2012-2017年高考文科数学真题汇编：直线和圆老师版(最新整理)
历届高考直线与圆试题汇编
历届高考直线与圆试题汇编专题九：解析几何第二十五讲直线与圆一、选择题1.(2018全国卷Ⅲ) 直线 x+y+2=0 分别与 x 轴，y 轴交于 A，B 两点，点 P 在圆 (x-2)²+y²=2 上，则ΔABP 面积的取值范围是：A。
[2,6]B。
[4,8]C。
[2,32]D。
[22,32]2.(2018天津) 已知圆 x+y-2x=0 的圆心为 C，直线 y=3-x相交于 A，B 两点，则ΔABC 的面积为：3.(2018北京) 在平面直角坐标系中，记 d 为点P(cosθ,sinθ) 到直线 x-my-2=0 的距离，当θ，m 变化时，d 的最大值为：A。
1B。
2C。
3D。
44.（2017新课标Ⅲ）已知椭圆C：(x²/a²)+(y²/b²)=1 (a>b>0) 的左、右顶点分别为 A1，A2，且以线段 A1A2 为直径的圆与直线 bx-ay+2ab=0 相切，则 C 的离心率为：A。
√(3/32)B。
1/√(3/32)C。
√(3/8)D。
1/√(3/8)5.（2017新课标Ⅲ）在矩形 ABCD 中，AB=1，AD=2，动点 P 在以点 C 为圆心且与 BD 相切的圆上。
若AP=λAB+μAD，则λ+μ 的最大值为：A。
3B。
2√2C。
5D。
26.（2015山东）一条光线从点 (-2,-3) 射出，经 y 轴反射后与圆 (x+3)²+(y-2)²=1 相切，则反射光线所在直线的斜率为：A。
-2/5 或 5/2B。
-5/2 或 2/5C。
-2/3 或 3/2D。
-3/2 或 2/37.（2015新课标2）已知圆 C1：(x-1)²+y²=1，圆 C2：(x-2)²+y²=4，则圆 C1 与圆 C2 的公共弦所在直线的斜率为：A。
1/3B。
1/2C。
2/3D。
3/48.（2015新课标2）过三点 A(1,3)，B(4,2)，C(1,-7) 的圆交于 y 轴于 M、N 两点，则 MN 的长度为：A。
20122017年高考文科数学真题汇编坐标系和参数方程老师版
学科教师辅导教案 学员姓名 年 级高三 辅导科目 数 学授课老师课时数2h第 次课授课日期及时段 2017年 月 日 ： — ：1.（2015年广东文）在平面直角坐标系x y O 中，以原点O 为极点，x 轴的正半轴为极轴建立极坐标系．曲线1C 的极坐标方程为()cos sin 2ρθθ+=-，曲线2C 的参数方程为222x ty t⎧=⎪⎨=⎪⎩（t 为参数），则1C 与2C 交点的直角坐标为 ()2,4- ．2.（2015年新课标2文）在直角坐标系xOy 中,曲线1cos ,:sin ,x t C y t αα=⎧⎨=⎩（t 为参数,且0t ≠ ）,其中0απ≤<,在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线23:2sin ,:23cos .C C ρθρθ==（I ）求2C 与3C 交点的直角坐标； （II ）若1C 与 2C 相交于点A ,1C 与3C 相交于点B ,求AB 最大值.试题分析：（I ）把2C 与3C 的方程化为直角坐标方程分别为2220x y y +-=,22230x y x +-=,联立解历年高考试题集锦——坐标系和参数方程3.（2015年陕西文）在直角坐标版权法xOy 吕，直线l 的参数方程为132(32x t t y t ⎧=+⎪⎪⎨⎪=⎪⎩为参数），以原点为极点，x 轴的正半轴为极轴建立极坐标系，C e 的极坐标方程为23sin ρθ=.(I)写出C e 的直角坐标方程；(II)P 为直线l 上一动点，当P 到圆心C 的距离最小时，求点P 的坐标.试题解析：(I)由23sin ρθ=，得223sin ρρθ=，从而有2223x y y +=所以()2233x y +-=(II)设133,22P t t ⎛⎫+ ⎪⎝⎭，又(0,3)C ，则22213331222PC t t t ⎛⎫⎛⎫=++-=+ ⎪ ⎪⎝⎭⎝⎭，故当0t =时，PC 取得最小值，此时P 点的坐标为(3,0).4、（2015新课标1）在直角坐标系xOy 中，直线1:2C x =-，圆()()222:121C x y -+-=，以坐标原点为极点,x 轴正半轴为极轴建立极坐标系. （I ）求12,C C 的极坐标方程. （II ）若直线3C 的极坐标方程为()πR 4θρ=∈，设23,C C 的交点为,M N ，求2C MN ∆ 的面积. 解：（I ）因为cos ,sin x y ρθρθ==，所以1C 的极坐标方程为cos 2ρθ=-，2C 的极坐标方程为22cos 4sin 40ρρθρθ--+=. ……5分（II ）将4πθ=代入22cos 4sin 40ρρθρθ--+=，得23240ρρ-+=，解得1222,2ρρ==.故122ρρ-=，即2MN =由于2C 的半径为1，所以2C MN ∆的面积为12.5、（2016年全国I ）在直角坐标系xOy 中，曲线C 1的参数方程为（t 为参数，a ＞0）.在以坐标原点为极点，x 轴正半轴为极轴的极坐标系中，曲线C 2：ρ=4cos θ. （I ）说明C 1是哪种曲线，并将C 1的方程化为极坐标方程；（II ）直线C 3的极坐标方程为θ=α0，其中α0满足tan α0=2，若曲线C 1与C 2的公共点都在C 3上，求a . 解：⑴ cos 1sin x a t y a t=⎧⎨=+⎩ （t 均为参数）∴()2221x y a +-= ①∴1C 为以()01，为圆心，a 为半径的圆．方程为222210x y y a +-+-=∵222sin x y y ρρθ+==，∴222sin 10a ρρθ-+-=即为1C 的极坐标方程⑵ 24cos C ρθ=：两边同乘ρ得22224cos cos x y x ρρθρρθ==+=Q ，224x y x ∴+=即()2224x y -+= ②3C ：化为普通方程为2y x =由题意：1C 和2C 的公共方程所在直线即为3C ①—②得：24210x y a -+-=，即为3C ∴210a -=∴1a =6、（2016年全国II ）在直角坐标系xOy 中，圆C 的方程为22(6)25x y ++=． （Ⅰ）以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，求C 的极坐标方程；（Ⅱ）直线l 的参数方程是cos sin x t y t αα=⎧⎨=⎩（t 为参数）, l 与C 交于,A B 两点，||10AB =，求l 的斜率．解：⑴整理圆的方程得2212110x y +++=，由222cos sin x y x y ρρθρθ⎧=+⎪=⎨⎪=⎩可知圆C 的极坐标方程为212cos 110ρρθ++=．⑵记直线的斜率为k ，则直线的方程为0kx y -=，由垂径定理及点到直线距离公式知：226102521kk ⎛⎫-=- ⎪ ⎪+⎝⎭， 即22369014k k =+，整理得253k =，则153k =±． 7、（2016年全国III ）在直角坐标系xOy 中，曲线1C 的参数方程为3cos ()sin x y θθθ⎧=⎪⎨=⎪⎩为参数，以坐标原点为极点，以x 轴的正半轴为极轴，，建立极坐标系，曲线2C 的极坐标方程为sin()224ρθπ+= .（I ）写出1C 的普通方程和2C 的直角坐标方程；（II ）设点P 在1C 上，点Q 在2C 上，求|PQ |的最小值及此时P 的直角坐标.8、(2016江苏)在平面直角坐标系xOy 中，已知直线l 的参数方程为11232x t y t ⎧=+⎪⎪⎨⎪=⎪⎩ （t 为参数），椭圆C 的参数方程为cos ,2sin x y θθ=⎧⎨=⎩ （θ为参数）.设直线l 与椭圆C 相交于A ，B 两点，求线段AB 的长.解：椭圆C 的普通方程为2214y x +=，将直线l 的参数方程11232x t y t⎧=+⎪⎪⎨⎪=⎪⎩，代入2214y x +=，得223()12(1)124t t ++=，即27160t t +=，解得10t =，2167t =-.所以1216||7AB t t =-=.9．（2013江苏理）在平面直角坐标系xoy 中，直线l 的参数方程为⎩⎨⎧=+=t y t x 21（t 为参数），曲线C 的参数方程为⎩⎨⎧==θθtan 2tan 22y x （θ为参数），试求直线l 与曲线C 的普通方程，并求出它们的公共点的坐标。
2012年高考真题文科数学汇编8：直线与圆
2012高考文科试题解析分类汇编：直线与圆一、选择题1.【2012高考山东文9】圆22(2)4x y ++=与圆22(2)(1)9x y -+-=的位置关系为 (A)内切 (B)相交 (C)外切 (D)相离 【答案】B考点：圆的位置关系解析：通过求出两圆心的距离为：17<5，因此选B2.【2012高考安徽文9】若直线01-+-y x 与圆2)(22=+-y a x 有公共点，则实数a 取值范围是 （A ） [-3，-1] （B ）[-1，3] （C ） [ -3，1] （D ）（-∞，-3]U[1，+∞） 【答案】C【解析】圆22()2x a y -+=的圆心(,0)C a 到直线10x y -+=的距离为d则 1231d r a a ≤=⇔≤+≤⇔-≤≤3.【2012高考重庆文3】设A ，B 为直线y x =与圆221x y += 的两个交点，则||AB =（A ）1 （B （C （D ）2 【答案】D【解析】：直线y x =过圆221x y +=的圆心(0,0)C 则||AB =2【考点定位】本题考查圆的性质，属于基础题．4.【2012高考浙江文4】设a ∈R ，则“a ＝1”是“直线l 1：ax+2y=0与直线l 2 ：x+(a+1)y+4=0平行的 A 充分不必要条件 B 必要不充分条件 C 充分必要条件 D 既不充分也不必要条件 【答案】A【命题意图】本题考查的知识为依托于简易逻辑的直线平行问题的考查。
【解析】当121a a =+，解得1a =或2a =-.所以，当a ＝1是，两直线平行成立，因此是充分条件；当两直线平行时，1a =或2a =-，不是必要条件，故选A.5.【2012高考陕西文6】已知圆22:40C x y x +-=，l 过点(3,0)P 的直线，则（ ） A.l 与C 相交 B. l 与C 相切 C.l 与C 相离 D. 以上三个选项均有可能 【答案】A.【解析】点(3,0)P 在圆内，则l 必与C 相交，故选A ． 6.【2012高考辽宁文7】将圆x 2+y 2-2x-4y+1=0平分的直线是 （A ）x+y-1=0 （B ） x+y+3=0 （C ）x-y+1=0 （D ）x-y+3=0【答案】C【解析】圆心坐标为（1，2），将圆平分的直线必经过圆心，故选C 【点评】本题主要考查直线和圆的方程，难度适中。
2012-2017年高考文科数学真题汇编：圆锥曲线老师版
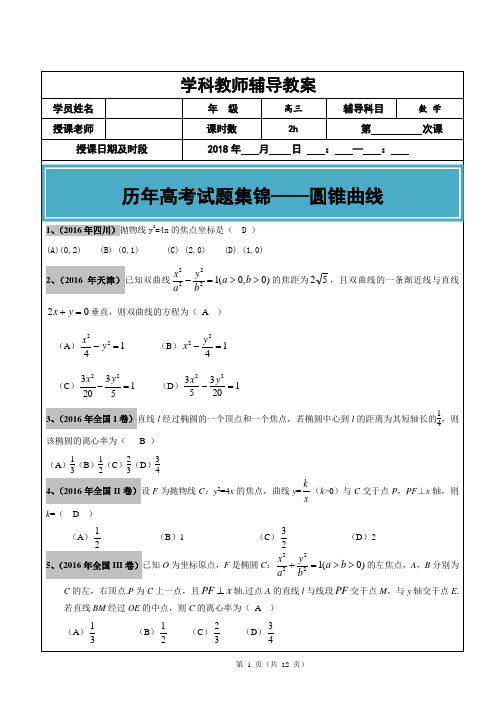
（Ⅱ）因为AB 过点(1,0)D 且垂直于x 轴，所以可设1(1,)A y ，1(1,)B y -. 直线AE 的方程为11(1)(2)y y x -=--.令3x =，得1(3,2)M y -. 所以直线BM 的斜率112131BM y y k -+==-.17.（2015年安徽文）设椭圆E 的方程为22221(0),x y a b a b+=>>点O 为坐标原点，点A 的坐标为(,0)a ,点B 的坐标为（0，b ）,点M 在线段AB 上，满足2,BM MA =直线OM 的斜率为510。
（1）求E 的离心率e;(2)设点C 的坐标为（0，-b ）,N 为线段AC 的中点，证明：MN ⊥AB 。
∴a b3231＝5525451511052222222=⇒=⇒=-⇒=⇒e a c a c a a b（Ⅱ）由题意可知N 点的坐标为（2,2b a -）∴a b a ba a bb K MN 56652322131==-+= abK AB-=∴1522-=-=⋅a b K K AB MN ∴MN ⊥AB18.（2015年福建文）已知椭圆2222:1(0)x y E a b a b+=>>的右焦点为F ．短轴的一个端点为M ，直线:340l x y -=交椭圆E 于,A B 两点．若4AF BF +=，点M 到直线l 的距离不小于45，则椭圆E 的离心率的取值范围是（ A ） A ． 3(0,]2 B ．3(0,]4 C ．3[,1)2 D ．3[,1)4119.（2015年新课标2文）已知双曲线过点()4,3,且渐近线方程为12y x =±,则该双曲线的标准方程为 ．2214x y -= 20.（2015年陕西文）已知抛物线22(0)y px p =>的准线经过点(1,1)-，则抛物线焦点坐标为（ B ） A ．(1,0)- B ．(1,0) C ．(0,1)- D ．(0,1) 【解析】试题分析：由抛物线22(0)y px p =>得准线2px =-，因为准线经过点(1,1)-，所以2p =， 所以抛物线焦点坐标为(1,0)，故答案选B 考点：抛物线方程.21.（2015年陕西文科）如图，椭圆2222:1(0)x y E a b a b+=>>经过点(0,1)A -，且离心率为22.(I)求椭圆E 的方程；2212x y += 22.（2015年天津文）已知双曲线22221(0,0)x y a b ab 的一个焦点为(2,0)F ,且双曲线的渐近线与圆222y 3x 相切,则双曲线的方程为（ D ）(A)221913x y (B) 221139x y (C)2213x y(D) 2213y x的等腰三角形，则新标2文221y b 0,0a b 的一条渐近线平行于直线210x ，双曲上，则双曲线的方程为（ A ）2120y （B ）221205x y （C ）2233125100x y 2233110025x y新标1) 已知双曲线2221x y =（0,0a b >>）的离心率为52，则14x B .13y =±12x ± D .y x[9,)+∞[9,)+∞C ．(0,1][4,)+∞D ．(0,3][4,)+∞【答案】A 【解析】当03m <<，焦点在x 轴上，要使C 上存在点M 满足120AMB ∠=，则tan 603ab≥=，即33m≥，得01m <≤；当3m >，焦点在y 轴上，要使C 上存在点M 满足120AMB ∠=，则tan 603a b ≥=，即33m ≥，得9m ≥，故m 的取值范围为(0,1][9,)⋃+∞，选A. 41、(2017·全国Ⅱ文，5)若a >1，则双曲线x 2a 2－y 2＝1的离心率的取值范围是( )A ．(2，＋∞)B ．(2，2)C ．(1，2)D ．(1,2)3．【答案】C 【解析】由题意得双曲线的离心率e ＝a 2＋1a .∴e 2＝a 2＋1a 2＝1＋1a 2.∵a ＞1，∴0＜1a 2＜1，∴1＜1＋1a2＜2，∴1＜e ＜ 2.故选C.42．(2017·全国Ⅱ文，12)过抛物线C ：y 2＝4x 的焦点F ，且斜率为3的直线交C 于点M (M 在x 轴上方)，l 为C 的准线，点N 在l 上且MN ⊥l ，则M 到直线NF 的距离为( )A. 5 B ．2 2 C ．2 3 D ．3 34．【答案】C 【解析】抛物线y 2＝4x 的焦点为F (1,0)，准线方程为x ＝－1.由直线方程的点斜式可得直线MF的方程为y ＝3(x －1)．联立得方程组⎩⎨⎧y ＝3(x －1)，y 2＝4x ，解得⎩⎨⎧x ＝13，y ＝－233或⎩⎨⎧x ＝3，y ＝2 3.∵点M 在x 轴的上方，∴M (3,23)．∵MN ⊥l ，∴N (－1,23)．∴|NF |＝(1＋1)2＋(0－23)2＝4， |MF |＝|MN |＝3－(－1)＝4.∴△MNF 是边长为4的等边三角形．∴点M 到直线NF 的距离为2 3. 故选C.43．(2017·全国Ⅲ文，11)已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右顶点分别为A 1，A 2，且以线段A 1A 2为直径的圆与直线bx －ay ＋2ab ＝0相切，则椭圆C 的离心率为( ) A ．63 B ．33 C ．23 D ．135．【答案】A 【解析】由题意知以A 1A 2为直径的圆的圆心坐标为(0,0)，半径为a .又直线bx －ay ＋2ab ＝0与圆相切，∴圆心到直线的距离d ＝2aba 2＋b 2＝a ，解得a ＝3b ， ∴b a ＝13，∴e ＝ca ＝a 2－b 2a ＝ 1－⎝⎛⎭⎫b a 2＝1－⎝⎛⎭⎫132＝63. 44．(2017·天津文，5)已知双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的右焦点为F ，点A 在双曲线的渐近线上，△OAF是边长为2的等边三角形(O 为原点)，则双曲线的方程为( ) A ．x 24－y 212＝1B ．x 212－y 24＝1C ．x 23－y 2＝1D ．x 2－y 23＝1 6．【答案】D 【解析】根据题意画出草图如图所示⎝⎛⎭⎫不妨设点A 在渐近线y ＝ba x 上.由△AOF 是边长为2的等边三角形得到∠AOF ＝60°，c ＝|OF |＝2.又点A 在双曲线的渐近线y ＝b a x 上，∴ba ＝tan 60°＝ 3.又a 2＋b 2＝4，∴a ＝1，b ＝3，∴双曲线的方程为x 2－y 23＝1.故选D. 45．(2017·全国Ⅲ文，14)双曲线x 2a 2－y 29＝1(a >0)的一条渐近线方程为y ＝35x ，则a ＝________.1．【答案】5【解析】∵双曲线的标准方程为x 2a 2－y 29＝1(a ＞0)，∴双曲线的渐近线方程为y ＝±3a x .又双曲线的一条渐近线方程为y ＝35x ，∴a ＝5.46、(2017·北京文，10)若双曲线x 2－y 2m＝1的离心率为3，则实数m ＝________. 【答案】2【解析】由双曲线的标准方程知a ＝1，b 2＝m ，c ＝1＋m ，故双曲线的离心率e ＝ca ＝1＋m ＝3，∴1＋m ＝3，∴m ＝2.47、(2017·全国Ⅱ理，16)已知F 是抛物线C ：y 2＝8x 的焦点，M 是C 上一点，FM 的延长线交y 轴于点N .若M 为FN 的中点，则|FN |＝________.【解析】如图，不妨设点M 位于第一象限内，抛物线C 的准线交x 轴于点A ，过点M 作准线的垂线，垂足为点B ，交y 轴于点P ，∴PM ∥OF .由题意知，F (2,0)，|FO |＝|AO |＝2.∵点M 为FN 的中点，PM ∥OF ，∴|MP |＝12|FO |＝1.又|BP |＝|AO |＝2，∴|MB |＝|MP |＋|BP |＝3.由抛物线的定义知|MF |＝|MB |＝3，故|FN |＝2|MF |＝6.48、(2017新课标1文)设A ，B 为曲线C ：y =24x 上两点，A 与B 的横坐标之和为4.（1）求直线AB 的斜率；（2）设M 为曲线C 上一点，C 在M 处的切线与直线AB 平行，且AM ⊥BM ，求直线AB 的方程. 【解析】（1）设()()1122,,,A x y B x y ，则2221212121214414AB x x y y x x K x x x x --+====-- （2）设200,4x M x ⎛⎫ ⎪⎝⎭，则C 在M 处的切线斜率'00112AB y K K x x x ====- ∴02x = 则()12,1A ，又AM ⊥BM ，22121212121111442222AM BMx x y y K K x x x x ----==---- ()()()121212222411616x x x x x x +++++===-即()12122200x x x x +++= 又设AB ：y=x ＋m 代入24x y = 得2440x x m --= ∴124x x +=，124x x m =- －4m ＋8＋20=0∴m=7故AB ：x ＋y=749.(2017年新课标Ⅱ文)设O 为坐标原点,动点M 在椭圆C :x 22＋y 2＝1上，过M 作x 轴的垂线,垂足为N ,点P满足→NP ＝2→NM . (1)求点P 的轨迹方程；(2)设点Q 在直线x ＝－3上,且→OP ·→PQ ＝1.证明:过点P 且垂直于OQ 的直线l 过C 的左焦点F . 【解析】(1)设P (x ,y ),M (x 0,y 0),则N (x 0,0),→NP ＝(x －x 0,y ),→NM ＝(0,y 0).由→NP ＝2→NM 得x 0＝x ,y 0＝22y .∵M (x 0,y 0)在C 上,∴x 22＋y 22＝1,∴点P 的轨迹方程为x 2＋y 2＝2.(2)由题意知F (－1,0).设Q (－3,t ),P (m ,n ),则→OQ ＝Q (－3,t ),→PF ＝(－1－m ,－n ),→OQ ·→PF ＝3＋3m －tn , →OP ＝(m ,n ),→PQ ＝(－3－m ,－tn ).由→OP ·→PQ ＝1得－3m －m 2＋tn －n 2＝1,。
历年高考直线与圆真题以及解析
【详解】（1）根据题意，圆C：（x﹣a）2+（y﹣b）2=1（a＞0）关于直线3x﹣2y=0对称，
【详解】（1） 直线 与直线 垂直，
，解得 ．
（2）当 时，直线 化为： 不满足题意．
当 时，可得直线 与坐标轴的交点 ， ．
直线 在两轴上的截距相等，
，解得： ．
该直线的方程为 ，即 .
11.
（1） ；（2）存在，理由见解析
【分析】
（1）根据题意得到 ，再解不等式即可得到答案.
（2）首先假设存在得以 为直径的圆过原点，设 ， ，直线与圆联立得到 ，再根据韦达定理和圆的性质即可得到答案.
化简可得： 即为点Q的轨迹方程.
【点睛】本题考查直线与圆的位置关系，考查直线被圆截得的弦长公式的应用，考查直线恒过定点问题和轨迹问题，属于中档题.
10.
（1） ；（2） ．
【分析】
（1）利用两条直线垂直的条件列方程，解方程求得 的值.
（2）分成 和 两种情况，结合直线 在两轴上的截距相等求得 ，由此求得所求直线方程.
②当切线斜率存在时，设切线斜率为 ，
则切线方程为 ，即
因为圆心到切线距离等于半径，
所以 ，解得 ，此时切线方程为 ，
综上所述，过点 的圆的切线方程为 和 ．
(2)因为 即 ， 为圆上任意一点，
所以 即原点到圆上一点的直线的斜率，
令 ，则原点到圆上一点的直线的方程为 ，即
2012-2017年高考文科数学真题汇编：坐标系和参数方程老师版
C的极坐标方程为C的直角坐标方程；为直线l上一动点，当到圆心C的距离最小时，求点ρ=(I)由2：化为普通方程为2=由题意：y x，（I ）求直线l 和圆C 的普通方程；（II ）若直线l 与圆C 有公共点，求实数a 的取值范围.【简解】（I ）直线l 的普通方程为220x y a --=.圆C 的普通方程为2216x y +=. （II ）因为直线l 与圆有公共点,故圆C 的圆心到直线l 的距离245a d -=≤,解得2525a -≤≤12. (2014新标1理)已知曲线C ：22149x y +=，直线l ：222x t y t =+⎧⎨=-⎩（t 为参数）. (Ⅰ)写出曲线C 的参数方程，直线l 的普通方程；（Ⅱ）过曲线C 上任一点P 作与l 夹角为o30的直线，交l 于点A ，求||PA 的最大值与最小值. 【简解】.(Ⅰ) 曲线C 的参数方程为：2cos 3sin x y θθ=⎧⎨=⎩（θ为参数）， 直线l 的普通方程为：260x y +-=（Ⅱ）在曲线C 上任意取一点P (2cos θ,3sin θ)到l 的距离为54cos 3sin 65d θθ=+-， 则()025||5sin 6sin 305d PA θα==+-，其中α为锐角．且4tan 3α=. 当()sin 1θα+=-时，||PA 取得最大值，最大值为2255； 当()sin 1θα+=时，||PA 取得最小值，最小值为255. 13.(2013新标2理) 已知动点P 、Q 都在曲线C ：2cos 2sin x ty t =⎧⎨=⎩(t 为参数)上，对应参数分别为t ＝α与t ＝2α(0<α<2π)，M 为PQ 的中点．(1)求M 的轨迹的参数方程； (2)将M 到坐标原点的距离d 表示为α的函数，并判断M 的轨迹是否过坐标原点．【简解】 (1)依题意有P (2cos α，2sin α)，Q (2cos 2α，2sin 2α)，因此M (cos α＋cos 2α，sin α＋sin 2α)． M 的轨迹的参数方程为{x ＝cos α＋cos 2α，y ＝sin α＋sin 2α，(α为参数，0<α<2π)． (2)M 点到坐标原点的距离d ＝x 2＋y 2＝2＋2cos α(0<α<2π)．当α＝π，d ＝0，故M 的轨迹过坐标原点．14、已知点A 的极坐标为(2,)4π，直线l 的极坐标方程为cos()4a πρθ-=，且点A 在直线l 上．（1）求a 的值及直线l 的直角坐标方程；。
2012-2017年高考文科数学真题汇编：基本不等式和线性规划老师版
学科教师辅导教案 学员 年 级高三 辅导科目数 学授课老师课时数2h第 次课授课日期及时段 2018年 月 日 ： — ：1．（2013文）设a ，b ，c R ∈，且a b >，则（ ）A ．ac bc >B ．11a b< C ．22a b > D ．33a b > 【答案】D2．（2013沪春招）如果0a b <<，那么下列不等式成立的是（ ） (A)11a b < (B) 2ab b < (C) 2ab a -<- (D) 11a b-<- 【答案】D3.(2014) 若0a b >>，0c d <<，则一定有（ ） A 、a b c d > B 、a b c d < C 、a b d c > D 、a b d c< 【答案】D4．（2013理）不等式220x x +-<的解集为 . 【答案】(-2,1)5．（2012文）不等式x 2-5x+6≤0的解集为______. 【答案】{}23x x ≤≤6．（2012文）不等式的解集是___________。
【答案】(3,2)(3,)-⋃+∞ 4．（2013文）不等式021xx <-的解为 ． 【答案】(0,1/2)7.(2014新标1文) 设函数()113,1,,1,x e x f x x x -⎧<⎪=⎨⎪≥⎩则使得()2f x ≤成立的x 的取值围是________【简解】作图象，得x ≤8历年高考试题集锦——基本不等式和线性规划20.(2012文) 设变量x,y 满足约束条件⎪⎩⎪⎨⎧≤-≥+-≥-+01042022x y x y x ,则目标函数z=3x-2y 的最小值为（A ）-5 （B ）-4 （C ）-2 （D ）3【答案】B21.（2013）设变量x ，y 满足约束条件⎩⎪⎨⎪⎧3x ＋y －6≥0，x －y －2≤0，y －3≤0，则目标函数z ＝y －2x 的最小值为( )A ．－7B ．－4C ．1D ．2 【答案】A22.(2013新标2文) 设x ，y 满足约束条件{ x －y ＋1≥0，x ＋y －1≥0，x ≤3，则z ＝2x －3y 的最小值是( ) A ．－7B ．－6C ．－5D ．－3【答案】B23.(2014新标2理) 设x,y 满足约束条件70310350x y x y x y +-⎧⎪-+⎨⎪--⎩≤≤≥，则2z x y =-的最大值为（ ）A. 10B. 8C. 3D. 2 【答案】B24.(2014新标2文)设x ，y 满足约束条件10,10,330,x y x y x y +-≥⎧⎪--≤⎨⎪-+≥⎩则2z x y =+的最大值为（A ）8 （B ）7 （C ）2 （D ）1 【答案】B25．(2012) 若函数y ＝2x图象上存在点(x ，y )满足约束条件30,230,,x y x y x m +-≤⎧⎪--≤⎨⎪≥⎩则实数m 的最大值为( )A ．12B ．1C ．32D ．2【简解】作图，由图可知当直线x ＝m 经过函数y ＝2x的图象与直线x ＋y －3＝0的交点P 时取得最大值；即得2x＝3－x ，即x ＝1＝m ．选B 26．（2013文）某旅行社租用A 、B 两种型号的客车安排900名客人旅行，A 、B 两种车辆的载客量分别为36人和60人，租金分别为1600元/辆和2400元/辆，旅行社要求租车总数不超过21辆，且B 型车不多于A 型车7辆．则租金最少为A ．31200元B ．36000元C ．36800元D ．38400元A ．10B ．8C ．5D ．2 【答案】C48.（2015年文科）变量,x y 满足约束条件02200x y x y mx y +≥⎧⎪-+≥⎨⎪-≤⎩，若2z x y =-的最大值为2，则实数m 等于（ ）A ．2-B ．1-C ．1D ．2 【答案】C49.（2015年新课标1理科）若x,y 满足约束条件则yx的最大值为 . 【答案】350.（2015年新课标2文科）若x ,y 满足约束条件50210210x y x y x y +-≤⎧⎪--≥⎨⎪-+≤⎩,则z =2x +y 的最大值为 ．【答案】851、（2016年高考）若变量x ，y 满足2,239,0,x y x y x +≤⎧⎪-≤⎨⎪≥⎩则x 2+y 2的最大值是（A ）4（B ）9（C ）10（D ）12 【答案】C52、（2016年高考）设x ∈R ，则不等式31x -<的解集为_______. 【答案】)4,2(53、（2016高考）若,x y 满足0,0,1,x y y x ≥⎧⎪≥⎨⎪≥+⎩则2x y -的最大值为____2-___.54．（2013文）若122=+yx，则y x +的取值围是（ ） A ．]2,0[ B ．]0,2[- C ．),2[+∞- D ．]2,(--∞ 【简解】用均值不等式，选D55.(2012文) 若正数x ，y 满足x+3y=5xy ，则3x+4y 的最小值是 A.245B.285C.5D.6【简解】135y x +=，3x+4y=113131213(34)()()555x y x y y x y x +⋅+=++≥113236555⨯⨯+=.选C 56.（2015年文科）若直线1(0,0)x ya b a b+=>>过点(1,1)，则a b +的最小值等于（ ） A ．2 B ．3 C ．4 D ．5 【答案】C57、（2016全国II 卷高考）若x ，y 满足约束条件103030x y x y x -+≥⎧⎪+-≥⎨⎪-≤⎩，则2z x y =-的最小值为__________【答案】5-58、（2016全国III 卷高考）若,x y 满足约束条件210,210,1,x y x y x -+≥⎧⎪--≤⎨⎪≤⎩则235z x y =+-的最大值为_____________. 【答案】10-59、（2016省高考）函数y =232x x --的定义域是 . 【答案】[]3,1-60、（2017全国I 卷文）设x ，y 满足约束条件33,1,0,x y x y y +≤⎧⎪-≥⎨⎪≥⎩则z =x +y 的最大值为（ D ）A ．0B ．1C ．2D ．361.(2017年新课标Ⅱ文)设x ,y 满足约束条件⎩⎪⎨⎪⎧2x ＋3y －3≤0，2x －3y ＋3≥0，y ＋3≥0，则z ＝2x ＋y 的最小值是( A )A.－15B.－9C.1D.962、（2017·）设变量x ，y 满足约束条件 ，则目标函数z=x+y 的最大值为（ D ）A、 B、1 C、 D、363、（2017•）已知x，y满足约束条件，则z=x+2y的最大值是（ C ）A、0B、2C、5D、664、（2017•新课标Ⅲ）若x，y满足约束条件，则z=3x﹣4y的最小值为____-1____。
20122017年高考文科数学真题汇编：坐标系和参数方程老师版.doc
C的极坐标方程为C的直角坐标方程；为直线l上一动点，当到圆心C的距离最小时，求点ρ=(I)由2：化为普通方程为2=由题意：y x，（I ）求直线l 和圆C 的普通方程；（II ）若直线l 与圆C 有公共点，求实数a 的取值范围.【简解】（I ）直线l 的普通方程为220x y a --=.圆C 的普通方程为2216x y +=. （II ）因为直线l 与圆有公共点,故圆C 的圆心到直线l 的距离245a d -=≤,解得2525a -≤≤12. (2014新标1理)已知曲线C ：22149x y +=，直线l ：222x t y t =+⎧⎨=-⎩（t 为参数）. (Ⅰ)写出曲线C 的参数方程，直线l 的普通方程；（Ⅱ）过曲线C 上任一点P 作与l 夹角为o30的直线，交l 于点A ，求||PA 的最大值与最小值. 【简解】.(Ⅰ) 曲线C 的参数方程为：2cos 3sin x y θθ=⎧⎨=⎩（θ为参数）， 直线l 的普通方程为：260x y +-=（Ⅱ）在曲线C 上任意取一点P (2cos θ,3sin θ)到l 的距离为54cos 3sin 65d θθ=+-， 则()025||5sin 6sin 305d PA θα==+-，其中α为锐角．且4tan 3α=. 当()sin 1θα+=-时，||PA 取得最大值，最大值为2255； 当()sin 1θα+=时，||PA 取得最小值，最小值为255. 13.(2013新标2理)已知动点P 、Q 都在曲线C ：2cos 2sin x ty t =⎧⎨=⎩(t 为参数)上，对应参数分别为t ＝α与t ＝2α(0<α<2π)，M 为PQ 的中点．(1)求M 的轨迹的参数方程； (2)将M 到坐标原点的距离d 表示为α的函数，并判断M 的轨迹是否过坐标原点． 【简解】 (1)依题意有P (2cos α，2sin α)，Q (2cos 2α，2sin 2α)，因此M (cos α＋cos 2α，sin α＋sin 2α)． M 的轨迹的参数方程为{ x ＝cos α＋cos 2α，＝sin α＋sin 2α，(α为参数，0<α<2π)．(2)M 点到坐标原点的距离d ＝x2＋y2＝2＋2cos α(0<α<2π)．当α＝π，d ＝0，故M 的轨迹过坐标原点． 14、已知点A 的极坐标为(2,)4π，直线l 的极坐标方程为cos()4a πρθ-=，且点A 在直线l 上．（1）求a 的值及直线l 的直角坐标方程； （2）圆c 的参数方程为1cos sin x y αα=+⎧⎨=⎩，（α为参数），试判断直线l 与圆的位置关系．2=，15．（2012辽宁）在直角坐标-3）(-3≤≤3) 16．(2013新标1) 已知曲线⎝⎛⎭⎫2，π4⎭⎫，π217．（2013辽宁）⎭⎪⎫－422. ＝2t3解⎨⎪⎧x2＋－＝4，得⎨⎪⎧x1＝0，⎨⎪⎧x2＝2，所以C 与C 交点的一个极坐标为 ⎛⎪⎫4，π，＝12|OA ⎭⎫－π3⎪⎪⎭⎫－π3－32＋ 3. ＝－π12时，＋ 3.＋ 3.23．(2017·全国Ⅲ文，22)在直角坐标系＝m k －2＝＝1k (设P (x ，y )，由题设得⎩⎪⎨⎪⎧y ＝－，y ＝1k＋消去k 得x －y ＝4(y ≠0)．所以C 的普通方程为x －y ＝4(y ≠0)．(2)C 的极坐标方程为ρ2(cos 2θ－sin 2θ)＝4(0＜θ＜2π，θ≠π)．联立⎩⎨⎧－＝4，＋－2＝0，得＝－13，从而＝910，＝110.的极径为 5.24．(2017·江苏，21)在平面直角坐标系中＝t222s22s 从而点P 到直线的距离d ＝|2s2－42s ＋8|5＝－2＋4|，当s ＝2时，d ＝45.。
20122017年高考文科数学真题汇编基本初等函数老师版
11、（2016年山东）已知函数f(x )的定义域为R.当x ＜0时，f(x )=x 3-1；当-1≤x ≤1时，f(-x )= —f(x )；当x ＞12时，f(x +12)=f(x —12).则f(6)=（ D ） （A ）-2 （B ）-1 （C ）0 （D ）212、（2016年天津）已知)(x f 是定义在R 上的偶函数，且在区间)0,(-∞上单调递增，若实数a 满足)2()2(|1|->-f f a ，则a 的取值范围是（ C ）（A ）)21,(-∞（B ）),23()21,(+∞-∞Y （C ）)23,21( （D ）),23(+∞13、（2016年全国I 卷）若a>b>0，0<c<1，则（ B ）（A ）log a c <log b c （B ）log c a <log c b （C ）a c <b c （D ）c a >c b 14、（2016年全国I 卷高考）函数y =2x 2–e |x |在[–2,2]的图像大致为（ D ）（A ）（B ）（C ）（D ）15、（2016年全国II 卷）下列函数中，其定义域和值域分别与函数y=10lg x 的定义域和值域相同的是（ D ）（A ）y =x （B ）y =lg x （C ）y =2x （D ）1y x=16、（2016年全国III 卷）已知4213332,3,25a b c ===，则（ A ）(A) b a c << (B)a b c <<(C) b c a << (D) c a b <<17、（2016年江苏）函数y =232x x --的定义域是 []3,1- .18、（2016年江苏）设f （x ）是定义在R 上且周期为2的函数，在区间[ −1,1)上，,10,()2,01,5x a x f x x x +-≤<⎧⎪=⎨-≤<⎪⎩其中.a ∈R 若59()()22f f -= ，则(5)f a 的值是 25- . 19、（2016年四川高考）若函数f （x ）是定义R 上的周期为2的奇函数，当0<x<1时，f （x ）=x 4，则f （25-）+f （2）= -2 。
高考数学真题汇编---专题9_直线和圆_理
【2012年高考试题】1.【2012高考真题重庆理3】任意的实数k ，直线1+=kx y 与圆222=+y x 的位置关系一定是（1） 相离 B.相切 C.相交但直线不过圆心 D.相交且直线过圆心2.【2012高考真题浙江理3】设a ∈R ，则“a ＝1”是“直线l 1：ax+2y=0与直线l 2 ：x+(a+1)y+4=0平行 的A 充分不必要条件B 必要不充分条件C 充分必要条件D 既不充分也不必要条件4.【2012高考真题陕西理4】已知圆22:40C x y x +-=，l 过点(3,0)P 的直线，则（ ） A.l 与C 相交 B. l 与C 相切 C.l 与C 相离 D. 以上三个选项均有可能 【答案】A.【解析】圆的方程可化为4)2(22=+-y x ，易知圆心为)0,2(半径为2，圆心到点P 的距离为1，所以点P 在圆内.所以直线与圆相交.故选A.5.【2012高考真题天津理8】设，若直线与圆相切，则m+n 的取值范围是（A ） （B ） （C ） （D ） 【答案】D【解析】圆心为)1,1(，半径为 1.直线与圆相切，所以圆心到直线的距离满足R n m ∈,02)1()1(=-+++y n x m 1)1()1(22=-+-y x ]31,31[+-),31[]31,(+∞+⋃--∞]222,222[+-),222[]222,(+∞+⋃--∞1)1()1(|2)1()1|22=+++-+++n m n m （，即2)2(1n m mn n m +≤=++，设z n m =+，即01412≥--z z ，解得,222-≤z 或,222+≥z6.【2012高考江苏12】（5分）在平面直角坐标系xOy 中，圆C 的方程为228150x y x +-+=，若直线2y kx =-上至少存在一点，使得以该点为圆心，1为半径的圆与圆C 有公共点，则k 的最大值是 ▲ ．8.【2012高考真题湖南理21】（本小题满分13分） 在直角坐标系xOy 中，曲线C 1的点均在C 2：（x-5）2＋y 2=9外，且对C 1上任意一点M ，M 到直线x=﹣2的距离等于该点与圆C 2上点的距离的最小值. （Ⅰ）求曲线C 1的方程；（Ⅱ）设P(x 0,y 0)（y 0≠±3）为圆C 2外一点，过P 作圆C 2的两条切线，分别与曲线C 1相交于点A ，B 和C ，D.证明：当P 在直线x=﹣4上运动时，四点A ，B ，C ，D 的纵坐标之积为定值. 【答案】（Ⅰ）解法1 ：设M 的坐标为(,)x y ，由已知得23x +=，易知圆2C 上的点位于直线2x =-的右侧.于是20x +>，所以5x =+.化简得曲线1C 的方程为220y x =.解法2：由题设知，曲线1C 上任意一点M 到圆心2C (5,0)的距离等于它到直线5x =-的距离，因此，曲线1C 是以(5,0)为焦点，直线5x =-为准线的抛物线，故其方程为220y x =.设四点A,B,C,D 的纵坐标分别为1234,,,y y y y ，则是方程③的两个实根，所以0112120(4).y k y y k +⋅=④同理可得0234220(4).y k y y k +⋅=⑤于是由②，④，⑤三式得010*******400(4)(4)y k y k y y y y k k ++=2012012124004()16y k k y k k k k ⎡⎤+++⎣⎦=22001212400166400y y k k k k ⎡⎤-+⎣⎦=.所以，当P 在直线4x =-上运动时，四点A ，B ，C ，D 的纵坐标之积为定值6400. 【2011年高考试题】 一、选择题:1．(2011年高考江西卷理科9)若曲线1C ：2220x y x +-=与曲线2C ：()0y y mx m --=有四个不同的交点，则实数m 的取值范围是 A ．(．(-0)∪(0) c ．[．(-∞，+∞) 、解析：选 B ，由题意，AC 为直径，设圆心为F ，则FE BD ⊥,圆的标准方程为()()221310x y -+-=，故()1,3F ，由此，易得：AC =又31210EF k -==-，所以直线BD 的方程为112y x =-+，F 到BD=BD =四边形ABCD的面积为1122AC BD =⨯=g 二、填空题:1.(2011年高考安徽卷理科15)在平面直角坐标系中，如果x 与y 都是整数，就称点(,)x y 为整点，下列命题中正确的是_____________（写出所有正确命题的编号）. ①存在这样的直线，既不与坐标轴平行又不经过任何整点 ②如果k 与b 都是无理数，则直线y kx b =+不经过任何整点 ③直线l 经过无穷多个整点，当且仅当l 经过两个不同的整点④直线y kx b =+经过无穷多个整点的充分必要条件是：k 与b 都是有理数 ⑤存在恰经过一个整点的直线2.(2011年高考重庆卷理科15)设圆C 位于抛物线22y x =与直线3x =所组成的封闭区域（包含边界）内，则圆C 的半径能取到的最大值为1。
历届高考直线与椭球试题汇编
历届高考直线与椭球试题汇编
本文档汇编了历届高考中与直线和椭球相关的试题，旨在帮助考生进行复备考。
以下是试题内容的总结：
直线
1. 2008年高考数学试题
- 题目：已知直线L1：2x-3y=7，直线L2：x+2y=2，求L1、L2的交点坐标。
- 解析：通过联立两条直线的方程，求得交点坐标。
2. 2012年高考数学试题
- 题目：直线L: 3x-4y=5，过点A(-1,2)的直线与直线L平行，求相应的方程。
- 解析：通过直线的斜率判断两条直线是否平行，然后根据已知条件构建方程。
椭球
1. 2010年高考数学试题
- 题目：已知椭球E：x^2/16 + y^2/9 = 1，点A(4,0)在椭球上，求A点在椭球上到x轴和y轴的距离。
- 解析：求点到坐标轴的距离可以根据已知条件和几何性质进行求解。
2. 2015年高考数学试题
- 题目：将椭球E：x^2/9 + y^2/4 + z^2/1 = 1，展开后得到的方程是什么？
- 解析：将椭球的方程按照特定顺序展开，最终得到展开后的方程。
以上是部分历届高考中与直线和椭球相关的试题，希望对考生的复习备考有所帮助。
请注意理解题意，并熟悉解题思路和方法。
高考数学真题汇编7 直线与圆 文(解析版)
2012高考试题分类汇编:7：直线与圆一、选择题1.【2012高考山东文9】圆22(2)4x y ++=与圆22(2)(1)9x y -+-=的位置关系为 (A)内切 (B)相交 (C)外切 (D)相离 【答案】B【解析】两圆的圆心分别为)0,2(-，)1,2(，半径分别为2=r ，3=R 两圆的圆心距离为17)10()22(22=-+--，则r R r R +<<-17，所以两圆相交，选B.2.【2012高考安徽文9】若直线01-+-y x 与圆2)(22=+-y a x 有公共点，则实数a 取值范围是（A ） [-3，-1] （B ）[-1，3] （C ） [ -3，1] （D ）（-∞，-3]U[1，+∞） 【答案】C【解析】圆22()2x a y -+=的圆心(,0)C a 到直线10x y -+=的距离为d ，则 1231d r a a ≤=⇔≤⇔+≤⇔-≤≤。
3.【2012高考重庆文3】设A ，B 为直线y x =与圆221x y += 的两个交点，则||AB =（A ）1 （B （C （D ）2 【答案】D【解析】直线y x =过圆221x y +=的圆心(0,0)C ，则AB 为圆的直径，所以||AB =2，选D.4.【2012高考浙江文4】设a ∈R ，则“a ＝1”是“直线l 1：ax+2y=0与直线l 2 ：x+(a+1)y+4=0平行的A 充分不必要条件B 必要不充分条件C 充分必要条件D 既不充分也不必要条件 【答案】A【解析】当121a a =+，解得1a =或2a =-.所以，当a ＝1是，两直线平行成立，因此是充分条件；当两直线平行时，1a =或2a =-，不是必要条件，故选A.5.【2012高考陕西文6】已知圆22:40C x y x +-=，l 过点(3,0)P 的直线，则（ ） A.l 与C 相交 B. l 与C 相切 C.l 与C 相离 D. 以上三个选项均有可能 6.【答案】A.【解析】圆的方程可化为4)2(22=+-y x ，易知圆心为)0,2(半径为2，圆心到点P 的距离为1，所以点P 在圆内.所以直线与圆相交.故选A.6.【2012高考辽宁文7】将圆x 2+y 2-2x-4y+1=0平分的直线是 （A ）x+y-1=0 （B ） x+y+3=0 （C ）x-y+1=0 （D ）x-y+3=0 【答案】C【解析】圆心坐标为（1，2），将圆平分的直线必经过圆心，故选C 【点评】本题主要考查直线和圆的方程，难度适中。
历届高考数学真题汇编专题9_直线和圆最新模拟_理
【备战2017年】历届高考数学真题汇编专题9 直线和圆最新模拟 理1、（2017济南一中模拟）直线1l :kx +(1-k )y -3=0和2l :(k -1)x +(2k +3)y -2=0互相垂直，则k =A. -3或-1B. 3或１C. -3或１D. -1或32、（2017滨州二模）直线l 与圆x 2＋y 2＋2x －4y ＋1＝0相交于A ，B 两点，若弦AB 的中点（－2,3），则直线l 的方程为：（A ）x ＋y －3＝0 （B ）x ＋y －1＝0 （C ）x －y ＋5＝0 （D ）x －y －5＝03、（2017德州一模）若直线100ax by (a,b (,))+-=∈+∞平分圆222220x y x y +---=，则12a b+的最小值是( )A ．．3+．2 D ．5 答案：B解析：圆方程化为：（x －1）2＋（y －1）2＝4，圆心坐标为（1,1），因为直线平分圆，所以它必过圆心，因此，有：a ＋b ＝1，12a b +＝121()a b +⨯＝12()(a b )a b ++＝3＋2b a a b+≥3＋3+，故选B 。
4、（2017临沂3月模拟）直线l 过点)04(，且与圆25)2()1(22=-+-y x 交于B A 、两点，如果8=AB ，那么直线l 的方程为____________。
【答案】020125=--y x 或4=x5、（2017临沂二模）设圆222x y +=的切线l 与x 轴的正半轴、y 轴的正半轴分别交于点A B 、，当AB 取最小值时，切线l 的方程为________________。
6、（2017青岛二模）函数y =等比数列，则以下不可能成为该等比数列的公比的数是A ．34B C D 【答案】D【解析】函数等价为0,9)5(22≥=+-y y x ，表示为圆心在)0,5(半径为3的上半圆，圆上点到原点的最短距离为2，最大距离为8，若存在三点成等比数列，则最大的公比q 应有228q =，即2,42==q q ，最小的公比应满足282q =，所以21,412==q q ，所以公比的取值范围为221≤≤q ，所以选D. 7、（2017青岛二模）已知直线y x a =+与圆224x y +=交于A 、B 两点，且0OA OB ⋅=，其中O 为坐标原点，则正实数a 的值为 .8、（2017青岛3月模拟）已知圆222()()x a y b r -+-=的圆心为抛物线24y x =的焦点,且与直线3420x y ++=相切,则该圆的方程为A.2264(1)25x y -+=B.2264(1)25x y +-= C. 22(1)1x y -+= D.22(1)1x y +-=9、（2017日照5月模拟）直线kx y =与函数)10(<<=a a y x 的图象交与A ，B 两点（点B 在A 上方），过B 点做x 轴平行线交函数x b y =图象于C 点，若直线y AC //轴，且3a b =，且A 点纵坐标为 .答案：3.【解析】设A 点的横坐标为)0(00≠x x ，由题意C 点的纵坐标为0xb ，又0033,x x a ba b ==∴B 点横坐标为03x ，又O B A ,,三点共线，3,3000003==∴x x x a x a x a .10、（2017泰安一模）过点A （2，3）且垂直于直线052=-+y x 的直线方程为 A.042=+-y x B.072=-+y x C.032=+-y xD.052=+-y x11、（2017烟台二模）已知倾斜角为α的直线l 与直线x 2y 20-+=平行，则tan 2α的值为A.45B.43C.34D.23答案：B解析：依题意，得：tan α＝12，22tan tan 21tan ααα=-＝1114-＝43。
2012-2017年高考文科数学真题汇编：坐标系和参数方程老师版
学科教师辅导教案 学员姓名 年 级高三 辅导科目 数 学授课老师课时数2h第 次课授课日期及时段 2017年 月 日 : - ：1。
(2015年广东文）在平面直角坐标系x y O 中，以原点O 为极点,x 轴的正半轴为极轴建立极坐标系．曲线1C 的极坐标方程为()cos sin 2ρθθ+=-，曲线2C 的参数方程为222x ty t⎧=⎪⎨=⎪⎩（t 为参数）,则1C 与2C 交点的直角坐标为 ()2,4- ．2.（2015年新课标2文）在直角坐标系xOy 中，曲线1cos ,:sin ,x t C y t αα=⎧⎨=⎩（t 为参数,且0t ≠ ),其中0απ≤<,在以O 为极点，x 轴正半轴为极轴的极坐标系中,曲线23:2sin ,:23cos .C C ρθρθ==（I)求2C 与3C 交点的直角坐标； (II ）若1C 与 2C 相交于点A ，1C 与3C 相交于点B ,求AB 最大值.试题分析：(I ）把2C 与3C 的方程化为直角坐标方程分别为2220x y y +-=,22230x y x +-=,联立解历年高考试题集锦——坐标系和参数方程3.（2015年陕西文）在直角坐标版权法xOy 吕，直线l 的参数方程为132(32x t t y t ⎧=+⎪⎪⎨⎪=⎪⎩为参数)，以原点为极点,x 轴的正半轴为极轴建立极坐标系，C 的极坐标方程为23sin ρθ=.（I)写出C 的直角坐标方程；（II ）P 为直线l 上一动点，当P 到圆心C 的距离最小时，求点P 的坐标.试题解析：（I ）由23sin ρθ=，得223sin ρρθ=，从而有2223x y y +=所以()2233x y +-=(II)设133,22P t t ⎛⎫+ ⎪⎝⎭，又(0,3)C ，则22213331222PC t t t ⎛⎫⎛⎫=++-=+ ⎪ ⎪⎝⎭⎝⎭，故当0t =时，PC 取得最小值，此时P 点的坐标为(3,0)。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
95 4 3
x
3
；
31（2016 年新课标 1 理）设圆 x2 y2 2x 15 0 的圆心为 A，直线 l 过点 B（1,0）且与 x 轴不重合，l
交圆 A 于 C，D 两点，过 B 作 AC 的平行线交 AD 于点 E.（I）证明 EA EB 为定值，并写出点 E 的轨迹
方程。
【详细解答】（I）圆心为 A(1, 0) ，圆的半径为 AD 4 ， AD AC ，
22.（2015 北京文）圆心为 1,1 且过原点的圆的方程是（ D ）
A． x 12 y 12 1
B． x 12 y 12 1
C． x 12 y 12 2
D． x 12 y 12 2
23.（2015 年广东理）平行于直线 2x y 1 0 且与圆 x2 y2 5 相切的直线的方程是（ D ）
学员姓名 授课老师
授课日期及时段
学科教师辅导教案
年级
高三
辅导科目
课时数
2h
第
2017 年 月 日 ： — ：
数学 次课
历年高考试题集锦——直线和圆
1．（2012 辽宁文）将圆 x2+y2 -2x-4y+1=0 平分的直线是（ C ）
（A）x）x-y+1=0 （D）x-y+3=0
4 的距离为
5 ，则圆 C 的方程为____ (x 2)2 y2 9. ______
5
19、（2016 年全国 I 卷）设直线 y=x+2a 与圆 C：x2+y2-2ay-2=0 相交于 A，B 两点，若
，则圆 C
的面积为 4π . 20、（2016 年全国 III 卷）已知直线 l ： x 3y 6 0 与圆 x2 y2 12 交于 A, B 两点，过 A, B 分别作 l
第 2 页（共 6 页）
的垂线与 x 轴交于 C, D 两点，则| CD | ____4_________.
21、（2016 年浙江）已知 a R ，方程 a2 x2 (a 2) y2 4x 8 y 5a 0 表示圆，则圆心坐标是_____，
半径是______.【答案】 (2, 4) ；5．
A.21 B.19 C.9 D. 11
4.（2012 山东文）圆 (x 2)2 y2 4 与圆 (x 2)2 ( y 1)2 9 的位置关系为（ B ）
(A)内切 (B)相交 (C)外切 (D)相离
5．（2013 江西文）若圆 C 经过坐标原点和点（4，0），且与直线 y=1 相切，则圆 C 的方程是
。
【答案】 (x 2)2 ( y 3)2 25 24
6.（2012 安徽文）若直线 x y 1 0 与圆 (x a)2 y2 2 有公共点，则实数 a 取值范围是（ C ）
( A) [3, 1]
(B) [1,3]
(C) [3,1]
(D) (, 3] [1, )
7.（2013 安徽文）直线 x 2 y 5 5 0 被圆 x2 y2 2x 4 y 0 截得的弦长为（ C ）
第 4 页（共 6 页）
ADC ACD ，又 BE / / AC ，ACD EBD ADC ， BE ED ， EA EB AD 4 .
所以点 E 的轨迹是以点 A(1, 0) 和点 B(1, 0) 为焦点，以 4 为长轴长的椭圆，
即 a 2, c 1 b 3 ，
所以点 E 的轨迹方程为： x2 y2 1 ( y 0) . 43
2.（2012 浙江文）设 a∈R ，则“a＝1”是“直线 l1：ax+2y=0 与直线 l2 ：x+(a+1)y+4=0 平行的（ A ）
A 充分不必要条件 B 必要不充分条件 C 充分必要条件
D 既不充分也不必要条件
3．（2014 湖南文）若圆 C1 : x2 y2 1 与圆 C2 : x2 y2 6x 8 y m 0 外切，则 m （ C ）
段 AB 的中点为 M ， O 为坐标原点.（I）求 M 的轨迹方程；（II）当 OP OM 时，求 l 的方程及 POM
的面积。
第 3 页（共 6 页）
【解析】（I）圆C的方程可化为 x2 y 42 16 ,所以圆心为 C(0,4),半径为 4.
设M(x,y),则 CM (x, y 4) ， MP (2 x, 2 y) ，,由题设知 CM AMP 0 ,故
则圆 C 的标准方程为 (x 2)2 ( y 1)2 4 。
15、（2016 年北京）圆（x+1）2+y2=2 的圆心到直线 y=x+3 的距离为（ C ）
（A）1 （B）2 （C） 2 （D）2 2
16、（2016 年山东）已知圆 M： x2 + y2 - 2ay = 0(a > 0) 截直线 x + y = 0 所得线段的长度是 2 2 ，则圆 M
（A）1
（B）2 （C）4
（D） 4 6
8.（2014 安徽文）过点 P（ 3,1）的直线 l 与圆 x2 y2 1有公共点，则直线 l 的倾斜角的取值范围是（
D）
A（. 0， ]
6
B（. 0， ]
3
C.[0， ]
6
D.[0， ]
3
9.（2012 福建文）直线 x 3y 2 0 与圆 x2 y 2 4 相交于 A, B 两点，则弦 AB 的长度等于（ B ）
因此，圆 N 的标准方程为 x 62 y 12 1.
(2)因为直线 l∥OA，所以直线 l 的斜率为 4 0 2 .设直线 l 的方程为 y=2x+m，即 2x-y+m=0， 20
则圆心 M 到直线 l 的距离 d
26 7 m
m5 .
5
5
因为 BC OA
32、（2016
年江苏） 如图，在平面直角坐标系
xOy
中，已知以
M
为圆心的圆
M:
x2
y2
12x
14
y
60
0
及其上一点 A(2，4)
（1）设圆 N 与 x 轴相切，与圆 M 外切，且圆心 N 在直线 x=6 上，求圆 N 的标准方程；
（2）设平行于 OA 的直线 l 与圆 M 相交于 B、C 两点，且 BC=OA,求直线 l 的方程；
1
29.（2015
年天津文）已知椭圆
x2 a2
+ y2 b2
=1(a > b > 0) 的上顶点为 B,左焦点为 F ,离心率为
5
,
5
（I）求直线 BF 的斜率； 【答案】（I）2；
30.（2015 年广东理）已知过原点的动直线 l 与圆 C1 : x2 + y2 - 6x +5 = 0 相交于不同的两点 A ， B . （1）求圆 C1 的圆心坐标；（2）求线段 AB 的中点 M 的轨迹 C 的方程；
A． 2x y 5 0 或 2x y 5 0 C. 2x y 5 0 或 2x y 5 0
B. 2x y 5 0 或 2x y 5 0 D. 2x y 5 0 或 2x y 5 0
24.（2015 年新课标 2 文）已知三点 A(1, 0), B(0, 3), C(2, 3) ,则△ ABC 外接圆的圆心到原点的距离为（
与圆 N：（x- 1）2 + ( y - 1)2 = 1 的位置关系是（ B ）
（A）内切（B）相交（C）外切（D）相离
17、（2016
年上海）已知平行直线
l1
:
2x
y
1
0, l2
:
2x
y
1
0
，则
l1, l2
的距离___
25 5
____
18、（2016 年天津）已知圆 C 的圆心在 x 轴的正半轴上，点 M (0, 5) 在圆 C 上，且圆心到直线 2x y 0
B）
A. 5 B. 21 C. 2 5 D. 4
3
3
3
3
25.(2013 新标 2 文) 在平面直角坐标系 xOy 中，已知圆 P 在 x 轴上截得线段长为 2 2，在 y 轴上截得线段长
2 为 2 3.(1)求圆心 P 的轨迹方程； (2)若 P 点到直线 y＝x 的距离为 ，求圆 P 的方程．
2 【简解】(1)设 P(x，y)，圆 P 的半径为 r.则 y2＋2＝r2，x2＋3＝r2.∴y2＋2＝x2＋3，即 y2－x2＝1.
x 2 x y 42 y 0 ，即 x 12 y 32 2
由于点P在圆C 的内部,所以M 的轨迹方程是 x 12 y 32 2
(Ⅱ)由(Ⅰ)可知M 的轨迹是以点N(1,3)为圆心, 2 为半径的圆.由于|OP|=|OM|,故O在线段PM的垂直平分线上,又P 在
圆N 上,从而ON⊥PM.因为ON 的斜率为3,所以 l 的斜率为 1 ,直线 l 的方程为： y 1 x 8
解：圆 M 的标准方程为 x 62 y 72 25 ，所以圆心 M(6，7)，半径为 5,.
（1）由圆心 N 在直线 x=6 上，可设 N 6, y0 .因为圆 N 与 x 轴相切，与圆 M 外切，
所以 0 y0 7 ，于是圆 N 的半径为 y0 ，从而 7 y0 5 y0 ，解得 y0 1 .
|x0－y0| 2 (2)设 P 的坐标为(x0，y0)，则 2 ＝ 2 ，即|x0－y0|＝1.∴y0－x0＝±1，即 y0＝x0±1. ①当 y0＝x0＋1 时，由 y20－x20＝1 得(x0＋1)2－x20＝1.∴Error!∴r2＝3. ∴圆 P 的方程为 x2＋(y－1)2＝3.
②当 y0＝x0－1 时，由 y20－x20＝1 得(x0－1)2－x20＝1∴Error!∴r2＝3. ∴圆 P 的方程为 x2＋(y＋1)2＝3.综上所述，圆 P 的方程为 x2＋(y±1)2＝3.