第13届中国北方数学奥林匹克试题及解析
中国西部数学奥林匹克试题及其解答

交流知识 共享智慧
文武光华
R A
Q
F
E
M
B
D
C N
P
证明:如图,连结 QR,则点 A 在线段 QR 上。连结 AP,则 AP⊥QR。设⊙P、⊙R、⊙Q 分别切 AB 于点 H、J、I。连结 MC、BN,则根据条件知 MC 平行且等于 QA,NB 平行且等于 QA。过点 C 作 CK∥MN 交 BN 延长线于点 K,则四边形 MCKN 为平行四边形,从而知 BK=BN+CM=QR。
2013年全国高中数学联赛黑龙江赛区预赛试卷及解析

2013年全国高中数学联赛黑龙江赛区预赛试卷注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题1.已知全集U=R,集合N ={x|(12)x≤1},M ={x|x 2−6x +8≤0}.则图中阴影部分所表示的集合为()A. {x|x ≤0}B. {x|2≤x ≤4}C. {x|0<x ≤2或x ≥4}D. {x|0≤x <2或x >4}2.已知i 为虚数单位.则i +i 2+i 3+i 4+⋯+i 2013=().A. iB. −iC. 0D. 13.命题“所有实数的平方都是正数”的否定为( ) A. 所有实数的平方都不是正数 B. 有的实数的平方是正数 C. 至少有一个实数的平方不是正数 D. 至少有一个实数的平方是正数4.直线l 过抛物线C: x 2=4y 的焦点且与y 轴垂直,则l 与C 所围成的图形的面积等于( ) A. 43 B. 2 C. 83 D. 16√235.将甲、乙、丙、丁四名学生分到三个不同的班,每个班至少分到一名学生,且甲、乙两名学生不能分到同一个班,则不同的分法的种数为 ( )A.24种B.30种C.36种D.81种 6.图是一立体的三视图.则该立体体积为().A. 4+5π2B. 4+3π2C. 4+π2D. 4+π7.程序框图如图所示.已知实数x ∈[1,9].则输出的x 不小于55的概率为()A. 13B. 23C. 38D. 588.已知定义在R 上的函数f (x )在(−∞,2)上是增函数,且f (x +2)的图像关于y 轴对称则()A. f (−1)<f(3)B. f (0)>f (3)C. f (−1)=f (3)D. f (0)=f (3)9.化简sin4α4sin 2(π4+α)⋅tan (π4−α)=()A. cos2αB. sin2αC. cosαD. sinα 10.设F 1、F 2分别是双曲线x 2a 2−y 2b2=1(a >0,b >0)的左、右焦点若双曲线右支上存在一点P ,使得 (OP ⃑⃑⃑⃑⃑⃑⃑ +OF 2⃑⃑⃑⃑⃑⃑⃑⃑⃑ )⋅F 2P ⃑⃑⃑⃑⃑⃑⃑⃑⃑ =0,其中, O 为坐标原点,且|PF ⃑⃑⃑⃑⃑⃑ 1|=√3|PF 2⃑⃑⃑⃑⃑⃑⃑⃑⃑ |,则该双曲线的离心率为()A. √6+√2B. √3+1C.√3+12D.√6+√2211.在直三棱柱A 1B 1C 1−ABC 中,∠BAC =π2,AB =AC =AA 1=1. 已知G与E分别为A 1B 1和CC 1的中点,D与F分别为线段AC 和AB 上的动点(不包括端点). 若GD ⊥EF ,则线段DF 的长度的取值范围为A. [√55,1) B. [15,2) C. [1,√2) D. [√55,√2)12.设正项等比数列{a n }满足a 7=a 6+2a 5,若存在两项a n 、a m 使得√a n a m =4a 1,则1m +4n的最小值为().A. 253B. 256C. 53D. 32第II 卷(非选择题)二、填空题13.已知变量x 、y 满足约束条件{x −y +2≤0,x ≥1,x +y −7≤0..则y x的取值范围为______. 14.定义()f x 是R 上的奇函数,且当0x ≥时, ()2f x x =.若对任意的[],2x a a ∈+均有()()2f x a f x +≥,则实数a 的取值范围为 . 15.已知OA=1,OB =3,OA ⃑⃑⃑⃑⃑ ⋅OB ⃑⃑⃑⃑⃑ =0,点C 在∠AOB 内,且∠AOC =30°,设OC⃑⃑⃑⃑⃑⃑⃑ =mOA ⃑⃑⃑⃑⃑⃑⃑ +nOB ⃑⃑⃑⃑⃑⃑⃑ (m 、n ∈R).则m n =______. 16.若正方形ABCD 的一条边在直线y=2x −17上,另外两个顶点在抛物线y =x 2上.则该正方形面积的最小值为________________.三、解答题17.已知函数f (x )=2sin2x −cos 2x −12(x ∈R ).(1)当x∈[−π12,5π12]时,求函数f (x )的最小值和最大值;(2)记△ABC 的内角∠A 、∠B 、∠C 的对应边分别为a 、b 、c ,且c =√3,f (C )=0,若向量α=(1,sinA )、β=(2,sinB )共线,求a 、b 的值.18.如图,在正△ABC 中,点D,E 分别在边AC, AB 上,且AD=13AC,AE=23AB,BD,CE 相交于点F.(Ⅰ)求证:A,E,F,D 四点共圆;(Ⅱ)若正△ABC 的边长为2,求A,E,F,D 所在圆的半径.19.一个口袋中有2个白球和n 个红球(2n ≥,且*n N ∈),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖. (1)试用含n 的代数式表示一次摸球中奖的概率p ;(2)若3n =,求三次摸球恰有一次中奖的概率;(3)记三次摸球恰有一次中奖的概率为()f p ,当n 为何值时,()f p 取最大值.20.数列{a n }的前n 项和为S n ,满足a 1=1,3t S n −(2t +3)S n−1=3t ,其中, t >0,n ≥2,且n ∈Z +.(1)证明:数列{a n }是等比数列;(2)记数列{a n }的公比为f (t )数列{b n }满足b 1=1,b n =f (1b n−1)(n ≥2),求b n 的通项公式; (3)记T n=∑(−1)i+1+b i b i+12ni=1,证明: T n≤−209.21.已知1(1,0)F -,2(1,0)F ,圆222:(1)1F x y -+=,一动圆在y 轴右侧与y 轴相切,同时与圆2F 相外切,此动圆的圆心轨迹为曲线C ,曲线E 是以1F ,2F 为焦点的椭圆。
2013中国女子数学奥林匹克试题及其解答

2013中国女子数学奥林匹克试题及其解答1.证明(张云华)1.证明(mavropnevma )Let , . The region is the triangle ,and , thus the triangles of largest possible area are and . But(equality for is for ,disallowed).(equality foris for ).EDIT. Referring to the next post - it is interesting to figure out the envelope of the linesis the parabola , but in some way it is irrelevant, since the problemfunctions for a fixed , with fixed on the parabola for some , and thetriangular area being delimited by the tangent to that parabola at .1.证明(kunny), thus theparabola is envelope of the linesWhich touches at .The domain of the family of the lines swept by is shown by the shaded region, excluded twopoints .Edit:I was misreading the context problem, thank you for pointing put it, mavropnevma.I have just attached another figure.Needless to say, mavropnevma's solution is perfect.P.S.I remember that the similar problem original problem has been posed in 1970's in Tokyo University entrance exam/Science.According to my memory, let be the maximum area of any triangle which is involved in theregion in original problem, then draw the graph of to find the extrema of .Here is the similar problem posed in Tokyo University entrance exam/Science, second round, 1978In the -plane, let be the part which is correspond to of the parabola ,that is to say, .Let the tangent Line of at intersects with the line at and intersects withthe line at .Let . We are to consider the questions as below in the range of.(1) Let denote the area of triangles by , respectively. Find the rangeof such that .(2) Let be the domain enclosed by line segments and .Note : contains line segments and .Let be the maximum area of the triangle with a vertex which is contained in .Find the function and draw the graph, then find the exterme value.Note : A function has local minimum (or local maximum) at a point, which means for all points which is closed to ,holds. We call local maximum, local minimum as extreme value.2.证明(Luis González)Let and Let be the incircleof touching at Clearly and are homothethic with incirclesbut since are symmetric about the midpoint of (isthe M-excircle of MAB), it follows that and are homotheticwith corresponding cevians2.证明(Andrew64)As shown in the figure below.is the intersection of and .Therefore , , meet at the same point .Attachments:link17.jpg [ 37.23 KiB | Viewed 52 times ]3.证明(mavropnevma)Since it is irrelevant which persons of the same gender know each other, we may assume there ore none such, and consider the bipartite graph having the left shore made ofthe boys and the right shore made of the girls, with an edge connecting a boy and a girl ifthey know each other. The condition means does not contain any induced cycle of length ,and the requirement is to show the number of edges satisfies .Thus it is an extremal graph theory question, for bipartite graphs with forbidden 's; bysymmetry we should also have .Denote by the set of girls that each knows exactly one boy, and by the set of girls that eachknows more than one boy; take and . We obviously have and.Let us count the number of objects , where is a girl, are distinctboys, and knows both . For each of the doubletons there is at mostone girl knowing them both (by the condition), so . Moreover, by pigeonholewe have .On the other hand, we have, by Jensen's inequality.We thus need , so.Finally, we get .For equality to be reached we obviously need , namely for each pair of boys having exactly one girl knowing both of them; and then we need .3.证明(crazyfehmy)Another solution: Consider the bipartite graph where there are girls andboys and denote the girls by 's and boys by 's as vertices.Let denote the number of edges from the vertex to set . If is connected to some andthen for any the girl must not connected to both and . Now let us count suchpairs. For every girl there are many pair of edges. Since all such edge pairs must bedistinct for all girls, and since there are at most such pairs, we haveor equivalentlyNow assume that are greater than or equal to and areor . Then we haveand we need to show that .Since for we have and hence .Now by Cauchy-Schwarz inequality we haveand if , we haveand we need to show that . Assume . Then we havewhich means that which is a contradiction. So, we are done.4.解(crazyfehmy)Let be called a nice pair if satisfies the conditionsstated in the problem.Firstly, we shall prove a lemma:If is a nice pair then for all integers and .Proof: Let or and divides for some integers and. Then we can find another pair such that and. (The proof is easy) Then consider the systemand . By the Chinese Remainder Theorem this system has a solution and such that both and isan element of which means that is not a nice pair becauseis divisible by .Now, we shall show that if or then has asolution for all integers . For the proof assume there exists an integer such thathas no solution in integers. Then it is easy to see thathas also no solution for all integers which are not divisibleby . Now take and consider the numbers . For all of these numbers,we have no solution and there are such numbers. Since all square residues have solutions(take ) and there are square residues modulo including zero, this means that forall nonsquare residues , the equation must have no solution. However, for the numberis not a square residue but so for we have asolution which is a contradiction. For the number is not a square residue buthas a solution since is a square residue. Hence we again obtain a contradiction so the second lemma is also proved.Now, since can take every value modulo and we must have andand also we must have and if is a nice pair. So, can take only three values. We will consider each case separately:If then we must have which meansIf then we must have whichmeansIf then we must have whichmeansIf we count these possibilities, if i am not wrong, we get.4.解(dinoboy)First, remark that it suffices for to be injective modulo and .For modulo simply note that we require .For modulo or we require for some thatNow, what values can take modulo ? It is a simple exercise to show allvalues modulo can be obtained (just express it as and then aswe can transform the problem to what values modulo can beexpressed as , which is known to be all of them). Therefore the only way this problemsworks out is if and .Therefore we simply require that and . For each value of there are valuesof modulo , 10 modulo and modulo so the answer should simply be.Note: To show takes all values modulo without relying onis not hard, but I'm lazy and felt like reducing it to an already solved problem.4.解(yunxiu),so ,hence satisfies the problem.So the answer should be .6.解(crazyfehmy)If let then satisfiessince is equivalent to whichhas always a solution in the set for all and since is odd.Now we will show that if then the condition does not satisfy. Let be theelements of the set . Consider the sums and let. Since 's are different modulo , the numbers 'sare also different modulo . On the other hand, none of 's can be equivalent to modulobecause otherwise we would have two equivalent terms. Hence is apermutation of and by adding up these equations we getwhich means. Now do the same procedure for all's to get. Let and. Then we have . So, we havemany numbers equivalent to each other modulo . However, we know that there are manynumbers modulo which are all equivalent to each other modulo . Hence in order for 's tobe different modulo, we must have which means that and hence. Soand we are done.Hence all possible values are .7.证明(Luis González ) Let cut again at Since is the exsimilicenter ofthen is midpoint of the arc ofbisects externally is midpoint of the arc ofis external bisector of andNote that is a Thebault circle of the cevian of externally tangent to itscircumcircle By Sawayama's lemma passes through its C-excenter isC-excenter ofis M-isosceles, i.e. Hence iscircumcenter of7.证明(Andrew64)As shown in the figure. Let be the intersection of and .It's fairly obviousSo we have, andare concyclic.So , andThus, Consequently .Namely is the bisector of.Attachments:link18.jpg [ 31.39 KiB | Viewed 93 times ]8.证明(duanby)hint:(a-b)(c-b)(a-d)(c-d)in detail: product (a-b)(c-b)(a-d)(c-d) for everya,c be the number on , b,d be the number onfor point x,y if they are not ajjectent then in the product, it will occur twice, if it's ajjectent it's appears only once, and also chick the point that are on and then we get it.iampengcheng1130 2013中国女子数学奥林匹克第7题的解答。
2014年第十三届中国女子数学奥林匹克试题及参考答案
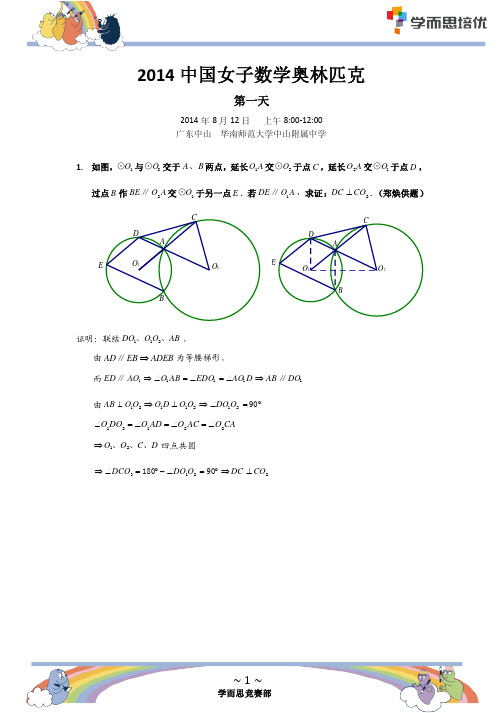
E D A O1 B O2 C
E
O1
B
证明:联结 DO1、O1O2、AB , 由 AD ∥ EB ADEB 为等腰梯形, 为等腰梯形
O1 AB EDO1 AO1 D AB ∥ DO1 而 ED ∥ AO1 DO1O2 90 由 AB O1O2 O1 D O1O2
∣A ∣= s , | B | 100 s, a t , a 5050 t, 解:记 a A a B
t p t 5050 t p 5050 t Ap f A f Bp f B 则F f s 1 s 99 s 100 s
Tm Fm 1 Fm Fm 2Km 则 1 Km 2Tm 1
Tm Tm 4Tm T 0, T4 6, T5 6, T6 6, 1 2 ,其中 3
1 7i 1 7i 解 x3 x2 2, , , 4得 x 2 2
n n 3
3 14 n Cn , 则 Tn An Bn ∣Bn∣=∣ Cn∣ 22 , 28 3 14 n 3 n 取 gn An , ∣ Tn gn∣≤∣ ∣≤ Bn∣ ∣ Cn∣ 22 22 2 gn 14 2
也即 g n 2 g n ≤ Tn ≤ g n +2 g n .
2 若2 d ,则 2∣a ,令每个男生与他左边 令每个男生与他左边
~3~
学而思竞赛部
,am 的个数: 4. 对整数 m ≥ 4 , 定义 Tm 为满足下列条件的数列 a1 ,a 2 , :
1,2 , ,m ,a i 1 ,2 ,3 ,4 ( 1 )对每个 i ;
国奥赛2013决赛真题及详解

2013年小学数学竞赛决赛试卷2013年4月13日上午10:00——11:30(每题10分 总分140分)1.计算:531)]125.021()4175.0(31[÷-+- = 。
解:原式 = 85]832131[⨯+⨯ = 852413⨯ = 19265 2.计算:252015105120151051151051105151++++++++++++++ = 。
解:原式 = 75150130115151++++ = 1502351030++++ = 31 3.用 a 表示正整数a 的不同约数的个数,如4的不同约数有1,2,4共3个。
所以4 = 3,那么(12 - 6)÷5 = 。
解:分解质因数。
12 = 2×2×3,不同的约数有:(2 + 1)×(1 + 1)= 6;6 = 2×3,不同的约数有:(1 + 1)×(1 + 1)= 4;5 = 5,不同的约数有:1 + 1 = 2;原式 =(6 - 4)÷2 = 14.右图是9个棱长为1米的正方体堆成的一个立体。
那么,这个立体的表面积 是 平方米。
解:三视图。
正面:6平方米侧面:4平方米上面:6平方米表面积:(6+4+6)×2 = 32平方米。
5.五个不同的整数,它们两两之和为6、7、8、10、13、14、15、16、17、18。
那么,这五个整数中,最大数是 ,最小数是 。
解:设这五个数为a 、b 、c 、d 、e ,那么有:a + b = 6;a + c = 7;a + d = 8;a + e = 10;b +c = 13;b + d = 14;b + e = 15;c +d = 16;c + e = 17;d +e = 18;所以,a + b + c + d + e =(6 + 7 + 8 + 10 + 13 + 14 + 15 + 16 + 17 + 18)÷4 = 31; 要使最大的数尽可能大,那么其余四个数要尽可能的小。
2013年中国女子数学奥林匹克(CGMO)试题及其解答
A 、A 中间,与A 、A 相邻矛盾。同理j、k奇偶性也不同。从而i、k奇偶性相同,于是线段 A A 中垂线所过的顶点A 在折线A A A 内,且不为A ,这与A 、A 、A 为三个相邻点矛盾。
综上所述,集合S对应的m个点必然等距排列。从而m|99。 另一方面,当m|99时,任取等间距为 的m个点,它们所对应的集合必然满足条件。
证明:如图,阴影部分即为区域 A。设直线y = t(2x − t)与 x 轴、y 轴的交点分别为 M、
N,则点M ,0 ,N 1,t(2 − t) 。显然点 P 在线段 MN 上。对于区域 A 内任一点 A,显然
有S△ ≤ max S△ ,S△ ,所以我们只需证明S△ ≤ 且S△ ≤ 。
作 PB⊥x 轴于 B,作 PC⊥QN 于 C,则S△ = · = S△ = · = ( )·( ) ≤ ( ) < 。命题得证。
⎩1 ≤ a、b ≤ 2013 ⎩1 ≤ a、b ≤ 2013
综上所述,满足条件的 a,b 共有(3 × 10 × 1) × (2 × 1 × 60) + (3 × 1 × 1) ×
(2 × 10 × 60) = 7200组。
五、给定正实数a 、a 、 … … 、a ,求证:存在正实数x 、x 、 … … 、x 满足
因为所有女孩只有m个,所以|A ⋃A ⋃ … … ⋃A | ≤ m。另一方面,对于任意两个男孩 和两个女孩,其中至少有一个男孩与一个女孩互不认识,所以对于任意i ≠ j, A ⋂A ≤ 1。 于是根据容斥原理知:
|A ⋃A ⋃ … … ⋃A | ≥ |A | + |A | + ⋯ + |A | − ∑ < A ⋂A ⇒ |A | + |A | + ⋯ + |A | ≤ |A ⋃A ⋃ … … ⋃A | + ∑ < A ⋂A ⇒ |A | + |A | + ⋯ + |A | ≤ m + C = m + ( ) 即男女孩无序对的个数不超过m + ( )。命题得证。
2021年第十三届全国大学生数学竞赛非数学类初赛参考答案

xn
.
【解】
记 a = 1011, yn = 1+ xn ,函数
f (x) = x + a 2x
(x 0) ,则 y1 = 2a ,且
yn+1 = f ( yn ) (n 1) .
------------ 5 分
2
2021 年初赛试题及参考解答
易知,当 x 2a 时, x f (x) 2a ,所以{yn} 是单调减少且有下界的数列,
n→
n
2
Bn
=
(b − a)2 f (b) −
24
f (a).
------------ 4 分
六、(14 分) 设{an} 与{bn}均为正实数列,满足: a1 = b1 = 1 ,且 bn = anbn−1 − 2 ,
n = 2,3,
.又设 {bn }
为有界数列,证明级数
n =1
1 a1a2
cos = x, cos = y, cos = z ,因此
------------ 2 分
( ) f (x, y, z)dS = 1
4
xf
x
(
x,
y,
z)
+
yf
y
(
x,
y,
z)
+
zf
z
(
x,
y,
z)
dS
= 1 4
cos
f
x
(
x,
y,
z)
+
cos
f
y
(
x,
y,
z)
+ cos
f
z
(
x,
y,
z)
中国数学奥林匹克(CMO)历届试题及解答(1986-2005)

0(i = 1, 2, . . . , n),则显然有a1 x1 + a2 x2 + · · · + an xn 0, ai −a1 > 0(i = 2, 3, . . . , n). ∴
√ sin ∠F AE FE AD 由正弦定理 sin AE 2 − AD2 = 5, ∠DAE = DE × AF .其中DE = √ √ F E = F D − DE = AF 2 − AD2 − DE = m2 − 122 − 5 > 0. ∴ m > 13, 且∠A为锐角等价于 ∠A为直角等价于 ∠A为钝角等价于 解得当13 < m < 当m = 当m >
∈ Z.
1 3 2n+1 (2n + 1)ϕ = (2l + 3 = 2t + 3 2 )π (l ∈ Z). ∴ (2n + 1)(2k + 6 ) = 2l + 2 , 6 2 , n = 6t + 4(t ∈ Z). 5(2n+1) 5 ) = 2l + 3 = 2t + 3 或(2n + 1)(2k + 6 2, 6 2 , 5|4t + 3, t ≡ 3 (mod 5)(t ∈ Z).
zk ∈A 2 , yk A,x2 k 4 2 1 √
1 4 ,即
2 x2 k + yk 2 x2 k + yk
√
2xk . yk |
zk ∈A zk ∈A
2004-2012历届北方数学奥林匹克试题PDF(无答案)

目录2005年北方数学奥林匹克 (2)2006年北方数学奥林匹克 (4)2007年北方数学奥林匹克 (6)2008年北方数学奥林匹克 (7)2009年北方数学奥林匹克 (10)2010年北方数学奥林匹克 (13)2011年北方数学奥林匹克 (15)2012年北方数学奥林匹克 (17)2005年北方数学奥林匹克1.AB是⊙O的一条弦,它的中点为M,过点M作一条非直径的弦CD,过点C和D作⊙O的两条切线,分别与直线AB相交于P、Q两点.求证:P A=QB.(裘宗沪供题)2.定义在R上的函数f(x)满足:(1)f(0)=0;(2)对任意xx∈(−∞,−1)∪(1,+∞),都有f�1x�+f�1y�=f(x+y1+xy);(3)当x∈(−1,0)时,都有f(x)>0.求证:f�119�+f�129�+⋯+ f�1n2+7n+11�>f(12),其中n∈N+. (刘贵谭祖春供题)3.在公差为d(d>0)的整数等差数列a1,a2,⋯,a3n(n≥2)中,任取n+2个数.证明:其中必存在两个数a i、a j(i≠j),满足不等式1<�a i−a j�nn<2. (刘康宁安振平供题)4.已知n位数的各位数字只能取集合{1,2,3,4,5}中的元素,设含有数字5且在5的前面不含3的n位数的个数为f(n).求f(n).(蒋西明供题)5.如果三个正实数x、y、z满足x2+xx+x2=254,x2+xy+y2=36,y2+yx+x2=1694.求xx+xy+yx的值. (张同君供题)6.设0≤α、β、γ≤π2,ccc2α+ccc2β+ccc2γ=1.求证:2≤(1+ccc2α)2cin4α+(1+ccc2β)2cin4β+(1+ccc2γ)2cin4γ≤(1+ccc2α)(1+ccc2β)(1+ccc2γ)(谭祖春供题)2006年北方数学奥林匹克1. 如图1,AB 为⊙O 的直径,非直径的弦CC ⊥AA ,E 是OC 的中点,连结AE 并延长交⊙O 于点P ,连结DP 交BC 于点F .求证:F 是BC 的中点.图12. 设p 是大于2的质数,数列{a n }满足na n+1=(n +1)a n −(p 2)4.求证:当a 1=5时,16|a 81. 3. 已知AD 是△ABC 的边BC 上的高,且AC +AC =AA +AC .求∠A 的取值范围.4. 设函数f (x )=x 2+ax +b (a 、b ∈R ).若存在实数m ,使得|f (m )|≤14,且|f (m +1)|≤14,求Δ=a 2−4b 的最大值和最小值.5. 已知正数a 、b 、c 满足a +b +c =3.求证:a 2+92a +(b+c )+b 2+92b +(c+a )+c 2+92c 2+(a+b )2≤5. 6. 组委会说明试题有误.7. 是否可以将正整数1,2,⋯,64分别填入8×8的64个方格 ,使得凡具备“”形的四个方格(方向课以任意转置)内的数之和都能被5整除?8. 已知数列{a n }满足a k+1=a k +12006a k 2,a 0=12,k ∈N .求证:A1−12008<a2006<1.1.在锐角△ABC中,BD、CE分别是AC、AB边上的高.以AB为直径作圆交CE于M,在BD上取点N是AN=AM.证明:AN⊥CN.2.设△ABC三边长分别为a、b、c,且a+b+c=3.求f(a,b,c)=a2+ b2+c2+43abc的最小值.3.在数列{a n}中,a n+1=a n2a n+1(n∈N).求证:当0≤n≤1004时,有[a n]=2007−n(其中[x]表示不超过x的最大整数).4.平面上每个点被染为n中颜色之一,同时满足:(1)每种颜色的点都有无穷多个,且不全在同一条直线上;(2)至少有一条直线上所有的点恰为两种颜色.求n的最小值,使得存在互不同色的4个点共圆.5.设α,β∈(0,π2),求A=(1−�tanα2tanβ2)2cctα+cctβ的最大值.6.已知f(x)=ll(x+1)−12lcl3x.(1)解方程f(x)=0;(2)求集合M={n|f(n2−214n−1998)≥0,n∈Z}.7.设n是正整数,a=�√n�(其中[x]表示不超过x的最大整数),求同时满足下列条件的n的最大值:(1)n不是完全平方数;(2)a3|n28.设△ABC的内切圆半径为1,三边长AC=a,CA=b,AA=c.若a、b、c都是整数,求证:△AAC为直角三角形.1. 如图1,⊙O 是梯形ABCD 的内切圆,切点分别为E 、F 、G 、H ,AB ∥CD .作BP ∥AD 交DC 的延长线于点P ,AO 的延长线交CP 于点Q .若AD =AD ,求证:∠CAQ =∠PAQ .图1 (张利民 供题)2. 已知∠A 、∠A 、∠C 是△AAC 的三个内角.证明:tan A 2+tan B 2+tan C 2√3≥�tan 2A 2+tan 2A 2+tan 2C 26 (张 雷 供题)3. 给定三角形数表如图2:1 2 3 4 ⋯ 97 98 99 100 3 5 7 ⋯ 195 197 199 8 12 ⋯ 392 396 20 ⋯ 788 ⋱ ⋯ ⋰ ⋱ ⋰ M图2其中,第一行各数依次是1,2,⋯,100,从第二行起,每个数分别等于它上面一行左、右两数的和.求M 的值.(焦和平 供题)4.证明:(1)存在无穷个正整数n,使n2+1的最大质因子小于n;(2)存在无穷个正整数n,使n2+1|n!. (张雷供题)5.如图3,已知□ABCD,过A、B、C三点的⊙O1分别交AD、BD 于点E、F,过C、D、F三点的⊙O2交AD于点G,设⊙O1、⊙O2R222.的半径分别为R1、R2.求证:AG图3(吕建恒刘康宁供题)6.设a、b、c为直角三角形的三边长,其中,c为斜边长.求使得a3+b3+c3abc≥k成立的k的最大值.(李铁汉供题)7.设n是正整数,整数a是方程x4+3ax2+2ax−2×3n=0的根.求所有满足条件的数对(n,a).(李铁汉供题)8.给定由n(n+1)2个点组成的正三角形点阵(如图4),记以点阵中三个点为顶点的所有正三角形的个数为f(n),求f(n)的表达式.图4(张利民供题)2009年北方数学奥林匹克1. 设数列{x n }满足x 1=1,x n =�x n−12+x n−1+x n−1(n ≥2).求数列{x n }的通项公式. (张 雷 供题)2. 如图1,在锐角△ABC 中,已知AA >AC ,cccA +cccC =1,E 、F 分别是AB 、AC 延长线上的点,且满足∠AAF =∠ACD =90°.(1) 求证:AD +CF =DF ;(2) 设∠DAC 的平分线与EF 交于点P ,求证:CP 平分∠ACF .图1(刘康宁 吕建恒 徐庆金 供题)3. 已知有26个互不相等的正整数,其中任意六个数中都至少有两个数,一个数整除另一个数.证明:一定存在六个数,其中一个数能被另外五个数整除.(张同君 供题)4. 船长和三位水手共得到2009枚面值相同的金币.四人商定按照如下规则对金币进行分配:水手1、水手2、水手3每人写下一个正整E数分别为b 1、b 2、b 3,满足b 1≥b 2≥b 3,且b 1+b 2+b 3=2009;船长在不知道水手写的数的情况下,将2009枚金币分成3堆,各堆数量分别为a 1、a 2、a 3,且a 1≥a 2≥a 3.对于水手k (k =1,2,3),当b k <a k 时,可以从第k 堆拿走b k 枚金币,否则不能拿.最后所有余下的金币归船长所有.若无论三位水手怎样写数,船长总可以确保自己拿到n 枚金币.试确定n 的最大值,并证明你的结论. (张 利 供题)5. 如图2,在给定的扇形AOB 中,圆心角为锐角.在弧AB 上取异于A 、B 的一点C ,在线段OC 上取一点P ,连结AP ,过点B 作直线BQ ∥AP 交射线OC 于点Q .证明:封闭图形OAQPBO 的面积与点C 、P 的选取无关.图2 (徐庆金 供题)6. 设x 、y 、z >0,且x 2+x 2+y 2=3,求证:∑x 2009−2008(x−1)y+z ≥12(x +x +y ). (杨海滨 贾应红 供题)7. 记[m ]为不超过实数m 的最大整数.设x 、y 均为正实数,且对所有的正整数n ,都有[x [nx ]]=n −1成立.证明xy =1,且y 是大于1的无O理数.(刘康宁供题)8.求能被209整除且各位数字之和等于209的最小正整数.(张雷供题)2010年北方数学奥林匹克1.已知数列{a n}满足a1=2,a n=22n a n−1+2n2n(n=2,3,⋯).求通项a n(n=1,2,⋯). (吴树勋供题)2.已知PA、PB是⊙O的切线,切点分别是A、B,PCD是⊙O的一条割线,过点C作PA的平行线,分别交弦AB、AD于点E、F.求证:CD=DF.(李新焕供题)3.求所有的正整数(x,x,y),使得1+2x×3y=5z成立.(张雷供题)4.在7×7的方格表的64个网格线交点(称为“结点”)处放棋子,每点至多放1枚,一共放了k枚棋子.若无论怎样放,总存在4枚棋子,它们所在的结点构成一个矩形(矩形的边平行于棋盘网格线)的四个顶点.试求k的最小值.(张利民供题)5.设正实数a、b、c满足(a+2b)(b+2c)=9.求证:�a2+b22+2�b3+c323≥3.(张雷供题)6.已知⊙O是△ABC的内切圆,D、E、N是切点,连结NO并延长交DE于点K,连结AK并延长交BC于点M.求证:M是BD的中点.(康春波供题)7.求[x,x,y]=(x,x)+(x,y)+(y,x)满足x≤x≤y,(x,x,y)=1的所以正整数解,其中,[m,n]和(m,n)分别表示正整数m、n的最小公倍数和最大公约数.(王全供题)8.设x、x、y∈[0,1],且|x−x|≤12,|x−y|≤12,|y−x|≤12.试求W=x+x+y−xx−xy−yx的最小值和最大值.(刘康宁安振平供题)2011年北方数学奥林匹克1.已知数列{a n}的通项a n=(√3+√2)2n(n∈N+),设b n=a n+1a n. (1)试求b n+2、b n+1、b n之间的递推关系;(2)求a2011整数部分的个位数字.(刘洪柱供题)2.如图1,△ABC的内切圆分别切BC、CA、AB、于点D、E、F,P 为内切圆内一点,线段PA、PB、PC分别于内切圆交于点X、Y、Z.证明:XD、YE、ZF三线共点.图1(徐庆金供题)3.求不定方程1+2x×7y=y2的全部正整数解(x,x,y). (翁世有供题)4.设n个集合A1,A2,⋯,A n是集合A={1,2,⋯,29}的一个分划,且A i(i=1,2,⋯,n)中任意个元素之和都不等于30.求n的最小可能值. 【注】若集合A的非空子集A1,A2,⋯,A n(n∈N+,n≥2)满足A i∩A j=∅(i≠j),A1∪A2∪⋯∪A n=A,则称A1,A2,⋯,A n是集合A的一个分划.(张雷供题)5. 若正整数a 、b 、c 满足a 2+b 2=c 2,则称(a ,b ,c )为勾股数组.求含有30的所有勾股数组. (杨春宏 供题)6. 如图2,过点P 引的切线P A 和割线PBC ,AC ⊥PP ,垂足为D .证明:AC 是△ABD 外接圆的切线.图2(吕建恒 供题) 7. 在△ABC 中,证明:11+ccs 2A+ccs 2A +11+ccs 2A+ccs 2C +11+ccs 2C+ccs 2A ≤2.(安振平 供题) 8. 已知n 是正整数,实数x 满足�1−|2−⋯|(n −1)−|n −x ||⋯|�=x .求x 的值. (张利民供题)P2012年北方数学奥林匹克1.如图1,在△ABC中,∠C=90°,I是内心.直线BI交AC于D,作DE平行于AI交BC于E,直线EI交AB于F.证明:DF垂直于AI.图12.正整数x1,x2,⋯,x n(n∈ℕ+),满足x12+x22+⋯+x n2=111,求S=x1+x2+⋯+x n n的最大可能值.3.设S={x|x=a2+ab+b2,a,b∈ℤ}.求证:(1)若m∈S,3|m,则3m∈S;(2)若m,n∈S,则m⋅n∈S.4.平面上有n(n≥4)条直线,对于直线a,b,在余下的n-2条直线中,如果至少存在两条直线与直线a,b都相交,则称直线a,b是相合的直线对,否则称其是相离的直线对.若n条直线中相合直线对的个数比相离直线对的个数多2012.求n的最小可能值(直线对中的两条直线不计顺序).5.已知数列{a n}:a0=0,a n=1a n−1−2,n∈ℕ+,在数列{a n}中任意取定一项a k,构造数列{b n}:b0=a k,b n=2b n−1+1b n−1,n∈ℕ+.试判断数列{b n}是有限数列还是无穷数列?并给出证明.6.设n是正整数,证明�1+13��1+13�⋯�1+13�<2.7.如图2在五边形ABCDE中,BC=DE,CD平行于BE,AB>AE,AA AA,求证:AC平分线段BE.若∠AAC=∠CAD,且图28.设p是奇素数,如果存在正整数a使p!|a p+1,证明:(1)�a+1,a p+1a+1�=p.(2)a p+1a+1没有小于p的素因子.p!|a+1.。
第十三届应用竞赛初赛试题及参考解答

第十三届北京高中数学知识应用竞赛初赛试题及参考解答一、(满分20分)一游客在马台长城游览后,乘坐缆车下山。
缆车运行了一会儿,她开始注意到,自己乘坐的是50号缆车,这时离自己最近的迎面上山的缆车是81号,接下来是82号,再往下的缆车上所标数字依次连续出现,她又记下了自己乘坐的缆车与对面相邻缆车相遇的时间间隔是9秒。
对面缆车号的最大数字是112,接着就是1号缆车。
(1)从与81号缆车相遇开始,50号缆车大约还有多久能够到站?(2)下山后,见牌子上写:“索道全长1200米”。
请计算一下缆车的速度是多少?解答:假设:1.缆车间隔相同;2.缆车匀速运动;3.当第49号缆车迎面出现时,所乘缆车到站。
…………………………………4分(1)t =(112−81+49)÷2×18=720(秒),即50号缆车还有12分钟到站。
………12分(2)根据已知条件,可得全程运行的总时间是T =(112−51+49)÷2×18=990(秒)。
于是,速度v =S/T =1200÷990≈1.21(米/秒)。
即缆车的速度约为1.21米/秒。
……………20分二、(满分20分)视野,是指人的眼睛固定注视一定目标时,所能见到的范围,常用角度来表示。
一般来说,在静止状态下,人的双眼视野可达210°;在驾驶车辆时,随着车速的增加,驾驶员的双眼视野度数减小。
右面是一组车速与视野关系的实验数据:(数据来自/bbs/thread-c-774-2558157-1.html )请根据这些数据估计车速在120km/h 时的视野。
解:用二次函数拟合,可以得到函数y =0.0155x 2−3.217x +208.75,其图像如下左图所示。
代入x =120得:y =45.9°。
这表示车速在120km/h 时的视野大于车速在100km/h 时的视野,显然不合理。
说明为估计车速在120km/h 时的视野而选择拟合二次函数是错的,故舍去此结论。
历届北方数学奥林匹克试题

目录2005年北方数学奥林匹克 (2)2006年北方数学奥林匹克 (4)2007年北方数学奥林匹克 (6)2008年北方数学奥林匹克 (7)2009年北方数学奥林匹克 (10)2010年北方数学奥林匹克 (13)2011年北方数学奥林匹克 (15)2012年北方数学奥林匹克 (17)2005年北方数学奥林匹克1.AB是⊙O的一条弦,它的中点为M,过点M作一条非直径的弦CD,过点C和D作⊙O的两条切线,分别与直线AB相交于P、Q两点.求证:P A=QB.(裘宗沪供题)2.定义在R上的函数f(x)满足:(1)f(0)=0;(2)对任意xx∈(−∞,−1)∪(1,+∞),都有f�1x�+f�1y�=f(x+y1+xy);(3)当x∈(−1,0)时,都有f(x)>0.求证:f�119�+f�129�+⋯+ f�1n2+7n+11�>f(12),其中n∈N+. (刘贵谭祖春供题)3.在公差为d(d>0)的整数等差数列a1,a2,⋯,a3n(n≥2)中,任取n+2个数.证明:其中必存在两个数a i、a j(i≠j),满足不等式1<�a i−a j�nn<2. (刘康宁安振平供题)4.已知n位数的各位数字只能取集合{1,2,3,4,5}中的元素,设含有数字5且在5的前面不含3的n位数的个数为f(n).求f(n).(蒋西明供题)5.如果三个正实数x、y、z满足x2+xx+x2=254,x2+xy+y2=36,y2+yx+x2=1694.求xx+xy+yx的值. (张同君供题)6.设0≤α、β、γ≤π2,ccc2α+ccc2β+ccc2γ=1.求证:2≤(1+ccc2α)2cin4α+(1+ccc2β)2cin4β+(1+ccc2γ)2cin4γ≤(1+ccc2α)(1+ccc2β)(1+ccc2γ)(谭祖春供题)2006年北方数学奥林匹克1. 如图1,AB 为⊙O 的直径,非直径的弦CC ⊥AA ,E 是OC 的中点,连结AE 并延长交⊙O 于点P ,连结DP 交BC 于点F .求证:F 是BC 的中点.图12. 设p 是大于2的质数,数列{a n }满足na n+1=(n +1)a n −(p 2)4.求证:当a 1=5时,16|a 81. 3. 已知AD 是△ABC 的边BC 上的高,且AC +AC =AA +AC .求∠A 的取值范围.4. 设函数f (x )=x 2+ax +b (a 、b ∈R ).若存在实数m ,使得|f (m )|≤14,且|f (m +1)|≤14,求Δ=a 2−4b 的最大值和最小值.5. 已知正数a 、b 、c 满足a +b +c =3.求证:a 2+92a +(b+c )+b 2+92b +(c+a )+c 2+92c 2+(a+b )2≤5. 6. 组委会说明试题有误.7. 是否可以将正整数1,2,⋯,64分别填入8×8的64个方格 ,使得凡具备“”形的四个方格(方向课以任意转置)内的数之和都能被5整除?8. 已知数列{a n }满足a k+1=a k +12006a k 2,a 0=12,k ∈N .求证:A1−12008<a2006<1.1.在锐角△ABC中,BD、CE分别是AC、AB边上的高.以AB为直径作圆交CE于M,在BD上取点N是AN=AM.证明:AN⊥CN.2.设△ABC三边长分别为a、b、c,且a+b+c=3.求f(a,b,c)=a2+ b2+c2+43abc的最小值.3.在数列{a n}中,a n+1=a n2a n+1(n∈N).求证:当0≤n≤1004时,有[a n]=2007−n(其中[x]表示不超过x的最大整数).4.平面上每个点被染为n中颜色之一,同时满足:(1)每种颜色的点都有无穷多个,且不全在同一条直线上;(2)至少有一条直线上所有的点恰为两种颜色.求n的最小值,使得存在互不同色的4个点共圆.5.设α,β∈(0,π2),求A=(1−�tanα2tanβ2)2cctα+cctβ的最大值.6.已知f(x)=ll(x+1)−12lcl3x.(1)解方程f(x)=0;(2)求集合M={n|f(n2−214n−1998)≥0,n∈Z}.7.设n是正整数,a=�√n�(其中[x]表示不超过x的最大整数),求同时满足下列条件的n的最大值:(1)n不是完全平方数;(2)a3|n28.设△ABC的内切圆半径为1,三边长AC=a,CA=b,AA=c.若a、b、c都是整数,求证:△AAC为直角三角形.1. 如图1,⊙O 是梯形ABCD 的内切圆,切点分别为E 、F 、G 、H ,AB ∥CD .作BP ∥AD 交DC 的延长线于点P ,AO 的延长线交CP 于点Q .若AD =AD ,求证:∠CAQ =∠PAQ .图1 (张利民 供题)2. 已知∠A 、∠A 、∠C 是△AAC 的三个内角.证明:tan A 2+tan B 2+tan C 2√3≥�tan 2A 2+tan 2A 2+tan 2C 26 (张 雷 供题)3. 给定三角形数表如图2:1 2 3 4 ⋯ 97 98 99 100 3 5 7 ⋯ 195 197 199 8 12 ⋯ 392 396 20 ⋯ 788 ⋱ ⋯ ⋰ ⋱ ⋰ M图2其中,第一行各数依次是1,2,⋯,100,从第二行起,每个数分别等于它上面一行左、右两数的和.求M 的值.(焦和平 供题)4.证明:(1)存在无穷个正整数n,使n2+1的最大质因子小于n;(2)存在无穷个正整数n,使n2+1|n!. (张雷供题)5.如图3,已知□ABCD,过A、B、C三点的⊙O1分别交AD、BD 于点E、F,过C、D、F三点的⊙O2交AD于点G,设⊙O1、⊙O2R222.的半径分别为R1、R2.求证:AG图3(吕建恒刘康宁供题)6.设a、b、c为直角三角形的三边长,其中,c为斜边长.求使得a3+b3+c3abc≥k成立的k的最大值.(李铁汉供题)7.设n是正整数,整数a是方程x4+3ax2+2ax−2×3n=0的根.求所有满足条件的数对(n,a).(李铁汉供题)8.给定由n(n+1)2个点组成的正三角形点阵(如图4),记以点阵中三个点为顶点的所有正三角形的个数为f(n),求f(n)的表达式.图4(张利民供题)2009年北方数学奥林匹克1. 设数列{x n }满足x 1=1,x n =�x n−12+x n−1+x n−1(n ≥2).求数列{x n }的通项公式. (张 雷 供题)2. 如图1,在锐角△ABC 中,已知AA >AC ,cccA +cccC =1,E 、F 分别是AB 、AC 延长线上的点,且满足∠AAF =∠ACD =90°.(1) 求证:AD +CF =DF ;(2) 设∠DAC 的平分线与EF 交于点P ,求证:CP 平分∠ACF .图1(刘康宁 吕建恒 徐庆金 供题)3. 已知有26个互不相等的正整数,其中任意六个数中都至少有两个数,一个数整除另一个数.证明:一定存在六个数,其中一个数能被另外五个数整除.(张同君 供题)4. 船长和三位水手共得到2009枚面值相同的金币.四人商定按照如下规则对金币进行分配:水手1、水手2、水手3每人写下一个正整E数分别为b 1、b 2、b 3,满足b 1≥b 2≥b 3,且b 1+b 2+b 3=2009;船长在不知道水手写的数的情况下,将2009枚金币分成3堆,各堆数量分别为a 1、a 2、a 3,且a 1≥a 2≥a 3.对于水手k (k =1,2,3),当b k <a k 时,可以从第k 堆拿走b k 枚金币,否则不能拿.最后所有余下的金币归船长所有.若无论三位水手怎样写数,船长总可以确保自己拿到n 枚金币.试确定n 的最大值,并证明你的结论. (张 利 供题)5. 如图2,在给定的扇形AOB 中,圆心角为锐角.在弧AB 上取异于A 、B 的一点C ,在线段OC 上取一点P ,连结AP ,过点B 作直线BQ ∥AP 交射线OC 于点Q .证明:封闭图形OAQPBO 的面积与点C 、P 的选取无关.图2 (徐庆金 供题)6. 设x 、y 、z >0,且x 2+x 2+y 2=3,求证:∑x 2009−2008(x−1)y+z ≥12(x +x +y ). (杨海滨 贾应红 供题)7. 记[m ]为不超过实数m 的最大整数.设x 、y 均为正实数,且对所有的正整数n ,都有[x [nx ]]=n −1成立.证明xy =1,且y 是大于1的无O理数.(刘康宁供题)8.求能被209整除且各位数字之和等于209的最小正整数.(张雷供题)2010年北方数学奥林匹克1.已知数列{a n}满足a1=2,a n=22n a n−1+2n2n(n=2,3,⋯).求通项a n(n=1,2,⋯). (吴树勋供题)2.已知PA、PB是⊙O的切线,切点分别是A、B,PCD是⊙O的一条割线,过点C作PA的平行线,分别交弦AB、AD于点E、F.求证:CD=DF.(李新焕供题)3.求所有的正整数(x,x,y),使得1+2x×3y=5z成立.(张雷供题)4.在7×7的方格表的64个网格线交点(称为“结点”)处放棋子,每点至多放1枚,一共放了k枚棋子.若无论怎样放,总存在4枚棋子,它们所在的结点构成一个矩形(矩形的边平行于棋盘网格线)的四个顶点.试求k的最小值.(张利民供题)5.设正实数a、b、c满足(a+2b)(b+2c)=9.求证:�a2+b22+2�b3+c323≥3.(张雷供题)6.已知⊙O是△ABC的内切圆,D、E、N是切点,连结NO并延长交DE于点K,连结AK并延长交BC于点M.求证:M是BD的中点.(康春波供题)7.求[x,x,y]=(x,x)+(x,y)+(y,x)满足x≤x≤y,(x,x,y)=1的所以正整数解,其中,[m,n]和(m,n)分别表示正整数m、n的最小公倍数和最大公约数.(王全供题)8.设x、x、y∈[0,1],且|x−x|≤12,|x−y|≤12,|y−x|≤12.试求W=x+x+y−xx−xy−yx的最小值和最大值.(刘康宁安振平供题)2011年北方数学奥林匹克1.已知数列{a n}的通项a n=(√3+√2)2n(n∈N+),设b n=a n+1a n. (1)试求b n+2、b n+1、b n之间的递推关系;(2)求a2011整数部分的个位数字.(刘洪柱供题)2.如图1,△ABC的内切圆分别切BC、CA、AB、于点D、E、F,P 为内切圆内一点,线段PA、PB、PC分别于内切圆交于点X、Y、Z.证明:XD、YE、ZF三线共点.图1(徐庆金供题)3.求不定方程1+2x×7y=y2的全部正整数解(x,x,y). (翁世有供题)4.设n个集合A1,A2,⋯,A n是集合A={1,2,⋯,29}的一个分划,且A i(i=1,2,⋯,n)中任意个元素之和都不等于30.求n的最小可能值. 【注】若集合A的非空子集A1,A2,⋯,A n(n∈N+,n≥2)满足A i∩A j=∅(i≠j),A1∪A2∪⋯∪A n=A,则称A1,A2,⋯,A n是集合A的一个分划.(张雷供题)5. 若正整数a 、b 、c 满足a 2+b 2=c 2,则称(a ,b ,c )为勾股数组.求含有30的所有勾股数组. (杨春宏 供题)6. 如图2,过点P 引的切线P A 和割线PBC ,AC ⊥PP ,垂足为D .证明:AC 是△ABD 外接圆的切线.图2(吕建恒 供题) 7. 在△ABC 中,证明:11+ccs 2A+ccs 2A +11+ccs 2A+ccs 2C +11+ccs 2C+ccs 2A ≤2.(安振平 供题) 8. 已知n 是正整数,实数x 满足�1−|2−⋯|(n −1)−|n −x ||⋯|�=x .求x 的值. (张利民供题)P2012年北方数学奥林匹克1.如图1,在△ABC中,∠C=90°,I是内心.直线BI交AC于D,作DE平行于AI交BC于E,直线EI交AB于F.证明:DF垂直于AI.图12.正整数x1,x2,⋯,x n(n∈ℕ+),满足x12+x22+⋯+x n2=111,求S=x1+x2+⋯+x n n的最大可能值.3.设S={x|x=a2+ab+b2,a,b∈ℤ}.求证:(1)若m∈S,3|m,则3m∈S;(2)若m,n∈S,则m⋅n∈S.4.平面上有n(n≥4)条直线,对于直线a,b,在余下的n-2条直线中,如果至少存在两条直线与直线a,b都相交,则称直线a,b是相合的直线对,否则称其是相离的直线对.若n条直线中相合直线对的个数比相离直线对的个数多2012.求n的最小可能值(直线对中的两条直线不计顺序).5.已知数列{a n}:a0=0,a n=1a n−1−2,n∈ℕ+,在数列{a n}中任意取定一项a k,构造数列{b n}:b0=a k,b n=2b n−1+1b n−1,n∈ℕ+.试判断数列{b n}是有限数列还是无穷数列?并给出证明.6.设n是正整数,证明�1+13��1+13�⋯�1+13�<2.7.如图2在五边形ABCDE中,BC=DE,CD平行于BE,AB>AE,AA AA,求证:AC平分线段BE.若∠AAC=∠CAD,且图28.设p是奇素数,如果存在正整数a使p!|a p+1,证明:(1)�a+1,a p+1a+1�=p.(2)a p+1a+1没有小于p的素因子.p!|a+1.。
第13届中国北方数学奥林匹克

而3一(cos p一√§sin p)‘
=3一(cos2臼+3sin2口一2√芋sin臼・cos p)
4.首先,假设IQI≥101. 若在某个排列中戈、y连续出现,则称 (菇,y)为一个“片段”. 由于每个排列恰有99个片段,于是,集 合Q中共有99×101=9 999个片段. 而不同的片段只有100×99=9 900个, 由抽屉原理,知存在一个片段在集合Q中出 现至少两次,矛盾. 从而,I Q I≤100. 其次,令
,,
,
/ P
2. 3. 4.
同基础班第3题 同基础班第4题 (1)当 n≥4时.
Q
C 图6
由正六边形的性质易知
(i)若6。 ,62,…,6。 中有两个偶数,则当
么甜E:60。:么埘Ⅳ
万方数据
2017年第10期
j么cAQ=么尉Ⅳ,
么ACQ=么AEⅣ=900,
取卜.1任一素因子p,于是, r三1(mod p). 任取n=(o。o一…口,),,在模p意义下有 n=(口,o,一1…口1),
[MDE=[NDF. 由正弦定理知
EM
口1+02+…+on<万;
当您≥4时,
口n
2歹j<歹曩F百2了×F
1
】
1
】
sin么删sin么ZⅥ纪
DF FN
DE
:亭口1+n,+…+8。
sin么DⅣF
万方数据
sin么ⅣDF
2017年第10期 =々EM=b?N=令AE+A壬?=BE+C}1.
么FDG=1200. 从而,D、F、M、G四点共圆. 又0F=DG,则
得对任意正整数后,61+玩1,62+尼02,…,6。+ 玩。两两互素? (张利民供题) 5.已知正六边形A曰优)EF边长为o,两 个动点M、Ⅳ分别在边BC、DE上运动,且满
2005-2013年第1-9届北方数学奥林匹克数学试题及解答

1 2
.
故原不等式成立 . 三、 在取出的 n + 2 个数中 , 设 al 为最 大 , 则
al ≤a3 n . 把每个数都加上 a3 n - al ,这样处理后不改
变任何两数差的绝对值 . 从而 , 总可以认为取出的
n + 2个数中包括 a3 n ,记 al = a3 n .
(1 ) 若 取 出 的 n + 2 个 数 中 , 除 a3 n 外 , 还 有
23 (2) 若取出的 n + 2 个数中 ,不含 an + 1 , an + 2 , …,
a2 n - 1 这 n - 1 个数中的任何一个数 . 把这些数及 a3 n
又 ( 1 + x 1 ) ( 1 - x 2 ) > 0 Ζ x1 - x 2 > x1 x 2 - 1 Ζ - 1 < x2 - x1 < 0. x 1 x2 - 1 由 (3) 得 f
| ai 平 供题)
第二天
四、 已知 n 位数的各位数字只能取集合 {1 ,2 ,3 ,4 ,5} 中的元素 , 设含有数字 5 且在 5 的前面不含 3 的 n 位数的个数为 f ( n ) . 求 ( 蒋西明 f ( n) . 供题) 五、 如果三个正实数 x 、 y、 z 满足 25 2 2 2 2 x + xy + y = , y + yz + z = 36 , 4
2 2 2 = ( ab + bc + ca) ( a + b + c )
①
② 因为 u ≥ 0,v ≥ 0 , 所以 , 式 ② 的左边显然成立 , π β、 γ 中两个取 、 且仅当 u = v = 0 , 即 α、 一个取 0 2 时等号成立 .
第13届中国北方数学奥林匹克试题及解析

BB第13届中国北方数学奥林匹克试题及解析(提高班)1.已知数列{}n a 满足()31221211,,2,,kk k nn n a e a e eaa an n Z k R -++-++===≥∈∈,求20171i i a =∏解:对12211kk k n n n ea a a -++-=两边同时取对数得()()()()111112ln ln 2ln 1ln 21ln 21ln n n n n n n k k a a k a a k a k a +----++=+⇒+=++-+ 设()()111ln 222n n n n n b a b k b kb n +-=+⇒=+-≥()()11222n n n n b b k b b n +-⇒-=-≥又211121ln 1ln 2,1ln 2nn n n b a e b a a e-=+=+==+=⇒=记()20172017201820191121is i i i S a e e -===-⇒==∑∏2.在ABC ∆中,D 为BC 的中点,,E F 分别为,AB AC 上的点,且DE DF =, 证明:AE AF BE CF EDF BAC +=+⇔∠=∠证明:如图,取,AB AC 的中点,M N , 延长DM 至点P ,使得MP MA = 联结,,EP MN DN一方面,若AE AF BE CF EM FN +=+⇒= 则由,PME MAN DNF MP MA DN ∠=∠=∠== 所以:PME DNF ∆∆≌所以:,PE DF DE NDF MPE PDE ==∠=∠=∠ 所以:EDF MND BAC ∠=∠=∠又因为:若EDF BAC MDE NDF ∠=∠⇒∠=∠ 由正弦定理得sin sin sin sin EM DE DF FNMDE DME DNF NDF===∠∠∠∠所以:EM FN AE AF BE CF =⇒+=+3.记Q 为1,2,,100L 的若干个排列组成的集合,且满足对于任意的1,100,,a b a b ≤≤≠至多存在一个Q σ∈使得在σ中a 的下一个数恰为b ;求集合Q 的元素个数的最大值解:首先,假设||101Q ≥。
历届北方数学奥林匹克试题

目录2005年北方数学奥林匹克 (2)2006年北方数学奥林匹克 (4)2007年北方数学奥林匹克 (6)2008年北方数学奥林匹克 (7)2009年北方数学奥林匹克 (10)2010年北方数学奥林匹克 (13)2011年北方数学奥林匹克 (15)2012年北方数学奥林匹克 (17)2005年北方数学奥林匹克1.AB是⊙O的一条弦,它的中点为M,过点M作一条非直径的弦CD,过点C和D作⊙O的两条切线,分别与直线AB相交于P、Q两点.求证:P A=QB.(裘宗沪供题)2.定义在R上的函数f(x)满足:(1)f(0)=0;(2)对任意xx∈(−∞,−1)∪(1,+∞),都有f�1x�+f�1y�=f(x+y1+xy);(3)当x∈(−1,0)时,都有f(x)>0.求证:f�119�+f�129�+⋯+ f�1n2+7n+11�>f(12),其中n∈N+. (刘贵谭祖春供题)3.在公差为d(d>0)的整数等差数列a1,a2,⋯,a3n(n≥2)中,任取n+2个数.证明:其中必存在两个数a i、a j(i≠j),满足不等式1<�a i−a j�nn<2. (刘康宁安振平供题)4.已知n位数的各位数字只能取集合{1,2,3,4,5}中的元素,设含有数字5且在5的前面不含3的n位数的个数为f(n).求f(n).(蒋西明供题)5.如果三个正实数x、y、z满足x2+xx+x2=254,x2+xy+y2=36,y2+yx+x2=1694.求xx+xy+yx的值. (张同君供题)6.设0≤α、β、γ≤π2,ccc2α+ccc2β+ccc2γ=1.求证:2≤(1+ccc2α)2cin4α+(1+ccc2β)2cin4β+(1+ccc2γ)2cin4γ≤(1+ccc2α)(1+ccc2β)(1+ccc2γ)(谭祖春供题)2006年北方数学奥林匹克1. 如图1,AB 为⊙O 的直径,非直径的弦CC ⊥AA ,E 是OC 的中点,连结AE 并延长交⊙O 于点P ,连结DP 交BC 于点F .求证:F 是BC 的中点.图12. 设p 是大于2的质数,数列{a n }满足na n+1=(n +1)a n −(p 2)4.求证:当a 1=5时,16|a 81. 3. 已知AD 是△ABC 的边BC 上的高,且AC +AC =AA +AC .求∠A 的取值范围.4. 设函数f (x )=x 2+ax +b (a 、b ∈R ).若存在实数m ,使得|f (m )|≤14,且|f (m +1)|≤14,求Δ=a 2−4b 的最大值和最小值.5. 已知正数a 、b 、c 满足a +b +c =3.求证:a 2+92a 2+(b+c )2+b 2+92b 2+(c+a )2+c 2+92c 2+(a+b )2≤5. 6. 组委会说明试题有误.7. 是否可以将正整数1,2,⋯,64分别填入8×8的64个方格 ,使得凡具备“”形的四个方格(方向课以任意转置)内的数之和都能被5整除?8. 已知数列{a n }满足a k+1=a k +12006a k 2,a 0=12,k ∈N .求证:A1−12008<a2006<1.1.在锐角△ABC中,BD、CE分别是AC、AB边上的高.以AB为直径作圆交CE于M,在BD上取点N是AN=AM.证明:AN⊥CN.2.设△ABC三边长分别为a、b、c,且a+b+c=3.求f(a,b,c)=a2+ b2+c2+43abc的最小值.3.在数列{a n}中,a n+1=a n2a n+1(n∈N).求证:当0≤n≤1004时,有[a n]=2007−n(其中[x]表示不超过x的最大整数).4.平面上每个点被染为n中颜色之一,同时满足:(1)每种颜色的点都有无穷多个,且不全在同一条直线上;(2)至少有一条直线上所有的点恰为两种颜色.求n的最小值,使得存在互不同色的4个点共圆.5.设α,β∈(0,π2),求A=(1−�tanα2tanβ2)2cctα+cctβ的最大值.6.已知f(x)=ll(x+1)−12lcl3x.(1)解方程f(x)=0;(2)求集合M={n|f(n2−214n−1998)≥0,n∈Z}.7.设n是正整数,a=�√n�(其中[x]表示不超过x的最大整数),求同时满足下列条件的n的最大值:(1)n不是完全平方数;(2)a3|n28.设△ABC的内切圆半径为1,三边长AC=a,CA=b,AA=c.若a、b、c都是整数,求证:△AAC为直角三角形.1. 如图1,⊙O 是梯形ABCD 的内切圆,切点分别为E 、F 、G 、H ,AB ∥CD .作BP ∥AD 交DC 的延长线于点P ,AO 的延长线交CP 于点Q .若AD =AD ,求证:∠CAQ =∠PAQ .图1 (张利民 供题)2. 已知∠A 、∠A 、∠C 是△AAC 的三个内角.证明:tan A 2+tan B 2+tan C 2√3≥�tan 2A 2+tan 2A 2+tan 2C 26 (张 雷 供题)3. 给定三角形数表如图2:1 2 3 4 ⋯ 97 98 99 100 3 5 7 ⋯ 195 197 199 8 12 ⋯ 392 396 20 ⋯ 788 ⋱ ⋯ ⋰ ⋱ ⋰ M图2其中,第一行各数依次是1,2,⋯,100,从第二行起,每个数分别等于它上面一行左、右两数的和.求M 的值.(焦和平 供题)4.证明:(1)存在无穷个正整数n,使n2+1的最大质因子小于n;(2)存在无穷个正整数n,使n2+1|n!. (张雷供题)5.如图3,已知□ABCD,过A、B、C三点的⊙O1分别交AD、BD 于点E、F,过C、D、F三点的⊙O2交AD于点G,设⊙O1、⊙O2R222.的半径分别为R1、R2.求证:AG图3(吕建恒刘康宁供题)6.设a、b、c为直角三角形的三边长,其中,c为斜边长.求使得a3+b3+c3abc≥k成立的k的最大值.(李铁汉供题)7.设n是正整数,整数a是方程x4+3ax2+2ax−2×3n=0的根.求所有满足条件的数对(n,a).(李铁汉供题)8.给定由n(n+1)2个点组成的正三角形点阵(如图4),记以点阵中三个点为顶点的所有正三角形的个数为f(n),求f(n)的表达式.图4(张利民供题)2009年北方数学奥林匹克1. 设数列{x n }满足x 1=1,x n =�x n−12+x n−1+x n−1(n ≥2).求数列{x n }的通项公式. (张 雷 供题)2. 如图1,在锐角△ABC 中,已知AA >AC ,cccA +cccC =1,E 、F 分别是AB 、AC 延长线上的点,且满足∠AAF =∠ACD =90°.(1) 求证:AD +CF =DF ;(2) 设∠DAC 的平分线与EF 交于点P ,求证:CP 平分∠ACF .图1(刘康宁 吕建恒 徐庆金 供题)3. 已知有26个互不相等的正整数,其中任意六个数中都至少有两个数,一个数整除另一个数.证明:一定存在六个数,其中一个数能被另外五个数整除.(张同君 供题)4. 船长和三位水手共得到2009枚面值相同的金币.四人商定按照如下规则对金币进行分配:水手1、水手2、水手3每人写下一个正整E数分别为b 1、b 2、b 3,满足b 1≥b 2≥b 3,且b 1+b 2+b 3=2009;船长在不知道水手写的数的情况下,将2009枚金币分成3堆,各堆数量分别为a 1、a 2、a 3,且a 1≥a 2≥a 3.对于水手k (k =1,2,3),当b k <a k 时,可以从第k 堆拿走b k 枚金币,否则不能拿.最后所有余下的金币归船长所有.若无论三位水手怎样写数,船长总可以确保自己拿到n 枚金币.试确定n 的最大值,并证明你的结论. (张 利 供题)5. 如图2,在给定的扇形AOB 中,圆心角为锐角.在弧AB 上取异于A 、B 的一点C ,在线段OC 上取一点P ,连结AP ,过点B 作直线BQ ∥AP 交射线OC 于点Q .证明:封闭图形OAQPBO 的面积与点C 、P 的选取无关.图2 (徐庆金 供题)6. 设x 、y 、z >0,且x 2+x 2+y 2=3,求证:∑x 2009−2008(x−1)y+z ≥12(x +x +y ). (杨海滨 贾应红 供题)7. 记[m ]为不超过实数m 的最大整数.设x 、y 均为正实数,且对所有的正整数n ,都有[x [nx ]]=n −1成立.证明xy =1,且y 是大于1的无O理数.(刘康宁供题)8.求能被209整除且各位数字之和等于209的最小正整数.(张雷供题)2010年北方数学奥林匹克1.已知数列{a n}满足a1=2,a n=22n a n−1+2n2n(n=2,3,⋯).求通项a n(n=1,2,⋯). (吴树勋供题)2.已知PA、PB是⊙O的切线,切点分别是A、B,PCD是⊙O的一条割线,过点C作PA的平行线,分别交弦AB、AD于点E、F.求证:CD=DF.(李新焕供题)3.求所有的正整数(x,x,y),使得1+2x×3y=5z成立.(张雷供题)4.在7×7的方格表的64个网格线交点(称为“结点”)处放棋子,每点至多放1枚,一共放了k枚棋子.若无论怎样放,总存在4枚棋子,它们所在的结点构成一个矩形(矩形的边平行于棋盘网格线)的四个顶点.试求k的最小值.(张利民供题)5.设正实数a、b、c满足(a+2b)(b+2c)=9.求证:�a2+b22+2�b3+c323≥3.(张雷供题)6.已知⊙O是△ABC的内切圆,D、E、N是切点,连结NO并延长交DE于点K,连结AK并延长交BC于点M.求证:M是BD的中点.(康春波供题)7.求[x,x,y]=(x,x)+(x,y)+(y,x)满足x≤x≤y,(x,x,y)=1的所以正整数解,其中,[m,n]和(m,n)分别表示正整数m、n的最小公倍数和最大公约数.(王全供题)8.设x、x、y∈[0,1],且|x−x|≤12,|x−y|≤12,|y−x|≤12.试求W=x+x+y−xx−xy−yx的最小值和最大值.(刘康宁安振平供题)2011年北方数学奥林匹克1.已知数列{a n}的通项a n=(√3+√2)2n(n∈N+),设b n=a n+1a n. (1)试求b n+2、b n+1、b n之间的递推关系;(2)求a2011整数部分的个位数字.(刘洪柱供题)2.如图1,△ABC的内切圆分别切BC、CA、AB、于点D、E、F,P 为内切圆内一点,线段PA、PB、PC分别于内切圆交于点X、Y、Z.证明:XD、YE、ZF三线共点.图1(徐庆金供题)3.求不定方程1+2x×7y=y2的全部正整数解(x,x,y). (翁世有供题)4.设n个集合A1,A2,⋯,A n是集合A={1,2,⋯,29}的一个分划,且A i(i=1,2,⋯,n)中任意个元素之和都不等于30.求n的最小可能值. 【注】若集合A的非空子集A1,A2,⋯,A n(n∈N+,n≥2)满足A i∩A j=∅(i≠j),A1∪A2∪⋯∪A n=A,则称A1,A2,⋯,A n是集合A的一个分划.(张雷供题)5. 若正整数a 、b 、c 满足a 2+b 2=c 2,则称(a ,b ,c )为勾股数组.求含有30的所有勾股数组. (杨春宏 供题)6. 如图2,过点P 引的切线P A 和割线PBC ,AC ⊥PP ,垂足为D .证明:AC 是△ABD 外接圆的切线.图2(吕建恒 供题) 7. 在△ABC 中,证明:11+ccs 2A+ccs 2A +11+ccs 2A+ccs 2C +11+ccs 2C+ccs 2A ≤2.(安振平 供题) 8. 已知n 是正整数,实数x 满足�1−|2−⋯|(n −1)−|n −x ||⋯|�=x .求x 的值. (张利民供题)P2012年北方数学奥林匹克1.如图1,在△ABC中,∠C=90°,I是内心.直线BI交AC于D,作DE平行于AI交BC于E,直线EI交AB于F.证明:DF垂直于AI.图12.正整数x1,x2,⋯,x n(n∈ℕ+),满足x12+x22+⋯+x n2=111,求S=x1+x2+⋯+x n n的最大可能值.3.设S={x|x=a2+ab+b2,a,b∈ℤ}.求证:(1)若m∈S,3|m,则3m∈S;(2)若m,n∈S,则m⋅n∈S.4.平面上有n(n≥4)条直线,对于直线a,b,在余下的n-2条直线中,如果至少存在两条直线与直线a,b都相交,则称直线a,b是相合的直线对,否则称其是相离的直线对.若n条直线中相合直线对的个数比相离直线对的个数多2012.求n的最小可能值(直线对中的两条直线不计顺序).5.已知数列{a n}:a0=0,a n=1a n−1−2,n∈ℕ+,在数列{a n}中任意取定一项a k,构造数列{b n}:b0=a k,b n=2b n−1+1b n−1,n∈ℕ+.试判断数列{b n}是有限数列还是无穷数列?并给出证明.6.设n是正整数,证明�1+13��1+132�⋯�1+13n�<2.7.如图2在五边形ABCDE中,BC=DE,CD平行于BE,AB>AE,AA AA,求证:AC平分线段BE.若∠AAC=∠CAD,且图28.设p是奇素数,如果存在正整数a使p!|a p+1,证明:(1)�a+1,a p+1a+1�=p.(2)a p+1a+1没有小于p的素因子.p!|a+1.。
2020最新奥数 第十三届地方复赛9年级B卷答案

九年级复赛B 卷答案一、选择题。
1.A2.D3.B4.A5.C6.B7.B8.B9.B 10.D3.B ∵1>cos6°=sin84°>sin45°,cot3°=tan87°>tan45°=1,∴sin45°<cos6°<tan45°<cot3°。
B 成立。
4.A 俯视图如下,最少有6个这样的正方体组成。
5.C 由于1+2+3+4=10,显然有4行台球在框内。
因此与框的任一边相接触的球数是4。
设台球的半径是r 毫米。
设从框角到与球的最近接触点的距离是x 毫米。
由图可知x =3r ,框的一边的长度是(6r +2x )毫米,即(6+23)r 毫米,这样,3(6+23)r =738,r =)326(3738+=33123+。
6.B 如图,CO =42,C 'O =22,由位似的定义可知,'AO AO =O C CO '=2,所以'AD AD =2,OD DO '=2,A 'D '=1,OD '=2,A '的坐标为(2,-1)。
7.B 用十进制表示:10×11=110,110=16×6+14转化成十六进制为6E 。
8.B 抛物线图象开口向上a >0,对称轴-a b 2=-21,得b =a ,所以方程ax 2+bx +c =0的两根之和-ab =-1<0,①错误。
当x =0时,c <0,所以a +b >c ,②正确。
当x =-1时,a -b +c <0,③正确。
当x =-2时,y =4a -2b +c<0,④正确。
正确的个数为3个。
9.B 依题意,设3x 2-4x =t ,则原方程化为(t -1)(t -5)=12,变形为t 2-6t -7=0,解得t =7或-1∴3x 2-4x =7或3x 2-4x =-1,解得,x =37或x =-1或31或1∵m 、n 是方程的两根,且m 、n 、2分别为三角形三边的边长,∴可能组合有37、1、2,那么三角形的周长只可能为316。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
BB第13届中国北方数学奥林匹克试题及解析(提高班)1.已知数列{}n a 满足()31221211,,2,,kk k nn n a e a e eaa an n Z k R -++-++===≥∈∈,求20171i i a =∏解:对12211kk k n n n ea a a -++-=两边同时取对数得()()()()111112ln ln 2ln 1ln 21ln 21ln n n n n n n k k a a k a a k a k a +----++=+⇒+=++-+ 设()()111ln 222n n n n n b a b k b kb n +-=+⇒=+-≥()()11222n n n n b b k b b n +-⇒-=-≥又211121ln 1ln 2,1ln 2nn n n b a e b a a e-=+=+==+=⇒=记()20172017201820191121is i i i S a e e -===-⇒==∑∏2.在ABC ∆中,D 为BC 的中点,,E F 分别为,AB AC 上的点,且DE DF =, 证明:AE AF BE CF EDF BAC +=+⇔∠=∠证明:如图,取,AB AC 的中点,M N , 延长DM 至点P ,使得MP MA = 联结,,EP MN DN一方面,若AE AF BE CF EM FN +=+⇒= 则由,PME MAN DNF MP MA DN ∠=∠=∠== 所以:PME DNF ∆∆≌所以:,PE DF DE NDF MPE PDE ==∠=∠=∠ 所以:EDF MND BAC ∠=∠=∠又因为:若EDF BAC MDE NDF ∠=∠⇒∠=∠ 由正弦定理得sin sin sin sin EM DE DF FNMDE DME DNF NDF===∠∠∠∠所以:EM FN AE AF BE CF =⇒+=+3.记Q 为1,2,,100L 的若干个排列组成的集合,且满足对于任意的1,100,,a b a b ≤≤≠至多存在一个Q σ∈使得在σ中a 的下一个数恰为b ;求集合Q 的元素个数的最大值解:首先,假设||101Q ≥。
若在某个排列中,x y 连续出现,则称(),x y 为一个“片段”。
由于每个排列恰有99个片段,于是,集合Q 中共有9910199999⨯=个片段;而不同的片段只有100999900⨯=个,,由抽屉原理,知存在一个片段在集合Q 中出现至少两次,矛盾, 从而, ||100Q ≤其次,令(1,100,2,99,,50,51)(099),i i i i i i i i σ=++++⋯++≤≤其中,所有元素均按模100处理,{|099}i Q i σ=≤≤;则对于()()00199,1x x x σσ≤≤+-不重复地取遍模100的除0外的完全剩余系, 故对a b ≠,可唯一找到199k ≤≤,使得()()()001mod100k k b a σσ+-≡- 然后,可找到唯一适当的i ,使得()i k a σ=,从而,此集合Q 满足要求。
综上,,Q 的最大值为1004.已知3(),n n Z n +≥∈个两两互素的正整数12,,,n a a a L 满足:可以适当添加+“”或“-”使它们的代数和为0;问:是否存在一组正整数12,,,n b b b ⋯ (允许相同),使得对任意正整数1122,,,,n n k b ka b ka b ka +++L 两两互素.解:(1)当4n >时(i )若12,,,n b b b ⋯中有两个偶数,则当k 为偶数时,1122,,,n n b ka b ka b ka +++L 中有两项同为偶数,不互素(ii )若12,,,n b b b ⋯中至多有一个偶数,则其中至少有三个奇数,设123,,b b b 为奇数,考虑123,,a a a ,由题设其中至少有两个奇数,不妨设12,a a 为奇数,则当k 为奇数时,1122,b ka b ka ++同为偶数,不互素.综上,4n ≥不存在(2)当3n =时,由题设,不妨设123a a a +=,注意到()12,1a a =由裴蜀定理,知存在整数,x y 使得121a x a y +=, 不妨设0x y >>,令12312,,b y b x b b b =-==+,则()()1221233221211211a b a b a b a b a b b a b b -=⇒-=+-+=-()()31131211121a b a b a a b a b b -=+-+=-所以:()()()()1222113111331,1a b a k a b a k a b a k a b a k +-+=+-+=- 故112233,,b ka b ka b a k +++两两互素。
所以,3n =时,这样的整数存在。
5.已知正六边形ABCDEF 边长为a ,两个动点,M N 分别在边,BC DE 上运动,且满足60MAN ∠=o, 证明:AM AN BM DN ⋅-⋅恒为定值.证明:如图,延长DC ,分别与,AB AM 的延长线交于点,P Q ,联结,AC AE 由正六边形的性质易知:60CAE MAN ∠==∠o,90,3,CAQ EAN ACQ AEN AC AE a CP a ⇒∠=∠∠=∠====oCAQ EAN ∴∆∆≌,,DN a EN a CQ PQ AM AN BM DN AM AQ BM PQ =-=-=⋅-⋅=⋅-⋅记:CAQ θ∠=,在ACM ∆中,由正弦定理得()()()333sin sin sin 30sin 302sin 30sin 30CM AM a a a AM CM θθ==⇒==+++o 所以:()()()sin 303cos 3sin 302sin 30BM a CM a a θθθθθθ+=-==++o o o在ACQ ∆中,注意到33sin cos 3sin 3tan a a AQ CQ a PQ a CQ θθθθ-====-= 则()()()223cos 32sin 30cos a AM AQ BM PQ θθθθ-⋅-⋅=+⋅o而()()2223cos 33cos 3sin 3cos θθθθθθ-=-+-⋅()()2cos cos 34cos sin 30θθθθθ==⋅+o所以22AM AN BM DN AM AQ BM PQ a ⋅-⋅=⋅-⋅=(定值),有6.定义()r S n 为n 在()1r r >进制下的数码和,例如()3381102=, ()33811024S =+++=;证明: (1)对于任意2r >,存在素数p ,使得对任意正整数n ,有()()mod r S n n p ≡ (2)对于任意1r >及素数p ,存在无穷多个正整数n 满足()()mod r S m n p ≡证明:(1)由2r >,知11r ->,从而,1r -有素国子,取1r -任一素因子p ,于是,()1mod r p ≡ 任取11()s s n a a a -=L ,在模p 意义下有()11111()ssk s s r k k r k k n a a a ra a S n --====≡=∑∑L ,即()()mod r S n n p ≡;(2)设p 的r 进制表示为11()k k r p a a a -=L , 令()()1110p kir k k i n prS n p a a a --==⇒=+++∑L ,所以()||p n p S n 且所以:存在无穷多个正整数n 满足()()mod r S n n p ≡7.给定正整数()1n n >,n 个实数12,,,n x x x L 满足[]12,,,0,n x x x n ∈L ,且()()()1212n n x x x n x n x n x =---L L ;试确定12n y x x x =+++L 的最大值.解:最大值为2n n -令(1,2,,)kk x y k n n ==⋯,于是[]()110,1,1n nk k k k k y y y ==∈=-∏∏ 若存在0k y =,则11nkk yn =≤-∏若对任意的1k n ≤≤,有01k k y y >⇒<令()1,2,,1k k k y z k n y ==⋯-于是,1kk k z y z =+,且11n k k z ==∏ 不妨设12n z z z ≤<⋯≤,则121z z ≤;所以:1212113121221111nnnk k k k k k kk z z z z z z y n z z z z z z ===++==+≤-+++++∑∑∑从而211nnkk k k y xn y n n ====≤-∑∑又当12,,,n x x x L 中恰有1n -个n ,1个为0时2y n n =-8.草原上生活着编号为1,2,,7L 的7只羊和编号为1,2,,2017L 的2017匹狼。
在该草原上有如下奇怪的规则:(1)定义()P n 为小于n 的素数个数,仅当()()mod7P i j ≡时,编号为i 的狼可以吃掉编号为j 羊(也可以不吃)(2)若编号为i 的狼吃了编号为j 的羊,则它会立刻变成编号为j 的羊(3)每匹狼在确保不会被吃的前提下都非常想体验作为一只羊的生活。
假设每匹狼都很聪明,求最后草原上会剩下多少匹狼?解:首先,考虑有1只羊和n 匹狼且所有狼均可以吃这只羊的情形: 当1n =时,这匹狼当然会把羊吃掉,不用担心自己变成羊后会被吃;当2n =时,这两匹狼均不敢吃羊,否则,会在变成羊之后被另外一匹狼吃掉;当3n =时,这三匹狼均想吃这只羊,因为即使自己变成羊,由2n =情形时的推论,另外两匹狼不敢吃自己;设当2n k =时,所有的狼均不敢吃羊,21n k =+时,所有的狼均想吃羊当22n k =+时,若某匹狼吃了羊,由21n k =+的推论,它会立刻被某匹狼吃掉,故22n k =+时所有的狼均不敢吃羊;当23n k =+时,若某匹狼吃了羊,由23n k =+的推论,,其它的狼均不敢吃自己,故23n k =+时所有的狼均想吃羊;由数学归纳法,知n 为奇数时,所有的狼均想吃羊,n 为妈数时,所有的狼均不敢吃羊;(1) 其次,记集合{}()(){}1,2,,2017,|mod7k S A n S P n k =⋯=∈≡,其中,1,2,,7,k =⋯⋯并约定以||A 表示集合A 的元素个数。
由前面的论述,只需考虑||k A 的奇偶性即可。
设不超过2017的所有素数为12,,,2017m p p p =L ,则满足()(),,P n k k m n S =∈的n 为11,2,,k k k p p p +++L 共1k k p p +-个当1k >时,||k A 为偶数; 当1k =时,1||A 为奇数;所以:1||A 为奇数,()||2k A k ≥为偶数; 由结论(1),知最后草原上会剩余2016匹狼.。
