最优投资组合实验共25页
最优投资组合模型课件

最优投资组合模型
1
教师信息
• 教师:张晓黎 • 电子信箱:
• 办公室:学院楼B420 • 电话:
最优投资组合模型
2
学习目标与学习重点
• 学习内容
• 多目标规划 • 最优投资组合模型
• 马克维茨投资组合模型 • 风险厌恶度模型
• Excel学习重点
• 多目标规划操作 • 协方差函数、转置函数 • 数组区域结果计算
• 收益率协方差、平均收益率区域计算方法同前
• 投资组合比例合计、投资组合收益率、风险计算方法同前
最优投资组合模型
4
示例1-多目标规划
• 某公司生产和销售两种产品,两种产品各生产一个单位需要 3工时和7工时,用电量4千瓦和5千瓦,需要原材料9公斤和 4公斤。公司可提供的工时为300,可提供的用电量为250千 瓦,可提供的原材料为420公斤。两种产品的单位利润分别 为12元和15元。假设两种产品各生产10个单位,试在Excel 中建立产品组合线性规划模型,用规划求解工具求解两种产 品的最优生产量,使总利润最大,总工时最少;把规划求解 参数保存在单元格中。
最优投资组合模型
10
示例2-步骤 • 步1-利用covar函数或者数据分析-协方差,计算项目间 的收益率协方差,得到收益率协方差区域数据.
步2-利用average函数计算各项目的平均收益率,设定初 始投资比例,计算投资比例合计
最优投资组合模型
11
示例2-步骤 • 步3-计算投资组合的收益率和风险(方差)。 • 利用sumproduct函数,根据各项目平均收益率和投资比例计算投资组合的 收益率。 • 根据风险计算公式,计算投资组合的风险 • 选中N4:P6区域,在函数编辑框输入“=TRANSPOSE(J10:L10)*J10:L10” • 同时按下CTRL+SHIFT+ENTER3个键,计算投资i和投资j在投资组合中的权重 • 利用sumproduct函数,根据上述计算结果和项目间的协方差矩阵计算投资组合 的风险(方差)
实验4:多种风险资产与无风险资产的最优投资组合决策

实验四:无风险资产与多种风险型资产最优投资组合的模型分析 一、实验目的通过上机实验,使学生充分理解Excel 软件系统管理和基本原理,掌握多资产投资组合优化的Excel 应用。
二、预备知识(一)相关的计算机知识: Windows 操作系统的常用操作;数据库的基础知识;Excel 软件的基本操作。
(二)实验理论预备知识现代资产组合理论发端于Markowitz(1952)提出的关于投资组合的理论。
该理论假设投资者只关心金融资产(组合)收益的均值(期望收益)和方差,在一定方差下追求尽可能高的期望收益,或者在一定的期望水平上尽可能降低投资收益的方差。
投资者的效用是关于投资组合的期望回报率和方差的函数,理性的投资者通过选择有效地投资组合以实现期望效用最大。
该理论第一次将统计学中期望与方差的概念引入投资组合的研究,提出用资产收益率的期望来衡量预期收益,用资产预期收益的标准差来度量风险的思想。
1、理论假设(Ⅰ)市场上存在n ≥2种风险资产,资产的收益率服从多元正态分布,允许卖空行为的存在。
{}12(,,,)T n ωωωωω=,代表投资到这n 种资产上的财富(投资资金)相对份额,它是n 维列向量,有11=∑=ni i ω,允许0<i ω,即卖空不受限制。
(Ⅱ) 用e 表示所有由n 种风险资产的期望收益率组成的列向量。
12(,,,)T n e R R R R == (1)p r 表示资产组合的收益率,)(p r E 和)(p r σ分别为资产组合p 的期望收益率和收益率标准差。
∑=⋅=⋅=ni ii Tp e r E 1)(μωω (2)(Ⅲ)假设n 种资产的收益是非共线性的(其经济意义为:没有任何一种资产的期望收益率可以通过其他资产的线性组合来得到,它们的期望收益是线性独立的。
)。
这样它们的方差-协方差矩阵可以表示为:⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=nn n n n n Q σσσσσσσσσ212222111211 (3)由于总是假定非负的总体方差,它还必须是一个正定矩阵,即对于任何非0的n 维列向量a ,都有0T a Qa >。
最优投资组合选择PPT课件

2 p
p2 M 2
因此,对于分散好的投资组合,就是要最小化 p
第6页/共39页
计算最优投资组合权重
计算出股票期望收益和风险水平后,就可以用PROC LP来找出在 最大可接受风险的前提下收益最大的投资组合权。该线性规划问题为以下 形式:
最大化:c'x 条件:Ax b 其中:li xi ui
•var col1 col2 col3;
•title 'Markowitz 模型';
•q u i t ;
第17页/共39页
计算股票投资组合的平均收益
•一 般 说 来 , 两 种 股 票 投 资 组 合 的 收 益 用 以 下 方 法 计 算 :
Rp x R1 (1 x) R2
/*数据集COV_OUTl1中,增加变量X,表示权重。例中,X从0到l, 步长为0.05。 */ data cov_out2(drop=_name_); set cov_out1; if _type_ ne 'MEAN' then delete; do x=0 to 1 by .05; output; end; rename col1=r000002 col2=r000007 col3=r000011; label x='投资组合的权重'; run;
•proc print data=lp_out4a; •title '整数规划'; •title2 '购买手数'; •r u n ; •注意,在PROC LP输出中,LOTS约束条件(限制投资金 额 ) 是 一 个 最 大 值 为 $第1 0130页0/0共03的9页不 等 式 约 束 。 在 这 $ 1 0 0 0 0 0
投资组合构建PPT课件

确立投资哲学的目的是要通过某种科学的过程和方法来提高组合投资的规范化程度,以减少投 资组合构建的随意性,从而使投资收益建立在可靠的基础之上.
马考维茨模型为构建能实现最有效这一目标的投资组 合提供了一种明确的修炼过程,这种过程被称为最优 化。
最优化过程已经被广泛地应用于大型计划的投资者确 定投资组合中各主要资产类型的最佳组合的活动中, 这种过程通常被称做资产配置。
实际中可考虑的主要资产类型是有限的,所以最优化
过程是可操作的。
第6页/共55页
第三章 投资组合构建
投资组合的构建过程 首先,需要界定适合的 证券选择范围。 主要资产类型:普通股票、债券和货币市场工具等 新 兴 资 产 类 型 : 国 际 股 票 、 非 美 元 债 券 、 房 地 产 和 风 险 资 本 等 全 球 性 资 产 进 行 投 资 所 形 成 投 资 组 合 的 价 值 很 大 程 度 上 取 于 这 些 所 选 证 券 的 质 量 。
第3页/共55页
第三章 投资组合构建
确立投资哲学首先要正确认识市场特征和自身条件. 所谓市场特征通常包括:
市场有效程度 市场定价机制 市场参与人与竞争特征 市场交易规则与投资限制等.
第4页/共55页
第三章 投资组合构建
所谓自身条件主要是指投资基金委托人的意志、来自于政府或有关机构的约束、研究与管理 能力等.
第8页/共55页
爱尔兰 智利 以色利 泰国 奥地利 波兰 印度尼西亚 新西兰 菲律宾 匈牙利 捷克 埃及 秘鲁 巴基斯坦身 委内瑞拉 哥伦比亚 摩洛哥 爱沙尼亚 克罗地亚 斯洛文尼亚 斯里兰卡 毛里求斯 立陶宛 黎巴嫩 斯洛伐克 约旦 罗马尼亚 拉托维亚
投资学报告---最优投资组合.

实验报告(文经管艺体类)课程名称:投资学原理及应用课程代码: 1207949 学院(直属系):工商管理学院年级/专业/班:2013级财务管理学生姓名:学号:实验总成绩:任课教师:开课学院:工商管理学院证券组合投资分析实验报告班级: 财务管理1班(一)、宏观经济分析2015年,制造业在结构调整的状态下继续出清过剩产能,工业生产总值的增幅将继续维持下行趋势,GDP等经济总量指标的增速也会相应放缓。
于此同时,服务业尤其是信息产业和智能技术相关的生产性服务业在国民经济中的比重将继续上升,产业结构将有所优化。
从增长动力来看,随着房地产增速的放缓和政府部门淡化直接投资者的角色,投资对国民经济增长的贡献度会有所下降,而随着劳动力供不应求状况的持续、产业工人工资收入的增长以及政府民生支出的增加,消费将保持较为稳定的增长,成为2015年经济增长的主要动力。
1.增长动力切换消费成为中国经济的引擎2015年是经济结构调整和改革全面深化的转型期。
随着房地产市场进入下行周期,投资拉动的增长时代终结,就业繁荣和居民收入增加构成经济增长的基础。
从人口结构数据来看,40-50岁这个收入和消费能力最强的年龄段人口占比达到18.5%,达到巅峰水平,收入所支持的社会消费水平将因此有所上升,此外,随着社会保障机制的改革,政府在民生支出上的增加,居民的预防性储蓄比率会相应降低,由预期所支撑的当前消费支出也会相应有所提高。
2.货币政策依然保持稳健和弹性从政策的制定基础来看,2015下调准备金率存在较大可能性。
随着人民币汇率双向波动的特征逐步确立,人民银行逐渐减轻对人民币汇率的干预力度,外汇占款不再是我国基础货币供应的基础,适度降低准备金率的环境也趋于成熟。
为了改善中小企业融资难融资贵的问题,2014年11月下旬,国务院出台的新融十条将其他金融机构的同业存款纳入一般存款统计口径以放松贷比考核,根据不同银行的存贷比现状,该项政策在理论上可释放近2-3万亿的信贷规模,但同业存款成本较高,该政策只能放松信贷规模的约束,对于降低融资成本并无直接助益。
投资学之最优投资组合与有效边界PPT59页课件

*
*
命题1:完全正相关的两种资产构成的机会集合是一条直线。 证明:由资产组合的计算公式可得
*
两种资产组合(完全正相关),当权重wD从1减少到0时可以得到一条直线,该直线就构成了两种资产完全正相关的机会集合(假定不允许买空卖空)。
收益 E(rp)
风险σp
D
E
*
两种完全负相关资产的可行集
两种资产完全负相关,即ρDE =-1,则有
*
4.4多个风险资产组合的最优资产组合求解
见Excel文件。
*
4.5马科维茨的资产组合选择模型
均值-方差(Mean-variance)模型是由Harry Markowitz于1952年建立的,其目的是寻找投资组合的有效边界。通过期望收益和方差来评价组合,投资者是理性的:害怕风险和收益多多益善。 因此,根据投资组合比较的占优原则,这可以转化为一个优化问题,即 (1)给定收益的条件下,风险最小化 (2)给定风险的条件下,收益最大化
*
*
*
两基金分离定理的意义
定理的前提:两基金(有效资产组合)的期望收益是不同的,即两基金分离。 金融含义:若有两家基金都投资于风险资产,且经营良好(即达到有效边界),则按一定比例投资于该两基金,可达到投资于其他基金的同样结果。这就方便了投资者的选择。 CAL、CML实际上是在有风险资产组合和无风险资产组合之间又进行了一次两基金分离。此时投资者仅需确定一个有风险组合,即可达到各种风险收益水准的组合。资本配置更加方便。
*
资产组合理论的缺点
当证券的数量较多时,计算量非常大,使模型应用受到限制。 均值方差分析的成立条件:收益正态分布或二次型效用函数
*
4.6不允许卖空的投资组合策略模型计算
第四章 最优投资组合(实际)(证券投资学-北大,杨云红)

期望值的估计方法
样本均值
在如下条件下合理
股票指标保持不变 将来的回报率和过去的回报率由同一个模型产生
否则,需要根据现在的环境调整 寻找现在可以观测,可以预测将来回报率的变量 一般不容易找到 已有的几个例子:红利收益、红利价格比、市盈率、一些利 率变量 回归
寻找特殊变量来预测回报率
第四章 最优ห้องสมุดไป่ตู้资组合(实际)
Estimation of the inputs A computer exercise using real data Implementation problem and some solutions
Estimation results in uncertainty Shrinkage and Bayesian inference to deal with uncertainty Imposing restrictions.
Theory is good
How much data should we use to estimate beta?
The further we go back in time, the higher the statistical precision of the estimate, but the bigger the possibility of introducing some old data bias. Unlike with sample averages, however, here it often pays to use more frequent data. For example, whereas the 95% confidence interval for GM's beta based on the monthly data is 0.65 to 1.57, this interval based on weekly data is tighter, 0.69 to 1.08. GM's beta estimated using weekly data is 0.88.
最优投资组合选择

实验软件
Wind, Excel
PART 03
实验方案设计
选择5只股票和1个无风险资产,绘制风险资产集的最小方差边界、有效边界及最优资本配置线,寻
找最优风险资产组合。
从 上 证50 中 选 择5 只 股 票,计算每只股票
2016.11.30-2019.11.29 每天的收益率,无风险 资产收益率设定为3.5%。
伊利股份 0.000070 0.000121 0.000208 0.000424 0.000134
海螺水泥 0.000092 0.000210 0.000123 0.000134 0.000421
PART 04
实验过程(实验步骤、记录、数据、分析)
求解有效边界的初始设置条件
无风险利率(R007) 日无风险利率 wj w1 w2 w3 w4 w5 sum
'600000.SH' H'
H'
H'
H'
浦发银行
三一重工 恒瑞医药 伊利股份 海螺水泥
2016/11/30
2016/12/1
-0.06% -0.62% 0.02% 0.96% 3.41%
2016/12/2
-0.29% -0.93% 0.36% -3.83% -0.75%
2016/12/5
1.16% -2.69% 0.11% -6.39% -1.73%
计算每只股票期 间3年的日平均 收益率。
根据每只股票的收益率 序列计算风险资产的样 本方差和协方差矩阵。
对这5只股票赋以初始权重, 计算出风险资产组合的期望 收益率Mean、标准差SD, 以及与无风险资产相连的资 本 配 置 线 的 斜 率 ( Sharp Ratio)。
投资学之最优投资组合与有效边界.pptx

有效组合 E
F C
B 可行组合,但非有效
D A
0.40
0.60Leabharlann 0.80组合标准差
1.00
1.20
13
命题1:完全正相关的两种资产构成的机会集 合是一条直线。 证明:由资产组合的计算公式可得
EP(rP
) wD
wD D
E
(rD )
wE E
wE
E
(rE
)
(1) ( 2)
wD wE 1
( 3)
➢ 资产组合的机会集合或可行集合(Portfolio opportunity set, Feasible set),即资产可构造 出的所有组合的期望收益和标准差。
➢ 有效组合点(Efficient portfolio ):给定风险 水平下的具有最高收益的组合或者给定收益水 平下具有最小风险的组合。每一个组合代表 E(r)和σ空间中的一个点。
则由y份风险资产和(1 y)份无风险资产组成的新组合C :
E(rC ) yE(rP ) (1 y)rf rf y[E(rP ) rf ]
C y P
E(rC ) rf
[E(rP ) rf
P
]
C
由该式得到图4 1可行投资组合(investment opportunity set)
4最优投资组合与有效边界
投资组合优化的五种形式 1C=F+P 2P=D+E 3C=F+D+E 4P=S1+S2+…+Sn 5C=F+ 4P=S1+S2+…+Sn
1
4.1 单一风险资产P与单一无风险资产 F的资产组合 C
记风险资产组合P的期望收益率为E
《最优投资组合理论》课件

资本资产定价模型(CAPM)
总结词
资本资产定价模型(CAPM)是一种用于评估风险和预期收益之间关系的投资组合理论 。
详细描述
CAPM认为资产的预期收益由两部分组成:无风险收益和市场风险溢价的线性组合。它 为投资者提供了评估风险和预期收益之间关系的方法,并帮助投资者理解市场对风险资
产的需求和供给。
套利定价理论(APT)
05 最优投资组合的实证分析
数据来源与预处理
数据来源
主要来自各大证券交易所、金融数据 库以及公开市场数据。
数据预处理
清洗数据、处理缺失值、异常值和重 复数据,确保数据准确性和完整性。
模型参数选择与调整
参数选择
根据投资目标和风险偏好,选择合适的 模型参数,如预期收益率、风险系数等 。
VS
参数调整
通过机器学习算法对市场数据进行实时分析,提高交易决策的准确 性和效率,降低交易成本。
研究动态最优投资组合策略
01
研究不同市场环境下的动态最优投资组合策 略
根据市场环境的变化,动态调整投资组合的配置比例究
根据投资者的风险偏好和收益目标,研究如何动态调整投 资组合以更好地满足投资者需求。
根据市场变化和投资组合表现,适时调整 模型参数,以实现最优投资组合。
模型评估与结果分析
模型评估
通过回测、蒙特卡洛模拟等方法评估模型的 有效性和稳健性。
结果分析
分析投资组合的实际表现与预期目标的差异 ,总结经验教训,优化投资策略。
06 最优投资组合理论的未来 研究方向
考虑市场非完全有效性的影响
投资者情绪对投资组合的影响
随着计算机技术的发展,现代投资组 合理论开始广泛应用,通过复杂的数 学模型和算法来优化投资组合。
最优投资组合安例

中国石化宝钢股份民生银行第45周0.096270.1320260.08742第44周-0.04621-0.04557-0.01435第43周0.0953640.0422340.045238第42周0.0244220.0056980.054305第41周0.0296770.0744850.001441第40周0.1-0.036530.004231第39周0.0192590.1555150.049231第38周0.0306280.0052630.120482第37周0.0604580.083682-0.01709第36周0.0912410.0610330.049911第35周-0.00367-0.013920.001709第34周-0.194120.026190.087199第33周0.0944630.0048430.033932第32周-0.00648-0.018820.050505第31周0.0557430.0343140.089912第30周0.003407-0.012140.049065第29周0.026087-0.011960.014151第28周0.0035090.0072820.03632第27周-0.039050.0122550.009732第26周-0.036860.01737-0.00246第25周0.052632-0.00247-0.04502第24周0.0119660.0049020.021583第23周-0.06879-0.00966-0.03917第22周-0.05692-0.028240.016393第21周-0.04012-0.022730.069048第20周-0.004370.0530120.029484第19周0.036697-0.004830.048718第18周0.115646-0.01651-0.00501第17周0.02109-0.04719-0.02975第16周0.071845-0.049890.009112第15周-0.01161-0.08758-0.05727第14周-0.009710.1224020.032037第13周-0.020990.0213780.110276第12周0.023438-0.04091-0.03283第11周0.0081630.004587-0.28319第10周-0.047170.007109-0.00354第9周0.0076190.0095010.072797第8周-0.009290.0023750.001934第7周-0.019310.0072120.057613第6周0.02-0.009460.024845第5周0.101952-0.00946-0.05133第4周-0.01706-0.03890.04158第3周0.0034480.0583940.079186第2周0.16-0.01442-0.02845第1周0.0460250.0147060.072816统计量计算单项期望值0.0173180.0099240.019172单项方差0.0036550.0023120.004011标准方差0.0604540.0480840.063336相关系数中国石化宝钢股份民生银行中国石化10.0932910.231708宝钢股份0.09329110.283083民生银行0.2317080.2830831模型决策变量股票1股票2债券投资比例之和投资比例0.3544670.3800830.265451 =1投资比例的平方0.1256470.1444630.070464总回报率期望值实际值要求值0.015〉=0.015总回报率方差0.001385总回报率标准差0.037219。
《最优投资组合理论》PPT课件

VCVoa~rv2~r,1~r1
Co~rv1,~r2 Va~r2
C Coo~r~rvv12,,~r~rN N
Co~rvN,~r1 Co~rvN,~r2 Va~r2
– 证券组合的期望收益率和方差 – 给定证券组合 1,2, ,NT – 期望回报率 – 方差 – 当证券的种类越来越多时,证券组合回报率的
证券组合选择问题
• 通过分析资本市场,一个中心的事实是,风 险资产的回报平均来说高于无风险资产 的回报,而且回报越高,风险越大.
• One interesting consequence of having these two conflicting objectives is that the investor should diversify by purchasing not just one security but
– 〔2〕利用期末价格计算证券组合的期望回报率
– 证券 在证券组合 每股的期末
– 名称 中的股数 预期价值 期末预期价值
总的
– A 100 46.48元 46.48元 100=4,648元
– B 200 43.61元 43.61元 200=8,722元
– C 100 76.14元 76.14元 100=7,614元
• 价格与回报率之间是一一决定的关系,给 定价格,就可算出回报率,反过来,给出了回 报率,就可决定价格.
• 在以下的章节里,通常以回报率为研究对 象,并假设,字母〔或者字母上加一波浪线〕 表示随机变量,字母上加一横线表示期望 值.
• 由于违约、通货膨胀、利率风险、再投 资风险等不确定因素,证券市场并不存在 绝对无风险的证券.
rP
G
=-1
=-0.1
投资组合实验报告

投资组合实验报告摘要:本实验旨在通过构建和分析不同投资组合来研究投资组合的效果和风险。
我们选择了一组不同资产类别的股票和债券,通过分配不同权重来构建投资组合,并评估其回报率和风险水平。
实验结果显示,合理的资产配置可以实现较高的回报并控制风险。
1. 引言:投资组合是将资金分配到不同资产类别的一种策略,旨在实现最佳的回报和风险平衡。
通过分散投资于不同的资产,投资者可以降低风险并提高回报的机会。
本实验旨在通过构建投资组合并分析其绩效来探索资产配置对投资结果的影响。
2. 方法:2.1 数据收集:从可靠的金融数据源收集了一段时间的股票和债券价格数据,并计算了每个资产的日回报率。
2.2 投资组合构建:选择了多个股票和债券作为投资组合的资产,根据不同的权重分配资金。
权重决定了每个资产在投资组合中的占比。
2.3 绩效指标计算:计算投资组合的综合回报率、标准差(风险)和夏普比率等绩效指标。
夏普比率衡量了每单位风险所获得的超额回报。
3. 实验结果:通过对不同权重的投资组合进行分析,我们得出以下结论:-合理的资产配置可以实现更好的绩效。
通过在股票和债券之间分配资金,可以获得更高的回报并降低整体风险。
-不同权重的投资组合对绩效和风险有显著影响。
高权重的股票投资组合可能带来更高的回报,但也伴随着更高的风险。
相比之下,高权重的债券投资组合可能带来较低的回报,但风险较低。
-夏普比率是评估投资组合绩效的重要指标。
较高的夏普比率表示在承担相同风险水平下,投资组合获得了更高的回报。
4. 讨论与结论:本实验结果表明,投资组合的资产配置对绩效和风险有重要影响。
通过分散投资于不同资产类别,投资者可以实现更好的回报和风险控制。
然而,投资组合的选择应根据投资者的风险承受能力、投资目标和时间期限进行定制。
此外,投资组合管理需要定期监测和再平衡。
市场条件的变化可能导致资产权重偏离原始配置,因此需要定期调整以恢复目标配置。
这可以通过定期审查投资组合绩效并进行必要的调整来实现。
《最优投资组合理论》课件

投资组合的实现
实施方式
投资组合可以通过交易所、基金 等不同的实施方式来进行买卖和 持有。
交易成本
交易成本是投资组合实施的一个 重要考虑因素,包括佣金、印花 税等。
维护和更新
投资组合需要定期维护和更新, 以适应市场变化和投资目标的变 化。
投资组合优化的应用
风险控制
投资组合优化可以帮助投资者实现风险控制,减少投资组合的波动性。
最优投资组合理论基于现代投资组合理
约束条件
2
论 (MPT) 和资本资产定价模型 (CAPM) 等 经典理论。
投资组合优化需要考虑投资者所设定的
约束条件,如最大风险、最小回报等。
3
求解算法
通过数学模型和计算技术,可以求解最 优投资组合,例如线性规划和蒙特卡罗 模拟等方法。
风险和收益
投资组合的风险来源包括市场风险、系统风险和个别风险,可以通过波动率 等指标度量。 收益可以来自资本增值、股息和利息等,通常用年化回报率来度量。 投资组合的优化需要在风险和收益之间进行权衡,以实现最佳的投资结果。
资产分配
投资组合优化可以帮助投资者在不同资产之间分配资金,以实现最佳的资产配置。
期望收益与风险平衡
投资组合优化可以帮助投资者在追求高收益的同时,保持风险的可控范围内。
最优投资组合的挑战和限制
1 数据取样误差
投资组合优化的结果受限于输入数据的准确性和可靠性。
2 优化方法的局限性
不同的优化方法可能对不同的情况表现更为适用,没有一种方法适用于所有情况。
3 实施成本
投资组合优化需要付出一定的实施成本,包括时间、资源和人力等。
总结
最优投资组合理论的贡献
最优投资组合理论帮助投资者在风险和回报之间做 出明智的选择,提升投资效益。
最优投资组合实验
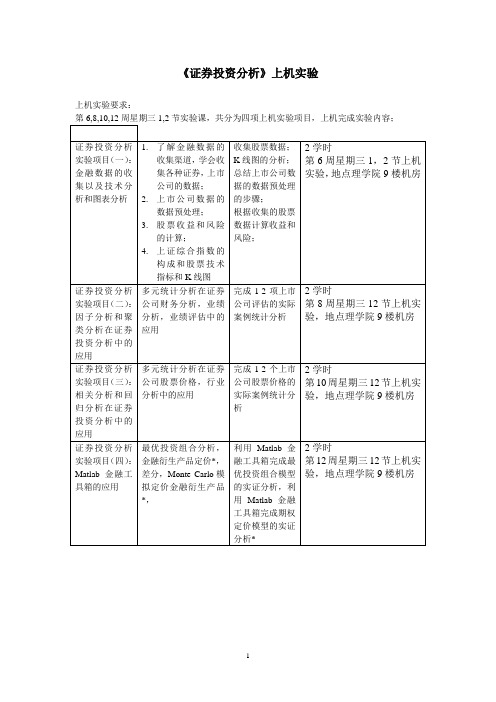
《证券投资分析》上机实验上机实验要求:第6,8,10,12周星期三1,2节实验课,共分为四项上机实验项目,上机完成实验内容;具体内容与步骤:(一)数据收集:3-5项股票的价格,上证指数(至少1年时间跨度),K线图,上市公司财务数据中国股市股票组合的适宜规模为5-10种股票为了达到组合风险充分分散的目的,随机股票组合大致需要9-13只股票,但是不同行业的股票组合只需要5-8只股票股票价格数据预处理与收益率的统计量的计算1 极端值的控制2 缺损值的处理3 周收益率的计算使用下面公式对原始数据进行处理:(1)(1)()it i t itit i t P P D r P ---+=其中:it r 为资产i 在第t 期的收益率;it P 、(1)i t P -分别为资产i 在第t 、t-1期的期末价格;it D 为资产i 在第t 期的红利;1,2,,t T = 。
1j jj js s r s +-=其中,j s 为上周末股价,1j s +为本周末股价 4各投资项目的数据特征运用MATLAB 或者Excel 软件中的mean(x)函数、std(x)函数和corrcoef(x)函数分别计算上面股票中的单项收益率期望值、单项收益率标准差以及各项目之间的相关系数上市公司评价数据预处理 1 极端值的控制所有上市公司所出的经营环境不尽相同,影响上市公司的基本素质、财务状况的不确定性因素也各有不同,如,地理位置、政府干预、生态环境等不确定因素。
为了避免这些不利因素的影响,所有上市公司的评价指标X 服从正态分布。
2 剔除不可比行业因素的影响因为上市公司各种行业都有,由于行业性质不同,导致了各种行业的财务指标也存在不同的特点,因此需要剔除行业之间不可比因素对财务指标的影响。
通过ij ij X X k '=-可以剔除行业之间的不可比因素,其中ij X 表示第i 家上市公司第j 项财务指标的观测值,k 是各上市公司第j 项财务指标的均值。
最优投资组合

Cov(Ri
,
Rj
)
T
1 1
t (Ri E (Ri ))(Rj E (Rj ))
确定协方差和相关系数
• 协方差的结果可能会因股票的波动方向不 同而发生变化,所以我们用相关系数来确 定两者的变动方向的联系
Corr (Ri , R j )
Cov(Ri , R j ) SD(Ri )SD(R j )
期望回报率
26% 6% 2%
投资组合
波动率
股票间的相关系数 英特尔 可口可乐 波尔实业
50%
1
0
0
25%
0
1
0
25%
0
0
1
多种股票构成的投资组合
股票从2只增加到3只,投资机会集随之扩大,有效边界就得以改进。
无风险储蓄和借款——无风险证 劵
• 考虑回报率为Rp的任意风险证劵投资组合, 如果将x比例的资金投资于风险证劵组合, 而将剩余(1-x)比例的资金投资于回报率为r 的无风险债券,则期望回报率为
股票
期望回报率
英特尔
26%
可口可乐
6%
波动率
50% 25%
股票见的相关系数
英特尔 可口可乐
1
0
0
1
风险与回报率:选择有效投资组
合
E R4060 xI E RI xc E RC
风险与回报率:选择有效投资组 合
相关系数的影响
风险与回报率:多种股票构成的
股票
英特尔 可口可乐 波尔实业
Cov(Ri , Rp ) Var(Rp )
计算投资组合的方差和波动率
• 了解不同投资项目之间的关系之后,我们 可以计算投资组合资深的方差和波动率
一文教你如何最优化投资组合

一文教你如何最优化投资组合最优投资组合建立——有约束条件的目标函数人们在构建一个量化组合时,需要三板斧的加持,即alpha信号,风险模型和优化器。
alpha信号刻画股票的预期收益率,它凝聚了投研人员的聪明才智,将他们对股票的研究判断封装成因子。
风险模型则代表股票的预期波动率,以及不同股票之间的相关程度。
而优化器,则涉及金融学中一个重要的基本模型。
这个模型就是均值方差模型,在1952年由Markowitz提出,开启了现代投资领域的大门。
它通过平衡组合的收益和风险,使量化投资得到了飞速发展。
优化器就是依照均值方差模型的理论设计出来的,它的作用是将alpha信号与风险模型作为输入,求解出最优的投资组合。
在求解组合的过程中,需要设定一个优化目标,标准的均值方差模型的优化目标是:但如很多理论模型一样,这个函数只适用于最简单的情形,忽略了实际情况可能要考虑的问题,例如交易成本。
除了上述目标函数之外,人们往往会需要设定一些约束条件来获得最优解。
常见的约束条件包括个股持仓比例、股票总仓位、行业偏离度、风格偏离度等,对每一个条件,我们都可以设置一个对应的上下限。
增加了约束条件后求解出来的最优投资组合x*,和没有约束条件的情况下的最优投资组合很可能会不一样。
在学术上这种现象称为Implementation inefficient,简单来说就是:alpha信号在有约束的情况下,没有得到完整的表达。
萝卜投资对约束条件的刻画业界通常使用Transfer Coefficient (TC)来刻画alpha信号表达的程度,如果没有约束,则TC=1。
但是这种方式无法精确衡量出每个约束条件如何限制了alpha信号的表达,也就是说它们无法精确衡量它们如何影响了最优投资组合x*。
萝卜投资开发了一套模型专门衡量约束条件带来的影响。
下面将会通过一个实例,从三个角度分别阐述。
我们以2019年7月26日这一天为例,选择个股的EPS作为因子。
为了方便起见,我们在沪深300投资域中,随机选择了10只股票,并且将它们中性化后形成alpha信号。
最优投资组合选择
091601005 091601011 091601012 091601009 091601024
姓名
曲婷婷 羊阳 施琇菁 吴梦楚 孙润
承担任务
策划 资料收集 撰写 多媒体制作 数据分析
最优投资组合选择
——案例分析
• 一、研究目的
运用统计学原理科学地为投资者分析选择最有效的投 资组合,帮助投资者以最小的风险获得较高的未来回报率, 从而获得最大的利润。
最优投资组合选择学号姓名承担任务091601005曲婷婷策划091601011资料收集091601012撰写091601009多媒体制作091601024数据分析案例分析一研究目的运用统计学原理科学地为投资者分析选择最有效的投资组合帮助投资者以最小的风险获得较高的未来回报率从而获得最大的利润
最优投资组合选择
二、统计方法
通过计算平均数测量概率的集中趋势,从而了解股票 投资的回报率,通过计算标准值测量概率的分散程度,从 而了解股票投资的风险。
三、分析
1、投资者遭受负的投资回报率的可能性分析 设事件A、B、C分别为股票组合X、Y、Z为负的投资 回报率。 依据X、Y、Z股票组合的回报率与概率分布情况得:
P(A)=0.1+0.05+0.03+0.1=0.19 P(B)=0.1+0.07+0.03=0.2 P(C)=0.07+0.05+0.03=0.15 因为P(B)>P(A)>P(C) 所以组合Y最有可能使投足者遭票组合的回报率与概率分布情况,运用 概率的相关公式得出以下数据:
X、Y、Z股票组合的回报率与概率分布
如数据所示,股票组合Z的平均数大于股票组合X的 平均数,即股票组合Z的收益大于股票组合X的收益;股 票组合Z的标准差小于股票组合X的标准差,即股票组合 Z的风险小于股票组合X的风险。
第6章 最优证券投资组合

最后讨论风险程度的改变对最优证券投资组合的 影响
➢ 考虑最优化问题的一阶条件,同时引入一个关于变 量a和y的二元函数g
g(a, y) u wrf ay rf y rf
➢ 我们可以证明,函数g是y的凹函数的充分条件是, 经济行为主体的相对风险厌恶系数是增函数,并且 小于或者等于1,而绝对风险厌恶系数是递减的。 如果风险证券的风险贴水是严格正值的,那么就意 味着当风险收益率的风险程度更大时,经济行为主 体对于风险证券的投资是递减的。
J
max
a2 ,,a j
E u
wrf
aj
j2
rj
rf
最优投资 a a1,, aJ 作为这个最优证券组 合 选择
问题的一个解得出。最优证券投资组合收益率为
J
ajrj
r j1
w
J
投资于无风险证券的财富量为 a1 w aj
➢类似结果同样适用于递增的和不变的相对风险 厌恶系数。
其次讨论收益率变动对最优证券投资组合的影响
无风险收益率变动对最优证券投资组合的影响
✓ 定理:如果一个经济行为主体是风险厌恶的,并且他 的绝对风险厌恶系数是递增的,如果这个经济行为主 体的最优证券投资组合对于风险证券的投资是正值的 并且风险贴水是正值的,那么他对风险证券的最优投 资a*对于无风险证券收益率的变动是严格递减的。
或者
wa
rf E u wrf a E u wrf a r
r rf rf
r rf r rf 2
可证明 wa 0
因此在设定的条件下,随着财富的增加,经济行为主
体投资于风险证券的价值将增加,风险证券是一种正 常商品。
最优股票投资组合本科生毕业设计

存档日期:存档编号:论文题目:摘要: 随着证券市场的发展,愈来愈多的风险资产可供人们选择,不同的风险资产有着不同的特点,让人们无从选择,证券市场上的风险与收益一直困扰着人们,本文从分散投资降低风险的角度,在马科维茨均值--方差理论的基础上,均衡风险与收益,找出最优的投资组合。
关键字:投资组合,风险,收益,最优。
绪论随着我国经济经济的飞速发展,居民的收入大幅度增加,生活条件也进一步改善,在保证日常必要消费及其他消费之外,还有很可观的资金留存,人们习惯性的喜欢把这部份资金存入银行,来保证资金的安全和获取一点利息收入。
随着居民收入的飞速增加,人们也不经意的发现此刻的物价水平也在飞速的增加,以前能买很多东西的钱此刻买不了几件东西,最明显的例子就是去一趟菜市场,篮子里没看买几样东西,身上的钱已经花的差不多了,人们在感慨“此刻的菜已经吃不起了”的时候,也开始注意到随着经济的发展,生活条件的提高,消费支出也在成倍的增加,看着刚拿得手的辛辛苦苦赚来的工资,盘算着接下来的开销,不由又深感无奈:这个月有无存下多少钱。
节约节约是我国的传统美德,人们舍不得吃舍不得穿,辛辛苦苦,兢兢业业,把省下来的钱存入银行,,等着碰到重要的时候再掏出来用。
眼看着这些年节衣缩食存下来的钱一天天的缩水,看在眼里,苦在心里。
这样下去实在是不行!可是这些钱不存银行能怎么办呢?高利贷,一种传统的牟取暴利的方式不由进入人们的脑海,人们把赚来的钱拿出去放高利贷,收入确实可观,尝到了甜头的人们加倍疯狂,把全数的积蓄,乃至向亲友老友借钱来放高利贷。
疯狂狂的结果往往是悲惨的下场,资金的断链,走投无路的债务人纷纷跑路,投入庞大的债主们损失惨重,乃至一贫如洗,走投无路,失望的债主选择了轻生来逃避。
惨重的事实,血的教训让人们警醒:高利贷真的不可取!证券交易市场的开放标志着我国资本市场的成立,在成立初期,人们由于对证券知识的缺乏和我国证券市场的不完善,法律的空白,致使股票市场出现极不稳定的现象,大涨大跌的情行让追求稳定的人们实在吃不消,更重要的是盲目的投资使得人们损失惨重。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《证券投资分析》上机实验上机实验要求:第6,8,10,12周星期三1,2节实验课,共分为四项上机实验项目,上机完成实验内容;具体内容与步骤:(一)数据收集:3-5项股票的价格,上证指数(至少1年时间跨度),K 线图,上市公司财务数据中国股市股票组合的适宜规模为5-10种股票为了达到组合风险充分分散的目的,随机股票组合大致需要9-13只股票,但是不同行业的股票组合只需要5-8只股票股票价格数据预处理与收益率的统计量的计算1 极端值的控制2 缺损值的处理3 周收益率的计算使用下面公式对原始数据进行处理:其中:it r 为资产i 在第t 期的收益率;it P 、(1)i t P -分别为资产i 在第t 、t-1期的期末价格;it D 为资产i 在第t 期的红利;1,2,,t T =L L 。
其中,j s 为上周末股价,1j s +为本周末股价4各投资项目的数据特征运用MATLAB 或者Excel 软件中的mean(x)函数、std(x)函数和corrcoef(x)函数分别计算上面股票中的单项收益率期望值、单项收益率标准差以及各项目之间的相关系数上市公司评价数据预处理1 极端值的控制所有上市公司所出的经营环境不尽相同,影响上市公司的基本素质、财务状况的不确定性因素也各有不同,如,地理位置、政府干预、生态环境等不确定因素。
为了避免这些不利因素的影响,所有上市公司的评价指标X 服从正态分布。
2 剔除不可比行业因素的影响因为上市公司各种行业都有,由于行业性质不同,导致了各种行业的财务指标也存在不同的特点,因此需要剔除行业之间不可比因素对财务指标的影响。
通过ijij X X k '=-可以剔除行业之间的不可比因素,其中ij X 表示第i 家上市公司第j 项财务指标的观测值,k 是各上市公司第j 项财务指标的均值。
3 指标同向化处理完成了上述步骤后,还要对适度指标和逆指标进行处理。
将逆指标转化为正指标,其转换方法如下:正向指标按下列公式变换:逆向指标按下列公式变换:适度指标则按下列公式转换:其中max ()max()ij X j X =,min ()min()ij X j X =,经过上述转换,所有指标都被压缩在区间[0,1]之内,而且ijX '总是越大越好,即越接近1越好。
财务指标中,适度指标有资产负债率、流动比率、速动比率、股东权益比率共4个,其余都是正指标,不存在逆指标。
根据国际惯例,资产负债率、流动比率、速动比率、股东权益比率的适度值分别为60%、200%、100%、50%。
4将数据进行标准化处理,消除指标量纲和数量级的影响。
(二)上市公司财务数据的因子分析和聚类分析利用SPSS ,SAS 等统计软件上机实验,保存实验结果(三)股票价格和上证指数的相关分析和回归分析利用SPSS,SAS等统计软件上机实验,保存实验结果(四)最优投资组合的求解和投资组合风险VaR值运用MATLAB或者Excel软件中的规划求解计算上面股票中的最优投资组合(风险最小或者收益最大)《证券投资分析》实验项目(一):证券与证券价值分析(一)——证券与证券市场分析【实验目的】通过实验,使学生了解证券,证券的种类,证券市场,证券机构,证券的发行与交易,证券投资分析,证券投资理论等基本概念。
【实验条件】1、个人计算机一台,预装Windows操作系统和浏览器;2、计算机通过局域网形式接入互联网;3、安装财经软件。
【知识准备】理论知识:证券,证券的种类,证券市场,证券机构,证券的发行与交易,证券投资分析,证券投资理论等理论。
参考资料:课本第一章,6份专题一证券学电子版补充材料。
【实验项目内容】1.安装财经软件或者浏览财经网站分别了解以下信息:(1)证券种类:国债,公司债券,股票,基金,金融衍生产品,期权,期货;(2)证券市场:证券发行市场,证券交易市场,证券交易所,场外市场;(3)股票价格指数:沪指,深指,香港恒生指数,日经指数,道琼斯指数,标准普尔指数,纳斯达克;(4)证券主体:上市公司,银行,投资银行,证券公司,券商,基金公司,信托公司;2.根据上述内容请举出你了解到的详例,下载相关数据。
【实验项目步骤与结果】【实验项目结论与心得】【注】1.学生根据实验内容进行上机实验,记录实验步骤,过程,实验结果,实验数据,编写的程序等,从而完成实验报告;2.如果有电子版的实验数据或者编写的程序需提交电子版的文件,并在课程报告中注明即可。
《证券投资分析》实验项目(二):证券与证券价值分析(二)——证券价值分析【实验目的】通过实验,使学生理解证券价值分析模型,进行证券价值分析计算。
【实验条件】1、个人计算机一台,预装Windows操作系统和浏览器;2、计算机通过局域网形式接入互联网;3、安装财经软件。
【知识准备】理论知识:债券估值模型,股票估值模型,期权定价模型等理论。
参考资料:课本第二章,6份专题二证券估值分析电子版补充材料。
【实验项目内容】利用matlab软件进行证券价值分析:1.固定收益证券的估值计算;2.股票的估值计算;3.衍生证券的估值计算。
【实验项目步骤与结果】【实验项目结论与心得】【注】1.学生根据实验内容进行上机实验,记录实验步骤,过程,实验结果,实验数据,编写的程序等,从而完成实验报告;2.如果有电子版的实验数据或者编写的程序需提交电子版的文件,并在课程报告中注明即可。
1.利用matlab软件进行利率的期限结构计算:(1)计算利率的期限结构;(2)计算特定时间利率1.理解证券的价值分析:债券估值分析,股票估值分析,衍生产品的估植分析;2.掌握利率的期限结构:计算利率的期限结构,计算特定时间利率。
第1章MATLAB运行环境及金融运用1.1MATLAB介绍1.1.1MATLAB的产生背景1.1.2MATLAB语言的优点1.1.3MATLAB金融工具箱的介绍1.2MATLAB在金融领域的应用1.2.1建模预测新兴市场的金融危机1.2.2建立和验证新的期权定价模型1.2.3MathWorks公司的金融业主要客户思考题第2章MATLAB数值计算初步2.1变量与常量2.1.1数字变量2.1.2字符串操作2.1.3单元型变量与结构变量2.2矩阵及向量运算2.2.1矩阵生成2.2.2向量运算2.2.3矩阵运算2.3插值与拟合2.3.1一维插值2.3.2样条插值2.3.3Hermite插值2.4符号计算2.5MATLAB编程基本知识2.5.1脚本文件与函数文件2.5.2编程注意事项2.5.3程序排版格式思考题第3章金融时间序列数据分析3.1MATLAB中时间序列变量的创立3.1.1时间序列数组的创立和数据文件的读取3.1.2时间序列数组运算3.2金融时间序列的统计特征3.2.1相关系数和偏相关系数3.2.2金融时间序列界面功能介绍3.3时间序列模型3.3.1时间序列模型介绍3.3.2时间序列模型估计3.3.3ARX与ARMAX模型的估计3.4GARCH模型参数估计3.4.1GARCH{模型介绍3.4.2GARCH(P,Q)模型参数估计思考题第4章固定收益证券计算4.1固定收益证券基本概念4.1.1美国的固定收益证券种类4.1.2固定收益证券相关概念4.1.3常见应计期间计算方法4.1.4美国国债报价方式4.1.5绝对利差、静态利差(StaticSpread)和期权调整后利差(OptionAdo ustedSpread,OAS)4.2现金流计算函数4.2.1固定收益证券基本概念4.2.2现金流基本计算4.2.3计算复杂形式现金流4.2.4短期债券回购计算4.2.5对美国短期债券进行定价4.2.6国库券收益4.2.7可转让定期存单(CD)定价4.2.8可转换债券定价4.2.9固定收益久期与凸度4.3利率期限结构4.3.1计算利率期限结构4.3.2计算特定时间利率思考题第5章资产组合计算5.1资产组合基本原理5.1.1收益率序列与价格序列间的转换5.1.2协方差矩阵与相关系数矩阵间的转换5.1.3资产组合收益率与方差5.1.4资产组合VaR(ValueAtRisk)5.2资产组合有效前沿5.2.1两种风险资产组合收益期望与方差5.2.2均值方差有效前沿5.2.3带约束条件资产组合有效前沿5.2.4考虑无风险资产及借贷情况下的资产配置5.2.5线性规划求解资产组合问题思考题第6章金融衍生品计算6.1金融衍生产品种类6.2欧式期权计算6.2.1Black-Scholes方程6.2.2欧式期权价格函数6.2.3欧式期权希腊字母6.2.4期货期权定价函数6.3衍生产品定价数值解6.3.1CRR二叉树模型6.3.2EQP型二叉树模型6.3.3二叉树定价函数6.4证券类衍生产品定价函数6.4.1标的资产输入格式6.4.2证券类衍生产品二叉树建立6.4.3证券类衍生产品定价函数介绍6.4.4证券类衍生产品输入格式6.4.5证券类衍生产品定价函数6.5利率类衍生产品定价函数6.5.1利率类衍生产品介绍6.5.2利率模型介绍6.5.3利率类衍生产品输入格式6.5.4利率树时间格式6.5.5说明利率期限结构函数6.5.6建立利率树6.5.7利率产品定价思考题第7章有限差分法定价7.1有限差分法基本原理7.2有限差分求解方法7.2.1显示法求解欧式看跌期权7.2.2显示法求解美式看跌期权7.2.3隐式法求解欧式看跌期权7.2.4隐式法求解美式看跌期权7.2.5Crank-Nicolson法求解欧式障碍期权思考题第8章蒙特卡洛模拟金融衍生产品定价8.1随机模拟基本原理8.1.1随机数生成函数8.1.2生成正态分布随机数8.1.3特定分布随机数发生器8.1.4蒙特卡洛模拟方差削减技术8.1.5随机模拟控制变量技术8.2蒙特卡洛方法模拟期权定价8.2.1蒙特卡洛方法模拟欧式期权定价8.2.2蒙特卡洛方法模拟障碍期权定价8.2.3蒙特卡洛方法模拟亚式期权定价8.2.4蒙特卡洛模拟经验等价鞅测度思考题第9章金融数据可视化技术9.1图形对象、对象句柄和句柄图形结构9.1.1MATLAB中图形图像基本内容9.1.2金融时间序列基本绘图函数9.1.3修改金融时间序列作图9.2金融时间序列精确绘图思考题第10章MATLAB和其他软件数据连接10.1MATLAB和Excel数据连接10.1.1MATLAB和Excel接口安装10.1.2MATLAB自动启动和Excel连接10.1.3利用Excel中的宏命令实现Excel和MATLAB数据连接10.2MATLAB与财经网站数据连接10.2.1获得Bloomberg网站数据10.2.2获得Yahoo网站数据10.2.3获取FactSet网站数据.10.2.4获取Hyperfeed中的数据10.2.5获得FT网站的数据10.2.6MATLAB和财经网站数据接口GUI10.3MATLAB和Word接口10.3.1启动Notebook10.3.2创建和运行Word中的计算区10.4MATLAB与ActiveX接口10.4.1ActiveX基本介绍10.4.2MATLABActiveX自动化服务器10.5MATLAB与Access数据连接10.5.1Access数据库介绍10.5.2MATLAB与Access数据连接思考题在欧美MATLAB现在已经成为金融工程人员的密切伙伴,世界上超过2000家金融机构运用MATLAB来管理公司资产。
