实验六抽样定理的MATLAB仿真

实验六 matlab采样定理的建模和验证

页眉内容
实验六
题目：采样定理的建模和验证
实验目的：通过建模与仿真验证采样定理，理解采样定理的物理实质实验要求：学习和回顾采样定理内容，对采样定理作建模和仿真
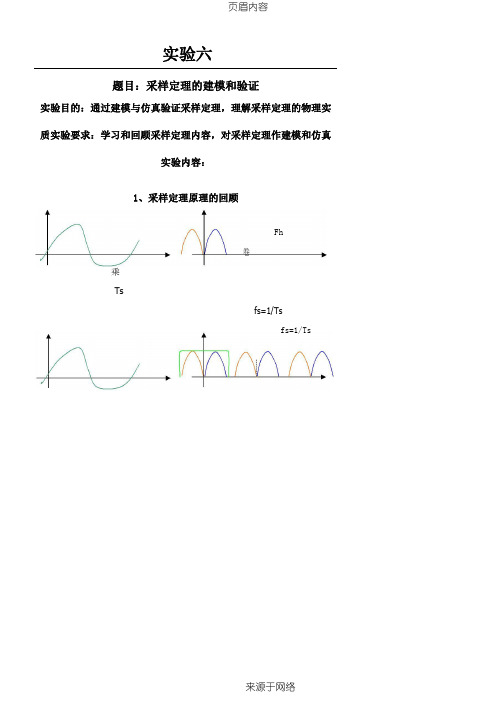
实验内容：
卷
乘
fs=1/Ts
2、建模参数要求：
设计模型,验证采样定理.
设基带波形频谱在 0Hz～200Hz 内. Fh=200Hz(信号最高频率)，采样率就应该大于 400Hz 。

用窄脉冲采样，要求窄脉冲宽度是采样周期的 1/10。

从而得到系统仿真步长: 小于等于 1/4000，仿真系统的仿真步长取 1/4000。

采样器用乘法器实现. 而恢复时用低通滤波器实现. 低通滤波器的带宽等于信
号最高频率 Fh,即等于 200Hz.
4、修改基带信号最高频率，如最高频率为200Hz、250Hz 等等，观察采样前后以及恢复的
波形和频谱。

请用实验方法得到频谱混叠后的频谱图和相应的波形。

5. 将被采样信号修改为正弦波、三角波和方波，观察采样前后和恢复非波形和频谱。

实验报告内容和要求：（！！注意每部分得分情况！！）
1.建立采样和恢复模型，说明关键模块的参数设置（30分）
仿真模型建立：
参数设置：
信源与滤波器参数：
2.修改采样率，如采样率为150Hz，200Hz、300Hz等等，观察采样前后以及恢复的波形和频谱。

请用实验方法得到频谱混叠后的频谱图和相应的波形。

（40分）
150Hz:
200Hz:
300Hz:。

MATLAB实现抽样定理探讨及仿真

应用 MATLAB 实现抽样定理探讨及仿真一．课程设计的目的利用MATLAB ，仿模信号抽样与恢复系统的实际实现，探讨过抽样和欠抽样的信号以及抽样与恢复系统的性能。

二．课程设计的原理模拟信号经过 (A/D) 变换转换为数字信号的过程称为采样，信号采样后其频谱产生了周期延拓，每隔一个采样频率 fs ，重复出现一次。

为保证采样后信号的频谱形状不失真，采样频率必须大于信号中最高频率成分的两倍，这称之为采样定理。

时域采样定理从采样信号恢复原信号必需满足两个条件： (1)必须是带限信号，其频谱函数在＞各处为零；（对信号的要求，即只有带限信号才能适用采样定理。

）(2) 取样频率不能过低，必须＞2（或＞2）。

（对取样频率的要求，即取样频率要足够大，采得的样值要足够多，才能恢复原信号。

）如果采样频率大于或等于，即（为连续信号的有限频谱），则采样离散信号能无失真地恢复到原来的连续信号。

一个频谱在区间（- ，）以外为零的频带有限信号，可唯一地由其在均匀间隔（＜）上的样点值所确定。

根据时域与频域的对称性，可以由时域采样定理直接推出频域采样定理。

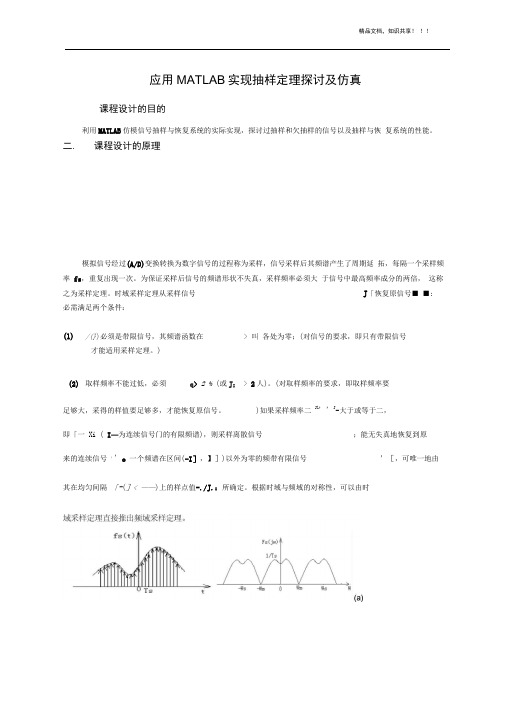
(a))(t f )()(t t s S T =)(t f s 连续信号取样脉冲信号抽样信号)(ωj H )(0t f 理想低通滤波器恢复信号(b)(c)图2.1抽样定理a) 等抽样频率时的抽样信号及频谱（不混叠） b) 高抽样频率时的抽样信号及频谱（不混叠） c) 低抽样频率时的抽样信号及频谱（混叠）2.1信号采样如图1所示，给出了信号采样原理图信号采样原理图（a ）由图1可见，)()()(t t f t f s T s δ⋅=，其中，冲激采样信号)(t s T δ的表达式为：∑∞-∞=-=n sT nT t t s)()(δδ其傅立叶变换为∑∞-∞=-n s s n )(ωωδω，其中ss T πω2=。

设)(ωj F ，)(ωj F s 分别为)(t f ，)(t f s 的傅立叶变换，由傅立叶变换的频域卷积定理，可得∑∑∞-∞=∞-∞=-=-=n ss n s s s n j F T n j F j F )]([1)(*)(21)(ωωωωδωωπω若设)(t f 是带限信号，带宽为m ω， )(t f 经过采样后的频谱)(ωj F s 就是将)(ωj F 在频率轴上搬移至 ,,,,,02ns s s ωωω±±±处（幅度为原频谱的s T 1倍）。

MATLAB实现抽样定理探讨及仿真讲解

应用MATLAB实现抽样定理探讨及仿真课程设计的目的利用MATLAB仿模信号抽样与恢复系统的实际实现，探讨过抽样和欠抽样的信号以及抽样与恢复系统的性能。

二.课程设计的原理模拟信号经过(A/D)变换转换为数字信号的过程称为采样，信号采样后其频谱产生了周期延拓，每隔一个采样频率fs，重复出现一次。

为保证采样后信号的频谱形状不失真，采样频率必须大于信号中最高频率成分的两倍，这称之为采样定理。

时域采样定理从采样信号J「恢复原信号■ ■:必需满足两个条件：(1)/(})必须是带限信号，其频谱函数在> 叫各处为零；(对信号的要求，即只有带限信号才能适用采样定理。

)(2)取样频率不能过低，必须q> 2 %(或J；> 2人)。

(对取样频率的要求，即取样频率要足够大，采得的样值要足够多，才能恢复原信号。

)如果采样频率二Jl' ' J-大于或等于二，即「一 Xi ( I—为连续信号门的有限频谱)，则采样离散信号；能无失真地恢复到原来的连续信号；' o 一个频谱在区间(-I］，】］)以外为零的频带有限信号’［，可唯一地由其在均匀间隔「-(］< ——)上的样点值-./J.：所确定。

根据时域与频域的对称性，可以由时傅立叶变换，由傅立叶变换的频域卷积定理，可得O01O0 F(j s '、( ’ 一 n 上)' F[j (一 n 「s)]n - ； T s n -I若设f(t)是带限信号，带宽为監，f(t)经过采样后的频谱 F s(j«)就是将F(jco)在频率轴上搬移至0,一 1，二’2s ，…厂’ns ，…处(幅度为原频谱的1 T s 倍)。

因此，当 \~2 -m时，频谱不发生(C)b) 高抽样频率时的抽样信号及频谱 c) 低抽样频率时的抽样信号及频谱(不混叠) (不混叠) (混叠)2.1信号采样如图1所示，给出了信号采样原理图孑相乘北)------- A速)信号采样原理图(a )由图1可见，f s(t)f (t) =T s (t)，其中，冲激采样信号% (t)的表达式为:□aT (t)八沁- nT s )n =^0其傅立叶变换为-召('- n 「s)，其中■ -^― n =T s设 F(j )，F s (j )分别为 f (t)，f s (t)的F s(j )1 2~等抽样频率时的抽样信号及频谱 a)精品文档，知识共享！！！混叠；而当•，s ：：： 2 -m 时，频谱发生混叠。

MATLAB实现抽样定理探讨及仿真

MATLAB实现抽样定理探讨及仿真应用 MATLAB 实现抽样定理探讨及仿真一．课程设计的目的利用MATLAB ，仿模信号抽样与恢复系统的实际实现，探讨过抽样和欠抽样的信号以及抽样与恢复系统的性能。

二．课程设计的原理模拟信号经过 (A/D) 变换转换为数字信号的过程称为采样，信号采样后其频谱产生了周期延拓，每隔一个采样频率 fs ，重复出现一次。

为保证采样后信号的频谱形状不失真，采样频率必须大于信号中最高频率成分的两倍，这称之为采样定理。

时域采样定理从采样信号恢复原信号必需满足两个条件： (1)必须是带限信号，其频谱函数在＞各处为零；（对信号的要求，即只有带限信号才能适用采样定理。

）(2) 取样频率不能过低，必须＞2 （或＞2）。

（对取样频率的要求，即取样频率要足够大，)(t f )()(t t s S T δ=)(t f s 连续信号取样脉冲信号抽样信号)(ωj H )(0t f 理想低通滤波器恢复信号采得的样值要足够多，才能恢复原信号。

）如果采样频率大于或等于，即（为连续信号的有限频谱），则采样离散信号能无失真地恢复到原来的连续信号。

一个频谱在区间（-，）以外为零的频带有限信号，可唯一地由其在均匀间隔（＜）上的样点值所确定。

根据时域与频域的对称性，可以由时域采样定理直接推出频域采样定理。

(a)(b)(c)图2.1抽样定理a) 等抽样频率时的抽样信号及频谱（不混叠） b) 高抽样频率时的抽样信号及频谱（不混叠）c) 低抽样频率时的抽样信号及频谱（混叠） 2.1信号采样如图1所示，给出了信号采样原理图信号采样原理图（a ）由图1可见，)()()(t t f t f s T sδ⋅=，其中，冲激采样信号)(t sT δ的表达式为：∑∞-∞=-=n sT nT t t s)()(δδ其傅立叶变换为∑∞-∞=-n ss n )(ωωδω，其中ssT πω2=。

设)(ωj F ，)(ωj F s分别为)(t f ，)(t f s的傅立叶变换，由傅立叶变换的频域卷积定理，可得∑∑∞-∞=∞-∞=-=-=n ss n s s s n j F T n j F j F )]([1)(*)(21)(ωωωωδωωπω若设)(t f 是带限信号，带宽为mω， )(t f 经过采样后的频谱)(ωj F s就是将)(ωj F 在频率轴上搬移至ΛΛ,,,,,02ns ssωωω±±±处（幅度为原频谱的sT 1倍）。

MATLAB实现抽样定理探讨及仿真

应用 MATLAB 实现抽样定理探讨及仿真一．课程设计的目的利用MATLAB ，仿模信号抽样与恢复系统的实际实现，探讨过抽样和欠抽样的信号以及抽样与恢复系统的性能。

二．课程设计的原理模拟信号经过 (A/D) 变换转换为数字信号的过程称为采样，信号采样后其频谱产生了周期延拓，每隔一个采样频率 fs ，重复出现一次。

为保证采样后信号的频谱形状不失真，采样频率必须大于信号中最高频率成分的两倍，这称之为采样定理。

时域采样定理从采样信号恢复原信号必需满足两个条件： (1)必须是带限信号，其频谱函数在＞各处为零；（对信号的要求，即只有带限信号才能适用采样定理。

）(2) 取样频率不能过低，必须＞2（或＞2）。

（对取样频率的要求，即取样频率要足够大，采得的样值要足够多，才能恢复原信号。

）如果采样频率大于或等于，即（为连续信号的有限频谱），则采样离散信号能无失真地恢复到原来的连续信号。

一个频谱在区间（-，）以外为零的频带有限信号，可唯一地由其在均匀间隔（＜）上的样点值所确定。

根据时域与频域的对称性，可以由时域采样定理直接推出频域采样定理。

(a))(t f )()(t t s S T δ=)(t f s 连续信号取样脉冲信号抽样信号)(ωj H )(0t f 理想低通滤波器恢复信号(b)(c)图2.1抽样定理a)等抽样频率时的抽样信号及频谱（不混叠）b)高抽样频率时的抽样信号及频谱（不混叠）c) 低抽样频率时的抽样信号及频谱（混叠）2.1信号采样如图1所示，给出了信号采样原理图信号采样原理图（a）由图1可见，)()()(ttftfsTsδ⋅=，其中，冲激采样信号)(ts Tδ的表达式为：∑∞-∞=-=nsTnTtts)()(δδ其傅立叶变换为∑∞-∞=-nssn)(ωωδω，其中ss Tπω2=。

设)(ωjF，)(ωjFs分别为)(tf，)(tfs的傅立叶变换，由傅立叶变换的频域卷积定理，可得∑∑∞-∞=∞-∞=-=-=nssnsssnjFTnjFjF)]([1)(*)(21)(ωωωωδωωπω若设)(tf是带限信号，带宽为mω，)(t f经过采样后的频谱)(ωjFs就是将)(ωjF在频率轴上搬移至,,,,,02nsssωωω±±±处（幅度为原频谱的sT1倍）。

MATLAB实现抽样定理探讨及仿真

MATLAB实现抽样定理探讨及仿真抽样定理，也被称为Nyquist定理或香农定理，是一种关于信号采样的基本理论。

它的核心观点是：如果对信号进行合适的采样，并且采样频率大于信号中最高频率的两倍，那么原始信号可以从采样信号中完全或几乎完全地恢复。

在MATLAB中，我们可以实现抽样定理的探讨和仿真。

下面将详细介绍如何进行这样的实现。

首先，我们可以通过使用MATLAB内置的函数来生成一个连续时间的信号。

例如，我们可以使用sinc函数生成一个带宽有限的信号，其频率范围为[-F/2, F/2]，其中F是信号的最大频率。

以下是一个示例代码：```MATLABFs=100;%采样率Ts=1/Fs;%采样周期t=-1:Ts:1;%连续时间序列f_max = 10; % 信号最大频率signal = sinc(2*f_max*t); % 生成带宽有限的信号```然后，我们可以使用MATLAB的plot函数来显示生成的信号。

以下是一个示例代码：```MATLABplot(t, signal);xlabel('时间');ylabel('信号幅度');title('连续时间信号');```生成的图形将显示带宽有限的信号在连续时间域中的波形。

接下来，我们需要对信号进行离散化采样。

根据抽样定理，理想情况下，采样频率应大于信号中最高频率的两倍。

我们可以使用MATLAB的resample函数来进行采样。

以下是一个示例代码：```MATLABFs_new = 2*f_max; % 新的采样率Ts_new = 1/Fs_new; % 新的采样周期t_new = -1:Ts_new:1; % 新的时间序列signal_sampled = resample(signal, Fs_new, Fs); % 信号采样```然后，我们可以使用MATLAB的stem函数来显示采样后的信号。

以下是一个示例代码：```MATLABstem(t_new, signal_sampled);xlabel('时间');ylabel('信号幅度');title('离散时间信号');```生成的图形将显示采样后的信号在离散时间域中的序列。

实验六抽样定理的MATLAB仿真设计

综合性、设计性实验报告贺鹤学号8专业通信工程班级2013级1班实验课程名称抽样定理的MATLAB仿真指导教师及职称玲香讲师开课学期 2014 至 2015 学年第二学期上课时间 2015年 6 月 17、27日科技学院教务处编印(2) 编程步骤（仿真实验）①确定f(t)的最高频率fm。

对于无限带宽信号，确定最高频率fm的方法：设其频谱的模降到10-5左右时的频率为fm。

②确定Nyquist抽样间隔TN 。

选定两个抽样时间：TS<TN，TS>TN。

③滤波器的截止频率确定：ωm <ωC <ωS -ωm 。

④采样信号f(nTs )根据MATLAB计算表达式的向量表示。

⑤重建信号f(t) 的MATLAB中的计算机公式向量表示。

根据原理和公式，MATLAB计算为：ft=fs*Ts*wc/pi*sinc((wc/pi)*(ones(length(nTs),1)*t-nTs'*ones(1,length(t)))); （3）电路连接原理（硬件实验）5．实验数据处理方法①自定义输入信号:f1=cos(2*pi*80*t)+2*sin(2*pi*30*t)+cos(2*pi*40*t-pi/3)②改变抽样频率，实现欠抽样、临界抽样和过抽样，调试结果分析:(1)频率sf<max2fm时，为原信号的欠采样信号和恢复，采样频率不满足时域采样定理，那么频移后的各相临频谱会发生相互重叠，这样就无法将他们分开，因而也不能再恢复原信号。

频谱重叠的现象被称为混叠现象。

如图1所示图1.fs=140Hz恢复后信号波形及频谱(2)频率sf=max2fm时，为原信号的临界采样信号和恢复，从下图2恢复后信号和原信号先对比可知，只恢复了低频信号，高频信号未能恢复。

如图2所示图2.fs=160Hz恢复后信号波形及频谱(3)频率sf>max2fm时，此时的采样是成功的，它能够恢复原信号，从时域波形可看出，比上面采样所得的冲激脉冲串包含的细节要多，在频域中也没出现频谱的交叠，这样我们可以利用低通滤波器得到无失真的重建。

MATLAB实现抽样定理探讨及仿真

应用 MATLAB 实现抽样定理探讨及仿真一．课程设计的目的利用MATLAB ，仿模信号抽样与恢复系统的实际实现，探讨过抽样和欠抽样的信号以及抽样与恢复系统的性能。

二．课程设计的原理模拟信号经过 (A/D) 变换转换为数字信号的过程称为采样，信号采样后其频谱产生了周期延拓，每隔一个采样频率 fs ，重复出现一次。

为保证采样后信号的频谱形状不失真，采样频率必须大于信号中最高频率成分的两倍，这称之为采样定理。

时域采样定理从采样信号恢复原信号必需满足两个条件： (1)必须是带限信号，其频谱函数在＞各处为零；（对信号的要求，即只有带限信号才能适用采样定理。

）(2) 取样频率不能过低，必须＞2（或＞2）。

（对取样频率的要求，即取样频率要足够大，采得的样值要足够多，才能恢复原信号。

）如果采样频率大于或等于，即（为连续信号的有限频谱），则采样离散信号能无失真地恢复到原来的连续信号。

一个频谱在区间（-，）以外为零的频带有限信号，可唯一地由其在均匀间隔（＜）上的样点值所确定。

根据时域与频域的对称性，可以由时域采样定理直接推出频域采样定理。

(a))(t f )()(t t s S T δ=)(t f s 连续信号取样脉冲信号抽样信号)(ωj H )(0t f 理想低通滤波器恢复信号(b)(c)图2.1抽样定理a)等抽样频率时的抽样信号及频谱（不混叠）b)高抽样频率时的抽样信号及频谱（不混叠）c) 低抽样频率时的抽样信号及频谱（混叠）2.1信号采样如图1所示，给出了信号采样原理图信号采样原理图（a）由图1可见，)()()(ttftfsTsδ⋅=，其中，冲激采样信号)(ts Tδ的表达式为：∑∞-∞=-=nsTnTtts)()(δδ其傅立叶变换为∑∞-∞=-nssn)(ωωδω，其中ss Tπω2=。

设)(ωjF，)(ωjFs分别为)(tf，)(tfs的傅立叶变换，由傅立叶变换的频域卷积定理，可得∑∑∞-∞=∞-∞=-=-=nssnsssnjFTnjFjF)]([1)(*)(21)(ωωωωδωωπω若设)(tf是带限信号，带宽为mω，)(tf经过采样后的频谱)(ωjFs就是将)(ωjF在频率轴上搬移至,,,,,02nsssωωω±±±处（幅度为原频谱的sT1倍）。

MATLAB实现抽样定理探讨及仿真

MATLAB实现抽样定理探讨及仿真抽样定理是信号处理与通信领域中的一个重要定理，它指出在进行信号采样时，为了避免失真和信息丢失，采样频率必须至少为信号带宽的两倍。

抽样定理还提供了信号的重构方法，可以从采样信号中恢复出原始信号的全部信息。

在这篇文章中，我们将使用MATLAB对抽样定理进行探讨，并进行相关的仿真实验。

首先，我们将介绍抽样定理的基本原理。

在信号处理中，信号可以被表示为时域函数或频域函数。

在时域中，信号可以用冲激函数的线性组合来表示，而在频域中，信号可以被表示为复指数函数的线性组合。

信号的带宽是指信号中包含的频率的范围，通常用赫兹（Hz）来表示。

根据抽样定理，为了准确地恢复信号，采样频率必须至少是信号带宽的两倍。

接下来，我们将使用MATLAB对抽样定理进行仿真实验。

首先，我们将生成一个具有限带宽的信号，并对其进行采样。

然后，我们将根据抽样定理的要求重新构建信号，以验证定理的有效性。

假设我们有一个信号x(t)，其频率范围为0至10赫兹，并且我们以20赫兹的采样频率对其进行采样。

我们可以使用MATLAB生成这个信号，并进行采样，代码如下所示：```matlabFs=20;%采样频率t=0:1/Fs:1-1/Fs;%1秒内的采样时刻x = sin(2*pi*10*t); % 10赫兹的正弦波信号stem(t,x);xlabel('时间（秒）');ylabel('幅度');title('原始信号');```接下来，我们将使用抽样定理的频率限制条件对信号进行重构，并绘制重构后的信号。

我们将使用插值的方法对采样信号进行重构，代码如下所示：```matlabt_recon = 0:1/(2*Fs):1-1/(2*Fs); % 重新构建信号时的采样时刻x_recon = interp1(t,x,t_recon); % 插值重构信号stem(t_recon,x_recon);xlabel('时间（秒）');ylabel('幅度');title('重构信号');```通过对原始信号和重构信号的比较，我们可以看到抽样定理的有效性。

MATLAB实现抽样定理探讨及仿真讲解

应用MATLAB 实现抽样定理探讨及仿真课程设计的目的利用MATLAB 仿模信号抽样与恢复系统的实际实现，探讨过抽样和欠抽样的信号以及抽样与恢复系统的性能。

二. 课程设计的原理模拟信号经过(A/D)变换转换为数字信号的过程称为采样，信号采样后其频谱产生了周期延拓，每隔一个采样频率 fs ，重复出现一次。

为保证采样后信号的频谱形状不失真，采样频率必须大于信号中最高频率成分的两倍，这称之为采样定理。

时域采样定理从采样信号 J 「恢复原信号■ ■:必需满足两个条件：才能适用采样定理。

)(2)取样频率不能过低，必须 q > 2 % (或J ； > 2人)。

(对取样频率的要求，即取样频率要足够大，采得的样值要足够多，才能恢复原信号。

)如果采样频率二 Jl ' ' J -大于或等于二，即「一 Xi ( I —为连续信号门的有限频谱)，则采样离散信号；能无失真地恢复到原来的连续信号-'Il 。

一个频谱在区间(-I],】])以外为零的频带有限信号,可唯一地由其在均匀间隔「-(]< ——)上的样点值-./J.：所确定。

根据时域与频域的对称性，可以由时f(t)连续信号取样脉冲信号S(t)二 TS (t)(1)--:必须是带限信号，其频谱函数在也〉叫各处为零；(对信号的要求，即只有带限信号2.1信号采样如图1所示，给出了信号采样原理图---- 北)T 相乘 ------- A昭)信号采样原理图由图1可见，f s (t) = f (t) ®s (t),其中，冲激采样信号 6s (t)的表达式为:□0T(t)八沁- nT s )n =^0傅立叶变换，由傅立叶变换的频域卷积定理，可得O01 O0F(j s ' 、( ’ 一 n 上)' F[j (一 n 「s )] n - ； Ts n -I若设f(t)是带限信号，带宽为監，f(t)经过采样后的频谱 F s (j«)就是将F(jco)在频率轴(c)b) 高抽样频率时的抽样信号及频谱(不混叠)c) 低抽样频率时的抽样信号及频谱其傅立叶变换为-召('- n 「s )，其中■ -^― n = T s设 F(j )，F s (j )分别为 f (t)，f s (t)的F s (j )1 2~ fs'tU等抽样频率时的抽样信号及频谱 (不混叠) a)上搬移至0,一1，二’2s，…厂’ns，…处(幅度为原频谱的1 T s倍)。

MATLAB实现抽样定理探讨及仿真讲解

应用 MATLAB 实现抽样定理探讨及仿真一．课程设计的目的利用MATLAB ，仿模信号抽样与恢复系统的实际实现，探讨过抽样和欠抽样的信号以及抽样与恢复系统的性能。

二．课程设计的原理模拟信号经过 (A/D) 变换转换为数字信号的过程称为采样，信号采样后其频谱产生了周期延拓，每隔一个采样频率 fs ，重复出现一次。

为保证采样后信号的频谱形状不失真，采样频率必须大于信号中最高频率成分的两倍，这称之为采样定理。

时域采样定理从采样信号恢复原信号必需满足两个条件： (1)必须是带限信号，其频谱函数在＞各处为零；（对信号的要求，即只有带限信号才能适用采样定理。

）(2) 取样频率不能过低，必须＞2（或＞2）。

（对取样频率的要求，即取样频率要足够大，采得的样值要足够多，才能恢复原信号。

）如果采样频率大于或等于，即（为连续信号的有限频谱），则采样离散信号能无失真地恢复到原来的连续信号。

一个频谱在区间（-，）以外为零的频带有限信号，可唯一地由其在均匀间隔（＜）上的样点值所确定。

根据时域与频域的对称性，可以由时域采样定理直接推出频域采样定理。

(a))(t f )()(t t s S T δ=)(t f s 连续信号取样脉冲信号抽样信号)(ωj H )(0t f 理想低通滤波器恢复信号(b)(c)图2.1抽样定理a)等抽样频率时的抽样信号及频谱（不混叠）b)高抽样频率时的抽样信号及频谱（不混叠）c) 低抽样频率时的抽样信号及频谱（混叠）2.1信号采样如图1所示，给出了信号采样原理图信号采样原理图（a）由图1可见，)()()(ttftfsTsδ⋅=，其中，冲激采样信号)(ts Tδ的表达式为：∑∞-∞=-=nsTnTtts)()(δδ其傅立叶变换为∑∞-∞=-nssn)(ωωδω，其中ss Tπω2=。

设)(ωjF，)(ωjFs分别为)(tf，)(tfs的傅立叶变换，由傅立叶变换的频域卷积定理，可得∑∑∞-∞=∞-∞=-=-=nssnsssnjFTnjFjF)]([1)(*)(21)(ωωωωδωωπω若设)(tf是带限信号，带宽为mω，)(t f经过采样后的频谱)(ωjFs就是将)(ωjF在频率轴上搬移至,,,,,02nsssωωω±±±处（幅度为原频谱的sT1倍）。

MATLAB实现抽样定理探讨仿真

应用MATLAB实现抽样定理探讨及仿真课程设计的目的利用MATLAB仿模信号抽样与恢复系统的实际实现，探讨过抽样和欠抽样的信号以及抽样与恢复系统的性能。

二.课程设计的原理模拟信号经过（A/D）变换转换为数字信号的过程称为采样，信号采样后其频谱产生了周期延拓，每隔一个采样频率fs，重复出现一次。

为保证采样后信号的频谱形状不失真，采样频率必须大于信号中最高频率成分的两倍，这称之为采样定理。

时域采样定理从采样信号_.. ：1 i恢复原信号「［I必需满足两个条件：（1）；必须是带限信号，其频谱函数在才能适用采样定理。

）叫〉2 %（或£> 2几）。

（对取样频率的要求，即取样频率要即.—id （in为连续信号GL的有限频谱），则采样离散信号''能无失真地恢复到原来的连续信号心。

一个频谱在区间（-三乙，口二）以外为零的频带有限信号Ji ，可唯一地由域采样定理直接推出频域采样定理。

f o（t）恢复信号由| > % 各处为零；（对信号的要求，即只有带限信号（2）取样频率不能过低，必须足够大，采得的样值要足够多，才能恢复原信号。

）如果采样频率—-大于或等于二）上的样点值八：所确定。

根据时域与频域的对称性，可以由时其在均匀间隔2其傅立叶变换为s ( n s ),其中s ——。

设F(j )，F s (j )分别为f(t)，f s (t)的 n T s傅立叶变换，由傅立叶变换的频域卷积定理，可得1 1F s (j ) —F(j )* s (n s ) - F[j( n s )]2nI s n若设f (t)是带限信号，带宽为m, f(t)经过采样后的频谱 F s (j )就是将F(j )在频率轴1/T sA/\ A(c)b) 高抽样频率时的抽样信号及频谱 c)低抽样频率时的抽样信号及频谱(不混叠) (不混叠) (混叠)2.1信号采样如图1所示，给出了信号采样原理图相乘—:- >0)r(a )由图1可见，f s (t) f (t)Ts(t)，其中，冲激采样信号Ts (t)的表达式为:(t)n(t nT s )等抽样频率时的抽样信号及频谱 a)上搬移至0, s, 2s, , ns,处(幅度为原频谱的1 T s倍)。

MATLAB实现抽样定理探讨及仿真剖析

应用 MATLAB 实现抽样定理探讨及仿真一．课程设计的目的利用MATLAB ，仿模信号抽样与恢复系统的实际实现，探讨过抽样和欠抽样的信号以及抽样与恢复系统的性能。

二．课程设计的原理模拟信号经过 (A/D) 变换转换为数字信号的过程称为采样，信号采样后其频谱产生了周期延拓，每隔一个采样频率 fs ，重复出现一次。

为保证采样后信号的频谱形状不失真，采样频率必须大于信号中最高频率成分的两倍，这称之为采样定理。

时域采样定理从采样信号恢复原信号必需满足两个条件： (1)必须是带限信号，其频谱函数在＞各处为零；（对信号的要求，即只有带限信号才能适用采样定理。

）(2) 取样频率不能过低，必须＞2（或＞2）。

（对取样频率的要求，即取样频率要足够大，采得的样值要足够多，才能恢复原信号。

）如果采样频率大于或等于，即（为连续信号的有限频谱），则采样离散信号能无失真地恢复到原来的连续信号。

一个频谱在区间（-，）以外为零的频带有限信号，可唯一地由其在均匀间隔（＜）上的样点值所确定。

根据时域与频域的对称性，可以由时域采样定理直接推出频域采样定理。

(a))(t f )()(t t s S T δ=)(t f s 连续信号取样脉冲信号抽样信号)(ωj H )(0t f 理想低通滤波器恢复信号(b)(c)图2.1抽样定理a)等抽样频率时的抽样信号及频谱（不混叠）b)高抽样频率时的抽样信号及频谱（不混叠）c) 低抽样频率时的抽样信号及频谱（混叠）2.1信号采样如图1所示，给出了信号采样原理图信号采样原理图（a）由图1可见，)()()(ttftfsTsδ⋅=，其中，冲激采样信号)(ts Tδ的表达式为：∑∞-∞=-=nsTnTtts)()(δδ其傅立叶变换为∑∞-∞=-nssn)(ωωδω，其中ss Tπω2=。

设)(ωjF，)(ωjFs分别为)(tf，)(tfs的傅立叶变换，由傅立叶变换的频域卷积定理，可得∑∑∞-∞=∞-∞=-=-=nssnsssnjFTnjFjF)]([1)(*)(21)(ωωωωδωωπω若设)(tf是带限信号，带宽为mω，)(t f经过采样后的频谱)(ωjFs就是将)(ωjF在频率轴上搬移至,,,,,02nsssωωω±±±处（幅度为原频谱的sT1倍）。

实验六-抽样定理的MATLAB仿真

综合性、设计性实验报告姓名贺鹤学号201308002118专业通信工程班级2013级1班实验课程名称抽样定理的MATLAB仿真指导教师及职称李玲香讲师开课学期 2014 至 2015 学年第二学期上课时间 2015年 6 月 17、27日湖南科技学院教务处编印(2) 编程步骤（仿真实验）① 确定f(t)的最高频率fm 。

对于无限带宽信号，确定最高频率fm 的方法：设其频谱的模降到10-5左右时的频率为fm 。

② 确定Nyquist 抽样间隔T N 。

选定两个抽样时间：T S <T N ，T S >T N 。

③ 滤波器的截止频率确定：ωm <ωC <ωS -ωm 。

④采样信号f(nTs )根据MATLAB 计算表达式的向量表示。

⑤ 重建信号f(t) 的MATLAB 中的计算机公式向量表示。

根据原理和公式，MATLAB 计算为：ft=fs*Ts*wc/pi*sinc((wc/pi)*(ones(length(nTs),1)*t-nTs'*ones(1,length(t)))); （3）电路连接原理（硬件实验）5．实验数据处理方法① 自定义输入信号:f1=cos(2*pi*80*t)+2*sin(2*pi*30*t)+cos(2*pi*40*t-pi/3) ② 改变抽样频率，实现欠抽样、临界抽样和过抽样，调试结果分析:(1)频率sf<max2fm 时，为原信号的欠采样信号和恢复，采样频率不满足时域采样定理，那么频移后的各相临频谱会发生相互重叠，这样就无法将他们分开，因而也不能再恢复原信号。

频谱重叠的现象被称为混叠现象。

如图1所示)(t f a )()(t t s S T δ=)(t f s 连续信号取样脉冲信号抽样信号)(ωj H )(0t f 理想低通滤波器恢复信号图1.fs=140Hz恢复后信号波形及频谱(2)频率sf=max2fm时，为原信号的临界采样信号和恢复，从下图2恢复后信号和原信号先对比可知，只恢复了低频信号，高频信号未能恢复。