单表代换密码
经典密码

一、经典密码
⑴.单表代换密码
只使用一个密文字母表,并且用密文字母表中的一 个字母来代换明文字母表中的一个字母。 明文字母表:A ={ a0 , a1 ,..., an-1 }
密文字母表:B ={ b0 , b1 ,..., bn-1 } 定义一个由A到 B的映射:f:A→B
–因此,单表代换密码可用统计分 析攻破。
三、经典密码的统计分析
• 英语的统计规律
–每个单字母出现的频率稳定。
最高频率字母
E
次高频率字母
TAOINSHR
中高频率字母
DL
低频率字母
CUMWFGYPB
最低频率字母 V K J X Q Z
三、经典密码的统计分析
• 英语的统计规律
–频率最高的双字母组: TH HE IN ER AN RE ED ON ES ST EN AT TO NT HA ND OU EA NG AS OR TI IS ET IT AR TE SE HI OF
三、经典密码的统计分析
• 英语的统计规律
–频率最高的三字母组: THE ING AND HER ERE ENT THA WAS ETH FOR DHT HAT SHE ION HIS ERS VER
其中THE的频率是ING的3倍!
三、经典密码的统计分析
• 英语的统计规律
–英字母的约占一
半。
–还有其它统计规律!
三、经典密码的统计分析
经得起统计分析是对近代 密码的基本要求!
一、经典密码
•(2)把明文按某一顺序排成一个矩阵, 然后
按另一顺序选出矩阵中的字母以形成密文, 最后截成固定长度的字母组作为密文。
例如:
密码学原理与实践答案

密码学原理与实践答案1.1 几个简单的密码体制注:小写代表明文,大写代表密文分组密码:单表代换密码:移位密码,代换密码,仿射密码多表代换密码:维吉尼亚密码,希尔密码非代换密码:置换密码流密码:同步流密码,异步流密码1.1.1 移位密码密码体制:令 P = C = K = Z 26 P=C=K=Z_{26} P=C=K=Z26 有 e K ( x ) = ( x + K ) m o d 26 d K ( y ) = ( x −K ) m o d 26 e_{K}(x)=(x+K)mod 26 \quad d_K(y)=(x-K)mod 26 eK(x)=(x+K)mod26dK(y)=(x−K)mod26 并且当K=3时叫凯撒密码。
密钥空间为261.1.2 代换密码密码体制:令 P = C = Z 26 P=C=Z_{26} P=C=Z26 对任意的置换π ∈ K \pi \in K π∈K,有 e π ( x ) = π ( x ) d π ( y ) = π − 1 ( y ) e_{\pi}(x)=\pi(x) \quadd_{\pi}(y)=\pi^{-1}(y) eπ(x)=π(x)dπ(y)=π−1(y)。
密钥空间为 26 ! 26! 26!1.1.3 仿射密码加密函数形式: e ( x ) = ( a x + b ) m o d 26e(x)=(ax+b)mod 26 e(x)=(ax+b)mod26,要求仿射函数必须是单射,也就是同余方程 a x ≡ y ( m o d 26 ) ax\equivy(mod 26) ax≡y(mod26)有唯一解。
上述同余方程有唯一解⇔ g c d ( a , 26 ) = 1\Leftrightarrow gcd(a,26)=1 ⇔gcd(a,26)=1 ,证明略。
此时a的取值为0~25之间与26互素的数,共12个,b的取值为0~25。
这时密钥空间为312。
实现单表代换加解密并对其攻击
5.程序运行。
(1)选择密文输入方式,K为从键盘输入,F为从文件读入。如果为从文件读取,输入文件名称。程序会把密文显示在屏幕上并输出字频统计的结果。如下图所示:
(2)输入保存破译出的可能密钥和可能明文的文件名称。程序把结果破译输出到屏幕和文件。程序中只输出可能性最大的16个可能明文。
解密时,输入密钥建立代换表,然后像加密一样,把密文中的字母代换成代换表中相应的字母,从而再现明文。
3.程序设计及实现。
程序设计中对输入变量的要求:
密钥key:是26个英文字母的排列,
明文plaintext:要求明文中只能有26个字母出现,不能有其他符号包括空格,大小写不限,长度不限,可从键盘输入,也可从txt文件读入。
intDecryption(void)
Decryption()和加密一样,根据输入的密钥和密文进行解密。
具体的程序源代码见代码文件:encryption.cpp
4.程序运行。
(1)选择加密功能,输入密钥:qwertyuiopasdfghjklzxcvbnm,选择从文件输入明文,输入保存明文的文件名:plaintext.txt,输入保存密文的文件名:ciphertext.txt。运行结果如下图所示:
加密所得密文如下:
(2)选择解密功能,输入密钥:qwertyuiopasdfghjklzxcvbnm,选择从文件读入密文,输入保存密文的文件名:ciphertext.txt,输入保存解密所得明文的文件名:decryption.txt。运行结果如下:
解密所得明文如下:
二、对单表代换密码进行攻击。
1.频率统计攻击方式的理解。
密文ciphertext:全部用大写字母,只能有26个字母出现,不能有其他符号包括空格,长度不限,可从键盘输入,也可从txt文件读入。
现代密码学02 - 古典密码

映射关系
24
频率分析:简单代换密码的终结者 字母出现频率差别很大 频率分布极不均匀
25
频率分析:简单代换密码的终结者
字母 出现频率 字母 出现频率
a
0.082
n
0.067
b
0.015
o
0.075
c
0.028
在这种大环境下,阿拉伯世界 成为东西方文明交流的中转站,其 成就对欧洲乃至全世界都产生了巨 大影响。
Abbasid Caliphate (850)
20
频率分析:简单代换密码的终结者
频率分析 最早记录于9世纪阿尔.金迪的
革命性著作《关于破译加密信息的手稿》。 这项伟大成就是语言学、统计学和宗教信
仰之间的卓越联合,它在密码学历史上掀起 一场革命。
使用不同的代换表进行加解密。
注意:在维吉尼亚密码中,代换表不再是密钥了。
44
维吉尼亚密码
维吉尼亚密码的代换表 如右图
每行都由前一行向左移一位得到。 实际就是26个移位密码的代换表。 具体使用哪一行代换表,是基于 密钥进行的,在代换过程中会不断 变换。
45
维吉尼亚密码
明文:ATTACKATDAWN 密钥:LEMON (m=5) •加密
Julius Caesar (100 BC – 44 BC)
a b c d e . . . wx y z DE F GH . . . ZABC
没有密钥,不安全
13
移位密码
工作原理 • 加密 : 把明文中每个字母代换为字母表中其后的第k个字母
• 解密 : 与加密相反,把密文中每个字母代换为字母表中其前的第k个字母
01古典密码

移位密码实例
打开 Windows 电脑的注册表的如下目录: HKEY_CURRENT_USER\Software\Microsoft\Windows\ CurrentVersion\Explorer\UserAssist\{75048700-EF1F11D0-9888-006097DEACF9}\Count
24
单字母频率图
25
频率分组表
26个英文字母: e t---a---o---i---n---s---h---r d---l c---u---m---w---f---g---y---p---b v—k---j---x---q---z
12% 6%--9%
4% 1.5%--2.8%
<1%
26
频度最高的前30个双字母
TH HE IN ER AN RE ED ON ES ST EN AT TO NT HA ND OU EA NG AS OR TI IS ET IT AR TE SE HI OF
27
其它频率特征
① the 的使用频率最高,是ing的三倍, ② 一半的单词以e s d t 结尾 ③ 一半的单词以t a s w开头 ④ y的使用频率90%都集中在单词的结尾
a-1表示a的逆元,即a-1a≡1 (mod 26)
19
仿射密码例子
假设a=7, b=21,则a-1=15
如果明文c为security,则加密之后的密文m为rxjfkzyh 如果密文m为vlxijh,则解密之后的明文为agency
20
对仿射密码的攻击
仿射密码是比较简单的密码类型,对它的已知明文 攻击都可以很轻易地成功。
28
统计分析法
对于单表密码,虽然加密之后每个字母都变成了另外的 字母,但是这样只是把明文字母出现的概率转移到密文 字母中去
密码学3 序列密码

仿射加密
加密: c (am b) mod26 解密: m a1(c b) mod 26
0 m,c 25
2020/1/27
3
3. 多表代换密码
Playfair密码
将明文字母按照两个字母一组分组,然后将这 些组按照字母矩阵替换为密文字母组合。基于 一个5×5字母矩阵.
m1
,
m2
,md
kd1 kd 2 kdd
解密:
k11 k12 k1d 1
m1
,
m2
,
,
md
c1
,
c2
,
cd
kd1 kd 2 kdd
2020/1/27
5
第3章 序列密码
重点: 掌握LFSR的使用。 熟悉RC4加密算法。 学时:4-6学时
2020/1/27
24
二 特征多项式
设n级线性移位寄存器的输出序列{ai}满足递 推关系
an+k=c1an+k-1 c2an+k-2 … cnak 其中ci=0或1。 这种递推关系可用一个一元高次多项式 P(x)=1+c1x+…+cn-1xn-1+cnxn 表示,称这个多项式为LFSR的特征多项式。
2020/1/27
14
一、同步流密码
优点: 容易检测出是否有插入、删除等主动攻击。 如果密文中只有某个字符产生了错误(不是
插入或删除),只影响此字符的解密,不影 响其他字符,即无错误传播。
2020/1/27
15
单表置换密码

源程序如下:import java.util.*;public class test {public static void main(String[] args) {int m;do{System.out.println("请选择操作:1、加密 2、解密 0、退出 ");Scanner input=new Scanner(System.in);m=input.nextInt();char[] ZhiHuanBiao=new char['z'+1];char[] fanZhiHuanBiao=new char['z'+1];if(m!=0)setZhiHuan(ZhiHuanBiao, fanZhiHuanBiao);switch(m) //判断m值,执行相应的功能{case 1: JiaMi(ZhiHuanBiao);break;case 2: JieMi(fanZhiHuanBiao);break;default:break;}}while(m!=0);System.out.println("程序结束!");}private static void JieMi(char[] fanZhiHuanBiao) {String jiewen;System.out.println("请输入密文");Scanner jie=new Scanner(System.in);jiewen=jie.nextLine();char[] mi=jiewen.toCharArray();System.out.println("解密后的明文为:");for(int i=0;i<mi.length;i++) //直接利用置换表输出密文{if(mi[i]>='A'&&mi[i]<='z'&&mi[i]!='\0')mi[i]=fanZhiHuanBiao[mi[i]];System.out.print(mi[i]);}System.out.println("");}private static void JiaMi(char[] zhiHuanBiao) {String mingwen;System.out.println("请输入明文");Scanner jia=new Scanner(System.in);mingwen=jia.nextLine();char[] ming=mingwen.toCharArray();System.out.println("加密后的密文为:");for(int i=0;i<ming.length;i++) //直接利用置换表输出密文{if(ming[i]>='A' && ming[i]<='z')ming[i]=zhiHuanBiao[ ming[i]];System.out.print(ming[i]);}}private static void setZhiHuan(char[] zhiHuanBiao, char[] fanZhiHuanBiao) {String s; //密钥System.out.println("请输入密钥:");Scanner zhihuan=new Scanner(System.in); //读入密钥s=zhihuan.nextLine(); //输出密钥System.out.println("置换表为:");String s1="";String s2="";for(int i = 0 ; i < s.length();i++)//对密钥去掉空格和重复的字符{boolean sign =false; //标志变量if((s.charAt(i) >= 'A' && s.charAt(i)<='Z')){for(int j = 0; j < s1.length();j++){if(s.charAt(i) == s1.charAt(j)){sign =true;break;}}if(!sign) s1=s1+s.charAt(i);else sign =true;}}for(int i = 0 ; i < s.length();i++) //对密钥去掉空格和重复的字符{boolean sign2 =false; //标志变量if((s.charAt(i) >= 'a' && s.charAt(i)<='z')){for(int j = 0; j < s2.length();j++){if(s.charAt(i) == s2.charAt(j)){sign2 =true;break;}}if(!sign2) s2=s2+s.charAt(i);else sign2 =true;}}char ch2='a';for(int i = 'A' ;i <= 'Z'; i++) //该循环利用密钥得到置换表{if(i < 'A' + s2.length()) //前面直接用s1代替{zhiHuanBiao[i] = s2.charAt(i-'A');}else//后面将剩下的"贴"上去{ for(int j = 'A'; j < 'A' + s2.length(); j++){if(ch2 == zhiHuanBiao[j]){ch2++;j= 'A'; //每次都从头开始搜索continue;}}zhiHuanBiao[i] = ch2;ch2++;}System.out.print(zhiHuanBiao[i]+" ");//同时输出置换表}char ch='A';System.out.println();for(int i = 'a' ;i <= 'z'; i++) //该循环利用密钥得到置换表{if(i < 'a' + s1.length()) //前面直接用s1代替{zhiHuanBiao[i] = s1.charAt(i-'a');}else//后面将剩下的"贴"上去{for(int j = 'a'; j < 'a' + s1.length(); j++){if(ch == zhiHuanBiao[j]){ch++;j= 'a'; //每次都从头开始搜索continue;}}zhiHuanBiao[i] = ch;ch++;}System.out.print(zhiHuanBiao[i]+" ");//同时输出置换表}System.out.println();for( int i='A'; i<= 'z'; i++) //该循环利用置换表得到反置换表{ if(zhiHuanBiao[i]!='\0')fanZhiHuanBiao[ zhiHuanBiao[i]] = (char) i;}for( int i='A'; i<= 'Z'; i++){ if(fanZhiHuanBiao[i]!='\0')System.out.print(fanZhiHuanBiao[i]+" ");}System.out.println();for( int i='a'; i<= 'z'; i++){ if(fanZhiHuanBiao[i]!='\0')System.out.print(fanZhiHuanBiao[i]+" ");}System.out.println();}}实验结果:。
密码学实验-实验1 凯撒密码与单表置换

ifkey.count(i) ==0:
AlphaBet1[k] = i
k +=1
#将key中重复的字母删除
chuli_key()
#将key加入到密码表中
add_key()
#判断字母大小写
foriinmiwen:
ifi.isspace() ==True:
mingwen = mingwen +' '
"J","K","L","M","N","O","P","Q","R",
"S","T","U","V","W","X","Y","Z"]
#小写字母表
alphaBet = ["a","b","c","d","e","f","g","h","i",
"j","k","l","m","n","o","p","q","r",
char f(int i)
{
for(int x=0;x<26;x++)
if(str_passtable[x]==(i+'a'))return (x+'a');
古典密码的演化(二)—密码学复习(三)

古典密码的演化(⼆)—密码学复习(三)前⾯介绍了⼏种古典密码算法(凯撒密码、仿射密码、维吉尼亚密码、希尔密码、置换密码),下⾯将对其中的⼏种密码算法站在攻击者的⾓度进⾏分析。
三、密码破译密码破译的原则:遵循观察和经验⽅法:采⽤归纳与演绎步骤:分析、假设、推测和证实三⼤要素:①语⾔频率特征:如E出现频率最⾼;②连接特征:q...u,Iex.③重复特征:th,tion,tious.3.1 单表代换——密码分析利⽤统计数据获得密码分析。
例:假设从仿射密码获得的密⽂为:FMXVE D KAPHFE R BN D K R X R S R EFMO R U D S D K D VSHVUFE D KAP R K D LYEVL R HH R H.通过上⾯的57个密⽂字母,就可以分析仿射密码。
最⾼频率的密⽂字母:R——8次 D——7次 E、H、K——各5次 F、S、V——各4次根据已知的26个英⽂字母的概率分布表: E——0.127 T——0.091 A——0.082 O——0.075①假定R是E的加密,D是T的加密数值化后有:e k(4)=17 d k(19)=3⽽加密函数 e k(x)=ax+b.可以得到两个包含两个未知数的线性⽅程组:4a+b=1719a+b=3解得 a=6,b=19 (mod 26)这是⼀个⾮法密钥,因为gcd(6,26)=2≠1,所以假设不成⽴。
②假设R是e的加密,E是t的加密,解得 a=13,gcd(a,26)=13≠1,故此时假设不成⽴。
③假设R是e的加密,K是t的加密,此时解得 a=3,b=5.⾄少这是⼀个合法密钥。
接着计算k=(3,5)时的解密函数,之后对密⽂进⾏解密,观察的到的明⽂是否有意义。
容易验证a=3,b=5是⼀个有效密钥,解得明⽂为:Algorithms are quite general definitions of arithmetic process.3.2 多表代换——密码分析3.2.1 希尔密码对希尔密码进⾏已知明⽂分析。
现代密码学第二讲:古典密码学

明文p ∈Z26,密文c ∈Z26 ,密钥k取[1,25],只有25个
凯撒密码
例:使用其后的第三个字母代换该字母
明文:meet me after the toga party 密文:PHHW PH DIWHU WKH WRJD SDUWB
恺撒密码的攻击
已知明文和密文、加密和解密算法,需要解 同余方程,可以恢复密钥 k = (c- p) mod (26); 穷举攻击:已知密文,且明文为有意义字符 ,至多尝试25次,可以恢复明文.
惟密文攻击
令R=E(e),D=E(t),得到方程组
a b c d e f g h i j k
0 1 2 3 4 5 6 7
l
m n
o
p
q
r
s
t
u
v
w
x
y
Z
8 9 10 11 12 13 14
15 16
17 18
19 20
21 22
23 24 25
4a + b = 17 19a + b = 3
多表代换密码
维吉尼亚密码:在长为m的密码中,任何一 个字母可被影射为26个字母中的一个
明文p ∈(Z26)m,密文c ∈ (Z26)m ,密钥k ∈ (Z26)m
加密 c= (p1+k1 ,,p2+k2 ,, …, pm+km) mod 26; 解密 p = (c1-k1 ,,c2-k2 ,, …, cm-km) mod 26.
希尔密码
已知m组明文和密文、加密和解密算法,需要解m 元同余方程组可以恢复密钥;
c11 M cm1 c12 M cm2 L c1m p11 M M = M L cmm pm1 p12 L M M pm2 L p1m k11 M M pmm km1 k12 M km2 L k1m M M L kmm
单表代换密码课程设计

单表代换密码课程设计一、课程目标知识目标:1. 学生能理解单表代换密码的定义和基本原理;2. 学生能够掌握至少一种单表代换密码的加密和解密方法;3. 学生能够解释单表代换密码在历史和现代通信中的应用和重要性。
技能目标:1. 学生能够运用所学知识,独立完成单表代换密码的加密和解密操作;2. 学生能够运用逻辑思维和分析能力,破解简单的单表代换密码;3. 学生能够运用单表代换密码进行简单信息的传递和解读。
情感态度价值观目标:1. 学生能够认识到密码学在信息安全中的重要作用,增强信息安全意识;2. 学生通过学习单表代换密码,培养对密码学的好奇心和探索精神;3. 学生能够体会到团队合作在解决问题中的优势,增强团队协作意识。
课程性质:本课程为信息技术与信息安全领域的拓展课程,旨在通过学习单表代换密码,提高学生的信息素养和逻辑思维能力。
学生特点:考虑到学生所在年级的特点,课程内容设计将结合学生的认知水平和兴趣,以实际操作和案例分析为主线,增强学生的学习兴趣和参与度。
教学要求:教师应注重理论与实践相结合,通过问题驱动的教学方式,引导学生主动探究和解决问题,确保学生达到课程目标所设定的具体学习成果。
同时,关注学生的个体差异,给予个性化指导,使全体学生都能在课程中取得进步。
二、教学内容1. 单表代换密码的定义与分类:介绍单表代换密码的基本概念、分类及其特点,结合教材相关章节,使学生理解其在密码学中的地位和作用。
2. 单表代换密码的加密方法:详细讲解至少一种单表代换密码的加密过程,如凯撒密码、替换密码等,让学生掌握其基本操作和原理。
3. 单表代换密码的解密方法:分析单表代换密码的解密技巧,指导学生学会如何逆向思考,破解加密信息。
4. 单表代换密码的应用实例:通过案例分析,介绍单表代换密码在历史和现代通信中的应用,让学生了解其实际价值。
5. 单表代换密码的安全性分析:探讨单表代换密码的安全性,分析其可能存在的弱点,引导学生思考如何提高密码的安全性。
单表代换密码课程设计

单表代换密码课程设计一、课程目标知识目标:1. 学生能理解单表代换密码的概念,掌握其基本原理和应用方法。
2. 学生能运用所学知识,分析并解决实际问题,如编制和破译简单的单表代换密码。
3. 学生了解单表代换密码在历史和现实生活中的应用,提高对密码学的认识。
技能目标:1. 学生能够独立完成单表代换密码的编制和破译,提高逻辑思维和推理能力。
2. 学生通过小组合作,培养团队协作能力和沟通技巧,共同解决复杂问题。
3. 学生能够运用信息技术手段,如计算机软件,辅助完成单表代换密码的编制和破译。
情感态度价值观目标:1. 学生培养对密码学的兴趣,激发学习主动性和积极性。
2. 学生通过学习单表代换密码,认识到信息安全的重要性,提高信息保护意识。
3. 学生在小组合作中,学会尊重他人意见,培养良好的团队精神和道德品质。
课程性质:本课程为信息技术与数学相结合的跨学科课程,注重培养学生的逻辑思维、动手能力和团队协作精神。
学生特点:六年级学生具有一定的信息素养和数学基础,对新鲜事物充满好奇心,喜欢动手操作和实践。
教学要求:结合学生特点,采用任务驱动、小组合作等教学方法,引导学生主动探究,提高课堂参与度。
将课程目标分解为具体的学习成果,便于教学设计和评估。
二、教学内容1. 单表代换密码的基本概念与原理:- 引导学生了解密码学发展简史,认识单表代换密码的地位与作用。
- 讲解单表代换密码的构成要素,如密钥、加密算法和加密过程。
2. 单表代换密码的编制与破译:- 介绍单表代换密码的编制方法,如凯撒密码、替换密码等。
- 指导学生通过实际操作,学会编制和破译简单的单表代换密码。
3. 单表代换密码的应用实例:- 分析历史上著名的单表代换密码案例,如二战时期的恩尼格玛密码机。
- 讨论单表代换密码在现实生活中的应用,如计算机安全、通信加密等。
4. 密码学相关信息技术:- 结合计算机软件,介绍单表代换密码的编程实现方法。
- 引导学生了解信息安全领域的基本概念,提高信息保护意识。
单表代替的缺点

置移动的密码。
换句话说,移位密码就是对明文字符的位置 进行重新排列的一种密码。移位密码有时也称为 易位密码、置换密码、换位密码等。
4
例1 明文:明晨五时发起总攻
移位规则:
密文字符位置
明文字符位置
1
5
2
4
3
6
4
8
5
7
6
3
7
2
8
1
该移位规则的含义是:第1个密文字符是第5个明文字符、 第2个密文字符是第4个明文字符,…。由该移位规则加密得到 的密文为:
10
在拼音文字国家,其早期大多采用代替密码,而现
代机器密码也大量采用代替密码法。
广义地讲,由于所有的加密算法都是密文对明文的
代替,因而都是代替密码。
代替密码可分为单表代替、多表代替。 其中在多表代替密码中,有一类在理论上是可以证
明能够做到不可破译的。
11
1、单表代替
在单表代替中, 始终使用一个代替表, 即代替表是固定的, 与被加密的明文字符组的序号无关。 设 是所有可能的明文字符组, 是对应的密文字符组,
符的统计规律之中.形态变但位置不变
24
英文字母使用频率
25
26
英语字母中常见的组合
27
单表代替的上述信息泄漏,直接导致了对单表代
替密码的破译方法。
在唯密文攻击条件下,由于敌手可以掌握明文字
符或明文字符组的统计规律,因而可利用不同的 明文字符或明文字符组的出现频次的不同,利用 密文字符或密文字符组的出现频次推断出代替关
单表代替的缺点:明文字符相同,则密文字符也相同 代替密码的代替规则就是其密钥。在例4中,由于10个数 字的全排列共有10!,因而由十个数字形成的单表代替的 总数是10!。
单表代替密码原理及算法实现

单表代替密码原理及算法实现 要了解单表替代密码就得先了解替代密码,在这⾥我就做⼀下简单的介绍:替代是古典密码中⽤到的最基本的处理技巧之⼀。
替代密码是指先建⽴⼀个替换表,加密时将需要加密的明⽂依次通过查表,替换为相应的字符,明⽂字符被逐个替换后,⽣成⽆任何意义的字符串,即密⽂,替代密码的密钥就是其替换表。
根据密码算法加解密时使⽤替换表多少的不同,替代密码⼜可分为单表替代密码和多表替代密码。
单表替代密码的密码算法加解密时使⽤⼀个固定的替换表。
单表替代密码⼜可分为⼀般单表替代密码、移位密码、、密钥短语密码。
这⾥讲单表替代密码的直接攻击。
对于⾃然语⾔,如果取⼀本⾮专业书籍,统计⾜够长的课⽂就会发现,字母(或字符)出现的频率会反映出相应语⾔的统计特性。
统计⼤量的课⽂定会发现,相应语⾔中每个字母在相应语⾔中出现的概率。
于是便得到该语⾔字母表上的⼀个概率分布。
⼀、英⽂字母⼀由独⽴试验产⽣明⽂单码,Beker在1982年统计的样本总数为100 362,得到单码的概率分布见下表:根据上表,英⽂字母出现的概率按⼤⼩排列如下:E T A O I N S H R D L C U M WFG Y P B V K J X Q Z在上表中,不少字母出现的概率近乎相等。
为了应⽤⽅便,常将英⽂字母表按字母出现的概率⼤⼩分类,分类情况见下表:--------------------------极⾼频 E次⾼频 T A O I N S H R中等频 D L低频 C U M W F G Y P B甚低频 V K J X Q Z--------------------------其它语⾔和数据也有类似于英语语⾔的单字母统计特性。
如果我们随意统计⼀段⾜够长的英⽂课⽂,只要内容不是太特殊,其结果⼀定和上表基本相同。
这表明英⽂的⼀篇⽂章中各个字母出现的概率是基本可预测的,它将为密码分析提供⼀个⽅⾯的依据。
语⾔的单字母统计特性⾄少在以下两个⽅⾯没有反映出英⽂语⾔的特征:⑴根据英⽂的单字母统计特性可以计算出双字母QE出现的概率为p(QE)=0.00095×0.12702≈1.21×10^(-4)这就是说,在10^6个双字母的抽样中,QE出现的次数⼤约应为121次,但这不符合英⽂课⽂的实际。
实现单表代换加解密并对其攻击

对单表代换加密算法的实现和攻击——PB09210277 阮琪森一、单表代换加密算法的实现1.对单表代换加密算法的理解。
单表代换加密算法是传统对称加密算法的一种,它主要是通过输入的密钥建立一个明文字符和密文字符的映射表来实现加密。
它的密钥空间为26!,因此它相对于Caesar 密码在抗穷举攻击方面有了很大的改进。
但是在抗频率统计攻击方面就显得很脆弱,只要密文的长度足够,就可以轻易地进行唯密文攻击。
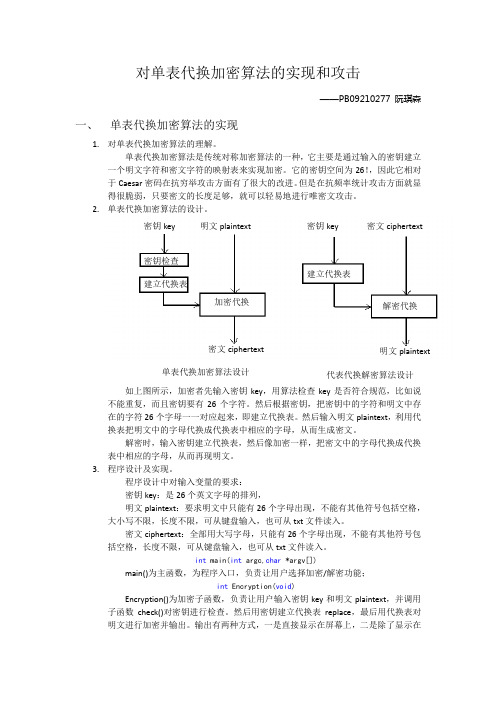
2.单表代换加密算法的设计。
如上图所示,加密者先输入密钥key ,用算法检查key 是否符合规范,比如说不能重复,而且密钥要有26个字符。
然后根据密钥,把密钥中的字符和明文中存在的字符26个字母一一对应起来,即建立代换表。
然后输入明文plaintext ,利用代换表把明文中的字母代换成代换表中相应的字母,从而生成密文。
解密时,输入密钥建立代换表,然后像加密一样,把密文中的字母代换成代换表中相应的字母,从而再现明文。
3.程序设计及实现。
程序设计中对输入变量的要求:密钥key :是26个英文字母的排列,明文plaintext :要求明文中只能有26个字母出现,不能有其他符号包括空格,大小写不限,长度不限,可从键盘输入,也可从txt 文件读入。
密文ciphertext :全部用大写字母,只能有26个字母出现,不能有其他符号包括空格,长度不限,可从键盘输入,也可从txt 文件读入。
int main(int argc,char *argv[])main()为主函数,为程序入口,负责让用户选择加密/解密功能;int Encryption(void )Encryption()为加密子函数,负责让用户输入密钥key 和明文plaintext ,并调用子函数check()对密钥进行检查。
然后用密钥建立代换表replace ,最后用代换表对明文进行加密并输出。
输出有两种方式,一是直接显示在屏幕上,二是除了显示密钥key密文ciphertext 密钥key 明文plaintext 密钥检查加密代换建立代换表建立代换表解密代换密文ciphertext 明文plaintext单表代换加密算法设计代表代换解密算法设计在屏幕上以外还输出到用户指定的文件中。
2.2_单表代替密码

明文 a b c d e f g h i j k l m 密文 A D G J M P S V Y B E H K 明文 n o p q r s t u v w x y z 密文 N Q T W Z C F I L O R U X
22
第二章 古典密码学
问题: 在(k, q) = 1时,如何求k模q的逆?
7
第二章 古典密码学
加密变换为: Ek(m) = m + k ≡ c (mod q) 0 ≤ m, c<q
解密变换为: Dk = Eq−k(c) ≡ m (mod q)
移位代替密码的密钥空间K = {k | 0≤ k < q}元素的个 数为q, 其中k = 0是恒等变换。
8
第二章 古典密码学
例2.3 凯撒密码(Caesar Cipher)是对英文字母表进 行移位代替的密码, 即q = 26。例如, 选择密钥k = 3, 则有 下述代替表:
13
第二章 古典密码学
定 理 2.1 在 乘 法 代 替 密 码 中 , 当 且 仅 当 gcd(k,q) = 1, Ek 才是一一映射。
14
第二章 古典密码学
证明: 对于任意的 j, k, i ∈ Zq, jk ≡ ik (mod q) ⇔ (j - i)k ≡ 0 (mod q)。
若 gcd(k, q) = 1, 则必有 j = i, 因而是一一映射。 若 gcd(k, q) = d>1, 则 j = i + q/d 也可使 (j−i)k ≡ 0 (modq), 因而对 j ≠ i, j 和 i 将被映射成同一字母, Ek 不再 是一一的。
27
第二章 古典密码学
这样, 我们就得到了一种易于记忆而代替表 又有多种可能选择的密码。用不同的密钥字就可得 到不同的代替表。q = 26时, 将可能有26! = 4×1026 种代替表。除去一些不太有用的代替表外, 绝大多 数代替表都是可用的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验报告
姓名:1111 学号:111111 班级:1111111 日期:111
1 古典密码(单表代换密码)
一、实验环境
1.硬件配置:处理器:Corei5 M ***********,内存2GB,主硬盘
320G
2.使用软件:
(1)操作系统:win7
(2)软件工具:Microsoft Visual C++6.0
二、实验设计的相关概念或基本原理
1.单表代换密码的基本原理:
对字母表中的每一个字母用别的字母代换形成密文。
明文和密文代换的规则可以是先任选一个易记的单词或短语或一句话作为密钥放在前面,然后从A到X的顺序中剔除前面出现过的字母后依次补在后面,形成代换表。
三、实验内容
根据实验原理的介绍,你先选取一个密钥,创建一个明文信息,编写实现程序,实现加密和解密的操作。
实验流程图:
四、实验总结分析
关键代码:
1.产生代换表:
void generate_alphabeta( )//产生代换表
{
int i,j;
cout<<"请先输入密钥句子,至少为1个字符,最多100个字符,且第一个字符必须是小写字母:"<<endl;
cin>>miyue;//输入的密钥句子,至少为1个字符,最多100个字符,且第一个必须为字母
cout<<miyue<<endl;
int length=strlen(miyue);
//cout<<"密钥句子的长度为:"<<length<<endl;
int pos=0;//指示填充位置
int tag=1;//
alphabeta[0] =miyue[0];//填充第0个位置
for(i=1;i<length;i++)
{
if (isalpha(miyue[i])!=0) //是字母
{
tag=1;
for (j=0;j<=pos;j++)
{
if(alphabeta[j]==miyue[i])//alphabet表中已经存在字母miyue[i]
{
tag=0;
break;
}
}
if(tag==1)
alphabeta[++pos]=miyue[i];
}
}
for(i=0;i<26;i++) //把英文字母表中还没有出现在代换字母表中的字母存入代换字母表
{
tag=1;
for (j=0;j<=pos;j++)
{
if(alphabeta[j]==str[i])//alphabet表中已经存在英文字母表中的第i个字母{
tag=0;
break;
}
}
if(tag==1)
alphabeta[++pos]=str[i];
}
cout<<"原始字母表为"<<str<<endl;
cout<<"代换密码表为"<<alphabeta<<endl;
}
2.加密算法
int encrepty( )//加密
{
int pos;
//alphabeta[0]是序号为0的字母a的密文,alphabeta[1]是序号为1的字母的密文...,依次类推
for(int i=strlen(source);i>=0;i--)
{
if(islower(source[i]))//假如当前字符是小写字母
{
pos=source[i]-'a';//计算出当前字母在字母表中的序号
cipher[i]=alphabeta[pos];
}
else //不是字母,原样复制
cipher[i]=source[i];
}
cout<<"密文为:"<<cipher<<endl;
return 1;
}
3.解密算法
int deciphring( )//解密
{
for(int i=strlen(cipher);i>=0;i--)
{
if(islower(cipher[i]))//假如当前字符是小写字母
{
for (int j=0;j<26;j++)
{
if(cipher[i]==alphabeta[j])
//当前密文字符,在代换字符表的第j个位置,在其明文字符为str[j];
{
source[i] =str[j];
break;
}
}
}
else //不是字母,原样复制
source[i]=cipher[i];
}
cout<<source<<endl;
return 1;
}
结果显示:
4.小结
此算法的难点在于如何通过密钥句子写出代换表,根据算法的思路,主要是要解决去掉密钥句子中重复字母,再将未出现过的字母依次填充代换表中,形成最终的代换表。
在编程的过程中,看似简单的过程却总是无法正常实现填充过程,后来在与同学讨论之后,发现使用布尔变量来作为是否已存在相同字母的填充标记,最终解决了如何填充的问题。
