2009考研数一真题及解析
北京邮电大学《电子电路》考研真题2009年

北京邮电大学《电子电路》考研真题2009年(总分:66.00,做题时间:90分钟)一、{{B}}选择题{{/B}}(总题数:1,分数:6.00)稳压管2CW22、2CW20的稳压值的电压温度系数分别为-0.05%/℃,0.095%/℃,在下图中的______、______接法能起到减小温度对稳压值的影响。
A. B. C.(分数:6.00)A.B. √C.解析:A.B.C. √解析:(3).集成运放的输入失调电压U IO是______。
• A.两个输入端电压之差• B.输入端都为零时的输出电压• C.输出端为零时输入端的等效补偿电压(分数:1.50)A.B.C. √解析:(4).电路如下图所示,欲使后级c点向前级引入负反馈,则应______。
• A.c端和b端连接• B.c端和d端连接• C.c端和a端连接(分数:1.50)A.B.C. √解析:二、{{B}}判断题{{/B}}(总题数:6,分数:9.00)1.输入电阻、输出电阻、增益、频率响应和非线性失真是衡量放大电路品质优劣的主要性能指标。
(分数:1.50)A.正确√B.错误解析:2.共集电路又称为电压跟随器;共基电路又称为电流跟随器。
(分数:1.50)A.正确√B.错误解析:3.改善放大电路低频响应的方法是采用直接耦合放大电路;改善高频响应的较好方法是采用共基电路。
(分数:1.50)A.正确√B.错误解析:4.用一定频率的方波信号去测试某放大电路的频率响应,若方波响应很好,则电路的频带较宽。
(分数:1.50)A.正确√B.错误解析:5.放大电路的图解分析法是针对电子器件的非线性特性的一种直观的信号分析方法。
(分数:1.50)A.正确√B.错误解析:6.在串联负反馈电路中,信号源内阻R s的值越小,反馈效果越好。
(分数:1.50)A.正确√B.错误解析:三、{{B}}计算题{{/B}}(总题数:3,分数:51.00)电路如图1所示,要求:图1(分数:16.00)(1).按图中给出的u i正方向给出u o的极性(分数:4.00)___________________________________________________________ _______________________________正确答案:(u o极性如图2所示。
2009考研数学一真题及答案

2009考研数学一真题及答案一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.(1)当0x →时,()sin f x x ax =-与()()2ln 1g x x bx =-等价无穷小,则( )()A 11,6a b ==-. ()B 11,6a b ==. ()C 11,6a b =-=-. ()D 11,6a b =-=. 【答案】 A【解析】2()sin ,()(1)f x x ax g x x ln bx =-=-为等价无穷小,则222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bx bx→→→→→---==-⋅---洛洛230sin lim 166x a ax a b b axa→==-=-⋅ 36a b ∴=- 故排除,B C 。
另外201cos lim3x a axbx →--存在,蕴含了1cos 0a ax -→()0x →故 1.a =排除D 。
所以本题选A 。
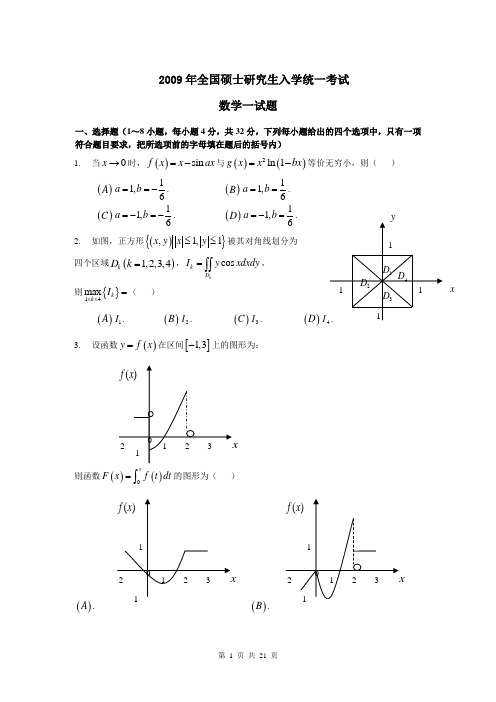
(2)如图,正方形(){},1,1x y x y ≤≤被其对角线划分为四个区域()1,2,3,4k D k =,cos kk D I y xdxdy =⎰⎰,则{}14max k k I ≤≤=( )()A 1I .()B 2I . ()C 3I .(D 【解析】本题利用二重积分区域的对称性及被积函数的奇偶性。
24,D D 两区域关于x 轴对称,而(,)cos (,)f x y y x f x y -=-=-,即被积函数是关于y 的奇函数,所以240I I ==;13,D D 两区域关于y 轴对称,而(,)cos()cos (,)f x y y x y x f x y -=-==,即被积函数是关于x 的偶函数,所以{}1(,),012cos 0x y y x x I y xdxdy ≥≤≤=>⎰⎰; x{}3(,),012cos 0x y y x x I y xdxdy ≤-≤≤=<⎰⎰.所以正确答案为A.(3)设函数()y f x =在区间[]1,3-上的图形为:则函数(F()A .()B .()C .()D .【答案】D【解析】此题为定积分的应用知识考核,由()y f x =的图形可见,其图像与x 轴及y 轴、0x x =所围的图形的代数面积为所求函数()F x ,从而可得出几个方面的特征:①[]0,1x ∈时,()0F x ≤,且单调递减。
2009年考研数学一真题及答案
2009年全国硕士研究生入学统一考试数学一试题一、选择题(1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内)1. 当0x →时,()sin f x x ax =-与()()2ln 1g x x bx =-等价无穷小,则( )()A 11,6a b ==-. ()B 11,6a b ==. ()C 11,6a b =-=-. ()D 11,6a b =-=.2. 如图,正方形(){},1,1x y x y ≤≤被其对角线划分为四个区域()1,2,3,4k D k =,cos kk D I y xdxdy =⎰⎰,则{}14max k k I ≤≤=( )()A 1I .()B 2I . ()C 3I .()DI 3. 设函数()y f x =在区间[]1,3-上的图形为:则函数()()0x F x f t dt =⎰的图形为( )()A .()B .x()C .()D .4. 设有两个数列{}{},n n a b ,若lim 0n n a →∞=,则( )()A 当1n n b ∞=∑收敛时,1n n n a b ∞=∑收敛.()B 当1n n b ∞=∑发散时,1n n n a b ∞=∑发散.()C 当1nn b∞=∑收敛时,221n nn a b∞=∑收敛.()D 当1nn b ∞=∑发散时,221n nn a b∞=∑发散.5. 设123,,ααα是3维向量空间3R 的一组基,则由基12311,,23ααα到基 122331,,αααααα+++的过渡矩阵为( )()A 101220033⎛⎫⎪⎪ ⎪⎝⎭. ()B 120023103⎛⎫⎪⎪ ⎪⎝⎭.()C 111246111246111246⎛⎫- ⎪ ⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭.()D 111222111444111666⎛⎫-⎪ ⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭. 6. 设,A B 均为2阶矩阵,**,A B 分别为,A B 的伴随矩阵,若2,3A B ==,则分块矩阵O A B O ⎛⎫⎪⎝⎭的伴随矩阵为( )()A **32O B A O ⎛⎫ ⎪⎝⎭.()B **23OB A O ⎛⎫⎪⎝⎭. ()C **32O A BO ⎛⎫ ⎪⎝⎭.()D **23O A BO ⎛⎫⎪⎝⎭.7. 设随机变量X 的分布函数为()()10.30.72x F x x -⎛⎫=Φ+Φ⎪⎝⎭,其中()x Φ为标准正态分布函数,则EX =( )()A 0.()B 0.3. ()C 0.7.()D 1.8. 设随机变量X 与Y 相互独立,且X 服从标准正态分布()0,1N ,Y 的概率分布为{}{}1012P Y P Y ====,记()Z F z 为随机变量Z XY =的分布函数,则函数()Z F z 的间断点个数为( )()A 0.()B 1. ()C 2.()D 3.二、填空题(9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.)9. 设函数(),f u v 具有二阶连续偏导数,(),z f x xy =,则2zx y∂=∂∂ 。
考研数学一二维随机变量及其分布历年真题试卷汇编2_真题(含答案与解析)-交互

考研数学一(二维随机变量及其分布)历年真题试卷汇编2(总分150, 做题时间180分钟)选择题1.[2009年] 设随机变量X与Y相互独立,且X服从标准正态分布N(0,1),Y(z)为随机变量Z=XY的分布函数,则函的概率分布P(Y=0)=P(Y=1)=1/2.记FZ数F(z)的间断点的个数为( ).ZSSS_SINGLE_SELAB1C2D3分值: 7.5答案:BF(z)=P(Z≤z)=P(XY≤z)=P(XY≤z|Y=0)P(Y=0)+P(XY≤z|Y=1)P(Y=1)Z=[P(XY≤z|Y=0)+P(XY≤z|Y=1)]/5.又X,Y相互独立,故 F(z)=[P(X·0≤z)+P(X≤z)]/2.Z(z)=[+ф(z)]/2=ф(z)/2.当z<0时, FZ(z)=[P(Ω)+P(X≤z)]/2=[1+ф(z)]/2.当z≥0时, FZ综上所述,得到因(z)只有一个间断点z=0.仅B入选.所以FZ2.[2012年] 设随机变量X与Y相互独立,且分别服从参数为1和参数为4的指数分布,则P(X<Y)=( ).SSS_SINGLE_SELA1/5B1/3C2/5D4/5分值: 7.5答案:A由题设有而X与Y相互独立,故f(x,y)=fX (x)fY(y)=则P(X<Y)= f(x,y)dxdy=∫0+∞∫x+∞4e-(x+4y)dxdy=一∫+∞e-x dx∫x+∞e-4y d(一4y)=∫0+∞e-x·e-4x dx=∫+∞e-5x dx=仅A入选.3.[2005年] 设二维随机变量(X,Y)的概率分布为若随机事件{X=0}与{X+Y=1}相互独立,则( ).SSS_SINGLE_SELAa=0.2,b=0.3Ba=0.4,b=0.1Ca=0.3,b=0.2Da=0.1,b=0.4分值: 7.5答案:B由=(a+0.4)+(b+0.1)=a+b+0.5=1(归一性)知,a+b=0.5.又由事件{X=0}与{X+Y=1}相互独立,有P(X=0,X+Y=1)=P(X=0)P(X+Y=1),而P(X=0,X+Y=1)=P(X=0,Y=1)=a,P(X=0)=a+0.4,P(X+Y=1)=P(X=0,Y=1)+P(X=1,Y=0)=a+b,故 a=(a+0.4)(a+b)=(a+0.4)×0.5.①所以a=0.4.从而b=0.5一a=0.1.填空题4.[2003年] 设二维随机变量(X,Y)的概率密度为则P(X+Y≤1)=______.SSS_FILL分值: 7.5答案:首先求出积分区域D ∩ G.D ∩ G实质上是G={(x,y)|0≤x≤y≤1}与D={(x,y)|x+y≤1}交集.可知,0≤x≤y≤1是在y=x上方的区域,而x+y≤1是直线x+y=1下方的区域.两者之交即为D ∩ G(见图),故5.[2015年] 设二维随机变量(X,Y)服从正态分布N(1,0;1,1;0),则P{XY—Y<0}=_______.SSS_FILL分值: 7.5答案:因(X,Y)~N(1,1;0,1;0),ρ=0,故X,Y相互独立,则P{XY—y<0}=P{(X一1)Y<0}=P{X一1<0,Y>0}+P{X一1>0,Y<0}=P{X<1}P{Y>0}+P{X>1}P{Y<0}.因X~N(1,1),故P{X<1}=P{X>1}=.因Y~N(0,1),故P{Y>0}=P{Y<0}=.所以6.[2006年] 设随机变量X与Y相互独立,且均服从区间[0,3]上的均匀分布,则P(max{X,Y}≤1)=______.SSS_FILL分值: 7.5答案:1/9P(max(X,Y)≤1)=P({X≤1}{Y≤1})=P(X≤1,Y≤1)=P(X≤1)P(Y≤1)=[(1一0)/(3—0)][(1一0)/(3一0)]=(1/3)×(1/3)=1/9.解答题[2008年] 设随机变量X与Y相互独立,X的概率分布为P(X=i)=1/3(i=一1,0,1),Y的概率密度为记Z=X+Y.SSS_TEXT_QUSTI7.求P(Z≤1/2|X=0);分值: 7.5答案:由于X,Y相互独立,有P(Z≤1/2 |X=0)=P(X+Y≤1/2|X=0)=P(y≤1/2|X=0)SSS_TEXT_QUSTI8.求Z的概率密度fZ(z).分值: 7.5答案:因X的可能取值为一1,0,1,而fY(y)取非零值的自变量的变化范围为0≤y≤1,一1≤z=x+y≤2.(1)当z≥2时,X,Y的所有取值均满足上式,故F(z)=P(Z≤z)=P(X+Y≤z)=1.(2)当z=x+y<一1时,X,Y的取值为空值,则P(X+Y≤z)==0.(3)当一1≤z<2时,下面用全概率公式求出FZ(z)的表示式:FZ(z)=P(Z≤z)=P(X+Y≤z)=P(X+Y≤z|X=一1)P(X=一1)+P(X+Y≤z|X=0)P(X=0)+P(X+Y≤z|X=1)P(X=1)(Fy(z)为y的分布函数),则fZ (z)=F'Z(z)=[FY(z+1)+fY(z)+fY(z—1)].当0<z+1<1或0<z<1或0<z—1<1,即一1<z<2时,FZ(z)=;其他情况下,fZ(z)=0.[2017年] 设随机变量X,Y相互独立,,Y的概率密度为fY(y)=SSS_TEXT_QUSTI9.求P{Y≤E(Y)};分值: 7.5答案:因E(Y)=∫-∞+∞yfY(y)dy=∫1y·2ydy=,故SSS_TEXT_QUSTI10.求Z=X+Y的概率密度.分值: 7.5答案:Z的分布函数FZ(Z)=P{X+Y≤z,X=0}+P{X+Y≤z,X=2} =P{X=0,Y≤z}+P{X=2,Y+2≤z}=,故Z的概率密度函数为[2014年] 设随机变量X的概率分布为P(X=1)=P(X=2)=,在给定X=i的条件下,随机变量y服从均匀分布U(0,i)(i=1,2).SSS_TEXT_QUSTI11.求Y的分布函数F(y);Y分值: 7.5答案:记U(0,i)的分布函数为F(x)(i=1,2),则i(y)=p(Y≤Y)=P(x=1)P(Y≤y|X=1)+P(X=2)P(Y≤y|X=2)于是FY因在X=i的条件下,Y服从均匀分布U(0,i)(i=1,2),故当y≤0时,(y)=0.Fi当0<y≤1时,当1<y<2时,当y≥2时,所以SSS_TEXT_QUSTI12.求期望E(Y).分值: 7.5答案:(y)可得概率密度函数为由Y的分布函数FY+∞yfy(y)dy=故E(Y)=∫-∞[2013年] 设随机变量X的概率密度为令随机变量,SSS_TEXT_QUSTI13.求y的分布函数;分值: 7.5答案:+∞f(x)dx=,得到a=9.此时,X的利用概率密度函数的归一性,由1=∫-∞概率密度为(y).由题设知,Y的取值范围为1≤Y≤2,故设Y的分布函数为FY(y)=P{Y≤y}=0;P(1≤Y≤2)=1.因而当y<1时,FY当1≤Y<2时,F(y)=P{Y≤y}=P{Y<1}+P{Y=1}+P{1<Y≤y}Y=0+P{X≥2}+P{1<X≤Y}=(y)=P{Y≤y}=P{Y≤2}=1.当Y≥2时,FY综上得到y的分布函数为SSS_TEXT_QUSTI14.求概率P{X≤Y}.分值: 7.5答案:由随机变量y的分段表示式易看出,满足x≤y的x的取值范围为x<2.因而所求概率为P{X≤Y}=P{X<2}=[2016年]设二维随机变量(X,Y)在区域D=((x,y)|0<x<1,x2<y<)上服从均匀分布.令SSS_TEXT_QUSTI15.写出(X,Y)的概率密度;分值: 7.5答案:易求得区域D的面积,故(X,Y)的概率密度SSS_TEXT_QUSTI16.问U与X是否相互独立?并说明理由;分值: 7.5答案:考查事件{U=0}与乘积的概率是否与事件{U=0}的概率的乘积相等.事实上,它们不相等.易求得显然,故U与X不独立.SSS_TEXT_QUSTI17.求Z=U+X的分布函数FZ(z).分值: 7.5答案:下面用全集分解法求f(u,v)的分布函数FZ(z)=P(Z≤z)=P(U+X≤z).FZ(z)=P(U+X≤z)=P(U=0,U+X≤z)+P(U=1,U+X≤z)=P(U=0,X≤z)+P(U=1,U≤z—1)=P(X>y,X≤z)+P(X≤Y,X≤z一1)注意到x取值的边界点为0,1,而U取值边界点也为0,1,因而z的取值的分段点为0,1,2.于是应分下述四种情况分别求出FZ(z)的表示式.①z<0时,则P(X≤z)==0,P(X≤z—1)==0,故FZ(z)=0.②0≤z<1时,③1≤z<2时,④z≥2时,FZ(z)=P(X>Y)+P(X≤y)=P(U=0)+P(U=1)=1.综上所述,Z的分布函数为[2009年] 袋中有一个红球、两个黑球、三个白球.现在有放回地从袋中取两次,每次取一个,以X,Y,Z分别表示两次取球所取得的红球、黑球与白球个数.SSS_TEXT_QUSTI18.求P(X=1|Z=0);分值: 7.5答案:(I)用缩减样本空间的方法求之.求时应注意两次取球取到的是不同类的球,要讲次序.因而两次都没取到白球(Z=0)的条件下,只能取红、黑两种球,且每次都要取到一个红球,其可能性为C11×C21+C21×C11=4,总的可能性为C 31×C31=3×3=9,故SSS_TEXT_QUSTI19.求二维随机变量(X,Y)的概率分布.分值: 7.5答案:由题设知X与Y的所有可能取值均为0,1,2,而取值的概率可由古典概率的计算公式得到.计算时要注意两次取球取到的是不同类的球要讲次序,取到的是同类的球不讲次序.故(X,Y)的概率分布为20.设随机变量X的概率密度为f(x)=e-|x|/2,一∞<x<+∞,问随机变量X 与|X|是否相互独立?为什么?SSS_TEXT_QUSTI分值: 7.5答案:因X和|X|为两个随机变量,下面证明对于给定的a(0<a<+∞),式P(X<x,Y<y)=P(X<x)P(Y<y)不成立,从而X与|X|不相互独立.事实上,因事件{|X|<a}包含在事件{X<a}之中,即{X<a} {|X|<a},故P(X<a,|X|<a)=P({X<a}∩{|X|<a})=P(|X|<a).又P(X<a)<1,P(|X|<a)>0,因而P(X<a)P(|X|<a)<P(|X|<a).于是P(X<a,|X|<a)=P(|X|<a)>P(X>a)P(|X|<a),故P(X>a,|X|<a)≠P(X<a)P(|X|<a) (0<a<+∞).可知,X与|X|不相互独立.1。
2009年全国考研数学一真题及答案.doc
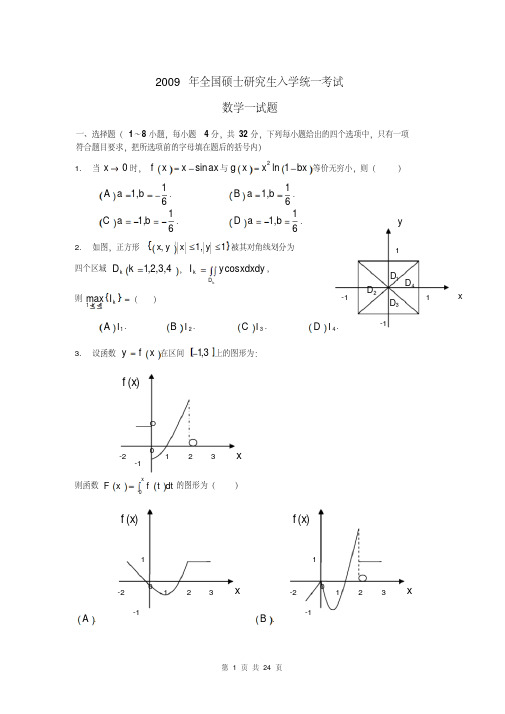
以 X ,Y , Z 分别表示两次取球所取得的红球、黑球与白球的个数。
(Ⅰ)求 p X 1 Z 0 ;
(Ⅱ)求二维随机变量 X , Y 概率分布。
第 4 页 共 24 页
9. (本题满分 11 分)
设总体 X 的概率密度为 f ( x)
2xe x , x 0 ,其中参数 (
0,其他
0) 未知, X 1 ,
S1
an , S2
a2 n 1 ,求 S1 与 S2 的值。
n1
n1
3.
x2 (本题满分 11 分)椭球面 S1 是椭圆
y2 1 绕 x 轴旋转而成,圆锥面 S2 是过点
43
第 3 页 共 24 页
x2 4,0 且与椭圆
4
y2 1
3
相切的直线绕 x 轴旋转而成。
(Ⅰ)求 S1及 S2 的方程
(Ⅱ)求 S1与 S2 之间的立体体积。
2z
9. 设函数 f u, v 具有二阶连续偏导数, z f x, xy ,则
。
xy
10. 若二阶常系数线性齐次微分方程
y ay by 0 的通解为 y C1 C2 x ex ,则非齐
次方程 y ay by x 满足条件 y 0 2, y 0 0的解为 y
。
11. 已知曲线 L : y x2 0 x
均值和样本方差。若 X kS2 为 np 2 的无偏估计量,则 k
。
三、解答题( 15- 23 小题,共 94 分 .请将解答写在答题纸指定的位置上 明、证明过程或演算步骤 .)
.解答应写出文字说
1. (本题满分 9 分)求二元函数 f ( x, y) x2 2 y2 y ln y 的极值。
2. (本题满分 9 分)设 an 为曲线 y xn 与 y xn 1 n 1,2,..... 所围成区域的面积,记
2009年1月考研管理类联考真题及答案解析

2009年1月考研管理类联考真题及答案解析一、问题求解1、一家商店为回收资金把甲乙两件商品均以480元一件卖出。
已知甲商品赚了%20,乙商品亏了%20,则商店盈亏结果为( )A 、不亏不赚B 、亏了50元C 、赚了50元D 、赚了40元E 、亏了40元2、某国参加北京奥运会的男女运动员的比例原为12:19,由于先增加若干女运动员,使男女运动员的比例变为13:20,后又增加了若干名男运动员,于是男女运动员比例最终变为19:30。
如果后增加的男运动员比先增加的女运动员多3人。
则最后运动员的总人数为( )A 、686B 、637C 、700D 、661E 、6003、某工厂定期购买一种原料。
已知该厂每天需用该原料6吨,每吨价格1800元,原料的保管等费用平均每吨3元,每次购买原料需支付费用900元,若该工厂要使平均每天支付的总费用最省,则应该每( )天购买一次原料。
A 、11B 、10C 、9D 、8E 、74、在某实验中,三个试管各盛水若干。
现将浓度为%12的盐水10克倒入A 试管中混合后取10克倒入B 管中,混合后再取10克倒入C 管中,结果A 、B 、C 三个试管中盐水的浓度分别为%5.0%2%6、、。
那么三个试管中原来盛水最多的试管及其成水量各是( ) A 、A 试管,10克 B 、B 试管,20克 C 、C 试管,30克D 、B 试管,40克E 、C 试管,50克5、一艘轮船往返航行于甲乙两个码头之间,若船在静水中的速度不变,则当这条河的水流速度增加%50时,往返一次所需的时间比原来将( )A 、增加B 、减少半小时C 、不变D 、减少一小时E 、无法判断6、方程412=+-x x 的根是( )A 、15=-=x x 或B 、15-=-=x x 或C 、353-==x x 或 D 、353=-=x x 或 E 、不存在 7、)0(032≠=++c c bx x 的两个根为βα、,如果βα+、αβ为根的一元二次方程是032=+-c bx x ,则b 和c 分别为( )A 、6,2B 、4,3C 、6,2--D 、6,3--E 、以上结果都不正确8、若n n n x na x a x a x x x )1()1(2)1()1()1()1(2212-++-+-=++++++ ,则=+++n na a a 212( )A 、213-nB 、2131-+n C 、2331-+n D 、233-n E 、433-n 9、在36人中,血型情况如下:A 型12人,B 型10人,AB 型8人,O 型6人。
2009至2019年计算机考研408历年真题及解析

2009年全国硕士研究生入学统一考试计算机科学与技术学科联考计算机学科专业基础综合试题一、单项选择题:第1~40小题,每小题2分,共80分。
下列每题给出的四个选项中,只有一个选项最符合试题要求。
1.为解决计算机主机与打印机之间速度不匹配问题,通常设置一个打印数据缓冲区,主机将要输出的数据依次写入该缓冲区,而打印机则依次从该缓冲区中取出数据。
该缓冲区的逻辑结构应该是。
A.栈B.队列C.树D.图2.设栈S和队列Q的初始状态均为空,元素a,b,c,d,e,f,g依次进入栈S。
若每个元素出栈后立即进入队列Q,且7个元素出队的顺序是b,d,c,f,e,a,g,则栈S的容量至少是。
A.1 B.2 C.3 D.43.给定二叉树如右图所示。
设N代表二叉树的根,L代表根结点的左子树,R代表根结点的右子树。
若遍历后的结点序列是3,1,7,5,6,2,4,则其遍历方式是。
A.LRN B.NRL C.RLN D.RNL4.下列二叉排序树中,满足平衡二叉树定义的是______。
5.已知一棵完全二叉树的第6层(设根为第1层)有8个叶结点,则该完全二叉树的结点个数最多是______。
A.39 B.52 C.111 D.1196.将森林转换为对应的二叉树,若在二叉树中,结点u是结点v的父结点的父结点,则在原来的森林中,u和v可能具有的关系是______。
Ⅰ.父子关系Ⅱ.兄弟关系Ⅲ.u的父结点与v的父结点是兄弟关系A.只有ⅡB.Ⅰ和ⅡC.Ⅰ和ⅢD.Ⅰ、Ⅱ和Ⅲ7.下列关于无向连通图特性的叙述中,正确的是______。
I.所有顶点的度之和为偶数II.边数大于顶点个数减1III.至少有一个顶点的度为1A.只有ⅠB.只有ⅡC.Ⅰ和ⅡD.Ⅰ和Ⅲ8.下列叙述中,不.符合m阶B树定义要求的是______。
A.根节点最多有m棵子树B.所有叶结点都在同一层上C.各结点内关键字均升序或降序排列D.叶结点之间通过指针链接9.已知关键字序列5,8,12,19,28,20,15,22是小根堆(最小堆),插入关键字3,调整后得到的小根堆是______。
考研数学一(矩阵的特征值和特征向量)历年真题试卷汇编1(题后含

考研数学一(矩阵的特征值和特征向量)历年真题试卷汇编1(题后含答案及解析)题型有:1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
1.设A是n阶实对称矩阵,P是n阶可逆矩阵,已知n维列向量α是A 的属于特征值λ的特征向量,则矩阵(P-1AP)T属于特征值λ的特征向量是( ).A.P-1αB.PTαC.PαD.(P-1)Tα正确答案:B解析:由题设有Aα=λα,且AT=A.令B=(P-1AP)T,则B=(P-1AP)T=PTAT(P-1)T=PTA(PT)-1,A=(PT)-1BPT.故Aα=(PT)-1BPTα,即(PT)-1B(PTα)=λα.两边乘以PT得到B(PTα)=λPTα.如能证明PTα≠0,则PTα为B的属于λ的特征向量.事实上,如PTα=0,则由P为可逆矩阵知,PT也为可逆矩阵,于是有(PT)-1PTα=(PT)-10=0,即a=0.这与a≠0矛盾.仅B 入选.知识模块:矩阵的特征值和特征向量2.[2016年] 设A,B是可逆矩阵,且A与B相似,则下列结论错误的是( ).A.AT与BT相似B.A-1与B-1相似C.A+AT与B+BT相似D.A+A-1与B+B-1相似正确答案:C解析:因A~B,故存在可逆矩阵P使得B=P-1AP.①在式①两边取转置,得到BT=(P-1AP)T=PTAT(P-1)T=[(PT)-1]-1AT[(PT)-1]故AT与BT相似,选项A正确.在式①两边求逆运算得到B-1=(P-1AP)-1=P-1A-1(P-1)-1=P-1A-1P,②故A与A-1相似,选项B正确.由式①+式②得到B+B-1=P-1AP+P-1A-1P=P-1(A+A-1)P,故A+A-1~B+B-1,选项D正确,仅C 入选.知识模块:矩阵的特征值和特征向量3.[2017年] 已知矩阵,则( ).A.A与C相似,B与C相似B.A与C相似,B与C不相似C.A与C不相似,B与C相似D.A与C不相似,B与C相似正确答案:B解析:显然A,B,C的特征值都为λ1=λ2=2,λ3=1.由2E—A=得秩(2E —A)=1,则A可以相似对角化,故A与C相似.由2E—B=得秩(2E—B)=2,则B不可相似对角化,故B与C不相似.综上,仅B入选.知识模块:矩阵的特征值和特征向量4.[2018年] 下列矩阵中,与矩阵相似的为( ).A.B.C.D.正确答案:A解析:记矩阵,则|λE—M|==(λ一1)3=0,所以矩阵M的特征值为λ1=λ2=λ3=1,且秩(λE—M)=秩(E—M)=2.设选项A,B,C,D的矩阵分别记为A,B,C,D,容易计算出其特征值均为1,且秩(λE—A)=秩(E—A)=2,秩(E —B)=秩(E—C)=秩(E—D)=1,若两矩阵相似,其对应的特征值矩阵也相似,故秩相等.所以可以判断选项A正确.知识模块:矩阵的特征值和特征向量5.[2013年] 矩阵与相似的充分必要条件为( ).A.a=0,b=2B.a=0,b为任意常数C.a=2,b=0D.a=2,b为任意常数正确答案:B解析:令,则=λ[λ2一(b+2)λ+2b—2a2],=λ(λ—2)(λ—b).因λ=2为B的特征值,故λ=2也必为A的特征值,则|2E一A|=2[22一(b+2)·2+2b—2a2]=2(一2a2)=0,所以a=0.因λ=b为B的特征值,故λ=b也必为A的特征值,则|bE—B|=b[b2一(b+2)b+2b]=b·0=0,即b可为任意常数.仅B入选.知识模块:矩阵的特征值和特征向量6.[2010年] 设A为四阶实对称矩阵,且A2+A=O,若A的秩为3,则A 相似于( ).A.B.C.D.正确答案:D解析:设λ为A的特征值,则由A2+A=O得到λ2+λ=(λ+1)λ=0,于是A 的特征值为一1或0.又因A为实对称矩阵,故A必与对角矩阵A相似.因A 的秩为3,知,A的非零特征值个数为3,故对角矩阵A的秩也为3.于是A=diag(一1,一1,一1,0).仅D入选.知识模块:矩阵的特征值和特征向量填空题7.设n阶矩阵A的元素全为1,则A的n个特征值是______.正确答案:n解析:因秩(A)=1,知A有n一1个零特征值λ1=λ2=…=λn-1=0,另一特征值为λn=a11+a22+…+ann=1+1+…+1=n.知识模块:矩阵的特征值和特征向量8.[2009年] 若三维列向量α,β满足αTβ=2,其中αT为α的转置,则矩阵βαT的非零特征值为______.正确答案:2解析:(βαT)T=(βαT)(βαT)=β(αTβ)αT=2βαT,则βαT的任意特征值λ满足λ2=2λ,故矩阵βαT的特征值λ只能为0或2.若λ只能取零,则A为零矩阵,故αTβ=0.这与αTβ=2矛盾,故βαT有非零特征值2.知识模块:矩阵的特征值和特征向量9.[2008年] 设A为二阶矩阵,α1,α2为线性无关的二维列向量,A α1=0,Aα2=2α1+α2,则A的非零特征值为______.正确答案:λ=1解析:因矩阵A满足矩阵等式,可用定义求出A的非零特征值.事实上,因Aα1=0,故A(2α1+α2)=2Aα1+Aα2一Aα2=2α1+α2=1·(2α1+α2).又因α1,α2线性无关,故2α1+α2≠0,由定义知λ=1为A的非零特征值.知识模块:矩阵的特征值和特征向量10.[2018年] 设二阶矩阵A有两个不同的特征值,α1,α2是A的线性无关的特征向量,且满足A2(α1+α2)=α1+α2,则|A|=______.正确答案:-1解析:由A2(α1+α2)=α1+α2可知(A2一E)(α1+α2)=0.α1,α2线性无关,因此方程(A2一E)x=0有非零解,从而|A2一E|=0,所以特征值λ满足方程λ2一1=0,即λ=1或λ=一1.又A有两个不同的特征值,所以|A|=1·(一1)=一1.知识模块:矩阵的特征值和特征向量解答题解答应写出文字说明、证明过程或演算步骤。
【合集打印】1987-2009年考研数学一真题【 72页 】

九、(本题满分8分) 问a,b为何值时,线性方程组
X1 + X2 + x3 + X4 = 0, x2 + 2x3 + 2x4 = 1, -x2 + (a-3)x3 -2x4 = b, 3x1 + 2x2 + x3 + ax4 = - l 有唯一 解,无解, 有无穷多组解?并求出有无穷多组解时的通解.
(D)某邻域内单调减少.
(3)设有空间区域fl1 :x2 +y2 +z2�R2,z�0 ; 及[12 :X2 十广+z2�R2'X�0'y�0,z�0'则( )
(A)fJJxdv = 4fJJxdv.
il1
纺
(B)fjJydv = 4fjJydv.
il1
{Ji
(C)fJJzdv = 4fJJzdv.
6
1989年真题
1989年全国硕士研究生招生考试试题
(试卷I)
-、填空题(本题共5小题,每小题3分,满分15分)
(1)已知f
'(3)
= 2,则lim h----+O
f(3
-h) -f(3)
2h
(2)设八x)是连续函数,且j(X) = X +2rj(t)dt,则J(x) =
.
Ji J (3)设平面 曲线L为下半圆y =- 二了,则曲线积分 (x2 +y2)ds =
1987年真题
率等于
.已知取出的球是自球,此球属于第二个箱子的概率为
.
7, (3)已知连续型随机变量X的概率密度函数为f(x) = 了 卫心-1' 则X的数学期望为
方差为
,X的
+-、(本题满分6分)
2009考研数农真题及解析

2009年全国硕士研究生入学统一考试农学门类联考数学试题一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内. (1) 在(,)ππ-内,函数tan xy x=的可去间断点的个数为 ( ) (A) 0.(B) 1. (C) 2.(D) 3.(2) 函数2ln(1)y x =+单调增加且其图形为凹的区间是 ( )(A) (,1)-∞-. (B) (1,0)-. (C) (0,1).(D) (1,)+∞.(3) 函数22()x x t f x e dt --=⎰的极值点为x = ( )(A)12.(B)14. (C) 14-.(D) 12-. (4) 设区域{}22(,)2,0D x y x x y x y =≤+≤≥,则在极坐标下二重积分Dxydxdy =⎰⎰( )(A) 2cos 220cos cos sin d r dr πθθθθθ⎰⎰.(B) 2cos 320cos cos sin d r dr πθθθθθ⎰⎰.(C)2cos 20cos cos sin d r dr πθθθθθ⎰⎰.(D)2cos 30cos cos sin d r dr πθθθθθ⎰⎰.(5) 设矩阵121242242A ab a ⎛⎫ ⎪=+ ⎪ ⎪+⎝⎭的秩为2,则 ( ) (A) 0,0a b ==. (B) 0,0a b =≠. (C) 0,0a b ≠=. (D) 0,0a b ≠≠.(6) 设A 为3阶矩阵,*A 为A 的伴随矩阵,A 的行列式2A =,则*2A -= ( )(A) 52- .(B) 32-. (C) 32. (D) 52.(7) 设事件A 与事件B 互不相容,则 ( )(A) ()0P AB =.(B) ()()()P AB P A P B =. (C) ()1()P A P B =-.(D) ()1P AB =.(8) 设随机变量X 的分布函数为()()10.30.72x F x x -⎛⎫=Φ+Φ⎪⎝⎭,其中()x Φ为标准正态分布的分布函数,则EX = ( ) (A) 0. (B) 0.3. (C) 0.7. (D) 1.二、填空题:9-14小题,每小题4分,共24分.请将答案写在答题纸指定位置上. (9) 20lim 1sin3xx x →⎛⎫+= ⎪⎝⎭. (10) 设2()ln(4cos 2)f x x x =+,则()8f π'= .(11) 设2()xf x e =,()ln x x ϕ=,则[]1(())(())f x f x dx ϕϕ+=⎰ .(12) 设(,)f u v 为二元可微函数,(sin(),)xyz f x y e =+,则zx∂=∂_______________. (13) 设向量组(1,0,1)T α=,(2,,1)T k β=-,(1,1,4)T γ=--线性相关,则k =__________. (14) 设总体X 的概率密度||1(;),,2x f x e x σσσ-=-∞<<+∞其中参数(0)σσ>未知.若12,,,n X X X 是来自总体X 的简单随机样本,11ˆ1ni i X n σ==-∑是σ的估计量,则ˆ()E σ=_____________.三、解答题:15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. (15)(本题满分10分)求极限[]24ln(1tan )limsin x x x x x→-+.(16)(本题满分10分)计算不定积分.(17)(本题满分10分)曲线L 过点(1,1),L 上任一点(,)(0)M x y x >处法线的斜率等于2yx,求L 方程. (18)(本题满分11分)讨论方程440x x k -+=实根的个数,其中k 为参数.11X -1122P1Y1344P(19)(本题满分11分)计算二重积分1Dx dxdy -⎰⎰,其中D 是第一象限内由直线0,y y x ==及圆222x y +=所围成的区域.(20)(本题满分10分)设1211211223A a a a a ⎛⎫ ⎪=++ ⎪ ⎪---⎝⎭,若存在3阶非零矩阵B ,使得AB O =.(Ⅰ) 求a 的值;(Ⅱ) 求方程组0Ax =的通解. (21)(本题满分11分)设3阶矩阵A 的特征值为1,1,2-,对应的特征向量依次为1010α⎛⎫ ⎪= ⎪ ⎪⎝⎭,2101α⎛⎫ ⎪= ⎪ ⎪⎝⎭,3101α⎛⎫⎪= ⎪ ⎪-⎝⎭.(Ⅰ) 求矩阵A ; (Ⅱ) 求2009A.(22)(本题满分11 分)设随机变量X 的概率密度为2,,()0,x a x b f x <<⎧=⎨⎩其他, 且21EX =.(Ⅰ) 求,a b 的值; (Ⅱ) 求{}1P X <.(23)(本题满分10 分)已知随机变量X 与Y 的概率分布分别为且{}14P X Y ==. (Ⅰ) 求二维随机变量(,)X Y 的概率分布; (Ⅱ) 求X 与Y 的相关系数XY ρ.2009年全国硕士研究生入学统一考试农学门类联考数学试题解析一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内. (1)【答案】(D) 【解析】函数tan x y x =在点0x =,2x π=±没有定义,而 0lim1tan x xx→=,所以0x =为可去间断点; 2lim0tan x xxπ→±=,所以2x π=±也为可去间断点.因此,在(,)ππ-内,函数tan xy x=的可去间断点的个数为3个,故选(D). (2)【答案】(C)【解析】由2222222200,122(1)(12)011,(1)(1)x y x x x y x x x x x x ⎧'=>⇒>⎪+⎪⎨-⎪''=⋅+-⋅=>⇒-<<⎪++⎩取交集可得()0,1x ∈,故应选(C). (3)【答案】(A)【解析】因 2222()2()()()(12)x x x x f x e x x x e ----''=⋅-=-,令()0f x '=,得12x =,又 222222()()2222()()2(12)()22(12)(),x xx xx x f x e x e x x x x x e ------'''⎡⎤=-+-⋅⋅--⎣⎦⎡⎤=-+-⋅-⎣⎦所以102f ⎛⎫''≠ ⎪⎝⎭,故12x =为极值点,应选(A). (4)【答案】(B)【解析】区域D 见右图所示.2cos 20cos 2cos 320cos cos sin cos sin .Dxydxdy d r r rdr d r dr πθθπθθθθθθθθ=⋅⋅=⎰⎰⎰⎰⎰⎰(5)【答案】(C)【解析】对矩阵A 进行初等变换:1211212420024200A ab ab a a ⎛⎫⎛⎫ ⎪ ⎪=+→ ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭,因为0a =时,()1r A =,所以0a ≠,1000000A ab a ⎛⎫⎪→ ⎪ ⎪⎝⎭.因为()2r A =,所以0b =,综上0,0a b ≠=. (6)【答案】(A)【解析】因为2A =,1312*22n A AAA --====,所以*3*3252(2)(2)22A A -=-⋅=-⋅=-.(7)【答案】(D)【解析】因为,A B 互不相容,所以()0P AB =. (A)()()1()P AB P AB P A B ==-,因为()P A B 不一定等于1,所以(A)不正确;(B)当(),()P A P B 不为0时,()B 不成立,故排除; (C)只有当,A B 互为对立事件的时候才成立,故排除; (D)()()1()1P AB P AB P AB ==-=,故()D 正确.(8)【答案】(C)【解析】因为()()10.30.72x F x x -⎛⎫=Φ+Φ⎪⎝⎭,所以 ()()0.710.322x F x x -⎛⎫'''=Φ+Φ ⎪⎝⎭, 因此, ()()10.30.352x EX xF x dx x x dx +∞+∞-∞-∞⎡-⎤⎛⎫'''==Φ+Φ ⎪⎢⎥⎝⎭⎣⎦⎰⎰()10.30.352x x x dx x dx +∞+∞-∞-∞-⎛⎫''=Φ+Φ ⎪⎝⎭⎰⎰.由于()x Φ为标准正态分布的分布函数,所以()0x x dx +∞-∞'Φ=⎰,()()()()11221222222,x x x dx u u u du u u du u du +∞+∞-∞-∞+∞+∞-∞-∞--⎛⎫''Φ=+Φ ⎪⎝⎭''=Φ+Φ=⎰⎰⎰⎰()10.30.3500.3520.72x EX x x dx x dx +∞+∞-∞-∞-⎛⎫''=Φ+Φ=+⨯= ⎪⎝⎭⎰⎰.二、填空题:9-14小题,每小题4分,共24分.请将答案写在答题纸指定位置上. (9)【答案】23e【解析】 0002sin2222233ln(1sin )lim ln(1sin )limlim 33300lim(1sin )lim 3x x x xx x xx x x xxx x xeeeee →→→⋅++→→+=====.(10)【答案】41π+【解析】2()ln(4cos 2)f x x x =+,[]22144sin 2cos 2()42cos 2(sin 2)24cos 24cos 2x xf x x x x x x x-'=+⋅-⋅=++, 44422()18122f πππ-'==++. (11)【答案】43【解析】2ln 22(()),(())ln 2xx f x ex f x e x ϕϕ====,所以[]13112200014(())(())(2)1333x f x f x dx x x dx x ϕϕ⎛⎫+=+=+=+=⎪⎝⎭⎰⎰.(12)【答案】12cos()xyf x y e yf ''++【解析】根据复合函数求导法,得12cos()xy zf x y yf e x∂''=++∂. (13)【答案】1【解析】令121(,,)01114A kαβγ-⎛⎫ ⎪== ⎪ ⎪--⎝⎭,由于,,αβγ线性相关,所以0A =,即3301k k -+=⇒=. (14)【答案】1nn σ- 【解析】11ˆ()11n i i i n E E X E X n n σ===--∑ 0001212121.11xt xxtt n n x n x e dx e dx te dt n n n n n te dt n n σσσσσσσ=--+∞+∞+∞--∞+∞-=⋅=⋅=---==--⎰⎰⎰⎰三、解答题:15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. (15)(本题满分10分) 【解析】 []2242200ln(1tan )ln(1tan )limlim sin sin sin x x x x x x x x xx x→→-+-+= 2200200ln(1tan )ln(1tan )limlimsin 11sec 1tan lim 2cos sin 1lim .2cos (sin cos )2x x x x x x x x x x xxxx x x x x →→→→-+-+==-+=-==⋅+(16)(本题满分10分)【解析】令2,2t x t dx tdt ===,则222ln(2)22ln(2)22ln(2)ln(2)2ln (2)ln (2.t tdtt t t dt t d t t t C C +=⋅++==+++=++=++⎰⎰⎰(17)(本题满分10分)【解析】设L 的方程为()y y x =,由题意得2dx y dy x-=. 分离变量得 2ydy xdx =-,两边积分得 222x y C =-+, 故 2222x y C +=. 又由已知条件3(1)12y C =⇒=, 所以L 的方程为2223,(0)x y x +=>.(18)(本题满分11分)【解析】设4()4f x x x k =-+,()f x 在(,)-∞+∞内连续.令3()440f x x '=-=得唯一驻点1x =.当1x <时,()0f x '<,()f x 单调减少;当1x >时,()0f x '>,()f x 单调增加, 故(1)3f k =-为最小值.则当3k =时,(1)0f =,方程4430x x -+=有唯一实根1x =;当3k >时,()(1)0f x f ≥>,方程无实根; 当3k <时,(1)0f <,而44lim ()lim (4),lim ()lim (4),x x x x f x x x k f x x x k →-∞→-∞→+∞→+∞=-+=+∞=-+=+∞根据零点定理可得,方程有两个实根.(19)(本题满分11分) 【解析】解法11211010111232221222441(1)(1)1)(1)(1)1)(2)2231111(22cos sin 23632DD D xx dxdy x dxdy x dxdyx dy dx x dyx x dx x x x x d x x tdt t t πππ-=-+-=-+-=-+-⎛⎫=----+- ⎪⎝⎭⎛⎫=---+=-+ ⎪⎝⎭⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰211.64ππ+=-解法2121(1)(1)DD D x dxdy x dxdy x dxdy -=-+-⎰⎰⎰⎰⎰⎰111011221101212400041)(1)22(222cos 2112sin 21.224yy dy x dx dy x dxx x x dy x dyy y dy y tdt t t πππ=-+-⎛⎛⎫=-+- ⎪⎝⎝⎭⎛⎫=-=-- ⎪⎝⎭⎛⎫=--+=- ⎪⎝⎭⎰⎰⎰⎰⎰⎰⎰(20)(本题满分10分)【解析】(I)由题设知方程组0Ax =有非零解,所以1211211210(2)01223022A a a a a a a a a a a =++==-=----,于是2a =或0a =.(II) 当2a =时,对A 施以初等行变换,121121022101143022022011101101101000A -⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=→→→⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦⎣⎦,取自由未知量31x =,得[]11,1,1Tξ=-,即0Ax =的通解为[]1111,1,1Tx k k ξ==-,(1k 为任意常数).当0a =时, 对A 施以初等行变换,121121120121000001123002000A ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=→→⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦⎣⎦,取自由未知量21x =,得[]22,1,0Tξ=-,即0Ax =的通解为[]2222,1,0Tx k k ξ==-,(2k 为任意常数).(21)(本题满分11分)【解析】(I)由题设知123123100(,,)(,,)010002A αααααα⎛⎫ ⎪= ⎪ ⎪-⎝⎭,即011011100100100010011011002A ⎛⎫⎛⎫⎛⎫ ⎪ ⎪⎪= ⎪ ⎪⎪ ⎪ ⎪⎪---⎝⎭⎝⎭⎝⎭. 由于0111020011=≠-,所以101110001110001010001100201101110002010311100010101020.22011002101301A -⎛⎫⎛⎫⎛⎫ ⎪⎪⎪= ⎪⎪⎪⎪⎪⎪---⎝⎭⎝⎭⎝⎭-⎛⎫⎛⎫⎛⎫⎛⎫ ⎪⎪⎪ ⎪== ⎪⎪⎪ ⎪ ⎪⎪⎪ ⎪----⎝⎭⎝⎭⎝⎭⎝⎭(II) 12009200901110001110001010001100(2)011A-⎛⎫⎛⎫⎛⎫ ⎪⎪⎪= ⎪⎪⎪ ⎪⎪⎪---⎝⎭⎝⎭⎝⎭200920092009200920090111000201100010101201100(2)101120121020.212012⎛⎫⎛⎫⎛⎫ ⎪⎪⎪= ⎪⎪⎪ ⎪⎪⎪---⎝⎭⎝⎭⎝⎭⎛⎫-+ ⎪= ⎪ ⎪+-⎝⎭(22)(本题满分11 分) 【解析】(Ⅰ)由()1f x dx +∞-∞=⎰得2221baxdx b a =-=⎰, ①由21EX =得223441()2()12baEX x f x dx x dx b a +∞-∞===-=⎰⎰, ② 联立①、②得2224421,1232.2a b a b a b ⎧=⎪⎧-=⎪⇒⎨⎨-=⎩⎪=⎪⎩Born to win第 11 页 共 11 页 Y X 110211144- 01 由概率密度函数的非负性,知0,0a b >>,则,2a b ⎧=⎪⎪⎨⎪=⎪⎩(Ⅱ)X 的概率密度为 2,,()0,x a x b f x <<⎧=⎨⎩其他, 所求概率为1111(1)()22P X f x dx xdx -<===⎰.(23)(本题满分10 分)【解析】(Ⅰ)由题设知()()11,14P X Y P X Y =====, 所以 ()()()11,011,14P X Y P X P X Y ====-===, 同理可得 ()()()1,001,00P X Y P Y P X Y =-===-===, ()()()11,111,12P X Y P Y P X Y =-===-===. 所以(,)X Y 的概率分布为(2)由(,)X Y 的概率分布可得 ()2222111,0,1,4243333,().44416E XY EX DX EX EY DY EY EY =-=-===⎛⎫==-=-= ⎪⎝⎭所以X 与Y 的相关系数为,3XY Cov X Y ρ===-.。
2009考研数一真题答案及详细解析

f(t)dt
I: > �f'.J<t)dt+ 八 t)dt�f (x) dx.'
又由定积分的几何意义知,『 g (x)dx>O,故 2<x<3 时 F(x)>O.故应选 D.
(4) C
解
I; 若令
an= bn=
(-l)n
嘉,则nl-im= a
n
=
O, n=
l
从收敛,却有
co
nI=;l a
n从
=
nI=;l — n1
1,1],
和函数为—
ln(l+x).
因为5 (x)=
= I;
(—l)n
X
n=
X
— ln(l+x),令
x= l,得
n= 2 n
S 2= n�= la 加一1 = S(1)= 1- ln 2.
(17) 解
(I)
椭球面 S1
的方程为X— 42
+
沪
+z 3
2 =
1.
。 设切点为
(x
口 Yo),
则
X—+
4
— y
y2dxdyd乏 = 』之2dxdyd之,
{l
所以
w 上�+ ill f I I z'dxd:
。 。 。 上 2
六
(x' 二三) dxdydz� 3
亢 d0
sin钊'P'r'dr�±. 穴. 15
{l
03) 2
n 解 设入是P矿的非零特征值, 是属于入的特征向量,从而p矿T/=入1
由于入=/=-0, TJ =/=-0,故a可=l=-0.
2009考研数学真题及答案详解

2009年全国硕士研究生入学统一考试数学一试题答案解析一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内. (1)当0x ®时,()sin f x x ax =-与()()2ln 1g x x bx =-等价无穷小,则()A 11,6a b ==-.()B 11,6a b ==.()C 11,6a b =-=-.()D 11,6a b =-=.【答案】 A【解析】2()sin ,()ln(1)f x x ax g x x bx =-=-为等价无穷小,则222200000()sin sin 1cos sinlim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bx bx ®®®®®---==-×---洛洛230sin lim 166x aax a b b ax a®==-=-× 36a b \=- 故排除,B C 。
另外201cos lim 3x a axbx ®--存在,蕴含了1cos 0a ax -®()0x ®故 1.a =排D 。
所以本题选A 。
(2)如图,正方形(){},1,1x y x y ££被其对角线划分为四个区域()1,2,3,4k D k =,cos kk D I y xdxdy =òò,则{}14max k k I ££=()A 1I .()B 2I . ()C 3I .()D 4I .【答案】A【解析】本题利用二重积分区域的对称性及被积函数的奇偶性。
24,D D 两区域关于x 轴对称,而(,)cos (,)f x y y x f x y -=-=-,即被积函数是关于y 的奇函数,所以240I I ==;13,D D 两区域关于y 轴对称,而(,)cos()cos (,)f x y y x y x f x y -=-==,即被积函数是-1 -1 1 1 xy 1D 2D3D4D关于x 的偶函数,所以{}1(,),012cos 0x y y x x I y xdxdy ³££=>òò;{}3(,),012cos 0x y y x x I y xdxdy £-££=<òò.所以正确答案为A. (3)设函数()y f x =在区间[]1,3-上的图形为:则函数()()0x F x f t dt =ò的图形为()A ()B()C ()D【答案】D【解析】此题为定积分的应用知识考核,由()y f x =的图形可见,其图像与x 轴及y 轴、0x x =所围的图形的代数面积为所求函数()F x ,从而可得出几个方面的特征:①[]0,1x Î时,()0F x £,且单调递减。
2009考研数学真题数一及解析

= lim
x →0
a 3 = −6b 意味选项 B,C 错误。
再由 lim =
x →0
1 − a cos ax 存在,应有 1 − a cos ax → 0( x → 0) ,故 a = 1 ,D 错误,所以选 A。 − 3bx 2
( 2 ) 如 图 , 正 方 形
{(x, y ) x ≤ 1, y ≤ 1} 被 其 对 角 线 划 分 为 四 个 区 域
【答案】B 【解析】由于分块矩阵 ⎜ ⎜
⎛0 ⎝B
−1
A⎞ 0 ⎟ 的行列式 0⎟ B ⎠
A = (−1) 2×2 A B = 2 × 3 = 6 ,即分块矩 0
阵可逆,根据公式 C* = C C ,
⎛0 ⎜ ⎜B ⎝
A⎞ 0 ⎟ = ⎟ 0⎠ B
∗
A⎛ 0 ⎜ 0⎜ ⎝B
A⎞ ⎟ 0⎟ ⎠
−1
⎛ 0 = 6⎜ ⎜ A −1 ⎝
P{Y = 0} = P{Y = 1} =
个数为( ) (A).0 (B).1
1 , 记 FZ ( z ) 为随机变量 Z=XY 的分布函数, 则函数 FZ ( z ) 的间断点 2
(C).2 (D).3
【解析】 FZ ( z ) = P( XY ≤ z ) = P XY ≤ z Y = 0 P (Y = 0 ) + P ( XY ≤ z Y = 1) P (Y = 1)
∗ ∗
⎛O ⎜ ⎜B ⎝
A⎞ ⎟ 的伴随矩阵为( ) 0⎟ ⎠
⎛ O ⎝2A
∗
(A) ⎜ ⎜
3B ∗ ⎞ ⎟ O ⎟ ⎠
(B) ⎜ ⎜
⎛ O ⎝ 3A
∗
⎛ O 2B ∗ ⎞ ⎟ (C) ⎜ ∗ ⎟ ⎜ 2B O ⎠ ⎝
2009年考研数学三真题及完整解析

2009年全国硕士研究生入学统一考试数学三试题一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内. (1)函数3()sin x xf x xπ-=的可去间断点的个数为:( )()A .1()B . 2 ()C .3()D .无穷多个(2)当0x →时,()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小,则( )()A .1a=,16b =-()B . 1a =,16b = ()C .1a =-,16b =-()D .1a =-,16b =(3)使不等式1sin ln xt dt x t>⎰成立的x 的范围是( )()A .(0,1)()B .(1,)2π ()C .(,)2ππ()D .(,)π+∞(4)设函数()y f x =在区间[]1,3-上的图形为:则函数()()0xF x f t dt =⎰的图形为( )()A .()B .()f x 02 3x1 -2-11()f x 0 2 3x1 -2 -11 1()f x -2 0 2 3x-1O()C .()D .(5)设,A B 均为2阶矩阵,*,A B *分别为,A B 的伴随矩阵,若||2,||3A B ==则分块矩阵 00A B⎛⎫⎪⎝⎭的伴随矩阵为( ) ()A .**0320B A ⎛⎫⎪⎝⎭()B . **230B A⎛⎫⎪⎝⎭ ()C .**0320A B⎛⎫⎪⎝⎭()D .**0230A B⎛⎫⎪⎝⎭(6)设,A P 均为3阶矩阵,TP 为P 的转置矩阵,且100010002TP AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭,若123122(,,),(,,)P Q ααααααα==+,则TQ A Q 为( ) ()A .210110002⎛⎫ ⎪ ⎪ ⎪⎝⎭()B . 110120002⎛⎫⎪⎪ ⎪⎝⎭ ()C .200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭()D .100020002⎛⎫⎪ ⎪ ⎪⎝⎭(7)设事件A 与事件B 互不相容,则( )()A .()0P A B =()B . ()()()P AB P A P B = ()C .()1()P A P B =-()D .()1P A B ⋃=(8)设随机变量X 与Y 相互独立,且X 服从标准正态分布(0,1)N ,Y 的概率分布为1{0}{1}2P Y P Y ====,记()z F Z 为随机变量Z XY =的分布函数,则函数()z F Z 的间断点个数为( )()A .()B . 1 ()C .2()D . 3二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.()f x 0 2 3x1 -2-11()f x 02 3x1 -1 1(9)cos 320lim11x x e ex →-=+- .(10)设()y x z x e =+,则(1,0)z x∂=∂(11)幂级数21(1)n nnn e x n∞=--∑的收敛半径为(12)设某产品的需求函数为()Q Q P =,其对应价格P 的弹性0.2p ξ=,则当需求量为10000件时,价格增加1元会使产品收益增加 元(13)设(1,1,1)T α=,(1,0,)T k β=,若矩阵T αβ相似于300000000⎛⎫⎪⎪ ⎪⎝⎭,则k = (14)设1X ,2X ,…n X 是来自二项分布总体(,)B n p 的简单随机样本,X 和2S 分别为样本均值和样本方差,记统计量2T X S =-,则E T =三、解答题:15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.(15)(本题满分9分)求二元函数()22(,)2ln f x y x y y y =++的极值。
2009年考研数学一真题及答案解析
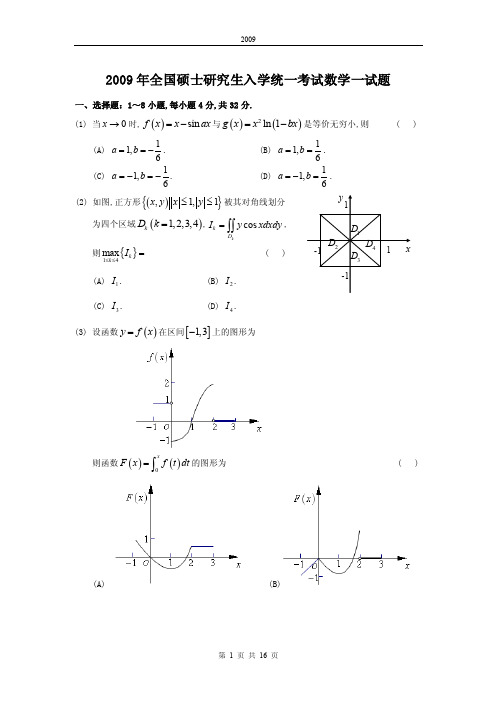
2009年全国硕士研究生入学统一考试数学一试题一、选择题:1~8小题,每小题4分,共32分.(1) 当0x →时,()sin f x x ax =-与()()2ln 1g x x bx =-是等价无穷小,则 ( )(A) 11,6a b ==-. (B) 11,6a b ==. (C) 11,6a b =-=-. (D) 11,6a b =-=.(2) 如图,正方形(){},1,1x y x y ≤≤被其对角线划分为四个区域()1,2,3,4k D k =,cos kk D I y xdxdy =⎰⎰,则{}14max k k I ≤≤= ( )(A) 1I .(B) 2I .(C) 3I .(D) 4I .(3) 设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为 ( )(A) (B)(C)(D)(4) 设有两个数列{}{},n n a b ,若lim 0n n a →∞=,则 ( )(A) 当1nn b∞=∑收敛时,1n nn a b∞=∑收敛. (B) 当1nn b∞=∑发散时,1n nn a b∞=∑发散.(C) 当1n n b ∞=∑收敛时,221n nn a b ∞=∑收敛.(D) 当1n n b ∞=∑发散时,221n n n a b ∞=∑发散. (5) 设123,,ααα是3维向量空间3R 的一组基,则由基12311,,23ααα到基122331,,αααααα+++的过渡矩阵为 ( )(A) 101220033⎛⎫ ⎪ ⎪ ⎪⎝⎭.(B) 120023103⎛⎫⎪⎪ ⎪⎝⎭.(C)111246111246111246⎛⎫- ⎪ ⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭.(D) 111222111444111666⎛⎫-⎪ ⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭. (6) 设,A B 均为2阶矩阵,**,A B 分别为,A B 的伴随矩阵,若2,3A B ==,则分块矩阵O A B O ⎛⎫ ⎪⎝⎭的伴随矩阵为 ( ) (A) **32O B A O ⎛⎫⎪⎝⎭. (B) **23O B A O ⎛⎫⎪⎝⎭.(C) **32O A BO ⎛⎫⎪⎝⎭.(D) **23OA BO ⎛⎫⎪⎝⎭.(7) 设随机变量X 的分布函数为()()10.30.72x F x x -⎛⎫=Φ+Φ⎪⎝⎭,其中()x Φ为标准正态分布的分布函数,则EX = ( ) (A) 0.(B) 0.3.(C) 0.7.(D) 1.(8) 设随机变量X 与Y 相互独立,且X 服从标准正态分布()0,1N ,Y 的概率分布为{}{}1012P Y P Y ====.记()Z F z 为随机变量Z XY =的分布函数,则函数()Z F z 的间断点个数为 ( ) (A) 0.(B) 1. (C) 2.(D) 3.二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.(9) 设函数(),f u v 具有二阶连续偏导数,(),z f x xy =,则2zx y∂=∂∂ .(10) 若二阶常系数线性齐次微分方程0y ay by '''++=的通解为()12xy C C x e =+,则非齐次方程y ay by x '''++=满足条件()()02,00y y '==的解为y = .(11) 已知曲线(2:0L y x x =≤≤,则Lxds =⎰ .(12) 设(){}222,,1x y z xy z Ω=++≤,则2z dxdydz Ω=⎰⎰⎰ .(13) 若3维列向量,αβ满足2T αβ=,其中Tα为α的转置,则矩阵T βα的非零特征值为.(14) 设12,,,m X X X 为来自二项分布总体(),B n p 的简单随机样本,X 和2S 分别为样本均值和样本方差.若2X kS +为2np 的无偏估计量,则k = .三、解答题:15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. (15)(本题满分9分)求二元函数()22(,)2ln f x y x y y y =++的极值.(16)(本题满分9分)设n a 为曲线n y x =与()11,2,n y xn +== 所围成区域的面积,记11,n n S a ∞==∑2211n n S a ∞-==∑,求1S 与2S 的值.(17)(本题满分11分)椭球面1S 是椭圆22143x y +=绕x 轴旋转而成,圆锥面2S 是由过点()4,0且与椭圆22143x y +=相切的直线绕x 轴旋转而成. (Ⅰ)求1S 及2S 的方程; (Ⅱ)求1S 与2S 之间的立体体积. (18)(本题满分11分)(Ⅰ)证明拉格朗日中值定理:若函数()f x 在[],a b 上连续,在(,)a b 可导,则存在(),a b ξ∈,使得()()()()f b f a f b a ξ'-=-.(Ⅱ)证明:若函数()f x 在0x =处连续,在()()0,0δδ>内可导,且()0lim x f x A +→'=,则()0f +'存在,且()0f A +'=.(19)(本题满分10分)计算曲面积分()32222xdydz ydzdx zdxdyI xy z∑++=++⎰⎰,其中∑是曲面222224x y z ++=的外侧.(20)(本题满分11分) 设111111042A --⎛⎫ ⎪=- ⎪ ⎪--⎝⎭,1112ξ-⎛⎫ ⎪= ⎪ ⎪-⎝⎭(Ⅰ)求满足22131,A A ξξξξ==的所有向量23,ξξ; (Ⅱ)对(Ⅰ)中的任意向量23,ξξ,证明:123,,ξξξ线性无关. (21)(本题满分11分)设二次型()()2221231231323,,122f x x x ax ax a x x x x x =++-+-(Ⅰ)求二次型f 的矩阵的所有特征值; (Ⅱ)若二次型f 的规范形为2212y y +,求a 的值. (22)(本题满分11分)袋中有1个红球,2个黑球与3个白球.现有放回地从袋中取两次,每次取一个球,以,,X Y Z 分别表示两次取球所取得的红球、黑球与白球的个数.(Ⅰ)求{}10P X Z ==;(Ⅱ)求二维随机变量(),X Y 的概率分布. (23)(本题满分11 分) 设总体X 的概率密度为2,0,()0,x xe x f x λλ-⎧>=⎨⎩其他, 其中参数(0)λλ>未知,12,,,n X X X 是来自总体X 的简单随机样本.(Ⅰ) 求参数λ的矩估计量;(Ⅱ )求参数λ的最大似然估计量.2009年全国硕士研究生入学统一考试数学一试题一、选择题:1~8小题,每小题4分,共32分. (1) 【答案】(A)【解析】()sin f x x ax =-与()()2ln 1g x x bx =-是0x →时的等价无穷小,则2200232000330()sin sin limlim lim ()ln(1)()sin 1cos sin lim lim lim 36sin lim 1,66x x x x x x x f x x ax x axg x x bx x bx x ax a ax a axbx bx bxa ax ab axb →→→→→→→--=-⋅---=---⎛⎫=-=-= ⎪⎝⎭等洛洛 即36a b =-,故排除B,C.另外,201cos lim3x a axbx→--存在,蕴含了1cos 0a ax -→()0x →,故1,a =排除D. 所以本题选A. (2) 【答案】(A)【解析】本题利用二重积分区域的对称性及被积函数的奇偶性.令(,)cos f x y y x =,24,D D 两区域关于x 轴对称,(,)cos (,)f x y y x f x y -=-=-,即被积函数是关于y 的奇函数,所以240I I ==;13,D D 两区域关于y 轴对称,(,)cos()cos (,)f x y y x y x f x y -=-==,即被积函数是关于x 的偶函数,所以{}{}1(,),013(,),012cos 0,2cos 0.x y y x x x y y x x I y xdxdy I y xdxdy ≥≤≤≤-≤≤=>=<⎰⎰⎰⎰所以正确答案为(A).(3) 【答案】(D)【解析】此题为定积分的应用知识考核,由()y f x =的图形可以看出,其图像与x 轴及y 轴、0x x =所围的图形的代数面积为所求函数()F x ,从而可得出下面几个方面的特征:① []1,0x ∈-时,()0F x ≤为线性函数,单调递增; ② []0,1x ∈时,()0F x ≤,且单调递减;③ []1,2x ∈时,()F x 单调递增; ④ []2,3x ∈时,()F x 为常函数; ⑤ ()F x 为连续函数. 结合这些特点,可见正确选项为(D). (4) 【答案】C【解析】解法1 举反例:取(1)nn n a b ==-,则lim 0n n a →∞=,1n n b ∞=∑是收敛的,但111n n n n a b n ∞∞===∑∑发散,排除(A);取1n n a b n ==,则lim 0n n a →∞=,1n n b ∞=∑是发散的,但2111n n n n a b n ∞∞===∑∑收敛,排除(B);取1n n a b n ==,则lim 0n n a →∞=,1n n b ∞=∑是发散的,但224111n n n n a b n∞∞===∑∑收敛,排除(D),故答案为(C).解法2 因为lim 0,n n a →∞=则由定义可知1,N ∃使得1n N >时,有1n a <;又因为1nn b∞=∑收敛,可得lim 0,n n b →∞=则由定义可知2,N ∃使得2n N >时,有1n b <,从而,当12n N N >+时,有22n nn a b b <,则由正项级数的比较判别法可知221n nn a b∞=∑收敛.(5) 【答案】(A)【解析】根据过渡矩阵的定义,知由基12311,,23ααα到122331,,αααααα+++的过渡矩阵M 满足:()12233112312311,,,,2310111,,220,23033M αααααααααααα⎛⎫+++= ⎪⎝⎭⎛⎫⎛⎫ ⎪= ⎪ ⎪⎝⎭ ⎪⎝⎭所以此题选(A). (6) 【答案】(B)【解析】分块矩阵O A B O ⎛⎫⎪⎝⎭的行列式221236O A A B B O⨯=-=⨯=(),即分块矩阵可逆,且1116112366.1132O A O A O A O B B O B O B O A O O B O B B O B A O A O A O A *---******⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫ ⎪ ⎪⎛⎫⎪=== ⎪ ⎪ ⎪ ⎪⎝⎭⎪ ⎪⎝⎭⎝⎭故答案为(B). (7) 【答案】(C)【解析】因为()()10.30.72x F x x -⎛⎫=Φ+Φ⎪⎝⎭,所以 ()()0.710.322x F x x -⎛⎫'''=Φ+Φ ⎪⎝⎭, 因此, ()()10.30.352x EX xF x dx x x dx +∞+∞-∞-∞⎡-⎤⎛⎫'''==Φ+Φ ⎪⎢⎥⎝⎭⎣⎦⎰⎰()10.30.352x x x dx x dx +∞+∞-∞-∞-⎛⎫''=Φ+Φ ⎪⎝⎭⎰⎰.由于()x Φ为标准正态分布的分布函数,所以()0x x dx +∞-∞'Φ=⎰,()()()()11221222222,x x x dx u u u du u u du u du +∞+∞-∞-∞+∞+∞-∞-∞--⎛⎫''Φ=+Φ ⎪⎝⎭''=Φ+Φ=⎰⎰⎰⎰()10.30.3500.3520.72x EX x x dx x dx +∞+∞-∞-∞-⎛⎫''=Φ+Φ=+⨯= ⎪⎝⎭⎰⎰.(8) 【答案】(B) 【解析】(){}{0}{0}{1}{1}11{0}{1}2211{00}{1},22Z F z P XY z P XY z Y P Y P XY z Y P Y P XY z Y P XY z Y P X z Y P X z Y =≤=≤==+≤===≤=+≤==⋅≤=+≤=由于,X Y 相互独立,所以11(){0}{}22Z F z P X z P X z =⋅≤+≤. (1) 当0z <时,1()()2Z F z z =Φ;(2) 当0z ≥时,11()()22Z F z z =+Φ,因此,0z =为间断点,故选(B).二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.(9) 【答案】12222xf f xyf '''''++ 【解析】12zf f y x∂''=+⋅∂, 21222212222zxf f yx f xf f xyf x y∂''''''''''=++⋅=++∂∂. (10) 【答案】(1)2x x e -+【解析】由常系数线性齐次微分方程0y ay by '''++=的通解为()12xy C C x e =+可知1x y e =,2x y xe =为其两个线性无关的解,代入齐次方程,有111222(1)010,[2(1)]020,x xy ay by a b e a b y ay by a a b x e a '''++=++=⇒++='''++=++++=⇒+=从而可见2,1a b =-=,非齐次微分方程为2y y y x '''-+=.设特解*y Ax B =+,代入非齐次微分方程,得2A Ax B x -++=,即11(2)202A A Ax A B x A B B ==⎧⎧+-+=⇒⇒⎨⎨-+==⎩⎩所以特解*2y x =+,通解()122xy C C x e x =+++.把()()02,00y y '==代入通解,得120,1C C ==-.所以所求解为2(1)2x x y xe x x e =-++=-+.(11)【答案】136【解析】由题意可知,2,0y x x =≤≤,则ds ==,所以()21148Lxds x ==+⎰11386==. (12) 【答案】415π 【解析】解法1:()212222002124013500sin cos cos cos cos 42.3515z dxdydz d d d d d d πππππθϕρϕρϕρθϕϕρρϕρππΩ==-⎛⎫=⋅-⋅= ⎪⎝⎭⎰⎰⎰⎰⎰⎰⎰⎰⎰解法2:由轮换对称性可知2z dxdydz Ω=⎰⎰⎰2x dxdydz Ω=⎰⎰⎰2y dxdydz Ω⎰⎰⎰ 所以,()212222400011sin 33z dxdydz x y z dxdydz d d r dr ππϕθϕΩΩ=++=⎰⎰⎰⎰⎰⎰⎰⎰⎰ 14002214sin sin 33515d r dr d ππππϕϕϕϕπ==⋅⋅=⎰⎰⎰. (13) 【答案】2【解析】2T αβ=,()2T T βαββαββ∴==⋅,又由于0β≠,T βα∴的非零特征值为2. (14) 【答案】1-【解析】由于2X kS +为2np 的无偏估计量,所以22()E X kS np +=,即2222()()()E X kS np E X E kS np +=⇒+=2(1)1(1)(1)1 1.np knp p np k p pk p p k ⇒+-=⇒+-=⇒-=-⇒=-三、解答题:15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. (15)(本题满分9分)【解析】 2(,)2(2)x f x y x y '=+,2(,)2ln 1y f x y x y y '=++.令(,)0,(,)0,x y f x y f x y ⎧'=⎪⎨'=⎪⎩解得唯一驻点1(0,)e .由于212(0,)1(0,)21(0,)11(0,)2(2)2(2),1(0,)40,11(0,)(2),xxexye yy eA f y e eB f xy eC f x e e y ''==+=+''===''==+= 所以 2212(2)0,B AC e e-=-+<且0A >. 从而1(0,)f e是(,)f x y 的极小值,极小值为11(0,)f e e =-.(16)(本题满分9分)【解析】曲线n y x =与1n y x +=的交点为(0,0)和(1,1),所围区域的面积112111111()()001212n n n n n a x x dx x x n n n n +++=-=-=-++++⎰, 111lim 1111111lim()lim(),2312222Nn nN n n N N S a a N N N ∞→∞==→∞→∞===-++-=-=+++∑∑22111211111111(1)22123456n n n n n S a n n n ∞∞∞-=====-=-+-++=-+∑∑∑ ().考查幂级数1(1)n nn x n ∞=-∑,知其收敛域为(1,1]-,和函数为ln(1)x -+.因为2(1)()ln(1)n nn S x x x x n ∞=-==-+∑,令1x =,得2211(1)1ln 2n n S a S ∞-====-∑.(17)(本题满分11分)【解析】(I)椭球面1S 的方程为222143x y z ++=.设切点为00(,)x y ,则22143x y +=在00(,)x y 处的切线方程为00143x x y y +=.将4,0x y ==代入切线方程得01x =,从而032y ==±. 所以切线方程为142x y ±=,从而圆锥面2S 的方程为222(1)44x y z +-=,即222(4)440x y z ---=.(II)1S 与2S 之间的体积等于一个底面半径为32、高为3的锥体体积94π与部分椭球体体积V 之差,其中22135(4)44V x dx ππ=-=⎰. 故所求体积为9544πππ-=.(18)(本题满分11分) 【解析】(Ⅰ)取()()()()()f b f a F x f x x a b a-=---,由题意知()F x 在[],a b 上连续,在(),a b 内可导,且 ()()()()()(),()()()()()().f b f a F a f a a a f a b af b f a F b f b b a f a b a -=--=--=--=-根据罗尔定理,存在(),a b ξ∈,使得()()()()0f b f a F f b aξξ-''=-=-,即()()()()f b f a f b a ξ'-=-.(Ⅱ)对于任意的(0,)t δ∈,函数()f x 在[]0,t 上连续,在()0,t 内可导,由右导数定义及拉格朗日中值定理()()000()0()0lim lim lim ()0t t t f t f f tf f t tξξ++++→→→-'''===-,其中()0,t ξ∈. 由于()0lim t f t A +→'=,且当0t +→时,0ξ+→,所以0lim ()t f A ξ+→'=,故(0)f +'存在,且(0)f A +'=.(19)(本题满分10分)【解析】取2221:1x y z ∑++=的外侧,Ω为∑与1∑之间的部分.()()()11322223322222222.xdydz ydzdx zdxdyI xy zxdydz ydzdx zdxdyxdydz ydzdx zdxdyxy zxy z∑∑-∑∑++=++++++=+++++⎰⎰⎰⎰⎰⎰根据高斯公式()13222200xdydz ydzdx zdxdydxdydz x y z∑-∑Ω++==++⎰⎰⎰⎰⎰ .()1122232222134.x y z xdydz ydzdx zdxdyxdydz ydzdx zdxdyxy zdxdydz π∑∑++≤++=++++==⎰⎰⎰⎰⎰⎰⎰所以4I π=.(20)(本题满分11分)【解析】(Ⅰ)对矩阵1()A ξ 施以初等行变换()11110221111111111012204220000A ξ⎛⎫-- ⎪---⎛⎫ ⎪⎪ ⎪=-→ ⎪ ⎪ ⎪--- ⎪⎝⎭ ⎪ ⎪⎝⎭可求得 2122122k k k ξ⎛⎫-+ ⎪ ⎪ ⎪=- ⎪⎪⎪ ⎪⎝⎭,其中k 为任意常数.又2220220440A ⎛⎫ ⎪=-- ⎪ ⎪⎝⎭,对矩阵21()A ξ 施以初等行变换()211110220122201000044020000A ξ⎛⎫-⎪-⎛⎫ ⎪ ⎪=--→ ⎪ ⎪ ⎪ ⎪-⎝⎭ ⎪⎝⎭,可求得 312a a b ξ⎛⎫-- ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭,其中,a b 为任意常数.(Ⅱ)解法1 由(Ⅰ)知12311122211,,102222ka ka kbξξξ--+--=-=-≠-, 所以123,,ξξξ线性无关.解法2 由题设可得10A ξ=.设存在数123,,k k k ,使得1122330k k k ξξξ++=, ①等式两端左乘A ,得22330k A k A ξξ+=,即21330k k A ξξ+=, ②等式两端再左乘A ,得2330k A ξ=,即310k ξ=.由于10ξ≠,于是30k =,代入②式,得210k ξ=,故20k =.将230k k ==代入①式,可得10k =,从而1,ξ23,ξξ线性无关.(21)(本题满分11分) 【解析】(Ⅰ)二次型f 的矩阵101111a A a a ⎛⎫ ⎪=- ⎪ ⎪--⎝⎭.由于01||01()((1))((2))111aE A aa a a a λλλλλλλ---=-=--+----+, 所以A 的特征值为123,1,2a a a λλλ==+=-.(Ⅱ)解法1 由于f 的规范形为2212y y +,所以A 合同于100010000⎛⎫ ⎪ ⎪ ⎪⎝⎭,其秩为2,故 1230A λλλ==,于是0a =或1a =-或2a =.当0a =时,1230,1,2λλλ===-,此时f 的规范形为2212y y -,不合题意. 当1a =-时,1231,0,3λλλ=-==-,此时f 的规范形为2212y y --,不合题意. 当2a =时,1232,3,0λλλ===,此时f 的规范形为2212y y +. 综上可知,2a =.解法2 由于f 的规范形为2212y y +,所以A 的特征值有2个为正数,1个为零. 又21a a a -<<+,所以2a =.(22)(本题满分11分)【解析】(Ⅰ) 12211{1,0}463(10)1{0}9()2C P X Z P X Z P Z ⋅========. (Ⅱ)由题意知X 与Y 的所有可能取值均为0,1,2.()()()()()()()()()1111332311116666111223111166661122116611221166110,0,1,0,461112,0,0,1,36311,1,2,10,910,2,91,20,2,20,C C C C P X Y P X Y C C C C C C C P X Y P X Y C C C C C C P X Y P X Y C C C C P X Y C C P X Y P X Y ⋅⋅========⋅⋅⋅⋅========⋅⋅⋅=======⋅⋅====⋅======故(,)X Y 的概率分布为(23)(本题满分11 分) 【解析】(Ⅰ)2202().x EX xf x dx x e dx λλλ+∞+∞--∞===⎰⎰令X EX =,即2X λ=,得λ的矩估计量为 12Xλ=. (Ⅱ)设12,,,(0,1,2,,)n i x x x x i n >= 为样本观测值,则似然函数为()12121,,,;,nii nx nn i i L x x x ex λλλ=-=∑=⋅∏11ln 2ln ln n ni i i i L n x x λλ===-+∑∑,由1ln 20n i i d L n x d λλ==-=∑,得λ的最大似然估计量为 22X λ=.。
2009考研数学三真题及答案解析
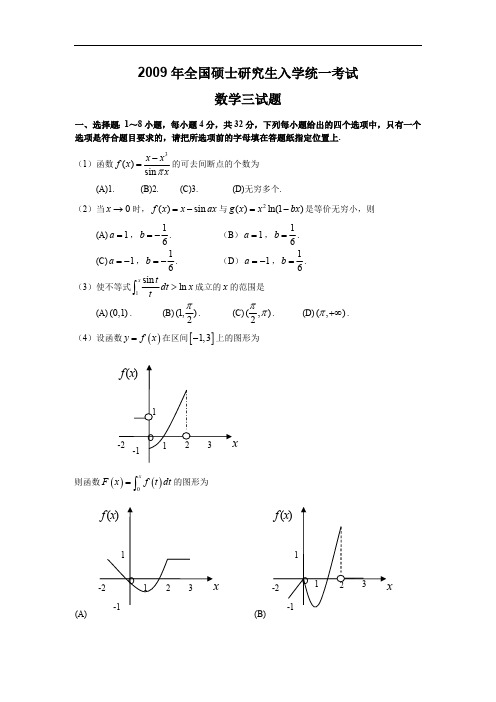
2009年全国硕士研究生入学统一考试数学三试题一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一个选项是符合题目要求的,请把所选项前的字母填在答题纸指定位置上.(1)函数的可去间断点的个数为3()sin x x f x xπ-=(A)1.(B)2.(C)3.(D)无穷多个.(2)当时,与是等价无穷小,则0x →()sin f x x ax =-2()ln(1)g x x bx =-(A),. (B ),. 1a =16b =-1a =16b =(C),. (D ),.1a =-16b =-1a =-16b =(3)使不等式成立的的范围是1sin ln x tdt x t>⎰x (A).(B). (C).(D).(0,1)(1,2π(,)2ππ(,)π+∞(4)设函数在区间上的图形为()y f x =[]1,3-则函数的图形为()()0xF x f t dt =⎰(A)(B)(C)(D)(5)设均为2阶矩阵,分别为的伴随矩阵,若,则分块矩,A B *,A B *,A B ||2,||3A B ==阵的伴随矩阵为O A B O ⎛⎫⎪⎝⎭(A).(B). **32O B A O ⎛⎫ ⎪⎝⎭**23OB A O ⎛⎫⎪⎝⎭(C).(D).**32O A B O ⎛⎫⎪⎝⎭**23O A BO ⎛⎫⎪⎝⎭(6)设均为3阶矩阵,为的转置矩阵,且,,A P T P P 100010002TP AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭若,则为1231223(,,),(,,)P Q ααααααα==+TQ AQ (A).(B).210110002⎛⎫⎪ ⎪ ⎪⎝⎭110120002⎛⎫⎪ ⎪ ⎪⎝⎭(C). (D).200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭100020002⎛⎫ ⎪ ⎪ ⎪⎝⎭(7)设事件与事件B 互不相容,则A (A). (B). ()0P AB =()()()P AB P A P B =(C).(D).()1()P A P B =-()1P A B ⋃=(8)设随机变量与相互独立,且服从标准正态分布,的概率分布为X Y X (0,1)N Y ,记为随机变量的分布函数,则函数1{0}{1}2P Y P Y ====()z F Z Z XY =()z F Z的间断点个数为(A)0.(B)1. (C)2.(D)3.二、填空题:9~14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.(9).0x →=(10)设,则.()y xz x e =+(1,0)zx ∂=∂(11)幂级数的收敛半径为 .21(1)n n nn e x n ∞=--∑(12)设某产品的需求函数为,其对应价格的弹性,则当需求量为()Q Q P =P 0.2p ξ=10000件时,价格增加1元会使产品收益增加元.(13)设,,若矩阵相似于,则.(1,1,1)T α=(1,0,)T k β=Tαβ300000000⎛⎫⎪ ⎪ ⎪⎝⎭k = (14)设,,…,为来自二项分布总体的简单随机样本,和分别为样1X 2X n X (,)B n p X 2S 本均值和样本方差,记统计量,则.2T X S =-ET =三、解答题:15~23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.(15)(本题满分9分)求二元函数的极值.()22(,)2ln f x y xy y y =++(16)(本题满分10 分)计算不定积分 .ln(1dx +⎰(0)x >(17)(本题满分10 分)计算二重积分,其中.()Dx y dxdy -⎰⎰22{(,)(1)(1)2,}D x y x y y x =-+-≤≥(18)(本题满分11 分)(Ⅰ)证明拉格朗日中值定理,若函数在上连续,在上可导,则()f x [],a b (),a b ,得证.(),a b ξ∈()'()()()f b f a f b a ξ-=-(Ⅱ)证明:若函数在处连续,在内可导,且()f x 0x =()0,,(0)σσ>,则存在,且.'0lim ()x f x A +→='(0)f +'(0)f A +=(19)(本题满分10 分)设曲线,其中是可导函数,且.已知曲线与直线()y f x =()f x ()0f x >()y f x =及所围成的曲边梯形绕轴旋转一周所得的立体体积值是该曲边梯0,1y x ==(1)x t t =>x 形面积值的倍,求该曲线的方程.t π(20)(本题满分11 分)设,.111A=111042--⎛⎫ ⎪- ⎪ ⎪--⎝⎭1112ξ-⎛⎫⎪= ⎪⎪-⎝⎭(Ⅰ)求满足,的所有向量,.21A ξξ=231Aξξ=2ξ3ξ(Ⅱ)对(Ⅰ)中的任意向量,,证明,,线性无关.2ξ3ξ1ξ2ξ3ξ(21)(本题满分11 分)设二次型.2221231231323(,,)(1)22f x x x ax ax a x x x x x =++-+-(Ⅰ)求二次型的矩阵的所有特征值.f (Ⅱ)若二次型的规范形为,求的值.f 2211y y +a (22)(本题满分11 分)设二维随机变量的概率密度为(,)X Y 0(,)0xe y xf x y -⎧<<=⎨⎩其他(Ⅰ)求条件概率密度;()Y X f y x (Ⅱ)求条件概率.11P X Y =⎡≤≤⎤⎣⎦(23)(本题满分11分)袋中有一个红球,两个黑球,三个白球,现在放回的从袋中取两次,每次取一个,求以、X 、分别表示两次取球所取得的红、黑与白球的个数.Y Z (Ⅰ)求;10P X Z ⎡==⎤⎣⎦(Ⅱ)求二维随机变量的概率分布.(,)X Y 2009年全国硕士研究生入学统一考试数学三试题解析一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一个选项是符合题目要求的,请把所选项前的字母填在答题纸指定位置上.(1)函数的可去间断点的个数为3()sin x x f x xπ-=(A)1. (B)2. (C)3.(D)无穷多个.【答案】C. 【解析】()3sin x x f x xπ-=则当取任何整数时,均无意义x ()f x 故的间断点有无穷多个,但可去间断点为极限存在的点,故应是的解()f x 30x x -=1,2,30,1x =±320032113211131lim lim sin cos 132lim lim sin cos 132lim lim sin cos x x x x x x x x x x x x x x x x x x x x x ππππππππππππ→→→→→-→---==--==--==故可去间断点为3个,即0,1±(2)当时,与是等价无穷小,则0x →()sin f x x ax =-2()ln(1)g x x bx =-(A),. (B ),. 1a =16b =-1a =16b =(C),.(D ),.1a =-16b =-1a =-16b =【答案】A.【解析】为等价无穷小,则2()sin ,()(1)f x x ax g x x ln bx =-=-222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bx bx→→→→→---==-⋅---洛洛 故排除(B)、(C).230sin lim 166x a ax a b b axa→==-=-⋅36a b ∴=-另外存在,蕴含了故排除(D).201cos lim3x a axbx →--1cos 0a ax -→()0x → 1.a =所以本题选(A).(3)使不等式成立的的范围是1sin ln xtdt x t>⎰x (A).(B). (C).(D).(0,1)(1,2π(,)2ππ(,)π+∞【答案】A.【解析】原问题可转化为求成立时的111sin sin 1()ln xx x tt f x dt x dt dt t t t =-=-⎰⎰⎰11sin 11sin 0x x t t dt dt t t--==>⎰⎰x 取值范围,由,时,知当时,.故应选(A).1sin 0tt->()0,1t ∈()0,1x ∈()0f x >(4)设函数在区间上的图形为()y f x =[]1,3-则函数的图形为()()0xF x f t dt =⎰(A)(B)(C)(D)【答案】D.【解析】此题为定积分的应用知识考核,由的图形可见,其图像与轴及轴、()y f x =x y 所围的图形的代数面积为所求函数,从而可得出几个方面的特征:0x x =()F x ①时,,且单调递减.[]0,1x ∈()0F x ≤②时,单调递增.[]1,2x ∈()F x ③时,为常函数.[]2,3x ∈()F x ④时,为线性函数,单调递增.[]1,0x ∈-()0F x ≤⑤由于F(x)为连续函数结合这些特点,可见正确选项为(D).(5)设均为2阶矩阵,分别为的伴随矩阵,若,则分块矩,A B *,A B *,A B ||2,||3A B ==阵的伴随矩阵为O A B O ⎛⎫⎪⎝⎭(A).(B). **32O B A O ⎛⎫ ⎪⎝⎭**23OB A O ⎛⎫⎪⎝⎭(C).(D).**32O A B O ⎛⎫⎪⎝⎭**23O A BO ⎛⎫⎪⎝⎭【答案】B.【解析】根据,若CC C E *=111,C C C CC C*--*==分块矩阵的行列式,即分块矩阵可逆O A B O ⎛⎫ ⎪⎝⎭221236O A A B B O ⨯=-=⨯=()1111661O B BO A O A O A O B B O B O B O AO A O A**---*⎛⎫ ⎪⎛⎫⎛⎫⎛⎫ ⎪=== ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎪⎝⎭1236132O B O B AO A O ****⎛⎫⎪⎛⎫== ⎪ ⎪ ⎪⎝⎭⎪⎝⎭故答案为(B).(6)设均为3阶矩阵,为的转置矩阵,且,,A P T P P 100010002TP AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭若,则为1231223(,,),(,,)P Q ααααααα==+TQ AQ (A).(B).210110002⎛⎫⎪ ⎪ ⎪⎝⎭110120002⎛⎫⎪ ⎪ ⎪⎝⎭(C). (D).200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭100020002⎛⎫ ⎪ ⎪ ⎪⎝⎭【答案】A.【解析】,即:122312312312100(,,)(,,)110(,,)(1)001Q E αααααααααα⎡⎤⎢⎥=+==⎢⎥⎢⎥⎣⎦12121212122112(1)[(1)][(1)](1)[](1)100(1)010(1)002110100100210010010110110001002001002T T TT Q PE Q AQ PE A PE E P AP E E E ===⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦(7)设事件与事件B 互不相容,则A (A).(B). ()0P AB =()()()P AB P A P B =(C).(D).()1()P A P B =-()1P A B ⋃=【答案】D.【解析】因为互不相容,所以,A B ()0P AB =(A),因为不一定等于1,所以(A)不正确.()()1()P AB P A B P A B ==- ()P A B (B)当不为0时,(B)不成立,故排除.(),()P A P B (C)只有当互为对立事件的时候才成立,故排除.,A B(D),故(D)正确.()()1()1P A B P AB P AB ==-= (8)设随机变量与相互独立,且服从标准正态分布,的概率分布为X Y X (0,1)N Y ,记为随机变量的分布函数,则函数1{0}{1}2P Y P Y ====()z F Z Z XY =()z F Z 的间断点个数为( )(A)0.(B)1. (C)2.(D)3.【答案】 B.【解析】()()(0)(0)(1)(1)Z F z P XY z P XY z Y P Y P XY z Y P Y =≤=≤==+≤==1[(0)(1)]21[(00)(1)]2P XY z Y P XY z Y P X z Y P X z Y =≤=+≤==⋅≤=+≤=独立,X Y 1()[(0)()]2Z F z P x z P x z ∴=⋅≤+≤(1)若,则0z <1()()2Z F z z =Φ(2)当,则0z ≥1()(1())2Z F z z =+Φ为间断点,故选(B).0z ∴=二、填空题:9~14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.(9).0x →=【答案】.32e 【解析】.00x x →→=02(1cos )lim13x e x x→-=20212lim 13x e x x →⋅=32e =(10)设,则.()y xz x e =+(1,0)zx ∂=∂【答案】.2ln 21+【解析】由,故()xy z x e=+()(),01xz x x =+()''ln(1)ln(1)1ln(1)1x x x x x dz x x e e x dx x ++⎡⎤⎡⎤⎡⎤=+==++⎣⎦⎢⎥⎣⎦+⎣⎦代入得,.1x =()ln 21,01ln 22ln 212z e x∂⎛⎫=+=+ ⎪∂⎝⎭(11)幂级数的收敛半径为 .21(1)n n nn e x n ∞=--∑【答案】.1e【解析】由题意知,()210nn n e a n--=>()()()()111122122111()11111n n n n n nn n nn e e ea n n e n a n e n e e +++++⎡⎤⎛⎫--⎢⎥ ⎪⎝⎭--⎢⎥⎣⎦=⋅=⋅→→∞⎡⎤+--+⎛⎫--⎢⎥⎪⎝⎭⎢⎥⎣⎦所以,该幂级数的收敛半径为1e(12)设某产品的需求函数为,其对应价格的弹性,则当需求量为()Q Q P =P 0.2p ξ=10000件时,价格增加1元会使产品收益增加 元.【答案】8000.【解析】所求即为()QP Q P Q ''=+因为,所以0.2p Q PQξ'==-0.2Q P Q '=-所以()0.20.8QP Q Q Q '=-+=将代入有.10000Q =()8000QP '=(13)设,,若矩阵相似于,则.(1,1,1)T α=(1,0,)T k β=Tαβ300000000⎛⎫ ⎪ ⎪ ⎪⎝⎭k =【答案】2.【解析】相似于,根据相似矩阵有相同的特征值,得到的特征值为T αβ300000000⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦Tαβ3,0,0.而为矩阵的对角元素之和,,.TαβT αβ1300k ∴+=++2k ∴= (14)设,,…,为来自二项分布总体的简单随机样本,和分别为样1X 2X n X (,)B n p X 2S 本均值和样本方差,记统计量,则 .2T X S =-ET =【答案】2np 【解析】由.222()(1)ET E X S E X ES np np p np =-=-=--=三、解答题:15~23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.(15)(本题满分9分)求二元函数的极值.()22(,)2ln f x y xy y y =++【解析】,,故.2(,)2(2)0x f x y x y '=+=2(,)2ln 10y f x y x y y '=++=10,x y e= =.2212(2),2,4xxyy xyf y f x f xy y''''''=+ =+ =则,,.12(0,)12(2xxef e ''=+1(0,)0xyef ''=1(0,)yyef e ''=而0xxf ''> 2()0xy xx yy f f f ''''''-<二元函数存在极小值.∴11(0,)f e e=-(16)(本题满分10 分)计算不定积分 .ln(1dx+⎰(0)x >得t =22212,1(1)tdtx dx t t -= =--2221ln(1ln(1)1ln(1)11111dx t d t t dt t t t +=+-+=---+⎰⎰⎰而22111112(11411(1)111ln(1)ln(1)2441dt dtt t t t t t t C t =---+-++--++++⎰⎰所以2ln(1)111ln(1ln 1412(1)1ln(1.2t t dx C t t t x C +++=+-+--+=+++⎰(17)(本题满分10 分)计算二重积分,其中.()Dx y dxdy -⎰⎰22{(,)(1)(1)2,}D x y x y y x =-+-≤≥【解析】由得,22(1)(1)2x y -+-≤2(sin cos )r θθ≤+32(sin cos )4()(cos sin )04Dx y dxdy d r r rdr πθθθθθπ+∴-=-⎰⎰⎰⎰332(sin cos )14(cos sin )034r d πθθθθθπ⎡+⎤=-⋅⎢⎥⎣⎦⎰2384(cos sin )(sin cos )(sin cos )34d πθθθθθθθπ=-⋅+⋅+⎰3384(cos sin )(sin cos )34d πθθθθθπ=-⋅+⎰.3344438814(sin cos )(sin cos )(sin cos )3344d πππθθθθθθπ=++=⨯+⎰83=-(18)(本题满分11 分)(Ⅰ)证明拉格朗日中值定理,若函数在上连续,在上可导,则()f x [],a b (),a b ,得证.(),a b ξ∈()'()()()f b f a f b a ξ-=-(Ⅱ)证明:若函数在处连续,在内可导,且()f x 0x =()0,,(0)σσ>,则存在,且.'0lim ()x f x A +→='(0)f +'(0)f A +=【解析】(Ⅰ)作辅助函数,易验证满足:()()()()()()f b f a x f x f a x a b aϕ-=----()x ϕ;在闭区间上连续,在开区间内可导,且()()a b ϕϕ=()x ϕ[],a b (),a b .''()()()()f b f a x f x b aϕ-=--根据罗尔定理,可得在内至少有一点,使,即(),a b ξ'()0ϕξ='()f ξ'()()0,()()()()f b f a f b f a f b a b aξ--=∴-=--(Ⅱ)任取,则函数满足:在闭区间上连续,开区间内可导,0(0,)x δ∈()f x []00,x ()00,x 从而有拉格朗日中值定理可得:存在,使得()()000,0,x x ξδ∈⊂……()0'00()(0)x f x f f x ξ-=-()*又由于,对上式(*式)两边取时的极限可得:()'lim x f x A +→=00x +→()()000000'''0000()00lim lim ()lim ()0x x x x x f x f f f f A x ξξξ++++→→→-====-故存在,且.'(0)f +'(0)f A +=(19)(本题满分10 分)设曲线,其中是可导函数,且.已知曲线与直线()y f x =()f x ()0f x >()y f x =及所围成的曲边梯形绕轴旋转一周所得的立体体积值是该曲边梯0,1y x ==(1)x t t =>x 形面积值的倍,求该曲线的方程.t π【解析】旋转体的体积为22()()11x x t t V f dx f dxππ==⎰⎰曲边梯形的面积为:,则由题可知()1x ts f dx =⎰22()()()()1111x x x x t t t tV ts f dx t f dx f dx t f dxπππ=⇒=⇒=⎰⎰⎰⎰两边对t 求导可得 22()()()()()()11t x t t t x t t f f dx tf f tf f dx =+⇒-=⎰⎰继续求导可得,化简可得''2()()()()()f t f t f t tf t f t --=,解之得'1(2())()2()12dt f t t f t f t t dy y-=⇒+=1223t c y y-=⋅+在式中令,则,代入得 1t =2(1)(1)0,()0,(1)1f f f t f -=>∴= 1223t cyy -=+.11,2)33c t y =∴=所以该曲线方程为:.230y x +=(20)(本题满分11 分)设,.111A=111042--⎛⎫ ⎪- ⎪ ⎪--⎝⎭1112ξ-⎛⎫⎪= ⎪⎪-⎝⎭(Ⅰ)求满足,的所有向量,.21A ξξ=231Aξξ=2ξ3ξ(Ⅱ)对(Ⅰ)中的任意向量,,证明,,线性无关.2ξ3ξ1ξ2ξ3ξ【解析】(Ⅰ)解方程21A ξξ=()1111111111111,111100000211042202110000A ξ---------⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=-→→ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭故有一个自由变量,令,由解得,()2r A =32x =0Ax =211,1x x =-= 求特解,令,得120x x ==31x = 故 ,其中为任意常数21101021k ξ⎛⎫⎛⎫ ⎪ ⎪=-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭1k解方程231Aξξ=2220220440A ⎛⎫ ⎪=-- ⎪ ⎪⎝⎭()21111022012,2201000044020000A ξ-⎛⎫ ⎪-⎛⎫ ⎪ ⎪=--→⎪ ⎪ ⎪ ⎪-⎝⎭ ⎪⎝⎭故有两个自由变量,令,由得231,0x x =-=20A x =11x =令,由得230,1x x ==-20A x =10x =求得特解21200η⎛⎫- ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭故 ,其中为任意常数3231102100010k k ξ⎛⎫-⎪⎛⎫⎛⎫⎪ ⎪ ⎪=-++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭ ⎪⎝⎭23,k k (Ⅱ)证明:由于12121212122111121112(21)()2((21)22221k k k k k k k k k k k k k -+--=+++-+-+-+102=≠故 线性无关. 123,,ξξξ(21)(本题满分11 分)设二次型.2221231231323(,,)(1)22f x x x ax ax a x x x x x =++-+-(Ⅰ)求二次型的矩阵的所有特征值.f (Ⅱ)若二次型的规范形为,求的值.f 2211y y +a【解析】(Ⅰ) 0101111a A a a ⎛⎫ ⎪=- ⎪⎪--⎝⎭0110||01()1111111aa aE A a a a a λλλλλλλλ-----=-=---+---+222()[()(1)1][0()]()[()(1)2]()[22]19(){[(12)]}24()(2)(1)a a a a a a a a a a a a a a a a a λλλλλλλλλλλλλλλλ=---+--+-=---+-=--++--=-+--=--+--.123,2,1a a a λλλ∴==-=+(Ⅱ) 若规范形为,说明有两个特征值为正,一个为0.则2212y y +1)若,则, ,不符题意10a λ==220λ=-<31λ=2)若 ,即,则,,符合20λ=2a =120λ=>330λ=>3)若 ,即,则 ,,不符题意30λ=1a =-110λ=-<230λ=-<综上所述,故2a =(22)(本题满分11 分)设二维随机变量的概率密度为(,)X Y 0(,)0x e y xf x y -⎧<<=⎨⎩其他(Ⅰ)求条件概率密度()Y X f y x (Ⅱ)求条件概率11P X Y =⎡≤≤⎤⎣⎦【解析】(Ⅰ)由得其边缘密度函数0(,)0x y xe f x y -<<⎧= ⎨⎩其它()0xx x x f x e dy xe x --== >⎰故 |(,)1(|)0()y x x f x y f y x y x f x x== <<即|1(|)0y x y xf y x x ⎧ 0<<⎪=⎨⎪⎩其它(Ⅱ)[1,1][1|1][1]P X Y P X Y P Y ≤≤≤≤=≤而11111[1,1](,)12xxx x y P X Y f x y dxdy dx e dy xe dx e ---≤≤≤≤====-⎰⎰⎰⎰⎰()|,0x x yY yf y e dx e e y y+∞---+∞==-= >⎰11101[1]|110y y P Y e dy e e e ----∴ ≤==-=-+=-⎰.11122[1|1]11e e P X Y e e ----∴ ≤≤==--(23)(本题满分11分)袋中有一个红球,两个黑球,三个白球,现在放回的从袋中取两次,每次取一个,求以、X 、分别表示两次取球所取得的红、黑与白球的个数.Y Z ①求.10P X Z ⎡==⎤⎣⎦②求二维随机变量的概率分布.(,)X Y 【解析】(Ⅰ)在没有取白球的情况下取了一次红球,利用压缩样本空间则相当于只有1个红球,2个黑球放回摸两次,其中摸了一个红球.12113324(10)9C P X Z C C ⨯∴====⋅(Ⅱ)X ,Y 取值范围为0,1,2,故()()()()()()()()()1111332311116666111223111166661122116611221166110,0,1,0461112,0,0,136311,1,2,10910,291,20,2,20C C C C P X Y P X Y C C C C C C C P X Y P X Y C C C C C C P X Y P X Y C C C C P X Y C C P X Y P X Y ⋅⋅========⋅⋅⋅⋅========⋅⋅⋅=======⋅⋅====⋅======012 XY01/41/61/36 11/31/9021/900。
研究生入学考试生物化学(激素)历年真题试卷汇编1

研究生入学考试生物化学(激素)历年真题试卷汇编1(总分:60.00,做题时间:90分钟)一、判断题请判断下列各题正误。
(总题数:7,分数:14.00)1.(复旦大学2008年考研试题)酪氨酸可以在人体内直接被加碘而转变为甲状腺素。
(分数:2.00)A.正确B.错误√解析:解析:碘化过程发生在甲状腺球蛋白的酪氨酸残基上,10%的酪氨酸残基可被碘化。
碘离子被摄入甲状腺腺泡上皮细胞后,在过氧化酶的作用下,迅速氧化为活化碘,然后经碘化酶的作用使甲状球蛋白中的酪氨酸残基碘化,生成一碘酪氨酸(MIT)和二碘酪氨酸(DIT)。
再在缩合酶的作用下,将它们缩合成T4或T3即有生物活性的甲状腺素激素。
所以酪氨酸不是直接加碘生成甲状腺素。
2.(南京大学2008年考研试题)肝素是带有大量负电荷的糖胺聚糖,临床上常用作抗凝剂。
(分数:2.00)A.正确√B.错误解析:3.(南京大学2008年考研试题)雌性激素和雄性激素虽然都是胆固醇的衍生物,但在体内不能相互转变。
(分数:2.00)A.正确B.错误√解析:解析:雌性激素和雄性激素都是胆固醇衍生而成的,可以相互转变。
雄性激素在机体内可变为雌性激素,由尿排出;雌性激素也可变为雄性激素,由尿排出。
4.(南开大学2009年考研试题)酷氨酸在碘化酶的作用下可直接生成甲状腺素。
(分数:2.00)A.正确B.错误√解析:解析:碘化过程发生在甲状腺球蛋白的酪氨酸残基上,10%的酪氨酸残基可被碘化。
碘离子被摄入甲状腺腺泡上皮细胞后,在过氧化酶的作用下,迅速氧化为活化碘,然后经碘化酶的作用使甲状球蛋白中的酪氨酸残基碘化,生成一碘酪氨酸(MIT)和二碘酪氨酸(DIT)。
再在缩合酶的作用下,将它们缩合成T4或T3即有生物活性的甲状腺素激素。
所以酷氨酸不是在碘化酶的作用下可直接生成甲状腺素。
5.(南开大学2008年考研试题)胰岛素受体具有酪氨酸激酶活性。
(分数:2.00)A.正确√B.错误解析:6.(山东大学2005年考研试题)含氮激素主要是通过与膜受体结合后,引起级联反应而发挥作用的。
2009年考研数学一真题及答案解析

2009年全国硕士研究生入学统一考试数学一试题一、选择题(1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)(1)当0x →时,()sin f x x ax =-与()()2ln 1g x x bx =-等价无穷小,则( )()A 11,6a b ==-. ()B 11,6a b ==. ()C 11,6a b =-=-. ()D 11,6a b =-=.(2)如图,正方形(){},1,1x y x y ≤≤被其对角线划分为四个区域()1,2,3,4k D k =,cos kk D I y xdxdy =⎰⎰,则{}14max k k I ≤≤=( )()A 1I .()B 2I . ()C 3I .()DI (3)设函数()y f x =在区间[]1,3-上的图形为:则函数()()0xF x f t dt =⎰的图形为( )()A .()B .x()C .()D .(4)设有两个数列{}{},n n a b ,若lim 0n n a →∞=,则( )()A 当1n n b ∞=∑收敛时,1n n n a b ∞=∑收敛.()B 当1n n b ∞=∑发散时,1n n n a b ∞=∑发散.()C 当1nn b∞=∑收敛时,221n nn a b∞=∑收敛.()D 当1nn b ∞=∑发散时,221n nn a b∞=∑发散.(5)设123,,ααα是3维向量空间3R 的一组基,则由基12311,,23ααα到基 122331,,αααααα+++的过渡矩阵为( )()A 101220033⎛⎫⎪⎪ ⎪⎝⎭. ()B 120023103⎛⎫⎪⎪ ⎪⎝⎭.()C 111246111246111246⎛⎫- ⎪ ⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭.()D 111222111444111666⎛⎫-⎪ ⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭. (6)设,A B 均为2阶矩阵,**,A B 分别为,A B 的伴随矩阵,若2,3A B ==,则分块矩阵O A B O ⎛⎫⎪⎝⎭的伴随矩阵为( )()A **32O B A O ⎛⎫ ⎪⎝⎭.()B **23OB A O ⎛⎫⎪⎝⎭. ()C **32O A BO ⎛⎫ ⎪⎝⎭.()D **23O A BO ⎛⎫⎪⎝⎭.(7)设随机变量X 的分布函数为()()10.30.72x F x x -⎛⎫=Φ+Φ⎪⎝⎭,其中()x Φ为标准正态分布函数,则EX =( )()A 0.()B 0.3. ()C 0.7.()D 1.(8)设随机变量X 与Y 相互独立,且X 服从标准正态分布()0,1N ,Y 的概率分布为{}{}1012P Y P Y ====,记()Z F z 为随机变量Z XY =的分布函数,则函数()Z F z 的间断点个数为( )()A 0.()B 1. ()C 2.()D 3.二、填空题(9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.)(9)设函数(),f u v 具有二阶连续偏导数,(),z f x xy =,则2zx y∂=∂∂ 。
2009-2010计算机考研真题及答案——数据结构部分

void leftShift(int r[],int n,int p) { if(p>0&&p<n) { reverse(r,0,n-1);//将全部数据逆置 reverse(r,0,n-p-1);//将前n-p个元素逆置 reverse(r,n-p,n-1);//将后p个元素逆置 } } (3)说明算法复杂性:上述算法的时间复杂度为O(n),空间复 杂度为O(1)。
10.若数据元素序列11,12,13,7,8,9, 10. 23,4,5是采用下列排序方法之一得到的第二 趟排序后的结果,则该排序算法只能是( ) A A. A.起泡排序 B.插入排序 B. C.选择排序 D.二路归并排序 C. D.
二、综合应用题(10分+15分) 综合应用题(10分+15分
41.(10分)带权图(权值非负,表示边连接 41. 的两顶点间的距离)的最短路径问题是找出从 初始顶点到目标顶点之间的一条最短路径。假 定从初始顶点到目标顶点之间存在路径,现有 一种解决该问题的方法: ①设最短路径初始时仅包含初始顶点,令当前 顶点u为初始顶点; ②选择离u最近且尚未在最短路径中的一个顶 点v,加入到最短路径中,修改当前顶点u=v; ③重复步骤②,直到u是目标顶点时为止。 请问上述方法能否求得最短路径?若该方法可 行,请证明之;否则,请举例说明。
42题答案解析 42题答案解析
(1)算法的基本设计思想: 定义两个指针变量p和q,初始时均指向头结点的下 一个结点。P指针沿链表移动;当p指针移动到第k个结点 时,q指针开始与p指针同步移动;当p指针移动到链表最 后一个结点时,q指针所指元素为倒数第k个结点。 以上过程对链表仅进行一遍扫描。 (2)算法的详细实现步骤: ①count=0,p和q指向链表表头结点的下一个结点; ②若p为空,转⑤; ③若count等于k,则q指向下一个结点;否则, count=count+1; ④p指向下一个结点,转步骤②; ⑤若count等于k,则查找成功,输出该结点的 data域的值,返回1;返回,查找失败,返回0; ⑥算法结束。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2009年全国硕士研究生入学统一考试数学一试题一、选择题:1~8小题,每小题4分,共32分.(1)当0x →时,()sin f x x ax =-与()()2ln 1g x x bx =-是等价无穷小,则()(A)11,6a b ==-.(B)11,6a b ==.(C)11,6a b =-=-.(D)11,6a b =-=.(2)如图,正方形(){},1,1x y x y ≤≤被其对角线划分为四个区域()1,2,3,4k D k =,cos kk D I y xdxdy =⎰⎰,则{}14max k k I ≤≤=()(A)1I .(B)2I .(C)3I .(D)4I .(3)设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为()(A)(B)-1-111xy1D 2D 3D 4D(C)(D)(4)设有两个数列{}{},n n a b ,若lim 0n n a →∞=,则()(A)当1nn b∞=∑收敛时,1n nn a b∞=∑收敛.(B)当1nn b∞=∑发散时,1n nn a b∞=∑发散.(C)当1nn b∞=∑收敛时,221n nn a b∞=∑收敛.(D)当1nn b∞=∑发散时,221n nn a b∞=∑发散.(5)设123,,ααα是3维向量空间3R 的一组基,则由基12311,,23αα到基122331,,αααααα+++的过渡矩阵为()(A)101220033⎛⎫ ⎪ ⎪ ⎪⎝⎭.(B)120023103⎛⎫ ⎪ ⎪ ⎪⎝⎭.(C)111246111246111246⎛⎫- ⎪ ⎪ ⎪-⎪ ⎪ ⎪- ⎪⎝⎭.(D)111222111444111666⎛⎫- ⎪ ⎪⎪- ⎪ ⎪ ⎪- ⎪⎝⎭.(6)设,A B 均为2阶矩阵,**,A B 分别为,A B 的伴随矩阵,若2,3A B ==,则分块矩阵O A B O ⎛⎫ ⎪⎝⎭的伴随矩阵为()(A)**32O B A O ⎛⎫⎪⎝⎭.(B)**23O B A O ⎛⎫⎪⎝⎭.(C)**32O A BO ⎛⎫⎪⎝⎭.(D)**23O A BO ⎛⎫⎪⎝⎭.(7)设随机变量X 的分布函数为()()10.30.72x F x x -⎛⎫=Φ+Φ⎪⎝⎭,其中()x Φ为标准正态分布的分布函数,则EX =()(A)0.(B)0.3.(C)0.7.(D)1.(8)设随机变量X 与Y 相互独立,且X 服从标准正态分布()0,1N ,Y 的概率分布为{}{}1012P Y P Y ====.记()Z F z 为随机变量Z XY =的分布函数,则函数()Z F z 的间断点个数为()(A)0.(B)1.(C)2.(D)3.二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.(9)设函数(),f u v 具有二阶连续偏导数,(),z f x xy =,则2zx y∂=∂∂.(10)若二阶常系数线性齐次微分方程0y ay by '''++=的通解为()12xy C C x e =+,则非齐次方程y ay by x '''++=满足条件()()02,00y y '==的解为y =.(11)已知曲线(2:0L y x x =≤≤,则Lxds =⎰.(12)设(){}222,,1x y z xy z Ω=++≤,则2z dxdydz Ω=⎰⎰⎰.(13)若3维列向量,αβ满足2T αβ=,其中T α为α的转置,则矩阵T βα的非零特征值为.(14)设12,,,m X X X 为来自二项分布总体(),B n p 的简单随机样本,X 和2S 分别为样本均值和样本方差.若2X kS +为2np 的无偏估计量,则k =.三、解答题:15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.(15)(本题满分9分)求二元函数()22(,)2ln f x y x y y y =++的极值.(16)(本题满分9分)设n a 为曲线ny x =与()11,2,n y xn +== 所围成区域的面积,记11,n n S a ∞==∑2211n n S a ∞-==∑,求1S 与2S 的值.(17)(本题满分11分)椭球面1S 是椭圆22143x y +=绕x 轴旋转而成,圆锥面2S 是由过点()4,0且与椭圆22143x y +=相切的直线绕x 轴旋转而成.(Ⅰ)求1S 及2S 的方程;(Ⅱ)求1S 与2S 之间的立体体积.(18)(本题满分11分)(Ⅰ)证明拉格朗日中值定理:若函数()f x 在[],a b 上连续,在(,)a b 可导,则存在(),a b ξ∈,使得()()()()f b f a f b a ξ'-=-.(Ⅱ)证明:若函数()f x 在0x =处连续,在()()0,0δδ>内可导,且()0lim x f x A +→'=,则()0f +'存在,且()0f A +'=.(19)(本题满分10分)计算曲面积分()32222xdydz ydzdx zdxdyI xy z ∑++=++⎰⎰,其中∑是曲面222224x y z ++=的外侧.(20)(本题满分11分)设111111042A --⎛⎫ ⎪=- ⎪ ⎪--⎝⎭,1112ξ-⎛⎫ ⎪= ⎪⎪-⎝⎭(Ⅰ)求满足22131,A A ξξξξ==的所有向量23,ξξ;(Ⅱ)对(Ⅰ)中的任意向量23,ξξ,证明:123,,ξξξ线性无关.(21)(本题满分11分)设二次型()()2221231231323,,122f x x x ax ax a x x x x x =++-+-(Ⅰ)求二次型f 的矩阵的所有特征值;(Ⅱ)若二次型f 的规范形为2212y y +,求a 的值.(22)(本题满分11分)袋中有1个红球,2个黑球与3个白球.现有放回地从袋中取两次,每次取一个球,以,,X Y Z 分别表示两次取球所取得的红球、黑球与白球的个数.(Ⅰ)求{}10P X Z ==;(Ⅱ)求二维随机变量(),X Y 的概率分布.(23)(本题满分11分)设总体X 的概率密度为2,0,()0,x xe x f x λλ-⎧>=⎨⎩其他,其中参数(0)λλ>未知,12,,,n X X X 是来自总体X 的简单随机样本.(Ⅰ)求参数λ的矩估计量;(Ⅱ)求参数λ的最大似然估计量.2009年全国硕士研究生入学统一考试数学一试题一、选择题:1~8小题,每小题4分,共32分.(1)【答案】(A)【解析】()sin f x x ax =-与()()2ln 1g x x bx =-是0x →时的等价无穷小,则2200232000330()sin sin limlim lim ()ln(1)()sin 1cos sin lim lim lim 36sin lim 1,66x x x x x x x f x x ax x axg x x bx x bx x ax a ax a ax bx bx bx a ax a b axb →→→→→→→--=-⋅---=---⎛⎫=-=-= ⎪⎝⎭等洛洛即36a b =-,故排除B,C.另外,201cos lim3x a axbx→--存在,蕴含了1cos 0a ax -→()0x →,故1,a =排除D.所以本题选A.(2)【答案】(A)【解析】本题利用二重积分区域的对称性及被积函数的奇偶性.令(,)cos f x y y x =,24,D D 两区域关于x 轴对称,(,)cos (,)f x y y x f x y -=-=-,即被积函数是关于y 的奇函数,所以240I I ==;13,D D 两区域关于y 轴对称,(,)cos()cos (,)f x y y x y x f x y -=-==,即被积函数是关于x 的偶函数,所以{}{}1(,),013(,),012cos 0,2cos 0.x y y x x x y y x x I y xdxdy I y xdxdy ≥≤≤≤-≤≤=>=<⎰⎰⎰⎰所以正确答案为(A).(3)【答案】(D)【解析】此题为定积分的应用知识考核,由()y f x =的图形可以看出,其图像与x 轴及y 轴、0x x =所围的图形的代数面积为所求函数()F x ,从而可得出下面几个方面的特征:①[]1,0x ∈-时,()0F x ≤为线性函数,单调递增;②[]0,1x ∈时,()0F x ≤,且单调递减;③[]1,2x ∈时,()F x 单调递增;④[]2,3x ∈时,()F x 为常函数;⑤()F x 为连续函数.结合这些特点,可见正确选项为(D).(4)【答案】C【解析】解法1举反例:取(1)nn n a b ==-,则lim 0n n a →∞=,1n n b ∞=∑是收敛的,但111n n n n a b n ∞∞===∑∑发散,排除(A);取1n n a b n ==,则lim 0n n a →∞=,1n n b ∞=∑是发散的,但2111n n n n a b n ∞∞===∑∑收敛,排除(B);取1n n a b n ==,则lim 0n n a →∞=,1n n b ∞=∑是发散的,但224111n n n n a b n ∞∞===∑∑收敛,排除(D),故答案为(C).解法2因为lim 0,n n a →∞=则由定义可知1,N ∃使得1n N >时,有1n a <;又因为1nn b∞=∑收敛,可得lim 0,n n b →∞=则由定义可知2,N ∃使得2n N >时,有1n b <,从而,当12n N N >+时,有22n nn a b b <,则由正项级数的比较判别法可知221n nn a b∞=∑收敛.(5)【答案】(A)【解析】根据过渡矩阵的定义,知由基12311,,23αα到122331,,αααααα+++的过渡矩阵M 满足:()12233112312311,,,,2310111,,220,23033M ααααααααααα⎛⎫+++= ⎪⎝⎭⎛⎫⎛⎫ ⎪= ⎪ ⎪⎝⎭ ⎪⎝⎭所以此题选(A).(6)【答案】(B)【解析】分块矩阵O A B O ⎛⎫⎪⎝⎭的行列式221236OA AB B O⨯=-=⨯=(),即分块矩阵可逆,且1116112366.1132O A O A O A O B B O B O B O A O O B O B B O B A O A O A O A *---******⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫ ⎪ ⎪⎛⎫⎪===⎪ ⎪ ⎪ ⎪⎝⎭⎪ ⎪⎝⎭⎝⎭故答案为(B).(7)【答案】(C)【解析】因为()()10.30.72x F x x -⎛⎫=Φ+Φ⎪⎝⎭,所以()()0.710.322x F x x -⎛⎫'''=Φ+Φ ⎪⎝⎭,因此,()()10.30.352x EX xF x dx x x dx+∞+∞-∞-∞⎡-⎤⎛⎫'''==Φ+Φ ⎪⎢⎥⎝⎭⎣⎦⎰⎰()10.30.352x x x dx x dx +∞+∞-∞-∞-⎛⎫''=Φ+Φ ⎪⎝⎭⎰⎰.由于()x Φ为标准正态分布的分布函数,所以()0x x dx +∞-∞'Φ=⎰,()()()()11221222222,x x x dx u u u du u u du u du +∞+∞-∞-∞+∞+∞-∞-∞--⎛⎫''Φ=+Φ ⎪⎝⎭''=Φ+Φ=⎰⎰⎰⎰()10.30.3500.3520.72x EX x x dx x dx +∞+∞-∞-∞-⎛⎫''=Φ+Φ=+⨯= ⎪⎝⎭⎰⎰.(8)【答案】(B)【解析】(){}{0}{0}{1}{1}11{0}{1}2211{00}{1},22Z F z P XY z P XY z Y P Y P XY z Y P Y P XY z Y P XY z Y P X z Y P X z Y =≤=≤==+≤===≤=+≤==⋅≤=+≤=由于,X Y 相互独立,所以11(){0}{}22Z F z P X z P X z =⋅≤+≤.(1)当0z <时,1()()2Z F z z =Φ;(2)当0z ≥时,11()()22Z F z z =+Φ,因此,0z =为间断点,故选(B).二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.(9)【答案】12222xf f xyf '''''++【解析】12zf f y x∂''=+⋅∂,21222212222zxf f yx f xf f xyf x y∂''''''''''=++⋅=++∂∂.(10)【答案】(1)2x x e -+【解析】由常系数线性齐次微分方程0y ay by '''++=的通解为()12xy C C x e =+可知1x y e =,2x y xe =为其两个线性无关的解,代入齐次方程,有111222(1)010,[2(1)]020,x x y ay by a b e a b y ay by a a b x e a '''++=++=⇒++='''++=++++=⇒+=从而可见2,1a b =-=,非齐次微分方程为2y y y x '''-+=.设特解*y Ax B =+,代入非齐次微分方程,得2A Ax B x -++=,即11(2)202A A Ax AB x A B B ==⎧⎧+-+=⇒⇒⎨⎨-+==⎩⎩所以特解*2y x =+,通解()122xy C C x e x =+++.把()()02,00y y '==代入通解,得120,1C C ==-.所以所求解为2(1)2x x y xe x x e =-++=-+.(11)【答案】136【解析】由题意可知,2,0y x x =≤≤ds ==,所以()21148Lxds x ==+⎰⎰11386==.(12)【答案】415π【解析】解法1:()212222002124013500sin cos cos cos cos 42.3515z dxdydz d d d d d d πππππθϕρϕρϕρθϕϕρρϕρπΩ==-⎛⎫=⋅-⋅= ⎪⎝⎭⎰⎰⎰⎰⎰⎰⎰⎰⎰解法2:由轮换对称性可知2z dxdydz Ω=⎰⎰⎰2x dxdydz Ω=⎰⎰⎰2y dxdydzΩ⎰⎰⎰所以,()212222400011sin 33z dxdydz x y z dxdydz d d r dr ππϕθϕΩΩ=++=⎰⎰⎰⎰⎰⎰⎰⎰⎰14002214sin sin 33515d r dr d ππππϕϕϕϕπ==⋅=⎰⎰⎰.(13)【答案】2【解析】2T αβ=,()2TTβαββαββ∴==⋅,又由于0β≠,Tβα∴的非零特征值为2.(14)【答案】1-【解析】由于2X kS +为2np 的无偏估计量,所以22()E X kS np +=,即2222()()()E X kS np E X E kS np +=⇒+=2(1)1(1)(1)1 1.np knp p np k p pk p p k ⇒+-=⇒+-=⇒-=-⇒=-三、解答题:15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.(15)(本题满分9分)【解析】2(,)2(2)x f x y x y '=+,2(,)2ln 1y f x y x y y '=++.令(,)0,(,)0,x y f x y f x y ⎧'=⎪⎨'=⎪⎩解得唯一驻点1(0,)e .由于212(0,)1(0,21(0,)11(0,)2(2)2(2),1(0,)40,11(0,)(2),xxexye yy eA f y e eB f xy eC f x e e y ''==+=+''===''==+=所以2212(2)0,B AC e e -=-+<且0A >.从而1(0,)f e 是(,)f x y 的极小值,极小值为11(0,)f e e=-.(16)(本题满分9分)【解析】曲线n y x =与1n y x +=的交点为(0,0)和(1,1),所围区域的面积112111111()()001212n n n n n a x x dx x x n n n n +++=-=-=-++++⎰,111lim 1111111lim ()lim (),2312222Nn nN n n N N S a a N N N ∞→∞==→∞→∞===-++-=-=+++∑∑ 22111211111111(1)22123456n n n n n S a n n n ∞∞∞-=====-=-+-+=-+∑∑∑ ().考查幂级数1(1)n nn x n ∞=-∑,知其收敛域为(1,1]-,和函数为ln(1)x -+.因为2(1)()ln(1)n nn S x x x x n ∞=-==-+∑,令1x =,得2211(1)1ln 2n n S a S ∞-====-∑.(17)(本题满分11分)【解析】(I)椭球面1S 的方程为222143x y z ++=.设切点为00(,)x y ,则22143x y +=在00(,)x y 处的切线方程为00143x x y y +=.将4,0x y ==代入切线方程得01x =,从而032y ==±.所以切线方程为142x y ±=,从而圆锥面2S 的方程为222(1)44x y z +-=,即222(4)440x y z ---=.(II)1S 与2S 之间的体积等于一个底面半径为32、高为3的锥体体积94π与部分椭球体体积V 之差,其中22135(4)44V x dx ππ=-=⎰.故所求体积为9544πππ-=.(18)(本题满分11分)【解析】(Ⅰ)取()()()()()f b f a F x f x x a b a-=---,由题意知()F x 在[],a b 上连续,在(),a b 内可导,且()()()()()(),()()()()()().f b f a F a f a a a f a b a f b f a F b f b b a f a b a -=--=--=--=-根据罗尔定理,存在(),a b ξ∈,使得()()()()0f b f a F f b aξξ-''=-=-,即()()()()f b f a f b a ξ'-=-.(Ⅱ)对于任意的(0,)t δ∈,函数()f x 在[]0,t 上连续,在()0,t 内可导,由右导数定义及拉格朗日中值定理()()00()0()0lim lim lim ()0t t t f t f f tf f t tξξ++++→→→-'''===-,其中()0,t ξ∈.由于()0lim t f t A +→'=,且当0t +→时,0ξ+→,所以0lim ()t f A ξ+→'=,故(0)f +'存在,且(0)f A +'=.(19)(本题满分10分)【解析】取2221:1x y z ∑++=的外侧,Ω为∑与1∑之间的部分.()()()11322223322222222.xdydz ydzdx zdxdyI xy zxdydz ydzdx zdxdyxdydz ydzdx zdxdyx y z xy z ∑∑-∑∑++=++++++=+++++⎰⎰⎰⎰⎰⎰根据高斯公式()13222200xdydz ydzdx zdxdydxdydz x y z ∑-∑Ω++==++⎰⎰⎰⎰⎰ .()1122232222134.x y z xdydz ydzdx zdxdyxdydz ydzdx zdxdyxy z dxdydz π∑∑++≤++=++++==⎰⎰⎰⎰⎰⎰⎰所以4I π=.(20)(本题满分11分)【解析】(Ⅰ)对矩阵1()A ξ 施以初等行变换()11110221111111111012204220000A ξ⎛⎫-- ---⎛⎫ ⎪ ⎪ ⎪=-→ ⎪ ⎪ ⎪--- ⎪⎝⎭ ⎪ ⎪⎝⎭ 可求得2122122k k k ξ⎛⎫-+ ⎪ ⎪⎪=- ⎪ ⎪⎪ ⎪⎝⎭,其中k 为任意常数.又2220220440A ⎛⎫ ⎪=-- ⎪ ⎪⎝⎭,对矩阵21()A ξ 施以初等行变换()211110220122201000044020000A ξ⎛⎫- ⎪-⎛⎫ ⎪ ⎪=--→⎪ ⎪ ⎪ ⎪-⎝⎭ ⎪⎝⎭ ,可求得312a a b ξ⎛⎫-- ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭,其中,a b 为任意常数.(Ⅱ)解法1由(Ⅰ)知12311122211,,102222ka ka k bξξξ--+--=-=-≠-,所以123,,ξξξ线性无关.解法2由题设可得10A ξ=.设存在数123,,k k k ,使得1122330k k k ξξξ++=,①等式两端左乘A ,得22330k A k A ξξ+=,即21330k k A ξξ+=,②等式两端再左乘A ,得2330k A ξ=,即310k ξ=.由于10ξ≠,于是30k =,代入②式,得210k ξ=,故20k =.将230k k ==代入①式,可得10k =,从而1,ξ23,ξξ线性无关.(21)(本题满分11分)【解析】(Ⅰ)二次型f 的矩阵101111a A a a ⎛⎫ ⎪=- ⎪ ⎪--⎝⎭.由于01||01()((1))((2))111a E A a a a a a λλλλλλλ---=-=--+----+,所以A 的特征值为123,1,2a a a λλλ==+=-.(Ⅱ)解法1由于f 的规范形为2212y y +,所以A 合同于100010000⎛⎫⎪ ⎪ ⎪⎝⎭,其秩为2,故1230A λλλ==,于是0a =或1a =-或2a =.当0a =时,1230,1,2λλλ===-,此时f 的规范形为2212y y -,不合题意.当1a =-时,1231,0,3λλλ=-==-,此时f 的规范形为2212y y --,不合题意.当2a =时,1232,3,0λλλ===,此时f 的规范形为2212y y +.综上可知,2a =.解法2由于f 的规范形为2212y y +,所以A 的特征值有2个为正数,1个为零.又21a a a -<<+,所以2a =.(22)(本题满分11分)【解析】(Ⅰ)12211{1,0}463(10)1{0}9()2C P X Z P X Z P Z ⋅========.(Ⅱ)由题意知X 与Y 的所有可能取值均为0,1,2.()()()()()()()()()1111332311116666111223111166661122116611221166110,0,1,0,461112,00,1,36311,1,2,10,910,2,91,20,2,20,C C C C P X Y P X Y C C C C C C C P X Y P X Y C C C C C C P X Y P X Y C C C C P X Y C C P X Y P X Y ⋅⋅========⋅⋅⋅⋅========⋅⋅⋅=======⋅⋅====⋅======故(,)X Y 的概率分布为X012Y01/41/61/3611/31/9021/9(23)(本题满分11分)【解析】(Ⅰ)2202().x EX xf x dx x e dx λλλ+∞+∞--∞===⎰⎰令X EX =,即2X λ=,得λ的矩估计量为 12Xλ=.(Ⅱ)设12,,,(0,1,2,,)n i x x x x i n >= 为样本观测值,则似然函数为()12121,,,;,nii nx n n ii L x x x ex λλλ=-=∑=⋅∏ 11ln 2ln ln nni i i i L n x x λλ===-+∑∑,由1ln 20n i i d L n x d λλ==-=∑,得λ的最大似然估计量为 22Xλ=.。
