理想气体实验定律共34页
气体定律

气体定律物质的状态在一定温度和压力下,物质总是以一定的聚集状态存在。
即存在为气态、液态或固态,条种状态都各有其特性。
在一定条件下,物质总是以一定的聚集状态参加化学反应的。
物质的状态对其化学行为是有重要影响的。
对于给定的反应,由于物质的状态不同,反应的速度和反应的能量关系也有所不同,还会影响反应条件。
本章将叙述气体的特性。
气体的特征是具有扩散性和压缩性。
将气体引入任何大小的容器中,由于气体分子的能量大,分子间引力小,分子在作无规则地运动,因而能自动扩散充满整个容器。
因此,气体没有一定的体各和形状。
又因为气体分子间的空隙很大,对气体加压,其体积就缩小。
同时气体还受到温度、气体的量的影响。
通常一定量的气体所处状态可以用压力、体积、温度来描述。
而反应这四个量的关系的式子就是气体的状态方程式。
理想气体的状态方程一般气体,在密度不太高、压强不太大和温度不太低的实验范围内,遵守玻意耳定律、盖-吕萨克和查理定律。
应该指出,对不同气体来说,这三条定律的适用范围是不同的,不易液化的气体,例如氮气、氢气等适用的范围比较大,而氨气的适用范围就要小得多。
实际上在任何情况下都服从上述三条理论定律的气体是没有的。
我们把实际气体抽象化,提出理想气体的概念,认为理想气体能无条件地服从这三条定律。
在这种情况下,理想气体的状态函数p、V、T之间的关系即理想气体的状态方程。
可以从这三条定律导出当物质的量为n的理想气体处于平衡态时,它的状态方程就是:其中包括了气体的三个状态量:p——压强;V——体积;T——气体的热力学温度。
这个方程就是理想气体的状态方程,只有理想气体才完全遵守这个关系式。
而对于真实气体,必须考虑到分子间的作用力和分子本身体积,将理想气体状态方程式修正后才能应用。
现在我们要关心的问题是式中的常数R,要应用这个方程必须要求出R.这个常数被称为气体常数,它是由实验测得的。
将具有一定物质的量的气体的三个状态量,即压强、体积和温度代入方程就可以求出气体常数。
气体定律实验题探索理想气体状态方程

气体定律实验题探索理想气体状态方程本实验旨在探究理想气体的状态方程,对气体定律进行实验验证,通过实验数据分析,得出实验结果并对理论做出合理解释。
通过本实验的实施,可以深入理解理想气体状态方程的基本原理以及与实验结果的关系。
实验材料与仪器:1. 气缸:用于封闭气体和调节气压。
2. 活塞:用于调节气缸的体积。
3. 温度计:用于测量气体的温度。
4. 压强计:用于测量气体的压强。
5. 大气压力表:用于测量环境的压强。
实验过程:步骤一:准备工作1. 将气缸清洗干净,并与温度计、压强计连接好。
2. 将气缸与大气压力表连接,用于测量环境的压强。
步骤二:探索压强与体积关系1. 调节气缸的活塞,使气缸体积变化,在每次变化后等待气缸内温度恢复平衡。
2. 同时记录下气缸的体积和相应的压强。
步骤三:探索温度与压强关系1. 固定气缸的体积。
2. 调节气缸内气体的温度,等待温度稳定。
3. 同时记录下温度和相应的压强。
数据记录与分析:根据实验过程中所记录的数据,我们可以绘制压强与体积、温度与压强的曲线图。
通过数据的分析,试图归纳出气体状态方程的表达形式。
结果与讨论:基于所获得的实验数据,我们可以得出以下结论:1. 压强与体积的关系符合玛丽特定律,即压强与体积成反比关系。
2. 温度与压强的关系符合查理定律,即温度与压强成正比关系。
3. 结合理想气体状态方程,我们可以得出P×V/T = R(其中P代表压强,V代表体积,T代表温度,R为气体常数)的表达形式。
结论:通过本实验的实施以及对实验数据的分析,我们探索了理想气体的状态方程,并验证了气体定律的准确性。
实验结果与理论相吻合,表明理想气体状态方程的适用范围广泛,并能够准确描述气体的行为。
总结:本实验通过实验验证与数据分析,详细探讨了理想气体状态方程以及气体定律的实验证明。
实验结果的准确性证明了理想气体状态方程的可靠性,对于进一步研究气体行为以及应用于相关领域具有积极的推动作用。
理想气体

盖·吕萨克定律:一定质量的气体,在压强不变的条件下, 温度每升高(或降低)1℃,它的体积的增加 (或减少)量等于0℃时体积的1/273。即V1/T1=V2/T2=C2(常量)。
2.两平衡状态间参数的计算
3.标准状态与任意状态或密度间的换算
4.气体体积膨胀系数
理想气体对外膨胀可以分为两种情况:一、理想气体周围有其他物体。二、理想气体自由膨胀,即周围没有 其他物体。第一种情况下,理想气体做功。第二种情况下,不做功。如果两个容器相连,其中一个容器内充满理 想气体,另一个容器内是真空,将两个容器相连后理想气体膨胀充满两个容器,此时,理想气体不做功,且选取 任何一个中间过程也不做功。一般情况下,如不做特别说明,则认为气体对外膨胀做功。
谢谢观看
综合以上三个定律可得pV/T=常量,这个称为联合气体方程。在此基础再加上阿伏伽德罗定律定律即V/n=恒 量(n表示摩尔数),得到理想气体状态方程。
说明
模型
高压低温
理想气体是一种理想化的模型,实际并不存在。实际气体中,凡是本身不易被液化的气体,它们的性质很近 似理想气体,其中最接近理想气体的是氢气和氦气。一般气体在压强不太大、温度不太低的条件下,它们的性质 也非常接近理想气体。因此常常把实际气体当作理想气体来处理。这样对研究问题,尤其是计算方面可以大大简 化。
推导
指 的 是 克 拉 伯 龙 方 程 来 源 的 三 个 实 验 定 律 : 玻 ( 意 耳 ) - 马 ( 略 特 ) 定 律 、 查 理 定 律 和 盖 ·吕 萨 克 定 律 , 以 及 直 接结论pV/T=常量。
气体实验定律-PPT课件

C.气体分子平均速率变大
D.单位时间单位面积器壁上受到气体分子撞击的次 数减少
小结:
• 一定质量的气体在等容变化时,遵守查理定 律. 一定质量的气体在等压变化时,遵守盖 · 吕萨 克定律.
•
气体实验定律(Ⅱ)
一、等容过程
1.等容过程:气体在体积不变的情况下发 生的状态变化过程叫做等容过程. 2.一定质量气体的等容变化
演示:
• 如图所示,研究瓶中一 定质量的气体,先使U 型管中两侧水银液面等 高,在左侧液面处标上 标记P,然后改变瓶内 气体温度(可分别放入 热水和冰水中),上下 移动A管,使左侧水银 面保持在P处(即使瓶 中气体体积不变).
4.等容线 ( l )等容线:一定质量的某种气体在等容变化 过程中,压强p跟热力学温度 T的正比关系 p- T在直角坐标系中的图象叫做等容线. (2)一定质量气体的等容线 p- T图象,其延长 线经过坐标原点,斜率反映体积大小,如图所 示.
(3)一定质量气体的等容线的物理意义. ①图线上每一个点表示气体一个确定的状态 ,同一根等容线上各状态的体积相 ②不同体积下的等容线,斜率越大,体积越 小(同一温度下,压强大的体积小)如图所 示,V2<V1.
查理定律的微观解释:
一定质量(m)的气体的总分子数(N) 是一定的,体积(V)保持不变时,其单 位体积内的分子数(n)也保持不变,当 温度(T)升高时,其分子运动的平均速 率(v)也增大,则气体压强(p)也增大; 反之当温度(T)降低时,气体压强(p) 也减小。
二、等压过程
1 .等压过程:气体在压强不变的情况下发 生的状态变化过程叫做等压过程. 2.一定质量气体的等压变化.
可得到,气体温度升 高,压强增大;气体 温度降低,压强减小.
气体实验定律及理想气体状态方程的应用PPT课件

典例:如图,一粗细均匀的U形管竖直放置,A侧
上端封闭,B侧上端与大气相通,下端开口处开
关K关闭,A侧空气柱的长度为ɭ1=10.0cm,B侧水 银面比A侧的高h1=3.0cm。现将开关K打开,从U 形管中放出部分水银,当两侧水银面
的高度差h2=10.0cm时将开关K闭合。 已知大气压强P0=75.0cmHg。 (1)求放出部分水银后A侧空气柱的高度ɭ2; (2)此后再向B侧注入水银,使A、B两侧的水
银面达到同一高度,求注入的水银在管内的高度
△h。
【定向导学,分组讨论,合作探究】
通过分组讨论以下问题来理解题意,从而体 会如何寻找的解题的思路及突破口
1、通过读题等效翻译获得的解题信息有哪些? 2、本题的研究对象是一部分气体还是多部分气 体? 3、如何寻找解决第一问的解题思路?即如何找 到解题的难点和突破方法? 4、解决本题第二问时可确定的气体的初态有几 个?最有助于解题的初态是那一个? 5、解决本题第二问时的难点是什么?如何突破 ?
根 据 玻 意 耳 定 律 p 1 V 1 p 1 'V 1 1 代 入 数 据 解 得 p 1 '= 9 0 c m H g
解 : 对 细 管 中 封 闭 气 体
初 态 : p 2p 07 5 cm H g,
V 2l1S1 2 s, T 2
末 态 : p 2 ' p 1 ' p h9 6 cm H g, V 2 ' l2
(1)由如图的U形管可以想起确定封闭气体压强
的方法为 连通器等液面法 。
(2)将粗管管口封闭说明粗管的封闭气体可以作
为 研究对象
。
(3)将细管管口用一活塞封闭说明细管内的封闭
气体也可以作为 研究对象
理想气体实验定律
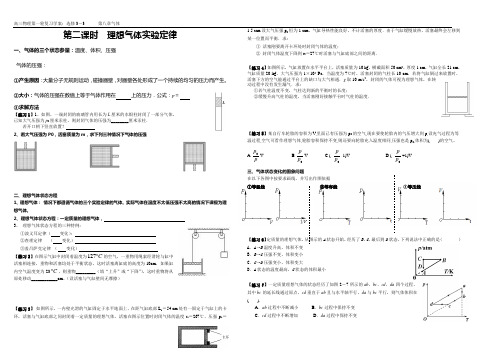
第二课时 理想气体实验定律一、气体的三个状态参量:温度、体积、压强 气体的压强: ①产生原因:大量分子无规则运动,碰撞器壁,对器壁各处形成了一个持续的均匀的压力而产生。
②大小:气体的压强在数值上等于气体作用在 上的压力.公式:p = ③求解方法【练习1】1、如图,一端封闭的玻璃管内用长为L 厘米的水银柱封闭了一部分气体, 已知大气压强为p 0厘米汞柱,则封闭气体的压强为________厘米汞柱. 若开口朝下竖直放置?2、若大气压强为P0,活塞质量为m ,求下列三种情况下气体的压强二、理想气体状态方程1、理想气体: 情况下都遵循气体的三个实验定律的气体。
实际气体在温度不太低压强不太高的情况下课视为理想气体。
2、理想气体状态方程:一定质量的理想气体,3、 理想气体状态方程的三种特例:①波义耳定律( 变化):②查理定律 ( 变化) ③盖吕萨克定律 ( 变化) 【练习2】在图示气缸中封闭着温度为127C ︒的空气,一重物用绳索经滑轮与缸中活塞相连接,重物和活塞均处于平衡状态,这时活塞离缸底的高度为10cm ,如果缸内空气温度变为-23C ︒,则重物_________(填“上升”或“下降”),这时重物将从原处移动____________cm 。
(设活塞与气缸壁间无摩擦)【练习3】 如图所示,一内壁光滑的气缸固定于水平地面上,在距气缸底部L 1=54 cm 处有一固定于气缸上的卡环,活塞与气缸底部之间封闭着一定质量的理想气体,活塞在图示位置时封闭气体的温度t 1=267℃、压强p 1=1.5 atm.设大气压强p 0恒为1 atm ,气缸导热性能良好,不计活塞的厚度.由于气缸缓慢放热,活塞最终会左移到某一位置而平衡.求:① 活塞刚要离开卡环处时封闭气体的温度;② 封闭气体温度下降到t 3=27℃时活塞与气缸底部之间的距离.【练习4】如图所示,气缸放置在水平平台上,活塞质量为10 kg ,横截面积50 cm 2,厚度1 cm ,气缸全长21 cm ,气缸质量20 kg ,大气压强为1×105 Pa ,当温度为7℃时,活塞封闭的气柱长10 cm ,若将气缸倒过来放置时,活塞下方的空气能通过平台上的缺口与大气相通.g 取10 m/s 2,封闭的气体可视为理想气体,在转动过程中没有发生漏气.求:①若气柱温度不变,气柱达到新的平衡时的长度;②缓慢升高气柱的温度,当活塞刚好接触平台时气柱的温度.【练习5】某自行车轮胎的容积为V ,里面已有压强为p 0的空气,现在要使轮胎内的气压增大到p,设充气过程为等温过程,空气可看作理想气体,轮胎容积保持不变,则还要向轮胎充入温度相同,压强也是p 0,体积为( )的空气。
气体实验定律 理想气体

气体实验定律理想气体一、理想气体(1)宏观上讲,把在任何温度、任何压强下都遵从的气体称为理想气体.在压强不太高(不超过大气压的几倍)、温度不太低时(不低于零下几十摄氏度),实际气体可以看做理想气体.(2)微观上讲,理想气体的分子间除碰撞外无其他作用力,因而没有分子势能二、气体的状态参量通常用压强、体积、温度描述一定质量的某种理想气体的状态,这三个物理量称为气体的状态参量.1.气体的压强(1)产生原因:由于气体分子无规则的热运动,大量的分子频繁地碰撞器壁产生持续而稳定的压力.作用在单位面积上的压力叫做气体的压强.(2)决定压强大小的因素从宏观来看,一定质量的气体其压强与气体的和有关.从微观角度说,决定气体压强大小的因素是分子的密集程度及气体分子的.(3)常用单位及换算关系国际单位:帕斯卡,符号:Pa,1 Pa=1 N/m2常用单位:标准大气压(atm);厘米汞柱(cmHg)换算关系:1 atm= cmHg= Pa≈10 m水柱产生的压强2.气体的温度(1)物理意义:宏观上温度表示物体的冷热程度,微观上温度是分子平均动能的标志.(2)国际单位:开尔文,简称开,符号:K(3)热力学温度与摄氏温度的关系:T=t+273.15 K说明:①摄氏温标规定标准大气压下冰的熔点为零度,即0℃,而热力学温标是把摄氏温度的-273.15℃规定为零度,即0K。
所以这两种温标的零度不同,但△T=△t,即每一度的大小是相同的②热力学温度的0K是低温的极限,永远达不到,即热力学温度无负值3.气体的体积气体体积为气体分子所能达到的空间的体积,即气体所充满容器的容积.国际单位:立方米,符号:m3常用单位:升(L)、毫升(mL)换算关系:1 m3=103 L,1 L=103 mL说明:当气体达到平衡态时,容器内各点的压强和温度都不再变化三、三个实验定律1.玻意耳定律(1)数学表达式:p1V1=p2V2或pV=C(常数)(2)微观解释:一定质量的某种理想气体,温度保持不变时,分子的平均动能是一定的。
理想气体(物理化学)

将这三个定律相结合,经过一定的数据处理 参看第三版 参看第三版), 将这三个定律相结合,经过一定的数据处理(参看第三版 ,可 得到理想气体状态方程: 得到理想气体状态方程 pV=nRT 或 pVm=RT 或
m pV = RT M
(R为摩尔气体常数 为摩尔气体常数) 为摩尔气体常数 为气体的摩尔体积) (Vm为气体的摩尔体积) 为气体的相对摩尔质量) (M为气体的相对摩尔质量) 为气体的相对摩尔质量
即混合气的平均摩尔质量是其中所有各组分的摩尔分数与 其摩尔质量乘积之和。
2. 道尔顿定律与分压力 道尔顿定律与分压力(part pressure) 气体的压力是分子对容器器壁碰撞的结果,混合气的压力是 构成该混合气的各组分对压力所作贡献之和, 因此在热力学计 算中,人们提出了一个分压力的概念: 分压力pB:混合气中任一组分对压力所作贡献。 p = ∑ pB 混合气总压力 B 且有 pB = y B p 或 y B =
物理量 ,如上图及下表 如上图及下表: 如上图及下表 单位
p/MPa
…………
………… pVm/J . mol-1 ↑ ↑ 表头中物理量的表示: 物理量 表中均为纯数
单位
低压气体可近似视作为理想气体。 ⑶ 低压气体可近似视作为理想气体。 即低压气体可近似使用理想气体状态方程计算p、T、V 关系。
理想气体的微观模型( ) 二 理想气体的微观模型(p9)
按照分子运动论,理想气体微观模型应该是: 1. 分子间无作用力; 分子间无作用力; 2. 分子本身没有体积 3. 分子不停顿地作无规则的热运动 分子不停顿地作无规则的热运动。 低压气体,气体密度小,分子间距离大,分子间作用 力及分子本身的体积均可忽略,故可当作理想气体处 理。
低压混合气(理想气体混合物) 三 低压混合气(理想气体混合物)(ideal gas mixture)(p11) ( ) 在工业生产中所遇到的气体在很多情况下为混合气体,实 验表明,低压混合气也服从理想气体状态方程,即低压混合气 可视为理想混合气处理
理想气体与热力学第一定律

理想气体与热力学第一定律一、理想气体模型与克拉珀龙方程。
⒈气体实验定律。
玻‐马定律pV = p0V0= C pV查理定律 p = p0(1+αp t)盖·吕萨克定律 V = V0(1+αV t)αp、αV分别为气体压强系数和体胀系数,且αp≈αV≈1/273.15℃⒉克拉珀龙方程。
比较气体实验定律中的查理定律和盖·吕萨克定律,可以很容易地看到共同之处。
如果我们改变温标的零点,令纯水的三相点为273.16K(1K=1℃),αp=αV=1/T0,则p = p0 T/T0V = V0 T/T0即p/T=p0/T0=C pT,V/T=V0/T0=C VT∴pV/T=p0V0/T0= C这样我们就得出了理想气体状态方程,即克拉珀龙方程pV=nRT。
例⒈⑴计算空气泡在水下多深处不会上浮(忽略温度变化)。
⑵试定量分析半杯水加纸盖后翻转的平衡态。
⒊理想气体模型。
实验表明,温度高、压强低的气体与气体实验定律符合得较好。
可以引入一个理想化模型,称为理想气体,它严格服从气体实验定律,且αp=αV=1/273.15℃。
理想气体被描述为这样一群粒子:⑴永不停歇地进行着无规则热运动。
⑵具有无限的可压缩性,即粒子本身的体积忽略不计。
⑶粒子间作用力为零。
⑷粒子不断相互碰撞或与器壁碰撞(产生压力),两次碰撞间粒子做匀速直线运动。
由理想气体模型可以得出理想气体状态方程。
考虑一边长为l的立方体容器,内盛N个质量为m的粒子,其平均速度为u,分子数密度为n*=N/l3。
粒子与器壁碰撞后动量改变量mu-(-mu)=2mu在t时间内与容器某一个面碰撞的粒子数n*utl2/6粒子与器壁碰撞产生压强p=2mu·n*utl2/6tl2=n*mu2/3=2n*(mu2/2)/3=2n*E K/3 粒子平动动能E K=3kT/2∴p=n*kT∵k=R/N A,n*=N/V∴pV=NRT/N A=nRT理想气体模型也可以类比于拥有大量运动粒子的系统,例如所谓的电子气、光子气等;在宇宙尺度上可与星系运动类比。
理想气体的状态方程 课件

答案:(1)330 K (2)1.1p0 (3)见解析图 解析:(1)活塞刚离开 B 处之前的状态变化可看做等容变化。
初状态:p1=0.9p0,T1=297 K,V1=V0;
末状态:p2=p0,T2=TB,V2=V0;
由查理定律p1
T1
=
p2 T2
得
0.9������0 297������
(盖—吕萨克定律)
由此可见,三个气体实验定律是理想气体状态方程的特例。
2.应用理想气体状态方程解题的一般步骤
ቤተ መጻሕፍቲ ባይዱ(1)明确研究对象,即一定质量的气体;
(2)确定气体在始末状态的参量 p1、V1、T1 及 p2、V2、T2;
(3)由理想气体状态方程列式求解;
(4)讨论结果的合理性。
目录 退出
二、气体的状态变化图象
目录 退出
迁移与应用 1
如图所示,粗细均匀、一端封闭一端开口的 U 形玻璃管,当 t1=31 ℃、 大气压强 p0=76 cmHg 时,两管水银面相平,这时左管被封闭的气柱长 L1=8 cm,求:
(1)当温度 t2 是多少时,左管气柱 L2 为 9 cm; (2)当温度达到上问中的温度 t2 时,为使左管气柱长 L 为 8 cm,应在 右管中加入多长的水银柱。 答案:(1)78 ℃ (2)11.75 cm
目录 退出
解析:(1)初状态:p1=p0=76 cmHg,
V1=L1S,T1=304 K; 末状态:p2=p0+2 cmHg=78 cmHg,
V2=L2S,T2=?
根据理想气体状态方程p1V1
T1
=
p2V2 T2
代入数据得 T2=351 K,t2=78 ℃。
(2)设应在左管中加入 h cm 水银
气体实验定律及应用答案

第2节气体实验定律及应用知识梳理一、气体分子运动速率的统计分布气体实验定律理想气体1.气体分子运动的特点1分子很小;间距很大;除碰撞外不受力.2气体分子向各个方向运动的气体分子数目都相等.3分子做无规则运动;大量分子的速率按“中间多;两头少”的规律分布.4温度一定时;某种气体分子的速率分布是确定的;温度升高时;速率小的分子数减少;速率大的分子数增多;分子的平均速率增大;但不是每个分子的速率都增大.2.气体的三个状态参量1体积;2压强;3温度.3.气体的压强1产生原因:由于气体分子无规则的热运动;大量的分子频繁地碰撞器壁产生持续而稳定的压力.2大小:气体的压强在数值上等于气体作用在单位面积上的压力.公式:p=错误!.3常用单位及换算关系:①国际单位:帕斯卡;符号:Pa;1 Pa=1 N/m2.②常用单位:标准大气压atm;厘米汞柱cmHg.③换算关系:1 atm=76 cmHg=1.013×105Pa≈1.0×105 Pa.4.气体实验定律1等温变化——玻意耳定律:①内容:一定质量的某种气体;在温度不变的情况下;压强p与体积V成反比.②公式:p1V1=p2V2或pV=C常量.2等容变化——查理定律:①内容:一定质量的某种气体;在体积不变的情况下;压强p与热力学温度T成正比.②公式:错误!=错误!或错误!=C常量.③推论式:Δp=错误!·ΔT.3等压变化——盖—吕萨克定律:①内容:一定质量的某种气体;在压强不变的情况下;其体积V与热力学温度T 成正比.②公式:错误!=错误!或错误!=C常量.③推论式:ΔV=错误!·ΔT.5.理想气体状态方程1理想气体:在任何温度、任何压强下都遵从气体实验定律的气体.①理想气体是一种经科学的抽象而建立的理想化模型;实际上不存在.②理想气体不考虑分子间相互作用的分子力;不存在分子势能;内能取决于温度;与体积无关.③实际气体特别是那些不易液化的气体在压强不太大;温度不太低时都可看作理想气体.2一定质量的理想气体状态方程:错误!=错误!或错误!=C常量.典例突破考点一气体压强的产生与计算1.产生的原因:由于大量分子无规则地运动而碰撞器壁;形成对器壁各处均匀、持续的压力;作用在器壁单位面积上的压力叫做气体的压强.2.决定因素1宏观上:决定于气体的温度和体积.2微观上:决定于分子的平均动能和分子的密集程度.3.平衡状态下气体压强的求法1液片法:选取假想的液体薄片自身重力不计为研究对象;分析液片两侧受力情况;建立平衡方程;消去面积;得到液片两侧压强相等方程.求得气体的压强.2力平衡法:选取与气体接触的液柱或活塞为研究对象进行受力分析;得到液柱或活塞的受力平衡方程;求得气体的压强.3等压面法:在连通器中;同一种液体中间不间断同一深度处压强相等.4.加速运动系统中封闭气体压强的求法选取与气体接触的液柱或活塞为研究对象;进行受力分析;利用牛顿第二定律列方程求解.例1.如图中两个汽缸质量均为M;内部横截面积均为S;两个活塞的质量均为m;左边的汽缸静止在水平面上;右边的活塞和汽缸竖直悬挂在天花板下.两个汽缸内分别封闭有一定质量的空气A、B;大气压为p0;求封闭气体A、B的压强各多大解析:题图甲中选m为研究对象.p A S=p0S+mg得p A=p0+错误!题图乙中选M为研究对象得p B=p0-错误!.答案:p0+错误!p0-错误!例2.若已知大气压强为p0;在下图中各装置均处于静止状态;图中液体密度均为ρ;求被封闭气体的压强.解析:在甲图中;以高为h的液柱为研究对象;由二力平衡知p气S=-ρghS+p0S所以p气=p0-ρgh在图乙中;以B液面为研究对象;由平衡方程F上=F下有:p A S+p h S=p0Sp气=p A=p0-ρgh在图丙中;仍以B液面为研究对象;有p A+ρgh sin 60°=p B=p0所以p气=p A=p0-错误!ρgh在图丁中;以液面A为研究对象;由二力平衡得p气S=p0+ρgh1S;所以p气=p0+ρgh1答案:甲:p0-ρgh乙:p0-ρgh丙:p0-错误!ρgh丁:p0+ρgh1例3.如图所示;光滑水平面上放有一质量为M的汽缸;汽缸内放有一质量为m的可在汽缸内无摩擦滑动的活塞;活塞面积为S.现用水平恒力F向右推汽缸;最后汽缸和活塞达到相对静止状态;求此时缸内封闭气体的压强p.已知外界大气压为p0解析:选取汽缸和活塞整体为研究对象;相对静止时有:F=M+ma再选活塞为研究对象;根据牛顿第二定律有:pS-p0S=ma解得:p=p0+错误!.答案:p0+错误!考点二气体实验定律及理想气体状态方程1.理想气体状态方程与气体实验定律的关系错误!=错误!错误!2.几个重要的推论1查理定律的推论:Δp=错误!ΔT2盖—吕萨克定律的推论:ΔV=错误!ΔT3理想气体状态方程的推论:错误!=错误!+错误!+……例4.如图;一固定的竖直汽缸由一大一小两个同轴圆筒组成;两圆筒中各有一个活塞.已知大活塞的质量为m1=2.50 kg;横截面积为S1=80.0 cm2;小活塞的质量为m2=1.50 kg;横截面积为S2=40.0 cm2;两活塞用刚性轻杆连接;间距保持为l=40.0 cm;汽缸外大气的压强为p=1.00×105 Pa;温度为T=303 K.初始时大活塞与大圆筒底部相距错误!;两活塞间封闭气体的温度为T1=495 K.现汽缸内气体温度缓慢下降;活塞缓慢下移;忽略两活塞与汽缸壁之间的摩擦;重力加速度大小g取10 m/s2.求:1在大活塞与大圆筒底部接触前的瞬间;汽缸内封闭气体的温度;2缸内封闭的气体与缸外大气达到热平衡时;缸内封闭气体的压强.解析1设初始时气体体积为V1;在大活塞与大圆筒底部刚接触时;缸内封闭气体的体积为V2;温度为T2.由题给条件得V1=S1错误!+S2错误!①V2=S2l②在活塞缓慢下移的过程中;用p1表示缸内气体的压强;由力的平衡条件得S1p1-p=m1g+m2g+S2p1-p③故缸内气体的压强不变.由盖-吕萨克定律有错误!=错误!④联立①②④式并代入题给数据得T2=330 K⑤2在大活塞与大圆筒底部刚接触时;被封闭气体的压强为p1.在此后与汽缸外大气达到热平衡的过程中;被封闭气体的体积不变.设达到热平衡时被封闭气体的压强为p′;由查理定律;有错误!=错误!⑥联立③⑤⑥式并代入题给数据得p′=1.01×105 Pa⑦答案1330 K 21.01×105 Pa例5.一氧气瓶的容积为0.08 m3;开始时瓶中氧气的压强为20个大气压.某实验室每天消耗1个大气压的氧气0.36 m3.当氧气瓶中的压强降低到2个大气压时;需重新充气.若氧气的温度保持不变;求这瓶氧气重新充气前可供该实验室使用多少天.解析:设氧气开始时的压强为p1;体积为V1;压强变为p22个大气压时;体积为V2.根据玻意耳定律得p1V1=p2V2①重新充气前;用去的氧气在p2压强下的体积为V3=V2-V1②设用去的氧气在p01个大气压压强下的体积为V0;则有p2V3=p0V0③设实验室每天用去的氧气在p0下的体积为ΔV;则氧气可用的天数为N=V0/ΔV④联立①②③④式;并代入数据得N=4天⑤答案:4天考点三气体状态变化的图象问题一定质量的气体不同图象的比较例6.为了将空气装入气瓶内;现将一定质量的空气等温压缩;空气可视为理想气体.下列图象能正确表示该过程中空气的压强p和体积V关系的是解析:选B.等温变化时;根据pV=C;p与错误!成正比;所以p-错误!图象是一条通过原点的直线;故正确选项为B.当堂达标1.如图所示;一个横截面积为S的圆筒形容器竖直放置;金属圆块A的上表面是水平的;下表面是倾斜的;下表面与水平面的夹角为θ;圆块的质量为M;不计圆块与容器内壁之间的摩擦;若大气压强为p0;则被圆块封闭在容器中的气体的压强p为________.解析:对圆块进行受力分析:重力Mg;大气压的作用力p0S;封闭气体对它的作用力错误!;容器侧壁的作用力F1和F2;如图所示.由于不需要求出侧壁的作用力;所以只考虑竖直方向合力为零;就可以求被封闭的气体压强.圆块在竖直方向上受力平衡;故p0S+Mg=错误!·cos θ;即p=p0+错误!.答案:p0+错误!2.某压缩式喷雾器储液桶的容量是5.7×10-3 m3.往桶内倒入4.2×10-3 m3的药液后开始打气;打气过程中药液不会向外喷出.如果每次能打进2.5×10-4m3的空气;要使喷雾器内药液能全部喷完;且整个过程中温度不变;则需要打气的次数是A.16次B.17次C.20次D.21次解析:选B.设大气压强为p;由玻意耳定律;npV0+pΔV=pV;V0=2.5×10-4m3;ΔV =5.7×10-3m3-4.2×10-3m3=1.5×10-3m3;V=5.7×10-3m3;解得n=16.8次≈17次;选项B正确.3.多选一定质量理想气体的状态经历了如图所示的ab、bc、cd、da四个过程;其中bc的延长线通过原点;cd垂直于ab且与水平轴平行;da与bc平行;则气体体积在A.ab过程中不断增大B.bc过程中保持不变C.cd过程中不断增大D.da过程中保持不变解析:选AB.首先;因为bc的延长线通过原点;所以bc是等容线;即气体体积在bc过程中保持不变;B正确;ab是等温线;压强减小则体积增大;A正确;cd是等压线;温度降低则体积减小;C错误;连接aO交cd于e;如图所示;则ae是等容线;即V a=V e;因为V d<V e;所以V d<V a;da过程中体积不是保持不变;D错误.4.已知湖水深度为20 m;湖底水温为4 ℃;水面温度为17 ℃;大气压强为1.0×105Pa.当一气泡从湖底缓慢升到水面时;其体积约为原来的取g=10 m/s2;ρ水=1.0×103 kg/m3A.2.8倍B.8.5倍C.3.1倍D.2.1倍解析:选C.一标准大气压约为10 m高的水柱产生的压强;所以气泡在湖底的压强p1约为3.0×105Pa;由理想气体状态方程得;错误!=错误!;而T1=4+273K=277 K;T2=17+273K=290 K;温度基本不变;压强减小为原来的错误!;体积扩大为原来的3倍左右;C项正确.5.如图所示;上端开口的光滑圆柱形汽缸竖直放置;横截面积为40 cm2的活塞将一定质量的气体和一形状不规则的固体A封闭在汽缸内.在汽缸内距缸底60 cm 处设有a、b两限制装置;使活塞只能向上滑动.开始时活塞搁在a、b上;缸内气体的压强为p0p0=1.0×105 Pa为大气压强;温度为300 K.现缓慢加热汽缸内气体;当温度为330 K时;活塞恰好离开a、b;当温度为360 K时;活塞上移了4 cm.g 取10 m/s2.求活塞的质量和物体A的体积.解析:设物体A的体积为ΔV;T1=300 K;p1=1.0×105Pa;V1=60×40 cm3-ΔV;T2=330 K;p2=错误!Pa;V2=V1;T3=360 K;p3=p2;V3=64×40 cm3-ΔV.由状态1到状态2为等容过程;则错误!=错误!;代入数据得m=4 kg.由状态2到状态3为等压过程;则错误!=错误!;代入数据得ΔV=640 cm3.答案:4 kg 640 cm3。
气体实验定律

气体实验定律一、气体实验定律1、玻意耳定律(1)内容:一定质量的气体,在温度不变的情况下,它的压强跟体积成反比;或者说压强跟体积的乘积是不变的。
玻意耳定律是实验定律,不论什么气体,只要符合压强不太大(和大气压比较)、温度不太低(和室温比较)的条件,都近似地符合这个定律。
(2)数学表达式: p 1V 1=p 2V 2或pV=恒量(3)等温线(P-V 图像如图):2、查理定律(1)内容:体积不变时,一定质量气体的压强与热力学温度成正比。
查理定律是个实验定律。
不论什么气体,只要符合压强不太大(和大气压比较)、温度不太低(和室温比较)的条件,都近似地符合这个定律。
(2)数学表达式:2121T T P P = (3)等容线(P-T 图像):2、盖·吕萨克定律(1)内容:压强不变时,一定质量气体的体积与热力学温度成正比。
盖·吕萨克定律是个实验定律。
不论什么气体,只要符合压强不太大(和大气压比较)、温度不太低(和室温比较)的条件,都近似地符合这个定律。
(2)数学表达式:2121T T V V = (3)等压线(V-T 图像):【典型例题】例1、一个气泡从水底升到水面时,它的体积增大为原来的3倍,设水的密度为ρ=1×103kg/m 3,大气压强p 0=1.01×105Pa ,水底与水面的温度差不计,求水的深度.取g=10m/s 2.例2、要求瓶内氢气在500℃时的压强不超过1atm,则在20℃下对瓶子充气时,瓶内压强最多为多少?瓶子的热膨胀不计.例3、内壁光滑的导热气缸竖直浸放在盛有冰水混合物的水槽中,用不计质量的活塞封闭压强为1.0×l05Pa、体积为2.0×l0-3m3的理想气体.现在活塞上方缓缓倒上沙子,使封闭气体的体积变为原来的一半,然后将气缸移出水槽,缓慢加热,使气体温度变为127℃.(1)求气缸内气体的最终体积;(2)在p-V图上画出整个过程中气缸内气体的状态变化.(大气压强为1.0×l05Pa)【反馈练习】1、两个半球壳拼成的球形容器内部已抽成真空,球形容器的半径为R,大气压强为p,使两个半球壳沿图中箭头方向互相分离,应施加的力F至少为[]A、4πR2pB、2πR2pC、πR2pD、πR2p2、一个气泡从水面下40m深处升到水面上,假定水的温度一定,大气压强为76cmHg,则气泡升到水面时的体积约为原来的[]A、3倍B、4倍C、5倍D、5.5倍3、密闭容器中装有某种理想气体,当温度从t1=50℃升到t2=100℃时,气体的压强从p1变化到p2,则[]A、p2/p1=2B、p2/p1=1/2C、p2/p1=1D、1<p2/p1<24、一定质量的气体,处于平衡状态I,现设法使其温度降低而压强增大,达到平衡状态II,则[ ]A、状态I时气体的密度比状态II时的大B、状态I时分子的平均动能比状态lI时的入C、状态I时分子间的平均距离比状态II时的大D、状态I时每个分子的动能都比状态II时的分子的平均动能大5、竖直的玻璃管,封闭端在上,开口端在下,中间有一段水银,若把玻璃管稍倾斜一些,但保持温度不变,则:[ ]A、封闭在管内的气体压强增大B、封闭在管内的气体体积增大C、封闭在管内的气体体积减小D、封闭在管内的气体体积不变6、如图所示,两端开口的U形玻璃管中,左右两侧各有一段水银柱,水银部分封闭着一段空气,己知右侧水银还有一段水平部分,则:(1)若向右侧管中再滴入少许水银,封闭气体的压强将.(2)若向左侧管中再滴入少许水银,封闭气体的压强将,右侧水银的水平部分长度变7、(1)下图中甲、乙均匀玻璃管中被水银封闭的气体压强分别为P1、P2、P3,己知大气压为76cmHg,h l=2cm,h2=3cm,求P1、P2、P3各为多少?(2)如图设气缸的质量为M,横截面为S,活塞的质量为m,当气缸搁于地上时,里面气体的压强为____.当通过活塞手柄提起气缸时,被封闭的气体的压强为____.(已知大气压强为p0)8、盛有氧气的钢瓶,在室内(17℃)测得瓶内氧气的压强是9.31×106Pa当把钢瓶搬到温度是-13℃的室外时,测得瓶内氧气的压强变为8.15×106Pa.试问钢瓶是否漏气?为什么?9、如图所示,截面积S=0.01m2的气缸内有一定质量的气体被光滑活塞封闭.已知外界大气压p0=105Pa,活塞重G=100N.现将气缸倒过来竖直放置,设温度保持不变,气缸足够长.求气缸倒转后气体的体积是倒转前的几倍?10、如图所示,一端封闭横截面积均为S、长为b的细管弯成L形,放在大气中,管的竖直部分长度为a,大气压强为P0,现在开口端轻轻塞上质量为m,横截面积也为S的小活塞。
气体实验定律PPT教学课件精选全文

单原子分子:
t
1 2
mv2
1 2
m vx2
1 2
m
v
2 y
1 2
m
v
2 z
3 2
kT
v
2 x
v
2 y
vz2
1 v2 3
1 2
m vx2
1 2
m
v
2 y
1 2
m
v
2 z
1 2
kT
能量均分定理:
在温度为T 的平衡态下,物质分子的每一个自 由度都具有相同的平均动能,其大小都等于kT/2。
分子平均能量: i kT “i”为刚性分子自由度
3.分子永不停息地作无规则的运动.
§2 气体的状态参量 平衡态
一、体积V 气体分子所能达到的空间范围. [单位: m3]
二、压强P 气体作用于容器壁单位面积的垂直作用力. [单位:Pa] 1Pa=1N/ m2
1.1mmHg=133.3Pa 2.标准大气压(atm)
1atm 760mmHg 1.013105 Pa
R 称为“普适气体常数 ”
代入: PV PoVo M PoVmol
T
To
M mol To
理想气体物态方程: PV M RT M mol
阿伏伽德罗常数: N A 6.022 1023 mol 1
玻耳兹曼常数: k R 1.38 1023 (J K 1) NA
设:分子质量为 m,气体分子数为N,分子数密度 n。
f (v) 4 (
m
)3
2
e
mv2 2 kT
v2
2 kT
f(v)
f (v)dv dN N
v
dv
f(v)
理想气体实验定律

A.T1>T2 B.T1=T2 C.T1<T2 D.无法判断 小结:在p-V图中,p与V的大小可直接由坐标轴上比较得出,而T的大小由 p、V的乘积决定,p、V乘积值大的,T大。
例2 图5是一定质量理想气体在p-T图中体积分别为V1、V2、V3的三条等容图线, 由此图象可知V1、V2、V3之间的关系是________。
三)、压强
气体作用在器壁单位面积上的压力叫做气体的压强. 在国际单位制中,压强的单位是帕斯卡,符号是Pa.其他如:
标准大气压 毫米汞柱等
问题:怎么样研究P.T.V三者关系?
控制变量法
二、气体的三大实验定律: 1.玻马定律:
⑴质量一定气体,保持温度不变,研究压强和体积的
关系(等温过程)
实验:用活塞封闭一定质量的气体
持温度不变,让体积膨胀③先保持温度不变,使 体积膨胀,再保持体积不变,使气体升温 ④先
保持温度不变,压缩气体,再保持体积不变,使 气体降温。可以断定( )
▪ A.①、②不可能
B.③、④不可能
▪ C.①、③不可能 可能
D.①、②、③、④都
▪ 例4. 如图6所示,在V-T图中A、B两点表示一定 质量的理想气体的两个状态(pA,VA,TA)和 (pB,VB,TB),则可从图中得出: PA______PB;VA______VB;TA______TB。 (填“>”、“=”或“<”)
体积______;温度______;在BC过程中:压强______;体积______;温度
______;在CA过程中:压强______;体积______;温度______;(以上空填
理想气体定律

气象学:理想气体定律在天气预报和气候研究中用于描述大气的压力、温度和密度
航天工程:理想气体定律在航天工程中用于计算火箭发动机的推力和效率
在化学中的应用领域和实例
化学反应速率的计算:利用理想气体定律计算反应物的浓度和温度,从而预测反应速率。
气体吸收和释放:利用理想气体定律计算气体吸收和释放过程中的压力和温度变化。
理想气体的定义:忽略分子间的相互作用,视为质点
状态方程:pV=nRT,其中p为压力,V为体积,n为物质的量,R为气体常数,T为热力学温度
结论:理想气体定律是描述理想气体状态的基本定律,对于实际气体也具有一定的适用性
理想气体定律的实验验证
4
实验验证的原理和方法
理想气体定律:PV=nRT
实验原理:通过改变气体的体积和温度,观察压力的变化,验证理想气体定律。
理想气体定律在工程和科学领域中有广泛的应用,例如在热力学、流体力学、气象学等领域中都有重要的应用。
理想气体定律可以帮助我们理解和解释许多自然现象,例如大气压力的变化、气体的膨胀和压缩等。
理想气体定律还可以帮助我们设计和优化各种设备和系统,例如制冷系统、热力系统等。
理想气体定律的适用范围
适用于气体的微观性质,如分子数、分子动量等
实验方法:使用气缸和温度计,改变气缸的体积,同时测量温度和压力,得出实验数据。
数据分析:通过计算得出气体的摩尔数,验证理想气体定律的准确性。
实验验证的过程和结果
ቤተ መጻሕፍቲ ባይዱ
单击此处输入你的项正文
实验目的:验证理想气体定律的正确性
单击此处输入你的项正文
实验结果:实验数据与理想气体定律的预测结果相符,验证了理想气体定律的正确性
理想气体定律的公式
