圆锥台侧面积公式
圆锥侧面积公式和扇形面积公式

圆锥侧面积公式和扇形面积公式
圆锥是一种由平面围绕着一个点旋转形成的几何体。
它由一个圆形底面和连接底面边缘与顶点的斜面组成。
圆锥的侧面积公式和扇形面积公式是计算圆锥侧面积和扇形面积的重要工具。
首先,让我们来看看圆锥的侧面积公式。
假设圆锥的底面半径为r,斜面的高度为h。
根据勾股定理,我们可以得到斜面的长度为l,即 l = √(r^2 + h^2)。
圆锥的侧面积可以通过计算底面周长与斜面长度
的乘积得到,即 S = πr * l。
所以圆锥的侧面积公式为 S = πr * √(r^2 + h^2)。
接下来,我们来看看扇形的面积公式。
扇形是圆的一部分,由圆心、圆弧和两条半径组成。
假设扇形的半径为r,圆心角度数为θ(以弧度为单位)。
扇形的面积可以通过计算扇形的圆心角度数与整个圆的
面积的比例来得到,即 S = (θ/360) * πr^2。
这个公式是基于圆
的面积公式πr^2,并乘以一个比例因子,该比例因子是扇形的圆心角度数与整个圆的圆心角度数的比例。
需要注意的是,上述公式中的角度必须以弧度为单位。
如果角度以度数给出,可以使用以下转换公式将其转换为弧度:弧度 = (度数 * π) / 180。
这些公式对于解决与圆锥和扇形相关的几何问题非常有用,例如计算圆锥的表面积、体积或扇形的面积。
掌握这些公式可以帮助我们更好地理解和解决与圆锥和扇形相关的数学和物理问题。
初数数学公式解析圆锥和圆柱的侧面积计算

初数数学公式解析圆锥和圆柱的侧面积计算圆锥和圆柱是初等数学中常见的几何图形,求解它们的侧面积是基础的数学技能之一。
在本文中,我们将解析圆锥和圆柱的侧面积计算公式,并提供一些例题帮助读者更好地理解和掌握这个概念。
一、圆锥的侧面积计算圆锥是由一个圆形底面和一个位于底面中心上方的顶点连成的直线围成的几何体。
为了计算圆锥的侧面积,我们需要知道底面的半径和侧面的斜高。
侧面积的计算公式为:侧面积= π * r * l其中,π为圆周率的近似值,约等于3.14159;r为圆锥底面的半径;l为圆锥的斜高。
举个例子,假设圆锥的底面半径为5 cm,斜高为8 cm。
我们可以通过代入公式来计算侧面积:侧面积 = 3.14159 * 5 * 8 = 125.6637 cm²因此,该圆锥的侧面积为约125.6637 cm²。
二、圆柱的侧面积计算圆柱是由一个圆形底面和平行于底面的另一个圆形面组成的几何体。
求解圆柱的侧面积需要提供底面的半径和高度。
侧面积的计算公式如下:侧面积= 2 * π * r * h其中,π为圆周率的近似值,约等于3.14159;r为圆柱底面的半径;h为圆柱的高度。
举个例子,假设圆柱的底面半径为6 cm,高度为10 cm。
我们可以通过代入公式来计算侧面积:侧面积 = 2 * 3.14159 * 6 * 10 = 376.99112 cm²因此,该圆柱的侧面积为约376.99112 cm²。
结论:通过以上的解析,我们了解到计算圆锥和圆柱的侧面积需要使用不同的公式,并且都需要提供底面的半径。
对于圆锥,我们还需要知道斜高;而对于圆柱,则需要底面与高度。
熟练掌握这些计算公式,能够帮助我们更好地理解和应用于数学问题中。
同时,理解几何图形的特点和计算方法,有助于拓宽我们对数学的认识和应用能力。
希望本文的解析能够帮助读者更好地理解圆锥和圆柱的侧面积计算,并在数学学习中取得更好的成绩。
圆锥侧面积公式是什么

圆锥侧面积公式是什么
圆锥的侧面展开是扇形,所以根据扇形的面积计算公式得到圆锥侧面积=πLR(L是圆锥的侧长,R是圆锥半径)。
圆锥侧面积公式是什么
1圆锥侧面积公式
圆锥的侧面积=母线的平方×π×(360分之扇形的度数)==1/2×母线长×底面周长=π×底面圆的半径×母线
其它相关公式:
圆锥的表面积=底面积+侧面积S=πr²+πrl (注l=母线);
圆锥的体积=1/3底面积乘高或1/3πr^2*h。
2圆锥
定义
圆锥面和一个截它的平面(满足交线为圆)组成的空间几何图形叫圆锥。
以直角三角形的直角边所在直线为旋转轴,其余两边旋转而成的曲面所围成的几何体叫做圆锥。
注意:圆锥不是特殊的圆柱。
组成
圆锥的高:圆锥的顶点到圆锥的底面圆心之间的最短距离叫做圆锥的高;
圆锥母线:圆锥的侧面展开形成的扇形的半径、底面圆周上任意一点到顶点的距离。
圆锥的侧面积:将圆锥的侧面沿母线展开,是一个扇形,这个扇形的弧长等于圆锥底面的周长,而扇形的半径等于圆锥的母线的长. 圆锥的侧面积就是弧长为圆锥底面的周长×母线/2;没展开时是一个曲面。
圆锥有一个底面、一个侧面、一个顶点、一条高、无数条母线,且底面展开图为一圆形,侧面展开图是扇形。
圆锥的表面积公式和侧面积公式

圆锥的表面积公式和侧面积公式
在我们的日常生活中,我们可能会经常遇到圆锥这个几何体。
圆锥是一个非常有趣的几何体,它的形状很特殊,既有圆形的底面,又有一个顶点,连接底面和顶点的部分叫做侧面。
在这篇文章中,我们将讨论圆锥的表面积公式和侧面积公式。
让我们来看一下圆锥的表面积公式。
圆锥的表面积是指圆锥的所有外表面积的总和。
它的计算公式是:表面积= 底面积+ 侧面积。
其中,底面积是指圆锥底面的面积,可以用圆的面积公式来计算:底面积= πr^2,其中π是一个数学常数,约等于3.14159,r是圆锥底面的半径。
侧面积是指圆锥侧面的面积,它的计算公式是:侧面积= πrℓ,其中ℓ是圆锥侧面的斜高。
这里需要注意的是,斜高是指从圆锥顶点到底面边缘的直线距离。
接下来,让我们来看一下圆锥的侧面积公式。
圆锥的侧面积是指圆锥侧面的总面积。
它的计算公式是:侧面积= πrℓ,其中r和ℓ的含义与上面相同。
侧面积实际上就是圆锥侧面的曲面积分,可以理解为将圆锥侧面展开后的面积。
通过这两个公式,我们可以计算出圆锥的表面积和侧面积。
这些公式是非常有用的,可以帮助我们在实际问题中计算圆锥的表面积和侧面积。
比如,当我们需要知道一个圆锥的表面积时,我们可以使用这些公式来计算。
同样地,当我们需要知道一个圆锥的侧面积时,
我们也可以使用这些公式来计算。
圆锥的表面积公式和侧面积公式是非常重要的几何公式。
它们可以帮助我们计算圆锥的表面积和侧面积,从而更好地理解和应用圆锥这个几何体。
希望通过这篇文章的介绍,读者们对圆锥的表面积和侧面积有了更深入的了解。
圆锥知识点总结大全

圆锥知识点总结大全一、圆锥的定义圆锥是由一个平面曲线(直角圆锥)或者一个曲线(斜圆锥)围绕着一条直线而形成的几何体,这条直线被称为圆锥的轴。
圆锥的侧面是由轴和平面曲线(或者直线)共同确定的。
二、圆锥的分类根据圆锥的底面形状,圆锥可以分为圆锥台、圆锥体和斜圆锥。
其中,圆锥台是底面为圆的圆锥,圆锥体是底面为椭圆的圆锥,而斜圆锥则是底面为三角形、四边形或者正多边形的圆锥。
三、圆锥的性质1. 圆锥的侧面是由轴和底面上的点连线组成的。
2. 圆锥的顶点是垂直于底面的轴上的定点。
3. 圆锥的底面形状决定了圆锥的几何性质,不同形状的底面对应不同的计算公式和应用。
四、圆锥的公式1. 圆锥的体积公式:对于圆锥台,其体积公式为V = 1/3πr^2h,其中r为底面半径,h为高度;对于圆锥体,其体积公式为V = 1/3πab h,其中a和b为椭圆的长轴和短轴,h为高度;对于斜圆锥,其体积公式则视底面形状而定。
2. 圆锥的侧面积公式:对于圆锥台,其侧面积公式为S = πrl,其中r为底面半径,l为斜高;对于圆锥体,其侧面积公式为S = πa l,其中a为椭圆长轴,l为斜高;对于斜圆锥,其侧面积公式则视底面形状而定。
3. 圆锥的表面积公式:对于圆锥台,其表面积公式为S = πr(l+r),其中r为底面半径,l为斜高;对于圆锥体,其表面积公式为S = πa(l+r),其中a为椭圆长轴,l为斜高;对于斜圆锥,其表面积公式则视底面形状而定。
五、圆锥的应用1. 圆锥的体积应用:圆锥的体积公式是解决容器容积、物体体积等问题的重要工具,比如计算桶、漏斗、锥形顶等的容积。
2. 圆锥的表面积应用:圆锥的表面积公式是解决圆锥包装、圆锥顶、锥形灯罩等问题的重要工具,比如计算油漆的表面积,勺子头的封闭面积等。
3. 圆锥的相似应用:圆锥的相似性性质是解决相关问题的重要方法,比如据求与已知圆锥相似的圆锥的侧面积、体积等。
4. 圆锥的几何证明:圆锥的几何性质是解决证明问题的重要素材,利用圆锥的性质来证明一些几何定理和公式。
圆锥所有的公式

圆锥所有的公式
圆锥是一个三维几何图形,由一条直线(生成元)和一个封闭曲面组成,曲面上的每个点到直线的距离都相等。
圆锥的公式涉及到它的各个部分,如底面、侧面、体积和表面积等。
下面是圆锥所有的公式:
1. 圆锥的侧面积公式:S = πrl,其中,r是底面半径,l是侧斜高。
2. 圆锥的表面积公式:S = πr + πrl,其中,r是底面半径,l是侧斜高。
3. 圆锥的体积公式:V = (1/3)πrh,其中,r是底面半径,h 是高度。
4. 圆锥的底面积公式:A = πr,其中,r是底面半径。
5. 圆锥的母线公式:l = √(r + h),其中,r是底面半径,h 是高度。
6. 圆锥的侧斜高公式:l = √(h + r),其中,r是底面半径,h是高度。
7. 圆锥的高度公式:h = l - r / 2l,其中,r是底面半径,l 是侧斜高。
8. 圆锥的底面半径公式:r = √(A / π),其中,A是底面积。
以上是圆锥的所有公式,它们有助于我们计算圆锥的各种参数和特性。
- 1 -。
圆锥侧面积的计算公式

圆锥侧面积的计算公式
圆锥侧面积公式为:S侧=πrl,l为母线。
圆锥的表面积由侧面积和底面积两部分组成。
全面积S=S侧+S底。
圆锥是一种几何图形,有两种定义。
几何定义:圆锥面和一个截它的平面(满足交线为圆)组成的空间几何图形叫圆锥。
立体几何定义:以直角三角形的直角边所在直线为旋转轴,其余两边旋转360度而成的曲面所围成的几何体叫做圆锥。
旋转轴叫做圆锥的轴。
垂直于轴的边旋转而成的曲面叫做圆锥的底面。
不垂直于轴的边旋转而成的曲面叫做圆锥的侧面。
无论旋转到什么位置,不垂直于轴的边都叫做圆锥的母线。
(边是指直角三角形两个旋转边)。
圆锥的表面积公式和侧面积公式

圆锥的表面积公式和侧面积公式表面积公式:
圆锥的表面积包括底面积和侧面积。
底面积即圆的面积,可以
用πr^2表示,其中r为圆锥底面的半径。
侧面积可以通过计算圆
锥的母线(斜边)与生成圆的周长的乘积来得到,公式为πrl,其
中r为底面半径,l为母线的长度。
综合起来,圆锥的表面积公式为:
πr^2 + πrl = πr(r + l)。
侧面积公式:
圆锥的侧面积即圆锥的母线(斜边)的长度乘以生成圆的周长,公式为πrl,其中r为底面半径,l为母线的长度。
这些公式可以帮助我们计算圆锥的表面积和侧面积,从而更好
地理解和解决与圆锥相关的问题。
圆锥的侧面积公式推导过程

圆锥的侧面积公式推导过程
圆锥侧面积的公式:圆锥侧面积=圆锥底面半径X圆周率X母线,即S侧=πrl。
第一种方法:把展开的扇形的弧微分为许多小段,那么每一个小段和扇形顶点形成一个三角形,扇形的面积就是这些小三角形的和。
设每小段长度为x,则每个小三角形的面积是(1/2)xl,所有x加起来为扇形弧长2πr。
所以圆锥侧面积=(1/2)(2πr)l=πrl。
第二种方法:因为圆锥侧面是展开后大圆的一部分,占大圆的面积为(弧长/大圆周长)=2πr/2πl。
因为大圆面积为πl^2,所以圆锥侧面积=(πl^2)·(2πr/2πl)=πrl。
圆锥组成:
圆锥的高:圆锥的顶点到圆锥的底面圆心之间的最短距离叫做圆锥的高。
圆锥母线:圆锥的侧面展开形成的扇形的半径、底面圆周上任意一点到顶点的距离。
圆锥的侧面积:将圆锥的侧面沿母线展开,是一个扇形,这个扇形的弧长等于圆锥底面的周长,而扇形的半径等于圆锥的母线的长.圆锥的侧面积就是弧长为圆锥底面的周长×母线/2;没展开时是一个曲面。
圆锥有一个底面、一条高、无数条母线,且底面展开图
为一圆形,侧面展开图是扇形。
圆锥台的表面积计算公式

圆锥台的表面积计算公式圆锥台是由一个圆锥和一个圆柱体组成的几何体。
它具有独特的形状和特征,可以通过计算其表面积来了解其大小和形态。
下面将介绍圆锥台的表面积计算公式及其应用。
圆锥台的表面积计算公式如下:表面积 = 圆锥的底面积 + 圆锥侧面的面积 + 圆柱体的侧面积我们需要计算圆锥的底面积。
圆锥的底面是一个圆形,其面积可以通过圆的面积公式来计算。
假设圆锥的底面半径为r,则底面积为πr²。
接下来,我们计算圆锥侧面的面积。
圆锥的侧面是一个斜面,其形状类似于一个三角形。
我们可以通过计算圆锥的母线和斜高来计算侧面积。
假设圆锥的母线为l,斜高为s,则侧面积为πrl。
我们计算圆柱体的侧面积。
圆柱体的侧面是一个矩形,其面积可以通过计算矩形的长和宽来求得。
假设圆柱体的高为h,底面周长为C,则侧面积为Ch。
将上述三部分的面积相加,即可得到圆锥台的表面积。
圆锥台的表面积计算公式为:表面积= πr² + πrl + Ch圆锥台的表面积计算公式可以应用于多个实际问题中。
例如,在建筑领域,我们可以利用该公式计算圆锥台形结构的表面积,以确定所需的材料数量和成本。
在制造业中,该公式可以用于计算各种圆锥形零件的表面积,从而进行加工和设计。
在数学教育中,该公式可以用于教授学生如何计算几何体的表面积,培养他们的几何思维能力。
除了计算圆锥台的表面积,该公式还可以帮助我们理解圆锥台的特征和性质。
例如,当圆锥的高度增加时,其表面积也会增加,这意味着圆锥台的体积也会增加。
当圆锥的底面半径增加时,表面积也会增加,这表明圆锥台的大小也会增加。
总结一下,圆锥台的表面积计算公式为表面积= πr² + πrl + Ch。
该公式可以应用于建筑、制造业和教育等领域,帮助我们计算和理解圆锥台的特征和性质。
通过对圆锥台的表面积进行计算和研究,我们可以更好地理解和应用这个几何体。
圆锥台面积公式
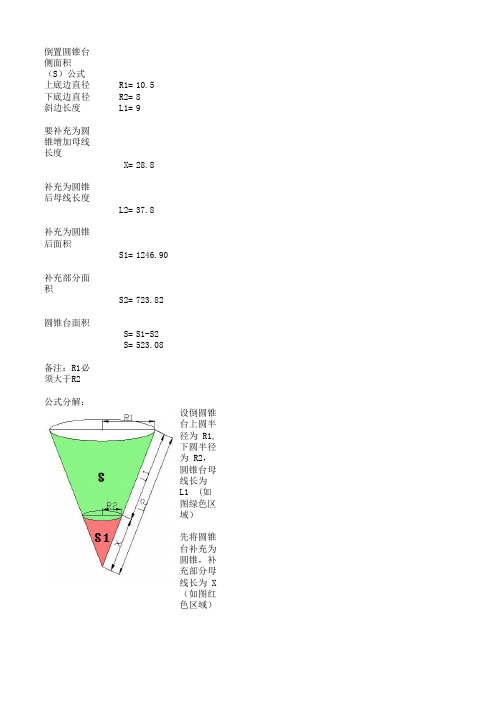
倒置圆锥台侧面积(S)公式计算
上底边直径R1=10.5
下底边直径R2=8
斜边长度L1=9
要补充为圆锥增加母线长度
X=28.8
补充为圆锥后母线长度
L2=37.8
补充为圆锥后面积
S1=1246.90
补充部分面积
S2=723.82
圆锥台面积
S=S1-S2
S=523.08
备注:R1必须大于R2
公式分解:
设倒圆锥台上圆半径为 R1,下圆半径为 R2,
圆锥台母线长为 L1 (如图绿色区域)
先将圆锥台补充为圆锥,补充部分母线长为 X
(如图红色区域)
根据三角形比例关系故此得出:
R2/R1=X/L2
L2=X+L1
即:R2/R1=X/(X+L1)
R2*(X+L1)=R1*X
R2*X+R2*L1=R1*X
R2*L1=R1*X-R2*X
R2*L1=(R1-R2)*X
X=R2*L1/(R1-R2)
故此得出上面公式数值,求得X值
倒圆锥台面积 S 为补充成完整圆锥后圆锥的侧面积 S2 减去补充部分圆锥的侧面积 S1
即:S=S2-S1
根据圆锥侧面积公式:S=π*L*R 得出:
S2=π*L2*R1S1=π*X*R2
大连海达玻璃幕墙工程有限公司
计算设计师2013年7月14日
王刚。
关于圆锥侧面积的公式

关于圆锥侧面积的公式圆锥是一种常见的几何体,它由一个圆形的底面和一个顶点连接底面的直线段组成。
圆锥侧面积是指圆锥除底面外的所有侧面的总面积。
下面我们来探讨一下关于圆锥侧面积的公式。
要计算圆锥的侧面积,我们需要知道圆锥的底面半径和侧面的斜高。
底面半径是指圆锥底面上的半径,也就是一个以圆锥底面圆心为中心的圆的半径。
侧面的斜高是指从圆锥顶点到底面上的某一点的直线段的长度。
在计算圆锥的侧面积时,我们可以使用以下公式:侧面积= π × r × l其中,π是一个常数,约等于3.14159,r是圆锥底面的半径,l是侧面的斜高。
这个公式的推导过程可以通过几何方法来进行。
我们可以将圆锥展开成一个扇形,然后再将这个扇形打开成一个等腰三角形和一个弧形。
等腰三角形的底边就是圆锥的底面周长,也就是2πr,而等腰三角形的高就是圆锥的斜高l。
所以,等腰三角形的面积为1/2 × 2πr × l = πrl。
而弧形的长度就是圆锥底面的周长,也是2πr。
所以,弧形的面积为1/2 × 2πr × r = πr^2。
将等腰三角形的面积和弧形的面积相加,就得到了圆锥的侧面积,即πrl + πr^2 = πr(l + r)。
通过这个公式,我们可以方便地计算出圆锥的侧面积。
举个例子,假设一个圆锥的底面半径为5cm,侧面的斜高为8cm。
那么根据公式,这个圆锥的侧面积为π × 5 × 8 = 40π ≈ 125.66平方厘米。
需要注意的是,圆锥的侧面积只包括了除底面外的所有侧面的面积。
如果要计算整个圆锥的表面积,还需要将底面的面积加上去。
底面的面积可以通过圆的面积公式来计算,即πr^2。
所以,整个圆锥的表面积为πr^2 + πrl。
除了圆锥的侧面积,还可以计算它的体积。
圆锥的体积可以通过以下公式计算:体积= 1/3 × 底面积× 高其中,底面积为圆锥底面的面积,高为圆锥顶点到底面的垂直距离。
