点到平面距离的若干典型求法知识交流
例谈空间距离——点到平面的距离求法

出或作 出有 关距离 的图形 ; 证 明它符 ②
合 定 义 ; 在 同一 平 面 内计 算 。 ③ 点 到 平 面 的 距 离 求 法 有 下 列 三 种 【 路 方 法 一 I 接 法 : 解 的关 键 思 直 求 是 正确 作 出 图形 , 确定 垂 足位 置 最 重 要 。 充 分 利 用 面 面 垂 直 要
【 路 方 法 二 】 体 积 法 : 所 求 距 离 转 化 为 求 锥 体 的高 。 思 等 把 (i 当0a2 ,()0f ) ( ,)(, ) i) << 时 f x> ,x在 一 1 ,1+ 为增 函数 。 , (
(当20d1 = 得一/ , i a , ,(0 x、Ox i > < 令x, ’ i 时 导< )解 = ) 譬 -
解 析 : 1 f x = x+ a + 由题 意 知P( ,) ( ) ,.+ + ( ) ( ) 3 '2 x b, , 14 在fx 上 .1 a ‘
c , 孚 ,一 — 一 √ t
f( ) x
.
(
, :4 ) b-且 I I- +4 { ) ,o o c ,
f X ()
x 化 时f()fx 的变 化 情 况 如 下 表 变 x ,()
f) ( ,/ 2 ,/兰,,, )增 数 (在一 一 a一 (! 1(+ 为 函 , x , - )、  ̄ )1
T a V a
一
3 ~ ,2 一 ( 2亍) 3 ( 1 l ( 3一 ) 2 一 , ÷, )
的 性 质 。 ( 图 1 如 )
图1
于 d 0 . 是: : P
J
: 巫
J
下 面 通 过 几 个 实 例 来 说 明点 到 平 面 的 距 离 求 法 。以 及 线 面 距 离 或 面 面
求点到平面的距离的方法公式

求点到平面的距离的方法公式求点到平面的距离是数学中的一种常见问题,也是几何学的基础知识之一。
在平面几何中,点到平面的距离是指从给定点到平面上的一点的最短距离。
本文将介绍两种常用的求解点到平面距离的方法。
方法一:点到平面的法向量距离公式要求解点到平面的距离,我们首先需要知道平面的方程以及点的坐标。
假设平面的方程为Ax + By + Cz + D = 0,点的坐标为(x0, y0, z0)。
根据向量的性质,平面上的任意一点P(x1, y1, z1)可以表示为平面上任意一点Q(x, y, z)加上平面的法向量N的倍数。
即P = Q + tN,其中t为实数。
将P的坐标代入平面方程,可以得到:A(x1 + tx) + B(y1 + ty) + C(z1 + tz) + D = 0整理后可以得到:t = - (Ax1 + By1 + Cz1 + D) / (Ax + By + Cz)根据点到平面的距离定义,点到平面的距离d可以表示为点P与平面上的任意一点Q之间的距离。
而点P与Q之间的距离可以使用向量的长度来表示,即d = ||PQ||。
将PQ的向量表示代入,可以得到:d = ||(x - x1, y - y1, z - z1)||将向量的长度公式代入,可以得到:d = sqrt((x - x1)^2 + (y - y1)^2 + (z - z1)^2)点到平面的距离公式为:d = sqrt((x - x1)^2 + (y - y1)^2 + (z - z1)^2)方法二:点到平面的投影距离公式除了使用法向量距离公式,我们还可以利用点在平面上的投影点来求解点到平面的距离。
点在平面上的投影点是指从给定点到平面上的一点的垂直线段与平面的交点。
假设平面的方程为Ax + By + Cz + D = 0,点的坐标为(x0, y0, z0)。
平面上的一点P(x1, y1, z1)为点(x, y, z)在平面上的投影点。
根据点在平面上的投影点的定义,可得到以下方程组:Ax + By + Cz + D = 0x = x0 + t(A - Ax0 - By0 - Cz0)y = y0 + t(B - Ax0 - By0 - Cz0)z = z0 + t(C - Ax0 - By0 - Cz0)将x, y, z代入平面方程,可以得到:t = - (Ax0 + By0 + Cz0 + D) / (A^2 + B^2 + C^2)将t代入x, y, z的方程中,可以得到P的坐标:x1 = x0 + t(A - Ax0 - By0 - Cz0)y1 = y0 + t(B - Ax0 - By0 - Cz0)z1 = z0 + t(C - Ax0 - By0 - Cz0)根据点到平面的距离定义,点到平面的距离d可以表示为点P与原点O的距离。
求点到面的距离的几种方法

求点到面的距离的几种方法1. 什么是点到面的距离在计算机图形学中,点到面的距离是指一个点到一个平面的最短距离。
点到面的距离是一个重要的计算问题,它在很多应用中都有广泛的应用,比如碰撞检测、物体投影等。
2. 求点到平面的距离的方法求点到平面的距离有多种方法,下面将介绍其中的几种常见方法。
2.1. 点到平面的法向量距离点到平面的法向量距离是一种常见的求解方法。
法向量是垂直于平面的一个向量,可以通过平面的法向量和点到平面的向量的点积来计算距离。
具体计算公式如下:distance = abs((P - A) · N) / ||N||其中,P为点的坐标,A为平面上的点的坐标,N为平面的法向量,||N||表示法向量的模。
2.2. 点到平面的投影距离点到平面的投影距离是另一种常见的求解方法。
它通过将点投影到平面上,然后计算点到投影点的距离来求解。
具体计算公式如下:distance = ||P - P_proj||其中,P为点的坐标,P_proj为点在平面上的投影点的坐标,||P - P_proj||表示点到投影点的距离。
2.3. 点到平面的有向距离点到平面的有向距离是一种考虑点在平面的哪一侧的求解方法。
它通过计算点到平面的距离,并根据点在平面的哪一侧来确定距离的正负。
具体计算公式如下:distance = (P - A) · N / ||N||其中,P为点的坐标,A为平面上的点的坐标,N为平面的法向量,||N||表示法向量的模。
3. 比较不同方法的优缺点不同的求解方法有各自的优缺点,下面将对比它们的优缺点。
3.1. 点到平面的法向量距离优点: - 计算简单,只需进行点积和模运算。
- 结果为非负数,可以直接表示距离。
缺点: - 不考虑点在平面的哪一侧。
3.2. 点到平面的投影距离优点: - 考虑了点在平面的投影位置。
缺点: - 需要额外计算点的投影点。
3.3. 点到平面的有向距离优点: - 考虑了点在平面的哪一侧。
点到平面距离的若干典型求法

点到平面距离的若干典型求法1.引言点到平面的距离是高考立体几何部分必考的热点题型之一,也是学生较难准确把握的难点问题之一。
本文将介绍七种较为典型的求解方法,包括几何方法(如体积法、二面角法)、代数方法(如向量法、公式法)以及常用数学思维方法(如转化法、最值法),以达到秒杀得分的效果。
2.预备知识1) 正射影的定义:从平面外一点P向平面α引垂线,垂足为P',则点P'叫做点P在平面α上的正射影,简称为射影。
同时,把线段PP'叫作点P与平面α的垂线段。
2) 点到平面距离定义:一点到它在一个平面上的正射影的距离叫作这点到这个平面的距离,也即点与平面间垂线段的长度。
3) 四面体的体积公式:V = Sh/3,其中V表示四面体体积,S、h分别表示四面体的一个底面的面积及该底面所对应的高。
4) 直线与平面垂直的判定定理:一条直线与一个平面内的两条相交直线垂直,则该直线与此平面垂直。
5) 三垂线定理:在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它和这条斜线也垂直。
3.求点到平面距离的若干求法3.1 定义法求点到平面距离定义法是最基本的求解方法之一,根据点到平面距离的定义,可以通过求点在平面上的正射影来求解点到平面的距离。
3.2 转化法求点到平面距离转化法是一种常用的求解方法,通过将问题转化为等价的问题来求解。
在点到平面距离的求解中,可以通过将平面方程转化为标准式,然后代入点的坐标,求解点到平面的距离。
3.3 等体积法求点到平面距离等体积法是一种几何方法,通过构造等体积的四面体来求解点到平面的距离。
具体方法是在点与平面之间构造一个四面体,使其与另一四面体等体积,然后根据四面体的体积公式来求解点到平面的距离。
3.4 利用二面角求点到平面距离二面角法是一种几何方法,通过求解点与平面所夹二面角的正弦值来求解点到平面的距离。
具体方法是求解点到平面的垂线与平面法线的夹角,然后根据正弦定理求解点到平面的距离。
求点到平面距离的基本方法

求点到平面距离的基本方法点到平面的距离是空间几何中一个重要的概念,它对于解决一些实际问题以及理论研究都有着重要的意义。
在本文中,我将介绍点到平面距离的基本方法,包括数学公式的推导、几何解法、向量法和线代法等。
首先,我们考虑三维空间中的一个平面,假设平面方程为Ax+By+Cz+D=0,其中A,B,C和D为常数,并且平面上有一点P(x0,y0,z0)。
我们的目标是求点P到平面的距离。
一、数学公式的推导为了推导出点到平面距离的公式,我们可以利用向量的知识。
首先,设平面上任意一点Q(x,y,z),则该点到平面的距离为点PQ的长度。
由于平面上的点Q一定满足平面方程,将Q的坐标代入平面方程可得:Ax+By+Cz+D=0然后,我们用向量表示点P到点Q的向量为向量v=PQ=(x-x0,y-y0,z-z0)。
由向量的点积定义可知,点积v·(A, B, C) = ,v, * ,(A, B, C),* cosθ,其中,v,表示向量v的长度,(A, B, C),表示向量(A, B, C)的长度,θ表示二者之间的夹角。
将向量v和(A,B,C)的定义代入点积公式可得:(A, B, C)·(x - x0, y - y0, z - z0) = ,v, * ,(A, B, C),* cosθ化简上式得:Ax - Ax0 + By - By0 + Cz - Cz0 = ,v, * (A^2 + B^2 + C^2) * cosθ由于点P和点Q都在平面上,点P到平面的距离与平面的法向量垂直,即θ = 90°,cosθ = 0。
因此,上式最后一项为0。
进一步得到点P到平面的距离公式为:d=,Ax0+By0+Cz0+D,/√(A^2+B^2+C^2)这就是点到平面的距离的数学公式。
二、几何解法除了数学公式,我们还可以利用几何的方法来求点到平面的距离。
首先,我们可以将平面方程转化为点法式方程,即n·(P-P0)=0,其中n为平面的法向量,P为平面上任意一点的坐标,P0为平面上已知的一点的坐标。
求点到面的距离的几种方法

求点到面的距离的几种方法点到面的距离是计算机图形学中的一个重要问题,它涉及到三维空间中点和平面之间的距离计算。
在实际应用中,点到面的距离计算常常用于计算三维模型的碰撞检测、物体运动轨迹的计算等方面。
本文将介绍几种常用的点到面距离计算方法。
一、点到平面的距离公式点到平面的距离公式是最基本的点到面距离计算方法。
假设点P(x,y,z)到平面Ax+By+Cz+D=0的距离为d,则有:d = |Ax + By + Cz + D| / sqrt(A^2 + B^2 + C^2)其中,|.|表示绝对值,sqrt(.)表示开方运算。
这个公式的推导可以通过向量的方法得到,具体可以参考相关的线性代数教材。
二、点到三角形的距离计算点到三角形的距离计算是点到面距离计算的一个特例,因为三角形是一个平面图形。
假设点P(x,y,z)到三角形ABC的距离为d,则有:d = |(P-A)·n| / |n|其中,·表示向量的点积运算,n为三角形ABC的法向量,|.|表示向量的模长。
这个公式的推导也可以通过向量的方法得到。
三、点到网格模型的距离计算在实际应用中,我们通常需要计算点到网格模型的距离,而不是单个平面或三角形的距离。
这个问题可以通过以下步骤解决:1. 遍历网格模型的所有三角形,计算每个三角形到点的距离。
2. 找到距离最小的三角形,将其距离作为点到网格模型的距离。
这个方法的实现比较简单,但是需要遍历整个网格模型,计算量较大。
四、点到包围盒的距离计算包围盒是一个能够完全包含三维模型的最小立方体或最小球体。
点到包围盒的距离计算可以通过以下步骤解决:1. 判断点是否在包围盒内部,如果是,则距离为0。
2. 如果点在包围盒外部,计算点到包围盒各个面的距离。
3. 找到距离最小的面,将其距离作为点到包围盒的距离。
这个方法的实现比较简单,但是需要先计算包围盒,然后再计算点到包围盒的距离。
总结点到面的距离计算是计算机图形学中的一个重要问题,涉及到三维空间中点和平面之间的距离计算。
点到平面的距离的几种求法

点到平面的距离的几种求法求点到平面的距离是立体几何教学中不可忽视的一个基本问题,是近几年高考的一个热点.本文试通过对一道典型例题的多种解法的探讨,结合《立体几何》(必修本)中的概念、习题,概括岀求点到平面的距离的几种基本方法.例已知ABCD是边长为4的正方形,E、F分别是AE、AD的中点,GC垂直于ABCD所在平面,且GC=2,求点B到平面EFG的距离.一、直接通过该点求点到平面的距离1 •直接作岀所求之距离,求其长.解法1.如图1,为了作出点B到平面EFG的距离,延长FE交CB的延长线于M, 连结GM,作BN丄BC,交GM于N,则有BN//CG,BN丄平面ABCD .作BPXEM,交EM于P,易证平面BPN丄平面EFG .作BQXPN,垂足为Q,则BQ丄平面EFG .于是BQ是点B到平面EFGr- 4BP2 BN2 =—的距离•易知BN=2 / 3,BP=.l,PN= 二,由BQ・PN=PB・BN,得BQ= ….图1 图22 •不直接作岀所求之距离,间接求之.(1)利用二面角的平面角.课本P. 42第4题,P. 46第2题、第4题给岀了“二面角一个面内的一个点,它到棱的距离、到另一个面的距离与二面角的大小之间所满足的关系”.如图2,二面角M - CD - N的大小为a,A€M,AB丄CD,AB=a,点A到平面N的距离AO=d, 则有d=asin a. ①①中的a也就是二面角的大小,而并不强求要作出经过AB的二面角的平面角.解法2.如图3,过B作BP丄EF,交FE的延长线于P,易知BP= 亞,这就是点B到二面角C - EF-G的棱EF的距离.连结AC交EF于H,连结GH,易证ZGHC就是二面角C -EF - G的平面角.T GC=2,A求点到平面的距离是立体几何教学中不可忽视的一个基本问题,是近几年高考的一个热点.本文试通过对一道典型例题的多种解法的探讨,结合《立体几何》(必修本)中的概念、习题,概括岀求点到平面的距离的几种基本方法.例已知ABCD是边长为4的正方形,E、F分别是AB、AD的中点,GC垂直于ABCD所在平面,且GC=2,求点B到平面EFG的距离.一、直接通过该点求点到平面的距离1 •直接作岀所求之距离,求其长.解法1.如图1,为了作出点B到平面EFG的距离,延长FE交CB的延长线于M, 连结GM,作BN丄BC,交GM于N,则有BN//CG,BN丄平面ABCD .作BP丄EM,交EM于P,易证平是EQ 是点E 到平面EFGPNDO①中的 这就是点E 到二面角C解法 角AH GHD F A)利用二面角的平面角图2图1面EPN 丄平面EFG .作EQ 丄PN ,垂足为Q,则EQ 丄平面EFG 易得平面EER 丄平面EFG,ER 为它们的交线,所以ZREB 就是EE 与平面EFG 所成的角04a 也就是二面角的大小,而并不强求要作出经过AB 的二面角的平面角 2 •不直接作岀所求之距离,间接求之9 .②9 •由CH=3 a 上的射影B,连结OB 得 9 .解法3.如图5,设M 为FE 与CB 的延长线的交点,作BR±GM,R 为垂足.又GMXEBEF - G 的平面2.如图 3,过B 作BP 丄EF ,交FE 的延长线于P,易知BPGC=2, AC=4 课本P.42第4题,P.46第2题、第 另一个面的距离与二面角的大小之间所满足的关系OP 与a 所成的角为9 ,A 到平面a EF -G 的棱EF 的距离.连结AC 交EF 于H,连结GH,易证ZGHC 就是二面角C(2)利用斜线和平面所成的角.如图4, OP 为平面 a 的一条斜线,A€OP,OA4题给岀了 二面角一个面内的一个点,它到棱的距离、到 ”.如图2,二面角M - CD -N 的大小为 a, AEM, ABAB = a ,点A 到平面N 的距离AO于是由①得所求之距离d = BP-sinZGHC则有d = asin a. ①经过OP 与a 垂直的平面与a 相交,交线与OP 所成的锐角就是②中的9,这里并不强求要作出点A 在22二 ,由BQ ・PN=PB ・BN的距离•易知BN=2 /3,BP 得 BQ=[J .的距离为d,则由斜线和平面所成的角的定义可知,有d=lsin2 加L : = u •解略△ MRB^^MCG ,可得BR= j ;,在Rt^REB 中,/E=90所以sin 0 =BR / ER=,于是由②得所求之距离d=i. I(3)利用三棱锥的体积公式.解法4.如图6,设点B 到平面EFG 的距离为d,则三棱锥B - EFG 的体积V= ( 1 / 3 ) S AE FG •d.另一方面又可得这个三棱锥的体积V= ( 1 / 3 ) S AFEB •CG,可求得S △ FEB = ( 1 / 4 ) S ADAB =2,2你S AEFG = J - i ,所以有1 / 3 •二-1 ・d=1 / 3・2・2,得d= IJ .二、不经过该点间接确定点到平面的距离1•利用直线到平面的距离确定解法5.如图7,易证BD//平面EFG ,所以BD 上任意一点到平面EFG 的距离就是点B 到平面EFG 的距离.由对称思想可知,取BD 中点0,求点0到平面EFG 的距离较简单.AC 交EF 于H,如图8,把平面EFG 补成一个正四棱柱的截面所在的平面,可使题设中的点、线、面之间的位置关系更加明朗.面GMT 是正四棱柱ABCD - A 1 B 1GD 1经过F 、E 、G 的截面所在的平面.MG 交BB1于N,TG 交DD 1于Q,作BP//MG ,交CG 于P,连结DP,则有平面GTM/平面PDB .它们之间 的距离就是所求之距离•于是可以把点B 平移到平面PDB 上任何一个位置,哪里方便就在哪里求.这两个平行平面的距离d 又同三棱柱GQN -PDB 的体积有关,所以也可以利用三棱柱的体积确定所求之距离•据此可得解法6.解法6.三棱柱GQN - PDB 的体积V=SA PDB d ,另一方面又有V=S A CDB BN ,可求得BN=2图5BR =_2_-1 ,EB = 2,2•利用平行平面间的距离确定4価迺/3,CP = 4 /3,PB = PD= 二,ED=仏匕,S = :: , S △c DB 27H=8・2 3,得d= 一一为所求之距离.8#i8,所以:;・d。
求点到平面的距离的方法

求点到平面的距离的方法
在学习几何学时,有些对于求点到平面的距离的问题会困惑很多学生。
其实,从数学的角度来看,求点到平面的距离是一个广泛而普遍的问题,而且其解决方案也有很多。
下面,我将介绍求点到平面的距离的几种方法。
第一种方法是直线和平面交点法。
首先,我们需要找到平面上与某一点最近的直线。
然后求出该直线和平面的交点,直线和点所组成的三角形的高即是点到平面的距离。
第二种方法是利用向量来求解。
根据几何学习的知识,我们知道,点到平面的距离是点到平面的垂线的长度。
从而可以通过向量的计算求出垂线的长度,从而求出点到平面的距离。
第三种方法称为“分段法”。
首先,我们需要将平面上的点进行分隔,每个分隔的点都可以用一条直线来描述,从而可以计算出每个点到每条直线的距离。
之后,该点到整个平面的距离就可以得到,因为点到平面的距离就等于点到每条直线的最短距离。
最后,我再介绍一种求点到平面的距离的方法,称为“三维空间中的点分层法”。
首先,将该点投影到三维空间中,然后求出点到每个层的距离,最后加总求出该点到整个空间的距离。
以上就是求点到平面的几种方法。
这些方法在现实生活中都有着广泛的应用,比如在测量物体时会使用。
同时,在解决一些几何学问题时,也会需要用到这些算法。
总之,求点到平面的距离的方法不仅有助于我们更好地理解它,也很实用,有助于我们更好地应用。
点到平面距离计算的五种方法

点到平面距离计算的五种方法一、五种方法1.定义法对于求点到面的距离问题,首先是根据点到面的距离的定义来求,过该点直接作平面的垂线,再在构造的直角三角形中,求出这条垂线段的长度.2.平移转化点到面的距离不好求时,可以通过求过该点且平行于平面的直线上另外一点(这个点到平面的距离比较好求)到该平面的距离,来解决问题.3.垂面法在用定义法求点到面的距离,垂足往往比较特殊,很难直接找到,此时就需要借助面面垂直的性质来完成,如图,过A 向平面β作垂线,可以先找到一个过点A 且垂直于面β的平面α,于是只需过A 向交线做垂线,垂足为B ,则AB 即为点A 到面β的距离,这种做点到面距离的方法具有很强的操作性,经常使用.4.等体积法利用体积公式求出距离.5.向量法如图,已知平面α的法向量为→n ,α⊥PQ ,垂足为Q ,A 为平面α内任一点,则平面外一点P 到平面α的距离为:||||||→→→→⋅=n n AP PQ,二、例题分析例1.在四棱锥P ABCD -中,PA ⊥平面ABCD ,2AP =,点M 是矩形ABCD 内(含边界)的动点,且1AB =,3AD =,直线PM 与平面ABCD 所成的角为π4.当三棱锥P ABM -的体积最小时,三棱锥P ABM -的外接球的表面积为().A.4πB.6πC.8πD.10π解析:如图,因为PA ⊥平面ABCD ,垂足为A ,则PMA ∠为直线PM 与平面ABCD 所成的角,所以π4PMA ∠=,因为2AP =,所以2AM =,所以点M 位于底面矩形ABCD 内的以点A 为圆心,2为半径的圆上,注意1AB =,3AD =,记点M 的轨迹为圆弧EF ,当点M 位于F 时,三棱锥P ABM -的体积最小,由AF、BF 在面ABCD 内,则π2PAF PBF ∠=∠=,三棱锥P ABM -的外接球球心为PF 的中点.因为222222PF =+=,所以三棱锥P ABM -的外接球的表面积()24π28πS ==.故选:C例2.如图.在直三棱柱111ABC A B C -中,12AB AA BC ===,平面1A BC ⊥平面11ABB A .(1)求点A 到平面1A BC 的距离;(2)设D 为1AC 的中点,求平面ABD 与平面CBD 夹角的正弦值.解析(1)方法1:垂面法:由于平面1A BC ⊥平面11ABB A ,而B A 1为交线,故过A 向B A 1作垂线,垂足为E ,显然2=AE 方法2:等体积法:在直三棱柱111ABC A B C -中,12AB AA BC ===,设点A 到平面1A BC 的距离为h ,取1A B 的中点E ,连接AE,则1AE A B ⊥,因为平面1A BC ⊥平面11ABB A ,平面1A BC ⋂平面111ABB A A B =,则有⊥AE平面1A BC ,又BC ⊂平面1A BC ,即有AE BC ⊥,因为1AA ⊥平面,ABC BC ⊂平面ABC ,则1AA BC ⊥,因为11,,AA AE A AA AE =⊂ 平面11ABB A ,于是BC ⊥平面11ABB A ,又AB ⊂平面11ABB A ,因此BC AB ⊥,1111142223323A ABC ABC V S AA -=⋅=⨯⨯⨯⨯=,111112332A A BC A BC V S h h -=⋅=⨯⨯⨯,又11A ABC A A BC V V --=,解得h ,所以点A 到平面1A BC例3.如图,四棱锥P ABCD -的底面是矩形,PD⊥底面ABCD,2PD DC ==,AD =为BC 的中点.(1)求D 到平面APM 的距离;(2)求平面ABCD 与平面APM 所成角的余弦值.解析:(1)因为四棱锥P ABCD -的底面是矩形,PD⊥底面ABCD,所以可以建立以D 为坐标原点,DA 方向为x 轴,DC 方向为y 轴,DP 方向为z 轴,如图所示的空间直角坐标系,又2PD DC ==,AD =M 为BC 的中点,所以(0,0,0)D,A,2,0)M ,(0,0,2)P ,所以2)PA =-,2,2)PM =-,DA = 设平面PAM 的法向量为(,,)n x y z = ,所以()()()),,220,,2,2220n PA x y z z n PM x y z y z ⎧⋅=⋅-=-=⎪⎨⋅=⋅-=+-=⎪⎩ ,取1x =,解得z =,2y =,所以2n = ,所以D 到平面APM 的距离为DA n n ⋅ (2)所以平面ABD与平面CBD .例4.如图,长方体111l ABCD A B C D -的底面ABCD 是边长为2的正方形,4l AA =,点E 为棱l AA 的中点.(1)求证:BE ⊥平面11EB C ;(2)求点A 到平面1CEB 的距离.解析:(2)方法一:取1CB 的中点,F BC 的中点P ,连接1,,,,EF AP PF PB PE ,可得//AE PF ,且AE PF =,则四边形APFE 为平行四边形,可得//AP EF ,又因为AP 平面1,CEB EF ⊂平面1CEB ,所以//AP 平面1CEB ,所以点A 到平面1CEB 的距离等于点P 到平面1CEB 的距离,易知11P CEB E PCB V V --=,在1CEB ∆中,2222222112223,222,4225CE EB CB =++==+=+,所以22211CE EB CB +=,从而1CEB ∆为直角三角形.设点P 到平面1CEB 的距离为dP ,所以111133CEB P PCB S d S AB ∆∆⨯⨯=⨯⨯,即1111321423232P d ⨯⨯=⨯⨯⨯,解得63P d =,所以点A 到平面1CEB 的距离为63;方法二:等体积法设点P 到平面1CEB 的距离为h ,因为112,5,3B E B C CE ===,所以三角形1CEB 是直角三角形,1126,2CEB AEB S S ∆∆==,而11A CEB C AEB V V --=,可得11262233h ⨯=⨯⨯,解得63h =,所以点A 到平面1CEB 的距离为63.例5.如图,在三棱柱111ABC A B C -中,1A C ⊥底面ABC ,190,2ACB AA ∠=︒=,1A 到平面11BCC B 的距离为1.(1)证明:1A C AC =;(2)已知1AA 与1BB 的距离为2,求1AB 与平面11BCC B 所成角的正弦值.【解析】(1)证明:∵1A C ⊥面,ABC BC ⊂面ABC ∴1A C BC ⊥,∵90ACB ∠=︒,即BC AC ⊥,且1,A C AC ⊂面111,ACC A A C AC C ⋂=,∴BC ⊥面11ACC A ,∵BC ⊂面11BCC B ∴面11ACC A ⊥面11BCC B ,过1A 作11A O CC ⊥交1CC 于点O ,且面11ACC A ⋂面111BCC B CC =,∴1A O ⊥面11BCC B ,∵1A 到面11BCC B 的距离为11,1A O ∴=,在Rt 11A CC ∆中,111111,2,A C A C CC AA A C AC ⊥===,设CO x =,则2212,11(2)4C O x x x =-+++-=,解得:1x =,∴1112AC A C A C ===,∴1A C AC =.(2)11113cos cos ,13||n AB n AB n AB θ⋅∴===。
例谈点面距离的求法

龙源期刊网
例谈点面距离的求法
作者:张彩霞
来源:《数学教学通讯(教师阅读)》2008年第08期
求点到平面的距离是高考中的一类常考题型,也是立体几何学习中的一个难点内容之一.现举例说明求点面距离的一些常用方法:
1 定义法
由定义点到平面的距离是指点到平面的垂线段的长,因此找或作平面的垂线就成了关键. 1.1 记住特殊图形里特殊点的射影位置找平面的垂线
四面体P-ABC中,若PA=PB=PC,则点P在△ABC内的射影为△ABC的外心;若侧棱与底面所成的角相等,则点P在△ABC内的射影为△ABC的外心;若P到△ABC的三边的距离相等,则点P在△ABC内的射影为△ABC的内心或旁心;若每个侧面与底面所成的二面角相等,则点P在△ABC内的射影为△ABC的内心;若对棱相互垂直,则点P在△ABC内的射影为△ABC的垂心;若三条侧棱两两互相垂直,则点P在△ABC内的射影为△ABC的垂心;由正三棱锥的定义知:正三棱锥的顶点在底面内的射影是底面的中心等等,利用这些结论,准确地定位垂足,从而找到平面的垂线.
注:用向量法求点到平面α的距离是过平面α内的任一点与该点所构造的向量在法向量n 方向上投影的绝对值,而非过该点的任一向量在法向量n方向上投影的绝对值.
“本文中所涉及到的图表、注解、公式等内容请以PDF格式阅读原文”。
利用向量法求点到平面的距离讲解学习

利用平面的法向量求点到平面的距离甘肃省 彭长军如图1,设n 是平面α的一个法向量,P 是α外一点,Q 是α内任意一点,则向量PQ u u u r 在法向量n 方向上的射影长d=PQ u u u r cos PQ,n <>uuu r u r =PQ n nu u u r r g r 就是点P 到平面α的距离.下面举几例予以说明.例1.已知A(2,3,1)、B(4,1,2)、C(6,3,7)、D(-5,-4,8)是空间不共面的四点,求点D 到平面ABC 的距离.解:设),,(z y x n =是平面ABC 的一个法向量,则由0n AB =g 及10n BC =g ,得2x 2y z 02x 2y 5z 0--+=⎧⎨++=⎩⇒2y x 32z x 3⎧=⎪⎪⎨⎪=-⎪⎩,取x=3,得)2,2,3(-=n ,于是点D 到平面ABC 的距离为d=DA n n u u u r r g r = 1749=171749. 例2.已知四边形ABCD 是边长为4的正方形,E 、F 分别是AB 和AD 的中点,GC ⊥平面ABCD ,且GC=2,求点B 到平面EFG 的距离.解:建立如图2所示的空间直角坐标系C-xyz ,则G(0,0,2),E(2,4,0),B(0,4,0), F(4, 2,0),∴GE =(2,4,-2),GF =(4,2,-2),BE =(2,0,0).设平面EFG 的一个法向量为),,(z y x n =,则由0n GE =g 及0n GF =g ,得2x+4y 2z 04x 2y 2z 0-=⎧⎨+-=⎩⇒ x=y z 3y⎧⎨=⎩,取y=1,得(1,1,3)n =,于是点B 到平面EFG 的距离为d=BE n n u u u r r g r =11112112=. 例3.在棱长为1的正方体ABCD-A 1B 1C 1D 1中,求点C 1到平面A 1BD 的距离。
解:建立如图3所示的空间直角坐标系D-xyz ,则A 1(1,0,1),B(1,1,0),C 1 (0, 1,1).设平面A 1BD 的一个法向量为),,(z y x n =,则由1DA 0n =g 及DB 0n =g ,得x z 0x y 0+=⎧⎨+=⎩⇒ z=-x y=-x ⎧⎨⎩,取x=-1,得n =(-1,1, 1),于是点C 1到平面A 1BD 的距离为d=1C D n n u u u u r r g r 3233. 例4.(06年福建高考题)如图4,四面体ABCD 中,O 、E 分别是BD 、BC 的中点,CA=CB=CD=BD=2,2,求点E 到平面ACD 的距离.解:由题设易知AO ⊥BD ,OC ⊥BD ,∴OA=1,3OA 2+OC 2=AC 2,∴∠AOC=90︒,即OA ⊥OC.以O 为原点,OB 、OC 、OA 所在直线为x 、y 、z 轴,建立空间直角坐标系O-xyz ,则A(0,0,1),B(1,0,0),C(0, 3,∴ E(12,32,0), AD =(-1,0,-1), AC =(0, 3ED =(-32,-32,0). 设平面ACD 的一个法向量为),,(z y x n =,则由AD 0n =g 及AC 0n =g ,得x z 03y z 0+=⎧⎪-=⇒ x=-z 3⎧⎪⎨⎪⎩,取3得n 33于是点E 到平面ACD 的距离为d=D E n nu u u r r g r 37=217.。
点到平面的距离的几种求法

点到平面的距离的几种求法大关一中 胡兴兆点到平面的距离是高中立体几何的一项基本要求,点到平面的距离涉及先面平行、线面垂直、面面垂直等关系,也是高考经常遇见的一个知识点。
下面就用几个列子说明点到平面的距离的几种求法。
一、直接法1、 直接过点作平面的垂线。
例1 已知:直线l 与平面α交于点O,点A 在直线l 上, OA=2cm.l 与α所成的角为300,求点A 到平面α的距离。
解:过点A 作AB ⊥α,垂足为B ,则∠AOB=300,在直角三角形ABO 中,AB=OA ⨯sin ∠AOB =3⨯sin300=3⨯21=23∴点A 到平面α的距离为23cm 。
2、直接过点作平面内某一直线的垂线。
例2 三棱柱ABC-A 1B 1C 1中,底面是边长为1的 正三角形,侧棱与底面垂直,M 是BC 的中点, 且MC 1=MA ,求点B 到平面AMC 1的距离. 解:过B 作BF ⊥C 1M 交C 1M 的延长线于F,M 是等边三角形ABC 中BC 边上的中点,∴ AM ⊥BCC 1C ⊥平面ABC, AM ⊂平面ABC∴ AM ⊥C 1CC 1M BC=C∴ AM ⊥平面BCC 1BF ⊂平面BCC 1∴BF ⊥A又 BF ⊥C 1F,C 1F AM=M∴BF ⊥平面AMC 1∴BF 的长就是点B 到平面AMC 1的距离,M FBAB 1C 1A 1ClA BO易知:AM=MC 1=23,MC=MB=21,CC 1=22在∆BFM 和∆C 1CM 中,∠BFM=∠C 1CM=900∠BMF=∠C 1CM,∴ ∆BFM ∽∆C 1CM, ∴BF cc 1=BMMC 1, ∴ BF=11MC CC ⨯BM=232122⨯=66, ∴点B 到平面AMC 1的距离是66。
二、等体积法例 已知三棱柱A 1B 1C 1-ABC 中,侧棱垂直于底面,且C 1C=AC=BC=2,求点C 到平面C 1AB 的距离。
分析:点C 到平面C 1AB 的距离就是三棱锥C-C 1AB 的高。
求点到平面距离的基本方法

求点到平面距离的基本方法北京农大附中 闫小川求点到平面的距离是立体几何中的一个基本问题,是高考的一个热点,也是同学学习中的一个难点.本文通过对一道典型例题的多种解法的探讨,概括出求点到平面的距离的几种基本方法.例 (2005年福建高考题)如图1,直二面角E AB D --中,四边形ABCD 是边长为2的正方形,EB AE =,F 为CE 上的点,且⊥BF 平面ACE .(Ⅰ)求证:⊥AE 平面BCE ; (Ⅱ)求二面角E AC B --的大小; (Ⅲ)求点D 到平面ACE 的距离.FEDCBA图1(Ⅰ)、(Ⅱ)解略,(Ⅲ)解如下: 一、直接法利用两个平面垂直,直接作出点到平面的距离. 如图2,β∈A ,αβ⊥,l =βα , l AM ⊥,则α⊥AM .AM 为点A 到平面α的距离.图2解:如图3,过点A 作AG EC ,连结CG DG ,,则平面ADG ∥平面BCE ,∵平面BCE ⊥平面ACE , ∴平面ADG ⊥平面ACE ,作,AG DH ⊥垂足为H ,则DH ⊥平面ACE . ∴DH 是点D 到平面ACE 的距离. 在ADG Rt ∆中,.332622=⋅=⋅=AG DG AD DH ABCDEFGH图3二、平行线法如图4,l A ∈,l ∥α,B 为l 上任意一点, α⊥AM ,α⊥BN ,则BN AM =.点A 到平面α的距离转化为平行于平面α的直线l 到平面α的距离,再转化为直线l 上任意一点B 到平面α的距离.图4解:如图5,过点D 作DMAE ,连结CM ,则DM ∥平面ACE ,点D 到平面ACE 的距离转化为直线DM 到平面ACE 的距离,再转化为点M 到平面ACE 的距离.作,CE MN ⊥垂足为N ,∵平面CEM ⊥平面ACE , ∴⊥MN 平面ACE ,∴MN 是点M 到平面ACE 的距离. 在CEM Rt ∆中,.332622=⋅=⋅=CE CM EM MN N MAB CDEF图5三、斜线法利用平面的斜线及三角形相似,转化为求斜线上的点到平面的距离. 如图6、7, O l =α ,l B A ∈,, α⊥AM ,α⊥BN ,若t BOAO=,则BN t AM ⋅=.点A 到平面α的距离转化为求直线l 上的点B 到平面α的距离.图6 图7解:如图8,BD 与AC 的交点为Q ,即 BD 平面Q ACE =, ∵BQ DQ =,∴点D 到平面ACE 的距离与点B 到平面ACE 的距离相等. ∵平面BCE ⊥平面ACE ,⊥BF 平面ACE , ∴BF 是点B 到平面ACE 的距离.在BCE Rt ∆中,.332622=⋅=⋅=CE BE BC BF Q AB CDEF图8四、线面角法如图9,OP 为平面α的一条斜线,OP A ∈,l OA =,OP 与α所成的角为θ,A 到平面α的距离为d ,则由斜线和平面所成的角的定义可知,有θsin l d =.经过OP 与α垂直的平面与α相交,交线与OP 所成的锐角就是OP 与α所成的角θ,这里并不强求要作出A 在α上的射影B ,连结OB 得θ.图9解:如图10,∵⊥BF 平面ACE , ∴平面BDF ⊥平面ACE ,BQF ∠为DQ 与平面ACE 所成的角为θ,则点D 到平面ACE 的距离θsin DQ d =.由(Ⅱ)知二面角E AC B --的正弦值为36,得36sin =θ. ∴D 到平面ACE 的距离332362=⨯=d .Q FEDCBA图10五、二面角法如图11,l =βα ,α、β所成二面角的大小为θ,β∈A ,l AB ⊥,a AB =,点A 到平面α的距离d AO =,则有θsin a d =.θ也就是二面角的大小,而不强求作出经过AB 的二面角的平面角.图11解:如图12,∵平面ACD 平面ACE AC =,⊂DQ 平面ACD ,AC DQ ⊥,设二面角E AC D --的大小为θ,则点D 到平面ACE 的距离θsin DQ d =.由(Ⅱ)知二面角E AC B --的正弦值为36,得36sin =θ. ∴D 到平面ACE 的距离332362=⨯=d .A BCDE F Q图12六、体积法解:如图13,过点E 作AB EO ⊥交AB 于点O ,1=OE . ∵二面角E AB D --为直二面角, ∴EO ⊥平面ABCD .设D 到平面ACE 的距离为h ,,ACD E ACE D V V --= ∴.3131EO S h S ACD ACE ⋅=⋅∆∆ ⊥AE 平面BCE ,∴EC AE ⊥.∴.3326221122212121=⨯⨯⨯⨯⨯=⋅⋅⋅=EC AE EODC AD h∴点D 到平面ACE 的距离为.332 OF EDCBA图13七、向量法解:如图14,以线段AB 的中点为原点O ,OE 所在直线为x 轴,AB 所在直线为y 轴,过O 点平行于AD 的直线为z 轴,建立空间直角坐标系xyz O -,⊥AE 平面BCE ,⊂BE 平面BCE ,∴BE AE ⊥,在AB O AB AEB Rt 为中,2,=∆的中点, ∴1=OE ,∴).2,1,0(),0,0,1(),0,1,0(C E A -).2,2,0(),0,1,1(==AC AE设平面ACE 的一个法向量为),,(z y x n =,则⎩⎨⎧=+=+⎪⎩⎪⎨⎧=⋅=⋅.022,0,0,0z y y x n AC n AE 即 解得⎩⎨⎧=-=.,x z x y令,1=x 得)1,1,1(-=n 是平面ACE 的一个法向量. ∵AD//z 轴,2=AD ,∴)2,0,0(=AD , ∴点D 到平面ACE 的距离33232|||,cos |||===><⋅=n n AD AD d. DA图14。
利用向量法求点到平面的距离知识讲解

利用向量法求点到平面的距离利用平面的法向量求点到平面的距离 甘肃省 彭长军 如图1,设n 是平面α的一个法向量,P 是α外一点,Q 是α内任意一点,则向量PQ u u u r 在法向量n 方向上的射影长d=PQ u u u r cos PQ,n <>uuu r u r =PQ n nu u u r r g r 就是点P 到平面α的距离.下面举几例予以说明.例1.已知A(2,3,1)、B(4,1,2)、C(6,3,7)、D(-5,-4,8)是空间不共面的四点,求点D 到平面ABC 的距离.解:设),,(z y x n =是平面ABC 的一个法向量,则由0n AB =g 及10n BC =g ,得2x 2y z 02x 2y 5z 0--+=⎧⎨++=⎩⇒2y x 32z x 3⎧=⎪⎪⎨⎪=-⎪⎩,取x=3,得)2,2,3(-=n ,于是点D 到平面ABC 的距离为d=DA n nu u u r r g r = 1749=171749. 例2.已知四边形ABCD 是边长为4的正方形,E 、F 分别是AB 和AD 的中点,GC ⊥平面ABCD ,且GC=2,求点B 到平面EFG 的距离.解:建立如图2所示的空间直角坐标系C-xyz ,则G(0,0,2),E(2,4,0),B(0,4,0), F(4, 2,0),∴GE =(2,4,-2),GF =(4,2,-2),BE =(2,0,0).设平面EFG 的一个法向量为),,(z y x n =,则由0n GE =g 及0n GF =g ,得2x+4y 2z 04x 2y 2z 0-=⎧⎨+-=⎩⇒ x=y z 3y ⎧⎨=⎩,取y=1,得(1,1,3)n =,于是点B 到平面EFG 的距离为d=BE n n u u u r r g r =11112112=. 例3.在棱长为1的正方体ABCD-A 1B 1C 1D 1中,求点C 1到平面A 1BD 的距离。
向量法求空间点到平面的距离讲解学习

分别是 求点 B
AB、AD 的中点,GC⊥平面 到平面 EFG 的距离.
ABCD,且
GC=2z,
G
解:如图,建立空间直角坐标系 C-xyz.
由题设 C(0,0,0),A(4,4,0),B(0,4,0),
D(4,0,0),E(2,4,0),
F(4,2,0),G(0,0,2).
xD
C
EF (2, 2, 0), EG (2, 4, 2), F
新课导入: 我们在路上行走时遇到障碍一般会绕过它,在生活中我们知道(zhī dào)转弯,那么在学 习上也一样,要想求空间一点到平面距离,就必须找到或间接找到它,而这样做恰恰 是一个比较困难的问题,今天我们就让思维转个弯,用向量法解决这个难题。
一、复习引入: 1、空间中如何求点到面距离? 方法1、直接做或找距离; 方法2、等体积法; 方法3、空间向量。
13
第十一页,共12页。
小结:向量法求点到平面的距离 要求一个点到平面的距离,可以分为以下三个步骤: (1)找出从该点出发的平面的任一条斜线段对应的向量; (2)求出该平面的一个法向量; (3)求出法向量与斜线段对应的向量的数量积的绝对值 再除以法向量的模,即可求出点到平面距离。
第十二页,共12页。
2、向量数量积公式
a • b a b cos (为a与b的夹角)
第二页,共12页。
二、新课
向量法求点到平面的距离
B
n
A
O
1、剖析:如图,BO 平面,垂足为O,则点B到平面的距离就是
线段BO的长度。
第三页,共12页。
2、若AB是平面的任一条斜线段,则在RtBOA中,BO BA • cos ABO
BA BA • BO BA • BO ,如果令平面的法向量为n,考虑到法向
求点到平面距离的基本方法
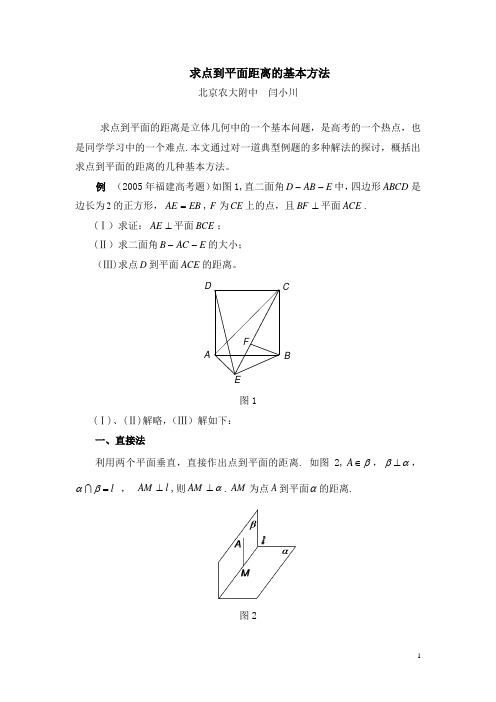
求点到平面距离的基本方法北京农大附中 闫小川求点到平面的距离是立体几何中的一个基本问题,是高考的一个热点,也是同学学习中的一个难点.本文通过对一道典型例题的多种解法的探讨,概括出求点到平面的距离的几种基本方法。
例 (2005年福建高考题)如图1,直二面角E AB D --中,四边形ABCD 是边长为2的正方形,EB AE =,F 为CE 上的点,且⊥BF 平面ACE .(Ⅰ)求证:⊥AE 平面BCE ; (Ⅱ)求二面角E AC B --的大小; (Ⅲ)求点D 到平面ACE 的距离。
FEDCBA图1(Ⅰ)、(Ⅱ)解略,(Ⅲ)解如下: 一、直接法利用两个平面垂直,直接作出点到平面的距离. 如图2,β∈A ,αβ⊥,l =βα , l AM ⊥,则α⊥AM .AM 为点A 到平面α的距离.图2解:如图3,过点A 作AG EC ,连结CG DG ,,则平面ADG ∥平面BCE ,∵平面BCE ⊥平面ACE , ∴平面ADG ⊥平面ACE ,作,AG DH ⊥垂足为H ,则DH ⊥平面ACE 。
∴DH 是点D 到平面ACE 的距离. 在ADG Rt ∆中,.332622=⋅=⋅=AG DG AD DH ABCDEFGH图3二、平行线法如图4,l A ∈,l ∥α,B 为l 上任意一点, α⊥AM ,α⊥BN ,则BN AM =。
点A 到平面α的距离转化为平行于平面α的直线l 到平面α的距离,再转化为直线l 上任意一点B 到平面α的距离。
图4解:如图5,过点D 作DMAE ,连结CM ,则DM ∥平面ACE ,点D 到平面ACE 的距离转化为直线DM 到平面ACE 的距离,再转化为点M 到平面ACE 的距离。
作,CE MN ⊥垂足为N ,∵平面CEM ⊥平面ACE , ∴⊥MN 平面ACE ,∴MN 是点M 到平面ACE 的距离. 在CEM Rt ∆中,.332622=⋅=⋅=CE CM EM MN N MAB CDEF图5三、斜线法利用平面的斜线及三角形相似,转化为求斜线上的点到平面的距离. 如图6、7, O l =α ,l B A ∈,, α⊥AM ,α⊥BN ,若t BOAO=,则BN t AM ⋅=.点A 到平面α的距离转化为求直线l 上的点B 到平面α的距离。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
点到平面距离的若干典型求法点到平面距离的若干典型求法目录1.引言 (1)2.预备知识 (1)3.求点到平面距离的若干求法 (3)3.1定义法求点到平面距离 (3)3.2转化法求点到平面距离 (5)3.3等体积法求点到平面距离 (7)3.4利用二面角求点到平面距离 (8)3.5向量法求点到平面距离 (9)3.6最值法求点到平面距离 (11)3.7公式法求点到平面距离 (13)1.引言求点到平面的距离是高考立体几何部分必考的热点题型之一,也是学生较难准确把握难点问题之一。
点到平面的距离的求解方法是多种多样的,本讲将着重介绍了几何方法(如体积法,二面角法)、代数方法(如向量法、公式法)及常用数学思维方法(如转化法、最值法)等角度等七种较为典型的求解方法,以达到秒杀得分之功效。
2.预备知识(1)正射影的定义:(如图1所示)从平面外一点P向平面α引垂线,垂足为P',则点P'叫做点P在平面α上的正射影,简称为射影。
同时把线段PP'叫作点P与平面α的垂线段。
图1(2)点到平面距离定义:一点到它在一个平面上的正射影的距离叫作这点到这个平面的距离,也即点与平面间垂线段的长度。
(3) 四面体的体积公式13V Sh = 其中V 表示四面体体积,S 、h 分别表示四面体的一个底面的面积及该底面所对应的高。
(4)直线与平面垂直的判定定理:一条直线与一个平面内的两条相交直线垂直,则该直线与此平面垂直。
(5)三垂线定理:在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它和这条斜线也垂直。
(6)二面角及二面角大小:平面内的一条直线l 把平面分为两部分,其中的每一部分都叫做半平面,从一条直线出发的两个半平面所组成的图形,叫做二面角,这条直线叫做二面角的棱,每个半平面叫做二面角的面。
图2所示为平面α与平面β所成的二面角,记作二面角l αβ--,其中l 为二面角的棱。
如图在棱l 上任取一点O ,过点O 分别在平面α及平面β上作l 的垂线OA 、OB ,则把平面角AOB ∠叫作二面角l αβ--的平面角,AOB ∠的大小称为二面角l αβ--的大小。
在很多时候为了简便叙述,也把AOB ∠称作α与平面β所成的二面角。
图2(7)空间向量内积:代数定义: 设两个向量111(,,)a x y z =,222(,,)b x y z =,则将两个向量对应分量的乘积之和定义为向量a 与b 的内积,记作a b ,依定义有a b =121212x x y y z z ++ 几何定义: 在欧几里得空间中,将向量a 与b 的内积直观地定义为||||cos ,a b a b a b =<>,这里||a 、||b 分别表示向量a 、b 的长度,,a b <>表示两个向量之间的夹角。
向量内积的几何意义为一个向量的模与另一个向量在这个向量正方向上投影向量模的乘积。
当0,90a b <>=,即a b ⊥时,0||||cos ,||||cos900a b a b a b a b =<>==。
下面说明这两种定义是等价的。
如图3所示,设O 、P 、Q 为空间的三点,令a OP =,b OQ =,c PQ =图3由余弦定理 222||||||2||||cos ,c a b a b a b =+-<>再设111(,,)a x y z =,222(,,)b x y z =,则212121(,,)c x x y y z z =---从而有222212121()()()x x y y z z -+-+-=2222221112222||||cos ,x y z x y z a b a b +++++-<>即121212||||cos ,x x y y z z a b a b ++=<>这就证得了两个定义是等价的。
3求点到平面距离的若干求法3.1 定义法求点到平面距离(直接法)定义法求点到平面距离是根据点到平面的定义直接作出或者寻找出点与平面间的垂线段,进而根据平面几何的知识计算垂线段长度而求得点与平面距离的一种常用方法。
定义法求点到平面距离的关键在于找出或作出垂线段,而垂线段是由所给点及其在平面射影间线段,应而这种方法往往在很多时候需要找出或作出点在平面的射影。
以下几条结论常常作为寻找射影点的依据:(1)两平面垂直的性质定理:如果两个平面互相垂直,那么在一个平面内垂直于他们交线的直线垂直于另一个平面。
(2) 如果一个角所在平面外一点到角的两边的距离相等,那么这个点在该平面内的射影在这个角的角平分线所在的直线上。
(3)经过一个角的顶点引这个角所在平面的斜线。
设斜线和已知两边的夹角为锐角且相等,则这条斜线在这个平面的射影是这个角的角平分线。
(4)若三棱锥的三条棱长相等,则顶点在底面上的射影是底面三角形的外心。
例 如图4所示,所示的正方体ABCD A B C D ''''- 棱长为a ,求点A '到平面AB D ''的距离。
(注:本文所有解法均使用本例)图4解法一(定义法):如图5所示,连结交B D ''于点E ,再连结AE ,过点A '作A H '垂直于AE ,垂足为H ,下面证明A H '⊥平面AB D ''。
图5AA '⊥平面A B C D ''''∴B D ''⊥AA '又在正方形A B C D ''''中,对角线B D A C ''''⊥,且AA A C A ''''=AA '⊂平面AA E ', A C ''⊂平面AA E '∴由线面垂直的判定定理知道B D ''⊥平面AA E 'A H '⊂平面AA E '∴A H '⊥B D ''又由A H '的作法知道A H '⊥AE ,且有B D ''AE E =,B D ''⊂平面AB D '',AE ⊂平面AB D ''∴由线面垂直的判定定理知道A H'⊥平面AB D''根据点到平面距离定义,A H'的长度即为点A'到平面AB D''的距离,下面求A H'的长度。
AB D''∆中,容易得到AB B D D A''''===,从而AB D''∆为正三角形,060AB D''∠=。
进而在Rt AB E'∆中,0sin sin60AE AB AB D'''=∠==。
由1122AA ES AA A E AE A H'∆'''=⨯=⨯得到123AA A C aAA A EA HAE AE'''⨯''⨯'====从而A'到平面AB D''的距离为3a。
3.2转化法求点到平面距离有时候限于几何体的形状,不易直接寻找出点在平面的射影,或者由直接法作出的射影线段在所给几何体中不易计算其长度,此时转化法不失为一种有效的方法。
转化法即是将点到平面的距离转化为另一点到平面间的距离的方法。
转化法依据主要有以下两点:(1)若直线l//平面α,则直线l上所有点到平面α的距离均相等。
(2)若直线AB与平面α交于点M,则点A、B到平面α的距离之比为:AM BM。
特别地,当M为AB中点时,A、B到平面α的距离相等。
下面用转化法重解上面例题解法二(转化法)如图6所示,连结AC、A C'、A C''、A B'、AB',A C''交B D''于点E,连结AE交AC于点H,延长A C''至点G使得12C G A C'''=,连结CG。
图6 CB ⊥平面AA B B ''∴从而斜线A C '在平面AA B B ''的射影为A B 'A B '、AB '为正方形AA B B ''对角线∴AB A B ''⊥,∴由三垂线定理知道AB A C ''⊥同理可以得到AD A C ''⊥ 又AB AD A ''=,AB '⊂平面AB D '',AD '⊂平面AB D ''∴A C '⊥平面AB D ''∴A H '⊥平面AB D '',即点H 为A '在平面AB D ''的射影,A H '的长度为所求//AC A C ''即//AC EG ,且1122EG EC C G A C A C A C AC ''''''''=+=+== ∴四边形ACGE 为平行四边形 ∴//AE CG在A CG '∆由等比性质有13A H AE A C EG '==' ∴13A H A C ''= 而在正方体ABCD ABCD ''''-中对角线2223A C A A AB BC a ''=++=∴3A H a '= 在本例中,未直接计算垂线段A H '的长度,而是找出了其与正方体ABCD ABCD ''''-中对角线A C '的数量关系,从而转化为求正方体ABCD A B C D ''''-对角线A C '长度,而A C '长度是极易计算的,故用这种转化方法降低了运算量。
本例运用的转化方法与依据(2)类似,都是寻求所要求的垂线段与某一已知或易求线段的数量关系,从而简化计算。
3.3等体积法求点到平面距离用等体积法求点到平面的距离主要是一个转换的思想,即要将所要求的垂线段置于一个四面体中,其中四面体的一个顶点为所给点,另外三点位于所给点射影平面上,这里不妨将射影平面上的三点构成的三角形称为底面三角形。
