计算机控制系统高金源版课后标准答案
计算机控制技术课后习题答案

第一章计算机控制系统概述习题及参考答案1.计算机控制系统的控制过程是怎样的计算机控制系统的控制过程可归纳为以下三个步骤:(1)实时数据采集:对被控量的瞬时值进行检测,并输入给计算机。
(2)实时决策:对采集到的表征被控参数的状态量进行分析,并按已定的控制规律,决定下一步的控制过程。
(3)实时控制:根据决策,适时地对执行机构发出控制信号,完成控制任务。
2.实时、在线方式和离线方式的含义是什么?(1)实时:所谓“实时”,是指信号的输入、计算和输出都是在一定时间范围内完成的,即计算机对输入信息以足够快的速度进行处理,并在一定的时间内作出反应并进行控制,超出了这个时间就会失去控制时机,控制也就失去了意义。
(2)“在线”方式:在计算机控制系统中,如果生产过程设备直接与计算机连接,生产过程直接受计算机的控制,就叫做“联机”方式或“在线”方式。
(3)“离线”方式:若生产过程设备不直接与计算机相连接,其工作不直接受计算机的控制,而是通过中间记录介质,靠人进行联系并作相应操作的方式,则叫做“脱机”方式或“离线”方式。
3.微型计算机控制系统的硬件由哪几部分组成?各部分的作用是什么?由四部分组成。
图1.1微机控制系统组成框图(1)主机:这是微型计算机控制系统的核心,通过接口它可以向系统的各个部分发出各种命令,同时对被控对象的被控参数进行实时检测及处理。
主机的主要功能是控制整个生产过程,按控制规律进行各种控制运算(如调节规律运算、最优化计算等)和操作,根据运算结果作出控制决策;对生产过程进行监督,使之处于最优工作状态;对事故进行预测和报警;编制生产技术报告,打印制表等等。
(2)输入输出通道:这是微机和生产对象之间进行信息交换的桥梁和纽带。
过程输入通道把生产对象的被控参数转换成微机可以接收的数字代码。
过程输出通道把微机输出的控制命令和数据,转换成可以对生产对象进行控制的信号。
过程输入输出通道包括模拟量输入输出通道和数字量输入输出通道。
最新计算机控制系统课后习题答案

2.1 在计算机控制系统中,为了获取系统的运行状态或设定信息,经常需要进行开关量信号的输入。
2.2 把从控制对象检测到的模拟信号,转换成二进制数字信号,经I/O接口送入计算机。
2.3 在计算机控制系统中,经常需要控制执行机构的开/关(如对电磁阀的控制)或启/停(如各种交、直流电机的控制),某些控制算法(如脉宽调制方法,最优控制中的乒乓控制算法等)也需要控制执行机构在一定时间T内全负荷工作一段时间t(0≤t≤T),这些控制可通过计算机开关量输出通道来实现。
2.4 把计算机输出的数字量转换成模拟量。
2.5 光电耦合器的作用:从工业现场获取的开关量或数字量的信号电平往往高于计算机系统的逻辑电平,即使输入开关量电压本身不高,也有可能从现场引入意外的高压信号,因此必须采取电隔离措施,以保障计算机系统的安全。
常用的隔离措施是采用光电耦合器件实现的。
光电耦合器的用法:下图为原理图。
当输入侧(即发光二极管)流过一定的电流IF时,发光二极管开始发光,它触发光敏三极管使其导通;当撤去该电流时,发光二极管熄灭、三极管截止。
这样,就实现了以光路来传递信号,保证了两侧电路没有电气联系,从而达到了隔离的目的。
2.5 光电耦合器的注意事项:① 输入侧导通电流要使光电隔离器件导通,必须在其输入侧提供足够大的导通电流,以使发光二极管发光。
不同的光电隔离器件的导通电流也不同,典型的导通电流IF=10mA。
② 频率特性受发光二极管和光敏元件响应时间的影响,光电隔离器件只能通过一定频率以下的脉冲信号。
因此,在传送高频信号时,应该考虑光电隔离器件的频率特性,选择通过频率较高的光电隔离器。
③ 输出端工作电流光电隔离器输出端的灌电流不能超过额定值,否则就会使元件发生损坏。
一般输出端额定电流在mA量级,不能直接驱动大功率外部设备,因此通常从光电隔离器至外设之间还需设置驱动电路。
2.5 光电耦合器的注意事项:④ 输出端暗电流这是指光电隔离器处于截止状态时,流经输出端元件的电流,此值越小越好。
计算机控制系统课后习题答案1

第一章课后参考答案1-1简述计算机控制系统的控制过程。
计算机控制系统的控制过程可以归纳为以下三个步骤:1)实时数据采集:对被控量进行采样测量,形成反馈信号;2)实时控制计算:根据反馈信号和给定信号,按一定的控制规律,计算出控制量;3)实时控制输出,向执行机构发出控制信号,实现控制作用。
1-2什么是实时性?有哪些因素影响系统的实时性?硬件:1)控制器计算速度2)传感器采集速度3)执行器反应时间4)A/D、D/A转换速度软件:1)操作系统调度2)中断响应处理方式(包括定时器)3)延时函数的设置实时性:即信号的输入、计算和输出都是在一定时间范围内即时完成的,超出这个时间就会失去控制时机,控制也就失去了意义。
1-3计算机控制系统的硬件由哪几部分组成?各部分作用是什么?计算机的硬件主要包括主机、输入输出通道和外部设备。
主机:主机是计算系统的核心,通过接口向系统的各个部分发出各种指令,对被控对象进行检测和控制。
输入输出通道:输入输出通道是计算机和生产对象之间进行信息交换的桥梁和纽带。
过程输入通道把生产对象的被控参数转换成计算机可以接收的数字信号,过程输出通道把计算机输出的控制命令和数据,转化成可以对生产对象进行控制的的信号。
过程输入输出通道包括模拟量输入输出通道和数字量输入输出通道。
外部设备:外部设备是实现计算机和外界进行信息交换的设备,简称外设,包括人机联系设备(操作台)、输入输出设备(磁盘驱动器、键盘、打印机、显示终端等)和外存贮器,其中操作台应具备显示功能,即根据操作人员的要求,能立即显示所要求的内容,还应有按键或开关,完成系统的启、停等功;操作台还要保证操作错误也不会造成恶劣后果,即应有保护功能。
1-4计算机控制系统的软件由哪几部分组成?各部分作用是什么?计算机控制系统软件分为系统软件、应用软件及数据库。
系统软件是有计算机生产厂家提供的专门用来使用和管理计算机的程序。
对用户来说,系统软件只是用来开发应用软件的工具,不需要自己设计。
计算机控制技术课后习题与答案

单路模拟量电路原理图如下列图所示。
10.采用DAC0832和PC/ISA总线工业控制机接口,请画出接口电路原理图,并编写D/A转换程序。
11.采用DAC1210和PC/ISA总线工业控制机接口,请画出接口电路原理图,并编写D/A转换程序。
答案:略。
12.请分别画出D/A转换器的单极性和双极性电压输出电路,并分别推导出输出电压与输入数字量之间的关系式。
①无源I/V变换
无源I/V变换主要是利用无源器件电阻来实现,并加滤波和输出限幅等保护措施,如下图。
无源I/V变换电路
对于0~10mA输入信号,可取R1=100Ω,R2=500Ω,且R2为精细电阻,这样当输入的I为0~10mA电流时,输出的V为0~5V.对于4~20mA输入信号,可取R1=100Ω,R2=250Ω,且R2为精细电阻,这样当输入的I为4~20mA时,输出的V为1~5V。
上世纪末期开展起来的单片机及嵌入式系统等以其价格低和体积小的优势,使智能仪器和智能仪表在控制场合中的应用也越来越广。现代工业生产规模的日益复杂化和大型化趋势,对控制计算机提出了更高的要求。计算机不仅要完成面向过程的控制和优化任务,还要在获取生产过程各种信息的根底上进展这个过程的信息综合和优化调度,完成生产、经营管理和其它综合管理工作。这种集企业的管理、监视与控制为一体的计算机综合自动化系统被称为计算机集成制造系统(CIMS)或计算机集成过程系统(CIPS)。此外,监视控制与数据采集系统(SCADA)、可编程自动化控制器(PAC)和无线传感器网络(WSN)等各种控制系统也为计算机控制方法提供了新的应用领域。
《计算机控制系统》课后题答案

1.14简述直接数字控制系统的结构和特点。
解答:直接数字控制系统DDC结构如图1.17所示。这类控制是计算机把运算结果直接输出去控制生产过程,简称DDC系统。这类系统属于闭环系统,计算机系统对生产过程各参量进行检测,根据规定的数学模型,如PID算法进行运算,然后发出控制信号,直接控制生产过程。它的主要功能不仅能完全取代模拟调节器,而且只要改变程序就可以实现其他的复杂控制规律,如前馈控制、非线性控制等。它把显示、打印、报警和设定值的设定等功能都集中到操作控制台上,实现集中监督和控制给操作人员带来了极大的方便。但DDC对计算机可靠性要求很高,否则会影响生产。
2 (1.3)
式中, 为输出的满幅值电压, 是二进制的最高有效位, 是最低有效位。
以4位二进制为例,图1.12给出了一个说明实例。在图1.12中每个电流源值取决于相应二进制位的状态,电流源值或者为零,或者为图中显示值,则输出电流的总和为:
(1.4)
我们可以用稳定的参考电压及不同阻值的电阻来替代图1.12中的各个电流源,在电流的汇合输出加入电流/电压变换器,因此,可以得到权电阻法数字到模拟量转换器的原理图如图1.13所示。图中位切换开关的数量,就是D/A转换器的字长。
图1.18 SCC加调节器的系统框图
(2)SCC加DDC的系统
在这种系统中,SCC计算机的输出直接改变DDC的设定值,两台计算机之间的信息联系可通过数据传输直接实现,其构成如图1.19所示。
这种系统通常一台SCC计算机可以控制数个DDC计算机,一旦DDC计算机发送故障时,可用SCC计算机代替DDC的功能,以确保生产的正常进行。
图1.17 直接数字控制系统
1.15简述计算机监督控制系统的结构和特点。
计算机控制系统课后答案 (3)

计算机控制系统课后答案问题1:什么是计算机控制系统?计算机控制系统是指利用计算机技术对物理过程或机械设备进行监控、控制和管理的系统。
它由计算机硬件、软件和工程配套设备等多个组成部分构成。
计算机控制系统具有实时性好、反应速度快、准确性高等特点,广泛应用于各种工业自动化领域。
问题2:计算机控制系统的组成部分有哪些?计算机控制系统由以下几个部分组成:1.传感器和执行器:传感器用于感知物理过程的状态和参数,并将其转换为电信号,以便计算机能够处理。
执行器根据计算机的指令来执行控制动作,控制物理过程或机械设备的运行。
2.计算机硬件:包括中央处理器(CPU)、内存、输入输出接口等。
计算机硬件负责接收传感器采集的数据,并根据预设的算法进行处理和判断,进而控制执行器的动作。
3.计算机软件:包括控制算法、界面程序等。
控制算法根据输入的传感器数据进行计算和判断,生成相应的控制指令。
界面程序提供控制系统的人机交互界面,使操作员能够对系统进行监控和控制。
4.工程配套设备:包括可编程逻辑控制器(PLC)、仪表仪器等。
这些设备与计算机系统相连,作为中间装置,用于完成不同领域的控制任务。
问题3:计算机控制系统的工作原理是什么?计算机控制系统的工作原理是通过传感器采集物理过程的状态和参数,将其转换为电信号输入到计算机系统中。
计算机根据预设的控制算法,对输入的数据进行处理和判断,生成相应的控制指令。
这些控制指令通过输出接口发送给执行器,执行器根据指令来执行相应的控制动作,从而实现对物理过程或机械设备的控制。
计算机的工作过程可以理解为以下几个步骤:1.信号采集:传感器采集物理过程的状态和参数,并将其转换为电信号。
2.信号处理:计算机系统接收传感器的电信号,对其进行滤波、放大、数字量化等处理,以获取准确的数据。
3.控制计算:根据输入的数据,计算机系统进行控制算法的计算和判断,生成相应的控制指令。
4.控制输出:控制指令通过输出接口发送给执行器,执行器根据指令来执行相应的控制动作。
计算机控制系统课后答案PPT文档39页

21、要知道对好事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
23、一切节省,归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰,决心到最后会全部推倒。——莎士比亚
计算机控制系统课后答案
6、法律的基础有两个,而且只有两个……公平和实用。——伯克 7、有两种和平的暴力,那就是法律和礼节。——பைடு நூலகம்德
8、法律就是秩序,有好的法律才有好的秩序。——亚里士多德 9、上帝把法律和公平凑合在一起,可是人类却把它拆开。——查·科尔顿 10、一切法律都是无用的,因为好人用不着它们,而坏人又不会因为它们而变得规矩起来。——德谟耶克斯
25、学习是劳动,是充满思想的劳动。——乌申斯基
谢谢!
计算机控制系统习题答案

( c )由系统结构图
C ( z ) NG2 ( z ) R ( z ) DD 2 ( z )Gh ( z )G1G2 ( z ) E ( z ) DD1 ( z )Gh ( z )G1G2 ( z ) E ( z ) R( z ) C ( z ) NG2 ( z ) R( z ) DD 2 ( z )Gh ( z )G1G2 ( z ) DD1 ( z )Gh ( z )G1G2 ( z ) R ( z ) C ( z ) C ( z) NG2 ( z ) R( z ) DD 2 ( z )Gh ( z )G1G2 ( z ) DD1 ( z )Gh ( z )G1G2 ( z ) R ( z ) 1 DD1 ( z )Gh ( z )G1G2 ( z ) 1 DD1 ( z )GhG1G2 ( z )
1
计算机监督控制 SCC 系统有两种类型,一种是 SCC+模拟调节器,另一种是 SCC+DDC 控制系统。SCC 的优点是不仅可进行复杂控制规律的控制,而且工作可靠性高,当 SCC 出现故障时,下级仍可继续执行控制任务。 1.4 实时、在线方式和离线方式的含义是什么? 解答:(1)实时:所谓“实时” ,是指信号的输入、计算和输出都是在一定时间范围内完成 的,即计算机对输入信息以足够快的速度进行处理,并在一定的时间内作出反应并进行 控制,超出了这个时间就会失去控制时机,控制也就失去了意义。 (2)“在线”方式:在计算机控制系统中,如果生产过程设备直接与计算机连接,生产过 程直接受计算机的控制,就叫做“联机”方式或“在线”方式。 (3)“离线”方式:若生产过程设备不直接与计算机相连接,其工作不直接受计算机的控 制,而是通过中间记录介质,靠人进行联系并作相应操作的方式,则叫做“脱机”方式 或“离线”方式。 1.5 如果按应用场合分类,计算机控制系统大致可以分为几类?各有什么主要特点? 解答: (1)数据采集与监视控制系统。特点:机构简单,控制灵活安全,特别适应于未 摸清控制规律的系统,常被用于计算机控制系统研究的初级阶段,或用于试验新的数学 模型和调制新的控制程序等。 (2)直接数字控制系统。特点:a、控制灵活。只要改变算法程序,就可以方便地改变 控制方法,无需改变系统任何硬件。b、可以有效地实现较复杂的控制,用来改善控制 品质。c、可以实现多回路控制,费用比模拟系统节省。 (3)计算机监督控制系统。特点:SCC 的优点是不仅可进行复杂控制规律的控制,而 且工作可靠性高,当 SCC 出故障时,下级仍可继续执行控制任务。 (4)分布式计算机控制系统。特点:a、分布式结构。b、具有较高的可靠性。c、设计, 开发与维护,操作方便。 1.6 为什么说计算机集成制造系统是工业自动化的发展趋势? 解答:大规模及超大规模集成电路的发展,提高了计算机的可靠性和性能价格比,从而 使计算机控制系统的应用也越来越广泛。为更好地适应生产力的发展,扩大生产规模, 以满足对计算机控制系统提出的越来越高的要求。
计算机控制技术课后习题答案

第一章计算机控制系统概述习题及参考答案1.计算机控制系统的控制过程是怎样的计算机控制系统的控制过程可归纳为以下三个步骤:1实时数据采集:对被控量的瞬时值进行检测,并输入给计算机;2实时决策:对采集到的表征被控参数的状态量进行分析,并按已定的控制规律,决定下一步的控制过程;3实时控制:根据决策,适时地对执行机构发出控制信号,完成控制任务;2.实时、在线方式和离线方式的含义是什么1实时:所谓“实时”,是指信号的输入、计算和输出都是在一定时间范围内完成的,即计算机对输入信息以足够快的速度进行处理,并在一定的时间内作出反应并进行控制,超出了这个时间就会失去控制时机,控制也就失去了意义;2“在线”方式:在计算机控制系统中,如果生产过程设备直接与计算机连接,生产过程直接受计算机的控制,就叫做“联机”方式或“在线”方式;3“离线”方式:若生产过程设备不直接与计算机相连接,其工作不直接受计算机的控制,而是通过中间记录介质,靠人进行联系并作相应操作的方式,则叫做“脱机”方式或“离线”方式;3.微型计算机控制系统的硬件由哪几部分组成各部分的作用是什么由四部分组成;图微机控制系统组成框图1主机:这是微型计算机控制系统的核心,通过接口它可以向系统的各个部分发出各种命令,同时对被控对象的被控参数进行实时检测及处理;主机的主要功能是控制整个生产过程,按控制规律进行各种控制运算如调节规律运算、最优化计算等和操作,根据运算结果作出控制决策;对生产过程进行监督,使之处于最优工作状态;对事故进行预测和报警;编制生产技术报告,打印制表等等;2输入输出通道:这是微机和生产对象之间进行信息交换的桥梁和纽带;过程输入通道把生产对象的被控参数转换成微机可以接收的数字代码;过程输出通道把微机输出的控制命令和数据,转换成可以对生产对象进行控制的信号;过程输入输出通道包括模拟量输入输出通道和数字量输入输出通道;3外部设备:这是实现微机和外界进行信息交换的设备,简称外设,包括人机联系设备操作台、输入输出设备磁盘驱动器、键盘、打印机、显示终端等和外存贮器磁盘;其中操作台应具备显示功能,即根据操作人员的要求,能立即显示所要求的内容;还应有按钮,完成系统的启、停等功能;操作台还要保证即使操作错误也不会造成恶劣后果,即应有保护功能;4检测与执行机构a.测量变送单元:在微机控制系统中,为了收集和测量各种参数,采用了各种检测元件及变送器,其主要功能是将被检测参数的非电量转换成电量,例如热电偶把温度转换成mV信号;压力变送器可以把压力转换变为电信号,这些信号经变送器转换成统一的计算机标准电平信号0~5V或4~20mA后,再送入微机;b.执行机构:要控制生产过程,必须有执行机构,它是微机控制系统中的重要部件,其功能是根据微机输出的控制信号,改变输出的角位移或直线位移,并通过调节机构改变被调介质的流量或能量,使生产过程符合预定的要求;例如,在温度控制系统中,微机根据温度的误差计算出相应的控制量,输出给执行机构调节阀来控制进入加热炉的煤气或油量以实现预期的温度值;常用的执行机构有电动、液动和气动等控制形式,也有的采用马达、步进电机及可控硅元件等进行控制;4.微型计算机控制系统软件有什么作用说出各部分软件的作用;软件是指能够完成各种功能的计算机程序的总和;整个计算机系统的动作,都是在软件的指挥下协调进行的,因此说软件是微机系统的中枢神经;就功能来分,软件可分为系统软件、应用软件及数据库;1系统软件:它是由计算机设计者提供的专门用来使用和管理计算机的程序;对用户来说,系统软件只是作为开发应用软件的工具,是不需要自己设计的;系统软件包括:a.操作系统:即为管理程序、磁盘操作系统程序、监控程序等;b.诊断系统:指的是调节程序及故障诊断程序;c.开发系统:包括各种程序设计语言、语言处理程序编译程序、服务程序装配程序和编辑程序、模拟主系统系统模拟、仿真、移植软件、数据管理系统等;d.信息处理:指文字翻译、企业管理等;2应用软件:它是面向用户本身的程序,即指由用户根据要解决的实际问题而编写的各种程序;应用软件包括:a.过程监视程序:指巡回检测程序、数据处理程序、上下限检查及报警程序、操作面板服务程序、数字滤波及标度变换程序、判断程序、过程分析程序等;b.过程控制计算程序:指的是控制算法程序、事故处理程序和信息管理程序,其中信息管理程序包括信息生成调度、文件管理及输出、打印、显示程序等;c.公共服务程序:包括基本运算程序、函数运算程序、数码转换程序、格式编码程序;3数据库:数据库及数据库管理系统主要用于资料管理、存档和检索,相应软件设计指如何建立数据库以及如何查询、显示、调用和修改数据等;5.微型计算机控制系统的特点是什么微机控制系统与常规的自动控制系统相比,具有如下特点:a.控制规律灵活多样,改动方便b.控制精度高,抑制扰动能力强,能实现最优控制c.能够实现数据统计和工况显示,控制效率高d.控制与管理一体化,进一步提高自动化程度6.操作指导、DDC和SCC系统工作原理如何它们之间有何区别和联系1操作指导控制系统:在操作指导控制系统中,计算机的输出不直接作用于生产对象,属于开环控制结构;计算机根据数学模型、控制算法对检测到的生产过程参数进行处理,计算出各控制量应有的较合适或最优的数值,供操作员参考,这时计算机就起到了操作指导的作用;其原理框图如图所示;图操作指导控制系统原理框图2直接数字控制系统DDC系统:DDCDirect Digital Control系统就是通过检测元件对一个或多个被控参数进行巡回检测,经输入通道送给微机,微机将检测结果与设定值进行比较,再进行控制运算,然后通过输出通道控制执行机构,使系统的被控参数达到预定的要求;DDC系统是闭环系统,是微机在工业生产过程中最普遍的一种应用形式;其原理框图如图所示;图 DDC系统原理框图3计算机监督控制系统SCC系统:SCCSupervisory Computer Control系统比DDC 系统更接近生产变化的实际情况,因为在DDC系统中计算机只是代替模拟调节器进行控制,系统不能运行在最佳状态,而SCC系统不仅可以进行给定值控制,并且还可以进行顺序控制、最优控制以及自适应控制等;SCC系统的原理框图如图所示;图 SCC系统原理框图SCC是操作指导控制系统和DDC系统的综合与发展;7.计算机控制系统的发展趋势是什么大规模及超大规模集成电路的发展,提高了计算机的可靠性和性能价格比,从而使计算机控制系统的应用也越来越广泛;为更好地适应生产力的发展,扩大生产规模,以满足对计算机控制系统提出的越来越高的要求,目前计算机控制系统的发展趋势有以下几个方面;a.普及应用可编程序控制器b.采用集散控制系统c.研究和发展智能控制系统本章作业简述几类常见的计算机控制系统的特点及其应用领域;第二章输入输出过程通道习题及参考答案1.什么是过程通道过程通道有哪些分类过程通道是在计算机和生产过程之间设置的信息传送和转换的连接通道;按信息传递的方向来分,过程通道可分为输入过程通道和输出过程通道;按所传递和交换的信息来分,过程通道又可分为数字量过程通道和模拟量过程通道;2.数字量过程通道由哪些部分组成各部分的作用是什么数字量过程通道包括数字量输入通道和数字量输出通道;数字量输入通道主要由输入缓冲器、输入调理电路、输入地址译码电路、并行接口电路和定时计数电路等组成;数字量输出通道主要由输出锁存器、输出驱动电路、输出口地址译码电路等组成;其中:输入调理电路将来自控制装置或生产过程的各种开关量,进行电平转换,将其通断状态转换成相应的高、低电平,同时还要考虑对信号进行滤波、保护、消除触点抖动,以及进行信号隔离等问题;3.简述两种硬件消抖电路的工作原理;采用积分电路的硬件消抖电路,首先利用积分电路将抖动的高频部分滤出,其次利用施密特触发器整形;采用RS触发器的硬件消抖电路,主要是利用RS触发器的保持功能实现消抖;4.简述光电耦合器的工作原理及在过程通道中的作用;光电耦合器由封装在一个管壳内的发光二极管和光敏三极管组成,如图所示;输入电流流过二极管时使其发光,照射到光敏三极管上使其导通,完成信号的光电耦合传送,它在过程通道中实现了输入和输出在电气上的完全隔离;图光电耦合器电路图5.模拟量输入通道由哪些部分组成各部分的作用是什么模拟量输入通道一般由I/V变换、多路转换器、采样保持器、A/D转换器、接口及控制逻辑电路组成;1I/V变换:提高了信号远距离传递过程中的抗干扰能力,减少了信号的衰减,为与标准化仪表和执行机构匹配提供了方便;2多路转换器:用来切换模拟电压信号的关键元件;3采样保持器:A/D转换器完成一次A/D转换总需要一定的时间;在进行A/D转换时间内,希望输入信号不再变化,以免造成转换误差;这样,就需要在A/D转换器之前加入采样保持器;4A/D转换器:模拟量输入通道的任务是将模拟量转换成数字量,能够完成这一任务的器件,称为之模/数转换器Analog/Digital Converter,简称A/D转换器或ADC;6.对理想多路开关的要求是什么理想的多路开关其开路电阻为无穷大,其接通时的导通电阻为零;此外,还希望切换速度快、噪音小、寿命长、工作可靠;7.采样保持器有什么作用试说明保持电容的大小对数据采集系统的影响;采样保持器的作用:A/D转换器完成一次A/D转换总需要一定的时间;在进行A/D 转换时间内,希望输入信号不再变化,以免造成转换误差;这样,就需要在A/D转换器之前加入采样保持器;保持电容对数据采集系统采样保持的精度有很大影响;保持电容值小,则采样状态时充电时间常数小,即保持电容充电快,输出对输入信号的跟随特性好,但在保持状态时放电时间常数也小,即保持电容放电快,故保持性能差;反之,保持电容值大,保持性能好,但跟随特性差;8.在数据采样系统中,是不是所有的输入通道都需要加采样保持器为什么不是,对于输入信号变化很慢,如温度信号;或者A/D转换时间较快,使得在A/D转换期间输入信号变化很小,在允许的A/D转换精度内,就不必再选用采样保持器;D转换器的结束信号有什么作用根据该信号在I/O控制中的连接方式,A/D转换有几种控制方式它们在接口电路和程序设计上有什么特点A/D转换器的结束信号的作用是用以判断本次AD转换是否完成;常见的A/D转换有以下几种控制方式,各自特点如下延时等待法:EOC可不和I/O口连接,程序设计时,延时大于ADC转换时间后,取数据;保持等待法:EOC与READY相连,EOC无效时,自动插入等待状态;直至EOC有效时,取数据;查询法: EOC可以和任意I/O口连接,程序设计时,反复判断EOC是否有效,直至EOC 有效时,取数据;中断响应法: EOC与外部中断相连,AD转换结束后,发中断申请,在中断服务程序中取数据;10.设被测温度变化范围为0o C~1200o C,如果要求误差不超过,应选用分辨为多少位的A/D 转换器 选择依据:124.0120012log ≈⎪⎭⎫ ⎝⎛+≥n 11.设计出8路模拟量采集系统;请画出接口电路原理图,并编写相应的8路模拟量数据采集程序;本例给出用8031、DAC0809设计的数据采集系统实例;把采样转换所得的数字量按序存于片内RAM 的30H~37H 单元中;采样完一遍后停止采集;其数据采集的初始化程序和中断服务程序如下:初始化程序:MOV R0,30H ;设立数据存储区指针MOV R2,08H ;设置8路采样计数值SETB IT0 ;设置外部中断0为边沿触发方式SETB EA ;CPU 开放中断SETB EX0 ;允许外部中断0中断MOV DPTR,FEF8H ;送入口地址并指向IN0LOOP : MOVX DPTR,A ;启动A/D 转换,A 的值无意义HERE : SJMP HERE ;等待中断中断服务程序:MOVX A,DPTR ;读取转换后的数字量MOV R0,A ;存入片内RAM 单元INC DPTR ;指向下一模拟通道INC R0 ;指向下一个数据存储单元DJNZ R2,INT0 ;8路未转换完,则继续CLR EA ;已转换完,则关中断CLR EX0 ;禁止外部中断0中断RETI ;中断返回INT0: MOVX DPTR,A ;再次启动A/D转换RETI ;中断返回12.模拟量输出通道由哪几部分组成各部分的作用是什么模拟量输出通道一般由接口电路、D/A转换器、功率放大和V/I变换等信号调理电路组成;1D/A转换器:模拟量输出通道的核心是数/模转换器Digital/Analog Converter,简称D/A转换器或DAC;它是指将数字量转换成模拟量的元件或装置;2V/I变换:一般情况下,D/A转换电路的输出是电压信号;在计算机控制系统中,当计算机远离现场,为了便于信号的远距离传输,减少由于传输带来的干扰和衰减,需要采用电流方式输出模拟信号;许多标准化的工业仪表或执行机构,一般是采用0~10mA或4~20mA的电流信号驱动的;因此,需要将模拟电压信号通过电压/电流V/I变换技术,转化为电流信号;13.采用DAC0832和PC总线工业控制机接口;请画出接口电路原理图,并编写产生三角波、梯形波和锯齿波的程序;设计一八路数据采集及其回放系统;要求八路数据巡回检测,存储10组数据,输数据为电压信号0-5V,检测精度<1%;CPU、AD、DA可任选;Uo第五章微机数控系统习题及参考答案1.什么是数控系统数控系统包括哪些数控系统是采用数字电子技术和计算机技术,对生产机械进行自动控制的系统,它包括顺序控制和数字程序控制两部分;2.什么是顺序控制系统它由哪几部分组成微机顺序控制方式是指以预先规定好的时间或条件为依据,按预先规定好的动作次序顺序地进行工作;一般地,把按时序或事序规定工作的自动控制称为顺序控制;它包括系统控制器、输入电路、输入接口、输出电路、输出接口、检测机构、显示与报警电路;3.微机数控系统由哪些部分组成各部分的作用是什么由五部分组成;1输入装置:一般指微机的输入设备,如键盘;其作用是输入数控系统对生产机械进行自动控制时所必需的各种外部控制信息和加工数据信息;2微机:微机是MNC系统运算和控制的核心;在系统软件指挥下,微机根据输入信息,完成数控插补器和控制器运算,并输出相应的控制和进给信号;若为闭环数控系统,则由位置检测装置输出的反馈信息也送入微机进行处理;3输出装置:一般包括输出缓冲电路、隔离电路、输出信号功率放大器、各种显示设备等;在微机控制下,输出装置一方面显示加工过程中的各有关信息,另一方面向被控生产机械输出各种有关的开关量控制信号冷却、启、停等,还向伺服机构发出进给脉冲信号等;4伺服机构:一般包括各种伺服元件和功率驱动元件;其功能是将输出装置发出的进给脉冲转换成生产机械相应部件的机械位移线位移、角位移运动;5加工机械:即数控系统的控制对象,各种机床、织机等;目前已有专门为数控装置配套设计的各种机械,如各种数控机床,它们的机械结构与普通机床有较大的区别;4.什么是逐点比较插补法直线插补计算过程和圆弧插补计算过程各有哪几个步骤逐点比较法插补运算,就是在某个坐标方向上每走一步即输出一个进给脉冲,就作一次计算,将实际进给位置的坐标与给定的轨迹进行比较,判断其偏差情况,根据偏差,再决定下一步的走向沿X轴进给,还是沿Y轴进给;逐点比较法插补的实质是以阶梯折线来逼近给定直线或圆弧曲线,最大逼近误差不超过数控系统的一个脉冲当量每走一步的距离,即步长;直线插补计算过程的步骤如下:1偏差判别:即判别上一次进给后的偏差值Fm是最大于等于零,还是小于零;2坐标进给:即根据偏差判断的结果决定进给方向,并在该方向上进给一步;3偏差计算:即计算进给后的新偏差值Fm+1,作为下一步偏差判别的依据;4终点判别:即若已到达终点,则停止插补;若未到达终点,则重复上述步骤;圆弧插补计算过程的步骤如下:1偏差判别2坐标进给3偏差计算4坐标计算5终点判别5.若加工第二象限直线OA,起点O0,0,终点A-4,6;要求:1按逐点比较法插补进行列表计算;2作出走步轨迹图,并标明进给方向和步数;解:由题意可知xe =4,ye=6,F=0,我们设置一个总的计数器Nxy,其初值应为Nxy=|6-0|+|-4-0|=10,则插补计算过程如表3—1所示;根据插补计算过程表所作出的直线插补走步轨迹图如下图所示;表3—11按逐点比较法插补进行列表计算;2作出走步轨迹图,并标明进给方向和步数;解:插补计算过程如表3—2所示;终点判别仍采用第二种方法,设一个总的计数器Nxy ,每走一步便减1操作,当Nxy=0时,加工到终点,插补运算结束;下图为插补过程中的走步轨迹;表3—2波形图;有三种工作方式: 1三相单三拍工作方式各相的通电顺序为A →B →C,各相通电的电压波形如图所示;图单三拍工作的电压波形图2三相双三拍工作方式双三拍工作方式各相的通电顺序为AB →BC →CA;各相通电的电压波形如图所示;图双三拍工作的电压波形图3三相六拍工作方式在反应式步进电机控制中,把单三拍和双三拍工作方式结合起来,就产生了六拍工作方式,其通电顺序为A →AB →B →BC →C →CA;各相通电的电压波形如图所示;图三相六拍工作的电压波形图8. 采用三相六拍方式控制X 轴走向步进电机; 主程序:MOV A,0FH;方向输入信号MOV P1,AXMM : MOV A,P1 JNB ,XM ;=0反转 LCALL STEP1;调正转子程序 SJMP XMMXM : LCALL STP2;调反转子程序SJMP XMM +X 走步子程序:STEP1: MOV DPTR,TAB ;指表头 CLR AMOVX A,A+DPTR ;取数非非非光电隔离功率放大步进电机AB C方向控制“1”正83CJNE A,05H,S11;是否最后单元 MOV DPTR,TAB;重置表头SJMP S12S11: INC DPTR ;地址加1S12: MOV R0,7FH;延时S13: DJNZ R0,S13;CLR A;MOVX A,A+DPTR;取数据MOV P1,ARET-X走步子程序:STEP2: MOV DPTR,TABCLR AMOVX A,A+DPTR;CJNZ A,01H,S21MOV DPTR,TABADD DPTR,0006HSJMP S12S21: CLR CDEC DPLSJMP S12TAB: DB 01H,03H,02H,06H,04H,05H本章作业若加工第二象限直线OA和圆弧AB,已知直线起点O0,0,终点A-4,6;圆弧起点A-4,6,终点A-6,10要求:1按逐点比较法插补进行列表计算;2作出走步轨迹图,并标明进给方向和步数;第四章 微型计算机控制系统的控制算法习题及参考答案1.数字控制器的模拟化设计步骤是什么 模拟化设计步骤:1设计假想的模拟控制器DS 2正确地选择采样周期T 3将DS 离散化为DZ4求出与DS 对应的差分方程 5根据差分方程编制相应程序; 2.某连续控制器设计为试用双线形变换法、前向差分法、后向差分法分别求取数字控制器DZ; 双线形变换法:把112+-•=z z T s 代入,则 前向差分法:把Tz-z 1=代入,则 后向差分法:把Tzz s 1-=代入,则3.在PID 调节器中系数p k 、i k 、d k 各有什么作用它们对调节品质有什么影响 系数p k 为比例系数,提高系数p k 可以减小偏差,但永远不会使偏差减小到零,而且无止境地提高系数p k 最终将导致系统不稳定;比例调节可以保证系统的快速性; 系数i k 为积分常数,i k 越大积分作用越弱,积分调节器的突出优点是,只要被调量存在偏差,其输出的调节作用便随时间不断加强,直到偏差为零;在被调量的偏差消除后,由于积分规律的特点,输出将停留在新的位置而不回复原位,因而能保持静差为零;但单纯的积分也有弱点,其动作过于迟缓,因而在改善静态品质的同时,往往使调节的动态品质变坏,过渡过程时间加长;积分调节可以消除静差,提高控制精度;系数d k 为微分常数,d k 越大微分作用越强;微分调节主要用来加快系统的相应速度,减小超调,克服振荡,消除系统惯性的影响;4.什么是数字PID 位置型控制算法和增量型控制算法试比较它们的优缺点;为了实现微机控制生产过程变量,必须将模拟PID 算式离散化,变为数字PID 算式,为此,在采样周期T 远小于信号变化周期时,作如下近似T 足够小时,如下逼近相当准确,被控过程与连续系统十分接近: 于是有:uk 是全量值输出,每次的输出值都与执行机构的位置如控制阀门的开度一一对应,所以称之为位置型PID 算法;在这种位置型控制算法中,由于算式中存在累加项,因此输出的控制量uk 不仅与本次偏差有关,还与过去历次采样偏差有关,使得uk 产生大幅度变化,这样会引起系统冲击,甚至造成事故;所以实际中当执行机构需要的不是控制量的绝对值,而是其增量时,可以采用增量型PID 算法;当控制系统中的执行器为步进电机、电动调节阀、多圈电位器等具有保持历史位置的功能的这类装置时,一般均采用增量型PID 控制算法;与位置算法相比,增量型PID 算法有如下优点:1位置型算式每次输出与整个过去状态有关,计算式中要用到过去偏差的累加值,容易产生较大的累积计算误差;而在增量型算式中由于消去了积分项,从而可消除调节器的积分饱和,在精度不足时,计算误差对控制量的影响较小,容易取得较好的控制效果;2为实现手动——自动无扰切换,在切换瞬时,计算机的输出值应设置为原始阀门开度u 0,若采用增量型算法,其输出对应于阀门位置的变化部分,即算式中不出现u 0项,所以易于实现从手动到自动的无扰动切换;3采用增量型算法时所用的执行器本身都具有寄存作用,所以即使计算机发生故障,执行器仍能保持在原位,不会对生产造成恶劣影响; 5.已知模拟调节器的传递函数为试写出相应数字控制器的位置型和增量型控制算式,设采样周期T=; 则()()()()s SE .s E s SU .s U 1700850+=+ 把T=代入得 位置型 增量型6.有哪几种改进的数字PID 控制器 有四种:1积分分离PID 控制算法 2不完全微分PID 控制算法 3带死区的PID 控制算法4消除积分不灵敏区的PID 控制10: 什么叫积分饱和 它是怎样引起的如何消除。
计算机控制系统课后习题附标准答案

1计算机控制系统概述习题参考答案1.计算机控制系统的控制过程是怎样的?计算机控制系统的控制过程可归纳为以下三个步骤:(1)实时数据采集:对被控量的瞬时值进行检测,并输入给计算机。
(2)实时决策:对采集到的表征被控参数的状态量进行分析,并按已定的控制规律,决定下一步的控制过程。
(3)实时控制:根据决策,适时地对执行机构发出控制信号,完成控制任务。
2.实时、在线方式和离线方式的含义是什么?(1)实时:所谓“实时”,是指信号的输入、计算和输出都是在一定时间范围内完成的,即计算机对输入信息以足够快的速度进行处理,并在一定的时间内作出反应并进行控制,超出了这个时间就会失去控制时机,控制也就失去了意义。
(2)“在线”方式:在计算机控制系统中,如果生产过程设备直接与计算机连接,生产过程直接受计算机的控制,就叫做“联机”方式或“在线”方式。
(3)“离线”方式:若生产过程设备不直接与计算机相连接,其工作不直接受计算机的控制,而是通过中间记录介质,靠人进行联系并作相应操作的方式,则叫做“脱机”方式或“离线”方式。
3.微型计算机控制系统的硬件由哪几部分组成?各部分的作用是什么? 由四部分组成。
图1.1微机控制系统组成框图(1)主机:这是微型计算机控制系统的核心,通过接口它可以向系统的各个部分发出各种命令,同时对被控对象的被控参数进行实时检测及处理。
主机的主要功能是控制整个生产过程,按控制规律进行各种控制运算(如调节规律运算、最优化计算等)和操作,根据运算结果作出控制决策;对生产过程进行监督,使之处于最优工作状态;对事故进行预测和报警;编制生产技术报告,打印制表等等。
(2)输入输出通道:这是微机和生产对象之间进行信息交换的桥梁和纽带。
过程输入通道把生产对象的被控参数转换成微机可以接收的数字代码。
过程输出通道把微机输出的控制命令和数据,转换成可以对生产对象进行控制的信号。
过程输入输出通道包括模拟量输入输出通道和数字量输入输出通道。
计算机控制技术课后习题详解答案

计算机控制技术课后习题详解答案文档编制序号:[KKIDT-LLE0828-LLETD298-POI08]第一章计算机控制系统概述习题参考答案1.计算机控制系统的控制过程是怎样的计算机控制系统的控制过程可归纳为以下三个步骤:(1)实时数据采集:对被控量的瞬时值进行检测,并输入给计算机。
(2)实时决策:对采集到的表征被控参数的状态量进行分析,并按已定的控制规律,决定下一步的控制过程。
(3)实时控制:根据决策,适时地对执行机构发出控制信号,完成控制任务。
2.实时、在线方式和离线方式的含义是什么(1)实时:所谓“实时”,是指信号的输入、计算和输出都是在一定时间范围内完成的,即计算机对输入信息以足够快的速度进行处理,并在一定的时间内作出反应并进行控制,超出了这个时间就会失去控制时机,控制也就失去了意义。
(2)“在线”方式:在计算机控制系统中,如果生产过程设备直接与计算机连接,生产过程直接受计算机的控制,就叫做“联机”方式或“在线”方式。
(3)“离线”方式:若生产过程设备不直接与计算机相连接,其工作不直接受计算机的控制,而是通过中间记录介质,靠人进行联系并作相应操作的方式,则叫做“脱机”方式或“离线”方式。
3.微型计算机控制系统的硬件由哪几部分组成各部分的作用是什么由四部分组成。
(1)主机:这是微型计算机控制系统的核心,通过接口它可以向系统的各个部分发出各种命令,同时对被控对象的被控参数进行实时检测及处理。
主机的主要功能是控制整个生产过程,按控制规律进行各种控制运算(如调节规律运算、最优化计算等)和操作,根据运算结果作出控制决策;对生产过程进行监督,使之处于最优工作状态;对事故进行预测和报警;编制生产技术报告,打印制表等等。
图微机控制系统组成框图(2)输入输出通道:这是微机和生产对象之间进行信息交换的桥梁和纽带。
过程输入通道把生产对象的被控参数转换成微机可以接收的数字代码。
过程输出通道把微机输出的控制命令和数据,转换成可以对生产对象进行控制的信号。
计算机控制系统高金源版课后答案

计算机控制系统高金源版课后答案第1章习题B 习题B1-1 举例说明2-3个你熟悉的计算机控制系统,并说明与常规连续模拟控制系统相比的优点。
B1-2 利用计算机及接口技术的知识,提出一个用同一台计算机控制多个被控参量的分时巡回控制方案。
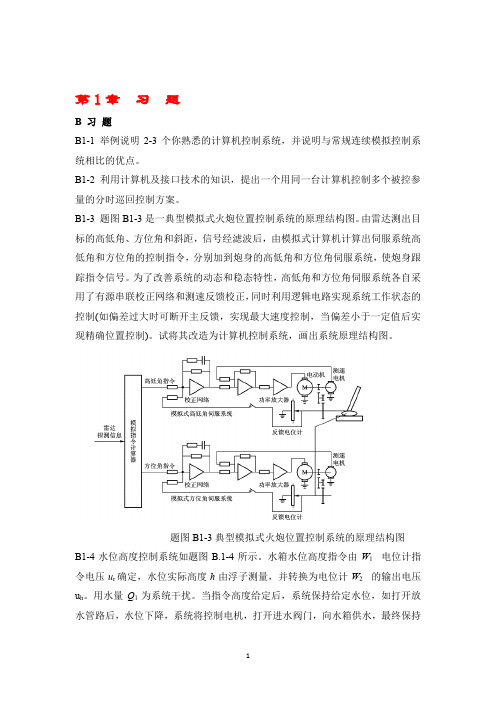
B1-3 题图B1-3是一典型模拟式火炮位置控制系统的原理结构图。
由雷达测出目标的高低角、方位角和斜距,信号经滤波后,由模拟式计算机计算出伺服系统高低角和方位角的控制指令,分别加到炮身的高低角和方位角伺服系统,使炮身跟踪指令信号。
为了改进系统的动态和稳态特性,高低角和方位角伺服系统各自采用了有源串联校正网络和测速反馈校正,同时利用逻辑电路实现系统工作状态的控制(如偏差过大时可断开主反馈,实现最大速度控制,当偏差小于一定值后实现精确位置控制)。
试将其改造为计算机控制系统,画出系统原理结构图。
题图B1-3典型模拟式火炮位置控制系统的原理结构图B1-4水位高度控制系统如题图B.1-4所示。
水箱水位高度指令由W1 电位计指令电压u r确定,水位实际高度h由浮子测量,并转换为电位计W2 的输出电压u h。
用水量Q1 为系统干扰。
当指令高度给定后,系统保持给定水位,如打开放水管路后,水位下降,系统将控制电机,打开进水阀门,向水箱供水,最终保持水箱水位为指令水位。
试把该系统改造为计算机控制系统。
画出原理示意图及系统结构图。
题图B1-4 水箱水位控制系统原理示意图B1-5 题图B1-5为一机械手控制系统示意图。
将其控制器改造为计算机实现,试画出系统示意图及控制系统结构图。
题图B1-5机械手控制系统示意图B1-6题图B1-6为仓库大门自动控制系统示意图。
试将其改造为计算机控制系统,画出系统示意图。
题图B1-6 仓库大门自动控制系统示意图B1-7车床进给伺服系统示意图如题图B1-7所示。
电动机经过齿轮减速机构带动丝杠转动,进而使工作台面实现直线运动。
该系统为了改进系统性能,利用测速电机实现测速反馈。
计算机控制系统高金源版课后答案

计算机控制系统高金源版课后答案
一、单选题
1.以下哪种计算机控制系统是采用时间事件触发技术()
A.分布式控制系统
B.嵌入式控制系统
C.单片机控制系统
D.PLC控制系统
答案:D
2.在控制系统中,控制元件、传感器、执行元件都属于()
A.关节
B.运动学
C.机构
D.构型
答案:D
3.在控制系统中,将实际状态与现实状态比较,发现实际状态与期望状态不一致时,采取措施将之调整到期望状态,该过程叫()
A.状态反馈
B.参数预估
C.控制
D.调节
答案:D
4.下列哪种调节器,不能自动满足控制目标()
A.继电器
B.单片机
C.自整定器
D.PLC
答案:A
5.以下哪种控制型式使用模型预测控制()
A.传统控制
B.人机控制
C.模糊控制
D.预测控制
答案:D
二、多选题
1.计算机控制系统常用的元件包括()
A.变送器
B.执行器
C.控制器
D.传感器
答案:A、B、C、D
2.常见的控制构型()
A.功率控制
B.比例控制
C.存储器控制
D.时间控制
答案:A、B、C、D
3.在计算机控制系统中,常使用的传感器有()
A.温度传感器
B.压力传感器
C.激光传感器
D.光电传感器。
《计算机控制系统》 第三章习题答案

z2Y (z) z 2 y(0) zy(1) 8zY (z) 8zy(0) 12Y ( z) 0
Y (z)
z2
z 8z
12
(z
z 2)(z
6)
1 4
( z
z 6
z
z) 2
查表得 y(k ) 1 (6k 2k ) 4
第三章习题答案
3.8 解:(1)G(z)
Y (s) E*(s)G(s)
G(s)R*(s) G(s)Y *(s)M *(s) G(s)Y *(s)
(z) Y(z)
G(z)
R(z) 1 G(z)M (z) G(z)
Y(z)
RG ( z )
1 GDM1(z) GM 2 (z)
(d ) Y (s) G2 (s)R1(s) G2 (s)M 2 (s)Y *(s)
其中 R1(s) G1(s)R(s) G1(s)M1(s)Y (s)
则 Y (s) G2 (s)G1(s)R(s) G2 (s)G1(s)M1(s)Y (s)
Z
[G(s)]
1 2
( 1
1 eT
z 1
1
1 e3T
z 1
)
第三章习题答案
(4)
G(s)
(s
10 2)2 (s
1)
10[ (s
1 2)2
1 s2
s
1] 1
Z
[G(z)]
10[ 1
1 eT
z1
1
1 e2T
z1
(完整版)计算机控制系统高金源版课后答案
第1章习题B 习题B1-1 举例说明2-3个你熟悉的计算机控制系统,并说明与常规连续模拟控制系统相比的优点。
B1-2 利用计算机及接口技术的知识,提出一个用同一台计算机控制多个被控参量的分时巡回控制方案。
B1-3 题图B1-3是一典型模拟式火炮位置控制系统的原理结构图。
由雷达测出目标的高低角、方位角和斜距,信号经滤波后,由模拟式计算机计算出伺服系统高低角和方位角的控制指令,分别加到炮身的高低角和方位角伺服系统,使炮身跟踪指令信号。
为了改善系统的动态和稳态特性,高低角和方位角伺服系统各自采用了有源串联校正网络和测速反馈校正,同时利用逻辑电路实现系统工作状态的控制(如偏差过大时可断开主反馈,实现最大速度控制,当偏差小于一定值后实现精确位置控制)。
试将其改造为计算机控制系统,画出系统原理结构图。
题图B1-3典型模拟式火炮位置控制系统的原理结构图B1-4水位高度控制系统如题图B.1-4所示。
水箱水位高度指令由W1 电位计指令电压u r确定,水位实际高度h由浮子测量,并转换为电位计W2 的输出电压u h。
用水量Q1 为系统干扰。
当指令高度给定后,系统保持给定水位,如打开放水管路后,水位下降,系统将控制电机,打开进水阀门,向水箱供水,最终保持水箱水位为指令水位。
试把该系统改造为计算机控制系统。
画出原理示意图及系统结构图。
题图B1-4 水箱水位控制系统原理示意图B1-5 题图B1-5为一机械手控制系统示意图。
将其控制器改造为计算机实现,试画出系统示意图及控制系统结构图。
题图B1-5机械手控制系统示意图B1-6题图B1-6为仓库大门自动控制系统示意图。
试将其改造为计算机控制系统,画出系统示意图。
题图B1-6 仓库大门自动控制系统示意图B1-7车床进给伺服系统示意图如题图B1-7所示。
电动机通过齿轮减速机构带动丝杠转动,进而使工作台面实现直线运动。
该系统为了改善系统性能,利用测速电机实现测速反馈。
试将该系统改造为计算机控制系统,画出系统示意图。
计算机控制技术课后习题详解答案

计算机控制技术课后习题详解答案计算机控制技术课后习题答案第一章计算机控制系统概述习题参考答案1.计算机控制系统的控制过程是什么?计算机控制系统的控制过程可归纳为以下三个步骤:(1)实时数据采集:检测控制量的瞬时值并输入计算机。
(2)实时决策:对采集到的表征被控参数的状态量进行分析,并按已定的控制规律,决定下一步的控制过程。
(3)实时控制:根据决策,及时向执行机构发送控制信号,完成控制任务。
2.实时、在线和离线模式的含义是什么?(1)实时:所谓“实时”,是指信号的输入、计算和输出都是在一定时间范围内完成的,即计算机对输入信息以足够快的速度进行处理,并在一定的时间内作出反应并进行控制,超出了这个时间就会失去控制时机,控制也就失去了意义。
(2)“在线”方式:在计算机控制系统中,如果生产过程设备直接与计算机连接,生产过程直接受计算机的控制,就叫做“联机”方式或“在线”方式。
(3)“离线”模式:如果生产工艺设备不直接与计算机连接,其工作不直接由计算机控制,而是通过中间记录介质,则称为“离线”模式或“离线”模式。
3.微型计算机控制系统的硬件由哪几部分组成?各部分的作用是什么?由四部分组成。
(1)主持人:这是微机控制系统的核心。
通过该接口,它可以向系统的各个部分发送各种命令,并实时检测和处理被控对象的被控参数。
主机的主要功能是控制整个生产过程,根据控制规律进行各种控制操作(如调整规律操作、优化计算等)和操作,并根据操作结果做出控制决策;监督生产过程,使其处于最佳工作状态;预测和报警事故;准备生产技术报告、打印和制表等。
1图1.1微机控制系统组成框图(2)输入输出通道:这是微机和生产对象之间进行信息交换的桥梁和纽带。
过程输入通道把生产对象的被控参数转换成微机可以接收的数字代码。
过程输出通道把微机输出的控制命令和数据,转换成可以对生产对象进行控制的信号。
过程输入输出通道包括模拟量输入输出通道和数字量输入输出通道。
计算机控制系统高金源第1章

25
7. 计算机控制系统应用概况
---各种空间飞行器的控制;
---现代工厂自动化中,广泛使用计算机实现 分散控制和集中监视系统。
26
1.2 课程内容 1.设计方法
计算机控制系统是一种混合信号系统
A A’ A/D CPU D/A 被控对象
图(a)
CPU
图(b)
B A/D 被控对象 D/A B’
从图(a)中AA’来看,将计算机系统看作黑箱,系统可以 看成是连续系统; 从图(b)中BB’来看又可将其看成离散信号系统,因此 在实际工程设计时亦有两种方法。 27
正确选择采样间隔时间是需要特别重视的问题。 软件编程值得注意。
28
Hale Waihona Puke 2.课程内容 -----采样理论、模型、分析、设计(与经典控制类似)
微分方程——差分方程; S传递函数——Z传递函数; 稳定性、控制特性分析; 控制器设计; 状态空间方程——离散状态空间方程; 可控可观性; CCS系统实现问题。
计算机发展水平:计算机系统速度慢、价格贵,也不可靠 计算机的作用:显示、报警 局限性:计算机的潜能没有得到充分发挥,需要常规的模拟 控制设备
监督操作方式:操作指导式且设定值控制
21
■ 直接数字控制期(DDC)—约1962年
代表产品:1962年,英国的帝国化学工业公司(ICI)制造的装置,过 程控制中的全部模拟仪表由一台计算机来代替。计算机直接测量224个 变量和控制129个阀门
3
1.1 概述 计算机实现了原控制系统中控制器及指令生成装 置的作用。
G D/A + 功率放大 M
控制 计算机
(包括 硬件及 相应 软件) (内含
天线 定向 位置 指令)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1章习题B 习题B1-1 举例说明2-3个你熟悉的计算机控制系统,并说明与常规连续模拟控制系统相比的优点。
B1-2 利用计算机及接口技术的知识,提出一个用同一台计算机控制多个被控参量的分时巡回控制方案。
B1-3 题图B1-3是一典型模拟式火炮位置控制系统的原理结构图。
由雷达测出目标的高低角、方位角和斜距,信号经滤波后,由模拟式计算机计算出伺服系统高低角和方位角的控制指令,分别加到炮身的高低角和方位角伺服系统,使炮身跟踪指令信号。
为了改善系统的动态和稳态特性,高低角和方位角伺服系统各自采用了有源串联校正网络和测速反馈校正,同时利用逻辑电路实现系统工作状态的控制(如偏差过大时可断开主反馈,实现最大速度控制,当偏差小于一定值后实现精确位置控制)。
试将其改造为计算机控制系统,画出系统原理结构图。
题图B1-3典型模拟式火炮位置控制系统的原理结构图B1-4水位高度控制系统如题图B.1-4所示。
水箱水位高度指令由W1 电位计指令电压u r确定,水位实际高度h由浮子测量,并转换为电位计W2 的输出电压u h。
用水量Q1 为系统干扰。
当指令高度给定后,系统保持给定水位,如打开放水管路后,水位下降,系统将控制电机,打开进水阀门,向水箱供水,最终保持水箱水位为指令水位。
试把该系统改造为计算机控制系统。
画出原理示意图及系统结构图。
题图B1-4 水箱水位控制系统原理示意图B1-5 题图B1-5为一机械手控制系统示意图。
将其控制器改造为计算机实现,试画出系统示意图及控制系统结构图。
题图B1-5机械手控制系统示意图B1-6题图B1-6为仓库大门自动控制系统示意图。
试将其改造为计算机控制系统,画出系统示意图。
题图B1-6 仓库大门自动控制系统示意图B1-7车床进给伺服系统示意图如题图B1-7所示。
电动机通过齿轮减速机构带动丝杠转动,进而使工作台面实现直线运动。
该系统为了改善系统性能,利用测速电机实现测速反馈。
试将该系统改造为计算机控制系统,画出系统示意图。
题图B1-7车床进给伺服系统示意图B1-8 现代飞机普遍采用数字式自动驾驶仪稳定飞机的俯仰角、滚转角和航向角。
连续模拟式控制系统结构示意图如题图B1-8所示。
图中所有传感器、舵机及指令信号均为连续模拟信号。
试把该系统改造为计算机控制系统,画出系统结构图。
题图B1-8 飞机连续模拟式姿态角控制系统结构示意图第2章 习 题A 习题(具有题解)A 2-1 下述信号被理想采样开关采样,采样周期为T ,试写出采样信号的表达式。
1)()1()f t t = 2)()e at f t t -= 3)()e sin()at f t t ω-= 解:1) *0()1()()k f t kT t kT δ∞==-∑;2) *()()()akT k f t kT e t kT δ∞-==-∑;3) *()sin()()akT k f t e kT t kT ωδ∞-==-∑A 2-2 已知f (t ) 的拉氏变换式F (s ) ,试求采样信号的拉氏变换式F * (s )(写成闭合形式) 。
11)()(1)F s s s =+ 12)()(1)(2)F s s s =++解:1) 首先进行拉氏反变换,得()1e t f t -=-;*(1)00()()e(1e)eee kTskTkTskTskT s k k k k F s f kT ∞∞∞∞-----+======-=-∑∑∑∑因为201e 1e e 1ekTs Ts Ts Tsk ∞----==+++⋅⋅⋅⋅⋅=-∑, 1Tse -<,(依等比级数公式) 类似,(1)(1)01e 1ek s T s Tk ∞-+-+==-∑,(1)e 1T s -+<,所以有*(1)11()1e 1e Ts T s F s --+=--- A 2-3 试分别画出10()5e t f t -=及其采样信号*()f t 的幅频曲线(设采样周期T =0.1s)。
解:连续函数10()5e t f t -=的频率特性函数为:5(j )10j F ωω=+。
连续幅频曲线可以用如下MATLAB 程序绘图:step=0.1; Wmax=100; w2=-Wmax;y2=5*abs(1/(10+w2*i)); W=[w2]; Y=[y2]; for w=-Wmax:step:Wmax y=5*abs(1/(10+w*i)); W=[W,w]; Y=[Y ,y]; endplot(W,Y); axis([-Wmax Wmax 0 0.6]) grid结果如题图A 2-3-1所示。
题图A 2-3-1该函数的采样信号幅频谱数学表达式为*s 1(j )(j j )n F F n T ωωω∞=-∞=+∑*s s 1(j )(j j )n F F n T ωωω∞=-∞≈+∑1(j j )Ns n NF n T ωω=-≈+∑显然,采用的项数N 越大,则计算得到的值越逼近于实际值。
这里采用9N =来进行计算。
采样幅频曲线可以用如下MATLAB 程序绘图: T=0.1;%采样周期ws=2*pi/T; %采样频率num=50;%每个采样周期的计算点数step=ws/num;%计算步长Wmax=150;%画图显示的频率范围GW=4*Wmax;%计算的频率范围g0=(1/T)*5*abs(1/(1+10*GW*i)); G00=[g0];g0=(1/T)*5*abs(1/(10+(GW+ws)*i)); G11=[g0];g0=(1/T)*5*abs(1/(10+(GW-ws)*i)); G12=[g0];g0=(1/T)*5*abs(1/(10+(GW+2*ws)*i)); G21=[g0]; g0=(1/T)*5*abs(1/(10+(GW-2*ws)*i)); G22=[g0];g0=(1/T)*5*abs(1/(10+(GW+3*ws)*i)); G31=[g0]; g0=(1/T)*5*abs(1/(10+(GW-3*ws)*i)); G32=[g0];g0=(1/T)*5*abs(1/(10+(GW+4*ws)*i)); G41=[g0]; g0=(1/T)*5*abs(1/(10+(GW-4*ws)*i)); G42=[g0];g0=(1/T)*5*abs(1/(10+(GW+5*ws)*i)); G51=[g0]; g0=(1/T)*5*abs(1/(10+(GW-5*ws)*i)); G52=[g0];g0=(1/T)*5*abs(1/(10+(GW+6*ws)*i)); G61=[g0]; g0=(1/T)*5*abs(1/(10+(GW-6*ws)*i)); G62=[g0];g0=(1/T)*5*abs(1/(10+(GW+7*ws)*i)); G71=[g0]; g0=(1/T)*5*abs(1/(10+(GW-7*ws)*i)); G72=[g0];g0=(1/T)*5*abs(1/(10+(GW+8*ws)*i)); G81=[g0]; g0=(1/T)*5*abs(1/(10+(GW-8*ws)*i)); G82=[g0];g0=(1/T)*5*abs(1/(10+(GW+9*ws)*i)); G91=[g0]; g0=(1/T)*5*abs(1/(10+(GW-9*ws)*i)); G92=[g0];其余类似,最后可得,结果如题图A 2-3-2所示。
题图A 2-3-2A 2-4 若数字计算机的输入信号为10()5t f t e -=,试根据采样定理选择合理的采样周期T 。
设信号中的最高频率为m ω定义为m ()0.1(0)F j F ω=。
解: 5()10F s s =+;5(j )j 10F ωω=+;所以有0.150.1(0)0.0510F ⨯=== 222max 0.05(10)25ω+=由此可得 max 99.5ω=依采样定理得:max 2199s ωω>=rad/sA 2-5 已知信号x =1cos()A t ω,试画出该信号的频谱曲线以及它通过采样器和理想滤波器以后的信号频谱。
设采样器的采样频率分别为4ω1,1.5ω1,和ω1 3种情况。
解释本题结果。
解:1cos()t ω的频谱为脉冲,如题图A 2-5-1所示。
当采样频率s 14ωω=时,采样频谱如题图A 2-5-1所示。
由于满足采样定理,通过理想滤波器后,可以不失真恢复原连续信号。
(见题图A 2-5-2)当采样频率s 11.5ωω=时,采样频谱如题图A 2-5-1所示。
由于不满足采样定理,采样频率发生折叠,当通过理想滤波器后,只保留了折叠后的低频信号,其频率为1111.50.5ωωω-=。
(见题图A 2-5-2)当采样频率s 1ωω=时,采样频谱如题图A 2-5-1所示。
由于不满足采样定理,采样频率发生折叠,折叠后的低频信号位于0ω=处,当通过理想滤波器后,只保留了折叠后的低频信号,其频率为0ω=,即直流信号。
(见题图A 2-5-2)题图A 2-5-1题图A 2-5-2A 2-6 已知信号x =1cos()A t ω,通过采样频率s 13ωω=的采样器以后。
又由零阶保持器恢复成连续信号,试画出恢复以后信号的频域和时域曲线;当s 110ωω=时,情况又如何?比较结果。
解:见题图A 2-6。
s 13ωω=题图A 2-6结果表明,当采样频率较低时,零阶保持器输出阶梯较大,高频分量较大。
A 2-7 已知信号s sin()sin(4),1,3,4,x t y t ω===和若试求各采样信号的x (kT )及y(kT),并说明由此结果所得结论。
解: ()sin()sin(2π/)s x kT kT k ω==;s ()sin(4)sin(8π/)y kT kT k ω==s s 1,()sin(2π/)sin(2π)0x kT k k ωω====;()sin(8π)0y kT k ==s 3,()sin(2π/)sin(2π/3)s x kT k k ωω===;s ()sin(4)sin(8π/)sin(8π/3)sin(2π2π/3)sin(2π/3)y kT kT k k k k k ω====+=。
s s 4,()sin(2π/)sin(2π/4)sin(π/2)x kT k k k ωω====;s ()sin(4)sin(8π/)sin(8π/4)sin(2π)y kT kT k k k ω==== 结果表明,不满足采样定理,高频信号将变为低频信号。
A 2-8 试证明ZOH 传递函数h 1e ()sTG s s--=中的s =0不是G h (s )的极点,而21e ()sTY s s --=中,只有一个单极点s =0。
