二氧化碳吸收与解吸实验
CO2吸收-解吸试验资料

附件6:CO 2吸收-解吸实验资料一、实验流程图本实验是在填料塔中用水吸收空气和CO 2混合气中的CO 2,和用空气解吸水中的CO 2以求取填料塔的吸收传质系数和解吸系数。
图1. 吸收与解吸实验流程图阀门:V A01—吸收液流量调节阀,V A02—吸收塔空气流量调节阀,V A03—解吸塔空气流量调节阀,V A04—解吸液流量调节阀,V A05—吸收塔CO 2流量调节阀,V A06—风机旁路调节阀,V A07—吸收泵放净阀,V A08—水箱放净阀,V A09—解吸液回流阀,V A10—吸收泵回流阀,AI01—吸收塔进气采样阀, AI02 —吸收塔排气采样阀, AI03—解吸塔进气采样阀, AI04—解吸塔排气采样阀,AI05—吸收塔塔顶液体采样阀,AI06—解吸塔塔顶液体采样阀,AI07—解吸塔塔底液体采样阀,V A11—吸收塔放净阀,V A12—解吸塔放净阀,V A13—缓冲罐放净阀风压6kPa,风量55m3/hCO2钢瓶温度:TI01—液相温度流量:FI01—吸收塔空气流量,FI02—吸收液流量,FI03—解吸塔空气流量,FI04—解吸液流量,FI05—CO2气体流量图2. CO2吸收‐解吸实验装置实物照片二、实验设备结构参数吸收塔:塔内径100 mm;填料层高550 mm;填料为陶瓷拉西环;丝网除沫解吸塔:塔内径100 mm;填料层高550 mm;填料为φ6不锈钢θ环;丝网除沫风机:旋涡气泵,6kPa,55m3/h;吸收泵:扬程12m,流量14L/min;解吸泵:扬程14m,流量3.6m3/h;饱和罐:PE,50L温度:Pt100传感器流量计:水涡轮流量计:200~1000L/h;气相质量流量计:0~1.2 m3/h;气相转子流量计:1~4 L/min;三、实验注意事项1.在实验中,两个水流量计的读数要尽量保持一致;2.测取液泛数据点时,等待时间不要过长,避免液泛过于强烈导致液体喷出塔外;3.调节解吸塔的空气流量时要求在不液泛的情况下,尽量维持在较大的气量;4.泵是机械密封,必须在泵有水时使用,若泵内无水空转,易造成机械密封件升温损坏而导致密封不严,严禁泵内无水空转;5.液相采样和滴定时,要保证规范操作,以免影响测定和数据分析;6.实验结束时,注意按顺序关闭风机、水泵和阀门等。
乙醇胺-二甲基亚砜无水溶液吸收-解吸二氧化碳性能

科 技·TECHNOLOGY62乙醇胺-二甲基亚砜无水溶液吸收-解吸二氧化碳性能文_姚靖1,2 梁怀勇1,2 潘艳艳1,2 周小斌1,21. 桂林理工大学环境科学与工程学院2.广西环境污染控制理论与技术重点实验室摘要:本研究以乙醇胺(MEA)为活性组分,二甲基亚枫(DMSO)为溶剂,配制MEA-DMSO无水吸收剂用于CO2捕集。
研究表明,在40℃下,MEA-DMSO的CO2吸收负荷可达0.71mol·mol-1,该结果比传统MEA水溶液的吸收负荷高24.6%;在120℃下,MEA-DMSO的最大CO2解吸速率和解吸负荷分别为0.23mol·min-1·kg-1和0.38mol·mol-1,远优于MEA水溶液;经历6次循环吸收,MEA-DMSO的CO2负荷仍可保持0.33mol·mol-1。
以上结果说明MEA-DMSO具有良好的CO2吸收-解吸性能,是一种颇具应用潜力的CO2吸收剂。
关键词:CO2捕集;乙醇胺;二甲基亚枫;吸收-解吸性能基金项目:广西自然科学基金项目(2020GXNSFBA297071)、广西科技计划项目(桂科AD18126018)和桂林理工大学科研基金项目(GUTQDJJ2019123)资助。
CO2 Absorption and Desorption Performance of Monoethanolamine-dimethylSulfoxide Nonaqueous SolutionYAO Jing LIANG Huai-yong PAN Yan-yan ZHOU Xiao-bin[ Abstract ] A nonaqeous absorbent comprising of monoethanolamine (MEA) and dimethyl sulfoxide (DMSO) was proposed for CO2 capture in this study. The experimental results showed that the CO2 absorption loading of the MEA-DMSO solution could realize 0.71 mol·mol-1 at 40℃, which was 24.6% higher than that of the conventional MEA aqueous solution. In addition, the MEA-DMSO solution had a high maximum desorption rate (0.23mol·min-1·kg-1) and desorption loading (0.38mol·mol-1) at 120℃, clearly outperforming the MEA aqueous solution. Moreover, the MEA-DMSO solution could be used repeatedly, its CO2 absorption loading was still 0.33mol·mol-1 after six absorption cycles. Therefore, the MEA-DMSO solution may be a promising candidate for CO2 capture due to its superior CO2 absorption-desorption performance.[ Key words ] CO2 capture; monoethanolamine; dimethyl sulfoxide;absorption-desorption performance减缓气候变暖,对CO2实施控制与减排已成为全球共识。
实验十CO2吸收专业实验讲义 - CO2分析
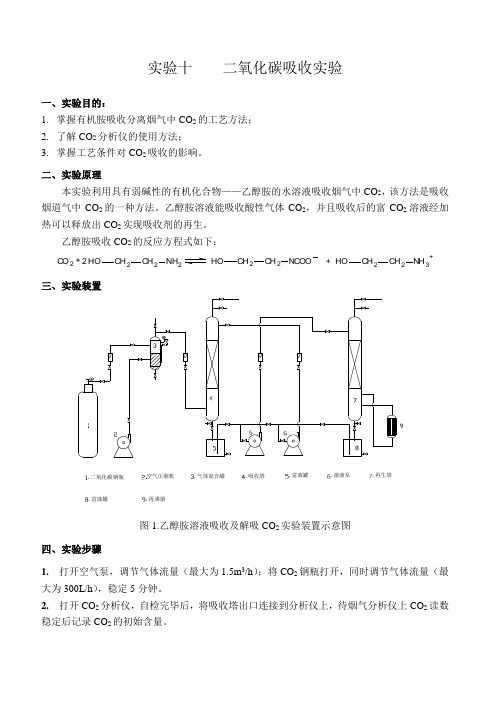
实验十 二氧化碳吸收实验一、实验目的:1. 掌握有机胺吸收分离烟气中CO 2的工艺方法;2. 了解CO 2分析仪的使用方法;3. 掌握工艺条件对CO 2吸收的影响。
二、实验原理本实验利用具有弱碱性的有机化合物——乙醇胺的水溶液吸收烟气中CO 2,该方法是吸收烟道气中CO 2的一种方法。
乙醇胺溶液能吸收酸性气体CO 2,并且吸收后的富CO 2溶液经加热可以释放出CO 2实现吸收剂的再生。
乙醇胺吸收CO 2的反应方程式如下:CO2+OH CH 2CH 2NH 22OH CH 2CH 2NCOOOH CH 2CH 2NH 3++三、实验装置.二氧化碳钢瓶.气体混合罐空气压缩机.吸收塔.富液罐.溶液泵.再生塔.贫液罐.再沸器工艺流程图图1.乙醇胺溶液吸收及解吸CO 2实验装置示意图 四、实验步骤1. 打开空气泵,调节气体流量(最大为1.5m 3/h );将CO 2钢瓶打开,同时调节气体流量(最大为300L/h ),稳定5分钟。
2. 打开CO 2分析仪,自检完毕后,将吸收塔出口连接到分析仪上,待烟气分析仪上CO 2读数稳定后记录CO 2的初始含量。
3.打开吸收塔溶液泵,调整进液流量(最大16L/h),记录吸收温度,待吸收稳定后记录分析仪上CO2的含量。
4.调整溶液泵的进液流量(至少调节5个流量),吸收稳定5分钟后,记录分析仪上CO2的含量。
五、注意事项注意观察储液罐液位,避免液位过低。
六、报告要求1.简明叙述实验目的、原理、操作要点。
不必绘制设备图;2.对结果进行讨论,得到一定吸收温度、一定CO2初始浓度下,吸收剂流量与CO2吸收率的关系图。
七、讨论题1.乙醇胺是否按照理论值完全吸收CO2;2.说明一下吸收剂流量对CO2出口浓度有何影响;3.你对自己的实验结果是否满意,如何解释实验失败的原因。
你有什么需要声明的问题。
化工原理实验装置图

2.二氧化碳吸收与解吸实验装置流程示意图(见图四)图四二氧化碳吸收与解吸实验装置流程示意图1- CO2流量计;2- CO2瓶减压阀;3- CO2钢瓶;4-吸收用空气流量计;5- 吸收用气泵;6、8-喷头; 7、19- 水箱放水阀;9- 解吸塔;10- 解吸塔塔底取样阀;11- 解吸液储槽;12、15- U型管液柱压强计;13- 吸收液流量计;14-解吸液液泵;16- 吸收液储槽;17- 吸收塔;18- 吸收塔塔底取样阀;20- 解吸液流量计;21- 吸收液液泵;22-空气流量计;23- 空气旁通阀;24- 风机2.离心泵性能测定流程示意图见图一、仪表面板示意图见图二:图一离心泵性能测定流程示意图1-水箱;2-泵入口真空表控制阀;3-离心泵;4-流量调节阀;5-泵出口压力表控制阀;6-泵入口真空表;7-泵出口压力表;8-涡轮流量计;9-灌泵入口; 10-灌水控制阀门;11-排水阀;12-底阀图二设备面板示意图四、实验装置的基本情况1.实验装置流程示意图(如图一所示):图-1 实验装置流程示意图1-调速器;2-电动搅拌器;3、5、6、7、9、16-阀门;4-虑浆槽;8-压力表;10-泥浆泵;11-后滤液入口阀;12-前滤液入口阀;13-后滤液出口阀;14-前滤液出口阀; 15-滤液槽; 17-过滤机组;18-压紧装置;19-反洗水箱;1.实验设备流程图(如图一所示):图一精馏实验装置流程图1-储料罐;2-进料泵;3-放料阀;4-料液循环阀;5-直接进料阀;6-间接进料阀;7-流量计;8-高位槽;9-玻璃观察段;10-精馏塔;11-塔釜取样阀;12-釜液放空阀;13-塔顶冷凝器;14回流比控制器;15-塔顶取样阀;16-塔顶液回收罐;17-放空阀;18-塔釜出料阀;19-塔釜储料罐;20-塔釜冷凝器;21-第六块板进料阀;22-第七块板进料阀;23-第八块板进料阀;T1-T12-温度测点3.洞道式干燥器实验装置流程示意图(见图一)图一洞道式干燥器实验装置流程示意图1-废气排出阀;2-废气循环阀;3-空气进气阀;4-洞道干燥器;5-风机;6-干燥物料;7-重量传感器;8-干球温度计;9-孔板流量计;10-湿球温度计;11-空气进口温度计;12-加热器;13-干球温度显示控制仪表;14-湿球温度显示仪表;15-进口温度显示仪表;16-流量压差显示仪表;17-重量显示仪表;。
二氧化碳的吸收与解析,实验的误差分析。

二氧化碳的吸收与解析,实验的误差分析。
二氧化碳的吸收与解析是化学分析学中一种基本的定量分析方法。
常用于测定空气、工业废气、汽车尾气、大气等中的二氧化碳含量。
方法是利用KOH(氢氧化钾)溶液可以吸收二氧化碳,并且有一个明确的化学反应式:
CO2 + 2KOH → K2CO3 + H2O
因此可以通过测定KOH溶液的消耗量来定量二氧化碳含量。
在实验中,误差可能产生于如下方面:
1. 试剂纯度:如果试剂的纯度不能保证,可能会影响吸收和解析过程中的化学反应,进而影响测量结果。
2. 装置漏气:实验装置如果出现气泡漏气等问题,会导致二氧化碳的流失,测量结果将不准确。
3. 操作技巧:实验操作不规范,包括倒液不准确、加热温度不够等等,也会导致实验误差。
4. 仪器准确性:实验中所使用的仪器可能存在读数误差和灵敏度等问题,这也可能导致测量结果的误差。
因此,在实验过程中,我们需要严格控制实验条件、使用高纯度试剂、保证操作技巧规范、使用准确的仪器和科学的数据处理方法,以尽可能减小误差并获得准确的二氧化碳含量测量结果。
吸收解吸实验
化工原理课程实验报告L K —以气相分压表示推动力的总传质系数,或简称为液相传质总系数,1-⋅s m 。
若气液相平衡关系遵循享利定律:A A Hp C =,则:l g G HK k K 111+= lg L k k H K 11+= (3-24)C A1,F L图3-10 双膜模型的浓度分布图 图3-11 填料塔的物料衡算图 当气膜阻力远大于液膜阻力时,则相际传质过程式受气膜传质速率控制,此时,g G k K =;反之,当液膜阻力远大于气膜阻力时,则相际传质过程受液膜传质速率控制,此时,l L k K =。
本实验采用转子流量计测得CO2、空气和水的流量。
根据实验条件(温度和压力)折算为实际流量,最后按有关公式换算成CO2、空气和水的摩尔流量。
填料塔物料衡算如图3-11所示。
气体校正公式:v =√ρ₀ρ (3-26)式中:V 。
——流量计读数;V ——被测流体实际流量;ρ₀,ρ——标定流体和被测流体在标定状态(T 。
,p 。
)下的密度。
测定塔顶和塔底液相组成C A1和C A2,利用滴定法测定吸收液浓度,根据吸收液消耗盐酸体积量可计算塔底吸收液浓度:C A1=2C Ba(OH)2V Ba(OH)2−C HCl V HCl2V 溶液(3-27)吸收剂(水)中含有少量的二氧化碳,根据吸收剂(水)滴定消耗盐酸体积量可计算出塔顶吸收剂(水)中CO ,浓度为:dh相 界 面距离液 膜气膜浓度图1 二氧化碳吸收与解吸实验装置流程示意图1-CO2钢瓶;2-减压阀;3-CO2流量计;4-吸收风机;5-吸收塔空气流量计;6-吸收水泵;7-吸收塔水流量计;8-吸收尾气传感器;9-吸收塔;10、15-液封;11-解吸液罐;12-解吸尾气传感器;13-吸收液罐;14-解吸塔;16-压差计;17-解吸水泵;18-解吸塔水流量计;19-解吸风机;20-解吸塔空气流量计; 21-空气旁路调节阀;22-π型管。
二氧化碳吸收与解吸实验问题讨论

二氧化碳吸收与解吸实验问题讨论1. 引言二氧化碳(CO2)是一种重要的温室气体,对地球的气候变化起着重要作用。
随着人类经济的发展和工业化进程的加快,CO2的排放量不断增加,导致大气中CO2的浓度上升,从而引发全球气候变化的问题。
因此,了解二氧化碳的吸收与解吸过程对于应对气候变化具有重要意义。
本实验旨在探究二氧化碳的吸收与解吸过程,分析其对环境的影响,并提出可能的解决方案。
本文将从实验的原理、实验方法、实验结果以及对结果的讨论等方面展开讨论。
2. 实验原理二氧化碳的吸收与解吸是通过物质在不同条件下的相变过程实现的。
一般来说,二氧化碳的吸收过程与温度、压力、浓度等因素有关。
在适当的温度和压力下,二氧化碳会从空气中溶解到溶液中;而在不同的条件下,溶液中的二氧化碳会释放出来,实现解吸过程。
3. 实验方法本实验采用溶液的吸收与解吸方法,具体的实验步骤如下:3.1 实验材料•二氧化碳气体•水•盐酸溶液•实验装置:气体收集瓶、试管、密封橡胶塞、恒温水浴器等3.2 实验步骤1.准备实验装置:将气体收集瓶、试管等清洗干净,放入恒温水浴器中加热,使其达到一定温度,以保证实验的稳定性。
2.将一定量的水倒入气体收集瓶中,加入少量盐酸溶液。
3.用实验装置连接好气体收集瓶与试管,确保气体通道畅通。
4.打开二氧化碳气体源,将二氧化碳气体缓慢通入试管中,观察二氧化碳溶解的过程。
5.当二氧化碳的通入量足够大时,观察溶液中是否有气泡产生,观察是否产生白色固体沉淀。
6.停止二氧化碳的通入,观察溶液中二氧化碳的解吸过程,记录相应的数据。
4. 实验结果与讨论经过实验观察,我们发现在二氧化碳通入试管的过程中,溶液中的二氧化碳逐渐增多,溶液颜色也发生了变化,变得更加浑浊。
同时,还观察到有气泡产生,并且溶液中产生了白色固体沉淀,这是由于二氧化碳与盐酸反应生成了碳酸,产生的碳酸较不溶于水,所以会形成沉淀。
在停止通气后,我们观察到沉淀逐渐消失,溶液的颜色变得更加清澈,气泡也停止产生。
二氧化碳的吸收与解吸实验报告

二氧化碳的吸收与解吸实验报告摘要:本实验旨在研究二氧化碳的吸收与解吸过程,并观察其对环境条件的敏感性。
通过使用氢氧化钠(NaOH)溶液作为吸收剂,测量二氧化碳溶液中的pH值和溶液的体积变化,以评估吸收和解吸的效果。
实验结果表明,二氧化碳能够被NaOH 溶液吸收,并在一定条件下释放。
1. 引言二氧化碳(CO2)是一种常见的气体,它在大气中的浓度增加与全球气候变化密切相关。
因此,研究CO2的吸收与解吸过程对于理解和控制大气中CO2浓度的变化至关重要。
本实验旨在模拟CO2吸收与解吸的过程,并观察其在不同条件下的反应情况。
2. 实验步骤2.1 实验材料:-氢氧化钠(NaOH)固体-蒸馏水-二氧化碳气源- pH计-称量器具-实验室玻璃器皿2.2 实验过程:(1)准备NaOH溶液:称取适量的NaOH固体,加入一定量的蒸馏水中,搅拌溶解。
(2)装置实验装置:将NaOH溶液倒入实验室玻璃器皿中,置于实验台上。
(3)测量初始条件:使用pH计测量NaOH溶液的初始pH 值,并记录初始溶液的体积。
(4)注入CO2气体:将二氧化碳气体缓慢地通入NaOH溶液中,观察溶液的变化,并记录每次通气的时间和CO2气体的体积。
(5)测量pH值:定期使用pH计测量溶液的pH值,并记录下来。
(6)测量溶液体积:测量在吸收和解吸过程中溶液的体积变化,并记录下来。
3. 实验结果实验期间,我们记录了二氧化碳气体通入溶液的时间、CO2气体的体积以及溶液的pH值变化。
根据实验结果,我们绘制了相应的数据表和图表。
4. 讨论与分析根据实验结果,我们观察到二氧化碳气体通入NaOH溶液后,溶液的pH值逐渐下降,说明二氧化碳被NaOH吸收并生成了碳酸。
随着二氧化碳的继续通入,溶液的体积也有所增加,这是由于二氧化碳的溶解导致溶液的体积增大。
在观察解吸过程时,我们停止通入二氧化碳气体,溶液开始释放二氧化碳,并逐渐恢复到初始状态。
此时,溶液的pH 值逐渐升高,说明碳酸在解吸过程中分解为二氧化碳和水,并释放出二氧化碳气体。
CO2吸收实验
CO2吸收实验一、实验目的1.了解填料吸收塔的结构、性能和特点,练习并掌握填料塔操作方法;通过实验测定数据的处理分析,加深对填料塔流体力学性能基本理论的理解,加深对填料塔传质性能理论的理解。
2.掌握填料吸收塔传质能力和传质效率的测定方法,练习对实验数据的处理分析。
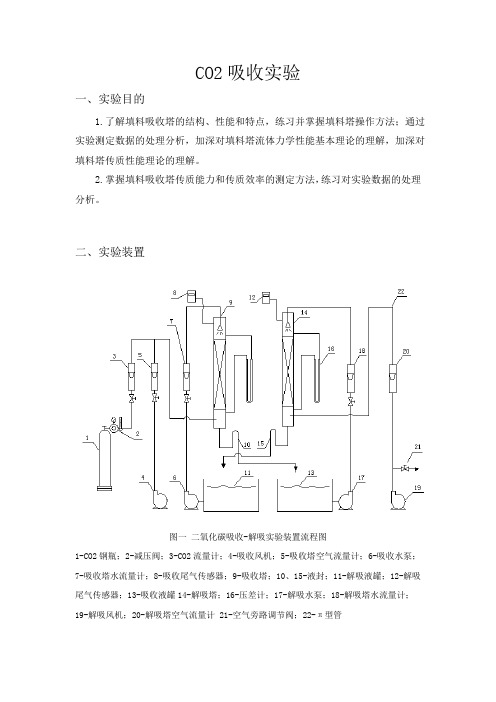
二、实验装置图一二氧化碳吸收-解吸实验装置流程图1-CO2钢瓶;2-减压阀;3-CO2流量计;4-吸收风机;5-吸收塔空气流量计;6-吸收水泵;7-吸收塔水流量计;8-吸收尾气传感器;9-吸收塔;10、15-液封;11-解吸液罐;12-解吸尾气传感器;13-吸收液罐14-解吸塔;16-压差计;17-解吸水泵;18-解吸塔水流量计;19-解吸风机;20-解吸塔空气流量计 21-空气旁路调节阀;22-π型管三、实验原理传质性能:吸收系数是决定吸收过程速率高低的重要参数,实验测定可获取吸收系数。
对于相同的物系及一定的设备(填料类型与尺寸),吸收系数随着操作条件及气液接触状况的不同而变化。
根据双膜模型的基本假设,气侧和液侧的吸收质A 的传质速率方程可分别表达为:气膜 )(Ai A g A p p A k G -= (1-1) 液膜 )(A Ai l A C C A k G -= (1-2)式中:A G —A 组分的传质速率,1-⋅s kmoI ;A —两相接触面积,m 2;A P —气侧A 组分的平均分压,Pa ;Ai P —相界面上A 组分的平均分压,Pa ;A C —液侧A 组分的平均浓度,3-⋅m kmolAi C —相界面上A 组分的浓度3-⋅m kmolg k —以分压表达推动力的气侧传质膜系数,112---⋅⋅⋅Pa s m kmol ;l k —以物质的量浓度表达推动力的液侧传质膜系数,1-⋅s m 。
以气相分压或以液相浓度表示传质过程推动力的相际传质速率方程又可分别表达为:)(*-=A A G A p p A K G (1-3))(A A L A C C A K G -=*(1-4)式中:*A p —液相中A 组分的实际浓度所要求的气相平衡分压,Pa ;*A C —气相中A 组分的实际分压所要求的液相平衡浓度,3-⋅m kmol ;G K —以气相分压表示推动力的总传质系数或简称为气相传质总系数,112---⋅⋅⋅Pa s m kmol ;L K —以气相分压表示推动力的总传质系数,或简称为液相传质总系数,1-⋅s m 。
二氧化碳的吸收与解吸实验思考题

二氧化碳的吸收与解吸实验思考题一、实验介绍二氧化碳是一种重要的气体,它在地球大气中起着重要的作用。
本实验主要是探究二氧化碳在水中的溶解过程,以及二氧化碳的吸收与解吸过程。
二、实验原理1. 二氧化碳在水中的溶解二氧化碳可以溶解在水中,形成碳酸。
当空气中的二氧化碳与水接触时,会发生以下反应:CO2 + H2O → H2CO3其中,H2CO3是碳酸。
2. 二氧化碳的吸收与解吸当空气中含有较多的二氧化碳时,它会被水吸收。
相反地,当空气中含有较少的二氧化碳时,水会释放出已经溶解在其中的二氧化碳。
三、实验步骤1. 准备一个透明的玻璃杯,并将其放置在平坦表面上。
2. 在玻璃杯里加入适量的自来水(约半杯)。
3. 将一张白纸放在玻璃杯下方,并将玻璃杯移到白纸上。
4. 将一个小碗放在玻璃杯旁边,并将其里面装满了小颗粒的碳酸钠。
5. 将一根吸管插入碳酸钠中,并将其另一端放在玻璃杯内,但不要让吸管接触到水面。
6. 观察玻璃杯内的水,当吸管中的气体流入水中时,会产生气泡。
这是因为二氧化碳溶解在水中时会产生气泡。
7. 等待几分钟,观察气泡是否消失。
如果消失了,说明二氧化碳已经被完全溶解在水中。
四、实验思考题1. 为什么二氧化碳会被水吸收?答:二氧化碳可以与水反应生成碳酸,而这个反应是一个可逆反应。
当空气中含有较多的二氧化碳时,它会被水吸收。
相反地,当空气中含有较少的二氧化碳时,水会释放出已经溶解在其中的二氧化碳。
2. 为什么加入小颗粒的碳酸钠?答:加入小颗粒的碳酸钠可以增加实验的效果,因为碳酸钠可以与酸反应,产生二氧化碳。
当吸管中的气体流入水中时,会产生气泡。
这是因为二氧化碳溶解在水中时会产生气泡。
3. 为什么要等待几分钟?答:等待几分钟是为了让二氧化碳充分地溶解在水中。
如果没有等待足够的时间,实验结果可能不准确。
4. 实验过程中有哪些注意事项?答:实验过程中需要注意以下事项:(1)使用透明的玻璃杯;(2)将玻璃杯放在平坦表面上;(3)不要让吸管接触到水面;(4)使用小颗粒的碳酸钠;(5)等待足够的时间,让二氧化碳充分地溶解在水中。
二氧化碳吸收与解吸实验报告

二氧化碳吸收与解吸实验报告一、实验目的通过实验观察二氧化碳在不同环境下的吸收和解吸情况,了解二氧化碳在自然界中的循环过程。
二、实验材料二氧化碳气体、水、氢氧化钠溶液、酚酞指示剂、容量瓶、试管、滴定管、酒精灯等。
三、实验原理二氧化碳在自然界中的循环过程包括二氧化碳的吸收和解吸,其中吸收后的二氧化碳可以被植物利用进行光合作用,解吸后的二氧化碳则会进入大气层中。
实验中,利用二氧化碳和水反应生成碳酸酸,再通过与氢氧化钠溶液反应,使碳酸酸转化为碳酸钠,观察其变化。
四、实验步骤1. 取一定量的二氧化碳气体,放入容量瓶中。
2. 加入一定量的水,使其中溶解的二氧化碳达到饱和状态。
3. 取一定量的氢氧化钠溶液,滴入试管中。
4. 加入少量的酚酞指示剂,观察其颜色变化。
5. 缓慢将第2步中的饱和二氧化碳气体通过试管中的氢氧化钠溶液中。
6. 观察指示剂的变化,记录颜色变化时间和颜色变化程度。
7. 重复实验,改变环境温度等条件,观察结果。
五、实验结果在常温下,通过饱和二氧化碳气体通入氢氧化钠溶液中,指示剂由粉红色变为无色,表明有二氧化碳吸收反应发生。
当环境温度提高时,吸收二氧化碳的速度会加快,颜色变化时间会缩短,颜色变化程度也会加深。
六、实验分析本实验通过观察酚酞指示剂颜色变化,可以判断二氧化碳气体是否被吸收。
在自然界中,植物通过光合作用吸收二氧化碳气体,并利用其进行生长等活动。
同时,二氧化碳也会通过植物的呼吸、动物的呼吸和燃烧等过程释放出来,进入大气层中。
通过本实验的观察,我们可以更加深入地了解二氧化碳在自然界中的循环过程。
七、实验结论通过本实验,我们可以得出以下结论:1. 二氧化碳气体可以被水吸收,并与水反应生成碳酸酸。
2. 碳酸酸可以与氢氧化钠溶液反应,生成碳酸钠。
3. 通过酚酞指示剂的变化,可以判断二氧化碳气体是否被吸收。
4. 环境温度的变化会影响二氧化碳的吸收速率。
八、实验注意事项1. 实验过程中要小心操作,防止产生危险。
二氧化碳吸收与解吸

六、附实验数据计算举例:1.实验数据计算及结果(以实验中所取得数据的第二组数据为例): (1)填料塔流体力学性能测定(以填料塔干填料数据为例)空气转子流量计读数:0.5m 3/h ; 填料层压降U 管读数:2.0 mmH 2O空塔气速:07.0050.0)4/36005.024/36002=⨯⨯⋅⨯=ππ(=)(iD Vu (m/s ) 单位填料层压降5.28.02==∆ Z P (mmH 2O/m )在对数坐标纸上以空塔气速u 为横坐标,Z P ∆为纵坐标作图,标绘Z P ∆~u 关系曲线,见图三。
(2)传质实验(以第一组数据为例)CO 2转子流量计读数0.200(m 3/h )、CO 2转子流量计处温度 16.1(℃) 16.1℃下二氧化碳气体密度2co ρ=1.976 Kg/m 3CO 2实际流量V CO2=2co Air ρρ=976.1204.1=0.156(m 3/h )空气转子流量计读数V Air =0.500 (m 3/h )(a ). 吸收液浓度计算吸收液消耗盐酸体积V 1=30.10 ml ,则吸收液浓度为:溶液V V C V C C HC HC OH Ba OH Ba A 22ll 2)()(12-==1021.30111.01017982.02⨯⨯⨯⨯-=0.01277 mol/L(b ).吸收剂二氧化碳浓度计算因纯水中含有少量的二氧化碳,所以纯水滴定消耗盐酸体积V=32.3ml ,则塔顶水中CO 2浓度为:溶液V V C V C C HClHCl OH Ba OH Ba A 222)()(22-==1023.32111.01017982.02⨯⨯-⨯⨯=0.00056mol/L(c ).塔底的平衡浓度计算塔底液温度t =7.9℃,由表一可查得CO 2亨利系数 E=0.9735×105 KPa 则CO 2的溶解度常数为EM H ww 1⨯=ρ =8109735.01181000⨯⨯=5.706×10-7 ( 13--⋅⋅Pa m kmol ) 塔底混和气中二氧化碳含量 y 1=5.0156.0156.0+=0.238=*1A C H ×P A1=H ×y 1×P 0=5.7×10-7×0.2857×101325=0.016521 (mol/l )(d ).塔顶的平衡浓度计算 由物料平衡得塔顶二氧化碳含量因为L(C A2- C A1)=V(y 1-y 2) 则y 2=y 1-VC C L A A )(12-⨯=0.238-)4.225.0()00056.001277.0()100040(-⨯=0.216*2A C = H ×P A2=H ×y 2×P 0=5.706×10-7×0.2638×101325=0.015256 mol/L(e ).液相平均推动力计算1*12*21*12*21221m ln )()ln A A A A A A A A A A A A A C C C C C C C C C C C C C -----∆∆∆∆∆(=-= =01277.001249.000056.00137.0ln)01277.0016521.0()00056.00137.0(-----= 0.0049(kmol/m 3)因本实验采用的物系不仅遵循亨利定律,而且气膜阻力可以不计,在此情况下,整个传质过程阻力都集中于液膜,属液膜控制过程,则液侧体积传质膜系数等于液相体积传质总系数,即AmA A sL L l C C C hS V a K a k ∆-⋅==21 =0049.0)00056.001277.0(4/)050.0(14.38.03600/104023-⨯⨯⨯⨯- =0.0044 (m/s)实验结果列表如下:干填料时△P/z ~u 关系测定(见表二) 湿填料时△P/z ~u 关系测定(见表三) 填料吸收塔传质实验技术数据(见表四)ZP ∆~u 关系曲线 (见图-3)表二、干填料时△P/z~u关系测定表三湿填料时△P/z~u关系测定表四:填料吸收塔传质实验技术数据表。
二氧化碳吸收与解吸实验解读

二氧化碳吸收与解吸实验一、实验目的1.了解填料吸收塔的结构、性能和特点,练习并掌握填料塔操作方法;通过实验测定数据的处理分析,加深对填料塔流体力学性能基本理论的理解,加深对填料塔传质性能理论的理解。
2.掌握填料吸收塔传质能力和传质效率的测定方法,练习实验数据的处理分析。
二、实验内容1. 测定填料层压强降与操作气速的关系,确定在一定液体喷淋量下的液泛气速。
2. 固定液相流量和入塔混合气二氧化碳的浓度,在液泛速度下,取两个相差较大的气相流量,分别测量塔的传质能力(传质单元数和回收率)和传质效率(传质单元高度和体积吸收总系数)。
3. 进行纯水吸收二氧化碳、空气解吸水中二氧化碳的操作练习,同时测定填料塔液侧传质膜系数和总传质系数。
三、实验原理:气体通过填料层的压强降:压强降是塔设计中的重要参数,气体通过填料层压强降的大小决定了塔的动力消耗。
压强降与气、液流量均有关,不同液体喷淋量下填料层的压强降P ∆与气速u 的关系如图一所示:图一 填料层的P ∆~u 关系当液体喷淋量00=L 时,干填料的P ∆~u 的关系是直线,如图中的直线0。
当有一定的喷淋量时,P ∆~u 的关系变成折线,并存在两个转折点,下转折点称为“载点”,上转折点称为“泛点”。
这两个转折点将P ∆~u 关系分为三个区段:既恒持液量区、载液区及液泛区。
传质性能:吸收系数是决定吸收过程速率高低的重要参数,实验测定可获取吸收系数。
对于相同的物系及一定的设备(填料类型与尺寸),吸收系数随着操作条件及气液接触状况的不同而变化。
1.二氧化碳吸收-解吸实验根据双膜模型的基本假设,气侧和液侧的吸收质A 的传质速率方程可分别表达为 气膜 )(Ai A g A p p A k G -= (1) 液膜 )(A Ai l A C C A k G -= (2) 式中:A G —A 组分的传质速率,1-⋅s kmoI ;A —两相接触面积,m 2;A P —气侧A 组分的平均分压,Pa ; Ai P —相界面上A 组分的平均分压,Pa ;A C —液侧A 组分的平均浓度,3-⋅m kmol Ai C —相界面上A 组分的浓度3-⋅m kmolg k —以分压表达推动力的气侧传质膜系数,112---⋅⋅⋅Pa s m kmol ;l k —以物质的量浓度表达推动力的液侧传质膜系数,1-⋅s m 。
实验10 吸收与解吸实验

⑵ ΔYm的计算
根据测出的水温可插值求出亨利常数E[atm],本实验为P=1 atm 则m=E/P
Ym
Y2 ln
Y1 Y2
Y1பைடு நூலகம்
Y2 Y2 Ye2 Y1 Y1 Ye1
ye2 m x2 ye1 m x1
根据公式 Y y 1 y
将ye换算成 Ye
三、实验装置及流程
1.装置流程示意图
气相质量流量计:0~1.5 m3/h,0~18 m3/h 气相转子流量计:1~4 L/min
四、操作步骤
1.单独吸收实验
⑴ 接通自来水,开启水流量调节阀VA01到第一个流量(按750、600、450、300 L/h 水量调节,从大流量开始做,最后是小流量,便于做解吸实验)。 ⑵ 全开VA02,启动风机,逐渐关小VA08,可微调VA07使FI01风量在0.4~0.5[m3/h]。 实验过程中维持此风量不变。 ⑶ 开启VA05,全开VA07,开启CO2钢瓶总阀,微开减压阀,根据CO2流量计读数 可微调VA07使CO2流量在约2~3[L/min]。实验过程中维持此流量不变。
3.单独解吸实验
⑴ 在单独解吸实验时,因液体中CO2浓度未知,因此我们需要做饱和液体,只要测得 液体温度,即可根据亨利定律求得其饱和浓度。所以,需要在饱和罐中制作饱和液。 在上面实验结束时,在饱和罐中有不饱和的液体(若没有作吸收解吸实验,可将水直 接从吸收塔送入饱和罐)。 ⑵ 启动加碳泵,开启VA06,全开VA07,开启CO2钢瓶总阀,微开减压阀,根据CO2 流量计读数可微调VA07使CO2流量在约2~3 [L/min],实验过程中维持此流量不变, 约10分钟后,饱和罐内的溶液饱和。
五、注意事项
1.在启动风机前,应检查三相动力电是否正常,若缺相,及易烧坏电 机;为保证安全,检查接地是否正常; 2.因为泵是机械密封,必须在泵有水时使用,若泵内无水空转,易造 成机械密封件升温损坏而导致密封不严,需专业厂家更换机械密封。 因此,严禁泵内无水空转!!!! 3.长期不用时,应将设备内水放净。 4.严禁学生打开电柜,以免发生触电。
二氧化碳吸收与解吸实验

二氧化碳吸收与解吸实验一、实验目的1.了解填料吸收塔的结构、性能和特点,练习并掌握填料塔操作方法;通过实验测定数据的处理分析,加深对填料塔流体力学性能基本理论的理解,加深对填料塔传质性能理论的理解。
2.掌握填料吸收塔传质能力和传质效率的测定方法,练习实验数据的处理分析。
二、实验内容1. 测定填料层压强降与操作气速的关系,确定在一定液体喷淋量下的液泛气速。
2. 固定液相流量和入塔混合气二氧化碳的浓度,在液泛速度下,取两个相差较大的气相流量,分别测量塔的传质能力(传质单元数和回收率)和传质效率(传质单元高度和体积吸收总系数)。
3. 进行纯水吸收二氧化碳、空气解吸水中二氧化碳的操作练习,同时测定填料塔液侧传质膜系数和总传质系数。
三、实验原理:气体通过填料层的压强降:压强降是塔设计中的重要参数,气体通过填料层压强降的大小决定了塔的动力消耗。
压强降与气、液流量均有关,不同液体喷淋量下填料层的压强降P ∆与气速u 的关系如图一所示:图一 填料层的P ∆~u 关系当液体喷淋量00=L 时,干填料的P ∆~u 的关系是直线,如图中的直线0。
当有一定的喷淋量时,P ∆~u 的关系变成折线,并存在两个转折点,下转折点称为“载点”,上转折点称为“泛点”。
这两个转折点将P ∆~u 关系分为三个区段:既恒持液量区、载液区及液泛区。
传质性能:吸收系数是决定吸收过程速率高低的重要参数,实验测定可获取吸收系数。
对于相同的物系及一定的设备(填料类型与尺寸),吸收系数随着操作条件及气液接触状况的不同而变化。
1.二氧化碳吸收-解吸实验根据双膜模型的基本假设,气侧和液侧的吸收质A 的传质速率方程可分别表达为 气膜 )(Ai A g A p p A k G -= (1) 液膜 )(A Ai l A C C A k G -= (2) 式中:A G —A 组分的传质速率,1-⋅s kmoI ;A —两相接触面积,m 2;A P —气侧A 组分的平均分压,Pa ;Ai P —相界面上A 组分的平均分压,Pa ; A C —液侧A 组分的平均浓度,3-⋅m kmolAi C —相界面上A 组分的浓度3-⋅m kmolg k —以分压表达推动力的气侧传质膜系数,112---⋅⋅⋅Pa s m kmol ; l k —以物质的量浓度表达推动力的液侧传质膜系数,1-⋅s m 。
DETA-PZ复合溶液吸收与解吸CO2实验研究

1.CO2钢瓶 ;2.N2钢瓶;3,4.气体减压阀;5,6.转子流量计;7.气体混合缓冲罐;8.三通阀;9.螺旋玻璃管;10.水浴锅;11,18.硅胶干燥管; 12,19.皂膜流量计;13.反应釜进气孔;14.多孔鼓泡管;15.油浴锅;16.精密增力电动搅拌器;17.智能电子 pH计
有机胺 类 捕 集 烟 气 中 CO2 的 主 流 工 艺 是 MEA法,虽 然 MEA法捕集 CO2吸收速率快、吸收能力强、设备尺寸较小[7-9], 但是该还存在 很 多 不 足 [10-13],比 如 溶 液 蒸 汽 压 较 高、易 挥 发、 MEA溶剂损失严重、热稳定性差、受热易分解等。另外 MEA与 CO2 反应生成的氨基甲酸盐类物质不易再生,再生能耗高;并且
溶液对设备的腐蚀 性 强,腐 蚀 产 生 的 铁、铬、镍、铜 等 离 子 的 存 在会进一步加速 MEA的分解;抗氧化能力差,MEA与氧气易发 生氧化降解,生成蚁酸、氨基乙酸和草酸等副产物[14],这些副产 物在加剧了设备腐蚀程度的同时又进一步加速了有机胺的氧 化降解,如此形成恶性循环使正常生产无法进行。
第 16期
朱立宾,等:DETA-PZ复合溶液吸收与解吸 CO2实验研究
·29·
DETA-PZ复合溶液吸收与解吸 CO2 实验研究
朱立宾1,陆诗建2
(1.山东泰克立德能源工程有限公司,山东 东营 257000; 2.中石化节能环保工程科技有限公司,山东 东营 257026)
摘要:以烯胺吸收剂 DETA(二乙烯三胺)为主吸收剂与辅助吸收剂 PZ(哌嗪)按物质的量配比 20∶1~20∶6进行复配,通过一次循环吸收、解 吸实验,对比其在 313K温度下的吸收量、吸收速率以及 393K温度下的再生速率、再生量以及它们的降解率。以筛选出较好的 20∶4DETA+ PZ烯胺复配药剂为基础,进行 6次循环吸收 -解吸实验,考察循环吸收、解吸性能与胺降解率;以智能高压反应釜分别考察了 20∶4DETA +PZ降解性能,对 CO2负载、温度、铁离子的对降解性能的影响进行了探讨。 关键词:二乙烯三胺;哌嗪;二氧化碳;吸收;解吸;降解 中图分类号:X701 文献标识码:A 文章编号:1008-021X(2019)16-0029-04
二氧化碳相变吸收解吸方法

二氧化碳相变吸收解吸方法二氧化碳是一种常见的化学物质,在大气中的含量较高。
它是一种无色无味的气体,但在特定条件下,它可以发生相变,即从气态转变为固态或液态,并释放或吸收热量。
本文将介绍二氧化碳的相变及其相关的吸收和解吸方法。
让我们了解一下二氧化碳的相变过程。
二氧化碳在常温常压下是一种气体,但在低温和高压下,它可以转化为固态或液态。
当二氧化碳气体遇到低温时,分子之间的相互作用增强,使得气体分子聚集在一起形成固态的二氧化碳,即干冰。
相反,当干冰受到高温的作用或者降低压力时,固态的二氧化碳会直接转变为气态。
在工业生产和实验室中,我们经常需要将二氧化碳从气态转变为固态或液态,并需要将其从固态或液态转变为气态。
这就需要使用相应的吸收和解吸方法。
下面将介绍几种常见的二氧化碳相变吸收解吸方法。
一种常见的方法是利用温度的变化来实现二氧化碳的相变吸收解吸。
当二氧化碳气体受到低温作用时,它会转变为固态或液态,并被吸收到相应的材料中。
这些材料通常具有较高的吸附能力和较大的表面积,如活性炭、分子筛等。
当需要释放二氧化碳气体时,可以通过升高温度来解吸,使二氧化碳从吸附材料中释放出来。
另一种方法是利用压力的变化来实现二氧化碳的相变吸收解吸。
当二氧化碳气体受到高压作用时,它会转变为液态,并被吸收到相应的容器中。
当需要释放二氧化碳气体时,可以通过降低压力来解吸,使液态的二氧化碳转变为气态并释放出来。
除了温度和压力的变化,还可以利用化学反应来实现二氧化碳的相变吸收解吸。
例如,一些化合物在特定条件下可以与二氧化碳发生化学反应,形成化合物的固态或液态,并吸收二氧化碳。
当需要释放二氧化碳气体时,可以通过改变反应条件或者添加适当的化学物质来解吸,使化合物中的二氧化碳释放出来。
总结起来,二氧化碳的相变吸收解吸方法可以通过温度、压力和化学反应来实现。
这些方法在工业生产、实验室研究和环境保护等领域都有广泛的应用。
了解和掌握这些方法对于高效利用二氧化碳资源以及减少二氧化碳排放具有重要意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二氧化碳吸收与解吸实验一、实验目的1.了解填料吸收塔的结构、性能和特点,练习并掌握填料塔操作方法;通过实验测定数据的处理分析,加深对填料塔流体力学性能基本理论的理解,加深对填料塔传质性能理论的理解。
2.掌握填料吸收塔传质能力和传质效率的测定方法,练习实验数据的处理分析。
二、实验内容1. 测定填料层压强降与操作气速的关系,确定在一定液体喷淋量下的液泛气速。
2. 固定液相流量和入塔混合气二氧化碳的浓度,在液泛速度下,取两个相差较大的气相流量,分别测量塔的传质能力(传质单元数和回收率)和传质效率(传质单元高度和体积吸收总系数)。
3. 进行纯水吸收二氧化碳、空气解吸水中二氧化碳的操作练习,同时测定填料塔液侧传质膜系数和总传质系数。
三、实验原理:气体通过填料层的压强降:压强降是塔设计中的重要参数,气体通过填料层压强降的大小决定了塔的动力消耗。
压强降与气、液流量均有关,不同液体喷淋量下填料层的压强降P ∆与气速u 的关系如图一所示:123L 3L 2L 1L 0 =>>0图一 填料层的P ∆~u 关系当液体喷淋量00=L 时,干填料的P ∆~u 的关系是直线,如图中的直线0。
ΔP , k P a当有一定的喷淋量时,P ∆~u 的关系变成折线,并存在两个转折点,下转折点称为“载点”,上转折点称为“泛点”。
这两个转折点将P ∆~u 关系分为三个区段:既恒持液量区、载液区及液泛区。
传质性能:吸收系数是决定吸收过程速率高低的重要参数,实验测定可获取吸收系数。
对于相同的物系及一定的设备(填料类型与尺寸),吸收系数随着操作条件及气液接触状况的不同而变化。
1.二氧化碳吸收-解吸实验根据双膜模型的基本假设,气侧和液侧的吸收质A 的传质速率方程可分别表达为 气膜 )(Ai A g A p p A k G -= (1) 液膜 )(A Ai l A C C A k G -= (2) 式中:A G —A 组分的传质速率,1-⋅s kmoI ;A —两相接触面积,m 2;A P —气侧A 组分的平均分压,Pa ; Ai P —相界面上A 组分的平均分压,Pa ;A C —液侧A 组分的平均浓度,3-⋅m kmol Ai C —相界面上A 组分的浓度3-⋅m kmolg k —以分压表达推动力的气侧传质膜系数,112---⋅⋅⋅Pa s m kmol ;l k —以物质的量浓度表达推动力的液侧传质膜系数,1-⋅s m 。
以气相分压或以液相浓度表示传质过程推动力的相际传质速率方程又可分别表达为: )(*-=A A G A p p A K G (3))(A A L A C C A K G -=*(4)式中:*A p —液相中A 组分的实际浓度所要求的气相平衡分压,Pa ;*A C —气相中A 组分的实际分压所要求的液相平衡浓度,3-⋅m kmol ;G K —以气相分压表示推动力的总传质系数或简称为气相传质总系数,112---⋅⋅⋅Pa s m kmol ;L K -以气相分压表示推动力的总传质系数,或简称为液相传质总系数,1-⋅s m 。
若气液相平衡关系遵循享利定律:A A Hp C =,则:lg G HK k K 111+= (5) lg L k k H K 11+= (6)P 2=P A2 C A2 ,LP AP AiC AiC A P A C AP A +d P A C A +dC AP 1=P A1 C A1,F L图二 双膜模型的浓度分布图 图三 填料塔的物料衡算图当气膜阻力远大于液膜阻力时,则相际传质过程式受气膜传质速率控制,此时,g G k K =;反之,当液膜阻力远大于气膜阻力时,则相际传质过程受液膜传质速率控制,此时,l L k K =。
如图三所示,在逆流接触的填料层内,任意载取一微分段,并以此为衡算系统,则由吸收质A 的物料衡算可得:A LLA dC F dG ρ=(7a )式中:L F ——液相摩尔流率,1-⋅s kmol ;dh相 界 面距离液 膜气膜浓度C AL ρ——液相摩尔密度,3-⋅m kmol 。
根据传质速率基本方程式,可写出该微分段的传质速率微分方程:aSdh C C K dG A A L A )(-=*(7b )联立上两式可得: AA A L L L C C dCaS K F dh -⋅=*ρ (8)式中:a ——气液两相接触的比表面积, m 2·m -1;S ——填料塔的横载面积,m 2。
本实验采用水吸收纯二氧化碳,且已知二氧化碳在常温常压下溶解度较小,因此,液相摩尔流率L F 和摩尔密度L ρ的比值,亦即液相体积流率L s V )(可视为定值,且设总传质系数K L 和两相接触比表面积a ,在整个填料层内为一定值,则按下列边值条件积分式(8),可得填料层高度的计算公式:0=h 2.A A C C = h h = 1A A C C =⎰-⋅=*12A A C C AA AL sL C C dC aS K V h (9) 令 aSK V H L sLL =,且称H L 为液相传质单元高度(HTU ); ⎰-=*12A A C C AA AL CC dC N ,且称N L 为液相传质单元数(NTU )。
因此,填料层高度为传质单元高度与传质单元数之乘积,即L L N H h ⨯= (10)若气液平衡关系遵循享利定律,即平衡曲线为直线,则式(9)为可用解析法解得填料层高度的计算式,亦即可采用下列平均推动力法计算填料层的高度或液相传质单元高度:AmA A L sL C C C aS K V h ∆-⋅=21 (11) SK V hH h N L sLL L α==(12) 式中m A C .∆为液相平均推动力,即2211221121.21ln )()(A A A A A A A A A A A A AmC C C C C C C C C C In C C C -----==∆∆∆-∆=∆**** (13) 其中:1110A A C Hp Hy p *==, 2220A A C Hp Hy p *==,0P 为大气压。
二氧化碳的溶解度常数:EM H ww1⋅=ρ 13--⋅⋅Pa m koml (14) 式中:w ρ——水的密度, ;3-⋅m kgw M ——水的摩尔质量, 1-⋅kmol kg ;E ——二氧化碳在水中的享利系数(见化工原理下册第78页),Pa 。
因本实验采用的物系不仅遵循亨利定律,而且气膜阻力可以不计,在此情况下,整个传质过程阻力都集中于液膜,即属液膜控制过程,则液侧体积传质膜系数等于液相体积传质总系数,亦即AmA A sL L l C C C hS V a K a k ∆-⋅==21 (15) 四、实验装置:1.实验装置主要技术参数:填料塔:玻璃管内径 D =0.050m 塔高1.00m 内装φ10×10mm 瓷拉西环; 填料层高度Z =0.78m ; 风机:XGB-12型 550W ; 二氧化碳钢瓶 1个; 减压阀1个(用户自备)。
流量测量仪表:CO 2转子流量计型号LZB-6 流量范围~0.6m 3/h ;空气转子流量计:型号LZB-10 流量范围~2.5m 3/h ;吸收水转子流量计: 型号LZB-10 流量范围16~160 L /h ; 解吸水转子流量计: 型号LZB-10 流量范围16~160 L /h浓度测量:吸收塔塔底液体浓度分析准备定量化学分析仪器(用户自备); 温度测量:PT100铂电阻,用于测定测气相、液相温度。
2.二氧化碳吸收与解吸实验装置流程示意图(见图四)图四二氧化碳吸收与解吸实验装置流程示意图1- CO2流量计;2- CO2瓶减压阀;3- CO2钢瓶;4-吸收用空气流量计;5- 吸收用气泵;6、8-喷头; 7、19- 水箱放水阀;9- 解吸塔;10- 解吸塔塔底取样阀;11- 解吸液储槽;12、15- U型管液柱压强计;13- 吸收液流量计;14-解吸液液泵;16- 吸收液储槽;17- 吸收塔;18- 吸收塔塔底取样阀;20- 解吸液流量计;21- 吸收液液泵;22-空气流量计;23- 空气旁通阀;24- 风机3.实验仪表面板图(见图五)图五实验装置面板图五、实验方法及步骤:1. 测量吸收塔干填料层(△P/Z)~u关系曲线(只做解吸塔):打开空气旁路调节阀5至全开,启动风机。
打开空气流量计,逐渐关小阀门5的开度,调节进塔的空气流量。
稳定后读取填料层压降△P即U形管液柱压差计11的数值,然后改变空气流量,空气流量从小到大共测定8-10组数据。
在对实验数据进行分析处理后,在对数坐标纸上以空塔气速 u为横坐标,单位高度的压降△P/Z为纵坐标,标绘干填料层(△P/Z)~u关系曲线。
2. 测量吸收塔在喷淋量下填料层(△P/Z)~u关系曲线:将水流量固定在104L/h(水流量大小可因设备调整),采用上面相同步骤调节空气流量,稳定后分别读取并记录填料层压降△P、转子流量计读数和流量计处所显示的空气温度,操作中随时注意观察塔内现象,一旦出现液泛,立即记下对应空气转子流量计读数。
根据实验数据在对数坐标纸上标出液体喷淋量为100L/h时的(△P/z)~u•关系曲线,并在图上确定液泛气速,与观察到的液泛气速相比较是否吻合。
3. 二氧化碳吸收传质系数测定:吸收塔与解吸塔(水流量控制在40L/h)(1)打开阀门5,关闭阀门9、13。
(2)启动吸收液泵2将水经水流量计14计量后打入吸收塔中,然后打开二氧化碳钢瓶顶上的针阀20,向吸收塔内通入二氧化碳气体(二氧化碳气体流量计15的阀门要全开),流量大小由流量计读出,控制在h 左右。
(3)吸收进行15分钟后,启动解吸泵2,将吸收液经解吸流量计7计量后打入解吸塔中,同时启动风机,利用阀门5 调节空气流量(约 m 3/h )对解吸塔中的吸收液进行解吸。
(4)操作达到稳定状态之后,测量塔底的水温,同时取样,测定两塔塔顶、塔底溶液中二氧化碳的含量。
(实验时注意吸收塔水流量计和解吸塔水流量计数值要一致,并注意解吸水箱中的液位,两个流量计要及时调节,以保证实验时操作条件不变)(5)二氧化碳含量测定用移液管吸取Ba (OH )2溶液10mL ,放入三角瓶中,并从塔底附设的取样口处接收塔底溶液10 mL ,用胶塞塞好振荡。
溶液中加入2~3滴酚酞指示剂摇匀,用的盐酸滴定到粉红色消失即为终点。
按下式计算得出溶液中二氧化碳浓度:溶液-V V C V C C HClHCl OH Ba OH Ba CO 222)()(22=1-⋅L mol六、实验注意事项:1.开启CO 2总阀门前,要先关闭减压阀,阀门开度不宜过大。
2.实验中要注意保持吸收塔水流量计和解吸塔水流量计数值一致,并随时关注水箱中的液位。
