第8章 二重积分
高数第八章

第25,26讲 第八章 重 积 分上一章把一元函数微分学推广到多元函数情形.现在要把一元函数定积分推广为多元函数的多重积分、曲线积分和曲面积分.定积分(特定构造的和式极限,“高级和”)所讨论的是分布在某区间上的几何量(曲边梯形面积)或物理量(变速直线运动路程)的积累问题.而多重积分,曲线、曲面积分则能求出分布在平面区域,平面曲线,空间曲面上的整体量,以扩大积分学的应用范围.第一节 二重积分的概念和性质一、二重积分的概念 1.两个实例例1 求曲顶柱体的体积.曲顶柱体是指:以平面上的有界闭区域D 为底,以D 上方的曲面S 为顶,周围是母线平行于z 轴的柱面(见P.306图8-1)今设曲顶方程为(,),(,)z f x y x y D =∈,且设(,)f x y 连续,,(,)0f x y ≥,求该曲顶柱体的体积.V 解 第一步 :“分割”— 化整为零.用一组曲线网将区域D 分成n 个小区域:12,,,n σσσ∆∆∆ ,并用它们记各小区域的面积.,于是大体积相应被分割为n 个曲顶柱体,记体积为:12,,,n v v v ∆∆∆ (见P.306图8-2).第二步:“近似代替”— 以平代曲.i σ∆上任意取一点(,)i i ξη,(,)f x y 在D 上连续,∴当分割充分细小时,可用小平顶柱体体积,()i i i f ξησ∆近似代替小曲顶柱体的体积(,)(1,2,,).i i i i v f i n ξησ∆≈∆= 第三步:“求和”— 积零为整. 11(,)nni i i i i i V v f ξησ===∆≈∆∑∑.第四步:“取极限”— 由近似到精确.1l i m (,)ni i i i V f λξησ→==∆∑,其中λ是n 个小区域i σ∆的直径最大者,即 1max ()i i nd λσ≤≤=∆.例2 求不均匀平面薄板的质量(薄即厚度可忽略不计).设有一块质量分布不均匀的薄板,在xoy 平面上占有区域D (见P.307图8-3), 面密度为ρ(,)x y ,求该薄板 的质量M .解 也分四步完成.“ 分割”: 在xoy 平面上将薄板D 分割为n 小块:12,,,n σσσ∆∆∆ .“近似代替”:在i σ∆上任取一点(,)i i ξη,将此小块近似看作是均匀的,则小块质量为: i M ∆≈ρ(,),(1,2,,)i i i i n ξησ∆= . “求和”: 11nni i i M M ===∆≈∑∑ρ(,)i i i ξησ∆.“取极限”:01lim ni M λ→==∑ρ(,)i i i ξησ∆.以上两例,虽内容不同,但解决问题的方法是一样的,都归结为求一种具有相同结构的“和式的极限”,我们把它抽象出来,得到2.二重积分的定义设二元函数(,)z f x y =在有界闭区域D 上有定义,用任意的曲线网分D 为n 个小区域 12,,,n σσσ∆∆∆ , 并用它们记小区域的面积. 又记 i σ∆的直径为()i d σ∆,并令1max ()i i nd λσ≤≤=∆,在i σ∆上任取一点(,)i i ξη,作乘积 (,),(1,2,,)i i i f i n ξησ∆= , 作和数(称为积分和,或Rimann 和)1(,)nn i i i i S f ξησ==∆∑,令0λ→,若积分和有极限 Ⅰ(它不依赖于区域D 的分法及中间点的取法),则称此极限值为函数(,)z f x y =在区域D 上的二重积分,记作:Ⅰ=01lim (,)(,)ni i i i Df f x y d λξησσ→=∆=∑⎰⎰ (1)其中D 称为积分区域,(,)f x y 称为被积函数,(,)f x y d σ称为被积表达式,d σ称为面积元素.若二重积分(,)Df x y d σ⎰⎰存在,则称(,)z f x y =在区域D 上可积.重要结论:二元连续函数是可积的.(不证)由二重积分的定义知:例1中取顶柱体的体积V 是曲顶柱体函数(,)f x y 在底面区域D 上的二重积分,即 (,)DV f x y d σ=⎰⎰.例2中平面薄板的质量M 是面密度函数ρ(,)x y 在所占区域D 上的二重积分, 即 DM =⎰⎰ρ(,)x y d σ.3.二重积分的几何意义 (1)当(,)0f x y ≥时,则(,)Df x y ⎰⎰d σ表示以(,)z f x y =为顶,以D 为底的曲顶柱体的体积.(2)当(,)0f x y ≤时,则(,)Df x y d σ⎰⎰表示曲顶柱体体积前面加了一个负号.(但不能说是负体积)(3)当(,)1f x y ≡时,(,)DDf x y d d σσσ==⎰⎰⎰⎰为D 的面积.二、二重积分的性质 (P.308)性质1 “常数因子提出来” 若(,)f x y 在区域D 上连续,则(,)(,),(DDkf x y d k f x y d k σσ=⎰⎰⎰⎰为常数)性质2 “一项一项分开积” 若(,),(,)f x y g x y 在D 上连续,则[](,)(,)(,)(,)DDDf x yg x y d f x y d g x y d σσσ±=±⎰⎰⎰⎰⎰⎰.性质3 设区域D 由1D 与2D 组成,且1D 与2D 除边界上点外无公共点,又(,)f x y 在D 上连续,则12(,)(,)(,).DD D f x y d f x y d f x y d σσσ=+⎰⎰⎰⎰⎰⎰性质4 若(,),(,)f x y g x y 在D 上连续,且 (,)(,)f x y g x y ≤,则有不等式(,)(,)DDf x y dg x y d σσ≤⎰⎰⎰⎰特殊地,由于(,)(,)(,)f x y f x y f x y -≤≤,又有不等式(,)(,).DDf x y d f x y d σσ≤⎰⎰⎰⎰性质5 设M ,m 分别是(,)f x y 在D 上的最大值和最小值,σ是D 的面积,则有 (,)Dm f x y d M σσσ≤≤⎰⎰ (估值不等式)性质6 (二重积分的中值定理)设(,)f x y 在闭区域D 上连续,σ为D 的面积,则在D 上至少存在一点(,)ξη,使得(,)(,)Df x y d f σξησ=⋅⎰⎰习 题 8-14 (1)—(4)5 (1)—(4)4. 根据二重积分的性质,比较下列积分的大小:(1) 2()d Dx y σ+⎰⎰与3()d Dx y σ+⎰⎰,其中积分区域D 是由x 轴、y 轴与直线1x y +=所围成;(2) 2()d Dx y σ+⎰⎰与3()d Dx y σ+⎰⎰,其中积分区域D 是由圆周22(2)(1)2x y -+-=所围成;(3)ln()d Dx y σ+⎰⎰与2[ln()]d Dx y σ+⎰⎰,其中D 是三角形闭区域,三顶点分别为(1,0),(1,1),(2,0);(4) ln()d Dx y σ+⎰⎰与2[ln()]d Dx y σ+⎰⎰,其中{(,)35,01}D x y x y =≤≤≤≤.解 (1) 在积分区域D 上,01x y ≤+≤,故有32()()x y x y +≤+,根据二重积分的性质4,可得32()d ()d .DDx y x y σσ+≤+⎰⎰⎰⎰(2) 由于积分区域D 位于半平面{(,)|1}x y x y +≥内,故在D 上有23()()x y x y +≤+.从而23()d ()d .DDx y x y σσ+≤+⎰⎰⎰⎰(3) 由于积分区域D 位于条形区域{(,)|12}x y x y ≤+≤内,故知D 上的点满足0l n ()1x y ≤+≤,从而有2[ln()]ln()x y x y +≤+.因此2[ln()]d ln()d .DDx y x y σσ+≤+⎰⎰⎰⎰ (4) 由于积分区域D 位于半平面{(,)|e}x y x y +≥内,故在D 上有ln()1x y +≥,从而有2[ln()]ln()x y x y +≥+.因此2[ln()]d ln()d .DDx y x y σσ+≥+⎰⎰⎰⎰5. 利用二重积分的性质估计下列积分的值:(1) ()d DI xy x y σ=+⎰⎰其中{(,)01,01}D x y x y =≤≤≤≤;(2) 22sin sin d DI x y σ=⎰⎰其中{(,)0,0}D x y x y ππ=≤≤≤≤;(3) (1)d DI x y σ=++⎰⎰其中{(,)01,02}D x y x y =≤≤≤≤;(4) 22(49)d DI x y σ=++⎰⎰其中22{(,)4}D x y x y =+≤.解 (1) 在积分区域D 上,01x ≤≤,01y ≤≤,从而0()2xy x y ≤+≤,又D 的面积等于1,因此0()d 2.Dxy x y σ≤+≤⎰⎰(2) 在积分区域D 上,0sin 1x ≤≤,0sin 1y ≤≤,从而220sin sin 1x y ≤≤,又D 的面积等于2π,因此2220sin sin d π.Dx y σ≤≤⎰⎰(3) 在积分区域D 上,014x y ≤++≤,D 的面积等于2,因此2(1)d 8.Dx y σ≤++≤⎰⎰(4) 在积分区域D 上,2204x y ≤+≤,从而22229494()925,x y x y ≤++≤++≤,又D 的面积等于4π,因此2236π(49)d 100π.Dx y σ≤++≤⎰⎰第27,28讲 第二节 二重积分的计算方法— 化为两个定积分,即累次积分. 一、在直角坐标系下计算二重积分当(,)f x y 在区域D 上可积时,其积分值与分割方法无关,因此取特殊的分割法来计算二重积分1.用两组分别平行于x 轴,y 轴的直线分割区域D ,这时面积元素d dxdy σ=, 从而(,)(,)DDf x y d f x y dxdy σ=⎰⎰⎰⎰.2.化二重积分为累次积分 设(,)0f x y ≥,则(,)Df x y dxdy ⎰⎰表示曲顶柱体的体积V ,用“切片法”求V(1)设区域D 由直线,x a x b == 及曲线12(),()y x y x ϕϕ==围成: 12()()x y x a x bϕϕ≤≤⎧⎨≤≤⎩(这称x -型区域)回忆:已知平行截面面积,求立体体积公式 8-4 ()a ()baV A x dx =⎰, ()A x 是平行截面面积.现用平行于yoz 的平面0x x =去截曲顶柱体,得截面,其面积为A 0()x (图8-5)是一个曲边梯形,曲边方程为:0(,)z f x y =,因此,由定积分的几何意义,2010()00()()(,)x x A x f x y dy ϕϕ=⎰ (1)'让0x 取遍整个[],a b ,得到截面面积 21()()()(,)x x A x f x y dy ϕϕ=⎰ (1)''于是,由“已知平行截面面积求立体体积公式”⇒ 22111()()()()()(,)(,)bbx b x aax a x V A x dxf x y dy dx dx f x y dy ϕϕϕϕ''⎡⎤===⎢⎥⎣⎦⎰⎰⎰⎰⎰()代入 (1)这叫累次积分.第一次对y 的积分,是求x 处的截面面积()A x ,将x 看作常数,第二次对x 积分,是沿x 轴加这些薄片的体积()A x dx ,这时x 是积分变量.注 公式(1)成立的条件是“(,)f x y 在D 上连续”,并不要求(,)0.f x y ≥公式(1)是在x -型积分域下,将二重积分化为先对y 后对x 的两次定积分.如何确定两次的积分限呢?先用平行于y 轴的直线在[],a b 内一点x 处穿入D 的下边界,穿出上边界,其交点的坐标12(),()x x ϕϕ为第一次先对y 积的下限与上限,再将D 投影到x 轴上,得交点,a b 为第二次对x 积分的下限与上限.(称“穿口法”,定限口诀是:后积先定限(常数),限内画条线,先交下限写,后交上限见.) 例1 化二重积分(,)Df x y d σ⎰⎰为累次积分.其中;(1) D 由1,2,0,2x x y y =-===围成; (2)D 由2,y x =及2x y =围成. (3)D 由2,,2y x y x y x ==-=-围成. 解 计算二重积分时,先画好积分区域的草图.(1)积分域是x -型的矩型域,由公式(1)⇒221(,)(,)Df x y d dx f x y dy σ-=⎰⎰⎰⎰.(2)解方程组求交点,画积分域草图2201,01x x y x y y x y ==⎧=⎧⎧⇒⎨⎨⎨===⎩⎩⎩这时x -型积分域,由公式(1)⇒(先对y 积分,将x 看作常数,积分限是x 的函数,第二次对x 积分,积分限为常数)21(,)(,).xDf x y d f x y d yσ=⎰⎰⎰(3)解方程组求交点,画积分区域草图1212y x x y x =-⎧⇒=-⎨=-⎩, 2212y xx y x =⎧⇒=⎨=-⎩如先对y 积分时,用平行y 轴的直线不能一次穿过区域D 时,需将D 分为1D 域2D ,然后由积分的可加性质3及公式(1),得到22122121(,)(,)(,).x x xxDD D f x y d dx f x y dy dx f x y dy σ----=+=+⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰例2 求ⅠDxyd σ=⎰⎰,其中D 由,y x =与2y x =围成. 解 解方程组求交点,画区域草图 1220,1y xx x y x=⎧⇒==⎨=⎩由公式(1)⇒222111350()211().224x x x xDy xyd xdx ydy x dxx x dx σ===-=⎰⎰⎰⎰⎰⎰例3 求Ⅰ(32),D x y d D σ=+⎰⎰由2x y +=及,x y 轴围成.解 由积分区域草图及定理1 Ⅰ2222222020(32)(3)2(2).3xx dx x y dy xy y dx x x dx --=+=+=+-=⎰⎰⎰⎰(2)若积分区域D 是由,y c y d ==及12(),()x y x y ψψ==围成,这称y -型积分域. 二重积分化为累次积分时,应先对x 后对y 积分,这时积分公式为: 21()()(,)(,)dy cy Df x y d dy f x y dx ψψσ=⎰⎰⎰⎰(2)对y -型积分域,如何确定两次的积分限呢? 图8-6 ()a 先用平行于x 轴的直线在[],c d 内一点y 处,穿入D 的左边界,穿出右边界,交点的坐标12(),()y y ψψ为第一次先对x 积分的下限与上限(是y 的函数),然后将D 投影到y 轴上得交点,c d 为第二次对y 积分的下限与上限(是常数).例4 求Ⅰ22Dx d yσ=⎰⎰,其中D 由2,,1y y x xy ===围成.解 解方程组求交点的坐标,画出积分域的草图11x yy xy =⎧⇒=⎨=⎩ 这是y -型积分域,先选择对x 后对y 积分, 及公式(2)⇒Ⅰ224222235122111111111127().3332464yy yyy y dy x dx x dy y y dy y y --⎡⎤⎡⎤===-=+=⎢⎥⎢⎥⎣⎦⎣⎦⎰⎰⎰⎰ 注 如若选择先对y 积分时,需把D 分块,则繁. 例5求ⅠDxyd σ=⎰⎰其中D 由抛物线2y x =及直线2y x =-围成. 解 解方程组求交点,画积分域草图214,122x x y xy y y x ⎧===⎧⎧⇒⎨⎨⎨=-==-⎩⎩⎩ 强调 积分次序的选择原则:① 考虑积分域的特点; ② 被积函数(下例说明)本题D 即是x -型域,又是y -型域,这时,根据D 的特点,应选择先对x 积分(因为平行x 轴直线可一次穿过D 的左,右边界,而先对y 积分时,D 应分块). 故由公式(2)⇒ Ⅰ222222211145().28y y y y ydy xdx y x dy ++--===⎰⎰⎰例6 求Ⅰsin Dy d yσ⎰⎰,其中D 由2y x =及y x =围成.解 解方程组求交点,画出积分区域草图 20,1y xy y y x=⎧⇒==⎨=⎩这时不能选择先对y 积分,因考虑到被积函数,积不出来,故应先对x 积分,由公式(2)⇒ Ⅰ2211sin sin 1y yy yy y dy dx dy dx yy==⋅⎰⎰⎰⎰11120sin ()sin sin y y y dy ydy y ydy y=-=-⎰⎰⎰110cos11cos cos y yydy =-++-⎰cos11cos1sin11sin10.1585.=-++-=⋅≈习 题 8-21 (1)(3) 2(2)(4) 4(1)(3)(5)1. 计算下列二重积分:(1) 22()d D xy σ+⎰⎰,其中{(,)|||1,||1}D x y x y =≤≤;(2) (32)d Dx y σ+⎰⎰,其中D 是由两坐标轴及直线2x y +=所围成的闭区域; (3)323(3)d D xx y y σ++⎰⎰,其中{(,)|01,01}D x y x y =≤≤≤≤;(4) cos()d Dx x y σ+⎰⎰其中D 是顶点分别为(0,0),(π,0)和(π,π)的三角形闭区域.解 (1) 1311112222221111128()d d ()d d (2)d .333Dy x y x x y y x y x x x σ-----⎡⎤+=+=+=+=⎢⎥⎣⎦⎰⎰⎰⎰⎰⎰ (2) D 可用不等式表示为03,02y x x ≤≤-≤≤,于是2222200022(32)d d (32)d [3]d 20(422)d .3xxDx y x x y y xy y xx x x σ--+=+=+=+-=⎰⎰⎰⎰⎰⎰(3)11323323(3)d d (3)d Dx x y y y x x y y x σ++=++⎰⎰⎰⎰ 1411333001d ()d 1.44x x y y x y y y y ⎡⎤=++=++=⎢⎥⎣⎦⎰⎰(4) D 可用不等式表示为0,0πy x x ≤≤≤≤,于是ππ00πcos()d d cos()d [sin()]d 3(sin 2sin )d π.2xxDx x y x x x y y x x y xx x x x σ+=+=+=-=-⎰⎰⎰⎰⎰⎰2. 画出积分区域,并计算下列二重积分:(1) Dσ⎰⎰,其中D是由两条抛物线y =,2y x =所围成的闭区域;(2)2d Dxy σ⎰⎰,其中D 是由圆周224xy +=及y 轴所围成的右半闭区域;(3) e d x y Dσ+⎰⎰,其中{(,)|||||1}D x y x y =+≤; (4)22()d Dxy x σ+-⎰⎰,其中D 是由直线2y =,y x =及2y x =所围成的闭区域.解 (1) D可用不等式表示为201x y x ≤≤≤≤,于是237111424000226d d (-)d .3355Dx x x y x y x x x x σ⎡====⎢⎥⎣⎦⎰⎰⎰⎰⎰(2) D可用不等式表示为022x y ≤≤-≤≤,于是22222222164d d d (4)d .215Dxy y y x y y y σ--==-=⎰⎰⎰⎰(3) 12D D D = ,其中1{(,)|11,10}D x y x y x x =--≤≤+-≤≤,1{(,)|11,01}D x y x y x x =-≤≤-+≤≤,于是121111101012112111e d e d e d e d e d e d e d (e e )d (e e )d e e .x y x y x yD D D x x x y x y x x x x x y x y x x σσσ+++++----+----=+=+=-+-=-⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰(4) D 可用不等式表示为,022y x y y ≤≤≤≤,于是22222023222232002()d d ()d 19313d d .322486yy Dyy x y x y x y x xx x y x y y y y σ+-=+-⎡⎤⎛⎫=+-=-=⎢⎥ ⎪⎝⎭⎣⎦⎰⎰⎰⎰⎰⎰4. 改换下列二次积分的积分次序:(1) 1d (,)d yy f x y x ⎰⎰ ; (2)2220d (,)d y y y f x y x ⎰⎰;(3) 10d (,)d y f x y x ⎰;(4)212d (,)d xx f x y y -⎰;(5)eln 1d (,)d xx f x y y ⎰⎰; (6)πsin 0sin2d (,)d xx x f x y y -⎰⎰.解 (1) 所给二次积分等于二重积分(,)d Df x y σ⎰⎰,其中{(,)|0,01}D x y x y y =≤≤≤≤,D 可改写为{(,)|1,01}x y x y x ≤≤≤≤,于是原式11d (,)d .xx f x y y =⎰⎰(2) 所给二次积分等于二重积分(,)d Df x y σ⎰⎰,其中2{(,)|2,02}D x y y x y y =≤≤≤≤,D可改写为{(,)|04}2x x y y x ≤≤≤≤,于是原式42d (,)d .x x f x y y =⎰⎰(3) 所给二次积分等于二重积分(,)d Df x y σ⎰⎰,其中{(,)|01}D x y x y =≤≤≤,D可改写为{(,)|011}x y y x ≤≤-≤≤,于是原式110d (,)d .x f x y y -=⎰(4) 所给二次积分等于二重积分(,)d Df x y σ⎰⎰,其中{(,)|212}D x y x y x =-≤≤≤≤,D可改写为{(,)|2101}x y y x y -≤≤+≤≤,于是原式1102d (,)d .yy f x y x -=⎰⎰(5) 所给二次积分等于二重积分(,)d Df x y σ⎰⎰,其中{(,)|0ln ,1e}D x y y x x =≤≤≤≤,D 可改写为{(,)|e e,01}y x y x y ≤≤≤≤,于是原式1ee d (,)d .yy f x y x =⎰⎰(6) 所给二次积分等于二重积分(,)d Df x y σ⎰⎰,将D 表示为12D D ,其中1{(,)|arcsin πarcsin ,01}D x y y x y y =≤≤-≤≤,2{(,)|2arcsin π,10}D x y y x y =-≤≤-≤≤,于是原式1πarcsin 0π0arcsin 12arcsin d (,)d d (,)d .yyyy f x y x y f x y x ---=+⎰⎰⎰⎰第29,30讲 二、在极坐标系下计算二重积分复习:直角坐标与极坐标(参见教材P.476附录4)的关系: (,)x y (,)r θcos sin x r y r θθ==tan r y xθ==1 圆心在极点,半径为a 的圆周222x y a += ,02r a θπ=≤≤ 2 圆心在(,0)a ,半径为a 的圆周222()x a y a -+= 22cos r ar θ= 222x y ax += 2cos ,22r a ππθθ=-≤≤3 圆心在(0,)a ,半径为a 的圆周22222()2x y a a x y ay+-=+=22sin 2sin ,0r ar r a θθθπ==≤≤在极坐标系下计算二重积分,需将被积函数(,)f x y ,积分域D 及面积元素d σ都用极坐标表示 :(,)f x y 的极坐标形式为 (cos ,sin )f r r θθ,为了得到极坐标系下面积元素d σ, 可用坐标曲线网去分割区域D , 即用 r =常数(一组同心圆) θ=常数 (一束射线),去分割D 面积元素可近似看作小矩形:两边长分别为dr 和(弧长)=rd θ(半径⨯圆心角) (见P.315图8-14) 所以 ()d rd dr rdrd σθθ=⋅=, 于是⇒ (,)(cos ,sin )DDf x y d f r r rdrd σθθθ=⎰⎰⎰⎰ (4)(ⅰ)当极点o 在D 的外部: 一般先对r 后对θ积分,定限时,用从极点出发的射线穿入区域, 入口的交线1()r θ,穿出区域出口的交线2()r θ为对r 积分的下限与上限,而θ的变范围则是后对θ积分的下限与上限. 图8-15(a )21()()(,)(cos ,sin (cos ,sin )DDr r f x y d f r r rdrd d f r r rdrβθαθσθθθθθθ⇒==⎰⎰⎰⎰⎰⎰(5)(ⅱ)当极点o 在D 的边界上,D 为曲边扇形()(cos ,sin ).r Dd f r r rdr βθαθθθ⇒=⎰⎰⎰⎰(6) 图8-17(ⅲ)当极点o 在D 的内部2()(cos ,sin ).r Dd f r r rdr πθθθθ⇒=⎰⎰⎰⎰(7)例1 化二重积分为累次积 图8-1822:,(0)D x y Rx R +=>解 222()()22RRx y -+= 这是圆心在(,0)2R ,半径为2R的圆,极坐标方程为:cos ,22r R ππθθ=-≤≤,这是极点在D 的边界上.由公式(6)⇒ cos 202(cos ,sin ).R Dd f r r rdr πθπθθθ-=⎰⎰⎰⎰例2 求Ⅰ=2Dxy d σ⎰⎰其中D 为 圆 221,x y +=和224x y +=之间在第一象限的部分(圆环) 解 这是极点在域D 外部的情形,由公式(5)⇒ Ⅰ=2cos (sin )Dr r rdrd θθθ⎰⎰=24221cos sin d r dr πθθθ⎰⎰=22421sin cos d r drπθθθ⎰⎰=用凑微分31.15例3 求Ⅰ=22x y De d σ--⎰⎰,其中D 是222,(0)x y a a +≤>在第一象限的部分. 解 因为 22,x y ee --的原函数不是初等函数,故在直角坐标系下积不出来.但D 是圆域,故可采用极坐标系.由于极点在边界上,由公式(6),得到 Ⅰ=2222(1).4ar r a oDe rdrd d e rdr e ππθθ--==-⎰⎰⎰⎰(这里用凑微分积) 利用此结果,可计算无穷积分(广义积分):2x e dx +∞-⎰(概率积分).例4利用二重积分证明概率积分22x e dx +∞-=⎰.(求正态分布的方差时用)证明22limax x a edx e dx +∞--→+∞=⎰⎰‘考虑正方形区域D ,在D 上计算二重积分 2222a axy x y De dxdy e dx e dy ----=⎰⎰⎰⎰=220a x e dx -⎡⎤⎢⎥⎣⎦⎰ 图8-19为了求出左端的二重积分,可以a (正方形对角线)为半径画圆,得到图中的区域12D D D ⊂⊂, 220xy e --> 22222212xy xy xy D DD e d e d e d σσσ------∴≤≤⎰⎰⎰⎰⎰⎰由例3知:22222(1)(1)44a xy a De e dxdy e ππ-----≤≤-⎰⎰(=22ax edx -⎡⎤⎢⎥⎣⎦⎰)令a →+∞,有 220lim 44a x a e dx ππ-→+∞⎡⎤≤≤⎢⎥⎣⎦⎰,即22044x e dx ππ+∞-⎡⎤≤≤⎢⎥⎣⎦⎰ 由极限的夹逼准则,所以 2204x e dx π+∞-⎡⎤=⎢⎥⎣⎦⎰ ,202x e dx +∞-==⎰例5 求球体22224x y z a ++≤被圆柱面222,(0)x y ax a +=>所截得部分的体积. 解 将圆柱面的方程化为:2222()x a y a -+= 被球面22224x y z a ++=所截,有对称性,只须求出图中第一卦限的体积1V ,再4倍,1V 的曲顶为z =11D V ⇒=其中 1D 如右图所示 采用极坐标系111D D V θ⇒==⎰⎰⎰⎰ 图8-20(a )(b )2cos 202cos 122222200322222cos 3320233301(4)(4)2128(4)((1sin )233882(sin )().32323a a a d d a r d a r a r d a d a d a πθπθππθπθθθθθππθθ==---=--⋅=-=-=-⎰⎰⎰⎰⎰⎰⎰所以 13224().323V V π==- 递推公式:3n =为奇数 Ⅰ212!!,1(21)!!m m m m +==+小结:何时用极坐标系计算二重积分? ① 积分区域是圆形或环形; ② 被积函数含22x y +.习 题 8-28(1)(3) 9(1)(4) 10(1)8. 化下列二次积分为极坐标形式的二次积分: (1) 11d (,)d x f x y y ⎰⎰ ;(2)2d (,)d xx f x y y ⎰;(3)11d (,)d xx f x y y -⎰ ; (4)21d (,)d x x f x y y ⎰⎰.解 (1) 用直线y x =将积分区域D 分成1D 、2D 两部分:1π{(,)|0sec ,0}4D ρθρθθ=≤≤≤≤,2ππ{(,)|0c ,}.42D cs ρθρθθ=≤≤≤≤, 于是原式sec csc 4204d (cos ,sin )d d (cos ,sin )d .f f ππθθπθρθρθρρθρθρθρρ=+⎰⎰⎰⎰(2) 在极坐标中,直线2,x y x ==和y =的方程分别是π2sec ,4ρθθ==和3πθ=。
二重积分概念与性质

的怎样划分以及 M i 在 i 上如何选取,只要
d 0 时恒有同一极限I ,则称此极限为f(M)
在几何形体 上的黎曼积分。
记为 : I lim
d 0
f (M )
i 1 i i
n
f ( M )d
根据几何形体的具体形式,可分别给出 各几何形体上的积分的具体表达式及名称: 1、若为一块可求面积的平面图形 D ,则 D 上的 积分称为:二重积分。 直角坐标系下记为: f ( x, y)d f ( x, y)dxdy
d e ,
a2
a2
ab e
D
( x 2 y2 )
d abe .
d 例 2 估计 I 的值, 2 2 x y 2 xy 16 D 其中 D: 0 x 1, 0 y 2 . 1 解: f ( x, y) , 区域面积 2 , ( x y)2 16
L
4、如果是可求面积的曲面块S,则 S上的积分称 为:第一类曲面积分。
记为: f ( x, y, z )dS
S
二、二重积分的概念
定义 设 f ( x , y )是有界闭区域 D 上的有界函数, 将 闭 区 域 D 任 意 分 成 n 个 小 闭 区 域 1 ,
2 , , n,其中 i 表示第 i 个小闭区域,
对上面五种情况:各自具体的对象不同,但归结为 处理同一种形式的和的极限问题,概括地给出下 面定义: Def: 有界闭区域 上黎曼积分定义: 设 为一几何形体,它是可度量的,在该几何体 上定义一函数f(M), M ,将 分为若干可度 量的小块 1 , 2 n ,并把它们的度量大 i ) 为最大直径; 小仍记为 i ,并令 d max( i M i ,做和式(黎曼 在每小分块 i 中任取一点 n 和数/积分和数) f (M i ) i ,若该和式不 i 1 论对
第八章 二重积分的计算

微积分
例12 计算
y sin( x 1) 2 x 1 dxdy, D : y x, y x 2 D
解 D {( x, y ) | 1 y 2, y 2 x y 2}
根据积分区域的特点 应先对 x 后对 y 积分
y sin( x 1) I dy dx x 1 1 y2 sin( x 1) 但由于 x 1 -1 对 x 的积分求不出,无法计算,
积分时必须考虑次序
D {( x, y ) | 0 y 1,0 x y}
x e
D
1 0
2 y2
dxdy
dy x e
1 y 0 0
2
2 y2
dx
e y
2
1 y3 y2 2 dy e y dy 0 3 6
1 2 (1 ). 6 e
a 2a
2a
2a
微积分
例 7 求 ( x 2 y )dxdy ,其中 D 是由抛物线
y x 和 x y 所围平面闭区域.
2 2
D
x y2
解 两曲线的交点
y x (0,0) , (1,1), 2 x y
2
y x2
D {( x , y ) | 0 x 1, x y x 2 }
化二重积分为累次积分时选择积分次序的 重要性,有些题目两种积分次序在计算上难易程 度差别不大,有些题目在计算上差别很大,甚至 有些题目对一种次序能积出来,而对另一种次序 却积不出来 另外交换累次积分的次序:先由累次积分 找出二重积分的积分区域,画出积分区域,交 换积分次序,写出另一种次序下的累次积分。
微积分
微积分
8.2 二重积分的计算法

ϕ1(θ) ≤ r ≤ϕ2(θ),α ≤θ ≤ β
表 ( 图 来 示如 )
中 数 其 函 ϕ1(θ),ϕ2 (θ) 区 [ 在 间α, β]上 续 连 。
O
r =ϕ2(θ)
D
β
r =ϕ1(θ)
α
x
10
D:ϕ1(θ) ≤ r ≤ϕ2(θ)
α ≤θ ≤ β
D
r =ϕ2(θ)
D
r =ϕ2(θ) r =ϕ1(θ)
o x
(2)从极点出发的一族射线:θ=常数, 从极点出发的一族射线: 常数 常数, 从极点出发的一族射线 个小区域( 把D分成 n个小区域(如上图) 分成 个小区域 如上图)
8
面积元素
∆σi ∆θi ∆r i
d σ = r d rd θ
dσ
x
o
∫∫ f (x, y)dσ = ∫∫ f (r cosθ , r sinθ )r d rdθ
D
D
注意:dσ = dxdy ≠ dx ⋅ dy
9
2、如何化为两次单积分 、 积分顺序:一般是先积 后积 积分顺序:一般是先积r后积θ 定限的方法:依D的特点: 定限的方法: 的特点: 的特点
D
r =ϕ2(θ)
(1) 极 在 外 点 D
β
O
α
r =ϕ1(θ)
x
设 分 域 可 不 式 积 区 D 用 等
z
V = ∫∫ R2 − x2dσ 1
= ∫ [∫
0
R 0
D R
R2 −x2
0
R2 − x2dy] dx
2 2
o R x
y
R
y
= ∫ [ R2 − x2 y]0 R −x dx
微积分-二重积分

3)、若 z f ( x, y) 在区域 D 上的值有正有负,则曲顶柱体
的体积取其二重积分的代数和。
(其中xoy面上方柱体的体积取正, xoy面下方柱体的体 积取负)。
三、二重积分的性质
calculus
性质1 被积函数的常数因子可以提到二重积分号 的外面,即:
kf x, yd k f x, yd
ms f ( x, y) d Ms
D
calculus
性质7 中值定理 如果 f ( x, y) 在闭区域 D 上连续,
s 是 D的面积,则在 D 内至少存在一点 ( ,) ,
使得
f ( x, y)d f ( ,) s
D
中值定理的几何意义:在区域 D 上以曲顶 z f (x, y)为顶 的曲顶柱体的体积,等于区域 D上以某一点( ,) 的函数值
dx
2(x) f ( x, y )dy
a
1(x)
D
注: 若 ƒ(x,y)≤0 仍然适用。
calculus
(2)Y-型域: c y d , 1( y) x 2( y).
d
x 1( y) c
D
d
x 1( y) x 2( y)
c
[Y-型] D
x 2( y)
Y型区域的特点:a、穿过区域且平行于x轴的直线与区 域边界的交点不多于两个;
D
D
(3,0) x
calculus
2) ln(x y)d 与 [ln(x y)]2d,其中区域 D为
D
D
顶点为A(1,0)B(1,1),C(2,0)的三角形闭区域。
解:BC的方程 x+y=2
B(1,1)
D内 1 x y 2, 0 ln(x y) 1
第八章 二重积分练习题

第八章 二重积分练习题A 题一 交换下列积分的积分次序(1)dy y x dx x ⎰⎰--+2402222(2)0(,)a a x dx f x y dy -⎰ (3)⎰⎰y y dx y x f dy 2202),( 二 计算下列二重积分 (1)D xdxdy ⎰⎰,其中D 为由21,2,0y x y x x =+==所围成的区域. (2)⎰⎰+D dxdy y x 22,其中D 是由圆环2222b y x a ≤+≤所围成的闭区域. (3)⎰⎰+D d xy σ)2(,其中=D {}x y x y x 2),(22≤+. (4)⎰⎰D xyd σ,其中D 为由直线2-=x y 及抛物线x y =2所围成的闭区域. (5)⎰⎰+Dd y x σ)2(,其中D 是由22x y =,12+=x y 围成的闭区域. (6)arctan Dy dxdy x ⎰⎰,其中D :2214,0,.x y y y x ≤+≤≥≤ 三 把积分dx e dy y y y x ⎰⎰-+222210化为极坐标形式并计算积分值.四 求以2,1y x x ==所围成的区域D为底,2(,)f x y xy =为顶的曲顶柱体的体积.B 题一 交换下列积分的积分次序(1)⎰⎰-x x dy y x f dx 2103),( (2)⎰⎰y dx y x f dy 2010),(+⎰⎰-y dx y x f dy 3031),(.二 计算下列二重积分(1)⎰⎰-+Ddxdy y x 422,其中D 是由圆1622≤+y x 所围成的闭区域. (2)⎰⎰+D dxdy y x x )cos(,其中D 是顶点分别为)0,0(,)0,(π和),(ππ的三角形闭区域.(3)x D exydxdy ⎰⎰其中D为由曲线y =与y =所围区域.(2012研三) 三 化二重积分⎰⎰--21110),(x x dy y x f dx 为极坐标下的二次积分.四 设),(y x f 连续,D 由2x y =,0=y ,1=x 围成,且),(y x f =⎰⎰+Ddxdy y x f xy ),(,求),(y x f .五 求由曲面222y x z +=及2226y x z --=所围成立体的体积.。
微积分 (第八章第1、2节)

即有 m ≤ f ( x , y ) ≤ M , σ 是 D 的面积 ,
则 mσ ≤ ∫∫ f ( x , y )dσ ≤ Mσ
D
—— 二重积分的估值定理
微积分A(3)
17
例2. 估计 ∫∫ ( x + y + 10)dσ , D : x2 + y2 ≤ 4 的值。
微积分A(3) 12
4. 二重积分的几何意义: 二重积分的几何意义 几何意义:
∫∫
D
f ( x, y)dσ
上的曲顶柱体体积的代数和 代数和. 表示 D 上的曲顶柱体体积的代数和 5. 曲顶柱体体积 V = ∫∫
D
f ( x , y ) dσ
平面薄片质量 M = ∫∫ ρ ( x , y )dσ
D
ρ ( x , y ) > 0 为面密度
1. 例 比较
∫∫
D
( x + y)2 dσ 与 ∫∫ ( x + y)3dσ 的大小。
D
其中 D : ( x − 2)2 + ( y −1)2 ≤ 2.
( x + y )2 dσ ≤ ∫∫ ( x + y )3dσ ∫∫D D
微积分A(3)
16
6. 设 m = min { f ( x , y )}, M = max { f ( x , y )},
利用被积函数的奇偶性及区域的对称性, 例3. 利用被积函数的奇偶性及区域的对称性 说明下列积分等式。 说明下列积分等式。 (1) ∫∫D )
( x + x3 y2 )dxdy = 0
x2 ydxdy = 0
2 2 其中D是半圆形闭区域: 其中 是半圆形闭区域:x + y ≤ 4, y ≥ 0 是半圆形闭区域
[理学]第八章二重积分_OK
![[理学]第八章二重积分_OK](https://img.taocdn.com/s3/m/0c543dfc7cd184254a353530.png)
2
0
2sin
I
0
ydy dx 2
d 0
r sin rdr
矩形域 半圆域
2
2 2
2
s
i
nd
[
r3 3
2sin
]
0
4
2
s i n
8si n3 3
d
令 t
4 8
2
s
i
n4
tdt
4
8
3
1
4
30
342 2
2 27
例5.计算I e y2 dxdy,其中D由y x, y 1和y轴
y x2
x
(0,0) y2
, (1,1),
0 x 1
x
2
y
x
x y2
yy xx22
22
( x2
y)dxdy
1[ 0
x x2
(
x
2
y)dy]dx
D
1
[
x
2
(
x x2 ) 1 ( x x4 )]dx
0
2
33 . 140
先对x后对y:
0 y 1
y
2
x
y
x y2 y x2
D
D
(9) f (x, y)d g(x, y)d,( f (x, y) g(x, y))
D
D
8
1 若D对称于x 轴,关于变量y被积函数 是奇函数,
其积分值为0;若是偶函数,其积分值两倍于y>0
的区域上的积分;
2 若D对称于y 轴,关于变量x被积函数 是奇函数,
其积分值为0;若是偶函数,其积分值两倍于x>0
第八章二重积分

D
嘉兴学院
2020年6月2日星期二
第八章 二重积分
第19页
例 2 估计I
d
的值,
D x2 y2 2 xy 16
其中 D: 0 x 1, 0 y 2.
解 f (x, y)
1
,
( x y)2 16
区域面积 2,
在D上 f ( x, y)的最大值 M 1 ( x y 0) 4
4)“取极限”
第10页
( k ) max P1P2 P1,P2 k
令
max 1k n
( k )
n
V
lim
0 k 1
f
(k , k ) k
f (k , k )
(k ,k ) k
嘉兴学院
2020年6月2日星期二
第八章 二重积分
第11页
二、二重积分的定义
定义: 设 f (x, y)是定义在有界区域 D上的有界函数 ,
2020年6月2日星期二
第八章 二重积分
第16页
性质2 对区域具有可加性 ( D D1 D2 且D1、D2 无公共内点,则
f ( x, y)d f ( x, y)d f ( x, y)d .
D
D1
D2
性质3 若 为D的面积, 1 d d .
D
D
性质4 若在D上 f ( x, y) g( x, y),
x
I2 I1 I3
嘉兴学院
2020年6月2日星期二
第八章 二重积分
第28页
6. 设D 是第二象限的一个有界闭域 , 且 0 < y <1,
则
I1 yx3 d ,
I3
y
1 2
x
习题详解-第8章 二重积分

习题8-11. 设有一平面薄片,在xOy 平面上形成闭区域D ,它在点(x ,y )处的面密度为μ(x ,y ),且μ(x ,y )在D 连续,试用二重积分表示该薄片的质量. 解:(,)Dm x y d μσ=⎰⎰.2. 试比较下列二重积分的大小: (1) 2()Dx y d σ+⎰⎰与3()Dx y d σ+⎰⎰,其中D 由x 轴、y 轴及直线x +y =1围成;(2)ln()Dx y d σ+⎰⎰与2ln()Dx y d σ+⎡⎤⎣⎦⎰⎰,其中D 是以A (1,0),B (1,1),C (2,0)为顶点的三角形闭区域.解:(1)在D 内,()()2301x y x y x y ≤+≤+≥+,故,23()()DDx y d x y d σσ+≥+⎰⎰⎰⎰.(2) 在D 内,212ln()1,ln()ln ()x y x y x y x y ≤+≤≤+≤+≥+,故0从而, 2ln()[ln()]DDx y d x y d σσ+≥+⎰⎰⎰⎰习题8-21. 画出积分区域,并计算下列二重积分:(1) ()Dx y d σ+⎰⎰,其中D 为矩形闭区域:1,1x y ≤≤;(2) (32)Dx y d σ+⎰⎰,其中D 是由两坐标轴及直线x +y =2所围成的闭区域;(3) 22()Dx y x d σ+-⎰⎰,其中D 是由直线y =2,y =x ,y =2x 所围成的闭区域;(4) 2Dx yd σ⎰⎰,其中D 是半圆形闭区域:x 2+y 2≤4,x ≥0;(5) ln Dx yd σ⎰⎰,其中D 为:0≤x ≤4,1≤y ≤e ;(6) 22Dx d σy ⎰⎰其中D 是由曲线11,,2xy x y x ===所围成的闭区域.解:(1) 111111()()20.Dx y d dx x y dy xdx σ---+=+==⎰⎰⎰⎰⎰(2) 22220(32)(32)[3(2)(2)]xDx y d dx x y dy x x x dx σ-+=+=-+-⎰⎰⎰⎰⎰223202220[224]4.330x x dx x x x =-++=-++=⎰(3) 3222222200193()()()248yy Dy x y x d dy x y x dx y dy σ+-=+-=-⎰⎰⎰⎰⎰43219113.96860y y -= (4) 因为被积函数是关于y 的奇函数,且D 关于x 轴对称,所以20.Dx yd σ=⎰⎰(5) 44201041ln ln (ln ln )2(1)2110e De e e x yd dx x ydy x y y y dx x e σ-==-==-⎰⎰⎰⎰⎰. (6) 122224111311122222119()()124642x Dx x x x x x d dx dy dx x x dx y y y x σ==-=-=-=⎰⎰⎰⎰⎰⎰.2. 将二重积分(,)Df x y d σ⎰⎰化为二次积分(两种次序)其中积分区域D 分别如下:(1) 以点(0,0),(2,0),(1,1)为顶点的三角形;(2) 由直线y =x 及抛物线y 2=4x 所围成的闭区域; (3) 由直线y =x ,x =2及双曲线1y x=所围成的闭区域;(4) 由曲线y =x 2及y =1所围成的闭区域. 解:(1) 1221201(,)(,)(,).xx y ydx f x y dy dx f x y dy dy f x y dx --+=⎰⎰⎰⎰⎰⎰(2) 24414(,)(,).y xy dx f x y dy dy f x y dx =⎰⎰⎰⎰(3) 12222111112(,)(,)(,).xyyxdy f x y dx dy f x y dx dx f x y dy +=⎰⎰⎰⎰⎰⎰(4)21111(,)(,).xdx f x y dy dy f x y dx -=⎰⎰⎰3. 交换下列二次积分的积分次序:(1) 1(,)ydy f x y dx ⎰⎰; (2)2220(,)yydy f x y dx ⎰⎰;(3) ln 10(,)e xdx f x y dy ⎰⎰; (4) 123301(,)(,)y ydy f x y dx dy f x y dx -+⎰⎰⎰⎰.解:(1) 111(,)(,)yxdy f x y dx dx f x y dy =⎰⎰⎰⎰.(2) 222402(,)(,).y x ydy f x y dx dx f x y dy =⎰⎰⎰⎰(3) ln 11(,)(,)y e xeedx f x y dy dy f x y dx =⎰⎰⎰⎰(4) 123323012(,)(,)(,)yyxxdy f x y dx dy f x y dx dx f x y dy --+=⎰⎰⎰⎰⎰⎰.4. 求由平面x =0,y =0,x =1,y =1所围成的柱体被平面z =0及2x +3y +z =6截得的立体体积.解:11100037(623)(62).22V dx x y dy x dx =--=--=⎰⎰⎰5. 求由平面x =0,y =0,x +y =1所围成的柱体被平面z =0及曲面x 2+y 2=6-z 截得的立体体积.解:3111222000(1)34(6)[6(1)(1)).312x x V dx x y dy x x x dx --=--=----=⎰⎰⎰习题8-3 1. 画出积分区域,把二重积分(,)Df x y d σ⎰⎰化为极坐标系下的二次积分,其中积分区域D是:(1) x 2+y 2≤a 2 (a >0); (2) x 2+y 2≤2x ;(3) 1≤x 2+y 2≤4; (4) 0≤y ≤1-x ,0≤x ≤1. 解:(1) 20(,)(cos ,sin ).aDf x y d d f r r rdr πσθθθ=⎰⎰⎰⎰(2) 2cos 20(,)(cos ,sin ).Df x y d d f r r rdr πθπσθθθ-=⎰⎰⎰⎰(3) 221(,)(cos ,sin ).D f x y d d f r r rdr πσθθθ=⎰⎰⎰⎰(4)12cos sin 0(,)(cos ,sin ).Df x y d d f r r rdr πθθσθθθ+=⎰⎰⎰⎰2. 把下列积分化为极坐标形式,并计算积分值:(1)220)ady x y dx +⎰;(2)21;xxdx ⎰⎰解:(1)4422320)248aaa a dy x y dx d r dr πππθ+==⋅=⎰⎰⎰.(2) 2sin 31244cos 600001sin 3cos x x dx d r dr d πθπθθθθθ==⎰⎰⎰⎰⎰244466400011c o s 111(c o s )[(c o s )(c o s )]cos cos cos d d d πππθθθθθθθ-=-=--⎰⎰⎰531cos cos 4()3530πθθ--=--+= 3. 在极坐标系下计算下列二重积分: (1) 22xy De d σ+⎰⎰,其中D 是圆形闭区域: x 2+y 2≤1;(2) 22ln(1)Dxy d σ++⎰⎰,其中D 是由圆周x 2+y 2=1及坐标轴所围成的在第一象限内的闭区域;(3)arctanDyd σx⎰⎰,其中D 是由圆周x 2+y 2=1,x 2+y 2=4及直线y =0,y =x 所围成的在第一象限内的闭区域;(4)Dσ其中D 由圆周x 2+y 2=Rx (R >0)所围成.解:(1) 22222100112(1).20xy r r De d d e rdr e e πσθππ+==⋅=-⎰⎰⎰⎰(2) 23112222201ln(1)ln(1)[ln(1)]2201Dr r x y d d r rdr r dr r ππσθ++=+=+-+⎰⎰⎰⎰⎰212(1)[ln 22](2ln 21)441r r r dr rππ+-=-=-+⎰. (3) 222244010133arctan arctan(tan ).32264Dy d d rdr d rdr x ππππσθθθθ=⋅==⋅=⎰⎰⎰⎰⎰⎰(4)Dσ3cos 222022cos 12()230R R d R r d ππθππθθθ--==--⎰⎰⎰ 3333221(s i n )33R R R d πππθθ-=--=⎰.4. 求由曲面z =x 2+y 2与z .解:两条曲线的交线为x 2+y 2=1,因此,所围成的立体体积为:2122200()]().6DV x y d d r r rdr ππσθ=+=-=⎰⎰⎰⎰习题8-41. 计算反常二重积分()x y De dx dy -+⎰⎰,其中D :x ≥0,y ≥x .2. 计算反常二重积分222()Ddx dyx y +⎰⎰,其中D :x 2+y 2≥1. 解:1.22201()2a aaax yx x aaa xe dx edy eedx e e ---------=-=-+-⎰⎰⎰所以2()211lim ().22a x y a a a De edxdy e e --+--→+∞-=-+-=⎰⎰2. 由232011112()22R d dr r R πθπ=-⎰⎰,得222211lim 2().2()2R Ddxdy x y R ππ→+∞=-=+⎰⎰复习题8(A )1. 将二重积分d d (,)Df x y x y ⎰⎰化为二次积分(两种次序都要),其中积分区域D 是:(1) ︱x ︱≤1,︱y ︱≤2;(2) 由直线y =x 及抛物线y 2=4x 所围成. 解:(1) 12211221(,)(,).dx f x y dy dy f x y dx ----=⎰⎰⎰⎰(2) 244004(,)(,).yy xdx f x y dy dy f x y dx =⎰⎰⎰⎰2. 交换下列两次积分的次序:(1)d d 10(,)yy f x y x ⎰;(2)d d 20(,)a x f x y y ⎰;(3)d d +d d 12201(,)(,)xxx f x y y x f x y y -⎰⎰⎰⎰.解:(1)211d (,)d d (,)d x yxy f x y x x f x y y =⎰⎰⎰.(2) 200d (,)d d (,)d aaa a x f x y y y f x y x =⎰⎰⎰.(3)1221201d (,)d +d (,)d d (,)d xxy yx f x y y x f x y y y f x y x --=⎰⎰⎰⎰⎰⎰.3. 计算下列二重积分:(1) e d x y Dσ+⎰⎰, D : ︱x ︱≤1,︱y ︱≤1;(2) d d 2Dx y x y ⎰⎰,D 由直线y =1,x =2及y =x 围成;(3) d d (1)Dx x y -⎰⎰,D 由y =x 和y =x 3围成;(4) d d 22()Dx y x y +⎰⎰,D :︱x ︱+︱y ︱≤1;(5) d 1sin Dy σy ⎰⎰,D 由22y x π=与y =x 围成;(6) d (4)Dx y σ--⎰⎰,D 是圆域x 2+y 2≤R 2;解: (1)1111111211111e d ()()()1x y x y x x x x Ddx e dy e e dx e e e e σ+++-+----==-=-=--⎰⎰⎰⎰⎰.(2) 5322224211121129d d ()()2253151xDx x x y x y dx x ydy x x dx ==-=-=⎰⎰⎰⎰⎰. (3) 3112430011117(1)d d (1)()325460x x Dx x y dx x dy x x x x dx -=-=--+=--+=-⎰⎰⎰⎰⎰.(4)1122220()d d 4()xDx y x y dx x y dy -+=+⎰⎰⎰⎰33241201412124(2)4()33323330x x x x x x dx x =--+=--+=⎰.(5) 222200sin 12sin d (sin sin )y y Dy y dy dx y y y dy y y πππσπ==-⎰⎰⎰⎰⎰ 222222sin (cos )1(cos sin )10ydy yd y y y y ππππππ=+=+-=-⎰⎰. (6)3222(4)d (4cos sin )[2(cos sin )]3R DR x y d r r rdr R d ππσθθθθθθ--=--=-+⎰⎰⎰⎰⎰3222[2(sin cos )]430R R R πθθθπ=--=. 4. 已知反常二重积分e d 2y Dx σ-⎰⎰收敛,求其值.其中D 是由曲线y =4x 2与y =9x 2在第一象限所围成的区域.解:设2249(0)a D y x y x y a a ===>是由曲线、和在第一象限所围成.则22222200015555ed ()236144144144aaa a y y y y a D x dy dx ye dy e d y e σ-----==⋅=--=-⎰⎰⎰⎰⎰. 所以225e d lime d 144ay ya DD x x σσ--→+∞==⎰⎰⎰⎰. 5. 计算e d 2x x +∞--∞⎰.解:由第四节例2以及2y =e x -是偶函数,可知2e d x x +∞--∞=⎰6. 求由曲面z =0及z =4-x 2-y 2所围空间立体的体积.解:曲面z =0和z =4-x 2-y 2的交线为x 2+y 2 =4.因此,所围空间立体的体积为:222220016(4)d d (4)2(8)8D x y x y d r rdr πθππ--=-=-=⎰⎰⎰⎰.7. 已知曲线y =ln x 及过此曲线上点(e ,1)的切线ey x 1=.(1) 求由曲线y =ln x ,直线ey x 1=和y =0所围成的平面图形D 的面积;(2) 求以平面图形D 为底,以曲面z =e y 为顶的曲顶柱体的体积.解:(1) 1ln (ln )12221e e e ee S xdx x x x =-=--=-⎰.(2) 221120013()()2220y y e y y y y y y e e V dy e dx e ye dy ye e ==-=-+=-⎰⎰⎰.(B )1. 交换积分次序:(1) 311(,)xxdx f x y dy -⎰⎰; (2)0112(,)y dy f x y dx --⎰⎰;(3) 224(,)x x f x y dy -⎰;(4) 110(,)dx x y dy ⎰.解:(1) 3111(,)(,)xxydx f x y dy dy f x y dx -=⎰⎰⎰.(2) 01101221(,)(,)yxdy f x y dx dx f x y dy ---=⎰⎰⎰⎰.(3) 2242402(,)(,)(,)x x f x y dy dy f x y dx dy f x y dx -=+⎰⎰⎰.(4) 211121(,)(,)(,)y dx f x y dy dy f x y dx dy f x y dx =+⎰⎰⎰⎰.2. 计算积分2122x xxdx dy x y +⎰⎰.解:222sin sin 144cos cos 2220000cos cos xxx r dx dy d rdr d dr x y r πθπθθθθθθθ==+⎰⎰⎰⎰⎰⎰ 4sin ln 24(ln cos )cos 20d ππθθθθ==-=⎰. 3. 计算积分112201yy dy dx x y ++⎰⎰.解:111114cos 4cos cos 222200000sin sin [sin ]111yy r dy dx d rdr d dr dr x y r r ππθθθθθθθθ==-++++⎰⎰⎰⎰⎰⎰⎰ 44001ln 21(tan sin arctan )arctan (cos )cos 2cos d d ππθθθθθθ=-⋅=+⎰⎰令cos t θ=,则原式211ln 21ln 21ln 211(arctan ln(12222dt dt t t t t t =+=+=+++ln 213ln 213ln ln 22242224ππ=---.4. 设函数f (x )在区间0,1⎡⎤⎣⎦上连续,且1()f x dx A =⎰,求11()()xdx f x f y dy ⎰⎰.解:设1'()()()(1)(0)F x f x f x dx F F A ==-=⎰,则.11111()()()[(1)()](1)()()(())xdx f x f y dy f x F F x dx F f x dx F x d F x =-=-⎰⎰⎰⎰⎰21()111(1)(1)[(1)(0)][(1)(0)](1)(1)(0)22220F x F A F A F F F F F A AF AF =-=--+=--21[(1)(0)]22A A F F =-=. 5. 计算2D x yd σ⎰⎰,其中D 是由直线y =0,y =1及双曲线x 2-y 2=1所围成的闭区域.解:11222022(13Dx yd dy ydx y y σ==+⎰⎰⎰⎰35122222011122(1)(1)(1)1)335150y d y y =++=⋅+=⎰. 6. 计算222y xdx e dy ⎰⎰.解:2222222240000211(1)220y y y y y x dx e dy dy e dx ye dy e e ====-⎰⎰⎰⎰⎰.7. 证明211()()d ()()d 1b xb n n aaadx x y f y y b y f y y n ---=--⎰⎰⎰,其中n 为大于1的正整数. 证:22()()d ()()bxbb n n aaaydx x y f y y dy x y f y dx ---=-⎰⎰⎰⎰11()()1b n b yax y f y dy n -=--⎰11()()d 1bn ab y f y y n -=--⎰。
高等数学微积分第八章第2节
zfx,y
用若干个小平 顶柱体体积之 和近似表示曲
顶柱体的体积, x
得到曲顶柱体的体积:
o
i
y
i,i
n
l i m 0
f (i ,i )i
f(x, y)d
i1
D
2。直角坐标系下的积分微元
我们利用直角
坐标网分割D
让分割充分细, yj
取D的被坐标网割出 yj 1
的一个典型子区域
Δσ,设它是如图
直线 y 2x 和抛物D线 y x2所围区域 .
[解] (1)求曲线的交点,作出曲线的草图:
y2x yx2
交点为(0,0),(2,4)
(2) 将区域D表示成不等式形式: D:x2 y2x,0x2
4。化二重积分为二次积分
( 3 ) 写 出 二 次 积 分 并 计 算
x2y
dxdy
2
dx
0
2xx2y dy
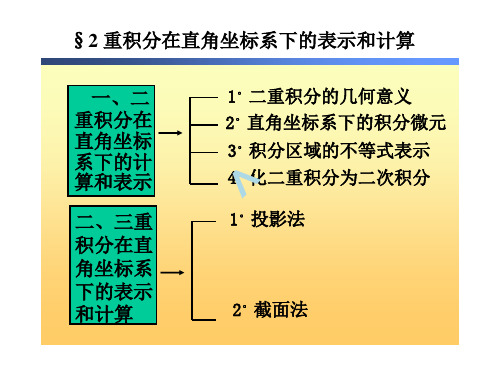
§2 重积分在直角坐标系下的表示和计算
一、二 重积分在 直角坐标 系下的计 算和表示
二、三重 积分在直 角坐标系 下的表示 和计算
1。二重积分的几何意义 2。直角坐标系下的积分微元 3。积分区域的不等式表示 4。化二重积分为二次积分 1。投影法
2。截面法
1。二重积分的几何意义
1 曲顶柱体的体积 曲顶柱体:
则D可以用不等式表示为:
D : x 1 y x x 2 y , c y b
3。积分区域的不等式表示
y型域
3。积分区域的不等式表示
例1.积分区域D为直线y=2x和抛物线y=x2 所围,写出区域D的不等式表示。
3。积分区域的不等式表示
[解] 解 方 程 组 y y 2 x x 2得 交 点 为 0 , 0 和 2 , 4
第八章 二重积分 第三节 广义二重积分

e
D
x2 y2
dxdy ,其中D是整个xy平面, 即
x , y .
解 整个xy平面用极坐标表示是D : 0 r ,0 2
e
D
x2 y2
dxdy bຫໍສະໝຸດ e
x2 y2
dxdy d e r rdr
§2.3 广义二重积分
类似于一元函数的广义积分,对于二元函数也有两类 广义二重积分. 即可分为积分区域无限与被积函数无界 两种,下面只研究无界区域上的二重积分的计算方法. 定义1 设D是xoy面上的无界区域, ƒ(x, y)在 D上连续且 G 是 D上的任意一个闭区域. 若 G 以任何方式无限扩展
lim f ( x , y )dxdy I 且趋于D 时, 均有 G D
G
则称此极限值 I 为ƒ(x, y)在无界区域 D上的二重积分,
并记为
f ( x , y )dxdy lim f ( x, y )dxdy
D GD G
当极限值I存在时, 则称广义二重积分 收敛;否则, 称广义二重积分发散.
f ( x , y )dxdy
D
注 由定义1知: 要求广义二重积分,只需仿照一元广 义积分, 先求二重积分, 再求二重极限即可. 例1 计算
( x, y) J 2 1 2 ( u, v )
故
1 2 1 2
1
e
( x 1 )2 ( x 2 )2 2 12 2 22
dxdy
e
u2 v 2
dudv 1
x2
dx.
的原函数不能用初等函数表示,故用
第八章 二重积分

第八章 二重积分(第7周第2次课)【教学目的和要求】掌握二重积分的概念、性质及计算(直角坐标、极坐标)。
【教学重点与难点】重点:二重积分的概念,二重积分的计算方法。
难点:极坐标下二重积分计算。
【教学方法】理论讲述与实例分析。
【总学时】6学时(理论讲述4学时,习题2学时)。
【教学过程】第一节 二重积分的概念与性质【教学目的和要求】掌握二重积分的概念、性质。
【教学重点与难点】二重积分的概念与性质。
【教学方法】理论讲述与实例分析。
【总学时】2学时。
【教学过程】引入:对面积、体积、质量等的几何量或物理量的计算导出了定积分的概念。
在一元函数定积分的基础上建立起来的二重积分因更接近于客观对象,故能处理更一般的问题。
二重积分和定积分一样,都是用和式的极限定义的。
但是,由于定积分的积分域通常只是区间,而二重积分的积分域则是平面区域,所以积分区域的恰当表示和积分顺序的合理选择是保证二重积分计算过程简捷正确的关键。
一、 二重积分的概念1.曲顶柱体的体积问题:定义并计算曲顶柱体的体积V :设有一立体,它的底是xoy 面上的闭区域D ,它的侧面是以D 的边界曲线为准线而母线平行于z 轴柱面,它的顶是曲面),(y x f z =,这里0),(≥y x f 且在D 上连续(图9-1,P363)。
这种立体叫作曲顶柱体。
求平顶柱体的体积:可以用公式来定义和计算:体积=高×底面积求曲顶柱体的体积:先用一组曲线网把D 分成n 个小区域:n σσσσ∆∆∆∆...,,,321分别以这些小闭区域的边界曲线为准线,作母线平行于Z 轴的柱面,这些柱面把原来的xoy 曲顶柱体分为n 个细曲顶柱体。
当这些小闭区域的直径很小时,由于),(y x f 连续,对同一个小闭区域来说,),(y x f 变化很小,这时细曲顶柱体可近似看作平顶柱体。
我们在每个i σ∆(这小闭区域的面积也记作i σ∆)中任取一点),(i i ηε,以),(i i f ηε为高而底为i σ∆的平顶柱体(图9-2)的体积为:),(i i f ηεi σ∆),...,2,1(n i =这n 个平顶柱体体积之和:∑=ni iif 1),(ηε,可以认为整个曲顶柱体的近似值。
第八章 二重积分

第八章 二重积分8.1 二重积分的概念设函数),(y x f 是闭区域D 上的有界函数,将区域D 任意分成n 个小区域1σ∆、2σ∆、…,n σ∆,其中i σ∆既是第i 个小区域也是第i 个小区域的面积。
在每个小区域i σ∆上任意取一点),(i i ηξ做乘积i i i f σηξ∆⋅),(,并作和式∑=∆⋅ni i i i f 1),(σηξ。
如果当各个小闭区间直径中的最大值0→λ时,极限i ni i i f σηξλ∆∑=→1),(lim 存在,则称为函数),(y x f 在D 上的二重积分,记为σd y x f D⎰⎰),(。
其中),(y x f 为被积函数,D 为积分区域,σd y x f ),(为被积表达式,σd 为面积微元。
(1)积分区域D 的划分和点的选取是任意的。
(2)σd y x f D⎰⎰),(的几何意义表示以积分区域D 为底面积,高为),(y x f 的曲顶柱体体积的代数和。
(3)函数),(y x f 可积的充分条件:若),(y x f 在D 上连续,则),(y x f 在D 上可积。
(4)函数),(y x f 可积的必要条件:若),(y x f 在D 上可积,则),(y x f 在D 上有界。
(5)直角坐标系下的面积微元dxdy d =σ。
8.2 二重积分的性质 (1)线性运算性质[]σβσασβαd y x g d y x f d y x g y x f DDD⎰⎰⎰⎰⎰⎰+=+),(),(),(),((βα,均为常数)(2)积分区域的可加性 )(),(),(),(2121D D D d y x f d y x f d y x f D D D+=+=⎰⎰⎰⎰⎰⎰σσσ(3)σσ=⎰⎰Dd (σ为积分区域D 的面积)(4)比较定理:设函数),(y x f 与),(y x g 在D 上有),(),(y x g y x f , 则σσd y x g d y x f DD⎰⎰⎰⎰),(),(推论:①若0),( y x f ,则0),( σd y x f D⎰⎰。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§8.1 二重积分的概念与性质教学内容1. 二重积分的概念;2. 二重积分的性质。
教学目的与要求1. 理解二重积分的概念;2. 熟悉二重积分的性质。
教学重点与难点二重积分的概念;二重积分的性质。
教学时数 2教学过程:一、二重积分的概念1.什么是曲顶柱体?设在有界闭区域D上),(yxf为非负连续函数,以曲面),(yxfz=为顶,以xoy平面的有界闭区域D为底、侧面是以D的边界曲线C作准线,而母线平行于z轴的柱面,称为曲顶柱体。
(如右图)2. 其体积V怎样计算?显然,平顶柱体的体积=底面积×高,而曲顶柱体的体积不能直接用上式计算,那么怎样来计算呢?由第五章求曲边梯形面积的方法就不难想到下面的解决办法:用一组曲线网将xoy面上的区域D划分为n个小区域:nσσσ∆∆∆,,,21,iσ∆也同时记为它们的面积),,2,1(ni=,分别以各小闭区域的边界曲线为准线,作母线平行于z轴的柱面,这些柱面把原曲顶柱体分为n个小曲顶柱体。
当这些小闭区域的直径很小时,连续函数),(yxfz=的变化不大,这时小曲顶柱体可近似看作平顶柱体.在每个iσ∆),,2,1(ni=任取一点),2,1(),(niPiii=ηξ,以),(iifηξ为高,而底为iσ∆的小平顶柱体的体积为iiifσηξ∆⋅),(),,2,1(ni=。
这n个平顶柱体体积之和∑=∆⋅niiiif1),(σηξ可作为整个曲顶柱体体积的近似值.令n个小闭区域的直径中的最大值(记作λ)趋于零,取上述和的极限,所得的极限就定义为所求曲顶柱体的体积。
综合起来,即所谓“分割、近似、作和、取极限”四步,即:xzyo曲顶柱体的体积∑=→∆⋅=niiiifV1),(limσηξλ。
3. 二重积分的概念定义设),(yxf在有界闭区域D上有定义,将闭区域D任意分成n个小闭区域1σ∆,,2σ∆,nσ∆,其中iσ∆表示第i个小闭区域,也表示它的面积,在每个iσ∆上任取一点),(iiηξ,作乘积),(iifηξiσ∆),,2,1(ni=,并作和iiniifσηξ∆∑=),(1,如果当各小闭区域的直径中的最大值λ趋近于零时,这和式的极限存在,则称此极限为函数),(yxf在闭区域D上的二重积分,记为⎰⎰Ddyxfσ),(,即⎰⎰Ddyxfσ),(iiniifσηξλ∆=∑=→),(lim1.其中),(yxf称为被积函数,σdyxf),(称为被积表达式,σd称为面积元素,D称为积分区域。
注:(1)在二重积分的定义中,对闭区域的划分是任意的;(2)当),(yxf在闭区域上连续时,或分片连续且有界,定义中和式的极限必存在,即二重积分必存在;(3)几何意义:当被积函数大于零时,二重积分表示曲顶柱体的体积,当被积函数小于零时,二重积分是曲顶柱体体积的负值;(4)上可积在存在,称若DyxfdyxfD),(),(⎰⎰σ;(5)在直角坐标系下,面积元素dxdyd=σ,二重积分也可写为⎰⎰Ddxdyyxf),(。
二、二重积分的性质(二重积分与定积分有类似的性质)性质1当k为常数时,.),(),(⎰⎰⎰⎰=DDdyxfkdyxkfσσ性质2 ⎰⎰±Ddyxgyxfσ)],(),([.),(),(⎰⎰⎰⎰±=DDdyxgdyxfσσ性质3 对区域具有可加性:⎰⎰⎰⎰⎰⎰+=21),(),(),(DDDdyxfdyxfdyxfσσσ(21DDD+=)。
性质4 若在D上,),(),(yxgyxf≤,则有⎰⎰⎰⎰≤DDdyxgdyxfσσ),(),(。
性质5 设A为区域D的面积,则AdD=⎰⎰σ。
性质6(二重积分的估计值定理)设m与M分别为),(yxf在区域D上的最大值与最小值,A为区域D的面积,则MAdyxfmAD≤≤⎰⎰σ),(。
性质7(二重积分的中值定理) 若),(yxf在闭区域D上连续,则在D上至少存在一点),(ηξ,使得AfdyxfD⋅=⎰⎰),(),(ηξσ成立,其中A为区域D的面积。
§8.2 二重积分的计算教学内容1. 直角坐标系下二重积分的计算;2. 极坐标系下二重积分的计算。
教学目的与要求1. 掌握直角坐标系下二重积分的计算;2. 掌握极坐标系下二重积分的计算。
教学重点与难点直角坐标系与极坐标系下二重积分的计算。
教学时数 4教学过程:一、直角坐标系下二重积分的计算1.基本积分区域(1)yD型(或X型)区域:设积分区域D由不等式组,bxa≤≤)()(21xyxϕϕ≤≤围成,则称这样的区域为yD型(或X型)区域(如下图所示)。
)(2xyϕ=a bD)(1xyϕ=Dba)(2xyϕ=)(1xyϕ=yD型(或X型)区域的特点:上、下边界各用一个方程表示;与y轴平行的直线和边界曲线相交,交点不超过两点。
(2)xD型(或Y型)区域:设积分区域D由不等式组,dyc≤≤)()(21yxyϕϕ≤≤围成,则称这样的区域为xD型(或Y型)区域(如下图所示)。
xD型(或Y型)区域的特点:左、右边界各用一个方程表示;与x轴平行的直线和边界曲线相交,交点不超过两点。
(3)对非X、Y型区域D:可将其化为若干个简单的X与Y型,利用可加性即可。
例1区域D是由xyxy==,2及2=x所围成,请用X型和Y型将D表示出来。
2.二重积分的计算步骤——化为两次单积分下面通过平行截面面积已知时立体体积的计算方法,引入二重积分的计算公式。
(1)积分区域是X型的情形设)}()(,),({21xyxbxayxDϕϕ≤≤≤≤=,0),(≥yxf。
如下图所示:)(2yxϕ=)(1yxϕ=Dcdcd)(2yxϕ=)(1yxϕ=D)(1xyϕ=ax bzyx)(xA),(yxfz=)(2xyϕ=一方面,曲顶柱体的体积:⎰⎰=Ddxdy y x f V ),(;另一方面由平行截面面积已知时立体体积的计算方法又知:dx x A V ba⎰=)(0,而⎰=)()(000201),()(x x dy y x f x A ϕϕ,当0x 在区间],[b a 上变化时,⎰=)()(21),()(x x dy y x f x A ϕϕ, (注意:任给一个x ,就有一个确定的一元函数值⎰)()(21),(x x dy y x f ϕϕ,此时x 视为常数)从而又有⎰⎰=bax x dx dy y x f V )()(21]),([ϕϕ。
于是就有:⎰⎰Ddxdy y x f ),(=⎰⎰bax x dx dy y x f )()(21]),([ϕϕ=⎰⎰bax x dy y x f dx )()(21),(ϕϕ。
上式右端的积分叫做先对y ,后对x 的二次积分,即先把x 看作常数,),(y x f 看作y 的一元函数,并对y 从)(1x ϕ到)(2x ϕ计算定积分,然后把计算的结果(是x 的函数)再对x 计算在区间],[b a 上的定积分。
(2)积分区域是Y 型的情形设}),()(),({21d y c y x y y x D ≤≤≤≤=ψψ,则同理有;⎰⎰Ddxdy y x f ),(=⎰⎰dcx x dx y x f dy )()(21),(ψψ。
其积分次序是先对x ,后对y 的二次积分,即先把y 看作常数,),(y x f 看作x 的一元函数,并对x 从)(1x ψ到)(2x ψ计算定积分,然后把计算的结果(是y 的函数)再对y 计算在区间],[d c 上的定积分。
(3)积分区域是非X 、Y 型区域D 时,可将其化为若干个简单的X 与Y 型,利用二重积分具有可加性分别计算即可。
例2 计算积分⎰⎰Dxy dxdy xe ,01,10:≤≤-≤≤y x D 。
例3 计算⎰⎰+Ddxdy y x )(,其中D 是由直线x y x y ===及2,1所围成的闭区域。
例4 改变积分 ⎰⎰-xdy y x f dx 101),(的次序。
例5 计算⎰⎰Dxydxdy ,其中D 是由抛物线2y x =与直线2-=x y 所围成的闭区域。
例6 计算⎰⎰Ddxdy y ysin ,其中D 是由抛物线2y x =与直线x y =所围成的闭区域。
二、极坐标系下二重积分的计算1. 极坐标简介(1)极坐标系的建立在平面内取一定点o,称为极点,从o引一条射线ox叫作极轴,对平面上任一点M,设其到极点的距离为r(称为极径),从极轴ox沿逆时针方向到射线oM的夹角为θ(极角),则称有序对),(θr为点M的极坐标。
注意θ以弧度为单位。
在极坐标系下,r=常数表示以极点o为心,常数r为半径的一族圆周;θ=常数表示从极点o出发,与极轴ox成夹角θ的一族射线。
(2)直角坐标与极坐标的互换⎪⎩⎪⎨⎧==+⇔⎩⎨⎧==xyryxryrxarctansincos222θθθ。
例7 把点M的极坐标)67,5(πM化为直角坐标。
例8 将曲线方程1,2,22222=+=+=+yxxyxayx化为极坐标方程。
2. 极坐标下的基本积分区域:rD型(1)极点在区域D的外部:。
{}βθαθϕθϕθ≤≤≤≤=),()(),(21rrDr特点:前后曲线分别只用一个方程表示;θ在两个常数之间;前后边界与过原点的射线相交,交点分别不超过一个(如右图)。
例9 将区域0,0,41:22≥≥≤+≤xyyxD用极坐标表示。
(2)极点在区域边界上,βθα≤≤).(0θϕ≤≤r例10 将区域axyxD2:22≤+,0≥y用极坐标表示。
(3)极点在区域内部πθ20≤≤,).(0θϕ≤≤roαβx)(1θϕ=r)(2θϕ=ro xD)(θϕ=rαβDo x)(θϕ=r例11 将区域1:22≤+yxD用极坐标表示。
3.极坐标系形式下的二重积分如右图所示小区域可以近似地看作是边长为ir∆和iirθ∆的小矩形,所以它的面积为iiiirrθσ∆∆≈∆,从而面积元素θσrdrdd=。
又⎩⎨⎧==θθsincosryrx所以,直角坐标系下的二重积分化为极坐标系下的二重积分如下:⎰⎰Ddyxfσ),(=⎰⎰Drdrdrrfθθθ)sin,cos(。
例12 计算dxdyeDyx⎰⎰--22,其中D是由中心在原点,半径为a的圆周所围成的闭区域。
例13 计算dxdyxyD⎰⎰arctan,其中D是由圆1,92222=+=+yxyx和直线0,==yxy 所围成的第一象限区域。
例14 将积分⎰⎰Ddxdyyxf),(化为极坐标系下的二次积分,其中xyxD2:22≤+。
例15 利用二重积分dxdyeDyx⎰⎰--22求广义积分⎰+∞∞--=dxeI x2。
作业:练习册第40、41次AoDiσ∆irr=iirrr∆+=iiθθθ∆+=θθ=。
