原子间相互作用势
晶体的结合能,内能,原子间的相互作用势能

晶体的结合能、内能、原子间的相互作用势能
晶体是由大量排列有序的原子或分子所组成的固体结构,在晶体中,原子或分
子之间存在着结合能和相互作用势能。
晶体的结合能、内能和原子间的相互作用势能密切相关,对于晶体的性质和稳定性起着至关重要的作用。
结合能
晶体的结合能是指晶体内部所有原子或分子之间相互结合所需要的能量。
晶体
的结合能决定了晶体的熔点、硬度、脆性等物理性质。
晶体的结合能可以通过实验方法或计算模拟方法来确定。
通常来说,结合能越大,晶体的稳定性越高,其熔点和硬度也会相应增加。
内能
晶体的内能是指晶体内部原子或分子的总能量。
内能包括晶体的结合能以及原
子或分子在晶体内部的动能和位能。
内能的大小与晶体的温度和压力有关。
晶体的内能是晶体的热力学性质的重要参数,可以通过实验测量或理论计算来确定。
原子间的相互作用势能
晶体中的原子或分子之间存在着相互作用势能,这种相互作用势能决定了晶体
的结构和稳定性。
原子间的相互作用势能可以通过简单的模型来描述,比如晶体中的键能、范德华力等。
不同种类的晶体,其原子间的相互作用势能也有所差异,这种差异导致了不同晶体的性质和行为。
在晶体学研究中,研究晶体的结合能、内能和原子间的相互作用势能是非常重
要的。
通过对这些能量的研究,可以更好地理解晶体的性质和行为,为合成新材料、优化材料性能等提供理论指导和实验依据。
总之,晶体的结合能、内能和原子间的相互作用势能是晶体学研究的核心内容,对于揭示晶体的本质和规律具有重要意义,也为材料科学和工程领域的发展做出了重要贡献。
原子间相互作用势解读

原子间相互作用势解读原子间相互作用势是描述两个或多个原子之间相互作用力的函数。
它是描述原子、分子或固体材料性质的关键因素,对于理解化学反应、材料力学性能、相变、晶体结构等都起着重要的作用。
本文将对原子间相互作用势进行解读。
一种显著的原子间相互作用势是范德华力(Van der Waals forces),它是由电荷偶极、氢键、格列高利亚力和弥散力等组成。
这些力可以通过公式来描述,例如Lennard-Jones势能公式:V(r)=4ε[(σ/r)^12-(σ/r)^6]这个公式中,r是两个原子间的距离,ε和σ是相互作用的参数。
这个公式表示了势能和原子间距离的关系,当两个原子非常接近时,势能会变得非常大,当原子间距离较大时,势能会变得非常小。
除了范德华力,库仑力也是原子间相互作用势的重要组成部分。
库仑力是由原子间的电荷交互作用引起的,它可以通过库仑电势公式来描述:V(r)=k*q1*q2/r其中r是两个原子间的距离,q1和q2是原子的电荷,k是电常数。
这个公式表示,当两个原子带有相同的电荷时,它们之间会存在排斥力;当两个原子带有相反的电荷时,它们之间会存在吸引力。
除了范德华力和库仑力,还有其他一些原子间相互作用势也非常重要。
例如,金属间相互作用势(Metal-Metal Interaction Potential)用于描述金属之间的相互作用力,分子间相互作用势(Molecule-Molecule Interaction Potential)用于描述分子之间的相互作用力。
通过使用原子间相互作用势,我们可以研究原子间的排列方式和结构稳定性。
例如,在材料科学中,人们可以使用原子间相互作用势预测材料的熔点、弹性模量、黏度等性质。
在化学反应中,通过分析原子间相互作用势,我们可以了解反应的速率和过程。
虽然原子间相互作用势是描述原子间相互作用的重要工具,但是它并不是完美的。
由于原子间相互作用力很复杂,我们通常只能采用近似的方法来描述这些力。
势晶体总的势能—N个原子两原子相互作用势能

dU
q2 6nb
dr
r0
N
4
0r02
r0n1
0
q2 6nb 4 0r02 r0n1
1
r0
(
e
)
24 0nb q 2
n1
电荷加倍时
1
1
r0 (
2e
)
240nb
2q2
n1
1 4
n1
r0
j
j
位移平方平均值为
m
2 n
m nj
m*nj
m
2 nj
m nj m*nj'
j
j
j
j j'
mnj取正和取负几率相等,第1项是主要项,忽略2nd项
m
2 n
m
2 nj
j
计算mnj平均值
m
2 nj
1 T0
T0 a 2
0j
sin2
wjt
naq j
dj
dt
a
r06
2
A12 A6
6
U (r0 )
1 N
2
A6 2 A12
Wbcc W fcc
U (r 0)bcc U (r 0) fcc
A6 2 A12
A'62 A'12
12.252
9.11 14.452
12.13
0.957
2.7 利用2-48式,可算出r0,将r0代入可得U
计算材料学第三章原子间相互作用势

• Reference system: an atom in a FCC crystal. The lattice constant of the reference crystal should match the density of the actual system. Use a measure for the local electron density as the map.
K.W. Jacobsen, M. Puska and J. K. Nørskov, Surf. Sci. 366, 394 (1996); Phys. Rev. B 35, 7423 (1987).
Effective medium theory (EMT)
• •
Blue lines: Electron density from blue atoms. Green line: Sum of contributions from blue atoms. This is the embedding density of red atom.
The Sutton-Chen potential provides a reasonable description of various bulk properties, with an approximate many-body representation of the delocalized metallic bonding. However, it does not include any directional terms, which are likely to be important for transition metals with partially occupied d shells.
固体物理第二章答案

第21. 有一晶体,平衡时体积为 0V , 原子间相互作用势为0.如果相距为 r 的两原子互作用势为 ()n m r r a r u β+-= 证明(1) 体积弹性模量为 K=.90V mnU (2) 求出体心立方结构惰性分子的体积弹性模量.[解答]设晶体共含有 N 个原子,则总能量为U(r)=()∑∑i jij r u '21. 由于晶体表面层的原子数目与晶体内原子数目相比小得多,因此可忽略它们之间的基异,于是上式简化为 U=().2'∑jijr u N设最近邻原子间的距离为R 则有j ij a r =R再令 A ,1'∑=j m j m a A ,1'∑=jn j n a 得到 U=.200⎪⎪⎭⎫ ⎝⎛+-n n m m R A R A N βα 平衡时R=R 0,则由已知条件U(R 0) = 0U 得0002U R A R A N n n m m =⎪⎪⎭⎫⎝⎛+-βα 由平衡条件 0)(0=R dRR dU得021010=⎪⎪⎭⎫⎝⎛-++n nm m R A n R A m N βα. 由(1),(2)两式可解得.)(2,)(20000n n m m nR n m N U A nR n m N U A -=-=βα利用体积弹性模量公式[参见《固体物理教程》(2.14)式]K=0220209R R U V R ⎪⎪⎭⎫ ⎝⎛∂∂得K= ⎥⎦⎤⎢⎣⎡+++-n n m m R A n n R A m m N V 000)1()1(291βα = ⎥⎦⎤⎢⎣⎡-++-+-)(2)1()(2)1(2910000000n m N mR U R n n n m N nR U R m m N V nnm m = .900V mn U - 由于,00<U 因此,00U U -= 于是 K= .90V mnU (1) 由《固体物理教程》(2.18)式可知,一对惰性气体分子的互作用能为.)(126r B r A r u +-=若令 61,42⎪⎭⎫⎝⎛==A B B A σε,则N 个惰性气体分子的互作用势能可表示为⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=6612122)(R A R A N r U σσε.由平衡条件0)(0=R dRR dU 可得 R .2616120⎪⎪⎭⎫ ⎝⎛=A A σ进一步得 .2)(122600A A N R U U ε-==代入K=.900V mn U 并取 m =6,n =12,V 300334R N =得 K=5126123233⎪⎪⎭⎫⎝⎛A A A σε.对体心立方晶体有 A .11.9,25.12126==A 于是.1.703σε=K 2. 一维原子链,正负离子间距为a ,试证:马德隆常数为2=μ1n2. [解答] 相距ij r 的两个离子间的互作用势能可表示成.4)(2n ijij ij r br q r u +=πμ设最近邻原子间的距离为R 则有 R a r j ij =, 则总的离子间的互作用势能 U=()∑∑∑-⎪⎪⎭⎫ ⎝⎛±-=jn jn j j j ij a bRa R q N r u N ''0'114[22πε. 基中 jja 1'±=∑μ 为离子晶格的马德隆常数,式中+;- 号分别对应于与参考离子相异和相同的离子.任选一正离子作为参考离子,在求和中对负离子到正号,对正离子取负号,考虑到对一维离子两边的离子是正负对称分布的,则有.413121112)1('⎥⎦⎤⎢⎣⎡+-+-=±=∑Λj ja μ利用正面的展开式 1n(1+x ),432432Λ+-+-x x x x 并令 1=x 得Λ+-+-41312111=1n(1+1)=1n2.于是,一维离子链的马德常数为2=μ1n23. 计算面心立方面简单格子的6A 和12A(1) 只计最近邻; (2) 计算到次近邻; (3) 计算到次近邻.[解答]图2.26示出了面心立方简单格子的一个晶胞.角顶O 原子周围有8个这样的晶胞,标号为1的原子是原子O 的最近邻标号为2的原子是O 原子的最近邻,标号为3的原子是O 原子的次次近邻.由此得到,面心立方简单格子任一原子有12个最近邻,6个次近邻及24个次次近邻.以最近邻距离度量,其距离分别为:.3,2,1===j j j a a a 由 .1,112'126'6⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛=∑∑jj j j a A a A图2.6 面心立方晶胞得(1) 只计最近邻时1211*12)1(66=⎪⎭⎫⎝⎛=A , 1211*12)1(1212\=⎪⎭⎫⎝⎛=A .(2) 计算到次近邻时.094.1221*611*12)2(,750.1221*611*12)2(121212666=⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛==⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛=A A(3) 计算到次次近邻时.127.12033.0094.1231*2421*611*12)3(,639.13899.0750.1231*2421*611*12)3(121212126666=+=⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛==+=⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛=A A 由以上可以看出,由于12A中的幂指数较大,12A 收敛得很快,而6A 中的幂指数较小,因此 6A 收敛得较慢,通常所采用的面心立方简单格子的 6A 和 12A 的数值分别是14.45与12.13.4. 用埃夫琴方法计算二维正方离子(正负两种)格子的马德隆常数. [解答]马德隆常数的定义式为 jja 1'±=∑μ,式中+、-号分别对应于与参考离子相异和相同的离子,二维正方离子(正负两种)格子,实际是一个面心正方格子,图 2.7示出了一个埃夫琴晶胞.设参考离子O 为正离子,位于边棱中点的离子为负离子,它们对晶胞的贡献为4*(1/2).对参考离子库仑能的贡献为图2.7二维正方离子晶格.121*4顶角上的离子为正离子,它们对晶胞的贡献为4*(1/4), 对参考离子库仑能的贡献为 .241*4-因此通过一个埃夫琴晶胞算出的马德隆常数为 .293.1241*4121*4=-=ν再选取422=个埃夫琴晶胞作为考虑对象,这时离子O 的最的邻,次近邻均在所考虑的范围内,它们对库仑能的贡献为,2414-而边棱上的离子对库仑能的贡献为 ,521*8221*4+- 顶角上的离子对为库仑能的贡献为 ,841*4-这时算出的马德隆常数为图 2.8 4个埃夫琴晶胞同理对932=个埃夫琴晶胞进行计算,所得结果为611.11841*41321*81021*8321*48458242414=⎪⎪⎪⎪⎭⎫ ⎝⎛-+-+⎪⎪⎭⎫ ⎝⎛-+-+⎪⎭⎫ ⎝⎛-=μ 对 1642=个埃夫琴晶胞进行计算,所得结果为614.13241*42521*81721*81021*8421*4184138108348458242414=⎪⎪⎪⎪⎭⎫ ⎝⎛-+-+-+⎪⎪⎭⎫ ⎝⎛-+-+⎪⎪⎭⎫ ⎝⎛-+-+⎪⎭⎫ ⎝⎛-=μ当选取 n 2个埃夫琴晶胞来计算二维正方离子(正负两种)格子的马德隆常数,其计算公式(参见刘策军,二维NaC1 晶体马德隆常数计算,《大学物理》,Vo1.14,No.12,1995.)为 [][].1,8411>+++=--n D C B A n n n n μ其中 ,21)1(,1)1(11111nB t A n n n t t n +-=+--=-=∑,1)1(1)1()2()1(1)1()1(2112212221112122122222222221⎪⎪⎪⎪⎪⎭⎫⎝⎛+--+--+-+-+--++⎪⎪⎭⎫⎝⎛+++-+⎪⎪⎭⎫ ⎝⎛+---n n n n n C n n ΛΛ.121)1()1(2181222222+-+-++++-=n n n n n D n n Λ5. 用埃夫琴方法计算CsCl 型离子晶体的马德隆常数(1) 只计最近邻 (2) 取八个晶胞 [解答](1) 图2.29是CsCl 晶胸结构,即只计及最近邻的最小埃夫琴晶胞,图2.29()a 是将Cs +双在体心位置的结构,图2.9(a)是将 Cl -取在体心位置的结构,容易求得在只计及最近邻情况下,马德隆常数为1.图2.29 (a )Cs 取为体心的CsC1晶胞,(b) C1取为体心的CsC1晶胞(2)图2.10是由8个CsCl 晶胞构成的埃夫琴晶胞,8个最近邻在埃夫琴晶胞内,每个离子对晶胞的贡献为1,它们与参考离子异号,所以这8个离子对马德隆常数的贡献为8埃夫琴晶胞6个面上的离子与参考离子同号,它们对埃夫琴晶胞的贡献是21,它们与参考离子的距离为32R 它们对马德隆常数的贡献为-()3/2*621图 2.10 8个CsCl 晶胞构成的一个埃夫琴晶胞埃夫琴晶胞楞上的12个离子,与参考离子同号,它们对埃夫琴晶胞的贡献是41它们与参考离子的距离为322R 它们对马德隆常数的贡献为-()3224/1*12埃夫琴晶胞角顶上的 8个离子,与参考离子同号,它们对埃夫琴晶胞的贡献是81它们与参考离子的距离为2R 它们对马德隆常数的贡献为 -()281*8,由8个CsCl 晶胞构成的埃夫琴晶胞计算的马德隆常数.064806.32)8/1(*8322)4/1(*123/2)2/1(*68=---=μ 为了进一步找到马德常数的规律,我们以计算了由27个CsCl 晶胞构成的埃夫琴晶胞的马德隆常数,结果发现,由27个CsCl 晶胞构成的埃夫琴晶胞的马德隆常数是0.439665.马德隆常数的不收敛,说明CsCl 晶胞的结构的马德隆常数不能用传统的埃夫琴方法计算.为了找出合理的计算方法,必须首先找出采用单个埃夫琴晶胞时马德隆常数不收敛的原因.为了便于计算,通常取参考离子处于埃夫琴晶胞的中心.如果以Cs +作参考离子,由于埃夫琴晶胞是电中性的要求,则边长为pa 2(p 是大于或等于1的整数)的埃夫琴晶胞是由(2p )3个CsCl 晶胞所构成,埃夫琴晶胞最外层的离子与参考离子同号,而边长为(2p +1)的埃夫琴晶胞是由(2p +1)3 个 CsCl 晶胞所构成,但埃夫琴晶胞的最外层离子与参考离子异号,如果以C1-作参考离子也有同样的规律,设参考离子处于坐标原点O ,沿与晶胞垂直的方向(分别取为x,y,z 图2.11示出了z 轴)看去,与参考郭同号的离子都分布在距O 点ia 的层面上,其中i 是大于等于 1的整数,与 O 点离子异号的离子都分布在距O 点(i -0.5)a 的层面上,图 2.11(a) 示出了同号离子层,图2.11(b)示出了异号离子层.图2.11 离子层示意图(a)表示同号离子层, O 离子所在层与 O '离子所在层相距ia(b)表示异号离子层, O 离子所在层和O ' 离子所在层相距(i -0.5)a当 CsCl 埃夫琴晶胞边长很大时,晶胞最外层的任一个离子对参考离子的库仑能都变得很小,但它们对参考离子总的库仑能不能忽略.对于由(2p )3个CsCl 晶胞所构成的埃夫琴晶胞来说,最外层有6*(2p )2个与参考离子同号的离子,它们与参考离子的距离为(1/2)pa ~(23)pa ,它们与参考离子的库仑能为a pe 024πε量级,这是一个相对大的正值.对于由(2p +1)3个CsCl 晶胞所构成的埃夫琴晶胞来说,离外层有6*(2p +1)2个与参考离子异号的离子,它们与参考离子的库仑能为a pe 024πε-量级,这是一个绝对值相对大的负值,因此,由(2p )3个CsCl 晶胞构成的埃夫琴晶胞所计算的库仑能,与由(2p +1)3个CsCl 晶胞构成的埃夫琴晶胞所计算的库仑能会有较大的差异.即每一情况计算的库仑能都不能代表CsCl 晶体离子间相互作用的库仑能.因此这两种情况所计算的马德隆常数也必定有较大的差异,由1个CsCl 晶胞、8个CsCl 晶胞和27个CsCl 晶胞构成的埃夫琴晶胞的计算可知, CsCl 埃夫琴晶胞体积不大时,这种现象已经存在.为了克服埃夫琴方法在计算马德隆常数时的局限性,可采取以下方法,令由 (2p )3个CsCl 晶胞构成的埃夫琴晶胞计算的库仑能为1U ,由(2p +1)3个CsCl 晶胞构成的埃夫琴晶胞所计算的库仑能为1U ,则CsCl 晶体离子间相互作用的库仑能可近似取作 )(2121U U U +=(1) 因子1/2 的引入是考虑除了(2p +1)3个CsCl 晶胞构成的埃夫琴晶胞最外层离子外,其他离子间的库仑能都累计了两偏,计算1U 和2U 时要选取体积足够大的埃夫琴晶胞,此时埃夫琴晶胞最外层离子数与晶胞内的离子数相比是个很小的数,相应的马德隆常数应为 )(2121μμμ+=(2) 其中:=1μ⎪⎪⎭⎫ ⎝⎛±∑i ja 1'是由(2p )3个CsC1晶胞构成的埃夫琴晶胞计算的值; =1μ⎪⎪⎭⎫ ⎝⎛±∑i ja 1'由 (2p +1)3 个CsC1晶胞构成的埃夫琴晶胞所计算成本的值.为简化计算,特选取晶胞边长a 为计算单位,由于,32a R =所以,23'μμ= ⎪⎪⎭⎫ ⎝⎛±=∑'''1i i a μ (3) 其中'i a 是某一离子到参点的距离与a 的比值.考虑到对称性,对选定的埃夫琴晶胞,把晶胞的离子看成分布在一个个以参考离子为对称心的正六面体的六个面上,体积不同的正六面六个面上的离子分别计算.由(2p )3个CsC1晶胞构成埃夫琴晶胞时,由分析整理可得,231111⎪⎪⎭⎫ ⎝⎛++=∑∑=-=p pi i p i i C B A μ (4) 由(2p +1)3个 CsC1 晶胸构成埃夫琴晶胞时,,231112⎪⎪⎭⎫ ⎝⎛++=∑∑=-=p pi i p i i D B A μ (5)其中:),1(''''22'2'p i i y x k A i x iy y x i <≤++-=∑∑(6)i A 表示与 O 点距离为ia 的6个面上所有的离子对马德隆常数的面贡献,因为这些离子与参考离子同号,故到负号.'x 、'y 是离子在平面 '''y x o 上的坐标, ''y x k 代表 6个面上等价离子的个数,其取值规则为:(1) 在角上(如E 点),即'x =i 且 'y = i. 时, ''y x k =8;(2) 在棱与坐标轴的交点(如 F 点),'x =i 且'y = 0或 'x =0且'y = 0时, ''y x k =6 (3) 在棱上的其他点(如H 、I 点)即不满足上述条件,且'x =i 或'y = i.时, ''y x k =12 (4) 在'O 点,即'x =0且'y = 0时, ''y x k =6(5) 在除'O 点外的面上的点(如J 点),即不满足上述条件时,''y x k =24.),1()5.0(5.05.05.05.022'2''''''p i i y x k B i x i y yx i ≤≤-++=∑∑-=-=(7)i B 代表距O 点距离为(i -0.5)a 的6个面上的离子对马德隆常数的贡献,因为这种些离子与参考离子异号,故取正号. 'x ,'y 是离子在平面'''y x o 上的坐标, '''y x k 代表这6个面上等价离子的个数,其取值规则为:(1) 在角上(如K 点),即'x =i 且 'y = i.时, '''y x k =8;(2) 在棱下(如L 、M 点),即不满足不述条件,且'x =i 或'y = i 时,'''y x k =12; (3) 在面上(如N 点)好不满足上述条件时, '''y x k =24.),(0022'2'"''''p i i y x k C i x iy i yx =++-=∑∑==i C 表示在边长为2pa 的晶胞最外层,即与参考离子相距pa 的6个面上的离子对马德隆常数的贡献,应取负号,与iA 的不同在于"''y x k的取值: (1) 在角上, "''y x k =''y x k /8; (2) 在棱上, "''y x k =''y x k /4; (3) 在面上, "''y x k=''y x k /2.),()5.0(5.05.05.05.022'2''''''''p i i y x k D i x i y yx i =-++=∑∑-=-=i D 表示在边长为2a p )1(+的晶胞最外层,即与参考离子相距(p +0.5)a 的离子层对马德隆常数的贡献,应取正号,与i B 的不同在于'''''yx k 的取值: (1) 在角上, '''''y x k ='''y x k /8; (2) 在棱上, '''''y x k ='''y x k /4; (3) 在面上, '''''y x k ='''y x k /2.表2.1给出了计算结果,给出的μ是由分别对应2p 和2p+1的1μ和2μ求得的,实际上, 1μ和2μ只需对应边长相近的埃夫琴晶胞即可,如取对应2p 和2p-1的埃夫琴晶胞也可得到一样的收敛结果,由以上数据可见,马德隆常数μ随晶胞边长的增大而迅速收敛.该方法适用于NaC1结构以外离子晶体马德隆常数的计算.6.只计及最近邻间的排斥作用时,一离子晶体离子间的互作用势为⎪⎪⎩⎪⎪⎨⎧±-=-)2(,)1(,)(22r e R e e r u R ρλ(1)最近邻(2)最近邻以外 式中ρλ,是常数,R 是最近邻距离,求晶体平衡时,原子间总的互作用势.[解 答]设离子数目为2N,以j ij a r =R 表示第j 个离子到参考离子i 的距离,忽略表面效应,则总的相互作用能可表示为U =N ⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛±-∑∑-ρλR j j e R a e 2' (∑表示最近邻)=N ,2⎥⎦⎤⎢⎣⎡+--ρλμR e Z R e其中⎪⎪⎭⎫⎝⎛±=∑j ia 1'μ 为马德隆常数,+号对应于异号离子,-号对应于同号离子;Z 为任一离子的最近邻数目,设平衡时R=R 0 ,由平衡条件,02020=⎥⎦⎤⎢⎣⎡+=-ρρλμR R e Z R e N dRdU 得.0202ρλμρR e Z R e -=平衡时的总相互作用为.1)(0020200⎪⎪⎭⎫⎝⎛-=⎥⎦⎤⎢⎣⎡+-=-R R e N e Z R e N R U R ρμλμρ 7. 设离子晶体中,离子间的互作用势为⎪⎪⎩⎪⎪⎨⎧±+-=最近邻以外最近邻,,)(22re R b R e r u m(1) 求晶体平衡时,离子间总的相互作用势能)(0R U (2) 证明: )(0R U 11-⎪⎪⎭⎫⎝⎛∝m mZ μ其中μ是马德隆常数,Z 是晶体配位数 [解答](1)设离子数目为2N , 以j ij a r =R 表示第j 个离子到参考离子i 的距离,忽略表面效应,则总的相互作用能可表示U =N ⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛±-∑∑m j j R b R a e 2'(∑表示最近邻) =N ,2⎥⎦⎤⎢⎣⎡+-m R b Z Re μ其中⎪⎪⎭⎫ ⎝⎛±=∑j i a 1'μ,为马德隆常数,+号对应于异号离子,-号对应于同号离子.Z 为任一离子的最近邻数目,设平衡时R=R 0由平衡条件,0102020=⎥⎦⎤⎢⎣⎡-=+m R R Zmb R e N drdUμ得10-m R Zmb=2e μ即1120-⎪⎪⎭⎫ ⎝⎛=m e Zmb R μ.于是,晶体平衡时离子间总的相互作用势能0U =).1(000--=⎥⎦⎤⎢⎣⎡+-m R NZbR b Z R Zmb N m m m(2)晶体平衡时离子间的相互作用势能可进一步化为0U =.)()()1()1(1111121211--------=⎪⎪⎭⎫ ⎝⎛--m m m m mm m m m m mb Ze Nbm e Zmb ZNbm μμ由上式可知 .110-⎪⎪⎭⎫⎝⎛∝m mZ U μ8.一维离子链,其上等间距载有正负2N 个离子,设离子间的泡利排斥只出现在最近邻离子之间,且为b/R n,b,n 是常R 是两最近邻离子的间距,设离子电荷为q ,(1) 试证明平衡间距下 )(0R U =;114212002⎪⎭⎫⎝⎛--n R n Nq πε(2) 令晶体被压缩,使0R )1(0δ-→R , 试证明在晶体被压缩单位长度的过程中外力作功的主项为c 2δ其中c=;21)1(02R n q n -(3) 求原子链被压缩了2)1(0<<e e NR δδ时的外力[解答](1) 因为离子间是等间距的,且都等于R ,所以认定离子与第j 个离子的距离j r 总可表示成为R a r j j =ja 是一整数,于是离子间总的互作用势能⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎪⎭⎫ ⎝⎛±-=⎥⎥⎦⎤⎢⎢⎣⎡+=∑∑n i in j j j R b a R q N r b r q N R U 214242)('202'0πεπεμ,其中+、-分别对应相异离子和相同离子的相互作用.一维离子晶格的马德隆常数(参见本章习题2)为=⎪⎪⎭⎫ ⎝⎛±∑i ia 1'21n2. 利用平衡条件0)(0=R dRR dU得到b=nq 01-n 0241n2R πε,)(R U =⎪⎪⎭⎫ ⎝⎛---n n nR R R Nq 102141n22πε. 在平衡间距下⎪⎭⎫⎝⎛--n R Nq R U 1141n22)(0020πε.(2) 将互作用势能在平衡间距附近展成级数Λ+-⎪⎪⎭⎫ ⎝⎛+-⎪⎭⎫⎝⎛+=202200)(21)()()(0R R dR U d R R dR dU R U R U R R 由外力作的功等于晶体内能的增量,可得外力作功的主项为W=20220)(21)()(0R R dR U d R U R U R-⎪⎪⎭⎫ ⎝⎛=-, 其中利用平衡条件,将R=R )1(0δ- ,代入上式,得到W=δδπε)2(421)1(2102002NR R n q n ⎥⎥⎦⎤⎢⎢⎣⎡-. 晶体被压缩单位长度的过程中,外力作的功的主项δ02W NR =δπε⎥⎥⎦⎤⎢⎢⎣⎡-2002421)1(21R n q n 令c=202421)1(R n q n πε-(CGS)得到在晶体被压缩单位长度的过程中,外力作的功的主项为2δc . (3)设e δδ=时外力为F e ,由于在弹性范围内,外力与晶格的形变成正比,所以 F= )2(0δαNR , F e = )2(0e NR δα,其中α为比例系数离子链被压缩e NR δ02过程中外力作的功W e =δδαδδd NR NR Fdx e eNR e 020002)]2([0⎰⎰== e e e F NR NR δδα022022121)2(=.由于 W e =)2(20e eNR c δδ,所以离子链被压缩了e NR δ02时的外力为F e =202)1(21R n n q c ee δδ-=.9.设泡利排斥项的形式不变,讨论电荷加倍对NaC1晶格常数,体积弹性模量以及结合能的影响。
双原子之间的作用力
r r0 du (r ) 0 dr r0
第二章 晶体的结合
第 14 页
f (r0 ) 0
r0
n m
Bn Am
(2) (3)
A m U C U (r0 ) m (1 ) r0 n
互作用势能达极小值,由此决定原子
间的平衡距离r0。
此时的状态称为稳定状态。
荷间的库仑吸引力,长程作用; +B/rn :代表排斥能,来自同性电荷 间的库仑斥力及泡利原理所引起的 排斥力,总体表现短程作用。
第二章
晶体的结合
第 13 页
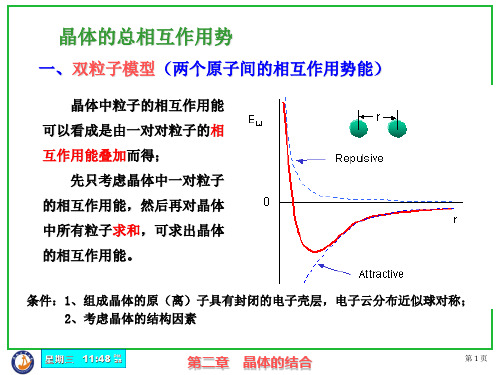
相互作用势能的一般性质
(1)平衡位置r0的确定: 图(a):互作用势能曲线
图(b): 互作用势能曲线的微商曲线
du( r ) mA nB f (r ) m 1 n 1 dr r r
1 k V
第二章
V P
T
第 12 页
晶体的结合
1、三维晶体参数与结合能的关系
相距r的两个原子之间的互作用势能用U(r)表示:
A B U (r ) m n r r
A、B、m、n皆为大于零的常数。
(1)
( m n)
-A/rm :代表吸引能,来自异性电
这表明,分子间的范德瓦尔斯-伦敦力引起的互作用势能与r-6成正比。 而由泡利原理产生的斥力作用,较难计算,一般由实验求得,排斥 势与r-12成反比 因此,一对分子间总的互作用势能为:
第二章
晶体的结合
第9页
Page 10
A B u( r ) 6 12 (11) r r or
12 6 u( r ) 4 (12) r r A2 B , 4B A
晶体的结合能、内能、原子间相互作用势能之间的区别

晶体的结合能、内能、原子间相互作用势能之间的区别晶体是由大量原子或分子组成的固体材料,它具有一定的结构和周期性,具有一定的热力学性质。
在研究和理解晶体性质的过程中,结合能、内能和原子间相互作用势能是重要的概念。
它们之间存在着一些区别和联系,接下来我将详细介绍这三个概念。
首先,我们来讨论结合能。
结合能是指晶体中各个原子之间的结合程度。
它代表了形成或破坏一个晶体所需要的能量。
结合能的大小可以反映晶体的稳定性和强度。
在晶体中,原子或分子之间通过化学键来相互结合,形成晶体的稳定结构。
不同类型的物质有不同的结合方式,例如离子晶体是通过离子键相互结合,而共价晶体是通过共价键相互结合。
结合能可以通过实验或计算方法来确定,它通常以能量的形式表示,单位为焦耳或电子伏特。
其次,我们来谈谈内能。
内能是指晶体中各个原子或分子的总能量。
它包括晶格振动能、电子能和其他能量形式。
晶体的内能与其温度和压力有关。
在晶体中,原子或分子通过振动和相互作用来形成晶格结构。
晶格振动能是晶体中原子或分子振动的能量,它与温度相关,随着温度的升高而增加。
电子能是晶体中电子的能量,它与原子或分子内部的电子分布和电子运动状态有关。
除了晶格振动能和电子能,晶体中还可能存在其他能量形式,例如电磁能、磁能等。
内能可以通过实验或计算方法来确定,它通常以能量的形式表示,单位为焦耳或电子伏特。
最后,我们来探讨原子间相互作用势能。
原子间相互作用势能是指晶体中相邻原子或分子之间相互作用的能量。
它描述了晶体中原子或分子之间的相互作用强度和性质。
在晶体中,原子或分子之间的相互作用可以通过势能函数来描述,其中吸引势能和排斥势能是两个主要成分。
吸引势能是由于原子或分子之间的吸引力而产生的,它使得晶体能够形成稳定的结构。
排斥势能是由于原子或分子之间的排斥力而产生的,它使得晶体中原子或分子之间保持一定的距离。
原子间相互作用势能可以通过实验或计算方法来确定,它通常以能量的形式表示,单位为焦耳或电子伏特。
《原子间作用势》课件

03
原子间作用势的应用
材料科学
材料强度与韧性
合金设计
原子间作用势在材料科学中用于描述 原子间的相互作用,有助于理解材料 的强度、韧性和其他力学性能,从而 优化材料的设计和制备。
利用原子间作用势,可以模拟合金的 微观结构和性能,预测合金的力学、 物理和化学性质,指导合金的成分设 计和优化。
相变与稳定性
原子间作用势的大小取决于原子 之间的距离和电子分布,其变化 规律对于理解物质性质和行为具 有重要意义。
原子间作用势的物理意义
原子间作用势反映了原子之间的吸引 力和排斥力,是决定物质稳定性和性 质的关键因素。
通过研究原子间作用势,可以深入了 解物质的物理、化学和材料科学性质 ,为新材料的开发和现有材料的优化 提供理论支持。
THANKS
感谢观看
《原子间作用势》PPT课件
目 录
• 原子间作用势概述 • 原子间作用势的数学模型 • 原子间作用势的应用 • 原子间作用势的发展趋势 • 原子间作用势面临的挑战与展望
01
原子间作用势概述
原子间作用势的定义
01
原子间作用势是指原子之间相互 作用的势能,它是描述原子之间 相互作用的重要物理量。
02
通过原子间作用势,可以研究材料在 不同温度和压力下的相变行为,以及 各种相的稳定性,为新型材料的开发 提供理论支持。
化学反应动力学
反应路径与能垒
原子间作用势在化学反应动力学 中用于描述化学键的生成、断裂 和转化,有助于确定反应路径、 能垒和活化能,从而深入理解化
学反应的机制。
反应速率常数
通过原子间作用势,可以计算化 学反应的速率常数,为反应机理 的确定和反应动力学模型的建立
提供重要依据。
原子间相互作用势Interatomic Potentials

微观尺度材料设计原子间相互作用势
原子间相互作用势-共价键势
共价键结合的原子间相互作用势在共价材料的计 算机模拟中占有极为重要的地位, 这主要是因为在共 价材料中原子间相互作用势不仅取决于原子间的距 离, 而且与原子间的成键方向有着密切的联系。所以, 为了正确地描述共价材料中原子间相互作用势的性 质, 不仅要考虑两个原子间的距离, 而且要体现成键 取向的变化对势函数的影响。
(6-12)势非常接近。
微观尺度材料设计原子间相互作用势
原子间相互作用势-对势
Born-Mayer势: Born-Mayer势是为了描述离子晶体中 离子间的闭壳层电子所产生的排斥作用而提出的, 其一般 形式为
(r ) Ae
Br
Born-Mayer势中的参数A, B一般是通过平衡态的晶体数 据确定的。
微观尺度材料设计原子间相互作用势
原子间相互作用势-对势
sp-价态金属的对势:对于sp-价态金属, 人们经常 可以利用准自由电子近似和弱赝势模型处理。在 这一理论模型中 , 内壳层电子的作用被记入原子 核, 从而构成有效电荷为Z的原子实。系统的总能 N 量为
E total
1 0 ij (rij ) E bs 2 i j 1
其中VR是排斥项, VA是吸引项, Bij是一个与键角ijk有关的 系数。
微观尺度材料设计原子间相互作用势
原子间相互作用势
在实际的材料研究和计算机模拟中, 原子间相互作用势 的选择主要取决于所研究的具体材料。 对于分子晶体, Lennard-Jones势就是合适的有效势; 对于共价晶体, 共价键结合的原子间相互作用势是非常 有效的; 对于过渡金属, 基于有效介质方法是一个理想的方案; 对于离子键占主导地位的陶瓷材料和金属氧化物, 人们
《原子间相互作用势》课件

多尺度模拟技术的发展
总结词
多尺度模拟技术能够同时考虑微观和宏观尺度上的相互作用,为全面理解物质性质提供有力工具。
详细描述
多尺度模拟技术能够将微观的原子、分子行为与宏观的物质性质相结合,为跨尺度研究提供便利。未来,多尺度 模拟技术将进一步应用于各种复杂系统的研究,如生物系统、材料系统等,为跨尺度研究和应用提供更多可能性 。
02
原子间相互作用势是量子力学中 的概念,它基于量子力学的原理 ,描述了原子之间的相互作用。
原子间相互作用势的重要性
原子间相互作用势是理解物质性质的关键因素之一,它决定了物质的物理性质和化 学性质。
在化学反应中,原子间相互作用势的变化会导致化学键的断裂和形成,从而影响化 学反应的进行。
在材料科学中,原子间相互作用势决定了材料的力学性质、热学性质和电学性质等 。
原子间相互作用势的应用
材料科学中的应用
01
可以更准确地模拟和预测 材料的性质,从而优化材 料设计。
材料性能预测
利用原子间相互作用势, 可以预测材料的力学、热 学、光学等性能,为新材 料的研发提供理论支持。
材料缺陷研究
通过原子间相互作用势, 可以深入了解材料中的缺 陷行为,为提高材料性能 和稳定性提供指导。
化学反应模拟中的应用
1 2 3
反应机理研究
利用原子间相互作用势,可以详细研究化学反应 的机理,包括反应中间体的行为和能量变化。
催化剂设计
通过原子间相互作用势,可以模拟催化剂与反应 物之间的相互作用,为新型催化剂的设计提供理 论依据。
药物合成优化
利用原子间相互作用势,可以模拟药物分子的合 成过程,优化合成路径,降低成本和提高效率。
大规模模拟技术的发展
原子间相互作用势解读

原子间相互作用势解读静电相互作用的形式可以用库伦定律来描述,即原子之间的电荷之间的相互作用力与它们之间的距离成反比。
具体来说,原子之间的相互作用势能可以表示为:V_Coulomb = k * (q1 * q2) / r其中,q1和q2是原子之间的电荷,r是它们之间的距离,k是一个常数。
范德华相互作用则更为复杂一些。
它可以用范德华力场模型来描述,其中最常用的是Lennard-Jones势函数。
Lennard-Jones势函数可以表示为:V_LJ=4ε[(σ/r)^12-(σ/r)^6]其中,ε是势能的尺度参数,σ是势能的距离参数,r是原子之间的距离。
Lennard-Jones势函数的形式可以分为两个部分:第一个部分是吸引项,即(σ/r)^12,它表示原子之间的瞬时电偶极引起的吸引力;第二个部分是排斥项,即(σ/r)^6,它表示原子之间的电子云重叠引起的排斥力。
这两个项的平衡决定了原子间的总体相互作用。
在实际应用中,原子间相互作用势通常还会加入其他修正项,以更准确地描述实际系统中的相互作用。
例如,对于离子化合物,静电相互作用势能可以通过考虑离子晶体间的库伦吸引力和斥力来表示。
而对于金属材料,电子间的交换和相关作用也需要被纳入考虑。
通过选择适当的参数,我们可以用原子间相互作用势来模拟和预测原子间的结合、位移和振动等行为。
这对于研究和理解固体材料的性质具有重要的意义。
例如,通过原子间相互作用势,我们可以解释和预测材料的热膨胀系数、热导率、机械性能等。
总而言之,原子间相互作用势是描述原子之间相互作用力的数学函数。
它包括静电相互作用和范德华相互作用,可以通过适当地选择参数来模拟和预测原子间的行为。
在分子动力学模拟和固体材料建模中具有广泛的应用。
原子间相互作用势解读

微观尺度材料设计原子间相互作用势
晶体的结合-晶体的类型
金属晶体:结合力主要依靠原子实和电子云间的静 电库仑力。金属晶体一般为密堆结构,配位数为 12 ; 少数金属具有体心立方结构,配位数为8。金属晶体 的结合能一般比较小,但过渡金属的结合能比较大。 金属晶体的导电性能好、一般熔点低,过渡金属的 熔点比较高。 典型的金属晶体:I、II及过渡元素
晶体的结合-晶体的类型
氢键晶体:结合力主要依靠氢原
子与电负性很大而原子半径较小
的两个原子结合成 XHY 强 键弱键形式。氢键晶体的结合 能一般比较低、氢键具有饱和性。 典型的氢键晶体:H2O
微观尺度材料设计原子间相互作用势
晶体的结合-结合力的一般性质
力函数 平衡位置
最大有效位置
du (r ) f (r ) dr du (r ) r0 0 0 dr d 2u ( r ) rm 0 2 dr
微观尺度材料设计原子间相互作用势
晶体的结合-晶体的类型
离子晶体:结合力主要依靠正、负离 子间的静电库仑力。离子晶体的结合 能一般在 800kJ/mol 、配位数最多为 8 。 离子晶体的结合稳定性导致导电性能 差、熔点高、热膨胀系数小等特征。 大多数离子晶体对可见光透明,在远 红外区有一个特征吸收峰。 典型的离子晶体:I-VII、II-VI
ij 也可以是的函数。
微观尺度材料设计原子间相互作用势
原子间相互作用势-对势
Lennard-Jones势
n m 0 A B r0 r0 (r ) n m m n r nm r r r
(r ) 4 r
12
Байду номын сангаас
碳原子和碳原子之间lj势

碳原子和碳原子之间lj势
碳原子之间的相互作用可以通过Lennard-Jones势来描述。
Lennard-Jones势是描述原子或分子之间相互作用的一种经典势能
模型,通常用于描述惰性气体和稀薄流体中的分子间相互作用。
对
于两个碳原子之间的Lennard-Jones势,它可以用以下公式来表示:V(r) = 4ε [ (σ/r)^12 (σ/r)^6 ]
在这个公式中,r是两个碳原子之间的距离,ε是势能的深度
参数,σ是势能的长度参数。
这个势能函数包含两项,一项是吸引项,即-(σ/r)^6,另一项是排斥项,即(σ/r)^12。
这两项分别描
述了范德华力的吸引和排斥效应。
从物理角度来看,当两个碳原子之间的距离很远时,势能趋于零,表示它们之间没有相互作用;当它们的距离很近时,势能会变
得非常大,表示排斥效应占据主导地位;而在某个距离范围内,势
能会出现吸引效应,使得两个碳原子会相互吸引。
另外,从化学角度来看,碳原子之间的Lennard-Jones势也可
以用于描述分子间的相互作用,比如在石墨或者纳米材料中,碳原
子之间的排列和相互作用对材料的性质有着重要影响。
因此,通过研究碳原子之间的Lennard-Jones势,可以更好地理解碳材料的性质和行为。
总的来说,碳原子之间的Lennard-Jones势是描述它们相互作用的重要模型,它既可以从物理角度解释范德华力的吸引和排斥效应,也可以从化学角度描述碳材料中分子间的相互作用。
这对于研究碳材料的性质和应用具有重要意义。
原子间相互作用势

原子间相互作用势
哎呀,一听到“原子间相互作用势”这个词,是不是感觉特别高大上,特别神秘?其实刚开始我也这么觉得,好像这是科学家们在实验室里研究的超级深奥的东西。
咱先不说那些复杂的科学定义,就想想咱们平时玩的弹珠。
弹珠碰到一起会弹开或者滚向别的地方,对不对?那原子就有点像特别特别小的弹珠。
原子之间也会有这样那样的“互动”。
比如说,有的原子靠得近了,就会互相排斥,就像两个脾气不太好的小朋友,谁也不想挨着谁;而有的原子靠得近了,又会紧紧地抱在一起,就跟好朋友手拉手一样亲密。
你可能会问啦,这跟我们的生活有啥关系呢?嘿,关系可大着呢!
比如说金属,为啥金属那么结实,能做成各种各样的工具?就是因为原子之间有一种特殊的“吸引力”,让它们乖乖地排好队,形成了坚固的结构。
再比如塑料,为啥塑料比较软,容易变形?也是因为原子间的作用方式和金属不一样。
想象一下,如果原子间的作用势突然乱套了,那这个世界会变成啥样?哇,简直不敢想!也许房子会一下子塌掉,汽车也开不了,甚至我们喝的水都可能变得奇奇怪怪。
老师给我们讲这些的时候,同学们都瞪大了眼睛,满脸的不可思议。
“这也太神奇了吧!”小明忍不住叫了出来。
“可不是嘛!”小红也跟着说,“原来我们身边的一切东西,都是因为原子间这样的作用才存在的。
”
我心里也在想,科学的世界真是充满了惊喜和未知,就像一个超级大的宝藏等着我们去挖掘。
所以说,原子间相互作用势虽然看不见摸不着,却在悄悄地影响着我们生活的方方面面。
我们得好好感谢科学家们,是他们努力探索,才让我们一点点了解这个神奇的世界。
这就是我对原子间相互作用势的理解啦,你是不是也觉得特别有趣呢?。
lammps lj势氢原子和铁原子

lammps lj势氢原子和铁原子LAMMPS是一款用于分子动力学模拟的软件,它可以模拟各种原子间相互作用力场。
其中,LJ势是一种常用的力场模型,用于描述非极性原子间的相互作用。
本文将以LAMMPS的LJ势模型为基础,讨论氢原子和铁原子的相互作用。
在LAMMPS中,氢原子和铁原子的相互作用力场可以通过定义原子类型和参数来实现。
氢原子可以使用LJ势模型的参数进行描述,而铁原子则需要根据具体的研究对象选择适当的参数。
LJ势模型是一种经验势函数,可以用于描述原子间的吸引力和斥力。
其基本形式为:V(r) = 4ε[(σ/r)^12 - (σ/r)^6]其中,V(r)表示两个原子间的相互作用势能,r表示原子间的距离,ε为势能尺度参数,σ为长度尺度参数。
对于氢原子,其LJ势的参数通常可以通过实验数据或计算方法得到。
以氢气(H2)为例,其LJ势的参数为ε = 36.0 kJ/mol,σ = 2.96 Å。
这意味着两个氢原子之间的相互作用势能会随着它们之间的距离变化而变化,当它们的距离为2.96 Å时,相互作用势能最小。
而对于铁原子,其LJ势的参数需要根据具体的研究对象来确定。
例如,在研究固体铁时,可以选择ε = 0.636 eV,σ = 2.556 Å作为模拟参数。
这样,铁原子之间的相互作用势能也会随着它们的距离变化而变化,当它们的距离为2.556 Å时,相互作用势能最小。
通过在LAMMPS中定义氢原子和铁原子的类型和参数,可以模拟它们之间的相互作用。
在模拟中,可以通过改变氢原子和铁原子的初始位置和速度,观察它们之间的相互作用和运动行为。
通过分析模拟结果,可以得到氢原子和铁原子之间的相互作用能量和力的信息,进一步研究它们的结构和性质。
除了LJ势模型,LAMMPS还支持其他力场模型的使用,如Coulomb 势、Morris potential等。
这些势模型可以用于模拟不同体系下的原子间相互作用,从而研究不同材料的性质和行为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
h,i j i aj (rij )
微观尺度材料设计原子间相互作用势
原子间相互作用势-基于有效介质方法
二阶动量近似和TB势:二阶动量近似和紧束缚方法起源 于能带理论的紧束缚模型。根据紧束缚理论, 电子态密度 的二阶动量与周围原子的径向函数和有关。带能量近似 地等于电子能带的宽度, 即二阶动量的平方根。
ij 也可以是的函数。
微观尺度材料设计原子间相互作用势
原子间相互作用势-对势
Lennard-Jones势
m r0 n 0 A B r0 (r ) n m m n r nm r r r
(r ) 4 r
微观尺度材料设计原子间相互作用势
原子间相互作用势-对势
对于由N个粒子组成的体系, 对势函数描述的系统总能量 N 为 1
E total
2
i j 1
ij
(rij ) U ()
其中ij(rij)为原子i、j相距为rij时的对势函数。对于第一类 对势U=0, 对于第二类对势U()为原子凝聚对系统总能量 的贡献, 它是原子平均体积或材料平均密度的函数, 同时
微观尺度材料设计原子间相互作用势
晶体的结合-结合力的一般性质
1 N N U (r ) u (rij ) 2 i 1 j i
2 U U U V P V 2 V V V0 V0
V 2U V P K V 2 V0 V V0 V0 0 2U K V 2 V0 V0
微观尺度材料设计原子间相互作用势
原子间相互作用势-对势
对势在早期的材料研究中发挥了极为重要的作用, 并仍 然活跃在计算机模拟的许多领域。 根据对系统总能量的贡献, 可以把对势分为两类。 系统的总能量完全由对势函数决定, 这类对势可以有效 地描述van der Waals相互作用占主导地位的体系; 对势函数仅描述恒定的材料平均密度下系统能量随原 子构型的变化, 这类对势适用于描述sp-价态金属。
晶体的结合-晶体的类型
氢键晶体:结合力主要依靠氢原
子与电负性很大而原子半径较小
的两个原子结合成XHY强 键弱键形式。氢键晶体的结合 能一般比较低、氢键具有饱和性。 典型的氢键晶体:H2O
微观尺度材料设计原子间相互作用势
晶体的结合-结合力的一般性质
力函数 平衡位置
最大有效位置
du (r ) f (r ) dr du (r ) r0 0 0 dr d 2u ( r ) rm 0 2 dr
微观尺度材料设计原子间相互作用势
原子间相互作用势-基于有效介质方法
多粒子体系的总能量的一般形式为
E total
1 N Fi f j (rij ) ij (rij ) j i 2 i j i
其中rij是原子i, j间的距离, F, f和则取决于所依据的物理 模型和处理方法。
微观尺度材料设计原子间相互作用势
原子间相互作用势-基于有效介质方法
以有效介质方法为基础, 先后发展出了原子 间相互作用势计算的有效介质理论(EMT)、嵌入 原子方法(EAM) 、紧束缚方法(TB) 、二阶动量近 似(SMA) 和胶体模型(Glue model) 等。尽管这些 原子间相互作用势所适用的范围有所不同, 但其 出发点都是有效介质方法。
晶体的结合-晶体的类型
微观尺度材料设计原子间相互作用势
晶体的结合-晶体的类型
金属晶体:结合力主要依靠原子实和电子云间的静 电库仑力。金属晶体一般为密堆结构,配位数为12; 少数金属具有体心立方结构,配位数为8。金属晶体 的结合能一般比较小,但过渡金属的结合能比较大。 金属晶体的导电性能好、一般熔点低,过渡金属的 熔点比较高。 典型的金属晶体:I、II及过渡元素
1 E total A Fi ( i ) ij (rij ) 2 i j i 其中F() = 1/2 j i (ri
原子间相互作用势-基于有效介质方法
EAM势比较适用于没有成键取向结构的密堆金 属; TB势更适用于具有体心立方结构的过渡金属; 而EMT势的势函数计算过于复杂。 然而, 这些问题都在随着人们认识的不断深入和 一些相关理论的发展而逐渐得以改善。
U
2
(rij )
i j k 1
U
3
(ri , r j , rk )
U3(ri, rj, rk) = h(rij, rik, jik)+ h(rjk, rji, kji)+ h(rki, rkj, ikj) 是
一个三体角关联项。
微观尺度材料设计原子间相互作用势
原子间相互作用势-共价键势
微观尺度材料设计原子间相互作用势
原子间相互作用势-共价键势
共价键结合的原子间相互作用势在共价材料的计 算机模拟中占有极为重要的地位, 这主要是因为在共 价材料中原子间相互作用势不仅取决于原子间的距 离, 而且与原子间的成键方向有着密切的联系。所以, 为了正确地描述共价材料中原子间相互作用势的性 质, 不仅要考虑两个原子间的距离, 而且要体现成键 取向的变化对势函数的影响。
微观尺度材料设计原子间相互作用势
原子间相互作用势-EAM势 EAM方法在解决固体声子谱、液态金属、 缺陷、合金、杂质、断裂、表面结构、 表面吸附、表面迁移、表面有序-无序相 变、表面有序合金、表面声子、团簇等 诸多领域均取得了巨大成功。
微观尺度材料设计原子间相互作用势
在一定的物理模型的基础上发展相应的原子间相 互作用势, 进而研究材料的性质和不同状态下的
行为, 成为材料研究中一种必要的研究手段。
早期的原子间相互作用势多数是一些纯经验拟合
势, 近年来人们更多地是通过基本电子结构的理
论计算, 发展一些合适的半经验的“有效势”。
其中为密度关联项。
微观尺度材料设计原子间相互作用势
原子间相互作用势-基于有效介质方法
基 于 有 效 介 质 方 法 (effective-medium-based Method)的原子间相互作用势在有关金属材料的 计算机模拟中有着广泛应用, 并取得了巨大成功。 基 于 有 效 介 质 方 法 也 被 称 为 对 泛 函 方 法 (pairfunctional method), 其理论基础是电子的密度泛 函理论。
微观尺度材料设计原子间相互作用势
原子间相互作用势
在实际的材料研究和计算机模拟中, 原子间相互作用势 的选择主要取决于所研究的具体材料。 对于分子晶体, Lennard-Jones势就是合适的有效势; 对于共价晶体, 共价键结合的原子间相互作用势是非常 有效的; 对于过渡金属, 基于有效介质方法是一个理想的方案; 对于离子键占主导地位的陶瓷材料和金属氧化物, 人们
Tersoff 势和Brenner势 :Tersoff 势和Brenner势起源于 Abell引入的有关C的处理方法。Tersoff 势和Brenner势 的一般形式为
E total
1 1 Vij [VR (rij ) BijVA (rij )] 2 i j 2 i j
其中VR是排斥项, VA是吸引项, Bij是一个与键角ijk有关的 系数。
基于壳层模型发展了相应的半经验势.。
微观尺度材料设计原子间相互作用势
原子间相互作用势-EAM势
EAM理论是Daw和Baskes在电子的密度泛函理论和有效 介质理论的基础上发展起来的一种构造原子间相互作用 势的方法。 Foiles等人对金属EAM势的构造做了重要改进, 并给出了 Au, Ag, Cu, Pt, Pd, Ni等金属的EAM势, 使之不仅适用于 纯金属材料的研究,而且可以对合金材料给出比较理想 的描述。 人们根据EAM理论, 先后构造出适用于不同材料的多种 形式的EAM势。
微观尺度材料设计原子间相互作用势
晶体的结合-晶体的类型
离子晶体:结合力主要依靠正、负离 子间的静电库仑力。离子晶体的结合 能一般在800kJ/mol、配位数最多为8。 离子晶体的结合稳定性导致导电性能 差、熔点高、热膨胀系数小等特征。 大多数离子晶体对可见光透明,在远 红外区有一个特征吸收峰。 典型的离子晶体:I-VII、II-VI
微观尺度材料设计原子间相互作用势
晶体的结合-晶体的类型
分子晶体:结合力主要依靠瞬时偶极 矩的相互作用 范德瓦耳斯力。分子 晶体的结合能很低、以密堆结构排列、 配位数为12。分子晶体导电性能差、
熔点低。分子晶体对可见光透明。分 子晶体分为极性和非极性两大类。
典型的分子晶体:VIII
微观尺度材料设计原子间相互作用势
微观尺度材料设计原子间相互作用势
原子间相互作用势-共价键势
Stilling-Weber势:Stilling-Weber势是针对硅的性质而提 出的一种包括两体和三体相互作用的经验势, 被广泛应用 于硅的体材料和表面的特性研究。Stilling-Weber势的一 般形式为
E total
i j 1
微观尺度材料设计原子间相互作用势
原子间相互作用势-基于有效介质方法
EMT和EAM势:有效介质理论和嵌入原子方法的物理思 想起源于Friedel提出的原子嵌入能概念。原子嵌入能的 基本思想是:原子的凝聚能主要取决于该原子所占据位 置的局域电子密度。
E total
1 Fi ( h,i ) ij (rij ) 2 i j i
微观尺度材料设计原子间相互作用势
原子间相互作用势-对势
sp-价态金属的对势:对于sp-价态金属, 人们经常 可以利用准自由电子近似和弱赝势模型处理。在 这一理论模型中, 内壳层电子的作用被记入原子 核, 从而构成有效电荷为Z的原子实。系统的总能 N 量为
E total
1 0 ij (rij ) E bs 2 i j 1
