七年级数学下册 3.3 探索三角形全等的条件(二)课件 (新版)北师大版
《探索三角形全等的条件》三角形PPT教学课件(第1课时)

所以△ABC≌△AED(SSS).
=× × =
课堂检测
基础巩固题
4.已知: 如图,点B,E,C,F在同一直线上 , AB = DE , AC = DF ,BE = CF .
试说明: (1)△ABC ≌ △DEF;
(2)∠A=∠D.
解: (1)因为BE = CF,
巩固练习
变式训练
如图, C是BF的中点,AB =DC,AC=DF.试说明:△ABC ≌ △DCF.
解:因为C是BF中点,
所以BC=CF.
在△ABC 和△DCF中, AB = DC, (已知) AC = DF, (已知) BC = CF, (已证) 所以 △ABC ≌ △DCF
(SSS).
探究新知 素养考点 2 利用三角形全等说明线段或角相等
D是BC的中点
探究新知
指明范 围
摆齐根 据
解:因为D 是BC中点, 所以BD =DC. 在△ABD 与△ACD 中,
准备条件
AB =AC (已知)
BD =CD (已证)
B
AD =AD (公共边)
所以 △ABD ≌ △ACD ( SSS ).
A C
D 写出结论
探究新知
书写步骤: ①准备条件:证全等时要用的条件要先证好; ②指明范围:写出在哪两个三角形中; ③摆齐根据:摆出三个条件用大括号括起来; ④写出结论:写出全等结论.
例 工人师傅在安装木制门框时,为防止变形常常如图中所示,钉上两条斜拉的 木条,这样做的原理是根据三角形的______性. 解稳析定:门框钉上斜拉的木条构成三角形,三角形具有稳定性.
巩固练习
变式训练
探索三角形全等的条件课件北师大版七年级数学下册

∴∠DAB=∠EAC
在ΔABD与ΔACE中
∠DAB=∠EAC
AB=AC
B
C
∠ABD=∠ACE
∴ΔABD≌ΔACE
∴BD=CE
三 角
01 三角形全等判定——SSS
形
全 02 三角形全等判定——SAS
等
的 判
03 三角形全等判定——AAS
定
条 件
04 三角形全等判定——SAS
判定两个三角形全等的思路:
针对练习:如图,已知OA=OC,OB=OD,∠AOC=∠BOD, 试说明:ΔAOB≌ΔCOD
D C
解:ΔAOB≌ΔCOD,理由如下:
∴∠AOC=∠BOD
∴∠AOC-∠AOD=∠BOD-∠AOD
∴∠COD=∠AOB
在ΔAOB与ΔCOD中
OA=OC
∠COD=∠AOB
OB=OD
O
∴ΔAOB≌ΔCOD
A B
A
全等判定——ASA
F
E
D
B
C
三角形全等的性质
全等判定——SSS
全等判定——SAS
选题背景
全等判定——AAS
针对练习:如图,AC=DC,AB=DE,CB=CE.
试说明:∠1=∠2
A
全等判定——ASA
解:∠1=∠2,理由如下: E 在ΔABC与ΔDEC中
AC=DC
AB=DE
CB=CE
B
∴ΔABC≌ΔDEC
E C
D
A
B
三角形全等的性质
全等判定——SSS
全等判定——SAS
选题背景
全等判定——AAS 全等判定——ASA
判定方法四: 两角及其夹边分别相等的两个三角形全等 ( 简写成“边角边”或“ASA”)
《探索三角形全等的条件(二)》课件 2022年北师大版数学课件

x 1 5.
x 1 5,
x1 6,x2 4 . ( 4 ) ( 2 x 1 ) 2 25 ,
4
2 x 1 25 5 . 42
2x 1 5. 2
x1
7 4
, x2
3. 4
想一想
(1) 52等 于 多 少?( (5)2等 于 多 少?
(2)
49
2
等 于 多 少?
∴ AB=CD BC=AD
〔全等三角形对应边相等〕
议一议
B A
利用“角边角〞可知, 带B块去,可以配到一 个与原来全等的三角形 玻璃。
完成以下推理过程:
在△ABC和△DCB中,A
∠ABC=∠DCB 3
∵ BC=CB〔公共边〕
∠2=∠1
B1
D
4
O 2C
∴△ABC≌△DCB〔 ASA〕
想一想:
如图,O是AB的中点,
E 800 5cm
700 300
B
A
700 300
D
F
请大家根据勾股定理,结合图形完成填空:
E
w1
z
D
A y1
1x
C 1
O1 B
x2= 2 , y2= 3 , z2= 4 , w2= 5 .
x2=2,幂和指 数,求底数x, 你能求出来吗?
注意!
一般地,如果一个正数 x 的平方等于 a,即 x2 = a ,那么这个正数 x 就叫做 a 的算术平方 根,记为“ ”,读作“根号 a ”. 特别地,我们规定0的算术平方根是0,即
F
A
BD
E
3、如图,在△ABC 中 ,∠B=∠C,AD是∠BAC的
角平分线,那么AB=AC吗?为什么?
七年级数学下册 第4章 三角形 4.3 探索三角形全等的条件课件 (新版)北师大版

例2 (2017四川宜宾中考)如图4-3-2,已知点B、E、C、F在同一条直线 上,AB=DE,∠A=∠D,AC∥DF.试说明:BE=CF.
图4-3-2 分析 由AC∥DF可得∠ACB=∠F,又∠A=∠D,AB=DE,可以利用AAS 得到△ABC≌△DEF,根据全等三角形的对应边相等可得BC=EF,都减 去EC即可得BE=CF.
AD BC,
因为DAB CBA,所以△ABD≌△BAC(SAS).
AB AB,
知识点一 判定三角形全等的条件——边边边 1.如图4-3-1,在△ABC和△FED中,AC=FD,BC=ED,要利用“SSS”来判 定△ABC和△FED全等,下面的4个条件中:①AE=FB;②AB=FE;③AE= BE;④BF=BE,可利用的是 ( )
AB=DE,BC=EF (2)已知两角
思路一(找第三边)
思路二(找角)
首先找出AC=DF,然后应用“SSS”判定全等
①找夹角:首先找出∠B=∠E,然后应用 “SAS”判定全等;②找直角用“HL”判定 全等(后面会学到)
思路一(找夹边)
思路二(找角的对边)
首先找出AB=DE,然后应用“ASA”判定全 等
A.①或②
B.②或③
图4-3-1 C.①或③ D.①或④
答案 A 由题意可得,要用“SSS”进行△ABC和△FED全等的判定, 只需AB=FE,若添加①AE=FB,则可得AE+BE=FB+BE,即AB=FE,故①可 以;显然②可以;若添加③AE=BE或④BF=BE,均不能得出AB=FE,故③④ 不可以,故选A.
架不变形,他至少要再钉上
根木条.
()
图4-3-5
A.0 解析 答案
B.1 C.2 D.3 连接AC或BD,构成三角形,三角形具有稳定性. B
数学(七下)3.3探索三角形全等的条件(二)

1、角.边.角;
2、角.角.边
每种情况下得到的三角形都全等吗?
做一做
1.角.边.角;
若三角形的两个内角分别是60°和80° 它们所夹的边为4cm,你能画出这个三角形吗?
2cm
60°
80°
做一做
2.角.角.边
若三角形的两个内角分别是60°和45°,且45° 所对的边为3cm,你能画出这个三角形吗?
2
C
∴△ABC≌△DCB( AAS )
巩固练习:
如图,O是AB的中点,∠A=∠B,△AOC 与△BOD全等吗?为什么? 我的思考过程如下: 两角与夹边对应相 等 A
C O B D
∴△AOC≌△BOD
补充练习
1﹑请在下列空格中填上适当的条件, 使△ABC≌△DEF。 在△ABC和△DEF中 A D
课堂小结
通过这堂课的学习你有 什么收获?知道了哪些 新知识?学会了做什么?
布置作业
P83 知识技能2.3; 问题解决。
第三章
三角形
3 探索三角形全等的条件(第2课时)
情境导入
我们已学过识别两个三角形全等的方法 是什么?识别三角形全等是不是还有其 它方法呢?
情境导入
有一块三角形纸片撕去了一个角, 要去剪一块新的,如果你手头没 有测量的仪器,你能保证新 剪的纸片形状、大小和原来的一 样吗?
实践探究
我们知道:如果给出一个三角形三条边的长度, 那么因此得到的三角形都是全等.如果已知一个 三角形的两角及一边,那么有几边对应相等的两个三 角形全等,简写成“角边角”或“ASA”
两角和其中一角的对边对应相等的两个 三角形全等,简写成“角角边”或“AAS”
练一练
1.如图,已知AB=DE, ∠A =∠D, ,∠B=∠E, 则△ABC ≌△DEF的理由是:角边角(ASA) 2.如图,已知AB=DE ,∠A=∠D,,∠C=∠F,则 △ABC ≌△DEF的理由是: 角角边(AAS)
北师大版七年级数学下册探索三角形全等的条件第2课时利用“角边角”“角角边”判定三角形全等

AB=AB(已证),
所以△ABD≌△A'B'D'.所以AD=A'D'.
课堂小结
内容
角边角 角角边
应用
有两角及夹边对应相等的两个三角 形全等(简写成“ASA”); 两角分别相等且其中一组等角的对 边相等的两个三角形全等(简写成 “AAS”)
为证明线段和角相等提供了新的证法
注意
注意“角角边”“角边角” 中两角与边的区分
第四章 三角形
3 探索三角形全等的条件
第2课时 利用“角边角”“角角边”判定三角形全等
学习目标
情境引入
1.探索并正确理解三角形全等的判定方法 “ASA”和“AAS”;
2.会用三角形全等的判定方法“ASA”和“AAS” 证明两个三角形全等.(重点)
情境导入
如图所示,某同学把一块三角形的玻璃不谨慎打碎成了三块, 现在要到玻璃店去配一块完全一样的玻璃,那么最省事的 办法是带哪块去? 学生活动:学生先自主探究出答案,然后再与同学进行交流. 教师点拨:显然仅仅带①或②是无法配成完全一样的玻璃的, 而仅仅带③则可以,为什么呢? 本节课我们继续研究三角形全等的判定方法.
所以AB=A'B'(全等三角形对应边相等),
D′ C′
∠ABD=∠A'B'D'(全等三角形对应角相等).
因为AD⊥BC,A'D'⊥B'C',所以∠ADB=∠A'D'B'=90°.
在△ABD和△A'B'D'中,
∠ADB=∠A'D'B'(已证), ∠ABD=∠A'B'D'(已证),
2023年北师大版七年级下册数学第四章三角形第7课时探索三角形全等的条件(2)

相等
·数学 的两个三角
∠A=∠A′, ቐ∠B=∠B′,
BC=B′C′,
所以△ABC≌ △A'B'C' ( AAS ).
·数学
3.如图,已知AC=EC,∠ACB=∠ECD,要利用“AAS”判 定△ABC≌△EDC,应添加的条件是 ∠B=∠D .
知识点四:AAS的应用 例:如图,已知∠B=∠DEF,AB=DE,要说明 △ABC≌△DEF.
BC=EF 所以△ABC≌△DEF(AAS).所以AC=DF.
·数学
8.【例4】如图,在△ABC中,高AD与BE相交于点H,且AD= BD,问△BHD≌△ACD吗?为什么? 解:△BHD≌△ACD. 理由如下:因为AD⊥BC,BE⊥AC, 所以∠ADC=∠BEC=90°. 所以∠DAC=∠EBC,即∠DAC=∠DBH.
几何直观 推理能力 角形全等的条件(ASA) 两角及其 夹边 分别相等的两个三角形全等(简写成“角边 角”或“ASA”). 几何语言:在△ABC与△A'B'C'中,
∠A=∠A′, ቐ AB=A′B′, 所以△ABC≌ △A'B'C' ( ASA ).
∠B=∠B′,
AD=AB 所以△ADE≌△ABC(AAS).
·数学 7.【例3】(北师7下P111、人教8上P44)如图,点B,F,C, E在一条直线上,BF=CE,AB∥DE,∠ACB=∠DFE.试 说明:AC=DF.
解:因为BF=CE,所以BC=EF. 又因为AB∥DE,所以∠B=∠E.
∠B=∠E 在△ABC和△DEF中,ቐ BC=EF ,
·数学
2.如图,点E在AB上,点C在AD上,AB=AD,∠B=∠D. 试说明:△ABC≌△ADE.
北师大版七年级数学下册:第2课时利用“角边角”“角角边”判定三角形全等课件

如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
A
A
它们能判定
两个三角形
全等吗?
B
图一
C
“两角及夹边”
B
图二 C
“两角和其中一角的对边”
做一做 如果“两角及一边”条件中的边是两角所夹的边,比如三
角形的两个内角分别是60°和80°,它们所夹的边为2cm,你能 画出这个三角形吗?你画的三角形与同伴画的一定全等吗?
改变角度和边长,你能得到同样的结论吗?
用直尺和量角 器或者尺规作 图可以来验证
先任意画出一个△ABC,再画一个△A ′ B ′ C ′ ,使A ′ B ′ =AB, ∠A ′ =∠A, ∠B ′ =∠B (即使两角和它们的夹边对应 相等).把画好的△A ′ B ′ C ′剪下,放到△ABC上,它们全等吗?
7. 我们把两组邻边相等的四边形叫做“筝形”. 如图,四边形ABCD是一个筝形,其中AB=CB, AD=CD.对角线AC,BD相交于点O,OE⊥AB, OF⊥CB,垂足分别是E,F. 试说明:OE=OF.
证明:因为在△ABD和△CBD中,
AB=CB, AD=CD,
所以△ABD≌△CBD(SSS).
应边上的中线是否相
等,你有办法吗?
B
FE D C
B ′ F' E' D ′ C ′
已知:如图,△ABC ≌△A′B′C′ ,AD和A′ D′ ,AE和 A'E'分别是△ABC 和△A′B′C′的高和角平分线.试说明 AD= A′D′ ,AE= A′E′ ,并用一句话说出你的发现.
随堂演练
1. 小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图 中标有1,2,3,4的四块),你认为将其中的哪块带去,就能配一块与本来一样大小的三角形玻璃?应该带( B ) A.第1块 B.第2块 C.第3块 D.第4块
探索三角形全等的条件 第二课时-七年级数学下册课件(北师大版)

1 如图,已知△ABC 的六个元素,则下列甲、乙、丙三个 三角形中一定和△ABC 全等的是( C )
A.甲、乙 B.甲、丙 C.乙、丙 D.乙
2 小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图 中标有1,2,3,4的四块),你认为将其中的哪块带去,就 能配一块与原来一样大小的三角形玻璃?应该带( B ) A.第1块 B.第2块 C.第3块 D.第4块
因为∠BAE=∠1+∠2=90°,
所以∠1=∠D.
1=D,
在△ABC 和△DEC 中,3=5,
所以△ABC ≌△DEC. BC=EC,
知识点
例5 我们把两组邻边相等的四边形叫做
“筝形”.如图,四边形ABCD 是 一个筝形,其中AB=CB,AD= CD.对角线AC,BD 相交于点O, OE⊥AB,OF⊥CB,垂足分别是 E,F. 试说明:OE=OF.
解:(1)因为AE 和BD 相交于点O, 所以∠AOD=∠BOE. 又因为在△AOD 和△BOE 中,∠A=∠B, 所以∠BEO=∠2. 又因为∠1=∠2,所以∠1=∠BEO. 所以∠AEC=∠BED. A= B, 在△AEC 和△BED 中, AE=BE,
AEC= BED,
所以△AEC ≌△BED (ASA).
导引:要说明BC=ED,需说明
它们所在的三角形全等,
由于∠B=∠E,AB=AE, 因此需说明∠BAC=∠EAD, 即需说明∠BAD+∠1=∠BAD+∠2,易知成立.
解:因为∠1=∠2,
所以∠1+∠BAD=∠2+∠BAD,
即∠BAC=∠EAD.
B=E,
在△BAC
和△EAD
中,因为
AB=AE,
所以△BAC ≌△EAD (ASA). BAC=EAD,
专题探索三角形全等的条件(SSS和SAS)(知识讲解)数学七年级下册(北师大版)
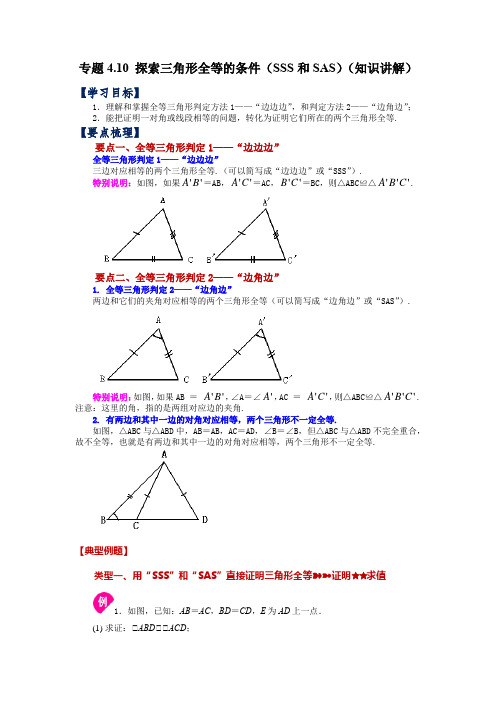
专题4.10 探索三角形全等的条件(SSS 和SAS )(知识讲解)【学习目标】1.理解和掌握全等三角形判定方法1——“边边边”,和判定方法2——“边角边”;2.能把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.【要点梳理】要点一、全等三角形判定1——“边边边”全等三角形判定1——“边边边”三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS ”).特别说明:如图,如果''A B =AB ,''A C =AC ,''B C =BC ,则△ABC ≌△'''A B C .要点二、全等三角形判定2——“边角边”1. 全等三角形判定2——“边角边”两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS ”).特别说明:如图,如果AB = ''A B ,∠A =∠'A ,AC = ''A C ,则△ABC ≌△'''A B C . 注意:这里的角,指的是两组对应边的夹角.2. 有两边和其中一边的对角对应相等,两个三角形不一定全等.如图,△ABC 与△ABD 中,AB =AB ,AC =AD ,∠B =∠B ,但△ABC 与△ABD 不完全重合,故不全等,也就是有两边和其中一边的对角对应相等,两个三角形不一定全等.【典型例题】类型一、用“SSS”和“SAS”直接证明三角形全等➽➼证明✮✮求值1.如图,已知:AB =AC ,BD =CD ,E 为AD 上一点.(1) 求证:△ABD △△ACD ;(2) 若△BED =50°,求△CED 的度数.【答案】(1) 证明见分析 (2) 50CED ∠=︒【分析】(1)根据SSS 即可证明△ABD △△ACD ;(2)只要证明△EDB △△EDC (SAS ),即可推出△BED =△CED ,进而得到答案. (1)证明:在△ABD 和△ACD 中, AB ACBDCD AD AD ⎧⎪⎨⎪⎩===,△△ABD △△ACD (SSS );(2)解:△△ABD △△ACD ,△△ADB =△ADC ,在△EDB 和△EDC 中,DB DC BDE CDE DE DE ⎧⎪∠∠⎨⎪⎩===,△△EDB △△EDC (SAS ),△△BED =△CED ,△△BED =50°,△△CED =△BED =50°.【点拨】本题考查全等三角形的判定和性质,解题的关键是根据图形题意,熟练掌握两个三角形全等判定与性质.举一反三:【变式1】如图,点A 、M 、N 、C 在同一条直线上,AB CD =,BN DM =,AM CN =,求证:AB CD ∥.【分析】根据AB CD =,BN DM =,AM CN =,利用SSS 定理证明ABN CDM ≌,从而得到A C ∠=∠,再根据内错角相等,两直线平行,AB CD ∥得证.解:证明:∵AM CN =∴AM MN CN MN∴AN CM =在ABN 和CDM 中AB CD BN DM AN CM =⎧⎪=⎨⎪=⎩,∴()ABN CDM SSS △≌△∴A C ∠=∠∴AB CD ∥(内错角相等,两直线平行)【点拨】本题考查了三角形全等的判定方法和性质,以及平行线的判定,解题关键是掌握全等三角形的判定方法,运用全等三角形的性质证明线段和角相等.【变式2】如图,已知AB AC =,AD AE =,BD CE =,求证:312.【分析】利用SSS 可证明△ABD△△ACE ,可得△BAD=△1,△ABD=△2,根据三角形外角的性质即可得△3=△BAD+△ABD ,即可得结论.解:在△ABD 和△ACE 中,AB=AC AD=AE BD=CE ⎧⎪⎨⎪⎩,△△ABD△△ACE ,△△BAD=△1,△ABD=△2,△△3=△BAD+△ABD ,△△3=△1+△2.【点拨】本题考查全等三角形的判定与性质及三角形外角性质,熟练掌握判定定理及外角性质是解题关键.2.已知:如图,AB AC =,F ,E 分别是AB AC ,的中点,求证:ABE ACF ≌.在ABE 与△AB AC A A AE AF =⎧⎪∠=∠⎨⎪=⎩ABE △≌△【点拨】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:ASAAAS 、、【变式1】如图,点D 在BC 上,,ADB B BAD CAE ∠=∠∠=∠.(1) 添加条件:____________(只需写出一个),使ABC ADE ≅;(2) 根据你添加的条件,写出证明过程.【答案】(1) AC AE = (2) 见分析【分析】(1)根据已知条件可得AB AD =,BAC DAE ∠=∠,结合三角形全等的判定条件添加条件即可;(2)结合(1)的条件,根据三角形全等的判定条件添加条件进行证明即可.解:(1)添加的条件是:AC AE =,故答案为AC AE =;(2)△,ADB B ∠=∠△AB AD =,△BAD CAE ∠=∠△BAD DAC CAE DAC ∠+∠=∠+∠,即BAC DAE ∠=∠,又AC AE =△ABC ADE ≅【点拨】本题主要考查了三角形全等的判定,确定出三角形全等判定条件是解答本题的关键.【变式2】如图所示,DC CA ⊥,EA CA ⊥,CD AB =,CB AE =,求证:(1) BCD EAB ≌△△;(2) DB BE ⊥.【分析】(1)利用SAS 判定定理证明三角形全等即可;(2)由()≌DCB BAE SAS △△,可得∠=∠DBC BEA ,∠=∠BDC EBA ,再利用90DBC BDC ∠+∠=︒,可得90∠+∠=︒DBC EBA ,即90DBE ∠=︒,所以DB BE ⊥.解:(1)证明:△DC CA ⊥,EA CA ⊥,△90∠=∠=︒DCB BAE ,在DCB △和BAE 中,CD AB DCB BAE CB AE =⎧⎪∠=∠⎨⎪=⎩△()≌DCB BAE SAS △△. (2)证明:由(1)可知()≌DCB BAE SAS △△, △∠=∠DBC BEA ,∠=∠BDC EBA ,△90DBC BDC ∠+∠=︒,△90∠+∠=︒DBC EBA ,即90DBE ∠=︒,△DB BE ⊥.【点拨】本题考查全等三角形的判定定理及性质,垂直的定义,解题的关键是掌握全等三角形的判定定理及性质.类型二、用“SSS”和“SAS”间接证明三角形全等➽➼证明✮✮求值3.已知:如图,A 、C 、F 、D 在同一直线上,AF =DC ,AB =DE ,BC =EF ,求证:△ABC≌≌DEF .【分析】首先根据AF=DC ,可推得AF ﹣CF=DC ﹣CF ,即AC=DF ;再根据已知AB=DE ,BC=EF ,根据全等三角形全等的判定定理SSS 即可证明△ABC△△DEF .解:△AF=DC ,△AF ﹣CF=DC ﹣CF ,即AC=DF ;在△ABC 和△DEF 中AC DF AB DE BC EF =⎧⎪=⎨⎪=⎩△△ABC△△DEF (SSS )举一反三: 【变式1】如图,已知:PA=PB,AC =BD ,PC =PD ,△PAD 和△PBC 全等吗?请说明理由.【分析】由AC=BD ,利用线段的和差关系可得AD=BC ,利用SSS 即可证明△PAD△△PBC.解:△AC =BD ,△AC+CD=BD+CD ,即AD =BC ,又△PA =PB ,PC =PD ,△△PAD△△PBC(SSS)【点拨】本题考查全等三角形的判定与性质,熟练掌握全等三角形的判定定理是解题关键.【变式2】如图,点D ,A ,E ,B 在同一直线上,EF =BC ,DF =AC ,DA =EB .试说明:△F =△C .【分析】根据SSS 的方法证明△DEF△△ABC,即可得到结论.解:因为DA =EB , 所以DE =AB.在△DEF 和△ABC 中, 因为DE =AB ,DF =AC ,EF =BC ,所以△DEF△△ABC(SSS),所以△F =△C.【点拨】本题考查了全等三角形的判定和性质,属于简单题,找到证明全等的方法是解题关键.4.如图,在ABCD 中,点E 、F 在BD 上,ABE 与CDF 全等吗?若全等,写出证明过程;若不全等,请你添加一个条件使它们全等,并写出证明过程.(1) 你添加的条件是__________.(2) 证明过程: 【答案】(1) BE DF =,答案不唯一; (2) 证明见分析; 【分析】(1)根据选择的全等三角形判定方法添加合适的条件即可;(2)由四边形ABCD 是平行四边形得到AB CD ∥,AB CD =,得ABE CDF ∠=∠,再用上添加的条件,即可证明结论.(1)解:BE DF =(答案不唯一)故答案为:BE DF =(答案不唯一)(2)证明:△四边形ABCD 是平行四边形,△AB CD ∥,AB CD =,△ABE CDF ∠=∠,在ABE 和CDF 中,AB CD ABE CDF BE DF =⎧⎪∠=∠⎨⎪=⎩,△ABE CDF △≌△(SAS ).【点拨】此题考查了平行四边形的性质、全等三角形的判定等知识,熟练掌握全等三角形的判定是解题的关键.举一反三:【变式1】如图,在ABC 和ADE 中,AB AD =,AC AE =,且BAD CAE ∠=∠,求证:ABC ADE △≌△.【分析】根据BADCAE ∠=∠可得BAC DAE ∠=∠,再根据SAS 即可证明.证明:△BAD CAE ∠=∠,△BAD DAC CAE DAC ∠+∠=∠+∠,即BAC DAE ∠=∠,在ABC 和ADE 中,AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩,△()SAS ABC ADE △≌△.【点拨】本题主要考查了用SAS 证明三角形全等,解题的关键是通过BAD CAE ∠=∠得出BAC DAE ∠=∠.【变式2】图,BE CF =,AC DF =,AC DF ∥.求证:ABC DEF ≌△△.【分析】首先根据BE CF =可得BC EF =,再由AC DF ∥可得ACB F ∠=∠,然后利用定理证明ABC DEF ≌即可.证明:△BE CF =,△BE EC CF EC ++=,即BC EF =,△AC DF ∥,△ACB F ∠=∠, 在ACB △和DFE △中,BC EF ACB F AC DF =⎧⎪∠=∠⎨⎪=⎩,△()SAS ABC DEF ≌.【点拨】此题主要考查了全等三角形的判定和平行线的性质,判定两个三角形全等的一般方法有:SSS SAS ASA AAS HL 、、、、.注意:AAA SSA 、不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.类型三、全等的性质与“SSS”和“SAS”综合➽➼证明✮✮求值 5.已知:如图,在ABC 中,AB AC AD =,是BC 边上的中线.求证:AD BC ⊥(填空).证明:在三角形ABD ACD 和中,△()()()______________BD AB ⎧=⎪⎪=⎨⎪⎪⎩已知已知公共边,△ ≌ ( ).△ADB ∠= (全等三角形的对应角相等).△1902ADB BDC ∠∠︒==(平角的意义). △(垂直的意义).【答案】,,,,SSS DC AC AD AD ABD ACD ADC AD BC =∠⊥,△△,,【分析】证明()SSS ADB ADC ≌△△.推出ADB ADC ∠∠=,可得结论. 证明:△AD 是BC 边上的中线,△BD CD =,在三角形ABD △和ACD 中,【变式1】如图:AB AC =,BD CD =,若28B ∠=︒,求C ∠的度数.【答案】28︒ 【分析】连接AD ,利用“SSS ”证明ABD ACD △≌△,即可得到答案.解:连接AD ,在ABD △和ACD 中,AB AC BD CD AD AD =⎧⎪=⎨⎪=⎩,()SSS ABD ACD ∴≌C B ∴∠=∠,28B ∠=︒,28C ∴∠=︒.【点拨】本题考查了全等三角形的判定和性质,正确作辅助线构造全等三角形是解题关键.【变式2】已知:如图,AC BD =,AD BC =,AD ,BC 相交于点O ,过点O 作OE AB ⊥,垂足为E .求证:(1) ABC BAD ≌.(2) AE BE =.【分析】(1)利用SSS 证明ABC BAD ≌;(2)根据全等三角形的性质得出DAB CBA ∠=∠,则OA OB =,根据等腰三角形的性质可得出结论.(1)证明:在ABC 和BAD 中,AC BD BC AD AB BA =⎧⎪=⎨⎪=⎩,△ABC BAD ≌(2)证明:△ABC BAD ≌△CBA DAB ∠=∠,△OA OB =,△OE AB ⊥,△AE BE =.【点拨】此题考查了全等三角形的判定与性质,利用SSS 证明ABC BAD ≌是解题的关键.6.如图,在ABC 中,CM 是AB 边上的中线,8AC =,12BC =,求CM 的取值范围.【答案】210CM <<【分析】倍长中线CM 至点N ,构造BNM ,易得ACM BNM ≅△△,再利用三角形的三边关系找到CN 的取值范围,进而得到CM 的取值范围.解:如图,延长CM 到点N ,使CM MN =,连接BN ,在ACM △和BNM 中,CM NM AMC BMN AM BM =⎧⎪∠=∠⎨⎪=⎩,∴ACM BNM ≅△△(SAS ),∴8AC BN ==, 在BCN △中,BC BN CN BC BN -<<+,∴128128CN -<<+,即420CN <<,∴4220CM <<,即210CM <<.【点拨】本题考查了全等三角形的性质与判定以及三角形的三边关系,解决本题的关键是倍长中线构造全等三角形.举一反三:【变式1】如图,已知在ABC 与ADE 中,90BAC DAE AB AC AD AE ∠=∠=︒==,,,点C ,D ,E 三点在同一条直线上,连接BD .图中的CE BD 、有怎样的数量和位置关系?请证明你的结论.【答案】CE BD =,证明见分析【分析】根据SAS 证明ACE ABD ≌△△,即可得到CE BD =.解:CE BD =,证明:△90BAC DAE ∠=∠=︒,△BAC CAD DAE CAD ∠+∠=∠+∠,即BAD CAE ∠=∠,在ACE △和ABD △中AC AB CAE BAD AE AD =⎧⎪∠=∠⎨⎪=⎩△()SAS ACE ABD ≌△CE BD =.【点拨】此题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定方法是解题的关键.【变式2】如图已知AOB 和MON △都是等腰直角三角形.(1) 如图1,连接AM ,BM ,此时AM ,BN 的数量关系为___________请说明理由.(2) 若将MON △绕点O 顺时针旋转,如图2,当点N 恰好在AB 边上时,求证:222BN AN MN +=.【答案】(1) AM BN =,理由见分析(2) 见分析 【分析】(1)由AOB 和MON △都是等腰直角三角形,得到AOM BON ≌,即可得到AM BN =(2)连接AM ,由AOB 和MON △都是等腰直角三角形,得到AOM BON ≌,即可得到AM BN =,再求得90MAN ∠=︒,利用勾股定理即可得到222BN AN MN +=解:(1)AM BN =,理由如下:△AOB 和MON △都是等腰直角三角形,△OA OB =,OM ON =,90AOB MON ∠=∠=︒,△AOM BON ∠=∠,在AOM 和BON △中:OA OB OM ON AOM BON =⎧⎪=⎨⎪∠=∠⎩, △AOM BON ≌,△AM BN =(2)如下图,连接AM ,△AOB 和MON △都是等腰直角三角形,△OA OB =,OM ON =,90AOB MON ∠=∠=︒,45B BAO ∠=∠=︒,△AOM BON ∠=∠,在AOM 和BON △中:OA OB OM ONAOM BON =⎧⎪=⎨⎪∠=∠⎩, △AOM BON ≌,△AM BN =,45B MAO ∠=∠=︒,△90MAN MAO BAO ∠=∠+∠=︒,△222AM AN MN +=,△222BN AN MN +=【点拨】本题考查了旋转的性质、全等三角形的判定和性质、等腰直角三角形的性质及勾股定理,熟练掌握全等三角形的判定和性质是解决问题的关键。
北师大版七年级数学下册教学课件4.3 探索三角形全等的条件——边角边

∴∵A∠DA=是∠△7EA.,B如C的图角,平分已线,知CA=CB,AD=BD, M,N分别是CA,CB的中点,试说明:
∴△ABC≌△EFD,
已知:如D图M,A=BD=ANC,.BD=CD,E为AD上一点,
∴ 【归纳】两边及其夹角分别相等的两个三角形全等,简写成“边角边”或“SAS”. 解: 连接CD,如图所示; AM=BN (重庆中考)如图,△ABC和△DEF分别在线段AE的两侧,点D、C在线段AE上,AC=DE, AB∥EF, AB=EF.
∠A=∠D ∴∠A=∠BB.
∴DM=DN.
又∵M,N分别是CA,CB的中点,
活动5 课堂小结
内 容
边角边 应 用 注 意
有两边及夹角对应相等的两个三角形全等(简写成“SAS”)
为证明线段和角相等提供了新的证法
1.已知两边,必须找“夹角” 2. 已知一角和这角的一夹边,必须找这角的另一夹边
∴∠BAD五=∠、EA作C. 业布置与教学反思
∴△AFD≌△CEB(SAS).
D
F C
练习
6.已知:如图,AB=AC,AD是△ABC的角平分线,
试说明:BD=CD. 解: ∵AD是△ABC的角平分线, ∴ ∠BAD=∠CAD, 在△ABD和△ACD中,
AB=AC(已知), ∠BAD=∠CAD(已证), AD=AD (已证), ∴△ABD≌△ACD (S∴ASB)D=. CD.
证明:∵AD是∠BAC的角平分线(已知) ∴∠BAD=∠CAD(角平分线的定义) ∵AB=AC(已知) ∠BAD=∠CAD(已证)
AD=AD(公共边) ∴△ABD≌△ACD(SAS) ∴BD=CD(全等三角形对应边相等)
A
BDC
【七年级数学下册】第三章 图形的全等课件 北师大版

∠D=∠C
∠DOA=∠COB
A
O
B
如图,若△ABC≌△EFC,且CF=3cm,∠EFC=64°,
3 64° 则BC=_____cm,∠B=_____.
你还能求出哪些边的长度,
A
F
哪些角的度数?
B
C
E
沿图形中的虚线,分别把下面图形划分为两个 全等图形(至少找出两种方法)
如果上图1是4×4的方格子有哪些分割方法?
课堂小结
通过这节课的学习,你对全等图形有哪些认识?
作 业
你能把下面的这个平行四边形 1.分成两个全等的图形吗? 2.分成四个全等的图形吗? 3.分成三个全等的图形吗?
图片欣赏:
D
B
C
E
F
你能找到图中的对应边和对应角吗?
表示方法: △ABC≌△DEF
A D
B
C
E
F
注意:要把表示对应顶点的字母写在 对应的位置上
用纸板、剪刀等工具制作全等三角形
改变它们的摆放位置,找出对应边,对应角.
全等三角形的性质
全等三角形的对应边相等,对应角相等.
练习:
找出下列图形中的全等图形
想一想:如图是由几种全等图形拼凑而成的
如图,做四个全等的小“L”型纸片,将它们拼 成一个与大“L”全等的图案。
与图1所示图形全等的图形是图1ABC
D
将图2绕A点顺时针转90°所得到的图形是
B
A 图2
C
A
B
C
D
本 课 概 要
两个能够重合
的图形称为全等图形;
如果两个图形全等,那么它们的
形状和大小一定都相同;
全等三角形的概念 ;
3.3《探索三角形全等的条件》 课件(北师大版) (1)

小明不慎将一块三角形模具打碎为两块, 他要到商店去配一块与原来一样的三角形模 具,该怎么办?
知识重现
问题一 图中的两个三角形全等吗?为什么?
3cm 3cm 2cm
2cm 4cm
4cm
问题二 如果已知一个三角形的两角及一边, 那 么有几种可能的情况呢?每种情况下得
到的三角形全等吗?
做一做
两角和其中一角的对边对应相等的 两个三角形全等,简写成“角角边”或 “AAS”
想一想
如图,O是AB的中点, A= △BOD全等吗?为什么? B, △AOC与
C O A D B
巩固练习
如图所示,AB=AC, CDA= BEA,你 能说出CD与BE相等的理由吗?
A
D
E
B
C
实践探索
如图,小明不 慎将一块三角形模 具打碎为两块,他 是否可以只带其中 一块碎片到商店去, 就能配一块与原来 一样的三角形模具 呢?如果可以,带 哪块去合适?为什 么?
1.如果“两角及一边”条件中的边是两角所 夹的边,比如三角形的两个内角分别是60 和80, 它们所夹的边为2cm,你能画出这个三角形吗?你 画的三角形与同伴画的一定全等吗?
2cm
60
80
做一做
2.如果“两角及一边”条件中的边是其中一角的 对边,比如三角形的两个内角分别是60 和45,一 条边长为3cm,情况会怎样呢?
60
45
3cm
(1)如果60°角所对的边为3cm,你能画出这个 三角形吗?这里的条件与1中的条件有什么相同点 与不同点?你能将它转化为1中的条件吗?你画的 三角形与同伴画的一定全等吗? (2)如果45°角所对的边为3cm,那么按这个条 件画出的三角形都全等吗?
4-3-2 探索三角形全等的条件(第2课时)(课件)-七年级数学下册同步精品课堂(北师大版)

转化的思想:
角角边
角边角
由三角形内角和定 理可知,两角相等, 则必然三角都相等!
探究新知
归纳总结 两角和其中一角的对边对应相等的两个三角形全等。
简写成“角角边”或“AAS”。 符号语言:∵在△ABC和△DEF中
∠B=∠E (已知) ∠C= ∠F (已知) AC = DF (已知) ∴ △ABC ≌△DEF (AAS)
∴△ADC≌△BDF(AAS). AC=BF,
随堂练习
7.已知:如图,△ABC ≌△A′B′C′ ,AD,A′ D′ 分别是 △ABC 和△A′B′C′的高.试说明AD= A′D′ ,并用一句话说 出你的发现.
A
A′
B
D C B′
D′ C′
随堂练习
解:因为△ABC ≌△A′B′C′ ,
所以AB=A'B'(全等三角形对应边相等),
A E
F
B
D
C
随堂练习
解:∵AD⊥BC, BE⊥AC, ∴∠ADC=∠BDF=∠BEA=90°. ∵∠AFE=∠BFD, ∠DAC+∠AEF+∠AFE=180°, B ∠BDF+∠BFD+∠DBF=180°
A E
F
C D
∴∠DAC=∠DBF. 在△ADC和△BDF中,∵
∠DAC=∠DBF, ∠ADC=∠BDF,
4.如图,Rt△ABC中,∠BAC=90°,AB=AC,分别过 点B,C作过点A的直线的垂线BD,CE,垂足分别为D, E,若BD=3,CE=2,则DE= 5 .
随堂练习
5.解决课前导入的问题:一张教学用的三角 形硬纸板不小心被撕坏了,如下图,你能制作一张 与原来同样大小的新教具吗?能恢复原来三角形的 原貌吗?
探索三角形全等的条件(第2课时)教学课件北师大版中学数学七年级(下)

A.一定不全等
B.一定全等
C.不一定全等
D.以上都不对
随堂训练
3.如图∠ACB=∠DFE,BC=EF,那么应补充一
个条件
,才能使△ABC≌△DEF
(写出一个即可).
AB=DE可以吗?×
B
A
AB∥DE
∠B=∠E (ASA)
C
F
或∠A=∠D (AAS)
D
E
随堂训练
4. 已知△ABC中,BE AD于E,CF AD于F ,
形全等. (简写成“角角边”或“AAS”)
C
几何语言:
在△和△中,
∠ = ∠,
ቐ∠ = ∠ ,
= ,
∴ △ ≌△ (AAS).
A
B
F
D
E
知识讲授
例4 已知:如图, AB⊥BC,AD⊥DC,∠1=∠2.
A
求证:AB=AD.
12
证明: ∵ AB⊥BC,AD⊥DC,
D
被撕坏了,如图,你能制作一张与本来
同样大小的新教具吗?
能
你能说明其中的理由吗?
C
E
B
新课导入
想一想:
探究三角形全等的条件:有三个条件对应相等时
三个角对应相等; 不能
三条边对应相等; SSS
两个角和一条边对应相等
?
知识讲授
探究:
两个角和一条边对应相等时,两三角形是否全等?
思考:已知一个三角形的两个角和一条边,那么这两个角与这条边的位
∴ AB=CD , BC=AD,(全等三角形对应边相等)
2
4
3
∴ ∠1=∠2 ,
C
1
A
B
北师大版数学七年级下册4.用“边边边”判定三角形全等课件

E
解:在△ABF和△ECD中, 解: ∵BD=CF,∴BD+DF=CF+DF.
AB=CE, AF=ED,
在△ABF和△ECD中,
AB=CE,
BDF C
BF=CD,
AF=ED,
∴△ABF≌△ECD(SSS).
BF=CD,
∴△ABF≌△ECD(SSS).
课堂小结
三 角 形 全 等 的 判 定
分类探讨 SSS
当堂小练
如图,△ABC中,AB = AC,EB = EC,则由SSS可以判定( B ) A.△ABD≌△ACD B.△ABE≌△ACE C.△BDE≌△CDE D.以上答案都不对
拓展与延伸
已知∠AOB,点C是OB边上的一点,用尺规作图,画出经过点C与
OA平行的直线.
D
解:作图如图所示:
作法:(1)以点 O 为圆心,任意长为半径画弧,
通过画图,你能得出什么样的结论?
新课讲授
知识点1 全等形的判定1
判定1:三边分别相等的两个三角形全等(可以简写成“边 边边”或者“SSS”). 符号语言表示:在△ABC和△A'B'C'中,
AB=A'B', AC=A'C', BC=B'C', ∴△ABC≌△A'B'C'.(SSS)
新课讲授
典例分析
分别交OA,OB于点 D,E;
(2)以点 C 为圆心,OD 长为半径画弧,交OB 于点 F;
(3)以点 F 为圆心,DE 长为半径画弧,
与第2步中所画的弧相交于点 P ;
(4)过C,P 两点作直线,直线 CP 即为要求作的直线.
布置作业
北师大版七年级下3.3.2探索三角形全等的条件(第2课时)课件ppt(金榜学案配套)

【解析】选C.根据题意AD∥BC得∠ADO=∠CBO,∠DOA=∠BOC,
又OD=OB,所以△DOA≌△BOC同理可证△DOC≌△BOA,
△DAB≌△BCD,△ACD≌△CAB,所以有4对.
1.在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,∠A=∠B′, AB=B′A′,则下列结论中正确的是( (A)AC=A′C′ (C)AC=B′C′ )
对边 相等的两个三 3.由2得:两角分别相等且其中一组等角的_____
角角边 AAS 角形全等,简写成:“_______”或“____”. 【归纳】在两个三角形中,有两角一边对应相等,则这两个三
角形全等.
【预习思考】
对于两个直角三角形,有一边和锐角对应相等,它们全等吗?
提示:全等,其中隐含条件是直角对应相等,故可由“ASA”或 “AAS”得两个三角形全等.
_________.
【解析】因为四边形ABCD是正方形,所以AB=AD, ∠ABC=∠BAD=90°.
因为BF⊥a于点F,DE⊥a于点E,
所以∠FAB+∠FBA=∠FAB+∠EAD=90°,所以∠FBA=∠EAD.
所 以 在 Rt△AFB 和 Rt△AED 中 , 因 为 ∠ AFB=∠DEA=90° ,
(B)BC=B′C′ (D)∠A=∠A′
【解析】选C.如图所示,因为∠C=∠C′=90°,∠A=∠B′, AB=B′A′,∴Rt△ABC≌Rt△B′A′C′,所以AC=B′C′(A不
正确,C正确),BC=A′C′(B不正确),∠A=∠B′(已知已给出,
D不正确).
2. 如图,某同学将一块三角形玻璃打碎成
故得AB=ED.
(3)由BC∥DF,得∠CBD=∠FDB,进而得∠ABC=∠EDF.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C=E(已知) BAC=DAE(已证) AB=AD(已知)
∴∠1+∠DAC=∠2+∠DAC
即∠BAC=∠DAE 在△ABC和△ADC 中
∴ △ABC≌△ADE
(AAS)
3﹑如图:已知AAEB==AADC,,∠∠BB==∠∠CC,,
△ABD与△ACE全等吗?为什么?
A
解:全等。
在 ABD 和 ACE 中
D
4
O 2C
巩固练习:
如图,O是AB的中点,∠A=∠B,△AOC 与△BOD全等吗?为什么?
我的思考过程如下: C≌△BOD D
A 2
1
E 2﹑如图,已知,∠C=∠E, ∠1=∠2,AB=AD,△ABC和
BD
C △ADE全等吗?为什么?
解: △ABC和△ADE全等。 ∵∠1=∠2(已知)
1、角.边.角; 2、角.角.边
每种情况下得到的三角形都全等吗?
做一做
1、角.边.角;
若三角形的两个内角分别是60°和80° 它们所夹的边为4cm,你能画出这个三角形吗?
2cm
60°
80°
60°
80°
你画的三角形与同伴画的一定全等吗?
2、角.角.边
若三角形的两个内角分别是60°和45°,且45° 所对的边为3cm,你能画出这个三角形吗?
B = ∠CB(=已∠C知)
AB
=
A∠CA(=已∠知A )
A
=
AAD(=公AE共角)
E
D
B
C
∴△ABD≌△ACE(ASAAA)S
实践探索
如图,小明不慎将一块 三角形模具打碎为两块, 他是否可以只带其中一 块碎片到商店去,就能 配一块与原来一样的三 角形模具呢?如果可以, 带哪块去合适?为什么?
第三章 三角形
3 探索三角形全等的条件(第2课时)
情境导入
我们已学过识别两个三角形全等的简便 方法是什么?识别三角形全等是不是还 有其它方法呢?
情境导入
有一块三角形纸片撕去了一个角, 要去剪一块新的,如果你手头没 有测量的仪器,你能保证新 剪的纸片形状、大小和原来的一 样吗?
实践探究
我们知道:如果给出一个三角形三条边的 长度,那么因此得到的三角形都是全等. 如果已知一个三角形的两角及一边,那么 有几种可能的情况呢?
60°
45°
分析:
这里的条件与1中的条件有什么相同点与不同 点?你能将它转化为1中的条件吗?
60°
75°
两角和它们的夹边对应相等的两个三 角形全等,简写成“角边角”或“ASA”
两角和其中一角的对边对应相等的两个 三角形全等,简写成“角角边”或“AAS”
练一练
1、如图,已知AB=DE, ∠A =∠D, ,∠B=∠E,则 △ABC ≌△DEF的理由是: 角边角(ASA)
2、如图,已知AB=DE ,∠A=∠D,,∠C=∠F,则 △ABC ≌△DEF的理由是: 角角边(AAS)
C
F
A
BD
E
巩固提高
1、完成下列推理过程:
在△ABC和△DCB中,
A
∠A3=BC∠=4∠DCB
∵ ∠B2C==C∠B1 (公共边 )
∠C2B==∠B1 C
B
3 1
∴△ABC≌△DCB( AAASSA)
课堂小结
通过这堂课的学习你有什 么收获?知道了哪些新知 识?学会了做什么?
布置作业
P85 知识技能2.3; 问题解决。
生活链接
课间,小明和小聪在操场上突然争论起 来。他们都说自己比对方长得高,这时 数学老师走过来,笑着对他们说:“你 们不用争了,其实你们一样高,瞧瞧地 上,你俩的影子一样长!”,你知道数 学老师为什么能从他们的影长相等就断 定它们的身高相同?你能运用全等三角 形的有关知识说明一下其中的道理吗? (假定太阳光线是平行的)
