传热学9-1
传热学第九章

9-1 辐射传热的角系数
(3)角系数的可加性
从表面1上发出而落到表面2上的总能量,等于落到表面2上 各部分的辐射能之和,于是有
注意,利用角系数可加性时,只有对角系数符号中第二个角码 是可加的,对角系数符号中的第一个角码则不存在类似的关系。
9-1 辐射传热的角系数 3. 角系数的计算方法
试计算: (1)板1的自身辐射; (2)板1的有效辐射; (3)板1的投入辐射; (4)板1的反射辐射; (5)板1,2的净辐射换热量。
§ 9-4 气体辐射的特点及其计算
辐射性气体: 具有发射和吸收辐射能的能力的气体。
工业上常见的温度范围内 常见的辐射性气体: 二氧化碳、水蒸气、二氧化硫、甲烷、氟里昂等三原子、多原子及 结构不对称的双原子气体(一氧化碳)
ቤተ መጻሕፍቲ ባይዱ
9.3.2 多表面封闭系统网络法求解的实施步骤
9.3.2 多表面封闭系统网络法求解的实施步骤
3. 求解代数方程组,计算各表面的有效辐射。
例如
已知三个表面温度T1, T2, T3;以及 A1, A2, A3, ε1, ε2, ε3, X1,2, X1,3, X2,3。
确定每个表面的有效辐射J1, J2, J3和 净辐射热量Φ1, Φ2, Φ3。
81
9.6 综合传热问题
82
9.6 综合传热问题
83
9.6 综合传热问题 解:
求解的结果为,
这样的测量误差在工业上是可以接受的。
84
85
9.6 综合传热问题 辐射传热系数
86
第9章 测试题
• 试述气体辐射的基本特点,气体能当做灰体来处 理吗?请说明原因。(2003年,华电,15分)
• 两块平行放置且相互靠得很近的灰体平壁,它们 的黑度均为0.8,壁1和2的温度分别为400和30℃ ,试计算壁2的(1)辐射换热量;(2)本身辐 射;(3)有效辐射。( 2003年,华电,15分)
传热学-第九章 辐射计算

X1, 2
1,2 1,2 A 1,2 B
X1, 2i
i 1
n
A1 Eb1 X 1,2 A1 Eb1 X 1,2 A A1 Eb1 X 1,2 B X 1,2 X 1,2 A X 1,2 B
再来看一下2 对 1 的能量守恒情况: 2 ,1 2 A ,1 2 B ,1
X 1,2 X 2,1
1 A1 1 A2
A1
A2
X d 1, d 2 dA1 X d 2, d 1dA2
A
A1 1
1
cos 1 cos 2 dA1dA2
A2
A1
1 A2
A2
A1
r cos 1 cos 2 dA1dA2
2
(9-4a)
A2
r
2
(9-4b)
的电流、电位差和电阻比拟热辐射中的热流、热势差与热
阻,用电路来比拟辐射热流的传递路径。但需要注意的是, 该方法也离不开角系数的计算,所以,必须满足漫灰面、 物性均匀以及投入辐射均匀的条件。
热势差与热阻
上节公式(9-12):
J Eb ( 1)q
1
改写为:
Eb J q 1
1, 2 A1 Eb1 X 1, 2 A2 Eb 2 X 2,1 A1 X 1, 2 ( Eb1 Eb 2 ) 的热辐射 到达表面 2的部分 的热辐射 到达表面 1的部分
图9-13 黑体系统的 辐射换热
表面1发出 表面 2发出
例题9-4 一直径d=0.75m的圆筒形埋地式加热炉采用电加热。 在操作过程中需要将炉子顶盖移去一段时间,设此时筒身温 度为 500K ,筒底为 650K 。环境温度为 300K 。试计算顶盖移 去期间单位时间内的热损失。设筒身及底面均可作为黑体。
传热学-第9章-辐射传热的计算

A2
cos1 cos2 r 2
dA1dA2
X 2,1
1 A2
A1
A2
cos1 cos2 r 2
dA1dA2
则有: A1 X1,2 A2 X 2,1
2
平面1
2
凸面1
3. 角系数的完整性
封闭空腔中: A2 两表面组成封闭空腔:
X1,1 X1,2 1
A1
多表面组成封闭空腔:
Eb 2
1 2
A11 A1 X1,2 A2 2
或:
1,2
(1
A1(Eb1 Eb2 ) 1) 1 A1 (
1
1)
1
X1,2 A2 2
1,2 s A1(Eb1 Eb2 )
系统黑度
两漫灰表面间的辐射换热网络图
Φ 1,2
Eb1
1 1 J1 1
J2 1 2
解:作辅助面A3(非自见面):
A2
A3
则: X1,2 X1,3 , X 2,1 X 2,3
A1
由角系数的相对性: A1 X1,3 A3 X 3,1
得: X1,3
A3 A1
X 3,1
A3 A1
X1,2
X 1,1
1
X 1, 2
1
A3 A1
同理:X 2,3
A3 A2
X 3,2
A11
A1 X1,2
A2 2
节点J3:
Eb3 J 3
13
J1 J3 1
J2
J3 1
0
A3 3
A1 X1,3 A2 X 2,3
3. 求解代数方程组,计算各表面的有效辐射。
《传热学》第9章-辐射换热的计算

J = E + ρG = εEb + (1 − α )G
漫灰表面之间的辐射换热
单位面积的辐射换热量=?
应该等于有效辐射与投入辐射之差
Φ= A
也等于自身辐射力与吸收的投入辐射能之差
J− Φ A
G = εEb
α =ε
− αG
Φ
=
Aε 1−ε
X
1,
2
1 ε1
− 1
+1+
X
2.1
1 ε2
− 1
= ε s A1 X1,2 (Eb1 − Eb2 )
εs
=
X
1,
2
1 ε1
−1 + 1 +
X
2.1
1 ε2
− 1 −1
系统黑度
6
两个漫灰表面构成的封闭空腔中的辐射换热
两块平行壁面构成的封闭空腔
角系数的曲线图
(a)平行的等面积矩形
(c)垂直的两个矩形
2 角系数的性质
(1) 相对性 (2) 完整性
A1 X 1,2 = A2 X 2,1
-互换性
封闭空腔的所有表面的角系数之和等于1
n
∑ X i , j = X i ,1 + X i ,2 +L+ X i ,i +L + X i ,n = 1
j =1
黑体辐射
Lb
=
Eb π
角系数的定义式
∫ ∫ Φ1→2 =
A1
A2
Eb1
cosθ1 cosθ 2 πr 2
传热学 第九章 辐射换热的计算

9-2 两表面之间的辐射换热过程
1. 黑体表面之间的辐射换热
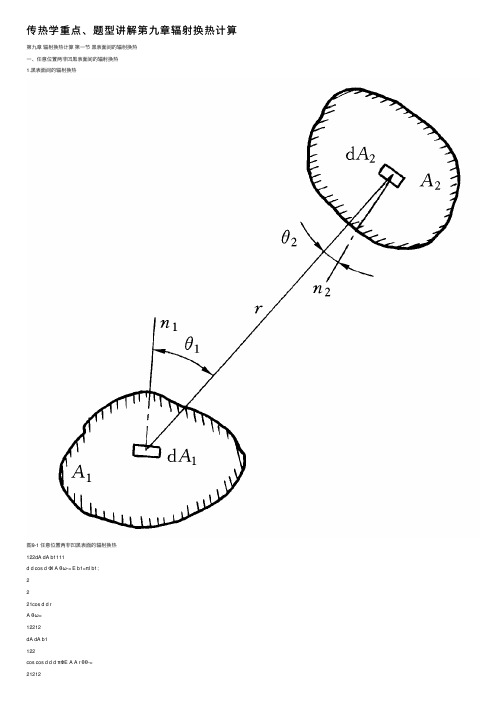
任意位置的两个黑体表面1、2,从表面1发出并直接投射
到表面2上的辐射能为
1 2 A1 X 1,2 E b1
从表面2发出并直接投射到表面1上的辐射能为
21 A2 X 2 ,1 E b 2
两个表面之间的直接辐射换热量为
X 1,2 X 2 ,1 1
A2 a
A1
9-1 角系数
4. 角系数的计算方法
(2) 代数法
由三个垂直于纸面方向无限长的非凹表面构成的封闭空腔,
三个表面的面积分别为A1、A2、A3 。
X i ,i 0
根据角系数的完整性
角系数的相对性
A1 X 1, 2 A1 X 1, 3 A1
A1 X 1,2 A2 X 2 ,1
Eb1 cos 1 cos 2 dA1dA2
1d 1
dd11
2
2 Lb1 dA1 cos
2
r
Eb1
dA2 cos 2
Lb1
d1
r2
9-1 角系数
2. 角系数的定义式
12
cos 1 cos 2
cos 1 cos 2
dA1dA2
E b1
dA1dA2 E b1
2
2
A1 A2
A1 A2
r
r
表面1对表面2的角系数为
X 1,2
12
A1 Eb1
1
A1
cos 1 cos 2
A1 A2 r 2 dA1dA2
1
A2
cos 1 cos 2
新大《传热学》复习题及解答第9章 辐射传热的计算

第9章辐射传热的计算(复习题解答)【复习题9-1]试述角系数的定义:”角系数是一个纯几何因子”的结论是在什么前提下得出的?答:表面1发出的辐射能中落到表面2的百分比称为表面1对表面2的角系数。
“角系数是一个纯几何因子”的结论成立的前提是(1)所研究的表面是漫射的;(2)在所研究表面的不同地点上向外发出的辐射热流密度是均匀的。
【复习题9-2】角系数有哪些特性?这些特性的物理背景是什么?答:角系数具有相对性、完整性和可加性。
相对性是在两物体处于热平衡时,净辐射换热量为零的条件下得出的。
完整性反映了一个由多表面组成的封闭系统中,任一表面所发出的辐射能,必全部落到封闭系统的各个表面上。
可加性表明从表面1发出的辐射,落到表面2的总能量,等于落到表面2上各部分的辐射能之和。
【复习题9-3]为什么计算一个表面与外界之间的净辐射传热量时要采用封闭腔的模型?答:因为任一表面与外界的辐射换热,包括该表面向空间各个方向发出的辐射,以及从空间各个方向投入到该表面上的辐射能。
【复习题9-4]实际表面系统与黑体系统相比,辐射传热计算增加了哪些复杂性?答:实际表面系统的辐射换热存在表面间的多次重复反射和吸收,光谱辐射力不服从普朗克定律,光谱吸收比与波长有关,辐射能在空间的分布不服从兰贝特定律,这都使辐射换热的计算更加复杂。
【复习题9-5】什么是一个表面的自身辐射、投入辐射及有效辐射?有效辐射的引入对于灰体表面系统辐射传热的计算有什么作用?答:由物体的内能转变而成的辐射能叫做自身辐射。
从外界投入到辐射表面的辐射能叫做投入辐射。
从一个辐射表面发出的辐射能(包括自身辐射和反射)叫做有效辐射。
引入有效辐射可避免实际物体辐射中出现的多次吸收和反射,从而简化计算。
【复习题9-6】对于温度已知的多表面系统,试总结求解每一表面净辐射传热量的基本步骤。
答:(1)画出等效的网络图;(2)列出节点的电流方程;(3)求解方程,得到各个节点电势;(4)确定每个表面的净辐射传热量。
传热学(第9章--对流换热)

— —
横向节距 纵向节距
23
9-3 流体有相变时的对流换热
一、凝结换热
1.特点:
——蒸汽和低于饱和温度的冷壁面相接触时会发 生凝结换热,放出凝结潜热。(如电厂中:凝汽 器和回热加热器内,管外蒸汽与管外壁的换热)
➢两种凝结方式:根据凝结液体依附在壁面上的形
态不同分.
tw ts
1)膜状凝结:凝结液体能润湿壁面,
腾换热设备安全经济的工作区为泡态沸腾区。
34
炉内高热负荷区水冷壁沸腾换热的强化
35
各种对流换热比较
液体对流换热比气体强;
对同一种流体,强制对流换热比自然对流换热强;
紊流换热比层流换热强;横向冲刷比纵向冲刷强;
有相变的对流换热比无相变换热强。
表9-5 各种对流换热平均换热系数的大致范围
换热系数 α[w/(m2.K)]
二是在蒸汽中混入油类或脂类物质。对紫铜管进行表面改 性处理,能在实验室条件下实现连续的珠状凝结,但在工 业换热器上应用,尚待时日。
26
2.影响蒸汽膜状凝结换热的因素:
(1)蒸汽中含有不凝结气体的影响 ➢ 蒸汽中含有不凝结气体(如空气)时,即使含量极微,
也会对凝结换热产生十分有害的影响。不凝结气体将会在 液膜外侧聚集而形成一层气膜,使热阻大大增加,从而恶 化传热。
21
(1)管束排列方式的影响
s1
s1
s2
顺排
s2
叉排
叉排:换热系数大,但流动阻力大. 顺排:换热系数小,但流动阻力小.
22
s1
s1
s2
s2
顺排
叉排
(2)流动方向上管排数的影响
后排管受前排管尾流的扰动作用对平均换热系 数的影响直到20排以上的管子才能消失。
传热学-第九章

当达到热平衡时,1,2 0
A1X1,2 A2 X 2,1
以上性质被称为角系数的相对性。
注意:
1,2、12、
21、1及
的区别
2
(2) 完整性
对于有n个表面组成的封闭系统,见图9-4所示,据能量
守恒可得:
n
X1,1 X1,2 X1,3 X1,n X1,i 1
i 1
上式称为角系数的完整性。若表面1为
非凹表面时,X1,1 = 0。
(3) 可加性
图9-4 角系数的完整性
如图9-5所示,表面2可分为2a和2b两个面,当然也可以分
为n个面,则角系数的可加性为
n
X1,2
X 1,2i
i 1
(9-4)
值得注意的是,上图中的表面2对表面1的角系数不存在上述
的可加性(9-5b)。
1,2 1,2 A 1,2B
X 1, 2
A2 A A2
X 2 A,1
A2 B A2
X 2B(,1 9 - 5b)
9.1.3 角系数的计算方法
1、直接积分法
X d1,2
A2
cos1 cos2dA2 r2
X1,2
1 A1
A1
A2
cos1cos r2
2dA2
dA1
工程中可直接查图线,如图9-7至图9-9.
2、代数分析法是利用角系数的各种性质,获得一组代数方 程,通过求解代数方程获得角系数。值得注意的是,利用该 方法的前提是系统一定是封闭的,如果不封闭可以做假想面, 令其封闭。下面以三个非凹表面组成的封闭系统为例,如图 9-10所示,面积分别为A1,A2和A3 ,则根据角系数的相对性 和完整性得:
第九章 辐射传热的计算
传热学 第9章-传热过程分析和换热器计算

第九章 传热过程分析和换热器计算在这一章里讨论几种典型的传热过程,如通过平壁、圆筒壁和肋壁的传热过程通过分析得出它们的计算公式。
由于换热器是工程上常用的热交换设备,其中的热交换过程都是一些典型的传热过程。
因此,在这里我们对一些简单的换热器进行热平衡分析,介绍它们的热计算方法,以此作为应用传热学知识的一个较为完整的实例。
9-1传热过程分析在实际的工业过程和日常生活中存在着的大量的热量传递过程常常不是以单一的热量传递方式出现,而多是以复合的或综合的方式出现。
在这些同时存在多种热量传递方式的热传递过程中,我们常常把传热过程和复合换热过程作为研究和讨论的重点。
对于前者,传热过程是定义为热流体通过固体壁面把热量传给冷流体的综合热量传递过程,在第一章中我们对通过大平壁的传热过程进行了简单的分析,并给出了计算传热量的公式 t kF Q ∆=, 9-1式中,Q 为冷热流体之间的传热热流量,W ;F 为传热面积,m 2;t ∆为热流体与冷流体间的某个平均温差,o C ;k 为传热系数,W/(⋅2m o C)。
在数值上,传热系数等于冷、热流体间温差t ∆=1 o C 、传热面积A =1 m 2时的热流量值,是一个表征传热过程强烈程度的物理量。
在这一章中我们除对通过平壁的传热过程进行较为详细的讨论之外,还要讨论通过圆筒壁的传热过程,通过肋壁的传热过程,以及在此基础上对一些简单的包含传热过程的换热器进行相应的热分析和热计算。
对于后者,复合换热是定义为在同一个换热表面上同时存在着两种以上的热量传递方式,如气体和固体壁面之间的热传递过程,就同时存在着固体壁面和气体之间的对流换热以及因气体为透明介质而发生的固体壁面和包围该固体壁面的物体之间的辐射换热,如果气体为有辐射性能的气体,那么还存在固体壁面和气体之间的辐射换热。
这样,固体壁面和它所处的环境之间就存在着一个复合换热过程。
下面我们来讨论一个典型的复合换热过程,即一个热表面在环境中的冷却过程,如图9-1所示。
传热学V4-第九章-辐射传热的计算1

传热学 Heat Transfer
Shanghai Jiao Tong University
9-1 角系数的定义、性质与计算 角系数的性质 相对性
1
完整性
可加性
角系数的相对性:
两个表面间的角系数 X1,2和X2,1 不是独立存在的。
(推导基于立体角概念和兰贝特定律)
两个有限大小表面
A1 X 1, 2 A2 X 2,1
2
代数分析法
几何分析法、蒙特卡罗法…
代数分析法: 利用角系数的性质,通过求解代数方程组获得角系数的方法。
X1,2
A1 A2 A3 2 A1
以线段长度表示
X1,2
三个非凹表面组成的封闭系统
l1 l2 l3 2l1
SJTU-OYH
(忽略垂直方向两端辐射能的逸出)
传热学 Heat Transfer
三个漫灰面组成的封闭空腔
SJTU-OYH
传热学 Heat Transfer
Shanghai Jiao Tong University
9-3 多表面系统辐射换热的计算 网络法求解辐射换热的步骤: 3. 根据等效网络图,利用电路基尔霍夫定律(所有流向节点J的热流量代数和=0),
列出节点的电流(热流量)方程;
X1, 2 X1, 2 A X1, 2 B
X 2,1 A2 A A X 2 A,1 2 B X 2 B ,1 A2 A2
角系数的直接相加仅适合角系数符号第二角码
SJTU-OYH
表面2到表面1
注意:
X 2,1 X 2 A,1 X 2 B,1
传热学 Heat Transfer
Shanghai Jiao Tong University
传热学9-1

第九章
辐射传热的计算
9-1
角系数的定义、性质及计算
一 角系数的定义
1 问题的引出
1 2 2
• 两表面之间的辐射换热量与它 们之间的相对位置有很大关系!
1 2 1
2 角系数的定义 • X1, 2 -表面 1对表面 2的角系数:表面 1发出 的辐射能落到表面2上的份额 • X2, 1 -表面 2对表面 1的角系数:表面 2发出 的辐射能落到表面1上的份额
传热学
如何确保以上两点呢?
• 计算的对象必须是一个包含所研究表面在 内的一个封闭腔
• 封闭腔的表面可以全部是真实的,也可以 部分是假想的
传热学
三 两黑体表面组成的封闭腔 如图,垂直于纸面方向无限长
假定出去为 “ + ”
1,2 A1Eb1 X1,2 A2 Eb2 X 2,1
A1 X 1, 2 Eb1 Eb 2 A2 X 2,1 Eb1 Eb 2
A2 X 2.1 A1
2 2.5 Z / X 1.33 X 2.(1 A) Y/X 1.67 1 .5 1.5 1 Z / X 0.67 X 2. A 0.11 Y / X 1.67 1.5
0.15
X 2.1 0.15 0.11 0.04
X 1 .2
关键!
传热学
四 两漫灰表面组成的封闭腔
以表面1为研究对象 • 投入到表面1上的辐射能 • 从表面1上出去的辐射能
1 投入辐射 G
12
1
T1
2
T2
• 单位时间内从外界投射到单位表面 积上的总辐射能
• 单位:W/m2
传热学
2 有效辐射 J • 单位时间内离开表面的单位表面积 上的总辐射能 • 单位:W/m2
传热学重点、题型讲解第九章辐射换热计算
传热学重点、题型讲解第九章辐射换热计算第九章辐射换热计算第⼀节⿊表⾯间的辐射换热⼀、任意位置两⾮凹⿊表⾯间的辐射换热1.⿊表⾯间的辐射换热图9-1 任意位置两⾮凹⿊表⾯的辐射换热122dA dA b1111d d cos d ΦI A θω-= E b1=πI b1;2221cos d d rA θω=12212dA dA b1122cos cos d d d πΦE A A r θθ-=21212dA dA b2122cos cos d d d πΦE A A r θθ-=12122122212dA ,dA dA dA dA dA b1b2122cos cos d d d ()d d πΦΦΦE E A A rθθ--=-=- 1212122121,2dA ,dA b1b2122cos cos d ()d d πA A A A ΦΦE E A A r θθ==- (9-1)2.⾓系数12121122b1122dA dA 12dA ,dA 22dA b11cos cos d d d cos cos πd d d πE A A Φr X A ΦE A r θθθθ-= ==12122121122dA dA 2dA A 12dA ,A 22dA dA d d cos cos d d d πA A ΦΦX A ΦΦr θθ--===12 1212 1112 2dA dA A A12 1,212 2A A1 dcos cos 1d dπA AA AΦΦX A A ΦΦA r θθ--(9-2a)212212AAA1,2ddπcoscos121212AArAΦΦXAA==-θθ(9-2b)21,212,1AXAX=(9-3)3.辐射空间热阻图9-2 辐射空间热阻21,2b2b112,1b2b12,1)(AXEEAXEEΦ-=-=(9-4)b1b21,21,211E EΦX A-=Φ1,2=(E b1-E b2)A = σb(T14- T24)A ⼆、封闭空腔诸⿊表⾯间的辐射换热图9-3 多个⿊表⾯组成的空腔图9-4 三个⿊表⾯组成空腔的辐射⽹络图9-5 例9-1附图:,1,2,,1ni i i i n i j j ΦΦΦΦΦ==++=∑将上式除以i Φ,按⾓系数定义,可得,1,2,n ,11ni i i i j j X X X X ==++=∑(9-5)∑∑∑∑====-=-==nj nj i j i nj i j i i j i nj j i i A X E A X E A X E E ΦΦ11,bj 1,bi ,bj bi 1,)(∑=-=nj j i j i i A X E A E Φ1,bj bi (9-6)【例9-1】∑=-=311,b 1b11j j j j A X E A E Φ(a )∑=-=312,b 2b22j j j j A X E A E Φ(b )0313,b 3b33=-=∑=j j j j A X E A E Φ(c )02,21,22,11,1====X X X X13,23,1==X X31,313,1A X A X =32,323,2A X A X =213,11,33,223/210.252A r X X X A r ππ==?==13,32,31,3=++X X X 5.03,3=X033,3b323,2b213,1b13b3=---A X E A X E A X E A E4b b T E σ=2424143T T T +=T 3=415.6K 或者142.6℃1b11b11,11b22,12b33,1344b11b31,3111344311b 244()()()100100473415.61 5.67()()1801.0W 2100100b ΦE A E X A E X A E X A E A E X A A T T T T AC σπ=---=-=-??=-=???-=????【讨论】π411212121=+=+=∑A A A A A AR 4444b1b2121,2()π5.67 4.73 3.13)1801.0W 4/π4b E E T T ΦRσ--===??-=∑(第⼆节灰表⾯间的辐射换热⼀、有效辐射图9-6 有效辐射⽰意图图9-7 辐射表⾯热阻1.有效辐射J 1=ε1E b1+ρ1G 1=ε1E b1+(1-α1)G 1 W/m 2(a )2.辐射表⾯热阻11b111111G E G J A Φαε-=-= W/m 2 (b ) 1111b11b111111)(1A J E J E A Φεεεε--=--=W (9-7)⼆、组成封闭腔的两灰表⾯间的辐射换热图9-8 两个灰表⾯组成封闭腔的辐射换热⽹络图9-9 空腔与内包壁⾯间的辐射换热22212,1111b2b12,1111A A X A E E Φεεεε-++--=W (9-8a ))11(1)11()(2212,112b 1b 12,1-++--=εεA A X E E A Φ 1,2112()W s b b X A E E ε=- (9-8b ))11()11(1121,212,1s -+-+=εεεX X1.⽆限⼤平⾏灰平壁的辐射换热A 1=A 2=A ,且X 1,2=X 2,1=1,)(111)(4241b s 212b b12,1T T A E E A Φ-=-+-=σεεε W (9-9)1121s -+=εεε2.其中⼀个表⾯为平⾯或凸表⾯的辐射换热)11(1)(22112b 1b 12,1-+-=εεA A E E A Φ W (9-10)A 2 >>A 1,且ε2的数值较⼤Φ1,2=ε1 A 1(E b1-E b2)W (9-11)三、封闭空腔中诸灰表⾯间的辐射换热1.⽹络法求解图9-10三个灰表⾯组成封闭腔辐射换热⽹络图9-11 例9-4附图图9-12 例题9-5附图节点1013,11312,1121111b1=-+-+-A X J J A X J J A J E εε(a )321,2212222b2=-+-+--A X J J A X J J A J E εε(b )节点3 011132,33231,3313333b3=-+-+--A X J J A X J J A J E εε(c )【例9-4】X 1,2= X 2,1=0.38X 1,3=X 2,3=1-X 1,2=1-0.38=0.62计算⽹络中的各热阻值:A 1=A 2=π?0.32=0.283m 21.14283.02.02.011111=?-=-A εε m -23.5283.04.04.011222=?=--A εε m -23.9283.038.01112,1=?=A X m -27.5283.062.011123,213,1=?==A X A X m -2流⼊每个节点的电流总和等于零07.53.91.141b3121b1=-+-+-J E J J J E 07.53.93.52b3212b2=-+-+-J E J J J E 202447731067.5484b1=??==-T E b σW/m 2 35445001067.5484b2=??==-T E b σW/m24593001067.5484b3=??==-T E b σW/m 2J 1=5129W/m 2J 2=2760W/m 2b1111112024451291072W 114.1E J ΦA εε--===- b22222235442760148W 1 5.3E J ΦA εε--===-312()(1072148)1220W ΦΦΦ=-+=-+=-【例9-5】1.1411111=-=A R εεm -23.512222=-=A R εεm -23.9112,12,1==A X R m -27.5113,13,23,1===A X R R m -2E b1=20244W/m 2E b2=3544W/m 2∑++++=23,23,12,11111R R R R R R =14.1+5.243.57.57.513.911=+++m -2b1b21,2202443544682W 24.5E E ΦR --===∑J 1=E b1-Φ1,2?R 1=20244-682?14.1=10627.8W/m 2J 2=E b2+Φ1,2?R 2=3544+682?5.3=7185.6 W/m 2J 3=(J 1+J 2)/2=8893.2 W/m 2J 3=G 3=E b3=σb T 341/41/45.6710b E T σ-=== ?2. 值解法图9-13 例9-6(a )(b )附图及其辐射换热⽹络∑==ni i j i i j j A X J G A 1,j j εα=∑=-+=ni i j i i j j j j j j A X J A E A J 1,b )1(εε(9-12)∑∑===ni i j i j ni i ji i X J A A XJ 1,1,b ,1(1)nj j j j i j i i J E J X εε==+-∑(9-13)4b 1,11j j j j jni i j i T J X J σεεε-=--∑= (9-14)4111,121,231,31,b 1114212,122,232,32,b 2221,12,231()()111()()11n n n n n n n J X J X J X J X T J X J X J X J X T J X J X J X εσεεεσεε-++++=--+-+++=--?++4,3,b 1()()11n n n n n n n J X T εσεε?++-=?--? (9-15)ii i i i i A J E Φεε--=1b i =1,2,…n (9-16)【例9-6】1,11,21,31,400.150.540.31X X X X ====、、、;2,12,22,32,40.2500.500.25X X X X ====、、、;3,13,23,33,40.270.140.320.27X X X X ====、、、;4,14,24,34,40.310.150.540X X X X ====、、、;4432198.267.5931.054.015.010??=---J J J J 4432183.267.5425.05.0525.0??=--+-J J J J4432186.267.5427.068.414.027.0??=-+--J J J J 4432184.267.55.15.254.015.031.0??=+---J J J JJ 1=440.45 W/m 2; J 2=370.28W/m 2; J 3=382.69W/m 2 ; J 4=380.80W/m 2。
传热学基本题-解答

t = 0.368t0 + 0.632t∞
答案:D
3-2 解析: ln θ = − hA τ , θ0 ρcV
τ
=
⎛θ
ln
⎜ ⎝
θ
0
⎞ ⎟ ⎠
⎛ ⎝⎜
−
hA ρcV
⎞ ⎠⎟
=
ln
⎛ ⎜⎜⎝
t t0
−tf −tf
⎞ ⎟⎟⎠
⎛ ⎝⎜
−
3h ρcR
⎞ ⎠⎟
ln 70 − 75
τ= −
15 − 75 3× 48
− t2 + δ2
=
t1
− tm δ1
=
tm − t2 δ2
λ1 λ2
λ1
λ2
答案:D
2-11 解析: dc
=
2λins hout
=
2× 0.12 12
= 0.02m =
20mm
答案:B
2
3 非稳态导热
3-1
解析:θ
= θ0
exp(−
hA ρcV
τ)
=
exp(− τ τr
)
;
当τ = τr , t − t∞ = (t0 − t∞ ) exp(−1) = 0.368× (t0 − t∞ )
气体
0.007--0.17
纯金属的导热系数银>铜>铝>铁,钢铁是合金。 答案:D
1-5 解析:空气热导率随温度升高而增大。 答案:A 。
1-6 解析:一维导热中,傅里叶定律的表达式: q = −λ dt ,或 Φ = −λ A dt
dx
dx
热流密度是单位面积的热流量,在傅里叶定律表述中,与温度梯度成正比,与传热面积无关。
传热学-9 传热过程和换热器

t
t
t1
t1
t1
t 2
t1
t 2
t 2 A
t 2 A
t
t
t1
t1
t1
t1
t 2
t 2
t 2
A
t 2 A
以顺流情况为例,作如下假设:
(1)冷、热流体的质量流量 qm2、qm1以及比热容 C2, C1是常数;
(2)传热系数是常数; (3)换热器无散热损失; (4)换热面沿流动方向的导热量可以忽略不计。
阻值。虽然 o 1,但 o 1 ,所以加肋侧总热
阻减小,传热热流量增加。
(2)调节壁面温度
9-1 传热过程的分析和计算
对于蒸汽加热的暖气包,由于蒸汽凝结换热系数 h1远远大于暖气包对室内空气自然对流时的h2,使这 一传热过程中的总热阻完全决定于h2一侧的换热热阻。 因此在h2一侧加导热热阻较小的肋片是最有效的改进 措施。
ho
1
1
hi Ai
hi dil
圆柱面导热: Φ= (twi two ) 1 ln do
2 l di
9-1 传热过程的分析和计算
外部对流:
Φ two t f 2 two t f 2
1
1
ho Ao ho dol
hi
Φ
t fi t fo
ho
1 1 ln( do ) 1
hi dil 2l di ho dol
在表面传热系数较小的一侧采用肋壁是强化传热 的一种行之有效的方法。
9-1 传热过程的分析和计算
四 临界热绝缘直径
圆管外加肋片是强化换热还是消弱传热(圆管外加保热 层)取决于增加表面积后所引起的对流换热热阻减小的程度 及导热热阻增加的程度的相对大小。
传热学-学习课件-9-1 辐射传热的角系数

A1 A2
由角系数相对性
A1 X 1,2 A2 X 2,1 A1 X 1,3 A3 X 3,1 A2 X 2,3 A3 X 3,2
A3
三表面封闭空间 角系数的确定
传热学 Heat Transfer
上述方程解得: X1,2
A1
A2 2 A1
A3
X 1,3
A1
A3 2A3
传热学 Heat Transfer
从表面2上发出而落到表面1上的辐射能,等于从 表面2的各部分发出而落到表面1上的辐射能之和,于 是有
A 2 E b 2 X 2 ,1 A 2 a E b 2 X 2 a ,1 A 2 b E b 2 X 2 b ,1
A2 X 2,1 A2a X 2a,1 A2b X 2b,1
X 2,1
X 2a,1
A2a A2
X 2b,1
A2b A2
角系数的上述特性可以用来求解许多情况下 两表面间的角系数值。
传热学 Heat Transfer
9.1.3 角系数的计算方法
求解角系数的方法
直接积分法 代数分析法
传热学 Heat Transfer
1、直接积分法
• 按角系数的基本定义通过求解多重积分而获得角 系数的方法
2、代数分析法
利用角系数的相对性、完整性及可加性,通过求解代数方 程而获得角系数的方法称为代数分析法。 (1)三个非凹表面组成的封闭系统
图9-10 三个非凹表面组成的封闭系统
传热学 Heat Transfer
由角系数完整性
X1,2 X1,3 1 X 2,1 X 2,3 1 X 3,1 X 3,2 1
传热学 Heat Transfer
《锅炉原理》备课笔记9

《锅炉原理》备课笔记9第九章炉内传热计算§9-1炉内传热的相似理论计算方法一.炉内辐射传热的基本概念1. 基本概念:投射辐射、有效辐射、系统黑度、炉膛黑度。
2. 计算公式是四次方差式,四次方差乘以系统黑度乘以辐射常数。
(通用)二.炉内传热计算的相似理论方法1.炉膛内辐射传热占95%以上。
对流传热占不到5%。
因此我们认为炉膛内完全是辐射传热,没有对流传热。
全部热量都是按照辐射的方式传递的。
2.理论燃烧温度的概念,应当叫绝热燃烧温度。
因为如果是理论的,参与燃烧的空气量应当是理论空气量(过量空气系数为1),而不是实际空气量(过量空气系数为实际的炉膛出口过量空气系数)。
从计算过程来看,只是没有对外传热所以应当叫绝热燃烧温度。
绝热燃烧温度就是把所有单位时间送入炉膛的热量当作焓,不对外传热,计算得到的相映的温度。
计算绝热燃烧温度的时候,因为烟气各个气体成分的比热是温度的函数,不能直接计算,只能用试算法计算。
3. 定性温度:用炉膛出口烟气温度作为定性温度。
4. 水冷壁面积:把与水冷壁相切的平面看作火焰的辐射表面,这个平面也是接受火焰辐射的水冷壁面积,叫做水冷壁面积。
5. 炉内传热的方程组:⎪⎩⎪⎨⎧''-=''-==)()(410l a p j l l j l T T VC B I Q B Q T Fa Q ϕϕσψ (9-12)(9-13) 6. 炉内有效放热量:包括修正后的1公斤燃料的有效放热量、1公斤燃烧用空气带进炉膛的热量。
7. 古尔维奇公式的推导过程:(1) 让(9-12)=(9-13),经过整理为(9-18)式。
(2) 带入卜略克—肖林公式(9-19)。
卜略克—肖林公式公式是描述炉膛内火焰平均温度与炉膛出口烟气温度的关系的经验公式。
卜略克—肖林公式从描述炉膛内沿炉膛高度的温度场的纯数学方法的公式演变而来。
(3) 经过数学数据整理得到古尔维奇公式(9-22)(9-23)(9-24)(9-25)。
[工学]第四版传热学第九章习题解答
![[工学]第四版传热学第九章习题解答](https://img.taocdn.com/s3/m/cea016fcc1c708a1284a44f4.png)
第九章思考题1、试述角系数的定义。
“角系数是一个纯几何因子”的结论是在什么前提下得出的?答:表面1发出的辐射能落到表面2上的份额称为表面]对表面2的角系数。
“角系数是一个纯几何因子”的结论是在物体表面性质及表面湿度均匀、物体辐射服从兰贝特定律的前提下得出的。
2、角系数有哪些特性?这些特性的物理背景是什么?答:角系数有相对性、完整性和可加性。
相对性是在两物体处于热平衡时,净辐射换热量为零的条件下导得的;完整性反映了一个由几个表面组成的封闭系统中。
任一表面所发生的辐射能必全部落到封闭系统的各个表面上;可加性是说明从表面1发出而落到表面2上的总能量等于落到表面2上各部份的辐射能之和。
3、为什么计算—个表面与外界之间的净辐射换热量时要采用封闭腔的模型?答:因为任一表面与外界的辐射换热包括了该表面向空间各个方向发出的辐射能和从各个方向投入到该表面上的辐射能。
4、实际表面系统与黑体系统相比,辐射换热计算增加了哪些复杂性?答:实际表面系统的辐射换热存在表面间的多次重复反射和吸收,光谱辐射力不服从普朗克定律,光谱吸收比与波长有关,辐射能在空间的分布不服从兰贝特定律,这都给辐射换热计算带来了复杂性。
5、什么是一个表面的自身辆射、投入辐射及有效辐射?有效辐射的引入对于灰体表面系统辐射换热的计算有什么作用?答:由物体内能转变成辐射能叫做自身辐射,投向辐射表而的辐射叫做投入辐射,离开辐射表面的辐射叫做有效辐射,有效辐射概念的引入可以避免计算辐射换热计算时出现多次吸收和反射的复杂性。
6、对于温度已知的多表面系统,试总结求解每一表面净辐射换热量的基本步骤。
答:(1)画出辐射网络图,写出端点辐射力、表面热阻和空间热阻;(2)写出由中间节点方程组成的方程组;(3)解方程组得到各点有效辐射;(4)由端点辐射力,有效辐射和表面热阻计算各表面净辐射换热量。
7、什么是辐射表面热阻?什么是辐射空间热阻?网络法的实际作用你是怎样认识的?答:出辐射表面特性引起的热阻称为辐射表面热阻,由辐射表面形状和空间位置引起的热阻称为辐射空间热阻,网络法的实际作用是为实际物体表面之间的辐射换热描述了清晰的物理概念和提供了简洁的解题方法。
高等传热学Chap9

1/ 2
Ts 16πσ 3 ∆Ts = Tl − Ts = 3 kT ln N kT / h ρv h fg l ( 0 l )
1/ 2
§9-1 沸腾传热的基本理论
543K过热水中的临界汽泡半径
∆Φ max J = N 0 f exp − kTl
N0为单位容积中分子数; 为单位容积中分子数;k为Boltzmann常数, 常数,k=1.38×10-23J/K; Tl为过热液体温度; 为过热液体温度;f为汽泡频率因子, 为汽泡频率因子,按下式计算: 按下式计算:
ED kTl f = exp − h kT l
Asv = π r 2 (1 − cos2 θ )
平壁上的汽化核心
§9-1 沸腾传热的基本理论
在加热壁面上形成该汽化核心时所引起的系统可用能的变 化∆Φ为
∆Φ = ( ml gl + mv gv + Alvσ lv + Asvσ sv ) − ( mgl + Aslσ sl )
注意: 注意:
Asv = Asl
Tl ( yb ) − Ts = 2σ Ts 2σ Ts sin θ = ρv h fg rb ρv h fg rm
或者写为: 或者写为:
Tl ( yb ) − Ts =
2σ Ts sin θ (1 + cos θ ) 2σ Ts = ρ v h fg rb ρv h fg yb
因此, 因此,汽泡长大的条件是: 汽泡长大的条件是:
σ sv = σ sl + σ lv cos θ
则有: 则有:
4 ∆Φ = π r 3 ρ v ( g v − gl ) + 4π r 2σ lv f (θ ) 3
传热学习题答案概要

传热学习题答案1-9 一砖墙的表面积为122m ,厚为260mm ,平均导热系数为1.5W/(m.K )。
设面向室内的表面温度为25℃,而外表面温度为-5℃,试确定次砖墙向外界散失的热量。
解:根据傅立叶定律有:WtA9.207626.05)(25125.1=--⨯⨯=∆=Φδλ1-11 夏天,阳光照耀在一厚度为40mm 的用层压板制成的木门外表面上,用热流计测得木门内表面热流密度为15W/m 2。
外变面温度为40℃,内表面温度为30℃。
试估算此木门在厚度方向上的导热系数。
解:δλtq ∆=,)./(06.0304004.015K m W t q =-⨯=∆=δλ1-12 在一次测定空气横向流过单根圆管的对流换热实验中,得到下列数据:管壁平均温度t w =69℃,空气温度t f =20℃,管子外径 d=14mm ,加热段长 80mm ,输入加热段的功率8.5w ,如果全部热量通过对流换热传给空气,试问此时的对流换热表面传热系数多大? 解:根据牛顿冷却公式()fw t t rlh q -=π2所以()f w tt d qh -=π=49.33W/(m 2.k) 1-14 一长宽各为10mm 的等温集成电路芯片安装在一块地板上,温度为20℃的空气在风扇作用下冷却芯片。
芯片最高允许温度为85℃,芯片与冷却气流间的表面传热系数为175W/(m 2.K)。
试确定在不考虑辐射时芯片最大允许功率时多少?芯片顶面高出底板的高度为1mm 。
解:()()[]⨯⨯⨯+⨯⨯=∆=Φ001.001.0401.001.0./1752max K m W t hA (85℃-20℃) =1.5925W1-15 用均匀的绕在圆管外表面上的电阻带作加热元件,以进行管内流体对流换热的实验,如附图所示。
用功率表测得外表面加热的热流密度为3500W/2m ;用热电偶测得某一截面上的空气温度为45℃,内管壁温度为80℃。
设热量沿径向传递,外表面绝热良好,试计算所讨论截面上的局部表面传热系数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4 4 523 K 300 K 3.14 0.05m 8m 5.67 W m 2 K 4 100 100 1 3.14 0.05 1 1 0.79 4 0.2 0.93 3710W 3.710 KW
s 1
高温管道间 热电偶测温的辐射误差
32/40
《传热学》讲义 五 例题
33/40
《传热学》讲义
例题 9-2 液氧储存容器为双壁镀银的夹层结构,外壁内表面温度 tw1=20℃,内壁外表面温度tw2=-183℃,镀银壁的发射率 ε=0.02,试计算由于辐射换热每单位面积容器壁的散热量。
• 液氧储存容器 • 表面镀银的作用
• 高温管道间
• 有两种处理方法
36/40
《传热学》讲义
解:因表面1非凹,可直接应用式(9-15)计算钢管的辐射热损失
T1 4 T2 4 A1C0 100 100 1 A 1 1 1 1 A2 2
X ab ,cd
bc ad ac bd
2ab
13/40
《传热学》讲义 • 从已知推出未知
求 X1,2=?
由P.400图9-8可以查出
X A, 2 X A1,2
1
2
A
由角系数的可加性
X 2, A1 X 2, A X 2,1
X A1, 2
A A1 X A, 2 X 1, 2 AA1 AA1
定义系统黑度(或称为系统发射率)
1 s 1 1 1 X 1, 2 1 X 2,1 1 1 2
1, 2 s A1 X1, 2 ( Eb1 Eb 2 )
29/40
《传热学》讲义 • 几种特殊情形
s
《传热学》讲义
三 角系数的性质
1 相对性
• 微元面和微元面
X d 1,d 2
I b1 cos1dA1d1 E b1dA1
dA2 cos1 cos 2 2 r
dA1 cos1 cos 2 X d 2,d 1 2 r
5/40
《传热学》讲义
dA1 X d 1, d 2 dA2 X d 2, d1
《传热学》讲义
第九章
辐射传热的计算
1/40
《传热学》讲义
9-1
角系数的定义、性质及计算
一 角系数的定义
1 问题的引出
1 2 2
• 两表面之间的辐射换热量与它 们之间的相对位置有很大关系!
2 1
1
2/40
《传热学》讲义 2 角系数的定义 • X1, 2 -表面 1 对表面 2 的角系数:表面 1 发出 的辐射能落到表面2上的份额 • X2, 1 -表面 2 对表面 1 的角系数:表面 2 发出 的辐射能落到表面1上的份额
表面积A1与表 面积A2相当且 无限靠近
s
1
1
1 1
2
1
31/40
《传热学》讲义
s
1 1 A1 1 1 X 1, 2 1 X 1, 2 A 1 2 2 1
表面积A2比表面 积A1大很多且表 面1为非凹表面
View factor, angle factor
3/40
《传热学》讲义
二 讨论角系数的假定
1 两个假定
• 物体表面为漫射表面 • 在所研究表面的不同地点上向外发射 的辐射热流密度是均匀的 2 优点 • 角系数完全是一个几何因子 • 物体表面温度及发射率的改变只影响 发射的辐射能的绝对大小
4/40
J E G Eb G
外 内
q1 J1 G1
q1 1Eb1 1G1
J1 Eb1 (
1
1
1)q1
假定出去为 “ + ”
26/40
《传热学》讲义 4 两漫灰表面组成的封闭腔 • 一般情形
1,2 A1J1 X1,2 A2 J 2 X 2,1
这是一个四重积分!
图9-7、9-8、9-9,查图时注意对数坐标
10/40
《传热学》讲义 2 代数分析法 ★
利用角系数的性质,通过求解代数方程组而 获得角系数的方法 • 三表面封闭系统 相对性 完整性 可加性
11/40
《传热学》讲义
X 1, 2 X 1,3 1 X 2,1 X 2,3 1 X 3,1 X 3, 2 1 A1 X 1, 2 A2 X 2,1 A1 X 1,3 A3 X 3,1 A2 X 2,3 A3 X 3, 2
20/40
《传热学》讲义 如何确保以上两点呢?
• 计算的对象必须是一个包含所研究表面在 内的一个封闭腔
• 封闭腔的表面可以全部是真是的,也可以 部分是假想的
21/40
《传热学》讲义 三 两黑体表面组成的封闭腔 如图,垂直于纸面方向无限长
假定出去为 “ + ”
1,2 A1Eb1 X1,2 A2 Eb2 X 2,1
24/40
《传热学》讲义 2 有效辐射 J • 单位时间内离开表面的单位表面积 上的总辐射能 • 单位:W/m2
1,2 A1J1 X1,2 A2 J 2 X 2,1
关键!
25/40
《传热学》讲义 3 有效辐射与表面净辐射换热量之间的关系
1,2 A1J1 X1,2 A2 J 2 X 2,1
∵ X ac,adc 1
ቤተ መጻሕፍቲ ባይዱ
∴ X adc ,ac
Aac Aadc
23/40
《传热学》讲义 四 两漫灰表面组成的封闭腔
以表面1为研究对象 • 投入到表面1上的辐射能 • 从表面1上出去的辐射能
1 投入辐射 G
12
1
T1
2
T2
• 单位时间内从外界投射到单位表面 积上的总辐射能
• 单位:W/m2
A2 A A2 B X 2,1 X 2 A,1 X 2 B ,1 A2 A2
注意:子区域不能重叠!
9/40
《传热学》讲义
四 角系数的计算
1 直接积分法
X d 1,d 2
X1,2
dA2 cos1 cos2 r2
1 2 1 2
1 cos1 cos2dA1dA2 1 A A A A X d1, d 2dA1 2 A1 A1 r
14/40
《传热学》讲义
例题:试确定右的表面1对表面2的角系数。 求 X1.2 但不能直接用,交换一下
X 2.(1 A) X 2.1 X 2. A
X 2.1 X 2.(1 A) X 2. A
由相对性知 先查
X 2.(1 A)
X 1.2
A2 X 2.1 A1
2 2.5 Z / X 1.33 X 2.(1 A) Y/X 1.67 1 .5 1.5 1 Z / X 0.67 X 2. A 0.11 Y / X 1.67 1.5
特例2
空调器室外机为 什么涂成白色?
这是有关抑 制辐射换热 的问题
34/40
《传热学》讲义
解: Tw1 t w1 273 K 20 273 K
Tw2 t w2 273 K 183 273 K 90 K
因容器夹层的间隙很小,可认为属于无 限大平行表面间的辐射换热问题。
28/40
1, 2
《传热学》讲义
1, 2 Eb1 Eb 2 1 1 1 1 2 1 A1 A1 X 1, 2 2 A2
1, 2
A1 X 1, 2 ( Eb1 Eb 2 ) 1 1 1 X 1, 2 1 1 X 2,1 1 2
J Eb (
1, 2 A1q1 2,1 A2 q2 1, 2 27/40 2,1
1
1)q
《传热学》讲义
1, 2
Eb1 Eb 2 1 1 1 1 2 1 A1 A1 X 1, 2 2 A2
Eb1 Eb 2 A1 X 1, 2 Eb1 Eb 2 1 A1 X 1, 2
• 有限大小表面
A1, T1
A1, T1
1, 2 A1Eb1 X1,2 A2 Eb 2 X 2,1
当T1=T2时,1, 2=0
A1 X1, 2 A2 X 2,1
6/40
《传热学》讲义
2 完整性 对于有n个表面组成的封闭系统, 见右图所示,据能量守恒可得:
X 1,1 X 1, 2 X 1,3 X 1,n X 1,i 1
4.18W m2
35/40
《传热学》讲义 例题9-3 一根直径d=50mm,长度l=8m的钢管,被 置于横断面为 0.2 m0.2m 的砖槽道内。若钢管温度 和发射率分别为t1=250℃,ε1= 0.79砖槽壁面温度 和发射率分别为t2=27℃,ε2=0.93,试计算该钢管 的辐射热损失。
Tw1 4 Tw2 4 c0 4 4 2 4 100 100 5 . 67 W m K 2 . 93 K 0 . 9 K q1,2 1 1 1 1 1 1 1 2 0.02 0.02
i 1 n
上式称为角系数的完整性
若表面1为非凹表面时,X1,1 = 0
7/40
《传热学》讲义
3 可加性 如图所示,表面2可分为 2A和2B两个面,当然也 可以分为n个面,则角系 数的可加性为
X1, 2
X1, 2i
i 1
8/40
n
注意:子区域不能重叠!
