三角函数转换关系
三角函数公式大全关系

三角函数公式大全关系三角函数是数学中常用的一类函数,与圆的周长、弧长、面积等有关,广泛应用于物理、工程、图像处理等领域。
以下是三角函数的一些基本公式和关系。
1.基本公式:- 正弦函数(sin):给定一个角θ,其正弦值由对边与斜边的比例给出,即sinθ=opposite/hypotenuse。
- 余弦函数(cos):给定一个角θ,其余弦值由邻边与斜边的比例给出,即cosθ=adjacent/hypotenuse。
- 正切函数(tan):给定一个角θ,其正切值由对边与邻边的比例给出,即tanθ=opposite/adjacent。
2.基本关系:- 三角函数之间的关系:sinθ=1/cscθ,cosθ=1/secθ,tanθ=1/cotθ。
-倍角公式:- sin(2θ) = 2sinθcosθ- cos(2θ) = cos²θ - sin²θ- tan(2θ) = 2tanθ / (1 - tan²θ)-半角公式:- sin(θ/2) = ±√[(1 - cosθ)/2]- cos(θ/2) = ±√[(1 + cosθ)/2]- tan(θ/2) = ±√[(1 - cosθ)/(1 + cosθ)]-和差公式:- sin(α ± β) = sinαcosβ ± cosαsinβ- cos(α ± β) = cosαcosβ ∓ sinαsinβ- tan(α ± β) = (tanα ± tanβ) / (1 ∓ tanαtanβ)-三角恒等式:- sin²θ + cos²θ = 1- 1 + tan²θ = sec²θ- 1 + cot²θ = csc²θ3.三角函数的周期性:- 正弦函数和余弦函数的周期均为2π,即sin(θ+2π) = sinθ,cos(θ+2π) = cosθ。
三角函数转换公式大全

三角函数转换公式大全三角函数是高中数学中的重要内容,它们在数学和物理学中有着广泛的应用。
在学习三角函数的过程中,我们经常会遇到需要进行三角函数的转换,而掌握三角函数的转换公式是十分重要的。
本文将为大家详细介绍三角函数的转换公式,希望能对大家的学习有所帮助。
1. 正弦函数转换公式。
正弦函数是三角函数中的一种基本函数,其转换公式包括:(1)正弦函数的奇偶性,sin(-x)=-sinx,sin(π-x)=sinx;(2)正弦函数的周期性,sin(x+2kπ)=sinx,其中k为整数;(3)正弦函数的同角变换,sin(π/2-x)=cosx,sin(π/2+x)=cosx。
2. 余弦函数转换公式。
余弦函数也是三角函数中的一种基本函数,其转换公式包括:(1)余弦函数的奇偶性,cos(-x)=cosx,cos(π-x)=-cosx;(2)余弦函数的周期性,cos(x+2kπ)=cosx,其中k为整数;(3)余弦函数的同角变换,cos(π/2-x)=sinx,cos(π/2+x)=-sinx。
3. 正切函数转换公式。
正切函数是三角函数中的另一种基本函数,其转换公式包括:(1)正切函数的奇偶性,tan(-x)=-tanx,tan(π-x)=-tanx;(2)正切函数的周期性,tan(x+π)=tanx;(3)正切函数的同角变换,tan(π/2-x)=cotx,tan(π/2+x)=-cotx。
4. 余切函数转换公式。
余切函数是三角函数中的第四种基本函数,其转换公式包括:(1)余切函数的奇偶性,cot(-x)=-cotx,cot(π-x)=-cotx;(2)余切函数的周期性,cot(x+π)=cotx;(3)余切函数的同角变换,cot(π/2-x)=tanx,cot(π/2+x)=-tanx。
5. 正割函数和余割函数转换公式。
正割函数和余割函数是三角函数中的补充函数,其转换公式包括:(1)正割函数的奇偶性,sec(-x)=secx,sec(π-x)=-secx;(2)正割函数的周期性,sec(x+2kπ)=secx,其中k为整数;(3)余割函数的奇偶性,csc(-x)=-cscx,csc(π-x)=-cscx;(4)余割函数的周期性,csc(x+2kπ)=cscx,其中k为整数。
高中三角函数角的转换公式
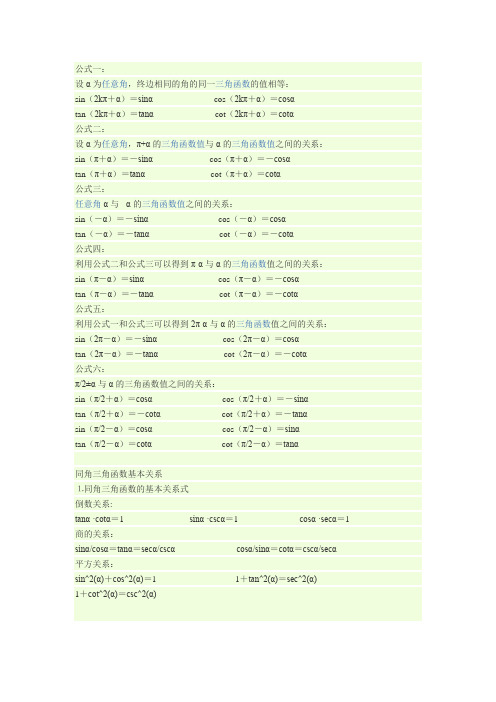
公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinα cos(2kπ+α)=cosαtan(2kπ+α)=tanα cot(2kπ+α)=cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinα cos(π+α)=-cosαtan(π+α)=tanα cot(π+α)=cotα公式三:任意角α与-α的三角函数值之间的关系:sin(-α)=-sinα cos(-α)=cosαtan(-α)=-tanα cot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinα cos(π-α)=-cosαtan(π-α)=-tanα cot(π-α)=-cotα公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinα cos(2π-α)=cosαtan(2π-α)=-tanα cot(2π-α)=-cotα公式六:π/2±α与α的三角函数值之间的关系:sin(π/2+α)=cosα cos(π/2+α)=-sinαtan(π/2+α)=-cotα cot(π/2+α)=-tanαsin(π/2-α)=cosα cos(π/2-α)=sinαtan(π/2-α)=cotα cot(π/2-α)=tanα同角三角函数基本关系⒈同角三角函数的基本关系式倒数关系:tanα ·cotα=1 sinα ·cscα=1 cosα ·secα=1 商的关系:sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=cscα/secα平方关系:sin^2(α)+cos^2(α)=1 1+tan^2(α)=sec^2(α)1+cot^2(α)=csc^2(α)。
三角函数变换的方法总结

三角函数变换的方法总结一、基础概念1.三角函数三角函数是以角度(x)作为自变量,单位圆上的坐标为函数值。
基本三角函数有正弦(sine)、余弦(cosine)、正切(tangent)、余切(cotangent)等。
定义域为实数集,值域为[-1,1]。
2.周期性三角函数都具有周期性,即函数值在一定范围内重复出现。
正弦和余弦的周期都为2π,正切和余切的周期为π。
3.基本关系三角函数之间有一系列基本关系:- 正弦、余弦关系:sin²(x)+cos²(x)=1- 正切、余切关系:tan(x)=1/cot(x)- 余弦、正切关系:cos(x)=1/sqrt(1+tan²(x))二、方法总结1.基本变换基本变换是通过改变角度的幅度和位置来改变三角函数的取值。
例如,sin(x)函数是以y轴为对称轴的偶函数,当角度发生变化时,sin(x)函数的值也会随之改变。
2.幅度变换幅度变换是通过改变系数a来改变函数的幅度。
在sin(ax)和cos(ax)中,a的取值决定了函数图像振动的频率和幅度,a越大,函数的振动越快,幅度越小。
3.位置变换位置变换是通过改变角度的平移来改变函数图像。
sin(x+b)和cos(x+b)中,b的取值决定了函数图像的位置,向右平移b单位,向左平移-b单位。
4.相关公式相关公式是一些常见的三角函数相互之间的变换式,它们可以简化计算,提高效率。
例如,sin(a+b)=sin(a)cos(b)+cos(a)sin(b)是常见的三角函数加法公式。
三、实际应用1.物理学2.电子工程3.统计学结论三角函数变换是解决三角函数关系和计算的一种重要方法,具有广泛的应用价值。
通过基本变换、幅度变换、位置变换和相关公式等方法,可以灵活地处理三角函数的计算和应用问题。
在物理学、电子工程和统计学等领域,三角函数变换对于解决实际问题起着重要的作用。
因此,熟练掌握三角函数变换的方法和技巧对于数学和实际应用都具有重要意义。
三角函数间的基本关系

三角函数间的基本关系一、三角函数间的基本关系1、平方和关系:1cos sin 22=+αα αα22s e c t a n 1=+ αα22c s c c o t 1=+ 2、倒数关系:ααcot 1tan = ααc o s 1s e c = ααsin 1csc =3、商数关系:αααtan cos sin = 二、诱导公式1、ααsin )360sin(=+︒⨯k ααcos )360cos(=+︒⨯k ααt a n )360t a n(=+︒⨯k 2、ααsin )360sin(-=-︒⨯k ααcos )360cos(=-︒⨯k ααtan )360tan(-=-︒⨯k 3、ααsin )180sin(-=+︒ ααcos )180cos(-=+︒ ααt a n )180tan(=+︒ 4、ααsin )180sin(=-︒ ααc o s )180c o s(-=-︒ ααt a n )180tan(-=-︒ 5、ααcos )90sin(=+︒ ααs i n)90cos(-=+ ααc o t )90tan(-=+ 6、ααcos )90sin(=-︒ ααs i n)90cos(=- ααc o t )90tan(=- 7、ααcos )270sin(-=+︒ ααsin )270cos(=+︒ ααc o t )270t a n(-=+︒ 8、ααcos )270sin(-=-︒ ααsin )270cos(-=-︒ ααc o t )270tan(=-︒ 9、ααsin )sin(-=- ααc o s )c o s(=- ααtan )tan(-=- 三、和、差公式1、βαβαβαsin cos cos sin )sin(+=+ βαβαβαs i n c o s c o s s i n )s i n (-=- 2、βαβαβαsin sin cos cos )cos(-=+ βαβαβαsin sin cos cos )cos(+=-3、βαβαβαtan tan 1tan tan )tan(-+=+ βαβαβαtan tan 1tan tan )tan(+-=-四、倍角公式αααcos sin 22sin =ααααα2222sin 211cos 2sin cos 2cos -=-=-= ααα2tan 1tan 22tan -=五、半角公式2cos 12sinαα-±= 2c o s 12c o s αα+±= αααc o s1c o s12t a n +-±= 六、和、差化积公式2cos2sin2sin sin ϕθϕθϕθ-∙+=+2sin 2cos 2sin sin ϕθϕθϕθ-∙+=-2cos 2cos 2cos cos ϕθϕθϕθ-∙+=+2sin 2sin 2cos cos ϕθϕθϕθ-∙+-=-七、积化和、差公式)]sin()[sin(21cos sin βαβαβα-++=∙)]sin()[sin(21sin cos βαβαβα--+=∙)]cos()[cos(21cos cos βαβαβα-++=∙)]cos()[cos(21sin sin βαβαβα--+=∙八、其他公式1、 弦化切公式α2tan 11+αα2tan 1tan +=αcos =αsinα2tan 11+-αα2tan 1tan +-αααα2tan 1tan cos sin +=2、 两点间距离公式 21221221)()(y y x x p p -+-=3、 万能公式2tan 12tan2sin 2αα+= 2t a n 12t a n1c o s 22ααα+-= 2t a n 12t a n2t a n 2αα-= 4、 线性和公式)sin(sin sin 22ϕβα++=+x b a b a (a,b)定ϕ的象限,ba =ϕtan 5、 升降次角公式 ⑴次降角升a )22sin cos sin ααα= b )22cos 1sin 2αα-=c )22cos 1cos 2αα+=⑵次升角降 a )2)2cos 2(sin sin 1ααα+=+ b )2)2cos2(sinsin 1ααα-=-c )2cos 2cos 12αα=+ d )2sin 2cos 12αα=-6、加减乘除公式 ⑴加减法公式a )]tan tan 1)[tan(tan tan βαβαβα +=± ⑵乘除法公式7、其他公式 1. αααααsin cos 1cos 1sin 2tan-=+=2. ααα2tan 2tan 1tan -=-3. αααααcos sin cos sin 2sin 1+=++4. ααααcos 2sin )2cos 1(sin =+5.ααα2cos )4sin(4sin(2=-+π)π6. ααααααtan 1tan 1sin cos cos sin 2122-+=-+ 7.αααααtan 2cos 2sin 12cos 2sin 1=++-+。
三角函数公式大全关系

三角函数公式大全关系:倒数tanα·cotα=1sinα·cscα=1cosα·secα=1商的关系:sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=cscα/secα平方关系:sin^2(α)+cos^2(α)=11+tan^2(α)=sec^2(α)1+cot^2(α)=csc^2(α)平常针对不同条件的常用的两个公式sin^2(α)+cos^2(α)=1tan α *cot α=1一个特殊公式(sina+sinθ)*(sina-sinθ)=sin(a+θ)*sin(a-θ)证明:(sina+sinθ)*(sina-sinθ)=2 sin[(θ+a)/2] cos[(a-θ)/2] *2 cos[(θ+a)/2] sin[(a-θ)/2] =sin(a+θ)*sin(a-θ)坡度公式我们通常半坡面的铅直高度h与水平高度l的比叫做坡度(也叫坡比),用字母i表示,即i=h / l, 坡度的一般形式写成l : m 形式,如i=1:5.如果把坡面与水平面的夹角记作a(叫做坡角),那么i=h/l=tan a.锐角三角函数公式正弦:sin α=∠α的对边/∠α的斜边余弦:cos α=∠α的邻边/∠α的斜边正切:tan α=∠α的对边/∠α的邻边余切:cot α=∠α的邻边/∠α的对边二倍角公式正弦sin2A=2sinA·cosA余弦1.Cos2a=Cos^2(a)-Sin^2(a)2.Cos2a=1-2Sin^2(a)3.Cos2a=2Cos^2(a)-1即Cos2a=Cos^2(a)-Sin^2(a)=2Cos^2(a)-1=1-2Sin^2(a) 正切tan2A=(2tanA)/(1-tan^2(A))三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a = tan a · tan(π/3+a)· tan(π/3-a)三倍角公式推导sin(3a)=sin(a+2a)=sin2acosa+cos2asina=2sina(1-sin²a)+(1-2sin²a)sina=3sina-4sin^3acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos²a-1)cosa-2(1-cos^a)cosa=4cos^3a-3cosasin3a=3sina-4sin^3a=4sina(3/4-sin²a)=4sina[(√3/2)²-sin²a]=4sina(sin²60°-sin²a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos^3a-3cosa=4cosa(cos²a-3/4)=4cosa[cos²a-(√3/2)^2]=4cosa(cos²a-cos²30°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]}=-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)现列出公式如下: sin2α=2sinαcosα tan2α=2tanα/(1-tan^2(α))cos2α=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α) 可别轻视这些字符,它们在数学学习中会起到重要作用。
三角函数基本转换公式与特殊三角函数值

三角函数基本转换公式与特殊三角函数值三角函数是数学中一个非常重要的概念,它描述了角度与直角三角形边长之间的关系。
在三角函数中,最常见的是正弦函数(sine)、余弦函数(cosine)和正切函数(tangent)。
在学习三角函数的过程中,我们会遇到一些基本转换公式和特殊三角函数值,它们在解题和证明中都会起到重要的作用。
首先,我们来介绍一下三角函数的基本转换公式。
这些公式是通过角度的周期性质和三角函数定义导出的,它们可以帮助我们将一个三角函数的表达式转换为另一个三角函数的表达式,从而简化计算和证明的过程。
1.正弦函数的基本转换公式:- 正弦函数是奇函数,即sin(-θ) = -sin(θ)- 正弦函数具有周期性,即sin(θ + 2πn) = sin(θ),其中n为整数- 正弦函数具有偶对称性,即sin(π - θ) = sin(θ)2.余弦函数的基本转换公式:- 余弦函数是偶函数,即cos(-θ) = cos(θ)- 余弦函数具有周期性,即cos(θ + 2πn) = cos(θ),其中n为整数- 余弦函数具有奇对称性,即cos(π - θ) = -cos(θ)3.正切函数的基本转换公式:- 正切函数是奇函数,即tan(-θ) = -tan(θ)- 正切函数具有周期性,即tan(θ + πn) = tan(θ),其中n为整数此外,我们还常常需要用到一些特殊角的三角函数值。
这些特殊角的三角函数值可以通过几何图形或其他方法来确定。
下面是一些常见的特殊角的三角函数值:1.0度角和360度角的三角函数值:- sin(0°) = 0,sin(360°) = 0- cos(0°) = 1,cos(360°) = 1- tan(0°) = 0,tan(360°) = 02.30度角和330度角的三角函数值:- sin(30°) = 1/2,sin(330°) = -1/2- cos(30°) = √3/2,cos(330°) = √3/2- tan(30°) = √3/3,tan(330°) = -√3/33.45度角和315度角的三角函数值:- sin(45°) = √2/2,sin(315°) = -√2/2- cos(45°) = √2/2,cos(315°) = √2/2- tan(45°) = 1,tan(315°) = -14.60度角和300度角的三角函数值:- sin(60°) = √3/2,sin(300°) = √3/2- cos(60°) = 1/2,cos(300°) = 1/2- tan(60°) = √3,tan(300°) = -√35.90度角和270度角的三角函数值:- sin(90°) = 1,sin(270°) = -1- cos(90°) = 0,cos(270°) = 0- tan(90°) = 无穷大,tan(270°) = 无穷大以上是一些常见的特殊角的三角函数值,它们在解题和证明中都会被广泛使用。
三角函数相互转化公式

三角函数相互转化公式三角函数是数学中的重要概念,其中三角函数相互转化公式更是解决许多数学问题的有力工具。
咱们先来说说正弦函数(sin)和余弦函数(cos)之间的转化公式。
这就好比两个人在跳舞,时而你在前,时而我在前,但总归跳的是同一支舞。
比如说,sin²α + cos²α = 1 ,这个公式就像定海神针一样,不管α是多少,这个等式都稳稳地成立。
我记得有一次给学生们讲这个公式的时候,有个学生特别可爱。
他瞪着大眼睛问我:“老师,这是不是就像孙悟空的金箍棒,永远不变呀?”我笑着回答他:“对呀,这就是咱们三角函数世界里的金箍棒,谁也动不了它。
”那咱们再看看正切函数(tan)和正弦、余弦函数的关系。
tanα =sinα / cosα ,这个公式就像是一座桥梁,把正弦和余弦紧密地联系在了一起。
在实际解题中,这些公式的相互转化用处可大了。
比如说,要求一个角的正切值,但是只知道它的正弦和余弦值,这时候用上这个转化公式,问题就能迎刃而解。
就像上次做的一道练习题,已知一个角的正弦值是 3/5 ,余弦值是-4/5 ,那这个角的正切值是多少?这时候,直接把数值代入tanα = sinα / cosα ,就能算出正切值是 -3/4 。
还有余切函数(cot),cotα = cosα / sinα 。
它和正切函数也是相互呼应的。
在解决一些几何问题或者物理中的波动问题时,这些三角函数相互转化公式就像是一把把神奇的钥匙,能打开难题的大门。
比如说,在计算一个物体做简谐运动时的位移和速度,就可能会用到三角函数的相互转化。
想象一下,一个小球在弹簧上做简谐运动,它的位移可以用正弦函数来表示,而速度就需要通过对位移函数求导,这时候三角函数的转化公式就能大显身手,帮助我们求出速度的表达式。
再比如,在三角形中,已知两条边和一个夹角,要求第三条边的长度。
这时候,我们可以利用正弦定理或者余弦定理,而这些定理的推导和应用都离不开三角函数的相互转化公式。
三角函数转换公式大全

三角函数转换公式大全1.正弦函数转换公式:(1)正弦函数的余弦函数表示:sin(x) = cos(π/2 - x)(2)正弦函数的正切函数表示:sin(x) = tan(x) / sec(x)(3)正弦函数的余切函数表示:sin(x) = cot(π/2 - x) / csc(π/2 - x)(4)正弦函数的正割函数表示:sin(x) = sec(x) / tan(x)(5)正弦函数的余割函数表示:sin(x) = csc(π/2 - x) / cot(π/2 - x) 2.余弦函数转换公式:(1)余弦函数的正弦函数表示:cos(x) = sin(π/2 - x)(2)余弦函数的正切函数表示:cos(x) = cot(π/2 - x) / csc(π/2 - x)(3)余弦函数的余切函数表示:cos(x) = tan(x) / sec(x)(4)余弦函数的正割函数表示:cos(x) = sec(π/2 - x) / cot(π/2 - x)(5)余弦函数的余割函数表示:cos(x) = csc(x) / tan(x)3.正切函数转换公式:(1)正切函数的正弦函数表示:tan(x) = sin(x) / sec(x)(2)正切函数的余弦函数表示:tan(x) = cos(x) / csc(x)(3)正切函数的余切函数表示:tan(x) = cot(π/2 - x)(4)正切函数的正割函数表示:tan(x) = sec(x) / sin(x)(5)正切函数的余割函数表示:tan(x) = csc(x) / cos(x)4.余切函数转换公式:(1)余切函数的正弦函数表示:cot(x) = csc(x) / sin(x)(2)余切函数的余弦函数表示:cot(x) = sec(x) / cos(x)(3)余切函数的正切函数表示:cot(x) = tan(π/2 - x)(4)余切函数的正割函数表示:cot(x) = sec(π/2 - x) / sin(π/2 - x)(5)余切函数的余割函数表示:cot(x) = csc(x) / cos(x)5.正割函数转换公式:(1)正割函数的正弦函数表示:sec(x) = sin(π/2 - x) / csc(π/2 - x)(2)正割函数的余弦函数表示:sec(x) = cos(π/2 - x) / cot(π/2 - x)(3)正割函数的正切函数表示:sec(x) = tan(x) / sin(x)(4)正割函数的余切函数表示:sec(x) = cot(x) / cos(x)(5)正割函数的余割函数表示:sec(x) = csc(π/2 - x) / cos(π/2 - x) 6.余割函数转换公式:(1)余割函数的正弦函数表示:csc(x) = sin(π/2 - x) / cos(π/2 - x)(2)余割函数的余弦函数表示:csc(x) = cos(x) / sec(x)(3)余割函数的正切函数表示:csc(x) = tan(π/2 - x) / cot(π/2 - x)(4)余割函数的余切函数表示:csc(x) = cot(x) / sin(x)(5)余割函数的正割函数表示:csc(x) = sec(π/2 - x) / cos(π/2 - x)这些转换公式可以帮助我们在计算过程中更方便地转换不同的三角函数,简化计算步骤,提高计算效率。
三角函数正余弦转换公式

三角函数正余弦转换公式1 三角函数的定义三角函数是用于描述三角形内角和边关系的函数。
其中最常见的三角函数包括正弦(sin)、余弦(cos)、正切(tan)等。
在三角函数中,正弦和余弦是最基本的两个函数,它们在数学、物理、工程等领域都有广泛应用。
2 正弦与余弦的关系在解决三角形问题时,我们常常需要用到正弦和余弦。
这两个函数在数学上有着紧密的联系。
正弦函数与余弦函数的定义式如下:sinθ=对边/斜边;cosθ=邻边/斜边。
其中,θ为角度,对边、邻边和斜边分别表示与角度θ相对应的三角形的对边、邻边和斜边。
当θ为锐角时,sinθ和cosθ的值都是正数。
当θ为直角时,cosθ的值为0,sinθ的值为1。
当θ为钝角时,sinθ和cosθ的值会出现负数。
3 正余弦转换公式在实际问题中,有时候我们需要将一个三角函数的函数值转换为另一个三角函数的函数值。
这时候就要用到正余弦转换公式。
3.1 正弦与余弦的转换公式根据三角函数的定义,可以得出以下正弦与余弦的转换公式:cosθ=±sin(90°-θ);sinθ=±cos(90°-θ);其中的±符号表示θ所在的象限。
3.2 例子分析例如,已知正弦函数sin35°=0.57,求余弦函数cos55°的值。
根据正余弦转换公式:cos55°=±sin(90°-55°)=±sin35°=±0.57;由于θ=55°位于第一象限,因此cos55°的值需要为正数,所以有:cos55°=0.57。
同样的,若已知余弦函数cos50°=0.64,求正弦函数sin40°的值。
根据正余弦转换公式:sin40°=±cos(90°-40°)=±cos50°=±0.64;由于θ=40°位于第一象限,因此sin40°的值需要为正数,所以有:sin40°=0.64。
【数学知识点】tanx与sinx和cosx的转换关系

【数学知识点】tanx与sinx和cosx的转换关系
tanx=sinx/cosx, 而且x不等于π/2+nπ,n为整数。
三角函数是基本初等函数之一,是以角度(数学上最常用弧度制)为自变量,角度对应任意角终边与单位圆交点坐标或其
比值为因变量的函数。
常见的三角函数包括正弦函数、余弦函数和正切函数。
在航海学、测绘学、工程学等
其他学科中,还会用到如余切函数、正割函数、余割函数、正矢函数、余矢函数、半正矢
函数、半余矢函数等其他的三角函数。
不同的三角函数之间的关系可以通过几何直观或者
计算得出,称为三角恒等式。
三角函数一般用于计算三角形中未知长度的边和未知的角度,在导航、工程学以及物
理学方面都有广泛的用途。
另外,以三角函数为模版,可以定义一类相似的函数,叫做双
曲函数。
常见的双曲函数也被称为双曲正弦函数、双曲余弦函数等等。
三角函数(也叫做
圆函数)是角的函数;它们在研究三角形和建模周期现象和许多其他应用中是很重要的。
三角函数通常定义为包含这个角的直角三角形的两个边的比率,也可以等价的定义为
单位圆上的各种线段的长度。
更现代的定义把它们表达为无穷级数或特定微分方程的解,
允许它们扩展到任意正数和负数值,甚至是复数值。
感谢您的阅读,祝您生活愉快。
高中三角函数角的转换公式

高中三角函数角的变换公式 1 / 1公式一:设 α为 随意角 ,终边同样的角的同一 三角函数 的值相等: sin ( 2k π+ α)= sinα tan ( 2k π+ α)=tan α 公式二:cos ( 2k π+ α)= cos α cot ( 2k π+ α)= cot α设 α为 随意角 , π+α的三角函数值 与 α的 三角函数值 之间的关系:sin ( π+α)=- sin αcos (π+ α)=- cos α tan ( π+ α)= tan αcot ( π+ α)= cot α公式三: 随意角 α与 -α的 三角函数值 之间的关系:sin (- α)=- sin αcos (- α)= cos α tan (- α)=- tan αcot (- α)=- cot α 公式四:利用公式二和公式三能够获得π-α与 α的 三角函数 值之间的关系: sin ( π-α)= sin αcos ( π- α)=- cos α tan ( π- α)=- tan αcot ( π- α)=- cot α 公式五:利用公式一和公式三能够获得2π-α与 α的 三角函数 值之间的关系: sin ( 2π-α)=- sin αcos ( 2π- α)= cos α tan ( 2π- α)=- tan αcot ( 2π-α)=- cot α公式六: π /2 ±α与α的三角函数值之间的关系:sin ( π /2+ α)= cos αcos (π /2+α)=- sin α tan ( π /2+ α)=- cot αcot ( π /2+ α)=- tan α sin ( π /2- α)= cos αcos (π /2-α)= sin α tan ( π /2- α)= cot α cot ( π /2- α)= tan α同角三角函数基本关系⒈同角三角函数的基本关系式倒数关系 :tan α ·=cot1 α sin α ·=csc1 α cos α · =sec1 α商的关系:sin α /cos =αtan α= sec α /csc α cos α /sin = αcot α= csc α /sec α平方关系: sin^2()α+ cos^2( α)=1 1+ tan^2( α)=sec^2( α) 1+ cot^2( α)=csc^2( α)。
高中三角函数角的转换公式

精品文档. 公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin (2k π+α)=sin α cos (2k π+α)=cos α tan (2k π+α)=tan α cot (2k π+α)=cot α 公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin (π+α)=-sin α cos (π+α)=-cos α tan (π+α)=tan α cot (π+α)=cot α 公式三:任意角α与-α的三角函数值之间的关系:sin (-α)=-sin α cos (-α)=cos α tan (-α)=-tan α cot (-α)=-cot α 公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin (π-α)=sin α cos (π-α)=-cos α tan (π-α)=-tan α cot (π-α)=-cot α 公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin (2π-α)=-sin α cos (2π-α)=cos α tan (2π-α)=-tan α cot (2π-α)=-cot α 公式六:π/2±α与α的三角函数值之间的关系:sin (π/2+α)=cos α cos (π/2+α)=-sin α tan (π/2+α)=-cot α cot (π/2+α)=-tan α sin (π/2-α)=cos α cos (π/2-α)=sin α tan (π/2-α)=cot α cot (π/2-α)=tan α同角三角函数基本关系⒈同角三角函数的基本关系式倒数关系:tan α ·cot α=1 sin α ·csc α=1 cos α ·sec α=1 商的关系:sin α/cos α=tan α=sec α/csc αcos α/sin α=cot α=csc α/sec α平方关系:sin^2(α)+cos^2(α)=11+tan^2(α)=sec^2(α)1+cot^2(α)=csc^2(α)。
