《非参数统计》与MATLAB编程 第二章 描述性统计
《非参数统计分析》课后计算题参考答案
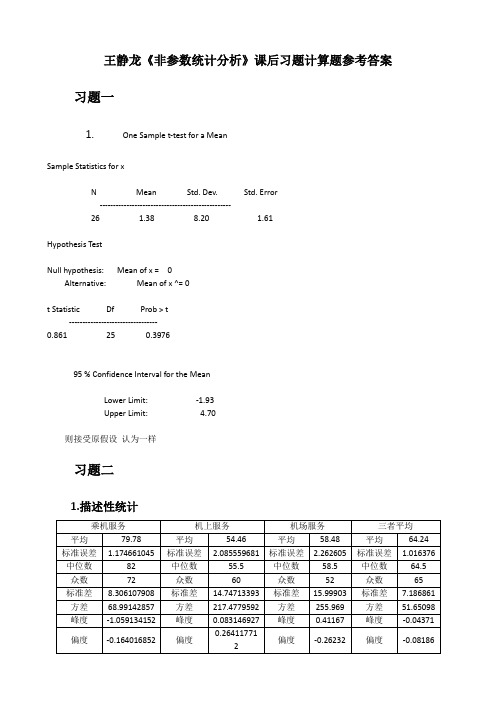
王静龙《非参数统计分析》课后习题计算题参考答案习题一1.One Sample t-test for a MeanSample Statistics for xN Mean Std. Dev. Std. Error-------------------------------------------------26 1.38 8.20 1.61Hypothesis TestNull hypothesis: Mean of x = 0Alternative: Mean of x ^= 0t Statistic Df Prob > t---------------------------------0.861 25 0.397695 % Confidence Interval for the MeanLower Limit: -1.93Upper Limit: 4.70则接受原假设认为一样习题二1.描述性统计习题三1.1{}+01=1339:6500:650013=BINOMDIST(13,39,0.5,1)=0.026625957S n H me H me P S +==<≤另外:在excel2010中有公式 BINOM.INV(n,p,a) 返回一个数值,它使得累计二项式分布的函数值大于或等于临界值a 的最小整数***0*0+1inf :2BINOM.INV(39,0.5,0.05)=141sup :1132S 1313n m i n d i n m m i n d d m i d αα==⎧⎫⎛⎫⎪⎪⎛⎫=≥⎨⎬⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭⎧⎫⎛⎫⎪⎪⎛⎫≤=-=⎨⎬ ⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭=≤=∑∑= 以上两种都拒绝原假设,即中位数低于65001.2****01426201inf :221inf :122BINOM.INV(40,0.5,1-0.025)=26d=n-c=40-26=14580064006200nn i c n m i n c c i n m m i x x me x αα==⎧⎫⎛⎫⎪⎪⎛⎫=≤⎨⎬⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭⎧⎫⎛⎫⎪⎪⎛⎫=≥-⎨⎬⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭====∑∑2.{}+01=4070:6500:65002402*(1-BINOMDIST(39,70,0.5,1))=0.281978922S n H me H me P S +==≠≥=则接受原假设,即房价中位数是65003.1{}+01=15521552527207911::22n 1552=5.33E-112S n H p H p P S φ+=+==>⎛≥≈ ⎝比较大,则用正态分布近似**+**0:=1552155252720791inf :221inf :122m=BINOM.INV(2079,0.5,0.975)=1084nn i c n m i S n n c c i n m m i αα===+=⎧⎫⎛⎫⎪⎪⎛⎫=≤⎨⎬⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭⎧⎫⎛⎫⎪⎪⎛⎫=≥-⎨⎬⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭∑∑另外则拒绝原假设,即相信孩子会过得更好的人多3.2P 为认为生活更好的成年人的比例,则1522=0.7465132079p 的比估计是:4.{}00.90610.90618154157860:65:6510.9060.094~(,)181541BINOMDIST(18153,157860,0.094,1)=0S n H P H P p S b n p P S +++===>=-=≥=-因为0〈0.05则拒绝原假设习题四1.()()++0.025+W =6+8+10+1+4+12+9+11+2+7=70p 2P W 70n=12c =65p 2P W 65=0.05≥≥符号秩和检验统计量:值为,当得所以值小于即拒绝原假设2.()()++0.025+W =2.5+2.5+7+7+7+7+10.5+14+14+14+14+14+17.5+17.5+19+20+23+24=234.5p 2P W 234.5n=25 c =236p 2P W 236=0.05≥≥符号秩和检验统计量:值为,当得所以值小于即接受原假设{}011826:0:02182*(1-BINOMDIST(17,25,0.5,1))=0.043285251S n H me H me P S +===≠≥=+符号检验:则拒绝原假设t t =0.861df=25 p=0.3976检验:统计量接受原假设3.(1)+0.0250.0250.025++=5+2+2=9833(1)322(3)0.052(9)0.05W n c n n d c P W P W ==+=-=≤=≤>查表可得:则 接受原假设(2)Walsh 平均由小到大排列:50 55 60 65 65 70 70 70 75 75 75 80 80 80 80 80 80 80 85 85 85 85 85 90 90 90 90 90 90 95 95 95 95 95 95 100 100 100 100 100 100 100 105 105105 105 105 110 110 110 110 110 115 115 120 N=55 则对称中心为()()^281/290N W W θ+===()()1/1/1/40.527.50.5 1.967.771011461/40.527.50.5 1.9647.22898853d n n U c n n U αα--=+--=--==+++++=因为c 不是整数,则^+1k d L k k w w θ()()介于与之间,其中表示比大的最小整数即为8 ^L θ为70与75之间,即为72.5 []-%72.5,105H L 则的点估计为90 95的区间估计为习题五1.171(,24,25,50)0.005060988i p P i p ===∑值很小,则拒绝原假设即认为女职工的收入比男职工的低。
如何使用Matlab进行非参数统计分析

如何使用Matlab进行非参数统计分析统计分析是一种用来处理和解释数据的方法,而在统计学中,非参数统计分析是指不对数据做出任何分布或参数假设的一种方法。
与参数统计分析相比,非参数统计分析更加灵活,适用于各种类型的数据,尤其是在数据分布未知或非正态分布时更为有用。
本文将介绍如何使用Matlab进行非参数统计分析,帮助读者更好地理解和应用这种方法。
1. 数据准备在进行非参数统计分析之前,首先需要准备好数据。
在Matlab中,可以通过导入、读取或生成数据的方式来准备数据。
例如,可以使用`xlsread`函数导入Excel文件中的数据,使用`load`函数读取.mat文件中的数据,或使用Matlab内置的函数生成符合特定要求的数据。
无论使用何种方式,确保数据被正确地导入到Matlab的工作环境中。
2. 非参数假设检验非参数假设检验是非参数统计分析的核心部分,用来验证某个假设在给定数据中是否成立。
Matlab提供了一系列函数用于进行非参数假设检验,包括`ranksum`、`kstest`、`signrank`等。
这些函数分别对应了Wilcoxon秩和检验、Kolmogorov-Smirnov检验和符号检验等常见的非参数检验方法。
通过调用这些函数并传入相应的参数,可以在Matlab中进行非参数假设检验并获取检验结果。
3. 非参数回归分析除了假设检验,非参数统计分析还可以用于回归分析。
在回归分析中,非参数方法可以更好地处理非线性关系和异方差性等问题,同时能够减轻对数据的假设和约束。
在Matlab中,可以使用`fitrgp`函数来进行非参数回归分析。
这个函数实现了高斯过程回归方法,通过拟合训练数据来推断模型,并提供了预测新数据的能力。
4. 非参数密度估计非参数密度估计是一种用于估计数据概率密度函数的方法,并且不需要对数据分布进行任何参数假设。
在Matlab中,可以使用`ksdensity`函数进行非参数密度估计。
深入剖析Matlab描述性统计:详解+实例PPT

91.9001
,H11 . 746-4
IO1.8319 ,日 Q.59 28
81 .251, 3
9.1.8 16
78.13 功
dr
1 分布函数
` T iIll`
I 逆分布函I 均值与方
X分布
.-chi,2
T分布
t
:
F分布
f
二项分布
b加0.
\ | \ stat,、
.`
:- 机数发生器
泊松分布 1
poiss
1、函数与说明
数名称
血 rmp df
说明:输入的参数可符合基本规则Ill
向
14j
例I、 质检员每天检验500个零件, 如果
校要求考试成绩符合正态分布
X ..., N(80妞共13 5个
计算各分数段理论上不及格同学个数问题描述: 正态分布 六 田 , 致 Y'= n or mcd 'fX
1=135自”“ 门mO, O『(础
HO, 1仇, il心l 不
y2=『135位(IDOlli'Jl1c d” 70j “ LI O,j-:no『 mcdn :
曾松涛
80
6010103
刘鹏飞
*
20
6010120
杨姗姗
81
37
6010213
张小兵
80
6010104
任时迁
82
21
6010121
姚丽娜
49
38
6010214
奚才
73
6010105
苏宏宇
80
22
6010122
张萌
91
39
MATLAB数据分析方法第2章数据描述性分析

MATLAB数据分析⽅法第2章数据描述性分析2.1 基本统计量与数据可视化1.均值、中位数、分位数、三均值均值、中位数:mean(A)、media(A)分位数:prctile(A,P),P∈[0,100]prctile(A,[25,50,75]) %求A的下、中、上分位数三均值:w=[0.25,0.5,0.75];SM=w*prctile(A,[25,50,75])%例:计算安徽16省市森林资源统计量A=xlsread('senlin.xls','sheet1')M=mean(A); %均值,MD=median(A); %中位数SM=[0.25,0.5,0.25]*prctile(A,[25,50,75]); %三均值[M;MD;SM]2.⽅差、标准误、变异系数⽅差:var(A,flag),flag默认0表⽰修正的⽅差,取1为未修正标准差:std(A,flag),同上变异系数:v=std(A)./abs(mean(A))k阶原点矩、中⼼距:ak=mean(A.^k)bk=mean((A-mean(A)).^k)%中⼼距系统命令bk=moment(A,k)3.极差、四分位极差(上、下分位数之差)R=rangr(A)R1=iqr(A)4.异常点判别(截断点)XJ=parctile(A,[25])-1.5*R1SJ=parctile(A,[75])+1.5*R15.偏度、峰度偏度:sk=skewness(A,flag),默认1,取0为样本数据修正的偏度峰度:ku=kurtosis(A,flg)-3,同上2.1.2 多维样本数据协⽅差:cov(A)相关系数:corr(A)标准化:zscore(A)2.1.3 样本数据可视化1.条形图bar(x)%样本数据x的条形图,横坐标为1:length(x)bar(x,y)%先把x和y⼀⼀对应,然后将x从⼩到⼤排序画图2.直⽅图hist(x,n)%数据x的直⽅图,n为组数,确省时n=10[h,stats]=cdfplot(x)%x的经验分布函数图,stats给出数据最⼤最⼩值、中位数、均值、标准差直⽅图基础上附加正态密度曲线histfit(x)histfit(x,nbins)%nbins指定bar个数,缺省时为x中数据个数的平⽅根3.盒图,五个数值点组成:最⼩值、下四分位数、中位数、上四分位数、最⼤值。
matlab数据的统计分析与描述课件

,
x
' 2
,
, xn' 各点,分别以
(
xi'
,
x' i 1
]
为底边,作高为
fi xi'
的矩形, xi'
xi'1 xi' , i 1,2,
, n 1,即得
频率直方图.
学习交流PPT
5
三、几个在统计中常用的概率分布
1.正态分布N (m,s 2 )
密度函数:p(x)
1
( xm )2
e 2s 2 分布函数:F (x)
s
2 1
s
2 2
s
2 1
s
2 2
F0 F1 (n1 , n2 )
F F1 (n1 1, n2 1)
Ⅲ
s
2 1
s
2 2
s
2 1
s
2 2
F0
1 F1 (n2 , n1 )
F
1
F1 (n2 1, n1 1)
F0
1 n1 1 n2
n1
( X i m1)2
i 1
n2
(Yi m2 )2
i 1
,
F
s12 s22
z u1
t t1 (n1 n2 2)
学习交流PPT
19
(四)两个正态总体方差的检验
设样本 X1,X2,…,Xn
与 Y1,Y2,…,Yn
分别来自正态总体
N
(m1
,s
2 1
)
与
1
2
N
(
m
2
,s
2 2
)
,检验假设:
H0
matlab中数据的统计描述和分析

matlab中数据的统计描述和分析MATLAB是一种基于计算机语言的数学软件包,它提供了处理各种数学和工程问题的工具,并在数据统计描述和分析方面发挥了重要作用。
在本文中,我们将探讨MATLAB中数据的统计描述和分析方法。
1. 数据的导入与预处理数据的导入是数据分析的第一步,MATLAB支持各种数据格式的导入,包括CSV,XLS,MAT等文件类型。
在导入数据后,预处理成为必要的步骤。
预处理的目的是删除异常值和不一致的数据点,以确保数据的准确性。
MATLAB提供了各种功能,例如删除重复值和缺失值、转换数据类型、缩放数据、标准化数据、去除噪声等,有助于准确性。
2. 数据的可视化数据的可视化是了解数据中存在的模式和趋势的重要方法,MATLAB提供了许多可视化工具,包括条形图、折线图、散点图、热力图等,以及专门用于可视化统计数据的Anova、Boxplot等工具。
3. 统计描述统计描述提供了对数据的整体理解的方法。
MATLAB提供了许多统计描述的函数,如mean(平均数)、median(中位数)、min(最小值)、max(最大值)、range(极差)、var(方差)、std(标准差)、skewness(偏度)、kurtosis(峰度)、cov(协方差)和corrcoef(相关系数)等函数可以用于计算数据的统计描述信息。
例如,假设我们有一个高斯分布的数据集,可以使用MATLAB的“randn”函数生成一个具有100项的随机高斯数据集。
data = randn(100,1);现在,使用MATLAB的“mean”和“std”函数可以计算出这些数据的统计描述信息。
平均数和标准差告诉我们有关数据的“中心”位置和分散程度的一些信息。
sigma = std(data)4. 假设检验假设检验是判断所提出的关于总体参数的假设是否显著的一种统计分析方法。
假设检验包括参数检验和非参数检验两类。
MATLAB中包含了各种假设检验的函数,例如单样本t检验、双样本t检验、方差分析、卡方检验、K-S检验等。
Matlab中常用的统计分析技巧介绍

Matlab中常用的统计分析技巧介绍统计分析是研究数据的特征、规律和变化趋势的一种方法。
作为一款功能强大的科学计算软件,Matlab提供了丰富的统计分析工具和函数,可用于处理和分析各种类型的数据。
本文将介绍Matlab中常用的统计分析技巧,帮助读者更好地利用Matlab进行数据分析和解释。
一、数据导入与处理在进行统计分析之前,首先需要将数据导入Matlab并进行相应的处理。
Matlab 提供了多种导入数据的函数,如`xlsread`、`csvread`和`importdata`等,可根据数据的来源和格式选择合适的函数进行导入。
同时,Matlab还提供了丰富的数据处理函数,如`reshape`、`sort`和`filter`等,可用于数据的重塑、排序和滤波等操作,便于后续的分析和计算。
二、描述性统计分析描述性统计分析是了解和概括数据特征的一种方法。
在Matlab中,我们可以使用`mean`、`median`、`std`、`max`和`min`等函数计算数据的均值、中位数、标准差、最大值和最小值等统计量。
此外,Matlab还提供了`hist`和`boxplot`等函数,可用于绘制数据的直方图和箱线图,直观展示数据的分布和离散情况。
三、假设检验假设检验是统计学中经典的方法之一,用于判断样本数据与假设之间的差异是否显著。
在Matlab中,我们可以使用`ttest`、`anova1`和`chisquare`等函数进行假设检验。
例如,`ttest`函数可以用于对比两组样本的均值是否存在显著差异,`chisquare`函数可以用于分析分类数据的关联性。
假设检验结果一般会给出显著性水平和p值,以帮助我们判断差异是否具有统计学意义。
四、回归和相关性分析回归和相关性分析是研究变量之间关系的一种常用方法。
Matlab中提供了`regress`和`corrcoef`等函数,可用于简单线性回归和相关性分析。
例如,`regress`函数可以用于求解线性回归模型的回归系数和拟合优度,`corrcoef`函数可以用于计算变量之间的相关系数矩阵。
Matlab数据的统计分析与描述

Matlab数据的统计分析与描述实验⽬的 (1)熟悉统计的基本概念、参数估计、假设检验。
(2.)会⽤参数估计和假设检验对实际问题进⾏分析。
实验要求 实验步骤要有模型建⽴,模型求解、结果分析。
实验内容(1)某校60名学⽣的⼀次考试成绩如下:93 75 83 93 91 85 84 82 77 76 77 95 94 89 91 88 86 83 96 81 79 97 78 75 67 69 68 84 83 81 75 66 85 70 94 84 83 82 80 78 74 73 76 70 86 76 90 89 71 66 86 73 80 94 79 78 77 63 53 551)计算均值、标准差、极差、偏度、峰度,画出直⽅图;2)检验分布的正态性;3)若检验符合正态分布,估计正态分布的参数并检验参数.(2)据说某地汽油的价格是每加仑115美分,为了验证这种说法,⼀位学者开车随机选择了⼀些加油站,得到某年⼀⽉和⼆⽉的数据如下:⼀⽉:119 117 115 116 112 121 115 122 116 118 109 112 119 112 117 113 114 109 109 118⼆⽉:118 119 115 122 118 121 120 122 128 116 120 123 121 119 117 119 128 126 118 1251)分别⽤两个⽉的数据验证这种说法的可靠性;2)分别给出1⽉和2⽉汽油价格的置信区间;3)给出1⽉和2⽉汽油价格差的置信区间.实验步骤1、解:主要使⽤MATLAB与SPSS求解,具体求解步骤如下, (1)编写MATLAB程序求解,代码如下1 %数据2 x=[93,75,83,93,91,85,84,82,77,76,77,95,94,89,91,88,86,83,96,81,79,97,78,75,67,69,68,84,83,81,75,66,85,70,94,84,83,82,80,78,74,73,76,70,86,76,90,89,71,66,86,73,80,94,79,78,77,63,53,55];3 %总样本数4 n=length(x);5 %平均值6 x_bar=sum(x)*1/n7 %标准差8 temp1=0;9for i=1:n10 c=x(i)-x_bar;11 temp1=temp1+c^2;12 end13 s=sqrt(temp1*(1/(n-1)))14 %极差15 x_max=max(x);16 x_min=min(x);17 x_jicha=x_max-x_min18 %偏度19 temp2=0;20for i=1:n21 c=x(i)-x_bar;22 temp2=temp2+c^3;23 end24 g1=(1/s)^3*temp225 %峰度26 temp3=0;27for i=1:n28 c=x(i)-x_bar;29 temp3=temp3+c^4;30 end31 g2=(1/s)^4*temp332 %画出直⽅图33 bar(x)题1_MATLAB 运⾏结果,平均值标准差极差偏度峰度80.109.7144.00-27.39 1.8380.109.7144.00-27.39 1.83 见图 (2)SPSS求解步骤: ⾸先,做出正态曲线直⽅图: 由上图可见,该校这60名学⽣的的成绩分布与正态分布相近。
使用Matlab进行统计分析的基本步骤

使用Matlab进行统计分析的基本步骤统计分析是指通过对收集到的数据进行整理、描述、分析和解释,从而揭示数据背后的规律和关联性。
Matlab是一种强大的数值计算和科学工程软件,广泛应用于各个领域的数据分析和建模。
本文将介绍使用Matlab进行统计分析的基本步骤。
一、数据准备和导入进行任何统计分析之前,首先需要准备和导入数据。
数据可以来自于实验、调查、采样等方式收集得到。
在Matlab中,可以通过各种途径导入数据,如文本文件、Excel文件、数据库等。
在导入数据之前,需要确保数据格式正确、无误,并进行必要的清洗和预处理。
二、数据的描述统计描述统计是对数据进行描述和分析的过程。
通过描述统计,可以获得数据的中心趋势、离散程度、分布特征等信息。
在Matlab中,可以使用一系列函数进行描述统计分析。
例如,mean函数可以计算数据的均值,std函数可以计算标准差,median函数可以计算中位数,hist函数可以绘制直方图等。
三、数据的可视化分析数据可视化是将数据以图形或图表的形式展示出来,以便更直观地理解数据之间的关系和趋势。
Matlab提供了强大的绘图功能,可以绘制散点图、柱状图、折线图等多种图形。
通过调用相应的绘图函数,可以将数据可视化展示出来,并进行进一步的分析和解读。
四、假设检验与推断统计假设检验与推断统计是统计学中重要的分析方法,用于对总体参数、分布或数据之间的关系进行推断。
在Matlab中,可以使用ttest函数进行单样本或双样本的假设检验,使用anova 函数进行方差分析,使用corrcov函数计算相关系数矩阵等。
这些函数可以帮助我们进行假设检验和推断统计,以得出对总体或样本的推断性结论。
五、回归分析和建模回归分析是研究变量之间相互依赖关系的一种统计方法,常用于预测、数据建模和因果推断。
在Matlab中,可以通过调用regress函数实现线性回归分析,使用fitlm函数进行多元线性回归分析,使用glm函数进行广义线性模型分析等。
003--matlab中数据的统计描述和分析

003--matlab中数据的统计描述和分析-122-数据的统计描述和分析数理统计研究的对象是受随机因素影响的数据,以下数理统计就简称统计,统计是以概率论为基础的一门应用学科。
数据样本少则几个,多则成千上万,人们希望能用少数几个包含其最多相关信息的数值来体现数据样本总体的规律。
描述性统计就是搜集、整理、加工和分析统计数据,使之系统化、条理化,以显示出数据资料的趋势、特征和数量关系。
它是统计推断的基础,实用性较强,在统计工作中经常使用。
面对一批数据如何进行描述与分析,需要掌握参数估计和假设检验这两个数理统计的最基本方法。
我们将用Matlab 的统计工具箱(Statistics Toolbox)来实现数据的统计描述和分析。
§1 统计的基本概念1.1 总体和样本总体是人们研究对象的全体,又称母体,如工厂一天生产的全部产品(按合格品及废品分类),学校全体学生的身高。
总体中的每一个基本单位称为个体,个体的特征用一个变量(如x )来表示,如一件产品是合格品记0=x ,是废品记1=x ;一个身高170(cm )的学生记170=x 。
从总体中随机产生的若干个个体的集合称为样本,或子样,如n 件产品,100名学生的身高,或者一根轴直径的10次测量。
实际上这就是从总体中随机取得的一批数据,不妨记作n x x x ,,,21 ,n 称为样本容量。
简单地说,统计的任务是由样本推断总体。
1.2 频数表和直方图一组数据(样本)往往是杂乱无章的,作出它的频数表和直方图,可以看作是对这组数据的一个初步整理和直观描述。
将数据的取值范围划分为若干个区间,然后统计这组数据在每个区间中出现的次数,称为频数,由此得到一个频数表。
以数据的取值为横坐标,频数为纵坐标,画出一个阶梯形的图,称为直方图,或频数分布图。
若样本容量不大,能够手工作出频数表和直方图,当样本容量较大时则可以借助Matlab这样的软件了。
让我们以下面的例子为例,介绍频数表和直方图的作法。
Matlab中常用的统计分析方法

Matlab中常用的统计分析方法统计分析是一项对数据进行收集、整理、分析和解释的过程,它对于研究和决策具有重要意义。
在各个领域中,Matlab作为一种强大的数据分析工具,为我们提供了许多常用的统计分析方法。
本文将介绍一些常见的统计分析方法,并讨论它们在Matlab中的应用。
一、描述性统计分析描述性统计分析是对数据进行描述和总结的一种方法。
它通过计算数据的均值、中位数、标准差、最大值、最小值等指标来揭示数据的集中趋势和离散程度。
在Matlab中,我们可以利用函数mean()、median()、std()、max()、min()等来进行描述性统计分析。
例如,我们可以使用mean()函数计算数据的均值:```matlabdata = [1, 2, 3, 4, 5];mean_value = mean(data);```二、假设检验假设检验是用来评估两个或多个数据集之间是否存在显著差异的方法。
在Matlab中,我们可以利用ttest2()函数来进行双样本t检验,利用anova1()函数来进行单因素方差分析。
双样本t检验常用于比较两个样本平均值是否有显著差异。
例如,我们想比较两组学生的成绩是否存在差异,可以使用ttest2()函数:```matlabgroup1 = [80, 85, 90, 95, 100];group2 = [70, 75, 80, 85, 90];[p, h] = ttest2(group1, group2); % p值表示差异的显著性```单因素方差分析用于比较多个样本平均值是否有显著差异。
例如,我们想比较三个不同条件下的实验结果是否有差异,可以使用anova1()函数:```matlabdata = [80, 85, 90; 70, 75, 80; 90, 95, 100];p = anova1(data); % p值表示差异的显著性```三、相关性分析相关性分析用于评估两个或多个变量之间的关联程度。
Matlab中常用的统计分析方法介绍

Matlab中常用的统计分析方法介绍统计分析是一种通过对数据的收集、整理、分析和解释,来推测并描述数据所呈现出的规律和规律性的方法。
作为一种重要的数据处理工具,Matlab提供了许多功能强大的统计分析方法,以帮助研究人员对数据进行深入的研究和解读。
在本文中,我们将介绍一些常用的统计分析方法,并对其原理和应用进行简要概述。
一、描述统计分析方法1. 均值与方差:均值是对样本数据的集中趋势进行度量的指标,可以通过Matlab的mean函数计算得到。
方差则是数据的离散程度度量,可以通过Matlab的var函数计算。
均值和方差是描述一个数据集的基本统计指标,可以帮助我们快速了解数据的分布情况。
2. 频数分布:频数分布可以将数据按照一定的区间划分,并统计每个区间中数据的数量。
Matlab提供了hist函数可以直接绘制频数直方图,进而帮助我们了解数据的分布情况和集中区间。
3. 分位数:分位数是将数据按大小顺序排列后分成若干部分的值。
常见的分位数有四分位数、百分位数等。
Matlab的quantile函数可以帮助我们计算任意分位数,从而得到数据分布的具体信息。
二、假设检验分析方法1. 单样本t检验:单样本t检验是一种用于判断样本均值与总体均值之间是否存在显著差异的方法。
在Matlab中,可以使用ttest函数进行单样本t检验。
通过设置显著性水平和计算得到的t值,我们可以对样本数据是否足够代表总体数据进行判断。
2. 独立样本t检验:独立样本t检验是一种用于比较两组独立样本均值是否存在显著差异的方法。
在Matlab中,可以使用ttest2函数进行独立样本t检验。
通过设置显著性水平和计算得到的t值,我们可以得出两组样本均值是否存在显著差异的结论。
3. 方差分析:方差分析是一种用于比较多组样本均值之间是否存在显著差异的方法。
在Matlab中,可以使用anova1或anova2函数进行方差分析。
通过计算得到的F值和p值,我们可以判断样本组间的差异是否显著。
Matlab技术统计分析方法解读

Mat1ab技术统计分析方法解读引言:在各个领域,统计分析方法在研究和决策过程中发挥着重要的作用。
Mat1ab作为一种强大的数值计算和编程软件,提供了多种统计分析方法的功能和工具。
本文将解读Mat1ab 中常用的技术统计分析方法,并探讨其在实际应用中的价值和限制。
一、描述性统计分析方法描述性统计分析方法是对数据进行统计描述和总结的方法。
在MatIab中,可以使用一系列函数来计算数据的均值、中位数、标准差等,以及绘制直方图、箱线图等可视化图形。
这些方法能够帮助我们对数据进行初步的了解和判断。
然而,由于描述性统计分析方法只能提供数据的整体情况,并不能对数据之间的关系和趋势进行分析,因此有时需要结合其他统计分析方法来进行深入研究。
二、假设检验方法假设检验方法用于根据已知数据样本对总体参数进行推断。
在MaUab中,可以使用t 检验、方差分析、卡方检验等常见的假设检验方法。
这些方法通过计算样本与理论分布之间的差异,判断总体参数是否具有统计显著性。
然而,需要注意的是统计显著性并不意味着实际意义上的显著性。
因此,在使用假设检验方法时,需要综合考虑具体问题和实际背景,慎重解读结果。
三、回归分析方法回归分析方法用于研究变量之间的相关关系和预测问题。
在Mat1ab中,可以使用线性回归、非线性回归等方法进行回归分析。
通过拟合模型,计算回归系数和拟合优度等指标,我们可以了解变量之间的线性或非线性关系,并通过预测结果进行决策。
然而,需要注意的是回归分析只能提供变量之间的相关性,并不能说明因果关系。
因此,在进行回归分析时,需谨慎解读结果,并结合领域知识和实际情境。
四、聚类分析方法聚类分析方法用于将数据对象进行分类和分组,以发现潜在的数据结构和规律。
在MaUab中,可以使用k均值聚类、层次聚类等方法进行聚类分析。
这些方法通过计算对象之间的相似性和距离,将相似的数据对象划分到同一组中。
聚类分析可以帮助我们对数据进行分类、发现异常点和预测未知数据。
非参数检验及matlab实现

非参数检验与matlab实现Kolmogorov-Smirnov test:检验两个样本是否有相同分布KstestTest statistics:()-max()()F xG x[h,p,ksstat,cv] = kstest<x,CDF,alpha,type>x:被测试的数据样本,以列向量输入〔continuous distribution defined by cumulative distribution function〕CDF:被检验的样本cumulative distribution function,缺省值为N<0,1> Alpha:显著性水平,缺省时为0.05Type:字符输入.'unequal'〔缺省值〕检验两者分布是否相同'larger' 检验x的CDF大于给定的CDF'smaller' 检验x的CDF小于给定的CDFh h=0不拒绝原假设,即两个分布相同h=1拒绝原假设,即两个分布不同p:拒绝原假设的最小显著性水平ksstat:假设为真时,满足student分布cv:critical value/cutoff value,determining if ksstat is significant. Kstest2:[h,p,ks2stat] = kstest2<x1,x2,alpha,type>详见ketestLilliefors test :检验两个样本是否有相同分布Test statistics :()max ()()xF xG x - 2-sided goodness-of-fit testlillietest[h,p,kstat,critval] = lillietest <x,alpha,distr,mctol>各参数参见kstest,特别的,mctol 为使用蒙特卡洛方法计算p 值 Jarque-Bera test检验样本是否来自均值和方差未知的正态分布two-sided goodness-of-fit test假设:x 为正态分布test statistic :()22364k n JB s ⎛⎫-=+ ⎪ ⎪⎝⎭, where n is the sample size, s is the sample skewness, and k is the sample kurtosis.test[h,p,stat,critval] = test<x,alpha,mctol>各个参数意义详见lillietest.Wilcoxon-Mann-Whitney Ranks Test检验两个样本是否来自于同一分布.以下function f=Wilcoxon_Rank_Test<x,y,alpha>直接是秩和检验方法,另有function f=Pre_Wilcoxon<x,y,alpha>是改进的秩和检验方法.区别在于样本的处理方式.function f=Wilcoxon_Rank_Test<x,y,alpha>;%x,y are vectors%x,y can be at different lengthZ=[x;y];%z1 for ranking from small to large%z2 for place[z1,z2]=sort<Z,'ascend'>;for i=1:size<x,1>for j=i:size<z1,1>if z1<j>==x<i>X<i,1>=j;endendend%X is the rank of x in vectorm=size<x,1>;n=size<y,1>;Ex=m*<m+n+1>/2;Varx=m*n*<m+n+1>/12;c=sqrt<Varx>*norminv<1-alpha/2>;beta=sum<X,1>;if abs<beta-Ex>>cdisp<'Reject Null Hypothesis'>;f=1;else disp<'Fail to Reject Null Hypothesis'>; f=0;endfunction f=Pre_Wilcoxon<x,y,alpha>;%to find whether division is neededmemo=zeros<size<x,1>,size<y,1>>;for i=1:size<x,1>for j=1:size<y,1>if x<i,1>==y<j,1>memo<i,j>=1;endendend%memo contains the information of division; %memo is a symmetric matrix;if memo==zeros<size<memo>>disp<'No need for division'>;disp<'Go on Rank Test straightly'>;disp<{'Reault as Following','significant level',num2str<alpha>}>; Wilcoxon_Rank_Test<x,y,alpha>;else disp<'Division is needed'>;[cx,cy]=find<memo>0>;if <cx<1,1>~=1>&&<cy<1,1>~=1>disp<'group 1'>;gamma=Wilcoxon_Rank_Test<x<1:cx<1>>,y<1:cy<1>>,alpha>; if gamma==1;returnendfor k=1:size<cx,1>disp<'group ',num2str<k+1>>;gamma=Wilcoxon_Rank_Test<x<cx<k>:cx<k+1>>,y<cy<k>:cy<k+1> >,alpha>;if gamma==1;breakendendelseif <<cx<1>==1>&&<cy<1>~=1>>||<<cx<1>~=1>&&<cy<1>==1>> gamma=0;disp<'Reject Null Hypothesis'>;end%<cx<1>==1>&&<cy<1>==1>for k=1:size<cx,1>disp<'group ',num2str<k+1>>;gamma=Wilcoxon_Rank_Test<x<cx<k>:cx<k+1>>,y<cy<k>:cy<k+1> >,alpha>;if gamma==1;breakendendendend另外matlab中也有相关的自带的秩和检验函数:signrank/signtestp = signrank<x,y> 为双侧检验,检验x,y是否来自中位数为0的整体;相似的,有p = signtest<x,y>ranksump = ranksum<x,y>为双侧检验,检验x,y之间是否相互独立,要求x,y之间有相同的中位数Chi-square goodness-of-fit test离散态的检验样本是否来自于已知分布.Test statistics:()221Ni ii iO EEχ=-=∑, where O i are the observed countsand E i are the expected counts. The statistic has an approximate chi-square distribution when the counts are sufficiently large.chi2gofh = chi2gof<x>H0:x<列向量>来自正态分布〔期望和方差来源于x〕〔default significance level: 0.05〕h=0 fail to reject H0h=1 rejectH0或者[h,p] = chi2gof<x,'cdf',{normcdf,mean<x>,std<x>}>关于样本是否来自对称的分布function f=symmetric_test<x,alpha>%x is a vector%alpha is the significant level[x1,x2]=sort<x,'ascend'>;%x1 is x from min to max%x2 is the placen=size<x,1>;x_ME=median<x,1>;%median in column x_IQR=iqr<x>;%IQR in columnx3=abs<x-x_ME>;x4=var<x3>;x5=norminv<1-alpha/2>;if abs<x3-x_IQR/2>>x5*sqrt<x4>disp<'Asymmetric Distribution'>;else disp<'Symmetric Distribution'>;end。
数据分析方法MATLAB实现ppt课件

MATLAB数据分析方法(机械工业出版社)
第2章 数据描述性分析
5/24
虽然均值与中位数都是描述数据集中位置的
数字特征,但是均值用了数据的全部信息,中位数
只用了部分信息(位置信息),因此通常情况下均
值比中位数有效.当数据有异常值时,中位数比较
稳健。为了兼顾两者的优势,因此人们提出三均值
17/24
例2.1.3 根据2007年华东地区各高校教职工数据, 计算专任教师、 行政人员、教辅人员以及工勤人
员占在职教工的百分比,以及百分比的极差、四分 位极差以及上、下截断点.
表2.4 2007年华东地区各高校教职工数据
地 区 在职教工 专任教师 行政人员 教辅人员
上海 江苏 浙江 安徽 福建
61385 134215 67763 59149 47864
第2章 数据描述性分析
1/24
第2章 数据描述性分析
数据描述性分析是从样本数据出发,概括分析数
据的集中位置、分散程度、相互关联关系等,分析数 据分布的正态或偏态特征.描述性分析是进行数据进一 步分析的基础.对不同类型量纲的数据有时还要进行变 换,然后再作出合理分析.本章主要介绍样本数据的基 本统计量、数据的可视化、数据分布检验及数据变换 等内容.
v s / x,或 s / | x | (2.1.9) 变异系数是一个无量纲的量,一般用百分数表示. 在MATLAB中,计算方差命令var,调用格式
S=var(x); 计算标准差命令std,调用格式
d=std(x) 其中输入x是样本数据,输出S为方差,d为标准差.当 输入x是矩阵时,输出x每列数据的方差与标准差. 由均值与方差命令,可设计变异系数的计算程序为 v=std(x)./mean(x),或者v=std(x)./abs(mean(x)) 当输入x是矩阵时,输出x每列数据的变异系数.
matlab统计种类

matlab统计种类Matlab是一种用于数值计算和数据可视化的高级编程语言和环境。
它在科学研究、数据分析和工程设计方面都有广泛的应用。
在数据统计方面,Matlab提供了多种用于统计分析、数据处理和模型建立的函数和工具箱。
下面将介绍一些常用的Matlab统计函数和工具箱。
1. 基本统计功能:Matlab提供了一系列基本的统计计算函数,如平均数、标准差、方差、中位数等。
这些函数可以直接应用于数据向量或矩阵。
2. 概率分布函数:Matlab提供了多种概率分布函数,如正态分布、二项分布、泊松分布等。
这些函数可用于生成服从指定分布的随机数,或计算概率密度函数和累积分布函数。
3. 统计图表:Matlab内置的绘图函数可以用于创建各种统计图表,如直方图、散点图、箱线图等。
这些图表可用于数据的可视化和分析。
4. 回归分析:Matlab提供了回归分析函数和工具箱,可用于拟合线性或非线性回归模型。
这些函数可用于评估变量之间的关系,并预测未来的观测值。
5. 方差分析:Matlab提供了方差分析函数和工具箱,可用于比较多个组别之间的均值差异。
方差分析可用于检验因素对观测值之间差异的显著性。
6. 非参数统计:Matlab提供了多种非参数统计函数和工具箱,如Mann-Whitney U检验、Wilcoxon符号秩检验等。
非参数统计方法可应用于不满足正态分布假设的数据。
7. 时间序列分析:Matlab提供了时间序列分析函数和工具箱,可用于模型拟合、趋势分析、季节性调整等。
时间序列分析可用于预测未来的观测值或分析时间序列数据的波动性。
8. 多元分析:Matlab提供了多元分析函数和工具箱,如主成分分析、因子分析、聚类分析等。
多元分析可用于降维、数据压缩和数据分类。
9. 假设检验:Matlab提供了多种假设检验函数和工具箱,可用于验证统计推断的显著性。
常见的假设检验方法包括t检验、卡方检验、F检验等。
10. 贝叶斯统计:Matlab提供了贝叶斯统计函数和工具箱,可用于贝叶斯推断和模型选择。
《非参数统计》与MATLAB编程 第二章 描述性统计-推荐下载

对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电通,力1根保过据护管生高线产中0不工资仅艺料可高试以中卷解资配决料置吊试技顶卷术层要是配求指置,机不对组规电在范气进高设行中备继资进电料行保试空护卷载高问与中题带资2负料2,荷试而下卷且高总可中体保资配障料置2试时32卷,3各调需类控要管试在路验最习;大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试,况卷要下安加与全强过,看度并25工且52作尽22下可护都能1关可地于以缩管正小路常故高工障中作高资;中料对资试于料卷继试连电卷接保破管护坏口进范处行围理整,高核或中对者资定对料值某试,些卷审异弯核常扁与高度校中固对资定图料盒纸试位,卷置编工.写况保复进护杂行层设自防备动腐与处跨装理接置,地高尤线中其弯资要曲料避半试免径卷错标调误高试高等方中,案资要,料求编试技5写、卷术重电保交要气护底设设装。备备置管4高调、动线中试电作敷资高气,设料中课并技3试资件且、术卷料中拒管试试调绝路包验卷试动敷含方技作设线案术,技槽以来术、及避管系免架统不等启必多动要项方高方案中式;资,对料为整试解套卷决启突高动然中过停语程机文中。电高因气中此课资,件料电中试力管卷高壁电中薄气资、设料接备试口进卷不行保严调护等试装问工置题作调,并试合且技理进术利行,用过要管关求线运电敷行力设高保技中护术资装。料置线试做缆卷到敷技准设术确原指灵则导活:。。在对对分于于线调差盒试动处过保,程护当中装不高置同中高电资中压料资回试料路卷试交技卷叉术调时问试,题技应,术采作是用为指金调发属试电隔人机板员一进,变行需压隔要器开在组处事在理前发;掌生同握内一图部线纸故槽资障内料时,、,强设需电备要回制进路造行须厂外同家部时出电切具源断高高习中中题资资电料料源试试,卷卷线试切缆验除敷报从设告而完与采毕相用,关高要技中进术资行资料检料试查,卷和并主检且要测了保处解护理现装。场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
描述性统计的matlab实现

描述性统计的matlab实现理论讲的再多不会做也⽩弄直接上⼿⼀.针对接近正态分布的(均值,⽅差,标准差,极差,变异系数,偏度,峰度)这⾥我必须提前说明⼀点就是,你在写好函数后,函数的名是dts,你保存的⽂件名也必须是dts.m才⾏,这样调⽤dts()函数的时候才不会出现错。
x=[ 1 2 0/0 4 5 6]function dts(x);a = x(:);nans = isnan(a);ind = find (nans); %nan是0/0.a(ind)=[];xbar= mean(a);disp(['均值是:',num2str(xbar)]);s2 = var(a);disp(['⽅差是:',num2str(s2)]);s = std(a);disp(['标准差是:',num2str(s)]);%数据⾥必须是元素的类型⼀样,所以要有num2str()函数转⼀下。
R = range(a);disp(['极差是:',num2str(R)]);cv = 100*s./xbar;%它是⼀个相对的数且没有量纲,所以更具有说明性。
disp(['变异系数是:',num2str(cv)]);g1 = skewness(a,0);disp(['偏度:',num2str(g1)]);g2=kurtosis(a,0);disp(['峰度',num2str(g2)]);⼆.针对有极端值(中位数,上下四分位数,四分位极差,三均值,上下截断点)function fws(x)a = x(:);a(isnan(a))=[];ss5 = prctile(a,50);disp(['中位数是:',num2str(ss5)]);ss25 = prctile(a,25);disp(['下四分位数是:',num2str(ss25)]);ss75 = prctile(a,75);disp(['上四分位数是:',num2str(ss75)]);RS = ss75-ss25;disp(['四分位极差:',num2str(RS)]);sss = 0.25*ss25+0.5*ss50+0.25*ss75;disp('三均值:',num2str(sss));三.⽤样本的分布描述总体的matlab茎叶图:a=[10 20 10;54 56 78]a=a(:)b=a-mod(a,10);b=unique(b);b=sort(b);N=length(b);for k=1:Ntmp=b(k);TT=sort(a');TT(TT<tmp)=[];TT(TT>tmp+10)=[];ts=mat2str(mod(TT,10));ts(ts=='[')=[];ts(ts==']')=[];disp([int2str(tmp),' : ',ts])end经验分布函数图X=[12,3,5,6;4,5,6,7];X=X(:)'X=sort(X)n=length(X)m=size(X)%写这⼀步是为了⽐较length 和 size两个函数的不同xsui=ones(size(X))B=cumsum(xsui)B=B/nx1=min(X)-(max(X)-min(X))*0.1xr=max(X)+(max(X)-min(X))*0.1x=[x1,X,xr]y=[0,B,1]h=stairs(x,y)set(h,'linewidth',2,'color','k')xlabel('x')ylabel('F(x)')grid onaxis([x1,xr,-0.05,1.05])title('经验分布函数')。
matlab在统计数据描述性分析的应用

一、实验目的
熟悉在matlab中实现数据的统计描述方法, 掌握基本统计命令: 样本均值、样本中位数、样本标准差、样本方差、概率密度函数pdf、概率分布函数df、随机数生成rnd。
二、实验内容
1、频数表和直方图
数据输入,将你班的任意科目考试成绩输入
>>data=[9178 90 88 76 81 77 74];
>>[N,X]=hist(data,5)
N=
3 1 1 0 3
75.7000 79.1000 82.5000 85.9000 89.3000 >>hist 94 36 88 90 92
2、基本统计量
1)样本均值
语法:m=mea n(x)
若x为向量,返回结果m是x中元素的均值;
若x为矩阵,返回结果m是行向量,它包含x每列数据的均值。
2)样本中位数
语法:m=media n(x)
若x为向量,返回结果m是x中元素的中位数;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章描述性统计2.1 表格法和图形法表2.1 灯丝寿命数据107 73 68 97 76 79 94 59 98 57 73 81 54 65 71 80 84 88 62 61 79 98 63 65 66 62 79 86 68 74 61 82 65 98 63 71 62 116 65 88 64 79 78 79 77 86 89 76 74 85 73 80 68 78 89 72 58 69 82 72 92 78 88 77 103 88 63 68 88 81 64 73 75 90 62 89 71 71 74 70 74 70 85 61 65 81 75 62 94 71 85 84 83 63 92 68 81 62 79 83 93 61 65 62 92 65 64 66 83 70 70 81 77 72 84 67 59 58 73 83 78 66 66 94 77 63 66 75 68 76 73 76 90 78 71 101 78 43 59 67 61 71 77 91 96 75 64 76 72 77 74 65 82 86 79 74 66 86 96 89 81 71 85 99 59 92 94 62 68 72 77 60 87 84 75 77 51 45 63 102 85 67 87 80 84 93 69 76 89 75 59 77 83 68 72 67 92 89 82 96a =Columns 1 through 17107 73 68 97 76 79 94 59 98 57 7381 54 65 71 80 8479 98 63 65 66 62 79 86 68 74 6182 65 98 63 71 6264 79 78 79 77 86 89 76 74 85 7380 68 78 89 72 5892 78 88 77 103 88 63 68 88 81 6473 75 90 62 89 7174 70 85 61 65 81 75 62 94 71 8584 83 63 92 68 8193 61 65 62 92 65 64 66 83 70 7081 77 72 84 67 5978 66 66 94 77 63 66 75 68 76 7376 90 78 71 101 7861 71 77 91 96 75 64 76 72 77 74 65 82 86 79 74 6681 71 85 99 59 92 94 62 68 72 77 60 87 84 75 77 5185 67 87 80 84 93 69 76 89 75 59 77 83 68 72 67 92Columns 18 through 2088 62 61116 65 8869 82 7271 74 7062 79 8358 73 8343 59 6786 96 8945 63 10289 82 96注:a不能复制到MATLAB中。
b=reshape(a,200,1);[min(b) max(b)]ans =43 116n=histc(b,[40,50,60,70,80,90,100,110,120])n =2105264452241n/200ans =0.01000.05000.26000.32000.22500.11000.02000.0050bar([40,50,60,70,80,90,100,110,120],n,'histc')表2.2 灯丝寿命数据频率分布灯丝寿命(小时)个数频率(%)40—50 2 150—60 10 560—70 52 2670—80 64 3280—90 45 22.590—100 22 11100—110 4 2110-120 1 0.5合计200 100c=[2 32 24 19 10 6 3 2 1 1]bar(c)表2.7 赔款样本数据直方图x=[1 2 2 2 2 3 3 5 7 8 9];y=[1 1 2 3 4 1 2 1 1 1 1];plot(x,y,'*','markersize',30,'linewidth',4)axis([0,10,0,5])图2.8[mean([1,2,2,2,2,3,3,5,7,8,9]) median([1,2,2,2,2,3,3,5,7,8,9])] ans =4 3切尾均值:trimmeantrimmean(x,percent) ,其中percent为0到100。
当x为向量时,切尾均值为:先去掉x的percent/2的最大值和最小值,再求算术平均值。
注意:若length(x)×percent/2恰好为整数时,则就x按大小排序后,两端去掉length(x)×percent/2个数,如果不是整数,则去掉length(x)×percent/2四舍五入数(若小数点后正好等于5,则取小的整数,如1.5还是取1)。
如:a=[4 9 12.4 23 33.5 45 56 67 76 99] 回车trimmean(a,50) 回车ans =39.4833(25/2)%×length(x)=2.5,两端切掉2个数。
即等于:mean([12.4 23 33.5 45 56 67]) 回车ans =39.4833然后当:trimmean(a,51) 回车ans =39.3750(51/2)%×length(x)=2.55,即两端切掉3个数。
mean([23 33.5 45 56]) 回车ans =39.3750Trimmean 也可处理矩阵,不过只是计算矩阵每列的切尾均值。
继续上面,如:b=a';c=[1:10]';d=[b,c];trimmean(d,51) 回车ans =39.3750 5.50002.2.2 表示离散程度的数值 [var(b) std(b) range(b)] ans =145.4548 12.0605 73.0000百分位数:prctile(x,percent) ,其中percent 为0到100,x 可为向量或矩阵。
[prctile(b,25) prctile(b,75)] ans =66.5000 84.0000四分位间距:iqr(x) 其中x 可为向量或矩阵,当x 为向量时,iqr(x)为x 的75%的百分位数减去25%的百分位数。
iqr(b) ans = 17.5000V a l u e sColumn NumberX-上四分位数>1.5IQR 或下四分位数-X>1.5IQR 时 ,X 为野值。
称“下四分位数-1.5IQR”和“上四分位数+1.5IQR”两个数为内篱笆,“下四分位数-3IQR”和“上四分位数+3IQR”两个数为外篱笆,位于内、外篱笆之间的数称为弱异常值,而在外篱笆的数称为强异常值。
区间估计:双侧均值的区间估计:[h,sig,ci,stats]=ttest(b,75,0.05)% 95%的置信区间h =sig =0.2197ci =74.3683 77.7317stats =tstat: 1.2312df: 199sd: 12.0605[mean(b)-tinv(0.975,199)*std(b)/(200^0.5)mean(b)+tinv(0.975,199)*std(b)/(200^0.5)]ans =74.3683 77.7317单侧区间估计:[h,sig,ci,stats]=ttest(b,75,0.05,1)h =sig =0.1098ci =74.6407 Infstats =tstat: 1.2312df: 199sd: 12.0605[h,sig,ci,stats]=ttest(b,75,0.05,-1)h =sig =0.8902ci =-Inf 77.4593stats =tstat: 1.2312df: 199sd: 12.0605[mean(b)-tinv(0.95,199)*std(b)/(200^0.5) mean(b)+tinv(0.95,199)*std(b)/(200^0.5)] ans =74.6407 77.4593§2.2.2 偏度 format longskewness(b)%不修正的偏度系数 ans =0.27494548340412 moment(b,3)/std(b,1)^3 ans =0.27494548340412 moment(b,3)/moment(b,2)^1.5 ans =0.27494548340412(sum((b-mean(b)).^3)/200)/std(b,1)^3 ans =0.27494548340412 不修正的偏度系数:()()()2/32333//∑∑--==n x x nx x u skewness σskewness(b,0) %修正的偏度系数 ans =0.27702753367296200*(200/(199*198))*moment(b,3)/std(b)^3 ans =0.27702753367296 修正的偏度系数:()3)2(1∑⎪⎪⎭⎫ ⎝⎛---=s x x n n n skewness i 2*(1-normcdf(bs*sqrt(200/6)))ans =0.10972748638965在0.05显著性水平下,接受原假设。
为正态分布。
§2.2.5 峰度x = -6:0.1:6;y = tpdf(x,8);z = normpdf(x,0,8/6);plot(x,y,'-.',x,z,'-','linewidth',5)legend('T 分布','正态分布')图2.12 正态分布和t 分布x1 = 3.5:0.01:6;y1= tpdf(x1,8);z1= normpdf(x1,0,8/6);plot(x1,y1,'-.',x1,z1,'-','linewidth',5)legend('T分布','正态分布')图2.13 正态分布和t分布的尾部kurtosis(b)ans =3.00483762647840moment(b,4)/std(b,1)^4ans =3.00483762647840kurtosis(b,0)ans =3.03557145622493ku=kurtosis(b,0)ku =3.035571456224932*(1-normcdf((ku-3)*sqrt(200/24)))ans =0.91821222565534。
