壳体稳定性分析报告
藕节形耐压壳体强度与稳定性有限元分析

考依据。
关键词 : 水下航行器 ; 耐压壳体 ; 强度 ; 稳定性
压力容器壳体的稳定性分析

• 弹塑性失稳 •当回转壳体厚度增大时,壳体中的应力超
•(非弹性失稳)
过材料屈服点才发生失稳,这种失稳称为 弹塑性失稳或非弹性失稳。
PPT文档演模板
压力容器壳体的稳定性分析
影响壳体稳定性的因素
• ----失稳破坏的型式和临界载荷取决于如下因素: 1)壳体的结构型式与结构参数
•■试验表明,圆环失稳破坏时的波纹数n=2。
•圆环的临界失稳压力为:pcr=3EJ/R3
•相交点变形为0
•n=2时:cos2×450=0,sin2×450=1 →C1=0,C2≠0;
•
每经过半个圆环,挠度周期性变化一次。
PPT文档演模板
•450 •cos2 ¢
•900
•180
0
•270
0
•3600
•¢
PPT文档演模板
压力容器壳体的稳定性分析
•2.5.2.1受均布周向外压的长圆筒的临界压 力 (1)圆环失稳的临界压力
1)外压→变形:曲率 1/R→1/R1 内力:弯矩(无剪力) M=( 1/R- 1/R1 )EJ
•R
•R1
•切入点:圆 环
•2)几何分析→圆环绕度曲线微分方程
PPT文档演模板
压力容器壳体的稳定性分析
•
状态附近振荡。
PPT文档演模板
压力容器壳体的稳定性分析
存在失稳破坏的常见结构:
• 压杆失稳(一维问题) :压力达到临界载荷时,稍受 扰动,压杆会因屈曲而破坏。 达到临界载荷时杆中的最大应力一般小于材料的屈服 极限。屈曲前为弹性,屈曲后的某个时刻,因弯矩过 大而屈服破坏。
• 外压容器失稳(二维或三维问题):真空容器、夹套 容器、水下结构、减压塔等,同样存在一个弹性临界 载荷,当外载达到这一载荷并存在扰动时,也会发生 屈曲破坏。
稳定性试验报告范文

摘要:xxx是,研究其稳定性是在考察其在温度、湿度、光线的影响下随时间变化的规律,为其生产、包装、贮存、运输条件和有效期的确定提供科学依据。
本试验采用高温、高湿、光照等试验方法,通过测定其含量,得出其稳定性较好,产品有效期以上,暂定其有效期为年。
关键词:稳定性试验、xxx、正文1 前言1.1 xxx简介1.2 xxx生产工艺(如工艺保密,可改为质量标准)1.3 取样信息:1.4 稳定性试验指导:化学药物稳定性研究技术指导原则2005年版2考察项目及检测方法2.1性状2.1.1 外观2.1.2 熔点2.13 水分等等2.2 含量测定检测方法:样品制备:实验条件:2.3 有关物质3 试验方法3.1高温试验试验设备取本品,在60℃条件下放置10天,于第5天、第10天取样,检测相关指标。
3.2高湿试验试验设备取本品,于25℃、RH90%±5%条件下放置10天,在第0天、第5天和第10天取样检测。
3.3光照试验取本品,在光强度为4500lx的光源下,距光源30cm,放置10天,在0天、5天和10天取样测定。
3.4加速试验试验条件包材类型、来源及相关证明文件取采用包装的三批次样品,试验条件为40℃±2℃、RH75%±5%,试验时间从开始,为6个月,分别于0、1、2、3、6个月取样检测。
3.5长期试验试验条件包材类型、来源及相关证明文件取采用包装的三批次样品,试验条件为25℃±2℃、RH60%±10%,试验时间从开始,取样时间点为第一年每3个月末一次,第二年每6个月末一次,以后每年末一次。
(如为阶段性试验报告,可如下描述:试验时间从开始,已完成月试验,接下来将持续到年月,此报告为阶段性试验报告。
)4 试验结果4.1高温试验4.2高湿试验4.3光照试验4.4加速试验4.5长期试验5 结论5.1小结5.1.1高温试验5.1.2高湿试验5.1.3光照试验5.1.4加速试验5.1.5长期试验5.2讨论(讨论内容包括:由前三个试验结果,初步确定包装材料和容器,结合加速试验和长期试验的稳定性研究的结果,进一步验证采用的包装材料和容器的合理性。
有机玻璃耐压壳的应力与稳定性分析

有机玻璃耐压壳的应力与稳定性分析摘要:全通透潜水器在深海下潜时要承受高静水压力、冲击、交变应力和振动等多种苛刻环境载荷,上述载荷因素都可能对其结构稳定性和安全性产生影响。
然而,全通透潜水器的耐压壳使用的是有机玻璃,材料具有黏弹性特性,结构的力学行为、性能随着时间而变化,分析这种特性对结构设计是非常重要的。
关键词:有机玻璃;耐压壳;稳定性分析深海全通透潜水器的耐压壳是使用材料为有机玻璃,其满足了科学家、探险爱好者以及游客可以近距离观察海洋生物、美丽的海底景色,海洋深处的地形地貌勘察、样本获取、拍摄及生物和矿产资源的勘测都扮演着重要角色。
有机玻璃耐压壳在材料性能以及制造、加工、工艺不断地发展进步,才能满足全通透潜水器下潜到海洋深处。
但是关于有机玻璃壳体的黏弹性特性、稳定性计算等方面的研究进展,较为缓慢,这使得上述问题得到各个国家的关注,对其研究是必要且具有应用价值。
1有机玻璃的概念有机玻璃(Polymethylmethacrylate)是一种通俗的名称,缩写为PMMA。
此高分子透明材料的化学名称叫聚甲基丙烯酸甲酯,是由甲基丙烯酸甲酯聚合而成的高分子化合物。
是一种开发较早的重要热塑性塑料。
有机玻璃分为无色透明、有色透明、珠光、压花有机玻璃四种。
有机玻璃俗称亚克力、中宣压克力、亚格力,有机玻璃具有较好的透明性、化学稳定性,力学性能和耐候性,易染色,易加工,外观优美等优点。
有机玻璃又叫明胶玻璃、亚克力等。
2有机玻璃耐压壳的结构形式及其构造特点有机玻璃耐压壳的结构形状及材料一般是根据深海潜水器的下潜深度与其承受的有效载荷来确定的,同时还要考虑很多方面包括:比刚度、比强度、腐蚀性能、优化性能以及加工难易成本。
但是有机玻璃的耐压壳与金属材料的耐压壳又有很大区别,在交接过渡处不能进行焊接,必须通过金属环肋与其进行连接,嵌入其中,与金属耐压壳相比重量大大的减少了,也要满足下潜很深的深度。
2.1柱形组合最常用的一般是球形和圆柱形。
压力容器壳体的稳定性分析

压力容器壳体的稳定性分析一、引言压力容器壳体是蒸发器、换热器、反应器等化工设备中重要的组成部分,它承受来自内部介质的压力,同时还需要经受外部环境的力作用。
为了保证压力容器壳体能够在工作过程中保持稳定并安全地承受压力,必须对其进行稳定性分析。
本文将介绍压力容器壳体的稳定性分析方法和相关理论知识。
二、压力容器壳体的稳定性分析1. 应力状态在工作过程中,压力容器壳体承受来自内部介质的压力载荷,同时还需要经受外部环境荷载的作用,如风荷载等。
这些外部荷载会导致壳体上出现正应力和剪应力。
在确定压力容器壳体稳定性时需要先了解其压力状态。
在壳体内部,应力状态由压力载荷引起,应力分为径向应力、周向应力和轴向应力,其大小与压力载荷大小有关。
在壳体上,轻荷载下剪应力很小,只有正应力比较大,而在重载荷下,正应力和剪应力都较大。
2. 稳定性分析方法在确定壳体的稳定性时需要考虑其受力情况和力的分布情况,分析其受力状态并选择合适的分析方法。
稳定性分析方法有很多种,其中常用的有力学方法、能量方法、虚功原理和位移法等。
其中,力学方法主要是根据材料力学性质,通过应力计算得出壳体受到的外力大小,在此基础上确定其稳定性;能量方法是将壳体受到的外力转化成内能来研究稳定性;虚功原理是通过计算虚功来判断壳体的稳定性;位移法是通过计算变形、位移来判断壳体的稳定性。
在实际应用中,选取合适的分析方法需要考虑具体情况和要求。
3. 稳定性分析步骤(1)确定受力情况在进行压力容器壳体稳定性分析前,首先需要确定其所受外界荷载的大小和方向,同时还要考虑其内部介质压力的影响。
根据受力情况可以计算出壳体的应力状态。
(2)确定分析方法根据具体情况和要求选取合适的稳定性分析方法,应注意考虑分析的范围、精度和可靠性等因素。
必要时还需进行有限元分析。
(3)建立数学模型在使用分析方法进行计算前,需要建立数学模型来描述压力容器壳体的几何结构、物理性质以及受力情况等。
通常情况下,可以采取二维或三维模型。
大跨度网壳结构的稳定性分析

大跨度网壳结构的稳定性分析xxxxxx摘要:空间结构是一种倍受瞩目的结构形式,其中网壳结构是近半个世纪以来发展最快、应用最广的空间结构之一。
随着大跨度单层网壳结构的不断涌现,其结构重要性不言而喻,结构的稳定性问题尤为突出。
本文主要介绍了网壳结构的稳定性问题并以某大跨度球类馆为工程实例,采用非线性有限元法针对承载力计算时的11种工况进行整体稳定计算,考虑了材料和几何非线性,对实际工程进行了第一类和第二类稳定分析,结果表明:该网壳结构的第一类稳定符合相关规范的要求;其第二类稳定性较差。
因此,第二类稳定分析应该受到重视。
关键词:网壳结构;稳定性;非线性有限元;大跨度;稳定系数STABILITY ANALYSIS OF LONG-SPAN LATTICED SHELLSxxxDepartment of Civil Engineering ,xxxAbstract: Space structure is a very attractive structure system, and the latticed shell is one of the furthest development and the most widely applied space structure in the recent half century. The stability analysis is the key problem in the design of latticed shells, especially in single-layer latticed shells. This paper introduces the stability of latticed shells and a long-span ball gymnasium is adopted as a practical work, and it is analyzed by nonlinear finite element method under the first and the second kinds of stability problems. The holistic calculation aimed at 11 conditions in bearing capacity, material and geometric nonlinearity are considered. The results show that the first kind of stability of this latticed shells accords with the requirements of correlative specifications; the second kind of stability is poorer. Therefore, the analysis of the second kind of stability should be paid attention..Keywords: latticed shells; stability; nonlinear finite element; long-span; stability factor1 前言自20世纪以来,大跨度、大空间的建筑在世界各地得到了迅猛发展。
壳体结构的稳定性分析与优化设计

壳体结构的稳定性分析与优化设计壳体结构的稳定性分析与优化设计是结构工程领域的重要研究内容之一。
壳体结构是指在一定的边界条件下,由曲面组成的薄壁结构,如圆顶、穹顶、圆柱、球壳等。
壳体结构具有较高的自重和外荷载承载能力,同时还具有较好的自重分布和刚度特性,因此在工程实践中得到了广泛应用。
壳体结构的稳定性分析是指对壳体结构在外部荷载作用下的变形、应力、变位等进行研究,以确定结构是否满足稳定性要求。
稳定性是指结构在外部荷载作用下不发生失稳或局部失稳的能力。
壳体结构的稳定性受到多种因素的影响,如几何形状、材料特性、边界条件等。
稳定性分析的目标是找出结构的失稳模式和临界荷载,以保证结构的安全可靠性。
壳体结构的稳定性分析可以采用理论计算和数值模拟两种方法。
理论计算方法主要是基于壳体结构的几何形状和材料特性,通过应力分析、变形分析、能量方法等来确定结构的稳定性。
数值模拟方法主要是基于有限元分析,通过将结构离散化为有限个单元,利用计算机进行数值计算,得到结构的应力、变形等信息,进而进行稳定性分析。
在壳体结构的优化设计中,稳定性是一个重要的考虑因素。
通过优化设计可以改善壳体结构的稳定性,提高结构的承载能力和安全性。
优化设计的目标是在满足结构稳定性要求的前提下,使结构的重量最小或成本最低。
常用的优化设计方法包括拓扑优化、形状优化、尺寸优化等。
拓扑优化是指在给定的设计空间内,通过改变结构的拓扑形状,使结构的重量最小。
拓扑优化的关键是确定结构的材料分布,即在哪些位置放置材料,哪些位置去除材料。
形状优化是指在给定的拓扑形状下,通过改变结构的形状参数,使结构的重量最小。
尺寸优化是指在给定的拓扑形状和形状参数下,通过改变结构的尺寸参数,使结构的重量最小。
壳体结构的稳定性分析与优化设计是结构工程领域的研究热点,对于提高结构的安全性和经济性具有重要意义。
随着计算机技术的发展,数值模拟方法在壳体结构的稳定性分析与优化设计中得到了广泛应用,为工程实践提供了有效的工具。
静水压力下纤维缠绕圆柱壳体的稳定性分析

潜航器是开发海洋资源与巩固海防的重要装 备,耐压壳体的结构稳定性是潜航器设备正常工作 和人员安全的重要保证,同时也是深海潜航器研发 的关键技术之一[1⁃2] 。 随着人类向深海探索步伐的 加快,对潜航器的搭载能力有了更高要求,因此,潜 航器应具备较大的储备浮力。 纤维复合材料是一种 新型的结构耐压材料,具有比强度大、比刚度高、可 设计等特点,能够减轻结构重量、提供正浮力、增加 负载能力;耐腐蚀、吸波和无磁性等特点对潜航器的 寿命周期和反侦察能力具有重要意义[3] 。
+
1 R
∂2 Mβ ∂β2
+
R
∂2 Mα ∂α2
+
Nβ
-
Fn
= 0 (3)
式中, Nα,Nβ,Nαβ 为圆柱壳体的薄膜内力,Mα,Mβ, Mαβ 为 弯 曲 内 力 矩。 Fα,Fβ,Fn 是 附 加 载 荷, 可 表 示为
Fα
=-
pR
∂ω ∂α
+
PR
∂2 u ∂α2
+
T R
∂2 u ∂β2
(4)
Fβ
2018 年 10 月 第 36 卷第 5 期
西北工业大学学报 Journal of Northwestern Polytechnical University
Oct. 2018 Vol.36 No.5
静水压力下纤维缠绕圆柱壳体的稳定性分析
沈克纯, 潘光, 姜军, 黄桥高, 施瑶
æ1.西北工业大学 航海学院, 陕西 西安 710072;
=
-
p
æ
ç
è
∂ω ∂β
压力容器应力分析_壳体的稳定性分析
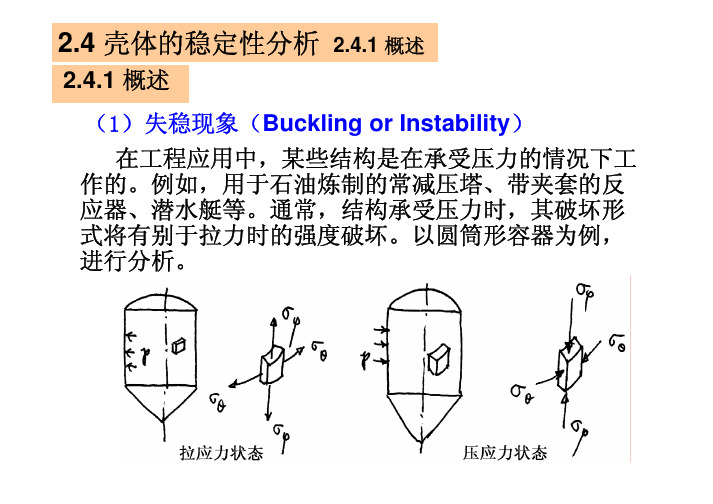
2.4 壳体的稳定性分析2.4.1 概述2.4.1 概述(1)失稳现象(Buckling or Instability) 在工程应用中,某些结构是在承受压力的情况下工 作的。
例如,用于石油炼制的常减压塔、带夹套的反 应器、潜水艇等。
通常,结构承受压力时,其破坏形 式将有别于拉力时的强度破坏。
以圆筒形容器为例, 进行分析。
2.4 壳体的稳定性分析2.4.1 概述圆筒在外压作用下,可能会有二种可能的失效形式: ① 因强度不足,导致压缩屈服失效;② 因刚度不 足,导致失稳破坏。
圆筒失稳破坏:承受外压的圆筒,当外压载荷增大到 某一值时,圆筒会突然失去原有的形状,被压瘪或出 现波纹,圆筒失去承载能力。
这种现象成为外压圆筒 的屈曲(Buckling)或失稳(Instability)。
实际上,当结构出现失稳后,最终导致结构破坏 的原因,是由于结构失稳变形后产生的附加弯矩。
下 面以杆件的失稳破坏过程进行说明。
2.4 壳体的稳定性分析2.4.1 概述2.4 壳体的稳定性分析(2)外压圆筒受载形式2.4.1 概述圆筒承受外载的形式,有以下三种:理论分析表明,在相同外载时,轴向外压对圆筒 壳体失稳的影响,要小于横向外压的影响。
本节主要 讨论横向受载失稳。
2.4 壳体的稳定性分析(3)外压圆筒失稳类型2.4.1 概述外压圆筒失稳类型有以下二种 ① 弹性失稳:圆筒为薄壁时,发生失稳时筒壁中的压 应力小于材料的屈服极限,即此时筒体的受力变形为 弹性阶段。
② 非弹性失稳:对于壁较厚的筒体,有可能在筒壁中 的应力应变进入塑性阶段后出现失稳,即此时筒体中 的压应力超过了材料的屈服点。
在本节的分析中,主要讨论弹性失稳计算。
而对 于非弹性失稳,则借助弹性失稳的结果,采用简化计 算方法。
2.4 壳体的稳定性分析(4)外压圆筒失稳形貌2.4.1 概述圆筒承受横向外载后的失稳形貌2.4 壳体的稳定性分析2.4.1 概述水下圆筒管节承受横向外载后的失稳形状2.4 壳体的稳定性分析2.4.1 概述水下圆锥形过渡管节承受横向外载后的失稳形状2.4 壳体的稳定性分析2.4.1 概述2.4 壳体的稳定性分析2.4.1 概述轴向外压圆筒的失稳形状(试验照片和计算结果)周向外压圆筒失稳后,其横截面形状如下表所示。
稳定性报告模板

稳定性报告模板1. 引言稳定性报告是对系统、软件或产品在一段时间内的稳定性进行评估和分析的报告。
本报告旨在提供一个稳定性报告的模板,以便对系统或软件的稳定性进行全面的评估和分析。
在本报告中,我们将介绍稳定性报告的结构、内容和关键要素。
2. 报告结构稳定性报告通常包含以下几个部分:2.1 背景在这一部分,我们将对所评估的系统或软件的背景进行简要的介绍。
包括系统或软件的名称、版本、用途和关键特性等。
此外,还应该明确报告的时间范围,以便读者能够了解评估的时段。
2.2 目标在这一部分,我们将明确本次稳定性评估的目标和重点。
这有助于读者了解评估的范围以及我们将着重关注的方面。
为了更好地评估系统或软件的稳定性,我们可以设定一些关键性能指标(KPIs)。
2.3 方法和数据收集在这一部分,我们将介绍评估的方法和数据收集过程。
我们可以使用各种工具和技术来监测系统或软件的稳定性,并收集相关数据。
这些数据可以包括系统的日志文件、错误报告、性能指标数据等。
2.4 结果分析在这一部分,我们将对评估的结果进行分析和总结。
我们可以根据事先设定的KPIs来评估系统或软件的稳定性,并比较不同时间段或不同版本之间的差异。
通过分析结果,我们可以发现稳定性问题和潜在的风险,并提出相应的改进建议。
2.5 结论在这一部分,我们将总结评估的结果,并给出对系统或软件稳定性的最终评价。
同时,我们还可以提供对未来改进的建议和措施。
3. 关键要素在编写稳定性报告时,以下几个要素是非常重要的:3.1 系统或软件日志系统或软件日志是评估稳定性的重要数据来源。
通过分析日志文件,我们可以了解系统或软件的运行情况,发现异常或错误,并进行相应的处理和修复。
3.2 错误报告错误报告是另一个重要的数据来源。
通过收集和分析错误报告,我们可以发现系统或软件的常见问题和故障,并提出解决方案。
3.3 性能指标性能指标是评估系统或软件稳定性的关键指标之一。
通过监测和分析性能指标数据,我们可以评估系统或软件的性能水平,并及时发现性能问题。
结构失稳和整体稳定性分析

结构失稳和整体稳定性分析失稳破坏是一种突然破坏,人们没有办法发觉及采取补救措施,所以其导致的结果往往比较严重。
正因为此,在实际工程中不允许结构发生失稳破坏。
导致结构失稳破坏的原因是薄膜应力,也就是轴向力或面内力。
所以在壳体结构、细长柱等结构体系中具有发生失稳破坏的因素和可能性。
这也就是为什么在网壳结构的设计过程中稳定性分析如此被重视的原因。
下面根据本人多年来的研究及工程计算经验,谈谈个人对整体稳定性分析的一点看法,也算做一个小结。
1稳定性分析的层次在对某个结构进行稳定性分析,实际上应该包括两个层次。
(一)是单根构件的稳定性分析。
比如一根柱子、网壳结构的一根杆件、一个格构柱(桅杆)等。
单根构件的稳定通常可以根据规范提供的公式进行设计。
不过对于由多根构件组成的格构柱等子结构,还是需要做试验及有限元分析。
(二)是整个结构的稳定分析。
比如整个网壳结构、混凝土壳结构等结构整体的稳定性分析。
整体稳定性分析目前只能根据有限元计算来实现。
2整体稳定性分析的内容通常,稳定性分析包括两个部分:Buckling分析和非线性“荷载-位移”全过程跟踪分析。
(1)Buckling分析Buckling分析是一种理论解,是从纯理论的角度衡量一个理想结构的稳定承载力及对应的失稳模态。
目前几乎所有的有限元软件都可以实现这个功能。
Buckling分析不需要复杂的计算过程,所以比较省时省力,可以在理论上对结构的稳定承载力进行初期的预测。
但是由于Buckling分析得到的是非保守结果,偏于不安全,所以一般不能直接应用于实际工程。
但是Buckling又是整体稳定性分析中不可缺少的一步,因为一方面Buckling 可以初步预测结构的稳定承载力,为后期非线性稳定分析施加的荷载提供依据;另一方面Buckling分析可以得到结构的屈曲模态,为后期非线性稳定分析提供结构初始几何缺陷分布。
另外本人认为通过Buckling分析还可以进一步校核单根构件截面设计的合理性。
壳体失稳应力分析

压力容器应力分析
CHAPTER Ⅱ STRESS ANALYSIS OF PRESSURE VESSELS
第五节 壳体的稳定性分析
1
主要内容
2.5.1 概述 2.5.2 外压薄壁圆柱壳弹性失稳分析 2.5.3 其他回转薄壳的临界压力
2
2.5.1 概述
一、失稳现象
1、外压容器举例 (1)真空操作容器、减压精馏塔的外壳
局部区域中的折皱、鼓胀、凹陷
内压下,有消除不圆度的趋势 影响 外压下,在缺陷处产生附加的弯曲应力
圆筒中的压缩应力增加
临界压力降低
实际失稳压力与理论计算结果不很好吻和的主要原因之一
对圆筒的初始不圆度严格限制
24
2.5.3 其他回转薄壳的的临界压力
半球壳 椭球壳 碟形壳 锥壳
25
半球壳
经典公式:
pcr
t D
3
(2-90)
代替EJ
长圆筒的临界压力计算公式:
2E p cr 1 2 0.3
长圆筒临界压力:
t pcr 2.2 E D o
3
(2-92)
长圆筒临界应力:
t pcr Do cr 1.1E D 2t o
K1见第四 章 P141, 表4 - 5) (
27
锥壳的临界压力 等效圆柱壳(α<60º )
等效长度Lx
等效长度半径R=锥壳两端第二曲率半径的平均值
28
锥壳
2.59 E te pcr D Le DL L
注意:
2 .5
(2-106)
Le——锥壳的当量长度; DL——锥壳大端外直径 DS——锥壳小端外直径 或锥壳上两刚性元件所 在处的大小直径
部分变速器壳体模态试验分析与验证

部分变速器壳体模态试验分析与验证摘要:本文通过对部分变速器壳体的模态试验进行分析与验证,探讨其在车辆工程领域中的应用。
首先介绍了部分变速器壳体的基本结构和工作原理,然后对其进行了有限元建模,并使用ANSYS有限元软件对其进行了模态分析。
根据模态分析的结果,我们对部分变速器壳体进行了优化,以提高其结构的稳定性。
最后,我们通过实验验证了本文的分析与改进,证明了我们的改进方案具有显著的效果。
关键词:部分变速器壳体;模态试验;有限元建模;ANSYS软件;结构优化;试验验证。
一、引言自动变速器是汽车的重要组成部分之一,而变速器壳体则是自动变速器的主要结构部件之一。
部分变速器壳体在汽车行驶中处于重要的负荷承载位置,其结构的稳定性影响着汽车的安全性能和使用寿命。
因此,对部分变速器壳体的研究具有重要的意义。
本文旨在通过对部分变速器壳体的模态试验进行分析与验证,探讨其在车辆工程领域中的应用。
文章首先介绍了部分变速器壳体的基本结构和工作原理,然后对其进行了有限元建模,并使用ANSYS有限元软件对其进行了模态分析。
根据模态分析的结果,我们对部分变速器壳体进行了优化,以提高其结构的稳定性。
最后,我们通过实验验证了本文的分析与改进,证明了我们的改进方案具有显著的效果。
二、部分变速器壳体的基本结构和工作原理部分变速器壳体是自动变速器中的一个组成部分,其作用是承担变速器内部传递动力的职责。
部分变速器壳体通常由铸件或冷镦加工而成,其底部一般采用多边形的形式,以适应变速器的各种形式和尺寸。
下图是部分变速器壳体的示意图。
部分变速器壳体中包含了多个部件,包括油泵、制动器和离合器等组件。
这些组件的工作往往会对部分变速器壳体的结构造成一定的冲击负荷,因此,部分变速器壳体需要具有足够的强度和刚度来承担这些负荷。
三、有限元建模和模态分析为了对部分变速器壳体的结构进行分析,我们采用了有限元建模的方法。
根据部分变速器壳体的外形和内部结构,我们进行了三维模型的建模,并在模型中添加了油泵、制动器和离合器等部件。
壳体的稳定性分析

5、受外压形式:
p
p
p a
轴向
b
周向
c
周 轴 向
本节讨论:受周向均匀外压薄壁回转壳体的弹性失稳问题
6
过程设备设计
二、临界压力
1、临界压力
壳体失稳时所承受的相应压力,称为临界压力,用pcr表示。
2、失稳现象
外载荷达到某一临界值,发生径向挠曲,并迅速增加,
沿周向出现压扁或波纹。 见表2-5
7
过程设备设计
Et
代替长、短圆筒
pcr
E
注意:
弹性失稳→
非弹性失稳→
各类钢E接近 ∴采用高强钢对提高圆筒的稳定性不显著 , 与材料强度有关, 变化大 ∴采用高强钢经济 ,使 。 压> p ↑p cr
, 与材料强度无关, 与E有关,但变化不大, 压 < p pcr
Et
pcr
24
过程设备设计
3 其他回转薄壳的的临界压力
内压下,有消除不圆度的趋势 影响: 外压下,在缺陷处产生附加的弯曲应力
圆筒中的压缩应力增加
临界压力降低
实际失稳压力与理论计算结果不很好吻和的主要原因之一
对圆筒的初始不圆度严格限制
23
过程设备设计
六、非弹性失稳的工程计算 —应变”曲线上的切线 时的“压缩 压> p 式中的弹性模量
近似利用材料 模量
各类钢E接近 ∴采用高强钢对提高圆筒的稳定性不显著 可提高承载能力,
pcr f (E, Do , t )
s
17
过程设备设计
二、受均布周向外压的短圆筒的临界压力
2.59 Et 2 pcr LDO DO t
(2-97)
拉姆公式,仅适合弹性失稳
压力容器应力分析壳体的稳定性分析

PPT文档演模板
压力容器应力分析壳体的稳定性分析
•该理论的局限
•(1)壳体失稳的本质是几何非线性的问题 •(2)经历成型、焊接、焊后热处理的实际圆筒,存在各种 • 初始缺陷,如几何形状偏差、材料性能不均匀等 •(3)受载不可能完全对称
•小挠度线性分析会与实验结果不吻合。
•工程中,在采用小挠度理论分析基础上,引进稳定性安全系数 m , •限定外压壳体安全运行的载荷。
讨论题
1、是否只有在外压作用下,压力容器才会失稳?试 举例说明。
2、工程上采取哪些措施,可以提高圆柱形容器的抗 失稳能力?
PPT文档演模板
压力容器应力分析壳体的稳定性分析
演讲完毕,谢谢听讲!
再见,see you again
PPT文档演模板
2024/2/8
压力容器应力分析壳体的稳定性分析
压力容器应力分析-壳体 的稳定性分析
PPT文档演模板
2024/2/8
压力容器应力分析壳体的稳定性分析
•主要内容
•2.4.1 概述 •2.4.2 外压薄壁圆柱壳弹性失稳分析 •2.4.3 其他回转薄壳的临界压力
PPT文档演模板
压力容器应力分析壳体的稳定性分析
•一、失稳现象
•2.4.1 概述
•1、外压容器举 例
•椭球壳: •同碟形壳计算,RO=K1DO
•K1见第四 章
PPT文档演模板
压力容器应力分析壳体的稳定性分析
•锥壳
•(2-106)
•注意:•Le——锥壳的当量长度;见表2-6
•DL——锥壳大端外直径 •或锥壳上两刚性元件所
•DS——锥壳小端外直 径•Te——锥壳当量厚度
•在处的大小直径
•适用于:
•若
压力容器壳体的稳定性分析

其它形式回转壳的临界压力
pcr
2E t 2
312 R
0.3
半球壳的临界压力
pc
r
1.21E
t R
2
(2)蝶形壳的临界压力
01
临界应力计算同球壳, 但R用碟形壳中央部
2
t 分的半径代替。 p 1.21E R cr
02
■ n=2.0→ →
pcr
3EJ R3
,此时有实际意义的最小压力解;
■试验表明,圆环失稳破坏时的波纹数n=2。
圆环的临界失稳压力为:pcr=3EJ/R3
相交点变形为0
n=2时:cos2×450=0,sin2×450=1 →C1=0,C2≠0;
每经过半个圆环,挠度周期性变化一次。
450
cos2¢
900
短圆筒: L/D0较小,D0/t较大,长度方向的中间部分 离边界较近,两端部的约束作用不可忽略, 壳体有一定刚性,失效形式为稳定性破坏, 失稳时呈两个以上皱折波数。
刚性圆筒:L/D0很小,壁厚t较大,D0/t较小,壳体刚 性很大,失效形式为强度破坏。
■圆筒、球壳和锥壳的临界载荷与失效形态各不相同。
60o
按平板计算,平板直径取锥壳最大直径。
其它型式的失稳
塔受风载时,迎风侧产生拉应力,而背风侧产 生压缩应力,当压缩应力达到临界值时,塔就 丧失稳定性。
短圆筒的特点临界压力计算式来自○ 端部约束作用的1. Mises(1914)
影响不能忽略;
受均布周向外压的短
公式(小挠度
○ 失稳时的波数大 于2;
圆筒的临界压力
解)
○ 该式对长短圆
壳体稳定性分析报告

§ 2-4壳体的稳定性分析一、概述(1 )失稳现象(2)临界压力概念临界压力一一承受外压的壳体失稳时的相应压力,以P er表示。
二、外压薄壁圆柱壳弹性失稳分析1、受均布周向外压的长圆筒的临界压力a.圆环的挠度曲线微分方程1 丄_ MR, 一R 一一EJEJ――圆环的抗弯刚度1 1 _ w d wR, R 一R2ds2圆环挠度曲线微分方程:d 2 w w Mds 2 R 2一一EJb.圆环的力矩平衡方程F°二p R - w°M =M0pAO AD -卫AB?2圆环的力矩平衡方程式:M = M 0- pR w0-wc.圆环的临界压力式中:n 2「 J圆环失稳时的最小临界压力:3EJ _f t 彳Pcr =巨=2E 6t —圆环的壁厚;R —圆环中性面半径,D=2R ;E —圆环材料的弹性模量。
d. 长圆筒的临界压力计算公式—泊松比;t —不包括壁厚附加量的器壁厚度E —圆筒材料在设计温度下的弹性模量对于钢质圆筒(卩=0.3)称为临界应力:2、受均布周向外压的短圆筒的临界压力Mises 短圆筒临界压力计算式:d 2w + PR 3 2 3-R M o pR W o 通解:ET 丿 ET w =G sinn 「 c 2cosn 「 2 3R M o pR w 0EJ pR 2将n=2代入上式,并令J 1 t 3122EP er 2 丨 1」2 DM PaD —圆筒的中面直径,可近似地取圆筒外径,D : D o P cr = 2.2E D o=1.1E2t D o2 n ,亠=0.3 ,可得与最小临界压力相应波数: 7.06 短圆筒最小临界压力计算式:3、临界长度 L>L cr --------- 长圆筒L<L cr ——短圆筒4、周向外压及轴向载荷组合作用下的失稳a.受均布轴向压缩载荷圆筒的临界应力Timoshenko 临界应力计算式:cr =对于钢材(」=0.3):= = 0.605》临界应力的经验公式:P er 二 Et R(n 2 —1)1 + nL 八3 121」R (n 2_1 片2n 一i P cr 22.59 EtLD °P cr D 0 1.30E适合条件: 2t LD 。
双层柱面网壳整体稳定性分析

[ ] 陈骥. 3 钢结构稳定理论 与设计 [ . M]北京 : 出版社 ,0 3 科学 20 .
C HEN J.Sa it h oya dds no te srcue[ .B in : ineP es 0 3 i tblyter n ei fsel tutrsM] e ig S e c rs,2 0 . i g j c
第 3 卷第 3期 3
V0 I 3 No 3 2 1 I3 . 0 2
青 岛 理 工 大 学 学 报
J u a fQig a c n lgc l ie s y o r l n d o Te h oo i v ri n o a Un t
双 层 柱 面 网 壳 整 体 稳 定 性 分 析
—
0
01 .
02 .
03 .
04 . 0. 0. 0. 5 6 7
08 .
位 移/ m
图5 水平荷 载作 用下 临界 荷载 对 比
_ 卜
—
1 / 0 —. -1 5 1 ;— 0 1 0; _ 2. / 00
1 / 00 —o. 1 . / 0 51 ; 75 1 0
sgn i .
Ke r s o b e ly rr tc ltd s el rt a o d p n r t y wo d :d u l-a e e iu a e h l;c i c lla ;s a ai i o;n n i e r n t li e— o l a ;i i a mp r n i
关键词: 双层柱面网 临界荷裁; 壳; 矢跨比; 非线性; 初始缺陷
中图分类号 : TU3 3 2 文献 标 志 码 : A 文 章 编 号 :6 3 4 O (O 2 0一 o 3一 O 1 7— 62 2 1 ) 3 0 1 4
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§2-4壳体的稳定性分析
一、概述
(1)失稳现象
(2)临界压力概念
临界压力——承受外压的壳体失稳时的相应压力,以p cr 表示。
二、外压薄壁圆柱壳弹性失稳分析
1、受均布周向外压的长圆筒的临界压力
a. 圆环的挠度曲线微分方程
EJ
M R R -=-111 EJ ——圆环的抗弯刚度
2
22111ds w d R w R R +=- 圆环挠度曲线微分方程:
EJ
M R w ds w d -=+222 b. 圆环的力矩平衡方程
()00w R p F -=
202
AB p AD AO p M M -⋅+= 圆环的力矩平衡方程式:
()w w pR M M --=00
c. 圆环的临界压力
ET w pR M R ET pR w d w d 03023221+-=⎪⎪⎭⎫ ⎝
⎛++ϕ 通解:
2
030221cos sin pR EJ w pR M R n c n c w ++-++=ϕϕ 式中:EJ pR n 3
2
1+= 将n=2代入上式,并令12
13
t J ⋅= 圆环失稳时的最小临界压力:
3323⎪⎭
⎫ ⎝⎛==D t E R EJ p cr t —圆环的壁厚;
R —圆环中性面半径,D=2R ;
E —圆环材料的弹性模量。
d. 长圆筒的临界压力计算公式
3
212⎪⎭
⎫ ⎝⎛-=D t E p cr μ M P a μ—泊松比;
t —不包括壁厚附加量的器壁厚度
E —圆筒材料在设计温度下的弹性模量
D —圆筒的中面直径,可近似地取圆筒外径,0D D ≈
对于钢质圆筒(μ=0.3) 3
2.2⎪⎪⎭
⎫ ⎝⎛=D t E p cr 称为临界应力: 3001.12⎪⎪⎭
⎫ ⎝⎛==D t E t D p cr cr
σ 2、受均布周向外压的短圆筒的临界压力
Mises 短圆筒临界压力计算式:
()()()
⎥⎥⎥
⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+--+-⎪⎭⎫ ⎝⎛-+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+-=22232222112111211R nL n n R t E R nL n R Et p cr πμμπ 令0=dn
dp cr ,并取3.0,122=≈-μn n ,可得与最小临界压力相应波数:⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=D t D L n 24
06
.7
短圆筒最小临界压力计算式:
t
D LD Et p cr 002
59.2= 5.10
0030.12⎪⎪⎭⎫ ⎝⎛==D t D L E t D p cr cr σ 适合条件:cr σ<t
y σ
3、临界长度
L >L cr ——长圆筒
L<L cr ——短圆筒
300
03059.222⎪⎪⎭⎫ ⎝⎛⋅=⎪⎪⎭⎫ ⎝⎛⋅D t D t D L E D t E cr 得:t
D D L cr 0017.1= 4、周向外压及轴向载荷组合作用下的失稳
a.受均布轴向压缩载荷圆筒的临界应力
Timoshenko 临界应力计算式: ()R
t E cr 213μσ-=
对于钢材(μ=0.3): R
Et cr 605
.0=σ 临界应力的经验公式:
R Et c
cr =σ 工程上,500≤t R 25.0500==c t
R ,取 R Et cr 25
.0=σ b. 组合载荷作用下园筒的失稳
三、其它回转薄壳的临界压力
1、半球壳的临界压力
()2
2132⎪⎭⎫ ⎝⎛-=R t E p cr μ 对于钢材(3.0=μ)
2
21.1⎪⎭
⎫ ⎝⎛=R t E p cr
修正公式: 225.0⎪⎭
⎫ ⎝⎛=R t E p cr 我国规范采用的工程实际应用公式为: 200833.0][⎪⎭⎫ ⎝⎛==
e cr t R E m p p [p]—许用外压力
E —材料弹性模量
R 0—球壳外半径
t e —球壳有效厚度
m —安全系数为3。
2、碟形壳和椭球壳的临界压力
可用球壳临界压力计算式来计算碟形壳的临界压力,R 0用碟形壳中央区域部分外半径代替。
椭球壳与碟形壳相类似,取当量半径R 0=KD 0作计算,系数K 由表2-9查得。
(3)锥壳的临界压力
R t R L R t E p e e cr 22259.22⎪⎭⎫ ⎝⎛'⎪⎭⎫ ⎝⎛=
Mpa 59.25.2⎪⎪⎭⎫ ⎝⎛⎪⎭
⎫ ⎝⎛=L e L e cr D t D L E p
四、具有圆环加强圈的圆筒
3324
3D EJ R EJ L p s cr ==
122
cr
S D tL J ε=
s
s
e L A
t t += 得:cr S S S L A
t L D J ε⎪⎪
⎭
⎫
⎝⎛+=122
考虑适当的安全系数1.1,得:
cr S S S L A t L D J ε⎪⎪⎭⎫
⎝⎛+=9.102。
