十大数学公式
世界著名的十大公式
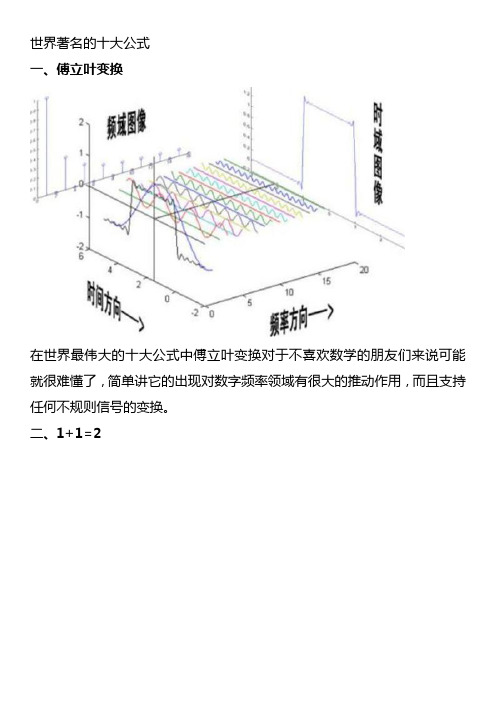
世界著名的十大公式一、傅立叶变换在世界最伟大的十大公式中傅立叶变换对于不喜欢数学的朋友们来说可能就很难懂了,简单讲它的出现对数字频率领域有很大的推动作用,而且支持任何不规则信号的变换。
二、1+1=21+1=2这个公式和上一个相比较应该就是无人不知了吧,从幼儿园开始它就伴随着我们,简单好理解,它的出现在整个数学领域可以说是引起轰动了的呢!三、毕达哥拉斯定理毕达哥拉斯定理也就是我们数学学习生涯中常见勾股定理,如今有四百多种图形被毕达哥拉斯定理给证明了,是非常伟大又典型的解决图形问题的公式。
四、麦克斯韦方程组人们评价说,如果没有麦克斯韦方程组就没有现代社会的文明,整个方程也是完美到无可挑剔,可以说宇宙间的任何电磁用这个方程组都能很好的被解释。
五、欧拉公式这个欧拉公式从形式上看非常的巧妙,没有任何多余的“杂质”,数学家们评论说凡是第一眼爱上这个公式的人必定会成为数学家,可见该公式的伟大之处。
六、质能方程在世界最伟大的十大公式中质能方程著名的物理学家爱因斯坦提出来的,该公式很好的揭示了质量和能量之间的关系,也正是质能方程的出现才有了当今的原子弹,氢弹等。
七、德布罗意方程组德布罗意方程组揭示出了任何物质都是有粒子性和波动性的,让波长和能量等之间有了一个很好的关系解释,提出者也在1929年获得了诺贝尔奖。
八、圆的周长公式圆的周长公式,这个伴随着整个数学学习生涯,如果用圆的周长公式来说计算太阳系包起来的周长,误差的直径不到百万分之一。
九、牛顿第二定律牛顿第二定律可以说是当下物理学的核心公式,它的出现可以是标志着真正物理学研究的开始,学习上好多的方程也都要依靠牛顿第二定律导出来。
十、薛定谔方程在世界最伟大的十大公式中薛定谔方程可谓是经典中的经典,它的出现很好的揭示了力学中位移和速度的关系,如今该公式在物理学的应用极为广泛,影响力也很大。
世界史上10个最伟大的公式,没有它们就没有现在的世界

世界史上10个最伟大的公式,没有它们就没有现在的世界1、麦克斯韦方程组:将电场和磁场有机地统一成完整的电磁场。
并创立了电磁场理论,而没有电磁学理论,就不会有现在的社会文明。
不管是对于我们对宇宙的理解,还是对于现代科技的发展,这一方程组都意义重大。
微观麦克斯韦方程组宏观麦克斯韦方程组2、薛定谔方程:薛定谔方程的解完备地描述物理系统里,微观尺寸粒子的量子行为;这包括分子系统、原子系统、亚原子系统;另外,薛定谔方程的解还可完备地描述宏观系统,可能乃至整个宇宙。
薛定谔方程3、圆周长公式:精确计算圆周长、圆面积、球体积等几何形状的关键值。
也可应用于工程师或物理学家要进行较精密的计算圆周长公式4、欧拉公式:欧拉公式也被称为世界上最完美的公式,在数学历史上有很多公式都是欧拉发现的,它们都叫做欧拉公式,它们分散在各个数学分支之中。
如:分式里的、复变函数论里的、三角形中的、拓扑学里的、初等数论里的欧拉公式等等。
欧拉公式5、牛顿第二定律:牛顿第二定律证明物体加速度的大小跟作用力成正比,跟物体的质量成反比,且与物体质量的倒数成正比;加速度的方向跟作用力的方向相同。
牛顿第二定律6、1+1=2:这个公式不需要名称,不需要解释,大家不要强行给它加戏码了。
1+1=27、勾股定理/毕达哥拉斯定理:勾股定理是几何学中的明珠,所以它充满魅力,千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者,有普通的老百姓,也有尊贵的政要权贵,甚至有国家总统。
也许是因为勾股定理既重要又简单,更容易吸引人,才使它成百次地反复被人炒作,反复被人论证。
勾股定理/毕达哥拉斯定理8、傅里叶变换:如果没有它,就没有今天的电子计算机,我们除了要感谢国家给我们上网以外,还得感谢它,另外虽然看上去是中文名,但他是法国人。
但不幸的是,傅里叶分析的公式看起来太复杂了,所以很多新生上来就懵圈并从此对它深恶痛绝。
傅里叶变换傅里叶变换9、德布罗意方程组:德布罗意认为电子不仅是一个粒子,也是一种波,它还有“波长”。
世界上十大著名公式

世界上十大著名公式
1. 欧拉公式:eπi + 1 = 0
2. 欧几里得定理:a² + b² = c²
3. 黎曼假设:没有一个数字可以同时被两个不同素数整除
4. 勒贝格定理:任何一个正整数都可以表示成若干个素数的乘积
5. 兰开斯特定理:每一个整数都可以写成四个整数的平方和
6. 马尔可夫定理:任何一个图都可以用四条边分割成四个面
7. 拉格朗日定理:任何一个多项式都可以用一系列的积分表示
8. 默尔定理:任何一个正整数都可以写成若干个素数的和
9. 哥德巴赫猜想:任何一个大于2的偶数都可以表示成两个质数的和
10. 布尔定理:任何一个自然数都可以表示成若干个素数的乘积。
高等数学十大定理公式

高等数学十大定理公式高等数学十大定理公式有有界性、最值定理、零点定理、费马定理、罗尔定理、拉格朗日中值定理、柯西中值定理、泰勒定理(泰勒公式)、积分中值定理(平均值定理)。
1、有界性|f(x)|≤K2、最值定理m≤f(x)≤M3、介值定理若m≤μ≤M,∃ξ∈[a,b],使f(ξ)=μ4、零点定理若f(a)⋅f(b)<0∃ξ∈(a,b) ,使f(ξ)=05、费马定理设f(x)在x0处:1,可导2,取极值,则f′(x0)=06、罗尔定理若f(x)在[a,b] 连续,在(a,b) 可导,且f(a)=f(b) ,则∃ξ∈(a,b) ,使得f′(ξ)=07、拉格朗日中值定理若f(x)在[a,b] 连续,在(a,b) 可导,则∃ξ∈(a,b) ,使得f(b)−f(a)=f′(ξ)(b−a)8、柯西中值定理若f(x)、g(x)在[a,b] 连续,在(a,b) 可导,且g′(x)≠0 ,则∃ξ∈(a,b) ,使得f(b)−f(a)g(b)−g(a)=f′(ξ)g′(ξ)9、泰勒定理(泰勒公式)n阶带皮亚诺余项:条件为在$x_0$处n阶可导$f(x)=f(x_0)f'(x_0)(x-x_0)+\dfrac{f''(x_0)}{2!}(x-x_0)^2+...+\dfra c{f^{(n)}(x_0)}{n!}(x-x_0)^n+o((x-x_0)^n)\ ,x\xrightarrow{} x_0$ n阶带拉格朗日余项:条件为n+1阶可导$f(x)=f(x_0)f'(x_0)(x-x_0)+\dfrac{f''(x_0)}{2!}(x-x_0)^2+...+\dfra c{f^{(n)}(x_0)}{n!}(x-x_0)^n+\dfrac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0 )^{n+1}\ ,x\xrightarrow{} x_0$10、积分中值定理(平均值定理)若f(x)在[a,b] 连续,则∃ξ∈(a,b),使得∫baf(x)dx=f(ξ)(b−a)。
十大著名数学公式

十大著名的数学公式
以下是十大著名的数学公式:
1 欧拉公式:e^(iπ) + 1 = 0。
这个公式将五个重要的数学常数联系在一起:自然对数的底e、虚数单位i、圆周率π、单位元素1 和零0。
2 皮亚诺公理:这是数学基础理论的公理系统,用于推导整数的性质和运算规则。
3 傅里叶变换:这个公式将一个函数在频域和时域之间进行转换,可以将一个信号分解成一系列不同频率的正弦和余弦分量。
4 黎曼猜想:由黎曼提出的一个关于素数分布的猜想,尚未被证明或者推翻。
5 二项式定理:(a + b)^n = C(n,0)a^nb^0 + C(n,1)*a^(n-1)*b^1 + ... + C(n,n)a^0b^n。
这个公式展示了如何展开一个二项式的幂。
6费马大定理:由费马提出的一个关于整数解存在性的问题,直到近几年才被安德鲁·怀尔斯证明。
7斯特林公式:这个公式给出了n 的阶乘的近似值,以及对数函数在正实数范围内的近似值。
8黑-斯科尔定理:这个公式用于计算曲线围成的面积,推广了基本的微积分概念。
9导数定义:f'(x) = lim(h->0) [f(x+h)-f(x)]/h。
这个公式给出了函数的导数定义,描述了函数在某一点的变化率。
10 矩阵乘法规则:矩阵乘法的公式,使得矩阵代数成为现代数学和应用中至关重要的工具。
这些公式在数学领域有着广泛的应用,对于数学研究和实际问题的解决起到了重要的作用。
十大数学公式

1. 欧拉恒等式这是一个非常著名的恒等式。
它给出了3个看似随机的量之间的联系:π、e和-1的平方根。
许多人认为这是数学中最漂亮的公式。
一个更一般的公式是e^(ix) =cosx+isinx (a^b表示a的b次方,下同)。
当x=π,cosx取值为-1,而isinx 取值为0。
由-1+1=0,我们得到了欧拉恒等式。
2. 欧拉乘积公式等式左边的符号是无穷求和,而右边的符号则是无穷乘积。
这个公式也是欧拉首先发现的。
它联系了出现在等式左边的自然数(如n=1,2,3,4,5等等)与出现在等式右边的素数(如p=2,3,5,7,11等等)。
而且我们可以选取s为任意大于1的数,并保证等式成立。
欧拉乘积公式的左边是黎曼ζ函数最常见的一种表示形式。
3. 高斯积分函数e^(-x²)本身在积分中是很难对付的。
可是当我们对它在整个实数轴上积分,也就是说从负无穷到正无穷时,我们却得到了一个十分干净的答案。
至于为什么曲线下面的面积是π的平方根,这可不是一眼就能看出来的。
由于这个公式代表了正态分布,它在统计中也十分重要。
4. 连续统的基数上面的公式说明了实数集的基数与自然数全体子集的基数相同。
这首先是被集合论的建立者康托尔证明的。
值得注意的是,这也说明了连续统是不可数,因为2^N > N。
一个相关的假设是连续统假设。
这个假设是说,在N和R之间不存在其它的基数。
有趣的是,这个假设有一个奇怪的性质:它既不能被证明也不能被证伪。
5. 阶乘函数的解析延拓阶乘函数通常被定义为n!=n(n-1)(n-2)……1。
但是这个定义只对n是正整数时有效,而上面积分方程则对分数和小数也有效,而且还可以用于负数、复数等等……同样的积分式中我们把n换成n-1就定义了伽马函数。
6. 勾股定理勾股定理恐怕是这个清单中最熟悉的公式了。
它给出了直角三角形三边的联系,其中a和b是直角边长,而c是斜边长。
这个公式还将三角形和正方形联系了起来。
7. 斐波那契数列的通项这里,注意到φ这个数字是黄金分割比例。
十个最伟大的公式

十个最伟大的公式1. 帕斯卡定理:组合数规律,表达式为C(n,m)=C(n-1,m)+C(n-1,m-1),其中C为组合数。
2. 欧拉公式:描述了立体图形中的面数、顶点数及边数之间的关系,即V-E+F=2。
3. 高斯定理:描述了向量场和曲面的关系,表达式为∬S rotF·dS=∮L F·dr,其中rot为旋度,∬S和∮L分别为曲面S和曲线L 上的积分。
4. 能量守恒定律:能量在一定条件下不会减少或增加,表达式为E=mc²,其中E为能量,m为质量,c为光速。
5. 万有引力定律:任意两个物体之间的万有引力与它们的质量成正比,与它们之间的距离的平方成反比,表达式为F=G·m1m2/r²,其中G为引力常数,m1、m2为物体的质量,r为它们之间的距离。
6. 热力学第一定律:能量不会被创造或毁灭,只会从一个物体传递到另一个物体,表达式为ΔU=Q-W,其中ΔU为内能变化,Q为吸收的热量,W为做功。
7. 热力学第二定律:热量不可能自发地从低温物体传递到高温物体,表达式为ΔS≥0,其中ΔS为熵变化。
8. 卢瑟福散射公式:描述了荷电粒子在靶核上碰撞后散射的角度分布,表达式为dσ/dΩ=(kZ/z)²cos²(θ/2),其中dσ/dΩ为散射截面,k为波数,Z为靶核的原子序数,z为入射粒子电荷数,θ为散射角度。
9. 波动方程:描述了波动传播的规律,表达式为∂²u/∂t²=c²∇²u,其中u为波函数,t为时间,c为波速,∇²为拉普拉斯算子。
10. 黎曼猜想:描述素数分布的规律,还未被证明或证伪,是数学领域中的一个重要难题。
初中数学十大公式

初中数学十大公式初中数学十大公式包括:1. 周长公式:长方形周长=(长+宽)×2,C=2(a+b);正方形周长=边长×4,C=4a。
2. 面积公式:长方形面积=长×宽,S=ab;正方形面积=边长×边长,S=a²;三角形面积=底×高÷2,S=ah/2;平行四边形面积=底×高,S=ah;梯形面积=(上底+下底)×高÷2,S=1/2(a+b)h;圆形面积=半径×半径×圆周率,S=πr²;扇形面积=半径×半径×圆周率×圆心角度数(n)÷360,S=nπr²/360。
3. 判别式:b²-4ac=0,注:方程有两个相等的实根;b²-4ac>0,注:方程有两个不等的实根;b²-4ac<0,注:方程没有实根,有共轭复数根。
4. 两角和公式:sin(A+B)=sinAcosB+cosAsinB。
5. 圆的有关公式:弧长L=nπR/180;扇形面积S扇形=nπR²/360=LR/2;内公切线长d-(R-r)=外公切线长d-(R+r)。
6. 正n边形的每个内角都等于(n-2)×180°/n。
7. 圆的切线判定定理:经过半径的外端点并且垂直于半径的直线是圆的切线。
8. 圆的切线性质定理:圆的切线垂直于过切点的半径。
9. 相交两圆的连心线垂直平分两圆的公共弦。
10. 圆和圆的位置关系:两圆外离d>R+r;两圆外切d=R+r;两圆相交R-r<d<R+r(R>r);两圆内切d=R-r(R>r);两圆内含d<R-r(R>r)。
以上是初中数学中的部分公式,初中数学还有许多其他重要的公式和定理,建议查看初中数学教材或咨询数学老师进行学习。
十大最美公式

以下是一些被认为具有美学价值的数学公式,这些公式不仅在数学上具有重要意义,而且被广泛认为是美丽和优雅的:1. 欧拉公式(Euler's formula):e^ix = cos(x) + i * sin(x)。
2. 二次方程(Quadratic equation):ax^2 + bx + c = 0。
3. 黄金比例公式(Golden ratio formula):(1 + √5) / 2。
4. 平面三角形面积公式(Triangle area formula):A = 1/2 * base * height。
5. 导数定义(Derivative definition):f'(x) = lim(h->0) (f(x + h) - f(x)) / h。
6. 泰勒级数展开公式(Taylor series expansion):f(x) = f(a) + f'(a)(x - a) + f''(a)(x - a)^2 + ...。
7. 牛顿万有引力定律公式(Newton's law of universal gravitation):F = G * (m1 * m2) / r^2。
8. 斐波那契数列公式(Fibonacci sequence formula):Fn = Fn-1 + Fn-2,其中F0 = 0,F1 = 1。
9. 傅里叶级数公式(Fourier series formula):f(x) = a0 + Σ(an * cos(nx) + bn * sin(nx))。
10. 矩阵变换公式(Matrix transformation formula):Ax = b,其中A是一个矩阵,x和b是向量。
以上是一些被认为具有美学价值的数学公式,它们展现了数学的优雅与深度。
世界上最伟大的十大公式

世界上最伟大的十大公式
1. 欧拉公式:e^(iπ) + 1 = 0。
它将数学中的五个基本常数(e、
i、π、1和0)结合在一起,以一种简洁而优雅的方式。
2. 直角三角形的勾股定理:a² + b² = c²。
这个公式描述了直角三角形中三条边之间的关系,是几何学中最重要的定理之一。
3. 爱因斯坦的质能方程:E = mc²。
这个公式描述了质量和能量之间的等价关系,揭示了相对论的基本原理。
4. 麦克斯韦方程组:这是一组描述电磁场的四个基本方程,包括高斯定律、法拉第电磁感应定律、安培环路定律和法拉第电磁感应定律。
它们统一了电磁学的基本原理。
5. 黎曼猜想:尚未被证明的数学猜想,涉及到复数域上的素数分布规律。
如果该猜想成立,将对数论产生深远的影响。
6. 波尔兹曼熵公式:S = k ln W。
它描述了统计物理学中系统的熵和系统的微观状态数之间的关系,是热力学第二定律的基础。
7. 黑-施陶尔兹迈尔方程:描述流体运动的偏微分方程,是流体力学的基本方程之一。
8. 熵增定律:描述了自然界中系统总是趋向于熵增加的趋势,是热力学和统计物理学中基本的原理之一。
9. 维里定律:描述了电阻产生的焦耳热与电流、电阻和时间的关系,是电学中的基本定律之一。
10. 斯特雷克公式:描述了光谱线的位移与外加电场的关系,揭示了原子和分子的结构与性质之间的关联。
世界上十大伟大公式

世界上十大伟大公式几年前英国科学期刊《物理世界》曾让读者投票评选了“最伟大的公式”,最终榜上有名的十个公式既有无人不知的1+1=2,又有著名的E=mc^2;既有简单的-圆周公式,又有复杂的欧拉公式……这些公式不仅仅是数学家和物理学家的智慧结晶,更是人类文明的集中体现。
每一个公式都深深影响了人类社会的变革,甚至塑造了人类的思想。
这些公式中有些你会很熟悉,有些你也许不那么熟悉。
作为人类的我们有必要了解这些公式,了解人类的思想历程。
10 圆的周长公式The Length of the Circumference of a Circle创立者:古人意义:自然界之美的数学表达。
09 傅立叶变换The Fourier Transform创立者:让·巴普蒂斯·约瑟夫·傅立叶意义:任何不规则的信号都可以表示为规则的正弦波无限叠加。
它是数字信号处理领域的很重要的方法。
08 德布罗意方程组The de Broglie Relations创立者:路易·维克多·德布罗意意义:德布罗意认为,任何物质既有粒子性,又有波动性,或者说,任何物质也可以看成是一种波,包括人本身。
人不但是作为一种物质存在,某种意义上也是一种波。
07 1+1=2这个公式不需要名称,不需要翻译,不需要解释。
06 薛定谔方程The Schr dinger Equation创立者:埃尔温·薛定谔意义:在量子力学中描述物体的状态不能像经典力学中一样用位移、速度等,而只能用一个物理量的函数来描述,这个物理量也不再是某个确定的值,而是一个随时间分布的概率,每一个微观系统都有相应的薛定谔方程。
薛定谔方程在量子力学中的意义与牛顿第二定律在经典力学中的意义一样。
05 质能方程Mass–energy Equivalence创立者:阿尔伯特·爱因斯坦意义:质能方程深刻地揭示了质量与能量之间的关系,在此之前,人们毫无疑问的认为:质量是质量,能量是能量,两者间没有联系。
十大必学公式

十大必学公式在学习数学的过程中,公式是不可或缺的一部分。
公式的掌握不仅可以帮助我们更好地理解数学知识,还可以在解题时提高效率。
下面是十大必学公式,希望对大家的学习有所帮助。
1.勾股定理:a²+b²=c²,其中a、b、c分别为直角三角形的两条直角边和斜边。
2.二次方程求根公式:对于ax²+bx+c=0,其根为x1=(-b+√(b²-4ac))/2a,x2=(-b-√(b²-4ac))/2a。
3.三角函数公式:sin²θ+cos²θ=1,tanθ=sinθ/cosθ,cotθ=cosθ/sinθ。
4.圆的面积公式:S=πr²,其中S为圆的面积,r为圆的半径。
5.立方体的体积公式:V=a³,其中V为立方体的体积,a为立方体的边长。
6.平行四边形的面积公式:S=bh,其中S为平行四边形的面积,b 为底边长,h为高。
7.三角形的面积公式:S=1/2bh,其中S为三角形的面积,b为底边长,h为高。
8.等差数列求和公式:Sn=n(a1+an)/2,其中Sn为等差数列的前n项和,a1为首项,an为末项。
9.等比数列求和公式:Sn=a1(1-qⁿ)/(1-q),其中Sn为等比数列的前n项和,a1为首项,q为公比。
10.导数公式:f'(x)=lim(h→0)(f(x+h)-f(x))/h,其中f'(x)为函数f(x)在x处的导数。
以上是十大必学公式,掌握这些公式可以帮助我们更好地理解数学知识,提高解题效率。
当然,公式的掌握并不是学习数学的全部,还需要不断地练习和思考,才能真正掌握数学的精髓。
改变世界十个数学公式

改变世界十个数学公式数学公式在改变世界中起着重要的作用,它们广泛应用于科学、工程、经济、计算机科学等领域。
下面是改变世界的十个数学公式:1. E=mc^2 - 爱因斯坦的质能方程改变了物理学的面貌。
它揭示了质量与能量之间的等价性,为核能、原子弹和核电站等带来了重大的技术突破。
2.无穷级数公式-数学无穷级数公式的发展促进了现代科学的发展。
例如,泰勒级数使我们能够使用多项式逼近函数,从而发展了微积分和数值计算方法。
3.黑-斯科利方程-黑-斯科利方程是描述光传播的非线性波动方程,它在光学通讯和激光技术中起着重要作用。
4.脑电图公式-脑电图记录了人脑发出的电活动,这对于了解大脑的功能和研究神经疾病至关重要。
脑电图公式描述了电极上记录到的电信号的特征。
5.马尔可夫链公式-马尔可夫链是在概率论和统计学中应用广泛的模型。
它描述了一系列状态之间的转移概率,并在自然语言处理、金融风险管理等领域有重要应用。
6.线性规划公式-线性规划是一种常见的优化方法,它通过最小化或最大化目标函数,同时满足一系列线性等式或不等式约束条件。
它在经济学、交通规划、物流等领域有广泛应用。
7.有限元法公式-有限元法是一种数值解法,用于求解具有复杂几何形状的物理问题。
它在工程学中广泛应用,如结构力学、热传导、流体力学和电磁学等领域。
8.傅里叶变换公式-傅里叶变换将一个函数表示为一组正弦和余弦函数的和,它在信号处理、图像处理和通信中起着重要作用。
傅里叶变换可以帮助我们理解和处理各种信号,如音频、图像和视频等。
9.黎曼猜想公式-黎曼猜想是数论中的一个重要问题,它要求找到一种函数,能够揭示素数之间的规律。
虽然迄今为止还没有被证明,但黎曼猜想促进了数论和素数研究的发展。
10.布莱克-斯科尔斯期权定价公式-布莱克-斯科尔斯期权定价公式是金融工程中的重要成果,它提供了一种用于估计期权价格的方法。
该公式在金融衍生品交易中广泛使用,为风险管理和投资决策提供了依据。
世界最美的十大数学公式

世界最美的十大数学公式数学公式是数学思想的高度凝结和精炼,它们是描述自然界和人类社会中普遍规律的有力工具。
世界上有许多优美而重要的数学公式,下面是我挑选的世界上最美的十大数学公式:1. 欧拉恒等式(Euler's identity):e^πi + 1 = 0欧拉恒等式被公认为数学中最美丽的公式之一、它涵盖了五个基本数学运算符:0、1、e(自然对数的底)、π(圆周率)和i(虚数单位)。
它将这些数学常数和运算符结合在一起,以惊人的方式得出了结果0。
2. 四色定理(Four-Color Theorem):四色定理是指任何一个平面上的地图或图形都可以用四种颜色进行涂色,使得任何两个相邻的区域不会有相同的颜色。
这个定理于1976年由Mathias Hebert和Wolfgang Haken在计算机的帮助下完成证明。
3. 爱因斯坦场方程(Einstein Field Equations):4. 黎曼假设(Riemann Hypothesis):黎曼假设是数论领域的著名问题,由Bernhard Riemann在1859年提出。
该假设可以用复数论的术语来描述,它关于质数分布的性质,被认为是解决质数分布问题的关键。
然而,至今尚未有人证明或反驳这个假设。
5. 莱布尼茨积分法则(Leibniz Rule):莱布尼茨积分法则是微积分中的基本定理,描述了求导和积分之间的关系。
它使我们能够计算复杂函数的导数和原函数,为物理、工程和经济学等领域中的问题提供了强大的工具。
6. 哈密顿四元数(Hamilton's Quaternions):哈密顿四元数是数学中一种扩充了复数的代数结构,由William Rowan Hamilton在1843年发现。
它具有复数的形式,但包含了三个虚数单位,使其能够进行三维旋转和方向计算,在计算机图形学和物理模拟中有广泛应用。
7. 奥氏定律(Ohm's Law):奥氏定律是电学中最基本的定律之一,描述了电流、电压和电阻之间的关系。
奥数需要掌握的十大公式

奥数需要掌握的十大公式奥数是指奥林匹克数学竞赛,是一个注重逻辑思维和数学运算能力的竞赛项目。
在奥数竞赛中,学生们需要熟练掌握各种数学公式,以解决复杂的数学问题。
在这篇文章中,我将介绍奥数竞赛中需要掌握的十大公式,并附上相关的例题来帮助读者更好地理解和应用这些公式。
公式一:二项式定理二项式定理是奥数竞赛中非常重要的公式之一,它可以用来展开任意一个二次多项式的幂。
二项式定理的数学表达式为:(a + b)ⁿ = C(n, 0)aⁿb⁰ + C(n, 1)aⁿ⁻¹b¹ + C(n, 2)aⁿ⁻²b² + ... + C(n, n-1)abⁿ⁻¹ + C(n, n)a⁰bⁿ其中,C(n, k)表示从n个元素中选取k个元素的组合数。
例题一:展开(a + b)⁵,并计算其结果。
解析:根据二项式定理,展开(a + b)⁵可得:(a + b)⁵ = C(5, 0)a⁵b⁰ + C(5, 1)a⁴b¹ + C(5, 2)a³b² + C(5, 3)a²b³ + C(5,4)ab⁴ + C(5, 5)a⁰b⁵计算出每一项的系数并整理可得展开结果:(a + b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵公式二:勾股定理勾股定理是一条关于直角三角形的定理,它可以用于求解直角三角形的任意边长、角度和面积。
根据勾股定理,直角三角形中两条较短的边的平方和等于斜边的平方。
数学表达式为:a² + b² = c²其中,a和b为直角三角形的两条较短的边,c为斜边的长度。
例题二:已知直角三角形的两条直角边分别为4cm和5cm,求斜边的长度。
解析:根据勾股定理,可得:4² + 5² = c²16 + 25 = c²41 = c²c ≈ 6.4因此,直角三角形的斜边长度为约6.4cm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
从什么时候起我们开始厌恶数学?这些东西原本如此美丽,如此精妙。这个地球上有多少伟大的智慧曾耗尽一生,才最终写下一个等号。每当你解不开方程的时候,不妨换一个角度想,暂且放下对理科的厌恶和对考试的痛恨。因为你正在见证的,是科学的美丽与人类的尊严。
No.4 勾股定理/毕达哥拉斯定理(Pythagorean Theorem)
做数学不可能没用到过吧,不on's Second Law of Motion)
有史以来最伟大的没有之一的科学家在有史以来最伟大没有之一的科学巨作《自然哲学的数学原理》当中的被认为是经典物理学中最伟大的没有之一的核心定律。动力的所有基本方程都可由它通过微积分推导出来。对于学过高中物理的人,没什么好多讲了。
No.5 质能方程(Mass–energy Equivalence)
好像从来没有一个科学界的公式有如此广泛的意义。在物理学“奇迹年”1905年,由一个叫做/爱因斯坦的年轻人提出。同年他还发表了《论动体的电动力学》——俗称狭义相对论。
这个公式告诉我们,爱因斯坦是牛逼的,能量和质量是可以互换的。副产品:原/子/弹。
积分形式:
微分形式:
任何一个能把这几个公式看懂的人,一定会感到背后有凉风——如果没有上帝,怎么解释如此完美的方程?这组公式融合了电的高斯定律、磁的高斯定律、法 拉第定律以及安培定律。比较谦虚的评价是:“一般地,宇宙间任何的电磁现象,皆可由此方程组解释。”到后来麦克斯韦仅靠纸笔演算,就从这组公式预言了电磁波的存在。我们不是总喜欢编一些故事,比如爱因斯坦小时候因为某一刺激从而走上了发奋学习、报效祖国的道路么?事实上,这个刺激就是你看到的这个方程组。 也正是因为这个方程组完美统一了整个电磁场,让爱因斯坦始终想要以同样的方式统一引力场,并将宏观与微观的两种力放在同一组式子中:即著名的“大一统理 论”。爱因斯坦直到去世都没有走出这个隧道,而如果一旦走出去,我们将会在隧道另一头看到上帝本人。
关于e,以前有一个笑话说:在一家精神病院里,有个病患整天对着别人说,“我微分你、我微分你。”也不知为什么,这些病患都有一点简单的微积分概 念,总以为有一天自己会像一般多项式函数般,被微分到变成零而消失,因此对他避之不及,然而某天他却遇上了一个不为所动的人,他很意外,而这个人淡淡地对他说,“我是e的x次方。”
No.6 薛定谔方程(The Schr?0?2dinger Equation)
也是一般人完全不明白的。因此我摘录官方评价:“薛定谔方程是世界原子物理学文献中应用最广泛、影响最大的公式。”由于对量子力学的杰出贡献,薛定谔获得1933年诺贝尔物理奖。
另外薛定谔虽然姓薛,但是奥地利人。
No.2 欧拉公式(Euler's Identity)
这个公式是上帝写的么?到了最后几名,创造者个个神人。欧拉是历史上最多产的数学家,也是各领域(包含数学的所有分支及力学、光学、音响学、水利、天文、化学、医药等)最多著作的学者。数学史上称十八世纪为“欧拉时代”。欧拉出生于瑞士,31岁丧失了右眼的视力,59岁双眼失明,但他性格乐观,有惊 人的记忆力及集中力。他一生谦逊,很少用自己的名字给他发现的东西命名。不过还是命名了一个最重要的一个常数——e。
No.10 圆的周长公式(The Length of the Circumference of a Circle)
这公式贼牛逼了,初中学到现在。目前,人类已经能得到圆周率的2061亿位精度。还是挺无聊的。现代科技领域使用的-圆周率值,有十几位已经足够了。如果用 35位精度的-圆周率值,来计算一个能把太阳系包起来的一个圆的周长,误差还不到质子直径的百万分之一。现在的人计算圆周率,多数是为了验证计算机的计算能力,还有就是为了兴趣。
这个东西也挺牛逼的,高中物理学到光学的话很多概念跟它是远亲。简要地说德布罗意这人觉得电子不仅是一个粒子,也是一种波,它还有 “波长”。于是搞啊搞就有了这个物质波方程,表达了波长、能量等等之间的关系。同时他获得了1929年诺贝尔物理学奖。
No.7 1+1=2
这个公式不需要名称,不需要翻译,不需要解释。
No.9 傅立叶变换(The Fourier Transform)
这个挺专业的,一般人完全不明白。不多作解释。简要地说没有这个式子没有今天的电子计算机,所以你能在这里上网除了感谢党感谢GV还要感谢这个完全看不懂的式子。另外傅立叶虽然姓傅,但是法国人。
No.8 德布罗意方程组(The de Broglie Relations)
这个公式的巧妙之处在于,它没有任何多余的内容,将数学中最基本的e、i、pie放在了同一个式子中,同时加入了数学也是哲学中最重要的0和1,再以简单的加号相连。
高斯曾经说:“一个人第一次看到这个公式而不感到它的魅力,他不可能成为数学家。”
No.1 麦克斯韦方程组(The Maxwell's Equations)
