SPC计数型数据统计模块
SPC计量与计数型控制图表格模板(全公式未加密-自动生成结果)

+5δ
+6δ
300.000
对照输入数据
返回数据登入
子组容量 n 总组数 Count 总样本数 N
平均值 X 最大值 Max X 最小值 Min X 平均中位数 Mid X 规范上限 USL
中心限 CL 规范下限 LSL 上限值 UCL (X) 中心限 CL (X) 下限值 LCL (X) 上限值 UCL (R) 中心限 CL (R) 下限值 LCL (R) 偏度 Skewness 峰度 Kurtosis 预估不良率(PPM) 标准差 Std.Dev.= 标准差 Sigma=
Sigma分布 规范值 频率分布 正态分布
350.000
通往初始面板
X-S图及过程能力分析
X控制图
生成报告
对比其他控制图
查看并填写报告
查看X-R图
查看中位数图
250.000
200.000
150.000
100.000
50.000
0.000
1
2
3
4
5
6
7
8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
Pp= Ppk= Ca= Cp= CPU= CPL= Cpk= Grade=
9 30 270 142.9852 300.0000 40.0000 143.5000 200.0000 150.0000 100.0000 178.177 143.500 108.823 152.847 84.167 15.487 0.8966 3.7034 85484.310 34.603 28.339 0.482 0.419 13.00% 0.588 0.665 0.512 0.512 E
SPC统计-计数型数据

SPC统计-计数型数据1. 简介SPC〔统计过程控制〕是一种统计方法,用于监测和控制过程的变异性。
计数型数据是SPC中常见的一种类型,它是指对一个过程中发生的事件进行计数或计量的数据。
在生产过程中,计数型数据常用于统计质量缺陷、产品故障等信息。
2. SPC统计-计数型数据的目的SPC统计-计数型数据的目的在于通过对计数型数据进行统计分析,了解和控制过程的变异性,从而实现生产过程的质量控制和改良。
3. SPC统计-计数型数据的方法SPC统计-计数型数据常用的方法有以下几种:3.1 控制图控制图是SPC统计-计数型数据中最常用的图表之一,通过绘制计数型数据的变化趋势以及控制限,可以及时发现过程的异常变异,并进行相应的调整和改良。
常见的控制图包括:•P图:用于统计不良事件的比例的控制图。
P图将观察时间分为假设干子组,然后统计每个子组内不良事件发生的比例,并计算上下控制限,以判断过程是否处于控制状态。
•C图:用于统计不良事件的数量的控制图。
C图将观察时间分为假设干子组,然后统计每个子组内不良事件的数量,并计算上下控制限,以判断过程是否处于控制状态。
•U图:用于统计不良事件的单位数的控制图。
U图将观察时间分为假设干子组,然后统计每个子组内不良事件的单位数〔如每个产品的不良事件数量〕,并计算上下控制限,以判断过程是否处于控制状态。
3.2 过程能力指数过程能力指数用于衡量过程的稳定性和一致性,是SPC统计-计数型数据评估过程能力的重要工具。
常见的过程能力指数有:•Cp指数:Cp指数用于评估过程的一致性,它比拟过程的控制限与规格限的距离。
Cp指数越大,说明过程越稳定,一致性越好。
•Cpk指数:Cpk指数用于评估过程的稳定性和一致性,考虑了过程的中心位置。
Cpk指数越大,说明过程的稳定性和一致性越好。
•Pp指数:Pp指数用于评估过程的一致性,考虑了样本大小的影响。
Pp指数越大,说明过程越稳定,一致性越好。
•Ppk指数:Ppk指数用于评估过程的稳定性和一致性,考虑了过程的中心位置和样本大小的影响。
SPC计数型(P图)
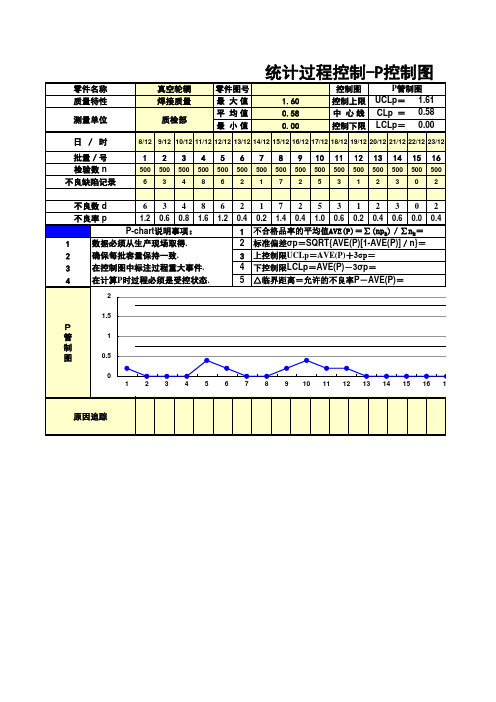
测量单位
日/时 批量/号 检验数 n 不良缺陷记录
真空轮辋 焊接质量
质检部
零件图号 最 大值 平 均值 最 小值
统计过程控制-P控制图
1.60 0.58 0.00
控制图 控制上限 中 心线 控制下限
P管制图 UCLp= 1.61 CLp = 0.58 LCLp= 0.00
8/12 9/12 10/12 11/12 12/12 13/12 14/12 15/12 16/12 17/12 18/12 19/12 20/12 21/12 22/12 23/12
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 6348621725312302
不良数 d
6348621725312302
不良率 p
1.2 0.6 0.8 1.6 1.2 0.4 0.2 1.4 0.4 1.0 0.6 0.2 0.4 0.6 0.0 0.4
6241301
73
1.2 0.4 0.8 0.2 0.6 0.0 0.2 0.58%
过程能力CPK
请设定参数
=
△临界距离/3σp
允许的P= 样本量n=
2.00% 500
=
1.3851
子组数k= 25
结论
满足
过程能力 ≥1.33
UCLp 说明栏 A分检 M反馈 R维修 S调整
CL p W工装 X换人
17 18 19 20 21 22 23 24 25
制定者
张明君
24/12 25/12 26/12 27/12 28/12 29/12 30/12 31/12 1/01
SPC统计-计数型数据

– 用附录7中的数据计算np 图的 UCL 和 LCL。
– 把数据标在图上并确定是否有任何超为 出控制范围的情况。
不合格数的
c图
• 何时使用 c 图
• 当数据为计数型数据时(一种可以计数的属 性)。
• 当不合格是分布于整个产品时,如油漆部件 上的缺陷数,装配工序上的缺陷数等。
• 当不合格现 象可从多个来源发现,或由多 种原因造成时。
SPC统计-计数型数据
课程目标
• 到本课程结束时,学员应能识别: 1. 计数型SPC数据控制图
2. 何时使用这些图最合适
如何选择正确的SPC图
计数型 数据
P图
计算零件数 N = 固定值或变 值
Np 图
计算零件数 N = 固定值
U图
计算发生次数 N = 变值
C图
计算发生次数 N = 固定值
不合格品率 p图
• 更重要的是,当您必须了解正在检验的一组 产品中不合格品的数量时。
• 当各子组样本容量均相等时。
np 图
• 计算np 图的方法
– 确定子组 的容量,通常为>50 个零件。 – 确定检验的频率。 – 收集数据。 – 确定该子组 中不合格品的数量。 – 在 np 图上记录有缺陷的零件数量。 – 在 np 图上描绘该数据。
• 在样本容量不等的情况下,当不合格数的情况分 布于整个产品时(如油漆零件的缺陷数,装配工 序的缺陷数)
• 当不合格现象可从多个来源发现,或由于多种原 因造成时。
单位产品不合格数的 u图
• 计算 u 图的方法
– 定义检验内容。 – 确定检验频率。 – 确定在该样本上发现的不合格数。 – 以样本容量除以所发现的不合格数。 – 在 u 图上记录不合格的比率。 – 在 u 图上描绘此数据。
SPC-计量型数据模块10

SPC-计量型数据模块10SPC(统计过程控制)是一种质量管理工具,旨在监控和控制过程的稳定性和可靠性。
计量型数据模块10是SPC中的一个重要组成部分,用于收集、分析和监控计量型数据,以帮助企业实现质量的持续改进。
本文档将详细介绍SPC-计量型数据模块10的功能和使用方法。
1. 功能介绍SPC-计量型数据模块10提供了以下主要功能:1.1 数据收集该模块可以从多种来源收集计量型数据,包括传感器、测量仪器和记录表等。
用户可以手动输入数据,或通过数据接口自动导入数据。
收集的数据可以是连续或离散的,并且可以包含多个测量指标。
1.2 数据分析SPC-计量型数据模块10能够对收集的数据进行各种分析,以获取统计特征和趋势。
这些分析包括:•均值和标准差的计算•直方图和箱线图的绘制•数据分布分析•数据关联和相关性分析用户可以根据自己的需要选择特定的分析方法,以便更好地理解数据的状态和性质,并采取相应的措施。
1.3 监控和控制SPC-计量型数据模块10可以监控数据的稳定性和可靠性,通过检测异常值、偏离控制限的数据和趋势变化等情况,及时发现潜在的问题。
用户可以设置上下控制限,并根据控制图上的警告信号进行相应的调整和改进。
2. 使用方法下面是使用SPC-计量型数据模块10的步骤:2.1 数据收集首先,需要收集计量型数据。
可以通过传感器、测量仪器或手动记录表等方式获取数据。
确保数据的准确性和完整性,并将其保存在电脑或服务器中。
2.2 数据导入如果数据已经保存在电脑或服务器中,可以通过数据接口将其导入到SPC-计量型数据模块10中。
选择相应的数据导入选项,并按照提示完成导入过程。
确保导入的数据格式正确,以便后续的分析和控制。
2.3 数据分析在导入数据后,可以开始进行数据分析。
选择要分析的数据集、测量指标和分析方法,然后点击开始分析按钮。
系统将根据选择的方法计算统计特征和绘制相应的图表。
查看分析结果,并对数据的分布、趋势和异常进行评估。
与SPC有关的定义

与SPC有关的定义1、统计过程控制(staristical. Process control)使用诸如控制图等统计技术来分析过程或其输出以便采取适当的措施来达到并保持统计控制状态从而提高过程能力。
2、计数型数据可以用来记录和分析的定性数据。
例如,要求的标识的出现,所有要求的紧固件安装,经费报告中不出现错误等特性量即为计数型数据的例子。
其他的例子如一些本来就可以测量(即可以作为计量型数据处理),但是其结果用简单的“是/否”的形式来记录。
例如,用通/止规来检验轴径的可接受性,或一张图样上任何设计更改的出现。
3、计量型数据定量的数据,可用测量值来分析。
例如:用毫米表示的轴承轴颈直径,用牛顿表示关门的力,用百分数表示电解液的浓度,用牛顿.米表示紧固件的力矩。
4、控制图用来表示一个过程特性的图形,图上标有根据该特性收集到的一些统计数据,如一条中心线,一条或两条控制线。
5、Ⅰ类错误拒绝真的假设,例如当过程实际没有改变(超出控制)时,而对过程采取适用于特殊原因的措施。
它和生产方风险或α风险相关。
6、Ⅱ类错误 没有拒绝错误的假设,例如:对实际上受特殊原因影响(受控)的过程没有采取适用的措施。
它和使用方风险或β风险相关。
7、二项分布 应用于合格与不合格品的计数型数据的离散概率分布,是p 图和np 图的基础。
8、正态分布 一种用于计量型数据的、连续的、对称的钟形频率分布,它是计量型数据用控制图的基础。
9、泊松分布 应用于不合格数的计数型数据的离散型概率分布,是c 和u 控制图的基础。
10、统计控制 描述一个过程的状态,这个过程中所有的特殊原因变差都已排除,并且仅存在普通原因。
即:观察到的变差可归咎与恒定系统的偶然原因;在控制图上表现为不存在超出控制限的点或在控制限范围内不存在非随机性的图形。
11、Cpk 稳定过程的能力指数,通常定义为CPU 或CPL 中的最小值。
12、Ppk 性能指数,通常定义为 的或 最小值。
s x USL δ3-sLSL X δ3-。
MES系统软件SPC模块介绍

MES系统软件SPC模块介绍实时SPC分析工具可减少工艺变化对质量和生产成本的影响。
制造商使用统计过程控制(SPC)和过程能力工具可以确保质量,满足客户需求并推动改进。
MES软件与质量管理模块一起提供SPC分析模块,以便:获得实时SPC分析以确保您的流程稳定出现过程异常时快速反应测量过程能力并生成能力报告将SPC数据添加到一致性证书预测不合格产品的数量通过将过程维持在“最佳位置”来降低材料成本【SPC模块特征】1.配置您的SPC图表根据收集到的所有质量数据自动生成SPC图表计算并设置控制限制设置分层SPC分析,例如跨线,钻入机器内的机器,在机器上钻头2.实时SPC分析和警报实时SPC图表无论当前是否查看图表,都会在输入时分析所有数据警惕违规行为:失控测量,外部控制限制,违反趋势规则等。
3.线路操作人员的图表定义要显示的SPC图表和要显示的计算结果设计屏幕以帮助负责过程质量的生产线操作人员。
可能有几个功能需要控制; 您可能想要并排创建具有主要功能的屏幕4.进一步的工艺变化分析从XR,XS,IXMR,MXMR,直方图,X和个人,能力概述,3D图表,NP,P,C,U,帕累托图表中选择需要的SPC图表...多头分析- 有许多过程实际上是并行连接但是独立的过程,例如多模/腔工具,多通道/通道,多切割/切片/铺设。
在这些过程中有一个共同的和个人的变异来源。
理解变异的共同和个体来源至关重要。
创建SPC图表的多个视图为不同的人和目的生成视图,例如查看跨多个生产运行的生产产品的功能; 或者即使在流程从一种产品切换到另一种产品时也可以查看流程趋势。
5.计算过程能力Cp,CpkPp,Ppk生成一致性证书使用每次生产运行期间收集的关键特征和数据。
【优点】提高质量- 管理和减少差异不仅可以避免浪费,而且可以减少价值链下方变化的影响,减少问题,减少对流程进行调整的需要满足客户要求- 许多客户要求您使用SPC软件并了解工艺变化。
SPC计数计量统计法

练习3 计算均值和标准差
下面的数据是一个样本中的8个观测值,求其极差 (R)和标准差s(计算s可采用下表计算)。数据为: 2.8 3.2 4.8 4.2 4.6 2.9 5.0 5.5
(1) Xi
(2) Xbar
(3) Xi-Xbar
(4) (Xi-Xbar)2
右偏态情形下分布集中程度与离散程度间的关系
Statistical Process Control
产品质量的 统计观点
产品质量具有变异性 (Variation)
产品质量的变异具 有统计规律性
作好质量管理首先应明确:
1 贯彻预防原则是现代质量管理的核心与 精髓;
2 质量管理科学有一个重要的特点,即对 于质量管理所提出的原则、方针、目标都 要有科学措施与科学方法来保证他们的实 现。
(3)根据上述计算可以得出什么结论?
90%
95%
98%
工序1
工序2
工序3
练习2 计算概率
若随意掷两个骰子,问 1、共有多少种可能的结果出现? 2、两个骰子的点数和有多少可能性? 3、点数和出现的概率是多少?分别用小数 和分数表示。 采用下表会有助于计算
练习2 计算概率(续)
÷ » × Ó A
123456
Xbar
Xi-Xbar (Xi-Xbar)2
计算样本标准差的步骤(续)
步骤 1、把样本数据排成一列放在第一列。 2、计算样本均值X,并将X填入第二列 。 3、计算Xi—X的值并填在第3列上。 4、将第3列的数值求平方,填入对应的第4列。 5、将第4列的数累加。 6、将累积数除以n-1即为样本方差。 7、对样本要求的平方根即是样本样准差。
时总变异是多少? 3、若将主要变异来源彻底根除,此时总变异又是多
SPC计量型数据15304

模块 10 - SPC 计量型数据
过程能力研究
• CpK 的计算
Cpk Z min , Zmin MIN (ZUSL, ZLSL) 3
USL - X
X - LSL
ZUSL
, ZLSL
R
R
d2
d2
n
d2
2
1.128
3
1.693
4
2.059
5
2.326
6
2.534
7
2.704
8
2.847
9
2.97
World Class Quality Pty Ltd - 1999年9月
模块 10 - SPC 计量型数据
X -S图
• 计算 X -S图的方法:
– 1. 确定子 组 的大小,一般为10或更大。 – 2. 确定进行测量的频率。 – 3. 收集数据。 – 4. 计算每个子 组 的均值并将结果记录下来。 – 5. 计算每个子 组 的标准差并将结果记录下来。 – 6. 在图上标出均值和标准差。 – 7. 对图作解释。
计量型数据
X &S
N=10 或更大
X &R
N= 2至 9
X & MR
N=1
中位数
N= 奇数
World Class Quality Pty Ltd - 1999年9月
模块 10 - SPC 计量型数据
X -R图
• 何时使用 X -R图
• 当有测量数据时 • 为了确定过程偏差 • 当您能获得一个大小不变的子组时,子组数大小在
D3 - - - - -
0.08 0.14 0.18 0.22
A2
1.88 1.19 0.8 0.69 0.55 0.51 0.43 0.41 0.36
SPC计数计量统计法

■ 乘法原则 —与条件 —互相独立 —P(A与B)=P(A)P(B)
练习一、计算概率
■ 某工序需经三道工序加工,假定各道工序彼此独立,其合格 品详细分别是90%、95%、98%,三道工序之后为检验工 序,假定检验工序可以检测出前三道工序中的缺陷。
问:(1)整条线的合格品率是多少?
(2)若在第1、2工序和第2、3工序增加两 个检验点, 此时整条线的合格率是多少?
缺点
■ 平均数受超常值的影 响。
■ 大量数据计算平均数 较为繁琐。
中位数的优、缺点
优点 中位数不受超常值的影响。
缺点 需要对数据排序,对大样本将非常繁琐。
众数的优缺点
优点
■ 众数不受超常值 影响。
■ 可应用于定性数 据。
缺点
■ 一组数据可能不存在 众数。
■ 有时一组数据会有一 个以上的众数。
数据的离散程度
0
1¦Ò 2¦Ò 3¦Ò 4¦Ò 5¦Ò 6¦Ò
标准正态分布曲线
-6¦Ò -5¦Ò -4¦Ò -3¦Ò -2¦Ò -1¦Ò
0 1¦Ò 2¦Ò 3¦Ò 4¦Ò 5¦Ò
推断正态分布的参数
总体参数
样本统计量
集中程度
μ
X
离散程度
σ
s
两个离散分布
■ 二项式分布
—试验次数固定 —每次试验相互独立 —每次试验结果只有二个 —每次试验概率保持不变
统计功能的计算器在计算方差时一般使用该
公式:
s2 n(
X
2 i
)
(
Xi )2
n(n 1)
举例:计算数据离散程度(续)
+
Xi
1.32 1.40 1.58 1.44 1.60 1.35 1.45 1.38 11.52
计数型数据SPC

计数型数据SPC
4
过程能力的度量
控制图种类 P图 Pn图 U图 C图
能力指数
P
P
U
C
计算公式
k
pni
P i1 N
k
pni
P i1 N
k
ci
U i1 N
k
ci
C i1 N
计数型数据SPC
5
过程能力的度量
上图计算公式中 K=子组数
计数型数据SPC
3
过程能力的度量
1、计数值数据控制图控制对象的过程能力的解释计 数值数据控制图的过程能力与计算值数据有所不 同,计数值数据控制图上的所有点直接表明了不 符合客户要求的百分数或不合格品数(或缺陷数), 而计量值数据控制图上的所有点显示的是过程实 际生产的产品与规格比较的结果。计数值数据控 制图控制对象的过程能力定义为不合格品,缺陷 数的平均不合格率或缺陷率。
制作P图前的准备 为了P图能顺利制作并发挥其应用作用,
在制作P图前应做以下准备: 1.取得高层对推行控制图的认可与支持。 2.确定需用P图控制的过程和特性。 3.定义测量系统。 4.消除明显的过程偏差。
计数型数据SPC
7
控制P控制图
正确制作P控制图,是进行过程控制及改善的基础, 制作P控制图的流程如下: 1、收集数据 (1)进行测量系统分析 (2)确定子组样本容量 一般而言,P图的每个子组的样本容量需大于50。 (3)确定子组额率 适当的子组频率可以区分特殊原因引起的过程变化, 在确定抽样频率时需综合考虑过程稳定性和经济性。 一般而言,P图的子组间时间间隔不可过大。 (4)确定子组数 一般来说,要求子组在25个以上,这样可以全面检 验过程的稳定性。
SPC-计数型数据控制图

World Class Quality Pty Ltd - 1999年9月
模块 11 - SPC 计数型数据
第 2片
如何选择正确的SPC图
计数型 数据
P图
Np 图
U图
C图
计算零件数
N = 固定值或变 值
计算零件数 N = 固定值
计算发生次数 N = 变值
计算发生次数 N = 固定值
World Class Quality Pty Ltd - 1999年9月
第 4片
p图
• 计算 p 图的方法
– 确定子组 的容量,一般大于50个零件。 – 确定检验的频率。 – 收集数据。 – 确定该子组 中不合格品的数量。 – 把有缺陷的产品的数量记录在P图上。 – 确定有缺陷零件的比率,即有缺陷零件的数量/子组 中
的零件数量。 – 在P图上描绘该值。
World Class Quality Pty Ltd - 1999年9月
模块 11 - SPC 计数型数据
第 11 片
不合格数的
c图
• 何时使用 c 图
• 当数据为计数型数据时(一种可以计数的属 性)。
• 当不合格是分布于整个产品时,如油漆部件 上的缺陷数,装配工序上的缺陷数等。
• 当不合格现 象可从多个来源发现,或由多 种原因造成时。
World Class Quality Pty Ltd - 1999年9月
World Class Quality Pty Ltd - 1999年9月
模块 11 - SPC 计数型数据
第 7片
不合格品数的
np 图
• 何时使用 np 图
• 当数据为计数型数据时(一种可以计数的属 性)。
• 更重要的是,当您必须了解正在检验的一组 产品中不合格品的数量时。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
)
第片
np 图
• 计算np 图的方法
– 确定子组 的容量,通常为>50 个零件。 – 确定检验的频率。 – 收集数据。 – 确定该子组 中不合格品的数量。 – 在 np 图上记录有缺陷的零件数量。 – 在 np 图上描绘该数据。
)
第片
np 图
• 计算 np 图控制线的示例
确定不合格品的平均数量 - np
)
Np 图
计算零件数 N = 固定值
U图
计算发生次数 N = 变值
C图
计算发生次数 N = 固定值
第片
不合格品率 p图
• 何时使用 p 图
• 当数据为计数型数据时(一种可以计数的属 性)。
• 当您希望确定正在检验的一组产品中不合格 品的比率时。
• 数据来自大小相等或不等的样品时。
)
第片
p图
• 计算 p 图的方法
• 计算 u 图控制线的示例
确定单位产品的平均不合格数 u
u u u u =
1+ 2 ++ k n1 + n2 + nk
UCLu u 3 u n
其中 c1, c2 等为 单位产品的不合 格数,n1, n2 等 为相应的样本容 量。
LCLu u 3 u n
)
第片
单位产品不合格数的 u图
• 课堂练习
– 确定检验频率。 – 确定在该样本上发现的不合格数。 – 把该不合格数记录在 c 图上。 – 在 c 图上描绘该数据。
)
第片
c图
• 计算 c 图控制线的示例
确定不合格平均数 c
c = c1 + c2 ++ ck k UCLc c 3 c
LCLc c 3 c
其中 k 为子组 数。
)
第片
c图
– 确定子组 的容量,一般大于50个零件。 – 确定检验的频率。 – 收集数据。 – 确定该子组 中不合格品的数量。 – 把有缺陷的产品的数量记录在P图上。 – 确定有缺陷零件的比率,即有缺陷零件的数量/子组 中
的零件数量。 – 在P图上描绘该值。
)
第片
p图
• 计算P图控制线的示例
确定不合格品的平均比率 - p
– 用附录8中的数据计算 u 图的 UCL 和 LCL。
– 在图上描绘数据并确定任何超出控 制范围的情况。
)
第片
•
生活中的辛苦阻挠不了我对生活的热 爱。20.11.1620.11.16Monday, November 16, 2020
•
人生得意须尽欢,莫使金樽空对月。23:51:3523:51:3523:5111/16/2020 11:51:35 PM
•
加强自身建设,增强个人的休养。2020年11月16日 下午11时51分20.11.1620.11.16
•
精益求精,追求卓越,因为相信而伟 大。2020年11月16日 星期一 下午11时51分35秒23:51:3520.11.16
•
让自己更加强大,更加专业,这才能 让自己 更好。2020年11月下 午11时51分20.11.1623:51November 16, 2020
• 课堂练习
– 用附录5中的数据计算P 图的 UCL 和 LCL 。
– 把数据标在图上并确定是否有任何超出 控制范围的情况。
)
第片
不合格品数的
np 图
• 何时使用 np 图
• 当数据为计数型数据时(一种可以计数的属 性)。
• 更重要的是,当您必须了解正在检验的一组 产品中不合格品的数量时。
• 当各子组样本容量均相等时。
• 课堂练习
– 用附录7中的数据计算c 图的 UCL 和 LCL。
– 在图上描绘该数据并确定任何超出控制 范围的情况。
)
第片
单位产品不合格数的 u图
• 何时使用 u 图
• 当数据为计数型数据时( 一种可以计数的属性 )。
• 在样本容量不等的情况下,当不合格数的情况分 布于整个产品时(如油漆零件的缺陷数,装配工 序的缺陷数)
• 当不合格现象可从多个来源发现,或由于多种原 因造成时。
)
第片
单位产品不合格数的 u图
• 计算 u 图的方法
– 定义检验内容。 – 确定检验频率。 – 确定在该样本上发现的不合格数。 – 以样本容量除以所发现的不合格数。 – 在 u 图上记录不合格的比率。 – 在 u 图上描绘此数据。
)
第片
单位产品不合格数的 u图
k np = np1 + np2 ++ npk
UCLnp np 3 np(1 np ) n np
LCLnp np 3 np(1 ) n
)
其中k为子组数 ,n为这些子组 的样本容量。
第片
np 图
• 课堂练习
– 用附录7中的数据计算np出控制范围的情况。
•
做一枚螺丝钉,那里需要那里上。20. 11.1623 :51:352 3:51No v-2016 -No v-2 0
•
日复一日的努力只为成就美好的明天 。23:51:3523:51:3523:51Monday, November 16, 2020
•
安全放在第一位,防微杜渐。20.11.1620.11.1623:51:3523:51:35November 16, 2020
•
相信命运,让自己成长,慢慢的长大 。2020年11月16日星 期一11时51分35秒Monday, November 16, 2020
•
爱情,亲情,友情,让人无法割舍。20.11.162020年 11月16日星期 一11时 51分35秒20.11.16
谢谢大家!
)
第片
SPC - 计数型数据
模块 11
编制: World Class Quality Pty Ltd 授课人: John Adamek
课程目标
• 到本课程结束时,学员应能识别: 1. 计数型SPC数据控制图
2. 何时使用这些图最合适
)
第片
如何选择正确的SPC图
计数型 数据
P图
计算零件数 N = 固定值或变 值
)
第片
不合格数的
c图
• 何时使用 c 图
• 当数据为计数型数据时(一种可以计数的属 性)。
• 当不合格是分布于整个产品时,如油漆部件 上的缺陷数,装配工序上的缺陷数等。
• 当不合格现 象可从多个来源发现,或由多 种原因造成时。
)
第片
c图
• 计算 c 图的方法
– 确保检验样本的容量都相等,如零件的数量,规定 的面积或体积。
•
这些年的努力就为了得到相应的回报 。2020年11月16日星 期一11时51分35秒23:51:3516 November 2020
•
科学,你是国力的灵魂;同时又是社 会发展 的标志 。下午11时51分35秒 下午11时51分23:51:3520.11.16
•
每天都是美好的一天,新的一天开启 。20.11.1620.11.1623:5123:51:3523:51:35Nov-20
p
=
n1p1 + n2p2 + + nkpk n1 + n2 +nk
p(1 p) UCLp p 3
n
p(1 p) LCLp p 3
n
注:如果 LCL 的计算结果为负值,则 LCL 应为默认值 0 。
)
注: n1p1 等是所发现 的不合格产品的数量 ,n1, n2 等是相应的 样品容量。
第片
p图
