三阶幻方专项练习题
三阶幻方练习题
同学们:
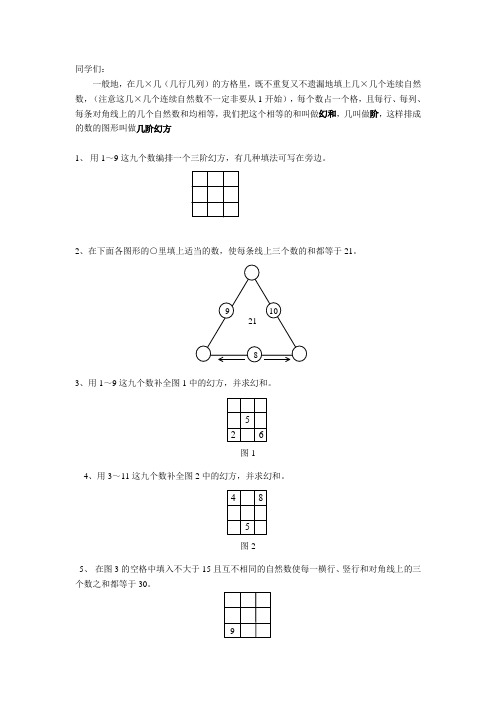
一般地,在几×几(几行几列)的方格里,既不重复又不遗漏地填上几×几个连续自然数,(注意这几×几个连续自然数不一定非要从1开始),每个数占一个格,且每行、每列、每条对角线上的几个自然数和均相等,我们把这个相等的和叫做幻和,几叫做阶,这样排成的数的图形叫做几阶幻方
1、用1~9这九个数编排一个三阶幻方,有几种填法可写在旁边。
2、在下面各图形的○里填上适当的数,使每条线上三个数的和都等于21。
3、用1~9这九个数补全图1中的幻方,并求幻和。
5
26
图1
4、用3~11这九个数补全图2中的幻方,并求幻和。
48
5
图2
5、在图3的空格中填入不大于15且互不相同的自然数使每一横行、竖行和对角线上的三个数之和都等于30。
9。
三阶幻方题目初一

三阶幻方题目初一
以下是关于三阶幻方的初一题目:
1. 什么是三阶幻方?
2. 在三阶幻方中填入数字1-9,使得每行、每列和每条对角线上的数字之和都相等,这个和是多少?
3. 如果在三阶幻方中填入数字1-9,使得每行、每列和每条对角线上的数字之和都是奇数,有哪些填法?
4. 在三阶幻方中填入数字1-9,使得每行、每列和每条对角线上的数字之和都是偶数,有哪些填法?
5. 在三阶幻方中填入数字1-9,使得每行、每列和每条对角线上的数字之和都是质数,有哪些填法?
6. 在三阶幻方中填入数字1-9,使得每行、每列和每条对角线上的数字之和都是3的倍数,有哪些填法?
7. 在三阶幻方中填入数字1-9,使得每行、每列和每条对角线上的数字之和都是平方数,有哪些填法?
8. 在三阶幻方中填入数字1-9,使得每行、每列和每条对角线上的数字之和都是立方数,有哪些填法?
这些题目可以作为初一学生的练习题,通过解答这些题目,可以加深学生对三阶幻方的理解。
三阶幻方练习题。之欧阳治创编

欧阳治创编 2021.03.101.用3、6、9、12、15、18、21、24、27这9个数作一个三阶幻方。
2.3.用0、2、4、6、8、10、12、14、16这9个数作一个三阶幻方。
12题4.在空格中填数,使每一行,每一列、每条对角线的和都等于30.4. 用9个连续自然数组成三阶幻方, 使每一行、每一列、每条对角线的和都是603题5.一个三阶幻方的幻和是60.这个幻方最中间的数是()。
组成幻方的9个数的和是()6..一个三阶幻方,最中间的数是30,这个幻方的幻和是()。
组成幻方的9个数的和是()7..一个三阶幻方的幻和是45.这个幻方最中间的数是()。
()8..一个三阶幻方,最中间的数是8,这个幻方的幻和是()。
组成幻方的9个数的和是()9. 用1,2,3,4,5,6,7,8,9 写一个三阶幻方。
用3、6、9、12、15、18、21、24、27这9个数作一个三阶幻方。
10. 将6,6,6,8,8,8,10,10,10这9个数填入幻方三阶幻方是每行每列对角线上三个数的和都相等。
欧阳治创编2021.03.10欧阳治创编 2021.03.1011.在空格里填数,使横竖对角线上三个数的和是21. 7. 使横竖对角线上三个数的和是30.12.填上其他8个数,使得方格中的9个数为9个连续自然数。
9. 有蜘蛛、蜻蜓、蝉三种昆虫共18只,共有腿118条。
翅膀20对,( 蜘蛛8条腿,蜻蜓6条腿,2对翅膀,蝉6条腿,1对翅膀),三种昆虫各多少只?10. 蜘蛛8条腿,蜻蜓6条腿,2对翅膀,蝉6条腿,1对翅膀。
这三种昆虫共有21只,有140条腿和23对翅膀.求每种昆虫各几只?11. 有一个车队以每秒行5米的速度通过一座长200米的大桥共用145秒.已知每辆车长5米.一个车队以每秒行五米的速度通过一座长200米的大桥共用一145秒.已知每辆车长5米,两车隔8米,这个车队有多少辆车?12. 小明步行上学,每分钟行70米,离家12分钟后,爸爸发现小明的文具盒忘记在家里,立即骑自行车以每分钟280米的速度去小明,那么爸爸出发后几分钟追上小明?13. 一队中学生到某地进行军事训练,他们以每小时5千米的速度前进,走了6小时后,学校派秦老师骑自行车以每小时15千米的速度追赶学生队伍,传达学校通知。
三阶幻方
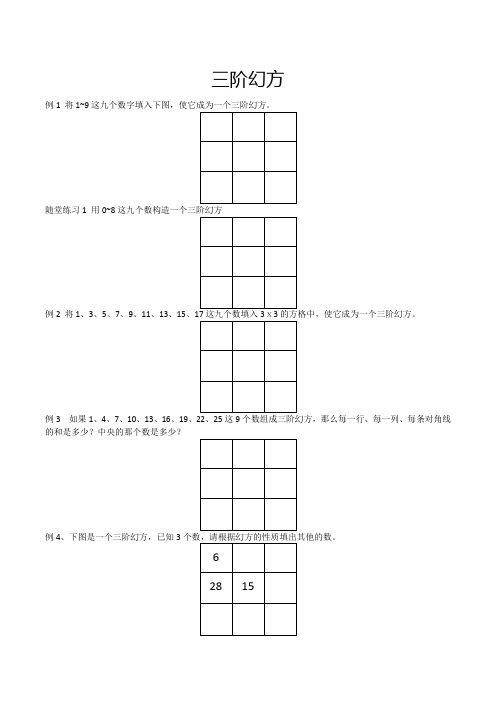
6
28
15
例5、已知下图中,每一行、每一列对角线上3个数的乘积都相等,请填出其他的数。
1
12
6
3
例6已知下图是一个三阶幻方,每一行、每一列、每条对角线的和都等于2037,求画有“?”的格子填的数是多少。
447
?
894
练习题
1、用3、6、9、12、15、18、21、24、27这9个数作一个三阶幻方。
三阶幻方
例1将1~9这九个数字填入下图,使它成为一个三阶幻方。
随堂练习1用0~8这九个数构造一个三阶幻方
例2将1、3、5、7、9、11、13、15、17这九个数填入3ⅹ3的方格中,使它成为一个三阶幻方。
例3如果1、4、7、10、13、16、19、22、25这9个数组成三阶幻方,那么每一行、每一列、每条对角线的和是多少?中央的那个数是多少?
2、用0、2、4、6、8、10、12、14、16这9个数作一个三阶幻方。
3、在空格中填数,使每一行、每一列、每条对角线的和都等于30.
5
8
4、在空格中填数,使每一行、每一列、每条对角线的和都等于30.
14
7
5、数独游戏
3
5
6
5
1
3
9
8
3
1
2
5
1
65Leabharlann 7843
4
9
1
4
8
3
1
5
7
7
5
4
2
8
9
7
1
5
8
4
9
三阶幻方练习题。精编版
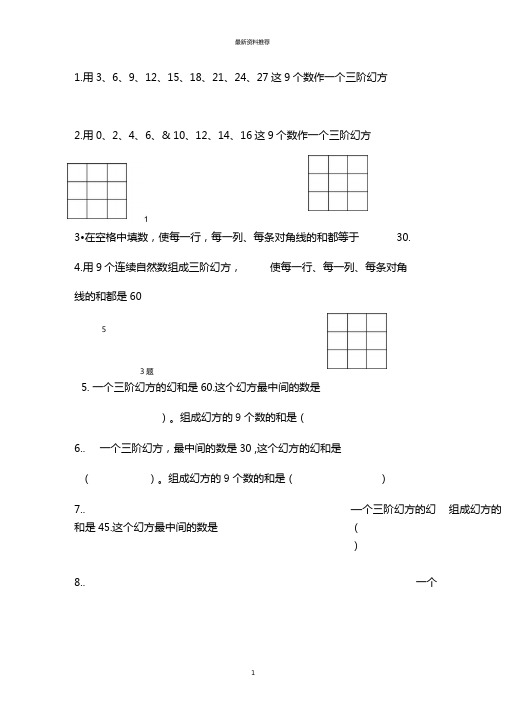
1.用3、6、9、12、15、18、21、24、27这9个数作一个三阶幻方2.用0、2、4、6、& 10、12、14、16这9个数作一个三阶幻方3•在空格中填数,使每一行,每一列、每条对角线的和都等于 4.用9个连续自然数组成三阶幻方, 使每一行、每一列、每条对角 线的和都是605.一个三阶幻方的幻和是60.这个幻方最中间的数是)。
组成幻方的9个数的和是(6.. 一个三阶幻方,最中间的数是30 ,这个幻方的幻和是( )。
组成幻方的9个数的和是( )7.. —个三阶幻方的幻和是45.这个幻方最中间的数是 ()8.. 一个□ 5□ □ □ □ □ □ 3题30.组成幻方的三阶幻方,最中间的数是8,这个幻方的幻和是()组成幻方的9个数的和是()9.用1,234,5,6,7,8,9 写一个三阶幻方。
用3、6、9、12、15、18、21、24、27这9个数作一个三阶幻方。
10.将6,6,6,8,8,8,10,10,10这9个数填入幻方格中, 5.用0—— -8 这9个数,做一个三阶幻方是每行每列对角线上三个数的和都相等。
r D 13 12 10 □td D D12填上其他8个数,使得方格中的9个数为9个连续自然数。
i i18 只,共有腿 118 条。
翅膀 20 对,( 蜘蛛 8 条腿,蜻蜓 6 条腿, 2对翅膀,蝉 6 条腿, 1 对翅膀),三种昆虫各多少只?7.使横竖对角线上三个数的和是□ □ 6n 7 □ □ j 9. 有蜘蛛、蜻蜓、蝉三种昆虫共 310.蜘蛛 8 条腿,蜻蜓 6 条腿, 2 对翅膀,蝉 6 条腿, 1 对翅膀。
这三种昆虫共有 21 只 , 有 140 条腿和23 对翅膀 . 求每种昆虫各几只?11.有一个车队以每秒行 5 米的速度通过一座长 200 米的大桥共用 145 秒.已知每辆车长 5 米.一个车队以每秒行五米的速度通过一座长200 米的大桥共用一 145 秒.已知每辆车长5 米,两车隔 8 米 ,这个车队有多少辆车?12.小明步行上学,每分钟行 70 米,离家 12 分钟后,爸爸发现小明的文具盒忘记在家里,立即骑自行车以每分钟 280 米的速度去小明,那么爸爸出发后几分钟追上小明?13.一队中学生到某地进行军事训练,他们以每小时 5 千米的速度前进,走了 6 小时后,学校派秦老师骑自行车以每小时 15 千米的速度追赶学生队伍,传达学校通知。
三阶幻方20道题

三阶幻方20道题一、基础数字型1. 用1 - 9这九个数字组成一个三阶幻方,使每行、每列、每条对角线上的数字之和都相等。
这就像是把9个性格各异的小伙伴(1 - 9这些数字)安排在一个九宫格的小房间里,让每行、每列、每条对角线上的小伙伴凑在一起的力量(数字之和)都一样呢。
2. 请用3、4、5、6、7、8、9、10、11这九个连续的数字构建一个三阶幻方。
想象一下,这就像把九个连续的小怪兽按照特殊的规则(幻方规则)关在九宫格的笼子里,让它们横竖斜都保持一种神秘的平衡。
3. 用5、6、7、8、9、10、11、12、13构建三阶幻方。
这九个数字就像九个魔法小精灵,要让它们在九宫格这个魔法阵里站好位置,使得每行、每列、每条对角线小精灵的魔力总和(数字之和)是一样的哦。
二、给定和值型4. 构建一个三阶幻方,要求每行、每列、每条对角线上的数字之和为15。
这就像是一场数字的聚会,每个数字都要找到自己的位置,让三个数字凑在一起的总和是15这个神奇的数字。
5. 构造一个三阶幻方,其每行、每列、每条对角线上的数字之和为18。
你可以把它想象成一个数字拼图游戏,把合适的数字放进九宫格,让它们达到18这个“小目标”。
6. 制作一个三阶幻方,使得每行、每列、每条对角线上的数字之和为21。
这就像要把数字当作小砖头,砌成一个九宫格的小房子,而且这个小房子的每条边(行、列、对角线)所用砖头数量之和(数字之和)得是21呢。
三、部分数字给定型7. 在三阶幻方中,左上角的数字是1,其他数字未知,请完成这个幻方。
这就像在一个神秘的九宫格迷宫里,你已经知道了入口(左上角数字1),现在要根据幻方的魔法规则找到其他数字的出口。
8. 已知三阶幻方中间一格的数字是5,构建完整的幻方。
这个5就像九宫格的中心小太阳,你要围绕着它放置其他数字,就像行星围绕太阳一样,让整个幻方符合规则。
9. 三阶幻方的右下角数字是9,请完成这个幻方。
这个9就像一个小尾巴,你得从这个小尾巴开始倒推,把其他数字合理地安排在九宫格中。
三阶幻方练习十二题之欧阳光明创编

把7—15这九个数构成一个三阶幻方。
欧阳光明(2021.03.07)
把3、4、5、8、9、10、13、14、15编成一个三阶幻方,并求出幻和是多少?
用3、6、9、12、15、18、21、24、27这9个数作一个三阶幻方。
用0、2、4、6、8、10、12、14、16这9个数作一个三阶幻方 。
构成一个三阶幻方,使其幻和是18。
用9个连续自然数组成三阶幻方, 使每一行、每一列、每条对角线的和都是60
用9个连续的自然数构造一个三阶幻方,使每一横行、竖列、对角线的三个数的和等于30。
用3~11这九个数补全图中的幻方,并求幻和。
在图的空格中填入不大于15
的自然数使每一横行、竖行和对角线上的三个数之
和都等于30。
条对角线的和都等于30.
在空格中填数,使每一行,每一列、每
条对角线的和都等于30.
下图是一个三阶幻方。
求“?”是多
少。
三阶幻方练习题。

1.用3、6、9、12、15、18、21、24、27这9个数作一个三阶幻方。
2.用0、2、4、6、8、10、12、14、16这9个数作一个三阶幻方。
1 2题3.在空格中填数,使每一行,每一列、每条对角线的和都等于30.4. 用9个连续自然数组成三阶幻方, 使每一行、每一列、每条对角线的和都是603题5.一个三阶幻方的幻和是60.这个幻方最中间的数是 ( )。
组成幻方的9个数的和是( )6. .一个三阶幻方,最中间的数是30,这个幻方的幻和是( )。
组成幻方的9个数的和是( )7..一个三阶幻方的幻和是45.这个幻方最中间的数是()。
组成幻方的8..一个三阶幻方,最中间的数是8,这个幻方的幻和是()。
组成幻方的9个数的和是()9. 用1,2,3,4,5,6,7,8,9 写一个三阶幻方。
用3、6、9、12、15、18、21、24、27这9个数作一个三阶幻方。
10. 将6,6,6,8,8,8,10,10,10这9个数填入幻方格中, 5. 用0---8这9个数,做一个三阶幻方是每行每列对角线上三个数的和都相等。
11.在空格里填数,使横竖对角线上三个数的和是21.7. 使横竖对角线上三个数的和是30.12.填上其他8个数,使得方格中的9个数为9个连续自然数。
9. 有蜘蛛、蜻蜓、蝉三种昆虫共18只,共有腿118条。
翅膀20对,(蜘蛛8条腿,蜻蜓6条腿,2对翅膀,蝉6条腿,1对翅膀),三种昆虫各多少只?10. 蜘蛛8条腿,蜻蜓6条腿,2对翅膀,蝉6条腿,1对翅膀。
这三种昆虫共有21只,有140条腿和23对翅膀.求每种昆虫各几只?11. 有一个车队以每秒行5米的速度通过一座长200米的大桥共用145秒.已知每辆车长5米.一个车队以每秒行五米的速度通过一座长200米的大桥共用一145秒.已知每辆车长5米,两车隔8米,这个车队有多少辆车?12. 小明步行上学,每分钟行70米,离家12分钟后,爸爸发现小明的文具盒忘记在家里,立即骑自行车以每分钟280米的速度去小明,那么爸爸出发后几分钟追上小明?13.一队中学生到某地进行军事训练,他们以每小时5千米的速度前进,走了6小时后,学校派秦老师骑自行车以每小时15千米的速度追赶学生队伍,传达学校通知。
三阶幻方练习题。

1. 用3、6、9、12、15、18、21、24、27这9个数作一个三阶幻方2. 用0、2、4、6、8、10、12、14、16这9个数作一个三阶幻方13. 在空格中填数,使每一行,每一列、每条对角线的和都等于30.4. 用9个连续自然数组成三阶幻方,使每一行、每一列、每条对角线的和都是60□5□□□□□□3题5. 一个三阶幻方的幻和是60.这个幻方最中间的数是()。
组成幻方的9个数的和是()6.. 一个三阶幻方,最中间的数是30 ,这个幻方的幻和是()。
组成幻方的9个数的和是()7.. —个三阶幻方的幻和是45.这个幻方最中间的数是()。
组成幻方的8.. —个三阶幻方,最中间的数是8,这个幻方的幻和是(组成幻方的9个数的和是() 9.用1,234,5,6,7,8,9 写一个三阶幻方。
18、21、24、27这9个数作一个三阶幻方。
10.将6,6,6,8,8,8,10,10,10 这9个数填入幻方格中, 5.用0 — --8这9个数,做一个三阶幻方11.在空格里填数,使横竖对角线上三个数的和是2 1 . 7.使横竖对角线上三个数的和是是每行每列对角线上三个数的 用 3、6、9、12、15、12.填上其他8个数,使得方格中的9个数为9个连续自然数。
9. 有蜘蛛、蜻蜓、蝉三种昆虫共18 只,共有腿118 条。
翅膀20 对,(蜘蛛8 条腿,蜻蜓6 条腿, 2 对翅膀,蝉 6 条腿, 1 对翅膀),三种昆虫各多少只?10. 蜘蛛8 条腿,蜻蜓 6 条腿, 2 对翅膀,蝉 6 条腿, 1 对翅膀。
这三种昆虫共有21 只,有140 条腿和23 对翅膀. 求每种昆虫各几只?11. 有一个车队以每秒行 5 米的速度通过一座长200 米的大桥共用145 秒.已知每辆车长 5 米.一个车队以每秒行五米的速度通过一座长200 米的大桥共用一145 秒.已知每辆车长5 米,两车隔8 米, 这个车队有多少辆车?12. 小明步行上学,每分钟行70 米,离家12 分钟后,爸爸发现小明的文具盒忘记在家里,立即骑自行车以每分钟280 米的速度去小明,那么爸爸出发后几分钟追上小明?13. 一队中学生到某地进行军事训练,他们以每小时 5 千米的速度前进,走了 6 小时后,学校派秦老师骑自行车以每小时15 千米的速度追赶学生队伍,传达学校通知。
三阶幻方练习题。

1.用3、6、9、12、15、18、21、24、27这9个数作一个三阶幻方。
2.用0、2、4、6、8、10、12、14、16这9个数作一个三阶幻方。
1 2题3.在空格中填数,使每一行,每一列、每条对角线的和都等于30.4. 用9个连续自然数组成三阶幻方, 使每一行、每一列、每条对角线的和都是603题5.一个三阶幻方的幻和是60.这个幻方最中间的数是 ( )。
组成幻方的9个数的和是( )6. .一个三阶幻方,最中间的数是30,这个幻方的幻和是( )。
组成幻方的9个数的和是( )7. 一个三阶幻方的幻和是45.这个幻方最中间的数是 ( )。
组成幻方的9个数的和是( )8..一个三阶幻方,最中间的数是8,这个幻方的幻和是( )。
组成幻方的9个数的和是( )9. 用1,2,3,4,5,6,7,8,9 写一个三阶幻方。
用3、6、9、12、15、18、21、24、27这9个数作一个三阶幻方。
10. 将6,6,6,8,8,8,10,10,10这9个数填入幻方格中, 5. 用0---8 这9个数,做一个三阶幻方是每行每列对角线上三个数的 和都相等。
11.在空格里填数,使横竖对角线上三个数的和是21. 7. 使横竖对角线上三个数的和是30.12.填上其他8个数,使得方格中的9个数为9个连续自然数。
9.有蜘蛛、蜻蜓、蝉三种昆虫共18只,共有腿118条。
翅膀20对,( 蜘蛛8条腿,蜻蜓6条腿,2对翅膀,蝉6条腿,1对翅膀),三种昆虫各多少只?10. 蜘蛛8条腿,蜻蜓6条腿,2对翅膀,蝉6条腿,1对翅膀。
这三种昆虫共有21只,有140条腿和23对翅膀.求每种昆虫各几只?11. 有一个车队以每秒行5米的速度通过一座长200米的大桥共用145秒.已知每辆车长5米.一个车队以每秒行五米的速度通过一座长200米的大桥共用一145秒.已知每辆车长5米,两车隔8米,这个车队有多少辆车?12. 小明步行上学,每分钟行70米,离家12分钟后,爸爸发现小明的文具盒忘记在家里,立即骑自行车以每分钟280米的速度去小明,那么爸爸出发后几分钟追上小明?13.一队中学生到某地进行军事训练,他们以每小时5千米的速度前进,走了6小时后,学校派秦老师骑自行车以每小时15千米的速度追赶学生队伍,传达学校通知。
2022年三阶幻方讲解和练习题

2022年三阶幻方讲解和练习题幻方起源于中国. 传说在大禹治水时,有只神龟在洛水中浮起,龟背上有奇特的图案,如右图. 人们称之为洛书.如果将龟背上的数字翻译出来,如下图.观察,你发现了什么? 观察发现,上图的每行每列,斜着的三个数之和都是15. 像这样,将九个不同的自然数填在3×3(三行三列)的正方形内,使每行、每列以及每条对角线上的三个数和都相等,这样的图形就叫三阶幻方. 三阶幻方是一种特殊的数阵图.上面的三阶幻方中,15是这个幻方的和,简称幻和. 5是幻方最中心的数字,简称中心数.三阶幻方的规律:(1)幻和= 九个数之和 ÷3; (2)中间数=幻和÷3(3)四个角上的数字 2=(3+1)÷2,8=(9+7)÷2例题1 在图中填上合适的数,使每行、每列、每一条对角线的三个数的和都相等。
巩固练习:在下图的方格中填上适合的数,使每行、每列、每一条对角线的三个数的和都等于21。
73 84 63 二、例题讲解 672159834例题2 在下图中填上适当的数,使每行、每列、每条对角线上的三个数的和都相等。
巩固练习:根据三阶幻方的特点,完成下列幻方。
例题3 在下图的每个空格中填入小于12且互不相同的九个自然数,使得每行、每列及每条对角线上的三个数之和都等于21。
巩固练习:在下列右图空着的方格内填上合适的数,使得每一横行、每一竖列和对角 线上的三个数之和都等于27。
例题4 将1~9这九个自然数填在下面图中的九个方格里,使每行、每列、两条对角线上的三个数的和都相等。
19 1410 18 812介绍杨辉法:介绍公式法:口诀:九子斜列,上下对易,左右相更,四维挺出。
想一想还有没有其他填法:第一种:816 357 492第二种:618 753 294第三种:492357816第四种:294753618第五种:672159834第六种:834159672第七种:276951438第八种:438951276巩固练习:用3-11构造一个三阶幻方课堂练习1、把4~12九个数填入方格中,使每行、每列、每一条对角线的三个数的和都相等。
