16位乘法器芯片设计 3月9日
16位有符号乘法器设计

对每个部分积,符号扩展的过程可以看成符号位取非,再上全 1 的扩展。这也是前面部 分积产生电路中取 E 为符号位的非的原因。 对于全 1 的扩展,可以预先计算出结果。如图 6 中的 1 阵列,经过计算,可以化简成 图 7 的样子。 然后,加上符号位的非,得图 8。类似前面符号位扩展,可以把 E+(11)b 变为 EEE 。(图 9)
1. 部分积的产生
我们知道,N 位补码表示的数,它的值等于
val ( X ) X N 1 2N 1 X N 2 2N 2
X 2 22 X1 21 X 0 20
2 / 12
根据 ( X k ) 2k ( X k ) 2k 1 (2 X k ) 2k 1 ,可以把一个奇数项分解成前后两个偶数项 (图 1),那么部分积的数量减少了一半。变换之后,X 的值可以表示为
表 1 Wallace 资源使用情况
资源 半加器 全加器
数量 22 个 91 个
7 / 12
16 bits
A
PP[i] 1 E E S Half Adder Full Adder
B
C
D
E
F
图 10 构造 Wallace Tree
3) 加法器的选择 使用 DC 综合时,可以指定加法器的实现方式。在 Verilog 代码中,通过注释指定 DC 综 合时选用的加法器类型, 如图 11。 根据 synopsys 提供的 DesignWare Building Block IP user guide,在设计中指定模块实现的方法如下。
二. 方案选择
编码方式: Booth2 编码 拓扑结构: Wallace 树 加法器:Carry look ahead Adder Booth2 编码可以使部分积的数量减半,并且解决了符号问题,也就是说,符号位不需要 单独处理。 部分积的累加采用 Wallace 树,和其它拓扑结构相比,Wallace 具有硬件节省,延时小的 优点,Wallace 树的传播延时等于 O(log3/2 N ) 。 最终相加使用的加法器使用的是 DesignWare 中的超前进位加法器,通过在 Verilog 中添 加 synopsis 控制命令来明确指定 DC 选择何种实现。
16位(8x8)硬件乘法器设计报告

EDA课程设计16位(8x8)硬件乘法器设计学校:华侨大学学院:信息与工程学院班级:10集成姓名:项传煜学号:1015251031老师:凌朝东目录摘要一.设计要求二.正文2.1. 系统设计2.1.1 系统设计方案 (3)2.1.2 系统设计原理 (4)2.2. 各子模块设计2.2.1 十进制加计数器设计 (5)2.2.2 BCD码转二进制码BCD_B的设计 (5)2.2.3 8位移位寄存器reg_8的设计 (6)2.2.4 8位加法器adder_8的设计 (7)2.2.5 1位乘法器multi_1的设计 (7)2.2.6 16位移位寄存器reg_16的设计 (8)2.2.7 16位二进制转BCD码B_BCD的设计 (9)2.3. 软件设计2.3.1 设计平台和开发工具 (10)2.3.2 程序流程方框图 (10)2.3.3 实现功能 (11)2.3.4 8位乘法器的顶层设计 (11)2.4. 系统测试2.4.1 乘法器使用 (13)2.4.2 仪器设备 (13)2.4.3 测试数据 (14)2.5. 结论 (14)三.测试结果仿真图 (14)四.参考文献 (15)五.附录:设计说明书及使用说明书 (15)摘要本设计通过对一个8×8的二进制乘法器的设计,学习利用VHDL语言来描述简单的算法,掌握利用移位相加方法实现乘法运算的基本原理。
在此次设计中该乘法器是由十进制计数器,BCD码(输入)转二进制码,8位寄存器,8位加法器,16位寄存器,8x1乘法器,二进制码转BCD码(输出显示)7个模块构成的以时序方式设计的8位乘法器,采用逐项移位相加的方法来实现相乘。
设计中乘数,被乘数的十位和个位分别采用cnt10(十进制加法器)来输入,经拼接符“&”拼接成8位BCD码,再由BCD_B(BCD码转二进制码)转化成二进制码后计算,计算结果由B_BCD(二进制转BCD码)转化成BCD码输入到数码管中显示。
十六位硬件乘法器电路设计报告

课程名称电子设计自动化题目十六位硬件乘法器电路院系班级信息学院11电子信息工程A班姓名学号指导老师凌朝东2013 年 12 月 5 日题目名称:十六位硬件乘法器电路摘要:设计一个16位硬件乘法器电路.要求2位十进制乘法,能用LED数码管同时显示乘数,被乘数和积的值.本设计利用Quartus II软件为设计平台,通过移位相加的乘法原理:即从被乘数的最低位开始,若为1,则乘数左移后与上一次的和相加;若为0,左移后以全零相加,直至被乘数的最高位。
经软件仿真和硬件测试验证后,以达到实验要求。
目录1.题目名称 (2)2.摘要 (2)3.目录 (3)4.正文 (4)4.1. 系统设计 (4)4.1 设计要求 (4)4.2 系统设计方案 (4)4.2 单元电路设计 (4)4.2.1十进制计算模块 (5)4.2.2 BCD码转二进制模块 (5)4.2.3 8位右移寄存器模块 (6)4.2.4 8位加法器模块 (7)4.2.5 1乘法器multi_1模块 (7)4.2.6 16位移位寄存器reg_16模块 (8)4.2.7 16位二进制转BCD码B_BCD模块 (9)4.2.8 8位乘法器multi_8x8顶层设计 (10)4.3 软件设计 (12)4.3.1设计平台和开发工具 (12)4.3.2程序流程方框图 (13)4.4 系统测试 (14)4.1仿真分析 (14)4.2硬件验证 (15)5. 结论 (15)6. 参考文献 (15)7. 附录 (15)4.正文4.1系统设计1.1设计要求题目要求设计一个16位硬件乘法器电路.要求2位十进制乘法;能用LED数码管同时显示乘数,被乘数和积的信息.设置一个乘法使能端,控制乘法器的计算和输出.1.2系统设计方案此设计问题可分为乘数和被乘数输入控制模块,乘法模块和输出乘积显示模块基本分.乘数和被乘数的输入模块使输入的十进制数转化为二进制数输入乘法模块,乘法模块利用移位相加的方法将输入的两组二进制数进行相乘,并将16位乘积输出到乘积输出显示模块.显示模块将输入的二进制数按千,百,十,个位分别转化为十进制数输出.乘数和被乘数的输入可用数据开关K1~K10分别代表数字1,2,…,9,0,用编码器对数据开关K1~K10的电平信号进行编码后输入乘法器进行计算.但此方案所用硬件资源较多,输入繁琐,故不采取.方案二是利用硬件箱自带16进制码发生器,由对应的键控制输出4位2进制构成的1位16进制码,数的范围是0000~1111,即0H~FH.每按键一次,输出递增1,输出进入目标芯片的4位2进制数将显示在该键对应的数码管.乘数和被乘数的输入模块将16进制码的A~F码设计成输出为null.使得减少了无用码的输入.两数相乘的方法很多,可以用移位相加的方法,也可以将乘法器看成计数器,乘积的初始值为零,每一个时钟周期将乘数的值加到积上,同时乘数减一,这样反复执行,直到乘数为零.本设计利用移位相加的方法使得程序大大简化.系统总体电路组成原理图如下图所示:4.2单元电路设计下面分解8位乘法器的层次结构,分为以下7个模块:1. 十进制计算模块:使用4个十进制计数模块,输入乘数的十位个位,被乘数的十位个位。
kk16位硬件乘法器

十六位硬件乘法器一、摘要1、设计要求:位宽十六,输入2个两位十进制相乘,能在数码管上显示积的信息!2、原理说明:十六位硬件乘法器可以分解为由2个8位2进制相乘得到,但要求输入十进制,故可用8421BCD码将2位十进制译成8位2进制即可,本次课设使用的是移位相加法来实现乘法!3、开发板使用说明:sw1到sw8开关是数据输入按键,即一次可同时输入八位数据,对于运算y=a*b,由于加入了辅助程序,总共要输入2次,每次输入的数据分别代表a转换为2进制的八位数,b转换成2进制的八位数,。
每按一次按键s3,即输入当前所设定的八位数据一次,,在数据输入完成后,按s2,进行运算,并由数码管输出用十进制表示的结果。
二、正文1、系统设计方案提出由于是2位的十进制,输入的数据不是很大,转换为二进制也是8位,故想到使用移位相加的方法来实现乘法的功能,同时移位相加是最节省资源的一种方法,其思路是乘法通过逐项移位相加来实现,根据乘数的每一位是否为1,若为1将被乘数移位相加,比较简单,适合本次课程设计。
2,电路划分,电路主要由3部分组成,第一部分是将输入的十进制译成2进制,第二部分是乘法器部分,第三部分是将得到的16位二进制结果译为十进制!第一部分LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;USE IEEE.STD_LOGIC_UNSIGNED.ALL;ENTITY chengshu ISPORT (a: IN STD_LOGIC_VECTOR(3 DOWNTO 0);cq : OUT STD_LOGIC_VECTOR(7 DOWNTO 0) );END chengshu;ARCHITECTURE behav OF chengshu ISBEGINprocess(a)begincase a iswhen "0000" => cq<="00000000";when "0001" => cq<="00001010";when "0010" => cq<="00010100";when "0011" => cq<="00011110";when "0100" => cq<="00101000";when "0101" => cq<="00110010";when "0110" => cq<="00111100";when "0111" => cq<="01000110";when "1000" => cq<="01010000";when "1001" => cq<="01011010";when others =>null;end case ;end process;end ARCHITECTURE behav;library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;entity add8 isport(a:in std_logic_vector(7 downto 0);b:in std_logic_vector(3 downto 0);qout:out std_logic_vector(7 downto 0));end add8;architecture ab of add8 issignal tmp1,tmp2,tmp:std_logic_vector(8 downto 0); begintmp1<='0'&a;tmp2<="00000"&b;tmp<=tmp1+tmp2;qout<=tmp(7 downto 0);end ab;第二部分:library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;entity cheng isport ( start : in std_logic;a : in std_logic_vector(7 downto 0);b : in std_logic_vector(7 downto 0);y : out std_logic_vector(15 downto 0)); end cheng;architecture behav of cheng issignal ql : std_logic_vector(7 downto 0);signal qz : std_logic_vector(7 downto 0);signal qy : std_logic_vector(15 downto 0);beginprocess(a,ql,qz,qy,b,start)variable q0 : std_logic_vector(15 downto 0); variable q1 : std_logic_vector(15 downto 0); variable q2 : std_logic_vector(15 downto 0); variable q3 : std_logic_vector(15 downto 0); variable q4 : std_logic_vector(15 downto 0); variable q5 : std_logic_vector(15 downto 0); variable q6 : std_logic_vector(15 downto 0); variable q7 : std_logic_vector(15 downto 0); variable q8 : std_logic_vector(15 downto 0); beginql<=a;qz<=b;q8:="0000000000000000";q7:="00000000"&ql;q0:="00000000"&ql;q7:=q7+q7;q1:=q7;q7:=q7+q7;q2:=q7;q7:=q7+q7;q3:=q7;q7:=q7+q7;q4:=q7;q7:=q7+q7;q5:=q7;q7:=q7+q7;q6:=q7;q7:=q7+q7;if start='1' thenif qz(0)='1' then q8:=q8+q0;end if;if qz(1)='1' then q8:=q8+q1;end if;if qz(2)='1' then q8:=q8+q2;end if;if qz(3)='1' then q8:=q8+q3;end if;if qz(4)='1' then q8:=q8+q4;end if;if qz(5)='1' then q8:=q8+q5;end if;if qz(6)='1' then q8:=q8+q6;end if;if qz(7)='1' then q8:=q8+q7;end if;end if;qy<=q8;end process;y<=qy;end behav;第三部分IBRARY ieee;USE ieee.std_logic_1164.all;USE ieee.std_logic_unsigned.all;USE ieee.std_logic_arith.all;ENTITY jian ISport( a: in std_logic_vector(15 downto 0) ;cnt : OUT std_logic_vector(15 downto 0) ;qout: OUT std_logic_vector(3 downto 0) );END ;ARCHITECTURE hdlarch OF jian ISBEGINprocess(a)beginif a>8999 then cnt<=a-9000;qout<="1001";elsif a>7999 then cnt<=a-8000;qout<="1000";elsif a>6999 then cnt<=a-7000;qout<="0111";elsif a>5999 then cnt<=a-6000;qout<="0110";elsif a>4999 then cnt<=a-5000;qout<="0101";elsif a>3999 then cnt<=a-4000;qout<="0100";elsif a>2999 then cnt<=a-3000;qout<="0011";elsif a>1999 then cnt<=a-2000;qout<="0010";elsif a>999 then cnt<=a-1000;qout<="0001";else cnt<=a ;qout<="0000";end if;end process;end hdlarch;LIBRARY ieee;USE ieee.std_logic_1164.all;USE ieee.std_logic_unsigned.all;USE ieee.std_logic_arith.all;ENTITY jian1 ISport( a: in std_logic_vector(15 downto 0) ;cnt : OUT std_logic_vector(15 downto 0) ;qout: OUT std_logic_vector(3 downto 0) );END ;ARCHITECTURE hdlarch OF jian1 ISBEGINprocess(a)beginif a>899 then cnt<=a-900;qout<="1001";elsif a>799 then cnt<=a-800;qout<="1000";elsif a>699 then cnt<=a-700;qout<="0111";elsif a>599 then cnt<=a-600;qout<="0110";elsif a>499 then cnt<=a-500;qout<="0101";elsif a>399 then cnt<=a-400;qout<="0100";elsif a>299 then cnt<=a-300;qout<="0011";elsif a>199 then cnt<=a-200;qout<="0010";elsif a>99 then cnt<=a-100;qout<="0001";else cnt<=a ;qout<="0000";end if;end process;end hdlarch;LIBRARY ieee;USE ieee.std_logic_1164.all;USE ieee.std_logic_unsigned.all;USE ieee.std_logic_arith.all;ENTITY jian2 ISport( a: in std_logic_vector(15 downto 0) ;cnt : OUT std_logic_vector(15 downto 0) ;qout: OUT std_logic_vector(3 downto 0) );END ;ARCHITECTURE hdlarch OF jian2 ISBEGINprocess(a)beginif a>89 then cnt<=a-90;qout<="1001";elsif a>79 then cnt<=a-80;qout<="1000";elsif a>69 then cnt<=a-70;qout<="0111";elsif a>59 then cnt<=a-60;qout<="0110";elsif a>49 then cnt<=a-50;qout<="0101";elsif a>39 then cnt<=a-40;qout<="0100";elsif a>29 then cnt<=a-30;qout<="0011";elsif a>19 then cnt<=a-20;qout<="0010";elsif a>9 then cnt<=a-10;qout<="0001";else cnt<=a ;qout<="0000";end if;end process;end hdlarch;但是由于2个8位2进制在开发板上不好输入和最后的16位不好译成十进制,故加入几段辅助程序减少其输入次数!library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;entity test_in isport(test_in: in std_logic_vector(7 downto 0);test_out_ah: out std_logic_vector(3 downto 0);test_out_al: out std_logic_vector(3 downto 0);test_out_bh: out std_logic_vector(3 downto 0);test_out_bl: out std_logic_vector(3 downto 0);clk: in std_logic;led: out std_logic);end entity;architecture one of test_in issignal test_temp: std_logic_vector(7 downto 0);signal cnt: std_logic;begin--process(clk)--begin--if(clk'event and clk='1')then--led<='1';--else--led<='0';--end if;--end process;process(clk)beginif(clk'event and clk='0')thencnt<=not cnt;test_temp<=test_in;end if;end process;process(cnt)begin--if(clk'event and clk='0')thenif(cnt='1')thentest_out_ah<=test_temp(7 downto 4);test_out_al<=test_temp(3 downto 0);elsetest_out_bh<=test_temp(7 downto 4);test_out_bl<=test_temp(3 downto 0);end if;--end if;end process;end architecture;library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;entity de_shake isport(key_in: in std_logic;key_out: out std_logic;clk_1_2hz: in std_logic);end entity;architecture one of de_shake issignal a,b,c: std_logic;beginprocess(clk_1_2hz)variable key_out_temp: std_logic;beginif(clk_1_2hz'event and clk_1_2hz='1')thena<= key_in;b<=a;c<=b;key_out_temp:=(a and b and c );end if;key_out<=key_out_temp;end process;end architecture;library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;entity fre_deshake isport(clk_50m: in std_logic;clk_deshake: out std_logic;clk_50: out std_logic);end entity;architecture one of fre_deshake issignal clk_temp: std_logic_vector(20 downto 0); beginclk_50<=clk_50m;process(clk_50m)beginif(clk_50m'event and clk_50m='1')thenclk_temp<=clk_temp+1;end if;end process;clk_deshake<=clk_temp(20);--clk_deshake(1)<=clk_temp(20);end architecture;library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;entity decode isport(clk_50M: in std_logic;input4: in std_logic_vector(3 downto 0);input3: in std_logic_vector(3 downto 0);input2: in std_logic_vector(3 downto 0);input1: in std_logic_vector(3 downto 0);output: out std_logic_vector(7 downto 0);address: out std_logic_vector(7 downto 0));end entity;architecture one of decode issignal div_clk: std_logic_vector(18 downto 0);signal mode: std_logic_vector(7 downto 0);signal data: std_logic_vector(3 downto 0);begindivclk:process(clk_50M)beginif(clk_50M'event and clk_50M='1')thendiv_clk<=div_clk+1;end if;end process;de_code_01: process(clk_50M,div_clk(18 downto 16))beginif(clk_50M'event and clk_50M='1')thencase div_clk(18 downto 16) iswhen "000"=>mode<="01111111";when "001"=>mode<="10111111";when "010"=>mode<="11011111";when "011"=>mode<="11101111";--when "100"=>--mode<="11110111";--when "101"=>--mode<="11111011";--when "110"=>--mode<="11111101";--when "111"=>--mode<="11111110";when others=>mode<="11111111";end case;end if;end process;de_code_02: process(mode)beginaddress <= mode;case mode iswhen "01111111"=>data<=input4;when "10111111"=>data<=input3;when "11011111"=>data<=input2;when "11101111"=>data<=input1;--when "11110111"=>--data<=input(15 downto 12);--when "11111011"=>--data<=input(11 downto 8);--when "11111101" =>--data<=input(7 downto 4);--when "11111110"=>--data<=input(3 downto 0);when others=>null;end case;end process;decode_03: process(data)begincase data iswhen "0000"=>output<="11000000";when "0001"=>output<="11111001";when"0010"=>output<="10100100";when"0011"=>output<="10110000";when"0100"=>output<="10011001";when"0101"=>output<="10010010";when"0110"=>output<="10000010";when"0111"=>output<="11111000";when"1000"=>output<="10000000";when"1001"=>output<="10010000";--when"1010"=>--output<="10001000";--when"1011"=>--output<="10000011";--when"1100"=>--output<="11000110";--when"1101"=>--output<="10100011";--when"1110"=>--output<="10000110";when others=>output<="10001110";end case;end process;end architecture;第二种方案(无硬件测试)library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;entity mult16_16 isport(clk: in std_logic;start: in std_logic;ina: in std_logic_vector(15 downto 0);inb: in std_logic_vector(15 downto 0);sout: out std_logic_vector(31 downto 0));end entity;architecture one of mult16_16 issignal cout1: std_logic_vector(19 downto 0);signal cout2: std_logic_vector(23 downto 0);signal cout3: std_logic_vector(27 downto 0);signal cout4: std_logic_vector(31 downto 0);signal a4b1: std_logic_vector(19 downto 0);signal a3b1: std_logic_vector(19 downto 0);signal a2b1: std_logic_vector(19 downto 0);signal a1b1: std_logic_vector(19 downto 0);signal a4b2: std_logic_vector(23 downto 0);signal a3b2: std_logic_vector(23 downto 0);signal a2b2: std_logic_vector(23 downto 0);signal a1b2: std_logic_vector(23 downto 0);signal a4b3: std_logic_vector(27 downto 0);signal a3b3: std_logic_vector(27 downto 0);signal a2b3: std_logic_vector(27 downto 0);signal a1b3: std_logic_vector(27 downto 0);signal a4b4: std_logic_vector(31 downto 0);signal a3b4: std_logic_vector(31 downto 0);signal a2b4: std_logic_vector(31 downto 0);signal a1b4: std_logic_vector(31 downto 0);beginprocess(clk)beginif(clk'event and clk='1')thena4b1<=((ina(15 downto 12)*inb(3 downto 0))&"000000000000");a3b1<=("0000"&(ina(11 downto 8)*inb(3 downto 0))&"00000000");a2b1<=("00000000"&(ina(7 downto 4)*inb(3 downto 0))&"0000");a1b1<=("000000000000"&(ina(3 downto 0)*inb(3 downto 0)));a4b2<=((ina(15 downto 12)*inb(7 downto 4))&"0000000000000000");a3b2<=("0000"&(ina(11 downto 8)*inb(7 downto 4))&"000000000000");a2b2<=("00000000"&(ina(7 downto 4)*inb(7 downto 4))&"00000000");a1b2<=("000000000000"&(ina(3 downto 0)*inb(7 downto 4))&"0000");a4b3<=((ina(15 downto 12)*inb(11 downto 8))&"00000000000000000000");a3b3<=("0000"&(ina(11 downto 8)*inb(11 downto 8))&"0000000000000000");a2b3<=("00000000"&(ina(7 downto 4)*inb(11 downto8))&"000000000000");a1b3<=("000000000000"&(ina(3 downto 0)*inb(11 downto 8))&"00000000");a4b4<=((ina(15 downto 12)*inb(15 downto 12))&"000000000000000000000000");a3b4<=("0000"&(ina(11 downto 8)*inb(15 downto 12))&"00000000000000000000");a2b4<=("00000000"&(ina(7 downto 4)*inb(15 downto 12))&"0000000000000000");a1b4<=("000000000000"&(ina(3 downto 0)*inb(15 downto 12))&"000000000000");end if;end process;process(clk)beginif(clk'event and clk='1')thencout1<=a4b1+a3b1+a2b1+a1b1;cout2<=a4b2+a3b2+a2b2+a1b2;cout3<=a4b3+a3b3+a2b3+a1b3;cout4<=a4b4+a3b4+a2b4+a1b4;end if;end process;process(clk,start)beginif(start='1')thensout<="00000000000000000000000000000000";elsesout<=("000000000000"&cout1)+("00000000"&cout2)+("0000"&cout3)+cout4;end if;end process;end architecture;仿真结果三,参考文献资料,EDA技术和VHDL,和同学一起讨论!四,仿真结果,随便输入几个数字后,进行仿真,结果正确,但只能用16进制看结果,因为是译成8421BCD码,是一位十进制数对应4位2进制,最终的结果范围是0~9801,需要16位2进制来对应!五,硬件测试在硬件上进行测试,结果正确!六,实验总结这次课设让我学会了很多东西,刚开始的时候对很多东西不是很理解,后来请教同学,查资料,虽然有些的程序不是自己写的,但跟同学讨论,请教,大概也懂得的那些程序是干什么用的,在最后测试的时候,在仿真阶段,刚开始一直仿真不对,以为是程序错误,但检验后程序并没有错误,由于是8421BCD码故应该用十六进制进行仿真。
EDA创新性实验项目——16位CPU设计

EDA创新性实验项目——16位CPU设计一、项目背景随着计算机科学和技术的不断发展,人们对计算机处理速度和性能的需求也在不断增加。
在这种背景下,为了满足人们对计算速度和性能的需求,研究者们开始将目光投向了新型的CPU设计。
传统的CPU设计多为32位或64位,但这种设计可能会带来一些不必要的复杂性和成本。
因此,设计一种16位CPU成为了当前研究的热点之一二、项目目标本实验项目旨在设计一款16位CPU,以满足轻量级计算需求,并保证其性能和效率。
通过设计一款16位CPU,可以降低处理器的成本和复杂度,提高计算性能,并且更好地满足轻量级计算需求。
三、项目内容1.CPU指令设计:设计新的16位CPU指令集,包括运算指令、数据传输指令、分支跳转指令等,以实现更加高效的计算功能。
2.CPU架构设计:设计16位CPU的整体架构,包括寄存器文件、数据通路、控制单元等,确保CPU的稳定性和高效性。
3.性能优化:对设计的CPU进行性能优化,提高其计算速度和响应速度,确保其在轻量级计算中的高效性。
4.性能评估:通过仿真和实验对设计的16位CPU进行性能评估,检验其计算速度和稳定性,以保证其满足设计需求。
四、项目实施步骤1.设计CPU指令集:根据实际需求设计新的16位CPU指令集,包括指令的格式、操作码和功能,保证其具有高效的计算能力。
2.设计CPU架构:设计16位CPU的整体架构,包括寄存器文件、数据通路和控制单元,确保其能够稳定运行和高效计算。
3.性能优化:对设计的CPU进行性能优化,优化数据通路和控制单元的设计,提高CPU的计算速度和响应速度。
4.实验仿真:通过基于EDA工具进行CPU的设计仿真,检验设计的CPU在不同场景下的计算性能和稳定性。
5.性能评估:对设计的CPU进行性能评估,比较其与传统32位CPU 的性能差异,确保16位CPU在轻量级计算中的优越性。
五、项目成果通过本实验项目的实施,设计一款16位CPU并进行性能评估1.设计一款高效、稳定的16位CPU,满足轻量级计算需求。
16位芯片

16位芯片16位芯片是指一个具有16位数据总线的微处理器芯片。
它具有更高的位宽,可以处理更多位的数据,在计算和运算上更为高效。
16位芯片的优势主要体现在以下几个方面:1. 更大的数据表示范围:16位芯片可以处理的数据范围更广,可以表示的整数范围为-32768到32767。
这使得它在一些需要处理大范围数据的应用中更加灵活。
2. 更高的计算精度:由于具有更多的位宽,16位芯片计算和运算的精度更高。
在一些需要高精度计算的领域,如科学计算、加密解密等,16位芯片能够提供更准确的结果。
3. 更高的性能表现:16位芯片相对于低位芯片,在计算和运算速度上更快。
它不仅可以更快地完成各种运算任务,还可以更好地处理大数据量的操作,提高了整体性能。
4. 更低的功耗:相对于32位或更高位芯片,16位芯片由于位宽较小,其功耗也相对较低。
在一些对电池寿命和功耗要求较高的设备中,16位芯片可以提供更长的使用时间和更节能的功耗。
5. 更低的成本:16位芯片相对于高位芯片来说,更为经济实惠。
这使得它在一些对成本要求较高的领域,如嵌入式系统、传感器网络等,更具竞争力。
当然,16位芯片也存在一些不足之处:1. 数据表示范围相对有限:相比于32位或更高位芯片,16位芯片的数据表示范围较小,无法处理超过其表示范围的数据。
在一些对数据范围要求较高的场景,可能需要使用更高位数的芯片。
2. 计算精度相对较低:虽然相对于低位芯片,16位芯片的计算精度更高,但相比于32位或更高位芯片,其计算结果的精度仍然有限。
在一些对计算精度要求较高的应用中,可能需要使用更高位数的芯片。
综上所述,16位芯片是一种能够提供更大数据范围、更高计算精度、更高性能表现、更低功耗和成本的微处理器芯片。
它在一些对数据范围和性能要求较高,同时对成本要求较低的应用中有着广泛的应用前景。
基于FPGA的16位乘法器的实现

目录引言....................................................................................................................................... - 1 - 摘要....................................................................................................................................... - 2 -一、乘法器概述....................................................................................................................... - 3 -1.1 EDA技术的概念........................................................................................................ - 3 -1.2 EDA技术的特点........................................................................................................ - 3 -1.3 EDA设计流程............................................................................................................ - 5 -1.4硬件描述语言(Verilog HDL)................................................................................ - 5 -二、16位乘法器的设计要求与设计思路.............................................................................. - 6 -2.2 设计要求.................................................................................................................... - 6 -三、16位乘法器的总体框图.................................................................................................. - 6 -四、16位乘法器的综合设计.................................................................................................. - 7 -4.1 16位乘法器功能........................................................................................................ - 7 -4.2 16位乘法器设计思路................................................................................................ - 8 -4.3 基于Verilog HDL 硬件语言的乘法器设计 ............................................................ - 8 -(1)输入模块......................................................................................................... - 8 -(2)乘法模块......................................................................................................... - 9 -五、总体调试与仿真结果..................................................................................................... - 10 -5.1乘法器的RTL Viewer .......................................................................................... - 10 -5.2 16位乘法器的系统程序:....................................................................................... - 11 -5.3计算结果仿真结果................................................................................................... - 12 -5.3.1仿真测试程序(a=6,b=10).............................................................................. - 12 - 总结......................................................................................................................................... - 16 - 参考文献................................................................................................................................. - 16 -引言随着微电子技术的飞速发展,集成电路工艺进入深亚微米阶段,特征尺寸变得越来越小。
16乘16乘法器电路

摘要随着现代数字技术的高速发展,乘法器在高速实时信号处理中特别是在数字信号处理和数字图像处理系统中起到了重要的作用。
乘法器已经是现代计算机中必不可少的一部分。
随着乘数和被乘数位数的增加,乘法器电路中的加法器位树也要相应的增加。
通过研究CLA电路的特性,也可以在乘法器中开发出更快的加法阵列。
纯组合逻辑构成的乘法器虽然工作速度比较快,但过于占用硬件资源,难以实现宽位乘法器。
这里介绍由十六位加法器构成的以时序逻辑方式设计的十六位乘法器,具有一定的实用价值,而且由FPGA\CPLD构成实验系统后,可以很容易的用ASIC大型集成芯片来完成,性价比高,可操作性强。
其运算速度是决定逻辑运算单元(ALU)工作频率的关键,并在很大程度上决定了系统的性能。
由于DSP芯片是串行执行,速度慢、功耗大,所以现在高速实时信号处理中一般采用FPGA\CPLD来进行并行处理。
现在很多系统设计中,要求速度越来越快,功耗越来越小,因此研究高速低功率的乘法器相当重要。
在此次课设中我将在modelsim的环境下完成十六位的乘法器的设计。
关键词FPGA;加法器;Modelsim;锁存器,;移位寄存器目录引言 (1)1总体电路结构设计 (2)1.1电路功能与性能 (2)1.2关键功能电路设计 (3)1.3电路接口 (3)1.4电路功能框图 (5)1.5验证方案 (6)2模块的设计 (7)2.1 输入信号处理模块设计 (8)2.2 16位移位寄存器模块 (9)2.3 16位计数器模块 (9)2.4 输出信号处理模块 (10)3 设计仿真与测试 (12)3.1仿真与测试的功能列表 (12)3.2 仿真平台构建和仿真结果 (12)3.2.1 顶层仿真平台与激励..................... 错误!未定义书签。
3.2.2 电路功能仿真结果....................... 错误!未定义书签。
3.2.3 电路后仿真结果......................... 错误!未定义书签。
EDA课程设计十六位乘加器华侨大学

EDA实验报告十六位硬件乘加器电路学号 1215102057姓名张凌枫班级 12电子信息工程A华侨大学电子工程系1、题目名称:十六位硬件乘加器电路2、摘要:采用流水线方式来实现对8个16位数据进行乘法和加法运算(yout=a0⨯b0+a1⨯b1+a2⨯b2+a3⨯b3),使用乘法器lpm_mult2、16位加法器ADDER16B、计数器cnt16以及锁存器en_dff四个模块。
当clock 出现上升沿时,对输入端输入的两个数dataa、datab进行乘法运算。
将结果输入锁存器中,锁存上一阶段计算得到的值, 16位加法器ADDER16B将锁存器锁存的上一阶段的值与进行完乘法计算得到的值dataa*datab加起来,并输出结果。
计数器cnt16用于区分四组乘加所得数,当有一个上升沿脉冲送入cnt16时,若计数不到5,则进行计数+1,若计数达到5,COUT输出进位信号到锁存器en_dff的reset 端口,将锁存器复位清零,重新进行计数。
此设计经过仿真与硬件测试检验后证实可行。
3、目录4.1系统设计 (4)4.1.1设计要求4.1.2系统设计方案(1)系统设计思路(2)总体方案的论证与比较(3)各功能块的划分与组成(4)系统的工作原理4.2单元电路设计 (6)4.2.1各单元电路的工作原理4.2.2各单元电路电路分析与设计4.3软件设计 (12)4.3.1软件设计平台、开发工具和实现方法4.3.2程序的流程方框图4.3.3实现的功能、程序清单4.4系统测试 (16)4.4.1系统的性能指标4.4.2功能的测试方法、步骤4.4.3仪器设备名称、型号4.4.4测试数据、图表4.5结论 (19)4.5.1对测试结果和数据的分析和计算4.5.2对于此设计的评价4、正文4.1系统设计4.1.1设计要求设计要求:位宽16位;能对8个16位数据进行乘法和加法运算(yout=a0⨯b0+a1⨯b1+a2⨯b2+a3⨯b3),并行、串行或流水线方式。
实验五、16位乘法器芯片设计

4
BJ-EPM240V2 学习板实验说明
else breg = bin; if(i==0) yout = 32'h00000000; if( (i<16) && areg[i]) yout[31:16] = yout[31:16]+breg; if(i==16)
begin
if(!rst_n)ຫໍສະໝຸດ beginareg <= 16'h0000;
breg <= 16'h0000;
done_r <= 1'b0;
yout_r <= 32'h00000000;
i <= 5'd0;
end else if(start)
//启动运算
begin
if(i < 5'd21) i <= i+1'b1; if(i == 5'd0) begin //锁存乘数、被乘数
//芯片输出标志信号。定义为 1 表示乘法运算完成.
reg[15:0] areg;//乘数 a 寄存器 reg[15:0] breg; //乘数 b 寄存器 reg[31:0] yout_r; //乘积寄存器
reg done_r;
reg[4:0] i;
//移位次数寄存器
always@(posedge clk)
信号无效。 start: 芯片使能信号。定义为 0 表示信号无效;定义为 1 表示芯片读入输
入管脚得乘数和被乘数,并将乘积复位清零。 ain:输入 a(被乘数),其数据位宽为 16bit. bin:输入 b(乘数),其数据位宽为 16bit.
16-16位Wallace乘法器测试激励文件设计

16*16位Wallace乘法器测试激励文件设计摘要课题首先要深入分析和掌握Wallace加法树的基本原理,Wallace树是对部分积规约,减小乘法器关键路径时延的一种算法。
设计的思想是为了加快乘法器的运行速度并减少芯片面积开销,采用阵列累加原理实现乘法运算。
本课题设计采用加法器阵列结构来完成部分积相加的,相加的研究和应用方法有多种,本课题基于Wallace加法树结构,并在Wallace加法树算法的基础上进行基于Wallace加法树的16位乘法器的Verilog设计与实现。
功能验证通过后,采用Synopsys公司EDA综合工具Design Compiler进行设计综合。
在此过程中,首先要对工具应用进行综合脚本文件的编写。
然后采用脚本文件对RTL代码进行设计综合,得到门级网表与电路实现。
关键词乘法器;Wallace加法树;Verilog硬件描述语言在乘法器的计算过程中,一般是通过减少部分积的总数,来减少部分积相加的次数,从而来提高计算的速度。
而对于Wallace Tree算法则是通过改进部分积累加的方式以减少部分积累加所需的时间,从而来加快运算的速度。
Wallace树算法的基本思想是通过3-2编码器来减少累加过程中所需要的时间。
加法器中的时延问题主要是出现在进位的过程中所花费大量的时间,如果我们单纯的使用串行的方式,逐级相加,那么所花费的时间也是很长的。
对于一个N比特的被乘数和一个N比特的乘数相乘的算法如下图所示:Y=Yn-1 Yn-2.....................Y2 Y1 Y0 被乘数X=Xn-1 Xn-2.....................X2 X1 X0 乘数一般来说:Y=Yn-1Yn-2....................... Y2Y1Y0X=Xn-1Xn-2 (X2X1X0)2Yn-1X0 Yn-2X0 Yn-3X0 ……Y1X0 Y0X0Yn-1X1 Yn-2X1 Yn-3X1 ……Y1X1 Y0X1Yn-1X2 Yn-2X2 Yn-3X2 ……Y1X2 Y0X2… … … ……. …. …. …. ….Yn-1Xn-2 Yn-2X0 n-2 Yn-3X n-2 ……Y1Xn-2 Y0Xn-2Yn-1Xn-1 Yn-2X0n-1 Yn-3Xn-1 ……Y1Xn-1 Y0Xn-1 ----------------------------------------------------------------------------------------------------------------P2n-1 P2n-2 P2n-3 P2 P1 P0例如:1101 4-bits1101 4-bits110100001101110110010101“与”门被用来产生部分乘积,如果被乘数是N比特,乘数是M比特,那么就会产生N*M个部分积,然而在不同结构和类型的乘法器当中,部分乘积的产生方式是不同的。
16位布斯算法乘法器和ALU

16位布斯算法乘法器和ALUBooth算法16位乘法器西安电子科技大学大三集成电路设计与集成系统专业尹俊镖一乘法器原理分析16位有符号乘法器可以分为三个部分:根据输入的被乘数和乘数产生部分积、部分积压缩产生和和进位、将产生的和和进位相加。
这三个部分分别对应着编码方式、拓扑结构以及加法器。
被乘数X(16-bit)符号位扩展S01?X(17-bit)X(17-比特)01?X2?XMUXADD/SUBBooth译码&ALU(17-bit)控制逻辑符号位扩展S乘积(低16-bit)乘数乘积(高16-bit)保留移出位右移2-bit1 编码方式:本设计采用booth2编码。
部分积是负数时S=1,部分积是正数时S=0;当部分积是+0时,E=1,部分积是-0时,E=0,其余情况E=S取反。
2 拓扑结构:本设计采用二进制树的拓扑结构。
二进制树拓扑结构排列的较为规整,且部分积压缩的速度也非常快。
部分积压缩的目的是为了减小进位传播的延时,采用进位保留加法器,根据当前位信息产生下一位的进位,仅仅产生而没有进位行波传播,这样就可以把当前的多位压缩到较少的位数。
经过几次压后,把部分积压缩成和以及进位。
部分积主要是通过counter和compressor进行压缩,通常使用(3:2)counter 和(4:2)compressor。
(3:2)counter其实质就是一个全加器,进位输入为ci,进位输出为c;(4:2)compressor可以由两个全加器组成,ci为进位输入,Coin为内部进位,输入到下一位的进位输入Ci,Coex为输出进位。
上图为二进制树的拓扑结构图,每4个部分积输入到一个(4:2)compressor 中,产生两个输出,则8个部分积使用3次(4:2)compressor就可以得到和和进位。
部分积的压缩方式可以见下图。
如图中所示,加上最后一个部分积的进位,共有9个部分积,本设计把最后的进位位移到第一个部分积上,使用5个全加器,把进位融合到第一个部分积,这样就转变成8个部分积了,再使用两级二进制树压缩,所以总共使用了三级压缩,最终得到部分积的和和进位。
16位乘法器

乘法器是众多数字系统中的基本模块。
从原理上说它属于组合逻辑范畴;但从工程实际设计上来说,它往往会利用时序逻辑设计的方法来实现,属于时序逻辑范畴。
通过这个实验使大家能够掌握利用FPGA/CPLD设计乘法器的思想,并且能够将我们设计的乘法器应用到实际工程中。
下面我们分别列举了十进制乘法运算和二进制乘法运算的例子。
下面这种计算乘法的方式是大家非常熟悉的:乘积项与乘数相应位对齐(即将乘积项左移),加法运算的数据宽度与被乘数的数据位宽相同。
下面例子中的被乘数和乘数都是无符号的整数,对于有符号数的乘法,可以将符号与数据绝对值分开处理,即绝对值相乘,符号异或。
乘法器的设计方法有两种:组合逻辑设计方法和时序逻辑设计方法。
采用组合逻辑设计方法,电路事先将所有的乘积项全部计算出来,最后加法运算。
采用时序逻辑设计方法,电路将部分已经得到的乘积结果右移,然后与乘积项相加并保存和值,反复迭代上述步骤直到计算出最终乘积。
在本次实验中我们就利用时序逻辑设计方法来设计一个16位乘法器,既然是利用时序逻辑设计方法那么我们就得利用时钟信号控制乘法器运算,那么这样用时序逻辑设计方法与用组合逻辑设计方法比较,它有什么好处呢?利用时序逻辑设计方法可以使整体设计具备流水线结构的特征,能适用在实际工程设计中。
IO口定义:clk:芯片的时钟信号。
rst_n:低电平复位、清零信号。
定义为0表示芯片复位;定义为1表示复位信号无效。
start: 芯片使能信号。
定义为0表示信号无效;定义为1表示芯片读入输入管脚得乘数和被乘数,并将乘积复位清零。
ain:输入a(被乘数),其数据位宽为16bit.bin:输入b(乘数),其数据位宽为16bit.yout:乘积输出,其数据位宽为32bit.done:芯片输出标志信号。
定义为1表示乘法运算完成,yout端口的数据稳定,得到最终的乘积;定义为0表示乘法运算未完成,yout端口的数据不稳定。
数据吞吐量的计算:数据吞吐量使指芯片在一定时钟频率条件下所能处理的有效数据量。
基于FPGA的16位乘法器设计与实现
l
将 移位 寄 存 器 mi 移 d右 位
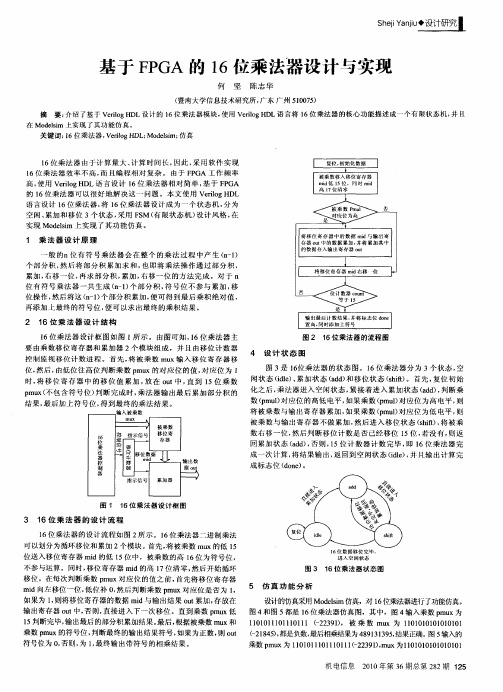
2 1 6位 乘 法 器 设 计 结 构 l 位 乘法 器 设计框 图如 图 l 示 。由 图可知 ,6位 乘法 器主 6 所 l
要 由乘 数移 位 寄存器 和 累加 器 2 模 块组 成 ,并 且 由移位 计 数器 个 控 制 监视 移位 计 数进 程 。首 先 , 被 乘 数 m x 入 移位 寄存 器移 将 a 输 位, 然后 , 由低位 往高 位判 断乘 数 p x的对 应位 的值 , mu 对应 位 为 l
I 乘 移 移 1 乘 法 器 设 计 原 理
一
般 的n 有 符 号 乘 法 器会 在 整 个 的 乘 法 过 程 中 产 生 ( ) 位 1 r1
将移位 寄存器 中的数据 mi d与输 出寄 存器 ot u 中的数据 累加 , 并将 累加 其中 的数 据 存 入 输 出寄 存 器 o t u
在 Mo es 上 实 现 了其 功 能 仿 真 。 d lm i 关 键 词 :6位 乘 法 器 , ro 1 Vei gHDL Mo es 仿 真 l ; d lm; i
1 6位乘 法 器 由于计 算 量大 、 算 时 间长 , 此 , 用软 件 实 现 计 因 采 l 6位乘 法 器效 率不 高 , 且编 程 相对 复 杂 。 由于 F G 工 作 频 率 而 PA
l 复 ,始 数 I 位初 化 据
●
高 , 用 V ro D 使 e l H L语言 设计 1 ig 6位乘 法 器相 对 简单 , 于 F G 基 PA
的 l 位 乘法 器可 以很好 地解 决 这一 问题 。本文 使 用 V ro D 6 el i gH L 语 言 设计 1 6位乘 法器 , 1 乘法 器设 计成 为一个 状 态机 , 将 6化 分为 空闲、 累加 和 移位 3 状态 , 用 F M ( 限状 态机 ) 计风 格 , 个 采 S 有 设 在 实现 Mo e i 上 实现 了其功 能 仿真 。 dl m s
16位乘法器芯片设计 3月9日

16位乘法器芯片设计1.方法乘法器的设计方法有两种:组合逻辑设计方法和时序逻辑设计方法。
采用组合逻辑设计方法,电路事先将所有的乘积项全部算出来,然后做加法运算。
采用时序逻辑设计方法,电路将部分已经得到的乘积结果右移,然后与乘积项相加并保存和值,反复迭代上述步骤直到计算出最终积。
2.组合逻辑的实现可以以16*3位的乘法器为例做出如下设想:A为16位二进制乘数,B为3位二进制乘数,C为A与B相乘的积。
则:C的结果实际上只能为如下值中的一个:0,A,2A,3A,4A,5A,6A,7A因为B为3位二进制,则B只能是000,001,010,011,100,101,110,111中的一个。
初步设想符合现实,由于要实现ASIC芯片的生产,所以对各端口定义如下:reset:芯片复位、清零信号。
值为0,芯片复位。
start:芯片使能信号。
值为1,芯片读入乘数和被乘数,并将乘积复位清零。
ain:被乘数,16bit。
bin:乘数,3bit。
yout:乘积输出,19bit。
done:芯片输出标志信号,值为1,乘法运算完成,yout端口的数据稳定,得到最终的乘积;值为0,乘法运算未完成,yout端口数据不稳定。
编写的Verilog程序如下:Module mult16(reset,start,ain,bin,done,yout);Parameter N=16;Input reset;Input start;Input [N-1:0] ain;Input [2:0]bin;Output [N+3:0] yout;Output done;Integer aa,ab,ac,temp;Integer su;Reg done;Always @(ain)BeginIf(start&&!reset)Beginaa=ain;ab=ain+ain;ac=ab+ab;temp=aa+ab;case(bin)3’b000: su=0;done=1’b1;3’b001: su<=aa;done=1’b1;3’b010: su<=ab;done=1’b1;3’b011: su<=aa+ab;done=1’b1;3’b100: su<=ac;done=1’b1;3’b101: su<=aa+ac;done=1’b1;3’b110: su<=ab+ac;done=1’b1;3’b111: su<=temp+ac;done=1’b1;default: su<=0;done=1’b0;else if (reset)beginsu=0;aa=0;ab=0;ac=0;done=1’b0;endelse if (!start)beginsu=0;done=1’b0;endendassign yout=su;endmodule基于组合逻辑的乘法器,在程序语言上通俗易懂,思路清晰,但是有致命缺点,当乘数和被乘数位数很多的时候,不可能一一列举各种乘积结果,用case语句就显得很繁琐,所以基于时序逻辑的乘法器的研制在所难免。
基于FPGA的16位乘法器芯片的设计

基于FPGA的16位乘法器芯片的设计
王荣海;赵丽梅
【期刊名称】《四川理工学院学报(自然科学版)》
【年(卷),期】2006(019)005
【摘要】文章简要地介绍了乘法器的工作原理,分析了组合逻辑电路设计方法的缺点,将流水线结构引入到设计中,采用时序逻辑电路的设计理念,利用迭代算法,在FPGA上实现了16bit的乘法器设计,在工程上得到了很好的应用.
【总页数】3页(P70-72)
【作者】王荣海;赵丽梅
【作者单位】四川绵阳职业技术学院,四川,绵阳,621000;四川绵阳职业技术学院,四川,绵阳,621000
【正文语种】中文
【中图分类】TP302.2
【相关文献】
1.基于FPGA的16位乘法器设计与实现 [J], 何坚;陈志华
2.基于FPGA的16位乘法器设计与实现 [J], 何坚;陈志华
3.基于FPGA的自顶向下乘法器电路设计 [J], 陈楚;吕石磊;孙道宗;刁寅亮
4.基于CSD编码的16位并行乘法器的设计 [J], 王瑞光;田利波
5.基于16位定点DSP的并行乘法器的设计 [J], 王叶辉;林贻侠;严伟
因版权原因,仅展示原文概要,查看原文内容请购买。
一种16×16位高速低功耗流水线乘法器的设计

一种16×16位高速低功耗流水线乘法器的设计
吴明森;李华旺;刘海涛
【期刊名称】《微电子学与计算机》
【年(卷),期】2003(20)8
【摘要】提出了一种16×16位的高速低功耗流水线乘法器的设计。
乘法器结构采用Booth编码和Wallace树,全加器单元是一种新型的准多米诺逻辑,其性能较普通CMOS逻辑全加器有很大改善。
使用0.5μmCMOS工艺模型,HSPICE模拟结果表明,在频率为150MHz条件下,电源电压3.0V,其平均功耗为11.74mW,延迟为6.5ns。
【总页数】3页(P151-153)
【关键词】16×16位高速低功耗流水线乘法器;设计;Booth编码;算术逻辑单元;乘法器
【作者】吴明森;李华旺;刘海涛
【作者单位】中国科学院上海微系统与信息技术研究所
【正文语种】中文
【中图分类】TP342.22
【相关文献】
1.一种可重构的高速流水线乘法器 [J], 田心宇;张小林;姚英
2.16×16位高速低功耗并行乘法器的实现 [J], 徐锋;邵丙铣
3.用EMODL实现的高速低功耗流水线乘法器 [J], 王颀;邵丙铣
4.一种高速低功耗可重构流水线乘法器 [J], 田心宇;杨银堂;朱樟明;姚英
5.一种新型高速低功耗可重构流水线乘法器设计 [J], 姚英;田心宇;韩晓聪
因版权原因,仅展示原文概要,查看原文内容请购买。
16bit∑△ADC的设计的开题报告

16bit∑△ADC的设计的开题报告题目:16bit ∑△ADC的设计一、选题的背景和意义模拟信号的数字化处理一直是信息领域研究的重点方向之一。
智能设备和嵌入式系统中要求数据精度和转换速率都越来越高,常规的低精度ADC已经不能满足需求,高精度ADC开始受到重视。
本课题主要是通过设计一款16bit ∑△ADC,提高ADC数据的精度和稳定性。
二、研究内容和技术路线1.设计16bit ∑△ADC的基础电路,包括160KSPS采样速率的运放、普通反向SPS和反向SAR等基础电路。
2.应用Sigma频率转换技术,实现高精度ADC的数据转换。
3.利用计数器、多路复用器等逻辑电路,实现ADC的控制与输出。
4.研究ADC的数字后处理方法,包括滤波、失调校正等。
5.验证和测试设计的ADC电路,包括功能和精度等参数的测试和分析。
技术路线:1.了解并掌握μFARADAY公司的FSK (Fast Sigma-delta K-order)架构,并应用在16bit ∑△ADC电路的设计中。
2.选定基于TSMC 0.18um技术的CMOS工艺流程,通过Circuital Embbedded Design Kit (CEDK)进行模块电路的仿真和验证。
3.选择模块化设计思路,逐步完善模块化结构,完成最终的ADC电路设计,并进行验证测试。
三、预期研究成果及实际应用本课题预期设计一款具有高精度、高速度的16bit ∑△ADC电路,预期转换精度可达到±1LSB,噪声水平低于-120dbFS,最高采样速率可达到160KSPS。
实际应用方面,该ADC电路可被应用于各种需要高精度和高速度ADC的场合,如智能仪器、音频处理设备、数据采集系统等。
四、进度安排第一期 10月-12月:研究技术路线,并进行仿真验证第二期 1月-3月:完善模块化设计,完成ADC的基础电路、Sigma频率转换、数字后处理电路等设计第三期 4月-6月:进行ADC的控制与输出设计,包括计数器、多路复用器等逻辑电路的设计第四期 7月-8月:进行ADC电路的测试与验证五、参考文献1.陶定刚. 模拟集成电路与信号处理 [M]. 北京:清华大学出版社,2002.2.Li X L, Zhao Y, Yi H Q, et al. Design and simulation of a 18-bit SAR ADC with current-mode edge-combining comparator [J]. Journal of Semiconductors, 2015. 3.Zhou J, Meng Y, Liu G, et al. A 15b 1.86MS/s CTAD-Based SAR ADC with 4-Level Calibration[J]. Journal of Semiconductors, 2014.4.van der Goes F, Galton I, Viagarajan A, et al. A 15-b, 50 MS/s, 52 mW, Multistage Pipeline ADC with Digital Calibration and Offset Compensation. IEEE Journal of Solid-State Circuits, 2012, 47(2): 465-475.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
16位乘法器芯片设计
1.方法
乘法器的设计方法有两种:组合逻辑设计方法和时序逻辑设计方法。
采用组合逻辑设计方法,电路事先将所有的乘积项全部算出来,然后做加法运算。
采用时序逻辑设计方法,电路将部分已经得到的乘积结果右移,然后与乘积项相加并保存和值,反复迭代上述步骤直到计算出最终积。
2.组合逻辑的实现
可以以16*3位的乘法器为例做出如下设想:
A为16位二进制乘数,B为3位二进制乘数,C为A与B相乘的积。
则:
C的结果实际上只能为如下值中的一个:
0,A,2A,3A,4A,5A,6A,7A
因为B为3位二进制,则B只能是000,001,010,011,100,101,110,111中的一个。
初步设想符合现实,由于要实现ASIC芯片的生产,所以对各端口定义如下:
reset:芯片复位、清零信号。
值为0,芯片复位。
start:芯片使能信号。
值为1,芯片读入乘数和被乘数,并将乘积复位清零。
ain:被乘数,16bit。
bin:乘数,3bit。
yout:乘积输出,19bit。
done:芯片输出标志信号,值为1,乘法运算完成,yout端口的数据稳定,得到最终的乘积;值为0,乘法运算未完成,yout端口数据不稳定。
编写的Verilog程序如下:
Module mult16(reset,start,ain,bin,done,yout);
Parameter N=16;
Input reset;
Input start;
Input [N-1:0] ain;
Input [2:0]bin;
Output [N+3:0] yout;
Output done;
Integer aa,ab,ac,temp;
Integer su;
Reg done;
Always @(ain)
Begin
If(start&&!reset)
Begin
aa=ain;
ab=ain+ain;
ac=ab+ab;
temp=aa+ab;
case(bin)
3’b000: su=0;done=1’b1;
3’b001: su<=aa;done=1’b1;
3’b010: su<=ab;done=1’b1;
3’b011: su<=aa+ab;done=1’b1;
3’b100: su<=ac;done=1’b1;
3’b101: su<=aa+ac;done=1’b1;
3’b110: su<=ab+ac;done=1’b1;
3’b111: su<=temp+ac;done=1’b1;
default: su<=0;done=1’b0;
else if (reset)
begin
su=0;
aa=0;
ab=0;
ac=0;
done=1’b0;
end
else if (!start)
begin
su=0;
done=1’b0;
end
end
assign yout=su;
endmodule
基于组合逻辑的乘法器,在程序语言上通俗易懂,思路清晰,但是有致命缺点,当乘数和被乘数位数很多的时候,不可能一一列举各种乘积结果,用case语句就显得很繁琐,所以基于时序逻辑的乘法器的研制在所难免。
3.时序逻辑实现
流程图如下:
1.数据入口定义
clk:时钟。
reset:芯片复位、清零信号。
start:芯片使能信号。
ain:被乘数a。
bin:被乘数b。
2.数据出口定义
yout:乘积输出。
done:芯片输出标志信号。
3.Verilog HDL 描述
module tmult16(clk,reset,start,done,ain,bin,yout); parameter N=16;
input clk, reset, start;
input [N-1:0] ain;
input [N-1:0] bin;
output [2*N-1:0] yout;
output done;
//乘法器的数据寄存器
reg [2*N-1:0] a;
reg [N-1:0] b;
reg [2*N-1:0] yout;
reg done;
//reset的信号下降沿启动复位过程
always @(posedge clk or negedge reset)
begin
if(~reset)
begin
a<=0;
b<=0;
yout<=0;
done<=1’b1;
end
else
begin
if(start)
begin
a<=ain;
b<=bin;
yout<=0;
done<=0;
end
else
begin
if(~done)
begin
if(b!=0)
begin
if(b[0])
begin
yout<=yout+a;
end
b<=b>>1;
a<=a<<1;
end
else begin
done<=1’b1;
end
end
end
end
end
endmodule。
