dsp-fir滤波器
基于DSP的FIR滤波器的设计和实现

/view/e6e44f4c2e3f5727a5e962d7.html/view/157f7f35eefdc8d376ee325f.html基于DSP的FIR滤波器的设计和实现摘要:DSP技术一般指将DSP 处理器用于完成数字信号处理的方法与技术。
目前的DSP芯片以其强大的数据处理功能在通信和其他信号处理领域得到广泛注意并已成为开发应用的热点技术。
许多领域对于数字信号处理器的应用都是围绕美国德州仪器所开发的DSP处理器来进行的。
DSP芯片是一种特别适合于进行数字信号处理运算的微处理器。
主要应用是实时快速的实现各种数字信号处理算法,如卷积及各种变换等。
其中利用DSP来实现数字滤波器就是很重要的一种应用,本文深入研究基于美国德州仪器公司(TI)TMS320C5410 DSP芯片的滤波器系统软件实现方法,用窗口设计法实现FIR滤波器,给出了MATLAB仿真结果,并在以TI TMS320C5410为微处理器的DSK上实现,实验结果表明滤波结果效果良好,达到了预期的性能指标,用时间抽取法实现的FFT/ IFFT算法,介绍了自适应滤波器的基本原理及应用,并对LMS算法进行了深入的研究。
关键词:DSP;TMS320C5410;FIR滤波器;FFT/IFFT;自适应滤波器The Design and Implemention of FIRFilter Based on DSP’sAbstract:DSP technology means the technology to accomplish digital signal processing.Nowadays DSP’ are getting more an d more attentions in the information field, due to its powerful signal processing ability, becoming a hot-point technique in communication and other relating signal processing areas. DSP chip is especially fit for digital signal processing, its main application is realizing all kinds of digital signal processing arithmetic such as clove hitch correlation、all kinds of transforms etc. Realizing digital filters with DSPis an important application.The paper discusses the filter’s software realization based on TMS320C5410 and finished the hardware system of noise-restraining. The arithmetic system was compiled with C and assemble language, The main works accomplished are as following: realization of FIR filter with window function, and to reach the simulation result through MATLAB,also realization on TMS320C5410 chip,the result of experiment to make clear that the effect is fine.realization of FFT/IFFT arithmetic with time-drawing.The paper begins with the principle of adptive filter.Based on the principle,Least Mean Square is researched deeply.Keywords:DSP; TMS320C5410; FIR Filter; FFT/IFFT; Adaptive Filtering第1章绪论1.1引言随着信息时代和数字世界的到来,数字信号处理已成为如今一门极其重要的学科和技术领域。
dsp_FIR滤波器

电子信息学院DSP结构原理及应用实验_FIR低通滤波器设计及滤波组员:蒋万欣;邓宏恩;谢兴轮实验报告书写:蒋万欣:2012141451177日期:第十四教学周四地点:基础教学楼B座520实验室实验五FIR滤波器一、实验目的:1,熟悉FIR滤波器‘C54X’实现的编程方法。
2,测试FIR滤波器的单位冲击响应曲线。
3,检查FIR滤波器的频率特性。
二、实验条件1,已经设计出的线性相位FIR滤波器的参数如下:滤波器名称:带通滤波器采样频率:Fs = 10 kHz通带:1 kHz ——4 kHz过渡带:1 kHz —— 1.375 kHz,3.625 kHz —— 4 kHz带类脉动:< 0.5dB阻带衰减:—60dB以下滤波器级数:N = 80滤波器系数:H(0) = FFDCH H(10) = 00A2H H(20) = 000BH H(30) = FAA3HH(1) = 001FH H(11) = FF6FH H(21) = FE7FH H(31) = 0347HH(2) = 0051H H(12) = FFFEH H(22) = FDBFH H(32) = FE3DHH(3) = FFE9H H(13) = FF70H H(23) = 0192H H(33) = 0747HH(4) = FFE6H H(14) = FEF4H H(24) = FFB5H H(34) = 09BBHH(5) = FFBAH H(15) = 00CBH H(25) = 026AH H(35) = FE3DHH(6) = FFB4H H(16) = 000BH H(26) = 0368H H(36) = 052BHH(7) = 004BH H(17) = 00E6H H(27) = FDC2H H(37) = DB59HH(8) = FFF9H H(18) = 0187H H(28) = 00C0H H(38) = DC2AHH(9) = 0069H H(19) = FEE5H H(29) = FC0AH H(39) = 2D57H2,生成正弦信号的数据文件的高级语言程序,程序名,sin_flt.exe.用法见附录2.3,线性相位FIR滤波器源程序Lab5.asm,以及链接命令文件Lab5.cmd,参看教材6.3节。
DSP实验报告——FIR和IIR滤波器设计

DSP 实验报告实验一 FIR 滤波器的设计1.实验目的利用所学DSP 知识,在CCS3.3平台上,对TMS320VC5416DSP 设计,编程实现FIR 滤波器。
从而学会使用CCS 软件和TMS320VC5416实验板。
2.实验要求设计一个10阶的FIR 滤波器,要求 =2.5kHZ ,定点实现。
并对 =8kHZ 的多正弦波合成文件进行滤波测试,显示出输入和输出信号。
3.实验原理一个截止频率为 的理想数字低通滤波器,其传递函数的表达式为:⎪⎩⎪⎨⎧≤≤≤=-πωωωωωτωc c j jd ee H ,0,)(这个滤波器是物理不可实现的。
为了产生有限长度的冲激响应函数,我们取样响应为)(n h ,长度为N 。
)(n h 表示截取)(n h d 后的冲激响应,即)()()(n h n n h d ω=,其中)(n ω即为窗函数,窗长为N 。
一般的FIR 滤波器差分方程如下:1()()()n k y n h k x n k -==-∑进行Z 变换得到FIR 的系统函数为:∑-=-=10)()(N n nz n h z HN 阶滤波器通常采用N 个延迟单元、N 个加法器与N+1个乘法器组成。
因此可以得到FIR 滤波器的结构图如图1所示。
图1 FIR 滤波器直接结构图4.设计思路对于FIR滤波器的设计,其系数()h n是关键。
由于matlab自带滤波器设计工具箱和滤波器设计函数,故借用matlab工具,设计满足条件的滤波器并导出系数以备编写滤波器程序时使用。
实验需要用到的输入数据是多正弦波合成文件,对于输入信号的设计,这里也借助matlab编程生成dat文件。
然后用C语言编写FIR滤波器的主程序,输入文件在程序运行后导入。
5.实验内容(1)滤波器系数的设计由于实验只给出滤波器条件为N=10,=2.5kHZ,并没有给出和,所以这里调用matlab工具箱函数fir1实现窗函数法设计滤波器。
fir1的调用格式为 ( ,),返回值为6dB截止频率为的N阶(单位脉冲响应h(n)长度=N+1)的FIR低通滤波器的系数向量(为标量),默认选用哈明窗。
基于DSP实现的FIR低通滤波器

基于DSP实现的FIR低通滤波器FIR(有限脉冲响应)低通滤波器是一种常见的数字信号处理(DSP)滤波器。
它的设计和实现非常灵活,可以用于去除数字信号中高频成分,使得信号能在一定的频率范围内进行平滑处理。
FIR低通滤波器有很多种设计方法,其中最简单的方法是基于窗函数设计,例如矩形窗、汉宁窗、布莱克曼窗等。
这些窗函数的选择取决于滤波器的性能要求和频率响应的形状。
在DSP中,FIR低通滤波器的实现可以采用直接形式、级联形式、并行形式和迭代形式等多种结构。
其中直接形式是最简单和直观的实现方式,也是最容易理解和实现的一种结构。
直接形式的FIR低通滤波器由一个延迟线、一组乘法器和加法器组成。
延迟线用于延迟输入信号,乘法器用于对延迟后的信号进行调制,而加法器则将调制后的信号相加得到输出信号。
```----------------------,,,x(n) -->, Delay ,-->, Multiply,-->--+ Sum ,--> y(n)Line ,,,----------------------```在实现过程中,需要注意的是延迟线的设置和乘法器的系数。
延迟线的长度决定了滤波器的阶数,即滤波器对输入信号的响应范围。
乘法器的系数则决定了滤波器的频率响应,可以通过窗函数的选取来确定。
通常,FIR滤波器的实现可以通过查表法或者卷积法来实现。
查表法通过预先计算所有可能的输入组合,并将其存储在一张查找表中,以减少计算量。
卷积法则通过将输入信号和滤波器的冲击响应进行卷积运算来得到输出信号。
当实现FIR低通滤波器时,还需要考虑滤波器的性能指标和算法的优化。
常见的性能指标包括滤波器的截止频率、抗混叠性能、通带和阻带的幅频特性等。
算法的优化可以从以下几个方面考虑:乘法器的系数选择、滤波器结构的选择、滤波器长度的选择和存储器的优化等。
总之,基于DSP实现的FIR低通滤波器是一种常用的数字信号处理滤波器,它可以用于去除数字信号中的高频成分,平滑信号的频谱。
FIR滤波器设计和DSP实现

FIR滤波器设计和DSP实现FIR滤波器(Finite Impulse Response Filter)又称为有限脉冲响应滤波器,是一种数字滤波器,其脉冲响应为有限长度。
FIR滤波器具有稳定性、线性相位等优点,广泛应用于数字信号处理(DSP)中。
1.窗函数法:窗函数法是FIR滤波器设计中最简单、最常用的方法之一、设计步骤主要有:选择合适的窗函数(如矩形窗、汉宁窗、哈宁窗等);确定滤波器的截止频率和通带或阻带波动范围;根据窗函数的特性进行滤波器系数的计算。
窗函数法设计得到的滤波器具有较好的频域响应,并且易于实现。
2.频率采样法:频率采样法是通过对滤波器在频域中的理想特性进行采样,然后进行逆变换得到滤波器系数。
设计步骤主要有:确定理想滤波器的频率响应;进行频率采样,得到取样频率上的实际频率响应;对实际频率响应进行逆变换,得到滤波器系数。
频率采样法设计的滤波器可以满足设计要求,但是需要进行逆变换,计算复杂度较高。
3.最小二乘法:最小二乘法是通过求解最小化均方差的优化问题,得到最佳滤波器系数。
设计步骤主要有:建立最小二乘优化问题的数学模型;对数学模型进行求解,得到最佳滤波器系数。
最小二乘法能够得到较好的滤波器性能,并且不需要进行逆变换,计算复杂度相对较低。
1.将滤波器的系数存储在系数寄存器中;2.将输入信号与相应的系数进行乘法运算;3.将乘法运算的结果累加得到输出信号;4.将输入信号和系数向右移动一个位置;5.重复步骤2-4,直到滤波器输出满足要求。
DSP实现可以采用硬件方法,如使用专用的FPGA或ASIC实现滤波器的计算单元;也可以采用软件方法,在DSP芯片上运行相应的滤波算法代码。
对于较复杂的滤波器设计,可以使用专门的滤波器设计软件进行设计和实现。
综上所述,FIR滤波器的设计和实现是数字信号处理中的重要内容,不同的设计方法和实现方式可以根据具体需求选择。
设计一个合适的FIR 滤波器可以满足信号处理的要求,并且在DSP实现中能够提高系统的运算效率和性能。
FIR滤波器及其DSP实现

FIR滤波器及其DSP实现FIR(Finite Impulse Response)滤波器是一种常见的数字滤波器,它具有有限的脉冲响应。
与IIR(Infinite Impulse Response)滤波器相比,FIR滤波器具有线性相位特性,并且可以实现稳定的滤波效果。
FIR滤波器的核心是其冲激响应,即滤波器的输出响应。
FIR滤波器的输出可以通过对输入信号和滤波器的冲激响应进行卷积来实现。
为了得到所需的滤波效果,需要设计滤波器的冲激响应。
常见的方法包括频域设计和时域设计两种。
频域设计方法主要利用频率响应来设计FIR滤波器的冲激响应。
这包括将所需滤波特性转化为频率域中的理想滤波器响应,然后通过反变换得到冲激响应。
常见的频域设计方法有窗函数法、最优逼近法和频带优化法等。
窗函数法是最简单的频域设计方法之一,通过将理想滤波器的频率响应与窗函数的频率响应相乘得到FIR滤波器的冲激响应。
常用的窗函数有矩形窗、汉宁窗、汉明窗等。
窗函数法的优点是简单易用,但实现的FIR 滤波器在频域存在较大的过渡带宽。
因此,需要根据具体应用需求选择合适的窗函数。
最优逼近法是一种基于最优化理论的频域设计方法。
它通过将所需滤波特性定义为目标函数,利用优化算法来最小化目标函数与实际滤波器响应之间的差距,从而得到FIR滤波器的冲激响应。
最优逼近法能够较好地满足滤波特性的要求,但计算复杂度较高。
时域设计方法主要通过对滤波器的冲激响应进行直接设计来实现。
常见的时域设计方法有零相位响应(Zero-Phase Response,ZPR)设计和线性相位设计。
零相位响应设计方法通过首先设计一个偶对称的冲激响应,并通过反转和平移来得到滤波器的冲激响应。
这样可以实现零相位的滤波效果。
零相位响应设计方法能够保持输入信号的相位信息,适用于对相位要求较高的应用,如音频信号处理。
线性相位设计方法主要通过对滤波器的延迟进行优化来实现。
线性相位设计方法能够使得滤波器的相位响应近似为线性函数,从而实现滤波器对不同频率的信号具有相同的延迟。
DSP_FIR实验报告
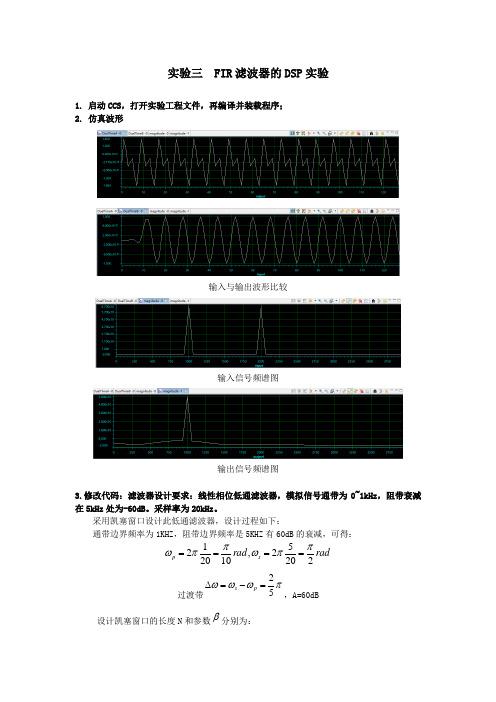
1. 启动CCS,打开实验工程文件,再编译并装载程序;
2. 仿真波形
输入与输出波形比较
输入信号频谱图
输出信号频谱图
3.修改代码:滤波器设计要求:线性相位低通滤波器,模拟信号通带为0~1kHz,阻带衰减在5kHz处为-60dB。采样率为20kHz。
采用凯塞窗口设计此低通滤波器,设计过程如下:
Fs=20000;
t=(0:200)/Fs;
s=sin(2*pi*t*1000)+sin(2*pi*t*5000);
subplot(1,1,1);
plot(t,s);
axis([0 0.005 -2 2]);
grid
产生了1000Hz和5000Hz的混叠波,并且变量Fs、t、s将显示在workspace列表中。
-0.003928668671765,-0.002911158381528, 0.004441058624642, 0.01416335142997,
0.01444447680484, -0.004466774967774,-0.03524603325736, -0.04900562431329,
-0.01223772579527, 0.0834377913716, 0.2040327190773, 0.2883076291491,
2)选择设计fir低通滤波器,阶数为29,采样频率fs=20000Hz,截止频率fc=3000Hz,窗口设置为凯塞窗口,凯塞窗口参数为5.65326
3)用SPtool 验证所设计滤波器的功能
在FDATool里设计了一个FIR低通滤波器后,用SPTool来分析所设计的滤波器.在MATLAB环境下产生一个混叠波信号,在MATLAB命令窗口输入:
通用DSP实现FIR滤波器实验报告

N -1一、试验目的:1、了解 FIR 滤波器的 DSP 实现方法;2、了解用 FIR 滤波器实现模拟信号滤波的全过程;3、把握 FIR 滤波器直接型构造的实现方法。
二、试验原理:FIR 滤波器是有限长单位脉冲响应数字滤波器,其系统函数一般式为:H (z ) = ∑ h (n )z - nn =0FIR 滤波器的通用 DSP 实现法与前面介绍的 IIR 滤波器构造的实现方法类似, 用 FIR 滤波器对模拟信进展滤波的构造图所示。
数字滤波器对模拟信号滤波的原理图本试验中在以通用DSP(TMS320)为核心的DSP 平台上承受窗函数设计法分别设计了 50 阶的高通、低通、带通 FIR 滤波器,其幅频特性分别如以下图形所示:50)B d (ed u t i n ga M 0 -50 -100-1501000 2023 3000 4000 5000 6000 7000 8000 9000 10000Frequency (Hz))s e r g e d ( e s a h P-500 -1000 -1500-20231000 2023 3000 4000 5000 6000 7000 8000 9000 10000Frequency (Hz)输入 保护滤波器输出A/D FIR 滤波器 D/A低通滤波器的频响特性)s e es no ps eRe dut i nga M1.510.510000 1000 2023 3000 4000 5000 6000 7000 8000Hertz9000 10000r g e d( e s a h P -1000-2023-3000-40000 1000 2023 3000 4000 5000 6000 7000 8000Hertz9000 10000es no ps eRe dut i nga Ms)1.510.50 1000 2023 3000 4000 5000 6000 7000 8000Hertz9000 10000e r ged(e sa hP-500-1000-15000 1000 2023 3000 4000 5000 6000 7000 8000Hertz9000 10000高通滤波器的频响特性带通滤波器的频响特性试验板信号源Input1GndGndOut3示波器试验名称:通用DSP 实现FIR 滤波器姓名:刘宇〔〕同组人:石龄佳〔〕三.试验原理图:图2-5 试验原理图四.试验仪器稳压电源一台,双踪示波器一台, 信号源一台,试验板一块五、试验内容及步骤:1、按试验连接图检查连线是否正确,然后依次翻开信号源﹑示波器﹑试验装置的电源开关。
基于DSP实现的FIR低通滤波器

基于DSP实现的FIR低通滤波器FIR(Finite Impulse Response)低通滤波器是一种数字信号处理(DSP)算法,用于滤除输入信号中高于一些截止频率的频域成分,并使输出信号只包含低于该截止频率的成分。
FIR低通滤波器通常由一组脉冲响应函数(Impulse Response)的加权和组成,其中权重决定了滤波器的频率响应。
实现FIR低通滤波器的一种常见方法是使用离散时间线性卷积运算。
滤波器的输入信号通过一个延迟线数组,然后与一组权重向量进行内积。
该内积计算的结果即为滤波器的输出。
在DSP领域,用于实现FIR低通滤波器的算法有很多种,其中最常用的是基于迭代结构(Direct Form)的算法。
此算法按照滤波器的脉冲响应函数的长度进行迭代,每次迭代处理输入信号的一个样本。
该算法的优点是实现简单、稳定可靠。
下面是一个基于DSP实现的FIR低通滤波器的伪代码示例:```python#定义滤波器的截止频率和脉冲响应函数长度def cutoff_frequency = 1000 # 截止频率为1kHzdef length = 101 # 脉冲响应函数长度为101#初始化滤波器的权重向量def weights = [0.0] * length#计算滤波器的脉冲响应函数for i in range(length):#计算当前权重对应的频率frequency = i * sampling_rate / length#如果当前频率小于截止频率,则设置权重为1,否则为0weights[i] = 1 if frequency <= cutoff_frequency else 0#初始化输入和输出信号数组def input_signal = [0.0] * signal_lengthdef output_signal = [0.0] * signal_length#循环处理输入信号的每个样本for i in range(signal_length):#延迟线数组移位,并将当前输入样本放入延迟线的第一个位置delay_line[1:] = delay_line[:-1]delay_line[0] = input_signal[i]#计算滤波器的输出output_signal[i] = sum(delay_line * weights)```这段示例代码实现了一个FIR低通滤波器,截止频率为1kHz,脉冲响应函数长度为101、首先,根据截止频率计算出权重向量。
通用DSP实现FIR滤波器

9
实验三、 FIR滤波器的硬件实现方法 实验三、 FIR滤波器的硬件实现方法
一、实验目的: 实验目的:
1、了解FIR滤波器的硬件实现方法; 了解FIR滤波器的硬件实现方法; FIR滤波器的硬件实现方法
二、实验原理: 实验原理:
本实验中FIR滤波器的硬件实现方法是以单片机为核心, 本实验中FIR滤波器的硬件实现方法是以单片机为核心,加上外扩展 FIR滤波器的硬件实现方法是以单片机为核心 的存储单元及其它电路来实现FIR的滤波运算, 的存储单元及其它电路来实现FIR的滤波运算,我们实现的是一个四阶的 FIR的滤波运算 FIR滤波器 选用的是直接型的结构, 其结构如图3 所示: 滤波器, FIR滤波器,选用的是直接型的结构, 其结构如图3-1所示: x(n) h(0) Z-1 h(1) Z-1 h(2) Z-1 h(3) y(n)
0
1000
2000
3000
4000 5000 6000 Frequency (Hz)
7000
8000
9000 10000
图2-2 低通滤波器的频响特性
3
高通滤波器的频率特性如图2 所示: 高通滤波器的频率特性如图2-3所示:
1.5 Magnitude Response
1
0.5
0
0
1000
2000
3000
2
低通滤波器的频率特性如图2 所示: 低通滤波器的频率特性如图2-2所示:
50 Magnitude (dB) 0 -50 -100 -150
0
1000
2000
3000
400Hz)
7000
8000
9000 10000
0 Phase (degrees) -500 -1000 -1500 -2000
FIR滤波器在DSP上的实现

FIR滤波器在DSP上的实现
1引言
近年来,随着数字信号处理(DSP)技术的发展,自由响应滤波器(FIR)已成为DSP系统的核心部分,广泛用于各种应用,如声学信号处理、通信器件、生物医学信号处理等。
本文首先介绍FIR滤波器的基本原理,之后介绍如何在DSP上实现FIR滤波器,主要介绍两种实现方法:延迟求和和移位加法(Shift-Add)。
最后,将对比分析两种实现方法的优劣,并分析哪些条件下使用移位加法。
2FIR滤波器的原理
输入的时域信号x[n]经过一系列不同阶数的延迟单元滤波器系数h[n]的乘法和求和运算,从而得到输出的时域信号y[n],即
y[n]=\sum_{k=0}^{k=N}h_{k}x[n-k]
其中,x[n]表示输入时域信号,h[n]表示滤波器系数,y[n]表示输出时域信号,N表示滤波器的阶数。
3在DSP上实现FIR滤波器。
DSP的FIR设计低通滤波C语言编写

DSP的FIR设计低通滤波C语言编写FIR(有限脉冲响应)滤波器是一种常用的数字滤波器,用于数字信号处理中的滤波操作。
FIR滤波器的设计通常包括两个主要步骤:滤波器的规格化和滤波器系数的计算。
滤波器的规格化是指确定滤波器的采样频率,截止频率以及陷波增益等参数。
在设计低通FIR滤波器时,我们需要确定滤波器的截止频率。
假设我们希望设计一个截止频率为Fs/4的低通FIR滤波器,其中Fs是采样频率。
根据滤波器设计的基本原理,我们可以得到滤波器的频率响应公式为:H(k) = (2 * Fs/4 * sin(2 * pi * Fs/4 * k))/(pi * k)其中,k是从0到N-1的整数序列,N是滤波器的长度。
经过频域设计,我们可以通过计算滤波器的频率响应公式来获得滤波器的系数。
接下来,我们将使用C语言编写一个低通FIR滤波器的代码示例。
在这个示例中,我们将实现一个截止频率为Fs/4的低通FIR滤波器,采样频率为Fs。
代码如下:```c#include <stdio.h>#include <stdlib.h>#include <math.h>//定义滤波器的长度#define N 51//定义采样频率//定义滤波器的截止频率#define Fc (Fs/4)//计算滤波器的系数void calculateCoefficients(float* coefficients)float sum = 0;for (int k = 0; k < N; k++)if (k == N/2)coefficients[k] = 2 * Fc/Fs;} elsecoefficients[k] = (sin(2.0 * M_PI * Fc * (k - N/2) / Fs)) / (M_PI * (k - N/2));}sum += coefficients[k];}//归一化滤波器的系数for (int k = 0; k < N; k++)coefficients[k] /= sum;}//应用滤波器void applyFilter(float* input, float* output, float* coefficients, int length)for (int n = 0; n < length; n++)output[n] = 0;for (int k = 0; k < N; k++)if (n - k >= 0)output[n] += input[n - k] * coefficients[k];}}}int mai//定义输入信号和输出信号的长度int length = 100;//为输入信号和输出信号分配内存空间float* input = (float*)malloc(length*sizeof(float));float* output = (float*)malloc(length*sizeof(float));//为滤波器的系数分配内存空间float* coefficients = (float*)malloc(N*sizeof(float));//生成输入信号for (int n = 0; n < length; n++)input[n] = sin(2.0 * M_PI * 1000 * n / Fs);}//计算滤波器的系数calculateCoefficients(coefficients);//应用滤波器applyFilter(input, output, coefficients, length); //打印输出信号for (int n = 0; n < length; n++)printf("%f\n", output[n]);}//释放内存空间free(input);free(output);free(coefficients);return 0;```在上面的代码示例中,我们首先定义了滤波器的长度、采样频率以及截止频率。
dsp实验报告 fir实验报告

dsp实验报告 fir实验报告DSP实验报告:FIR实验报告引言:数字信号处理(Digital Signal Processing,DSP)是一门研究如何对数字信号进行处理和处理的学科。
其中,滤波器是数字信号处理中最常用的技术之一。
本实验报告旨在介绍FIR(Finite Impulse Response)滤波器的原理、设计和实现过程,并通过实验验证其性能。
一、FIR滤波器的原理FIR滤波器是一种线性时不变系统,其输出信号仅由输入信号的有限个历史样本决定。
其基本原理是将输入信号与滤波器的冲激响应进行卷积运算,以实现对输入信号的滤波处理。
二、FIR滤波器的设计方法1. 理想低通滤波器设计方法理想低通滤波器的频率响应在截止频率之前为1,在截止频率之后为0。
通过对理想低通滤波器的频率响应进行采样和离散化,可以得到FIR滤波器的系数序列。
2. 窗函数法设计FIR滤波器窗函数法是一种常用的FIR滤波器设计方法。
其基本思想是将理想低通滤波器的频率响应与一个窗函数进行乘积,从而得到实际可实现的FIR滤波器的系数序列。
常用的窗函数有矩形窗、汉宁窗、汉明窗等。
三、FIR滤波器的实现FIR滤波器可以通过直接形式和间接形式两种方式实现。
直接形式是按照滤波器的差分方程进行计算,而间接形式则是利用FFT(Fast Fourier Transform)算法将滤波器的系数序列转换为频域进行计算。
四、FIR滤波器的性能评估1. 幅频响应幅频响应是评估FIR滤波器性能的重要指标之一。
通过绘制滤波器的幅频响应曲线,可以直观地观察滤波器在不同频率下的衰减情况。
2. 相频响应相频响应是评估FIR滤波器性能的另一个重要指标。
相频响应描述了滤波器对输入信号的相位延迟情况,对于某些应用场景,相频响应的稳定性和线性性非常重要。
3. 稳态误差稳态误差是指FIR滤波器在达到稳态后输出信号与理想输出信号之间的差异。
通过对滤波器的输入信号进行模拟或实际测试,可以计算出滤波器的稳态误差,并评估其性能。
dsp-fir滤波器

基于DSP的FIR低通滤波器的设计学号:电子与控制工程学院一、设计要求通过ICETEK–VC5509-A 评估板实现FIR滤波功能,将输入的方波信号通过评估板上的AD模块,滤波模块,以及DA模块后输出正弦波信号并在示波器上观察方波滤除后所产生的正弦波。
在CCS下编写C语音和汇编语言程序分别实现滤波器功能,并且比较c语言和汇编语言的执行速度进行比较。
二、设计原理数字信号处理技术的应用领域非常广泛,而数字滤波器的设计是数字信号处理中最重要的设计环节。
数字滤波器分为IIR滤波器和FIR滤波器。
本次课设使用的是FIR 滤波器。
FIR滤波器即有限长单位响应滤波器,是数字信号处理系统中最基本的原件。
可以在保证任意频率特性的同时具有严格的线性相位特性。
同时其单位冲激响应是有限长的,因而滤波器是稳定的系统。
FIR滤波器在通信、图像处理、模式识别等领域具有广泛的应用。
在进入FIR滤波器前,首先要将信号通过A/D器件进行模数转换,把模拟信号转化为数字信号;为了使信号处理能够不发生失真,信号的采样速度必须满足奈奎斯特定理,一般取信号频率上限的4-5倍做为采样频率;一般可用速度较高的逐次逼进式A/D转换器,不论采用乘累加方法还是分布式算法设计FIR滤波器,滤波器输出的数据都是一串序列,要使它能直观地反应出来,还需经过数模转换。
FIR滤波器误反馈回路,是一种稳定系统,可以设计成具有线性相位特性。
设FIR 滤波器的系数为h(0)、h(1)……h(N-1),X(n)表示滤波器在n时刻的输入,则那时刻的输出为:y(n)=h(0)*x(n)+h(1)*x(n-1)+……+h(N-1)*x[n-(N-1)]FIR滤波器的差分方程为:∑-=-=1) ()(Nkkknxany对上式进行Z变换得到FIR滤波器的传递函数为:∑-=-==1)()z (z N i kKzb z X Y H )(FIR 数字滤波器的结构图如图1所示:MATLAB 辅助DSP 实现FIR ,其总体过程为在DSP 中编写处理程序,在MATLAB 中利用滤波器设计、分析工具( FDATOOL) ,根据指定的滤波器性能快速设计一个FIR ,把滤波器系数以头文件形式导入CCS 中,头文件中MATLAB 辅助DSP 实现FIR 数字滤波器含滤波器阶数和系数数组,在MATLAB 中调试、运行DSP 程序并显示、分析处理后的数据。
DSP软件编程(fir滤波器)

FIR滤波器的单位冲激响应 FIR滤波器的单位冲激响应h(n)为有限长序列。 滤波器的单位冲激响应h 为有限长序列。 若h(n)为实数,且满足偶对称或奇对称的条件, 为实数,且满足偶对称或奇对称的条件, 则FIR滤波器具有线性相位特性。 FIR滤波器具有线性相位特性。 滤波器具有线性相位特性 偶对称: 偶对称:h(n)= h(N-1-n); 奇对称: 奇对称:h(n)= -h(N-1-n)。 偶对称线性相位FIR滤波器的差分方程: FIR滤波器的差分方程 偶对称线性相位FIR滤波器的差分方程:
FIR滤波器的DSP实现 FIR滤波器的DSP实现 滤波器的DSP
在数字信号处理中,滤波占有极其重要的地位。 在数字信号处理中,滤波占有极其重要的地位。 数字滤波是语音处理、图像处理、模式识别、 数字滤波是语音处理、图像处理、模式识别、频谱分 析等应用中的基本处理算法。 DSP芯片实现数字滤 析等应用中的基本处理算法。用DSP芯片实现数字滤 波除了具有稳定性好、精确度高、 波除了具有稳定性好、精确度高、不受环境影响等优 点外,还具有灵活性好等特点。 点外,还具有灵活性好等特点。 数字滤波器是DSP的基本应用, DSP的基本应用 数字滤波器是DSP的基本应用,分为有限冲激响 应滤波器FIR和无限冲激响应滤波器IIR 应滤波器FIR和无限冲激响应滤波器IIR。 FIR和无限冲激响应滤波器IIR。 本节主要讨论FIR滤波器的基本结构、 FIR滤波器的基本结构 本节主要讨论FIR滤波器的基本结构、设计方法 DSP实现方法 实现方法。 和DSP实现方法。
y (n) = ∑ bi x( n − i )
DSP中的fir

main() { unsigned int i; float signal; unsigned int n=0; int index=0; for(i=0;i<L;i++) { in[i]=0; out[i]=0; } while(1) { signal = a1*cos((float)w1*n); signal += a2*cos((float)w2*n); signal += a3*cos((float)w3*n); n++; in[index] = (int)((0x7fff*signal)+0.5); out[index] = fir(in,coeff,L,index); index--; if(index==-1) index=L-1; } }
N / 21
y(n)
b x(n i) x(n N 1 i)
i i 0
FIR滤波器的C语言编程实现
,直接型FIR滤波器的C语言编程实现。
/******************************************************** * fir.c 该程序用于实现FIR滤波器 * L——滤波器的阶数 * b[i]——滤波器的系数,i=0,1,…,L-1 * x[i]——输入信号向量,i=0,1,…,L-1;x[0]对应于当前值,x[1]对应于上一 采样值 * x_in —— 输入信号的当前值 * y_out—— 输出信号的当前值 ********************************************************/
extern int fir(int *,int *,unsigned int,int ); /* Low-pass FIR filter coefficients */ int coeff[L]={ -26,-13,14,36,31,-8,-58,-71,-15,83,139,76,-90,-231,-194,50,331,383,78,-405, -654,-347,403,1024,863,-228,-1577,-1972,-453,2910,6836,9470,9470,6836, 2910,-453,-1972,-1577,-228,863, 1024,403,-347,-654,-405,78,383,331,50,-194,-231,-90,76,139,83,-15,-71, -58,-8,31,36,14,-13,-26}; int in[L]; int out[L]; /* input buffer */ /* Output buffer */
DSP系统实验_FIR滤波器

四.实验过程及结果1.使用Matlab中的Fdatool设计滤波器,设计一个采样频率为20000Hz,截止频率fL=1000Hz,fH=4000Hz的FIR 带通滤波器。
(1)在Matlab的Start菜单中选择Toolboxes -> FilterDesign -> Filter Design & Analysis Tools(fdatool),或者在命令行中输入fdatool来启动滤波器设计分析器。
启动成功后界面如下图所示。
(2)在选项中选择或输入滤波器参数,然后点击“Design Filter”按钮,完成滤波器的设计。
具体参数及设计成功后的结果如下图所示。
(3)从Matlab中导出FIR滤波器系数。
在Fdatool 中,选择Targets -> Code Composer Studio (tm) IDE。
在出现的对话框中选择输出文件类型为C header file,输出系数类型为signed 16-bit integer,如下图所示。
点击Generate按钮,选择路径,即可输出前一步设计出的FIR滤波器的系数表。
(假设生成的系数表文件为fdacoefs.h,此头文件中数组B中的数据就是滤波器系数)导出十进制的系数列表,如下图所示。
最终生成.fcf文件,为下一步的Matlab 仿真所使用。
2.利用Matlab产生噪声信号用于滤波器测试,并进行仿真将下面代码另存为M 文件,在Matlab 中运行后将会生成input.dat 文件。
该数据文件中含有500Hz、3000Hz、8000Hz 三种频率的信号,用于滤波器滤波效果测试。
用Matlab进行仿真分别如下所示。
最后运行程序后会产生一个input.dat 文件,这个文件将会在后面的CCS中被用到。
代码如下所示:11=500; %/Hzf12=3000; %/Hzf13=8000; %/Hzfs=20000; %/ 采样 HzN=200 %数据个T=1/fs; % 采样周期n= 0:N;x11=sin(2*pi*f11*n*T);x12=0.7*sin(2*pi*f12*n*T);x13=0.5*sin(2*pi*f13*n*T);x_base=(x11+x12+x13);figure(1)subplot(211)plot(x_base) ; %待滤波信号形title( '待滤波信号形');Subplot(212)yff=abs(fft(x_base));df=(1:N/2)*(fs/N);plot(df,yff(1:N/2)); %待%将 1.3 中 d. 步骤生成的文件中系数复制,并赋值给 b b=[ 0.0015488099260604208-0.000639162226711395180.00000276175440328235950.0049050931002711240.0124676214730609050.013823224770750035-0.00026535232996076602-0.027038289777890162-0.04744269065963877-0.0393776956774877780.000131327872218974470.0462401856615866150.0644421182359068280.041726101066870809-0.00021601367549392082-0.025586149487005817-0.019584633178667085-0.00128851056756914320.0000036241074212133984-0.021008366929296321-0.039658785664257422-0.030892497493987696-0.0000577033839905187980.022210135405908792-0.0018716902153898345 -0.000064100972310515318 0.029127795779719676 0.054818958402419453 0.042884583593487118 -0.00003996438375069266 -0.029259239394713532 -0.014935307528602806 0.015078402779768362 -0.000043450394824481051 -0.079516267912042804 -0.15948637498492943 -0.14273465660088808 -0.000047883173032453426 0.18167944030096761 0.26439813485415459 0.18167944030096761 -0.000047883173032453426 -0.14273465660088808 -0.15948637498492943 -0.079516267912042804 -0.000043450394824481051 0.015078402779768362 -0.014935307528602806 -0.029259239394713532 -0.00003996438375069266 0.042884583593487118 0.054818958402419453 0.029127795779719676 -0.000064100972310515318 -0.0018716902153898345 0.016335005170358768 0.022210135405908792 -0.000057703383990518798 -0.030892497493987696 -0.039658785664257422 -0.021008366929296321 0.0000036241074212133984 -0.0012885105675691432 -0.019584633178667085 -0.025586149487005817 -0.00021601367549392082 0.0417261010668708090.0462401856615866150.00013132787221897447-0.039377695677487778-0.04744269065963877-0.027038289777890162-0.000265352329960766020.0138232247707500350.0124676214730609050.0049050931002711240.0000027617544032823595-0.000639162226711395180.0015488099260604208 ];figure(2);subplot(211);xf=filter(b,1,x_base); %滤波plot(xf); % 滤波之后的信号title( '滤波之后信号形' );yfff=abs(fft(xf));df=(1:N/2)*(fs/N);Subplot(212);plot(df,yfff(1:N/2)); % 滤波之后的信号频谱title ('滤波之后的信号频谱' );%生成 input.data 文件xout=x_base/max(x_base); % 归一化xto_ccs=round(32767*xout);fid=fopen('input.dat','w'); % 打开文件fprintf(fid,'1651 1 0 \n'); % 输出文件头fprintf(fid,'%d \n',xto_ccs);% 输出fclose(fid);仿真结果如下所示:3.在CCS中编写FIR滤波器程序(1)新建一个工程,编写C语言源代码并添加到工程中,代码如下所示:(2)添加cmd文件到工程中(3)分别将"tmwtypes.h","fdacoefs.h ",rst.lib,input.dat文件添加到工程中,最后进行编译链接,成功后则可以在工程所在目录下看到一个Debug文件夹下产生.out文件。
DSP:fir滤波器软硬件实现

设计:
-过渡带宽度=阻带边缘频率-通带边缘频率=22-10=12 kHz
-采样频率:
F1=通带边缘频率+(过渡带宽度)/2=10000+12000/2=16 kHz
Ω1=2Πf1/fs=0.64Π
--理想低通滤波器脉冲响应:
h1[n]=sin(nΩ1)/n/Π=sin(0.64Πn)/n/Π
--根据要求,选择布莱克曼窗,窗函数长度为:
N=5.98fs/过渡带宽度=5.98*50/12=24.9
--选择N=25,窗函数为:
W[n]=0.42+0.5cos(2лn/24)+0.8cos(4лn/24)
--滤波器脉冲响应为:
intnGraphBuf3[ADCNUMBER];
intci=0,keyflage,nAD;
Uint16nMixing[1024];
//液晶----------------------------------------------------------
#define CTRLED (*(unsignedint*)0x108004) // port8004
PORTR PA1,*AR2+0%
.end
链接命令文件
FIR2.obj
vectors.obj
-o FIR2.out
-m FIR2.map
-e start
MEMORY
{
PAGE0:
EPROM:org=0E000h,
len=1000h
VECS: org=0FF80h,
len=0080h
PAGE1:
用DSP实现FIR数字滤波器

用DSP实现FIR数字滤波器FIR滤波器具有幅度特性可随意设计、线性相位特性可严格精确保证等优点,因此在要求相位线性信道的现代电子系统,如图像处理、数据传输等波形传递系统中,具有很大吸引力。
本文简单介绍了其线性相位条件和设计方法,并且提供了一种用DSP实现的方法。
一、引言在许多信息处理过程中,如对信号的过滤、检测、预测等,都要广泛地用到滤波器,而数字滤波器则因其设计灵活、实现方便等特点而广为接受。
所谓数字滤波器就是具有某种选择性的器件、网络或以计算机硬件支持的计算程序。
其功能本质是按事先设计好的程序,将一组输入的数字序列通过一定的运算后转变为另一组输出的数字序列,从而改变信号的形式和内容,达到对信号加工或滤波以符合技术指标的要求。
二、数字滤波器的两种类型对于一般的数字滤波器,按照单位冲激响应可分为无限长冲激响应IIR (Infinite Impulse Response)系统和有限长冲激响应FIR(Finite Impulse Response)系统。
在IIR系统中,用有理分式表示的系统函数来逼近所需要的频率响应,即其单位冲激响应h(n)是无限长的;而在FIR系统中,则用一个有理多项式表示的系统函数去逼近所需要的频率响应,即其单位冲激响应h(n)在有限个n值处不为零。
IIR滤波器由于吸收了模拟滤波器的结果,有大量的图表可查,可以方便、简单、有效地完成设计,效果很好,但是其相位特性不好控制,必须用全通网络进行复杂的相位较正,才能实现线性相位特性的要求。
FIR滤波器则可在幅度特性随意设计的同时,保证精确、严格的线性相位特性。
这在要求相位线性信道的现代电子系统,如图像处理、数据传输等波形传递系统中,是具有很大吸引力的。
而且,其单位冲激响应是有限长的,不存在不稳定的因素,并且可用因果系统来实现。
下面着重讨论具有线性相位特性的FIR滤波器。
三、 FIR滤波器线性相位特性的条件及设计方法1.线性相位条件为保证滤波器带内输出信号的形状保持不变,常常要求滤波器单位冲激响应h(n)的频率响应H(ejω)应具有线性的相频特性,即 H(ejω)=H(ω)e-jωk,其中H(ω)为幅频特性,k为正整数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
经过这次课设对FIR滤波器的原理有了一定的了解,对于在滤波器设计中MATLAB的相关使用也加深了认识,知道如何通过FDATOOL工具快速设置一个滤波器。在ccs操作过程中通过比较C语言与汇编语言所设计的滤波器的处理速度有了一定的认识。同时通过此次课设也发现自身所存在的欠缺,在接下的时间需要加以锻炼提升。
FIR滤波器误反馈回路,是一种稳定系统,可以设计成具有线性相位特性。设FIR滤波器的系数为h(0)、h(1)……h(N-1),X(n)表示滤波器在n时刻的输入,则那时刻的输出为:
y(n)=h(0)*x(n)+h(1)*x(n-1)+……+h(N-1)*x[n-(N-1)]
FIR滤波器的差分方程为:
对上式进行Z变换得到FIR滤波器的传递函数为:
mov hi(AC0),T0;用Q15格式存放结果
popm ST3_55;恢复ST1, ST2和ST3
popm ST2_55
popm ST1_55
ret
.end
4、实验结果
实验设计的FIR滤波器的采样频率Fs为25KHz,截止频率Fc为1KHz,当输入700Hz的方波时候,其处理波形显示如下:
输入为2KHz的时候,显示如下:
三、实验过程及结果
1、FIR滤波器的系数
在matlab中可以通过分析工具FDATOOL来快速设计一个FIR,并得到相关的系数,其设计界面如图所示:
得到其相关系数:
2、fir的C程序的实现
首先要创建一个数组,数组的大小等于滤波器的阶数,用来存放用MATLAB生成的滤波器的系数,另外再定义一个数据缓冲区,来存放采集来的数据,该缓冲区的大小要和滤波器的系数数组的大小相同。然后进行数据移位,将数据缓冲区中的数据向下一个单元移1位,然后将刚采进来的数据放到缓冲区的首位。最后用for循环来实现乘加运算,得到这一时刻的卷积值。
3、Fir的汇编语言的实现
处理信号缓冲器的最有效方法,是把信号采样加载到循环缓冲器中。在循环缓冲器中,采取数据保持固定、反时针方向移动地址的方式,代替保持缓冲器地址固定且正方向移动数据。信号采样的起点由指针x(n)指定,其它诸采样则沿着顺时针方向,从起点开始依次顺序加载。当接收到一个新的采样时,它会被配置在位置x(n)上,并且完成滤波算法。计算完输出量y(n)以后,指针反时针方向移动一个单元到x(n-L+1)位置,并且当作下一次迭代运算的x(n)。FIR滤波器系数的循环缓冲器如图所示,它总是从第一个系数开始运行。
float fir( float x_in,float *x,float *b,int L) //
{
float y_out;
int i;
for(i=L-1;i>0;i--)
{
x[i]=x[i-1];
}
x[0]=x_in;
y_out=0.0;
for(i=0;i<L;i++)
{
y_out=y_out+b[i]*x[i];
由于不同的窗函数对信号频谱的影响是不一样的,这主要是因为不同的窗函数,产生泄漏的大小不一样,频率分辨能力也不一样。信号的截断产生了能量泄漏,而用FFT算法计算频谱又产生了栅栏效应,从原理上讲这两种误差都是不能消除的,但是我们可以通过选择不同的窗函数对它们的影响进行抑制。在MATLAB设计中采用海明窗。
FIR数字滤波器的结构图如图1所示:
MATLAB辅助DSP实现FIR ,其总体过程为在DSP中编写处理程序,在MATLAB中利用滤波器设计、分析工具( FDATOOL) ,根据指定的滤波器性能快速设计一个FIR ,把滤波器系数以头文件形式导入CCS中,头文件中MATLAB辅助DSP实现FIR数字滤波器含滤波器阶数和系数数组,在MATLAB中调试、运行DSP程序并显示、分析处理后的数据。使用该方法,便于采用汇编语言来实现程序。
bset SMUL ;置位SMUL(P50)
mov mmap(AR0),BSA01 ; AR0=输入信号循环缓冲区的起始地址
mov mmap(AR1),BSAT0),BK03;设置循环缓冲区大小
or #0x5,mmap(ST2_55) ; AR0和AR2为循环缓冲区指针
二、设计原理
数字信号处理技术的应用领域非常广泛,而数字滤波器的设计是数字信号处理中最重要的设计环节。数字滤波器分为IIR滤波器和FIR滤波器。本次课设使用的是FIR滤波器。
FIR滤波器即有限长单位响应滤波器,是数字信号处理系统中最基本的原件。可以在保证任意频率特性的同时具有严格的线性相位特性。同时其单位冲激响应是有限长的,因而滤波器是稳定的系统。FIR滤波器在通信、图像处理、模式识别等领域具有广泛的应用。
在进入FIR滤波器前,首先要将信号通过A/D器件进行模数转换,把模拟信号转化为数字信号;为了使信号处理能够不发生失真,信号的采样速度必须满足奈奎斯特定理,一般取信号频率上限的4-5倍做为采样频率;一般可用速度较高的逐次逼进式A/D转换器,不论采用乘累加方法还是分布式算法设计FIR滤波器,滤波器输出的数据都是一串序列,要使它能直观地反应出来,还需经过数模转换。
}
return(y_out);
}
直接型FIR滤波器的实现涉及到两个基本操作,一个是输入信号向量与滤波器系数向量的内积计算,另一个是输入信号向量的更新处理。在每个采样周期信号缓冲器都要更新一次,最老的采样被抛弃,而其他的信号则向缓冲器的右方移动一个单元,一个新的采样被插入存储单元,并被标记。如果这个操作过程不用DSP硬件完成,那么它需要很多的时间。
;参数2: T0 - FIR滤波器的阶数L
;参数3: T1 -输入信号当前值在循环缓冲区的序数
;返回值: T0 -输出信号当前值
.def _fir
_fir
pshm ST1_55 ;现场ST1,ST2和ST3入栈
pshm ST2_55
pshm ST3_55
or #0x340, mmap(ST1_55) ;设置FRCT,SXMD,SATD
mov T1,AR0 ; AR0从index偏移量开始
mov #0,AR2 ; AR2从0偏移量开始
sub #2,T0;T0=L-2
mov T0,CSR;设置外部循环次数为L-1
mpym *AR0+,*AR2+,AC0;执行第一次运算
|| rpt CSR;启动循环
macm *AR0+,*AR2+,AC0
基于以上方法的FIR滤波器,其汇编语言实现如下。
汇编语言整数fir滤波器函数:fir.asm
; fir.asm该程序用于实现FIR滤波器,可被C语言程序调用
; int fir(int *,int *, unsigned int,int)
;参数0: AR0 –输入信号缓冲区指针
;参数1: AR1 - FIR滤波器系数向量指针
基于DSP的FIR低通滤波器的设计
学 号:
电子与控制工程学院
一、设计要求
通过ICETEK–VC5509-A评估板实现FIR滤波功能,将输入的方波信号通过评估板上的AD模块,滤波模块,以及DA模块后输出正弦波信号并在示波器上观察方波滤除后所产生的正弦波。在CCS下编写C语音和汇编语言程序分别实现滤波器功能,并且比较c语言和汇编语言的执行速度进行比较。
