管道的屈曲分析
第11章 屈曲分析17讲解
第11章 屈曲分析11.1 屈曲分析概述静力分析方法认为杆件的破坏取决于材料的强度，当杆件承受的应力小于其许用应力时，杆件便可安全工作，对于细长受压杆件这却并不一定正确。
压杆在承受的应力小于其许用应力时，杆件会发生变形而失去承载能力，这类问题称为压杆屈曲问题，或者压杆失稳问题。
工程中许多细长构件如发动机中的连杆、液压缸中的活塞杆和订书机中的订书针等，以及其他受压零件，如承受外压的薄壁圆筒等，在工作的过程中，都面临着压杆屈曲的问题。
临界载荷是受压杆件承受压力时保持杆件形状的载荷上限。
压杆承受临界载荷或更大载荷时会发生弯曲，如图11-1所示。
经典材料力学使用Euler 公式求取临界载荷：()22l EJ F cr μπ= （11-1）图11-1临界载荷下压杆发生屈曲该公式在长细比超过100有效。
针对不同的压杆约束形式，参数的μ取值如表11-1所示。
表11-1 Euler 公式中参数μ的取值对于压杆屈曲问题，ANSYS 中一方面可以使用线性分析方法求解Euler 临界载荷，另一方面可以使用非线性方法求取更为安全的临界载荷。
ANSYS 提供两种技术来分析屈曲问题，分别为非线性屈曲分析法和线性屈曲分析法（也称为特征值法）。
因为这两种方法的结果可能截然不同（见图11-2），故需要理解它们的差异： ✧ 非线性屈曲分析法通常较线性屈曲分析法更符合工程实际．使用载荷逐渐增大的非线性静力学分析，来求解破坏结构稳定的临界载荷。
使用非线性屈曲分析法，甚至可以分析屈曲后的结构变化模式。
✧ 线性屈曲分析法可以求解理想线性弹性理想结构的临界载荷，其结果与Euler 方程求得的基本一致。
图11-2不同分析方法的屈曲分析结果11.2线性屈曲分析步骤由于线性屈曲分析基于线性弹性理想结构的假设进行分析，所以该方法的结果安全性不佳，那么在设计中不宜直接采用分析结果。
线性屈曲分析包含以下步骤。
11.2.1前处理建立模型，包括：（1）定义单元类型，截面结构、单元常数等。
管子的弯曲1讲解
7.3.1管子弯曲的受力分析和变形计算
(1)受力分析及易产生的缺陷
管子也有薄壁和厚壁之分，
S 0.06 时是薄壁，反之是厚壁。 当 Dm
(1)受力分析及易产生的缺陷
管子在弯矩M的 作用下产生自由 弯曲， 中性轴处不受力， 中性轴以外受拉 伸，中性轴内侧 受压缩。 当管子不是纯弯 曲时侧壁厚减薄量
min b 100%
估算见表7-19。计算公式见7-57。
7.3.2 弯管方法
（1）手工弯管 手工弯管可分为热弯和冷弯。
管子在室温下的弯曲习惯上称作冷弯，由于冷 弯效率高，质量好，操作环境好，所以直径 108mm以下的管子多采用冷弯。
直径大于108mm或直径60mm以上的厚壁 管，弯管阻力较大，容易出现缺陷，所以一般 不再 使用冷弯法。
(2) 冷弯机弯管
冷弯机是弯管机械化的设备之一，用在冷态 下，不用填充物弯管，可以用芯棒也可以不用。 结构形式主要有两种：辊轮式和导槽式 。 导槽与管子接触面积大 ，控制管子截面变形
方面比辊轮优越 。
a. 有 芯 弯 管
O
O
a. 有 芯 弯 管
b. 无 芯 弯 管
b. 无 芯 弯 管
b. 手 工 热 弯
热弯时一般要以砂子作填充物。
弯管前在管内装砂子的作用是阻止弯曲变形时管 的 截面变成椭圆形或内侧表面起皱。
因为砂子的吸热性和保温性都较好，用它做热载体允许 管子缓慢成形而不用重复加热，并且经济、易于操作。 加热温度：低碳钢 950-1000℃，普通低合金钢 850-1000℃，18-8型不锈钢1100-1200℃。
C.电动卷扬机弯管
电动卷扬机 拉弯管 1- 钢丝绳 2- 轨道 3- 拉轮
管道弯曲问题的弹性力学分析
管道弯曲问题的弹性力学分析引言管道是现代工业中不可或缺的设施，广泛应用于输送液体、气体和固体颗粒等物质。
然而，在实际应用中，管道通常会遇到弯曲问题，这可能导致管道的变形和损坏。
因此，对管道弯曲问题进行弹性力学分析，可以帮助我们更好地理解其受力特性，进而优化设计和维护管道系统。
一、管道弯曲的原因管道弯曲的原因主要有两种：外力作用和温度变化。
外力作用包括重力、压力和振动等，而温度变化会引起管道的热胀冷缩。
这些因素都会导致管道产生弯曲应力和变形。
二、弯曲管道的力学模型为了对弯曲管道进行弹性力学分析，我们可以采用梁的力学模型。
将管道视为一根悬臂梁，可以简化问题的复杂性，并得到较为准确的结果。
三、管道弯曲的受力分析在管道弯曲时，受力分析是非常重要的。
首先，我们需要考虑管道的自重作用，即重力对管道的影响。
其次，管道内的流体压力也会对管道产生作用力。
此外，管道的振动和温度变化也会引起额外的受力。
四、管道弯曲的应力分析在管道弯曲过程中，应力分析是评估管道强度和稳定性的关键。
通过应用弹性力学理论，我们可以计算出管道在弯曲过程中的应力分布。
这有助于我们判断管道是否能够承受外力和温度变化的影响，以及预测其寿命和安全性。
五、管道弯曲的变形分析除了应力分析外，变形分析也是管道弹性力学分析的重要内容。
管道在受力作用下会发生弯曲和拉伸，这可能导致管道的变形和位移。
通过计算管道的弯曲角度、拉伸量和位移等参数，我们可以评估管道的变形程度，并进一步优化设计和维护方案。
六、管道弯曲问题的解决方法针对管道弯曲问题，我们可以采取多种解决方法。
一种常见的方法是增加管道的壁厚，以提高其强度和刚度。
另外，可以使用支撑结构来减小管道的变形和位移。
此外，合理的材料选择和施工工艺也可以降低管道弯曲问题的发生概率。
七、案例分析：石油管道的弯曲问题石油管道是管道工程中的重要组成部分，其弯曲问题对于石油输送的安全和稳定性具有重要影响。
以某石油管道为例，我们可以通过弹性力学分析，评估管道在弯曲过程中的受力、应力和变形情况，从而为管道的设计和维护提供依据。
国内外海底管道屈曲研究进展
《海洋工程结构力学》国内外海底管道屈曲研究进展摘要：海底管道铺设过程中，往往在海底与铺管作业船之间的管道存在着相当长一段的悬跨段，悬跨段长度与水深有关。
在悬跨段经常可能因管子原始的或铺设过程中造成的局部凹陷或损伤而发生屈曲失稳现象。
这种屈曲一旦在管道局部形成，将容易因外部超静水压作用而沿着管道出现纵向屈曲迅速传播，造成危害性较大的传播型屈曲。
这将会严重阻碍管道的正常运行和造成较大的经济损失。
本文即简单评述了国内外海底管道屈曲研究进展情况。
关键词：管道铺设屈曲超静水压Advances on local & global buckling of subsea pipelinesAbstract：When the laying of submarine pipes, there often existence a long period of the suspension span between the seabed and pipe laying ship channel, which length have realated to the depth of water. In spanning the original tubes may often be due to the process or installation or damage caused by depression, while local buckling phenomena occur. Once this form of local buckling in the pipeline made, it will be vulnerable to the external role of super-hydrostatic pressure along the pipeline buckling of vertical spread rapidly, causing the spread of harmful larger type buckling. This will seriously impede the normal operation of pipeline and cause large economic losses. This paper briefly reviews the domestic and buckling of submarine pipelines progress.Key words：Pipe laying Buckling Super-hydrostatic pressure1国内外研究现状当前，海底管道铺设过程的受力性能和屈曲问题引起了广泛的关注，针对该类问题国内外相关学者进行了较为深入的研究。
薄管屈曲问题
1 前言冲击作用是在建筑桩基施工、金属加工和动力机械设计等问题中常见的现象，结构在冲击载荷下的材料强度以及动力响应问题（主要是变形和屈曲问题）一直是一项很重要的动力学研究课题。
各种冲击动力学问题的最基本特征为冲击物的速度或位移在与结构接触后的一个极短时间内迅速地改变，冲击作用的（加载）过程非常短暂。
本文以薄壁钢管在轴向冲击作用下的屈曲分析为例，介绍在ANSYS/LS-DYNA中进行冲击动力学分析的方法。
ANSYS/LS-DYNA将显式计算程序LS-DYNA 与ANSYS仿真分析环境有机的结合在一起，可以完成高度非线性的瞬态动力过程的分析。
两者的结合既克服了ANSYS在瞬态动力过程分析方面的弱点，同时也克服了LS-DYNA在建模方面的不方便性，两者的合并，无疑克服了各自的缺点，同时将两者的优点保留了下来。
2 模型建立与数值讨论实际生活中经常使用薄壁钢管支撑重物用，但是经常会发生这样的问题：但重物的重量慢慢增加时，薄壁钢管突然会发生弯曲。
这就是所谓的屈曲。
一旦结构发生了屈曲，结构已经丧失了稳定性，轻则不能承载重物，重则会危机生命。
用理论可以分析简单的结构屈曲，但是实际生活中的结构太复杂，以至于不能简单的运用理论进行分析了，必须借助CAE软件了，因此本文有很大的实用价值。
要分析的问题描述如下：圆钢管直径为D=500mm，壁厚t=3mm，长度L=1000mm，一端完全固定，另一端按强制性位移进行加载，使端面在20ms内沿轴向发生500mm的压缩位移，分析钢管在整个过程中的变形以及应力分布情况，最后进行一些讨论。
在分析中采用SHELL163显式分析单元，单元变形方法选用Belytschko-Wong方法，这种单元算法比较适合于处理有表面翘曲的大变形问题。
材料的密度为7800kg/m3，泊松比为0.27，弹性模量为2.07e11，屈服应力为300MPa，切线模量为1e10。
由于钢管表面在冲击压缩过程中，可能会发生表面折叠和自相接触的现象，因此需要定义接触，接触算法采用单面的自动接触算法ASSC，接触面的摩擦系数取为0.1。
管材弯曲技术简介
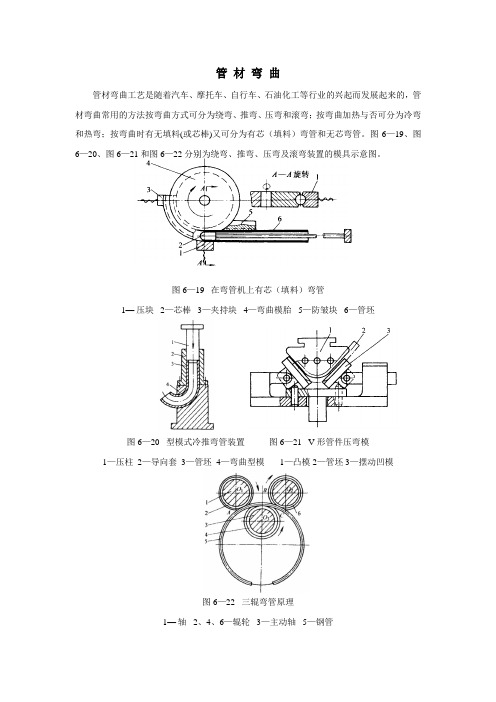
管材弯曲管材弯曲工艺是随着汽车、摩托车、自行车、石油化工等行业的兴起而发展起来的，管材弯曲常用的方法按弯曲方式可分为绕弯、推弯、压弯和滚弯；按弯曲加热与否可分为冷弯和热弯；按弯曲时有无填料(或芯棒)又可分为有芯（填料）弯管和无芯弯管。
图6—19、图6—20、图6—21和图6—22分别为绕弯、推弯、压弯及滚弯装置的模具示意图。
图6—19 在弯管机上有芯（填料）弯管1—压块2—芯棒3—夹持块4—弯曲模胎5—防皱块6—管坯图6—20 型模式冷推弯管装置图6—21 V形管件压弯模1—压柱2—导向套3—管坯4—弯曲型模1—凸模 2—管坯 3—摆动凹模图6—22 三辊弯管原理1—轴2、4、6—辊轮3—主动轴5—钢管一、管材弯曲变形及最小弯曲半径管材弯曲时，变形区的外侧材料受切向拉伸而伸长，内侧材料受到切向压缩而缩短，由于切向应力θσ及应变θε沿着管材断面的分布是连续的，可设想为与板材弯曲相似，外侧的拉伸区过渡到内侧的压缩区，在其交界处存在着中性层，为简化分析和计算，通常认为中性层与管材断面的中心层重合，它在断面中的位置可用曲率半径ρ表示(图6—23)。
管材的弯曲变形程度，取决于相对弯曲半径D R 和相对厚度D t (R 为管材断面中心层曲率半径，D 为管材外径，t 为管材壁厚)的数值大小，D R 和D t 值越小，表示弯曲变形程度越大(即D R 和D t 过小)，弯曲中性层的外侧管壁会产生过度变薄，甚至导致破裂；最内侧管壁将增厚，甚至失稳起皱。
同时，随着变形程度的增加，断面畸变(扁化)也愈加严重。
因此，为保证管材的成形质量，必须控制变形程度在许可的范围内。
管材弯曲的允许变形程度，称为弯曲成形极限。
管材的弯曲成形极限不仅取决于材料的力学性能及弯曲方法，而且还应考虑管件的使用要求。
对于一般用途的弯曲件，只要求管材弯曲变形区外侧断面上离中性层最远的位置所产生的最大伸长应变m ax ε不致超过材料塑性所允许的极限值作为定义成形极限的条件。
埋设悬跨海底管道的屈曲分析
第23卷第2期 V ol.23 No.2 工 程 力 学 2006年 2 月 Feb. 2006 ENGINEERING MECHANICS173———————————————收稿日期：2004-03-26；修改日期：2004-05-27作者简介：*邢静忠(1966)，男，甘肃人，教授，博士，从事海洋石油工程力学研究(E-mail: hsingjzh@)； 柳春图(1935)，男，江苏人，研究员，博士生导师，从事固体力学、断裂和疲劳研究； 徐永君(1964)，男，河北人，博士，从事工程力学研究。
文章编号：1000-4750(2006)02-0173-04埋设悬跨海底管道的屈曲分析*邢静忠1,2，柳春图1，徐永君1(1. 中国科学院力学研究所, 北京 100080; 2. 兰州理工大学理学院, 兰州 730050)摘 要：考虑海床刚度，研究了埋设悬跨海底管道在热膨胀引起的轴向压力下的屈曲问题。
传统方法是将悬跨管道简化为两端简支或者两端固支梁来处理。
基于欧拉-伯努利梁理论，考虑线弹性海床刚度和轴向压力，建立并求解了埋设段管道和悬跨段管道在自重作用下的四阶常微分方程，获得了两段管道的静挠度和内力的解析公式。
通过对静挠度的特性分析，给出了埋设管道段和悬跨管道段的稳定性判断准则。
关键词：屈曲；海底管道；悬跨；弹性地基；热膨胀 中图分类号：O343 文献标识码：ABUCKLING ANALYSIS OF BURIED SPANNING SUBMARINE PIPELINE*XING Jing-zhong 1,2 , LIU Chun-tu 1 , XU Yong-jun 1(1. Institute of Mechanics, Chinese Academy of Sciences, Beijing 100080, China; 2. School of Science, Lanzhou University of Science, Lanzhou 730050, China)Abstract: This paper presents a buckling analysis of buried spanning submarine pipelines under axial compressive force caused by thermal expansion, in which the seabed stiffness is taken into account. Traditional methods treat each span segment as a simply-supported beam or clamped-clamped beam in practice. A new approach is developed based on Euler-Bernoulli beam theory, taking into account the linear elastic stiffness of seabed and temperature-driving axial force. A fourth order ordinary differential equation governing buried segment in elastic seabed and spanning segment under self-weight and axial compressive force is established and solved. The static deflection and internal force function of both segments are obtained in closed form. Stability criteria of buried segment and spanning segment are established through analyzing the characteristics of static deflection.Key words: buckling; submarine pipeline; spanning; elastic foundation; thermal expansion由于海床不平整，或者海流淘蚀，海底管道经常出现悬跨(Spanning)情况。
第四章-管道的屈曲分析
临界载荷
直线管道的挠曲微分方程式
A y P 2 B y C 0 y
各系数分别为
A EI
B
K u D 1
1 D
C
K 0 D 1
2 D
K0 2K u
EI—管道的弯曲刚度； Ku —土壤对管道的轴向系 抗数 力； K0 —土壤的压缩抗力系数；
逆解法：假设管道失稳时的弯曲形状为
y f
q0——管道所受的向下压力, ｑ0=q1+q2 ，N/m；
q1——管子本身和管内流体重量，N/m；
q2——压重物（如土壤和固定支墩）的重量或锚栓对 管道的拉力，N/m；
n ——土壤的载荷系数，n=0.8~1.2；
qcr——土壤抗管道作向上的横向位移时的临界支承力， N/m。
土壤的临界支承力
q cr sD oh 0 0 .3D 9 sh o 0 2 tg 0 .7 c 0 .7 o 0 C .7 0 s h
限于两止屈器之间。
止屈器的形式
a）活动式（套 筒式）屈曲限 制器；
b）厚壁管筒式 （或整体式） 屈曲限制器；
c）焊接固定式 屈曲限制器。
本章小结
• 几种常见的屈服形式有：轴向屈曲、上浮屈曲、 压扁、外压下的屈曲、屈曲传播等；
• 陆上管道的屈曲验算的安全系数取0.60~0.75; • 在陆地管道的屈曲分析中需要考虑土壤刚度的影
安全温升
不同摩擦系数
T(℃ )
150温
120 90 60 30
f=0.01 f=0.05 f=0.1 f=0.2 f=0.4
0
f=0.6
0
20
40
60
80
100
L(m)
不同覆盖土层载荷
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
可以求得
EI
4
K0 D 1
2
D
Pcr
2
Ku D 1
1 D
EIK0
D
1
2 D
• 失稳时，轴向位移与横向位移相比只是一个二 阶小数，可忽略不计。
4 EI
K0D Pcr 2 EIK0D
适用于直线管道（或曲率半 径1000D的弯曲管道）。
土壤的压缩抗力系数K0
弯曲屈曲 U形屈曲 双凹屈曲 变平化屈曲
屈曲分析的内容
轴向屈曲 地下埋设管道
屈 曲
上浮屈曲
局部屈曲
地下埋设管道 海底埋设管道
机械作用 外压
屈曲传播
4-1 地下管道的轴向稳定性
• 在嵌固段，管道所受到的最大轴向力为：
P pD ET A
2t
• 管道轴向稳定性的验算条件
P nPcr
n——安全系数，可取n=0.6~0.75。
• 压扁深度大于管道直径8%时，影响管道的爆破 强度；
• 压扁处容易在疲劳载荷下产生裂纹。
压扁分析的Wierzbicki（维兹比基）模式
• 忽略了环向弯曲和轴向拉伸的塑性相互作用； • 忽略了弹塑性变形的相互作用； • 忽略了应变硬化； • 假定冲击载荷作用于垂直于管道的平面内。
塑性铰
压扁处的位移
2 210 103 (1 0.32 )
6
3
273
4.90MPa
4-5 海底管道的屈曲传播
• 局部屈曲 • 屈曲传播 • 止屈措施
1、局部屈曲
• 对管子局部屈曲可定义为：管子截面扁平化或翘 曲折皱超过规定的限度。
• 实际管子存在残余的椭圆度，而且还可能产生显 著的塑性变形。因此，管道的失稳的临界外压是 材料屈服极限的函数。
q0——管道所受的向下压力, ｑ0=q1+q2 ，N/m；
q1——管子本身和管内流体重量，N/m；
q2——压重物（如土壤和固定支墩）的重量或锚栓对 管道的拉力，N/m；
n ——土壤的载荷系数，n=0.8~1.2；
qcr——土壤抗管道作向上的横向位移时的临界支承力， N/m。
土壤的临界支承力
qcr
so Dh0
0
w=1200N/m w=2400N/m w=3600N/m w=4800N/m w=6000N/m
10 20 30 40 50 60 70 80 90 100 L(m)
4-3 压扁
在冲击载荷的作用下，会产生较大的塑性变形，
即被压扁。
压扁的影响
• 压扁深度大于管道直径5%时，影响清管球的通 过；
3、止屈器
为了防止屈曲和屈曲的传播，可以采取以下两种 措施： –加大全线管壁厚度：可行，但不经济 –管道局部加厚，或采用止屈器，使屈曲传播只
限于两止屈器之间。
止屈器的形式
持圆形形状或完全坍塌。
• 考虑实际管子不是理想的圆形，并且受环向和弯 曲应力的联合作用，其临界压力值会大大减小。
例： Ф273×6钢管能承受的极限外压
C
2E
(1
2
)
t D
3
式中：C — 极限外压； D —外径；
t —壁厚；
—泊松比(0.3);
E —弹性模量(210GPa)。
计算结果：
C
ud
3
32
P2
y2t3
ud — 压扁处的位移 P — 压扁处的集中力 y — 屈服应力 t — 壁厚
4-4 管道在外压作用下的稳定性
• 对于外压作用下的管子，稳定性是必须优先考虑 的因素。
• 理想圆管的临界压力：
C
2E
(1
2
)
t D
3
• 当管子承受的外压大于临界值时，管子将不能保
• 上浮屈曲产生过量的垂直位移和塑性变形，被认 为是一种失效情形。
• 和铁路铁轨中的热胀屈曲相类似。
上浮屈曲的形状
A B B'
y C'
C Lx
D' D E
y
k
q 2P
c osk x c osk L
2
k 2 L2 8
1
k 2 x2 2
临界载荷与长度
EI Pcr 80.73 L2
P0
Pcr
• 屈曲起始压力和屈曲传播压力。
pi p p 一旦造成管道屈曲，肯定传播
pe pi 屈曲发生
pe p p 屈曲传播 pe p p 屈曲传播停止
pi
pp
管道的屈曲传播压力的确定（试验和理论研究）
Battelle
pp
6
s
2t D
2.5
DNV
pp
1.15
t
s
DLeabharlann t2 传播压力只取决于屈服极限和径厚比。
0.39D
soh02tg0.7
0.7Ch0
cos0.7
式中： γso——管顶填土的容重，N/m3； φ——土壤内摩擦角； C——土壤粘着力。
当向上弯曲管道的轴向稳定性得不到保证时，可采 用增加埋深、设置固定墩或锚固等方法。
4-2 海底管线的上浮屈曲
• 海底（或地震液化土）覆盖土层的刚性较小，管 子容易因屈曲而产生向上拱的弯曲变形，称为上 浮屈曲。
pcr
2
t D
e
2 3
s
pcr
2
s
t D
1
1 3
2 s e
e
2 3
s
考虑实际管子不可能是理想的圆形，并且受环向和 弯曲应力的联合作用，其临界压力值会大大减小。
M M cr
pe 1 pcr
1
300 D/t
pe pcr
Mcr和pcr分别是管道单独受弯曲和外压时的临界值。
2、屈曲传播
• 管道的局部屈曲可以传播，传播的速度异常迅速， 屈曲传播的长度有几百米至上千米。
qL EI
1.598EAf qL5
0.25 fEI2
1 2
两式须联立求Pcr。
安全温升
不同摩擦系数
T(℃ )
150温 120 90 60 30
0 0
f=0.01 f=0.05 f=0.1 f=0.2 f=0.4 f=0.6
20
40
60
80
100
L(m)
不同覆盖土层载荷
T(℃)
150
120
90 60 30 0
土壤性质 密度小的土壤
中等密度的土壤
土壤名称
泥煤土 流砂 软湿土 新填砂 压实砂 砾石 湿粘土
K0,kgf/cm3
0.05~0.1 0.1~0.5 0.1~0.5 0.1~0.5 0.5~5.0 0.5~5.0 0.5~5.0
向上弯曲时 式中:
Pcr 0.375 q0
0——计算曲率半径，m； q——管道向上位移时的土壤极限阻力，ｑ=q0+qcr ，N/m；
临界载荷
直线管道的挠曲微分方程式
Ay P 2By Cy 0
各系数分别为
A EI
B
Ku D1
1
D
C
K 0 D1
2
D
K0
2Ku
EI —管道的弯曲刚度； Ku —土壤对管道的轴向抗力系数； K0 —土壤的压缩抗力系数；
逆解法：假设管道失稳时的弯曲形状为
y f x
y f sin x