【全国大学生数学建模竞赛获奖优秀论文作品学习借鉴】1992年A题 施肥效果分析
1992年A题农作物施肥效果分析
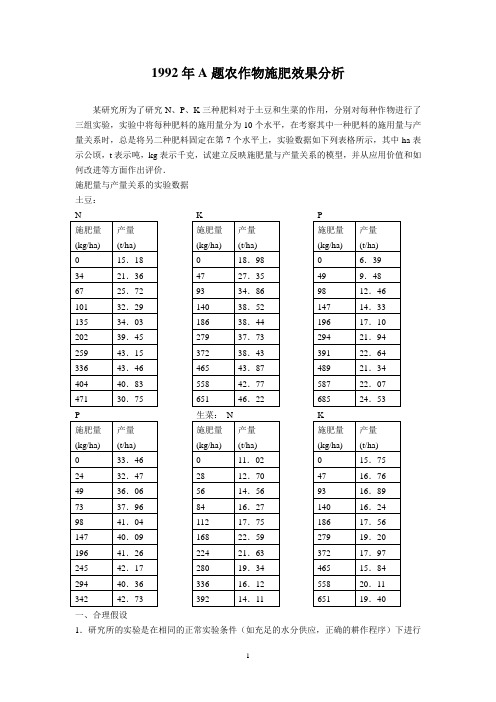
1992年A题农作物施肥效果分析某研究所为了研究N、P、K三种肥料对于土豆和生菜的作用,分别对每种作物进行了三组实验,实验中将每种肥料的施用量分为10个水平,在考察其中一种肥料的施用量与产量关系时,总是将另二种肥料固定在第7个水平上,实验数据如下列表格所示,其中ha表示公顷,t表示吨,kg表示千克,试建立反映施肥量与产量关系的模型,并从应用价值和如何改进等方面作出评价.施肥量与产量关系的实验数据土豆:一、合理假设1.研究所的实验是在相同的正常实验条件(如充足的水分供应,正确的耕作程序)下进行的,产量的变化是由施肥量的改变引起的,产量与施肥量之间满足一定的规律. 2.土壤本身已含有一定数量的氮、磷、钾肥,即具有一定的天然肥力. 3.每次实验是独立进行的,互不影响. 符号说明: W :农作物产量. x :施肥量.N 、P 、K :氮、磷、钾肥的施用量. Tw :农产品价格. Tx :肥料价格.Tn,Tp,Tk :氮、磷、钾肥的价格.a,b,b 0,b 1,b 2,c,c 0,c 1,c ’0,c ’1:常数(对特定肥料,特定农作物而言). 二、问题分析农学规律[2]表明,施肥量与产量满足下图所示关系,它分成三个不同的区段,在第一区段,当施肥量比较小时,作物产量随施肥量的增加而迅速增加,第二区段,随着施肥量的增加,作物产量平缓上升,第三区段,施肥量超过一定限度后,产量反而随施肥量的增加而下降. 图14-1 施肥量与产量的一般关系为考察氮、磷、钾三种肥料对作物的施肥效果,我们以氮、磷、钾的施用量为自变量;土豆和生菜的产量为因变量描点作图.从中看出,氮肥对于作物产量的贡献大致呈指数关系,磷肥对于作物产量的关系大致为分段直线形式,至于钾肥,对土豆而言,大致呈指数关系,对生菜而言,随着施用量的增加,产量的上升幅度很小.这样,我们得到了对施肥效果的定性认识.在长期的实践中,农学家们已经总结出关于作物施肥效果的经验规律,并建立了相应的理论[3].1.Nicklas 和Miller 理论:设h 为达到最高产量时的施肥量,边际产量(即产量W 对施肥量x 的导数)dxdW 与(h-x)成正比例关系.dW/dx=a(h-x),(1) 从而 W=b 0+b 1x+b 2x 2.(2)2.米采利希学说:只增加某种养分时,引起产量的增加与该种养分供应充足时达到的最高产量A 与现在产量W 之差成正比. dW/dx=c(A-W),(3)从而 W=A (1-exp(-cx)).(4)考虑到土壤本身的天然肥力,上式可修正为 W=A (1-exp(-cx+b)).(5)3.英国科学家博伊德发现,在某些情况下,将施肥对象按施肥水平分成几组,则各组的效应曲线就呈直线形式.若按水平分成二组,可以用下式表示:,)x x x (x c c )x x 0(x c c n i 10i 10⎩⎨⎧<≤'+'<≤+(6) 我们假设该研究所的实验是在正常条件下进行的,因而表14-1所示的施肥量与产量的数据应该满足上述规律(对不同肥料,不同作物而言可以满足不同的规律).以这些理论为依据,就可以对作物施肥效果进行回归分析.从实验设计的角度来看,该研究所采用的设计方案是因素轮换法,即在考察每一种肥料的效应时,总将另二种肥料的施用量固定在第7个水平上.采用这种设计方法,无法估算出三种肥料间的交互效应,因此,我们将每组实验看成单因素实验,并根据实验结果,给出反映施肥量与产量关系的一元肥料效应方程及效应曲线. 三、模型与结果我们建立了一元肥料效应回归模型,并在回归分析之前,用Chauvenent 准则进行修正,剔除异常值.根据对问题的初步分析,氮肥的施肥效果应满足Nicklas 和Miller 理论所描述的关系,运用二次多项式回归,得到氮肥对土豆的效应方程:W=14.74+0.197n-0.00034n 2.(7) 氮肥对生菜的效应方程:W=10.23+0.101n-0.00024n 2.(8) 氮肥的效应曲线如图14-2,图14-3所示.磷肥的施用对作物产量的增加表现为分段直线形式,运用线性回归,得到磷肥对土豆的效应方程:⎩⎨⎧≤≤+<≤+=).342p 04.101(p 0059.0968.39),04.101p 0(p 084.0077.32w (9)磷肥对生菜的效应方程:⎩⎨⎧≤≤+<≤+=).685k 54.202(k 00472.0196.20),54.202k 0(k 052.0809.6w (10)磷肥对作物的效应曲线如图14-4,图14-5所示.从钾肥对土豆的实验数据可以看出,当施用量超过一定限度后,产量的增加很不明显,因此用(5)式来描述其施肥效果是合理的,用指数回归分析得到 钾肥对土豆的效应方程:W(k)=42.17(1-exp(-0.01k-0.641)).(11) 对生菜来说,钾肥的施用对产量的影响很小.通过线性回归得到 钾肥对生菜的效应方程:W (k )=16.2269+0.00395k.(12) 钾肥对生菜的效应曲线如图14-6,图14-7所示.可以得到每种肥料的最佳施用量,这无疑为生产提供了极为重要的信息.此外,模型的建立并不依赖于任何特殊条件,这种方法可以适用于任何地区,考察任意一种肥料对于作物产量的效应,具有一定的推广价值.本文没有给出三种肥料用量的最佳组合,因为试验方法本身决定了无法估计肥料的交互效应,因而无法计算最佳施肥比例.如果对实验方法加以改进,可以将我们的模型推广为总效应模型,并根据下列式子(当肥料的边际产量之比等于其价格的反比时,即为肥料施用量的最佳配比)来计算最佳施肥比例:⎪⎪⎩⎪⎪⎨⎧=∂∂∂∂=∂ω∂∂∂.T :T K )k ,p ,n (w :P )k ,p ,n (W ,T :T P)k ,p ,n (:N )k ,p ,n (W p k N p (14) 七、关于交互效应的深入讨论和实验方法的建议 在农业学中[4],可以用三元二次多项式来描述氮、磷、钾三种肥料的综合施肥效果,用下列式子表示:W (N ,P ,K )=B 0+B N N+B P P+B K K+B NN N 2+B PP P 2+B KK K 2+B NP NP+B NK NK+B KP KP . 可以用回归的方法,求出回归系数,但对本题而言,下列处理[1]表明,交互系数是无法确定的,由于所给出的实验全都分布于三条平行于坐标轴的直线上,并且这三条直线交于公共点(n0,p0,k0),以n=N-n0,p=P-p0,k=K-k0作为现的变量,称为相对施肥量,则相对产量W(n,p,k)可表示为w(n,p,k)=b0+b n n+b p p+b k k+b nn n2+b pp p2+b kk k2+b np np+b nk nk+b kp kp.在新的坐标系中,所有的试验点都在坐标轴上,至少有两个坐标为0,这样所有的交叉项全消失了,即不可能由实验结果来确定交互系数,因而试验方法本身注定了交互效应是无法求出的.为估计肥料的交互效应,我们建议该研究所进行正交试验设计[5],将氮、磷、钾肥的用量以第7个水平为中心等问题分为五个水平,作一个五水平三因子的正交表,总共需进行15次实验,将所得数据运用直观分析和方差分析,可以方便地得到氮、磷、钾肥对作物的总效应.试验安排如下.表正交设计表。
全国大学生数学建模优秀论文(A题) 国家一等奖

地下储油罐的变位分析与罐容表标定摘要加油站地下储油罐在使用一段时间后,由于地基变形等原因会发生纵向倾斜及横向偏转,导致与之配套的“油位计量管理系统”受到影响,必须重新标定罐容表。
本文即针对储油罐的变位时罐容表标定的问题建立了相应的数学模型。
首先从简单的小椭圆型储油罐入手,研究变位对罐容表的影响。
在无变位、纵向变位的情况下分别建立空间直角坐标系,在忽略罐壁厚度等细微影响下,运用积分的方法求出储油量和测量油位高度的关系。
将计算结果与实际测量数据在同一个坐标系中作图,经计算得误差均保持在3.5%以内。
纵向变位中,要分三种情况来进行求解,然后将三段的结果综合在一起与变位前作比较,可以得到变位对罐容表的影响。
通过计算,具体列表给出了罐体变位后油位高度间隔为1cm 的罐容表标定值。
进一步考虑实际储油罐,两端为球冠体顶。
把储油罐分成中间的圆柱体和两边的球冠体分别求解。
中间的圆柱体求解类似于第一问,要分为三种情况。
在计算球冠内储油量时为简化计算,将其内油面看做垂直于圆柱底面。
根据几何关系,可以得到如下几个变量之间的关系:测量的油位高度0h 实际的油位高度h 计算体积所需的高度H于是得到罐内储油量与油位高度及变位参数(纵向倾斜角度α和横向偏转角度β )之间的一般关系。
再利用附表2中的数据列方程组寻找α与β最准确的取值。
αβ一、问题重述通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。
按照有关规定,需要定期对罐容表进行重新标定。
题目给出了一种典型的储油罐尺寸及形状示意图,其主体为圆柱体,两端为球冠体。
数模 国赛题目 1992-2010

1992年 (A) 施肥效果分析问题(北京理工大学:叶其孝) (B) 实验数据分解问题(华东理工大学:俞文此; 复旦大学:谭永基) 1993年 (A) 非线性交调的频率设计问题(北京大学:谢衷洁) (B西安电子科技大学:何大可) (B) 锁具装箱问题(复旦大学:谭永基,华东理工大学:俞文此) 1995年 (A) 飞行管理问题(复旦大学:谭永基,华东理工大学:俞文此) (B) 天车与冶炼炉的作业调度问题(浙江大学:刘祥官,李吉鸾) 1996年 (A) 最优捕鱼策略问题(北京师范大学:刘来福) (B) 节水洗衣机问题(重庆大学:付鹂) 1997年 (A) 零件参数设计问题(清华大学:姜启源) (B) 截断切割问题(复旦大学:谭永基,华东理工大学:俞文此) 1998年 (A) 投资的收益和风险问题(浙江大学:陈淑平) (B) 灾情巡视路线问题(上海海运学院:丁颂康)
四项题
1999年 (A) 自动化车床管理问题(北京大学:孙山泽) (B) 钻井布局问题(郑州大学:林诒勋) (C) 煤矸石堆积问题(太原理工大学:贾晓峰) (D) 钻井布局问题(郑州大学:林诒勋) 2000年 (A) DNA序列分类问题(北京工业大学:孟大志) (B) 钢管订购和运输问题(武汉大学:费甫生) (C) 飞越北极问题(复旦大学:谭永基) (D) 空洞探测问题(东北电力学院:关信) 2001年 (A) 血管的三维重建问题(浙江大学:汪国昭) (B) 公交车调度问题(清华大学:谭泽光) (C) 基金使用计划问题(东南大学:陈恩水) (D) 公交车调度问题(清华大学:谭泽光) 2002年 (A) 车灯线光源的优化设计问题(复旦大学:谭永基,华东理工大学:俞文此) (B) 彩票中的数学问题(解放军信息工程大学:韩中庚) (C) 车灯线光源的优化设计问题(复旦大学:谭永基,华东理工大学:俞文此) (D) 赛程安排问题(清华大学:姜启源) 2003年 (A) SARS的传播问题(组委会) (B) 露天矿生产的车辆安排问题(吉林大学:方沛辰) (C) SARS的传播问题(组委会) (D) 抢渡长江问题(华中农业大学:殷建肃) 2004年 (A) 奥运会临时超市网点设计问题(北京工业大学:孟大志) (B) 电力市场的输电阻塞管理问题(浙江大学:刘康生) (C) 酒后开车问题(清华大学:姜启源) (D) 招聘公务员问题(解放军信息工程大学:韩中庚) 2005年 (A) 长江水质的评价和预测问题(解放军信息工程大学:韩中庚) (B) DVD在线租赁问题(清华大学:谢金星等) (C) 雨量预报方法的评价问题(复旦大学:谭永基) (D) DVD在线租赁问题(清华大学:谢金星等) 2006年 (A) 出版社的资源配置问题(北京工业大学:孟大志) (B) 艾滋病疗法的评价及疗效的预测问题(天津大学:边馥萍) (C) 易拉罐的优化设计问题(北京理工大学:叶其孝) (D) 煤矿瓦斯和煤尘的监测与控制问题(解放军信息工程大学:韩中庚) 2007年 (A) 中国人口增长预测 (B) 乘公交,看奥运 (C) 手机“套餐”优惠几何 (D) 体能测试时间安排 2008年 (A)数码相机定位, (B)高等教育学费标准探讨, (C)地面搜索, (D)NBA赛程的分析与评价 2009年 (A)制动器试验台的控制方法分析 (B)眼科病床的合理安排 (C)卫星和飞船的跟踪测控 (D)会议筹备 2010年 (A)储油罐的变位识别与罐容表标定 (B)2010年上海世博会影响力的定量评估 (C)输油管的布置 (D)对学生宿舍设计方案的评价
11520-数学建模-1992年A题《施肥的效果分析》题目、论文、点评

1992年A题《施肥的效果分析》题目、论文、点评
回归模型
题目:1992年A题施肥效果分析.pdf (8.11 KB)
出题人:北京理工大学叶其孝
主要建模方法:回归模型
优秀论文:1、《施肥方案对作物、蔬菜的影响》
作者:北京师范大学喻梅、金青松、唐福明,
指导老师:刘来福;
论文摘要:对土豆和生菜,分别建立了产量与施肥水平之间的多元二次回归模型.运用SAS/STAT 软件依次采用全回归、逐步回归和二次响应面回归.在确认模型具完美适度性基础上,进行线性相关、交互作用、最佳响应水平、强影响变量、回归曲面形状等分析.同时,将两种作物进行比较,得出一系列颇有实用价值的结论.分析结果表明:土豆的产量对 N 具有强线性依赖性,而生菜是对 P;施肥的交互作用对土豆影响较大,对生菜则无强影响;最佳施肥方案中 N,P,K 的用量土豆为292,246,542(公斤/公顷),生菜为213,667,427(公斤/公顷)对应产量为45.18和23.13吨/公顷,且均在试验范围内达到,可信性强;对土豆,强影响因子依次为N→K→P,对生菜为P→N→K;回归曲面上凸,沿(N,P,K)=(1,0,0)方向下降迅速.
因此,施肥中应特别注意 N 的使用量.
论文下载:施肥方案对作物_蔬菜的影响.pdf (381.06 KB)
专家点评:《关于施肥效果分析问题的评注》
作者:项可风,中国科学院系统科学研究所
点评下载:关于施肥效果分析问题的评注.pdf (234.18 KB)。
全国大学生数学建模竞赛赛题综合评析
社会热点
叶其孝、周义仓
开放性强、社会关注性强,突出数据来源的可靠性、结论解释的合理性
数据收集与处理、问题的分析与假设,初等数学方法、一般统计方法、多目标规划、回归分析、综合评价方法、灰色预测
2009年
A题:制动器试验台的控制方法分析
工业问题
方沛辰、刘笑羽
问题具体、专业性强,要花时间读懂、理解清楚问题
出版社的资源配置
孟大志
艾滋病疗法的评价及疗效的预测
边馥萍
易拉罐形状和尺寸的最优设计(C题)
叶其孝
煤矿瓦斯和煤尘的监测与控制(D题)
韩中庚
2007年
中国人口增长预测
唐云
乘公交,看奥运
方沛辰、吴孟达
手机“套餐”优惠几何(C题)
韩中庚
体能测试时间安排(D题)
刘雨林
2008年
数码相机定位
谭永基
高等教育学费标准探讨
叶其孝、周义仓
地面搜索(C题)
肖华勇
NBA赛程的分析与评价(D题)
姜启源
2009年
制动器试验台的控制方法分析
方沛辰、刘笑羽
眼科病床的合理安排
吴孟达、毛紫阳
卫星和飞船的跟踪测控(C题)
周义仓
会议筹备(D题)
王宏健
2010年
储油罐的变位识别与罐容表标定
韩中庚
2010年上海世博会影响力的定量评估
杨力平
输油管的布置(C题)
1
6
8
付鹂
重庆大学
1
6
9
姜启源
清华大学
4
3
10
陈叔平
浙江大学、贵州大学
2
5
11
全国数学建模大赛A题获奖论文

全国数学建模大赛A题获奖论文城市表层土壤重金属污染分析摘要本文旨在对城市土壤地质环境的重金属污染状况进行分析,建立模型对金属污染物的分布特点、污染程度、传播特征以及污染源的确定进行有效的描述、评价和定位。
对于重金属空间分布问题,首先基于克里金插值法,应用Surfer 8软件对各数据点的分布情况进行模拟,得到了直观的重金属污染空间分布图形;随后,分别用内梅罗综合污染指数以及模糊评价标准和模型对城区内不同区域重金属的污染程度进行了评判。
对于金属污染的主要原因分析问题,基于因子分析法、问题一的结果和对各个金属污染物的来源分析等因素,判断出金属污染的主要原因有:工业生产、汽车尾气排放、石油加工并推测该区域是镍矿富集区。
随后讨论了污染源之间的相互关系和不同金属的污染贡献率。
针对污染源位置确定问题,我们建立了两个模型:模型一以流程图的形式出现,基于污染传播的一般规律建立模型,求取污染源范围,模型作用更倾向于确定污染源的位置;模型二基于最小二乘法原理,建立了拟合二次曲面方程,在有效确定污染源的同时也反映了其传播特征,模型更加清楚,理论性也更强。
在研究城市地质环境的演变模式问题中,我们对针对污染源位置确定问题所建模型的优缺点进行了评价,同时建立了考虑了时间,地域环境和传播媒介的污染物传播模型,从而反映了地质的演变。
综上所述,本文模型的特点是从简单的模型建立起,强更准确的数学模型发展,逐步达到目标期望。
关键词:重金属污染,克里金插值最小二乘法因子分析流程图一、问题重述问题背景随着城市经济的快速发展和城市人口的不断增加,人类活动对城市环境质量的影响日显突出。
对城市土壤地质环境异常的查证,以及如何应用查证获得的海量数据资料开展城市环境质量评价,研究人类活动影响下城市地质环境的演变模式,日益成为人们关注的焦点。
评价和研究城市土壤重金属污染程度,讨论土壤中重金属的空间分布,研究城市土壤重金属污染特征、污染来源以及在环境中迁移、转化机理,并对城市环境污染治理和城市进一步的发展规划提出科学建议,不仅有利于城市生态环境良性发展,有利于人类与自然和谐,也有利于人类社会健康和城市可持续发展[1]。
全国数学建模大赛获奖优秀论文.doc

全国数学建模大赛获奖优秀论文者T.L.Satty于代提出了以定性与定量相结合,系统化、层次化分析解决问题的方法,简称AHP。
传统的层次分析法算法具有构造判断矩阵不容易、计算繁多重复且易出错、一致性调整比较麻烦等缺点。
本文利用微软的Excel电子表格的强大的函数运算功能,设置了简明易懂的计算表格和步骤,使得判断矩阵的构造、层次单排序和层次总排序的计算以及一致性检验和检验之后对判断矩阵的调整变得十分简单。
关键词:Excel 层次分析法模型一、层次分析法的基本原理层次分析法是解决定性事件定量化或定性与定量相结合问题的有力决策分析方法。
它主要是将人们的思维过程层次化、,逐层比较其间的相关因素并逐层检验比较结果是否合理,从而为分析决策提供较具说服力的定量依据。
层次分析法不仅可用于确定评价指标体系的权重,而且还可用于直接评价决策问题,对研究对象排序,实施评价排序的评价内容。
用AHP分析问题大体要经过以下七个步骤:⑴建立层次结构模型;首先要将所包含的因素分组,每一组作为一个层次,按照最高层、若干有关的中间层和最低层的形式排列起来。
对于决策问题,通常可以将其划分成层次结构模型,如图1所示。
其中,最高层:表示解决问题的目的,即应用AHP所要达到的目标。
中间层:它表示采用某种措施和政策来实现预定目标所涉及的中间环节,一般又分为策略层、约束层、准则层等。
最低层:表示解决问题的措施或政策(即方案)。
⑵构造判断矩阵;设有某层有n个元素,X={Xx1,x2,x3xn}要比较它们对上一层某一准则(或目标)的影响程度,确定在该层中相对于某一准则所占的比重。
(即把n个因素对上层某一目标的影响程度排序。
上述比较是两两因素之间进行的比较,比较时取1~9尺度。
用表示第i个因素相对于第j个因素的比较结果,则A则称为成对比较矩阵比较尺度:(1~9尺度的含义)如果数值为2,4,6,8表示第i个因素相对于第j个因素的影响介于上述两个相邻等级之间。
1992—2008年全国大学生数学建模竞赛获奖论文
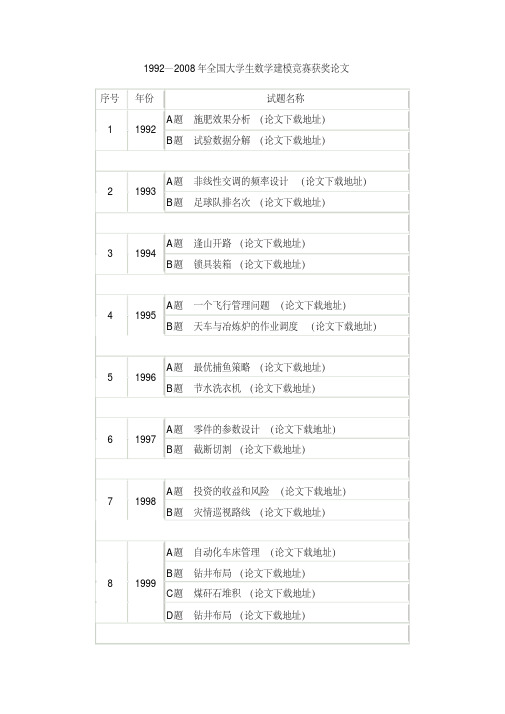
1992—2008年全国大学生数学建模竞赛获奖论文序号年份试题名称11992A题施肥效果分析(论文下载地址)B题试验数据分解(论文下载地址)21993A题非线性交调的频率设计(论文下载地址)B题足球队排名次(论文下载地址)31994A题逢山开路(论文下载地址)B题锁具装箱(论文下载地址)41995A题一个飞行管理问题(论文下载地址)B题天车与冶炼炉的作业调度(论文下载地址)51996A题最优捕鱼策略(论文下载地址)B题节水洗衣机(论文下载地址)61997A题零件的参数设计(论文下载地址)B题截断切割(论文下载地址)71998A题投资的收益和风险(论文下载地址)B题灾情巡视路线(论文下载地址)81999A题自动化车床管理(论文下载地址)B题钻井布局(论文下载地址)C题煤矸石堆积(论文下载地址)D题钻井布局(论文下载地址)92000B题钢管订购和运输(论文下载地址)C题飞跃北极(论文下载地址)D题空洞探测(论文下载地址)102001A题血管的三维重建(论文下载地址)B题公交车调度(论文下载地址)C题基金使用计划(论文下载地址)D题公交车调度(论文下载地址)112002A题车灯线光源的优化设计(论文下载地址)B题彩票中数学(论文下载地址)C题车灯线光源的计算(论文下载地址)D题赛程安排(论文下载地址)122003A题 SARS的传播(论文下载地址)B题露天矿生产的车辆安排(论文下载地址)C题 SARS的传播(论文下载地址)D题抢度长江(论文下载地址)132004A题奥运会临时超市网点设计(论文下载地址)B题电力市场的输电阻塞管理(论文下载地址)C题饮酒驾车(论文下载地址)D题公务员招聘(论文下载地址)142005A题长江水质的评价和预测(论文下载地址)B题 DVD在线租赁(论文下载地址)C题雨量预报方法的评价(论文下载地址)152006A题出版社的资源配置(论文下载地址)B题艾滋病疗法的评价及疗效的预测(论文下载地址)C题易拉罐形状和尺寸的最优设计(论文下载地址)D题煤矿瓦斯和煤尘的监测与控制(论文下载地址)162007A题中国人口增长预测(论文下载地址)B题乘公交,看奥运(论文下载地址)C题手机“套餐”优惠几何(论文下载地址)D题体能测试时间安排(论文下载地址)172008A题数码相机定位(论文下载地址【1】【2】)B题高等教育学费标准探讨(下载地址【1】【2】)C题地面搜索(论文下载地址)D题 NBA赛程的分析与评价(论文下载地址)。
高教社杯全国大学生数学建模竞赛获奖论文(精品)

高教社杯全国大学生数学建模竞赛获奖论文(精品)2010高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):赛区评阅记录(可供赛区评阅时使用):评阅人评分备注全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):关于2010年上海世博会影响力的评估——从历史文化交流方面进行讨论摘要本文从各国人民在历史文化方面的交流评估了2010年上海世博会的影响力。
根据题意以及互联网收集到的数据,建立了数学模型并定量估计了上海世博会的影响力,突出上海世博的主题“城市,让生活更美好”的基本理念。
首先,运用灰色聚类法对互联网收集到的数据进行灰类等级划分,再对数据进行无量纲化处理。
其次,建立各灰类白化函数,再对各组数据进行聚类权F运算,进而得出各因素的相应数据。
最后,通过白化函数得到的矩阵和聚类n权运算得到的函数,应用求聚类公式,求得各聚类对象的,,,fd*,LjjLLj,,,jL,1j各灰色聚类系数及结果。
然后应用层次分析法,推导出一种进行加权分析的方法,利用本方法对影响世博会的各个因素进行加权,得出了各个世博城市关于T,通过比较得到上海世博会影影响力的组合权重数据为(0.3634,0.3620,0.2743)响力均高于爱知、汉诺威世博会。
合适的评估体系是本课题的关键。
我们充分利用互联网收集到的数据进行分析及统计,并考虑到方案的可操作性。
通过组合权重数据,得到了三个世博城市关于影响力的权重。
由于此模型不受指数的影响,有很好的灵活性,使得我们可以根据实际情况灵活选取指数,减少模型的工作量,增加模型精度。
关键字:定量估计、层次分析法、灰色聚类法1一、问题重述2010年上海世博会是首次在中国举办的世界博览会。
从1851年伦敦的“万国工业博览会”开始,世博会正日益成为各国人民交流历史文化、展示科技成果、体现合作精神、展望未来发展等的重要舞台。
可以从我们感兴趣的某个侧面,建立数学模型,利用互联网数据,定量评估2010年上海世博会的影响力。
数学建模——经验公式与施肥效果分析的数学模型

理论研究 8
k ∈ [ 0, 1 ] 如果用上面求出的拟合函数来表示相应的产量
与施肥量的函数关系 , 从拟合曲线的图形来看 , 只有 产量与 N肥的用量函数有唯一极大值点。其它函数都 不具有这一性质 ,其规律是 : P、N 的施用量越多 ,产量 都会增加。如果只从增加产量的角度 , 就应尽量多施 这两种肥料 。但多施肥的同时也会增加购买肥料的费 用 ,从经济的角度来看 ,并不一定合算。应综合考虑产 量和施肥的成本因素 , 以单位面积上的收益 (即农作 物的销售收入与施肥的费用之差 ) 为目标函数 , 以单 位面积的收益最大为最优准则 ,来确定最优解 。
理论研究 6
从图上可看出 , N、P、K的取值范围不一样 ,可 以将它们的取值范围转化成区间 [ 0, 1 ] ,这样它们 的变化范围就都一样了 。转化后的数据图形如下 :
1 模型的建立及求解
要分析施肥量与产量之间的关系 ,首先要建立 施肥量与产量之间的函数关系 。可以用数据拟合的 方法来建立这种函数关系 。这又需要确定拟合的函 数的形式 ,即所谓经验公式 。
优秀数学建模论文(全国一等奖)

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写):我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):参赛队员(打印并签名) :1.2.3.指导教师或指导教师组负责人(打印并签名):日期:年月日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):A题:出版社的资源配置摘要本文根据题目的要求建立了合理的有限资源分配优化模型,我们借助多种数学软件的优势挖掘出大量数据潜在的信息,并将其合理运用,在此基础上,以利润最大为目标,长远发展为原则,制定出信息不足条件下的量化综合评价体系,并为出版社在2006年如何合理有效地分配有限的书号资源提供了最佳的分配方案。
在本文所建立的模型中,我们采取了层次分析法(AHP)、数据统计拟合以及整数线性规划相结合的手段,这样既借鉴了层次分析法综合评价的优势,又克服了该法中主观因素的不确定性,使模型更具有科学性,作出了出版社2006年的分配方案,如下表经过对模型的检验,单从生产计划准确度一项来看,模型所得出的结果就比以往的高,这样就首先保证了出版社获得年度稳定利润的前提,其他几个评价指标也都可以得出相似的结论。
以2006年与2005年生产计划的准确度为例,作比较:2005年的各分社平均生产计划的准确度为0.702006年的各分社平均生产计划的准确度为0.85平均准确度提高约21%从数据的对比中,我们很容易看出本模型具有较高的有效性和合理性。
数学建模 综合题目参考答案

综合题目参考答案1. 赛程安排(2002年全国大学生数学建模竞赛D 题)(1)用多种方法都能给出一个达到要求的赛程。
(2)用多种方法可以证明n 支球队“各队每两场比赛最小相隔场次r 的上界”(如n =5时上界为1)是⎥⎦⎤⎢⎣⎡-23n ,如: 设赛程中某场比赛是i ,j 两队, i 队参加的下一场比赛是i ,k 两队(k ≠j ),要使各队每两场比赛最小相隔场次为r ,则上述两场比赛之间必须有除i ,j ,k以外的2r 支球队参赛,于是32+≥r n ,注意到r 为整数即得⎥⎦⎤⎢⎣⎡-≤23n r 。
(3)用构造性的办法可以证明这个上界是可以达到的,即对任意的n 编排出达到该上界的赛程。
如对于n =8, n =9可以得到:可以看到,n =8时每两场比赛相隔场次数只有2,3,4,n =9时每两场比赛相隔场次数只有3,4,以上结果可以推广,即n 为偶数时每两场比赛相隔场次数只有22-n ,12-n ,2n ,n 为奇数时只有23-n ,21-n 。
(4)衡量赛程优劣的其他指标如平均相隔场次 记第i 队第j 个间隔场次数为ij c ,2,2,1,,,2,1-==n j n i ,则平均相隔场次为∑∑=-=-=n i n j ij c n n r 121)2(1 r 是赛程整体意义下的指标,它越大越好。
可以计算n =8,n =9的r ,并讨论它是否达到上界。
相隔场次的最大偏差 定义||,r c M a x f ij j i -=∑-=--=21|)2(|n j ij r n c Max gf 为整个赛程相隔场次的最大偏差,g 为球队之间相隔场次的最大偏差,它们都是越小越好。
可以计算n =8,n =9的f ,g ,并讨论它是否达到上界。
参考文献工程数学学报第20卷第5期20032. 影院座位设计建立满意度函数),(βαf ,可以认为α和β无关, ()()βαβαh g f -=),(,g ,h 取尽量简单的形式,如αα=)(g ;0)(=βh (030≤β),0)(h h =β)30(0>β。
历年全国赛数学建模题目

目录1996年全国大学生数学建模竞赛题目 (2)A题最优捕鱼策略 (2)B题节水洗衣机 (2)1997年全国大学生数学建模竞赛题目 (3)A题零件的参数设计 (3)B题截断切割 (4)1998年全国大学生数学建模竞赛题目 (5)A题投资的收益和风险 (5)B题灾情巡视路线 (6)1999创维杯全国大学生数学建模竞赛题目 (7)A题自动化车床管理 (7)B题钻井布局 (8)C题煤矸石堆积 (9)D题钻井布局(同 B 题) (9)2000网易杯全国大学生数学建模竞赛题目 (10)A题 DNA分子排序 (10)B题钢管订购和运输 (12)C题飞越北极 (15)D题空洞探测 (15)2001年全国大学生数学建模竞赛题目 (17)A题血管的三维重建 (17)B题公交车调度 (18)C题基金使用计划 (20)D题公交车调度 (20)2002高教社杯全国大学生数学建模竞赛题目 (21)A题车灯线光源的优化设计 (21)B题彩票中的数学 (21)C题车灯线光源的计算 (23)D题赛程安排 (23)2003高教社杯全国大学生数学建模竞赛题目 (24)A题 SARS的传播 (24)B题露天矿生产的车辆安排 (28)C题 SARS的传播 (29)D题抢渡长江 (30)2004高教社杯全国大学生数学建模竞赛题目 (31)A题奥运会临时超市网点设计 (31)B题电力市场的输电阻塞管理 (35)C题饮酒驾车 (39)D题公务员招聘 (39)2005高教社杯全国大学生数学建模竞赛题目 (42)A题: 长江水质的评价和预测 (42)B题: DVD在线租赁 (43)C题雨量预报方法的评价 (44)D题: DVD在线租赁 (45)2006高教社杯全国大学生数学建模竞赛题目 (46)A题: 出版社的资源配置 (46)B题: 艾滋病疗法的评价及疗效的预测 (46)C题: 易拉罐形状和尺寸的最优设计 (47)D题: 煤矿瓦斯和煤尘的监测与控制 (48)2007高教社杯全国大学生数学建模竞赛题目 (53)A题:中国人口增长预测 (53)2008高教社杯全国大学生数学建模竞赛题目 (56)A题数码相机定位 (56)B题高等教育学费标准探讨 (57)C题地面搜索 (57)2009高教社杯全国大学生数学建模竞赛题目 (59)A题制动器试验台的控制方法分析 (59)B题眼科病床的合理安排 (60)C题卫星和飞船的跟踪测控 (61)D题会议筹备 (61)2010全国高教社杯数学建模题目 (65)A题储油罐的变位识别与罐容表标定 (65)B题 2010年上海世博会影响力的定量评估 (66)A题最优捕鱼策略为了保护人类赖以生存的自然环境,可再生资源(如渔业、林业资源)的开发必须适度.一种合理、简化的策略是,在实现可持续收获的前提下,追求最大产量或最佳效益.考虑对某种鱼(鳀鱼)的最优捕捞策略:假设这种鱼分四个年龄组,称1龄鱼,…,4龄鱼,各年龄组每条鱼的平均重量分别为 5.07,11.55,17.86,22.99(g),各年龄组鱼的自然死亡率为0.8(1/年),这种鱼为季节性集产卵繁殖,平均每条4龄鱼的产卵量为1.109× (个),3龄鱼的产卵量为这个数的一半,2龄鱼和1龄鱼不产卵,产卵和孵化期为每年的最后4个月,卵孵化并成活为1龄鱼,成活率(1龄鱼条数与产卵总量n之比)为1.22× /(1.22× +n).渔业管理部门规定,每年只允许在产卵孵化期前的8个月内进行捕捞作业.如果每年投入的捕捞能力(如渔船数﹑下网次数等)固定不变,这时单位时间捕捞量与各年龄组鱼群条数成正比,比例系数不妨称捕捞强度系数.通常使用13mm网眼的拉网,这种网只能捕3龄鱼和4龄鱼,其两个捕捞强度系数之比为0.42:1.渔业上称这种方式为固定努力量捕捞.1)建立数学模型分析如何实现可持续捕获(即每年开始捕捞时鱼场中各年龄组鱼群不变),并且在此前提下得到最高的年收获量(捕捞总重量).2)某渔业公司承包这种鱼的捕捞业务5年,合同要求5年后鱼群的生产能力不能受到太大破坏. 已知承包时各年龄组鱼群的数量分别为:122,29.7,10.1,3.29(×条),如果任用固定努力量的捕捞方式,该公司应采取怎样的策略才能使总收获量最高.(北京师范大学刘来福提供)B题节水洗衣机我国淡水资源有限,节约用水人人又责,洗衣在家庭用水中占有相当大的份额,目前洗衣机已相当普及,节约洗衣机用水十分重要.假设在放入衣服和洗涤剂后洗衣机的运行过程为:加水-漂水-脱水-加水-漂洗-脱水-…-加水-漂洗-脱水(称"加水-漂洗-脱水"为运行一轮).请为洗衣机设计一种程序(包括运行多少轮﹑每轮加水量等),使得在满足一定洗涤效果的条件下,总用水量最少.选用合理的数据进行计算,对照目前常用的洗衣机的运行情况,对你的模型和结果做出评价.A题零件的参数设计一件产品由若干零件组装而成,标志产品性能的某个参数取决于这些零件的参数。
数学建模论文——施肥效果分析
[ 责任编辑: 张艳芳]
●
( 上接第 618 页) 间几乎呈线性关系, 因此考虑拟合该曲线为指数函数
是合理的。
( 2) 确定各变量间函数关系
由上段的讨论, 可以确定土豆产量与各营养素施用水平之间的函
数关系为:
y=a1n2+b1n+c1 y= p
a2p+b2 y=a3+b3ec3 k 其中 n, p, k 为氮肥、磷肥和钾肥的 不 同 施 用 水 平 , y 是 土 豆 产 量 ,
【关键词】施肥效果; 最小二乘法; 土豆
一 、问 题 的 提 出 某地区 作 物 生 长 所 需 要 的 营 养 素 主 要 是 氮(N)、钾(K)、磷(P), 某 作 物研究所在该地区对土豆做了一定数量的实验, 实验数据如表 1 所 示, 其中 ha 表示公顷, t 表示吨, kg 表示公斤。当一个营养素的施肥量 变化时, 总将另两个营养素的施肥量保持在第七个水平上, 如对土豆 产 量 关 于 N 的 施 肥 量 做 实 验 时 , P 与 K 的 施 肥 量 分 别 取 为 196kg/ha 与 372kg/ha。试分析施肥量与产量之间的关系。
图 1 土豆产量与氮肥、磷肥、钾肥施用量之间关系的散点图
考虑土豆产量与氮肥之间的数据变化, 可以看到, 当保持磷肥和 钾肥施放水平不变时, 随着氮肥施用量的增加, 土豆产量也随之增加, 但 当 施 肥 量 达 到 一 定 程 度 ( 336kg/ha) 后 , 再 增 加 施 肥 量 时 , 就 会 造 成 产量的下滑, 结合散点图, 可以判断土豆产量与氮肥施用量之间应该 可以用二次函数关系来拟合。
全国大学生数学建模竞赛竞赛题目汇编(1992-2000)

K
产量
(t/ha) 18.98 27.35 34.86 38.52 38.44 37.73 38.43 43.87 42.77 46.22
施肥量
(kg/ha) 0 47 93 140 186 279 372 465 558 651
K
产量
(t/ha) 15.75 16.76 16.89 16.24 17.56 19.20 17.97 15.84 20.11 19.40
全国大学生数学建模竞赛 竞赛题目汇编(1992-2000)
[注]相关优秀论文已经汇编成册正式出版:全国大学生数学建模竞赛组委会编,《全国大学 生数学建模竞赛优秀论文汇编(1992-2000)》,北京:中国物价出版社,2002 年 3 月出版。
1992 年赛题
A 题 施肥效果分析 某地区作物生长所需的营养素主要是氮(N)、钾(K)、磷(P)。某作物研究所在该地区对
2.25 6.80 20.15 35.70 56.40 75.10 87.85 98.50
输入信号为 u(t) = A1 cos2πf1t + A2 cos2πf 2t + A3 cos2πf 3t ,其中 A1 = 25,A2 = 10,A3 = 45
是输入信号的振幅。对输入信号频率 f1、f2、f3 的设计要求为:
产量 (t/ha) 33.46 32.47 36.06 37.96 41.04 40.09 41.26 42.17 40.36 42.73
产量 (t/ha) 6.39 9.48 12.46 14.38 17.10 21.94 22.64 21.34 22.07 24.53
施肥量
(kg/ha) 0 47 93 140 186 279 372 465 558 651
全国大学生数学建模竞赛C题国家奖一等奖优秀论文

脑卒中发病环境因素分析及干预摘要本文主要讨论脑卒中发病环境因素分析及干预问题。
根据题中所给出的数据,利用SPSS20 软件进行相关性统计分析,分别对各气象因素进行单因素分析,进而建立后退法线性回归分析模型,得到脑卒中与气压、气温、相对湿度之间的关系。
同时在广泛收集各种资料并综合考虑环境因素,对脑卒中高危人群提出预警和干预的建议方案。
首先,利用SPSS20软件,从患病人群的性别、年龄、职业进行统计分析,得到2007-2010年男性患病人数高于女性,且男性所占比例有逐年下降趋势,女性则有上升趋势,因此,性别比例呈减小趋势。
分析不同年龄段患病人数,得到患病高峰期为75-77岁之间,且青少年比例逐年呈增长趋势,可见患病比例趋于年轻化。
同时在不同的职业中,农民发病人数最多,教师,渔民,医务人员,职工,离退人员的发病人数较少。
其次,由题中所给数据先进行单因素分析,剔除对脑卒中影响不显著的因素,得出气温、气压、相对湿度对脑卒中的影响程度大小,进而采用后退法线性回归分析建立模型,利用SPSS20对数据进行分析,求得脑卒中发病率与气温、气压、相对湿度之间的关系。
即发病率与平均温度成正相关,与最高温度成负相关,发病率与平均气压成正相关,与最低气压成负相关,与平均相对湿度成负相关,与最小相对湿度成正相关。
最后,通过查找资料发现,影响脑卒中的因素有两类,一类是不可干预因素,如年龄、性别、家族史,另一类是可干预因素,如高血压、高血脂、糖尿病、肥胖、抽烟、酗酒等因素。
分析这些因素,建立双变量因素分析模型,并结合问题1和问题2,对高危人群提出预警和干预的建议方案。
关键词脑卒中单因素分析后退法线性回归分析双变量因素分析一问题的重述脑卒中(俗称脑中风)是目前威胁人类生命的严重疾病之一,它的发生是一个漫长的过程,一旦得病就很难逆转。
这种疾病的诱发已经被证实与环境因素,包括气温、湿度之间存在密切的关系。
对脑卒中的发病环境因素进行分析,其目的是为了进行疾病的风险评估,对脑卒中高危人群能够及时采取干预措施,也让尚未得病的健康人,或者亚健康人了解自己得脑卒中风险程度,进行自我保护。
数学建模-优化题目[精华]
![数学建模-优化题目[精华]](https://img.taocdn.com/s3/m/3ac17ea489eb172dec63b74a.png)
c ij x ij
总运价
i1 j1
n
x ij a i , j1
s .t . m x ij b j i1 x ij 0
i 1,..., m
j 1,..., n i 1,..., m ; j 1,..., n
产量限制 需量限制 运量非负
线性规划模型
假设产销平衡:
m
n
ai bj
线性规划模型
m f 0 . 1 x 1 0 i . 3 x 2 n 0 . 9 x 3 0 x 4 1 . 1 x 5 0 . 2 x 6 0 . 8 x 7 1 . 4 x 8
2x1 x2 x3 x4 100
s.t.x12xx2333xx3432xx5623xx67x47x8101000 不同方法
Ⅰ
Ⅱ
现有原 材料
A1
21 8
A2
10 3
A3
01 4
线性规划模型
解:设生 ,产 两 种产品 x1,x分 2吨 ,别为
max f= 5x1 +2x2
求最大利润
2x1 + x2 8
s.t .
x1 3
x2 4
x1,x2 0
三种材料量的限制 生产量非负
线性规划模型
运输问题
有两个粮 A1,库 A2向三个粮 B1,站 B2,B3调运大, 米 两个粮库现存大为米 4吨分 ,8吨 别,三个粮站至少需要 大米分别 2,4为 ,5吨,两个粮库到三个距粮离 (站 单的 位 :公里 )如下 ,问如何调运使运。费最低
约 束 条 件
30
矩阵形式
线性规划模型
记 c(c1,c2, cn)A ,aijm n,xx1,x2, xnT,
bb 1,b2, bnT,矩 阵 形 式 为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
K 施肥量
(kg/ha) 0 47 93 140 186 279 372 465 558 651
产量
(t/ha) 18.98 27.35 34.86 38.52 38.44 37.73 38.43 43.87 42.77 46.22
K 施肥量
(kg/ha) 0 47 93 140 168 279 372 465 554 651
N 施肥量
(kg/ha) 0 28 56 84 112 168 224 280 336 392
产量
(t/ha) 11.02 12.70 14.56 6.17 17.25 22.59 21.63 19.34 16.12 14.11
P 施肥量
(kg/ha) 0 24 49 73 98 147 196 245 294 342
产量
(t/ha) 15.75 16.76 16.89 16.24 17.56 19.20 17.97 15.84 20.11 19.40
1992 年题 A 施肥效果分析
某地区作物生长所需的营养素主要是氮(N),磷(P),钾(K) 某作物研究所在该地区对土豆 与生菜作乐一定数量的实验 实验数据如下列表格所示 其中 ha 表示公顷 t 表示吨 kg 表示公斤 当一个营养素的施肥量变化时 总将另二个营养素的施肥量保持在第七个水平上 如对土豆产量关于 N 的施肥量做实验时 P 与 K 的施肥量分别取为 195kg/ha 与 372kg/ha
试分析施肥量与生产量之间关系 并队所得结果从应用价值与如何改进等方面作出估 价
土豆:
生菜
Nห้องสมุดไป่ตู้施肥量
(kg/ha) 0 34 67 101 135 202 259 336 404 471
产量
(t/ha) 15.18 21.36 25.72 32.29 34.03 39.45 43.15 43.46 40.83 30.75
产量
(t/ha) 33.46 32.47 36.06 37.96 41.04 40.09 41.26 42.17 40.36 42.73
P 施肥量
(kg/ha) 0 49 98 147 196 294 394 489 587 685
产量
(t/ha) 6.39 9.48 12.46 14.33 17.10 21.94 22.64 21.34 22.07 24.53
