示波器CSV波形数据导入M精编b进行FFT分析
matlab处理波信息

matlab处理波信息Matlab是一种强大的科学计算软件,可以用于处理波信号。
以下是一些常见的用Matlab处理波信息的方法:1. 导入和可视化波信号数据:首先,你需要将波信号数据导入到Matlab中。
可以使用`importdata`函数或`load`函数加载数据文件。
然后,使用Matlab中的绘图函数(例如`plot`)将波信号可视化。
2. 时域分析:通过对波信号进行时域分析,可以获得关于波的时间特性的信息。
在Matlab中,你可以使用`fft`函数进行快速傅里叶变换,计算波信号的频谱。
另外,还可以使用`ifft`函数进行逆傅里叶变换,将频域信号转换回时域信号。
3. 频域分析:频域分析可以提供有关波信号频率特性的信息。
在Matlab中,你可以使用`fft`函数计算频谱,并使用`abs`函数获取幅度谱。
还可以使用`angle`函数获取相位谱。
通过对频谱的分析,可以提取波信号的频率分量和相位信息。
4. 滤波处理:滤波是一种常见的波信号处理技术,用于去除噪声或提取感兴趣的频率成分。
Matlab提供了各种滤波函数,例如`filter`函数用于滤波,`fir1`函数用于设计FIR滤波器,`butter`函数用于设计巴特沃斯滤波器等。
5. 谱分析:谱分析是一种用于估计波信号频谱的方法。
在Matlab中,你可以使用`pwelch`函数或`periodogram`函数进行谱估计。
这些函数可用于计算功率谱密度(PSD)估计,并提供了不同的参数和选项,以满足不同的分析需求。
6. 波形合成:如果你希望生成具有特定频率和幅度特性的波信号,可以使用Matlab中的合成函数。
例如,`sin`函数可以生成正弦波信号,`sawtooth`函数可以生成锯齿波信号,`square`函数可以生成方波信号等。
除了上述方法,还有许多其他功能和工具可用于处理波信号。
Matlab提供了丰富的文档和示例代码,可以帮助你更深入地了解和应用这些功能。
示波器CSV波形数据导入Matlab进行FFT分析
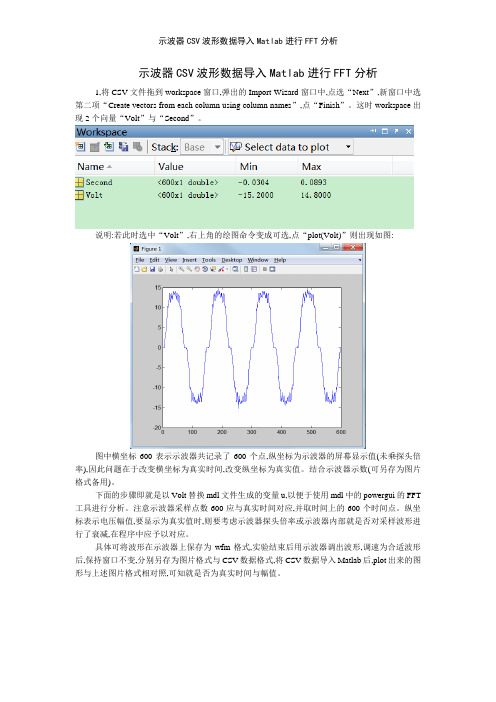
示波器CSV波形数据导入Matlab进行FFT分析1,将CSV文件拖到workspace窗口,弹出的Import Wizard窗口中,点选“Next”,新窗口中选第二项“Create vectors from each column using column names”,点“Finish”。
这时workspace出现2个向量“Volt”与“Second”。
说明:若此时选中“Volt”,右上角的绘图命令变成可选,点“plot(Volt)”则出现如图:图中横坐标600表示示波器共记录了600个点,纵坐标为示波器的屏幕显示值(未乘探头倍率),因此问题在于改变横坐标为真实时间,改变纵坐标为真实值。
结合示波器示数(可另存为图片格式备用)。
下面的步骤即就是以Volt替换mdl文件生成的变量u,以便于使用mdl中的powergui的FFT 工具进行分析。
注意示波器采样点数600应与真实时间对应,并取时间上的600个时间点。
纵坐标表示电压幅值,要显示为真实值时,则要考虑示波器探头倍率或示波器内部就是否对采样波形进行了衰减,在程序中应予以对应。
具体可将波形在示波器上保存为wfm格式,实验结束后用示波器调出波形,调速为合适波形后,保持窗口不变,分别另存为图片格式与CSV数据格式,将CSV数据导入Matlab后,plot出来的图形与上述图片格式相对照,可知就是否为真实时间与幅值。
可见,横坐标为120ms,纵坐标为10倍衰减后的值,在编程中应有相应体现。
2,打开forFFT、mdl,并运行仿真,完成后wordspace出现新的变量“u”与“tout”;Mdl文件中scope的设置已设置为保存波形名称为u,Structure with time格式,不限制最后5000个点。
由于powergui自带的FFT功能只能对该mdl文件中的scope保存的变量u进行分析,以下考虑将u中的数据替换为示波器保存的数据,注意横坐标真实时间点数0~0、1198s,(间隔0、0002s 包含两端共计600个点)与采样点数600相对应。
示波器CSV波形数据导入M精编b进行FFT分析精选文档

示波器C S V波形数据导入M精编b进行F F T分析精选文档 TTMS system office room 【TTMS16H-TTMS2A-TTMS8Q8-示波器CSV波形数据导入Matlab进行FFT分析1,将CSV文件拖到workspace窗口,弹出的Import Wizard窗口中,点选“Next”,新窗口中选第二项“Create vectors from each column using column names”,点“Finish”。
这时workspace出现2个向量“Volt”和“Second”。
说明:若此时选中“Volt”,右上角的绘图命令变成可选,点“plot(Volt)”则出现如图:图中横坐标600表示示波器共记录了600个点,纵坐标为示波器的屏幕显示值(未乘探头倍率),因此问题在于改变横坐标为真实时间,改变纵坐标为真实值。
结合示波器示数(可另存为图片格式备用)。
下面的步骤即是以Volt替换mdl文件生成的变量u,以便于使用mdl中的powergui的FFT工具进行分析。
注意示波器采样点数600应与真实时间对应,并取时间上的600个时间点。
纵坐标表示电压幅值,要显示为真实值时,则要考虑示波器探头倍率或示波器内部是否对采样波形进行了衰减,在程序中应予以对应。
具体可将波形在示波器上保存为wfm格式,实验结束后用示波器调出波形,调速为合适波形后,保持窗口不变,分别另存为图片格式和CSV数据格式,将CSV数据导入Matlab后,plot出来的图形与上述图片格式相对照,可知是否为真实时间与幅值。
可见,横坐标为120ms,纵坐标为10倍衰减后的值,在编程中应有相应体现。
2,打开,并运行仿真,完成后wordspace出现新的变量“u”和“tout”;Mdl文件中scope的设置已设置为保存波形名称为u,Structure with time格式,不限制最后5000个点。
由于powergui自带的FFT功能只能对该mdl文件中的scope保存的变量u 进行分析,以下考虑将u中的数据替换为示波器保存的数据,注意横坐标真实时间点数0~,(间隔包含两端共计600个点)与采样点数600相对应。
matlab示波器信号傅里叶变换

一、引言Matlab是一种非常流行的工具,被广泛用于处理和分析信号。
在许多应用中,我们需要对信号进行傅里叶变换来分析其频谱特性。
而Matlab中的示波器可以帮助我们对信号进行实时观测和分析。
本文将介绍在Matlab中如何使用示波器对信号进行傅里叶变换。
二、Matlab示波器简介Matlab中自带的示波器工具可以帮助我们实时观测信号的波形。
通过示波器,我们可以清晰地看到信号的振幅、频率和相位等特性。
示波器也支持对信号进行傅里叶变换来分析其频谱。
这为我们分析信号提供了非常有力的工具。
三、示波器信号傅里叶变换步骤在Matlab中,使用示波器对信号进行傅里叶变换可以分为以下几个步骤:1. 载入信号数据我们需要将待分析的信号数据加载到Matlab中。
这可以通过直接导入数据文件或者使用Matlab内置的信号生成函数来实现。
2. 打开示波器界面在Matlab的命令窗口中输入“scope”即可打开示波器界面。
在示波器界面中,我们可以选择已载入的信号数据并进行实时观测。
3. 设置傅里叶变换参数在示波器界面中,我们可以选择对当前观测的信号进行傅里叶变换。
在设置参数时,我们可以选择变换的类型(如单边频谱或双边频谱)、变换的窗函数和采样频率等。
4. 执行傅里叶变换在设置好参数后,我们可以执行傅里叶变换操作。
示波器会对当前观测的信号数据进行傅里叶变换,并实时显示频谱图像。
5. 分析频谱特性我们可以在示波器界面中对生成的频谱图像进行分析。
通过频谱图像,我们可以清晰地看到信号的频率成分和能量分布情况,从而更深入地了解信号的特性。
四、示波器信号傅里叶变换实例为了更具体地演示示波器对信号进行傅里叶变换的过程,这里我们以一个简单的正弦波信号为例进行说明。
假设我们有一个正弦波信号的采样数据,我们将通过示波器来对其进行傅里叶变换并分析频谱特性。
1. 载入信号数据我们将正弦波信号的采样数据加载到Matlab中。
2. 打开示波器界面在Matlab命令窗口中输入“scope”,即可打开示波器界面。
matlab csv 傅里叶变换 单边频谱 双边频谱

matlab csv 傅里叶变换单边频谱双边频谱本文介绍如何使用Matlab进行CSV文件的傅里叶变换,并生成单边频谱和双边频谱。
首先,导入 CSV 文件。
使用 `csvread` 函数可以将 CSV 文件导入到 Matlab 中。
例如,导入名为 `data.csv` 的 CSV 文件:```data = csvread('data.csv');```然后,对数据进行傅里叶变换。
使用 `fft` 函数可以进行傅里叶变换。
例如,对数据 `data` 进行傅里叶变换:```fft_data = fft(data);```接下来,生成单边频谱。
单边频谱是指只显示傅里叶变换结果的一半,因为另一半是对称的。
使用 `abs` 函数可以得到傅里叶变换结果的幅值,使用 `fftshift` 函数可以将傅里叶变换结果的直流分量移到频谱的中间位置。
使用 `length` 函数可以得到数据的长度。
例如,生成单边频谱:```N = length(data);single_spectrum = abs(fftshift(fft_data)) / N;single_spectrum = single_spectrum(N/2+1:end);```最后,生成双边频谱。
双边频谱是指显示傅里叶变换结果的全部,包括正频率和负频率。
使用 `abs` 函数可以得到傅里叶变换结果的幅值,使用 `fftshift` 函数可以将傅里叶变换结果的直流分量移到频谱的中间位置。
使用 `length` 函数可以得到数据的长度。
例如,生成双边频谱:```N = length(data);double_spectrum = abs(fftshift(fft_data)) / N;```以上是使用 Matlab 进行 CSV 文件的傅里叶变换,并生成单边频谱和双边频谱的简单介绍。
在实际应用中,需要根据具体情况进行适当调整和优化。
示波器波形参数测量和FFT分析

示波器波形参数测量和FFT分析示波器波形参数测量和FFT分析当示波器正确捕获波形后,示波器可以对波形参数进行自动测量。
这些波形参数主要包括下面几个类别:1)电压参数/幅度参数:幅度,峰峰值,最大值,最小值,过冲,有效值等2)时间参数:上升时间/下降时间,周期/频率,脉冲宽度,占空比,时间差,建立时间/保持时间等3)眼图参数:交叉百分比,占空比失真,眼高,眼宽,抖动等4)如果示波器带有抖动分析软件,还可以测量抖动参数,如:时间间隔误差,周期到周期抖动,抖动成分分解(RJ,DJ,ISI,DCD,PJ)等。
下面介绍典型的电压参数和时间参数测量。
电压参数和时间参数测量,都需要参考点,这是测量的关键点之一。
在示波器里,一般称为:Vtop 和Vbase。
Vtop 和Vbase 的测量计算是:采用幅度统计方法。
示波器的工作过程是:先对整个屏幕进行幅度统计分析,可以得出最大电压的位置和最小电压的位置,然后对最大最小幅度的上面40%部分进行统计分析,得到的平均值,此为Vtop 值;对最大最小幅度的下面40%部分进行统计分析,得到的平均值,此为Vbase 值。
不用统计分析中间的20%部分,防止被测波形是3 态信号,而得出错误的结论。
如图1 所示。
图1 示波器Vtop 和Vbase 参数的测量一旦测试出Vtop 和Vbase,基于我们设置的测量门限(示波器的测量门限默认是10%,50%,90%),示波器可以对电压和时间参数进行自动测量。
图2 幅度/最大值/最小值/峰峰值的测量图3 过冲的测量图4 上升时间/下降时间的测量图5 周期/频率/脉宽/占空比的测量。
fft实验分析实验报告

fft实验分析实验报告FFT实验分析实验报告一、引言傅里叶变换(Fourier Transform)是一种重要的信号分析工具,它能够将一个信号分解成不同频率的成分。
快速傅里叶变换(Fast Fourier Transform,FFT)是一种高效的计算傅里叶变换的算法。
本实验旨在通过实际操作,探究FFT在信号分析中的应用。
二、实验设备与方法1. 实验设备:本实验使用的设备包括示波器、信号发生器和计算机。
2. 实验方法:(1)将信号发生器的输出接入示波器的输入端。
(2)调节信号发生器的参数,如频率、振幅等,产生不同的信号。
(3)通过示波器观察信号的波形,并记录相关数据。
(4)将示波器与计算机通过USB接口连接,将示波器上的数据传输到计算机上。
(5)使用计算机上的软件进行FFT分析,得到信号的频谱信息。
三、实验结果与分析1. 实验一:正弦波信号的FFT分析(1)设置信号发生器的频率为1000Hz,振幅为5V,产生一段正弦波信号。
(2)通过示波器观察信号的波形,并记录相关数据。
(3)将示波器上的数据传输到计算机上,进行FFT分析。
实验结果显示,正弦波信号的频谱图呈现出单个峰值,且峰值位于1000Hz处。
这说明FFT能够准确地分析出信号的频率成分,并将其可视化展示。
2. 实验二:方波信号的FFT分析(1)设置信号发生器的频率为500Hz,振幅为5V,产生一段方波信号。
(2)通过示波器观察信号的波形,并记录相关数据。
(3)将示波器上的数据传输到计算机上,进行FFT分析。
实验结果显示,方波信号的频谱图呈现出多个峰值,且峰值位于500Hz的倍数处。
这说明方波信号由多个频率成分叠加而成,FFT能够将其分解出来,并显示出各个频率成分的强度。
3. 实验三:复杂信号的FFT分析(1)设置信号发生器的频率为100Hz和200Hz,振幅分别为3V和5V,产生一段复杂信号。
(2)通过示波器观察信号的波形,并记录相关数据。
(3)将示波器上的数据传输到计算机上,进行FFT分析。
Matlab仿真波形转到Word以及FFT波形处理

仿真波形如何转到Word的文档一、仿真波形如何转到Word,及如何修改与标注坐标步骤如下:1、先从Matlab/Simulink中选出时钟Clock 以及To Workspace模块并连接起来,如下图1-1。
然后打开To Workspace,如下图1-2,接着设置参数:修改Variable name为t(可自己定义),Sample time为2e-4(可自己定义),Save format为Array。
图1-1图1-22、选择To Workspace接到需要的位置,比如要测A相电流,打开To Workspace,设置如下图1-3,同图1-2类似,只要修改Variable name为ia(可自己定义)。
注:Sample time必须与步骤1中的Sample time一致。
图1-33、步骤1、2完成后,开始仿真运行,仿真完成后,在Matlab命令行中输入plot(t,ia),然后单机Enter键确定后,便可显示如下图1-4所示的仿真波形。
图1-44、点击Edit,如下图1-5所示,然后选择Edit图标下的Axes Properties…,显示结果如下图6所示。
图1-5图1-65、在图1-6下方的方框内点击X Axis,选择X Label:输入t/s,即标注了横坐标时间t,单位为秒(s),如下图1-7所示。
然后可以修改X Limits参数,即横坐标范围。
图1-7同理设置Y Axis。
选择Y Label:输入i a/A,即标注了纵坐标电流i a,单位为安培(A)。
6、完成上述步骤后,选择Edit图标下的Copy Figure命令,如图1-8所示。
最后粘帖到Word中,得到所需a相电流波形i a如图1-9所示。
图1-8图1-9注:可以采用Edit 图标下的Axes Properties 中的grid 命令,会产生如下图1-10所示的效果。
当然还可以采用Subplot 等命令,将2、3个仿真波形放到一个图中对比显示。
用MATLAB进行FFT谐波分析

FFT是离散傅立叶变换的快速算法,可以将一个信号变换到频域。
有些信号在时域上是很难看出什么特征的,但是如果变换到频域之后,就很容易看出特征了。
这就是很多信号分析采用FFT变换的原因。
另外,FFT可以将一个信号的频谱提取出来,这在频谱分析方面也是经常用的。
虽然很多人都知道FFT是什么,可以用来做什么,怎么去做,但是却不知道FFT之后的结果是什意思、如何决定要使用多少点来做FFT。
现在就根据实际经验来说说FFT结果的具体物理意义。
一个模拟信号,经过ADC采样之后,就变成了数字信号。
采样定理告诉我们,采样频率要大于信号频率的两倍,这些我就不在此罗嗦了。
采样得到的数字信号,就可以做FFT变换了。
N个采样点,经过FFT之后,就可以得到N个点的FFT结果。
为了方便进行FFT运算,通常N取2的整数次方。
假设采样频率为Fs,信号频率F,采样点数为N。
那么FFT之后结果就是一个为N点的复数。
每一个点就对应着一个频率点。
这个点的模值,就是该频率值下的幅度特性。
具体跟原始信号的幅度有什么关系呢?假设原始信号的峰值为A,那么FFT的结果的每个点(除了第一个点直流分量之外)的模值就是A的N/2倍。
而第一个点就是直流分量,它的模值就是直流分量的N倍。
而每个点的相位呢,就是在该频率下的信号的相位。
第一个点表示直流分量(即0Hz),而最后一个点N的再下一个点(实际上这个点是不存在的,这里是假设的第N+1个点,也可以看做是将第一个点分做两半分,另一半移到最后)则表示采样频率Fs,这中间被N-1个点平均分成N等份,每个点的频率依次增加。
例如某点n所表示的频率为:Fn=(n-1)*Fs/N。
由上面的公式可以看出,Fn所能分辨到频率为为Fs/N,如果采样频率Fs 为1024Hz,采样点数为1024点,则可以分辨到1Hz。
1024Hz的采样率采样1024点,刚好是1秒,也就是说,采样1秒时间的信号并做FFT,则结果可以分析到1Hz,如果采样2秒时间的信号并做FFT,则结果可以分析到0.5Hz。
用simulink对示波器波形fft分析

示波器保存为csv格式,电脑上吧非数据部分文字删除,然后在matlab上输入数据
导进去的数据有两列,第一列是时间轴,第二列是数据,把两行分别导出来,用语句t=s3(:,1),数组t就保存了s3中第一列的时间轴数据
同理导出第二列数据到数组s中
>> s=s3(:,2);
注意时间轴是从-0.05开始的,要把时间轴整体往右移0.05,从0开始
t1就是右移后的时间轴数组
新建一个simulink文件,使用from workspace将数据t1和s输出到scope
From workspace设置如下
仿真步长设置,设置开始时间为0,结束时间为数组t1最后一个数字,步长为数组t1步长
运行,scope就能出来波形了,再用powergui里的FFT分析。
使用示波器进行信号的频谱分析

使用示波器进行信号的频谱分析频谱分析是一种用于研究信号频域特征的常见方法,它能够让我们了解信号中包含的各种频率成分。
而示波器是一种电子测量仪器,广泛应用于电路测试、信号显示和分析等领域。
在示波器中进行频谱分析,通常是采用快速傅里叶变换(FFT)算法。
1.准备工作首先,我们需要准备一台示波器,确保其具备进行FFT分析的功能。
同时,也需要一款支持FFT分析的信号源,可以是一个信号发生器或者其他能够产生信号的设备。
2.连接与设置将信号源与示波器连接,确保信号源输出的信号能够正常输入到示波器中。
在示波器菜单中选择FFT功能,并根据需要设置采样率和FFT点数。
采样率决定了FFT分析的频率范围,通常选择一个适当的采样率可以确保准确的频谱分析。
3.信号输入与观察将信号源的输出接入示波器的输入通道,信号源可以输出一个单一频率的正弦波,也可以输出复杂的信号。
通过观察示波器的显示,可以直观地观察到信号的时域波形。
在示波器的FFT选项中选择启用FFT功能,并设置FFT点数。
FFT点数决定了频谱的分辨率,一般选择更高的FFT点数可以提高频谱显示的清晰度和准确性。
然后,示波器会自动计算信号的频谱。
5.频谱结果分析当示波器计算完毕后,会显示出信号的频谱结果。
频谱结果通常以频率和幅度为坐标进行绘制。
频率表示信号中各个频率分量,而幅度表示该频率分量的能量或功率。
6.频谱分析应用通过频谱分析,我们可以得到信号中各个频率分量的强度信息。
这对于研究信号的特性、检测频率畸变、找出信号的谐波等应用非常有帮助。
在电子工程、通信工程、音频处理等领域中,频谱分析常常被用于信号分析、故障检测、设备调试等方面。
总结:使用示波器进行频谱分析(FFT分析),可以快速、准确地了解信号频域特征。
通过连接信号源和示波器,并进行设置,示波器会自动计算信号的频谱,并将结果以图形方式显示。
通过观察频谱,可以得到信号中各个频率分量的强度信息,进而进行信号分析、故障检测、设备调试等应用。
使用示波器的FFT对信号进行频域分析(上)

http ://从根本上说,示波器是时域仪器,我们使用示波器从电路或被测设备获取信号,示波器在时域中显示它们,在垂直轴上显示信号的电压,我们看到电压在水平轴上随时间的变化。
在时域中,我们可以使用许多参数来表征信号,例如,如果谈论正弦波,这些参数包括频率(瞬时和平均)、幅度(平均值和峰峰值)、偏移、RMS 值,标准偏差,周期等参数。
但是在频域中会是什么样呢?在频域中,信号也有一些有用的参数,示波器用于将信号从时域转换到频域的基本机制是众所周知的傅立叶变换。
示波器中用于从时域转换到频域是离散傅立叶变换(DFT ),在这种情况下,基本假设是波形是重复的。
例如,时基设置为2μs/div ,则采集窗口(如图1所示)的总宽度为20μs ,当执行DFT 时,在20μs 范围内发生的事情每20μs 重复一次。
我们可以使用离散傅立叶变换来识别信号的频率分量,但是,有一些限制。
最重要的限制是离散傅立叶变换仅允许识别谐波,即一次谐波频率的倍数,即“1/采集窗口”。
因此,在图1的示例中,采集窗口是20μs ,定义了我们能够为该波形计算的最低频率,使用“1/采集窗口”确定频率,1/20μs=50kHz 。
这告诉我们,我们只会看到频率分量是50kHz 的倍数,当我们采用该周期性波形并假设它在20μs 的这个时间间隔内反复重复时,我们就可以计算出谐波幅度。
如我们所见,最低频率分量是一次谐波(1/20μs=50kHz ),频率分量之间的间距也是一次谐波。
我们解析的下一个频率成分是100kHz ,然后是150kHz ,依此类推。
离散傅立叶变换作为从时域到频域的路径的唯一问题是,当有非常多的数据点时,计算需要很长时间。
解决这个问题的方法是使用快速傅立叶变换(FFT )。
关于快速傅立叶变换中的数据截断上面我们讨论了如何使用离散傅立叶变换将示波器采集的时域信号转换到频域。
我们注意到,只有当信号重复时才使用傅立叶变换(图1),并且它允许我们仅识别一次谐波频率的谐波,即1/采集窗使用示波器的FFT 对信号进行频域分析(上)美国力科公司供稿图1离散傅立叶变换的基本假设是重复波形62http ://图2FFT 采集的示例口。
CSV示波器数据导入MATLAB中进行FFT分析操作
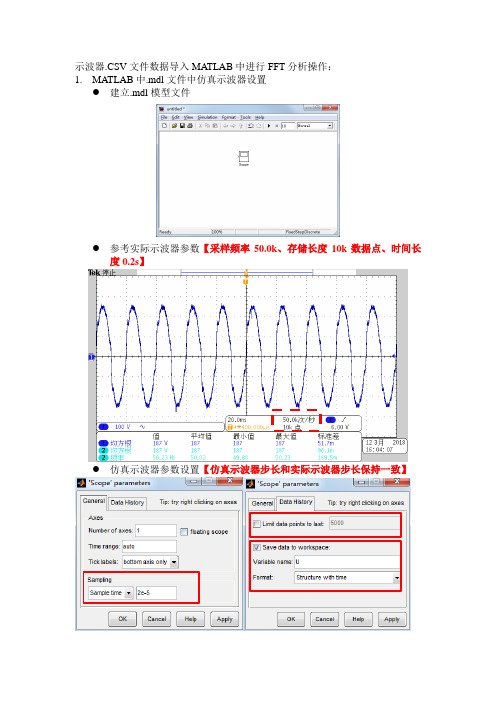
示波器.CSV文件数据导入MATLAB中进行FFT分析操作:1.MATLAB中.mdl文件中仿真示波器设置●建立.mdl模型文件●参考实际示波器参数【采样频率50.0k、存储长度10k数据点、时间长度0.2s】●仿真示波器参数设置【仿真示波器步长和实际示波器步长保持一致】2.仿真环境参数设置●配置仿真环境参数【仿真时间长度一致、定步长模式且选择离散solver且仿真步长和实际示波器步长一致】●.mdl文件仿真并在workspace中观察仿真结果【长度为10001数据点,和示波器真实10000数据点不匹配、注意变量名U.signals.values】3.导入CSV文件数据●观察示波器CSV文件信息【10000数据点、第20行为临近数据点最近一行、第21行数据为数据点个数不匹配人为正确加入1组数据点】●导入数据【file->Import Data】10001个,和仿真示波器数据点数一致,不人为加入一组数据点则会差一个数据,后续会影响结果4.执行FFT分析代码:U.signals.values=CH1;Power_fftscope谐波电压源给定与CSV文件数据进行MATLAB的FFT分析结果进行各次谐波含量对比如下:电压谐波给定/FFT测量频率基波180V/184.9V 50 Hz3次10%/9.46% 3*50Hz5次5%/4.86% 5*50Hz7次5%/4.97% 7*50Hz9次5%/5.22% 9*50Hz11次3%/3.16% 11*50Hz13次3%/3.07% 13*50Hz5.参考说明本操作参考博客及文库资料并结合自身仿真总结如上。
博客内容如下:附对比图如下:。
matlab fft谱分析实验报告

Matlab FFT 谱分析实验报告介绍本实验报告旨在通过使用Matlab进行FFT(快速傅里叶变换)谱分析,详细介绍该方法的步骤和应用。
FFT是一种常用的信号处理技术,可将时域信号转换为频域信号,并提供了对信号频谱特征进行分析的能力。
实验步骤以下是进行FFT谱分析的步骤:1. 导入信号数据首先,我们需要将待分析的信号数据导入Matlab中。
可以使用load函数加载存储信号数据的文件,或者直接在脚本中定义信号数据。
2. 对信号数据进行预处理在进行FFT谱分析之前,通常需要对信号数据进行预处理。
这可能包括去除噪声、滤波等操作。
在本实验中,我们将假设信号数据已经经过了必要的预处理步骤。
3. 执行FFT变换使用fft函数对信号数据执行FFT变换。
该函数将信号从时域转换为频域,并返回频谱数据。
4. 计算频谱幅度通过对FFT变换结果应用幅度函数,可以计算出信号在不同频率下的幅度。
这将揭示信号中包含的主要频率分量。
5. 绘制频谱图通过使用Matlab的绘图功能,可以将频谱数据可视化为频谱图。
频谱图可以帮助我们更好地理解信号的频谱分布情况。
6. 分析结果根据频谱图,我们可以观察信号的主要频率成分以及它们的幅度。
这有助于我们了解信号的频域特征,并可以用于识别信号中的噪声或其他异常。
实验应用FFT谱分析在许多领域中都有广泛的应用。
以下是一些常见的应用领域:1. 信号处理FFT谱分析可用于处理和分析各种类型的信号,例如音频信号、生物医学信号和电力信号等。
通过分析信号的频谱特征,我们可以提取出信号中的重要信息。
2. 通信系统在通信系统中,FFT谱分析可以用于频谱分配、频谱监测和信号调制等方面。
通过分析信号的频谱特征,我们可以更好地设计和优化通信系统。
3. 振动分析FFT谱分析可用于振动分析领域,用于分析和诊断机械系统的振动特征。
通过分析振动信号的频谱,可以检测到机械系统中的故障和异常。
4. 音频处理在音频处理中,FFT谱分析可用于音频信号的频谱分析、音频合成和音频特征提取等方面。
使用示波器的FFT对信号进行频域分析(下)

当对采集的波形执行快速傅里叶变换时,经常会遇到波形不能整齐地位于示波器采集窗口内的情况,因此,窗口的开始和结束时的电压是不相同的。
随之而来的从窗口到窗口的不连续性导致高频频谱泄露,并且解决该问题的方法是称为“窗口化”的技术。
这带来了另一个问题,即有大量的窗口函数可供选择,它们在产生的分辨率和从一个频率分量到另一个频率分量的高频泄漏方面都有所不同。
我们应该在FFT中使用哪一个?不同的窗函数对信号频谱的影响是不一样的,这主要是因为,不同的窗函数产生泄漏的大小不一样,频率分辨能力也不一样。
信号的截短产生了能量泄漏,而用FFT算法计算频谱又产生了栅栏效应,从原理上讲这两种误差都是不能消除的,但是我们可以通过选择不同的窗函数对它们的影响进行抑制。
矩形窗主瓣窄、旁瓣大、频率识别精度最高、幅值识别精度最低;布莱克曼窗主瓣宽、旁瓣小、频率识别精度最低,但幅值识别精度最高。
为了减少频谱旁瓣和栅栏效应的影响,我们在FFT运算中使用窗函数,图1显示了Hanning(汉宁窗)使用后的效果。
窗函数位于下图中左上角的栅格中红色的波形,叠加在黄色的时域信号上。
窗函数与时域信号时域相乘。
结果显示在左下角的蓝色波形。
右下角的粉色波形显示了进行FFT计算之后的频谱图,相对于右上角的使用窗函数之前的频谱图来说,旁瓣的幅度已经大大减低。
对于不同的应用需求,有多种不同的窗函数供工程师选择,Hanning(汉宁窗)是使用最广泛的一种窗函数,除此之外,Hamming(海明窗),Flat-top窗和Balckman-Harris窗的效果,在下图中做了对比,图中的信号是500MHz正弦波,矩形窗产生最窄的谱线,加Flat-top窗谱线最宽。
图2中显示了同样的窗函数对比,但是采用495MHz正弦波进行FFT运算,矩形窗显示了最差旁瓣效果,Flat-top窗函数基本上保持了与图3一样的旁瓣效果,所以我们看到旁瓣的影响和精确频率分辨率有时候是不可兼得的。
使用示波器的FFT对信号进行频域分析之一---FFT概述

使用示波器的FFT对信号进行频域分析之一---FFT概述从根本上说,示波器是时域仪器,我们使用示波器从电路或被测设备获取信号,示波器在时域中显示它们,在垂直轴上显示信号的电压,我们看到电压在水平轴上随时间的变化。
在时域中,我们可以使用许多参数来表征信号,例如,如果谈论正弦波,这些参数包括频率(瞬时和平均)、幅度(平均值和峰峰值)、偏移、RMS值,标准偏差,周期等参数。
但是在频域中会是什么样呢?在频域中,信号也有一些有用的参数,示波器用于将信号从时域转换到频域的基本机制是众所周知的傅立叶变换。
示波器中用于从时域转换到频域是离散傅立叶变换(DFT),在这种情况下,基本假设是波形是重复的。
例如,时基设置为2μs/ div,则采集窗口(如图1所示)的总宽度为20μs,当执行DFT时,在20μs 范围内发生的事情每20μs重复一次。
我们可以使用离散傅立叶变换来识别信号的频率分量,但是,有一些限制。
最重要的限制是离散傅立叶变换仅允许识别谐波,即一次谐波频率的倍数,即1/采集窗口。
因此,在图1的示例中,采集窗口是20μs,定义了我们能够为该波形计算的最低频率,使用1/采集窗口确定频率,1/20μs=50 kHz。
图1:离散傅立叶变换的基本假设是重复波形这告诉我们,我们只会看到频率分量是50kHz的倍数,当我们采用该周期性波形并假设它在20μs的这个时间间隔内反复重复时,我们就可以计算出谐波幅度。
如我们所见,最低频率分量是一次谐波(1/20μs=50 kHz),频率分量之间的间距也是一次谐波。
我们解析的下一个频率成分是100kHz,然后是150kHz,依此类推。
离散傅立叶变换作为从时域到频域的路径的唯一问题是,当有非常多的数据点时,计算需要很长时间。
解决这个问题的方法是使用称为快速傅立叶变换(FFT)。
关于快速傅立叶变换中的数据截断上面我们讨论了如何使用离散傅立叶变换将示波器采集的时域信号转换到频域。
我们注意到,只有当信号重复时才使用傅立叶变换(图1),并且它允许我们仅识别一次谐波频率的谐波,即1/采集窗口。
matlab csv 傅里叶变换 单边频谱 双边频谱

matlab csv 傅里叶变换单边频谱双边频谱本文主要介绍如何使用matlab对csv格式的数据进行傅里叶变换,并生成单边频谱和双边频谱的图形。
首先,我们需要导入csv文件的数据。
可以使用matlab自带的csvread函数进行导入。
例如,导入名为data.csv的文件:```data = csvread('data.csv');```接下来,我们可以使用matlab的fft函数对数据进行傅里叶变换。
例如,计算data的傅里叶变换:```fft_data = fft(data);```得到的fft_data为复数形式的结果,其中实部表示信号的幅度,虚部表示信号的相位。
接着,我们可以利用fftshift函数将fft_data转换为双边频谱。
例如:```fft_shift_data = fftshift(fft_data);```得到的fft_shift_data为双边频谱,其中x轴表示频率,y轴表示信号的幅度。
如果我们只需要单边频谱,可以利用matlab的abs函数和fftshift函数计算。
例如:```fft_shift_data = fftshift(fft_data);single_side_data = abs(fft_shift_data).^2;single_side_data =single_side_data(1:length(single_side_data)/2+1);single_side_data(2:end-1) = 2*single_side_data(2:end-1);```得到的single_side_data为单边频谱,其中x轴表示频率,y 轴表示信号的幅度。
最后,我们可以使用matlab的plot函数将频谱图形绘制出来。
例如,绘制名为“单边频谱”的图形:```plot(frequency, single_side_data);title('单边频谱');xlabel('频率');ylabel('幅度');```其中,frequency为频率轴的数据。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
示波器C S V波形数据导入M精编b进行
F F T分析
公司标准化编码 [QQX96QT-XQQB89Q8-NQQJ6Q8-MQM9N]
示波器CSV波形数据导入Matlab进行FFT分析
1,将CSV文件拖到workspace窗口,弹出的Import Wizard窗口中,点选“Next”,新窗口中选第二项“Create vectors from each column using column names”,点“Finish”。
这时workspace出现2个向量“Volt”和“Second”。
说明:若此时选中“Volt”,右上角的绘图命令变成可选,点“plot(Volt)”则出现如图:
图中横坐标600表示示波器共记录了600个点,纵坐标为示波器的屏幕显示值(未乘探头倍率),因此问题在于改变横坐标为真实时间,改变纵坐标为真实值。
结合示波器示数(可另存为图片格式备用)。
下面的步骤即是以Volt替换mdl文件生成的变量u,以便于使用mdl中的powergui的FFT工具进行分析。
注意示波器采样点数600应与真实时间对应,并取时间上的600个时间点。
纵坐标表示电压幅值,要显示为真实值时,则要考虑示波器探头倍率或示波器内部是否对采样波形进行了衰减,在程序中应予以对应。
具体可将波形在示波器上保存为wfm格式,实验结束后用示波器调出波形,调速为合适波形后,保持窗口不变,分别另存为图片格式和CSV数据格
式,将CSV数据导入Matlab后,plot出来的图形与上述图片格式相对照,可知是否为真实时间与幅值。
可见,横坐标为120ms,纵坐标为10倍衰减后的值,在编程中应有相应体现。
2,打开,并运行仿真,完成后wordspace出现新的变量“u”和“tout”;
Mdl文件中scope的设置已设置为保存波形名称为u,Structure with time格式,不限制最后5000个点。
由于powergui自带的FFT功能只能对该mdl文件中的scope保存的变量u 进行分析,以下考虑将u中的数据替换为示波器保存的数据,注意横坐标真实时间点数0~,(间隔包含两端共计600个点)与采样点数600相对应。
3,打开,并运行该文件,完成后出现FFT窗口如图:
4,选择要分析的波形的周期数(这里的周期数并不一定是标准意义上的同期),选择要显示的频谱展示范围,点“Display”;如果报错如图
则原因是所要分析的波形周期数过大,而所需分析的波形频率设置过小,这两个值为反比关系。
如图我的波形真实值是,所以Fundamental frequency 应设置为,如果出现以上报错,则应减小Number of cycles设置值。
本次实验减小为3后,不再报错。
理论上分析的周期数越大越准确。
其中,THD值描述波形的正弦化,该值越小则表示波形越接近正弦波,即波形的谐波含量越小。
5,想要对该结果进行进一步修改调速,则可以点击View->Property Editor进行调速,如改变横纵坐标名称、显示范围等。
不需要调速则略过此步。
6,菜单栏中,点Edit->Copy Figure后,即可在word中进行粘贴。
最后,分析出来的柱形图中,为以为基波进行分析时的基波幅值;THD为波形总的谐波含量,即%谐波含量;理论上THD越小,则原波形越接近正弦波。
