展开与折叠综合练习题

合集下载

四年级上数学8、展开与折叠(练习)

八、展开与折叠 ——正方体展开图的规律1. 判断下列平面图形能折叠成正方体吗？（）（）（）（）（）（）1.在下面的12个展开图中，哪些可以做成没有顶盖的小方盒？（）（）（）（）（）（）（）（）（）（）（）（）2. 将下图中左边的图形折叠起来围成一个正方体，应该得到右图中的( )，先想一想，再做一做。

3.（1）如果“你”在前面，那么谁在（2）“坚”在下，“就”在后，胜后面？利在哪里？4.如下图是一个正方体的展开图，图中已标出三个滚动思考组号学号姓名利胜持是就坚太了你棒！们AB CDFR实践百花园面在正方体中的位置，F ：前面；R ：右面；D ：下面。

试判定另外三个面A 、B 、C 在正方体中的位置。

5.如右图是一个正方体的展开图，每个面内部都标注了字母，请根据要求填空：（1）如果D 面在左面，那么F 面在（）；（2）如果B 面在后面，从左面看是D 面，那么上面是（）。

6.将下面两幅图沿虚线折成一个正方体，图1相交于一个顶点处的三个面上的数字之和的最大值是多少？图2相对两个面上的数字之和最大是几？653432452611图1 图21. 在下图中所示的一个立方体的六个面上分别写有A 、B 、C 、D 、E 五个字母，其中两个面写有相同的字母。

下面是它的三种放置图，请问：哪个字母写了两遍？AC B（1）BCD（2）DEC（3）2．有四枚相同的骰子，展开图如下，将这四枚骰子依次码好，由上往下数，第二、三、四枚骰子的上顶面的点数之和是多少？想做就做怪味豆七嘴八舌说说你的收获！生活随处课件几何形体，我们会根据展开图判断各个面的位置，还能确定正方体展开图上各个面的位置。

我还知道六连方图中能折成正方体的规律是我觉得这节课我的表现可以评（）（）（）A BC DEF。

专题-展开与折叠测试-初中数学七年级上册同步讲练

专题1.2展开与折叠一、选择题(本大题共14个小题，每题2分，共28分，在每个小题的四个选项中只有一项是符合题目要求的)1．是正方体的展开图的是()A．B．C．D．2．下列各图中，经过折叠不能围成一个棱柱的是()A．B．C．D．3．围成下列立体图形的各个面中，每个面都是平的是()A．长方体B．圆柱体C．球体D．圆锥体4．如图是一个正方体展开图，把展开图折叠成正方体后，“抗”字一面相对面上的字是()A．新B．冠C．病D．毒5．(2020·柘城县实验中学初三二模)下列图形中为正方体的平面展开图的是()A．B．C．D．6．如图是某几何体的展开图，则该几何体是()A．四棱锥B．三棱锥C．四棱柱D．长方体7．下列选项中，左边的平面图形能够折成右边封闭的立体图形的是()A．B．C．D．8．如图是一个正方体的表面展开图，在这个正方体中，与点A重合的点为()A．点C和点N B．点B和点M C．点C和点M D．点B和点N 9．下列图形经过折叠不能围成棱柱的是()A．B．C．D．10．下列图形不可能是长方体展开图的是()A．B．C．D．11．如果有一个正方体，它的展开图可能是下列四个展开图中的()A．B．C．D．12．如图是一个正方形盒的展开图，若在其中的三个正方形a、b、c内分别填入适当的数，使得它们折成正方体后相对的面上的两个数互为相反数，则填入正方形a、b、c内的三个数依次为()A．3，0，4-B．0，3，4-C．3-，0，4D．3，4-，013．如图是无盖长方体盒子的表面展开图(重叠部分不计)，则盒子的容积为()A．4B．6C．12D．15==；F，H为CD边14．如图所示，在长方形纸片ABCD中，E，G为AB边上两点，且AE EG GB==．沿虚线EF折叠，使点A落在点G上，点D落在点H上；然后再沿虚线GH 上两点，且DF FH HC折叠，使B落在点E上，点C落在点F上．叠完后，剪一个直径在EF上的半圆，再展开，则展开后的图形为()A．B．C．D．二、填空题(本题共4个小题；每个小题3分，共12分，把正确答案填在横线上)15．如图为某几何体的展开图，该几何体的名称是___.16．将面积为225cm2的正方形硬纸片围成圆柱的侧面，则此圆柱的底面直径为______cm(结果保留π)．17．下列各图都是正方体的表面展开图，若将它们折成正方体，则其中两个正方体各面图案完全一样的是____________．(填序号)18．一个小立方块的六个面分别标有数字1，-2，3，-4，5，-6，从三个不同方向看到的情形如图,则如图放置时的底面上的数字之和等于_____。

展开与折叠同步练习及答案

展开与折叠同步练习及答案展开与折叠同步练习及答案以下是查字典数学网为您推荐的展开与折叠同步练习及答案，希望本篇文章对您学习有所帮助。

展开与折叠同步练习及答案【问题情境】用六个完全一样的正方形做成如图所示的拼接图形，它折叠后能得到一个密封的正方体纸盒吗?若不能，如何改?【自主探究】1、改一改能否移动上图中某一个正方形的位置，使其折叠后可以得到一个密封的正方体纸盒。

画出移动后的图形，并用纸复制下来，折一下验证你的想法。

2、想一想上述问题，还有其他的移动方法吗，画出图形，与同学交流。

3、做一做除了上面自主探究1、2中的图形外，你还能画出哪些正方体的平面展开图?请与同学交流，然后把所有的正方体的平面展开图分类整理一下。

4、练一练马小虎准备制作一个有盖的正方体纸盒，他先用5个大小一样的正方形制成如图所示的拼接图形(实线部分)，经折叠后发现还少一个面，请你在图中拼接图形上再接一个正方形(用实线在图中画出来)，使得接成的图形经过折叠后能成为一个封闭的正方体盒子，再用纸复制下来，然后折叠验证你的想法。

M、N的位置。

8.下列图形是正方体的展开图，还原成正方体后，其中完全一样的是( )(1) (2) (3) (4)A.(1)和(2)B.(1)和(3)C.(2)和(3)D.(3)和(4)【拓展应用】9.一个正方体的骰子，1和6，2和5，3和4是分别相对的面上的点。

现在有12个正方形格子的纸上画好了点状的图案，如图所示，若要经过折叠能做成一个骰子，你认为应剪掉哪6个正方形格子?(请用笔在要剪掉的正方形格子上打，不必写理由)答案：情景问题不能。

自主探究略回顾反思需且仅需6个正方形每个正方形最多有两边与其他正方形相连基础演练 1.C; 2.略; 3. 。

能力升级 4.1; 5. ; 6.D; 7. ; 8.D。

拓展应用 9. 。

数学：5.3展开与折叠同步练习(苏科版七年级上)

5.3展开与折叠姓名_____________班级____________学号____________分数_____________一、选择题1 ．如图1是一个小正方体的侧面展开图,小正方体从如图2所示的位置依次翻到第1格、第2格、第3格,这时小正方体朝上面的字是( ) A.和 B.谐 C.社D.会2．下列各图中,( )是长方体的展开图A 、B 、C 、D 、3 ．圆锥侧面展开图可能是下列图中的( )4 ．下列图形中,是正方体表面展开图的是 ( ).(A) (B) (C) (D)5．一个正方体的侧面展开图如图4所示,用它围成的正方体只可能是( )A ．B ．C ．D ．图1 图2O O O A B C D二、填空题6．一个长、宽、高分别为15cm,10cm,5cm 的长方体包装盒的表面积为________cm 2. 7．将一个立方体展开后如图所示 ,请在空格处填上适当的整数,使相对的面的两数积为-24 (要求数字不能重复使用)｡8．如图,长方体的长BE=5cm,宽AB=3cm,高BC=4cm,一只小蚂蚁从长方体表面由A 点爬到D 点去吃食物,则小蚂蚁走的最短路程是___________cm ｡EDCBA9．如图是一个正方体的表面展开图,已知正方体相对两个面上的数字互为倒数,则a =_______,b =_______,c =_________.三、解答题10．如图是一个多面体展开图,每个面内都标注了字母,请根据要求回答问题: (1)如果面A 在多面体的底部,那么在上面的一面是_____(2)如果面F 在前面,从左面看面B,那么在上面的一面是___(3)从右面看是面C,面D 在后面,那么在上面的一面是____11．某长方体包装盒的展开图如图所示.如果长方体盒子的长比宽多4cm,求这个包装盒的体积.a b c 1 2.53参考答案一、选择题1 ．D2 ．B3 ．D4 ．D5．A二、填空题6．5507．8．749．-1,25,13; 三、解答题10．F CA11．解:设这种药品包装盒的宽为cm x ,高为cm y ,则长为(4)cm x +,根据题意得,22144213x y x y +=⎧⎨++=⎩　,解得52x y =⎧⎨=⎩ (9分,其中列式正确给4分) 故长为9cm,宽为5cm,高为2cm. 体积395290(cm )V =⨯⨯= 答:这种药品包装盒的体积为390cm .。

北师大版七年级数学上册展开与折叠优化练习(附答案)

北师大版七年级数学上册展开与折叠优化练习（附答案）一、单选题1.如图是正方体的平面展开图，则与“梅”字相对的字是（）A. 侨B. 香C. 牛D. 旺2.一个正方体的每一个面都有一个汉字，其平面展开图如图所示，那么在该正方体中和“城”字相对的字是（）A. 丹B. 东C. 创D. 联3.如图是正方形的展开图，原正方体相对两个面上的数字之和的最小值是（）A. 4B. 5C. 6D. 74.如图，透明的圆柱形玻璃容器（容器厚度忽略不计）的高为16cm，在容器内壁离容器底部4cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在容器外壁，位于离容器上沿4cm的点A处，若蚂蚁吃到蜂蜜需爬行的最短路径为20cm，则该圆柱底面周长为（）A. 12cmB. 14cmC. 20cmD. 24cm5.下列四个图形中，是三棱柱的平面展开图的是（）A. B. C. D.二、填空题6.如图是一个正方体的表面展开图，则原正方体中“喜”面所对面上的字是________．7.立方体木块的六个面分别标有数字1、2、3、4、5、6，如图，是从不同方向观察这个立方体木块看到的数字情况，数字1和5对面的数字的和是________．8.如图是一个正方体的表面展开图,还原成正方体后,标注了字母A的面是正方体的正面,若正方体的左面与右面所标注代数式的值相等,则x的值是________.9.如图，5个边长相等的小正方形拼成一个平面图形，小丽手中还有1个同样的小正方形，她想将它与图中的平面图形拼接在一起，从而可以构成一个正方体的平面展开图，则小丽总共能有________种拼接方法.10.一个几何体的表面展开图如图所示，则这个几何体是 ________．8题9题10题三、解答题11.一个正方体6个面分别写着1、2、3、4、5、6，根据下列摆放的三种情况，那么每个数对面上的数是几？12.如图，在无阴影的方格中选出两个画出阴影，使它们与图中4个有阴影的正方形一起可以构成一个正方体的表面展开图．（在图1和图2中任选一个进行解答，只填出一种答案即可）四、作图题13.马小虎准备制作一个封闭的正方体盒子，他先用5个大小一样的正方形制成如图所示的拼接图形（实线部分），经折叠后发现还少一个面，请你在图中的拼接图形上再接一个正方形，使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子（添加所有符合要求的正方形，添加的正方形用阴影表示）五、综合题14.一个正方体的六个面分别标有字母A，B，C，D，E，F，从三个不同方向看到的情形如图．（1）A对面的字母是________，B对面的字母是________；（请直接填写答案）（2）已知A＝x，B＝﹣x2+3x，C＝﹣3，D＝1，E＝x2019，F＝6．①若字母A表示的数与它对面的字母表示的数互为相反数，求E的值；②若2A﹣3B+M＝0，求出M的表达式．15.我们知道，将一个正方体或长方体的表面沿某些棱剪开，可以展成一个平面图形．（1）下列图形中，是正方体的表面展开图的是________．（2）如图所示的长方体，长、宽、高分别为4、3、6，若将它的表面沿某些棱剪开，展成一个平面图形．则下列图形中，可能是该长方体表面展开图的有________（填序号）（3）下列图是题（2）中长方体的一种表面展开图，它的外围周长为52，事实上，题（2）中长方体的表面展开图还有不少，聪明的你能画出一个使外围周长最大的表面展开图吗？请画出这个表面展开图，并求出它的外围周长．答案一、单选题1. A2. C3. B4. D5. B二、填空题6. 数7. 78. 19. 4 10. 四棱锥三、解答题11. 解：根据正方体的特征知，相邻的面一定不是对面，所以面“1”与面“4”相对，面“2”与面“5”相对，“3”与面“6”相对．1对4，2对5，3对612. 解：只写出一种答案即可．图1：图2：四、作图题13. 解：五、综合题14. （1）D；E（2）解：①∵字母A表示的数与它对面的字母D表示的数互为相反数，∴x＝﹣1，∴E＝（﹣1）2019＝﹣1；②∵2A﹣3B+M＝0，∴2x﹣3（﹣x2+3x）+M＝0，∴M＝﹣2x+3（﹣x2+3x）＝﹣3x2+7x．15. （1）B（2）①②③（3）解：外围周长最大的表面展开图，如图：观察展开图可知，外围周长为6×8+4×4+3×2=48+16+6=70．。

2.2展开与折叠同步练习北师大版数学五年级下册(含解析)

………○………装……○…………订…………○…2.2展开与折叠 24100 注意事项： 1．答题前填写好自己的姓名、班级、考号等信息 2．注意书卷整洁一、选择题 1．下面的图形能折成正方体的是（）。

A ． B ． C ． D ． 2．如图，是一个正方体展开图，把它折成正方体后与6相对的面是（）。

A ．1 B ．2 C ．3 D ．4 3．下面图形中，折叠后不能围成正方体的是（）。

A ． B ． C ． D ．4．（如图）一个正方体平面展开图折成正方体时，与顶点K 重合的点是（）。

A ．点F 、点N B ．点F 、点B C ．点F 、点M D ．点F 、点A 5．下面图形不能围成正方体的是( )。

A．B．C．D．6．笑笑沿下图中所示的粗实线和粗虚线剪开正方体纸盒，然后将纸盒各面向外展开，与展开后的图形形状相似的是（）。

A．B．C．D．7．下面的4个展开图中，____是图中所示的正方体展开图。

①①①①A．①①B．①①C．①① D．①①二、填空题8．长方体的展开图由( )个长方形组成，且相对面的面积( )；正方体的展开图是由( )个( )的正方形组成的。

9．如下图，正方体的展开图上有编号，请你写出相对面的号码：3的相对面是( )，4的相对面是( )，5的相对面是( )。

10．下面的图形折叠后，能围成长方体的图形是( )，能围成正方体的图形是( )。

○…………装…………○…………订……………………线…………○…11．最常见的骰子有6个面，它是一个正方体，上面分别有一到六个孔（或数字），其相对两个面数字的和是7。

明明想用纸板做一个骰子，已经写好了3个数字，剩下的数字你能帮忙填上吗？ 12．下图是一个长方体的展开图，围成长方体时，点C 与点( )重合。

13．下图是一个正方体的展开图，请说出与1号、2号、3号面相对的各是几号面， ( )——( ) ( )——( ) ( )——( ) 14．下图是一个正方体的展开图，在正方体中，与1号面相对的是( )号面，与2号面相对的是( )号面，与3号面相对的是( )号面。

第一章展开与折叠同步练习3

展开与折叠（3）(识别图形及概念) 姓名一．选择题：1．下图中哪些不能够沿虚线折叠成棱柱？现想一想，再折一折：（）(A)(B)(C)(D)2．下图中哪个是六棱柱的平面展开图（）(A)(B)(C)(D)3．如图，把一个等边三角形三边的中点用虚线连结，沿虚线折叠后取得的立体图形是（）（A）三棱柱（B）三棱锥（C）正方体（D）圆锥4．三棱柱中棱的条数是（）（A）3条（B）6条（C）8条（D）9条5．八棱柱共有（）（A）2个面（B）8个面（C）10个面（D）12个面6．下面图形能折叠起来能做成一只开口的盒子的有（）（A）1个（B）2个（C）3个（D）4个7．如图，通过折叠能够围成一个长方体的图形有（）（A）1个（B）2个（C）3个（D）4个8．下列说法中，正确的是（）（A）棱柱的侧面能够是三角形（B）由六个大小一样的正方形所组成的图形是正方体的展开图（C）正方体的各条棱都不相等（D）棱柱的各条棱都相等9．一个三面带有标记的正方体：若是把它展开，应是下列展开图形中的（）二．指出下列平面图形是什么几何体的展开图（6分）：B三．有一正方体木块，它的六个面别离标上数字1——6，这是那个正方体木块从不同面所观察到的数字情形。

请问数字1和5对面的数字各是多少？125214461四．推理猜想题（1）三棱锥有____条棱，四棱锥有_____条棱，十棱锥有____条棱。

（2）_____棱锥有30条棱。

（3）_____棱柱有60条棱。

一个多面体的棱数是8，则那个多面体的面数是_____展开与折叠（3）(识别图形及概念)参考答案一．（1）D；（2）B；（3）A；（4）D；（5）C；（6）D；（7）B；（8）D；（9）D；二．长方体，圆锥，圆柱；三．1对3，5对4；四．（1）6，8，20；（2）15；（3）20；10A C。

展开与折叠综合练习

展开与折叠综合练习
1、下图中的图形经过折叠能围成正方体的有。

2、将一个正方体的表面沿某些棱剪开，能展成下面平面图形的有。

3、在下图中增加两个小正方形，使所的图形经过折叠能围成一个正方体。

4、下图中的图形经过折叠能围成棱柱的有。

5、右上图中是圆锥表面展开图的有。

6、下面的实物图中，是圆柱体的有。

7、若“进”表示“前面”，“步”表示“右面”，“习”表示“下面”。

则，“祝”表示面，“你”表示面，“学”表示面。

8、下面的图形可以折成一个正方体形的盒子，折好以后，与1相邻的数是，相对的数是。

9、将正方体的表面分别标上数字1、2、3、4、5、6，使它的任意两个相对面的数字之和为7，将它沿某些棱剪开，能展成下面的平面。

10、已知一不透明的正方体的六个面上分别写着1至6六个数字，如图是我们能看到的三种情况，那么1和5的对面数字分别是____和_____.
11、如图是一个直三棱柱的表面展开图，其中，黄色和绿色的部分都是边长等于1的正方形．问这个直三棱柱的体积是。

12、如图所示的立方体，如果把它展开，可以是下列图形中的（）
13、如图，把左边的图形折叠起来，它会变成右边的正方体（）。

初一数学展开与折叠试题

初一数学展开与折叠试题1.右图是一个由相同小正方体搭成的几何体俯视图,小正方形中的数字表示在该位置上的小正方体的个数,则这个几何题的主视图是 ( )【答案】A【解析】本题考查的是三视图俯视图中的每个数字是该位置小立方体的个数，分析其中的数字，得主视图有3列，从左到右分别是3，2，1个正方形．由俯视图中的数字可得：主视图有3列，从左到右分别是3，2，1个正方形．故选A．2.如图是正方体的平面展开图,每个面上标有一个汉字, 与“油”字相对的面上的字是( )A．北B．京C．奥D．运【答案】A【解析】本题考查了正方体的的表面展开图正方体的平面展开图中，相对面的特点是中间必须间隔一个正方形，据此作答即可．因为正方体的平面展开图中，相对面的特点是中间必须间隔一个正方形，所以与“油”字相对的字是“北”．故选A.3.下面四个图形中,经过折叠能围成如图只有三个面上印有图案的正方体纸盒的是( )【答案】B【解析】本题考查的是正方体的展开图根据图中符号所处的位置关系作答．三角形图案的顶点应与圆形的图案相对，而选项A，C与此不符，所以错误；三角形图案所在的面应与圆形的图案所在的面相邻，而选项D与此也不符，正确的是B，故选B．4.圆锥侧面展开图可能是下列图中的( )【答案】D【解析】本题考查的是圆锥的侧面展开图根据圆锥的侧面展开图是一个扇形即可得到结果。

圆锥的侧面展开图是一个扇形，故选D。

5.将圆柱形纸筒沿母线剪开铺平,得到一个矩形(如图).如果将这个纸筒沿线路剪开铺平,得到的图形是A．矩形B．半圆C．三角形D．平行四边形【答案】D【解析】此题主要考查了图形的剪拼利用展开图可以得出将这个纸筒沿线路B→M→A剪开铺平时，AB与另对应点仍然连接，得出得到的图形是平行四边形．∵将圆柱形纸筒沿母线AB剪开铺平，则得到一个矩形（如图）．若将这个纸筒沿线路B→M→A剪开铺平，AB与另对应点仍然连接，∴得到的图形是平行四边形．故选D．6.下列图中,左边的图形是立方体的表面展开图,把它折叠成立方体｡它会变成右边的【答案】C【解析】本题考查正方体的表面展开图及空间想象能力在验证立方体的展开图式，要细心观察每一个标志的位置是否一致，然后进行判断．根据展开图中各种符号的特征和位置，可得能变成的是C．故选C．7.小红将考试时自勉的话“细心·规范·勤思”写在一个正方体的六个面上,其平面展开图如图所示,那么在该正方体中,和“细”相对的字是__________.【答案】范【解析】本题考查了正方体的的表面展开图正方体的平面展开图中，相对面的特点是中间必须间隔一个正方形，据此作答即可．因为正方体的平面展开图中，相对面的特点是中间必须间隔一个正方形，所以与“细”字相对的字是“范”．8.圆锥侧面展开图可能是下列图中的（）【答案】D【解析】本题考查的是圆锥的侧面展开图根据圆锥的侧面展开图是一个扇形即可得到结果。

立体图形的展开与折叠综合测试题

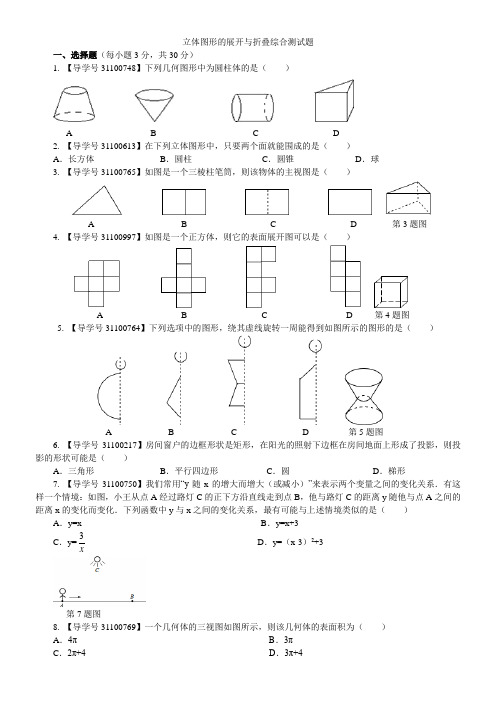
立体图形的展开与折叠综合测试题一、选择题（每小题3分，共30分）1. 【导学号31100748】下列几何图形中为圆柱体的是（）A B C D2. 【导学号31100613】在下列立体图形中，只要两个面就能围成的是（）A．长方体B．圆柱C．圆锥D．球3. 【导学号31100765】如图是一个三棱柱笔筒，则该物体的主视图是（）A B C D 第3题图4. 【导学号31100997】如图是一个正方体，则它的表面展开图可以是（）A B C D 第4题图5. 【导学号31100764】下列选项中的图形，绕其虚线旋转一周能得到如图所示的图形的是（）A B C D 第5题图6. 【导学号31100217】房间窗户的边框形状是矩形，在阳光的照射下边框在房间地面上形成了投影，则投影的形状可能是（）A．三角形B．平行四边形C．圆D．梯形7. 【导学号31100750】我们常用“y随x的增大而增大（或减小）”来表示两个变量之间的变化关系．有这样一个情境：如图，小王从点A经过路灯C的正下方沿直线走到点B，他与路灯C的距离y随他与点A之间的距离x的变化而变化．下列函数中y与x之间的变化关系，最有可能与上述情境类似的是（）A．y=x B．y=x+3C．y=3xD．y=（x-3）2+3第7题图8. 【导学号31100769】一个几何体的三视图如图所示，则该几何体的表面积为（）A．4π B．3πC．2π+4 D．3π+4第8题图第10题图9. 【导学号31100752】一个直角三角形的三条边分别为3，4，5，将这个三角形绕它的直角边所在直线旋转一周得到的几何体的体积是（）A．12π B．16πC．12π或16π D．36π或48π10. 【导学号31100742】如图是由一些完全相同的小正方体搭成的几何体的主视图和左视图，组成这个几何体的小正方体的个数最少是（）A．5个B．6个C．7个D．8个二、填空题（每小题4分，共32分）11. 【导学号31100759】把如图形状的硬纸板折成一个四棱锥，那么与E点重合在一起的是_____________.第11题图第12题图12. 【导学号31100996】如图是一个三棱柱，它的正投影是下图中的________（填序号）．13. 【导学号31100763】星期天，小明和小华在村后的小山岭上玩，突然，小明说“我捡到了一块非常好看的石头，它类似于我们刚学过的棱柱.”小华问：“几棱柱啊？”小明说：我说不上来，只知道它有9个面，14个顶点，21条棱.小华说：“我知道了，它是_______棱柱.”14. 【导学号31100957】图①是一个正方体的展开图，该正方体从图②所示的位置依次翻到第1格、第2格、第3格、第4格、第5格，此时这个正方体朝上一面的字是__________.①②第14题图15.【导学号31100751】如图，一块直角三角形板ABC，∠ACB=90°，BC=12cm，AC=8cm，测得BC边的中心投影B1C1长为24cm，则A1B1长为____________cm.第15题图第16题图16. 【导学号31100757】如图是由若干个棱长为1cm的小正方体堆砌而成的几何体，那么其三视图中面积最小的是_________cm217. 【导学号31100745】如图是一个几何体的三视图，已知左视图是一个等边三角形，根据图中尺寸（单位：cm），这个几何体的体积为__________cm3；表面积为__________cm2．第17题图第18题图18. 【导学号31100744】如图是一个由若干个正方体搭建而成的几何体的主视图与左视图，那么下列图形中可以作为该几何体的俯视图的序号是：_____________．三、解答题（共58分）19.【导学号31100741】（10分）画出下面几何体的三种视图.第19题图20.【导学号31100755】（12分）在一次数学活动课上，李老师带领学生去测教学楼的高度．在阳光下，测得身高1.65米的黄丽同学（ＢＣ）的影长ＢＡ为1.1米，与此同时，测得教学楼ＤＥ的影长ＤＦ为12.1米，如图．（１）请你在图中画出此时教学楼ＤＥ在阳光下的投影ＤＦ；（２）请你根据已测得的数据，求出教学楼ＤＥ的高度（精确到0.1米）．第20题图21.【导学号31100369】（12分）如图，某同学想测量旗杆的高度，他在某一时刻测得1ｍ长的竹竿竖直放置时影长为1.5ｍ，在同一时刻测量旗杆的影长时，因旗杆靠近一楼房，影子不全落在地面上，有一部分落在墙上，他测得落在地面上的影长为21ｍ，留在墙上的影高为2ｍ，求旗杆的高度．第21题图22.【导学号31100304】（12分）如图是一个包装纸盒的三视图（单位：cm）（1）该包装纸盒的几何形状是__________；（2）画出该纸盒的平面展开图．，精确到个位）（3）计算制作一个纸盒所需纸板的面积．（3 1.73第22题图23.【导学号31100879】（12分）如图，某光源下有三根杆子，甲杆GH的影子GM，乙杆EF的影子一部分是照在地面上的EA，一部分是照在斜坡AB上的AD．（1）请在图中画出形成影子的光线，确定光源所在的位置R，并画出丙杆PQ在地面上的影子．（2）在（1）的结论下，若过点F的光线FD⊥AB，斜坡与地面夹角为60°，AD=1米，AE=2米，请求出乙杆EF的高度．（结果保留根号）第23题图立体图形的展开与折叠综合测试题一、1.C 2.C 3.C 4.B 5.C 6.B 7.D 8.D 9.C 10.A二、11. A和C 12. ②13. 七14. 我15.81316. 3 17. 3318+2318. ①②③三、19. 解：20.解：（1）连接AC,过点E作EF∥AC交AD于点F，则DF即为所求，如图所示.第20题图（2）由题意，得1.121.165.1DE =，解得DE=18.15≈18.2．所以教学楼DE 的高度约为18.2米. 21.解：过C 作CE ⊥AB 于E ，如图.∵CD ⊥BD ，AB ⊥BD ，∴∠EBD=∠CDB=∠CEB=90°.∴四边形CDBE 为矩形，则BD=CE=21，CD=BE=2. 设AE=xm ，则1:1.5=x:21，解得x=14. 故旗杆高AB=AE+BE=14+2=16（m ）.第21题图第22题图22. 解：（1）正六棱柱（2）如图所示：（3）由图可知正六棱柱的侧面是边长为5的正方形，上、下底面是边长为5的正六边形，侧面面积：6×5×5=150（cm 2），底面积：2×6×21×5×235=753，制作一个纸盒所需纸板的面积：150753+≈280（cm 2）． 23. 解：（1）如图，QN 即为PQ 在地面的影子．（2）分别延长FD 、EA 交于点S.在Rt △ADS 中，∠ADS=90°，∠DAS=60°，所以∠S=30°. 又AD=1，∴AS=2.∴ES=AS+AE=2+2=4.在Rt △EFS 中，∠FES=90°，EF=ES•tan ∠FSE=4•tan30°=4×33＝433（米）．所以乙杆EF 的高度为433米.第23题图。

折叠几何综合专题---16道题目(含答案)

折叠几何综合专题---16道题目(含答案) -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN01如图，将矩形ABCD沿AF折叠，使点D落在BC边的点E 处，过点E作EG∥CD交AF于点G，连接DG.(1)求证：四边形EFDG是菱形；(2)探究线段EG，GF，AF之间的数量关系，并说明理由；(3)若AG＝6，EG＝25，求BE的长．(1)证明：由折叠性质可得，EF ＝FD ，∠AEF ＝∠ADF ＝90°，∠EFA ＝∠DFA ，EG ＝GD ，∵EG ∥DC ，∴∠DFA ＝∠EGF ， ∴∠EFA ＝∠EGF ，∴EF ＝EG ＝FD ＝GD ，∴四边形EFDG 是菱形；(2)解：EG 2＝12GF ·AF .理由如下：如解图，连接ED ，交AF 于点H ，∵四边形EFDG 是菱形，∴DE ⊥AF ，FH ＝GH ＝12GF ，EH ＝DH ＝12DE ， ∵∠FEH ＝90°－∠EFA ＝∠FAE ，∠FHE ＝∠AEF ＝90°， ∴Rt △FEH ∽Rt △FAE ，∴EFAF ＝FHEF ，即EF 2＝FH ·AF ，又∵FH ＝12GF ，EG ＝EF ，∴EG 2＝12GF ·AF ；(3)解：∵AG ＝6，EG ＝25，EG 2＝12AF ·GF ，∴(25)2＝12(6＋GF )·GF ，解得GF ＝4或GF ＝－10(舍)，∴GF ＝4，∴AF ＝10.∵DF ＝EG ＝25，∴AD ＝BC ＝AF 2－DF 2＝45，DE ＝2EH ＝2EG 2－（12GF ）2＝8，∵∠CDE ＋∠DFA ＝90°，∠DAF ＋∠DFA ＝90°，∴∠CDE ＝∠DAF ，∵∠DCE ＝∠ADF ＝90°，∴Rt △DCE ∽Rt △ADF ，∴EC DF ＝DE AF ，即EC 25＝810，∴EC ＝855，∴BE ＝BC －EC ＝1255.02如图，将矩形ABCD 沿对角线BD 对折，点C 落在E 处，BE 与AD 相交于点F ，若DE ＝4，BD ＝8.(1)求证：AF ＝EF ；(2)求证：BF 平分∠ABD .证明：(1)在矩形ABCD 中，AB ＝CD ，∠A ＝∠C ＝90°， ∵△BED 是△BCD 对折得到的，∴ED ＝CD ，∠E ＝∠C ，∴ED ＝AB ，∠E ＝∠A ，(2分)又∵∠AFB ＝∠EFD ，∴△ABF ≌△EDF (AAS)，∴AF ＝EF ；(4分)(2)在Rt △BCD 中，∵DC ＝DE ＝4，BD ＝8，∴sin ∠CBD ＝DC BD ＝12， ∴∠CBD ＝30°，(5分)∴∠EBD ＝∠CBD ＝30°，∴∠ABF＝90°－30°×2＝30°，(7分)∴∠ABF＝∠EBD，∴BF平分∠ABD.(8分)03把一张矩形ABCD纸片按如图方式折叠，使点A与点E重合，点C与点F 重合（E、F两点均在BD上），折痕分别为BH、DG。

北师大版七年级上册数学第二章《展开与折叠》单元综合测试卷(含答案)

北师大版七年级上册数学第二章《展开与折叠》单元综合测试卷（含答案）一、选择题(每题3分，共30分)1．如果温度上升3 ℃，记作＋3 ℃，那么温度下降2 ℃记作( ) A．－2 ℃ B．＋2 ℃ C．＋3 ℃ D．－3 ℃2．【2021·吉林】化简－(－1)的结果为( )A．－1 B．0 C．1 D．23．【2021·陕西】计算：3×(－2)＝( )A．1 B．－1 C．6 D．－64．【2020·湘西州】下列各数中，比－2小的数是( )A．0 B．－1 C．－3 D．35．【2020·绍兴】某自动控制器的芯片，可植入2 020 000 000粒晶体管，2 020 000 000这个数用科学记数法可表示为( )A．0.202×1010 B．2.02×109 C．20.2×108 D．2.02×108 6．【2020·枣庄】数a，b在数轴上对应点的位置如图所示，下列判断正确的是( )A．|a|＜1 B．ab＞0 C．a＋b＞0 D．1－a＞17．若a为有理数，则下列说法正确的是( )A．|a|一定是正数 B．|a|一定是负数C ．－|a |一定是负数D ．|a |＋1一定是正数 8．下列计算正确的是( )A ．⎝ ⎛⎭⎪⎫－78×15×⎝ ⎛⎭⎪⎫－117＝－⎝ ⎛⎭⎪⎫78×87×15＝－15B ．12×⎝ ⎛⎭⎪⎫13－14－1＝4－3－1＝0C ．(－9)×5×(－4)×0＝9×5×4＝180D ．(－5)×(－4)×(－2)×(－2)＝5×4×2×2＝809．【2020·包头】点A 在数轴上，点A 所对应的数用2a ＋1表示，且点A 到原点的距离等于3，则a 的值为( )A ．－2或1B ．－2或2C ．－2D ．110．【2021·镇江】如图，输入数值1 921，按所示的程序运算(完成一个方框内的运算后，把结果输入下一个方框继续进行运算)，输出的结果为( )A ．1 840B ．1 921C ．1 949D ．2 021 二、填空题(每题3分，共24分)11．－3的绝对值是________；－2 023的倒数是________．12．一只虫子从数轴上表示－3的点A 出发，沿着数轴正方向爬行了5个单位长度到达点B ，则点B 表示的数是________．13．用四舍五入法取近似数：2.952≈________(精确到0.1)． 14．如图是某市某一天的天气预报，则该天的温差是________℃.15．已知数a 在数轴上所对应的点在原点的左侧，且|a |＝2 023，则a ＝________．16．若x ，y 为有理数，且(5－x )4＋|y ＋5|＝0，则⎝ ⎛⎭⎪⎫x y 2 023＝________．17．定义一种新运算：对任意有理数a ，b 都有a ▽b ＝－a －b 2，例如：2▽3＝－2－32＝－11，则(2 022▽1) ▽2＝________．18．如图，某校园学子餐厅把WIFI 密码做成了数学题，小亮在餐厅就餐时，思索了一会儿，输入密码，顺利地连接到了学子餐厅的网络，那么他输入的密码是__________．三、解答题(19题16分，20题9分，21题7分，23题10分，其余每题12分，共66分)19．(1)【教材P 25随堂练习T 2改编】把下列各数填在相应的集合中：15，－12，0.81，－3，227，－3.1，－4，171，0，3.14，π，1.6·正数集合：{ …}；负分数集合：{ …}；非负整数集合：{ …}；有理数集合：{ …}． (2)在数轴上表示下列各数，并用“＜”将它们连接起来．－4，|－2.5|，－|3|，－112，－(－1)，020．计算：(1)－12＋20－(－2)＋(－3)；(2)－12022＋⎝⎛⎭⎪⎫－112－38＋712×(－24)；(3)(－2)3×⎣⎢⎡⎦⎥⎤－0.75＋⎝ ⎛⎭⎪⎫－38－|－3|2÷(－32)．21．【教材P 75复习题T 13变式】已知a ，b 互为相反数，c ，d 互为倒数，m 的绝对值为2，求a ＋ba ＋b ＋c＋m 2－cd 的值．22．【教材P 26习题T 6变式】某种水果的包装标准质量为每箱10 kg ，现抽取8箱样品进行检测，称重如下(单位：kg)：10.2，9.9，9.8，10.1，9.6，10.1，9.7，10.2.为了求得这8箱样品的总质量，我们可以选取一个恰当的基准质量进行简化运算．(1)你认为选取的这个恰当的基准质量为________kg；(2)根据你选取的基准质量，用正、负数填写下表；(3)这8箱样品的总质量是多少？23．如图，A，B，C三点在数轴上，点A表示的数为－10，点B表示的数为14，点C在点A与点B之间，且AC＝BC.(1)求点C表示的数；(2)甲、乙分别从A，B两点同时相向运动，甲的速度是每秒1个单位长度，乙的速度是每秒2个单位长度，求相遇点D表示的数．24．【教材P 76复习题T 26拓展】已知A ，B 两点在数轴上表示的数分别为m ，n . (1)对照数轴填写下表：(2)若将A ，B 两点之间的距离记为d ，试问d 与m ，n 有何数量关系？并用文字描述出来．(3)已知A ，B 两点在数轴上表示的数分别为x 和－1，则A ，B 两点之间的距离d 可表示为__________．如果d ＝3，求x 的值．参考答案一、1．A 2．C 3．D 4．C 5．B 6．D 7．D 8．D 9．A 10．D 二、11．3；－12 02312．2 13．3.0 14．10 15．－2 023 16．－1 17．2 019 18．143549三、19．解：(1)正数集合：{15，0.81，227，171，3.14，π，1.6·，…}；负分数集合：⎩⎨⎧⎭⎬⎫－12，－3.1，…；非负整数集合：{15，171，0，…}；有理数集合：{15，－12，0.81，－3，227，－3.1，－4，171，0，3.14，1.6·，…}．(2)|－2.5|＝2.5，－|3|＝－3，－(－1)＝1.在数轴上表示各数如图所示．故－4＜－|3|＜－112＜0＜－(－1)＜|－2.5|.20．解：(1)原式＝－12＋20＋2－3＝7；(2)原式＝－1＋⎝ ⎛⎭⎪⎫－32×(－24)＋⎝ ⎛⎭⎪⎫－38×(－24)＋712×(－24)＝－1＋36＋9－14＝30；(3)原式＝(－8)×⎝ ⎛⎭⎪⎫－34－38－9÷(－9)＝(－8)×⎝ ⎛⎭⎪⎫－98＋1＝10.21．解：由题意得a ＋b ＝0，cd ＝1，m ＝±2，所以m 2＝4.故a ＋b a ＋b ＋c ＋m 2－cd ＝00＋c＋4－1＝0＋4－1＝3. 22．解：(1)10(2)填表如下：(3)这8箱样品的总质量是10×8＋(0.2－0.1－0.2＋0.1－0.4＋0.1－0.3＋0.2)＝80－0.4＝79.6(kg)． 23．解：(1)|－10|＋|14|＝24，24÷2＝12，14－12＝2，故点C表示的数为2.(2)24÷(1＋2)×2＝16，16－14＝2.由于点D在原点左边，因此相遇点D表示的数为－2.24．解：(1)2；6；10；2；10；0(2)d＝|m－n|.数轴上两点之间的距离，等于这两点表示的数之差的绝对值．(3)|x－(－1)|当d＝3时，|x－(－1)|＝3，所以x＝2或x＝－4.。

五年级展开折叠练习题

五年级展开折叠练习题
五年级同学们，今天我们将进行展开折叠练习题。

这是一种既有趣
又有挑战性的练习，可以帮助你们提高空间想象能力和逻辑思维能力。

下面给出了一些练习题，希望你们能认真思考并找出正确答案。

1. 将一张正方形纸张从中间剪开，再将两片纸张叠叠在一起，用剪
刀一次剪一个圆孔。

展开纸张，你会看到什么图形？
2. 将一张长方形纸张按照一条边折叠，再将其打开。

这时，纸上会
出现什么图形？
3. 在一张正方形纸上，从一角向对角线方向对折两次，然后将纸的
两个角剪下。

展开纸张后，你会看到什么图形？
4. 如果将一个正方形纸张沿着对角线方向对折，然后再向中间对折，再将其打开，形成的图形是什么？
5. 将一张长方形纸张沿着宽度的方向对折，再展开，然后再沿着长
度的方向对折，再展开。

这时，纸张上会出现什么图形？
请你们以个体的形式完成练习题，并将你们的答案写在下面的空白处。

1. 答案：
展开后，你会看到两个同心圆。

2. 答案：
展开后，你会看到一条直线。

3. 答案：
展开后，你会看到一个正方形。

4. 答案：
展开后将会得到一个正方形和一个三角形。

5. 答案：
展开后，你会看到一条直线。

通过完成以上的练习题，你们应该对展开折叠有了更深入的理解。

展开折叠是一项培养空间想象能力和逻辑思维能力的重要活动，可以帮助你们解决实际生活中的问题。

继续努力，相信你们会在展开折叠这个领域中取得更大的成果！。

展开与折叠练习题

一、填空题1.棱柱中至少有_______个面的形状完全相同.2.如图所示棱柱（1）这个棱柱的底面是_______边形.（2）这个棱柱有_______个侧面，侧面的形状是_______边形.（3）侧面的个数与底面的边数_______.（填“相等”或“不相等”）（4）这个棱柱有_______条侧棱，一共有_______条棱.（5）如果CC′=3 cm，那么BB′=_______cm.二、判断题1. 棱柱是根据它总共有多少条棱来命名的. （）2.五棱柱中五条侧棱长度相同. （）3.三棱柱中底面三条边都相同. （）4. 长方体和正方体不是棱柱. （）三、剪一剪，折一折，然后选择正确答案1.下面图形不能围成一个长方体的是（）2.如果有一个正方体，它的展开图可能是下面四个展开图中的（）3．将一圆形纸片对折后再对折，得到图5，然后沿着图中的虚线剪开，得到两部分，其中一部分展开后的平面图形是 ( )A B CD图3图54、观察下列图形，其中不是．．正方体的展开图的为（）5.已知一个正方体的每一表面都填有唯一一个数字，且各相对表面上所填的数互为倒数. 若这个正方体的表面展开图如图2所示，则A 、B 的值分别是( ) A.13，12 B. 13，1 C. 12，13 D. 1，136、（2007四川乐山）图（3）为一个多面体的表面展开图，每个面内都标注了数字．若数字为3的面是底面，则朝上一面所标注的数字为（）Ａ．2 Ｂ．4 Ｃ．5 Ｄ．67、下列图形中，不是三棱柱的表面展开图的是( )．D8、如图是每个面上都标有一个汉字的正方体的平面展开图，在此正方体上与“水”字相对的面上的汉字是（）A ．“秀”B ．“丽”C ．“江”D ．“城”9回忆正方体表面展开图形口诀图2 AB CD 第5题图。

五年级数学展开与折叠试题

五年级数学展开与折叠试题1.据分析可知：当一个圆柱的底面周长和高相等时，展开这个圆柱的侧面，可以得到一个正方形( )A．B．C．D．【答案】C【解析】C图正确的是正方体展开图的“141”结构。

2.下面这个几何体的展开图形是( )A．B．C．D．【答案】D【解析】是正确的立方体展开图的“141”结构。

3.下面的图形是哪个图形的展开图？( )A.B.C.【答案】B【解析】由分析知：黑白点面相对，且两个阴影三角形面相邻，锐角端点相接。

4.下面是一个正方体的不同展开图，用相同符号标出了相对的面，不正确的是（）A．B．C．【答案】C【解析】C项中相同花纹的面相邻，而不是对面。

5.下面（）号图形是正方体的展开图．A．B．C．D．【答案】D【解析】选项D折叠后可以围成正方体，而A，B，C折叠后有两个面无法折起来，而且下边没有面，不能折成正方体。

6.下面图形折叠后能围成正方体的有（）A．B．C．【答案】C【解析】图A、图B不能围成正方体；图C纵着的四个正方形可以围成正方体的四个面，另外两个在这四正方形的两旁，能围成正方体的另外两个面，所以它能围成正方体。

7.如图是一个正方体的展开图，图上已经标出了正方体的上面和后面，那B的位置应该是正方体的（）面．A．前B．左C．右D．下【答案】A【解析】把这个正方体展开图折成正方体后，B面与后面相对，因此，判断B面是前面。

8.把一个底面半径是4厘米，高是5厘米的圆柱的侧面展开，得到一个长方形，这个长方形的长是______厘米，宽是______厘米。

【答案】25.12，5【解析】长是：2×3.14×4=25.12（厘米），宽是5厘米。

9.下图可以折成一个正方体，面1与面______相对；面2与面______相对。

【答案】3，6【解析】面1与面3相对；面2与面6相对。

10.下列各图中，哪几个是长方体表面的展开图？是的在括号内画“√”。

①②③（）（）（）④⑤（）（）【答案】①√；③√；⑤√【解析】②侧面是两个大的长方形相邻，两个小的长方形相邻；④有7个面，这与事实不符。