搜索顺序的选取与剪枝策略共43页文档
搜索剪枝常见方法与技巧

搜索剪枝常见方法与技巧关键字搜索方法,剪枝摘要搜索是计算机解题中常用的方法,它实质上是枚举法的应用。
由于它相当于枚举法,所以其效率是相当地的。
因此,为了提高搜索的效率,人们想出了很多剪枝的方法,如分枝定界,启发式搜索等等。
在竞赛中,我们不仅要熟练掌握这些方法,而且要因地制宜地运用一些技巧,以提高搜索的效率。
正文搜索的效率是很低的,即使剪枝再好,也无法弥补其在时间复杂度上的缺陷。
因此,在解题中,除非其他任何方法都行不通,才可采用搜索。
既然采用了搜索,剪枝就显得十分的必要,即使就简简单单的设一个槛值,或多加一两条判断,就可对搜索的效率产生惊人的影响。
例如N后问题,假如放完皇后再判断,则仅仅只算到7,就开始有停顿,到了8就已经超过了20秒,而如果边放边判断,就算到了10,也没有停顿的感觉。
所以,用搜索就一定要剪枝。
剪枝至少有两方面,一是从方法上剪枝,如采用分枝定界,启发式搜索等,适用范围比较广;二是使用一些小技巧,这类方法适用性虽不如第一类,有时甚至只能适用一道题,但也十分有效,并且几乎每道题都存在一些这样那样的剪枝技巧,只是每题有所不同而已。
问题一:(最短编号序列)表A和表B各含k(k<=20)个元素,元素编号从1到k。
两个表中的每个元素都是由0和1组成的字符串。
(不是空格)字符串的长度<=20。
例如下表的A和B两个表,每个表都含3个元素(k=3)。
表A 表B对于表A和表B,存在一个元素编号的序列2113,分别用表A中的字符串和表Array对表A和表B,具有上述性质的元素编号序列称之为S(AB)。
对于上例S(AB)=2113。
编写程序:从文件中读入表A和表B的各个元素,寻找一个长度最短的具有上述性质的元素编号序列S(AB)。
(若找不到长度<=100的编号序列,则输出“No Answer”。
对于这道题,因为表A和表B不确定,所以不可能找到一种数学的方法。
因为所求的是最优解,而深度优先搜索很容易进入一条死胡同而浪费时间,所以必须采用广度优先搜索的方法。
剪枝算法综述

剪枝算法综述
x
介绍
剪枝算法是一类从评价值最优化问题中获得最优解的算法,是机器学习和搜索引擎的重要基础,其结果可以用于优化计算机程序、算法以及计算机系统的性能。
它的本质是探索检索空间以找到最优解的方法。
剪枝算法的主要功能是消减搜索空间,通过消减搜索空间来获取最优解。
它通过对搜索树进行搜索,避免了在不必要的节点上浪费资源,最后得到更好的搜索效果。
剪枝算法分为两类。
一类是前剪枝算法,它的原理是在搜索树中寻找最佳点,在搜索到最佳点时,舍弃比它低的点,从而减小搜索空间;另一类是后剪枝算法,它的原理是在所有子树被访问完后,删除没有影响最终结果的节点,从而减小搜索空间。
剪枝算法的典型应用如下:
1.最优组合搜索:可以使用剪枝算法找出给定数据集中可能存在的最优解。
2.图像特征提取:可以使用剪枝算法从图像中提取最有价值的特征集合。
3.机器学习:可以使用剪枝算法减少模型的复杂度,从而提高模型的精度和效率。
剪枝算法具有计算效率高、性能优良以及易于实现等特点,广泛
应用于计算机科学中的优化问题处理中。
其结果可以有效提升计算机系统的性能,实现极致优化。
NOI导刊 搜索顺序的选取与剪枝策略

生日蛋糕(NOI99)
条件1:V = nπ
H=m层
形状:每层都是一个圆柱体。
条件2:
设从下往上数第i(1<=i<=m)层蛋糕是半径为Ri, 高度为Hi的圆柱。 当i<m时,要求Ri>Ri+1且Hi>Hi+1。 条件3:
表面积Q最小,令Q= Sπ
问题:
给出的n和m,
]
Else if Vi =0 then 更新最优值
• Problem-Cake
1. 计算MINi和MAXi R,H ; 2. for R1m to sqrt ( n ) do
/*假设 H1=1,只做一层蛋糕 */
3. for H1n div (R1*R1) downto m do [
4.
S1=2 * R1* H1+ R1* R1
mi
MINi k3 k1
因此,剪枝条件为, if Vi< MINi then exit
优化??
(3)如果剩下的蛋糕材料太多,以最大的方式做完m层, 仍有材 料剩余,那么没有必要继续往下做了,设, 第i+1层半径和高分别为,Ri+1 = Ri – 1 , Hi+1 = Hi –1 第i+2层半径和高分别为,Ri+2 = Ri – 2 , Hi+2 = Hi –2 ………… 第 m层半径和高分别为,Ri+m = Ri –m ,Hi+m= Hi –m 这样, 余下的m-i层的最大体积为
then exit; {剪枝1} {剪枝2} {剪枝3}
if i<m then
for Ri + 1 Ri downto i for Hi + 1min(Vi div (Ri + 1*Ri + 1), Hi) downto i [ Si + 1Si + 2 * Ri + 1* Hi + 1 Vi + 1Vi - Ri + 1* Ri + 1* Hi + 1 Search ( i+1, Ri + 1, Hi + 1, Si + 1,Vi + 1)
序列检索 剪枝算法

序列检索剪枝算法
序列检索是指在一组序列中查找特定序列的过程。
在很多实际应
用中,以及在机器学习和数据挖掘中,序列检索都是非常常见的问题。
然而,由于序列的数量很大,且搜索特定序列的复杂度很高,因此需
要使用剪枝算法来提高效率。
剪枝算法是一种在搜索中减少搜索空间的技术,其基本思想是根
据某些已知条件,排除一些不可能包含所需信息的部分,从而缩小搜
索的范围,减少搜索时间。
在序列检索中,剪枝算法可以通过比较特
定序列和已有序列的一些属性来判断特定序列是否存在,从而减少搜
索的次数和搜索的时间。
在实践中,剪枝算法有很多种,比如基于Pattern Growth的Apriori算法、基于封闭性的FP-Growth算法等等。
这些算法可以在不同的场景下实现不同的剪枝策略,从而提高搜索效率。
例如,Apriori
算法通过利用Apriori原则,每次只加入频繁项集的超集,来达到剪
枝的目的;而FP-Growth算法则是通过构建频繁模式树,减少了扫描
数据库的次数,从而加快了搜索速度。
综上所述,剪枝算法是序列检索中的一种重要技术,可以减少搜
索时间,提高搜索效率。
不同的剪枝策略可以根据具体的情况进行选择,以达到更好的效果。
商品搜索排序算法及其优化策略

商品搜索排序算法及其优化策略在当今电商快速发展的时代,搜索是电商网站的核心功能之一。
商品搜索是为了方便消费者快速找到所需商品而设计的,而搜索排序又是搜索的一个重要环节。
搜索排序的好坏直接影响消费者的购物体验和销售额,因此各大电商平台花费大量精力和资源优化商品搜索排序算法。
商品搜索排序原理商品搜索排序是根据搜索词、商品属性、消费者历史行为等多种因素参考排名的排序模式。
在搜索时,系统将搜索词与商品数据库匹配后,会按照某种规则组合相似度、销售量、价格、评价等信息进行排名。
排名越高的商品会被展示在搜索结果的前面,以此提升商品曝光度和点击率。
不同的电商平台可能会有自己的搜索排序算法,但总体来说,商品、用户、环境是影响排序的三个方面。
影响商品搜索排序的因素1. 商品属性商品属性直接影响排序效果。
平台会对商品信息进行标准化、SEO、评价、促销等多维度数据录入,进行排名。
属性中的品类、商户、价格、评论数、发货地等都会影响排序效果。
同时,在销量、收藏、浏览数等方面也会有所体现。
2. 用户行为用户行为也是排序中的一个重要因素。
平台会记录用户的登录情况、搜索历史、浏览过的商品等信息进行参考排序。
根据个人偏好进行相关性匹配的同时也增加了个性化推荐产品的可能性。
3. 环境因素环境因素包括了时间、地点、网络环境等。
如果用户搜索的商品与当前流行市场热度相似,那么搜索结果就会将相关商品展示在前面;不同的地区、时间、网络环境也会导致搜索排序的差异,这也是一种智能化的算法体现。
如何优化商品搜索排序1. 商品信息完整性商品完整、准确、鲜明的文案内容,对于搜索算法影响较大。
因此,平台会要求商家更多地提供商品信息,如商品简介、尺码表、材料等,提高商品信息的完整性。
2. 产品的质量与服务商品质量和服务也是消费者购物时非常关注的因素,过低的服务质量不仅会导致退货率增加,同时也会影响整体的店铺和产品评价排名,对店铺销量和口碑有一定的负面影响。
剪枝算法的搜索顺序

剪枝算法的搜索顺序剪枝算法是一种常用于解决搜索问题的算法,其核心思想是通过排除无效解,从而减少搜索空间的大小,从而提高搜索效率。
而在剪枝算法中,搜索顺序的选择对算法的性能和结果都有很大的影响。
本文将介绍剪枝算法的搜索顺序以及如何选择适合的搜索顺序。
一、剪枝算法概述剪枝算法是一种在搜索树上进行剪枝操作的算法,用于减少搜索空间的大小,从而节省搜索时间。
在进行搜索过程中,根据特定的剪枝条件,可以减少无效解的生成和判断。
这些剪枝条件可以基于问题的特征,也可以是启发式的。
二、搜索顺序的重要性搜索顺序决定了算法在搜索树上的遍历顺序。
不同的搜索顺序可能导致算法的效率和结果有很大的差异。
一个好的搜索顺序应当尽可能避免搜索无效解,提高搜索效率。
三、深度优先搜索深度优先搜索是一种常见的搜索顺序,其特点是沿着搜索树的深度方向先进行搜索。
在剪枝算法中,深度优先搜索可以方便地进行剪枝操作,因为在搜索的过程中会遇到大量的中间状态。
当遇到不满足剪枝条件的状态时,可以立即剪枝并进行回溯操作。
四、广度优先搜索广度优先搜索是另一种常见的搜索顺序,其特点是按层次逐层搜索。
在剪枝算法中,广度优先搜索无法很好地进行剪枝操作,因为搜索树的广度较大,难以判断无效解。
因此,在某些问题中,广度优先搜索可能不是最佳的选择。
五、启发式搜索启发式搜索是一种基于特定启发信息的搜索顺序,其目标是尽可能提高搜索效率。
启发式搜索常常利用问题本身的特征来进行剪枝,通过合适的搜索顺序能够更加快速地找到最优解。
例如,在旅行商问题中,可以优先访问距离当前位置最近的点。
六、选择适合的搜索顺序选择适合的搜索顺序需要根据问题的特点和需求进行判断。
对于剪枝算法,需要考虑剪枝条件的判断和剪枝操作的执行效率。
一般来说,启发式搜索可以较为准确地找到最优解,但其计算量较大。
深度优先搜索可以很好地进行剪枝操作,但可能错过最优解。
广度优先搜索则适用于某些特殊问题。
七、总结剪枝算法的搜索顺序对于算法的性能和结果有很大的影响。
搜索深度优先剪枝

定义 Hk 为队友需对第 k 号队员支援的高度, 对1号队员,H1 = 3;对2号队员,H2 = 2; 对3号队员,H3 = 1;4号队员不需他人支援,H4 = 0。 令 need(k) 表示 k 个人登山,保证 1人登顶所需给养; 令 take(k) 表示 k 个人登山共携带的给养; 令 d(k) 表示 k 个人一共差多少给养。 还是用图1的情况来说明上述参数的计算方法。 k = 1,让1号队员独自一人登山 need(1) = 2 * N = 2 * 4 = 8 take(1) = M = 5 d(1) = need(1) – take(1) = 8 – 5 = 3 1号队员如果单枪匹马登顶,缺3天给养, 因此需别人支援,要计算需队友支援的高度 H1 = d(1) / 1 = 3
take(k) d(k) 支援高度 说明 48 0 0 48 剪枝 剪枝 剪枝 剪枝 剪枝 25 7 3 33 11 3 剪枝 剪枝 剪枝
22
k 登山者 3 4 4 3 3 1#4#3# 1#4#3#5# 1#4#3#6# 1#4#5# 1#4#6#
2
编程要求:用键盘输入天数N(N<10)、俱乐部人 数P(P<10)之后,依次输入E[k]和M[k],k=1, 2, …, P, 分别输出两个登山组队计划, 计划1,要求参加登山的人数最少,在满足这一条 件之下消耗的总给养量最少。 计划2,要求消耗的总给养量最少。 输出的内容是:有多少队员参加登山,消耗的总 给养量,在出发时每人分别携带多少给养,每人分别 在出发几天后返回(几天后开始下山)。题目数据保 证有解。 【输入格式】第1行为2个小于10的整数N和P, 两个 整数之间有一个空格。第2行为P个整数,分别是 E[1],E[2],…,E[P], 相邻两整数之间有一个空格。第3行 为P个整数,分别是M[1],M[2],…,M[P], 相邻两整数之 间有一个空格。
搜索方法中的剪枝优化
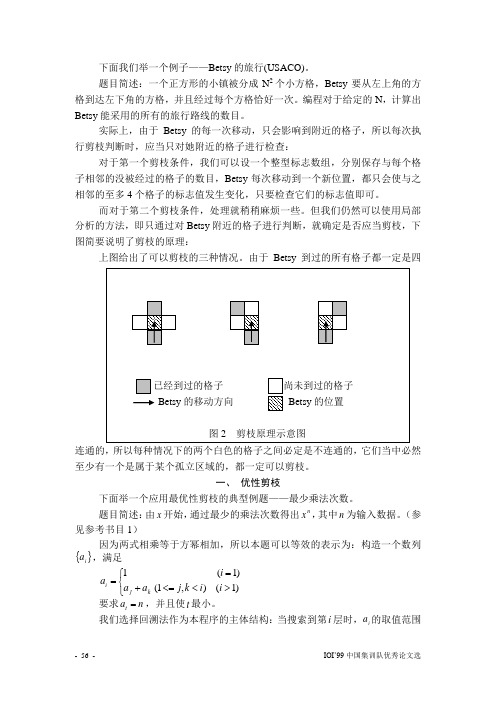
下面我们举一个例子——Betsy 的旅行(USACO)。
题目简述:一个正方形的小镇被分成N 2个小方格,Betsy 要从左上角的方格到达左下角的方格,并且经过每个方格恰好一次。
编程对于给定的N ,计算出Betsy 能采用的所有的旅行路线的数目。
实际上,由于Betsy 的每一次移动,只会影响到附近的格子,所以每次执行剪枝判断时,应当只对她附近的格子进行检查:对于第一个剪枝条件,我们可以设一个整型标志数组,分别保存与每个格子相邻的没被经过的格子的数目,Betsy 每次移动到一个新位置,都只会使与之相邻的至多4个格子的标志值发生变化,只要检查它们的标志值即可。
而对于第二个剪枝条件,处理就稍稍麻烦一些。
但我们仍然可以使用局部分析的方法,即只通过对Betsy 附近的格子进行判断,就确定是否应当剪枝,下图简要说明了剪枝的原理:上图给出了可以剪枝的三种情况。
由于Betsy 到过的所有格子都一定是四连通的,所以每种情况下的两个白色的格子之间必定是不连通的,它们当中必然至少有一个是属于某个孤立区域的,都一定可以剪枝。
一、 优性剪枝下面举一个应用最优性剪枝的典型例题——最少乘法次数。
题目简述:由x 开始,通过最少的乘法次数得出n x ,其中n 为输入数据。
(参见参考书目1)因为两式相乘等于方幂相加,所以本题可以等效的表示为:构造一个数列{}i a ,满足⎩⎨⎧><<=+==)1(),1()1(1i i k j a a i a k ji 要求n a t =,并且使t 最小。
我们选择回溯法作为本程序的主体结构:当搜索到第i 层时,i a 的取值范围搜索中的剪枝优化在11+-i a 到2*1-i a 之间,为了尽快接近目标n ,应当从2*1-i a 开始从大到小为i a 取值,当然,选取的数都不能大于n 。
当搜索到n 出现时,就得到了一个解,与当前保存的解比较取优。
最终搜索结束之后,即得到最终的最优解。
DFS(四):剪枝策略

DFS(四):剪枝策略顾名思义,剪枝就是通过⼀些判断,剪掉搜索树上不必要的⼦树。
在采⽤DFS算法搜索时,有时候我们会发现某个结点对应的⼦树的状态都不是我们要的结果,这时候我们没必要对这个分⽀进⾏搜索,砍掉这个⼦树,就是剪枝。
在DFS搜索算法中,剪枝策略就是寻找过滤条件,提前减少不必要的搜索路径。
应⽤剪枝策略的核⼼问题是设计剪枝判断⽅法,即确定哪些枝条应当舍弃,哪些枝条应当保留的⽅法。
剪枝策略按照其判断思路可⼤致分成两类:可⾏性剪枝及最优性剪枝。
1.可⾏性剪枝可⾏性剪枝就是把能够想到的不可能出现的情况给它剪掉。
该⽅法判断继续搜索能否得出答案,如果不能直接回溯。
【例1】Sum It Up (POJ 1564)DescriptionGiven a specified total t and a list of n integers, find all distinct sums using numbers from the list that add up to t. For example, if t = 4, n = 6, and the list is [4, 3, 2, 2, 1, 1], then there are four different sums that equal 4: 4, 3+1, 2+2, and 2+1+1. (A number can be used within a sum as many times as it appears in the list, and a single number counts as a sum.) Your job is to solve this problem in general.InputThe input will contain one or more test cases, one per line. Each test case contains t, the total, followed by n, the number of integers in the list, followed by n integers x 1 , . . . , x n . If n = 0 it signals the end of the input; otherwise, t will be a positive integer less than 1000, n will be an integer between 1 and 12 (inclusive), and x 1 , . . . , x n will be positive integers less than 100. All numbers will be separated by exactly one space. The numbers in each list appear in nonincreasing order, and there may be repetitions.OutputFor each test case, first output a line containing `Sums of', the total, and a colon. Then output each sum, one per line; if there are no sums, output the line `NONE'. The numbers within each sum must appear in nonincreasing order. A number may be repeated in the sum as many times as it was repeated in the original list. The sums themselves must be sorted in decreasing order based on the numbers appearing in the sum. In other words, the sums must be sorted by their first number; sums with the same first number must be sorted by their second number; sums with the same first two numbers must be sorted by their third number; and so on. Within each test case, all sums must be distinct; the same sum cannot appear twice.Sample Input4 6 4 3 2 2 1 15 3 2 1 1400 12 50 50 50 50 50 50 25 25 25 25 25 250 0Sample OutputSums of 4:43+12+22+1+1Sums of 5:NONESums of 400:50+50+50+50+50+50+25+25+25+2550+50+50+50+50+25+25+25+25+25+25(1)编程思路。
c语言技巧之搜索剪枝

搜索问题计算机学院2006级师范班程文华搜索被称为“通用的解题法”,在算法和人工智能方面占有非常重要的低位,特别是在各类ACM程序设计比赛中非常常见,在题目中一般位于中间位置,作为中等难度的题目出现。
因此我们需要着重掌握各类的搜索算法,才能面对各类即将到来的ACM大赛。
“只要功夫深,铁棒磨成针”,“冰冻三尺,非一日之寒”,要能熟练的掌握和AC比赛中的题目,必须在熟练掌握各类搜索算法的基础上勤加练题,也是唯一的好方法。
本次讲解中,首先给出有关搜索的基本概念,然后针对各类专题,讲解具体的几个例题并加于分析(注:题目全部选自poj中的题目)。
一概念介绍状态(state)问题在某一时刻的进展情况的数学描述。
算符(operator)/ 状态转移问题从一种状态变换成另一种(或几种)状态的操作。
解答树搜索的过程实际是在遍历一个图,它的结点就是所有的状态,有向边对应于算符,而一个可行解就是一条从起始节点出发到目标状态集中任意一个结点的路径。
特个图称为状态空间(state space),这样的搜索称为状态空间搜索(Single-Agent Search),得到的遍历树称为解答数。
基本搜索法:枚举枚举法的基本思想是根据提出的问题枚举所有可能状态,并用问题给定的条件检验哪些是需要的,哪些是不需要的。
能使命题成立,即为其解。
枚举算法的特点比较单纯,往往容易写出程序,也容易证明算法的正确性和分析算法的时间复杂度,可以解决一些很小的问题。
它的缺点是效率特别低,往往很多题目不能用枚举方法,用了只会超时。
所以它适应于容易找到状态并且状态较少的题目。
没有信心确定其状态较少,请勿立即动手写程序!深度优先搜索DFS(有时称为回溯法)遵循的搜索策略是尽可能深地搜索图,在深度优先搜索中,对于最新发现的顶点,如果它还有以此为起点而未探索到的边,就沿此边继续搜索下去。
当结点V的所有边都已被探寻过时,搜索将回溯到发现结点V有那条边的始结点。
这一过程一直进行到已发现从源结点可达的所有结点为止。
搜索顺序的选取与剪枝策略45页PPT

41、学问是异常珍贵的东西,从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
42、只有在人群中间,才能认识自 己。——德国
43、重复别人所说的话,只需要教育; 而要挑战别人所说的话,则需要头脑。—— 玛丽·佩蒂博恩·普尔
搜索顺序的选取与剪枝策略
1、纪律是管理关系的形式。——阿法 纳西耶 夫 ห้องสมุดไป่ตู้、改革如果不讲纪律,就难以成功。
3、道德行为训练,不是通过语言影响 ,而是 让儿童 练习良 好道德 行为, 克服懒 惰、轻 率、不 守纪律 、颓废 等不良 行为。 4、学校没有纪律便如磨房里没有水。 ——夸 美纽斯
5、教导儿童服从真理、服从集体,养 成儿童 自觉的 纪律性 ,这是 儿童道 德教育 最重要 的部分 。—— 陈鹤琴
44、卓越的人一大优点是:在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自己知道。——苏联
深搜的剪枝技巧

深搜的剪枝技巧⾸先是深搜的模板:int ans = 最坏情况, now; // now为当前答案void dfs(传⼊数值) {if (到达⽬的地) ans = 从当前解与已有解中选最优;for (遍历所有可能性)if (可⾏) {进⾏操作;dfs(缩⼩规模);撤回操作;}}1.剪枝的概念:实际上,对于搜索,其实就是⼀棵树:(树丑,莫要介意)那么对于没有剪枝的dfs,需要搜索整棵树,⽽剪枝,就是将其中⼀部分枝⼲减掉,使时间复杂度降低。
2.剪枝的原则:三个原则:正确性(这是剪枝优化的前提),准确性,⾼效性;3.深搜的优化技巧:1. 优化搜索顺序2. 排除等效冗杂3. 记忆化4. 最优性剪枝5. 可⾏性剪枝1.优化搜索顺序:不同的搜索顺序会产⽣不同的搜索树形态,其规模⼤⼩也相差甚远2.排除等效冗杂:在搜索中,若我们发现沿某⼏条线路所达到的效果是⼀样的,那么我们可以只搜索其中的⼀条3.记忆化:是啥?:不依赖任何外部变量答案以返回值的形式存在,⽽不能以参数的形式存在(就是不能将 dfs 定义成这⾥⾯的 nowans 不符合要求)。
对于相同⼀组参数,dfs 返回值总是相同的模板:int g[MAXN]; //定义记忆化数组int ans = 最坏情况, now;void dfs f(传⼊数值) {if (g[规模] != ⽆效数值) return; //或记录解,视情况⽽定if (到达⽬的地) ans = 从当前解与已有解中选最优; //输出解,视情况⽽定for (遍历所有可能性)if (可⾏) {进⾏操作;dfs(缩⼩规模);撤回操作;}}int main() {... memset(g, ⽆效数值, sizeof(g)); //初始化记忆化数组...}4.最优性剪枝:在搜索中导致运⾏慢的原因还有⼀种,就是在当前解已经⽐已有解差时仍然在搜索,那么我们只需要判断⼀下当前解是否已经差于已有解。
模板:int ans = 最坏情况, now;void dfs(传⼊数值) {if (now⽐ans的答案还要差) return;if (到达⽬的地) ans = 从当前解与已有解中选最优;for (遍历所有可能性)if (可⾏) {进⾏操作;dfs(缩⼩规模);撤回操作;}}5.可⾏性剪枝:在搜索中如果当前解已经不可⽤了还运⾏,也是在搜索中导致运⾏慢的原因。
搜索方法中的剪枝优化

搜索方法中的剪枝优化一、引子搜索是人工智能中的一种基本方法,也是信息学竞赛选手所必须熟练掌握的一种方法。
我们在建立一个搜索算法的时候,首要的问题不外乎两个:1. 建立算法结构。
2. 选择适当的数据结构。
然而众所周知的是,搜索方法的时间复杂度大多是指数级的,简单的不加优化的搜索,其时间效率往往低的不能忍受,更是难以应付信息学竞赛严格的运行时间限制。
本文所讨论的主要内容就是在建立算法的结构之后,对程序进行优化的一种基本方法——剪枝。
图1 搜索树首先应当明确的是,“剪枝”的含义是什么。
我们知道,搜索的进程可以看作是从树根出发,遍历一棵倒置的树——搜索树的过程。
而所谓剪枝,顾名思义,就是通过某种判断,避免一些不必要的遍历过程,形象的说,就是剪去了搜索树中的某些“枝条”,故称剪枝。
我们在编写搜索程序的时候,一般都要考虑到剪枝。
显而易见,应用剪枝优化的核心问题是设计剪枝判断方法,即确定哪些枝条应当舍弃,哪些枝条应当保留的方法。
设计出好的剪枝判断方法,往往能够使程序的运行时间大大缩短;否则,也可能适得其反。
那么,我们就应当首先分析一下设计剪枝判断方法的时候,需要遵循的一些原则。
二、剪枝的原则原则之一:正确性。
我们知道,剪枝方法之所以能够优化程序的执行效率,正如前文所述,是因为它能够“剪去”搜索树中的一些“枝条”。
然而,如果在剪枝的时候,将“长有”我们所需要的解的枝条也剪掉了,那么,一切优化也就都失去了意义。
所以,对剪枝的第一个要求就是正确性,即必须保证不丢失正确的结果,这是剪枝优化的前提。
为了满足这个原则,我们就应当利用“必要条件”来进行剪枝判断。
也就是说,通过解所必须具备的特征、必须满足的条件等方面来考察待判断的枝条能否被剪枝。
这样,就可以保证所剪掉的枝条一定不是正解所在的枝条。
当然,由必要条件的定义,我们知道,没有被剪枝不意味着一定可以得到正解(否则,也就不必搜索了)。
原则之二:准确性。
在保证了正确性的基础上,对剪枝判断的第二个要求就是准确性,即能够尽可能多的剪去不能通向正解的枝条。
搜索深度优先剪枝PPT文档共53页

41、实际上,我们想要的不是针对犯 罪的法 律,而 是针对 疯狂的 法律。 ——马 克·吐温 42、法律的力量应当跟随着公民,就 像影子 跟随着 身体一 样。— —贝卡 利亚 43、法律和制度必须跟上人类思想进 步。— —杰弗 逊 44、人类受制于法律,法律受制于情 理。— —托·富 勒
23、一切节省,归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰,决心到最后会全部推倒。——莎士比亚
25、学习是劳动,是充满思想的劳动。——乌申斯基
谢谢!
45、法律的制定是为了保证每一个人 自由发 挥自己 的才能 ,而不 是为了 束缚他 的才能 。——们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
序列检索 剪枝算法

序列检索剪枝算法
序列检索是一种在序列数据库中查找指定序列的有效方法。
由于序列数据库中的数据量很大,因此需要一些剪枝算法来加快检索速度。
剪枝算法基于一些预处理步骤,可以减少需要搜索的序列数量,并且在搜索过程中尽早舍弃不可能包含查询序列的序列。
目前,许多剪枝算法已经被提出来,包括简单排序剪枝算法、动态距离剪枝算法、基于位置相关剪枝算法等。
这些算法使用了不同的策略来减少搜索空间,并且基于不同的前提假设,有些算法可能适用于某些序列类型,而不适用于其他序列类型。
简单排序剪枝算法是一种基于序列相似度的剪枝算法。
该算法首先对序列进行排序,然后搜索与查询序列相似度高的序列。
由于排序本身需要时间和空间,因此该算法在处理大型序列数据库时可能效率较低。
动态距离剪枝算法是一种基于动态距离阈值的剪枝算法。
该算法根据查询序列的长度和动态距离阈值计算可能包含查询序列的序列。
如果搜索过程中发现一个序列的距离超过了阈值,则可以舍弃该序列并继续搜索其他序列。
基于位置相关剪枝算法是一种基于位置相关性的剪枝算法。
该算法假设序列中的不同部分具有不同的重要性,并且查询序列的部分在数据库序列中的位置也很重要。
该算法首先计算查询序列的位置相关性,然后对可能包含查询序列的序列进行排序。
在搜索过程中,该算法能够尽早舍弃不可能包含查询序列的序列。
总之,剪枝算法是序列检索中的重要技术,它可以减少搜索空间并提高检索效率。
不同的剪枝算法基于不同的前提假设和策略,应根据具体情况选择适当的算法。
