矢量.ppt
合集下载
矢量地图信息图表PPT模板-(01)
pleasure and praising pain was…
辽宁地图
YOUR LOCATION
But I must explain to you how all this mistaken idea of denouncing
pleasure and praising pain was…
湖南地图
海南地图
YOUR LOCATION
But I must explain to you how all this mistaken idea of denouncing
pleasure and praising pain was…
四川地图
YOUR LOCATION
But I must explain to you how all this mistaken idea of denouncing
张家口市
承德市
秦皇岛市 唐山市
廊坊市
保定市
沧州市
衡水市 石家庄市
邢台市 邯郸市
江苏地图
YOUR LOCATION
But I must explain to you how all this mistaken idea of denouncing
pleasure and praising pain was…
pleasure and praising pain was…
大同市 朔州市
忻州市
太原市
阳泉市
吕梁市
晋中市
临汾市 运城市
长治市 晋城市
宁夏地图
YOUR LOCATION
But I must explain to you how all this mistaken idea of denouncing
辽宁地图
YOUR LOCATION
But I must explain to you how all this mistaken idea of denouncing
pleasure and praising pain was…
湖南地图
海南地图
YOUR LOCATION
But I must explain to you how all this mistaken idea of denouncing
pleasure and praising pain was…
四川地图
YOUR LOCATION
But I must explain to you how all this mistaken idea of denouncing
张家口市
承德市
秦皇岛市 唐山市
廊坊市
保定市
沧州市
衡水市 石家庄市
邢台市 邯郸市
江苏地图
YOUR LOCATION
But I must explain to you how all this mistaken idea of denouncing
pleasure and praising pain was…
pleasure and praising pain was…
大同市 朔州市
忻州市
太原市
阳泉市
吕梁市
晋中市
临汾市 运城市
长治市 晋城市
宁夏地图
YOUR LOCATION
But I must explain to you how all this mistaken idea of denouncing
山东省矢量地图动态PPT模板(图文)

山东是儒家文化发源地,儒家思想的创立人有曲阜的孔子、邹城的孟子,以及墨家思想的创始人滕州的墨子、军事 家孙子等,均出生于今山东。姜太公在临淄建立齐国,成就了齐桓公、管仲、晏婴、鲍叔牙、孙武、孙膑、邹衍等 一大批名人志士;齐国还创建了世界上第一所官方举办、私家主持的高等学府——稷下学宫PPT模板
矢量素材 ︱可以编辑︱精美大气︱框架完整
矢量素材 ︱可以编辑
中 国 地 图
新疆 西藏
黑龙江
吉林
甘肃 青海
内蒙古
宁夏
北京
天津
河北
山西
山东
辽宁
陕西 河南
江苏
四川
云南
贵州 广西
湖北 湖南
安徽 上海
江西
浙江
福建
广东
海南
【选中地图】-【右键】-【组合】-【取消组合】,可对地图进行任意的拆分
新疆 西藏
黑龙江
吉林
甘肃 青海
内蒙古
辽宁
北京
天津
河北
宁 夏
山西
山东
四川 云南
陕西 河南
江苏
重庆
湖北
安徽
上海
浙江
贵州
湖南
江西 福建
钓鱼岛
台
广西
广东
湾
海南
香港 澳门
矢量素材 ︱可以编辑
山 东 省
德州市
滨州市
东营市
聊城市
济南市
淄博市
莱芜市 泰安市
潍坊市
菏泽市
济宁市 枣庄市
临沂市
日照市
【选中地图】-【右键】-【组合】-【取消组合】,可对地图进行任意的拆分
济宁市
任城区 微山县 鱼台县 金乡县 嘉祥县 汶上县 泗水县 梁山县 曲阜市 兖州区 邹城市
矢量素材 ︱可以编辑︱精美大气︱框架完整
矢量素材 ︱可以编辑
中 国 地 图
新疆 西藏
黑龙江
吉林
甘肃 青海
内蒙古
宁夏
北京
天津
河北
山西
山东
辽宁
陕西 河南
江苏
四川
云南
贵州 广西
湖北 湖南
安徽 上海
江西
浙江
福建
广东
海南
【选中地图】-【右键】-【组合】-【取消组合】,可对地图进行任意的拆分
新疆 西藏
黑龙江
吉林
甘肃 青海
内蒙古
辽宁
北京
天津
河北
宁 夏
山西
山东
四川 云南
陕西 河南
江苏
重庆
湖北
安徽
上海
浙江
贵州
湖南
江西 福建
钓鱼岛
台
广西
广东
湾
海南
香港 澳门
矢量素材 ︱可以编辑
山 东 省
德州市
滨州市
东营市
聊城市
济南市
淄博市
莱芜市 泰安市
潍坊市
菏泽市
济宁市 枣庄市
临沂市
日照市
【选中地图】-【右键】-【组合】-【取消组合】,可对地图进行任意的拆分
济宁市
任城区 微山县 鱼台县 金乡县 嘉祥县 汶上县 泗水县 梁山县 曲阜市 兖州区 邹城市
《Stokes矢量》课件

在量子光学中的应用
总结词
Stokes矢量在量子光学中用于描述光子 的偏振状态,是量子通信和量子计算中 的重要工具。
VS
详细描述
在量子光学中,光子的偏振状态是其量子 态的重要特征之一。Stokes矢量可以用于 描述光子的偏振态,从而在量子通信和量 子计算中实现精确的量子态操控。例如, 利用Stokes矢量可以制备具有特定偏振态 的光子,用于量子密钥分发、量子隐形传 态等量子通信协议。此外,在量子计算中 ,Stokes矢量还可以用于实现量子比特的 逻辑门操作和量子算法的执行。
《Stokes矢量》PPT 课件
目 录
• Stokes矢量定义 • Stokes矢量的性质 • Stokes矢量在光学中的应用 • Stokes矢量的测量技术 • Stokes矢量的应用前景
01
Stokes矢量定义
Stokes矢量的物理意义
描述光的偏振状态
Stokes矢量包含了光的四个偏振 态信息,可以全面描述光的偏振 状态。
03
Stokes矢量在光学中 的应用
描述光的偏振状态
总结词
Stokes矢量可以用来描述光的偏振状态,包括线偏振、椭圆偏振和圆偏振等。
详细描述
Stokes矢量由四个分量组成,可以用来描述光的偏振态。通过测量这四个分量 ,可以得到光的偏振状态,包括线偏振、椭圆偏振和圆偏振等。这些偏振态在 光学实验和工程中有广泛的应用。
光学测量
Stokes矢量可以用于测量光学元件的偏振特性, 如偏振片、波片和晶体等。
光学通信
在光纤通信中,Stokes矢量可以用于描述光的偏 振态,提高通信的可靠性和稳定性。
生物医学成像
在生物医学成像中,Stokes矢量可以用于描述光 的偏振态,提高成像的质量和分辨率。
矢量地图信息图表PPT模板-(12)

Female
Features Slides
Canada Map
Population
Lorem ipsum dolor sit amet, consectetur adipiscing elit. In in tortor in urna pulvinar blandit. Aliquam dolor nulla, interdum non quam ac, ultricies porttitor tellus. Vivamus vitae vestibulum mauris. In ut congue arcu. In lectus nibh, ultricies a elit ac, laoreet dictum nulla. Proin sed nisi justo. Cras quis placerat ipsum.
Paris Bordeaux Toulouse Marseille
45% 67% 35% 86%
Features Slides
Scandanavia Vector Map
POPULATION
93% Lorem ipsum dolor sit amet, consectetur adipiscing elit. Aliquam tincidunt ante nec sem congue convallis.
Help
Lorem ipsum dolor sit amet, consectetur adipiscing elit.
Design
Lorem ipsum dolor sit amet, consectetur adipiscing elit.
Features Slides
SEA - South East Asia
01 第一章 矢量分析

t t0
⑴极限:设 F (t ) 在点 t 0 的某个邻域内有定义(但在 t 0 点
则称,当 t t0
⑵连续:若矢性函数 F (t )在点 t 0 的某个邻域内有定义,且 lim F t F t0 t t0 则称F (t ) 在 t t0 处连续。
(x)
ui
2
(
2 y 2 ) ( z ) ui ui
4、拉梅系数的几何意义
u i 线上的弧微分
x 2 y 2 z 2 dli ( ) ( ) ( ) dui hi dui ui ui ui
dli hi dui
表明:拉梅系数hi是M点处曲线坐标ui的微分dui与该坐标线ui 上弧微分的比例系数。
r(M )
hi
根据全微分运算法则
r r r dl d r du1 du 2 du3 u1 u2 u3
y 矢量线元
引入拉梅系数,矢量线元表示为
图1-7
dl h1du1e1 h2 du2 e2 h3 du3e3 dl1e1 dl2 e2 dl3 e3
2、拉梅系数
空间任意一点 M (u1 , u 2 , u 3 ) ,矢径
若M点在 u1 线上,则矢径 于是,单位矢量表示为
r e1 u1 r u1
r r (u1 , u 2 , u3 )
r (u1 , u 2 c2 , u3 c3 )
M
F (t )
说明:矢径函数对其矢端曲线弧长的导数为曲线上的单位矢量。
3、积分
⑴不定积分:若 A(t ) F (t ) ,则称 A(t )为 F (t )的一个原函数, F (t ) 的原函数的集合叫做的F (t ) 不定积分,记作 )d t A(t ) C F (t ⑵定积分:若矢性函数 F (t ) 在区间 [T1 , T2 ]上的极限
⑴极限:设 F (t ) 在点 t 0 的某个邻域内有定义(但在 t 0 点
则称,当 t t0
⑵连续:若矢性函数 F (t )在点 t 0 的某个邻域内有定义,且 lim F t F t0 t t0 则称F (t ) 在 t t0 处连续。
(x)
ui
2
(
2 y 2 ) ( z ) ui ui
4、拉梅系数的几何意义
u i 线上的弧微分
x 2 y 2 z 2 dli ( ) ( ) ( ) dui hi dui ui ui ui
dli hi dui
表明:拉梅系数hi是M点处曲线坐标ui的微分dui与该坐标线ui 上弧微分的比例系数。
r(M )
hi
根据全微分运算法则
r r r dl d r du1 du 2 du3 u1 u2 u3
y 矢量线元
引入拉梅系数,矢量线元表示为
图1-7
dl h1du1e1 h2 du2 e2 h3 du3e3 dl1e1 dl2 e2 dl3 e3
2、拉梅系数
空间任意一点 M (u1 , u 2 , u 3 ) ,矢径
若M点在 u1 线上,则矢径 于是,单位矢量表示为
r e1 u1 r u1
r r (u1 , u 2 , u3 )
r (u1 , u 2 c2 , u3 c3 )
M
F (t )
说明:矢径函数对其矢端曲线弧长的导数为曲线上的单位矢量。
3、积分
⑴不定积分:若 A(t ) F (t ) ,则称 A(t )为 F (t )的一个原函数, F (t ) 的原函数的集合叫做的F (t ) 不定积分,记作 )d t A(t ) C F (t ⑵定积分:若矢性函数 F (t ) 在区间 [T1 , T2 ]上的极限
矢量场与标量场以及计算方法PPT课件

场: 如果在某一空间区域内的每一点,都对应着某个物理量 的一个确定的值,则称在此区域内确定了该物理量的一个场。
换句话说, 在某一空间区域中,物理量的无穷集合表示 一种场。如在教室中温度的分布确定了一个温度场,在空间电 位的分布确定了一个电位场。(物理量的值可相等)
场的一个重要的属性是它占有一定空间,而且在该空间
•终点一般称为矢性函数A(t)的矢端曲线。
第3页/共60页
z
Z
P(X, Y, Z)
r
Aazz Aaxx O
Y Aayy
y
X
x
图1-1 直角坐标系中一点的投影
第4页/共60页
02. 矢量的乘积
•矢量的乘积包括标量积和矢量积。
1) 标量积
任意两个矢量A与B的标量积
(Scalar Product)是一个标量,
第28页/共60页
2. 旋度
设 A ex Ax ey Ay ez Az dl exdx eydy ezdz
得
A dl
L
L ( Axdx Aydy Azdz)
s
(
Az y
Ay z
)dydz
(Ax z
Az x
)dzdx (Ay x
Ax y
)dxdy
•上式右面的积分可以看成是矢量
M为S中的某一点,令 向S p点收缩,则
有旋度定义的极限形式:
第30页/共60页
rotn
A
=
lim
S 0
l A dl lim d
S
S0 S ds
由此可见, rotnA表示矢量场A在P点的环量密度,它与该 点的曲面元的法线方向有关。当旋度rotA与n的方向相同时, 环量密度取得最大值。
换句话说, 在某一空间区域中,物理量的无穷集合表示 一种场。如在教室中温度的分布确定了一个温度场,在空间电 位的分布确定了一个电位场。(物理量的值可相等)
场的一个重要的属性是它占有一定空间,而且在该空间
•终点一般称为矢性函数A(t)的矢端曲线。
第3页/共60页
z
Z
P(X, Y, Z)
r
Aazz Aaxx O
Y Aayy
y
X
x
图1-1 直角坐标系中一点的投影
第4页/共60页
02. 矢量的乘积
•矢量的乘积包括标量积和矢量积。
1) 标量积
任意两个矢量A与B的标量积
(Scalar Product)是一个标量,
第28页/共60页
2. 旋度
设 A ex Ax ey Ay ez Az dl exdx eydy ezdz
得
A dl
L
L ( Axdx Aydy Azdz)
s
(
Az y
Ay z
)dydz
(Ax z
Az x
)dzdx (Ay x
Ax y
)dxdy
•上式右面的积分可以看成是矢量
M为S中的某一点,令 向S p点收缩,则
有旋度定义的极限形式:
第30页/共60页
rotn
A
=
lim
S 0
l A dl lim d
S
S0 S ds
由此可见, rotnA表示矢量场A在P点的环量密度,它与该 点的曲面元的法线方向有关。当旋度rotA与n的方向相同时, 环量密度取得最大值。
矢量分析课件2-56页文档资料

数.
lz l
l x o
l
ly y
cosl x,cosl y,cosl z
x
l
l
l
第二章 场论
§2 数量场的方向导数和梯度
例4 求函数 u x2在y点2z2 处沿M(1,0,1)
li2j2k
方向的方向导数.
解: u x , u y , u z x x 2 y 2 z 2 y x 2 y 2 z 2 z x 2 y 2 z 2
通过点 M(2,的1,1矢)量线方程。
解: 矢量场满足的微分方程为
dxdy dz xz yz (x2y2)
由 dx dy xz yz
y C1x
由
dy yz
dz (x2
y2)
x2y2z2C2
第二章 场论
§1 场
M(2,1,1)
C1
1 2
y C1x x2y2z2C2
C2 6
所以过点 M(2,的1,1矢) 量线方程为:
的l 方向余弦为: co s1,co s2,co s2
3
3
3
则 uuco suco sucos
l x
y
z
u x 1 y 2 z 2 l x 2 y 2 z 23 x 2 y 2 z 23 x 2 y 2 z 23
u 1 l M 2
第二章 场论
§2 数量场的方向导数和梯度
二、梯度 u
u
l2
u l1
uuco suco suco l3 s
l x
y
z
uG l 0G coG s,l (0) l
l 0 co i c so j c so k
G uiu juk
x y z
当 coG ,sl0 ()1,即 l 方向与 G 方向一致.
lz l
l x o
l
ly y
cosl x,cosl y,cosl z
x
l
l
l
第二章 场论
§2 数量场的方向导数和梯度
例4 求函数 u x2在y点2z2 处沿M(1,0,1)
li2j2k
方向的方向导数.
解: u x , u y , u z x x 2 y 2 z 2 y x 2 y 2 z 2 z x 2 y 2 z 2
通过点 M(2,的1,1矢)量线方程。
解: 矢量场满足的微分方程为
dxdy dz xz yz (x2y2)
由 dx dy xz yz
y C1x
由
dy yz
dz (x2
y2)
x2y2z2C2
第二章 场论
§1 场
M(2,1,1)
C1
1 2
y C1x x2y2z2C2
C2 6
所以过点 M(2,的1,1矢) 量线方程为:
的l 方向余弦为: co s1,co s2,co s2
3
3
3
则 uuco suco sucos
l x
y
z
u x 1 y 2 z 2 l x 2 y 2 z 23 x 2 y 2 z 23 x 2 y 2 z 23
u 1 l M 2
第二章 场论
§2 数量场的方向导数和梯度
二、梯度 u
u
l2
u l1
uuco suco suco l3 s
l x
y
z
uG l 0G coG s,l (0) l
l 0 co i c so j c so k
G uiu juk
x y z
当 coG ,sl0 ()1,即 l 方向与 G 方向一致.
CAGD中矢量、点与直线PPT(35张)

曲面的参数化
• 曲面上一点的u线与v线 • 曲面的u向切矢与v向切矢 • 曲面上一点的单位法矢 • 曲面的等距面
曲线曲面的几何不变性
• 概念
– 曲线曲面的数学表示及其所表达的形状不依赖于坐标 系
• 规范基表示具有几何不变性,仅需将原表示中的 系数矢量作相同的坐标变换即可获得变换后的曲 线与曲面
• 部分规范基表示具有几何不变性,需将原表示中 的绝对系数矢量作相同的坐标变换,而相对矢量 仅作旋转变换
程符合直纹面的形成规律,可以准确保证母线的直线度。 • 方案c为环切法,一般用于加工内槽。在加工螺旋桨叶片时,采用由
里到外的环切,刀具切削部位受毛坯刚性边框的支持,有利于减少工 件在加工中的变形。
脉冲当量
数控机床的数控系统发出一个脉冲指令后,经伺服系统的 转换、放大、反馈后推动数控机床上的工件(或刀具)实际移 动的位移量叫做数控机床的最小设定单位,又称最小指令增 量或脉冲当量。简言之即为每个脉冲信号所产生的机床移动 部件的位移量称为脉冲当量。常用的脉冲当量为0.01mm/ 脉冲、0.005mm/脉冲以及0.001mm/脉冲,视不同档次的 机床而选定。
选择走刀路线
走刀路线是指数控加工中刀位点相对于被加工工件的运动轨迹。 确定走刀路线的原则是: • 保证零件的加工精度和光洁度; • 方便数值计算,减少编程工作量; • 缩短走刀路线,减少空程; • 尽量减少程序段数。
选择走刀路线
• 方案a优点是便于加工后检验翼型的精度 • 方案b的优点是每次按直线走刀,刀位点计算简单,程序短;加工过
点位控制机床
这类机床的数控装置只能控制刀具从一个位置精确地移动 到另一个位置,在移动过程中不作任何加工。至于两相关点 之间的移动速度和轨迹,并不影响工件的加工质量,只影响 生产率。这类机床有数控钻床、数控镗床、数控冲孔床等。 数控钻铆床也属于点位控制机床。
矢量
20
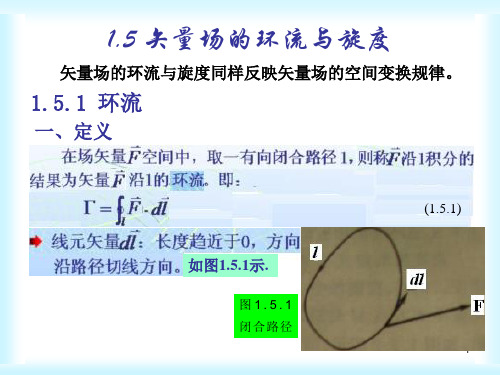
直角坐标系中 由梯度公式(1.3.7):
和散度公式 (1.4.9):
可得▽2u的表达式为:
u u u u 2 2 2 x y z
2 2 2 2
(1.7.1)
21 圆柱坐标系中源自由梯度公式(1.3.10):
和散度公式 (1.4.11):
可得▽2u的表达式为:
2
1 u 1 u u u ( ) 2 ( 2 ) 2 z
一、概念
(1.5.3)
即环流面密度取得最大值的面元正法线单位矢量
4
二、物理意义
矢量的旋度为矢量,是空间位置的函数; 矢量在空间某点处的旋度表征矢量场在该点处的漩涡源密 度; 矢量场在某个方向的环量密度是旋度在该方向上的投影。 如图1.5.2所示,即:
rotn F en rotF
MC模拟发展的背景、意义
作 业
1.23、1.27、 1.28、 1.31
32
2
S
dS n
(1.7.7)
由式(1.7.6)与式(1.7.7)相减,得到格林第二恒等式为:
V
( )dV
2 2
S
( )dS n n
(1.7.8)
格林定理描述了两个标量场之间满足的关系。如果已知 其中一个场的分布,就可以用格林定理求解另一个场的分 布。
23
二、 矢量场的拉普拉斯运算
F ( F ) ( F )
2
矢量场F的拉普拉斯运算定义为:
(1.7.4)
在直角坐标系中为:
2 2 2 F ex Fx ey Fy ez Fz
2
(1.7.5)
24
中国分省矢量地图 ppt课件

中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
中国分省矢量地图
矢量分析-PPT

0
2 2 2 2
x2 y2 z2
1 .4 .2 格林定理
将散度定理中矢量A表示为某标量函数的梯度 ψ与另一标 量函数 φ的乘积, 则有
A ( ) 2
取上式在体积V内的积分, 并应用散度定理, 得
(2 )dv
V
s( ) nˆds
s
n
ds
(1 -49)
式中S是包围体积V的封闭面, nˆ 是封闭面S的外法线方向单位矢
量。此式对于在体积V内具有连续二阶偏导数的标量函数φ和ψ都 成立, 称为格林( G .Green)第一定理。
divA A
A
xˆ
x
yˆ
y
zˆ
z
(xˆAx
yˆAy
zˆAz
)
Ax Ay Az x y z
利用哈密顿算子, 读者可以证明, 散度运算符合下列规则:
(A B) A B
(A) A A
1 .2 .3 散度定理
既然矢量的散度代表的是其通量的体密度, 因此直观地可知, 矢量场散度的体积分等于该矢量穿过包围该体积的封闭面的总 通量, 即
ds nˆds
nˆ 是面元的法线方向单位矢量。nˆ 的取法(指向)有两种情形: 对
开曲面上的面元, 设这个开曲面是由封闭曲线l所围成的, 则当选
定绕行l的方向后, 沿绕行方向按右手螺旋的姆指方向就是 nˆ 的方 向, 如图1 -4所示; 对封闭曲面上的面元, nˆ 取为封闭面的外法线方
向。
图 1 -4 开曲面上的面元
为A , B崐所在平面的右手法向 n:ˆ
A B nˆAB sin aAB
它不符合交换律。 由定义知,
A B (B A)
并有
xˆ xˆ yˆ yˆ zˆ zˆ 0 xˆ yˆ zˆ, yˆ zˆ xˆ, zˆ xˆ yˆ
《Stokes矢量》课件

Stokes矢量的性质
1 归一化
Stokes矢量可以进行归一化处理,使其各个分量在特定范围内。
2 对称性
Stokes矢量的分量之间存在一定的对称性关系。
3 上下偏振状态的判断
根据Stokes矢量的分量值可以判断光线的上下偏振状态。
Stokes矢量的测量
1
实验测量
通过使用偏振片和光学仪器,可以测量光的Stokes矢量分量。
《Stokes矢量》PPT课件
在这个《Stokes矢量》PPT课件中,我们将介绍Stokes矢量的基础知识和应用领 域,帮助您深入了解这一重要概念。
什么是Stokes矢量?
Stokes矢量是一种量化描述光偏振信息的工具。它通过四个分量来描述光的偏 振状态,包括偏振度、偏振方向、椭圆度和偏振椭圆旋转角。
矢量基础
矢量的定义
矢量是有大小和方向的量,可表示力、速度、位移等物理量。
矢量的运算
矢量之间可以进行加法、减法和数量乘法的运算。
Stokes矢量的定义
Hale Waihona Puke 分量含义Stokes矢量的四个分量分别表示偏振度、偏振方 向、椭圆度和偏振椭圆旋转角。
与线偏光的关系
Stokes矢量可以用来描述线偏光的偏振状态和偏 振特性。
2
应用样例
Stokes矢量的测量在光通信、材料科学和生物医学等领域有广泛应用。
总结
优缺点
Stokes矢量作为描述光的偏振状态的工具,既有 优点也有局限性。
未来发展趋势
随着科学技术的进步,Stokes矢量的应用领域将 不断扩大。
参考文献
1. 相关文献和资料的推荐
矢量数据结构课件

03
添加点
在矢量数据Leabharlann 构中,可以 通过添加点来构建几何图 形。
删除点
对于不再需要的点,可以 将其从矢量数据结构中删 除。
移动点
通过移动点,可以改变几 何图形的形状和位置。
线的操作
绘制线
使用线段连接一系列点, 形成所需的线条。
删除线
对于不再需要的线,可以 将其从矢量数据结构中删除。
修改线
可以通过添加、删除或移 动线上的点来修改线的形 状和长度。
它能够准确地表示空间几何实体, 并且可以通过几何运算进行数据 更新和操作。
矢量数据结构还支持拓扑关系和 几何对象的层次结构,方便进行
空间关系查询和地图可视化。
矢量数据结构的应用场景
矢量数据结构广泛应用于地理信息系统 (GIS)、地图绘制、遥感图像处理、计 算机图形学等领域。
在计算机图形学中,矢量数据结构用于 生成三维模型和场景,实现逼真的图形 渲染和动画效果。
矢量数据结构课件
• 矢量数据结构概述
01
矢量数据结构概述
矢量数据结构的定义
01
矢量数据结构是一种基于几何对 象(如点、线、面)的数据结构, 用于表示和存储空间信息。
02
它通过使用坐标系和几何对象的 位置、形状、方向等属性来表示 空间实体。
矢量数据结构的特点
矢量数据结构具有精度高、数据 量小、易于进行空间分析等特点。
优势,而栅格数据结构在表示大范围连续空间现象(如地形表面)方面更为合适。
与其他数据结构的比较
除了栅格数据结构外,还有许多其他的数据结构可以用于表示空间信息,如不规则三角 形网格(TIN)和基于文本的地理编码系统等。这些数据结构各有优缺点,适用于不同 的应用场景。矢量数据结构在表示几何形状方面具有优势,但在表达空间关系和现象的
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
OM O A ( OB OM )
得
即
o
A
B M
返回 结束
OM 1 ( OA OB 1 1 (x x , y y , z z ) 2 1 2 1 2 1 1
机动 目录 上页 下页
说明: 由
1 (x x , y y , z z ) 2 1 2 1 2 1 1 A 得定比分点公式: M x1 x2 y1 y2 , , B 1 1 z1 z 2 o 1 A 当 1时, 点 M 为 AB 的中点 ,于是得
机动 目录 上页 下页 返回 结束
一、向量的概念
向量: 既有大小, 又有方向的量称为向量 (又称矢量).
表示法: 有向线段 M1 M2 , 或 a ,
向量的模 : 向量的大小,
向径 (矢径): 起点为原点的向量. 自由向量: 与起点无关的向量. 单位向量: 模为 1 的向量, 零向量: 模为 0 的向量,
MC 1 ( a b ) 2
2 MA 2 MB
MD 1 ( b a ) 2
机动 目录
D
b
C
M
MA 1 ( a b ) MB 1 ( b a ) A 2 2
a
B
上页
下页
返回
结束
三、空间直角坐标系
1. 空间直角坐标系的基本概念 过空间一定点 o , 由三条互相垂直的数轴按右手规则 组成一个空间直角坐标系.
可见 总之: a a 1a a ; 运算律 : 结合律 ( a ) ( a ) a 1 a a ;
(a b ) a b 1 则有单位向量 a a a. 因此 a a a
z
z 轴(竖轴)
• 坐标原点
Ⅲ Ⅳ
Ⅱ
• 坐标轴 • 坐标面
yoz 面
o xoy面
Ⅰ
• 卦限(八个) Ⅶ
y
y轴(纵轴)
Ⅵ
x
x轴(横轴)
Ⅷ
Ⅴ
机动 目录 上页 下页 返回 结束
在直角坐标系下
点 M 有序数组 ( x, y, z ) 向径 r (称为点 M 的坐标) 特殊点的坐标 :
解: 对角线的长为
|mn|
m n ( 1, 1,1) m n (1, 3 , 1)
|mn 3 | m n 11
n
m
该平行四边形的对角线的长度各为 3, 11
机动
目录
上页
下页
返回
结束
例6. 已知两点
解: A B
和
求
AB
AB 3 1 2 , , 14 14 14
1 (3 ,1, 2) 14
机动 目录 上页 下页 返回 结束
2. 方向角与方向余弦 设有两非零向量 记作 类似可定义向量与轴, 轴与轴的夹角 . 与三坐标轴的夹角 , , 为其方向角. 方向角的余弦称为其方向余弦. x x cos 2 2 2 r x y z
OA O A OA 6 ( 1 , 2
2 1 , ) 2 2
(3 , 3 2 , 3)
故点 A 的坐标为 (3 , 3 2 , 3) .
第二节 目录
上页
下页
返回
结束
备用题 1. 设 m i j , n 2 j k , 求以向量 m , n 为边的平 行四边形的对角线的长度 .
机动
任取空间一点 O ,
称 =∠AOB (0≤ ≤ ) 为向量
的夹角. a ,b
z
r
o
上页
y
返回 结束
x
目录 下页
x x cos r x2 y2 z 2 y y cos r x2 y2 z 2 z z cos r x2 y2 z 2
两向量共线 .
若 k (≥3)个向量经平移可移到同一平面上 , 则称此 k 个向量共面 .
机动 目录 上页 下页 返回 结束
二、向量的线性运算
1. 向量的加法 平行四边形法则:
(a b) c a (b c)
c
bc b
b ab
三角形法则:
a
ab b
ab
a
运算规律 : 交换律
ab ba 结合律 ( a b ) c a ( b c ) a b c
M1 M2
机动
目录
上页
下页
返回
结束
若向量 a 与 b大小相等, 方向相同, 则称 a 与 b 相等,
记作 a=b ;
若向量 a 与 b 方向相同或相反, 则称 a 与 b 平行, 记作
a∥b ; 规定: 零向量与任何向量平行 ;
与 a 的模相同, 但方向相反的向量称为 a 的负向量,
记作-a ; 因平行向量可平移到同一直线上, 故两向量平行又称
2 2
9
故所求点为 M (0 , 0 , 14 ) .
思考: (1) 如何求在 xoy 面上与A , B 等距离之点的轨迹方程?
(2) 如何求在空间与A , B 等距离之点的轨迹方程 ?
机动
目录
上页
下页
返回
结束
提示: (1) 设动点为 M ( x , y , 0) , 利用 M A M B , 得 且 (2) 设动点为 M ( x , y , z ) , 利用 M A M B , 得
Hale Waihona Puke r x i y j z k (x , y , z )
此式称为向量 r 的坐标分解式 ,
C r M k j B o y i A N x
z
沿三个坐标轴方向的分向量.
机动 目录 上页 下页 返回 结束
四、利用坐标作向量的线性运算 设 a ( a x , a y , a z ), b (bx , b y , bz ) , 为实数 , 则 a b (a x bx , a y by , a z bz ) ( a , a , a ) a x y z
o
y
x
坐标面 :
机动
目录
上页
下页
返回
结束
2. 向量的坐标表示
以 i , j , k 分别表示 x , y , z 轴上的单位向量 , 设点 M
的坐标为 M ( x , y , z ) , 则
在空间直角坐标系下, 任意向量 r 可用向径 OM 表示.
OM ON NM OA OB OC
故 0 , 即 .
机动 目录 上页 下页 返回 结束
“
” 已知 b= a , 则 b=0 a , b 同向
a∥b
a , b 反向
例1. 设 M 为 解: ABCD 对角线的交点,
试用 a 与 b 表示 MA , MB , MC , MD .
a b AC b a BD
2 cos 2 3 4
机动 目录 上页 下页 返回 结束
3
,
例6. 设点 A 位于第一卦限, 向径 OA 与 x 轴 y 轴的夹 角依次为 , , 且 O A 6 , 求点 A 的坐标 . 3 4
, , 则 解: 已知 3 4 cos 2 1 cos 2 cos 2 1 4 因点 A 在第一卦限 , 故 cos 1 , 于是 2
方向余弦的性质:
z
r
o
y
x
机动
目录
上页
下页
返回
结束
例5. 已知两点
和
计算向量
的模 、方向余弦和方向角 .
解:
M 1M 2 ( 1 2 , 3 2 , 0 2 )
(1, 1, 2 )
(1) 2 12 ( 2 ) 2 2
1 cos , 2 2 , 3
机动 目录 上页 下页 返回 结束
分配律
定理1. 设 a 为非零向量 , 则 a∥b 证: “ ”. 设 a∥b , 取 =± ( 为唯一实数)
, a , b 同向时
取正号, 反向时取负号, 则 b 与 a 同向, 且
b
故 b a.
再证数 的唯一性 . 设又有 b= a , 则 ( ) a 0
即 M1M 2 M 3 为等腰三角形 .
机动 目录 上页
M1 M2
下页
M3
返回
结束
例4. 在 z 轴上求与两点 离的点 .
及
等距
解: 设该点为 M (0 , 0 , z ) , 因为 M A M B ,
(4) 2 12 (7 z ) 2
解得
(2 z ) 2 3 5
中点公式:
x1 x2 , 2
y1 y2 , 2
z1 z 2 2
机动 目录 上页 下页 返回
B M
结束
五、向量的模、方向角、投影
设 r ( x , y , z ), 作 OM r , 则有 r OM OP OQ OR
由勾股定理得
1. 向量的模与两点间的距离公式
R
z
M Q y
N
2 2 2
o
P x
r OM
对两点 与 因
x y z
得两点间的距离公式:
( x2 x1 ) 2 ( y2 y1 ) 2 ( z2 z1 ) 2
机动 目录 上页 下页 返回 结束
例3. 求证以
的三角形是等腰三角形 .
得
即
o
A
B M
返回 结束
OM 1 ( OA OB 1 1 (x x , y y , z z ) 2 1 2 1 2 1 1
机动 目录 上页 下页
说明: 由
1 (x x , y y , z z ) 2 1 2 1 2 1 1 A 得定比分点公式: M x1 x2 y1 y2 , , B 1 1 z1 z 2 o 1 A 当 1时, 点 M 为 AB 的中点 ,于是得
机动 目录 上页 下页 返回 结束
一、向量的概念
向量: 既有大小, 又有方向的量称为向量 (又称矢量).
表示法: 有向线段 M1 M2 , 或 a ,
向量的模 : 向量的大小,
向径 (矢径): 起点为原点的向量. 自由向量: 与起点无关的向量. 单位向量: 模为 1 的向量, 零向量: 模为 0 的向量,
MC 1 ( a b ) 2
2 MA 2 MB
MD 1 ( b a ) 2
机动 目录
D
b
C
M
MA 1 ( a b ) MB 1 ( b a ) A 2 2
a
B
上页
下页
返回
结束
三、空间直角坐标系
1. 空间直角坐标系的基本概念 过空间一定点 o , 由三条互相垂直的数轴按右手规则 组成一个空间直角坐标系.
可见 总之: a a 1a a ; 运算律 : 结合律 ( a ) ( a ) a 1 a a ;
(a b ) a b 1 则有单位向量 a a a. 因此 a a a
z
z 轴(竖轴)
• 坐标原点
Ⅲ Ⅳ
Ⅱ
• 坐标轴 • 坐标面
yoz 面
o xoy面
Ⅰ
• 卦限(八个) Ⅶ
y
y轴(纵轴)
Ⅵ
x
x轴(横轴)
Ⅷ
Ⅴ
机动 目录 上页 下页 返回 结束
在直角坐标系下
点 M 有序数组 ( x, y, z ) 向径 r (称为点 M 的坐标) 特殊点的坐标 :
解: 对角线的长为
|mn|
m n ( 1, 1,1) m n (1, 3 , 1)
|mn 3 | m n 11
n
m
该平行四边形的对角线的长度各为 3, 11
机动
目录
上页
下页
返回
结束
例6. 已知两点
解: A B
和
求
AB
AB 3 1 2 , , 14 14 14
1 (3 ,1, 2) 14
机动 目录 上页 下页 返回 结束
2. 方向角与方向余弦 设有两非零向量 记作 类似可定义向量与轴, 轴与轴的夹角 . 与三坐标轴的夹角 , , 为其方向角. 方向角的余弦称为其方向余弦. x x cos 2 2 2 r x y z
OA O A OA 6 ( 1 , 2
2 1 , ) 2 2
(3 , 3 2 , 3)
故点 A 的坐标为 (3 , 3 2 , 3) .
第二节 目录
上页
下页
返回
结束
备用题 1. 设 m i j , n 2 j k , 求以向量 m , n 为边的平 行四边形的对角线的长度 .
机动
任取空间一点 O ,
称 =∠AOB (0≤ ≤ ) 为向量
的夹角. a ,b
z
r
o
上页
y
返回 结束
x
目录 下页
x x cos r x2 y2 z 2 y y cos r x2 y2 z 2 z z cos r x2 y2 z 2
两向量共线 .
若 k (≥3)个向量经平移可移到同一平面上 , 则称此 k 个向量共面 .
机动 目录 上页 下页 返回 结束
二、向量的线性运算
1. 向量的加法 平行四边形法则:
(a b) c a (b c)
c
bc b
b ab
三角形法则:
a
ab b
ab
a
运算规律 : 交换律
ab ba 结合律 ( a b ) c a ( b c ) a b c
M1 M2
机动
目录
上页
下页
返回
结束
若向量 a 与 b大小相等, 方向相同, 则称 a 与 b 相等,
记作 a=b ;
若向量 a 与 b 方向相同或相反, 则称 a 与 b 平行, 记作
a∥b ; 规定: 零向量与任何向量平行 ;
与 a 的模相同, 但方向相反的向量称为 a 的负向量,
记作-a ; 因平行向量可平移到同一直线上, 故两向量平行又称
2 2
9
故所求点为 M (0 , 0 , 14 ) .
思考: (1) 如何求在 xoy 面上与A , B 等距离之点的轨迹方程?
(2) 如何求在空间与A , B 等距离之点的轨迹方程 ?
机动
目录
上页
下页
返回
结束
提示: (1) 设动点为 M ( x , y , 0) , 利用 M A M B , 得 且 (2) 设动点为 M ( x , y , z ) , 利用 M A M B , 得
Hale Waihona Puke r x i y j z k (x , y , z )
此式称为向量 r 的坐标分解式 ,
C r M k j B o y i A N x
z
沿三个坐标轴方向的分向量.
机动 目录 上页 下页 返回 结束
四、利用坐标作向量的线性运算 设 a ( a x , a y , a z ), b (bx , b y , bz ) , 为实数 , 则 a b (a x bx , a y by , a z bz ) ( a , a , a ) a x y z
o
y
x
坐标面 :
机动
目录
上页
下页
返回
结束
2. 向量的坐标表示
以 i , j , k 分别表示 x , y , z 轴上的单位向量 , 设点 M
的坐标为 M ( x , y , z ) , 则
在空间直角坐标系下, 任意向量 r 可用向径 OM 表示.
OM ON NM OA OB OC
故 0 , 即 .
机动 目录 上页 下页 返回 结束
“
” 已知 b= a , 则 b=0 a , b 同向
a∥b
a , b 反向
例1. 设 M 为 解: ABCD 对角线的交点,
试用 a 与 b 表示 MA , MB , MC , MD .
a b AC b a BD
2 cos 2 3 4
机动 目录 上页 下页 返回 结束
3
,
例6. 设点 A 位于第一卦限, 向径 OA 与 x 轴 y 轴的夹 角依次为 , , 且 O A 6 , 求点 A 的坐标 . 3 4
, , 则 解: 已知 3 4 cos 2 1 cos 2 cos 2 1 4 因点 A 在第一卦限 , 故 cos 1 , 于是 2
方向余弦的性质:
z
r
o
y
x
机动
目录
上页
下页
返回
结束
例5. 已知两点
和
计算向量
的模 、方向余弦和方向角 .
解:
M 1M 2 ( 1 2 , 3 2 , 0 2 )
(1, 1, 2 )
(1) 2 12 ( 2 ) 2 2
1 cos , 2 2 , 3
机动 目录 上页 下页 返回 结束
分配律
定理1. 设 a 为非零向量 , 则 a∥b 证: “ ”. 设 a∥b , 取 =± ( 为唯一实数)
, a , b 同向时
取正号, 反向时取负号, 则 b 与 a 同向, 且
b
故 b a.
再证数 的唯一性 . 设又有 b= a , 则 ( ) a 0
即 M1M 2 M 3 为等腰三角形 .
机动 目录 上页
M1 M2
下页
M3
返回
结束
例4. 在 z 轴上求与两点 离的点 .
及
等距
解: 设该点为 M (0 , 0 , z ) , 因为 M A M B ,
(4) 2 12 (7 z ) 2
解得
(2 z ) 2 3 5
中点公式:
x1 x2 , 2
y1 y2 , 2
z1 z 2 2
机动 目录 上页 下页 返回
B M
结束
五、向量的模、方向角、投影
设 r ( x , y , z ), 作 OM r , 则有 r OM OP OQ OR
由勾股定理得
1. 向量的模与两点间的距离公式
R
z
M Q y
N
2 2 2
o
P x
r OM
对两点 与 因
x y z
得两点间的距离公式:
( x2 x1 ) 2 ( y2 y1 ) 2 ( z2 z1 ) 2
机动 目录 上页 下页 返回 结束
例3. 求证以
的三角形是等腰三角形 .
