拉普拉斯变换ppt课件
合集下载
高数第10章 拉普拉斯变换PPT课件
L [sit]n dtarc t t an arc stan
t s t2 1
s2
或
L [stit]n s t2 d 1 令 tt u 11 s 0 1 d u 2u 0 1 s1 d u 2u aru c0 1 s ta arnc 1 st
第三节 拉氏逆变换的运算
❖ 重点:拉氏逆变换的求法 ❖难点:拉氏逆变换的求法
5. 积分性质: L[f(t)]F(s) ,( s 0 ) ,且 f ( t ) 连续,则
L[1f(x)dx]L[f(t)]F(s)
0
s
s
性质5表明,一个函数积分后取拉氏变换,等于这个函数
的拉氏变换除以参数 s .
性质5可以推广到有限次积分的情形:
n次
t t
L[ dt dt 00
t 0
f(t)dt]Fs(ns)
(s1)2 3
(s1)2 3
24
24
f(t)e2 t co3 st3e2 t sin 3t
2
2
例2
求
F(s)s2
s3 3ss
的拉氏逆变换。
解: 先将F (s) 分解为两个简单分式之和,
s 3 s 3 AB s2 3 ss (s 1 )s( 2 ) s 1s 2
其中AB为待定的常数,上式两边同乘以(s1)s(2),得
1 s
1 ss
e as
1 s
n!
(s ) n1
13
et sin t
14
et cost
15
tet sint
16
tet cost
17
sht
(s )2 2
s (s )2 2
2(s ) [(s )2 2 ]2
第6章拉普拉斯变换.ppt

Re{s} 0 而求得X(jw)
例2: x(t) eatu(t) 求拉氏变换
解:
X (s) 0 eat est dt e(sa)t
sa
0
1 sa
Re{s} 0
可见,不同的x(t)可能有相同的X(s),关键在于 收敛域不同。
收敛域(简称ROC):使拉普拉斯变换收敛 的S值的范围。ROC的图示——复平面(S平 面)。
T1
T1
T1
Re{s} 1位于ROC内 即
Re{
s}
的全部
1
s值位于
ROC
内
右边信号 对应 右半平面的ROC
• 性质5:如果x(t)是左边信号,且若 Re{s} 0 位于ROC内,则 Re{s} 0 的全部S值都位于 ROC内。
左边信号 : t T2 时x(t)=0, 对应 左半平面的ROC
Re{s} 1
6.1.2 零极点图
上述各X(s)称为有理的,
只要x(t)是实指数或复指数的线性组合,
N (s)
X(s)就一定是有理的
ቤተ መጻሕፍቲ ባይዱ
D(s)
对有理拉普拉斯变换,可用零极点图来形象地表示:分子
多项式的根——零点
分母多项式的根——极点
除常数因子外,零极点图+ROC就是有理拉普拉斯变换的S 平面表示。
Re{s}>-a
得所以
teatu(t) L d ds
eatu(t) L (s
(1 1s a a)2
)
1 -
(s a)2
Re{s}>-a
一般式:(当x(s)有多重极点时有用)
t n-1 eatu(t)L 1
例2: x(t) eatu(t) 求拉氏变换
解:
X (s) 0 eat est dt e(sa)t
sa
0
1 sa
Re{s} 0
可见,不同的x(t)可能有相同的X(s),关键在于 收敛域不同。
收敛域(简称ROC):使拉普拉斯变换收敛 的S值的范围。ROC的图示——复平面(S平 面)。
T1
T1
T1
Re{s} 1位于ROC内 即
Re{
s}
的全部
1
s值位于
ROC
内
右边信号 对应 右半平面的ROC
• 性质5:如果x(t)是左边信号,且若 Re{s} 0 位于ROC内,则 Re{s} 0 的全部S值都位于 ROC内。
左边信号 : t T2 时x(t)=0, 对应 左半平面的ROC
Re{s} 1
6.1.2 零极点图
上述各X(s)称为有理的,
只要x(t)是实指数或复指数的线性组合,
N (s)
X(s)就一定是有理的
ቤተ መጻሕፍቲ ባይዱ
D(s)
对有理拉普拉斯变换,可用零极点图来形象地表示:分子
多项式的根——零点
分母多项式的根——极点
除常数因子外,零极点图+ROC就是有理拉普拉斯变换的S 平面表示。
Re{s}>-a
得所以
teatu(t) L d ds
eatu(t) L (s
(1 1s a a)2
)
1 -
(s a)2
Re{s}>-a
一般式:(当x(s)有多重极点时有用)
t n-1 eatu(t)L 1
复变函数与积分变换———拉普拉斯变换ppt

对并返回结果 F ( s )。
(2) f = ilaplace (F ) 对函数 F ( s ) 进行 Laplace 逆变换, 对并返回结果 f ( t )。
22
3t 例 求函数 f ( t ) t e sin 2t
的 Laplace 变换。
解 Matlab 程序
clear; syms t; f = t*exp(3*t)*sin(2*t); F = laplace(f);
若L[f(t)]=F(s), 则有
F (s) L t f (t ) (2.6)
一般地有
F ( n ) (s) L [(t )n f (t )] (2.7)
利用(2.6) 式
【例2.3】求L[tsinkt]
2ks (答案: 2 2 2 ) (s k )
目录 上页 下页 返回 结束
2 a 2 s 【例3.5】求 L s( s2 a2 )2 t cos at
1
1 【例3.6】求 L1 ( s1)( s2)( s 3)
1 1 1 1 t 1 2t 1 3t 1 6 15 10 L s 1 s 2 s 3 e e e 6 15 10
注:书上对例4,例5,例6的计算是用“查表”的方法作 的.
目录 上页 下页 返回 结束
* 三、利用 Matlab 实现 Laplace 变换
在数学软件 Matlab 的符号演算工具箱中,提供了专用函数 来进行 Laplace 变换与 Laplace 逆变换。 (1) F = laplace (f ) 对函数 f ( t ) 进行 Laplace 变换,
输出 F=atan(1/s)
其中, atan 为反正切函数。
工程控制理论-拉普拉斯变换ppt

L
df (t) dt
sF (s)
f
(0)
证明:
L
df (t) dt
df (t) estdt 0 dt
estdf (t)
0
est f (t) s f (t)estdt sF (s) f (0)
0
0
同理,对于二阶导数的拉普拉斯变换:
L
d2 f dt
(t)
2
s2F
(s)
t
s0
2.2.4 拉普拉斯变换的基本性质
(6) 初值定理
若: L f (t) F(s)
则:
lim f (t) lim sF (s)
t 0
s
证明:根据拉普拉斯变换的微分定理,有
lim
s
0
df (t dt
拉普拉斯变换简表 (续3)
序号
原函数 f(t) (t >0)
象函数 F(s) = L[f(t)]
13
1 a
(1-e -at )
1 s(s+a)
14
1
b-a
(e -at -e -bt )
1 (s+a) (s+b)
15
1
b-a
(be
-bt
-ae
–at
)
s (s+a) (s+b)
16
sin(t + )
cos + s sin s2+2
L eat eatestdt e(sa)tdt 1
0
0
sa
2.2.3 典型时间函数的拉普拉斯变换
(5) 正弦信号函数
正弦信号函数定义:
两 e jt cost jsin t
《拉普拉斯变换 》课件

详细描述
对于线性时不变控制系统,通过拉普拉斯变换分析其极点和零点,可以判断系 统的稳定性。如果所有极点都位于复平面的左半部分,则系统稳定;否则系统 不稳定。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
05
总结与展望
拉普拉斯变换的重要性和应用前景
拉普拉斯变换在数学、物理和工程领域中具有广泛的应用,是解决线性常微分方程 、积分方程、偏微分方程等数学问题的有力工具。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
03
拉普拉斯变换的运算技 巧
积分性质的运用
积分性质
如果函数f(t)的拉普拉斯变换为F(s), 那么对于任意常数a,函数f(at)的拉普 拉斯变换为aF(as)。
应用场景
在求解某些物理问题时,可能需要将 时间变量乘以常数,此时可以利用积 分性质简化拉普拉斯变换的运算。
REPORT
《拉普拉斯变换》 PPT课件
CATALOG
DATE
ANALYSIS
SUMMARY
目录
CONTENTS
• 拉普拉斯变换的基本概念 • 拉普拉斯变换的应用 • 拉普拉斯变换的运算技巧 • 拉普拉斯变换的实例分析 • 总结与展望
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
随着科学技术的发展,拉普拉斯变换的应用 领域也在不断拓展,例如在人工智能、机器 学习、数据科学等领域中的应用前景值得关 注。
未来需要进一步加强拉普拉斯变换 的理论研究,提高其在实际问题中 的应用效果,同时探索新的应用领 域,推动科学技术的发展。
对于线性时不变控制系统,通过拉普拉斯变换分析其极点和零点,可以判断系 统的稳定性。如果所有极点都位于复平面的左半部分,则系统稳定;否则系统 不稳定。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
05
总结与展望
拉普拉斯变换的重要性和应用前景
拉普拉斯变换在数学、物理和工程领域中具有广泛的应用,是解决线性常微分方程 、积分方程、偏微分方程等数学问题的有力工具。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
03
拉普拉斯变换的运算技 巧
积分性质的运用
积分性质
如果函数f(t)的拉普拉斯变换为F(s), 那么对于任意常数a,函数f(at)的拉普 拉斯变换为aF(as)。
应用场景
在求解某些物理问题时,可能需要将 时间变量乘以常数,此时可以利用积 分性质简化拉普拉斯变换的运算。
REPORT
《拉普拉斯变换》 PPT课件
CATALOG
DATE
ANALYSIS
SUMMARY
目录
CONTENTS
• 拉普拉斯变换的基本概念 • 拉普拉斯变换的应用 • 拉普拉斯变换的运算技巧 • 拉普拉斯变换的实例分析 • 总结与展望
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
随着科学技术的发展,拉普拉斯变换的应用 领域也在不断拓展,例如在人工智能、机器 学习、数据科学等领域中的应用前景值得关 注。
未来需要进一步加强拉普拉斯变换 的理论研究,提高其在实际问题中 的应用效果,同时探索新的应用领 域,推动科学技术的发展。
电路原理-拉普拉斯变换PPT课件
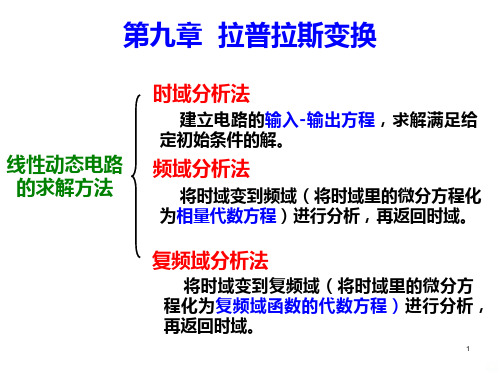
收敛域为s平面的右半平面
[ (t)] 1
s
7
例2 求单位冲激函数 (t)的拉普拉斯象函数。
解:
[ (t)] (t)estdt 0
0
(t
)e
st
dt
(t)estdt
0
0
est t0 1
收敛域包括整个s平面。
[ (t)] 1
[sint (t)] s2 2
10
2. 微分定理 (differentiation theorem)
d dt
f (t)
s
f (t) f (0 )
*证明:
d
dt
f (t)
e st d f (t )dt
0
dt
e stdf (t )
f (t)
0
f ()
f (0 )
lim sF(s)
s0
f
(0 )
lim f (t) limsF(s)
t
s0
利用初值定理和终值定理,根据已知的象函数
F(s)可直接在复频域中确定其对应原函数f(t)的初值
和终值。
21
例8 设 f (t) (1 et ) (t) 验证初值定理和终值定理。
2!
t (t)
1 s3
t (n
n1
1)!
(
t
)
1 sn
1
1 sn
t n1 (n 1)!
(t )
16
4. 时域位移定理 (time-shift theorem)
第3章 拉普拉斯变换 128页 6.1M ppt版

6.3 拉氏变换的性质:
揭示信号时域特性与复频域描述的关系,主要讨论 ROC
1、 线性。
ax1(t) bx2 (t) aX1(s) bX 2 (s)
ROC:包括 R1 R2
若 R1 与R2 无公共部分,则表明ax1(t) bx2 (t) 的拉氏变换不存在。
当 aX1(s) bX 2 (s) 中有零极点抵消时,ROC 可能会扩大。
第三章 拉普拉斯变换
本章要点 拉氏变换的定义——从傅立叶变换到拉 氏变换 拉氏变换与傅氏变换的关系 拉氏变换的性质,收敛域 卷积定理(S域) 系统函数和单位冲激响应
1
第六章 拉普拉斯变换
6.0 引言
第四章已经讨论过复指数信号est 是 LTI 系统的特征函数 s j ,并对
s j 的情况进行了研究,即傅立叶分析。本章对更一般的情况( s j )
7
例三: x(t) ea t eatu(t) eatu(t)
j
X (s) 0 eatestdt eatestdt
0
1 1 sa sa
( a, a)
-a
a
当 a>0 时,这两部分地收敛域有共同部分
a a
此时
X (s)
1 sa
1 sa
2a s2 a2
存在
当 a<0 时这两个 ROC 无公共区域 x(s)不存在。
立叶变换地推广。
3
如果Xx(s) 在 s j 收敛,则 即 s 可以取j
X ( j) Xx(t))eejjtdt tdt
是x(t) 的拉付氏里变叶换变换
X ( j) X (s) 表明傅立叶变换氏是拉氏变换在j 轴上的特例 s j
由傅立叶反变换得到拉斯反变换
拉普拉斯积分变换 PPT课件

记为 F(s) L f (t)
F(s)称为 f (t)的拉氏变换(或称为象函数)。
2
若F(s)是f (t) 的拉氏变换,则称 f (t) 为F(s)的拉 氏逆变换(或称为象原函数),记为
f (t) L1F(s)
可以看出,f (t) (t 0)的拉氏变换,实际上就是 f (t)u(t)e t 的傅氏变换。
解 Lsin kt sin ktestdt 0
e st s2 k2
(s sin
kt
k
cos kt)
0
s2
k
k2
(Re(s) 0)
同样可得余弦函数的拉氏变换:
Lcoskt
s2
s
k2
(Re(s) 0)
9
例6 求单位脉冲函数 (t) 的拉氏变换。
解
利用性质: f (t) (t)dt f (0) ,有
即
L
t 0
f
(t )dt
1 s
L
f
(t)
1 s
F (s)
这个性质表明:一个函数积分后再取拉氏 变换等于这个函数的拉氏变换除以复参数s。
20
重复应用积分性质可得:
L
t
dt
t
dt
0
0
n次
t 0
f
(t)dt
1 sn
F (s)
此外,由拉氏变换存在定理,还可以得到象函数 的积分性质:
L
7
则 f (t) 的拉氏变换
F (s) f (t) est dt 0
在半平面 Re(s) c上一定存在,右端的积分在 Re(s) c1 c 上绝对收敛而且一致收敛,并且在 Re(s) c 的半平面内,F(s)为解析函数。
第二章拉普拉斯变换.ppt

K11 (s s1)r
(s
K12 s1)r1
...
K1r s s1
F2 (s)
(s s1)r F(s) K11 (s s1)K12 ... (s s1)i1K1i ...
(s s1)r1K1r (s s1)r F2(s)
K11
s2 2
cost 1 d sin t dt
线性、微分定理
Lcost
1
s
s2
2
s2
s
2
Example 3
sin t 1 d cost dt
线性、微分定理
?
Lsin t
1
s
s2
s
2
s2 / s2 2
cos
m
m1
s X c (s) an1s X c (s) a0 X c (s)
n
n1
用 s 替代微分,用1/s 替代积分
五、时域积分特性(定理)
f t Fs
n重f积t分dt n
s n
1
m1
F(s)
f
s nm1 (0 )
n (m)
1(t) F (s) 0 (t)e dt
st
s 1
2)e-at
eat F(s) 0eatestdt
sa 1
前一页 后一页
3)tn(n为整数)
tn F(s)
0t
nest dt
s
t n est
s
0
n
0t
n1est
拉普拉斯变换(The Laplace Transform)课件

L
设
1 : X ( s) ( s 1)( s 2)
( s) 2
1 1 , ( s 1) ( s 2)
对X(s) 进行部分分式展开:
X ( s)
1 A B 1 1 ( s 1)( s 2) (s 1) (s 2) ( s 1) ( s 2)
S平面
j 0
j
s0 0 j0
0
• S平面上虚轴上的所有点代表整个周期 jt 复指数信号集 {e }
9.1 拉氏变换
一个信号x(t)的拉氏变换定义如下:
X (s) x(t )e dt ( where s j )
st
记作:
x(t ) X (s)
假设信号x(t)的拉氏变换X(s)没有多阶极 点,且分母多项式的阶次高于分子多项 式的阶次(有理真分式),那么X(s) 就可以展开成如下形式:
Ai X ( s) i 1 s ai
L {Ai /(s ai )}
1
M
Ai eait u(t )
Re{s} ai
Ai eait u(t ) Re{s} ai
性质3:如果x(t)是有限持续期,并 且是绝对可积的,那么ROC就是 整个s平面。
Im
s平面
Re
性质4:如果x(t)是右边信号,而且如果 Re{s} 0 这条线位于ROC内,那么 Re{s} 0 的全部s值都一定在ROC内。
0
Im s平面 Re
• 性质5:如果x(t)是左边信号,而且如果 • Re{s} 0 这条线位于ROC内,那么 • Re{s} 0 的全部s值都一定在ROC内。
1 2
设
1 : X ( s) ( s 1)( s 2)
( s) 2
1 1 , ( s 1) ( s 2)
对X(s) 进行部分分式展开:
X ( s)
1 A B 1 1 ( s 1)( s 2) (s 1) (s 2) ( s 1) ( s 2)
S平面
j 0
j
s0 0 j0
0
• S平面上虚轴上的所有点代表整个周期 jt 复指数信号集 {e }
9.1 拉氏变换
一个信号x(t)的拉氏变换定义如下:
X (s) x(t )e dt ( where s j )
st
记作:
x(t ) X (s)
假设信号x(t)的拉氏变换X(s)没有多阶极 点,且分母多项式的阶次高于分子多项 式的阶次(有理真分式),那么X(s) 就可以展开成如下形式:
Ai X ( s) i 1 s ai
L {Ai /(s ai )}
1
M
Ai eait u(t )
Re{s} ai
Ai eait u(t ) Re{s} ai
性质3:如果x(t)是有限持续期,并 且是绝对可积的,那么ROC就是 整个s平面。
Im
s平面
Re
性质4:如果x(t)是右边信号,而且如果 Re{s} 0 这条线位于ROC内,那么 Re{s} 0 的全部s值都一定在ROC内。
0
Im s平面 Re
• 性质5:如果x(t)是左边信号,而且如果 • Re{s} 0 这条线位于ROC内,那么 • Re{s} 0 的全部s值都一定在ROC内。
1 2
拉普拉斯变换ppt

机电工程学院
第二章 拉普拉斯变换
二、延时定理(Time-Shift Theorem)
若有 L[ f (t )] F ( s ) ,对任意实数 a ,则
控
L[ f (t a)] e asF (s)
制
工
程
基
础
page21
机电工程学院
第二章 拉普拉斯变换
三、周期函数的拉氏变换
若函数 f 是(t)以T 为周期的周期函数,即
则有
f (t T ) f ,(t )
L f t f t estdt
控
0
制
工 程 基
T f t e stdt 2T f t e stdt n1T f t e stdt
0
T
nT
础
n1T f t e stdt
nT
n0
page22
机电工程学院
第二章 拉普拉斯变换
若 L[ f (t)] F (s)则
L[ d f (t)] sF (s) f (0) dt
f (0)为时间函数 f (t)在t =0处的初始值。注意,本书假设
f (0-) = f (0+) = f (0) 。
控
制 工
推论 若
L[ f (t)], F则(s)
2j 0
s2 2
page14
机电工程学院
第二章 拉普拉斯变换
(七)余弦函数 余弦函数(Cosine Function)的数学表达式为
r (t ) co s t (t≥0)
控 制
其拉氏变换为
工 程 基
L[cos t] cos testdt 0
础
1 (e jt e jt )e st d t 20
信号与系统 拉普拉斯变换ppt课件

s1 s1
所 f(0 以 ) l s is m (F s ) k s l s i s m 2 s 2 1 2 s
2s
2
lim lim 2
ss1
s 1 1
所f以 (0)2
.
s
35
4.4 拉普拉斯逆变换
• 由象函数求原函数的三种方法 • 部分分式法求拉氏逆变换 • 两种特殊情况
ftL1ft
1
σj
Fs
estds
2πj σj
一般求函数的单边拉氏变换可以不加注其收敛范围。
.
14
三.一些常用函数的拉氏变换
1.阶跃函数
Lu(t) 1esd t t 1 est 1
0
s 0 s
2.指数函数
Leαt eαtesd t t eα st
0
αs
1 α s
σα
3.单位冲激信号
dt
lim f(t)lim sF (s)
t
s 0
终值存在的条件:
sF s在右j 半 ω 轴 (原 平点 面 )上 除 和 无 外
证明: 根据初值定理证明时得到的公式
sF (s)f00 dd ft(t)esd t t
ls i0s m ( F s)f0 ls i0m 0 d d ft(t)e sd tt
0
L t0 tesd t t1 全s域平面收敛
Lt t00 t t0.e sd tt e s0t15
4.tnu(t)
Ltn tnesd t t 0
1stest 0 0esd t t
Байду номын сангаас
t n e st s
n 0s
tn1estdt
0
1s1sest 0s12
所 f(0 以 ) l s is m (F s ) k s l s i s m 2 s 2 1 2 s
2s
2
lim lim 2
ss1
s 1 1
所f以 (0)2
.
s
35
4.4 拉普拉斯逆变换
• 由象函数求原函数的三种方法 • 部分分式法求拉氏逆变换 • 两种特殊情况
ftL1ft
1
σj
Fs
estds
2πj σj
一般求函数的单边拉氏变换可以不加注其收敛范围。
.
14
三.一些常用函数的拉氏变换
1.阶跃函数
Lu(t) 1esd t t 1 est 1
0
s 0 s
2.指数函数
Leαt eαtesd t t eα st
0
αs
1 α s
σα
3.单位冲激信号
dt
lim f(t)lim sF (s)
t
s 0
终值存在的条件:
sF s在右j 半 ω 轴 (原 平点 面 )上 除 和 无 外
证明: 根据初值定理证明时得到的公式
sF (s)f00 dd ft(t)esd t t
ls i0s m ( F s)f0 ls i0m 0 d d ft(t)e sd tt
0
L t0 tesd t t1 全s域平面收敛
Lt t00 t t0.e sd tt e s0t15
4.tnu(t)
Ltn tnesd t t 0
1stest 0 0esd t t
Байду номын сангаас
t n e st s
n 0s
tn1estdt
0
1s1sest 0s12
拉普拉斯变换ppt课件

2)在(-∞,+∞)上满足
绝对可积的条件
| f (x) | dx
3)在整个数轴上有定义
实际应用中,绝对可积的条件比较强,许多 函数都不满足该条件,如正弦,余弦,阶跃, 线性函数等;另外,在无线电技术中,函数 往往以t作为自变量,t<0无意义。
4
2 拉普拉斯变换研究的对象函数
1)函数满足这样的条件:
A, B,C, D代入原式得
1
1
s 1
I 2(s 3) 2(s 3) s2 9
1
1
s
1
2(s 3) 2(s 3) s2 9 s2 9
44
二 查表法反演
例4:求 F (s) e s 的原函数。
s
解 由表查得
L1
1 s
1
t
s3 2s2 9s 36 (s 3)(s 3)(s2 9)
1 2(s
3)
1 2(s
3)
s 3 s2 9 3(s2 32 )
因此原函数为
f (t) 1 (e3t e3t ) cos3t 1 sin 3t
2
3
43
I
s3 2s2 9s 36 (s 3)(s 3)(s2 9)
28
九 像函数积分定理
F(s) d s
s
ℒ
f
(t) t
即: 像函数求积分,相当于原函数 除 t 的像函数。
29
十 关于参数的运算
对于含参数α的函数f(t,α)的拉氏变换来说, 由于关于t的积分(即拉氏变换)与关于α的 运算顺序可以交换,所以
拉普拉斯变换(与“变换”有关优秀PPT文档)

第3页,共4页。
需要掌握什么技能?
• 如何获得“拉氏变换式”?
• “拉氏变换式”有哪些简化运算的运算定理?
• 如何通过“拉氏反变换”求取原函数?
• 如何应用拉氏变换求解微分方程?
典型机电控制系统
第4页,共4页。
拉如普何拉 获斯得变“换拉(氏变Th换e L式a”pla?ce Transform)(简称拉氏变化)是一种函数的变换,经变换后,可将微分方程式变换成代数方程式,并且在变换的同
时拉如如即普何何将 拉 通 获初斯过得可始变““条换拉拉将件(氏氏微引反变Th入变换e分L,换式a方避””pla免求?程ce了取式T经原ra变典函ns解数换fo法?rm成中)代求(积数简分方称常拉程数氏式的变,麻化并烦),且是因在一此种变这函换种数的方的同法变可时换以即,使经将微变初分换始方后条程,求件可解引将的微入过分,程方避大程免为式简了变化经换。成典代解数法方中程求式积,并分且常在数变的换的同
时他即认将 为初数麻始学条只烦件是,引一因入种此,解这避决免问种了题方经的法典工可解具以法,使中但求在微积运分分用方常数程数学求的时解麻创烦造的,和过因发程此展大这了为种许简方多法新化可的。以数使学微方分法方。程求解的过程大为简化。
法国数学家、天文学家拉普拉斯(1749─1827年),主要研究天体力学和物理学。
拉普拉斯变换及其典型机电控制系统
拉普拉斯变换 法国数学家、天文学家拉普拉斯(1749─1827年),主要研究天体力学和物理学。他认为数学只是
一种解决问题的工具,但在运用数学时创造和发展了许多新的数学方法。 1812年拉普拉斯在《概率的分析理论》中总结了当时整个概率论的研究,论述了概率在选举、审判调查、气
如时何即获 将得初建“始拉条立氏件在变引拉换入氏式,”避变?免换了的经基典解础法上中的求,积分因常此数,的拉麻烦氏,变因换此是这种经方典法控可制以理使微论分的方数程学求基解础的过。程大为简化。
需要掌握什么技能?
• 如何获得“拉氏变换式”?
• “拉氏变换式”有哪些简化运算的运算定理?
• 如何通过“拉氏反变换”求取原函数?
• 如何应用拉氏变换求解微分方程?
典型机电控制系统
第4页,共4页。
拉如普何拉 获斯得变“换拉(氏变Th换e L式a”pla?ce Transform)(简称拉氏变化)是一种函数的变换,经变换后,可将微分方程式变换成代数方程式,并且在变换的同
时拉如如即普何何将 拉 通 获初斯过得可始变““条换拉拉将件(氏氏微引反变Th入变换e分L,换式a方避””pla免求?程ce了取式T经原ra变典函ns解数换fo法?rm成中)代求(积数简分方称常拉程数氏式的变,麻化并烦),且是因在一此种变这函换种数的方的同法变可时换以即,使经将微变初分换始方后条程,求件可解引将的微入过分,程方避大程免为式简了变化经换。成典代解数法方中程求式积,并分且常在数变的换的同
时他即认将 为初数麻始学条只烦件是,引一因入种此,解这避决免问种了题方经的法典工可解具以法,使中但求在微积运分分用方常数程数学求的时解麻创烦造的,和过因发程此展大这了为种许简方多法新化可的。以数使学微方分法方。程求解的过程大为简化。
法国数学家、天文学家拉普拉斯(1749─1827年),主要研究天体力学和物理学。
拉普拉斯变换及其典型机电控制系统
拉普拉斯变换 法国数学家、天文学家拉普拉斯(1749─1827年),主要研究天体力学和物理学。他认为数学只是
一种解决问题的工具,但在运用数学时创造和发展了许多新的数学方法。 1812年拉普拉斯在《概率的分析理论》中总结了当时整个概率论的研究,论述了概率在选举、审判调查、气
如时何即获 将得初建“始拉条立氏件在变引拉换入氏式,”避变?免换了的经基典解础法上中的求,积分因常此数,的拉麻烦氏,变因换此是这种经方典法控可制以理使微论分的方数程学求基解础的过。程大为简化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
满足傅立叶变换的要求:
f (t)et 1 F ()eitd
2
F () 1 [ f (t)u(t)et ]eitdt
2
1
[
f
(t )e t
]eit
dt
2 0
令s i,则d ds F (s) f (t)est dt
i
0
f (t) 1 i f (s)est ds
2i i 6
1 e(sa)td[(s a)t] sa 0
1 sa
de(sa)t 1 e(sa)t
0
sa
0
1 sa
(Re s Re a)
13
例2 Heaviside阶跃 函数:
u(t)
1,
0,
t 0 t0
L [ f (t)] 1 est dt 1
0
s
(Re s 0)
14
例3 线性函数 f (t) = t (t > 0):
1
i
s2
2
(Re s 0)
ℒ
[cos t] 1 ℒ [eit ] ℒ
2
[eit ]
s
s2 2
(Re s 0)
23
二 原函数导数定理:
ℒ [ f '(t)] sF (s) f (0)
ℒ [ f (n) (t)] snF (s) sn1 f (0) sn2 f '(0)
0+i
解 析 区 域
0-i
22
一 线性定理:与 Fourier 变换一样。
ℒ[c1 f1(t) c2 f2 (t)] c1F1(s) c2F2 (s)
例 ℒ [sin t] 1 ℒ [eit ] ℒ [eit ]
ℒ[est ]
1 ps
2i
(Re p Re s)
1 2i
s
1
i
s
a) t<0时,f(t)=0
b) t=0时,f(t)右侧连续,lim f (t) f (0) t 0
f (t) f (t)
t 0, f (t)为t的实变函数
0 t0
2f)(t设),单研位究阶函跃数函为数f(,tu)(ut() t)。10
t0 t0
则原函数
5
3 从傅里叶变换推导拉普拉斯变换
当 f (t)et dt为有限值时,函数f (t)u(t)et 0
的下界称为收敛横标,以0 表示。
大多数函数都满足这个充分条件。
10
s 平面
0+i
o
i s
收敛横标
0-i
11
2 定理:若f(t)满足上述条件,则像函数 F(s)在半平面Res>δ上有意义,而且是一 个解析函数。
12
三 例题 例1 指数函数 eat (a为复常数)
L [eat ] e(sa)tdt 0
第六章 拉普拉斯变换
1
本章基本要求
• 理解和掌握导数和积分的拉普拉斯变换
• 掌握有理分式反演法
• 掌握延迟定理,位移定理和卷积定理
• 理解黎曼-梅林反演公式;运算微积方法 求解微积分方程。
2
6.1 拉普拉斯变换的概念
3
一 Laplace 变换的定义
1 傅里叶变换的限制:1)函数满足狄利克雷条件
9
二 Laplace变换的存在条件 1 Laplace 变换存在的充分条件是:
(1)在 0 t < 的任一有限区间上, 除了有限个第一类间断点外,函数f(t)
及其导数是处处连续的。
(2) 存在常数 M > 0 和 0,使对 于任何t (0 t < ), 有
f (t) Met即 f (t)et M
18
一 单位阶跃函数
二 δ(t)函数
L[ (t t0 )]
0
est
(t
t0
)dt
est0
当t0 0,L[ (t)] 1
19
三 函数tn(n>-1)的拉氏变换
L[t n ] t nest dt 0
令x st,则
L[tn ]
( x)nex 0s
dx s
1 s n1
0
xnexdx
0
sa 0
1 sa
t e(sa)t
|
0
e (sa)t
0
dt
s
1 a
0
s
1
a
e (sa)t
0
d[(s
a)t]
(s
1 a)2
e(sa)t
|
0
(s
1 a)2
(Re s Re a)
同理
L [t neat
]
(s
n! a)n1
(Re s Re a)
16
例5 求 ℒ[t f (t)]
从上面推导可知,函数f(t)(t≥0)拉普 拉斯变换,实际上就是函数f(t)u(t)e-δt 的傅里叶变换。
7
4 Laplace变换的定义
设f(t)为定义在[0,∞)上的实变函数或复
值函数,若含 s i( ,为实数)( 0)
复变量的积分
f (t)est dt f (t)et dt为有限值
(n 1) s n1
20
6.3 Laplace 变换的基本性质
21
Laplace 变换F(s) 的特性:
(1) F(s) 在 Re(s)>0 的半
平面代表一个解析函数。
(2)当 | s | ,
s 平面
|Arg s| /2 - ε (ε > 0) 时:
o
F(s) 存在,
பைடு நூலகம்
且满足 lim F(s) 0 s
L [ f (t)] test dt 1 t d(est )
0
s0
1 test s
|
0
1 s
e st dt
0
1 s2
e st
0
d( st )
1 s2
est
|
0
1 s2
(Res 0)
15
例4 f (t) t eat
L[teat ]
t
e(sa)t
dt
1
t d e(sa)t
2)在(-∞,+∞)上满足
绝对可积的条件
| f (x) | dx
3)在整个数轴上有定义
实际应用中,绝对可积的条件比较强,许多 函数都不满足该条件,如正弦,余弦,阶跃, 线性函数等;另外,在无线电技术中,函数 往往以t作为自变量,t<0无意义。
4
2 拉普拉斯变换研究的对象函数
1)函数满足这样的条件:
解: dF(s) d e-st f (t)dt e-st (t) f (t)dt
ds ds 0
0
e-st t f (t)dt 0
从而 ℒ [t f (t)] (1) dF(s) ds
类推 ℒ [t n f (t)] (1)n dnF (s) ds n
17
6.2 基本函数的拉普拉斯变换
0
0
在s的某个区域内存在,则由此积分定义的
复函数
F (s) f (t)est dt 0
称为函数f(t)的Laplace变换或像函数, 记作F(s)=L[f(t)],
8
f (t) 1 i f (s)est ds
2i i
而f(t)称为F(s)的拉氏逆变换或原函数, 记作f(t)=L-[F(s)],上式也称作黎曼-梅林 反演公式。
f (t)et 1 F ()eitd
2
F () 1 [ f (t)u(t)et ]eitdt
2
1
[
f
(t )e t
]eit
dt
2 0
令s i,则d ds F (s) f (t)est dt
i
0
f (t) 1 i f (s)est ds
2i i 6
1 e(sa)td[(s a)t] sa 0
1 sa
de(sa)t 1 e(sa)t
0
sa
0
1 sa
(Re s Re a)
13
例2 Heaviside阶跃 函数:
u(t)
1,
0,
t 0 t0
L [ f (t)] 1 est dt 1
0
s
(Re s 0)
14
例3 线性函数 f (t) = t (t > 0):
1
i
s2
2
(Re s 0)
ℒ
[cos t] 1 ℒ [eit ] ℒ
2
[eit ]
s
s2 2
(Re s 0)
23
二 原函数导数定理:
ℒ [ f '(t)] sF (s) f (0)
ℒ [ f (n) (t)] snF (s) sn1 f (0) sn2 f '(0)
0+i
解 析 区 域
0-i
22
一 线性定理:与 Fourier 变换一样。
ℒ[c1 f1(t) c2 f2 (t)] c1F1(s) c2F2 (s)
例 ℒ [sin t] 1 ℒ [eit ] ℒ [eit ]
ℒ[est ]
1 ps
2i
(Re p Re s)
1 2i
s
1
i
s
a) t<0时,f(t)=0
b) t=0时,f(t)右侧连续,lim f (t) f (0) t 0
f (t) f (t)
t 0, f (t)为t的实变函数
0 t0
2f)(t设),单研位究阶函跃数函为数f(,tu)(ut() t)。10
t0 t0
则原函数
5
3 从傅里叶变换推导拉普拉斯变换
当 f (t)et dt为有限值时,函数f (t)u(t)et 0
的下界称为收敛横标,以0 表示。
大多数函数都满足这个充分条件。
10
s 平面
0+i
o
i s
收敛横标
0-i
11
2 定理:若f(t)满足上述条件,则像函数 F(s)在半平面Res>δ上有意义,而且是一 个解析函数。
12
三 例题 例1 指数函数 eat (a为复常数)
L [eat ] e(sa)tdt 0
第六章 拉普拉斯变换
1
本章基本要求
• 理解和掌握导数和积分的拉普拉斯变换
• 掌握有理分式反演法
• 掌握延迟定理,位移定理和卷积定理
• 理解黎曼-梅林反演公式;运算微积方法 求解微积分方程。
2
6.1 拉普拉斯变换的概念
3
一 Laplace 变换的定义
1 傅里叶变换的限制:1)函数满足狄利克雷条件
9
二 Laplace变换的存在条件 1 Laplace 变换存在的充分条件是:
(1)在 0 t < 的任一有限区间上, 除了有限个第一类间断点外,函数f(t)
及其导数是处处连续的。
(2) 存在常数 M > 0 和 0,使对 于任何t (0 t < ), 有
f (t) Met即 f (t)et M
18
一 单位阶跃函数
二 δ(t)函数
L[ (t t0 )]
0
est
(t
t0
)dt
est0
当t0 0,L[ (t)] 1
19
三 函数tn(n>-1)的拉氏变换
L[t n ] t nest dt 0
令x st,则
L[tn ]
( x)nex 0s
dx s
1 s n1
0
xnexdx
0
sa 0
1 sa
t e(sa)t
|
0
e (sa)t
0
dt
s
1 a
0
s
1
a
e (sa)t
0
d[(s
a)t]
(s
1 a)2
e(sa)t
|
0
(s
1 a)2
(Re s Re a)
同理
L [t neat
]
(s
n! a)n1
(Re s Re a)
16
例5 求 ℒ[t f (t)]
从上面推导可知,函数f(t)(t≥0)拉普 拉斯变换,实际上就是函数f(t)u(t)e-δt 的傅里叶变换。
7
4 Laplace变换的定义
设f(t)为定义在[0,∞)上的实变函数或复
值函数,若含 s i( ,为实数)( 0)
复变量的积分
f (t)est dt f (t)et dt为有限值
(n 1) s n1
20
6.3 Laplace 变换的基本性质
21
Laplace 变换F(s) 的特性:
(1) F(s) 在 Re(s)>0 的半
平面代表一个解析函数。
(2)当 | s | ,
s 平面
|Arg s| /2 - ε (ε > 0) 时:
o
F(s) 存在,
பைடு நூலகம்
且满足 lim F(s) 0 s
L [ f (t)] test dt 1 t d(est )
0
s0
1 test s
|
0
1 s
e st dt
0
1 s2
e st
0
d( st )
1 s2
est
|
0
1 s2
(Res 0)
15
例4 f (t) t eat
L[teat ]
t
e(sa)t
dt
1
t d e(sa)t
2)在(-∞,+∞)上满足
绝对可积的条件
| f (x) | dx
3)在整个数轴上有定义
实际应用中,绝对可积的条件比较强,许多 函数都不满足该条件,如正弦,余弦,阶跃, 线性函数等;另外,在无线电技术中,函数 往往以t作为自变量,t<0无意义。
4
2 拉普拉斯变换研究的对象函数
1)函数满足这样的条件:
解: dF(s) d e-st f (t)dt e-st (t) f (t)dt
ds ds 0
0
e-st t f (t)dt 0
从而 ℒ [t f (t)] (1) dF(s) ds
类推 ℒ [t n f (t)] (1)n dnF (s) ds n
17
6.2 基本函数的拉普拉斯变换
0
0
在s的某个区域内存在,则由此积分定义的
复函数
F (s) f (t)est dt 0
称为函数f(t)的Laplace变换或像函数, 记作F(s)=L[f(t)],
8
f (t) 1 i f (s)est ds
2i i
而f(t)称为F(s)的拉氏逆变换或原函数, 记作f(t)=L-[F(s)],上式也称作黎曼-梅林 反演公式。
