钢结构原理与设计第2版__课后答案
《钢结构原理与设计第二版》章课后答案.docx

4. 1解:N = Y G N GK +Y Q N QK =1.2X |X 315 + 1.4X |X 315 = 420^焊缝质量为三级,用引弧板施焊。
查表得E43焊条的//= 185/V/mm 2,Q235 钢的 / = 215/V/mm 2。
N 420 X103 「北 t> ------ : ■ bf. = ---------- =1135mm 200x185 故取 f = 12mm o4. 2解:N = Y G N GK +Y Q N QK =1.2X O.2A/A +1.4X O.8A/A =l36N k 焊缝质量为二级,f t w =215N/mm 2未用引弧板施焊 l w — 400 — 2x12 = 316mmN = f ;v l w t = i.36N kf t w l w t. 1.36 = 215X376X12 亍山册1.364. 4解: 1)焊脚尺寸仰hf 、> 1 珀匚唤=l-5xV10 = 4.74mm h f[ < 1.2/inin = 1.2x8 = 9.6mm趾部尺寸! h /2 !-5At = 1.5x VlO = 4.74m/n WV^/2 "nin - (1 〜2)= 8-(1 〜2) = 6 〜7mm 为方便备料,取h f i = hf2 = hf = 6mm ,满足上述要求。
2) 轴心力N 的设计值N= Y C >N C .K ^Y Q N QK=1.2X 0」x 180 +1.4x 0.9x 180 = 248.4^按角钢背与趾部侧面角焊缝内力分配系数可知:等边角钢内力分配系 数 勺=0.3— = 0.7 bh对角钢趾部取力矩平衡得:N\b = N®N\=^N = 0.3N = 0.3x248.4 = 74.52RN 1 b N 2=N-N } =0.7^ =0.7X 24&4 = 173.88RN3) 焊缝长度。
《钢结构原理与设计第二版》中国建筑工业出版社夏志斌_部分课后答案

,
h f tmin (1 ~ 2) 8 ~ 9mm
取 h f 6mm 时, lW 不可行;
N 598.4 103 445.2mm 60h f 360mm 2 0.7h f f fW 2 0.7 6 160
取 h f 7mm 时, lw 381.6mm , lw 60h f 420 mm 可行, l 381.6 2h f 395.6mm ,取 l 400 mm 取 h f 9mm 时, lw 296.8mm , lw 60h f 540 mm 可行, l 296.8 2h f 314.8mm ,取 l 320 mm 故最小的焊脚尺寸可取 7mm ,钢板搭接长度为 400 mm 最大的焊脚尺寸可取 9mm ,钢板搭接长度为 320 mm
故取 t 12mm 。
4.2解:
N G NGK Q NQK 1.2 0.2 N k 1.4 0.8N k 1.36 N k
焊缝质量为二级, f tW 215 N / mm2 未用引弧板施焊
lW 400 2 12 376mm
f tW N , N f tW lW t 1.36 N k lW t
趾部尺寸
为方便备料,取 h f 1 h f 2 h f 6mm ,满足上述要求。 2)轴心力 N 的设计值
N G NGK Q NQK 1.2 0.1180 1.4 0.9 180 248.4kN
按角钢背与趾部侧面角焊缝内力分配系数可知:等边角钢内力分配系 数
f
f
M 10 106 186.0 N / mm2 2 2 0.7h f lW 6 0.7 8 240 6 N 50 103 37.2 N / mm2 0.7h f lW 0.7 8 240
钢结构基本原理课后习题答案
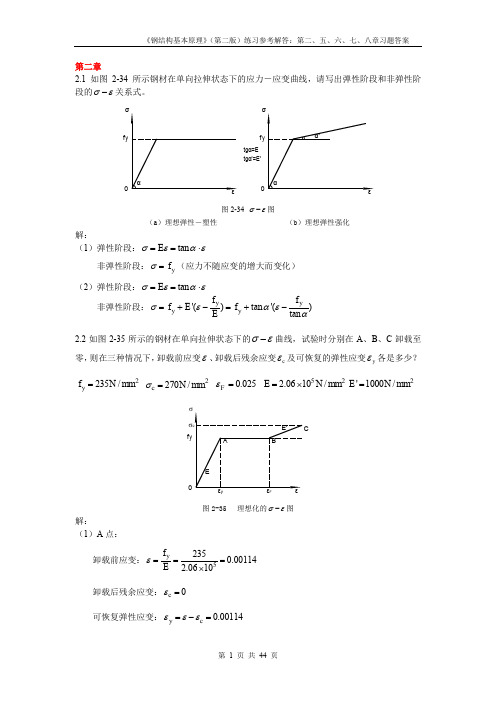
第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f yσF图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢结构基本原理(第二版)习题参考解答第七章

7.1 一压弯构件长15m ,两端在截面两主轴方向均为铰接,承受轴心压力1000N kN =,中央截面有集中力150F kN =。
构件三分点处有两个平面外支承点(图7-21)。
钢材强度设计值为2310/N mm 。
按所给荷载,试设计截面尺寸(按工字形截面考虑)。
解:选定截面如下图示:图1 工字形截面尺寸下面进行截面验算:(1)截面特性计算()23002026502021420540A mm =⨯⨯+-⨯⨯=339411300650286610 1.45101212x I mm =⨯⨯-⨯⨯=⨯ 63/325 4.4810x x W I mm ==⨯337411220300610149.01101212y I mm =⨯⨯⨯+⨯⨯=⨯ 53/150 6.0110y y W I mm ==⨯266.2x i mm ==66.2y i m m = (2)截面强度验算36226100010562.510172.3/310/20540 4.4810x M N N mm f N mm A W σ⨯⨯=+=+=<=⨯ 满足。
(3)弯矩作用平面内稳定验算 长细比1500056.3266.2x λ== 按b 类构件查附表4-4,56.368.2,查得0.761x ϕ=。
2257222.061020540' 1.20101.1 1.156.3EX x EA N N ππλ⨯⨯⨯===⨯⋅⨯ 弯矩作用平面内无端弯矩但有一个跨中集中荷载作用:371000101.00.2 1.00.20.981.2010 1.1mx EX N N β⨯=-⨯=-⨯=⨯⨯, 取截面塑性发展系数 1.05x γ= 363611000100.98562.5100.7612054010001010.8 1.05 4.481010.8' 1.2010mx x x x x EX M N A N W N βϕγ⨯⨯⨯+=+⨯⎛⎫⎛⎫⨯-⨯⨯⨯-⨯ ⎪ ⎪ ⎪⨯⎝⎭⎝⎭ 22189.54/310/N mm f N mm =<= ,满足。
(精品)钢结构原理与设计第2版__课后答案

For personal use only in study and research; not forcommercial use4-1解:焊缝质量为三级,用引弧板施焊。
查表得E43焊条的2/185mm N f W t =,Q235钢的2/215mm N f =。
故取mm t 12=。
4-2解:焊缝质量为二级,2/215mm N f W t =未用引弧板施焊tl N f W W t =,k W W t N t l f N 36.1== 4-4解:1)焊脚尺寸f h 背部尺寸⎪⎩⎪⎨⎧=⨯=≤=⨯=≥mm t h mm t h f f 6.982.12.174.4105.15.1min 1max 1 趾部尺寸()()⎪⎩⎪⎨⎧=-=-≤=⨯=≥mmt h mm t h f f 7~62~182~174.4105.15.1min 2max 2 为方便备料,取mm h h h f f f 621===,满足上述要求。
2)轴心力N 的设计值按角钢背与趾部侧面角焊缝内力分配系数可知:等边角钢内力分配系数对角钢趾部取力矩平衡得: 21Ne b N =3)焊缝长度。
当构件截面为一只角钢时,考虑角钢与节点板单面连接所引起的偏心影响, W t f 应乘以折减系数0-85。
角钢趾:mm h mm f h N l f W f f W 48813016085.067.01052.7485.07.0311=>=⨯⨯⨯⨯=⋅≥ 取mm l 1401= (mm h f 1422130=+,取10mm 的整数倍) 角钢背:mm h mm f h N l f W f f W 3606030416085.067.01088.17385.07.0322=<=⨯⨯⨯⨯=⋅≥ 取mm l 3202= (mm h f 3162304=+,取10mm 的整数) 4-5解:腹板受到轴心拉力k N 作用焊脚尺寸f hmm t h f 6.55.1max =≥,mm t h f 9~8)2~1(min =-≤取mm h f 6=时,mm h mm f h N l f W f f W 360602.44516067.02104.5987.023=>=⨯⨯⨯⨯=⨯≥ 不可行;取mm h f 7=时,mm l w 6.381≥,mm h l f w 42060=≤ 可行,mm h l f 6.39526.381=+=,取mm l 400= 取mm h f 9=时,mm l w 8.296≥,mm h l f w 54060=< 可行,mm h l f 8.31428.296=+=,取mm l 320= 故最小的焊脚尺寸可取mm 7,钢板搭接长度为mm 400 最大的焊脚尺寸可取mm 9,钢板搭接长度为mm 320 4-7解:(1)直接计算法解得:mm h f 85.7=采用()mmt mm t mm h f 9~82~136.6185.15.18min max =-≤=⨯=≥=,可 (2)试算法取mm h f 8=222222/160/9.1562.3722.1186mm N f mm N W f f f f =≤=+⎪⎭⎫ ⎝⎛=+⎪⎪⎭⎫ ⎝⎛τβσ,可 故mm h f 8=4-8解:取焊脚尺寸mm h f 6= mm h h f e 2.47.0==(1)几何关系水平焊缝计算长度mm h l l f h Wh 64670=-=-= 全部焊缝计算长度mm l l l Wh W 4286423002=⨯+=+= 全部焊缝有效截面W e W l h A = 形心位置cm h h A l l h x e e W Wh Wh e 96.08.4224.64.6222=⨯⨯⨯⨯=⋅=略去3e h 项焊缝有效截面对形心O 的极惯性矩(2)强度验算剪力和扭矩共同作用下的强度条件 ()222222/160/6.1554.9722.17.1123.35mm N f mm N W f T f f V f Tf =≤=+⎪⎭⎫ ⎝⎛+=+⎪⎪⎭⎫ ⎝⎛+τβσσ,可5-1解:QK Q GK G N N N γγ+=则:N N k 8.772560%904.1560%102.1=⨯⨯+⨯⨯=。
钢结构基本原理(第二版)习题参考解答第二章

钢结构基本原理(第二版)习题参考解答第二章第二章钢结构的基本材料和构件习题参考解答1. 钢材的基本性能指标有哪些?请简要描述各项性能指标的含义。
答:钢材的基本性能指标包括强度、韧性、可塑性和耐腐蚀性。
- 强度:钢材的强度是指钢材抵抗外力的能力,通常以屈服强度、抗拉强度和抗压强度来表示。
屈服强度是指钢材在受到外力作用时,开始产生塑性变形的应力值;抗拉强度是指钢材在拉伸状态下最大的抵抗外力的应力值;抗压强度是指钢材在受到压缩状态下最大的抵抗外力的应力值。
强度的高低决定了钢材的承载能力。
- 韧性:钢材的韧性是指钢材在受到外力作用时,能够发生塑性变形而不断延展的能力。
韧性的好坏决定了钢结构在受到冲击或震动时的抵抗能力。
- 可塑性:钢材的可塑性是指钢材在受到外力作用时,能够发生塑性变形而不断延展的能力。
可塑性的好坏决定了钢材的加工性能和成型性能。
- 耐腐蚀性:钢材的耐腐蚀性是指钢材在受到各种腐蚀介质(如大气、水、酸等)的侵蚀时,能够保持其力学性能和表面的完整性。
耐腐蚀性的好坏决定了钢结构的使用寿命。
2. 钢材的分类方法有哪些?请简要描述各种分类方法。
答:钢材的分类方法有按化学成分分类、按用途分类和按加工方法分类。
- 按化学成分分类:钢材按化学成分可分为碳素钢、合金钢和不锈钢。
碳素钢的主要成分是碳和铁,其含碳量通常在0.08%~2.11%之间;合金钢是在碳素钢中添加其他合金元素(如铬、钼、锰等)来改善钢材的性能;不锈钢是指含有至少12%的铬元素,在大气或酸性介质中形成一层致密的氧化铬膜,起到防腐蚀的作用。
- 按用途分类:钢材按用途可分为结构钢、机械钢、特种钢和工具钢等。
结构钢是用于制造各种钢结构的钢材,如建筑、桥梁、船舶等;机械钢是用于制造机械零部件的钢材,如轴承、齿轮、轴等;特种钢是用于特殊工作条件下的钢材,如高温、低温、高压等环境下的钢材;工具钢是用于制造各种切削工具和模具的钢材,如刀具、冲压模具等。
- 按加工方法分类:钢材按加工方法可分为热轧钢材、冷轧钢材和锻制钢材。
《钢结构原理与设计第二版》中国建筑工业出版社夏志斌 部分课后答案

4.1解:kN N N N QK Q GK G 420315324.1315312.1=⨯⨯+⨯⨯=+=γγ焊缝质量为三级,用引弧板施焊。
查表得E43焊条的2/185mm N f W t =,Q235钢的2/215mm N f =。
mm bf N t W t 35.11185200104203=⨯⨯=≥ 故取mm t 12=。
4.2解:k k k QK Q GK G N N N N N N 36.18.04.12.02.1=⨯+⨯=+=γγ焊缝质量为二级,2/215mm N f W t =未用引弧板施焊mm l W 376122400=⨯-= tl Nf W W t =,k W W t N t l f N 36.1== kN t l f N W W t k 3.71336.11237621536.1=⨯⨯==4.4解: 1)焊脚尺寸f h背部尺寸⎪⎩⎪⎨⎧=⨯=≤=⨯=≥mmt h mmt h f f 6.982.12.174.4105.15.1min 1max 1趾部尺寸()()⎪⎩⎪⎨⎧=-=-≤=⨯=≥mmt h mmt h f f 7~62~182~174.4105.15.1min 2max 2 为方便备料,取mm h h h f f f 621===,满足上述要求。
2)轴心力N 的设计值kN N N N QK Q GK G 4.2481809.04.11801.02.1=⨯⨯+⨯⨯=+=γγ按角钢背与趾部侧面角焊缝内力分配系数可知:等边角钢内力分配系数3.01=b e 7.02=be对角钢趾部取力矩平衡得: 21Ne b N =kN N N be N 52.744.2483.03.021=⨯===kN N N N N 88.1734.2487.07.012=⨯==-=3)焊缝长度。
当构件截面为一只角钢时,考虑角钢与节点板单面连接所引起的偏心影响, W t f 应乘以折减系数0.85。
钢结构第二版课后习题答案

钢结构第二版课后习题答案【篇一:钢结构基础(第二版)课后习题第四章答案】q235钢,翼缘为火焰切割边,沿两个主轴平面的支撑条件及截面尺寸如图所示。
已知构件承受的轴心压力为n=1500kn。
l?4m解:由支承条件可知l0x?12m,0y11?500?12?64ix??8?5003??250?123?2?250?12476.6?10 mm12122?? 50031iy??8?2??12?2503?31.3?106mm412122a?2?250?12?500?8?10000mmix??21.8cmiy5.6cm,l0y400l0x120071.4?x?55?y?i5.6ix21.8y,,2翼缘为火焰切割边的焊接工字钢对两个主轴均为b类截面,故按y查表得?=0.747n1500?103200.8mpa?f?215mpa整体稳定验算:?a0.747?10000,稳定性满足要求。
4.13图示一轴心受压缀条柱,两端铰接,柱高为7m。
承受轴心力设计荷载值n=1300kn,钢材为q235。
已知截面采用2[28a,单个槽钢的几何性质:a=40cm2,iy=10.9cm,ix1=2.33cm,解:柱为两端铰接,因此柱绕x、y轴的计算长度为:l0x?l0y?7m22b26??ix?2?ix1?a??y02?218?40??2.19940.8cm422l0y700l0x70064.263.1ix???11.1cmyxiy10.9ix11.10x格构柱截面对两轴均为b类截面,按长细比较大者验算整体稳定既可。
由?0x?65.1,b类截面,查附表得??0.779,65.1n1300?103208.6mpa?f?215mpa2整体稳定验算:?a0.779?2?40?10 所以该轴心受压的格构柱整体稳定性满足要求。
4.17焊接简支工字形梁如图所示,跨度为12m,跨中6m处梁上翼缘有简支侧向支撑,材料为q345钢。
集中荷载设计值为p=330kn,间接动力荷载,验算该梁的整体稳定是否满足要求。
钢结构基本原理(第二版)习题参考解答第二章
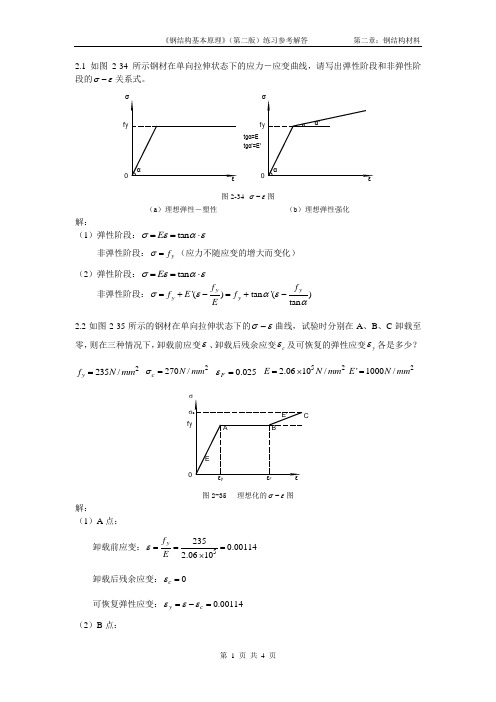
2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y0f y 0tgα=E图2-34 σε-图(a )理想弹性-塑性 (b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化)(2)弹性阶段:tan E σεαε==⋅非弹性阶段:'()tan '()tan yyy y f f f E f E σεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少? 2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f y 0σF图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610yf E ε===⨯卸载后残余应变:0c ε= 可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f E εε=-= 可恢复弹性应变:0.00114y c εεε=-=(3)C 点:卸载前应变:0.0250.0350.06'c y F f E σεε-=-=+= 卸载后残余应变:0.05869c c E σεε=-= 可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
《钢结构原理与设计第二版》中国建筑工业出版社夏志斌_部分课后答案详解

713.3kN
4.4解: 1)焊脚尺寸 hf
背部尺寸
h
f
1
hf
1.5 tmax 1.5 1 1.2tmin 1.2
10 8
4.74mm 9.6mm
趾部尺寸
h
f
h
2
f2
1.5 tmin
tmax 1.5 10
1 ~ 2 8 1 ~ 2
4.74mm 6 ~ 7mm
为方便备料,取 hf 1 hf 2 hf 6mm,满足上述要求。
y1
l 2
150mm
T f
Tx1 I0
14.3106 54.4 2202.4 10 4
35.3N
/ mm2
598.4103 2 0.7 6 160
445.2mm 60hf
360mm
不可行;
取 hf 7mm 时, lw 381.6mm, lw 60hf 420mm 可行, l 381.6 2hf 395.6mm,取 l 400mm 取 hf 9mm 时, lw 296.8mm, lw 60hf 540mm 可行, l 296.8 2hf 314.8mm,取 l 320mm 故最小的焊脚尺寸可取 7mm ,钢板搭接长度为 400mm
74.52kN
N2 N N1 0.7N 0.7 248.4 173.88kN
3)焊缝长度。
当构件截面为一只角钢时,考虑角钢与节点板单面连接所引起的偏心
影响, ftW 应乘以折减系数 0.85。
角钢趾: lW1 0.7hf
N1
0.85
f
W f
74.52103 0.7 6 0.85 160
f f
2
2 f
f
W f
同济大学版钢结构基本原理(第二版)习题参考解答

5.1 影响轴心受压稳定极限承载力的初始缺陷有哪些?在钢结构设计中应如何考虑?5.2 某车间工作平台柱高2.6m,轴心受压,两端铰接.材料用I16,Q235钢,钢材的强度设计值2215/d f N mm =.求轴心受压稳定系数ϕ及其稳定临界荷载.如改用Q345钢2310/d f N mm =,则各为多少?解答:查P335附表3-6,知I16截面特性,26.57, 1.89,26.11x y i cm i cm A cm === 柱子两端较接, 1.0x y μμ== 故柱子长细比为 1.0260039.665.7x x xli μλ⨯===,2600 1.0137.618.9y y y l i μλ⨯===因为x y λλ<,故对于Q235钢相对长细比为137.61.48λπ=== 钢柱轧制, /0.8b h ≤.对y 轴查P106表5-4(a)知为不b 类截面。
故由式5-34b得()223212ϕααλλλ⎡=++⎢⎣ ()2210.9650.300 1.48 1.482 1.48⎡=+⨯+⎢⎣⨯ 0.354=(或计算137.6λ=,再由附表4-4查得0.354ϕ=)故得到稳定临界荷载为20.35426.1110215198.7crd d N Af kN ϕ==⨯⨯⨯=当改用Q365钢时,同理可求得 1.792λ=。
由式5-34b 计算得0.257ϕ= (或由166.7λ=,查表得0.257ϕ=)故稳定临界荷载为20.25726.1110310208.0crd d N Af kN ϕ==⨯⨯⨯=5.3 图5-25所示为一轴心受压构件,两端铰接,截面形式为十字形.设在弹塑性范围内/E G 值保持常数,问在什么条件下,扭转屈曲临界力低于弯曲屈曲临界力,钢材为Q235.5.4 截面由钢板组成的轴心受压构件,其局部稳定计算公式是按什么准则进行推导得出的.5.5 两端铰接的轴心受压柱,高10m,截面为三块钢板焊接而成,翼缘为剪切边,材料为Q235,强度设计值2205/d f N mm =,承受轴心压力设计值3000kN (包括自重).如采用图5-26所示的两种截面,计算两种情况下柱是否安全.图5-26 题5.5解答:截面特性计算: 对a)截面:32394112(5002020500260)8500 1.436101212x I mm =⨯⨯⨯+⨯⨯+⨯⨯=⨯ 3384112205005008 4.167101212y I mm =⨯⨯⨯+⨯⨯=⨯ 2250020500824000A mm =⨯⨯+⨯=244.6x i mm ==131.8y i mm==对b)截面:32384112(4002540025212.5)104009.575101212x I mm =⨯⨯⨯+⨯⨯+⨯⨯=⨯ 33841122540040010 2.667101212y I mm =⨯⨯⨯+⨯⨯=⨯ 24002524001024000A mm =⨯⨯+⨯=199.7x i mm ==105.4y i mm==整体稳定系数的计算:钢柱两端铰接,计算长度10000ox oy l l mm == 对a)截面: 1000040.88244.6ox x x l i λ=== 1000075.87131.8ox y y l i λ=== 对b)截面: 1000050.08199.7kx x x l i λ=== 1000094.88105.4ox y y l i λ=== 根据题意,查P106表5-4(a),知钢柱对x 轴为b 类截面,对y 轴为c 类截面.对a)截面:对x 轴:40.880.440x λπ===()223212x x x x ϕααλλλ⎡=++⎢⎣()2210.9650.30.440.4420.44⎡=⨯+⨯+-⎢⨯⎣0.895=(或计算40.88λ=,再由附表4-4查得0.896xϕ)对y 轴:25.870.816y λπ===()223212y y y y ϕααλλλ⎡=++⎢⎣()2210.9060.5950.8160.81620.816⎡=⨯+⨯+⎢⨯⎣0.604=(或计算75.87λ=,再由附表4-5查得0.604yϕ)故取该柱的整体稳定系数为0.604ϕ=对b)截面,同理可求得0.852x ϕ=,0.489y ϕ=,故取该柱截面整体稳定系数为0.489ϕ= 整体稳定验算:对a)截面 0.604240002052971.68 3000 crd d N Af kN kN ϕ==⨯⨯=<不满足。
同济大学钢结构基本原理(第二版)习题参考解答第五章

5.1 影响轴心受压稳定极限承载力的初始缺陷有哪些?在钢结构设计中应如何考虑?5.2 某车间工作平台柱高2.6m,轴心受压,两端铰接.材料用I16,Q235钢,钢材的强度设计值2215/d f N mm =.求轴心受压稳定系数ϕ及其稳定临界荷载.如改用Q345钢2310/d f N mm =,则各为多少?解答:查P335附表3-6,知I16截面特性,26.57, 1.89,26.11x y i cm i cm A cm === 柱子两端较接, 1.0x y μμ== 故柱子长细比为 1.0260039.665.7x x xli μλ⨯===,2600 1.0137.618.9y y y l i μλ⨯===因为x y λλ<,故对于Q235钢相对长细比为137.61.48λπ=== 钢柱轧制, /0.8b h ≤.对y 轴查P106表5-4(a)知为不b 类截面。
故由式5-34b得()223212ϕααλλλ⎡=++⎢⎣ ()2210.9650.300 1.48 1.482 1.48⎡=+⨯+⎢⎣⨯ 0.354=(或计算137.6λ=,再由附表4-4查得0.354ϕ=)故得到稳定临界荷载为20.35426.1110215198.7crd d N Af kN ϕ==⨯⨯⨯=当改用Q365钢时,同理可求得 1.792λ=。
由式5-34b 计算得0.257ϕ= (或由166.7λ=,查表得0.257ϕ=)故稳定临界荷载为20.25726.1110310208.0crd d N Af kN ϕ==⨯⨯⨯=5.3 图5-25所示为一轴心受压构件,两端铰接,截面形式为十字形.设在弹塑性范围内/E G 值保持常数,问在什么条件下,扭转屈曲临界力低于弯曲屈曲临界力,钢材为Q235.5.4 截面由钢板组成的轴心受压构件,其局部稳定计算公式是按什么准则进行推导得出的.5.5 两端铰接的轴心受压柱,高10m,截面为三块钢板焊接而成,翼缘为剪切边,材料为Q235,强度设计值2205/d f N mm =,承受轴心压力设计值3000kN (包括自重).如采用图5-26所示的两种截面,计算两种情况下柱是否安全.图5-26 题5.5解答:截面特性计算: 对a)截面:32394112(5002020500260)8500 1.436101212x I mm =⨯⨯⨯+⨯⨯+⨯⨯=⨯ 3384112205005008 4.167101212y I mm =⨯⨯⨯+⨯⨯=⨯ 2250020500824000A mm =⨯⨯+⨯=244.6x i mm ==131.8y i mm==对b)截面:32384112(4002540025212.5)104009.575101212x I mm =⨯⨯⨯+⨯⨯+⨯⨯=⨯ 33841122540040010 2.667101212y I mm =⨯⨯⨯+⨯⨯=⨯ 24002524001024000A mm =⨯⨯+⨯=199.7x i mm ==105.4y i mm==整体稳定系数的计算:钢柱两端铰接,计算长度10000ox oy l l mm == 对a)截面: 1000040.88244.6ox x x l i λ=== 1000075.87131.8ox y y l i λ=== 对b)截面: 1000050.08199.7kx x x l i λ=== 1000094.88105.4ox y y l i λ=== 根据题意,查P106表5-4(a),知钢柱对x 轴为b 类截面,对y 轴为c 类截面.对a)截面:对x 轴:40.880.440x λπ===()223212x x x x ϕααλλλ⎡=++⎢⎣()2210.9650.30.440.4420.44⎡=⨯+⨯+-⎢⨯⎣0.895=(或计算40.88λ=,再由附表4-4查得0.896xϕ)对y 轴:25.870.816y λπ===()223212y y y y ϕααλλλ⎡=++⎢⎣()2210.9060.5950.8160.81620.816⎡=⨯+⨯+⎢⨯⎣0.604=(或计算75.87λ=,再由附表4-5查得0.604yϕ)故取该柱的整体稳定系数为0.604ϕ=对b)截面,同理可求得0.852x ϕ=,0.489y ϕ=,故取该柱截面整体稳定系数为0.489ϕ= 整体稳定验算:对a)截面 0.604240002052971.68 3000 crd d N Af kN kN ϕ==⨯⨯=<不满足。
钢结构基础(第二版)课后习题答案

3.7:解:由附录1中附表1可得I20a 的截面积为3550mm 2,扣除孔洞后的净面积为3249275.213550A n =⨯⨯-=mm 2。
工字钢较厚板件的厚度为11.4mm ,故由附录4可得Q235钢材的强度设计值为215f =N/mm 2,构件的压应力为2155.138324910450A N 3n<≈⨯==σN/mm 2,即该柱的强度满足要求。
新版教材工字钢为竖放,故应计入工字钢的自重。
工字钢I20a 的重度为27.9kg/m ,故19712.19.8169.27N g =⨯⨯⨯=N ;构件的拉应力为215139.113249197110450A N N 3ng<≈+⨯=+=σN/mm 2,即该柱的强度满足要求3.8解:1、初选截面假定截面钢板厚度小于16mm ,强度设计值取215f =,125f v =。
可变荷载控制组合:24kN .47251.410.22.1q =⨯+⨯=, 永久荷载控制组合:38.27kN 250.71.410.235.1q =⨯⨯+⨯= 简支梁的支座反力(未计梁的自重)129.91kNql/2R ==,跨中的最大弯矩为m 63kN .1785.547.2481ql 81M 22max ⋅≈⨯⨯==,梁所需净截面抵抗矩为36x maxnx 791274mm2151.051063.178fM W ≈⨯⨯==γ,梁的高度在净空方面无限值条件;依刚度要求,简支梁的容许扰度为l/250,参照表3-2可知其容许最小高度为229mm 24550024l h min ≈==,按经验公式可得梁的经济高度为347mm 3007912747300W 7h 33x e ≈-=-=,由净截面抵抗矩、最小高度和经济高度,按附录1中附表1取工字钢 I36a ,相应的截面抵抗矩3nx 791274mm875000W >=,截面高度229mm 360h >=且和经济高度接近。
同济大学版钢结构基本原理(第二版)习题参考解答

5.1 影响轴心受压稳定极限承载力的初始缺陷有哪些?在钢结构设计中应如何考虑?5.2 某车间工作平台柱高2.6m,轴心受压,两端铰接.材料用I16,Q235钢,钢材的强度设计值2215/d f N mm =.求轴心受压稳定系数ϕ及其稳定临界荷载. 如改用Q345钢2310/d f N mm =,则各为多少? 解答:查P335附表3-6,知I16截面特性,26.57, 1.89,26.11x y i cm i cm A cm === 柱子两端较接,1.0x y μμ==故柱子长细比为 1.0260039.665.7x x xli μλ⨯=== ,2600 1.0137.618.9y y y l i μλ⨯=== 因为x y λλ<,故对于Q235钢相对长细比为137.61.48λπ==钢柱轧制, /0.8b h ≤.对y 轴查P106表5-4(a)知为不b 类截面。
故由式5-34b 得()223212ϕααλλλ⎡=++⎢⎣()2210.9650.300 1.48 1.482 1.48⎡=+⨯+⎢⎣⨯ 0.354=(或计算137.6λ=,再由附表4-4查得0.354ϕ=)故得到稳定临界荷载为20.35426.1110215198.7crd d N Af kN ϕ==⨯⨯⨯= 当改用Q365钢时,同理可求得 1.792λ=。
由式5-34b 计算得0.257ϕ=(或由166.7λ=,查表得0.257ϕ=)故稳定临界荷载为20.25726.1110310208.0crd d N Af kN ϕ==⨯⨯⨯=5.3 图5-25所示为一轴心受压构件,两端铰接,截面形式为十字形.设在弹塑性范围内/E G 值保持常数,问在什么条件下,扭转屈曲临界力低于弯曲屈曲临界力,钢材为Q235.5.4 截面由钢板组成的轴心受压构件,其局部稳定计算公式是按什么准则进行推导得出的.5.5 两端铰接的轴心受压柱,高10m,截面为三块钢板焊接而成,翼缘为剪切边,材料为Q235,强度设计值2205/d f N mm =,承受轴心压力设计值3000kN (包括自重).如采用图5-26所示的两种截面,计算两种情况下柱是否安全.图5-26 题5.5解答:截面特性计算: 对a)截面:32394112(5002020500260)8500 1.436101212x I mm =⨯⨯⨯+⨯⨯+⨯⨯=⨯ 3384112205005008 4.167101212y I mm =⨯⨯⨯+⨯⨯=⨯ 2250020500824000A mm =⨯⨯+⨯=244.6x i mm ==131.8y i mm ==对b)截面:32384112(4002540025212.5)104009.575101212x I mm =⨯⨯⨯+⨯⨯+⨯⨯=⨯ 33841122540040010 2.667101212y I mm =⨯⨯⨯+⨯⨯=⨯ 24002524001024000A mm =⨯⨯+⨯=199.7x i mm ==105.4y i mm==整体稳定系数的计算:钢柱两端铰接,计算长度10000ox oy l l mm == 对a)截面: 1000040.88244.6ox x x l i λ=== 1000075.87131.8ox y y l i λ=== 对b)截面: 1000050.08199.7kx x x l i λ=== 1000094.88105.4ox y y l i λ=== 根据题意,查P106表5-4(a),知钢柱对x 轴为b 类截面,对y 轴为c 类截面.对a)截面:对x 轴:40.880.440x λπ===()223212x x x x ϕααλλλ⎡=++⎢⎣()2210.9650.30.440.4420.44⎡=⨯+⨯+⎢⨯⎣0.895=(或计算40.88λ=,再由附表4-4查得0.896x ϕ )对y 轴:25.870.816y λπ==()223212y y y y ϕααλλλ⎡=++⎢⎣()2210.9060.5950.8160.81620.816⎡=⨯+⨯+⎢⨯⎣0.604=(或计算75.87λ=,再由附表4-5查得0.604y ϕ )故取该柱的整体稳定系数为0.604ϕ=对b)截面,同理可求得0.852x ϕ=,0.489y ϕ=,故取该柱截面整体稳定系数为0.489ϕ= 整体稳定验算:对a)截面 0.604240002052971.68 3000 crd d N Af kN kN ϕ==⨯⨯=<不满足。
同济大学版钢结构基本原理(第二版)习题参考解答

5.1 影响轴心受压稳定极限承载力的初始缺陷有哪些?在钢结构设计中应如何考虑?5.2 某车间工作平台柱高2.6m,轴心受压,两端铰接.材料用I16,Q235钢,钢材的强度设计值2215/d f N mm =.求轴心受压稳定系数ϕ及其稳定临界荷载.如改用Q345钢2310/d f N mm =,则各为多少?解答:查P335附表3-6,知I16截面特性,26.57, 1.89,26.11x y i cm i cm A cm === 柱子两端较接, 1.0x y μμ== 故柱子长细比为 1.0260039.665.7x x xli μλ⨯===,2600 1.0137.618.9y y y l i μλ⨯===因为x y λλ<,故对于Q235钢相对长细比为137.61.48λπ=== 钢柱轧制, /0.8b h ≤.对y 轴查P106表5-4(a)知为不b 类截面。
故由式5-34b 得()223212ϕααλλλ⎡=++⎢⎣()2210.9650.300 1.48 1.482 1.48⎡=+⨯+⎢⎣⨯ 0.354=(或计算137.6λ=,再由附表4-4查得0.354ϕ=)故得到稳定临界荷载为20.35426.1110215198.7crd d N Af kN ϕ==⨯⨯⨯=当改用Q365钢时,同理可求得 1.792λ=。
由式5-34b 计算得0.257ϕ=(或由166.7λ=,查表得0.257ϕ=)故稳定临界荷载为20.25726.1110310208.0crd d N Af kN ϕ==⨯⨯⨯=5.3 图5-25所示为一轴心受压构件,两端铰接,截面形式为十字形.设在弹塑性范围内/E G 值保持常数,问在什么条件下,扭转屈曲临界力低于弯曲屈曲临界力,钢材为Q235.5.4 截面由钢板组成的轴心受压构件,其局部稳定计算公式是按什么准则进行推导得出的.5.5 两端铰接的轴心受压柱,高10m,截面为三块钢板焊接而成,翼缘为剪切边,材料为Q235,强度设计值2205/d f N mm =,承受轴心压力设计值3000kN (包括自重).如采用图5-26所示的两种截面,计算两种情况下柱是否安全.图5-26 题5.5解答:截面特性计算: 对a)截面:32394112(5002020500260)8500 1.436101212x I mm =⨯⨯⨯+⨯⨯+⨯⨯=⨯ 3384112205005008 4.167101212y I mm =⨯⨯⨯+⨯⨯=⨯ 2250020500824000A mm =⨯⨯+⨯=244.6x i mm ==131.8y i mm==对b)截面:32384112(4002540025212.5)104009.575101212x I mm =⨯⨯⨯+⨯⨯+⨯⨯=⨯ 33841122540040010 2.667101212y I mm =⨯⨯⨯+⨯⨯=⨯ 24002524001024000A mm =⨯⨯+⨯=199.7x i mm ==105.4y i mm==整体稳定系数的计算:钢柱两端铰接,计算长度10000ox oy l l mm == 对a)截面: 1000040.88244.6ox x x l i λ=== 1000075.87131.8ox y y l i λ=== 对b)截面: 1000050.08199.7kx x x l i λ=== 1000094.88105.4ox y y l i λ=== 根据题意,查P106表5-4(a),知钢柱对x 轴为b 类截面,对y 轴为c 类截面.对a)截面:对x 轴:40.880.440x λπ===()223212x x x x ϕααλλλ⎡=++⎢⎣()2210.9650.30.440.4420.44⎡=⨯+⨯+-⎢⨯⎣0.895=(或计算40.88λ=,再由附表4-4查得0.896xϕ)对y 轴:25.870.816y λπ===()223212y y y y ϕααλλλ⎡=++⎢⎣()2210.9060.5950.8160.81620.816⎡=⨯+⨯+⎢⨯⎣0.604=(或计算75.87λ=,再由附表4-5查得0.604yϕ)故取该柱的整体稳定系数为0.604ϕ=对b)截面,同理可求得0.852x ϕ=,0.489y ϕ=,故取该柱截面整体稳定系数为0.489ϕ= 整体稳定验算:对a)截面 0.604240002052971.68 3000 crd d N Af kN kN ϕ==⨯⨯=<不满足。
钢结构基本原理课后习题集答案解析(第二版)

第二章如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图(a )理想弹性-塑性 (b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =σf yCσF图2-35 理想化的σε-图 解: (1)A 点: 卸载前应变:52350.001142.0610y f E ε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=(2)B 点: 卸载前应变:0.025Fεε==卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢结构第二版习题答案

钢结构第二版习题答案1. 材料力学性质:在钢结构设计中,了解材料的力学性质是基础。
习题答案会解释如何根据材料的屈服强度、抗拉强度、弹性模量等参数来选择合适的材料。
2. 构件的应力分析:对于梁、柱、板等基本构件,习题答案会展示如何计算其在不同荷载作用下的应力分布,以及如何判断构件是否满足强度和稳定性要求。
3. 连接节点设计:在钢结构中,连接节点的设计对于整个结构的稳定性至关重要。
习题答案会说明如何根据连接方式(如焊接、螺栓连接等)来设计节点,确保其在受力时的可靠性。
4. 荷载分析:包括静荷载和动荷载的计算方法,习题答案会指导学生如何正确地将各种荷载(如自重、风荷载、雪荷载等)转化为作用在结构上的力。
5. 结构的稳定性分析:对于高层建筑和大跨度结构,稳定性分析是设计中的关键。
习题答案会解释如何评估结构在各种荷载作用下的稳定性,以及如何采取措施提高结构的抗倾覆能力。
6. 抗震设计:在地震多发地区,钢结构的抗震设计尤为重要。
习题答案会介绍抗震设计的原则和方法,包括如何计算地震作用力以及如何设计减震系统。
7. 疲劳分析:对于承受重复荷载的钢结构,疲劳分析是必不可少的。
习题答案会说明如何评估构件在长期重复荷载作用下的疲劳寿命。
8. 施工和维护:习题答案还会涉及到钢结构的施工方法和后期维护问题,包括焊接、螺栓连接的施工技巧,以及如何进行结构的检查和加固。
9. 案例研究:习题答案可能会包含一些实际工程案例,通过案例分析来加深学生对钢结构设计和施工的理解。
结束语:通过这些习题答案的学习,学生可以更深入地理解钢结构设计的复杂性和挑战性,为将来在工程实践中遇到的问题打下坚实的基础。
同时,习题答案也是检验学生学习成果的重要手段,有助于他们发现并弥补知识上的不足。
希望这些答案能为学习钢结构的学生提供帮助,促进他们对这一领域的深入理解和掌握。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4-1解:kN N N N QK Q GK G 420315324.1315312.1=⨯⨯+⨯⨯=+=γγ焊缝质量为三级,用引弧板施焊。
查表得E43焊条的2/185mm N f W t =,Q235钢的2/215mm N f =。
mm bf N t W t 35.11185200104203=⨯⨯=≥ 故取mm t 12=。
4-2解:k k k Q K Q G K G N N N N N N 36.18.04.12.02.1=⨯+⨯=+=γγ焊缝质量为二级,2/215mm N f W t =未用引弧板施焊mm l W 376122400=⨯-=tl Nf W W t =,k W W t N t l f N 36.1== kN t l f N W W t k 3.71336.11237621536.1=⨯⨯==4-4解: 1)焊脚尺寸f h背部尺寸⎪⎩⎪⎨⎧=⨯=≤=⨯=≥mmt h mmt h f f 6.982.12.174.4105.15.1min 1max 1趾部尺寸()()⎪⎩⎪⎨⎧=-=-≤=⨯=≥mmt h mmt h f f 7~62~182~174.4105.15.1min 2max 2 为方便备料,取mm h h h f f f 621===,满足上述要求。
2)轴心力N 的设计值kN N N N Q K Q G K G 4.2481809.04.11801.02.1=⨯⨯+⨯⨯=+=γγ按角钢背与趾部侧面角焊缝内力分配系数可知:等边角钢内力分配系数3.01=be 7.02=b e对角钢趾部取力矩平衡得: 21Ne b N =kN N N be N 52.744.2483.03.021=⨯===kN N N N N 88.1734.2487.07.012=⨯==-=3)焊缝长度。
当构件截面为一只角钢时,考虑角钢与节点板单面连接所引起的偏心影响, W t f 应乘以折减系数0-85。
角钢趾:mm h mm f h N l f W f f W 48813016085.067.01052.7485.07.0311=>=⨯⨯⨯⨯=⋅≥取mm l 1401= (mm h f 1422130=+,取10mm 的整数倍)角钢背:mm h mm f h N l f Wf f W 3606030416085.067.01088.17385.07.0322=<=⨯⨯⨯⨯=⋅≥ 取mm l 3202= (mm h f 3162304=+,取10mm 的整数)4-5解:腹板受到轴心拉力k N 作用kN N N N Q K Q G K G 4.5984408.04.14402.02.1=⨯⨯+⨯⨯=+=γγ焊脚尺寸f hmmt h f 6.55.1max =≥,mm t h f 9~8)2~1(min =-≤取mm h f 6=时,mm h mm f h N l f Wf f W 360602.44516067.02104.5987.023=>=⨯⨯⨯⨯=⨯≥ 不可行;取mm h f 7=时,mm l w 6.381≥,mm h l f w 42060=≤ 可行,mm h l f 6.39526.381=+=,取mm l 400= 取mm h f 9=时,mm l w 8.296≥,mm h l f w 54060=< 可行,mm h l f 8.31428.296=+=,取mm l 320=故最小的焊脚尺寸可取mm 7,钢板搭接长度为mm 400 最大的焊脚尺寸可取mm 9,钢板搭接长度为mm 3204-7解:(1)直接计算法m kN Nl M ⋅=⨯==102.0502262/1.148862407.0101067.0mm N h h l h M ff W f f =⨯⨯==σ23/6.2972407.010507.0mm N h h l h N f f W f f =⨯⨯==τW f f ff f ≤+⎪⎪⎭⎫⎝⎛22τβσ 1606.29722.11.148822≤⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛f f h h 解得:mm h f 85.7= 采用()mmt mmt mmh f 9~82~136.6185.15.18min max =-≤=⨯=≥=,可(2)试算法()⎩⎨⎧=-≤=⨯=≥m m t m mt h f 9~82~136.6185.15.1min max取mm h f 8=2134424087.07.0mm l h l h A W f W e W =⨯⨯===3225376024087.06161mm l h W W e W =⨯⨯⨯==2262/0.186624087.0101067.0mm N l h M W f f =⨯⨯⨯==σ 23/2.3724087.010507.0mm N l h N W f f =⨯⨯⨯==τ222222/160/9.1562.3722.1186mm N f mm N W f f ff =≤=+⎪⎭⎫ ⎝⎛=+⎪⎪⎭⎫ ⎝⎛τβσ,可 故mm h f 8=4-8解:kN R R R k k 405%754.1%252.1=⨯+⨯=mm l 300= mm l h 701080=-=取焊脚尺寸mm h f 6= mm h h f e 2.47.0== (1)几何关系水平焊缝计算长度mm h l l f h Wh 64670=-=-= 全部焊缝计算长度mm l l l Wh W 4286423002=⨯+=+= 全部焊缝有效截面W e W l h A = 形心位置cm h h A l l h x e e WWhWh e 96.08.4224.64.6222=⨯⨯⨯⨯=⋅=略去3e h 项423236.21542304.642.02123042.02212cm l l h l h I Wh e e x =⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛⨯⨯⨯+⨯=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛⋅+=42232238.4796.04.642.096.024.64.642.0124.642.022122cm x l h x l l h l h I Wh e Wh Wh e Wh e y =⨯⨯+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-⨯⨯+⨯⨯=+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-+=焊缝有效截面对形心O 的极惯性矩404.22028.476.2154cm I I I y x =+=+=(2)强度验算kN R V 5.2022== mm x a 4.7080=-= m kN Ra T ⋅=⨯⨯==-3.142104.7040523mm x l x Wh 4.546.9641=-=-= mm ly 15021==↑=⨯⨯⨯==24601/3.35104.22024.54103.14mm N I Tx T fσ ←=⨯⨯⨯==2461/4.97104.2202150103.14mm N I Ty Tfτ↑=⨯⨯==23/7.1124282.4105.202mm N A V V fσ剪力和扭矩共同作用下的强度条件()222222/160/6.1554.9722.17.1123.35mmN f mm N W f Tf f Vf Tf =≤=+⎪⎭⎫ ⎝⎛+=+⎪⎪⎭⎫⎝⎛+τβσσ,可5-1解:QK Q GK G N N N γγ+=则:N N k 8.772560%904.1560%102.1=⨯⨯+⨯⨯=查表,得:钢板螺栓孔壁承压承载力设计值:2/405mm N f b c = 螺栓的强度设计值为:2/190mm N f b v =)(32.1191019044002432kN f d n N bv e vbv =⨯⨯⨯⨯==-ππ)(1621040520203kN tf d N bc b c =⨯⨯⨯=∑=-取)(32.119},min{kN N N N b c b v b == 需要的螺栓数目:48.632.1198.772===b N N n 最少采用7=n试取螺栓距mm mm d p o 655.613≈== 端距mm mm d a o 45412≈== 边距mm mm d c o 3575.305.1≈==因为板宽mm b 250=,若边距为mm 35则不满足间距不大于mm t 12012=要求,故最外排每列螺栓应设3个,取螺栓横向间距为mm 90,端距为mm 45,螺栓数增加为8个。
取螺栓纵向间距为mm 65,边距为mm 35。
第二列布置2个螺栓,符合不大于mm t 24024=的构造要求。
已知,在最外侧螺栓处的截面,钢板受力最大,截面上有3个螺栓孔,其净面积为最小,即:21377020)5.203250()3(mm t d b A o n =⨯⨯-=-=净截面平均拉应力为:2231/205/2053770108.772mm N f mm N A N n =≤=⨯==σ,(1n A 为mm 20钢板面积,f 应该按照mm 20钢板取)可下面再验算拼接板四角处有无块状拉剪破坏的危险。
则每一块板呗抗剪破坏所需之力为)(9.2071021510)5.205.035(1012510)5.205.265245(331kN N =⨯⨯⨯⨯-+⨯⨯⨯⨯-⨯+=--拼缝一侧上、下两块拼接板同时有4角拉剪破坏时所需轴向力为)(8.772)(6.8319.207441kN kN N N >=⨯==因而此处不会发生块状拉剪破坏。
5-4解:2/190mm N f b v = 2/405mm N f b c =设螺栓单列为n 个。
kN P P P k k 544%804.1%202.1=⨯+⨯= m kN Pe T ⋅=⨯⨯==682505442121 (1)单个螺栓受剪承载力设计值: 螺栓杆被剪断承载力:kN f d n N b v vb v 2.721902241422=⨯⨯⨯==ππ螺栓孔承压破坏承载力:kN f t d N b b 56.1424051622=⨯⨯==∑c v min (2)求每列螺栓的个数n 的值。
取b T N N min =由修正公式(5-10):83.535.6135.670102.722106861636=⎪⎭⎫ ⎝⎛-⨯⨯⨯⨯⨯=⎪⎭⎫ ⎝⎛-=n n p mN T n T 取n=6(3)强度验算:螺栓除受扭转作用外,还受到竖向的剪力。
()kN y x Ty N i i i T xi93.47175105354801217510682222622=++⨯+⨯⨯⨯=+=∑∑ ()kN y x Tx N ii i Tyi91.2117510535480128010682222622=+++⨯⨯⨯=+=∑∑ kN nPN P y 67.222==由偏心剪力作用下强度条件:()()()kN N N NN bP yT yi T xi2.7246.6567.2291.2193.47min 2222=≤=++=++,可5-5解:2/140mm N f b v = 2/170mm N f b t = 2/305mm N f b c =设螺栓单列为n 个。
