巧算平均数
掌握计算平均数的方法

掌握计算平均数的方法计算平均数是数学中常用的一种方法,它用于计算一组数据的平均值。
平均数反映了一组数据的集中趋势,帮助我们更好地理解和分析数据。
本文将介绍几种常见的计算平均数的方法。
1. 算术平均数算术平均数是最常见的计算平均数的方法。
它是将一组数据中的所有数值相加,然后除以数据的个数。
算术平均数可以用于计算一组数据的平均成绩、平均年龄等。
例如,计算数列1,2,3,4,5的算术平均数可以按照以下步骤进行:- 将数列中的数值相加:1+2+3+4+5=15- 将总和除以数据的个数:15÷5=3因此,数列1,2,3,4,5的算术平均数为3。
2. 加权平均数加权平均数在某些情况下比算术平均数更为准确。
当不同数据对结果的贡献度不相同时,可以使用加权平均数。
加权平均数的计算方法是先将每个数据与其对应的权重相乘,然后将乘积相加,并且将总和除以权重的总和。
例如,假设一个班级的数学成绩组成为平时成绩占40%,期末考试成绩占60%,那么可以使用加权平均数计算出该班级的数学平均成绩。
3. 几何平均数几何平均数主要用于计算一组数据的乘积平均数。
这种平均数常用于计算比率、增长率等涉及乘法运算的问题。
几何平均数的计算方法是将一组数据中的所有数值相乘,然后开n次方,其中n是数据的个数。
例如,计算数列1,2,3,4,5的几何平均数可以按照以下步骤进行:- 将数列中的数值相乘:1×2×3×4×5=120- 开平方根:√120≈10.954所以,数列1,2,3,4,5的几何平均数约为10.954。
4. 中位数中位数是一组数据中位于中间位置的数值,它将一组数据分为两个部分,使得有一半的数据小于中位数,另一半的数据大于中位数。
中位数可以用来反映数据的集中趋势,并且不受极端值的影响。
计算中位数的方法是将一组数据按照从小到大的顺序排列,然后找出中间位置的数值。
如果数据的个数是奇数,则中位数是位于中间位置的数值;如果数据的个数是偶数,则中位数是中间两个数值的算术平均数。
巧奥数 4年级 第17讲 巧求平均问题

答案
问题
5个数的平均数是32,如果把这5个数从小到大排列, 那么,前3个数的平均数是28,后3个数的平均数是36, 问中间的一个数是多少?
答案
问题 既然这次要考99分,平均分才能到85分,说明这次测验要给前几次测 验补上(99-85)=14分,这样才能使平均分提高到2分,共补了 (14÷2)=7次。加上这一次共测验8次。 分析与解2 (99-83)÷(85-83)=8(次) 分析与解3 设一共测验了x次,则 83×(x-1)+99=85×x x=8
巧求平均问题
四年级奥数- 基础点睛
巧求平均问题
求平均数一般有如下两种方法: 方法1:(基数+每个数与基数的差求和)÷数的个数=平均数 方法2:总数量÷总份数=平均数
宇宇前4次语文测验的平均成绩是90分,第5次测验得了95 分。问他5次测验的平均成绩是多少?
问题
答案
分析1 先求出前4次测验的总分, 加上第5次测验的总分,除以测 验的次数(5次)就得到平均每 次测验的成绩。 解 (90×4+95)÷5=91(分)
问题
答案
一辆汽车在相距450千米的两地间来回行驶,去时每小时行45千米, 返回时每小时行15千米。问这辆汽车往返平均每小时行多少千米?
问题
答案
四年级奥数- 更上层楼
巧求平均问题
有3个小朋友去测体重,小华和小新的平均体重是50千克;小华、小新和小玲3 人的平均体重是48千克。问小玲体重是多少千克?又知小新比小华重4千克,问 他们3人各重多少千克?
问题
有3个小朋友去测体重,小华和小新的平均体重是50千克;小华、 小新和小玲3人的平均体重是48千克。问小玲体重是多少千克?又 知小新比小华重4千克,问他们3人各重多少千克?
算平均数的计算公式

算平均数的计算公式在数学中,平均数是一组数字的总和除以数字的个数。
它是用来表示一组数据的中间值,可以帮助我们了解数据的集中趋势。
平均数的计算公式是非常简单的,但它在日常生活和统计学中都有着广泛的应用。
平均数的计算公式可以表示为:平均数 = 总和 / 数字的个数。
其中,总和是指一组数字的所有数值相加的结果,数字的个数就是这组数字的数量。
通过这个公式,我们可以很容易地计算出一组数字的平均值。
举个例子来说,如果我们有一组数字,2, 4, 6, 8, 10。
我们可以先将这些数字相加起来,得到总和为30。
然后再将总和30除以这组数字的个数5,就可以得到平均数为6。
因此,这组数字的平均数为6。
在日常生活中,平均数的计算公式可以帮助我们更好地理解一组数据的整体情况。
比如,在购物时,我们可以计算出一家超市的平均价格,来了解商品的价格水平。
在学校教育中,老师可以通过计算学生的平均成绩,来评估班级整体的学习水平。
在经济学和统计学中,平均数也被广泛应用来表示一组数据的中心趋势,以便更好地分析和比较不同数据集之间的差异。
除了简单的平均数计算公式外,还有一些其他类型的平均数,比如加权平均数和几何平均数。
加权平均数是指在计算平均数时,给不同数值分配不同的权重。
计算加权平均数的公式可以表示为:加权平均数 = Σ(数值权重) / 总权重。
其中,Σ表示求和,数值和权重分别表示一组数字的数值和权重,总权重表示所有权重的总和。
通过加权平均数的计算,我们可以更加精确地表示一组数据的平均情况,尤其适用于不同数据对结果的影响程度不同的情况。
另外,几何平均数是指一组数字的乘积的n次方根,其中n表示数字的个数。
计算几何平均数的公式可以表示为:几何平均数 = (数值1 数值2 ... 数值n)的1/n次方。
通过计算几何平均数,我们可以更好地表示一组数据的整体增长率或变化趋势,特别适用于表示复合增长率或复利利率的情况。
总的来说,平均数的计算公式是一种非常重要的数学工具,它可以帮助我们更好地理解和分析一组数据的整体情况。
求平均数的方法

求平均数的方法平均数怎么计算,有几种计算的方法?不知道的考生看过来,下面由小编为你精心准备了“求平均数的方法”仅供参考,持续关注本站将可以持续获取更多的资讯!求平均数的方法1、算术平均法用到最多的莫过于算术平均法,考试平均分、平均工资等等,都是用到这个。
=AVERAGE(B2:B11)2、修剪平均法这种用于各种体育比赛的评分比较多,去除异常值,也就是去除最大值、最小值后求平均分。
=(SUM(B2:B11)-MAX(B2:B11)-MIN(B2:B11))/8内置函数法:=TRIMMEAN(B2:B11,0.2)3、加权平均法=SUMPRODUCT(B2:B11,C2:C11)/SUM(C2:C11)4、移动平均法就是每几个值,求算术平均值,这里以4为例。
在第C5输入公式下拉。
=AVERAGE(B2:B5)5、存货的移动平均法计算规则如下:-存货的移动平均单位成本=(原有结存存货的实际成本+本次进货的实际成本)/(原有结存存货数量+本次进货的数量)-本次发出存货的成本=本次发出存货的数量×本次发货前存货的单位成本-本月月末结存存货的成本=月末结存存货的数量×本月月末存货单位成本将相应的规则换成单元格,即可得出。
=(B2*C2+D2*E2)/(C2+E2)拓展阅读:平均值怎么算计算平均值,一般常用的有两种方法:一种是简单平均法,一种是加权平均法。
例如,某企业生产A产品10台,单价100元;生产B 产品5台,单价50元;生产C产品3台,单价30元,计算平均价格。
简单平均法:平均价格=∑各类产品单价/产品种类。
平均价格=(100+50+30)/3 =60(元)。
加权平均法:平均价格=∑(产品单价×产品数量)/∑(产品数量)。
平均价格=(100×10+50×5+30×3)/(10+5+3)=74.44(元)可以看出,简单平均与加权平均计算出来的平均值差距较大,而后者更贴近事实,属于精确计算。
平均数的简便算法

平均数的简便算法平均数的简便算法平均数是统计学中最基本的概念之一,它是指所有数据数值的总和除以数据的个数。
在实际应用中,计算平均数是非常常见的操作。
本文将介绍几种简便算法来计算平均数。
一、简单算术平均数1.定义简单算术平均数是指所有数据之和除以数据的个数。
2.计算公式设有n个数据,分别为a1,a2,...,an,则它们的简单算术平均数为:$$\bar{a}=\frac{a_1+a_2+...+a_n}{n}$$3.优缺点优点:简单易懂,适用于各种类型的数据。
缺点:对于极端值(异常值)比较敏感,容易受到极端值的影响。
二、加权平均数1.定义加权平均数是指每个数据乘以相应权重后求和再除以总权重。
2.计算公式设有n个数据,分别为a1,a2,...,an,相应权重为w1,w2,...,wn,则它们的加权平均数为:$$\bar{a}=\frac{w_1a_1+w_2a_2+...+w_na_n}{w_1+w_2+...+w_n} $$3.优缺点优点:能够对数据进行加权处理,可以更加准确地反映数据的特征。
缺点:需要确定权重,不适用于所有类型的数据。
三、中位数1.定义中位数是指一组数据按照大小顺序排列后处于中间位置的数值。
如果数据个数为偶数,则取中间两个数的平均值作为中位数。
2.计算方法将一组数据按照大小顺序排列后,找出处于中间位置的数值即可。
如果数据个数为偶数,则取中间两个数的平均值作为中位数。
3.优缺点优点:不受极端值影响,能够反映出一组数据的集中趋势。
缺点:只考虑了一部分数据,不能全面反映一组数据的特征。
四、众数1.定义众数是指在一组数据中出现次数最多的那个值。
2.计算方法统计每个数字出现的次数,找出出现次数最多的数字即可。
3.优缺点优点:能够反映出一组数据中最常见的数字。
缺点:可能存在多个众数或没有众数,不能全面反映一组数据的特征。
五、平均增长率1.定义平均增长率是指某个变量在一段时间内的平均增长速度。
多种方法巧求平均数

多种方法巧求平均数□吴国和蔡鑫芹解答平均数问题的关键,在于确定“总数”以及相对应的“总份数”,然后根据“总数÷总份数”求出平均数。
这是求平均数的基本解法,除此以外,还可以用以下方法巧算平均数。
一、假设法例1.一个班有12名男生,平均身高140厘米;有24名女生,平均身高143厘米。
全班同学的平均身高是多少厘米?我是这样解的假设12名男生和24名女生的平均身高都是140厘米,那么全班同学的实际总身高就多出了(143-140)×24=72(厘米)。
把多出的72厘米平均分成12+24=36份,每份与140厘米的和就是全班同学的实际平均身高,即140+(143-140)×24÷(12+24)=142(厘米)。
当然,我们也可以假设12名男生和24名女生的平均身高都是143厘米,那又该怎样算呢?你不妨试试看。
二、画图法例2.小芳与四名同学一起参加健康知识竞赛,那四名同学的成绩分别为66分、92分、83分、79分。
小芳的成绩比五人的平均成绩高8分。
求小芳的竞赛成绩。
我是这样解的要求小芳的竞赛成绩,我们可以通过画图的方法来解。
小芳的成绩四人的平均分五人的平均分8分四人的平均成绩为(66+92+83+79)÷4=80(分),从图中不难看出把小芳比五人平均成绩高的8分,平分给小芳的四名同学,每人能得到8÷4=2(分),这样,四人的平均分加上2分,就得到五人的平均分为80+2=82(分)。
根据小芳的成绩比五人的平均成绩高8分,可知小芳的竞赛成绩为82+8=90(分)。
三、移多补少法例3.下表是本周最高气温记录表。
星期最高气温/℃日24一22二21三22四23五24六25根据此表,求本周平均每天的最高气温是多少?由于每天的气温都在23℃左右,因此可以通过移多补少,使原来几个不相等的数达到相等,同时总数保持不变。
我们不妨把表中最高气温度数按从小到大的顺序排列,然后通过观察,移多补少,问题就能很快解决。
求平均数的方法三种

求平均数的方法三种在数学中,平均数是一组数的总和除以这组数的个数。
它是一种常见的统计量,用来表示一组数据的集中趋势。
在现实生活中,我们经常需要计算平均数,比如计算学生的平均成绩、家庭的平均收入等。
那么,接下来我们将介绍三种常用的求平均数的方法。
1. 算术平均数。
算术平均数是最常见的一种平均数,也是最直观的一种平均数。
计算算术平均数的方法是将一组数的总和除以这组数的个数。
假设有n个数,分别为a1,a2,a3,...,an,那么这组数的算术平均数可以表示为:平均数 = (a1 + a2 + a3 + ... + an) / n。
举个例子,如果我们有一组数:2,4,6,8,10,那么这组数的算术平均数为:(2 + 4 + 6 + 8 + 10) / 5 = 6。
因此,这组数的算术平均数为6。
2. 加权平均数。
加权平均数是一种考虑了权重的平均数。
在某些情况下,不同的数可能具有不同的重要性或者权重,这时候就需要使用加权平均数来计算平均值。
计算加权平均数的方法是将每个数乘以其对应的权重,然后将所有的乘积相加,最后除以总的权重的和。
假设有n个数,分别为a1,a2,a3,...,an,对应的权重分别为w1,w2,w3,...,wn,那么这组数的加权平均数可以表示为:加权平均数 = (a1w1 + a2w2 + a3w3 + ... + anwn) / (w1 + w2 + w3 + ... + wn)。
举个例子,如果我们需要计算一个班级的平均成绩,但是数学成绩的权重是2,语文成绩的权重是1,那么班级的加权平均数可以通过以下公式计算得出:(数学成绩总和2 + 语文成绩总和1) / (学生人数2 + 学生人数1)。
3. 几何平均数。
几何平均数是一组数的乘积的n次方根,其中n为这组数的个数。
计算几何平均数的方法是将一组数相乘,然后开n次方。
假设有n个数,分别为a1,a2,a3,...,an,那么这组数的几何平均数可以表示为:几何平均数 = (a1 a2 a3 ... an)^(1/n)。
平均数的求解方法

平均数的求解方法平均数是统计学中常用的概念,用来表示一组数据的集中趋势。
在实际应用中,我们常常需要计算数据的平均数,从而更好地了解数据的整体特征。
本文将介绍几种常见的平均数求解方法。
一、算术平均数算术平均数也被称为平均值,是最常见的一种求解平均数的方法。
它的计算公式如下:平均数 = 所有数据之和 / 数据个数举个例子来说明,假设有一组数据:80、85、90、95、100。
那么这组数据的平均数计算如下:平均数 = (80 + 85 + 90 + 95 + 100) / 5 = 450 / 5 = 90所以这组数据的平均数为90。
二、加权平均数加权平均数是一种考虑数据权重的求解平均数的方法。
在某些情况下,一些数据可能比其他数据更重要,因此需要对不同数据进行加权处理。
其计算公式如下:加权平均数 = 每个数据值 * 对应的权重之和 / 权重之和的总和假设有一组数据:80、85、90、95、100,对应的权重分别为1、2、3、4、5。
那么这组数据的加权平均数计算如下:加权平均数 = (80*1 + 85*2 + 90*3 + 95*4 + 100*5) / (1+2+3+4+5) = 90.71所以这组数据的加权平均数为90.71。
三、几何平均数几何平均数常用于计算一组数据的比率或增长率。
它的计算公式如下:几何平均数 = 所有数据之积的n次方根举个例子来说明,假设有一组数据:2、4、8、16。
那么这组数据的几何平均数计算如下:几何平均数 = (2 * 4 * 8 * 16)的1/4次方 = 8所以这组数据的几何平均数为8。
四、调和平均数调和平均数常用于计算一组数据的平均速度或平均效率。
它的计算公式如下:调和平均数 = 数据个数 / (所有数据之和的倒数)举个例子来说明,假设有一组数据:2、4、8、16。
那么这组数据的调和平均数计算如下:调和平均数 = 4 / (1/2 + 1/4 + 1/8 + 1/16) = 5.33所以这组数据的调和平均数为5.33。
求平均数的方法

求平均数的方法平均数是统计学中常用的一种描述数据集中趋势的指标,它能够反映出一组数据的集中程度。
在实际生活和工作中,我们经常需要求取一组数据的平均数,以便更好地理解和分析数据。
本文将介绍几种求平均数的方法,希望能够帮助读者更好地掌握这一统计学方法。
首先,最常见的求平均数的方法是算术平均数。
算术平均数是指将一组数据中的所有数值相加,然后除以数据的个数,即可得到平均数。
这是最直观、最简单的一种求平均数的方法,适用于各种类型的数据集。
例如,如果我们有一组数据,5,8,12,15,20,那么这组数据的算术平均数可以通过将这些数相加,然后除以5来得到。
其次,另一种常见的求平均数的方法是加权平均数。
加权平均数是指在计算平均数时,给不同的数据赋予不同的权重,以反映它们在整体中的重要程度。
这种方法常用于处理不同数据之间存在着不同影响力的情况。
例如,在考试成绩中,数学和语文的权重可能不同,这时可以使用加权平均数来计算总平均分。
另外,几何平均数是一种用于计算一组正数的平均值的方法。
它是将所有数值相乘,然后开n次方,其中n为数据的个数。
几何平均数常用于计算比率、指数和百分比等方面。
例如,在计算连续几年的增长率时,可以使用几何平均数来更好地反映出数据的变化趋势。
此外,调和平均数是一种用于计算一组数倒数的平均值的方法。
它是将所有数值的倒数相加,然后除以数据的个数,最后再取倒数。
调和平均数常用于计算速度、比率和周期性数据等方面。
例如,在计算两个人合作完成某项工作的效率时,可以使用调和平均数来更好地反映出他们的合作效率。
最后,除了上述几种常见的求平均数的方法外,还有一些其他特殊情况下的平均数计算方法,如中位数、众数等。
这些方法在不同的数据分布和应用场景下都有其独特的作用和意义。
总之,求平均数是统计学中的一项基本技能,掌握好求平均数的方法对于数据分析和决策具有重要意义。
希望本文介绍的几种方法能够帮助读者更好地理解和运用平均数的计算方法,提高数据分析的能力和水平。
巧算平均分

巧算平均分
作者:陶云娥
来源:《数学小灵通·3-4年级》2015年第07期
数学课上,马老师对同学们说:“昨天我们举行了‘生活与数学’知识竞赛,第一小组7名同学的成绩分别是:88分、82分、90分、80分、84分、86分和78分。
请大家算一算,他们的平均分是多少?看谁算法巧。
”
根据“平均分=总分÷人数”得出,他们的平均分是(88+82+90+80+84+86+78)÷7=588÷7=84(分)。
假设这7名同学都得了最高分90分(作为基数),那么另外6名同学的得分与这个基数相比分别少了90-88=2(分)、90-82=8(分)、90-80=1 O(分)、90-84=6(分)、90-86=4(分)和90-78=1 2(分),一共少了2+8+1 O+6+4+12=42(分),平均每人要减少42÷7=6(分),所以他们的平均分是90-6=84(分)。
把基数定为最低分78分,那么其他6名同学的得分与这个基数相比分别多了10分、4分、12分、2分、6分和8分,一共多了10+4+1 2+2+6+8=42(分),平均每人应增加42÷7=6(分),所以他们的平均分是78+6=84(分)。
把7名同学的成绩从高到低依次排列是90、88、86、84、82、80、78。
可以发现:每相邻两个数的差都是2,数的个数7是单数。
我听妈妈说过,这样一列数中的正中间一个数,就是这列数的平均数,所以他们的平均分就是正中间的84分。
小朋友,你认为哪种算法最巧呢?。
计算简单的平均数找出一组数的平均值

计算简单的平均数找出一组数的平均值平均数是我们在日常生活中经常会用到的一个数学概念。
它代表了一组数的平均值,可以用来描述这组数的集中趋势。
在本文中,我们将介绍如何计算简单的平均数,并演示如何找出一组数的平均值。
一、什么是平均数?平均数是一组数据的总和除以数据的个数得到的值。
它是统计学中最基本的测量指标之一。
我们可以通过求和来获得一组数的总和,并将总和除以数据的个数来得到平均数。
二、计算平均数的步骤计算平均数的步骤如下:步骤一:将一组数相加,得到总和。
步骤二:确定这组数的个数。
步骤三:将总和除以数据的个数,得到平均数。
三、示例演示为了更好地理解如何计算平均数,我们先来看一个简单的示例。
假设有一组数:5,7,9,11,13。
现在我们将演示如何计算这组数的平均值。
步骤一:将这组数相加,得到总和:5 + 7 + 9 + 11 + 13 = 45。
步骤二:确定这组数的个数,这里有5个数。
步骤三:将总和除以数据的个数,得到平均数:45 / 5 = 9。
所以,这组数的平均值是9。
四、应用场景平均数是一种常见的统计指标,在各个领域都有广泛的应用。
以下是一些常见的应用场景:1. 考试成绩:老师可以计算学生的平均成绩来评估整体学习水平。
2. 财务分析:企业可以计算每月销售额的平均数来了解销售趋势。
3. 市场调研:调查员可以计算一组受访者的年龄平均数来了解受访者的整体特征。
五、总结通过本文的介绍,我们了解了计算简单的平均数的方法。
平均数能够帮助我们从一组数中找出其集中趋势,是一种重要的统计指标。
在实际应用中,我们可以根据需要计算不同数据集的平均数,并用它来支持决策和分析工作。
当然,平均数只是统计学中众多测量指标的其中之一,还有更多的概念和方法等待我们去探索和应用。
希望本文对您理解计算平均数有所帮助,同时也能激发您对统计学的兴趣,让您能够更好地应用它于实际生活和工作中。
四年级求平均数的方法

四年级求平均数的方法
平均数问题在四年级学习当中出现的一类问题。
一组数据的和除以这组数据的个数,所得的商叫做平均数。
平均数能较好地反映一组数据的总体情况,也可以用平均数作为比较两组或几组同类数据的一个标准。
具体的解答方法有以下两类:
1、直接求法:利用平均数数量公式“总数量÷总份数=平均数”求出平均数,这是由“均分”思想产生的方法。
2、基数求法:利用公式“(基数×总份数+各数与基数的差的总和)÷总份数=平均数”求出平均数,这是由“补差”思想产生的方法。
平均数的简便算法

平均数的简便算法介绍在统计学和数学中,平均数是最常用的指标之一。
它用于表示一组数据的中心位置,是对数据集中值的一种度量。
平均数可以帮助我们理解数据的整体趋势,并进行比较和分析。
本文将介绍一些简便的算法来计算平均数。
这些算法不需要复杂的数学计算,通常适用于小规模的数据集和快速计算的场景。
我们将详细讨论这些算法的原理和实现方法,并提供示例代码来帮助读者更好地理解。
算法一:简单平均数简单平均数是计算平均数最基本的方法。
它的计算公式如下:平均数=所有数据之和数据个数这个算法非常直观和易于理解。
我们只需要将所有数据相加,然后除以数据的个数,就可以得到平均数。
让我们来看一个简单的例子,计算以下数据集的平均数:Data: [2, 4, 6, 8, 10]计算过程如下:平均数=2+4+6+8+105=6所以,这组数据的平均数是6。
算法二:加权平均数加权平均数是一种在计算平均数时给不同数据赋予不同权重的方法。
这些权重通常是根据数据的重要性或者其他因素来确定的。
计算加权平均数的公式如下:加权平均数=每个数据与对应权重的乘积之和权重之和我们可以使用加权平均数来处理对不同数据有不同重要性的情况。
例如,在某个班级中,数学成绩占总成绩的60%,英语成绩占总成绩的40%。
为了计算学生的综合平均成绩,我们可以使用加权平均数算法。
让我们看一个例子来计算以下数据集的加权平均数:Data: [3, 4, 5]Weights: [0.4, 0.3, 0.3]计算过程如下:加权平均数=(3×0.4)+(4×0.3)+(5×0.3)0.4+0.3+0.3=4.1所以,这组数据的加权平均数是4.1。
算法三:移动平均数移动平均数是一种用于平滑数据的方法。
它通过计算一组连续数据的平均值来减少数据中的噪声和波动。
移动平均数的计算公式如下:移动平均数=某段连续数据的和数据个数移动平均数通常用于时间序列分析和技术指标计算。
平均数的求解

平均数的求解平均数是描述一组数集中“典型”值的一种统计指标,计算平均数的方法通常是将所有数值相加,然后除以总数。
平均数的公式为:平均数 = 总和 / 总数平均数可以反映出一组数据的集中趋势,是统计学中最基本的概念之一。
在实际生活中,我们经常使用平均数来描述某种特征的典型值,比如人口平均年龄、班级成绩的平均分等。
下面将以几个例子来说明如何求解平均数。
例子一:求解一组数的平均数假设有一组数据:2, 4, 6, 8, 10。
我们想知道这组数据的平均数是多少。
解法:将所有数相加,然后除以总数。
即 (2 + 4 + 6 + 8 + 10) / 5 =30 / 5 = 6。
所以这组数据的平均数为6。
例子二:求解一组含有小数的数的平均数假设有一组数据:1.5, 2.5, 3.5, 4.5, 5.5。
我们想知道这组数据的平均数是多少。
解法:将所有数相加,然后除以总数。
即 (1.5 + 2.5 + 3.5 + 4.5 + 5.5) / 5 = 17.5 / 5 = 3.5。
所以这组数据的平均数为3.5。
例子三:求解一组数据中的缺失值平均数假设有一组数据:1, 2, 缺失, 4, 5。
其中有一个值缺失,我们想求解平均数。
解法:将已知值相加,然后除以总数。
即 (1 + 2 + 4 + 5) / 4 = 12 / 4= 3。
所以这组数据的平均数为3。
通过以上例子,我们可以看出平均数的求解方法相对简单,但需要注意以下几点:1. 平均数只适用于数值型数据,对于非数值型数据无法计算平均数。
2. 平均数对极端值(离群值)较为敏感,可能会导致平均数与数据整体情况不符。
在处理含有离群值的数据时,可以考虑使用中位数等其他统计指标。
3. 当数据样本较小时,平均数可能不太准确,容易受到抽样误差的影响。
此时可以考虑使用加权平均数。
综上所述,平均数是一种简单而常用的统计指标,能够有效地描述一组数据的集中趋势。
在实际应用中,我们可以根据数据类型和需求的不同,选择适当的求解方法来计算平均数,以得到准确的结果。
四年级上册数学教案8.1:掌握平均数求解技巧

作为小学数学教师,我们的目标不仅是教授学生基本的计算技能,更是希望学生能够理解数学,懂得如何将数学知识应用到生活中。
这一次,我们要来学习一个重要的数学概念——平均数,并掌握平均数求解技巧。
1.什么是平均数?平均数是数学中的一个概念,通常指一些数的算术平均数。
如果有 n 个数 a1,a2,a3...an,这些数的平均数就是:平均数 = (a1+a2+a3+...+an) / n举个例子,假设学生的语文成绩分别为 98,92,85,77,这些成绩的平均数就是:平均数 = (98 + 92 + 85 + 77 ) / 4 ≈ 882.平均数求解技巧(1)如果已知一些数的平均数以及其中 n-1 个数,就可以通过求出一个数来计算出这些数的平均数了。
例如,一个数的平均数为 n,其中有 n-1 个数的和为 S,这 n 个数的和就是 n^2。
当我们知道 3 个数 2、4、6 的平均数为 4 时,可以通过下列计算来得到第 3 个数的值:3×4−(2+4)=6第 3 个数的值为 6。
(2)如果希望求出一段数据的平均数,但是其中某些数无法得到,可以利用这些已知数的平均数来求得缺失的数。
例如,你知道一段数列的平均数为 6,其中仅知道四个数 1、3、4、5,而不知道剩余两个数。
我们可以通过以下计算来推算剩余两个数:6×6−(1+3+4+5)=17这段数的平均数加上这两个数就是:(1 + 3 + 4 + 5 + 17)/ 6 ≈ 5这样,我们就求出了这段数的平均数。
3.实际生活中的应用平均数是一个常用的数学概念,它可以应用于我们生活的许多方面。
下面,我们就来看一下平均数在哪些场合下有用。
(1)成绩的平均数成绩的平均数是评定学生平均水平最常用的方法之一。
学生们在期末考试中取得的成绩,经过统计计算后,可以得到班级平均数、学校平均数,甚至全省或者全国的平均数。
这些数据可以帮助学生了解自己的学习水平以及其他同学的表现情况。
求均值的高级方法

一、什么是求均值的高级方法呢?
哎呀,咱先来说说均值是啥,均值嘛,简就不是那种简单粗暴的相加再除喽。
二、一种高级方法——加权平均
比如说,咱们算成绩的时候。假如数学成绩占总成绩的60%,语文成绩占40%。你要是想求总成绩的均值,就不能简单把数学和语文成绩直接加起来除以2了。得用加权平均的方法。就拿数学80分,语文70分来说。先算数学的加权分,80乘以60%等于48分,语文的加权分就是70乘以40%等于28分,然后把这两个加权分加起来,48加28等于76分,这个76分就是加权平均后的成绩啦。这加权平均在很多地方都能用呢,像评估投资组合的收益,不同投资产品占比不一样,就得用加权平均来算收益的均值。
七、众数也能和均值联系起来
众数就是一组数据里出现次数最多的那个数。虽然它不是严格意义上的均值,但在某些情况下也能反映数据的集中趋势。比如说1,1,2,3,3,3,4。这里的众数是3。如果数据的分布比较特殊,众数可能是一种很有用的参考,在市场调研里,如果调查消费者最喜欢的颜色,众数那个颜色就是最受欢迎的,也可以从某种程度上看作是一种“均值”的体现,就是大家最倾向的那个值。
六、中位数其实也能当作一种求均值的高级方法
当数据分布不均匀的时候,中位数能很好地反映数据的“中心”。比如说1,2,3,4,10。这里的中位数是3,它就像是一个中间的代表值。有时候中位数比传统的算术平均更能体现数据的真实情况。像统计房价的时候,如果有少数超级豪宅价格特别高,那中位数房价可能比平均房价更能反映普通居民能承受的房价水平。
四、几何平均也很高级哦
几何平均主要用于计算比率或者增长率之类的均值。比如说,有一个投资,第一年增长了20%,第二年增长了30%。要算这两年的平均增长率,可不能简单地(20%+30%)÷2哦。得用几何平均。先把增长率都加上1,变成1.2和1.3,然后相乘得到1.56,再开平方(因为是两年)得到约1.25,再减去1,得到25%,这个25%就是这两年的几何平均增长率。这种方法在金融领域,计算连续期间的平均回报率之类的特别常用。
平均数速算技巧

平均数速算技巧——中位数法在涉及平均数的数学运算题目中,巧妙利用中位数是可以大大简化运算过程的。
将一组数据按大小依次排列,把处在最中间位置的一个数叫做这组数据的中位数。
那么将这个特性移植到自然数列等等差数列中时,中位数即为数列的平均数。
自然数列的中位数特性:1、位置特性:一定在数列的最中间位置。
2、数值特性:为整数或*.5计算方法:a中=(a1+an)÷2下面以例题来说明中位数是如何运用的。
2008年中央国家机关公务员考试真题小华在练习自然数求和,从1开始,数着数着他发现自己重复数了一个数。
在这种情况下,他将所数的全部数求平均数,结果为7.4,请问他重复的那个数是:A.2B.6C.8D.10平均数为7.4显然不符合自然数列的中位数规则。
那么这个自然数列的中位数可能是7.5,即1—14的平均数,1—14的和为105。
由于中间重复数了一个数字,那么他数了15个数,此时的数列和为7.4×15=111。
所以小华数重复的数字为111-105=6。
09公务员考试行测资料分析部分运算技巧举例分数是除法的一种形式,用来表达两个量之间的数量对比关系。
它本身有一些对于我们快速解答题目非常有益处的性质。
性质:当c/d=a/b时,c/d=(a+c)/(b+d)=a/b;当c/d>a/b时,c/d>(a+c)/(b+d)>a/b当c/d(a、b、c、d均是正数)例:节选自2008年北京市行测真题表一 2001年部分省(市)国民经济主要指标及在全国的位次指标省份 GDP(亿元)年末总人口(万人)城镇居民人均可支配收入(元)农民人均纯收入(元)绝对值位次绝对值位次绝对值位次绝对值位次上海 4951 8 1614 25 128831 5871 1湖北 4662 9 5975 9 5856 17 2352 11四川 4422 10 8640 3 6360 15 1987 19福建 4254 11 3440 18 8313 6 3381 7湖南 3983 12 6596 7 6781 11 2299 12黑龙江 3561 13 3811 15 5426 27 2280 13安徽 3290 14 6328 8 5669 21 2020 18北京 2846 15 1383 26 115782 5026 2问:根据各省(市)年末总人口推算,在2001年人均GDP比较中,下列正确的是A.湖北>四川>福建>湖南B.湖北>福建>湖南>四川C.福建>湖北>湖南>四川D.福建>湖北>四川>湖南解析:首先,人均GDP=GDP绝对值÷年末总人口,则湖北、四川、福建、湖南四省的人均GDP分别为4662/5975、4422/8640、4254/3440、3983/6596。
平均数问题巧算
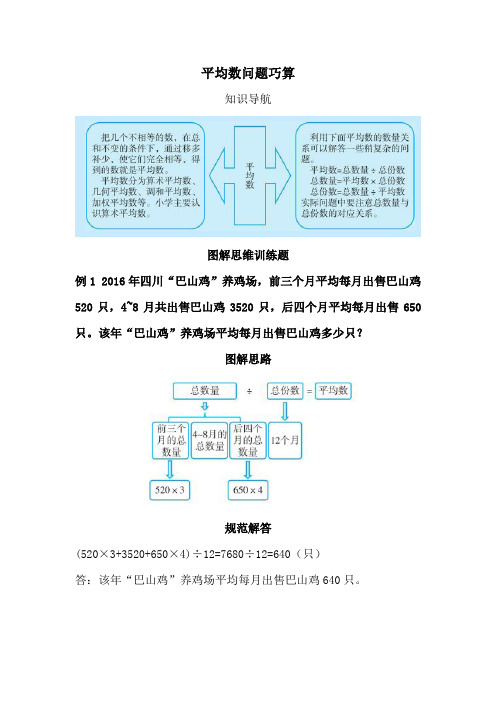
平均数问题巧算知识导航图解思维训练题例1 2016年四川“巴山鸡”养鸡场,前三个月平均每月出售巴山鸡520只,4~8月共出售巴山鸡3520只,后四个月平均每月出售650只。
该年“巴山鸡”养鸡场平均每月出售巴山鸡多少只?图解思路规范解答(520×3+3520+650×4)÷12=7680÷12=640(只)答:该年“巴山鸡”养鸡场平均每月出售巴山鸡640只。
例2五位评委给一位歌手打分,如果去掉一个最高分和一个最低分,平均得分是9.4分;如果只去掉一个最高分,平均得分是9.3分;如果只去掉一个最低分,平均得分是9.5分。
则这位歌手得的最高分与最低分分别是多少?图解思路规范解答最低分:9.3×4-9.4×3=9(分)最高分:9.5×4-9.4×3=9.8(分答:这位歌手得到的最高分是9.8分,最低分是9分。
例3有4人学习小组,在一次数学检测中,已知陈敏、千弘、星伶三位同学的平均分是93分,千弘、星伶、丽杨三位同学的平均分是92分,陈敏和丽杨的平均分是94.5分。
问:陈敏与丽杨各得多少分?图解思路规范解答丽杨:[94.5×2-(93×3-92×3)]÷2=[189-3]÷2=186÷2=93(分)陈敏:94.5×2-93=96(分)答:陈敏96分,丽杨93分。
例4在一次英语检测中,何坤、李想、晓春、玲梅四位同学的分数分别是85分、90分、86分、87分,第五位同学鲁力的分数比他们五个人的平均分多8分,鲁力得了多少分?图解思路鲁力的分数比五个人的平均分多8分,说明鲁力的分数一定比四个人的平均分数高,五个人的平均分也比四个人的平均分数高。
把她比五个人平均分多的8分,平均分给前面4人,每人得2分,也就是五个人的平均分比前四人平均分多2分,就成了五人的平均分。
再加上8分,就是鲁力的分数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1,2,0,3,5,8,4,9,6,2,6,5
计算这组数的平均数:
1 2 0 3 5 8 4 9 6 2 6 5 12 11 12 1.
答:全队同学的平均身高约为 164 厘米.
