电工基础 第三节 正弦量的复数表示法
正弦量的相量表示方法

正弦量的相量表示方法
正弦量的表示方法有: 数学表达式、波形图、 相量表达式
1.1 复数及四则运算
1.复数
在数学中常用 A a bi 表示复数,其中a为实部,b为虚部,i 1
称为虚单位。在电工技术中,为区别于电流的符号,虚单位常用j表示。
+j
3
A
+j
b
P
r
O
4
+1
O
a +1
图4.7 复数在复平面上的表示 图4.8 复数的矢量表示
解
A B (8 j6) (6 j8) 14 j2
A B (8 j6)(6 j8) 10 36.9 10 53.1 100 16.2
正弦量的相量表示方法
1.2 正弦量的相量表示法
给出一个正弦量 u U m sin(t ) 在复平面上作一矢量,如图4.10所示。
(1)矢量的长度按比例等于振幅值U m
(在第四象限)
A1 5 36.9
A2的模 r2 (3)2 42 5
辐角2
arctan
4 3
126.9
则 A2 极坐标形式为
A2 5 126.9
(在第二象限)
正弦量的相量表示方法
例 4.7 写出复数 A 220 60 的三角形式和代数形式。
解 三角形式 A 220(cos60 jsin 60)
u2 2U 2 sin(t 2 ) 40 sin(100t 30) V
电工基础
(2) 复数的三角形式
A r cos jr sin
(3) 复数的指数形式
A re j
(4) 复数的极坐标形式
A r
正弦量的相量表示方法
例4.6 写出复数 A1 4 j3 A2 3 j4 的极坐标形式。 解 A1 的模 r1 42 (3)2 5
03-正弦量的相量表示法知识点

正弦量相量表示1、基本概念(1)正弦电路相量表示方法。
正弦量的相量表示实质上就是用复数表示正弦量。
为与一般的复数相区别,将表示正弦量的复数称为相量。
正弦量的相量表示如表1所示。
表1正弦量的相量式三角函数式相量的极坐标式相量的直角坐标式电压tU u ωsin 2=o 0∠=U U )(o o 0sin j 0cos +=U U 电流)30sin(2o +=t I i ωo 30∠=I I )(o o 30sin j 0cos3+=I I电动势)30sin(2o -=t I e ωo 30-∠=E E)(o o 30sin j 0cos3-=E E (2)相量的实质与目的。
相量表示的实质上就是用复数表示正弦量。
正弦量可用三角函数式、波形图等表示,但以此方法分析正弦交流电路比较困难,引入相量的目的是为了简化正弦交流电路的分析方法,即将正弦交流电路的计算变成复数式的代数运算。
2、正弦交流电路的相量分析方法正弦交流电路引入相量后,正弦交流电路就有相量式法和相量图法两种分析方法。
(1)相量式法1)将电路中已知的正弦量电压、电流、电动势用相量表示;2)将电路中无源元件用阻抗表示,如R 、jX L 、-jX C ;3)用各种电路分析方法求解,所有方程均为相量方程。
一般加减运算用代数式;乘除运算用指数式或极坐标式。
(2)相量图法1)选取参考相量,一般并联电路选电压U 、串联电路选电流I ,复联电路要视具体情况而定;2)以参考相量为基础,根据元件上电压与电流的相位关系画出电路的相量图;3)根据相量的几何关系(平行四边形法则)求解待求物理量。
2、注意事项(1)正弦量与相量间为对应关系,不是“相等”或“等效”关系。
(2)相量法是分析计算正弦交流电路的一种辅助数学工具,可使正弦量的数学运算更为简便,且只适应于同频率的正弦量的分析计算。
(3)分析和计算正弦交流电路时,必要时可借助相量图的几何关系,同一相量图中各正弦量必须频率相同。
电工电子技术基础知识点详解2-1-正弦量的相量表示法(1)
电压的有效值相量
注意:
(1) 相量只是表示正弦量,而不等于正弦量,两者只有对应关系。
? i Imsin(ωt ψ) = Imejψ Im ψ
正弦量是时间的函数,而相量仅仅是表示正弦量的复数,两者不 能划等号!
(2) 只有正弦周期量才能用相量表示,非正弦量不能用相量表示。 因此,只有表示正弦量的复数才能称之为相量。
三角式
r a2 b2b ψ arctan
复数的模 复数的辐角
a
A r cos ψ j r sin ψ r (cos ψ jsin ψ)
2. 正弦量的相量表示 实质:用复数表示正弦量。
+j
b
A
r
(1) 复数表示形式
O
a +1
由欧拉公式:
ej ψ ej ψ
cos ψ
,
2
可得: ej ψ cosψ jsin ψ
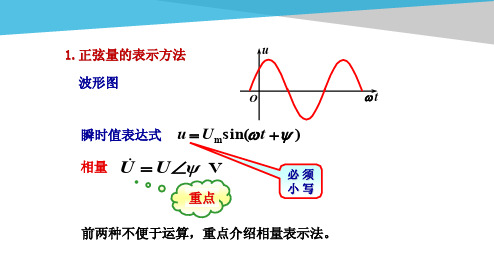
1.正弦量的表示方法
u
波形图
O
t
瞬时值表达式 u Umsin( t )
相量 U Uψ V
必须
重点
小写
前两种不便于运算,重点介绍相量表示法。
正弦量的相量表示法
2. 正弦量的相量表示 实质:用复数表示正弦量 (1) 复数表示形式
设A为复数
代数式 A =a + jb
+j b
r
O
A a +1
式中: a r cos ψ b r sinψ
正弦量的相量表示法
3. 相量的两种表示形式
相量式: U Uejψ Uψ U(cos ψ jsin ψ)
相量图: 把相量在复平面中用有向线段表示出来
U1 220 20V U2 110 45V
正弦量的复数表示法

教后记
教学程序
教学内容
教学方法与
教学手段
一、正弦量的复数表示法
正弦交流电的解析式和复数之间的对应关系可表示为 Nhomakorabea1、电压
u= Usin(ωt+φu0)
=U∠φu0
2、电流
i= Isin(ωt+φi0)
=I∠φi0
例如:
u=220 sin(ωt+30°)V,i=5 sin(ωt-60°)A
将它们表示成有效值的相量式为
二、复数形式的欧姆定律
1、复数形式的欧姆定律
2、电阻、感抗和容抗的复数表示
教学程序
教学内容
教学方法与
教学手段
Ⅰ
Ⅱ
Ⅲ
课前复习
(作业讲评)
新课导入
由于正弦量可以用矢量表示,而复数也可以用矢量表示。因此正弦量也可以用复数表示。确切地说,正弦量和复数之间存在着对应关系,应用这种对应关系,就可以用复数的模表示正弦电压或电流的有效值,用辐角表示正弦电压或电流的初相角。这种与正弦电压(或电流)相对应的复数电压(或电流)称为相量。电压相量和电流相量分别以和表示。
所以,电阻R的复数仍为R,感抗的复数表示为jXL,容抗的复数表示为-jXC。
课堂小结
复阻抗是阻抗的一种新的表达形式,它既能把电压和电流间的相位关系表示出来,又能把电路参数R、XL和XC表示出来。引人复阻抗的概念,得到复数形式的欧姆定律,它既表示出电压和电流有效值间的关系,又给出了它们之间的相位关系。
布置作业
教后记
举例讲解
板书作图
例题1
教后记
教学程序
教学内容
教学方法与
教学手段
解:i1和i2分别用相量表示为
电工基础正弦量的复数表示法ok
2002年4月19日课题正弦量的复数表示法复数形式的欧姆定律课型新授授课日期2002.4.30 授课时数2(总第7~8)教学目标1、掌握正弦量的复数表示法2、掌握复数形式的欧姆定律教学重点复数形式的欧姆定律教学难点公式Z= /与|Z|=U/I板书设计一、正弦量的复数表示法1、电压2、电流3、电压、电流的计算二、复数形式的欧姆定律1、复数形式的欧姆定律2、电阻、感抗与容抗的复数表示教学程序教学内容教学方法与教学手段ⅠⅡⅢ课前复习(作业讲评)新课导入由于正弦量可以用矢量表示,而复数也可以用矢量表示。
因此正弦量也可以用复数表示。
确切地说,正弦量与复数之间存在着对应关系,应用这种对应关系,就可以用复数的模表示正弦电压或电流的有效值,用辐角表示正弦电压或电流的初相角。
这种与正弦电压(或电流)相对应的复数电压(或电流)称为相量。
电压相量与电流相量分别以与表示。
新课讲授教后记教学程序教学内容教学方法与教学手段一、正弦量的复数表示法正弦交流电的解析式与复数之间的对应关系可表示为1、电压u=Usin(ωt+φu0)=U∠φu02、电流i=Isin(ωt+φi0)=I∠φi0例如:u=220sin(ωt+30°)V,i=5sin(ωt-60°)A 将它们表示成有效值的相量式为=220∠30°V,=5∠-60°A这也就是正弦交流电有效值的复数表示式。
上述电压相量与电流相量的相量图,如图所示。
3、电压、电流的计算用相量表示正弦交流电后,正弦交流电路的分析与计算就可以用复数来进行。
例题1、已知两个正弦交流电流为i1=6sin(ωt+120°)A,i2=8sin(ωt+30°)A,用相量来表示它们,并求它们的与。
举例讲解板书作图例题1教后记教学程序教学内容教学方法与教学手段解:i1与i2分别用相量表示为1=6∠120°A2=8∠30°A将复数的极坐标表示式变换为代数表示式,分别为1=6∠120°A=(-3+j5.2)A2=8∠30°A=(6.9+j4)A所以=1+2=(-3+j5.2+6.9+j4)A=(3.9+j9.2)A=10∠67°A最后,将电流相量写成对应的解析式i=10sin(ωt+67°)A。
正弦量的相量表示法

小结:
❖ 正弦量能够用相量表达,正弦量也能够用复数 表达。
❖ 正弦量旳相量旳幅角等于正弦量旳初相角, 相 量旳模等于正弦量旳最大值或有效值。
❖ 为了使计算成果能直接表达正弦量旳有效值, 一般使相量旳模等于正弦量旳有效值,即能够 表达为: U Ue j U
❖ 将几种同频率旳正弦量用相应旳相量表达并画 在同一种坐标平面上,这么旳图叫做相量图。
❖ 在同一量图中,以t=0时刻旳相量表达正弦量。
作业:
❖ 课后复习本节内容。 ❖ 预习下一节“交流电路基本元件”。
谢谢,再见!
2023年9月
( 4 ) 正弦量旳瞬时值=相量虚部
u U
例1: 已知 i1 10 2sin t 30A
+j
试i2 写 5出I21s和inI2旳t 体 6现0式A,并
画出其向量图。
I1 解: i1 和 i2 相应旳电流向量
30
体现式分别为
0 -60
+1
I1 1030 A
I2
I2 5 60A
I1旳长度是I2旳二倍。
例2:
已知 A1 10 j5,A2 3 j4
求
A1 A2 和
A1 A2
。
解: A1 10 j5 11.1826.57
A2 3 j4 553.13
A1 A2 11.1826.57 553.13
55.9079.70
A1 A2
11.1826.57 553.13
2.236 26.56
这么,表达正弦电压 u Umsin t
旳相量为
U m Ume j Um
为了使计算成果能直接表达正弦量旳有 效值,一般使相量旳模等于正弦量旳有效 值,即能够表达为:
电工基础3、3正弦量的相量表示法

3.3.1
1、复数的图形表示
1)复数用点表示
A1=1+j A2=-3 A3=-3-j2 A4=3-j
复数及其运算规律
+j
3
2
Байду номын сангаасA2
1
A1
-3 -2 -1 0 1 2 3 +1
-1
-2
A4
A3
-3
2)复数用矢量表示
复数A在复平面上是一个点,
原点指向复数的箭头称为它的模,
模r与正向实轴之间的夹角称为复 +j
1、复数的表示方法
复数的代数表达式为: A=a+jb 复数的三角形式为: A=rcos θ +jrsin θ
复数的极坐标形式为: A=r θ
复数的指数形式为: A=ae j θ
2、复数的四则运算
加减运算 •A±B=(a1±a2)+j(b1±b2)
乘除运算 A·B=r1r2 θ1+θ2 3、复数与相量的对应关系
A-B=(4-6)+j[5-(-2)]=-2+j7≈7.28 1060
A=4+j5=6.4 51.30
B=6-j2=6.32 -18.40
A×B=6.4×6.32 51.30+(-18.40) =4.04 32.90
A÷B=6.4÷6.32 51.30-(-18.40) =1.01 69.70 第2题课下做练习.
1、复数的几种表示方法
复数的代数表达式为: A=a+jb
复数的三角形式为: A=rcos θ +jrsin θ
复数的极坐标形式为: A=r θ
复数的指数形式为: A=re j θ
2、加减运算
三角函数的复数表示与运算

三角函数的复数表示与运算复数表示法是描述三角函数的常用方法之一。
在这篇文章中,我们将探讨三角函数的复数表示与运算,并介绍它们在实际问题中的应用。
一、三角函数的复数表示三角函数可以表示为一个实部和一个虚部的复数形式。
以正弦函数为例,正弦函数的复数表示可以如下表示:sin(x) = (e^ix - e^(-ix))/(2i),其中,e为自然对数的底,i为虚数单位。
同样地,余弦函数和正切函数的复数表示分别为:cos(x) = (e^ix + e^(-ix))/2,tan(x) = (e^ix - e^(-ix))/(e^ix + e^(-ix))。
其他三角函数如正割、余割和余切的复数表示也可以通过类似的方法得到。
二、三角函数的复数运算基于复数表示法,我们可以利用复数的运算规则对三角函数进行运算。
以下是一些常见的三角函数复数运算:1. 复数的加法和减法:可以直接将两个复数表示的三角函数进行加法或减法运算,实部与实部相加减,虚部与虚部相加减。
例如,sin(x + y) = sin(x)cos(y) + cos(x)sin(y),cos(x + y) =cos(x)cos(y) - sin(x)sin(y)。
2. 复数的乘法和除法:将两个复数表示的三角函数进行乘法运算时,实部和虚部相乘分别得到新复数的实部和虚部。
而除法运算则是将被除数与除数的共轭复数相乘,然后分别除以除数模长的平方。
例如,sin(x)sin(y) = (1/2)[cos(x - y) - cos(x + y)],cos(x)cos(y) =(1/2)[cos(x - y) + cos(x + y)]。
三、三角函数的复数表示在实际问题中的应用三角函数的复数表示在实际问题中有着广泛的应用。
以下是其中几个典型的应用:1. 信号处理:复数表示法可用于分析和处理信号,在音频处理、图像处理等领域有着重要作用,例如频域滤波和傅里叶变换等。
2. 电路分析:在交流电路分析中,复数表示法可以简化计算,并且更加直观地描述电路中电压和电流之间的相位关系。
电路基础-§3-2正弦量的相量表示法

第三章正弦交流电路§3-2 正弦量的相量表示法前面讲述过正弦量的两种基本表示方法,分别用解析式和波形图表示。
前者方便于求出正弦量的瞬时值,而后者形象直观。
但在进行几个正弦量的加减等运算时,用这两种表示法分析就显得比较复杂。
在正弦交流电路中,所有的电压、电流、电动势都是和电源同频率的正弦量,也就是说频率往往是已知的,只要确定了这些正弦量的最大值(有效值)和初相,那么正弦量就完全确定了。
由此,在本节引入正弦量的相量表示法,就是利用复数来表示正弦交流量的一种方法。
它是交流电路分析计算中最为方便的一种。
一、复数(一)复数的四种表示形式1、复数的代数形式。
jba A +=2、复数的三角形式)sin (cos sin cos ψψψψj A A j A A +=+=ψj eA A =ψ∠=A A 3、复数的指数形4、复数的极坐标形式(二)复数的运算1、加减运算复数相加(或相减)时,将实部与实部相加(或相减),虚部与虚部相加(或相减)。
设两个复数:11111ψ∠=+=A jb a A 22222ψ∠=++=A jb a A )()()()(2121221121b b j a a jb a jb a A A ±+±=+±+=±2、乘除运算通常情况下,将复数转化为极坐标形式(或指数形式)来进行乘除运算,更加方便些。
相乘运算时,乘积的模等于各复数的模相乘,乘积的辐角等于各复数幅角相加;相除运算时,商的模等于各复数的模相除,商的辐角等于各复数幅角相减。
即)(2121221121ψψψψ+∠=∠⨯∠=A A A A A A )(212121ψψ-∠=A A A A32.17101j A -=566.82j A +=212121,,A A A A A A -【例3-4】已知两复数求602032.17101-∠=-=j A3010566.82∠=+=j A 7.834.1232.1234.1)532.17()66.810(21∠=+=----=-j j A A 29023010602021j A A =-∠=∠-∠=1002.173302003010602021j A A -=-∠=∠⨯-∠= 解二、正弦量的相量表示法在正弦量的三要素中,只有有效值(或最大值)和初相两个要素是待求的未知量,而数学中的每个复数对应着唯一的模和幅角两个要素,因此,频率已知的正弦量和复数之间存在着对应的关系。
最新2.3 正弦量的相量表示法-J

有效值相量U、I 包含幅度与相位信息。 U、I 19
2、正弦量相量的书写方式
设正弦量: uU m si(ω ntψ )
用相量表示:
U Ujψ eUψ
相量的模=正弦量的有效值 相量辐角=正弦量的初相角
电压的有效值相量 20
3、
由于正弦交流电路中的电压、电 流都是同频率的正弦量,故角频率这 一共同拥有的要素在分析计算过程中 可以略去,只在结果中补上即可。这 样在分析计算过程中,只需考虑最大 值和初相两个要素。 (课本P37)
(3)指数式:由尤拉公式ejθ=cosθ+j sinθ,得
A=r ejθ (4) 极坐标式: 在电路中,复数的模和幅角通 常用更简明的方式表示
A=r∠θ
9
【补充例题】 写出1, -1, j, -j的极坐标式,
并在复平面内做出其矢量图。 (参见课本P36 下至 P37 上)
解:
1)复数1的实部为1, 虚部为0,
2)画在同一个复平面上表示相量的图 称为相量图。 (课本P37)
24
【例】写出下列相量对应的正弦量。 (见课本
P37 例2.10)
(1) U • 22 0 45V,f 5H 0 z
(2)
一般情况下,复数的加减运算应把复数写成 代数式。
12
复数的加减运算还可以用做图法进行: 用平行四边形法则与三角形法则 (参见课本P35—36)
+j B 0
A+B
A +1
平行四边形法则
+j
A+B
0
B
A +1
三角形法则(加法)
+j
B A
0 A-B -B +1 三角形法则(减法)
电工电子技术基础知识点详解2-3正弦量的相量表示

正弦量的相量表示正弦量除了采用三角函数式表示,或者用正弦波形图来表示外,还可以用相量来表示。
相量表示法的基础是复数,即用复数表示正弦量。
要将两个正弦量相加或相减时,这种方法将使计算简便而又形象。
1. 复数复数的表示形式及相互关系设复平面有一复数A ,其模为r ,幅角为ψ ,如图1所示。
它可以用以下几种形式表示;(1) 复数的代数式: b a A j +=22b a r += 复数的模ab arctan =ψ 复数的辐角(2) 复数的三角式:)sin j (cos sin j cos ψψψψ+=+=A A A A(3) 复数的指数式: ψj re A =(4) 复数的极坐标式: ψ∠=r A上述复数的四种表达形式,可以互相转换。
ψψψψ∠==+=+=r re r b a A j )sin j (cos j复数的加减运算可用代数式,复数的乘除运算可用指数式或极坐标式。
说明:数学中虚数用i 表示。
电工中在相量表示时,为了不与电流i 相混淆,改用j 表示虚数。
2.正弦量的相量表示由上可知:复数由模和幅角两个特征来确定,而正弦量由幅值、角频率、初相角三个特征来确定。
在分析线性电路时,正弦激励和响应均为同频率的正弦量,频率是已知的,可以不考虑。
因此,一个正弦量由幅值(或有效值)何初相位就可确定。
比照复数,正弦量可用复数表示。
复数的模即为正弦量的幅值(或有效值)复数的辐角即为正弦量的初相角为了与一般复数相区别,把表示正弦量的复数称相量。
用大写字母加“·”表示。
若已知正弦电压为)sin(m ψω+=t U u ,相量式可写为ψψψψ∠==+=mj m m m )sin j (cos U e U U U 最大值相量 相量的模=正弦量的最大值相量辐角=正弦量的初相角或:ψψψψ∠==+=U e U U Uj )sin j (cos 有效值相量相量的模=正弦量的有效值相量辐角=正弦量的初相角综上所述,正弦量的相量表示,其实质是将同频率的正弦量变换成它的复数形式,这样就把正弦稳态交流电路中繁琐的三角函数运算变换成复数运算,从而简化了运算过程。
周绍敏电工基础第二版-全部-教案

课题1-1电路1-2电流教学目标1.路的组成及其作用,电路的三种基本状态。
2.理解电流产生的条件和电流的概念,掌握电流的计算公式。
教学重点1.电路各部分的作用及电路的三种状态。
2.电流的计算公式。
教学难点对电路的三种状态的理解。
第一节电路一、电路的组成1.电路:由电源、用电器、导线和开关等组成的闭合回路。
2.电路的组成:电源、用电器、导线、开关(画图讲解)。
(1) 电源:把其他形式的能转化为电能的装置。
如:干电池、蓄电池等。
(2) 用电器:把电能转变成其他形式能量的装置,常称为电源负载。
如电灯等。
(3) 导线:连接电源与用电器的金属线。
作用:把电源产生的电能输送到用电器。
(4) 开关:起到把用电器与电源接通或断开的作用。
二、电路的状态(画图说明)1.通路(闭路):电路各部分连接成闭合回路,有电流通过。
2.开路(断路):电路断开,电路中无电流通过。
3.短路(捷路):电源两端的导线直接相连。
短路时电流很大,会损坏电源和导线,应尽量避免。
三、电路图1.电路图:用规定的图形符号表示电路连接情况的图。
2.几种常用的标准图形符号。
第二节电流一、电流的形成1.电流:电荷的定向移动形成电流。
(提问)2.在导体中形成电流的条件(1) 要有自由电荷。
(2) 必须使导体两端保持一定的电压(电位差)。
二、电流1.电流的大小等于通过导体横截面的电荷量与通过这些电荷量所用时间的比值。
qI =t2.单位:1A = 1C/s;1mA = 10-3 A;1μA = 10-6A3.电流的方向实际方向—规定:正电荷定向移动的方向为电流的方向。
提问:金属导体、电解液中的电流方向如何?参考方向:任意假定。
4.直流电:电流方向和强弱都不随时间而改变的电流。
(画图说明练习习题(《电工基础》第2版周绍敏主编)1.是非题(1) ~ (3)小结1.电路的组成及其作用。
2.电路的三种工作状态。
3.形成电流的条件。
4.电流的大小和方向。
5.直流电的概念。
正弦量的复数表示法

或
= /Z
这就是复数形式的欧姆定律。
例题讲解
学生练习
教后记
教学程序
教学内容
教学方法与
教学手段
Ⅳ
Ⅴ
|Z|=U/I
2、电阻、感抗和容抗的复数表示
(1)纯电阻电路
Z= R/ =UR∠φu0/I∠φi0=R
(2)纯电感电路
Z= L/ =UL∠φu0/I∠φi0=XL∠90°=jXL
(3)纯电容电路
Z= C/ =UC∠φu0/I∠φi0=XC∠-90°=-jXC
举例讲解
板书作图
例题1
教后记
教学程序
教学内容
教学方法与
教学手段
解:i1和i2分别用相量表示为
1=6∠120°A
2=8∠30°A
将复数的极坐标表示式变换为代数表示式,分别为
1=6∠120°A=(-3+j5.2)A
2=8∠30°A=(6.9+j4)A
所以
= 1+ 2=(-3+j5.2+6.9+j4)A
=(3.9+j9.2)A
所以,电阻R的复数仍为R,感抗的复数表示为jXL,容抗的复数表示为-jXC。
课堂小结
复阻抗是阻抗的一种新的表达形式,它既能把电压和电流间的相位关系表示出来,又能把电路参数R、XL和XC表示出来。引人复阻抗的概念,得到复数形式的欧姆定律,它既表示出电压和电流有效值间的关系,又给出了它们之间的相位关系。
2006年4月19日
课题
正弦量的复数表示法
复数形式的欧姆定律
课型
新授
授课日期
2006.4.30
授课时数
2(总第7~8)
教学目标
1、掌握正弦量的复数表示法
2、掌握复数形式的欧姆定律
三角函数的复数表示及其性质

三角函数的复数表示及其性质三角函数是数学中重要的函数之一,它们在物理、工程和计算机科学等领域都有广泛的应用。
本文将介绍三角函数的复数表示以及其性质。
一、正弦函数的复数表示及性质正弦函数可以通过欧拉公式进行复数表示。
欧拉公式表示为:e^(ix) = cos(x) + i * sin(x)其中,e是自然对数的底数,i是虚数单位。
根据欧拉公式可以得到正弦函数的复数表示:sin(x) = (e^(ix) - e^(-ix)) / (2i)正弦函数有以下重要性质:1. 奇函数:sin(-x) = -sin(x),即正弦函数关于原点是奇函数。
2. 周期性:sin(x + 2π) = sin(x),正弦函数的周期为2π。
3. 反函数:对于给定的值y,正弦函数的反函数记为arcsin(y),满足-sin(arcsin(y)) = y。
二、余弦函数的复数表示及性质与正弦函数类似,余弦函数也可以通过欧拉公式进行复数表示:cos(x) = (e^(ix) + e^(-ix)) / 2余弦函数有以下重要性质:1. 偶函数:cos(-x) = cos(x),即余弦函数关于原点是偶函数。
2. 周期性:cos(x + 2π) = cos(x),余弦函数的周期为2π。
3. 反函数:对于给定的值y,余弦函数的反函数记为arccos(y),满足cos(arccos(y)) = y。
三、正切函数的复数表示及性质正切函数是正弦函数和余弦函数的商:tan(x) = sin(x) / cos(x)通过正弦函数和余弦函数的复数表示,可以得到正切函数的复数表示:tan(x) = (e^(ix) - e^(-ix)) / (i * (e^(ix) + e^(-ix)))正切函数有以下重要性质:1. 奇函数:tan(-x) = -tan(x),即正切函数关于原点是奇函数。
2. 周期性:tan(x + π) = tan(x),正切函数的周期为π。
3. 反函数:对于给定的值y,正切函数的反函数记为arctan(y),满足tan(arctan(y)) = y。
《复数正弦量的相量表示》

《复数 正弦量的相量表示》 1.复数的实部、虚部和模复数叫虚单位,数学上用i 来代表它,因为在电工中i 代表电流,所以改用j 代表虚单位,即j=-1。
如图4.5所示,有向线段A 可用下面的复数表示为 A =a +j b图4.5 有向线段的复数表示 由图4.5可见, r 表示复数的大小,称为复数的模。
有向线段与实轴正方向间的夹角,称为复数的幅角,用Φ表示,规定幅角的绝对值小于180°。
2.复数的表达方式复数的直角坐标式 :复数的指数形式 :复数的极坐标形式 :实部相等、虚部大小相等而异号的两个复数叫做共轭复数。
用A *表示A 的共轭复数, 则有 A =a +j bA *=a-j b例 写出下列复数的直角坐标形式。
5∠48°;1∠90°; 解:复 数 的 运 算 1复数的加减若两个复数相加减,可用直角坐标式进行。
如:A 1=a 1+j b 1 A 2=a 2+j b 2 则 A 1±A 2=(a 1+j b 1)±a 2+j b 2)=(a 1±a 2)+j (b 1±b 2)即几个复数相加或相减就是把它们的实部和虚部分别相加减。
复数与复平面上的有向线段(矢量)对应,复数的加减与表示复数的有向线段(矢量)的加减相对应, 并且复平面上矢量的加减可用对应的复数相加减来计算。
2.复数的乘除两个复数进行乘除运算时,可将其化为指数式或极坐标式来进行。
)sin (cos sin cos ϕϕϕϕj r jr r jb a A +=+=+=ϕj re A =ϕ∠=r A 72.335.348sin 548cos 5485j j +=︒+︒=︒∠(1)jj =︒+︒=︒∠90sin 90cos 901(2) A 1=a 1+jb 1= 11ϕ∠r A 2=a 2+jb 2=22ϕ∠r)(2121221121ϕϕϕϕ-∠=∠∠=r r r r A A 22b a r +=如将复数A 1=re j φ乘以另一个复数e j α则得同理,如以e j α除复数A 1=re j φ,则得A 1=re j φ-α相量法正弦量的表示方法:三角函数式:波 形 图:相 量 法: 用复数的方法表示正弦量一个正弦量可以用旋转的有向线段表示。
正弦量的表示方法

正弦量的表示方法一、复数的概念及其运算1.复数的有关概念和性质1)虚数单位j规定2j1=−,形如a+bj 的数称为复数,其中a,b∈R。
2)复数的分类(下面的a,b 均为实数)3)复数的相等设复数,那么的充要条件是:且。
4)复数的几何表示复数z=a+bj(a,b∈R)可用平面直角坐标系内点Z(a,b)来表示。
这时称此平面为复平面,x轴称为实轴,y轴除去原点称为虚轴。
这样,全体复数集C与复平面上全体点集是一一对应的。
5)共轭复数a −bj 称为复数的共轭复数,记为,那么z与对应复平面上的点关于实轴对称。
且(1)(2)6)复数的模与复数的向量表示称为复数z=a +bj 的模,记为。
复数的模是非负实数。
特别。
复数在复平面内还可以用以原点O为起点,以点Z(a ,b)为终点的向量OZ来表示。
复数集C和复平面内所有以原点为起点的向量所成的集合也是一一对应的。
(例外的是复数0对应点O,看成零向量。
)7)复数与实数的不同(1)任意两个实数可以比较大小,而任意两个复数中至少有一个不是实数时就不能比较大小。
(2)实数对于四则运算是通行无阻的,但不是任何实数都可以开偶次方.而复数对四则运算和开方均通行无阻。
2.有关计算(1)怎样计算?(先求n被4除所得的余数,(2)是1的两个虚立方根,并且:。
(3)复数集内的三角形不等式是:,其中左边在复数对应的向量共线且反向(同向)时取等号,右边在复数z1、z2对应的向量共线且同向(反向)时取等号。
(4)棣莫佛定理是:(5)若非零复数,则z的n次方根有n个,即:思考:它们在复平面内对应的点在分布上有什么特殊关系?答:它们都位于圆心在原点,半径为的圆上,并且把这个圆n等分。
(6)若,复数z1、z2对应的点分别是A、B,则△AOB(O为坐标原点)的面积是。
(7)复平面内复数z 对应的点的几个基本轨迹:①argz=θ(θ为实常数)↔轨迹为一条射线。
②arg(z −z0)=θ(z是复常数,θ是实常数)↔轨迹为一条射线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
则为
设 Z1= a + jb =|Z1|/ ,Z2 = c + jd = |Z2|/ ,复数的运算规
1.加减法 2.乘法 3.除法 4.乘方
Z1 Z2 = (a c) + j(b d) Z1 · Z2 = |Z1| · |Z2|/ +
Z1 Z1 / Z2 Z2
初相 u = 30,所以它的相量为
= U/u = 220/30 V U
(2) 正弦电流 I 的有效值为 I = 0.7071 4.24 = 3 A,初相 i = 45,所以它的相量为 = I/ = 3/45 A I
i
例2: 将 u1、u2 用相量表示
u1 220 2 sin(ω t 20 ) V
④相量的两种表示形式
Ue jψ U ψ U ( cos ψ jsinψ) 相量式: U 相量图: 把相量表示在复平面的图形
可不画坐标轴
I
U
⑤相量的书写方式 、 I 模用最大值表示 ,则用符号:U m m
பைடு நூலகம்
、 I 实际应用中,模多采用有效值,符号:U
u2 110 2 sin(ω t 45) V
解: (1) 相量式
+j
U 2
U 1
+1
220 20V U 1 110 45 V U 2
(2) 相量图
落后于U U 2 1
U 2
45 20
超前 落后 U 1 ?
【例3】 把下列正弦相量用三角函数的瞬时值表达示,设角频
n Z1 Z1 n
/n
新课教学
第三节 正弦量的复数表示法
正弦量可以用矢量表示,复数也可以用矢量表示,所以正 弦量可以用复数表示,这种复数称为相量,有最大值相量或有 效值相量两种表示方法,但通常用有效值相量表示。其表示方 法是用正弦量的有效值作为复数相量的模、用初相角作为复数 相量的辐角。 正弦电流 i = Imsin( t i)的相量表达式为
率均为 : (1) (2)
=120/37 V ; U
I
= 5/60 A 。
解: u =120 2 sin( t 37) V,i = 5 2 sin( t + 60) A。
【例4】已知 i1 = 3 2sin( t 30 ) A, i2 = 4 2 sin( t 60 ) A。 试求:i1 i2。 解:首先用复数相量表示正弦量 i1、i2,即 I1= 3/30 A = 3(cos30 + jsin30 ) = 2.598 j1.5 A I2 = 4/60 A = 4(cos60 jsin60 ) = 2 j3.464 A 然后作复数加法: I1 + I2 = 4.598 j1.964 = 5/23.1 A 最后将结果还原成正弦量:i1 i2 = 5 2 sin( t 23.1 ) A
小结
正弦量的复数表示法
正弦交流电流 i = Imsin( t i) 的相量表达式为
I/ I i
正弦交流电压 u = Umsin( t u) 的相量表达式为
U/u U
作业
1、完成P156 1题第⑵⑷⑸ ⑹题,2题第⑵⑶⑷题, 3题 第⑶⑷题,4题第⑷题 2、练习册本节内容 3、预习下一节
如:已知u 220 sin(ω t 45 )V 220 j45 j45 U 220 e V e V 则 m 或U 2
用相量表示正弦交流电时,正弦交流电路的分析与计算就 可以用复数进行。 【例1】把正弦量
u = 311sin(314t 30) V,i = 4.24sin(314t 45) A 用相量表示。 解:(1) 正弦电压 u 的有效值为 U = 0.7071 311 = 220 V,
电压的有效值相量
或:
U e U ψ U m m m
jψ
注意:
相量的模=正弦量的最大值
相量辐角=正弦量的初相角
电压的幅值相量
①相量只是表示正弦量,而不等于正弦量。
i Imsin(ω t ψ ) = I me
?
jψ
Im ψ
②只有正弦量才能用相量表示, 非正弦量不能用相量表示。 ③只有同频率的正弦量才能画在同一相量图上。 I U
正弦电压 u = Umsin( t u)的相量表达式为
U m j u U e = U/u 2
I m j I/i I e 2
i
相量: 表示正弦量的复数称相量 设正弦量: u U msin( ω t ψ ) 相量表示:
Ue U
jψ
U ψ
相量的模=正弦量的有效值 相量辐角=正弦量的初相角
