第8章最优消费和投资离散时间
第8章 相关分析-2. 离散相关

第8章 相关分析2. 离散相关与离散序列的卷积运算一样,离散序列的相关运算也可以分为线性相关和循环相关两种类型。
2.1 基本定义线性相互关的计算对应公式(8-1)的离散化形式,计算离散序列][n x 和][n y 的线性互相关,可得:∑+∞-∞=+⋅=i xy n i y i x n r ][][][ (8-6)对有限长度的离散序列][n x ,1,1,0-=L n 、][n y ,1,1,0-=P n ,且二者的长度分别为L 和P 。
那么,有如下公式成立:∑--=+⋅=nP i xy n i y i x n r 10][][][ (8-7)当P n i ≥+时,0][=+n i y ,所以公式(8-7)中的求和上限为n P --1。
因为序列][n r xy 下标n 的取值范围为:11-≤≤-P n M ,所以与线性卷积的长度一样,序列][n x 和][n y 的线性互相关序列的最大长度也是1-+P L 。
与离散Fourier 变换的相关特性对应的是循环相关(或称圆周相关),循环互相关的定义已在第二章中出现过,笔者在下面重新书写一遍。
∑-=+⋅=10])[(][][N i N xy n i y i x n r (8-8)其中,N n i )(+表示)(n i +除以N 的余数,][n r xy 下标n 的取值范围为:2/2/N n N <≤-。
可以利用循环相关来计算两个序列的线性相关,只是要对原有序列进行补零处理。
把长度为L 的序列][n x 和长度为P 的序列][n y 补零后拓展序列长度为N 的新序列][n x 和][n y ,只要满足1-+≥P L N ,两个新序列的循环相关就等同于原有两个序列的线性相关。
与连续函数的互相关函数一样,互相关序列][n r xy 既不是偶序列,也不是奇序列,但满足等式:][][n N r n r yx xy -=。
2.2 快速算法计算两个长度相等的序列的循环相关时,如果直接采用公式(8-8)的定义,计算量是非常大的,尤其在N 较大的情况下。
第八章资产组合理论

如果我们的资产组合中的风险资产仍然 是债券基金与股票基金,但是,现在我 们也投资于年收益率为5%的无风险的国 库券,那会发生什么情况呢?我们从图 解开始,图8 - 6显示了根据表8 - 1计算出 的股票基金与债券基金的联合概率分布 的机会集合。
两条可能的资本配置线( C A L)从无风险 利率( rf=5%)连到两种可行的资产组合。
8.2 两种风险资产的资产组合
在上一节我们考虑了几种证券等权重的分散资 产组合。现在开始研究有效分散,这可以构建 任意给定期望收益条件下的最低风险的资产组 合。
两种资产的资产组合相对易于分析,它们体现 的原则与思考可以适用于多种资产的资产组合。 我们将考察一个包括两个共同基金的资产组合, 一个是专门投资于长期债券的债券资产组合D, 一个是专门投资于股权证券的股票基金E,表8 - 1列出了影响这些基金收益率的参数,这些参 数可以从真实的基金中估计得出。
在上一节,我们推导了资产组合中两种风险资产的比例, 在此基础上,我们引入第三种选择—无风险的资产组合。 这可以使我们处理好资金在三种关键资产:股票、债券与 无风险货币市场证券之间的配置,一旦投资者掌握了这个 原则,他将可以很容易地构造由多种风险资产组成的资产 组合。
最优风险资产组合:两种风险资产和一种 无风险资产
低于组合中各个资产的标准差。
信号与系统 第8章 离散时间系统的时域与变换域分析

4
8.1.1 线性时不变离散时间系统
例8.1-1 设某离散系统激励x[n]与响应y[n]之间的关系为
y[n] = nx[n],判断该系统是否为线性时不变系统。
1 M2
1
M2
k M1
(x1[n
k]
x1[n
k ])
1
M2
1
M2
M1 M 2 1 kM1 x1[n k] M1 M 2 1 kM1 x2[n k]
y1[n] y2[n]
该系统满足叠加性,所以该系统是线性系统。
(3)假设输入信号为x[n]= x1[n-m],则输出信号为
y[n]
y[n] = x[n] + ay[n-1] = a n
此范围仅限于n ≥ 0,
故
y[n] = anu[n] 12
8.2 常系数线性差分方程的求解
N
M
ak y[n k] br x[n r]
k 0
r0
(8.2-2)
8.2.1 线性常系数差分方程的时域经典法求解
一般地,常系数线性差分方程的解由齐次解和特解组成。
的完全解。
其中激励信号为x[n] n2,且边界条件为 y[1] 1
解:(1)齐次解为 yh[n] C(2)n
(2)将 x[n] n代2 入差分方程的右端,得自由项为
2n 1
从而特解为 yp[n] D1n D2
其中,D1和D2为待定系数,代入原方程得
3D1n 3D2 2D1 2n 1
第8章_离散模型(投影版)
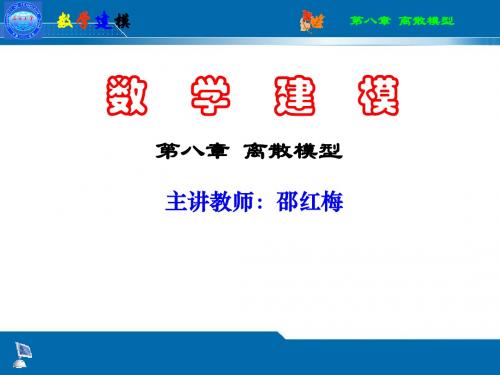
A的秩为1,A的惟一非零特征根为n
由成对比较阵求 A的任一列向量都是对应于特征根n的特征向量
A的归一化特征向量可作为权向量
权向量的特征根 法
对于不一致(但在允许范围内)的成对比较阵A,建议用对应于最大特征 根λ的特征向量作为权向量w ,即A w = A λ 层次分析模型
数学建模
一致性检验 对A确定不一致的允许范围 n阶一致阵A的惟一非零特征根为n
aij · ajk=(wi / wj) · (wj / wk)= wi / wk= aik
所以当aij离一致性的要求不远时, 表示诸因素 n阶一致阵A有下列性质 C1 ,…,Cn对上 A的特征根和特征向量也与一致阵的相差不大。
如果一个正互反阵A满足aij · ajk = aik , i,j,k = 1,2,…,n 因为矩阵A的特征根和特征向量连续地依赖于矩阵的元素aij, 则A称为一致性矩阵,简称一致阵。
随机一致性指标RI的数值 4 0.90 5 6 7 n RI 1 0 2 0 3 0.58 8 9 10 11
计算A'的一致性指标 CI 1,2阶的正互反 是因为
表中n = 1,2时RI = 0,
随机一致性指标RI之比称为一致性比率CR。 CI A的不一致程度在容许范围之内,可用其 CR 0.1 RI 特征向量作为权向量:通过一致性检验 层次分析模型
1.12 1.24 1.32 1.41 1.45 1.49 1.51 0.1的选取是带有 一定主观信度的 对于n≥3的成对比较阵A,将它的一致性指标 CI与同阶(指n相同)的
数学建模
第八章 离散模型
―选择旅游地”中准则层对目标的权向量及一致性检验
3 1 1/ 2 4 3 2 1 7 5 5 A 1 / 4 1 / 7 1 1 / 2 1 / 3 1 / 3 1 / 5 2 1 1 当检验不通过时, 1 1 / 3 1 / 5 3 1 要重新进行成对比较, 或对已有的A进行修正。
信号与系统_第八章 z变换、离散时间系统的z域分析

Re(z)
C是包围X(z)zn-1所有极点之逆时针闭合积分路线,通常选 择z平面收敛域内以原点为中心的圆。
➢ 求X(z)的反z变换的三种方法 ✓留数法 ✓幂级数展开和长除法 ✓部分分式展开法
中国民航大学 CAUC
8.3 逆z变换
二、部分分式展开法求逆z变换(1)
✓ 步骤 (1)将X(z)除以z,得到X(z)/z=X1(z); (2)将X1(z)按其极点展成部分分式(其方法与拉氏变换 的部分分式展开完全一致);
3.x(n)为左边序列
x(n)是无始有终的序列,即当n n2 时, x(n)=0 。
X (z)
n2
x(n)
z
n
x(n)z n
jIm(z)
n
n n2
✓若n20,0z RX2
0
RX2 Re(z)
✓若n20,0z RX2
中国民航大学 CAUC
8.2 z变换的收敛域
4.x(n)为双边序列
x(n)是从n =延伸到n = 的序列 。
(3)X(z)=zX1(z),得到X(z)的部分分式展开式;
(4)对X(z)的每一个部分分式进行反z变换,就得到X(z) 对应的序列x(n)。
[例]求 X (z)
z2
( z 1) 的逆z变换。
(z 1)( z 0.5)
中国民航大学 CAUC
8.3 逆z变换
二、部分分式展开法求逆z变换(2)
[例]求收敛域分别为z1和 z1 两种情况下, X (z) 1 2z 1
➢X(z)收敛域的确定必须同时依赖于 ✓ 序列的性质(有限长,右边,左边,双边) ✓ 是对x(n)进行单边还是双边z变换 ✓ X(z)的极点
中国民航大学 CAUC
信号与系统第8章 离散时间系统的z域分析

零状态响应为
Yf
(z)
(1 z 1 z 2 ) 2 3z 1 z 2
1 1 z 1
1/ 6 0.5 5 / 6 1 z1 1 z1 1 0.5z1
yf [k] Z 1{Yf (z)}{1/ 6 0.5(1)k (5/ 6)(0.5)k}u[k]
y[k] yx[k] yf [k] {1/ 6 3.5(1)k (4 / 3)(0.5)k}u[k]
离散时间信号与系统的Z域分析
• 离散时间信号的Z域分析 • 离散时间系统的Z域分析 • 离散时间系统函数与系统特
性
离散时间信号的Z域分析
• 理想取样信号的拉普拉斯变换 • 单边Z变换定义 • 单边Z变换的收敛域 • 常用序列的Z变换 • 单边Z变换的性质 • Z反变换
理想取样信号的拉普拉斯变换
fs (t) f (t) (t kT) f (kT) (t kT)
Re(z)
三、常用序列的Z变换
1) Z{ (k)} 1, z 0
2) 3)
Z{u(k)} 1 1 z
Z{aku(k)}
1 , 1
1 a
z
z
1
1 z
a
4)
Z{e
j0k
u(k
)}
1
e
1
j0
z
1
z z e j0
5)
Z{e-
j0k u (k
)}
1
1 e- j0
z
1
z z e- j0
z e j0 z e j0
解代数方程
二阶系统响应的z域求解
y[k] a1 y[k 1] a2 y[k 2] b0 f [k] b1 f [k 1] k 0
初始状态为y[1], y[2] 对差分方程两边做Z变换,利用
离散数学第8章图论
第8章 图论
两图同构的必要条件:
(1) 结点数相等; (2) 边数相等; (3) 度数相同的结点数相等。 但这不是充分条件。例如下图中(a)、(b)两图虽然满足以上 3条件,但不同构。(a)中的x应与(b)中的y对应,因为次数都是3。 但(a)中的x与两个次数为1的点u,v邻接,而(b)中的y仅与一个次数 为1的点w邻接。
A
C
B
第8章 图论
8.1 图的基本概念
8.1.1 图 定义8.1―1 一个图G是一个三重组〈V(G),E(G),ΦG〉,其中
V(G)是一个非空的结点(或叫顶点)集合,E(G)是边的集合,ΦG是从
边集E到结点偶对集合上的函数。一个图可以用一个图形表示。 例1设G=〈V(G),E(G),ΦG〉,其中V(G)={a,b,c,d},E(G)={e1,e2,e3,e4, e5,e6,e7},ΦG(e1)=(a,b),ΦG(e2)=(a,c),ΦG(e3)=(b,d), ΦG(e4)=(b,c),ΦG(e5)=(d,c),ΦG(e6)=(a,d),ΦG(e7)=(b,b)
第8章 图论
定理8.2―2在一个具有n个结点的简单图G=〈V,E〉
中,如果经v1有一条简单回路,则经v1有一条长度不超过n 的基本回路。
定义 8.2―3 在图 G=〈V,E〉中 , 从结点 vi 到 vj 最短路径
的长度叫从 vi 到 vj 的距离 , 记为 d(vi,vj) 。若从 vi 到 vj 不存在 路径,则d(vi,vj)=∞。 注意,在有向图中,d(vi,vj)不一定等于d(vj,vi),但一般地 满足以下性质:
其中V3=V1∩V2,E3=E1∩E2,记为G3=G1∩G2。 (3)G1与G2的差,定义为图G3=〈V3,E3〉,记为G3=G1-G2。 其中E3=E1-E2,V3=(V1-V2)∪{E3中边所关联的顶点}。 (4)G1与G2的环和,定义为图G3=〈V3,E3〉, G3=(G1∪G2)-(G1∩G2),记为G3=G1G2。
陈后金《信号与系统》(第2版)课后习题(离散时间信号与系统的z域分析)

第8章离散时间信号与系统的z域分析8-1 根据定义求以下序列的单边z变换及其收敛域。
解:根据序列单边z变换的定义即可求出上述信号的z变换及收敛域。
8-2 根据单边z变换的位移性质,求以下序列的z变换及其收敛域。
解:单边z变换的位移特性有以下3种形式(8-1)(8-2)(8-3)对于因果序列的位移,利用式(8-1);非因果序列的位移,利用式(8-2)和(8-3)。
(1)利用因果序列的位移特性,有(2)利用因果序列的位移特性,有(3)利用因果序列的位移特性,有(4)利用因果序列的位移特性,有(5)由于,直接应用指数信号的z变换,可得(6)将改写成,利用因果序列的位移特性,可得8-3 根据z变换的性质,求以下序列的单边z变换及其收敛域。
解:利用z变换的性质求信号z变换的关键是根据待分析信号的构成,确定合适的信号作为基本信号,采用相应的z变换性质。
(1)由,以及z域微分特性,有(2)将改写为利用(1)题结果及因果序列的位移特性,可得(3)将改写为利用的z变换及z域微分特性,有故(4)将改写为利用(3)题结论及因果序列的位移特性,可得(5)将改写为利用卷积特性(6)利用(5)题结果及指数加权特性,有8-4 求以下周期序列的单边z变换。
解:周期为N的单边周期序列可以表示为第一个周期序列及其位移的线性组合,即这样,若计算出的z变换,利用因果序列的位移特性和线性特性,则可求得其单边周期序列的变换为(1)可表示为利用的变换及因果序列的位移特性,可得(2)将改写为利用(1)题的结果及卷积特性,可得8-5 已知,利用z变换的性质,求下列各式的单边z变换及其收敛域。
解:本题的关键是判断各信号是经过什么运算得到的,然后根据其运算,利用相应的z变换性质即可求出它们的z变换。
(1)利用因果序列的位移特性,可得(2)利用指数加权特性,可得(3)利用(1)题结果及指数加权特性,可得(4)利用z域微分特性,可得(5)利用(4)题结果及线性加权特性,可得(6)可以表示为,利用卷积特性可得(7)可以表示为,利用卷积特性可得(8)可以表示为,利用因果序列的位移特性及卷积特性,可得8-6 已知因果序列的z变换式,试求的初值和终值解:利用初值定理和终值定理即可求出的初值和终值。
现代投资组合理论知识

哈里▪马科维茨
生于美国伊利诺伊州。在芝加哥大学
1950年获得经济学硕士、1952年博士
学位。
马科维茨是享誉美国和国际金融经济
学界的大师,曾任美国金融学会主席、
管理科学协会理事、计量学会委员和
美国文理科学院院士。 1989年美国运
筹学会、管理科学协会联合授予马科
维茨、冯?诺伊曼运筹学理论奖,以表
分别为j:i, j1
j i, j 1
j i, j 1
(w1w212 w1w313 ) (w2w1 21 w2w3 23 )
(Ewr23pww11w32E(112wn3w2ww2i1rwi3)23)=13 n2ww(2iw3Er2i3)
同理,当i,ij1 n 时 i1
n
其中 w 1 n
第8章 现代投资组合理论
马柯维茨的资产组合理论
马柯维兹(Harry Markowitz)1952年在 Journal of Finance发表了论文《资产组合的选择》,标志着现代 投资理论发展的开端。
马克维茨1927年8月出生于芝加哥一个店主家庭,大 学在芝大读经济系。在研究生期间,他作为库普曼的助 研,参加了计量经济学会的证券市场研究工作。他的导 师是芝大商学院院长《财务学杂志》主编凯彻姆教授。 凯要马克维茨去读威廉姆斯的《投资价值理论》一书。
马的贡献是开创了在不确定性条件下理性投资者进行 资产组合投资的理论和方法,第一次采用定量的方法证 明了分散投资的优点。他用数学中的均值方差,使人们 按照自己的偏好,精确地选择一个确定风险下能提供最 大收益的资产组合。获1990年诺贝尔经济学奖。
第8章 现代投资组合理论
2.现代证券组合理论的基本假设:为了弄清资产是如何 定价的,需要建立一个模型即一种理论,模型应将 注意力集中在最主要的要素上,因此需要通过对环 境作一些假设,来达到一定程度的抽象。
郑君里《信号与系统》(第3版)笔记和课后习题(含考研真题)详解-第8章 z变换、离散时间系统的z域分

(7)
X
z
1 2
n
u
n
u
n
10
z
n
9 n0
1 2
n
z
n
9 n0
1 2z
n
1
1 2z
1 1
10
z 0
2z
X(z)的零、极点分布图如图 8-2-1(g)所示。
(8)
8 / 75
圣才电子书
十万种考研考证电子书、题库视频学习平
X
z
n台
1 2
圣才电子书
十万种考研考证电子书、题库视频学习平
台
第 8 章 z 变换、离散时间系统的 z 域分析
8.1 复习笔记
从本章开始陆续讨论 Z 变换的定义、性质以及它与拉氏变换、傅氏变换的联系。在此 基础上研究离散时间系统的 z 域分析,给出离散系统的系统函数与频率响应的概念。通过 本章,读者应掌握对于离散时间信号与系统的研究,是先介绍 z 变换,然后引出序列的傅 里叶变换以及离散傅里叶变换(第九章)。
4 / 75
圣才电子书
十万种考研考证电子书、题库视频学习平
台
于实轴的直线映射到 z 平面是负实轴;
(3)在 s 平面上沿虚轴移动对应于 z 平面上沿单位圆周期性旋转,每平移 ωs,则沿
单位圆转一圈。
2.z 变换与拉氏变换表达式
Z
x nT X z zesT X s Z
n
u
n
1 3
n
u
n
z
n
n
(3)
X
z
n
1 3
n
u
n
z
n
n0
离散数学第8章

N= 3C(100,3) + 1003 = 1485100
15
基本计数公式的应用(续)
例2 求1000!的末尾有多少个0?
解: 1000!=1000 999 998 … 21 将上面的每个因子分解,若分解式中共有i 个5, j 个2, 那么min(i, j)就是0的个数. 1, …,1000中有
1 2n! (2n 2)! 2! (2n)!
...
n! (2n 2)! 2 (2n 4)! 2 0! 2 2n n!
21
实例(续)
例8 从S={1, 2, … , n}中选择 k 个不相邻的数,有多少种 方法?
解 使用一一对应的思想求解这个问题.
a1, a2, …, ak :k个不相邻的数, 属于集合{1, 2, …, n} b1, b2, …, bk:k个允许相邻的数, 属于集合{1, …, n(k1)} 对应规则是
n 1
k1kn
k
1
n [(k
k 1
1)
1]
k
1
常量外提
n
n(
k 1
k
1)
n k
11
n
n
k 1
n k
11
n1
nk
k0
n
k
1
n2n1
变限
n(n 1)2n2 n2n1 n(n 1)2n2
30
恒等式——变上项求和
n l n 1
8. l0 k k 1, n, k N
证明 组合分析. 令S={a1, a2, … , an+1}为n+1元集合. 等式右边是 S 的 k+1子集数. 考虑另一种分类计数的方
第八章_离散时间系统的z域分析4_北京交通真题库_大学915916通信系统及原

z0
七阶极点
j Im[z]
z
1 3
一阶极点
Re[z]
z 0
27
§8.4 逆z变换
X (z) ZT[x(n)] x(n)zn n
x(n) ZT 1[ X (z)] 1 X (z)zn1dz
2 j C
C是包围X(z)zn-1所有极点的逆时针闭合积分路线,一
般取z平面收敛域内以原点为中心的圆。
n0
n
an zn 1 bn zn
n0
n0
z a, z b
X (z) z 1 b za zb zz
za zb
25
jIm(z)
a
0
Re(z)
jIm(z)
a
0 b
Re(z)
图8.1序列单边Z变换的收敛域
图8.2序列双边Z变换的收敛域
当 z a时,X (z) z 当a z b时,X (z) z z
d s j
j
)
!
d
zs
j
(z
zi )s
X (z)
z
zzi
32
或X (z)
A0
M m1
1
Am zm
z
1
s j 1
Cj (1 zi z1) j
A0
M m1
Am z z zm
C1z z zi
C2 z2 (z zi )2
Cs (z
zs zi )s
Cs
1 zi z1
s
X
(
z
)
z
6
§8.2 z变换的定义、典型序列的z变换
➢ 借助于抽样信号的拉氏变换引出。 ➢ 连续因果信号x(t)经均匀冲激抽样,则抽样信号xs(t)
离散时间信号处理奥本海姆第二版课后答案第八章

第八章 离散傅立叶变换8.1 假设()t x c 是一个周期的连续时间信号,其周期为1ms ,它的傅立叶级数为()()∑-=-=9910/23k kt j kc e a t x π. 对于9>k ,傅立叶系数k a 为零,以采样间隔s T 31061-⨯=对()t x c 采样得到[]n x : []⎪⎪⎭⎫⎝⎛=-6103n x n x c .(a) []n x 是周期的吗?如果是,周期为多少?(b) 采样率是否高于奈奎斯特采样率,也就是说T 是否充分小而且可以避免混叠? (c) 利用k a 求出[]n x 的离散傅立叶级数系数。
解:(a )[]∑∑-=-=⎪⎪⎭⎫ ⎝⎛⨯-==⎪⎪⎭⎫ ⎝⎛=--996299610102333610k kn jkk n k j k c ea e a n x n x ππ而() 1,0,62662==+l ee kn jl n k jππ[][]l n x n x 6+=∴∴ []n x 是周期的,周期为6。
(b )30102-=Ωπ而采样频率为03321012106122Ω>=⨯==Ω--πππT 所以T 足够小,而可以避免混叠。
(c )[][]()()()∑∑∑∑∑∑-=---==-=--=-=--=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛==99335995062506299621011k k l k l lk n k l n j l n kn j l nl j l N n knNeea e a e e a w n x k X πππππ 8.2 设[]n x ~是一个周期为N 的周期序列,[]n x ~还是一个周期为3N 的周期序列。
令[]k X ~表示作为周期为N 的周期序列的[]n x ~的DFS 系数,[]k X ~3表示作为周期为3N 的周期序列的[]n x ~的DFS 系数。
(a) 用[]k X ~表示出[]k X ~3。
(b) 用公式计算[]k X ~和[]k X ~3,当[]n x ~为图P8.2中给定的序列时,证明你在(a)中得出的结果。
第8章 线性离散时间控制系统

一阶保持器复现原信号的准确度与零阶保持器相比有所 提高。但由于在式(8-16)中仍然忽略了高阶微分,一阶保持器 的输出信号与原连续信号之间仍有不同。
第8章 线性离散时间控制系统 由式(8-16)可知,一阶保持器的响应可以分解为阶跃响应
和斜坡输入响应之和。将式(8-16)的微分形式变换成式(8-17) 的差分形式,对应的传递函数为式(8-18)。
第8章 线性离散时间控制系统
图8-6 零阶保持器输入信号与输出信号的关系
第8章 线性离散时间控制系统 下面推导零阶保持器的表达式。利用泰勒级数展开公式,
可以得到
如果略去含 Δt、(Δt)2等项,可得
第8章 线性离散时间控制系统 这就是零阶保持器的公式。由式(8-11)可得零阶保持器输出 信号的完整表达式为
第8章 线性离散时间控制系统
第8章 线性离散时间控制系统
8.1 信号采样与采样定理 8.2 信号保持器 8.3 离散系统的数学模型 8.4 离散系统的稳定性分析 8.5 离散系统的稳态误差 8.6 离散系统的动态性能 8.7 离散系统的校正
第8章 线性离散时间控制系统
8.1 信号采样与采样定理
8.1.1 概述 离散时间系统(简称离散系统)是指系统中全部或一部分
进而输入给计算机控制器。也就是说,采样后的离散信号必 须能够保留有原连续信号的完整或近似完整的信息。因此, 周期T 的设定非常重要。
采样定理(也叫Shannon定理)从理论上给出了必须以多 快的采样周期(或多高的采样频率)对连续信号进行采样,才能 保证采样后离散信号可以不失真地保留原连续信号的信息。 换句话说,采样定理给出了对采样周期的限定条件,即采样周 期要在多短时间之内,才能保证采样后的离散信号保留有采 样之前的连续信号的尽量多的信息。
第8章 最优消费投资决策连续时间解析

第三步:假定在上一步骤中,我们已经求出 了价值函数 J (W , t ) ,就可以把它和它的偏 导数代入在第一步中获得的C *和w *的函数 式中,从而得到它们的显性解(explicit solution)。这时它们仅仅是W 、 r、t、、、 的函数。
综上所述,我们可以把一般最优化条件打包 起来,写成一个由两个一阶条件和一个偏微 分方程构成的方程组
假定投资者决定不留任何遗产,而且 效用函数采用HRHA 形式
解得
结论:风险资产的需求与财富之间存在线性关系,而且 HARA 族函数是惟一能够体现这种线性关系的凹的效用 函数。
多种资产:n 维几何布朗运动
把上述关于两种资产的结论,推广到多种资 产情形并不很复杂。只需要假定2 修改为: 市场上有 n + 1种资产,第0 种仍然是收益为r 的无风险资产,其他n 种为风险资产,它们 的价格运动遵循n 维几何布朗运动:
在以上三种情况下,最优资产组合都可以简化为 这就是上一小节中,假定资产价格遵循几何布朗 运动时,也就是资产价格呈对数正态分布时的结 论。 进一步,令 显然有1TwT=1。wT是最小方差曲线上与无风险借 贷线(no risk borrowing lending line)相切的切 点资产组合。
如何理解该最优资产组合的经济意义呢?可以把( 2-108)式右边分解为两个独立的部分:
互助基金定理
先考虑第二部分即第二项等于0 的情形,下列情形可能会导致第二项为0。 (1)投资机会集方面。这又有两种情况: ① 状态变量Sj,(j=1,2, m)的变化是非随机的,这样就有 gj=0,(j=0,1,2,m); ② 在整个投资期间内市场参数——风险资产收益率、方差、协方差和无风 险资产收益率,都独立于状态变量S(t),即ij=0。 这两种情况下,都会使得=0 ,从而使等(2-108)式的第二项为0,这被 统称为不变投资机会集(constant investment opportunity set)。 (2)效用函数方面。如果投资者引至效用函数J 中财富的边际效用,即W J 不依赖于状态变量 S(t ) ,则这时混合偏导数JW s =0,(s=1,2,m) 。 根据包络条件,这只有当最优消费 C *不依赖于状态变量 S(t ) 时才成立。 如果投资者具有对数形式的效用函数,则间接效用函数 J(W ,S ) 是W 的 函数和S 的函数的简单加总,从而使得(2-108)式中的第二项为0。
最优消费和投资离散时间分析

基本分析框架
典型消费者个人将生存一段时期[0,T],他会有一 个大于0 的初始财富或者说资源禀赋W(0) ;在生 存过程中,他会获得一些非资本(non-capital) 收入(t) (例如工资);在生存的每一天中,他 必须决定把可供支配的财富(资源),用于当前 消费C 和投资积累I 上(投资将提供下一时刻的资 本收入);在最后时刻留下一部分遗产W(T ) 给 后人。这时,两个基本选择问题,即消费多少( 也就是投资多少)和如何投资(资产组合),必 须同时被决定。消费者这种不断的选择行为的目 的就是使得他们终身效用最大化。
简单地说,它表示在每 一时点上,股票价格要 么以4/9 的概率上涨一倍 ,要么以(1-4/9)的概 率下跌一半。用w(0) 和 w(1) 表示该投资者在0、 1 时刻上,投资于风险资 产(股票)上的财富分 额。
(3)投资者的非资本收入为0,效用函数 具有以下特定形式:
U (x) =
(4)为了简化分析,假定投资者也不进行 任何消费,这样最优决策的惟一目标就是 最大化他来自最终财富的期望效用。
所谓随机最优控制,就是试图在一个由随机因素驱动的成 长路径上,通过采用适当的策略来最优化目标函数。这里 的消费多少和如何投资,就是由投资者决定的控制变量( controlled variable )或者说决策(decision),通过一系 列遵循某种原则的最优的决策,即最优策略(policy), 个人可以得到最大的效用满足。这里的原则,指的就是贝 尔曼(Bellman R.)最优化原则(principle of optimality) :
“一个最优策略有这样的特征:无论初始状态和初始决策 是什么,余下的决策在考虑到第一个决策导致的状态的影 响下,都必须是最优的策略。”
第8章 z变换离散时间系统的z变换分析

-n -n
收敛域 为 z >1
3. 斜变序列
间接求 解方法 已知 两边对(z -1)求导
两边乘(z -1)
∴
同理,两边再求导,得
…
4. 指数序列
x(n) a n u(n)
运用留数定理来进行运算。又称为留数法,即
f (n) Res[F ( z )z n1 ]z pm
m
略!
二、幂级数展开法(长除法)
F ( z ) f (n)z n f (0) f (1)z 1 f ( 2)z -2
n 0
!
一般为变量z的有理分式,可用长除法,
例
s = 2,
例题 解
求x(n) = ?
∴
∴
见P60~61,表8-2、8-3、8-4(逆z变换表) 作业:P103,8-5 (1)(2)
8.5 z变换的基本性质
一、线性 若 x(n) ←→ X(z) y(n) ←→ Y(z)
则
Rx1 < |z| < Rx2 Ry1 < |z| < Ry2
ax(n) + by(n) ←→ aX(z) + bY(z)
F ( z ) f (0) f (1) z 1 f (2) z 2
所以
f (0) 0, f (1) 1, f (2) 0, f (3) 3, f (4) 4,
重点!
三、部分分式展开法
一般Z变换式是有理函数
以下研究因果序列的逆变换,即
X(z) (|z|>R) ← Z → x(n)
对于N阶LTI离散系统的差分方程:
离散数学第8章 图论

软件学院
图论原理 两个图同构的必要条件: 1.结点个数相等. 2.边数相等. 3.度数相同的结点数相等. 4.对应的结点的度数相等. 下面是同构的图:
a b c e d 3 5 1 4 2 b c d a f e 2 4 6 1 3 5
软件学院
图论原理
软件学院
图论原理
图的同构 设G=<V,E>和G’=<V’,E’>是图,如果存在双射f:VV’ 且任何 vi,vj∈V,若边(vi,vj)∈E,当且仅当 边(f(vi),f(vj))∈E’, (则称G与G’同构,记作G≌G’. (同构图要保持边的“关联”关系) 例如:右边所示的两个图: a b 1 4 G=<V,E> G’=<V’,E’> c d 3 2 构造映射f:VV’ a 1 b 2 c 3 d 4 a 1 b 2 c 3 d 4
c
d
v2
v4 v6 G2
v3
v5
f g h G1
软件学院
图论原理
欧拉通路的判定方法: 定理:无向连通图G中结点a和b间存在欧拉通路的充分必要 条件是a与b的次数均为奇数而其他结点的次数均为偶数。 如果G有两个奇数度结点:就从一个奇数度结点出发,每当到 达一个偶数度结点,必然可以再经过另一条边离开此结点, 如此重复下去,经过所有边后到达另一个奇数度结点 如果G无奇数度结点,则可以从任何一个结点出发,去构造一 条欧拉路. a b 1 2 c d 4 3
v3
是一个结点,则称此路 是一个回路. 如果一条路中所有边都不同,则称此路为迹或简单通路. 如果一条回路中所有边都不同,则称此回路为闭迹或简 单回路. 如果一条路中所有结点都不同,则称此路为基本通路. 如果一条回路中所有结点都不同,则称此路为基本回路. 一条基本通路一定是简单通路,但是一条简单通路不 一定是基本通路
第八章1Z变换

1.离散时间信号-序列 2.离散时间系统的数学模型 3.常系数线性差分方程的求解 4.离散时间系统的单位样值(冲激)响应 5.卷积 6.反卷积
差分方程与微分方程的转换
差分方程与微分方程:
对连续y(t ), 若在t nT 各点取样值y(nT ), 且T 足够小
y(nT ) n 1 T dy(t ) y 则 dt T
小结
j Im[z]
有限长序列
Re[z ]
1 例:已知 x(n) [u (n) u (n 8)] 3 求其Z变换,并作出极零点图 ,画出收敛域。
n
j Im[z]
右边序列
Rx1
Re[z ]
1 例:已知 x(n) u (n) 3 求其Z变换,并作出极零点图 ,画出收敛域。
例:RC低通滤波器
dy(t ) Rc y (t ) x (t ) dt y (n 1) y (n ) RC y (n) x(n) T T T y (n 1) (1 ) y (n ) x(n) RC RC
课后习题7-26
差分方程可以解决很多实际中的离散问题 习题7-27:海诺塔问题
y(10) 1023
N-1个移动 N-1个移动
汉诺塔:汉诺塔(又称河内塔)问题是源于印度一个 古老传说的益智玩具(也说起源于越南河內附近一個 不知名小村庄的寺庙)。
在印度,有这么一个古老的传说:在世界中心贝拿勒斯(在印度北 部)的圣庙里,一块黄铜板上插着三根宝石针。印度教的主神梵天 在创造世界的时候,在其中一根针上从下到上地穿好了由大到小的 64片金片,这就是所谓的汉诺塔。不论白天黑夜,总有一个僧侣 在按照下面的法则移动这些金片:一次只移动一片,不管在哪根针 上,小片必须在大片上面。僧侣们预言,当所有的金片都从梵天穿 好的那根针上移到另外一根针上时,世界就将在一声霹雳中消灭, 而梵塔、庙宇和众生也都将同归于尽。
第八章两时期模型消费—储蓄决策与信贷市场

第八章两时期模型消费—储蓄决策与 信贷市场
MRSC, C’:当期消费对未来消费的边际替代率
图8.2 消费者的无差异曲线
第八章两时期模型消费—储蓄决策与 信贷市场
4、消费者优化条件
• 消费者最优
第八章两时期模型消费—储蓄决策与 信贷市场
贷款者
图8.3 借出资金的消费者(s>0)实现最优
的实际利率不相等;
2、假设借出资金的实际利率为r1,借入资金 的实际利率为r2,且 r2>r1。
• 政府能以私人市场借出资金利率借款(只 要低于私人借入资金利率即可)
• 李嘉图等价不再成立
第八章两时期模型消费—储蓄决策与 •8-44
信贷市场
预算约束
• 借出资金者(s≥0)一生的预算约束 • 借入资金者(s≤0)一生的预算约束
2、完全基金制(fully-funded)
完全用过去积累的缴款所挣取的利息收入提供保险金的制度。 具体说来,就是一个人在就业期间向政府管理的基金缴款,该 基金随着时间的推移不断生息增值,当这个人退休后,其所获 养老金来自于该基金的利息收入。
第八章两时期模型消费—储蓄决策与 信贷市场
1.现收现付制
• 现收现付制(pay-as-you-go)对工作人口 征收社会保障税,将资金转移给退休人员。
练习:
• 假设y-t=110,y’-t’=110,r=0.1。消费者效 用函数为U=c0.5+(c’)0.5,
• (1)从效用函数求出MRSc,c’ • (2)消费者一生预算约束 • (3)消费者效用最大化时当前期消费和储
蓄 • (4)如果r降为0,(3)结果有何变化?
第八章两时期模型消费—储蓄决策与 •8-25
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
为了找到最优投资比例w(1) ,只要对f [w(1)]求导,并令一阶导数等于0 就可以了, 容易得到:
再考察当股票价格p = 50 时的情形, 我们发现仍 旧可以使用上式。因为
依然表示股票价格上涨一倍的情况下,投资在两种 资产上,给投资者带来的期末财富的期望效用; 而
则是投资机会相对较差时,期末财富的效用水平。 所以最优解还是w(1) =13 /19 ,因此这个最优投 资比例决策独立于1 时刻股票价格和财富的绝对 水平。
逆向归纳法:从倒数第一期,即T -1期开始。 这就是说,我们必须获得t = 1时期,股票 价格在p = 200或者p = 50 两种情况下的最
优投资比例,这是一个单期静态优化问题。 一旦获得了t =1时的相应结果w(1) 和W(1) , 就可以按照同样的结构,进一步推测t = 0
时刻的最优投资比例,从而一层层地逐步 解决了问题。
第8章 最优消费和投资:离散时间
基本分析框架
典型消费者个人将生存一段时期[0,T],他会有一 个大于0 的初始财富或者说资源禀赋W(0) ;在生 存过程中,他会获得一些非资本(non-capital) 收入(t) (例如工资);在生存的每一天中,他 必须决定把可供支配的财富(资源),用于当前 消费C 和投资积累I 上(投资将提供下一时刻的资 本收入);在最后时刻留下一部分遗产W(T ) 给 后人。这时,两个基本选择问题,即消费多少 (也就是投资多少)和如何投资(资产组合), 必须同时被决定。消费者这种不断的选择行为的 目的就是使得他们终身效用最大化。
Байду номын сангаас
目前的任务就是找到 最优的投资决策变量 (最优控制) w(0) 和 w(1) ,使以上最优化 问题得以解决。
模型求解
“向前”推导的方法:即从t = 0 时刻开始,事先 决定一个策略w(0) ,但它是不是最优还不清楚。 根据w(0) ,我们仅仅能够知道t =1时刻的期望财 富水平的函数表达式,但是最大化这个函数得到 的“最优的”w(0) ,并不一定是最优决策过程 [w(0), w(1)]的必然组成部分,除非可以明确地知 道在所有不同情况状态下的w(1) ,并且它是惟一 的。因此向前推导的方法是行不通的。
w(0) =13 /19, w(1) = 13/19
尽管实际的问题要比这个简单的例子复杂得多, 但从上述求解过程中,仍然可以归纳出最优个人 消费/投资决策的动态规划解法的最显著特征—— 即它是向后追溯的。而这正是贝尔曼最优化原理 的体现。
一般情形
现在考察多期离散时间情况下,个人最优 消费/投资决策问题的标准建模方法和它的 一般解法。
目标函数
其中T 是投资者的寿命;C(t) 是 投资者年龄为t 时选择的消费数 量;W (t) 是t 时刻的财富(或 者遗产);Et (.) t是基于t 时刻 所有已经揭示出的信息的条件 期望算子。Ut[C (t), t] 是效用函 数,在整个定义域内,它被假 定是单调递增和凹的;U2[W (T),T] 是基于期末财富或者 说遗产的效用函数(bequest valuation function),它也是单 调递增和凹的。
简单地说,它表示在每 一时点上,股票价格要 么以4/9 的概率上涨一倍, 要么以(1-4/9)的概率 下跌一半。用w(0) 和w(1) 表示该投资者在0、1 时 刻上,投资于风险资产 (股票)上的财富分额。
(3)投资者的非资本收入为0,效用函数 具有以下特定形式:
U (x) =
(4)为了简化分析,假定投资者也不进行 任何消费,这样最优决策的惟一目标就是 最大化他来自最终财富的期望效用。
“一个最优策略有这样的特征:无论初始状态和初始决策 是什么,余下的决策在考虑到第一个决策导致的状态的影 响下,都必须是最优的策略。”
简单地说,这就意味着任何最优过程的最后一段过程必定 是最优的。这一原则将在后面的分析中一再的出现。
简化的例子
假定: (1)典型个人生存两个时期,他可以在两个时点
第一步: t = 1时刻
假定此时的财富W(1) 为任意一正数(它是 由上一期t = 0 时的最优决策所产生的)。 投资到股票上的财富比例为w(1) ,则投向 无风险资产上的就是1- w(1) 。我们来计算 最后的t = 2 时刻,积累的财富的期望效用 是多少。先考虑当股票价格p = 200时的情 形,根据二项树模型:
第二步: t = 0 时刻
根据上面的推理,我们只要知道1 时刻的财 富水平W(1) ,就可以知道最终财富的期望 效用水平是多少,而1 时期的财富水平 W(1) ,也是由同第一步类似的决策过程所 决定的,即:
同样对f [w(0)]求导数,并令一阶导数等于0,得到 最优化条件还是:w(0) = 13 /19 。因此最优投资 决策方案就是:
约束条件
其中 就是非资本收入,广 义上I 泛指各种投资,但这 里实际上仅仅包括对市场上 可交易的有价证券的投资。 经济体系中的风险, 就源自
于非资本收入和投资机会集 合(investment opportunity set)(也即资本收入)的不 确定性。
最优消费/投资决策:离散时间
所谓随机最优控制,就是试图在一个由随机因素驱动的成 长路径上,通过采用适当的策略来最优化目标函数。这里 的消费多少和如何投资,就是由投资者决定的控制变量 (controlled variable )或者说决策(decision),通过一 系列遵循某种原则的最优的决策,即最优策略(policy), 个人可以得到最大的效用满足。这里的原则,指的就是贝 尔曼(Bellman R.)最优化原则(principle of optimality):
上,即t = 0 、1上做决策( t = 3时,他就死亡 了);他被赋予一定量的初始资源W(0) > 0 。 (2)理想化的资本市场上存在两种资产。一种是 无风险的现金或者债券,它的价格在任何时刻都 没有变化,始终为1;另一种是有风险的股票,它 的价格过程假定由以下二项树描绘
股票价格运动的二项树模型
