02 热力学第一定律-3(2学时2011材料)
02热力学第一定律2

一粒粒取走砂粒
P终,V
终
可逆过程 , 外压和内压相差无穷 小,p环境 = p
P始,V
始
T
T
W p环境 dV
V1
V2
pdV
V1
V2
3、可逆过程的体积功:
可逆过程,外压和内压相差无穷小
W pdV
不同过程的体积功
一次 -18 72 二次 -24 48 三次 -26 44 (1)功与过程有 关。同样是膨 胀(压缩)过程, 它们的功各不 相同。
膨胀过程 W/kJ
压缩过程 W/kJ
(2)正、逆过程的功绝对值不相等。W正≠W逆 (3)膨胀次数越多,膨胀功越大。
可逆过程的体积功
P终 p
始
物理化学
第二章 热力学第一定律
第二章
2.1
2.2
热力学第一定律
热力学基本概念
热力学第一定律
2.3
2.4
恒容热、恒压热、焓
变温过程热的计算
第二章 热力学第一定律
2.5 可逆过程和可逆体积功的计算
2.6
2.7 2.8
相变热的计算
化学反应热的计算 气体的节流膨胀
2.1
热力学基本概念
一.系统[体系]和环境
系统(system) 在科学研究时必须先确定研究对象,把 研究的对象称为系统或体系。 环境(surroundings) 系统以外的与系统相联系的那部分物质 称为环境。 隔开系统与环境的界面可以是实际存在 的,也可以是想象的,实际上并不存在的。
根据系统与环境之间的关系,把系统分为三类:
第02章 热力学第一定律 2011-02-24

H2与N2以3:1的比例在绝热钢瓶中反应生成NH3,此过程:
(A) H = 0 (B) p = 0 (C) U = 0 (D) T = 0
3. 理想气体的热力学能和焓 焦耳实验(1845)图2.2.1
§2.4
热
容
或
δQV dU m
CV ,m
或
U m ( )V f (T ) T
热力学第一定律表述之一:
自然界一切物质都有能量,能量有各种不同形式并可互相转 化,在转化过程中总值不变(即能量守恒与转化定律)。
热力学第一定律表述之二:
第一类永动机是造不成的。
热力学第一定律的数学表述: 系统从状态 (1) 状态(2),与环境交换热Q,交换功W, 则有: U2 = U1 + Q + W, 或 U = Q +W dU = Q + W (封闭系统)
4. 过程与途径 系统的一切变化均称之为过程。 在相同的始终态间,可有不同的变化方式,称之为 途径 。状态函数的变化与途径无关!。 常见的过程有: 恒温过程:T2 = T1 = T (环) 恒压过程:p2 = p1 = p (环) 恒容过程:V = 0 绝热过程:无热交换,但可以有功的传递 循环过程:回到初始状态 5. 热力学平衡态(无环境影响下) (1) 热平衡 (2) 力平衡 (3) 相平衡 (4) 化学平衡 T (环)为环境温度 p (环)为环境压力
W 与途径有关,微小变化用W表示(不能用dW).
p(环)
p(环)
A
体积功的计算:
W = Fdl
= p(环) Adl
= p(环) dV
(能否用系统的压力p ?) dl
对于一有限过程:
若环境压力恒定, V1 = p(环)(V2 V1) = p(环)V (恒外压过程) 与恒压过程比较。 V2 V
2.2热力学第一定律

3.焦耳实验 3.焦耳实验
将两个容量相等的容器,放在水浴中, 将两个容量相等的容器,放在水浴中, 左球充满气体,右球为真空。打开活塞, 左球充满气体,右球为真空。打开活塞, 气体由左球冲入右球,达平衡。 气体由左球冲入右球,达平衡。
焦耳实验的讨论, 焦耳实验的讨论,理想气体的热力学能 •水温未变,dT=0,δQ = 0 ;气体由 球向 水温未变, 气体由B球向 水温未变 , A球自由膨胀, = 0 ;因此,dU=0。 球自由膨胀, 因此, 球自由膨胀 δW 。
§2.2 热力学第一定律
1.热力学第一定律 热力学第一定律
是能量守恒定律在热现象领域内的特殊形式,说明热 能量守恒定律在热现象领域内的特殊形式, 在热现象领域内的特殊形式 力学能、热和功之间可以相互转化,但总的能量不变。 力学能、热和功之间可以相互转化,但总的能量不变。 也可以表述为:第一类永动机是不可能制成的。 也可以表述为:第一类永动机是不可能制成的。 第一定律是人类经验的总结。 第一定律是人类经验的总结 第一类永动机(first kind of perpetual motion mechine) 一种既不靠外界提供能量,本身也不减少能量, 却可以不断对外作功的机器称为第一类永动机,它 显然与能量守恒定律矛盾。历史上曾一度热衷于制 造这种机器,均以失败告终,也就证明了能量守恒 定律的正确性。
∂U ∂U ) = 0 ( ∂V T
∂U ∂U ( )T = 0 ∂p
U = f (T )
2.封闭系统热力学第一定律的数学形式 2.封闭系统热力学第一定律的数学形式
∆U = Q + W
对微小变化: dU =δQ +δW 对微小变化 因为热力学能是状态函数, 因为热力学能是状态函数,数学上具有全微 分性质, 表示; 分性质,微小变化可用dU 表示;Q 和W 不是状态 表示,以示区别。 函数, 函数,微小变化用δ表示,以示区别。
热力学第一定律 (2)

末态 p1=50.663kPa V1= 44.8 dm3 T1= 273.15K
求:三个过程的体积功各为多少?
解:
W1=-pamb(V2-V1) = 0(效率为0,完全不可逆)
W2=-pamb(V2-V1) =-50.663103(44.8-22.4) 10-3 J
由热力学第一定律可得:
Qp U W U (p2V2 p1V1) (U2 p2V2)(U1 p1V1) (dp = 0,W’=0)
3.焓的导出:
定义 : H = U + pV 称H为焓,H为状态函数,广延量 于是:
Qp=H2-H1=H 或 : Qp=dH (dp = 0,W′= 0)
H 的计算:基本公式: H= U+ (pV)
热和功不是状态函数,而是过程函数
1)热 Q
系统与环境由温差而引起的能量交换称为热
显热 单纯pVT变化时,系统吸收或放出的热 热 潜热 相变时,T不变,系统吸收或放出的热
反应热 化学反应时,系统吸收或放出的热
2)功
除热之外,系统与环境交换能量的另一种形式
体积功Biblioteka 功 电功电化学一章讨论 非体积功
表面功
p1,V1,T1
W =?
末态2 p2,V2,T2
V2
W W pambdV pambdV
V1
体积功的计算式
(1)恒(外)压过程(isobaric or constant pamb)
恒外压过程:W=-pamb(V2-V1)
恒压过程(pamb=p):W=-p(V2-V1)
(2)自由膨胀过程(free expansion process)
热力学第一定律

热力学第一定律热力学第一定律是热力学的基本原理之一,也被称为能量守恒定律。
它描述了能量的转化和守恒,对于揭示物质的能量变化和热力学性质具有重要的意义。
本文将深入探讨热力学第一定律的概念、原理和应用。
热力学第一定律的概念热力学第一定律是由英国物理学家焦耳在19世纪提出的。
它可以简洁地表述为能量守恒定律,即能量既不能被创造也不能被摧毁,只能在不同形式之间转化。
这意味着一个封闭系统中的能量总量是恒定的,能量既不能消失也不能产生。
当一个系统经历能量的转化时,其总能量保持不变,只是能量的形式和分布发生改变。
热力学第一定律的原理热力学第一定律的原理可以通过以下公式表示:ΔU = Q - W其中,ΔU表示系统内部能量的变化,Q表示系统吸收的热量,W表示系统对外做的功。
这个公式表明,系统内部能量的变化等于系统吸收的热量与系统对外做的功之间的差值。
当系统吸热时,ΔU为正,系统内部能量增加;当系统放热时,ΔU为负,系统内部能量减少;当系统对外做功时,ΔU 为负,系统内部能量减少;当系统由外界做功时,ΔU为正,系统内部能量增加。
热力学第一定律的应用热力学第一定律在工程和科学领域有着广泛的应用。
下面将介绍热力学第一定律的几个重要应用。
1. 热机效率计算热力学第一定律在热机效率计算中起着重要的作用。
热机的效率是指能够转化为有效功的热量与燃料能量之间的比例。
通过热力学第一定律的应用,我们可以计算出热机的效率,从而评估其性能。
2. 平衡热量计算在热平衡过程中,热力学第一定律可以用于计算平衡热量。
平衡热量是指系统从一个状态到另一个状态的过程中吸收或释放的热量。
通过应用热力学第一定律,我们可以计算系统在不同温度下的平衡热量,并进一步了解能量转化过程。
3. 定常流动计算在工程领域中,很多设备和系统都涉及流体的流动。
热力学第一定律可以用于定常流动过程的计算。
这种定常流动的例子包括空调系统、燃料电池、蒸汽涡轮等。
通过应用热力学第一定律,我们可以计算能量损失和效率,从而优化系统性能。
热力学第一定律 课件

(3)若过程的始末状态物体的内能不变,即 ΔU=0,则 W+Q=0 或 W=-Q,
外界对物体做的功等于物体放出的热量。
4.判断是否做功的方法
一般情况下外界对物体做功与否,需看物体的体积是否变化。
(1)若物体体积增大,表明物体对外界做功,W<0;
(2)若物体体积变小,表明外界对物体做功,W>0。
为另一种形式,或者从一个物体转移到别的物体,在转化或转移的过程中,能
量的总量保持不变。
2.意义
(1)能量守恒定律告诉我们,各种形式的能量可以相互转化。
(2)各种互不相关的物理现象——力学的、热学的、电学的、磁学的、
光学的、化学的、生物学的等可以用能量守恒定律联系在一起。
三、永动机不可能制成
1.第一类永动机:人们设想中的不需要任何动力或燃料,却能不断地对
提示前者能制成而后者不能制成。这是因为可以用太阳能、电能等
能源代替石油能源制造出太阳能汽车、电动汽车等,但是不消耗任何能量
的汽车不可能制成,因为它违背能量守恒定律。
2.热力学第一定律与能量守恒定律是什么关系?
提示能量守恒定律是各种形式的能相互转化或转移的过程,总能量保
持不变,它包括各个领域,其范围广泛。热力学第一定律是物体内能与其他
(2)突破了人们关于物质运动的认识范围,从本质上表明了各种运动形
式之间相互转化的可能性。能量守恒定律比机械能守恒定律更普遍,它是物
理学中解决问题的重要思维方法。能量守恒定律与细胞学说、生物进化论
并称 19 世纪自然科学中三大发现,其重要意义由此可见。
(3)具有重大实践意义,即彻底粉碎了永动机的幻想。
外做功的机器。
2.第一类永动机不可制成的原因:违背了能量守恒定律。
(完整版)第二章热力学第一定律.doc
第二章热力学第一定律1、如果一个系统从环境吸收了40J 的热,而系统的热力学能却增加了200J ,问系统从环境中得到了多少功?如果该系统在膨胀过程中对环境作了 10kJ 的功,同时收了 28kJ 的热,求系统的热力学能变化值。
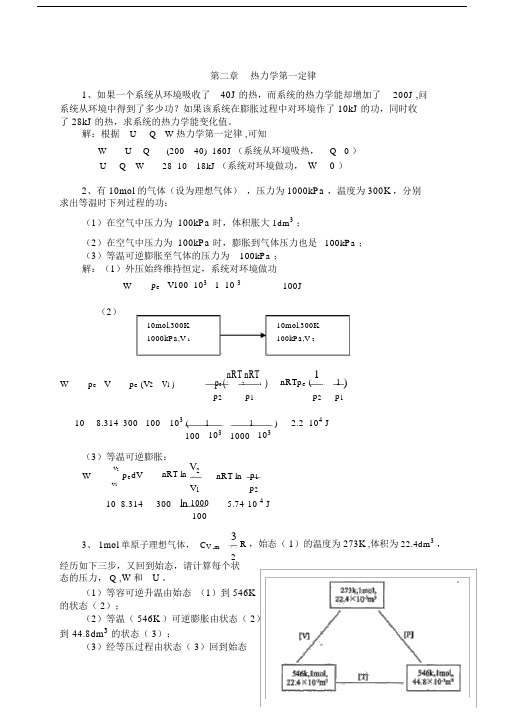
解:根据U Q W 热力学第一定律,可知W U Q (200 40) 160J (系统从环境吸热,Q 0 )U Q W 28 10 18kJ (系统对环境做功,W 0 )2、有 10mol 的气体(设为理想气体),压力为 1000kPa ,温度为 300K ,分别求出等温时下列过程的功:(1)在空气中压力为 100kPa 时,体积胀大1dm3;(2)在空气中压力为 100kPa 时,膨胀到气体压力也是100kPa ;(3)等温可逆膨胀至气体的压力为100kPa ;解:(1)外压始终维持恒定,系统对环境做功W p e V100 103 1 10 3 100J(2)10mol,300K10mol,300K1000kPa,V 1100kPa,V 2W p e V p e (V2 V1 ) p e(nRT2nRT1) nRTp e (11 )p2 p1 p2 p110 8.314 300 100 103 ( 1 1103 ) 2.2 104 J100 103 1000(3)等温可逆膨胀:V2p e dV nRT ln V2 nRT ln p1WV1 V1 p210 8.314 300 ln 1000 5.74 10 4 J1003、 1mol 单原子理想气体,C V ,m 3R ,始态(1)的温度为273K ,体积为 22.4dm3,2经历如下三步,又回到始态,请计算每个状态的压力, Q ,W和U 。
(1)等容可逆升温由始态(1)到 546K 的状态( 2);(2)等温( 546K )可逆膨胀由状态( 2)到44.8dm3的状态( 3);(3)经等压过程由状态( 3)回到始态( 1);解:(1)等容可逆升温过程:W P e V 0UQ WQ VT 2 nC V ,m dT 138.314 546 273 3404.58 JT 12(2)等温可逆膨胀过程:U 0WnRT lnV 21 8.314 546ln 44.83146.50JV 122.4Q W 3146.50J(3)等压过程 :WP e VnRT V 1 V 2 1 8.314 273 22.4 44.8 10 3 2269.72 JV 1 22.4 10 3Q pH T 2nC P ,m dT n 3 R 273 546 5 8.314 273 5674.31J T 1 R 12 2UQ W 5674.31 2269.72 3404.59 J4、在 291K 和 100kPa 下, 1molZn (s) 溶于足量稀盐酸中, 置换出 1molH 2 ( g) ,并放热 152kJ 。
02 热力学第一定律-2(2学时2011材料)

华南师范大学物理化学研究所
第二章 热力学第一定律 U Q W
2.3 热力学第一定律
1. 热 2. 功 3. 热力学能 4. 热力学第一定律 5. 可逆过程
热和功
封闭体系的状态发生变化时,有两种与环境 交换能量的方式:
热(heat);J(焦耳)
体系与环境之间因温差而传递的能量称为 热,用符号Q 表示。 Q的取号:
上述准静态膨胀过程若没有因摩擦等因素造成能量 的耗散,可看作是一种可逆过程。过程中的每一步都接 近于平衡态,可以向相反的方向进行,从始态到终态, 再从终态回到始态,体系和环境都能恢复原状。
可逆过程(reversible process)
可逆过程的特点:
(1)状态变化时推动力与阻力相差无限小,体系 与环境始终无限接近于平衡态;
准静态过程是一种理想过程,实际上是办不到 的。上例无限缓慢地压缩和无限缓慢地膨胀过程可 近似看作为准静态过程。
可逆过程(reversible process)
体系经过某一过程从状态(1)变到状态(2)之 后,如果能使体系和环境都恢复到原来的状态而未留 下任何永久性的变化,则该过程称为热力学可逆过程。 否则为不可逆过程。
种粒子之间的相互作用位能……等。(如没有特殊的外力场存在, 如电磁场、离心力场等,则只考虑热力学能)
(1)是状态函数,它的变化值决定于始态和终态, 与变化途径无关。
(2)其绝对值不可测量,只能计算它的变化值。
(3)是系统的广延性质,而摩尔热力学能是强度性质
Um
U n
U
单位
m
:
J mol1
(4)热力学能在数学上具有全微分的性质
V V1
V2
这种过程近似地可看作可逆过程,所作的功最大。
《热力学第一定律》 讲义

《热力学第一定律》讲义一、热力学第一定律的引入在探索自然界能量转化和守恒的奥秘中,热力学第一定律应运而生。
它就像是一把万能钥匙,为我们打开了理解热现象和能量转换的大门。
想象一下,我们的日常生活中充满了各种能量的转换。
比如,汽车燃烧汽油产生动力,电灯将电能转化为光能,甚至我们的身体通过消化食物将化学能转化为活动所需的能量。
在这些看似纷繁复杂的能量变化背后,是否存在着某种统一的规律呢?这就是热力学第一定律要回答的问题。
二、热力学第一定律的表述热力学第一定律可以简洁地表述为:能量既不会凭空产生,也不会凭空消失,它只会从一种形式转化为另一种形式,或者从一个物体转移到另一个物体,而在转化和转移的过程中,能量的总量保持不变。
这看似简单的一句话,却蕴含着深刻的物理意义。
让我们来仔细拆解一下。
首先,“能量既不会凭空产生”意味着不存在无中生有的能量。
比如,你不能期望在一个封闭的系统中,突然就多出了一股能量来推动某个物体运动。
其次,“也不会凭空消失”表示能量不会莫名其妙地消失无踪。
如果一个物体的能量减少了,那么必然是转化成了其他形式的能量或者转移到了其他物体上。
“从一种形式转化为另一种形式”则涵盖了众多常见的能量转换过程。
比如,摩擦生热是机械能转化为内能;发电是机械能或热能转化为电能。
而“从一个物体转移到另一个物体”常见的例子有热传递,高温物体的热量会传递给低温物体。
三、热力学第一定律的数学表达式为了更精确地描述热力学第一定律,我们引入了数学表达式:ΔU= Q + W其中,ΔU 表示系统内能的变化,Q 表示系统吸收或放出的热量,W 表示系统对外界做功或外界对系统做功。
当 Q 为正,表示系统吸收热量;Q 为负,表示系统放出热量。
当 W 为正,表示系统对外做功;W 为负,表示外界对系统做功。
例如,一个气体在绝热膨胀过程中,由于没有热量交换(Q =0),气体对外做功(W < 0),根据热力学第一定律,气体的内能会减少(ΔU < 0)。
物理化学第2章热力学第一定律

第二章热力学第一定律2.1 热力学的理论基础与方法1.热力学的理论基础热力学涉及由热所产生的力学作用的领域,是研究热、功及其相互转换关系的一门自然科学。
热力学的根据是三件事实:①不能制成永动机。
②不能使一个自然发生的过程完全复原。
③不能达到绝对零度。
热力学的理论基础是热力学第一、第二、第三定律。
这两个定律是人们生活实践、生产实践和科学实验的经验总结。
它们既不涉及物质的微观结构,也不能用数学加以推导和证明。
但它的正确性已被无数次的实验结果所证实。
而且从热力学严格地导出的结论都是非常精确和可靠的。
不过这都是指的在统计意义上的精确性和可靠性。
热力学第一定律是有关能量守恒的规律,即能量既不能创造,亦不能消灭,仅能由一种形式转化为另一种形式,它是定量研究各种形式能量(热、功—机械功、电功、表面功等)相互转化的理论基础。
热力学第二定律是有关热和功等能量形式相互转化的方向与限度的规律,进而推广到有关物质变化过程的方向与限度的普遍规律。
利用热力学第三定律来确定规定熵的数值,再结合其他热力学数据从而解决有关化学平衡的计算问题。
2.热力学的研究方法热力学方法是:从热力学第一和第二定律出发,通过总结、提高、归纳,引出或定义出热力学能U,焓H,熵S,亥姆霍茨函数A,吉布斯函数G;再加上可由实验直接测定的p,V,T等共八个最基本的热力学函数。
再应用演绎法,经过逻辑推理,导出一系列的热力学公式或结论。
进而用以解决物质的p,V,T变化、相变化和化学变化等过程的能量效应(功与热)及过程的方向与限度,即平衡问题。
这一方法也叫状态函数法。
热力学方法的特点是:(i)只研究物质变化过程中各宏观性质的关系,不考虑物质的微观结构;(ii)只研究物质变化过程的始态和终态,而不追究变化过程中的中间细节,也不研究变化过程的速率和完成过程所需要的时间。
因此,热力学方法属于宏观方法。
2.2 热力学的基本概念1.系统与环境系统:作为某热力学问题研究对象的部分;环境:与系统相关的周围部分;按系统与环境交换内容分为:(1)敞开系统(open system) :体系与环境间既有物质交换又有能量交换的体系。
第一节 热力学第一定律

第一节热力学第一定律
一、热力学第一定律
热力学第一定律又称“平衡状态原理”,又称“达到热平衡状态的原则”,是物理学家拉瓦锡和开普勒于19世纪50年代提出的一个基本定律。
它指出,只要一个热系统达到热平衡的状态,它的物理量必定满足某种定律。
该定律可以用如下的数学表达式表示:
U=Q-W
其中,U表示可用热量,Q表示向系统中输入的热量,W表示从系统中放出的热量。
热力学第一定律可以用来定义热力学系统的热平衡状态,以及实现这种状态所需要采取的步骤。
热力学第一定律可以用来研究物理热系统中的热量在系统中的流动情况,从而为热工程领域的设计提供参考。
由于热力学第一定律只阐述了关于热量的流动情况,因此它只能认为热平衡是否能达到由热量的流动情况来决定,而不能推断系统中物理量是否已经达到平衡状态。
对物理量的平衡情况,则必须依赖其他的定律,例如力学和物理化学等定律。
- 1 -。
第2章 热力学第一定律

第2章热力学第一定律一、教学目标1.理解热力学能的定义及对它的微观解释;掌握热力学第一定律的文字表述及数学表述2.理解热与功的概念并掌握其正、负号的规定;掌握体积功的定义及体积功计算,同时理解平衡过程和可逆过程的意义特点。
3.熟悉热容的定义及等压热容、等容热容的概念;掌握成立条件;掌握热力学第一定律对理想气体和实际气体的运用,即熟知理想气体的热力学性质并了解焦尔-汤姆生效应的原理特点及实际用途。
4.掌握热力学第一定律在热化学中的应用,即深刻理解反应进度、热化学方程式、热力学标准态、盖斯定律诸概念,并掌握相变、化学变化时的和的意义及其彼此间关系。
5.掌握以各种标准摩尔热力学量变(如相变焓、生成焓、燃烧焓等)数据和克希荷甫方程进行“298K下、非298K下及非等温下”诸过程热的计算。
二、教学内容1.热力学第一定律2.功与可逆过程3.热容4.理想气体的热力学性质5.焦耳-汤姆生效应6.热化学7.过程热计算与摩尔焓变8.过程热与温度的关系9.绝热反应-非等温过程的热衡算三、重点难点(一)严格区分状态函数与非状态函数(Q、W),并熟练掌握状态函数的数学特征1.体系始终态一旦确定,其状态函数改变量可通过设计途经而求算。
2.体系状态发生变化,其状态函数值可能发生变化,但并不一定全部状态函数都一定发生变化。
3.求算过程的热与功,不能随意设计途径。
唯有在特定条件下Q,W能与状态函数改变量相关联(如等压无其他功Q p =ΔH),才与途径无关。
4.体系状态函数具备五个数学特征。
(二)热力学第一定律数学表达式及其在理想气体中的应用1.表达式ΔU =Q+W =Q+W V+W′或,只适用于封闭体系,随着条件变化,存在ΔU与Q、W之间的转换关系。
2.一定量理想气体U和H,均决定于温度(但若有相变发生,或并非自始至终为理想气体,则不属此列)。
故它无论发生p,V怎样变化,只要有T变化,可直接引用或。
3.弄清节流过程与绝热过程的区别。
热力学第一定律课件ppt

解:方法一:取整个压气机(包括水冷部分)为系统,忽 略动能差及位能差则:
解:取缸内气体为热力系—闭口系。
分析:突然取走100 kg负载,气体 失去平衡,振荡后最终建立新的平衡 态。虽不计摩擦,因非准静态,故过 程不可逆,可应用第一定律解析式。
首先计算状态1及2的参数:
p1
pb
F1 A
(771133.32)
Pa
195 100
98
100
Pa 2.941105
Pa
宏观动能 宏观位能
总能
外部储存能
4
宏观动能与内动能的区别
三、热力学能是状态参数
dU 0
测量 p、V、T 可求出
四、热力学能单位 J
U
kJ
五、工程中关心 U
5
2–3 热力学第一定律基本表达式 加入系统的能量总和-热力系统输出的能量总和=
热力系总储存能的增量
δWtot
δmiei
E
δm je j
E+dE
功的基本表达式
8
讨论:
Q U W q u w
δQ dU δW δq du δw
1)对于可逆过程 δQ dU pdV
2)对于循环
δQ dU δW Qnet Wnet
3)对于定量工质吸热与升温关系,还取决于W 的 “+”、“–”、数值大小。
9
例 自由膨胀
如图, 抽去隔板,求 U 解:取气体为热力系
可逆过程
δwt pdv d pv vdp
25
2)第一定律第二解析式
wt
ws
1 2
cf2
gz
1
q h2 h1 2
cf22 cf21
《热力学第一定律》 讲义

《热力学第一定律》讲义一、热力学第一定律的引入在深入探讨热力学第一定律之前,让我们先思考一个日常生活中的现象。
当我们使用炉灶加热一锅水时,燃料燃烧释放出的能量使得水温升高。
那么,这些能量从何而来?又如何转化和守恒?这就引出了热力学研究的范畴,而热力学第一定律正是回答这些问题的关键。
想象一下,一个封闭的系统,比如一个绝热的容器。
如果对这个系统做功,或者向它传递热量,系统的内能就会发生变化。
这一简单而又深刻的观察,是热力学第一定律的基础。
二、热力学第一定律的表述热力学第一定律可以表述为:一个热力学系统的内能增量等于外界向它传递的热量与外界对它所做的功的和。
用数学表达式来写就是:ΔU = Q + W 。
其中,ΔU 表示系统内能的变化量,Q 表示系统从外界吸收的热量,W 表示外界对系统所做的功。
需要注意的是,这里的功和热量都是有正负之分的。
当系统从外界吸收热量时,Q 为正值;当系统向外界放出热量时,Q 为负值。
当外界对系统做功时,W 为正值;当系统对外界做功时,W 为负值。
三、对表达式的深入理解让我们来详细解读一下这个表达式。
首先看热量 Q 。
热量的传递是由于系统与外界之间存在温度差。
例如,将一杯热水放在室温环境中,热水会逐渐冷却,这是因为热水向周围环境散失了热量。
再看功 W 。
功的形式多种多样,比如压缩气体时,外界对气体做功;气体膨胀时,气体对外界做功。
而内能ΔU ,它是系统内部微观粒子的动能和势能的总和。
当系统的温度升高时,微观粒子的运动加剧,内能增加;当系统的体积变化或者物质的状态改变时,内能也会相应地发生变化。
举个例子,假如我们对一个气缸中的气体进行压缩,在这个过程中,外界对气体做功,同时气体与外界没有热交换(绝热过程),那么气体的内能就会增加,表现为温度升高。
四、热力学第一定律的应用热力学第一定律在许多领域都有着广泛的应用。
在热机中,燃料燃烧产生的热量一部分用于对外做功,一部分散失到环境中。
通过热力学第一定律,我们可以计算热机的效率,找到提高热机效率的途径。
热力学第一定律

热力学第一定律热力学第一定律,也被称为能量守恒定律,是热力学基本定律之一。
它阐述了能量在物理系统中的守恒原理,即能量不会被创造或消灭,只会在不同形式之间转换或传递。
该定律在许多领域都有广泛的应用,包括工程、物理、化学等。
1. 定律的表述热力学第一定律可从不同的角度进行表述,以下是几种常见的表述方式:1.1 内能变化根据热力学第一定律,一个封闭系统内能的变化等于系统所吸收的热量与系统所做的功的代数和。
数学表达式如下:ΔU = Q + W其中,ΔU表示系统内能的变化,Q表示系统吸收的热量,W表示系统所做的功。
1.2 能量守恒根据能量守恒定律,能量既不能被创造也不能被摧毁,只会在不同形式之间传递或转换。
能量的总量在一个封闭系统中保持不变。
2. 系统内能的变化系统内能的变化是热力学第一定律的核心内容之一。
系统内能的变化是由系统吸收或释放的热量以及系统所做的功决定的。
2.1 系统吸收的热量系统吸收的热量指的是系统从外界获得的热能。
当一个热源与系统接触时,能量会以热量的形式从热源传递到系统中。
系统吸收的热量可以引起系统内能的增加。
2.2 系统所做的功系统所做的功指的是系统对外界做的能量转移。
当系统对外界施加力并移动时,能量会以功的形式从系统传递到外界。
系统所做的功可以引起系统内能的减少。
3. 热力学第一定律的应用3.1 工程应用热力学第一定律在工程领域有着广泛的应用。
例如,在能源系统的设计与优化中,需要根据系统的能量转换过程,计算系统的内能变化和热功效率等参数,以提高能源利用效率。
3.2 物理学应用在物理学研究中,热力学第一定律通常用于分析热力学过程中的能量转化。
例如,在热力学循环中,通过计算各个环节的能量转换情况,可以确定工作物质的热效率,从而评估系统的性能。
3.3 化学反应在化学反应中,热力学第一定律对于研究反应的能量变化和平衡状态具有重要意义。
通过计算反应过程中释放或吸收的热量,可以确定反应的放热性或吸热性,并预测反应的发生与否。
【物理化学】2-02热力学第一定律

结论: 当始, 终态确定的条件下, 不 同途径有不同大小的热量.
热是途径函数!
2功 系统与环境间除热量外的另一种能量交换形式 (由微观粒子的有序运动所引起的) 环境对系统作功取“ + ”, 反之取“ - ”
体积功(本节) 功
电功(电化学章) 非体积功
表面功(表面现象章)
dl F (环) = p (环) A
•又要马儿跑, 又要马儿不吃草是不可能的. •将欲取之, 必先与之. •天上不会掉下馅饼. •一份耕耘, 一份收获.
的热“量”(Q), 而不是象状态函数那样的始, 终态
之间的“增量” ( T =T2-T1, Q=Q2-Q1 );
• 一个微小途径对应微小热“量”(dQ), 同时对应
各状态函数的微小“增量”(如 dT, T2 = T1 + dT );
• 上述提醒对“功”同样有效!
我们拥有一个家 名字叫状态函数 兄弟姐妹都很多 但是没有功和热
式中U是状态函数, Q和W是途径函数. 当系统从状态1
变化到状态2, 不同途径Q和W的不同, 但Q + W却与途径无
关.
状态1 U1
QW Q W
状态2 U2 U = U2-U1
Q + W = Q + W = U
5. 热力学第一定律的其它叙述方式
第一类永动机是不能创造的. 内能是系统的状态函数.
…………
T
V
n
p
一定状态的系统 Cp
U
A
HS
G
WQ
H2 1mol, 0℃ 101325Pa
Q=0
Q = 1135J
恒温 热源 0℃
11m01oH3l2,25H0P2℃5a, 15m66o真3lP,空a0℃p环, =0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:因为此过程为 乙醇正常沸点下的相变过程 ( 等温 351K、等压 101.325KPa ),即为可逆相变过程. C2H5OH (l) == C2H5OH (g)
热力学一定律计算例题
等压过程 W= -Pe dv =- p (V2 - V1) ≈ -p V2 ; 因为: 乙醇 Mr= 46.0 g•mol-1) 蒸汽的密度为ρ= 1.647 g•dm-3。 所以:1.0 mol蒸汽的体积 V2 = 46.0 / 1.647 = 27.93 dm3 W = - 101.325×27.93 / 1000 =-2.830 kJ Q = 39.49 kJ•mol-1 ΔU = Q + W = 36.7 kJ ΔH = Qp= 39.49 kJ
热力学一定律计算例题
[例4】在298.15K、标准大气压下,
单位反应 C(s)+ O2(g)→CO(g),若经过以下二条途 径: (1) 直接接触发生反应,已知单位反应放热 110.52 -1 kJ mol ; (2) 若反应在原电池中进行,对环境作电功 -1 60.15 kJ mol 。求二途径的Q , W ,ΔU及ΔH
Q0
气体真空膨胀,未对环境做功, W 0 所以,根据热力学第一定律 U 0
Joule实验
从Joule实验得到的结论: 在封闭系统中,理想气体的热力学能仅是温度的函数
U U 0 0 V T p T 对于理想气体 H U pV 如何证明? H U ( pV ) U (nRT ) 如何解释?
U 0 V T
U dU dT CV dT T V
说明什么 问题?
H H (T , p)
H H dH dp C p dT dT T p p T
作了两项修正: (1)1 mol 分子自身占有体积为 b (2)1 mol 分子之间有作用力,即内压力
a /V
2 m
van der Waals 方程为:
a p 2 Vm b RT Vm
van der Waals 方程
van der Waals 方程为:
a p 2 Vm b RT Vm
解:(1)等容升温过程
始态
n p0V0 4.403mol RT0
末态
p0 = 1000 kPa V0 = 10 dm3 T0 = 273.2 K
等容
p1 n = 4.403mol =1366 kPa
nRT1 V1
V1 = V0= 10 dm3 T1 = 373.2 K
等容过程: dv =0
T1
T2
[4.403 (12.471 8.314) (373.2 273.2)]J 9.152 103 J
(2)等压升温过程
末态
始态
pV n 1 1 4.403mol RT1
p2 = p1 = 1000 kPa
等压
n 4.403mol
p0 = 1000 kPa V0 = 10 dm3 T0 = 273.2 K
解:(1)等温,等压无其它功的条件下进行单位化学反应: Q1 = -110.52 kJ.mol-1 W1 = - (1-0.5)×8.314×298.15 = - 1.24 kJ.mol-1 ΔU1 = Q1+W1 = - 110.52 - 1.24 = - 111.76 kJ mol-1 ΔH1 = Qp = Q1 = -110.52 kJ mol-1
为什么 Q2≠ ΔH2
请思考:
如何计算不同过程的△U 、 △H、 W、 Q ? 1.简单物理状态变化过程?
等温?等压?等容?恒外压?等压变温?等容变温? 绝热过程?真空膨胀过程?
2.等温等压下的可逆相变过程?不可逆相变过程?
3.等温、等压下的化学变化过程?
例:不可逆相变过程 H2O (l) = 101.325 105℃ H2O (g) 101.325 105℃
T2
W p环 dV
V1
V2
=0
QV U1 nCV ,mdT nCV ,m (T2 T1 ) [4.403 12.471 (373.2 273.2)]J 5.491103 J
T1
H 1 nC p,m dT nC p,m (T2 T1 ) n(CV ,m R)(T2 T1 )
热力学一定律计算例题
【例 2】1mol 理想气体初态为 373.15K , 10.0dm3 ,反 抗 恒 外 压 P100KPa 迅 速 膨 胀 到 终 态 温 度 244.0K , 100.0KPa。求此过程的W, Q , ΔU , ΔH。
解:理想气体n =1 mol ,
T1=373.15K V1=10.0dm3
热力学一定律计算例题
[ 例 3】 1.0 mol 乙 醇 在 正 常 沸 点 ( 351K , 101.325KPa )下蒸发成气体,求此过程的W, Q , ΔU , ΔH。
g 已知乙醇正常沸点下的蒸发热 = 39.49 l Hm -1 -3
kJ•mol , 蒸汽的密度为ρ= 1.647 g•dm 。
U U (T )
所以封闭系统中,理想气体的焓也仅是温度的 函数
H H (T )
H 0 V T
H 0 p T
Joule定理—— 在封闭系统中,理想气体的热力学能仅是温度的函数
• 实际气体的热力学能为分子的动能和分子间相互作 用的位能之和。 • 分子的动能与分子热运动有关,为温度的函数;而 分子间相互作用的位能与分子间的距离有关,即与 气体体积有关。 • 理想气体为没有体积的自由运动的弹性质点,是实 际气体当压力趋向于零时的极限情况。此时,分子 间的相互作用可以忽略,所以理想气体的热力学能 仅是热运动的动能之和,只是温度的函数。
此过程为过热水的蒸发过程,为不可逆相变过程.求 此过程 △U 、 △H、 W、 Q .已知:水正常沸点蒸发焓 为 (101.325KPa.100 ℃)为40.668KJ/mol.
例:化学反应热的计算
已知反应:
H2(g) +1/2 O2 (g) = H2O (l)
在101.325KPa、 298.15K 时,摩尔反应焓变为 - 285.84 KJ/ mol。问:如何计算800K 时的反应焓变?
2 n a 或 p 2 V nb nRT V
a 的单位:
Pa m mol
6
2
b 的单位:
m mol
3
1
a,b 称为van der Waals 常数
还有其他ቤተ መጻሕፍቲ ባይዱ状态方程……。
理想气体的热力学能和焓-Joule实验
Joule 实验
实验前后,作为系统的气体和作为环境的水浴温度都未变
实际气体的状态方程?
低温、高压时,真实气体的行为偏离理想气体定 律,称为为实际气体。 实际气体分子不再是自由运动的弹性质点,即低 温、高压下,气体密度增大,分子之间距离缩小,分 子之间的相互作用以及分子自身的体积不可忽略。 因此,理想气体的分子运动模型要予以修正。
实际气体的状态方程?
荷兰科学家 van der Waals 对理想气体状态方程
1 2
热力学一定律计算例题
(2) 等温,等压有电功的条件下进行单位化学反应: W2 = W +W‘ = -1.240 - 60.15 =- 61.39 kJ mol-1 因途径1,2初、终态相同 ΔU 2 = ΔU 1 =(298.15K,)=-111.76 kJ mol-1 ΔH2 = ΔH1 (298.15K, )=-110.52 kJ mol-1 Q2=ΔU 2 – W 2 =-111.76 + 61.39 =-56.37 kJ mol-1
此为等温等压下的化学反应,在没有其 他功存在的条件下,摩尔反应焓变表示发生 单位反应所放出的热量.
2.5
理想气体的热力学能和焓
1. Joule 实验
2. 理想气体 U 和H 的计算
3. 理想气体的绝热可逆过程
问题:什么是理想气体?什么是实际气体?
什么是理想气体? — 任何温度、任何压力下都能够严格遵守 PV = nRT 的气体叫做理想气体。 气体的行为偏离理想气体定律,称为为实际气体。 理想气体体系将分子看作是没有体积的自由运动的弹 性质点;即
→T2=244.0K
p2=100.0 kPa
气体迅速膨胀可视为绝热过程,所以该过程是绝热恒外压膨胀。
因此 ,Q = 0 ; W =- pe (V2 - V1)
V2= nRT2 / p2 =1×8.314×244.0 / 100.0
= 20.3 dm
3
热力学一定律计算例题
W = -Pe(V2-V1) W =-100.0 (20.3 -10.0)=-1.03 kJ 根据热力学第一定律 ΔU = Q + W =-1.03 kJ (迅速膨胀 Q=0) 根据 焓的定义 ΔH =ΔU +Δ(pV) =ΔU +(P2V2 - p1V 1) = ΔU +nR (T2 - T1) =-1.03 +8.314(244.0-373.15)/1000 • =-2.10 kJ
即:在恒温时,改变体积或压力,理想气体的热力学 能和焓保持不变。还可以推广为理想气体的Cv,Cp也仅 为温度的函数。
理想气体ΔU、Δ H的计算
设理想气体的热力学能是
T ,V
的函数
U U (T ,V )
从Joule实验得 所以 同理
U U dU dT dV T V V T
U 2 nCV ,m dT nCV ,m (T2 T1 ) U1 5.491 10 J
