初二上作图题归纳
尺规作图专题详尽归纳

考点名称:尺规作图【学习目标】1.了解什么是尺规作图.2.学会用尺规作图法完成下列五种基本作图:(1)画一条线段等于已知线段;(2)画一个角等于已知角;(3)画线段的垂直平分线;(4)过已知点画已知直线的垂线;(5)画角平分线.3.了解五种基本作图的理由.4.学会使用精练、准确的作图语言叙述画图过程.5.学会利用基本作图画三角形等较简单的图形.6.通过画图认识图形的本质,体会图形的内在美.【基础知识精讲】1.尺规作图:①定义:限定只用直尺和圆规来完成的画图,称为尺规作图.注意:这里所指的直尺是没有刻度的直尺,由于免去了度量,因此,用尺规作图法画出的图形的精确度更高,它在工程绘图等领域应用比较广泛.②步骤:(1)根据给出的条件和求作的图形,写出已知和求作部分;(2)分析作图的方法和过程;(3)用直尺和圆规进行作图; (4)写出作法步骤,即作法。
(根据题目要求来定是否需要写出作法)2.尺规作图中的最基本、最常用的作图称为基本作图.任何尺规作图的步骤均可分解为以下五种.3.基本作图共有五种:(1)画一条线段等于已知线段.如图24-4-1,已知线段DE.求作:一条线段等于已知线段.作法:①先画射线AB.②然后用圆规在射线AB上截取AC=MN.线段AC就是所要作的线段.(2)作一个角等于已知角.如图24-4-2,已知∠AOB.求作:∠A′O′B′,使∠A′O′B′=∠AOB.作法:①作射线O′A′;②以点O为圆心,以任意长为半径作弧,交OA于C,交OB于D.③以点O′为圆心,以OC长为半径作弧,交O′A′于C′.④以点C′为圆心,以CD为半径作弧,交前弧于D′.⑤经过点D′作射线O′B′,∠A′O′B′就是所求的角.(3)作线段的垂直平分线.如图24-4-3,已知线段AB.求作:线段AB的垂直平分线.作法:①分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于点C和D.②作直线CD.直线CD就是线段AB的垂直平分线.注意:直线CD与线段AB的交点,就是AB的中点.(4)经过一点作已知直线的垂线.a.经过已知直线上的一点作这条直线的垂线,如图24-4-4.已知:直线AB和AB上一点C,求作:AB的垂线,使它经过点C.作法:作平角ACB的平分线CF.直线CF就是所求的垂线,如图24-4-4.b.经过已知直线外一点作这条直线的垂线.如图24-4-5,已知:直线AB和AB外一点C.求作:AB的垂线,使它经过点C.作法:①任意取一点K,使K和C在AB的两旁.②以C为圆心,CK长为半径作弧,交AB于点D和E.③分别以D和E为圆心,大于的长为半径作弧,两弧交于点F.④作直线CF.直线CF就是所求的垂线.注意:经过已知直线上的一点,作这条直线的垂线转化成画线段垂直平分线的方法解决.(5)平分已知角.如图24-4-6,已知∠AOB.求作:射线OC,使∠AOC=∠BOC.作法:①在OA和OB上,分别截取OD、OE.②分别以D、E为圆心,大于的长为半径作弧,在∠AOB内,两弧交于点C.③作射线OC.OC就是所求的射线.注意:以上五种基本作图是尺规作图的基础,一些复杂的尺规作图,都是由基本作图组成的,同学扪要高度重视,努力把这部分内容学习好.通过这一节的学习,同学们要掌握下列作图语言:(1)过点×和点×画射线××,或画射线××.(2)在射线××上截取××=××.(3)以点×为圆心,××为半径画弧.(4)以点×为圆心,××为半径画弧,交××于点×.(5)分别以点×,点×为圆心,以××,××为半径作弧,两弧相交于点×.(6)在射线××上依次截取××=××=××.(7)在∠×××的外部或内部画∠×××=∠×××.注意:学过基本作图后,在作较复杂图时,属于基本作图的地方,不必重复作图的详细过程,只用一句话概括叙述就可以了.如:(1)画线段××=××.(2)画∠×××=∠×××.(3)画××平分∠×××,或画∠×××的角平分线.(4)过点×画××⊥××,垂足为点×.(5)作线段××的垂直平分线××,等等.但要注意保留全部的作图痕迹,包括基本作图的操作程序,不能因为作法的叙述省略而作图就不按程序操作,只有保留作图痕迹,才能反映出作图的操作是否合理.【经典例题精讲】例1已知两边及其夹角,求作三角形.如图24-4-7,已知:∠α,线段a、b,求作:△ABC,使∠A=∠α,AB=a,AC=b.作法:①作∠MAN=∠α.②在射线AM、AN上分别作线段AB=a,AC=b.③连结BC.如图24-4-8,△ABC即为所求作的三角形.注意:一般几何作图题,应有下面几个步骤:已知、求作、作法,比较复杂的作图题,在作图之前可根据需要作一些分析.例2如图24-4-9,已知底边a,底边上的高h,求作等腰三角形.已知线段a、h.求作:△ABC,使AB=AC,且BC=a,高AD=h.分析:可先作出底边BC,根据等腰三角形的三线合一的性质,可再作出BC的垂直平分线,从而作出BC边上的高AD,分别连结AB和AC,即可作出等腰△ABC来.作法:(1)作线段BC=a.(2)作线段BC的垂直平分线MN,MN与BC交于点D.(3)在MN上截取DA,使DA=h.(4)连结AB、AC.如图24-4-10,△ABC即为所求的等腰三角形.例3已知三角形的一边及这边上的中线和高,作三角形.如图24-4-11,已知线段a,m,h(m>h).求作:△ABC使它的一边等于a,这边上的中线和高分别等于m和h(m>h).分析:如图24-4-12,假定△ABC已作出,其中BC=a,中线AD=m,高AE=h,在△AED中AD=m,AE=h,∠AED=90°,因此这个Rt△AED可以作出来(△AED为奠基三角形).当Rt△AED作出后,由的关系可作出点B和点C,于是△ABC即可得到.作法:(1)作△AED,使∠AED=90°,AE=h,AD=m.(2)延长ED到B,使.(3)在DE或BE的延长线上取.(4)连结AB、AC.则△ABC即为所求作的三角形.注意:因为三角形中,一边上的高不能大于这边上的中线,所以如果h>m,作图题无解;若m=h,则作出的图形为等腰三角形.例4如图24-4-13,已知线段a.求作:菱形ABCD,使其半周长为a,两邻角之比为1∶2.分析:因为菱形四边相等,“半周长为a”就是菱形边长为,为此首先要将线段a等分,又因为菱形对边平行,则同旁内角互补,由“邻角之比为1∶2”可知,菱形较小内角为60°,则菱形较短对角线将菱形分成两个全等的等边三角形.所以作图时只要作出两个有公共边的等边三角形,则得到的四边形即为所求的菱形ABCD.作法:(1)作线段a的垂直平分线,等分线段a.(2)作线段AC,使.(3)分别以A、C为圆心,为半径,在AC的两侧画弧,两弧分别交于B,D.(4)分别连结AB、BC、CD、DA得到四边形ABCD,则四边形ABCD为所求作的菱形(如图24-4-14).注意:这种通过先画三角形,然后再画出全部图形的方法即为“三角形奠基法”.例5如图24-4-15,已知∠AOB和C、D两点.求作一点P,使PC=PD,且使点P到∠AOB的两边OA、OB的距离相等.分析:要使PC=PD,则点P在CD的垂直平分线上,要使点P到∠AOB的两边距离相等,则P应在∠AOB的角平分线上,那么满足题设的P点就是垂直平分线与角平分线的交点了.作法:(1)连结CD.(2)作线段CD的中垂线l.(3)作∠AOB的角平分线OM,交l于点P,P点为所求.注意:这类定点问题应需确定两线,两直线的交点即为定点,当然这两直线应分别满足题目的不同要求.【中考考点】例6 (2000·安徽省)如图24-4-16,直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )A.一处 B.二处C.三处 D.四处分析:到直线距离相等的点在相交所构成的角的平分线上,可利用作角平分线的方法找到这些点.解:分别作相交所构成的角平分线,共可作出六条,三条角平分线相交的交点共有四个.答案:D.注意:本题应用了角平分线的性质,在具体作图时,不可只作出位于中心位置的一处,而要全面考虑其他满足条件的点.例7 (2002·陕西省)如图24-4-17,△ABC是一块直角三角形余料,∠C=90°,工人师傅要把它加工成—个正方形零件,使C为正方形的—个顶点,其他三个顶点分别在AB、BC、AC边上.(1)试协助工人师傅用尺规画出裁割线(不写作法,保留作图痕迹);(2)工人师傅测得AC=80 cm,BC=120cm,请帮助工人师傅算出按(1)题所画裁割线加工成的正方形零件的边长.解:(1)作∠ACB的平分线与AB的交点E即为正方形—顶点,作CE线段的中垂线HK 与AC、BC的交点F、D即为所作正方形另两个顶点,如图24-4-17.(2)设这个正方形零件的边长为x cm,∵DE∥AC,∴,∴.∴x=48.答:这个正方形零件的边长为48cm.注意:本题是几何作图和几何计算相结合题目,要求读者对基本作图务必掌握,同时对作出图形的性质要清楚.例8 (2002·山西省)如图24-4-18①,有一破残的轮片(不小于半个轮),现要制作一个与原轮片同样大小的圆形零件,请你根据所学的有关知识,设计两种方案,确定这个圆形零件的半径.分析:欲确定这个圆形零件的半径,可以借助三角板,T形尺或尺规作图均可,图②中是这个零件的半径,图③中OB是这个零件半径.解:如图24-4-18②③所示.【常见错误分析】例9如图24-4-19,已知线段a、b、h.求作△ABC,使BC=a,AC=b,BC边上的高AD=h.并回答问题,你作出的三角形唯一吗?从中你可以得到什么结论呢?错解:(1)作法:①作Rt△ADC,使AD=h,AC=b.②在直线CD上截取CB=a.如图24-4-20,则△ABC就是所求作的三角形.(2)作出的三角形唯一.(3)得出结论:有两边及一边上的高对应相等的两三角形全等.误区分析:本题错解在于忽略了三角形的高可能在三角形内部也可能在三角形的外部.正解:如图24-4-21,作法:①作Rt△ADC,使AD=h,AC=b.②在直线CD上截取CB=a(在点C的两侧).则△ABC,△AB′C都是所求作三角形.(2)作出的三角形不唯一.(3)得出结论有两边及—边上的高对应相等的两三角形不一定全等.注意:与三角形的高有关的题目应慎之又慎.【学习方法指导】学习基本作图,主要是运用观察法,通过具体的操作,了解各种基本作图的步骤,掌握作图语言.【规律总结】画复杂的图形时,如一时找不到作法,—般是先画出一个符合所设条件的草图,再根据这个草图进行分析,逐步寻找画图步骤.有时,也可以根据已知条件和基本作图,先作局部三角形,再以此为基础,根据有关条件画出其余部分,从而完成全图,这种方法称为三角形奠基法.拓展: 1.利用基本作图作三角形:(1)已知三边作三角形; (2)已知两边及其夹角作三角形; (3)已知两角及其夹边作三角形; (4)已知底边及底边上的高作等腰三角形;(5)已知一直角边和斜边作直角三角形.2.与圆有关的尺规作图:(1)过不在同一直线上的三点作圆(即三角形的外接圆). (2)作三角形的内切圆.(3)作圆的内接正方形和正六边形.附件:尺规作图简史:“规”就是圆规,是用来画圆的工具,在我国古代甲骨文中就有“规”这个字.“矩”就像现在木工使用的角尺,由长短两尺相交成直角而成,两者间用木杠连接以使其牢固,其中短尺叫勾,长尺叫股.矩的使用是我国古代的一个发明,山东历城武梁祠石室造像中就有“伏羲氏手执矩,女娲氏手执规”之图形.矩不仅可以画直线、直角,加上刻度可以测量,还可以代替圆规.甲骨文中也有矩字,这可追溯到大禹治水(公元前2000年)前.《史记》卷二记载大禹治水时“左准绳,右规矩”.赵爽注《周髀算经》中有“禹治洪水,……望山川之形,定高下之势,……乃勾股之所由生也.”意即禹治洪水,要先测量地势的高低,就必定要用勾股的道理.这也说明矩起源于很远的中国古代.春秋时代也有不少著作涉及规矩的论述,《墨子》卷七中说“轮匠(制造车子的工匠)执其规矩,以度天下之方圆.”《孟子》卷四中说“离娄(传说中目力非常强的人)之明,公输子(即鲁班,传说木匠的祖师)之巧,不以规矩,不能成方圆.”可见,在春秋战国时期,规矩已被广泛地用于作图、制作器具了.由于我国古代的矩上已有刻度,因此使用范围较广,具有较大的实用性.古代希腊人较重视规、矩在数学中训练思维和智力的作用,而忽视规矩的实用价值.因此,在作图中对规、矩的使用方法加以很多限制,提出了尺规作图问题.所谓尺规作图,就是只有限次地使用没有刻度的直尺和圆规进行作图.古希腊的安那萨哥拉斯首先提出作图要有尺寸限制.他因政治上的纠葛,被关进监狱,并被判处死刑.在监狱里,他思考改圆成方以及其他有关问题,用来打发令人苦恼的无所事事的生活.他不可能有规范的作图工具,只能用一根绳子画圆,用随便找来的破木棍作直尺,当然这些尺子上不可能有刻度.另外,对他来说,时间是不多了,因此他很自然地想到要有限次地使用尺规解决问题.后来以理论形式具体明确这个规定的是欧几里德的《几何原本》.由于《几何原本》的巨大影响,希腊人所崇尚的尺规作图也一直被遵守并流传下来.由于对尺规作图的限制,使得一些貌似简单的几何作图问题无法解决.最著名的是被称为几何三大问题的三个古希腊古典作图难题:立方倍积问题、三等分任意角问题和化圆为方问题.当时很多有名的希腊数学家,都曾着力于研究这三大问题,虽然借助于其他工具或曲线,这三大难题都可以解决,但由于尺规作图的限制,却一直未能如愿以偿.以后两千年来,无数数学家为之绞尽脑汁,都以失败而告终.直到1637年笛卡尔创立了解析几何,关于尺规作图的可能性问题才有了准则.到了1837年万芝尔首先证明立方倍积问题和三等分任意角问题都属于尺规作图不可能问题.1882年林德曼证明了π是无理数,化圆为方问题不可能用尺规作图解决,这才结束了历时两千年的数学难题公案.。
初二数学尺规作图典型例题归纳

初二数学尺规作图典型例题归纳典型例题一例已知线段a、b,画一条线段,使其等于.分析所要画的线段等于,实质上就是.画法:1.画线段.2.在AB的延长线上截取.线段AC就是所画的线段.说明1.尺规作图要保留画图痕迹,画图时画出的所有点和线不可随意擦去.2.其它作图都可以通过画基本作图来完成,写画法时,只需用一句话来概括叙述基本作图.典型例题二例如下图,已知线段a和b,求作一条线段AD使它的长度等于2a-b.图(2)正解如图(2),(1)作射线AM;(2)在射线AM上,顺次截取AB=BC=a;(3)在线段CA上截取CD=b,则线段AD就是所求作的线段.典型例题三例求作一个角等于已知角∠MON(如图1).图(1)图(2)正解如图(2),(1)作射线;(2)在图(1)上,以O为圆心,任意长为半径作弧,交OM于点A,交ON于点B;(3)以为圆心,OA的长为半径作弧,交于点C;(4)以C为圆心,以AB的长为半径作弧,交前弧于点D;(5)过点D作射线.则∠就是所要求作的角.典型例题四例如下图,已知∠α及线段a,求作等腰三角形,使它的底角为α,底边为a.分析先假设等腰三角形已经作好,根据等腰三角形的性质,知两底角∠B=∠C=∠α,底边BC=a,故可以先作∠B=∠α,或先作底边BC=a.作法如下图(1)∠MBN=∠α;(2)在射线BM上截取BC=a;(3)以C为顶点作∠PCB=∠α,射线CP交BN于点A.△ABC就是所要求作的等腰三角形.说明画复杂的图形时,如一时找不到作法,一般是先画出一个符合条件的草图,再根据这个草图进行分析,逐步寻找画图步骤.典型例题五例如图(1),已知直线AB及直线AB外一点C,过点C作CD∥AB(写出作法,画出图形).分析根据两直线平行的性质,同位角相等或错角相等,故作一个角∠ECD=∠EFB即可.作法如图(2).图(1)图(2)(1)过点C作直线EF,交AB于点F;(2)以点F为圆心,以任意长为半径作弧,交FB于点P,交EF于点Q;(3)以点C为圆心,以FP为半径作弧,交CE于M点;(4)以点M为圆心,以PQ为半径作弧,交前弧于点D;(5)过点D作直线CD,CD就是所求的直线.说明作图题都应给出证明,但按照教科书的要求,一般不用写出,但要知道作图的原由.典型例题六例如下图,△ABC中,a=5cm,b=3cm,c=3.5cm,∠B=,∠C=,请你从中选择适当的数据,画出与△ABC全等的三角形(把你能画的三角形全部画出来,不写画法但要在所画的三角形中标出用到的数据).分析本题实质上是利用原题中的5个数据,列出所有与△AB C全等的各种情况,依据是SSS、SAS、AAS、ASA.解与△ABC全等的三角形如下图所示.典型例题七例正在修建的北路有一形状如下图所示的三角形空地需要绿化.拟从点A出发,将△ABC分成面积相等的三个三角形,以便种上三种不同的花草,请你帮助规划出图案(保留作图痕迹,不写作法).(2003年,)分析这是尺规作图在生活中的具体应用.要把△ABC分成面积相等的三个三角形,且都是从A点出发,说明这三个三角形的高是相等的,因而只需这三个三角形的底边也相等,所以只要作出BC边的三等分点即可.作法如下图,找三等分点的依据是平行线等分线段定理.典型例题八例已知∠AOB,求作∠AOB的平分线OC.错解如图(1)作法(1)以O为圆心,任意长为半径作弧,分别交OA、OB于D、E两点;(2)分别以D、E为圆心,以大于DE的长为半径作弧,两弧相交于C点;(3)连结OC,则OC就是∠AOB的平分线.错解分析对角平分线的概念理解不够准确而致误.作法(3)中连结OC,则OC是一条线段,而角平分线应是一条射线.图(1)图(2)正解如图(2)(1)以点O为圆心,任意长为半径作弧,分别交OA、OB于D、E两点;(2)分别以D、E为圆心,以大于DE的长为半径作弧,两弧交于C点;(3)作射线OC,则OC为∠AOB的平分线.典型例题九例如图(1)所示,已知线段a、b、h(h<b).求作△ABC,使BC=a,AB=b, BC边上的高AD=h.图(1)错解如图(2),(1)作线段BC=a;(2)作线段BA=b,使AD⊥BC且AD=h.则△ABC就是所求作的三角形.错解分析①不能先作BC;②第2步不能同时满足几个条件,完全凭感觉毫无根据;③未考虑到本题有两种情况.对于这种作图题往往都是按照由里到外的顺序依次作图,如本题先作高AD,再作AB,最后确定BC.图(2)图(3)正解如图(3).(1)作直线PQ,在直线PQ上任取一点D,作DM⊥PQ;(2)在DM上截取线段DA=h;(3)以A为圆心,以b为半径画弧交射线DP于B;(4)以B为圆心,以a为半径画弧,分别交射线BP和射线BQ于和;(5)连结、,则△(或△)都是所求作的三角形.典型例题十例如下图,已知线段a,b,求作Rt△ABC,使∠ACB=90°,BC=a,AC=b (用直尺和圆规作图,保留作图痕迹).分析本题解答的关键在于作出∠ACB=90°,然后确定A、B两点的位置,作出△ABC.作法如下图(1)作直线MN:(2)在MN上任取一点C,过点C作CE⊥MN;(3)在CE上截取CA=b,在CM上截取CB=a;(4)连结AB,△ABC就是所求作的直角三角形.说明利用基本作图画出所求作的几何图形的关键是要先分析清楚作图的顺序.若把握不好作图顺序,要先画出假设图形.典型例题十一例如下图,已知钝角△ABC,∠B是钝角.求作:(1)BC边上的高;(2)BC边上的中线(写出作法,画出图形).分析(1)作BC边上的高,就是过已知点A作BC边所在直线的垂线;(2)作BC边上的中线,要先确定出BC边的中点,即作出BC边的垂直平分线.作法如下图(1)①在直线CB外取一点P,使A、P在直线CB的两旁;②以点A为圆心,AP为半径画弧,交直线CB于G、H两点;③分别以G、H为圆心,以大于GH的长为半径画弧,两弧交于E点;④作射线AE,交直线CB于D点,则线段AD就是所要求作的△ABC中BC边上的高.(2)①分别以B、C为圆心,以大于BC的长为半径画弧,两弧分别交于M、N两点;②作直线MN,交BC于点F;③连结AF,则线段AF就是所要求作的△ABC中边BC上的中线.说明在已知三角形中求作一边上的高线、中线、角平分线时,首先要把握好高线、中线、角平分钱是三条线段;其次,高线、中线的一个端点必须是三角形中这边所对的顶点,而关键是找出另一个端点.典型例题十二例如图(1)所示,在图中作出点C,使得C是∠MON平分线上的点,且AC=OC.图(1)图(2)分析由题意知,点C不仅要在∠MON的平分线上,且点C到O、A两点的距离要相等,所以点C应是∠MON的平分线与线段OA的垂直平分线的交点.作法如图(2)所示(1)作∠MON的平分线OP;(2)作线段OA的垂直平分线EF,交OP于点C,则点C就是所要求作的点.说明(1)根据题意弄清要求作的点的特征是到各直线距离相等,还是到各端点距离相等.(2)两条直线交于一点.典型例题十三例如下图,已知线段a、b、∠α、∠β.求作梯形ABCD,使AD=a,BC=b,AD∥BC,∠B=∠α;∠C=∠β.分析假定梯形已经作出,作AE∥DC交BC于E,则AE将梯形分割为两部分,一部分是△ABE,另一部分是AECD.在△ABE中,已知∠B=∠α,∠AEB=∠β,BE=b-a,所以,可以首先把它作出来,而后作出AECD.作法如下图.(1)作线段BC=b;(2)在BC上截取BE=b-a ;(3)分别以B、E为顶点,在BE同侧作∠EBA=∠α,∠AEB=∠β,BA、EA 交于A;(4)以EA、EC为邻边作AECD.四边形ABCD就是所求作的梯形.说明基本作图是作出较简单图形的基础,三角形是最简单的多边形,它是许多复杂图形的基础.因此,要作一个复杂的图形,常常先作一个比较容易作出的三角形,然后以此为基础,再作出所求作的图形.典型例题十四例如下图,在一次军事演习中,红方侦察员发现蓝方指挥部在A区,到铁路与公路的距离相等,且离铁路与公路交叉处B点700米,如果你是红方的指挥员,请你在图示的作战图上标出蓝方指挥部的位置.(2002年,)分析依据角平分线的性质可以知道,蓝方指挥部必在A区两条路所夹角的平分线上,然后由蓝方指挥部距B点的距离,依据比例尺,计算出图上的距离为3.5cm,就可以确定出蓝方指挥部的位置.解如下图,图中C点就是蓝方指挥部的位置.典型例题十五例如图(1),已知有公共端点的线段AB、BC.求作⊙O,使它经过点A、B、C(要求:尺规作图,不写作法,保留作图痕迹).(2002年,)图(1)图(2)分析因为A、B、C三点在⊙O上,所以OA=OB=OC=R.根据到线段AB、BC 各端点距离相等的点在线段的垂直平分线上,故分别作线段AB、BC垂直平分线即可.解如图(2)说明角平分线的性质、线段垂直平分线的性质在作图题中的应用是近几年中考中的又一道风景,它往往与实际问题紧密联系在一起.典型例题十六例如图,是一块直角三角形余料,.工人师傅要把它加工成一个正方形零件,使C为正方形的一个顶点,其余三个顶点分别在AB、BC、AC边上.试协助工人师傅用尺规画出裁割线.分析要作出符合条件的正方形,可先作出有三个角为90°的四边形,并设法让相邻的一组边相等即可.作法如图.1 作的角平分线CD,交AB于点G;②过G点分别作AC、BC的垂线,垂足为E、F.则四边形ECFG就是所要求作的正方形.。
(完整版)八上数学尺规作图归纳总结

八上数学教师辅导讲义学员编号:年级:新初二课时数:学员姓名:辅导科目:数学学科教师:赵老师课题尺规作图授课日期及时段教学目的教学内容一、知识梳理(一)尺规作图的定义:尺规作图是指用没有刻度的直尺和圆规作图。
(二)五种基本作图:1、作一条线段等于已知线段;已知:如图,线段a .求作:线段AB,使AB = a . 訂〈己知)作法:A 1H p①作射线AP;:作线段等干记知线段)②在射线AP上截取AB=a .则线段AB就是所求作的图形。
2、作一个角等于已知角;3、作已知线段的垂直平分线;已知:如图,线段MN.求作:点O,使MO=NQ即0是MN的中点)作法:完美WORD 格式.整理①分别以M N为圆心,大于1/2MN的相同线段为半径画弧,两弧相交于P, Q;②连接PQ交MN于O.则点O就是所求作的MN的中点。
(试问:PQ与MN有何关系?)4、作已知角的角平分线;已知:如图,/ AOB求作:射线OP,使/ AOP=Z BOP (即卩OP平分/ AOB 。
作法:①以O为圆心,任意长度为半径画弧,分别交OA OB于M N;②分别以M N为圆心,大于1/2MN的相同线段为半径画弧,两弧交/ AOB内于P;③作射线OP则射线OP就是/ AOB的角平分线。
5、过一点作已知直线的垂线;①以已知点为圆心,以任意长为半径作弧,交直线于②分别以A、B为圆心,以大于1/2AB长为半径分别作弧,两弧分别交于点M点N;③连接MN则直线MN为所求作的直线。
6、过直线外一点作直线的平行线(三)尺规作图拓展(1)已知三边作三角形。
已知:如图,线段a, b, c.求作:△ ABC 使AB = c , AC = b , BC = a.作法:(作线段的中点)(作角平分线)B两点;--------------------- b(巳知)(已知三边作三凭形)作线段AB = c ;以A 为圆心b 为半径作弧,以 B 为圆心 为半径作弧与前弧相交于 C ;连接AC, BG则厶ABC 就是所求作的三角形。
尺规作图 知识归纳+真题解析

尺规作图知识归纳+真题解析【知识归纳】一)尺规作图1.定义只用没有刻度的和作图叫做尺规作图.2.步骤①根据给出的条件和求作的图形,写出已知和求作部分;②分析作图的方法和过程;③用直尺和圆规进行作图;④写出作法步骤,即作法.二)五种基本作图1.作一条线段等于已知线段;2.作一个角等于已知角;3.作已知角的平分线;4.过一点作已知直线的垂线;5.作已知线段的垂直平分线.三)基本作图的应用1.利用基本作图作三角形(1)已知三边作三角形;(2)已知两边及其夹角作三角形;(3)已知两角及其夹边作三角形;(4)已知底边及底边上的高作等腰三角形;(5)已知一直角边和斜边作直角三角形.2.与圆有关的尺规作图(1)过不在同一直线上的三点作圆(即三角形的外接圆).(2)作三角形的内切圆.【知识归纳答案】一)尺规作图1.定义只用没有刻度的直尺和圆规作图叫做尺规作图.2.步骤①根据给出的条件和求作的图形,写出已知和求作部分;②分析作图的方法和过程;③用直尺和圆规进行作图;④写出作法步骤,即作法.二)五种基本作图1.作一条线段等于已知线段;2.作一个角等于已知角;3.作已知角的平分线;4.过一点作已知直线的垂线;5.作已知线段的垂直平分线.三)基本作图的应用1.利用基本作图作三角形(1)已知三边作三角形;(2)已知两边及其夹角作三角形;(3)已知两角及其夹边作三角形;(4)已知底边及底边上的高作等腰三角形;(5)已知一直角边和斜边作直角三角形.2.与圆有关的尺规作图(1)过不在同一直线上的三点作圆(即三角形的外接圆).(2)作三角形的内切圆.真题解析一.选择题(共8小题)1.如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是()A.6 B.8 C.10 D.12【考点】N2:作图—基本作图;L5:平行四边形的性质.【分析】连接EG,由作图可知AD=AE,根据等腰三角形的性质可知AG是DE的垂直平分线,由平行四边形的性质可得出CD∥AB,故可得出∠2=∠3,据此可知AD=DG,由等腰三角形的性质可知OA=AG,利用勾股定理求出OA的长即可.【解答】解:连接EG,∵由作图可知AD=AE,AG是∠BAD的平分线,∴∠1=∠2,∴AG⊥DE,OD=DE=3.∵四边形ABCD是平行四边形,∴CD∥AB,∴∠2=∠3,∴∠1=∠3,∴AD=DG.∵AG⊥DE,∴OA=AG.在Rt△AOD中,OA===4,∴AG=2AO=8.故选B.2.如图,在△AEF中,尺规作图如下:分别以点E,点F为圆心,大于EF的长为半径作弧,两弧相交于G,H两点,作直线GH,交EF于点O,连接AO,则下列结论正确的是()A.AO平分∠EAF B.AO垂直平分EF C.GH垂直平分EF D.GH平分AF【考点】N2:作图—基本作图;KG:线段垂直平分线的性质.【分析】直接根据线段垂直平分线的作法即可得出结论.【解答】解:由题意可得,GH垂直平分线段EF.故选C.3.如图,已知线段AB,分别以A、B为圆心,大于AB为半径作弧,连接弧的交点得到直线l,在直线l上取一点C,使得∠CAB=25°,延长AC至M,求∠BCM的度数为()A.40°B.50°C.60°D.70°【考点】N2:作图—基本作图;KG:线段垂直平分线的性质.【分析】根据作法可知直线l是线段AB的垂直平分线,故可得出AC=BC,再由三角形外角的性质即可得出结论.【解答】解:∵由作法可知直线l是线段AB的垂直平分线,∴AC=BC,∴∠CAB=∠CBA=25°,∴∠BCM=∠CAB+∠CBA=25°+25°=50°.故选B.4.下列四种基本尺规作图分别表示:①作一个角等于已知角;②作一个角的平分线;③作一条线段的垂直平分线;④过直线外一点P作已知直线的垂线,则对应选项中作法错误的是()A.①B.②C.③D.④【考点】N2:作图—基本作图.【分析】利用作一个角等于已知角;作一个角的平分线;作一条线段的垂直平分线;过直线外一点P 作已知直线的垂线的作法进而判断得出答案.【解答】解:①作一个角等于已知角的方法正确;②作一个角的平分线的作法正确;③作一条线段的垂直平分线缺少另一个交点,作法错误;④过直线外一点P作已知直线的垂线的作法正确.故选:C.5.如图,在△ABC中,∠ACB=90°,∠A=30°,BC=4,以点C为圆心,CB长为半径作弧,交AB于点D;再分别以点B和点D为圆心,大于BD的长为半径作弧,两弧相交于点E,作射线CE交AB于点F,则AF的长为()A.5 B.6 C.7 D.8【考点】N2:作图—基本作图;KO:含30度角的直角三角形.【分析】连接CD,根据在△ABC中,∠ACB=90°,∠A=30°,BC=4可知AB=2BC=8,再由作法可知BC=CD=4,CE是线段BD的垂直平分线,故CD是斜边AB的中线,据此可得出BD的长,进而可得出结论.【解答】解:连接CD,∵在△ABC中,∠ACB=90°,∠A=30°,BC=4,∴AB=2BC=8.∵作法可知BC=CD=4,CE是线段BD的垂直平分线,∴CD是斜边AB的中线,∴BD=AD=4,∴BF=DF=2,∴AF=AD+DF=4+2=6.故选B.6.如图,用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心,以任意长为半径画弧①,分别交OA、OB于点E、F,那么第二步的作图痕迹②的作法是()A.以点F为圆心,OE长为半径画弧B.以点F为圆心,EF长为半径画弧C.以点E为圆心,OE长为半径画弧D.以点E为圆心,EF长为半径画弧【考点】N2:作图—基本作图.【分析】根据作一个角等于一直角的作法即可得出结论.【解答】解:用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心,以任意长为半径画弧①,分别交OA、OB于点E、F,第二步的作图痕迹②的作法是以点E为圆心,EF长为半径画弧.故选D.学科网7.如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.步骤1:以C为圆心,CA为半径画弧①;步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;步骤3:连接AD,交BC延长线于点H.下列叙述正确的是()A.BH垂直平分线段AD B.AC平分∠BADC.S△ABC=BC•AH D.AB=AD【考点】N2:作图—基本作图;KG:线段垂直平分线的性质.【分析】根据已知条件可知直线BC是线段AD的垂直平分线,由此一一判定即可.【解答】解:A、正确.如图连接CD、BD,∵CA=CD,BA=BD,∴点C、点B在线段AD的垂直平分线上,∴直线BC是线段AD的垂直平分线,故A正确.B、错误.CA不一定平分∠BDA.C、错误.应该是S△ABC=•BC•AH.D、错误.根据条件AB不一定等于AD.故选A.8.下列尺规作图,能判断AD是△ABC边上的高是()A.B.C.D.【考点】N2:作图—基本作图.【分析】过点A作BC的垂线,垂足为D,则AD即为所求.【解答】解:过点A作BC的垂线,垂足为D,故选B.学科网二.填空题(共5小题)9.如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于MN的长为半径作弧,两弧相交于点P;③作AP 射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为15.【考点】N2:作图—基本作图;L5:平行四边形的性质.【分析】根据角平分线的性质可知∠DAQ=∠BAQ,再由平行四边形的性质得出CD∥AB,BC=AD=3,∠BAQ=∠DQA,故可得出△AQD是等腰三角形,据此可得出DQ=AD,进而可得出结论.【解答】解:∵由题意可知,AQ是∠DAB的平分线,∴∠DAQ=∠BAQ.∵四边形ABCD是平行四边形,∴CD∥AB,BC=AD=3,∠BAQ=∠DQA,∴∠DAQ=∠DQA,∴△AQD是等腰三角形,∴DQ=AD=3.∵DQ=2QC,∴QC=DQ=,∴CD=DQ+CQ=3+=,∴平行四边形ABCD周长=2(DC+AD)=2×(+3)=15.故答案为:15.10.如图所示,已知∠AOB=40°,现按照以下步骤作图:①在OA,OB上分别截取线段OD,OE,使OD=OE;②分别以D,E为圆心,以大于DE的长为半径画弧,在∠AOB内两弧交于点C;③作射线OC.则∠AOC的大小为20°.【考点】N2:作图—基本作图.【分析】直接根据角平分线的作法即可得出结论.【解答】解:∵由作法可知,OC是∠AOB的平分线,∴∠AOC=∠AOB=20°.故答案为:20°.11.如图,依据尺规作图的痕迹,计算∠α=56°.【考点】N2:作图—基本作图.【分析】先根据矩形的性质得出AD∥BC,故可得出∠DAC的度数,由角平分线的定义求出∠EAF的度数,再由EF是线段AC的垂直平分线得出∠AEF的度数,根据三角形内角和定理得出∠AFE的度数,进而可得出结论.【解答】解:∵四边形ABCD是矩形,∴AD∥BC,∴∠DAC=∠ACB=68°.∵由作法可知,AF是∠DAC的平分线,∴∠EAF=∠DAC=34°.∵由作法可知,EF是线段AC的垂直平分线,∴∠AEF=90°,∴∠AFE=90°﹣34°=56°,∴∠α=56°.故答案为:56.学科网12.如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧在第二象限内交于点P(a,b),则a与b的数量关系是a+b=0.【考点】N2:作图—基本作图;D5:坐标与图形性质;J5:点到直线的距离.【分析】根据作图方法可得点P在第二象限的角平分线上,根据角平分线的性质和第二象限内点的坐标符号,可得a与b的数量关系为互为相反数.【解答】解:根据作图方法可得,点P在第二象限角平分线上,∴点P到x轴、y轴的距离相等,即|b|=|a|,又∵点P(a,b)第二象限内,∴b=﹣a,即a+b=0,故答案为:a+b=0.13.图1是“作已知直角三角形的外接圆”的尺规作图过程已知:Rt△ABC,∠C=90°,求作Rt△ABC的外接圆.作法:如图2.(1)分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于P,Q两点;(2)作直线PQ,交AB于点O;(3)以O为圆心,OA为半径作⊙O.⊙O即为所求作的圆.请回答:该尺规作图的依据是到线段两端点的距离相等的点在这条线段的垂直平分线上;两点确定一条直线;90°的圆周角所对的弦是直径;圆的定义..【考点】N3:作图—复杂作图;MA:三角形的外接圆与外心.【分析】由于90°的圆周角所对的弦是直径,所以Rt△ABC的外接圆的圆心为AB的中点,然后作AB 的中垂线得到圆心后即可得到Rt△ABC的外接圆.【解答】解:该尺规作图的依据是到线段两端点的距离相等的点在这条线段的垂直平分线上;90°的圆周角所对的弦是直径.故答案为到线段两端点的距离相等的点在这条线段的垂直平分线上;两点确定一直线;90°的圆周角所对的弦是直径;圆的定义.三.解答题(共8小题)14.如图,△ABC中,∠ACB>∠ABC.(1)用直尺和圆规在∠ACB的内部作射线CM,使∠ACM=∠ABC(不要求写作法,保留作图痕迹);(2)若(1)中的射线CM交AB于点D,AB=9,AC=6,求AD的长.【考点】N2:作图—基本作图;S9:相似三角形的判定与性质.【分析】(1)根据尺规作图的方法,以AC为一边,在∠ACB的内部作∠ACM=∠ABC即可;(2)根据△ACD与△ABC相似,运用相似三角形的对应边成比例进行计算即可.【解答】解:(1)如图所示,射线CM即为所求;(2)∵∠ACD=∠ABC,∠CAD=∠BAC,∴△ACD∽△ABC,∴=,即=,∴AD=4.15.如图,在Rt△ABC中,∠B=90°,∠A=30°,AC=2.(1)利用尺规作线段AC的垂直平分线DE,垂足为E,交AB于点D,(保留作图痕迹,不写作法)(2)若△ADE的周长为a,先化简T=(a+1)2﹣a(a﹣1),再求T的值.【考点】N2:作图—基本作图;KO:含30度角的直角三角形.【分析】(1)根据作已知线段的垂直平分线的方法,即可得到线段AC的垂直平分线DE;(2)根据Rt△ADE中,∠A=30°,AE=,即可求得a的值,最后化简T=(a+1)2﹣a(a﹣1),再求T的值.【解答】解:(1)如图所示,DE即为所求;(2)由题可得,AE=AC=,∠A=30°,∴Rt△ADE中,DE=AD,设DE=x,则AD=2x,∴Rt△ADE中,x2+()2=(2x)2,解得x=1,∴△ADE的周长a=1+2+=3+,∵T=(a+1)2﹣a(a﹣1)=3a+1,∴当a=3+时,T=3(3+)+1=10+3.16.如图,已知△ABC,请用圆规和直尺作出△ABC的一条中位线EF(不写作法,保留作图痕迹).【考点】N3:作图—复杂作图;KX:三角形中位线定理.【分析】作线段AB的垂直平分线得到AB的中点E,作AC的垂直平分线得到线段AC的中点F.线段EF即为所求.【解答】解:如图,△ABC的一条中位线EF如图所示,方法:作线段AB的垂直平分线得到AB的中点E,作AC的垂直平分线得到线段AC的中点F.线段EF即为所求.17.如图,已知△ABC,∠B=40°.(1)在图中,用尺规作出△ABC的内切圆O,并标出⊙O与边AB,BC,AC的切点D,E,F(保留痕迹,不必写作法);(2)连接EF,DF,求∠EFD的度数.【考点】N3:作图—复杂作图;MI:三角形的内切圆与内心.【分析】(1)直接利用基本作图即可得出结论;(2)利用四边形的性质,三角形的内切圆的性质即可得出结论.【解答】解:(1)如图1,⊙O即为所求.(2)如图2,连接OD,OE,∴OD⊥AB,OE⊥BC,∴∠ODB=∠OEB=90°,∵∠B=40°,∴∠DOE=140°,∴∠EFD=70°.18.在数学课本上,同学们已经探究过“经过已知直线外一点作这条直线的垂线“的尺规作图过程:已知:直线l和l外一点P求作:直线l的垂线,使它经过点P.作法:如图:(1)在直线l上任取两点A、B;(2)分别以点A、B为圆心,AP,BP长为半径画弧,两弧相交于点Q;(3)作直线PQ.参考以上材料作图的方法,解决以下问题:(1)以上材料作图的依据是:线段垂直平分线上的点到线段两端点的距离相等(3)已知,直线l和l外一点P,求作:⊙P,使它与直线l相切.(尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)【考点】N3:作图—复杂作图;MD:切线的判定.【分析】(1)根据线段垂直平分线的性质,可得答案;(2)根据线段垂直平分线的性质,切线的性质,可得答案.【解答】解:(1)以上材料作图的依据是:线段垂直平分线上的点到线段两端点的距离相等,故答案为:线段垂直平分线上的点到线段两端点的距离相等;(2)如图.19.“直角”在初中几何学习中无处不在.如图,已知∠AOB,请仿照小丽的方式,再用两种不同的方法判断∠AOB是否为直角(仅限用直尺和圆规).【考点】N3:作图—复杂作图;KS:勾股定理的逆定理;M5:圆周角定理.【分析】(1)根据勾股定理的逆定理,可得答案;(2)根据圆周角定理,可得答案.【解答】解:(1)如图1,在OA,OB上分别,截取OC=4,OD=3,若CD的长为5,则∠AOB=90°(2)如图2,在OA,OB上分别取点C,D,以CD为直径画圆,若点O在圆上,则∠AOB=90°.20.如图,已知正七边形ABCDEFG,请仅用无刻度的直尺,分别按下列要求画图.(1)在图1中,画出一个以AB为边的平行四边形;(2)在图2中,画出一个以AF为边的菱形.【考点】N3:作图—复杂作图;L5:平行四边形的性质;L8:菱形的性质.【分析】(1)连接AF、BE、CG,CG交AF于M,交BE于N.四边形ABNM是平行四边形.(2)连接AF、DF,延长DC交AB的延长线于M,四边形AFDM是菱形.【解答】解:(1)连接AF、BE、CG,CG交AF于M,交BE于N.四边形ABNM是平行四边形.(2)连接AF、DF,∠延长DC交AB的延长线于M,四边形AFDM是菱形.21.图①、图②、图③都是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点称为格点.线段AB的端点在格点上.(1)在图①、图2中,以AB为边各画一个等腰三角形,且第三个顶点在格点上;(所画图形不全等)(2)在图③中,以AB为边画一个平行四边形,且另外两个顶点在格点上.【考点】N4:作图—应用与设计作图;KI:等腰三角形的判定;KK:等边三角形的性质;L6:平行四边形的判定.【分析】(1)根据等腰三角形的定义作图可得;(2)根据平行四边形的判定作图可得.【解答】解:(1)如图①、②所示,△ABC和△ABD即为所求;(2)如图③所示,▱ABCD即为所求.。
中考专题复习——初中最基本的尺规作图总结与典型例题

初中基本尺规作图总结与典型例题一、理解“尺规作图”的含义1.在几何中,我们把只限定用直尺(无刻度)和圆规来画图的方法,称为尺规作图.其中直尺只能用来作直线、线段、射线或延长线段;圆规用来作圆和圆弧.由此可知,尺规作图与一般的画图不同,一般画图可以动用一切画图工具,包括三角尺、量角器等,在操作过程中可以度量,但尺规作图在操作过程中是不允许度量成分的.2.基本作图:(1)用尺规作一条线段等于已知线段;(2)用尺规作一个角等于已知角. 利用这两个基本作图,可以作两条线段或两个角的和或差.二、熟练掌握尺规作图题的规范语言1.用直尺作图的几何语言:①过点×、点×作直线××;或作直线××;或作射线××;②连结两点××;或连结××;③延长××到点×;或延长(反向延长)××到点×,使××=××;或延长××交××于点×;2.用圆规作图的几何语言:①在××上截取××=××;②以点×为圆心,××的长为半径作圆(或弧);③以点×为圆心,××的长为半径作弧,交××于点×;④分别以点×、点×为圆心,以××、××的长为半径作弧,两弧相交于点×、×. 三、了解尺规作图题的一般步骤尺规作图题的步骤:1.已知:当作图是文字语言叙述时,要学会根据文字语言用数学语言写出题目中的条件;2.求作:能根据题目写出要求作出的图形及此图形应满足的条件;3.作法:能根据作图的过程写出每一步的操作过程.当不要求写作法时,一般要保留作图痕迹.对于较复杂的作图,可先画出草图,使它同所要作的图大致相同,然后借助草图寻找作法.在目前,我们只要能够写出已知,求作,作法三步(另外还有第四步证明)就可以了,而且在许多中考作图题中,又往往只要求保留作图痕迹,不需要写出作法,可见在解作图题时,保留作图痕迹很重要.尺规作图的定义:尺规作图是指用没有刻度的直尺和圆规作图。
初中作图题归纳

初中物理作图题汇总一、光的直线传播:1、在图中画出小孔成像光路图。
2、下图中,S 是光源,A 是不透明的物体,L 是竖直墙面,试画出光源S 照不到墙面的范围。
3、室内一盏电灯通过木板隔墙上的两个小洞,透出两条细小光束(如图所示)。
请根据这两条光束的方向确定室内电灯的位置。
二、光的反射:4、图所示的a 、b 是经平面镜反射后的反射光线,画出对应的入射光线:5、有一和水平面成30度的光线,要使它垂直射入井底,根据已知条件确定平面镜的位置,并注明反射角和入射角的度数。
6、一条光线与镜面成30°角射在平面镜上,如图所示,请画出反射光线并标出反射角的大小。
7、请你完成如图所示的光路。
三、平面镜成像:8、根据平面镜成像特点,在图中画出物AB 在平面镜MN 中的像A ′B ′。
9、有一束光通过A 点射到镜面,反射后过B 点,请画出入射光线和反射光线。
10、利用平面镜成像的原理作出点S 的像。
11、如图1所示,S ’为点光源S 在平面镜MN 中的像,SA 为光源S 发出的一条光线,请画出平面镜MN ,并完成光线SA 的光路。
12、小黄坐的位置与电视机红外线接收窗口之间刚好有张椅子,如图所示。
若不移动位置仍要遥控电视,在图14中画出遥控器发出红外线传播到电视机红外线接收窗口的光路:四、光的折射:13、如图所示,一束光线斜射向一块玻璃砖的侧面。
请画出光线进入玻璃砖的折射光线和从玻璃砖的另一侧面射出时的折射光线。
14、请在图12中画出对应的反射光线和折射光线。
15、请在下图中标出入射线,反射线,折射线 16、画出图所示的折射光线的入射光线。
五、透镜:17、图中,画出了光通过透镜前后的方向。
在图(a )、(b)中填上适当类型的透镜。
18、请你根据透镜对光线的作用完成下面的光路图.七、串、并联电路:19、按要求在虚线框内画好电路图,再根据电路图,在右边连接出对应的实物图.电路要求: (1)L 1与L 2组成并联电路, (2) S 1控制L 1, S 2同时控制L 1与L 2;20、按图所示的实物图画电路图:21、根据电路图连接实物图:22、现有小灯泡L1和L2,开关S1和S2,电源和导线若干 请在虚线框内设计一个电路图同时满足下列要求。
初中物理作图题总结归纳

初中物理作图题总结归纳物理学作为一门实验科学,实践操作能力的培养是十分重要的。
作图题作为物理实验的一种形式,旨在通过图形的绘制和数据的分析来加深学生对物理概念和规律的理解。
在初中物理学习中,作图题是一种常见的题型,需要学生灵活运用所学知识进行图形的绘制和分析。
本文将对初中物理作图题进行总结归纳,并探讨学生解题过程中可能遇到的难点。
一、作图题的基本要求作图题通常要求学生根据实验数据或已知条件绘制出合适的图形,并通过图形来分析问题。
在解答作图题时,学生需要注意以下几个基本要求:1. 使用合适的坐标系:学生应根据题目要求,选择合适的坐标系,如直角坐标系、时间坐标系等。
同时,要注意标注坐标轴的名称和刻度,并保证图形的大小适中,能够清晰地展示所要表达的信息。
2. 准确绘制曲线:学生需要根据给定的数据点,使用直尺和铅笔绘制出准确的曲线。
绘制曲线时,要注意点的标注要清晰、准确,且曲线要平滑、连续。
3. 注重正确的分析和解释:作图题的目的是为了通过图形来分析问题并得出结论。
学生在作图的过程中,应注意对图形的解读和分析,结合物理知识给出准确的解释。
同时要确保解答与图形相符,避免出现矛盾和错误的结论。
二、常见的作图题类型1. 动力学作图题:此类作图题通常要求学生根据物体的运动情况,绘制出相应的速度-时间图或位移-时间图。
通过观察图形的特征,分析物体的运动规律和相关的物理量。
2. 波动作图题:波动作图题主要涉及波的传播或波的干涉、衍射等现象。
学生需要根据给定的数据或条件,绘制出波的传播、波峰波谷位置等图形,并通过图形来描述和解释相关现象。
3. 电路作图题:电路作图题要求学生根据电路图和已知条件,绘制出电流的变化曲线或电压的变化曲线。
通过观察图形,学生需要分析电路元件的作用、电流的大小和方向等。
4. 光学作图题:光学作图题通常涉及光的传播、反射、折射等现象。
学生需要根据给定的条件,绘制出光线的传播路径、入射角、折射角等图形,并通过图形来解释和分析光学现象。
初二数学作图题举例义务几何试题

卜人入州八九几市潮王学校作图题举例义务几何【学习目的】1.知道几何作图题的一般步骤.2.能用根本作图作出满足某些条件的三角形,会写出、求作、作法.【主体知识归纳】1.一般几何作图题,应有、求作、作法、证明四个步骤.目前,我们只要求写出、求作、作法三个步骤.2.利用根本作图作三角形.三边作三角形;两边及其夹角作三角形;两角及其夹边作三角形;底边及底边上的高作等腰三角形;底边上的高及腰作等腰三角形;一直角边及斜边作直角三角形.【根底知识精讲】1.在中要画出图形,把条件详细化;在求作中,通常先明确求作什么图形,再写明图形应满足的条件.遇有属于根本作图的地方,写作法时,不必重写作图的详细过程,只用一句话概括表达就可以了.例如:(1)作线段××=××;(2)作∠×××=∠×××;(3)作××(射线)平分∠×××;(4)过点×作××⊥××,垂足为×;(5)作线段××的垂直平分线××.2.比照拟复杂的作图题,能经过严格分析,找到作图的方法,再进展作图,是本节的难点.复杂的作图题常用三角形奠基法,通过三角形过渡来完成.在作图之前,往往要先画一个假定适宜所设条件的草图,根据这个草图进展分析,寻找作图步骤.【例题精讲】[例1]:线段a和∠α(图3—134),求作:△ABC,使∠B=∠α,AB=AC=a.剖析:如图3—135,假设△ABC为所求作的三角形,其AB=AC=a,∠B=∠α,假设先作出∠B,那么可利用圆规在∠B一边上确定点A,AB=a,从而又可在∠B另一边上确定点C,于是可得所求作的△ABC.作法:(1)作∠EBF =∠α.(2)在BE 上截取BA =a ,以A 为圆心,a 为半径作弧,交BF 于点C .(3)连结AC .△ABC 为所求作的三角形(如图3—136).说明:此题也可先作线段AB =a ,再作∠B =∠α,最后确定点C (AC =a ).[例2]一角和这角的平分线及这角对边上的高,求作三角形.:线段m 、h 和∠α(图3—137).求作:△ABC ,使∠BAC =∠α,高线AD =h ,角平分线AE =m .剖析:假设△ABC 已作出,那么高AD =h ,角平分线AE =m ,∠BAE =∠CAE =21∠α(如图3—138).由Rt △AED 可先作出,再以AE 为一边,在两侧作∠EAB =∠EAC =21∠α,交直线DE 于B 、C ,可得所求的△ABC .作法:(1)作Rt △AED ,使∠ADE =90°,AE =m ,AD =h .(2)以A 为顶点,AE 为一边,在AE 两侧作∠EAB =∠EAC =21∠α,交直线DE 于B 、C . △ABC 即为所求(图3—139)作的三角形.说明:这种先作一个根本三角形的方法称为三角形奠基法.【同步达纲练习】1.填空题(1)一般几何作图题,应有下面几个步骤:__________、__________、__________、证明.比较复杂的作图题,在作图之前可作__________,有时还要对作图的__________进展讨论.目前,我们只要求写出__________、__________、__________三个步骤.(2)在几何作图题中,要反复应用学过的__________种根本作图,作法中不需要重述__________过程.(3)课本的例1中,有多处用到根本作图:①作∠MAN =∠α,是应用了__________;②在射线AM 、AN 上分别作线段AB =a ,AC =b ,两次应用了__________;课本例2中也屡次应用了根本作图,其中作线段BC =a 是应用了__________;作线段BC 的垂直平分线MN ,是应用了__________;在MN 上截取DA ,使DA =h ,是应用了__________.(4)尺规作图是指用__________来画图.2.选择题(1)如图3—140,∠AOB ,求作射线OC ,使OC 平分∠AOB ,作法的合理顺序是①作射线OC ②在OA 和OB 上,分别截取OD 、OE ,使OD =OE ③分别以D 、E 为圆心,大于21DE 的长为半径作弧,在∠AOB 内,两弧交于点CA .①②③B .②①③C .②③①D .③②①(2)线段a 、b 和m ,求作△ABC ,故BC =a ,AC =b ,BC 边上的中线AD =m ,作法的合理顺序为 ①延长CD 到B ,使BD =CD ②连结AB ③作△AD C ,使DC =21a ,AC =b ,AD =mA .③①②B .①②③C .②③①D .③②①(3)利用根本作图不可作的等腰三角形是A .底边及底边上的高B .底边上的高及腰C .底边及顶角D .两底角(4)用尺规作图,不能作出惟一三角形的是A .两角和夹边B .两边和夹角C .两边和其中一边的对角D .两角和其中一角的对边(5)用尺规作图,不能作出惟一直角三角形的是A .两条直角边B .两个锐角C .一直角边和一锐角D .斜边和一直角边(6)只用无刻度直尺就能作出的是A .延长线段AB 至C ,使BC =ABB .过直线l 上一点A 作l 的垂线C .作角的平分线D .从点O 再经过点P 作射线OP3.线段a 、b 、m ,求作△ABC ,使BC =a ,AC =b ,BC 上的中线AD =m .4.求作等腰三角形,使它的底边和底边上的高等于同一条线段(写出、求作、作法,不要求证明,但要求准确作图,保存作图痕迹).5.如图3—141,线段a ,求作:△ABC ,使AB =AC =a ,BC 边上的高AD =21a .6.如图3—142,线段a 和b ,求作:△ABC ,使AB =AC =a ,BC 边上的中线等于b .7.一直角边和它相邻的一个锐角,求作直角三角形(写出、求作、作法).8.腰长和底边上的高,求作等腰三角形(写出、求作、作法).9.三角形的一边及这边上的高和中线,求作三角形(写出、求作、作法).[参考答案]【同步达纲练习】1.(1)求作作法分析结果求作作法(2)五根本作图(3)①作一个角等于角②作一条线段等于线段作一条线段等于线段作线段的垂直平分线作一条线段等于线段(4)直尺和圆规2.(1)C(2)A(3)D(4)C(5)B(6)D3.提示:先作△ACD ,使AC =b ,CD =21a ,AD =m . 4~8.(略)9.提示:先作奠基三角形Rt △A ED ,使A E 、AD (斜边)分别等于高和中线.。
初二数学规作图典型例题归纳

初中尺规作图典型例题归纳典型例题一例 已知线段a 、b ,画一条线段,使其等于b a 2+.分析 所要画的线段等于b a 2+,实质上就是b b a ++.画法:1.画线段a AB =.2.在AB 的延长线上截取b BC 2=.线段AC 就是所画的线段.说明1.尺规作图要保留画图痕迹,画图时画出的所有点和线不可随意擦去.2.其它作图都可以通过画基本作图来完成,写画法时,只需用一句话来概括叙述基本作图. 典型例题二例 如下图,已知线段a 和b ,求作一条线段AD 使它的长度等于2a -b .图(2)正解 如图(2),(1)作射线AM ;(2)在射线AM 上,顺次截取AB =BC =a ;(3)在线段CA 上截取CD =b ,则线段AD 就是所求作的线段.典型例题三例 求作一个角等于已知角∠MON (如图1).图(1) 图(2)正解 如图(2),(1)作射线11M O ;(2)在图(1)上,以O 为圆心,任意长为半径作弧,交OM 于点A ,交ON 于点B ;(3)以1O 为圆心,OA 的长为半径作弧,交11M O 于点C ;(4)以C 为圆心,以AB 的长为半径作弧,交前弧于点D ;(5)过点D 作射线D O 1. 则∠D CO 1就是所要求作的角.典型例题四例 如下图,已知∠α及线段a ,求作等腰三角形,使它的底角为α,底边为a .分析 先假设等腰三角形已经作好,根据等腰三角形的性质,知两底角∠B =∠C =∠α,底边BC =a ,故可以先作∠B =∠α,或先作底边BC =a .作法 如下图(1)∠MBN =∠α;(2)在射线BM 上截取BC =a ;(3)以C 为顶点作∠PCB =∠α,射线CP 交BN 于点A .△ABC 就是所要求作的等腰三角形.说明 画复杂的图形时,如一时找不到作法,一般是先画出一个符合条件的草图,再根据这个草图进行分析,逐步寻找画图步骤.典型例题五例 如图(1),已知直线AB 及直线AB 外一点C ,过点C 作CD ∥AB (写出作法,画出图形).分析 根据两直线平行的性质,同位角相等或内错角相等,故作一个角∠ECD =∠EFB 即可.作法 如图(2).图(1) 图(2)(1)过点C 作直线EF ,交AB 于点F ;(2)以点F 为圆心,以任意长为半径作弧,交FB 于点P ,交EF 于点Q ;(3)以点C 为圆心,以FP 为半径作弧,交CE 于M 点;(4)以点M 为圆心,以PQ 为半径作弧,交前弧于点D ;(5)过点D 作直线CD ,CD 就是所求的直线.说明 作图题都应给出证明,但按照教科书的要求,一般不用写出,但要知道作图的原由.典型例题六例 如下图,△ABC 中,a =5cm ,b =3cm ,c =3.5cm ,∠B =︒36,∠C =︒44,请你从中选择适当的数据,画出与△ABC 全等的三角形(把你能画的三角形全部画出来,不写画法但要在所画的三角形中标出用到的数据).分析 本题实质上是利用原题中的5个数据,列出所有与△ABC 全等的各种情况,依据是SSS 、SAS 、AAS 、ASA .解 与△ABC 全等的三角形如下图所示.典型例题七例 正在修建的中山北路有一形状如下图所示的三角形空地需要绿化.拟从点A 出发,将△ABC 分成面积相等的三个三角形,以便种上三种不同的花草,请你帮助规划出图案(保留作图痕迹,不写作法).(2003年,桂林)分析 这是尺规作图在生活中的具体应用.要把△ABC 分成面积相等的三个三角形,且都是从A 点出发,说明这三个三角形的高是相等的,因而只需这三个三角形的底边也相等,所以只要作出BC 边的三等分点即可.作法 如下图,找三等分点的依据是平行线等分线段定理.典型例题八例 已知∠AOB ,求作∠AOB 的平分线OC .错解 如图(1)作法 (1)以O 为圆心,任意长为半径作弧,分别交OA 、OB 于D 、E 两点;(2)分别以D 、E 为圆心,以大于21DE 的长为半径作弧,两弧相交于C 点; (3)连结OC ,则OC 就是∠AOB 的平分线.错解分析 对角平分线的概念理解不够准确而致误.作法(3)中连结OC ,则OC 是一条线段,而角平分线应是一条射线.图(1) 图(2)正解 如图(2)(1)以点O 为圆心,任意长为半径作弧,分别交OA 、OB 于D 、E 两点;(2)分别以D 、E 为圆心,以大于21DE 的长为半径作弧,两弧交于C 点; (3)作射线OC ,则OC 为∠AOB 的平分线.典型例题九例 如图(1)所示,已知线段a 、b 、h (h <b ).求作△ABC ,使BC =a ,AB =b , BC 边上的高AD =h .图(1)错解 如图(2),(1)作线段BC =a ;(2)作线段BA =b ,使AD ⊥BC 且AD =h .则△ABC 就是所求作的三角形.错解分析 ①不能先作BC ;②第2步不能同时满足几个条件,完全凭感觉毫无根据;③未考虑到本题有两种情况.对于这种作图题往往都是按照由里到外的顺序依次作图,如本题先作高AD ,再作AB ,最后确定BC .图(2) 图(3)正解 如图(3).(1)作直线PQ ,在直线PQ 上任取一点D ,作DM ⊥PQ ;(2)在DM 上截取线段DA =h ;(3)以A 为圆心,以b 为半径画弧交射线DP 于B ;(4)以B 为圆心,以a 为半径画弧,分别交射线BP 和射线BQ 于1C 和2C ;(5)连结1AC 、2AC ,则△1ABC (或△2ABC )都是所求作的三角形.典型例题十例 如下图,已知线段a ,b ,求作Rt △ABC ,使∠ACB =90°,BC =a ,AC =b (用直尺和圆规作图,保留作图痕迹).分析 本题解答的关键在于作出∠ACB =90°,然后确定A 、B 两点的位置,作出△ABC .作法 如下图(1)作直线MN :(2)在MN 上任取一点C ,过点C 作CE ⊥MN ;(3)在CE 上截取CA =b ,在CM 上截取CB =a ;(4)连结AB ,△ABC 就是所求作的直角三角形.说明 利用基本作图画出所求作的几何图形的关键是要先分析清楚作图的顺序.若把握不好作图顺序,要先画出假设图形.典型例题十一例 如下图,已知钝角△ABC ,∠B 是钝角.求作:(1)BC 边上的高;(2)BC 边上的中线(写出作法,画出图形).分析 (1)作BC 边上的高,就是过已知点A 作BC 边所在直线的垂线;(2)作BC 边上的中线,要先确定出BC 边的中点,即作出BC 边的垂直平分线. 作法 如下图(1)①在直线CB 外取一点P ,使A 、P 在直线CB 的两旁;②以点A 为圆心,AP 为半径画弧,交直线CB 于G 、H 两点;③分别以G 、H 为圆心,以大于21GH 的长为半径画弧,两弧交于E 点; ④作射线AE ,交直线CB 于D 点,则线段AD 就是所要求作的△ABC 中BC 边上的高.(2)①分别以B 、C 为圆心,以大于21BC 的长为半径画弧,两弧分别交于M 、N 两点; ②作直线MN ,交BC 于点F ;③连结AF ,则线段AF 就是所要求作的△ABC 中边BC 上的中线.说明 在已知三角形中求作一边上的高线、中线、角平分线时,首先要把握好高线、中线、角平分钱是三条线段;其次,高线、中线的一个端点必须是三角形中这边所对的顶点,而关键是找出另一个端点.典型例题十二例 如图(1)所示,在图中作出点C ,使得C 是∠MON 平分线上的点,且AC =OC .图(1) 图(2)分析 由题意知,点C 不仅要在∠MON 的平分线上,且点C 到O 、A 两点的距离要相等,所以点C 应是∠MON 的平分线与线段OA 的垂直平分线的交点.作法 如图(2)所示(1)作∠MON 的平分线OP ;(2)作线段OA 的垂直平分线EF ,交OP 于点C ,则点C 就是所要求作的点.说明(1)根据题意弄清要求作的点的特征是到各直线距离相等,还是到各端点距离相等.(2)两条直线交于一点.典型例题十三例如下图,已知线段a、b、∠α、∠β.求作梯形ABCD,使AD=a,BC=b,AD∥BC,∠B=∠α;∠C=∠β.分析假定梯形已经作出,作AE∥DC交BC于E,则AE将梯形分割为两部分,一部分是△ABE,另一部分是AECD.在△ABE中,已知∠B=∠α,∠AEB=∠β,BE=b-a,所以,可以首先把它作出来,而后作出AECD.作法如下图.(1)作线段BC=b;(2)在BC上截取BE=b-a;(3)分别以B、E为顶点,在BE同侧作∠EBA=∠α,∠AEB=∠β,BA、EA交于A;(4)以EA、EC为邻边作AECD.四边形ABCD就是所求作的梯形.说明基本作图是作出较简单图形的基础,三角形是最简单的多边形,它是许多复杂图形的基础.因此,要作一个复杂的图形,常常先作一个比较容易作出的三角形,然后以此为基础,再作出所求作的图形.典型例题十四例如下图,在一次军事演习中,红方侦察员发现蓝方指挥部在A区内,到铁路与公路的距离相等,且离铁路与公路交叉处B点700米,如果你是红方的指挥员,请你在图示的作战图上标出蓝方指挥部的位置.(2002年,青岛)分析依据角平分线的性质可以知道,蓝方指挥部必在A区内两条路所夹角的平分线上,然后由蓝方指挥部距B点的距离,依据比例尺,计算出图上的距离为3.5cm,就可以确定出蓝方指挥部的位置.解如下图,图中C点就是蓝方指挥部的位置.典型例题十五例如图(1),已知有公共端点的线段AB、BC.求作⊙O,使它经过点A、B、C(要求:尺规作图,不写作法,保留作图痕迹).(2002年,大连)图(1)图(2)分析因为A、B、C三点在⊙O上,所以OA=OB=OC=R.根据到线段AB、BC各端点距离相等的点在线段的垂直平分线上,故分别作线段AB、BC垂直平分线即可.解如图(2)说明角平分线的性质、线段垂直平分线的性质在作图题中的应用是近几年中考中的又一道风景,它往往与实际问题紧密联系在一起.典型例题十六例 如图,是一块直角三角形余料,︒=∠90C .工人师傅要把它加工成一个正方形零件,使C 为正方形的一个顶点,其余三个顶点分别在AB 、BC 、AC 边上.试协助工人师傅用尺规画出裁割线.分析 要作出符合条件的正方形,可先作出有三个角为90°的四边形,并设法让相邻的一组边相等即可.作法 如图.① 作ACB ∠的角平分线CD ,交AB 于点G ;②过G 点分别作AC 、BC 的垂线,垂足为E 、F .则四边形ECFG 就是所要求作的正方形.。
初中数学中考复习:尺规作图及命题、证明

14
考点三:与圆有关的尺规作图 • 与圆有关的尺规作图:
• (1)过不在同一条直线上的三点作圆(即三角形的外接圆); • (2)作三角形的内切圆; • (3)作圆的内接正方形及正六边形.
• 有关中心对称或轴对称的作图以及设计图案是中考常见的类型.
15
考点三:与圆有关的尺规作图
• 【例 如图,已知△ABC,∠B=40°.
题;
•
若甲错,即x≤14,则y≥6,则乙错,故D不是真命题.
•
根据以上分析,故选B.
• 【答案】 B
30
考点五:命题、定理、证明 • 基本事实与定理:
• (1)经过长期实践后公认为正确的命题,作为判断其他命题的依据,这些命题称为 基本事实.例如,“两点之间线段最短”,“两点确定一条直线”.
• (2)用推理的方法判断为正确的命题叫做定理.例如,“对顶角相等”,“三角形任何 两边的和大于第三边”.
1 2
AC的长为半径画弧,两弧相交于M,N两点,作直线MN交AD于点E,则△CDE的周长是(
B
)
•
A.7
B.10
C.11
D.12
22
考点四:尺规作图的综合应用
• 【例】(2018·湖州)尺规作图特有的魅力曾使无数人沉湎其中.传说拿破仑通过下列尺规作 图考他的大臣:
• ①将半径为r的⊙O六等分,依次得到A,B,C,D,E,F六个分点; • ②分别以点A、D为圆心,AC长为半径画弧,G是两弧的一个交点; • ③连结OG. • 问:OG的长是多少? • 大臣给出的正确答案应是( )
1 2
AC的长为半径画弧,两弧相交于M,N两点,作直线MN交AD于点E,则△CDE的周长是(
)
•
初中尺规作图总结

2. 基本作图:(1)用尺规作一条线段等于已知线段; (2)用尺规作一个角等于已知角 .
利用这两个基本作图,可以作两条线段或两个角的和或差 . 二、熟练掌握尺规作图题的规范语言 1. 用直尺作图的几何语言: ①过点×、点×作直线××;或作直线××;或作射线××;
②连结两点××;或连结××;
③延长××到点×;或延长(反向延长)××到点×,使××=××;或延长××交
则线段 AB就是所求作的图形。 题目二:作已知线段的中点。 已知:如图,线段 MN. 求作:点 O,使 MO=N(O即 O是 MN的中点) . 作法: (1)分别以 M、N为圆心,大于
的相同线段为半径画弧, 两弧相交于 P,Q; (2)连接 PQ交 MN于 O. 则点 O就是所求作的MN的中点。 (试问: PQ与MN有何关系?) 题目三:作已知角的角平分线。 已知:如图,∠ AOB, 求作:射线 OP, 使∠ AOP=∠ BOP(即 OP平分∠ AOB)。 作法: (1)以 O为圆心,任意长度为半径画弧,
题时,保留作图痕迹很重要 . 尺规作图的定义: 尺规作图是指用没有刻度的直尺和圆规作图。最基本
规作图 , 通常称 基本作图 。一些复杂的尺规作图都是由基本作图组成的。 五种基本作图: 1、 作一条线段等于已知线段;
2 、作一个角等于已知角; 3 、作已知线段的垂直平分线; 4 、作已知角的角平分线; 5 、过一点作已知直线的垂线; 题目一:作一条线段等于已知线段。 已知:如图,线段 a . 求作:线段 AB,使 AB = a . 作法: ( 1)作射线 AP; ( 2)在射线 AP上截取 AB=a .
图( 2)
图( 3)
正解 如图( 3). (1)作直线 PQ,在直线 PQ上任取一点 D,作 DM⊥ PQ; (2)在 DM上截取线段 DA=h;
专题01 八年级物理 利用光的反射定律的作图题

专题01 利用光的反射定律的作图题1.光的反射定律内容(1)反射光线、入射光线和法线都在同一平面内。
(2)反射光线和入射光线分居法线两侧。
(3)反射角等于入射角。
(4)光路是可逆的。
2.利用光的反射定律作图考法(1)根据要求作出入射光线或反射光线;(2)根据光的发射定律以及入射角大小,标出反射角大小;(3)根据给定的入射光线和出射光线,作出法线。
(4)根据给定的入射光线和出射光线,画出入射面。
3.利用光的反射定律作图注意事项(1)注意“箭头”方向;(2)法线一定要画成“虚线”;(3)一般涉及角度的作图题,要标出入射角、反射角的大小。
【例题1】(2020湖北襄阳)根据给出的入射光线,请画出其反射光线。
【例题2】(2020山东德州)光与平面镜成30角射在平面镜上,如图所示,请根据光的反射定律画出它的反射光线,并标明反射角的大小。
【例题3】如图所示,射向平面镜的一束光经镜面反射后沿水平为向射出,图中ON是∠AOB的角平分线,请在图中画出平面镜放置的位置并标出入射角.1.在图中,画出入射光线AO的反射光线,并标明反射角和它的大小。
2.(2020南京)如图所示,入射光线AO射向平面镜,画出反射光线OB并标出反射角的大小。
3.(2020安徽)图中MN为平面镜,OB为入射光线AO的反射光线。
请在图中画出光线AO并标出入射角的度数。
4.如图所示,一束光线AO射向平面镜,请画出其反射光线.(保留作图痕迹)5.画出图中入射光线AO的反射光线并标出反射角的大小.6.(2020牡丹江鸡西)图中,入射光线AO与镜面的夹角为60 ,请在图中画出的反射光线,并标明反射角的大小。
7.如图所示,小明利用一块平面镜使此时的太阳光水平射入隧道内,请你通过作图画出平面镜,并在图中标出反射角的度数。
8.(2020湖北黄冈)北京天坛的圜丘体现了我国古代高水平的建筑声学成就,它将建筑学和声学完美结合。
当人站在圜丘中心处说话,会觉得声音特别洪亮。
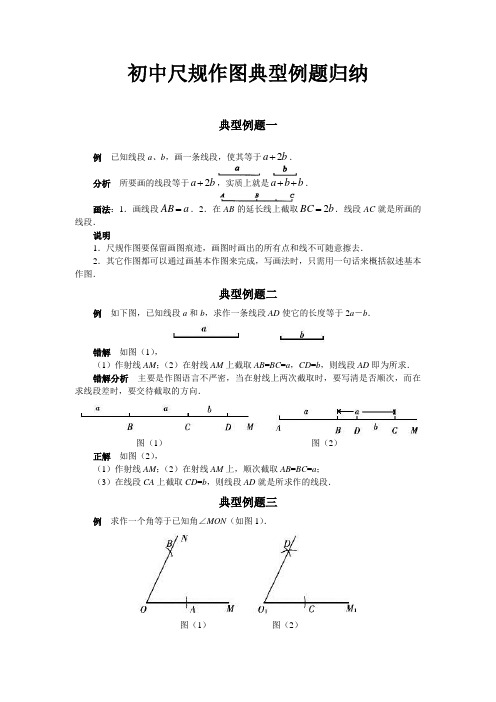
(完整版)初中尺规作图典型例题归纳总结
初中尺规作图典型例题归纳典型例题一例 已知线段a 、b ,画一条线段,使其等于b a 2+.分析 所要画的线段等于b a 2+,实质上就是b b a ++.画法:1.画线段a AB =.2.在AB 的延长线上截取b BC 2=.线段AC 就是所画的线段.说明1.尺规作图要保留画图痕迹,画图时画出的所有点和线不可随意擦去.2.其它作图都可以通过画基本作图来完成,写画法时,只需用一句话来概括叙述基本作图.典型例题二例 如下图,已知线段a 和b ,求作一条线段AD 使它的长度等于2a -b .错解 如图(1),(1)作射线AM ;(2)在射线AM 上截取AB =BC =a ,CD =b ,则线段AD 即为所求. 错解分析 主要是作图语言不严密,当在射线上两次截取时,要写清是否顺次,而在求线段差时,要交待截取的方向.图(1) 图(2)正解 如图(2),(1)作射线AM ;(2)在射线AM 上,顺次截取AB =BC =a ;(3)在线段CA 上截取CD =b ,则线段AD 就是所求作的线段.典型例题三例 求作一个角等于已知角∠MON (如图1).图(1) 图(2)错解 如图(2),(1)作射线11M O ;(2)在图(1),以O 为圆心作弧,交OM 于点A ,交ON 于点B ;(3)以1O 为圆心作弧,交11M O 于C ;(4)以C 为圆心作弧,交于点D ;(5)作射线D O 1.则∠D CO 1即为所求的角.错解分析 作图过程中出现了不准确的作图语言,在作出一条弧时,应表达为:以某点为圆心,以其长为半径作弧.正解 如图(2),(1)作射线11M O ;(2)在图(1)上,以O 为圆心,任意长为半径作弧,交OM 于点A ,交ON 于点B ;(3)以1O 为圆心,OA 的长为半径作弧,交11M O 于点C ;(4)以C 为圆心,以AB 的长为半径作弧,交前弧于点D ;(5)过点D 作射线D O 1. 则∠D CO 1就是所要求作的角.典型例题四例 如下图,已知∠α及线段a ,求作等腰三角形,使它的底角为α,底边为a .分析 先假设等腰三角形已经作好,根据等腰三角形的性质,知两底角∠B =∠C =∠α,底边BC =a ,故可以先作∠B =∠α,或先作底边BC =a .作法 如下图(1)∠MBN =∠α;(2)在射线BM 上截取BC =a ;(3)以C 为顶点作∠PCB =∠α,射线CP 交BN 于点A .△ABC 就是所要求作的等腰三角形.说明 画复杂的图形时,如一时找不到作法,一般是先画出一个符合条件的草图,再根据这个草图进行分析,逐步寻找画图步骤.典型例题五例 如图(1),已知直线AB 及直线AB 外一点C ,过点C 作CD ∥AB (写出作法,画出图形).分析 根据两直线平行的性质,同位角相等或内错角相等,故作一个角∠ECD =∠EFB 即可.作法 如图(2).图(1) 图(2)(1)过点C 作直线EF ,交AB 于点F ;(2)以点F 为圆心,以任意长为半径作弧,交FB 于点P ,交EF 于点Q ;(3)以点C 为圆心,以FP 为半径作弧,交CE 于M 点;(4)以点M 为圆心,以PQ 为半径作弧,交前弧于点D ;(5)过点D 作直线CD ,CD 就是所求的直线.说明 作图题都应给出证明,但按照教科书的要求,一般不用写出,但要知道作图的原由.典型例题六例 如下图,△ABC 中,a =5cm ,b =3cm ,c =3.5cm ,∠B =︒36,∠C =︒44,请你从中选择适当的数据,画出与△ABC 全等的三角形(把你能画的三角形全部画出来,不写画法但要在所画的三角形中标出用到的数据).分析 本题实质上是利用原题中的5个数据,列出所有与△ABC 全等的各种情况,依据是SSS 、SAS 、AAS 、ASA .解 与△ABC 全等的三角形如下图所示.典型例题七例 正在修建的中山北路有一形状如下图所示的三角形空地需要绿化.拟从点A 出发,将△ABC 分成面积相等的三个三角形,以便种上三种不同的花草,请你帮助规划出图案(保留作图痕迹,不写作法).(2003年,桂林)分析 这是尺规作图在生活中的具体应用.要把△ABC 分成面积相等的三个三角形,且都是从A 点出发,说明这三个三角形的高是相等的,因而只需这三个三角形的底边也相等,所以只要作出BC 边的三等分点即可.作法 如下图,找三等分点的依据是平行线等分线段定理.典型例题八例 已知∠AOB ,求作∠AOB 的平分线OC .错解 如图(1)作法 (1)以O 为圆心,任意长为半径作弧,分别交OA 、OB 于D 、E 两点;(2)分别以D 、E 为圆心,以大于21DE 的长为半径作弧,两弧相交于C 点; (3)连结OC ,则OC 就是∠AOB 的平分线.错解分析 对角平分线的概念理解不够准确而致误.作法(3)中连结OC ,则OC 是一条线段,而角平分线应是一条射线.图(1) 图(2)正解 如图(2)(1)以点O 为圆心,任意长为半径作弧,分别交OA 、OB 于D 、E 两点;(2)分别以D 、E 为圆心,以大于21DE 的长为半径作弧,两弧交于C 点; (3)作射线OC ,则OC 为∠AOB 的平分线.典型例题九例 如图(1)所示,已知线段a 、b 、h (h <b ).求作△ABC ,使BC =a ,AB =b , BC 边上的高AD =h .图(1)错解 如图(2),(1)作线段BC =a ;(2)作线段BA =b ,使AD ⊥BC 且AD =h .则△ABC 就是所求作的三角形.错解分析 ①不能先作BC ;②第2步不能同时满足几个条件,完全凭感觉毫无根据;③未考虑到本题有两种情况.对于这种作图题往往都是按照由里到外的顺序依次作图,如本题先作高AD ,再作AB ,最后确定BC .图(2) 图(3)正解 如图(3).(1)作直线PQ ,在直线PQ 上任取一点D ,作DM ⊥PQ ;(2)在DM 上截取线段DA =h ;(3)以A 为圆心,以b 为半径画弧交射线DP 于B ;(4)以B 为圆心,以a 为半径画弧,分别交射线BP 和射线BQ 于1C 和2C ;(5)连结1AC 、2AC ,则△1ABC (或△2ABC )都是所求作的三角形.典型例题十例 如下图,已知线段a ,b ,求作Rt △ABC ,使∠ACB =90°,BC =a ,AC =b (用直尺和圆规作图,保留作图痕迹).分析 本题解答的关键在于作出∠ACB =90°,然后确定A 、B 两点的位置,作出△ABC .作法 如下图(1)作直线MN :(2)在MN 上任取一点C ,过点C 作CE ⊥MN ;(3)在CE 上截取CA =b ,在CM 上截取CB =a ;(4)连结AB ,△ABC 就是所求作的直角三角形.说明 利用基本作图画出所求作的几何图形的关键是要先分析清楚作图的顺序.若把握不好作图顺序,要先画出假设图形.典型例题十一例 如下图,已知钝角△ABC ,∠B 是钝角.求作:(1)BC 边上的高;(2)BC 边上的中线(写出作法,画出图形).分析 (1)作BC 边上的高,就是过已知点A 作BC 边所在直线的垂线;(2)作BC 边上的中线,要先确定出BC 边的中点,即作出BC 边的垂直平分线. 作法 如下图(1)①在直线CB 外取一点P ,使A 、P 在直线CB 的两旁;②以点A 为圆心,AP 为半径画弧,交直线CB 于G 、H 两点;③分别以G 、H 为圆心,以大于21GH 的长为半径画弧,两弧交于E 点; ④作射线AE ,交直线CB 于D 点,则线段AD 就是所要求作的△ABC 中BC 边上的高. (2)①分别以B 、C 为圆心,以大于21BC 的长为半径画弧,两弧分别交于M 、N 两点; ②作直线MN ,交BC 于点F ;③连结AF ,则线段AF 就是所要求作的△ABC 中边BC 上的中线.说明 在已知三角形中求作一边上的高线、中线、角平分线时,首先要把握好高线、中线、角平分钱是三条线段;其次,高线、中线的一个端点必须是三角形中这边所对的顶点,而关键是找出另一个端点.典型例题十二例 如图(1)所示,在图中作出点C ,使得C 是∠MON 平分线上的点,且AC =OC .图(1) 图(2)分析 由题意知,点C 不仅要在∠MON 的平分线上,且点C 到O 、A 两点的距离要相等,所以点C 应是∠MON 的平分线与线段OA 的垂直平分线的交点.作法 如图(2)所示(1)作∠MON 的平分线OP ;(2)作线段OA 的垂直平分线EF ,交OP 于点C ,则点C 就是所要求作的点.说明(1)根据题意弄清要求作的点的特征是到各直线距离相等,还是到各端点距离相等.(2)两条直线交于一点.典型例题十三例 如下图,已知线段a 、b 、∠α、∠β.求作梯形ABCD ,使AD =a ,BC =b ,AD ∥BC ,∠B =∠α;∠C =∠β.分析 假定梯形已经作出,作AE ∥DC 交BC 于E ,则AE 将梯形分割为两部分,一部分是△ABE ,另一部分是AECD .在△ABE 中,已知∠B =∠α,∠AEB =∠β,BE =b -a ,所以,可以首先把它作出来,而后作出AECD .作法 如下图.(1)作线段BC=b;(2)在BC上截取BE=b-a;(3)分别以B、E为顶点,在BE同侧作∠EBA=∠α,∠AEB=∠β,BA、EA交于A;(4)以EA、EC为邻边作AECD.四边形ABCD就是所求作的梯形.说明基本作图是作出较简单图形的基础,三角形是最简单的多边形,它是许多复杂图形的基础.因此,要作一个复杂的图形,常常先作一个比较容易作出的三角形,然后以此为基础,再作出所求作的图形.典型例题十四例如下图,在一次军事演习中,红方侦察员发现蓝方指挥部在A区内,到铁路与公路的距离相等,且离铁路与公路交叉处B点700米,如果你是红方的指挥员,请你在图示的作战图上标出蓝方指挥部的位置.(2002年,青岛)分析依据角平分线的性质可以知道,蓝方指挥部必在A区内两条路所夹角的平分线上,然后由蓝方指挥部距B点的距离,依据比例尺,计算出图上的距离为3.5cm,就可以确定出蓝方指挥部的位置.解如下图,图中C点就是蓝方指挥部的位置.典型例题十五例如图(1),已知有公共端点的线段AB、BC.求作⊙O,使它经过点A、B、C(要求:尺规作图,不写作法,保留作图痕迹).(2002年,大连)图(1) 图(2)分析 因为A 、B 、C 三点在⊙O 上,所以OA =OB =OC =R .根据到线段AB 、BC 各端点距离相等的点在线段的垂直平分线上,故分别作线段AB 、BC 垂直平分线即可.解 如图(2)说明 角平分线的性质、线段垂直平分线的性质在作图题中的应用是近几年中考中的又一道风景,它往往与实际问题紧密联系在一起.典型例题十六例 如图,是一块直角三角形余料,︒=∠90C .工人师傅要把它加工成一个正方形零件,使C 为正方形的一个顶点,其余三个顶点分别在AB 、BC 、AC 边上.试协助工人师傅用尺规画出裁割线.分析 要作出符合条件的正方形,可先作出有三个角为90°的四边形,并设法让相邻的一组边相等即可.作法 如图.① 作ACB ∠的角平分线CD ,交AB 于点G ;②过G 点分别作AC 、BC 的垂线,垂足为E 、F .则四边形ECFG 就是所要求作的正方形.。
初二上作图题归纳

初二上画图题总结一、角平分线作图 已知:AOB ∠(1)求作:AOB ∠的平分线(要求:保留作图痕迹,不写做法)(2)若AOB ∠=60°,点P 为AOB ∠的平分线上一点,OP=800,求P 点到OA 的距离。
角平分线做法:1. 以 O 为圆心,任意长度为半径作弧,分别与角的两边交于点 D 、E;2. 分别以 D 、E 为圆心,大于DE 一半的相同长度为半径作弧,两弧在角的内部交于 C;3. 作射线 OC.∴射线 OC 为∠BOA 的角平分线二、作垂直平分线作图1、如图,在Rt ABC ∆中,C ∠=90°,B ∠=30°,作边AB 的垂直平分线交AB 于点D ,交BC 于点E (不写做法,保留作图痕迹,)并说明线段DE 和BC 边的数量关系。
线段垂直平分线做法:(1)分别以点A 、B 为圆心,以大于AB 21长为半径作弧,两弧相交于C 、D (2)作直线CD2、在一次军事演习中,红方侦查员发现蓝方的指挥部P 设在S 区,到公路a 与公路b 的距离相等,并且到水井M与小树N的距离也相等,请你帮助侦查员在图上标出蓝方指挥部P 的位置(不写做法吗,保留作图痕迹)垂直平分线规律:只要是说,到线段两边(即线段的两个端点)距离相等,则做垂直平分线。
角平分线规律:只要说,到两边的距离相等,则做角平分线。
3、最短路径作图OX 、OY 是两条公路,在两条公路夹角的内部有一油库A ,现在想在两条公路上分别建一个加油站M 、N ,为使运油的油罐车从油库A 先出发到加油站M ,再到另一个加油站N ,最后回到油库的路程最短,问加油站M 、N 应该如何选址?最短路径做法:选取对称点,一个点关于直线的对称点,关于另一条直线的对称点,则连接对称点后,交直线的交点,即为所求。
三、作对称图像(1)如图,分别画出△PQR 关于直线m 和直线n 的对称图形;(2)若点A (x ,y )在△PQR 上,写出点A 关于直线m 和直线n 对称的对应点21,A A 的点的坐标。
初二数学-尺规作图总结

初二数学尺规作图一、理解“尺规作图”的含义1.在几何中,我们把只限定用直尺(无刻度)和圆规来画图的方法,称为尺规作图.其中直尺只能用来作直线、线段、射线或延长线段;圆规用来作圆和圆弧.由此可知,尺规作图与一般的画图不同,一般画图可以动用一切画图工具,包括三角尺、量角器等,在操作过程中可以度量,但尺规作图在操作过程中是不允许度量成分的.2.基本作图:(1)用尺规作一条线段等于已知线段;(2)用尺规作一个角等于已知角. 利用这两个基本作图,可以作两条线段或两个角的和或差.二、熟练掌握尺规作图题的规范语言1.用直尺作图的几何语言:①过点×、点×作直线××;或作直线××;或作射线××;②连结两点××;或连结××;③延长××到点×;或延长(反向延长)××到点×,使××=××;或延长××交××于点×;2.用圆规作图的几何语言:①在××上截取××=××;②以点×为圆心,××的长为半径作圆(或弧);③以点×为圆心,××的长为半径作弧,交××于点×;④分别以点×、点×为圆心,以××、××的长为半径作弧,两弧相交于点×、×. 三、了解尺规作图题的一般步骤尺规作图题的步骤:1.已知:当作图是文字语言叙述时,要学会根据文字语言用数学语言写出题目中的条件;2.求作:能根据题目写出要求作出的图形及此图形应满足的条件;3.作法:能根据作图的过程写出每一步的操作过程.当不要求写作法时,一般要保留作图痕迹.对于较复杂的作图,可先画出草图,使它同所要作的图大致相同,然后借助草图寻找作法.在目前,我们只要能够写出已知,求作,作法三步(另外还有第四步证明)就可以了,而且在许多中考作图题中,又往往只要求保留作图痕迹,不需要写出作法,可见在解作图题时,保留作图痕迹很重要.尺规作图的定义:尺规作图是指用没有刻度的直尺和圆规作图。
作图题训练

· P
D B
的长为半径作弧,两弧交于点Q. 步骤3 作直线PQ.
ห้องสมุดไป่ตู้
Q
∴直线PQ就是经过直线AB外一点P的AB的垂线. 5.归纳总结. 经过一点可用直尺和圆规作一条直线与已知直线垂直.
2、已知:如图,在△ABC中,∠A=30°, ∠B=60°。 (1)作∠B的平分线BD,交AC于点D;作 AB的中点E(要求:尺规作图,保留作图痕 迹,不必写作法和证明); (2)连接DE,求证:△ADE≌△BDE。
P
A
B
3.比较
O
D
B
直线l 点O OM⊥直线l
直线AB 点P PQ⊥直线AB
分析:作图的关键是在 直线AB上确定C、D两点, 使得PC=PD;确定点Q, 使得CQ=DQ.
1.3 探索三角形全等的条件(7)
4.作法. 步骤1 以点P为圆心,适当的 长为半径作弧,使它与直线AB 交于C、D. 步骤2 分别以点C、D为圆心,大于 1 2 CD
6.如图,直线a.b.c 表示三条相互交叉 的公路,现在拟建一个货物中转站,要求它 到 三条公路的距离都相等,刚可供选择 的地址有: 处;
a
b c
B
A
C
用直尺和圆规作一个直角三角形, 使它的两条直角边分别等于a、b.
a b
3.(2013广东汕头,17,7分)如图,在 △ABC中,AB=AC,∠ABC=72°. (1)用直尺和圆规作∠ABC的平分线BD 交AC于点D(保留作图痕迹,不要求写作 法); (2)在(1)中作出∠ABC的平分线BD 后,求∠BDC的度数.
A
B
如图,为了促进当地旅游发展,某地要在三条公 路围成的一块平地上修建一个度假村.要使这个度 假村到三条公路的距离相等,应在何处修建?
初中中考尺规作图十例(打印)

BPAaOQPNM 尺规做图之阳早格格创做【知识归纳】1、尺规做图的定义:尺规做图是指用不刻度的曲尺战圆规做图.最基原,最时常使用的尺规做图,常常称基原做图.一些搀纯的尺规做图皆是由基原做图组成的.2、五种基原做图:1、做一条线段等于已知线段;2、做一个角等于已知角;3、做已知线段的笔曲仄分线;4、做已知角的角仄分线;5、过一面做已知曲线的垂线; (1)题目一:做一条线段等于已知线段. 已知:如图,线段a .供做:线段AB ,使AB = a . 做法:(1) 做射线AP ;(2) 正在射线AP 上截与AB=a .则线段AB 便是所供做的图形. (2)题目二:做已知线段的中面. 已知:如图,线段MN.供做:面O ,使MO=NO (即O 是MN 的中面). 做法:ONMBPANM BOA③②①A'A'N'O'B'M'O'A'N'M'M'O'(1)分别以M 、N 为圆心,大于的相共线段为半径绘弧, 二弧相接于P ,Q ;(2)对接PQ 接MN 于O .则面O 便是所供做的MN的中面. (3)题目三:做已知角的角仄分线. 已知:如图,∠AOB ,供做:射线OP, 使∠AOP =∠BOP (即OP 仄分∠AOB ).做法:(1)以O 为圆心,任性少度为半径绘弧,分别接OA ,OB 于M ,N ;(2)分别以M 、N为圆心,大于 的线段少为半径绘弧,二弧接∠AOB 内于P;(3) 做射线OP.则射线OP 便是∠AOB 的角仄分线. (4)题目四:做一个角等于已知角. 已知:如图,∠AOB. 供做:∠A ´O ´B ´,使∠A ´O ´B ´=∠AOB 做法: (1)做射线O ´A ´;(2)以O 为圆心,任性少度为半径绘弧,接OA 于M ,接OB 于N ;(3)以O ´为圆心,以OM 的少为半径绘弧,接O ´A ´于M ´;PB(4)以M ´为圆心,以MN 的少为半径绘弧,接前弧于N ´; (5)对接O ´N ´并延少到B ´. 则∠A ´O ´B ´便是所供做的角.(5)题目五:通过曲线上一面干已知曲线的垂线. 已知:如图,P 是曲线AB 上一面. 供做:曲线CD ,是CD 通过面P 做法:(1)以P 为圆,任性少为半径绘弧,接AB 于M 、N ;(2)分别以M 、N 为圆心,大于MN 21的少为半径绘弧,二弧接于面Q ;(3)过D 、Q 做曲线CD. 则曲线CD 是供做的曲线.(6)题目六:通过曲线中一面做已知曲线的垂线 已知:如图,曲线AB 及中一面P. 供做:曲线CD ,使CD 通过面P ,且CD ⊥AB.做法:(1)以P 为圆心,任性少为半径绘弧,接AB 于M 、N ;(2)分别以M 、N 圆心,大于MN 21少度的一半为半径绘弧,二弧接于面Q ;(3)过P 、Q 做曲线CD. 则曲线CD 便是所供做的曲线.ca b mn (7)题目七:已知三边做三角形. 已知:如图,线段a ,b ,c.供做:△ABC ,使AB = c ,AC = b ,BC = a. 做法:(1) 做线段AB = c ;(2) 以A 为圆心,以b 以B 为圆心,以a前弧相接于C ;(3) 对接AC ,BC.则△ABC 便是所供做的三角形.(8)题目八:已知二边及夹角做三角形. 已知:如图,线段m ,n, ∠α. 供做:△ABC ,使∠A=∠α,AB=m ,AC=n. 做法:(1) 做∠A=∠α; (2) 正在AB 上截与AB=m ,AC=n ; (3) 对接BC.则△ABC 便是所供做的三角形.(9)题目九:已知二角及夹边做三角形. 已知:如图,∠α,∠β,线段m .供做:△ABC ,使∠A=∠α,∠B=∠β,AB=m. 做法:(1)做线段AB=m;正在AB的共旁做∠A=∠α,做∠B=∠β,∠A与∠B的另一边相接于C.则△ABC便是所供做的图形(三角形).(10)题目十:已知三角形,做三角形的中接圆战内切圆.已知:如图,△ABC.供做:△ABC中接圆战内切圆.做法:(1)中接圆的圆心是△ABC三条边的笔曲仄分线的接面(转移为做AB、BC的笔曲仄分线接面,半径是接面与△ABC其中一个顶面的少度)(2)内切圆的圆心是△ABC三个角的角仄分线的接面(转移为做∠B、∠C的角仄分线接面,半径是接面到△ABC其中一条边的少度)。
八年级上册物理光学作图专题

八年级上册物理光学作图专题(基础版)1.根据光的反射定律,完成下面左图中的光路图,并标出反射角的大小。
2.如图所示,一束光经平面镜反射后,竖直向下射向井中,请你做出法线并画出平面镜的位置。
3.光线射向半球形玻璃砖,请画出完整的反射和折射光路图。
4.如图是一束光线射到平面镜上的反射光线,请你画出入射光线。
5.点发出一束光射向水面,一部分光经水面反射后射向A点,还有一部分光折射入水中射向B点,请完成反射和折射光路图。
6.如图所示,小明想要利用一块平面镜使此时的太阳光竖直射入井中。
请你通过作图画出反射光线,并标出平面镜的位置。
7.根据“平面镜成像特点”,分别画出图中的像点和光源,并完成光路图。
8.如图所示,L1为入射光线,L2为反射光线。
请在图中画出平面镜的位置。
(请保留作图痕迹。
)9.图中S点是水中鱼所在的位置,S'点是人的眼睛在P处看到的鱼的像的位置。
请完成人眼在P处看到鱼的光路图,并画出该光线在水面发生反射的反射光线。
10.如图,水下射灯发出一束光从水斜射向空气,请画出反射光线和折射光线的大致方向。
11.如图是经过平面镜反射后射向凸透镜的一束光线,请在图中补全经凸透镜折射的光线与射向平面镜的入射光线。
12.如图所示,一束光从空气射向半圆形玻璃砖的圆心,OA是经玻璃砖上表面反射的光,同时有一部分光通过玻璃砖并从其下表面射出,请完成这束光通过玻璃砖的光路图。
13.根据光的反射定律,完成下图中的光路图。
14.将一平面镜斜放在水槽中,有一束光线垂直射入水面,如图所示,请画出这束光线进入水中的折射光线和入射到平面镜后的反射光线。
15.如图,S是发光源,请你依据光的反射定律作出S光经反射后经过A点的光线。
16.请在图中画出物体在平面镜中的像,并画出一条眼睛能看到物体点的像的光路图。
17.光线BF从凸透镜射出后射到位于凸透镜焦点的镜面上,请画出进入凸透镜前的入射光线和经平面镜反射后的反射光线。
18.如图,ABC为一直角三角形玻璃砖的横截面。
初二数学尺规作图典型例题归纳

初二数学尺规作图典型例题归纳典型例题一例已知线段a、b,画一条线段,使其等于.分析所要画的线段等于,实质上就是.画法:1.画线段.2.在AB的延长线上截取.线段AC就是所画的线段.说明1.尺规作图要保留画图痕迹,画图时画出的所有点和线不可随意擦去.2.其它作图都可以通过画基本作图来完成,写画法时,只需用一句话来概括叙述基本作图.典型例题二例如下图,已知线段a和b,求作一条线段AD使它的长度等于2a-b.图(2)正解如图(2),(1)作射线AM;(2)在射线AM上,顺次截取AB=BC=a;(3)在线段CA上截取CD=b,则线段AD就是所求作的线段.典型例题三例求作一个角等于已知角∠MON(如图1).图(1)图(2)正解如图(2),(1)作射线;(2)在图(1)上,以O为圆心,任意长为半径作弧,交OM于点A,交ON于点B;(3)以为圆心,OA的长为半径作弧,交于点C;(4)以C为圆心,以AB的长为半径作弧,交前弧于点D;(5)过点D作射线.则∠就是所要求作的角.典型例题四例如下图,已知∠α及线段a,求作等腰三角形,使它的底角为α,底边为a.分析先假设等腰三角形已经作好,根据等腰三角形的性质,知两底角∠B=∠C=∠α,底边BC=a,故可以先作∠B=∠α,或先作底边BC=a.作法如下图(1)∠MBN=∠α;(2)在射线BM上截取BC=a;(3)以C为顶点作∠PCB=∠α,射线CP交BN于点A.△ABC就是所要求作的等腰三角形.说明画复杂的图形时,如一时找不到作法,一般是先画出一个符合条件的草图,再根据这个草图进行分析,逐步寻找画图步骤.典型例题五例如图(1),已知直线AB及直线AB外一点C,过点C作CD∥AB(写出作法,画出图形).分析根据两直线平行的性质,同位角相等或内错角相等,故作一个角∠ECD=∠EFB即可.作法如图(2).图(1)图(2)(1)过点C作直线EF,交AB于点F;(2)以点F为圆心,以任意长为半径作弧,交FB于点P,交EF于点Q;(3)以点C为圆心,以FP为半径作弧,交CE于M点;(4)以点M为圆心,以PQ为半径作弧,交前弧于点D;(5)过点D作直线CD,CD就是所求的直线.说明作图题都应给出证明,但按照教科书的要求,一般不用写出,但要知道作图的原由.典型例题六例如下图,△ABC中,a=5cm,b=3cm,c=3.5cm,∠B=,∠C=,请你从中选择适当的数据,画出与△ABC全等的三角形(把你能画的三角形全部画出来,不写画法但要在所画的三角形中标出用到的数据).分析本题实质上是利用原题中的5个数据,列出所有与△A BC全等的各种情况,依据是SSS、SAS、AAS、ASA.解与△ABC全等的三角形如下图所示.典型例题七例正在修建的中山北路有一形状如下图所示的三角形空地需要绿化.拟从点A出发,将△ABC分成面积相等的三个三角形,以便种上三种不同的花草,请你帮助规划出图案(保留作图痕迹,不写作法).(2003年,桂林)分析这是尺规作图在生活中的具体应用.要把△ABC分成面积相等的三个三角形,且都是从A点出发,说明这三个三角形的高是相等的,因而只需这三个三角形的底边也相等,所以只要作出BC边的三等分点即可.作法如下图,找三等分点的依据是平行线等分线段定理.典型例题八例已知∠AOB,求作∠AOB的平分线OC.错解如图(1)作法(1)以O为圆心,任意长为半径作弧,分别交OA、OB于D、E两点;(2)分别以D、E为圆心,以大于DE的长为半径作弧,两弧相交于C点;(3)连结OC,则OC就是∠AOB的平分线.错解分析对角平分线的概念理解不够准确而致误.作法(3)中连结OC,则OC是一条线段,而角平分线应是一条射线.图(1)图(2)正解如图(2)(1)以点O为圆心,任意长为半径作弧,分别交OA、OB于D、E两点;(2)分别以D、E为圆心,以大于DE的长为半径作弧,两弧交于C点;(3)作射线OC,则OC为∠AOB的平分线.典型例题九例如图(1)所示,已知线段a、b、h(h<b).求作△ABC,使BC=a,AB=b, BC边上的高AD=h.图(1)错解如图(2),(1)作线段BC=a;(2)作线段BA=b,使AD⊥BC且AD=h.则△ABC就是所求作的三角形.错解分析①不能先作BC;②第2步不能同时满足几个条件,完全凭感觉毫无根据;③未考虑到本题有两种情况.对于这种作图题往往都是按照由里到外的顺序依次作图,如本题先作高AD,再作AB,最后确定BC.图(2)图(3)正解如图(3).(1)作直线PQ,在直线PQ上任取一点D,作DM⊥PQ;(2)在DM上截取线段DA=h;(3)以A为圆心,以b为半径画弧交射线DP于B;(4)以B为圆心,以a为半径画弧,分别交射线BP和射线BQ于和;(5)连结、,则△(或△)都是所求作的三角形.典型例题十例如下图,已知线段a,b,求作Rt△ABC,使∠ACB=90°,BC=a,AC=b (用直尺和圆规作图,保留作图痕迹).分析本题解答的关键在于作出∠ACB=90°,然后确定A、B两点的位置,作出△ABC.作法如下图(1)作直线MN:(2)在MN上任取一点C,过点C作CE⊥MN;(3)在CE上截取CA=b,在CM上截取CB=a;(4)连结AB,△ABC就是所求作的直角三角形.说明利用基本作图画出所求作的几何图形的关键是要先分析清楚作图的顺序.若把握不好作图顺序,要先画出假设图形.典型例题十一例如下图,已知钝角△ABC,∠B是钝角.求作:(1)BC边上的高;(2)BC边上的中线(写出作法,画出图形).分析(1)作BC边上的高,就是过已知点A作BC边所在直线的垂线;(2)作BC边上的中线,要先确定出BC边的中点,即作出BC边的垂直平分线.作法如下图(1)①在直线CB外取一点P,使A、P在直线CB的两旁;②以点A为圆心,AP为半径画弧,交直线CB于G、H两点;③分别以G、H为圆心,以大于GH的长为半径画弧,两弧交于E点;④作射线AE,交直线CB于D点,则线段AD就是所要求作的△ABC中BC边上的高.(2)①分别以B、C为圆心,以大于BC的长为半径画弧,两弧分别交于M、N两点;②作直线MN,交BC于点F;③连结AF,则线段AF就是所要求作的△ABC中边BC上的中线.说明在已知三角形中求作一边上的高线、中线、角平分线时,首先要把握好高线、中线、角平分钱是三条线段;其次,高线、中线的一个端点必须是三角形中这边所对的顶点,而关键是找出另一个端点.典型例题十二例如图(1)所示,在图中作出点C,使得C是∠MON平分线上的点,且AC=OC.图(1)图(2)分析由题意知,点C不仅要在∠MON的平分线上,且点C到O、A两点的距离要相等,所以点C应是∠MON的平分线与线段OA的垂直平分线的交点.作法如图(2)所示(1)作∠MON的平分线OP;(2)作线段OA的垂直平分线EF,交OP于点C,则点C就是所要求作的点.说明(1)根据题意弄清要求作的点的特征是到各直线距离相等,还是到各端点距离相等.(2)两条直线交于一点.典型例题十三例如下图,已知线段a、b、∠α、∠β.求作梯形ABCD,使AD=a,BC=b,AD∥BC,∠B=∠α;∠C=∠β.分析假定梯形已经作出,作AE∥DC交BC于E,则AE将梯形分割为两部分,一部分是△ABE,另一部分是AECD.在△ABE中,已知∠B=∠α,∠AEB=∠β,BE=b-a,所以,可以首先把它作出来,而后作出AECD.作法如下图.(1)作线段BC=b;(2)在BC上截取BE=b-a ;(3)分别以B、E为顶点,在BE同侧作∠EBA=∠α,∠AEB=∠β,BA、EA 交于A;(4)以EA、EC为邻边作AECD.四边形ABCD就是所求作的梯形.说明基本作图是作出较简单图形的基础,三角形是最简单的多边形,它是许多复杂图形的基础.因此,要作一个复杂的图形,常常先作一个比较容易作出的三角形,然后以此为基础,再作出所求作的图形.典型例题十四例如下图,在一次军事演习中,红方侦察员发现蓝方指挥部在A区内,到铁路与公路的距离相等,且离铁路与公路交叉处B点700米,如果你是红方的指挥员,请你在图示的作战图上标出蓝方指挥部的位置.(2002年,青岛)分析依据角平分线的性质可以知道,蓝方指挥部必在A区内两条路所夹角的平分线上,然后由蓝方指挥部距B点的距离,依据比例尺,计算出图上的距离为3.5cm,就可以确定出蓝方指挥部的位置.解如下图,图中C点就是蓝方指挥部的位置.典型例题十五例如图(1),已知有公共端点的线段AB、BC.求作⊙O,使它经过点A、B、C(要求:尺规作图,不写作法,保留作图痕迹).(2002年,大连)图(1)图(2)分析因为A、B、C三点在⊙O上,所以OA=OB=OC=R.根据到线段AB、BC 各端点距离相等的点在线段的垂直平分线上,故分别作线段AB、BC垂直平分线即可.解如图(2)说明角平分线的性质、线段垂直平分线的性质在作图题中的应用是近几年中考中的又一道风景,它往往与实际问题紧密联系在一起.典型例题十六例如图,是一块直角三角形余料,.工人师傅要把它加工成一个正方形零件,使C为正方形的一个顶点,其余三个顶点分别在AB、BC、AC边上.试协助工人师傅用尺规画出裁割线.分析要作出符合条件的正方形,可先作出有三个角为90°的四边形,并设法让相邻的一组边相等即可.作法如图.1 作的角平分线CD,交AB于点G;②过G点分别作AC、BC的垂线,垂足为E、F.则四边形ECFG就是所要求作的正方形.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初二上画图题总结
一、角平分线作图
已知:AOB ∠
(1)求作:AOB ∠的平分线(要求:保留作图痕迹,不写做法)
(2)若AOB ∠=60°,点P 为AOB ∠的平分线上一点,OP=800,求P 点到OA 的距离。
角平分线做法:
1. 以 O 为圆心,任意长度为半径作弧,分别与角的两边交于点 D 、E;
2. 分别以 D 、E 为圆心,大于DE 一半的相同长度为半径作弧,两弧在角的内部交于 C;
3. 作射线 OC.
∴射线 OC 为∠BOA 的角平分线
二、作垂直平分线作图
1、如图,在Rt ABC ∆中,C ∠=90°,B ∠=30°,作边AB 的垂直平分线交AB 于点D ,交BC 于点E (不写做法,保留作图痕迹,)并说明线段DE 和BC 边的数量关系。
线段垂直平分线做法:
(1)分别以点A 、B 为圆心,以大于AB 2
1长为半径作弧,两弧相交于C 、D (2)作直线CD
2、在一次军事演习中,红方侦查员发现蓝方的指挥部P 设在S 区,到公路a 与公路b 的距
离相等,并且到水井M 与小树N 的距离也相等,请你帮助侦查员在图上标出蓝方指挥部P 的位置(不写做法吗,保留作图痕迹)
垂直平分线规律:
只要是说,到线段两边(即线段的两个端点)距离相等,则做垂直平分线。
角平分线规律:
只要说,到两边的距离相等,则做角平分线。
3、最短路径作图
OX 、OY 是两条公路,在两条公路夹角的内部有一油库A ,现在想在两条公路上分别建一个加油站M 、N ,为使运油的油罐车从油库A 先出发到加油站M ,再到另一个加油站N ,最后回到油库的路程最短,问加油站M 、N 应该如何选址?
最短路径做法:
选取对称点,一个点关于直线的对称点,关于另一条直线的对称点,则连接对称点后,交直线的交点,即为所求。
三、作对称图像
(1)如图,分别画出△PQR 关于直线m 和直线n 的对称图形;
(2)若点A (x ,y )在△PQR 上,写出点A 关于直线m 和直线n 对称的对应点21,A A 的点的坐标。
对称图形画法:
寻找特殊点,特殊点关于直线对称,连接特殊点,完成对称图形。
对称轴画法:
寻找特殊点和特殊点的对称点,取中点,两个中点能确定一条直线,即为对称轴。
