概率统计6 贝努利概型

合集下载

概率论与数理统计(chapt1-6 n重贝努利试验)

设A:恰好4次命中，B:至少4次命中，C:至多4次命中
（1） P( A) P5( 4) C54 0.840.2 0.4096
（2） P( B) P5( 4) P5( 5)
C
4 5
0.840.2
C
5 5
0.85
0.7373
（3） P(C ) 1 P(C) 1 P5( 5)
1
C
5 5
n重贝努利（Bernoulli ）试验的例子 1.已知在指定时间内某十字路口的事故率为p，现在此时间段内对经过的n 辆机动车进行观察每辆车是否经过这个十字路口是相互独立的，而且观
察结果有且只有这是一个贝努利试验
2.某射手每次射击命中目标的概率都是 p，现对同一目标独立射击 n 次，观察射击结果此射手独立射击n次，每次射击命中目标的概率都是p，所以这n次射击构成独立试验序列，每次射击
比如 s 3, a 1, b 1 则再赌3局必分胜负
P{甲赢} P{X 2} P{X 2} P{X 3}
C32
(1)2 2
1 2
C33
( 1 )3 2
1 2
又如 s 3, a 1, b 2
则再赌2局必分胜负
P{甲赢}
P{X
2} C22
( 1 )2 2
1 4
第一章小结
设事件A：10件中至少有两件次品，则
10
p( A) p10 (k) 1 p10 (0) p10 (1) k 2 1 0.9610 C110 0.04 0.969 0.0582
（2）设事件B：前 9 次中抽到 8 件正品一件次品；事件C：第 10 次抽到次品，则所求概率为
P(BC) P(B)P(C)
0.1 0.4 0.7

1.5_伯努利(Bernoulli)概型

2017年3月25日星期六
4
目录
上页
下页
返回
解设系队得胜人数为 X ，则在上述三种方案中，系队胜利的概率分别为
(1) P X 2 C 0.4 0.6
k 2 5 k 3 k k 5 k
3
3 k
0.352. 0.317. 0.290.
(2) P X 3 C 0.4 0.6
§1.5 伯努利(Bernoulli)概型
2017年3月25日星期六
1
目录
上页
下页
返回
定义 1：如果随机试验只有两个可能结果： A 与 A ，其中 P(A)=p, P( A )=1-p=q, 为伯努利试验 .
__
__
0＜p＜1, 则称该试验
定义 2：独立地重复 n 次伯努利试验，称为 n 重伯努利试验，也称伯努利概型.
在 n 重伯努利试验中，我们将事件 A 发生 k 次的概率记作 B(k;n,p).
2017年3月25日星期六
2
目录
上页
下页
返回
在 n 重伯努利试验中，设 P( A) p ， P( A) 1 p q (其中 0 p 1 )，则事件 A 恰好发生 k 次的概率为： k k n k k k n k P ( k ) C p (1 p ) C , (k 0,1, 2,, n) . n n n p q 定理
2017年3月25日星期六
7
目录
上页
下页
返回
【例】某人有一串 m 把外形相同的钥匙，其中只有一把能打开家门．有一天该人酒醉后回家，下意识地每次从 m 把钥匙中随便拿一只去开门，问该人在第 k 次才把门打开的概率多大？

贝努里概型

ＨＮ０Ｌ０ＧＹｌＮＦＯＲＭＡＴＩＯＮ
学术论坛
贝努里概型
许文琰（苏州技师学院江苏苏州２１５０００）摘要：贝努里概型是一种既简单又非常重要的概型，这种概型是概率论中最早研究的模型之一，也是得到最多研究的模型之一。在概率论中对概率分布的学＞－ｊ、概率的近似计算有着非常重要的作用。它在现实生活生产中和在自然科学试验中也有着直接的应用，并在其中发挥着重要的作用，为其解决问题提供了理论支持。该文就贝努里概型及其应用展开了解。关键词：贝努里概型贝努里试验中图分类号：０２１文献标识码：Ａ文章编号：１６７２－３７９１（２０１５）０１（ａ）一０１９６ —０２
Ｂ（４０００，０．００２），故所求概率为：
Ｐ（Ｘ ≥２）＝１一ＪＰ（＝０）一Ｐ（Ｘ＝１）
＝
１一００ｘ０．９９８。０ｏ ×０．００２。一０００ｘ０９９８ ” ｘ０００２。
随身带有两盒火柴，吸烟时从任一盒中取至少有２人发生过敏反应的概率。根火柴，经过若干时间后，发现一盒火柴解以表示４０００人中发生过敏反已经用完。如果最初两盒火柴中各有ｎ根应的人数，那么服从二项分布
．．

贝努里概型

贝努里概型作者：许文琰来源：《科技资讯》2015年第01期摘要：贝努里概型是一种既简单又非常重要的概型，这种概型是概率论中最早研究的模型之一，也是得到最多研究的模型之一。

在概率论中对概率分布的学习、概率的近似计算有着非常重要的作用。

它在现实生活生产中和在自然科学试验中也有着直接的应用，并在其中发挥着重要的作用，为其解决问题提供了理论支持。

我们就贝努里概型及其应用展开了解。

关键词：贝努里概型贝努里试验中图分类号： O21文献标识码：A 文章编号：1672-3791（2015）01（a）-0000-00伯努利家族在数学与科学上的地位正如巴赫家族在音乐领域的地位一样的显赫。

这个非凡的瑞士家族在三代时间里产生了十余位数学家和物理学家，其中有八位数学家，其中三位是杰出的，他们是雅可布、约翰、丹尼尔。

而贝努里概型就是雅可布.贝努里提出来的。

贝努里概型是一种既简单又非常重要的概型，这种概型是概率论中最早研究的模型之一，也是得到最多研究的模型之一。

在概率论中对概率分布的学习、概率的近似计算有着非常重要的作用。

它在现实生活生产中和在自然科学试验中也有着直接的应用，并在其中发挥着重要的作用，为其解决问题提供了理论支持。

而且，揭示这种简单概型的规律，对于以后研究更复杂的概型有着一定的指导意义和理论支撑。

下面我们就贝努里概型及其应用展开了解。

1 预备知识在许多概率问题中，试验中某事件是否发生受到的关注较多。

例如，在产品调查中注意的是抽到次品还是抽到正品；在掷硬币时注意的是出现正面还是反面等，在这类问题中试验产生的结果只有两个，即和。

像这样只有两个可能结果的试验成为贝努里试验，投币试验就是最简单的贝努里概型。

在相同的条件下，将同一个试验独立重复进行次，这种随机试验称为重贝努里试验。

现在我们来看看重贝努里试验的定义。

1.1贝努里概型的定义关于重贝努里概型的定义，尽管在各种教材的叙述不尽相同，但都是指满足下列条件的一系列实验：（1）次试验时独立的，即每次试验的结果都与其它各次试验的结果无关；（2）每次试验只有两个结果和，且它们出现的概率，在每次试验中是不变的。

高中数学中几种常见的概率模型

高中数学中几种常见的概率模型高中数学中几种常见的概率模型：古典概型、几何概型、贝努利概型、超几何分布概型1、古典概型：也叫传统概率、其定义是由法国数学家拉普拉斯提出的。

如果一个随机试验所包含的单位事件是有限的，且每个单位事件发生的可能性均相等，则这个随机试验叫做拉普拉斯试验，这种条件下的概率模型就叫古典概型。

在这个模型下，随机实验所有可能的结果是有限的，并且每个基本结果发生的概率是相同的；古典概型是概率论中最直观和最简单的模型，概率的许多运算规则，也首先是在这种模型下得到的。

2、几何概型：是概率模型之一，别名几何概率模型，如果每个事件发生的概率只与构成该事件区域的长度成比例，则称这样的概率模型为几何概率模型。

在这个模型下，随机实验所有可能的结果都是无限的，并且每个基本结果发生的概率是相同的。

一个试验是否为几何概型在于这个试验是否具有几何概型的两个特征，无限性和等可能性，只有同时具备这两个特点的概型才是几何概型。

3、贝努利模型：为纪念瑞士科学家雅各布·贝努利而命名。

对随机试验中某事件是否发生，实验的可能结果只有两个，这个只有两个可能结果的实验被称为贝努利实验；重复进行n次独立的贝努利试验，这里“重复”的意思是指各次试验的条件是相同的，它意味着各次试验中事件发生的概率保持不变。

“独立是指是指各次试验的结果是相互独立的。

基于n重贝努利试验建立的模型，即为贝努利模型。

4、超几何分布：是统计学上一种离散概率分布。

它描述了从有限N个物件（其中包含M个指定种类的物件）中抽出n个物件，成功抽出该指定种类的物件的次数（不放回）。

称为超几何分布，是因为其形式与“超几何函数”的级数展式的系数有关。

超几何分布中的参数是M,N,n，上述超几何分布记作X~H(n,M,N) 。

贝努利概率型公式

贝努利概率型公式贝努利概率是一种用来计算两个事件发生的概率的方法。

它的基本公式如下：P(A) = p其中，P(A)表示事件A发生的概率，p表示事件A发生的概率（介于0到1之间）。

例如，如果你想计算一枚硬币抛出后正面朝上的概率，则可以使用贝努利概率公式。

假设你抛出了一枚硬币，则事件A为硬币正面朝上，概率p为0.5。

根据贝努利概率公式，硬币正面朝上的概率P(A)就是0.5。

贝努利概率公式通常用于计算两个互斥事件发生的概率，即两个事件中至少有一个事件发生。

在这种情况下，公式为：P(A or B) = P(A) + P(B)其中，P(A or B)表示事件A或B中至少有一个发生的概率，P(A)和P(B)分别表示事件A和B 发生的概率。

例如，假设你有两枚硬币，你想计算至少有一枚硬币正面朝上的概率。

如果每枚硬币正面朝上的概率都是0.5，则根据贝努利概率公式，至少有一枚硬币正面朝上的概率P(A or B)就是0.5 +0.5 = 1。

这意味着两枚硬币中至少有一枚正面朝上的概率是100%。

贝努利概率公式也可以用来计算两个事件同时发生的概率。

在这种情况下，公式为：P(A and B) = P(A) * P(B)其中，P(A and B)表示事件A和B同时发生的概率，P(A)和P(B)分别表示事件A和B发生的概率。

例如，假设你有两枚硬币，你想计算两枚硬币同时正面朝上的概率。

如果每枚硬币正面朝上的概率都是0.5，则根据贝努利概率公式，两枚硬币同时正面朝上的概率P(A and B)就是0.5 * 0.5 = 0.25。

这意味着两枚硬币同时正面朝上的概率是25%。

贝努利概率公式是概率计算的基础公式之一，在许多方面都有广泛的应用。

例如，它可以用来计算赌博、保险、医学等领域的概率。

此外，贝努利概率公式也是机器学习和数据分析中经常使用的公式之一。

贝努里概型

(1) 恰有k粒种子出苗的概率； (2) 至少有一粒出苗的概率； (3) 要保证出苗率为98% ，应每穴至少播几粒？
解恰有k粒种子出苗的概率为
P6 (k) C6k 0.67k0.336k , (k 0,1, 2, 3, 4, 5, 6).
K P6(k)
0
0.0013
1
0.0157
2
0.0798
其中 p + q = 1。
山东农业大学
概率论与数理统计
主讲人：程述汉苏本堂
证明 n次试验中事件A在某k次发生，在其余 n-k次
不发生，由试验的独立性，有
P Ai1Ai2 L Aik Ai,k1L Ain pk (1 p)nk pk qnk .
在n次试验中，A发生k次的方式有Cnk 种。且任何两种方式都是互不相容的，于是有
将E独立地重复n次的试验，称为n重贝努里试验。
如：掷硬币，射击，种子发芽，投篮等。
3. 贝努里公式
定理1 在n重贝努里试验中，事件A在每次试验中发生的概率为p，0＜p＜1，则在n次试验中事件A恰好发生k次（0≤k≤n）的概率为
Pn(k) Cnk pk qnk , k 0, 1, 2, , n
加了人寿保险，在一年里每人死亡的概率为0.002，每个参加保
险的人一年付120元保险费，而在死亡之时家属可在公司里领取
20000元，问（不计利息）
（1）A={保险公司亏本}的概率是多少？
（2）B={保险公司每年获利不少于100000元}的概率是多少？
解若一年死亡X人，则保险公司支出20000X（元），一年中保险公司收入为2500×120=300000（元），于是
1 P( A1 A2 An ) 1 (1 r)n 1, (n )

1-7 独立性和贝努里概型

证明: 容易算出 P(A)=1/2, P(B)=1/2, P(C)=1/2, P(AB)=1/4, P(AC)=1/4, P(BC)=1/4, P(ABC)=0.
从而具有等式 P(AB)=P(A)P(B); P(AC)=P(A)P(C); P(BC)=P(B)P(C)
所以A,B,C两两独立. 容易看出 P(ABC)=0≠P(A)P(B)P(C)
定理设A，B是两事件，且P(A)>0(P(B)>0)，则A，B相互独立的充要条件是
P(B|A)=P(B) (或 P(A|B)=P(A))。
2、三个事件的独立性
定义1 设A，B，C是三事件，如果具有等式 P(AB)=P(A)P(B), P(BC)=P(B)P(C), P(AC)=P(A)P(C).
=P(A)+P(B)-P(A)P(B)=rn+rn-r2n=RⅠ
Ⅱ 第一对元件可靠性
P(A1∪B1)=P(A1)+P(B1)-P(A1)P(B1)=2r-r2，第二对元件的可靠性
P(A2∪B2)=P(A2)+P(B2)-P(A2)P(B2)=2r-r2, ……
第n对元件的可靠性 P(An∪Bn)=P(An)+P(Bn)-P(An)P(Bn)=2r-r2
设E为贝努里试验，将E独立地重复进行n次，（这里的“重复”是指试验E在相同条件下进行）而且每次试验中结果A出现的概率保持不变。我们把这n次独立重复贝努利试验总起来看成一个试验，称这种试验叫n重贝努里试验。总之，n重贝努里试验有下面四个约定：
（1）每次试验的结果只能是两个可能的结果A和A之一, （2）A在每次试验中出现的概率p保持不变, （3）各次试验相互独立, （4）共进行了n次.
条件概率

概率统计6 贝努利概型教学设计

《概率统计II》教学设计全概率公式贝努利概型教学设计【教学题目】§1.4 贝努利概型【教学目的】根据《教学大纲》要求理解贝努利概型定义，掌握二项概率公式及其应用【教学思想】1、贝努利概型是事件独立性问题中的典型而又重要的概率模型问题，在该问题教学中，体现出了如何化难为简，类比抽象出具有一般规律性的二项概率公式，使问题轻松得到解决。

2、通过引例，引导学生主动学习、思考，并通过实际问题案例的分析及应用，由特殊到一般，达到“授人以渔”的目的。

3、讲课中穿插数学家情况介绍，激励学生努力学习，体现出“既教书，又育人”的教育思想。

【教学分析】1、本次课主要包括以下内容：（1）回顾事件独立性，分析引例；（2）贝努利概型的定义；（3）二项概率公式及证明；（4）二项概率公式的应用。

2、重难点分析：因为利用贝努利概型解决具体问题时是使用二项概率公式解决，故二项概率公式为本次课的重点。

但在判断一个实际问题是否是贝努利概型时，学生往往感到比较困难，故要通过实际问题与贝努利概型特征对比分析，故二项概率公式应用是难点。

【教学方法和策略】黑板板书结合PP T演示，采用启发、提问式教学，利用一个简单的抛掷硬币问题，引出二项概率的简单形式。

先从特殊到一般，由表及里、层层递进、步步设问，再从一般到特殊，利用实例问题引导学生主动思考，达到理解并掌握知识点的目的。

【教学安排】引入（3分钟）：前面我们学习了随机事件的概率与古典概型，古典概型是概率论中最早、也最基础的一类概率模型。

后来，数学家们从实际问题出发，研究了很多其他概率模型。

例如（PPT）引例：将一枚质地不均匀的硬币抛掷了3次，每次出现正面的概率均为2/3, 问结果恰好出现1次正面的概率是多少？分析：记A i =“第i 次出现正面”，i=1, 2, 3B =“结果恰好出现一次正面”1。

贝努里概型

k P(B) = ∑ P( Bi ) = mP( B1 ) = Cn P k (1 − P)n −k i =1 m
概率论
一般地，有如下的定理：定理1 (贝努里定理)设一次试验中事件A发生的概率
为p，(0<p<1),则n重贝努里试验中，事件A恰好发生 k次的概率Pn (k)为
k Pn ( k ) = Cn p k q n −k ,( k = 0,1,..., n )
n
n
此式刚好是二项式(p+q)n 的展开式中的第的亦称为二项概率公式。
例1 有一批棉花种子，出苗率为0.67，现每穴播六有一批棉花种子，出苗率为，求解下列问题：粒，求解下列问题： (1) 恰有粒种子出苗的概率；恰有k粒种子出苗的概率粒种子出苗的概率； (2) 至少有一粒出苗的概率；至少有一粒出苗的概率； (3) 要保证出苗率为要保证出苗率为98% ，应每穴至少播几粒？应每穴至少播几粒？解恰有粒种子出苗的概率为恰有k粒种子出苗的概率为
4 = C3 0.630.42 + C5 0.640.4 + 0.65 =0.6826 5
在三局两胜赛制中，甲获胜的概率为 P3(2)+P3(3)
2 = C3 0.620.4 + 0.63 =0.648
甲应选择五局三胜制。
贝努里（ §1.6 贝努里（Bernoulli)概型概型
概率论
则事件A、相互独立相互独立。若P(AB) = P(A)P(B) ，则事件、B相互独立。在重复试验中，每次试验结果互不影响，如果在重复试验中，每次试验结果互不影响，也就是说各次试验结果发生的概率互不影响，是说各次试验结果发生的概率互不影响，称这类试验是独立的。是独立的。如： (1) 一枚硬币抛 n 次； (2) 一次抛 n 枚硬币；枚硬币； (3)有放回地抽样：10件产品中有件次品，从中任有放回地抽样：件产品中有件次品，件产品中有3件次品有放回地抽样取一件，取后放回，连取三次。取一件，取后放回，连取三次。 1. n重独立性试验若E可以在相同的条件下重复进重独立性试验可以在相同的条件下重复进各次试验的结果相互独立，行 n 次，各次试验的结果相互独立，则称这 n 次试验是独立的，重独立试验（独立试验序列）是独立的，或称 n 重独立试验（独立试验序列）。

贝努力大数定律

贝努利大数定律的深入研究一、定律的基本表述贝努利大数定律是概率论中的一条基本定律，它表明当一个实验进行了大量重复时，某一事件发生的频率趋近于该事件发生的概率。

换句话说，随着实验次数的增加，某一事件的相对频率趋于其相对概率。

这一原理在日常生活和科学实验中有着广泛的应用。

二、定律的数学形式贝努利大数定律的数学形式可以表述为：当一个实验进行了n 次独立重复，且每次实验中某一事件A发生的概率为p，那么对于任意的正数ε，有lim(n->∞) [|(1/n)∑(i=1->n) [xi] - p|<ε] = 1，其中xi是实验中事件A是否发生的指示变量，即如果A发生xi=1，否则xi=0。

三、定律的应用领域贝努利大数定律在许多领域都有广泛的应用，以下列举一些例子：统计和抽样：在统计学和抽样调查中，贝努利大数定律可以用来估计样本均值和总体均值的差异，以及估计样本比例和总体比例的差异。

保险业：保险业中常常需要根据历史数据来预测未来的风险，贝努利大数定律可以用来估计未来的风险和损失。

计算机科学：在计算机科学中，贝努利大数定律可以用来研究随机算法的性能和效率。

物理学：在物理学中，贝努利大数定律可以用来研究随机过程和热噪声的性质。

社会学：在社会学中，贝努利大数定律可以用来研究社会现象和人类行为的随机性和规律性。

四、定律的局限性虽然贝努利大数定律具有广泛的应用和理论意义，但也有其局限性：独立性假设：贝努利大数定律的前提假设是实验必须是独立的重复，事件之间没有相互影响。

如果实验不是独立的，或者事件之间存在相互影响，那么贝努利大数定律可能不成立。

有限性假设：贝努利大数定律需要实验次数是有限的或者至少是可数的，这意味着实验不能无限进行下去。

如果实验次数是无限的，那么贝努利大数定律的结论可能不成立。

概率的估计：贝努利大数定律需要估计事件发生的概率。

如果概率的估计不准确，那么贝努利大数定律的结论可能不成立。

数据的处理：贝努利大数定律要求数据的处理必须符合该定律的数学形式，例如计算频率和概率时要保持一致性。

贝努力概型

由全概率公式知：P(B） P( Ai )P(B | Ai ) i0 由贝努利概型的公式知：P(Ai ) C4i pi (1 p)4i,(i 0,1, 2,3, 4)
所以：P(B) C40(0.3)0(0.7)4 0.2 C41(0.3)1(0.7)3 0.5 [C42(0.3)2(0.7)2 C43(0.3)1(0.7)3 C44(0.3)4(0.7)0]0.8
例2 从一批灯泡中，任取n只作寿命试验，而每只灯泡的寿命结果不会影响其它灯泡的寿命结果，故此亦为n次重复且相互独立试验。
注意到例1 与例2的试验，前者每次试验只有两个结果{H， T}，而后者有无穷多结果{t | t0},本节重在讨论前一种试验类型，即贝努利概型。
二、贝努利概型
1、定义设试验E的结果只有两个，即A或A,且P(A) p,
i2
i 1
等价于 : 3 p3 8 p2 7 p 2 0
等价于 : ( p 1)2(3p 2) 0
所以 :
p

2 3
例巴拿赫火柴盒问题）某数学家有两盒火柴，
每盒有ｎ根火柴，每次用火柴时他在两盒中任取
一盒并从中任取一根。试求他首次摸到空盒时另
一个盒中还有ｒ根火柴的概率。 (1 r n)
i1
1
C
k n
pk
(1
p)nk
k 0
i
Pቤተ መጻሕፍቲ ባይዱ (A至多发生i次)
C
k n
pk
(1
p)nk
k 0
n
1
C
k n
pk
(1
p)nk
k i1
例：进行一系列独立试验，每次成功的概率
为p，求下面的概率(1)第k次才成功的概率.(2)n次试验中恰有k次成功的概率.(3)在第 n次成功前已有k-1次成功的概率.

1_6贝努里概型

概率论的奠基人
Jacob Bernoulli 1654-1705 瑞士数学家
下页
1695年提出著名的贝努里方程
dx / dy p( x) y q( x) y
n
此外贝努里对对数螺线深有研究, 发现对数螺线经过各种变换后, 结果还是对数螺线,在惊叹此曲线的奇妙之余, 遗言把对数螺线刻在自己的墓碑上, 并附以颂词:
En: 可看成将 E 重复了n次, 这是一个n重贝努里试验. 设在n次试验中，A恰好出现 k 次的概率为：
k Pn ( k ) Cn p k (1 p) nk
下页
(1) 采用三局二胜制,甲最终获胜, 至少需比赛 2 局,
且最后一局必需是甲胜, 而前面甲需胜1 局.
胜局情况可能是:
“甲甲”, “乙甲甲”,
下页
三、贝努里概型应用举例
例1.有一批棉花种子，出苗率为0.67，现每穴播六粒，求解下列问题：①至少有一粒出苗的概率；②要保证出苗率为98% ，每穴应至少播几粒？解：这是一个贝努里概型问题. ① 至少有一粒出苗的概率为
0 P6 (k ) 1 P6 (0) 1 C6 (0.67)0 (0.33)6 0.9987 .
Bayes公式
i 1
条件概率 P ( A | B )
P ( AB) P( B)
P ( Bi | A ) P ( Bi ) P ( A | B i )
P( B j ) P( A | B j )
j 1
n
下页
• 不确定性；试验的每个• 可重复性. 可能的结果基本事件 —— 不能再分解随机事件复合事件 —— 多于一个的基本事件构成基本概念必然事件 P( )=1，反之不真！不可能事件 P( )=0，反之不真！样本空间 —— 所有样本点(基本事件)构成的集合事件的关系及运算 —— 四种关系和三种运算

概率论中几种概率模型方法总结

概率论中几种概率模型方法总结绪论：概率论中几种常用的概率模型是古典概型、几何概型、贝努里概型.本文对概率论中几种概率模型方法进行了总结。

1 古典概型古典概型及其概率是概率论的基础知识,它既是进一步学习概率的基础,下面就一些典型事件的分析来说明古典概型的概率计算方法。

古典概型的概率计算可以分为三个步骤:确定所研究的对象为古典概型;计算样本点数;利用公式计算概率。

即如果随机试验只有有限个可能结果,而且每一个可能结果出现的可能性相同,那么这样的随机试验就是古典概型问题。

若设Ω是一个古典概型样本空间, 则对任意事件A 有: A m P ( A ) ==Q n中的样本点数中的样本点数。

在计算m 和n 时,经常使用排列与组合计算公式。

在确定一个试验的每个基本事件发生的可能性相同时,经常根据问题本身所具有的某种“对称性”,即利用人们长期积累的关于“对称性”的实际经验,认为某些基本事件发生的可能性没有理由偏大或偏小。

关于古典概型的数学模型如下:1.1 袋中取球问题1.1.1 随机地同时从袋中取若干球问题随机地同时从袋中取若干球问题是古典概型中的一类最基本问题,其特点是所考虑的事件中只涉及球的结构而不涉及取球的先后顺序,计算样本点数时只需考虑组合数即可。

概率中的很多问题常常可以归结为此类问题来解决。

事件1 一袋中有m + n 个球,其中m 个黑球, n 个白球,现随机地从袋中取出k 个球( k ≤m + n) ,求其中恰好有l 个白球( l ≤n)的概率。

分析:随机地从袋中取出k 个球有km+n C 种可能的结果,其中“恰好有l 个白球”这一事件包含了l k-l n mC C 种结果,因此所求概率为lk - ln m k m + n C C P =C 这个结论可以作为一个公式来应用。

用它可以解决一些类似的问题。

1.1.2 随机地从袋中不放回地取球若干次随机地从袋中不放回地取球若干次就是指随机地从袋中每次只取一个球,取后不再放回袋中,连续进行若干次。

伯努利概型

C p (1 p)
k n k
n k

e
k
k!
其中 np
实际计算中， n
100, np 10 时近似效果就很好
请看演示
二项分布的泊松近似
我们把在每次试验中出现概率很小的事件称作稀有事件. 如地震、火山爆发、特大洪水、意外事故等等
由泊松定理，n重贝努里试验中稀有事件出现的次数近似地服从泊松分布.
泊松分布的图形特点：X~P( λ)
二项分布与泊松分布
历史上，泊松分布是作为二项分布的近似，于1837年由法国数学家泊松引入的 . 近数十年来，泊松分布日益显示其重要性 , 成为概率论中最重要的几个分布之一. 在实际中，许多随机现象服从或近似服从泊松分布.
泊松定理: 设随机变量X~B(n,p). 当 n很大时，p 很小. 有以下近似式：
P ( X k ) e

k
k!
, k0,1,2,,
k
E X xk pk ke e
k 0
k 0
k!
k 1k 1 !Fra bibliotekk
e

k 1 !
k 1

k 1

P ( X k ) e
E X

k(1-p)1-k,k=0,1 P ( X = k )= p 称X服从参数为n和p的二项分布，记作称X服从0-1分布
n
k 0
X~B(n,p)
例某类灯泡使用时数在1000小时以上的概率是0.2，求三个灯泡在使用1000 小时以后最多只有一个坏了的概率. 解: 设X为三个灯泡在使用1000小时已坏的灯泡数 . X ~ B (3, 0.8)，

1-5全概率公式贝叶斯公式1-6伯努利概型

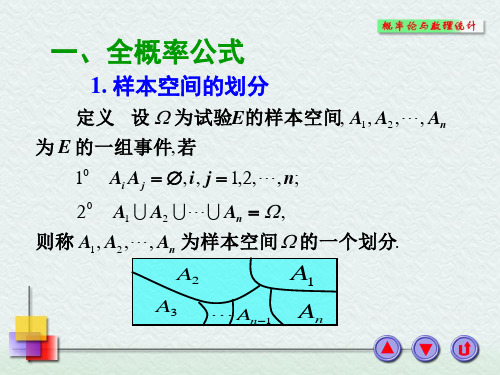
定义如果试验E只有两个基本事件A及A，且P(A) p, P(A) 1 p(0 p 1), 将E独立地进行n次，则这一系列试验称为n重伯努利试验或n重伯努利概型，简称伯努利概型.
定理在n重伯努利试验中，设每次试验中事件A发生的概率为p(0 p 1), 则在n次重复试验中，事件A恰好发生k次的概率为
解假设接待站的接待时间没有
规定,且各来访者在一周的任一天
中去接待站是等可能的.
17 27
37
47
172
周一周二周三周四周五周六周日
故一周内接待 12 次来访共有 712种.
12 2
32
42
122
周一周二周三周四周五周六周日
12 次接待都是在周二和周四进行的共有 212种.
解设 A 为事件 "产品合格".
B 为事件 "机器调整良好". 则有
P( A B) 0.98, P( A B) 0.55,
P(B) 0.95, P(B) 0.05, 由贝叶斯公式得所求概率为
P(B A)
P( A B)P(B)
P(AB)P(B) P(AB)P(B)
0.98 0.95
0.97.
解设X表示这一年内的死亡人数, 则保险公司在1年的收入是2500120=300000元
保险公司这一年里付出20000X元
当20000X ＞300000, 即X ＞ 15人时公司亏本
于是, P{公司亏本} =P{ X ＞ 15} =1-P{X≤ 15}
15
P{公司亏本} 1
Ck 2500
(0.002)k
贝叶斯公式
P ( Bi
A)

伯努利概型

(0.8)
C55
(0.2)5
(0.8)0
0.9933.
例.甲、乙两名棋手比赛，已知甲每盘获胜的概率为p.假定每盘棋胜负是相互独立，且不会出现和棋。在下列情况下，试求甲最终获胜的概率。(1)采用三盘两胜制;(2)采用五盘三胜制。
解:设事件A={采用三盘两制甲胜}，A1= {甲前两盘获胜} A2= {甲前两盘一胜一负而第三盘获胜}，则
第五节伯努利概型
一、独立试验系列二、二项概率公式
一、独立试验系列
独立重复试验：某个随机试验多次重复进行，各次试验结果相互独立。
重复次数称为重数。典型实例：多次投掷、有放回抽取。
二、二项概率公式
定义1.11、n重伯努利试验（或n重伯努利试验）
在相同条件下，重复n次做同一试验，每次试验只有两个可能结果A,A；
P(A)=P(A1)+P(A2) p2 C21 p1 p p 3 p2 2 p3.
设事件B={采用五盘三制甲胜}，B1= {甲前三盘获胜} B2= {甲前三盘两胜一负而第四盘获胜}，
B3= {甲前四盘两胜两负而第五盘获胜}，则 P(B)=P(B1)+P(B2)+P(B3)
p3 C32 p2 1 p p C42 p2 1 p2 p 10 p3 15 p4 6 p5.
用伯努里定理中的p和q 1 p代入上式
可得
n
n
( p q)n Cnk pkqnk Cnk pk 1 p nk 1
k0
k0
可见事件A发生k次的概率为( p q) Nhomakorabea展开后的
p的k次项.
故又称为二项概型。
例.从次品率为p=0.2的一批产品中，有放回抽取5件，每次抽取一件，分别求抽到恰有3件次品以及至多3件次品的概率。

贝努里概型

贝努里概型伯努利家族在数学与科学上的地位正如巴赫家族在音乐领域的地位一样地显赫。

这个非凡的瑞士家族在三代时间里产生了十余位数学家和物理学家，其中有八位数学家（其中三位是杰出的，他们是雅可布、约翰、丹尼尔），他们又生出了在许多领域里崭露头角的成群后代。

雅可布发明了极坐标，他和他的弟弟约翰是莱布尼茨的朋友，经常书信往来讨论数学问题。

他们对于莱布尼茨发明的微积分方法极为推崇，迅速地接受了莱布尼茨的学说，并且加以发扬光大。

雅可布曾当过洛必达的私人教师，最先提出洛必达法则，是欧拉的老师。

雅可布和约翰两兄弟有时致力于研究同一个问题，但是由于彼此嫉妒和易于激动，这一情况是很遗憾的。

有时两人之间的摩擦爆发成为公开的嫉恨诟骂。

由于解决“最速降线”问题，兄弟两个因为解法的优劣而争论不休，两人之间的口角纷争达数年之久，其所用言辞之粗野很像市井上的对骂而非科学讨论。

这两人之中约翰的脾气似乎更坏，因为多年之后，由于他的二儿子丹尼尔获得了他自己渴望获得的法兰西科学院奖金，约翰竟把他摔出窗外。

n次重复独立试验：（1）相同的条件下重复地做某试验n次；可重复性（2）每次试验结果不受其它各次试验影响；独立性如：掷骰子n重贝努里试验：每次试验结果只有两种可能的n重独立试验1．共进行n次试验；2．各次试验相互独立；3．在每次试验中某事件A或者发生或者不发生；4．在每次试验中事件A出现的概率都是p(0p1)。

n重贝努里试验中事件A恰好发生k(0kn)次的概率为kknkPn(k)Cnp(1p)证明：设Ai＝{第i次贝努里试验中出现A}，B＝{n重贝努里试验中A出现k次}分步：（1）A在指定的前k次试验中出现，后n-k次中不出现pP(A1...Akk1...n)P(A1)...P(Ak)P(k1)...P(n)pkqnkk（2）事件A可能出现在n次试验中的任何k次，共Cn中情况。

kknk所以Pn(k)Cnpq例1（1）将一个对称的硬币掷2次，求出现：恰好一次正面的概率；（2）将一个对称的硬币掷10次，求出现：恰好4次正面的概率。

概率论与数理统计1_6贝努里概型

《概率统计》返回
06 : A1 A2 A3 A4 A5 07 : A1 A2 A3 A4 A5 08: A1 A2 A3 A4 A5 09 : A1 A2 A3 A4 A5
10 : A1 A2 A3 A4 A5
下页结束
倡议：请大家自觉关闭手机 (李老师：2010-5-10)
上课自觉关手机尊重别人守纪律道德修养重细节不拘小节成恶习上课自觉关手机莫让手机牵精力影响自己可内疚扰乱别人人痛惜上课自觉关手机维护大局爱集体文明风尚靠大家高尚情怀靠律已
k 1 6
②要保证出苗率为98%，只要1-Pn(0) ≥0.98即可, 解得，n=4. 注：这里的Pn(0) 表示{n粒都不出苗}事件的概率.
《概率统计》
返回
下页
结束
例2. 某车间有10台同类型的机床，每台机床配备的电动机功
率为10千瓦，已知每台机床工作时，平均每小时实际开动12分钟，且开动与否是相互独立的.现因当地电力供应紧张，供电部门只提供50千瓦的电力给这10台机床，问这10台机床能够正常工作(即电力够用)的概率有多大？解： “电力够用”，其含义是“同一时刻开动的机床数不超过5 台”，因为有不少于6台机床同时工作时，其工作就不会正常.
作业：24页
21，
《概率统计》
返回
Байду номын сангаас
下页
结束
考察：事件A在5次试验中出现2次的情况,所有方式共
有C52 种. 其中Ai={A在第i次试验中发生} (1≤ i≤ 5).
01: A1 A2 A3 A4 A5
02 : A1 A2 A3 A4 A5 03: A1 A2 A3 A4 A5 04 : A1 A2 A3 A4 A5 05: A1 A2 A3 A4 A5

概率统计6 贝努利概型

引例再分析
问题：如何求n重贝努利试验中事件A 恰好发生k次的概率？
引例再分析：
A=“抛掷1枚硬币出现正面”，
P(A) 2 , P(A) 1
3
3
3重贝努利试验中， A 恰好发生1次（ A 发生2次）的概率
P(B)
C31P( A)P( A)P( A)
3
2 3
1 2 3
2 9
二项概率公式
一般地，二项概率公式：
内容小结
• 本节课主要学习了伯努利概型的定义，二项概率公式及应用，要求理解定义，熟记公式，会用公式解决具体问题
• 在解决具体问题时，首先要分析是否符合伯努利概型特征，进而确定n和P(A)，使用二项概率公式计算时应尽量结合概率的性质简化计算
课后作业
练习册1-4：第1（2）（4）、4题。
（1）5件中恰有3件次品的概率（2）5件中至少有1件次品的概率
例2 “七星彩”彩票能否中一等奖问题提示：每次买相同的号
思考与讨论
二项概率公式 Pn (k) Cnk pkqnk 中 k 可以取哪些值？k 值取遍是否完整表现出该k重贝努利试验的所有问题？
用二项概率公式计算一般概率问题时，计算量较大，能否有办法避开这个繁杂的计算呢？
P( A) p, P( A) 1 p q
n重贝努利试验中 A 恰好发生k次的概率
Pn (k) ?
Pn (k )
C
k n
pkqnk
A1 A2 ALeabharlann … Ank次An-k次 A 积事件
注：Pn (k) 可视为二项式 (q p)n 展开式中
一般项，故称为二项概率公式。
应用
例1 一批产品中有20%的次品，现进行抽样检查，共取5件产品，求：

概率统计6 贝努利概型

概率论与数理统计(chapt1-6 n重贝努利试验)

1.5_伯努利(Bernoulli)概型

贝努里概型

贝努里概型

高中数学中几种常见的概率模型

贝努利概率型公式

贝努里概型

1-7 独立性和贝努里概型

概率统计6 贝努利概型 教学设计

贝努里概型

贝努力大数定律

贝努力概型

1_6贝努里概型

概率论中几种概率模型方法总结

伯努利概型

1-5全概率公式贝叶斯公式1-6伯努利概型

伯努利概型

贝努里概型

概率论与数理统计1_6贝努里概型

概率统计6 贝努利概型

概率统计6 贝努利概型教学设计