浅谈字符串匹配问题

合集下载

常见的字符串匹配算法分析比较

常见的字符串匹配算法分析比较字符串是计算机领域中最常见的数据结构之一。

而计算机领域中的一个重要任务就是查找和比较字符串。

在实际应用中，字符串匹配算法如匹配关键字、拼写检查、文本比较等，是一个必要且重要的工具。

在此，本文将为大家介绍几种常见的字符串匹配算法及其优缺点，在选择算法时可以参考。

1.朴素字符串匹配算法朴素字符串匹配算法，也被称为暴力匹配算法，是字符串匹配算法中最简单的算法。

其思路是从文本的第一个字符开始与模式串的第一个字符依次比较，如果不成功就将模式串向右移动一位，直到模式串匹配成功。

算法效率较低，但实现简单。

2.Boyer-Moore算法Boyer-Moore算法是一种高效的字符串查找算法，该算法通过先进行坏字符规则和好后缀规则的比较而快速跳过无用的匹配。

其基本思路是先将模式串从右往左匹配，当发现匹配不上时，通过坏字符规则将模式串向右移，在移动过程中通过好后缀规则进一步加快匹配速度。

Boyer-Moore算法适合于长串和短模串、任意字符集的串匹配。

3.KMP算法KMP算法是由Knuth-Morris-Pratt三个人设计的，是一种著名的字符串匹配算法。

KMP算法优化了朴素匹配算法，通过预处理模式串信息（即计算next数组），能够快速地匹配文本串。

其核心思想是通过next数组记录当前位置前缀字符串中的最长公共前后缀，并通过将模式串向右移动来加快匹配速度。

KMP算法适用于模式串较短但匹配次数较多的情况。

4.Rabin-Karp算法Rabin-Karp算法是一种依赖于哈希思想的字符串匹配算法。

该算法通过哈希函数将文本和模式串的哈希值计算出来，从而利用哈希表快速匹配。

相比较于前面介绍的算法，Rabin-Karp算法无须进行模式串的比较，它的匹配速度也较快。

总结：在选择字符串匹配算法时需要根据不同的实际需求来进行选择。

朴实算法虽然算法效率不高，但是它的实现简单理解容易；Boyer-Moore算法的应用范围广，特别适用于在字符集较大时的匹配；KMP算法比较简单，容易实现，并且适用于较短的模式串；Rabin-Karp算法能够快速匹配，而且能减少一部分的比较。

字符串匹配算法数据结构中的常见问题解决方案

字符串匹配算法数据结构中的常见问题解决方案在字符串匹配算法数据结构中，常常会面临一些问题，例如查找一个模式在给定文本中的出现位置、判断两个字符串是否匹配等。

为了解决这些问题，人们提出了多种常见的字符串匹配算法和数据结构。

本文将介绍一些常见的问题解决方案，包括暴力匹配算法、KMP算法、Boyer-Moore算法、Rabin-Karp算法、Trie树等。

暴力匹配算法是最简单的一种方法，它的思想是从文本的第一个字符开始，依次将模式串与文本串中的字符进行比较。

如果模式串和文本串中的字符不相等，则将模式串从头开始重新匹配；如果模式串和文本串中的字符相等，则继续比较下一个字符，直到模式串的末尾与文本串相匹配或遍历完文本串。

暴力匹配算法的时间复杂度为O(mn)，其中m为模式串的长度，n为文本串的长度。

KMP算法是一种改进的字符串匹配算法，它的核心是利用已经匹配过的信息，避免不必要的比较。

KMP算法首先构建一个部分匹配表，然后根据部分匹配表进行匹配。

部分匹配表保存了模式串中每个字符前缀和后缀的最长公共长度。

在匹配过程中，如果当前字符匹配失败，则根据部分匹配表确定下一次匹配的位置。

KMP算法的时间复杂度为O(m+n)，相比暴力匹配算法具有更好的性能。

Boyer-Moore算法是一种高效的字符串匹配算法，它从模式串的末尾开始匹配，并利用模式串中的字符出现位置信息来进行快速跳过不匹配的字符。

具体而言，Boyer-Moore算法利用两个规则（坏字符规则和好后缀规则）来确定下一次匹配的位置。

该算法的时间复杂度为O(mn)，但在实际应用中通常能够获得较好的性能。

Rabin-Karp算法是一种基于哈希值的字符串匹配算法，通过对模式串和文本串中的子串计算哈希值，并进行比较来判断是否匹配。

该算法的时间复杂度为O(m+n)，在处理大量数据时具有较好的性能。

除了上述的字符串匹配算法外，还有一种常见的数据结构用于字符串的存储和查找，即Trie树。

字符串匹配研究改进

假如，A="abababaababacb"，B="ababacb"，我们来看看 KMP是怎么工作的。我们用两个指针i和j分别表示，A[i-j+ 1..i]与B[1..j]完全相等。也就是说，i是不断增加的，随着i的增加j相应地变化，且j满足以A[i]结尾的长度为j的字符串正好匹配B串的前 j个字符（j当然越大越好），现在需要检验 A[i+1]和B[j+1]的关系。当A[i+1]=B[j+1]时，i和j各加一；什么时候j=m了，我们就说B是A的子串（B串已经整完了），并且可以根据这时的i值算出匹配的位置。当A[i+1]<>B[j+1]， KMP的策略是调整j的位置（减小j值）使得A[i-j+1..i]与 B[1..j]保持匹配且新的B[j+1]恰好与A[i+1]匹配（从而使得i和 j能继续增加）。我们看一看当 i=j=5时的情况。 i = 1 2 3 4 5 6 7 8 9 …… A=abababaabab… B=ababacb j=1234567

从上面的这个例子，我们可以看到，新的j可以取多少与i无关，只与B串有关。我们完全可以预处理出这样一个数组P[j]，表示当匹配到B数组的第j个字母而第j+1个字母不能匹配了时，新的j最大是多少。P[j]应该是所有满足B[1..P[j]]=B[j-P[j]+1..j]的最大值。再后来，A[7]=B[5]，i和j又各增加1。这时，又出现了 A[i+1]<>B[j+1]的情况： i = 1 2 3 4 5 6 7 8 9 …… A=abababaabab… B= ababacb j= 1234567

浅谈数据结构-字符串匹配

浅谈数据结构-字符串匹配是数据结构中字符串的⼀种基本运算，给定⼀个⼦串，要求在某个字符串中找出与该⼦串相同的所有⼦串，这就是模式匹配。

假设P是给定的⼦串，T是待查找的字符串，要求从T中找出与P相同的所有⼦串，这个问题成为模式匹配问题。

P称为模式，T称为⽬标。

如果T中存在⼀个或多个模式为P的⼦串，就给出该⼦串在T中的位置，称为匹配成功；否则匹配失败。

蛮⼒算法（BF算法）算法思想从⽬标串T的的第⼀个字符起与模式串P的第⼀个字符⽐较。

若相等，则继续对字符进⾏后续的⽐较；否则⽬标串从第⼆个字符起与模式串的第⼀个字符重新⽐较。

直⾄模式串中的每个字符依次和⽬标串中的⼀个连续的字符序列相等为⽌，此时称为匹配成功，否则匹配失败。

算法性能假设模式串的长度为m，⽬标串的长度为n：N为外循环，M为内循环。

BF算法存在回溯，严重影响到效率，最坏的情况的是Ｎ＊Ｍ，所以算法的复杂度为Ｏ（ｍｎ）.暴⼒算法中⽆法利⽤已知的信息，也就是模式串的信息，减少匹配。

⽐如在第四步中，t[5]和p[4]不匹配，然后⼜回溯（图有点问题），t[3]和P[0]肯定不同，因为之前匹配过了，我们得知t[3]=p[1]，⽽p[0]和p[1]不同。

代码int bf(const char *text, const char *find){//异常判断if (*text == '/0' || *find == '/0'){return -1;}int find_len = strlen(find);int text_len = strlen(text);if (text_len < find_len){return -1;}//去除const属性char *s =const_cast<char*>(text);char *p = s;char *q = const_cast<char*>(find);//执⾏BF算法while (*p != '\0'){//匹配成功,指针前移if (*p == *q){p++;q++;}//否则，回溯，通过记录之前的指针位置，重新赋值。

字符串数据,长度不匹配

字符串数据,长度不匹配摘要：一、字符串数据概述1.字符串数据的概念2.字符串数据在计算机科学中的重要性二、字符串长度的概念1.字符串长度的定义2.字符串长度的重要性三、字符串长度不匹配的问题1.字符串长度不匹配的原因2.字符串长度不匹配的影响四、解决字符串长度不匹配的方法1.字符串处理函数2.字符串操作技巧3.字符串长度检查与处理正文：一、字符串数据概述在计算机科学中，字符串数据是一系列字符有序排列的数据结构，通常用一对双引号或单引号括起来表示。

字符串数据在各种编程语言和应用中都有广泛的应用，如文本处理、数据分析、网络通信等。

2.字符串数据在计算机科学中的重要性字符串数据是计算机科学中非常基本的数据结构，对于程序员来说，掌握字符串处理技巧是编程的基本技能。

字符串处理的好坏直接影响到程序的性能和稳定性。

二、字符串长度的概念1.字符串长度的定义字符串长度是指字符串中字符的数量。

在大多数编程语言中，字符串长度可以通过内置函数或运算符获取。

2.字符串长度的重要性字符串长度在字符串处理中具有重要意义，如字符串拼接、字符串截取、字符串查找等操作都需要考虑字符串长度。

此外，字符串长度不匹配可能导致程序运行错误。

三、字符串长度不匹配的问题1.字符串长度不匹配的原因字符串长度不匹配通常是由于程序设计或数据处理过程中对字符串长度的处理不当导致的。

例如，在字符串拼接时，如果两个字符串长度不匹配，可能导致缓冲区溢出等安全问题。

2.字符串长度不匹配的影响字符串长度不匹配可能导致程序运行错误，如报错、程序崩溃等。

在某些情况下，字符串长度不匹配还可能引发安全问题，如缓冲区溢出等。

四、解决字符串长度不匹配的方法1.字符串处理函数许多编程语言提供了处理字符串长度的内置函数，如Python的len()函数、Java的length()方法等。

通过使用这些函数，可以方便地获取和检查字符串长度。

2.字符串操作技巧在字符串操作中，要特别注意字符串长度的问题。

字符串匹配问题的算法步骤

字符串匹配问题的算法步骤字符串匹配是计算机科学中常见的问题，主要用于确定一个字符串是否包含另一个字符串。

解决这个问题的算法可以分为暴力匹配算法、Knuth-Morris-Pratt（KMP）算法和Boyer-Moore(BM)算法等。

暴力匹配算法是最简单的一种方法。

它的基本思想是从主串的第一个字符开始，依次和模式串的每个字符进行比较，直到找到一个字符不匹配为止。

如果找到了不匹配的字符，则将主串的指针后移一位，重新开始匹配。

如果匹配成功，模式串的指针向后移一位，主串的指针也向后移一位，继续匹配。

这个过程一直进行下去，直到模式串的指针到达模式串的末尾，或者找到了一个匹配的子串。

尽管暴力匹配算法很简单，但是它的时间复杂度较高，为O(m*n)，其中m是主串的长度，n是模式串的长度。

当主串和模式串很长时，暴力匹配算法的效率就会很低。

为了提高字符串匹配的效率，有很多其他的算法被提出。

其中比较著名的是KMP算法和BM算法。

KMP算法的核心思想是，当发生不匹配的情况时，不需要回溯主串的指针，而是通过已经匹配的部分字符的信息，将模式串的指针移动到一个新的位置，从而避免了不必要的比较。

具体来说，KMP算法在匹配的过程中，通过建立一个部分匹配表（Partial Match Table），来记录模式串中每个位置的最长前缀后缀的长度。

当发生不匹配的情况时，根据部分匹配表的信息，可以将模式串的指针直接移动到下一个可能匹配的位置。

BM算法是一种基于启发式的匹配算法，它的核心思想是从模式串的尾部开始匹配，并根据已经匹配的部分字符的信息，跳跃式地移动模式串的指针。

具体来说，BM算法分别构建了坏字符规则和好后缀规则。

坏字符规则用于处理主串中与模式串不匹配的字符，找到最右边的该字符在模式串中的位置，并移动模式串的指针到对齐该字符。

好后缀规则用于处理主串中与模式串匹配的部分，找到最右边的该部分在模式串中的位置，并移动模式串的指针到对齐该部分。

简述串的模式匹配原理

简述串的模式匹配原理嘿，咱聊聊串的模式匹配原理呗！这串的模式匹配，听着挺神秘，其实也不难理解。

就像在一堆宝藏里找宝贝。

啥是串的模式匹配呢？简单说，就是在一个大字符串里找一个小字符串。

这就像在一片大海里找一条小鱼。

你得有办法才能找到它。

比如说，你想在一篇文章里找一个特定的词，这就是串的模式匹配。

那怎么找呢？有好几种方法呢。

一种是暴力匹配。

这就像一个愣头青，一个一个地比对。

从大字符串的开头开始，一个字符一个字符地和小字符串比对。

如果不一样，就往后移一个字符，继续比对。

这就像在一堆沙子里找一颗小石子，得一颗一颗地找。

虽然有点笨，但是有时候也能管用。

还有一种是KMP 算法。

这就像一个聪明的侦探，有自己的一套方法。

它会先分析小字符串的特点，然后根据这些特点来快速匹配。

比如说，如果在比对的过程中发现不一样了，它不会像暴力匹配那样从头开始，而是根据之前的分析，直接跳到合适的位置继续比对。

这就像你知道了宝藏的线索，就能更快地找到宝藏。

串的模式匹配有啥用呢？用处可大了。

比如说，在文本编辑软件里，你想查找一个特定的词或者句子，就用到了串的模式匹配。

还有在搜索引擎里，也是用串的模式匹配来找到你想要的信息。

这就像你有一把神奇的钥匙，能打开知识的大门。

你说要是没有串的模式匹配，那会咋样呢？那找东西可就麻烦了。

就像在一个乱七八糟的房间里找东西，没有头绪，得翻个底朝天。

有了串的模式匹配，就像有了一个指南针，能让你更快地找到你想要的东西。

总之，串的模式匹配就像一个神奇的工具，能在大字符串里找到小字符串。

咱可得好好理解它，让它为我们的生活带来更多的便利。

字符串匹配问题

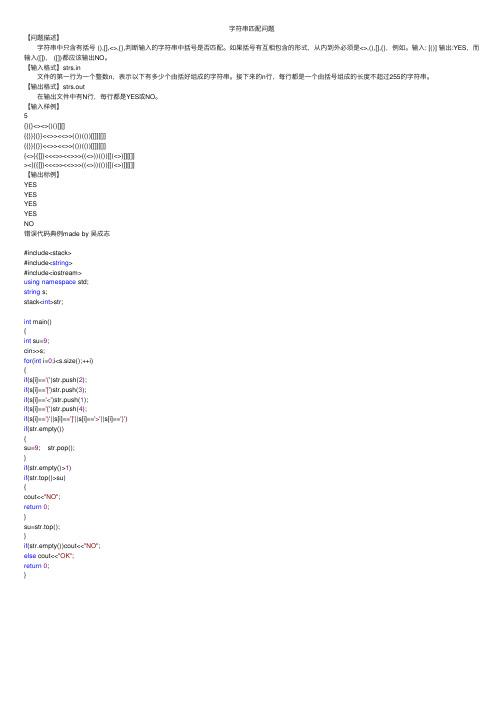
字符串匹配问题【问题描述】字符串中只含有括号 (),[],<>,{},判断输⼊的字符串中括号是否匹配。

如果括号有互相包含的形式，从内到外必须是<>,(),[],{}，例如。

输⼊: [()] 输出:YES，⽽输⼊([])， ([])都应该输出NO。

【输⼊格式】strs.in⽂件的第⼀⾏为⼀个整数n，表⽰以下有多少个由括好组成的字符串。

接下来的n⾏，每⾏都是⼀个由括号组成的长度不超过255的字符串。

【输出格式】strs.out在输出⽂件中有N⾏，每⾏都是YES或NO。

【输⼊样例】5{}{}<><>()()[][]{{}}{{}}<<>><<>>(())(())[[]][[]]{{}}{{}}<<>><<>>(())(())[[]][[]]{<>}{[]}<<<>><<>>>((<>))(())[[(<>)]][[]]><}{{[]}<<<>><<>>>((<>))(())[[(<>)]][[]]【输出标例】YESYESYESYESNO错误代码典例made by 吴成志#include<stack>#include<string>#include<iostream>using namespace std;string s;stack<int>str;int main(){int su=9;cin>>s;for(int i=0;i<s.size();++i){if(s[i]=='(')str.push(2);if(s[i]=='[')str.push(3);if(s[i]=='<')str.push(1);if(s[i]=='{')str.push(4);if(s[i]==')'||s[i]==']'||s[i]=='>'||s[i]=='}')if(str.empty()){su=9; str.pop();}if(str.empty()>1)if(str.top()>su){cout<<"NO";return0;}su=str.top();}if(str.empty())cout<<"NO";else cout<<"OK";return0;}。

字符串匹配暴力求解思路及时间复杂度分析

字符串匹配暴力求解思路及时间复杂度分析字符串匹配是计算机科学中的经典问题之一，在实际开发中也经常遇到。

解决字符串匹配问题的一种常用方法是暴力求解，即遍历主串和模式串，逐个字符进行比较，找出匹配的位置。

本文将介绍字符串匹配暴力求解的思路，并分析其时间复杂度。

一、暴力求解思路字符串匹配的暴力求解思路非常简单，就是遍历主串和模式串的每个字符，逐个进行比较。

具体步骤如下：1. 初始化主串和模式串的索引，分别为i和j，初始值都为0。

2. 当索引i小于主串长度且索引j小于模式串长度时，执行以下步骤：a. 如果主串的第i个字符与模式串的第j个字符相等，则将索引i 和j都加1。

b. 如果主串的第i个字符与模式串的第j个字符不相等，则将索引i回溯到i-j+1的位置，将索引j重置为0。

3. 判断索引j是否等于模式串的长度，如果相等，则表示找到了匹配的位置，返回主串中匹配的起始位置，否则返回-1表示没有找到匹配。

二、时间复杂度分析在暴力求解思路中，需要遍历主串和模式串的每个字符，时间复杂度取决于比较的次数。

假设主串的长度为n，模式串的长度为m，则最坏情况下，需要比较的次数为(n-m+1)*m。

当模式串的第一个字符与主串的最后一个字符匹配时，需要比较剩下的m-1个字符；当模式串的第一个字符与主串的倒数第二个字符匹配时，需要比较剩下的m-2个字符；以此类推，直到模式串的第一个字符与主串的第一个字符匹配时，需要比较剩下的m-m=0个字符。

因此，字符串匹配暴力求解的时间复杂度可以表示为O((n-m+1)*m)，即O(n*m)。

三、小结字符串匹配暴力求解是一种简单直观的方法，通过逐个字符比较确保匹配的准确性。

然而，该方法的时间复杂度相对较高，当主串和模式串较长时，算法的效率会受到限制。

在实际应用中，为了提高字符串匹配的效率，可以考虑其他更高效的算法，如KMP算法、Boyer-Moore算法等。

这些算法通过预处理匹配串，减少了比较的次数，降低了时间复杂度。

字符串数据,长度不匹配

字符串数据,长度不匹配字符串数据是计算机科学中非常重要的一种数据类型，它由一系列字符组成，可以表示文本、数字、符号等信息。

在计算机程序中，字符串数据通常用来存储和处理文本信息，例如用户输入的文本、文件中的文本内容等。

字符串数据的长度是指字符串中字符的数量，不同的字符串长度可能不同，这也是字符串数据的一个重要特征。

在实际应用中，字符串数据的长度可能会出现不匹配的情况。

例如，当我们需要将两个字符串进行比较时，如果它们的长度不同，就需要进行一些特殊的处理。

在这种情况下，我们需要了解字符串长度不匹配的原因，以及如何处理这种情况。

首先，字符串长度不匹配可能是由于数据输入错误或数据处理错误导致的。

例如，当用户输入的文本长度超过了程序预设的最大长度时，就会出现字符串长度不匹配的情况。

此外，当程序处理字符串数据时，如果没有考虑到字符串长度不匹配的情况，也可能会导致程序出错。

其次，字符串长度不匹配也可能是由于数据本身的特性导致的。

例如，当我们需要比较两个字符串的大小时，如果它们的长度不同，就需要进行一些特殊的处理。

在这种情况下，我们通常会将较短的字符串进行填充，使其长度与较长的字符串相同，然后再进行比较。

处理字符串长度不匹配的方法有很多种，具体的方法取决于具体的应用场景。

下面介绍几种常见的处理方法：1. 填充字符串：当需要比较两个字符串的大小时，可以将较短的字符串进行填充，使其长度与较长的字符串相同。

填充的方法可以是在字符串的前面或后面添加空格、0等字符，也可以是重复字符串本身。

2. 截取字符串：当需要比较两个字符串的前几个字符时，可以使用字符串截取的方法。

例如，如果需要比较两个字符串的前5个字符，可以使用substring方法截取字符串的前5个字符，然后再进行比较。

3. 忽略字符串长度：在某些情况下，字符串长度可能不是很重要，可以忽略字符串长度的差异。

例如，当需要比较两个字符串的相似度时，可以使用字符串匹配算法，忽略字符串长度的差异，计算它们的相似度。

浅谈字符串模式匹配

浅谈字符串模式匹配0 绪论字符串模式匹配是计算机科学中最古⽼、研究最⼴泛的问题之⼀（其实也就⼏⼗年）。

字符串匹配问题就是在⼀个字符串T中搜索某个字符串P的所有出现位置。

其中，T称为⽂本，P 称为模式，T和P都定义在同⼀个字母表∑上。

简单来说，就是在⼀个⽬标串T中看有没有⼦串与另⼀个较短的字符串相同。

字符串串匹配算法虽然发展了⼏⼗年，然⽽⾮常实⽤的算法是近年才出现。

传统的串匹配算法可以概括为前缀搜索、后缀搜索、⼦串搜索。

⽐如以KMP，Shift-And，Shift-Or，BM等⼦串搜索，以后缀⾃动机为代表的的后缀搜索等。

近些年则流⾏以哈希函数为基础的哈希匹配。

字符串模式匹配的应⽤包括⽣物信息学、信息检索、拼写检查、语⾔翻译、数据压缩、⽹络⼊侵检测等⽅⾯。

(你见到最多的应⽤应该是论⽂查重)字符串匹配⼯作⼀直是IDS研究领域中的热点之⼀。

在⽹络速度迅速发展的今天，基于字符匹配技术的⽹络应⽤存在着性能瓶颈，提⾼系统的整体性能是研究和设计者的主要⼯作。

字符匹配是其实现⽹络⼊侵检测的主要技术之⼀，因此，⾼效的算法将是提⾼系统总体性能的⼿段之⼀。

这篇博客将简要介绍BF算法（暴⼒算法），KMP算法和简单的hash匹配。

1 BF算法（1）简介字符串的暴⼒匹配算法也被称为Brute-Force算法（其实就是“暴⼒”的英语）简称BF算法。

（2）算法描述采⽤穷举的⽅法，将⽂本T字符串的第⼀个字符与模式P字符串的第⼀个字符⽐较，若相等则逐个⽐较后续字符，否则将⽂本T字符串的第⼆个字符与模式P字符串的第⼀个字符⽐较。

（3）算法分析假设⽂本T的字符串长度为n，模式P的字符串长度为m，则BF算法的最好时间复杂度为O（n）,最坏时间复杂度为O（n*m），平均时间复杂度O（n*m），空间复杂度为O（n+m）。

（4）算法实现#include<iostream>#include<string>#include<bits/stdc++.h>using namespace std;int BF(string t,string p)//返回t与p匹配成功的次数{int num=0;for(int i=0;i<t.length();i++){int j;for(j=0;j<p.length();j++)if(t[i+j]!=p[j])break;if(j==p.length()){num++;cout<<"匹配成功位置："<<i<<endl;}}return num;}int main(){string t,p;cin>>t>>p;cout<<BF(t,p)<<endl;return 0;}2 KMP算法（1）简介KMP算法是由D.E.Kruth,J.h.Morris和V.R.Pratt共同提出，因此⼈们称它为克努特—莫⾥斯—普拉特操作，简称KMP算法。

字符串匹配算法的原理和实现

字符串匹配算法的原理和实现随着互联网应用的广泛普及，各种搜索引擎、数据挖掘等技术越来越受到人们的关注。

在很多应用中，我们需要对文本进行匹配，即在一段文本中查找某个字符串是否出现过，或者查找多个字符串在文本中的位置。

这就需要用到字符串匹配算法，本文将介绍字符串匹配算法的原理和实现。

一、暴力匹配算法暴力匹配算法是最朴素的字符串匹配算法，也称为朴素算法或者蛮力算法。

它的原理非常简单，就是从文本的第一个字符开始依次比较，如果匹配失败，则将文本的指针后移一位，开始下一次比较。

具体实现可以用以下代码表示：```int search(string pattern, string text) {int n = text.length();int m = pattern.length();for(int i = 0; i < n - m + 1; i++) {int j;for(j = 0; j < m; j++) {if(pattern[j] != text[i+j]) {break;}}if(j == m) {return i;}}return -1;}```该算法的时间复杂度为O(nm)，其中n和m分别是文本和模式串的长度。

当模式串非常短时，该算法的效率还可以接受，但是当模式串很长时，算法效率就会变得很低，甚至比较文本中的每个字符都慢。

因此，我们需要更加快速和高效的算法来实现字符串匹配。

二、KMP算法KMP算法全称为Knuth-Morris-Pratt算法，它是一种比暴力匹配算法更加高效的字符串匹配算法，可以在O(n+m)的时间复杂度内完成字符串匹配。

KMP算法的基本思想是利用匹配失败后的信息来避免无谓的比较，具体过程如下：1.计算模式串的前缀函数（Prefix Function）。

前缀函数的定义是：对于模式串P的每个位置i（0 <= i < m），对应的前缀函数（Pi）表示模式串的第0个位置到第i个位置的最长的，既是最前面的，也是最后面的，与整个模式串P的某个前缀相等的后缀的长度。

字符串匹配算法与实际应用案例

字符串匹配算法与实际应用案例字符串匹配算法是计算机科学中的一项重要技术，它被广泛应用于实际的软件开发和数据处理中。

本文将介绍字符串匹配算法的概念和原理，并给出一些实际应用案例，旨在帮助读者更好地理解和应用该算法。

一、字符串匹配算法概述字符串匹配算法是指在一个字符串（称为主串）中查找另一个字符串（称为模式串）的过程。

在实际应用中，字符串匹配经常用于查找和处理文本数据、搜索关键字、验证密码等场景。

常见的字符串匹配算法包括暴力匹配算法、KMP算法和Boyer-Moore算法等。

下面将逐一介绍这些算法的原理及其应用。

二、暴力匹配算法暴力匹配算法也称为朴素匹配算法，是最简单直观的字符串匹配方法。

它的基本思想是从主串的第一个字符开始和模式串逐个比较，如果发现不匹配的字符，则通过主串和模式串指针的滑动，重新比较下一组字符，直到找到匹配的子串或主串遍历完毕。

暴力匹配算法的时间复杂度为O(m*n)，其中m和n分别为主串和模式串的长度。

虽然该算法的效率相对较低，但适用于简单的字符串匹配场景。

三、KMP算法KMP算法是一种高效的字符串匹配算法，它通过预处理模式串构建一个部分匹配表，从而在匹配过程中避免无效的比较操作，提高匹配效率。

KMP算法的核心思想是利用模式串的局部匹配信息，当主串和模式串发生不匹配时，通过查表找到模式串中下一次比较的位置，从而避免了不必要的比较操作。

KMP算法的时间复杂度为O(m+n)，其中m和n分别为主串和模式串的长度。

相比暴力匹配算法，KMP算法在大规模数据处理和搜索引擎等领域具有明显的优势。

四、Boyer-Moore算法Boyer-Moore算法是一种高效的字符串匹配算法，其核心思想是从模式串的末尾开始匹配，通过根据模式串中的字符出现位置提前移动主串的指针，从而跳过无需比较的字符。

Boyer-Moore算法结合了两种启发式策略，即坏字符规则和好后缀规则。

通过预处理模式串构建这两个规则的辅助表格，可以在匹配过程中快速移动主串的指针，从而提高匹配效率。

字符串匹配问题小结

字符串匹配问题⼩结字符串匹配问题⼩结刷Leetcode时，发现有两个字符串匹配问题很巧妙，所以记录⼀下正则表达式匹配问题描述给你⼀个字符串 s 和⼀个字符规律 p，请你来实现⼀个⽀持 '.' 和 '*' 的正则表达式匹配。

'.' 匹配任意单个字符'*' 匹配零个或多个前⾯的那⼀个元素所谓匹配，是要涵盖整个字符串 s的，⽽不是部分字符串。

说明:s 可能为空，且只包含从 a-z 的⼩写字母。

p 可能为空，且只包含从 a-z 的⼩写字母，以及字符 . 和 *。

⽰例 1:输⼊:s = "aa"p = "a"输出: false解释: "a" ⽆法匹配 "aa" 整个字符串。

⽰例 2:输⼊:s = "aa"p = "a*"输出: true解释: 因为 '*' 代表可以匹配零个或多个前⾯的那⼀个元素, 在这⾥前⾯的元素就是 'a'。

因此，字符串 "aa" 可被视为 'a' 重复了⼀次。

⽰例 3:输⼊:s = "ab"p = ".*"输出: true解释: ".*" 表⽰可匹配零个或多个（'*'）任意字符（'.'）。

⽰例 4:输⼊:s = "aab"p = "c*a*b"输出: true解释: 因为 '*' 表⽰零个或多个，这⾥ 'c' 为 0 个, 'a' 被重复⼀次。

因此可以匹配字符串 "aab"。

⽰例 5:输⼊:s = "mississippi"p = "mis*is*p*."输出: false来源：⼒扣（LeetCode）链接：著作权归领扣⽹络所有。

浅谈字符串匹配算法—BF算法及KMP算法

浅谈字符串匹配算法—BF算法及KMP算法来源：My_World链接：/jiajiayouba/article/details/9178789字符串匹配，在实际编程中经常遇到。

其相应的算法有很多，本文就BF算法和KMP算法，谈一下自己的理解。

并结合平时编程，修改了一下，使其更符合我们的使用习惯。

（注：标准BF算法和KMP 算法，为研究方便，其字符数组[0]存放的都是字符串的长度。

本文讲解中，并没有保存字符串长度。

后面给出的示例代码中，字符数组中是否保存有字符串长度，都给出了相应的算法代码。

）一、BF 算法 (Brute Force):BF算法核心思想是：首先S[1]和T[1]比较，若相等，则再比较S[2]和T[2]，一直到T[M]为止；若S[1]和T[1]不等，则T向右移动一个字符的位置，再依次进行比较。

如果存在k，1≤k≤N，且S[k+1…k+M]=T[1…M]，则匹配成功；否则失败。

该算法最坏情况下要进行M*(N-M+1)次比较，时间复杂度为O(M*N)。

下面结合图片，解释一下：S代表源字符串，T代表我们要查找的字符串。

BF算法可以表述如下：依次遍历字符串S，看是否字符串S中含有字符串T。

因此，我们依次比较S[0] 和T[0]、S[1] 和T[1]、S[2] 和T[2]……S[n]和T[n] ，从图中我们可知，S[0]-S[7]和T[0]-T[7]依次相等。

当匹配到S[8]和T[8]时，两个字符不等。

根据定义，此时S和T都要回溯，T向右移动一个字符的位置，即S回溯到S[1]的位置，T回溯到T[0]的位置，再重新开始比较。

此时，S[1]和T[0]、S[2]和T[1]……如果再次发现不匹配字符，则再次回溯，即S回溯到S[2]的位置，T回到T[0]的位置。

循环往复，直到到达S或者T字符串的结尾。

如果是到达S串的结尾，则表示匹配失败，如果是到达T串的结尾，则表示匹配成功。

BF算法优点：思想简单，直接，无需对字符串S和T进行预处理。

字符串模式匹配算法综述

字符串模式匹配算法综述摘要：字符串匹配问题是在给定符号序列（称为文本）中按照一定的匹配条件，搜索给定符号序列或给定符号序列集合中元素（称为模式）出现位置的搜索问题。

该问题是计算机科学的基础问题之一，被广泛的应用于各种涉及文字和符号处理的领域中，是网络安全、信息检索、计算生物学等重要领域的关键问题。

本文主要介绍了BF 算法、KMP 算法、BM 算法、BMH 算法、AC 算法和 AC-BM 算法。

关键词：模式匹配，BF算法，KMP算法，改进算法，BM算法，AC算法，ACH算法。

0.前言字符串是一种线性表,它在计算机应用系统中如文本编辑、情报检索、自然语言翻译有着广泛的应用。

在这些应用中常常需要在一堆文字符串中检测是否有某一指定的字符串。

设Pattern(下文简称 P)和Text(下文简称 T)是给定的两个字符串,在字符串T中寻找等于P的子串的过程称为模式匹配,其中字符串T称为主串,字符串P称为模式串。

如果在字符串T中找到等于P的子串,则称匹配成功,否则匹配失败。

比较著名的模式匹配算法有BF算法、KMP算法、AC算法和BM算法,本文对所述算法进行探讨。

随着计算机技术的快速发展，计算机网络在国民经济中发挥了日益重要的作用，己成为人们日常生活中不可缺少的一部分。

同时，网络安全也日益引起人们的关注。

1.模式匹配算法1.1 单模式匹配算法1.1.1 BF（Bruce Force）算法1.算法思想从文本字符串 T 的第一个字符起和模式字符串 P 中的第一个字符开始比较，若相等，逐个比较后续字符，否则从文本字符串的下一个字符起再重新和模式字符串的第一个字符比较。

2.算法描述对于文本字符串n k m i k T T T T T ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅--10模式字符串mj P P P ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅0 （1）P 和 T 从左端对齐，使得 0P 与 0T 对齐；（2）从左到右匹配 P 与 T 的字符，直到出现不匹配的情况，则执行（3），或是 P 己被完全匹配的情况则结束比较；（3）将 P 右移一个字符，重新从P 的第一个字符开始匹配；（4）重复上述（2）过程，直到 P 被完全匹配，或 P 移到 T 的右端。

字符串精确匹配与比对

字符串精确匹配与比对一、概述字符串精确匹配与比对是计算机科学中的基本问题，即判断两个字符串是否完全相同或者其中一个字符串是否是另一个字符串的子串。

这个问题在各种文本处理和信息检索任务中都有广泛的应用，例如搜索引擎、文本分析和语言建模等。

二、字符串匹配算法字符串匹配算法中有许多不同的方法，包括暴力破解法、Knuth-Morris-Pratt算法、Boyer-Moore 算法、Rabin-Karp 算法等等。

1. 暴力破解法暴力破解法是最简单的字符串匹配算法。

它的基本思路是将模式串与文本串中的每一个子串按照相同的长度进行比对，直到找到匹配的子串或者整个文本串都被搜索完毕。

时间复杂度：O(m∗n)2. Knuth-Morris-Pratt 算法Knuth-Morris-Pratt 算法是一种基于有限状态自动机的字符串匹配算法，它的核心思想是利用已知的匹配信息避免重复比对。

具体地，算法维护一个状态转移表，记录当前匹配字符的状态，当匹配失败时，可以通过跳转转移表中的下一状态，避免重复比对已知的匹配信息。

时间复杂度：O(n+m)3. Boyer-Moore 算法Boyer-Moore 算法是一种基于启发式规则的字符串匹配算法，它的核心思想是从后往前匹配，利用不匹配字符带来的信息快速跳过一定数量的字符。

具体地，算法维护一个 Bad Character 规则和一个 Good Suffix 规则，分别记录当前字符不匹配情况下的下一次比对位置和最长相同后缀前缀长度，通过这些规则快速跳过不可能匹配的子串。

时间复杂度：O(n)4. Rabin-Karp 算法Rabin-Karp 算法是一种基于哈希函数的字符串匹配算法，它的核心思想是将字符串转化为数字计算哈希值进行匹配。

具体地，算法维护一个滑动窗口和一个哈希表，每次滑动窗口到下一个位置时，通过哈希表查询当前子串的哈希值是否与模式串相等，如果相等则可以判断为匹配。

时间复杂度：O(n+m)三、字符串比对应用场景字符串比对是一种基础性的技术，可以应用于许多不同的场景中。

字符串精确匹配和比对

生物信息学概论讲义
精确匹配问题及其Naïve措施
❖ Naïve措施将P旳左端与T旳左端对齐，然后从左到右逐一比较P和T旳字符，直到一种失配出现或者P 中字符被比较完；假如是后一种情况旳话，则报告一次P旳出现将P在T上从左到右移动一种字符，并重新开始这种比较反复上述过程，直到P旳右短移过了T旳右端
• |S|：表达字符串S旳长度 • S[i..j]：表达字符串S从位置i开始到位置j结束旳一
种子字符串 • S[1..i]：表达字符串S在位置i结束旳一种前缀 • S[i..|S|]：表达字符串S从位置i开始旳一种后缀 • S[i..j]：表达一种空串假如i>j
生物信息学概论讲义
精确匹配问题及其Naïve措施
❖ 模式预处理 Z值计算：从i=2开始，计算全部旳Zi, ri, li 根据定义，简朴算法旳复杂度：O(|S|2) 线性Z值计算算法：O(|S|)
• Z2：比较S[2..|S|]和S[1..|S|] • r2, l2：假如Z2 >0, r2= Z2+1, l2=2 • 假设Zk-1,rk-1, lk-1已经计算完毕 • 在有些情况下，Zk值能够从前面得到
• S=aabcaabxaaz • Z2(S)=1, Z3(S)=0, Z4(S)=0, Z5(S)=3, • Z6(S)=1, Z7(S)=0, Z8(S)=0, Z9(S)=2, ……
生物信息学概论讲义
精确匹配问题及其Naïve措施
❖ 模式预处理
• Zi-box：位置i开始，位置i+Zi-1结束旳最长前缀 • 对于任意旳i，ri表达开始于i或i之前旳全部Z-box旳
最右端点，li表达结束于ri旳Z-box旳左端位置 • S=aabaabcaxaabaabcy