第02章 热力学第一定律 2011-02-24
热力学第一定律

热力学第一定律热力学是一门研究能量转换与传递规律的学科,它主要研究热现象与其他物理现象之间的相互关系。
热力学第一定律,也称作能量守恒定律,是热力学的基本原理之一。
本文将介绍热力学第一定律的基本概念和应用。
一、热力学第一定律的概念热力学第一定律是能量守恒定律在热学领域的表述。
它指出:在一个孤立系统中,总能量的变化等于系统所接受的热量与所做的功之和。
这个定律可以用以下公式表示:ΔE = Q - W其中,ΔE表示系统内能的变化,Q表示系统所接受的热量,W表示系统所做的功。
二、热力学第一定律的应用1. 热力学循环热力学循环是指一系列经历几个步骤的热能转换过程,最后回到初始状态的过程。
根据热力学第一定律,一个理想的热力学循环的净输入输出功为零,即总输入热量等于总输出功。
这一定律被广泛应用于热能转换设备的设计和研究中。
2. 热机效率热机效率是衡量热能转化的性能指标,是指输出功与输入热量之比。
根据热力学第一定律,对于一个正循环热机,其效率可以通过以下公式计算:η = 1 - Qc / Qh其中,η表示热机效率,Qc表示效率造成的能量损失,Qh表示输入的热量。
3. 热力学过程热力学过程是一个系统经历的状态变化过程,根据热力学第一定律,对于一个孤立系统来说,其内能的变化等于系统所接受的热量和所做的功之和。
这一定律不仅适用于准静态过程,也适用于非准静态过程,为热力学过程的分析提供了基础。
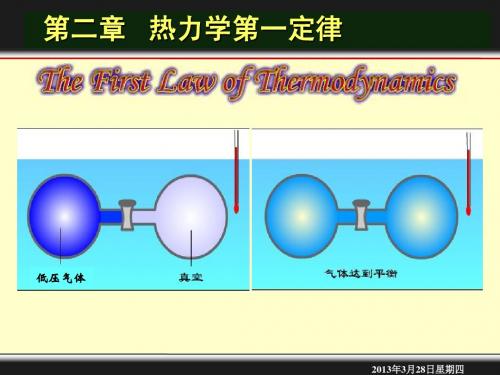
4. 热力学平衡热力学平衡是指在一个封闭系统中,各部分之间没有能量的净交换,即系统内外没有能量的流动。
根据热力学第一定律,当一个系统达到热力学平衡时,系统内能的变化为零,即ΔE = 0。
热力学平衡在热力学研究中起着重要的作用。
三、总结热力学第一定律是热力学的基本原理之一,它描述了系统能量转换与传递的规律。
在热力学循环、热机效率、热力学过程和热力学平衡等方面都有广泛的应用。
热力学第一定律的核心是能量守恒定律,对于热学领域的研究具有重要意义。
02章 热力学第一定律

系统与环境
系统(system)
在科学研究时必须先确定
研究对象,把一部分物质与其
环境
余分开,这种分离可以是实际 系统
的,也可以是想象的。
这种被划定的研究对象称 为系统,亦称为体系或物系。
环境(surroundings)
与系统密切相关、有相互作用或 影响所能及的部分称为环境。
系统与环境
h
8
系统的分类 根据系统与环境之间的关系,把系统分为三类: (1)敞开系统(open system) 系统与环境之间既有物质交换,又有能量交换
•能判断变化能否发生以及进行到什么程度, 但不考虑变化所需要的时间。
h
4
局限性 不知道反应的机理和反应速率 不研究系统的宏观性质与微观结构之间的关系
可以指出进行实验和改进工作的方向,讨 论变化的可能性,但无法指出如何将可能性变 为现实的方法和途径
h
5
§2.2 热平衡和热力学第零定律
温度的概念 将A和B用绝热壁隔开,而让A和B 分别与C达成 热平衡。
C
C
A
B
A
B
绝热
导热
然后在A和B之间换成导热壁,而让A和B 与C之
间用绝热壁隔开
h
6
A和B分别与C达成热平衡,则A和B也处于热平 衡,这就是热平衡定律或第零定律。
C
C
AB
Байду номын сангаас
AB
当A和B达成热平衡时,它们具有相同的温度 由此产生了温度计,C相h 当于起了温度计的作用 7
§2.3 热力学的一些基本概念
强度性质(intensive properties) 它的数值取决于系统自身的特点,与系统的数量无 关,不具有加和性,如温度、压力等。它在数学上 是零次齐函数。指定了物质的量的容量性质即成为 强度性质,或两个容量性h 质相除得强度性质。 13
02章 热力学第一定律

We' ,2 = − ∫ p e dV = − p1 (V1 − V2 )
V1 V2
We' ,3 = − p" (V " −V2 ) − p' (V ' −V " ) − p1 (V1 − V ' ) We' ,4 = − ∫ ( p i + dp )dV ≈ − ∫ p i dp = − nRT ln
V2 V2 V1 V1
V1 = −We ,4 V2
We ,4 = We' ,4
ΔU = Q + W
(W = We, Wf = 0)
一、等容过程(isochoric process) ΔV = 0
适用条件:封闭体系平衡态,不做非体积功的等容过程。 二、等压过程(isobaric process) p1 = p2 = pe
热力学概论
程
Su
n
2.3
热力学的一些基本概念 P67
一.系统(体系 System)与环境(surroundings) (1)定义: (2)体系的分类:① 敞开体系(open system)② 封闭体系(closed system) ③ 孤立体系(isolated system) 二.体系的性质(状态性质、热力学性质、热力学变量) 分类 广度性质(extensive properties) : 其数值与体系的物质的量成正比, 具加和性, 是 n 的一次齐函数。 如体积、 又称为容量性质, 质量、熵等。 强度性质(intensive properties) : 其数值取决于体系自身的特点,不具加和性,是 n 的零次齐函数。如温度、压力等。
热力学第一定律

热力学第一定律热力学是研究能量转化和能量传递规律的学科,其核心定律是热力学第一定律。
热力学第一定律是指能量守恒定律,亦即能量既不可以被创造也不可以被毁灭,只能由一种形式转化为另一种形式。
本文将详细探讨热力学第一定律的原理和应用。
一、热力学第一定律的原理热力学第一定律的原理可以用以下数学表达式表示:ΔU = Q - W其中,ΔU表示系统内能的变化,Q表示系统所吸收的热量,W表示系统所做的功。
根据能量守恒定律,系统内能的变化等于系统所吸收的热量减去系统所做的功。
这个表达式也可以解释为:系统内能的增加等于热量增加减去工作所做的减少。
二、热力学第一定律的应用热力学第一定律在热力学领域的应用非常广泛,下面将介绍几个常见的应用。
1. 热功等价关系根据热力学第一定律,热量和功可以相互转化。
当系统吸收热量时,系统内能增加,从而可以转化为对外做功;反之,当系统对外做功时,系统内能减少,相应地会释放热量。
这种热量和功的转化关系被称为热功等价原理。
2. 热机效率热机是指将热能转化为机械能的装置,例如蒸汽机、内燃机等。
根据热力学第一定律,热机的效率可以用以下公式表示:η = (W_net / Q_in) * 100%其中,η表示热机的效率,W_net表示净功,Q_in表示输入的热量。
热机的效率即净功和输入热量的比值,通常以百分比表示。
通过热力学第一定律的应用,可以评估和改善热机的性能。
3. 热力学循环热力学循环是指在特定条件下,将工质(如气体、液体等)依次进行一系列热量转换和功转换后回到起始状态的过程。
常见的热力学循环有卡诺循环和斯特林循环等。
热力学第一定律在热力学循环研究中起到了重要的作用,通过应用该定律可以分析循环系统内能的变化和热量转化情况,从而优化循环效率。
4. 热传导热传导是指通过物质内部的振动和碰撞,热能从高温区传递到低温区的现象。
根据热力学第一定律,热能传导的过程中不会产生或消耗热量,能量守恒。
通过热力学第一定律的应用,可以计算热传导的速率和热量的流动情况,为热传导的工程应用提供理论依据。
02章_热力学第一定律
始态
中间态 变温变压
理气 1mol理气 T = 300K 2 p2 = p′ = 1010kPa V2
终态
途径Ⅱ 途径Ⅱ只有一个过程
2011年4月14日星概念
3、过程的分类
有无相变化与化学变化 单纯状态变化过程 (单纯pVT 变化过程) 变化过程)
体系与环境之间是有边界 边界的 体系与环境之间是有边界的,但此边界可以是实 际存在的,也可以是假想的。 际存在的,也可以是假想的。 环境与体系之间是有联系的 可以在边界上发生 有联系的, 环境与体系之间是有联系的,可以在边界上发生 能量交换或物质交换,有时也可以不发生。 能量交换或物质交换,有时也可以不发生。
2011年4月14日星期四 年 月 日星期四
2.2
可逆过程与可逆功
途径Ⅰ 途径Ⅰ:一次膨胀
dT=0 dT=0
p1, T1, V1 p1= 4 Pa p2, T2, V2 p2 =1 Pa p1=4p2 =4p V2= 4V1 4V
WΙ ,膨胀 = − ∫ pamb dV
= − pamb (V2 − V1 ) = −3V1
2011年4月14日星期四 年 月 日星期四
2.1
热力学基本概念
⑵状态函数的特点 状态函数的改变量只与体系的始终态有关, 状态函数的改变量只与体系的始终态有关, 而与途径无关。 而与途径无关。
80 ºC 10 ºC 0 ºC 30 ºC
∆T = T终 − T始 = ( 30 − 10)o C = 20o C
西
2011年4月14日星期四 年 月 日星期四
2.1
热力学基本概念
途径Ⅰ 途径Ⅰ由两个过程组成
理气 1mol理气 T = 273 K dT=0 = 1 p1 = 101kPa V1
第二章 热力学第一定律

第二章热力学第一定律1.1概述本章的主要内容是通过热力学第一定律计算系统从一个平衡状态经过某一过程到达另一平衡状态时,系统与环境之间交换的能量。
、恒压条件下,△H =Q p 。
系统状态变化时,计算系统与环境间交换的能量状态),m dT1.2主要知识点1.2.1状态函数的性质状态函数也称热力学性质或变量,其值由系统所处的状态决定。
当系统的状态变化时,状态函数Z 的改变量Z 只决定于系统始态函数值1Z 和终态函数值2Z ,而与变化的途径过程无关。
即21Z Z Z 如21T T T ,21U U U 。
另外,状态函数也即数学上的全微分函数,具有全微分的性质。
例如,(,)U f T V ,则d (/)d (/)d V T U U T T U V V热力学方法也即是状态函数法,所谓状态函数法就是利用状态函数①改变值只与始、末态有关而与具体途径无关以及②不同状态间的改变值具有加和性的性质,即殊途同归,值变相等;周而复始,其值不变的特点,用一个或几个较容易计算的假设的变化途径代替一个难以计算的复杂变化过程,从而求出复杂的物理变化或化学变化过程中系统与环境之间交换的能量或其它热力学状态函数的变化值。
1.2.2平衡态在一定条件下,将系统与环境隔开,系统的性质不随时间改变,这样的状态称为平衡态。
系统处于平衡态一般应满足如下四个条件:①热平衡:系统各点温度均匀;②力学平衡:系统各点压力相等;③相平衡:即宏观上无相转移;④化学平衡:化学反应已经达到平衡。
应该特别注意平衡态与稳态的不同。
一个处于热力学平衡态的系统必然达到稳态,即各热力学性质不随时间而变化。
但是处于稳态的系统并不见得达到平衡态。
稳态只不过是系统的各物理量不随时间变化而已。
例如,稳定的热传导过程,系统各处温度并不相等,但不随时间变化;还有,稳定的扩散过程,各点浓度并不相等,但却不随时间变化。
1.2.3热系统与环境间由于温差而交换的能量。
热是物质分子无序运动的结果,是过程量。
热力学第02章 第一定律

推动工质移动所作的功;或因工
质在开口系统中流动而传递的功。
pAx pV mpv
推动功作用在质量m上。m被推入系统内,所以推动功随质量 m一起进入系统。 推动功的意义:工质m流入系统所带入的功(外界对系统作功);
工质m流出系统所带出的功(系统对外界作功)。
2.推动功(flow work; flow energy): p,v ⊿x 如果工质在传递推动功的时候没有热力状态的变化,当然也不 会有能量形态的变化。此时工质所起的作用只是单纯的运输能 量,就像传送带一样,把这部分推动功传递到其他地方。 p
热力学第一定律:
进入系统的能量 —
离开系统的能量 = 系统内部能量的增量
第一定律定第一表达式 第一定律定第二表达式
Q dU W
Q dH Wt
上节课内容回顾
第一定律第一解析式 —— 热 功的基本表达式
Q U W q u w
1)对于可逆过程
δQ dU δW δq du δw
第二章 热力学第一定律
the first law of thermodynamics
§2-1 热力学第一定律的实质
实质:能量传递和形态转化以及总量的守恒。(在工程
热力学的研究范围内,主要考虑的是热能和机械能之间的 相互转化和守恒的规律) 热力学第一定律是实践经验的总结。第一类永动机迄今都 不存在,而且由第一定律所得出的一切推论都和实际经验 相符,可以充分说明它的正确性。 第一类永动机(不消耗能量而作功)是不可能造出来的。
出口2 假如工质从状态1到状态2做膨胀功是w。那么在不考虑工质宏 观动能和位能变化时,开口系和外界交换的功量是膨胀功与流 动功的差值: 注:如需要考虑工质的动能和位能变化,还应该计算动能差 和位能差
02章_热力学第一定律(小结)

C p BC p,m (B)
如在该温度区间内有物质发生相变,就要分段积分。
T2
T1
C p dT
19.绝热反应——非等温反应
燃烧和爆炸反应的最高温度
计算恒压燃烧反应最高火焰温度的依据是
Q p ΔH 0
。计算恒容爆炸反应的最高温度的依据是 QV ΔU 0 。
第二章 热力学第一定律△U =Q+W 1.各类过程Q、W 、△U 、 △H的计算
B
B H H
过程的焓变为:
H H H
摩尔相变焓为:
H H m n
H 比相变焓为 h m
几种相态间的互相转化关系如下: 气相 晶型 转变 (trs)
固相
固相
熔化(fus) 凝固
对于宏观过程:
pe dV
W pedV
环境的压力 pe
理想气体等温可逆过程
We
V1 nRT ln V2
自由膨胀pe=0,We=0; 恒容过程dV=0,We=0.
对于恒外压过程:
W pe V
pe const
相变化、化学变化 W=-pe(V2-V1)
若A(L)→A(G) W=-pVG=-nRT
f H m (物质,相态,温度)
稳定相态单质本身的标准摩尔生成焓为零。
r Hm
B f H m (B) B
17.标准摩尔燃烧焓
T,100kPa 1mol物质 B
氧气
完全燃烧反应 规定的燃烧产物
标准摩尔燃烧焓 c H m 燃烧产物规定 C H N S Cl CO2(g) H2O(l) N2(g) SO2(g) HCl(aq)
第二章 热力学第一定律

第二章热力学第一定律§2-1 热力学概论1.热力学热力学是研究能量相互转换过程中所应遵循的规律的科学。
它所研究的基本问题有:(1)利用热一律解决各种变化过程的能量效应问题。
(2)利用热二律解决某指定过程的可能性、方向和限度问题。
如,在一定的条件下,某过程能否自动进行,如能进行,进行到什么程度。
(3)利用热第三律和热力学数据解决有关平衡计算问题。
热力学的基础主要是热力学第一、第二定律,它们是人类经验的总结,具有牢固的实践基础、严密的逻辑推理。
之后,又建立了热力学第三律和热力学第零定律。
2. 化学热力学化学热力学,就是热力学基本原理在化学过程以及与化学过程密切相关的物理过程(化学-物理过程)中的应用。
主要研究的问题是:(1)化学过程以及化学-物理过程中的能量效应问题。
(2)化学反应的方向和限度问题、相平衡和化学平衡等问题。
具体就是:判断在一定条件下,某一反应能否进行,如能进行,限度如何;确定一定条件下,某物质的稳定性;确定某一反应取得最大产率的条件,等等。
3. 热力学的局限性(1)热力学的研究对象是具有大量微观粒子的集合体-宏观物体,研究物质的宏观性质,对物质的微观性质-个别粒子行为,无从作出解答。
结论具有统计性。
(2)热力学只考虑平衡问题以及变化前后总结果。
热力学只要知道系统始、终态以及过程外界条件,就可进行计算,从而得出结论,无需知道物质的微观结构以及过程进行的机理,因而热力学简易而方便地得到广泛应用。
正因为如此,热力学对过程能否进行的判断,只知其然,而不知其所以然,不知变化的根本原因和变化的具体途径。
(3)热力学没有时间的概念,不涉及过程进行的速度问题。
它只指出过程能否发生以及进行到什么程度,至于什么时候发生,什么时候终止,需多少时间无法预知。
§2-2几个基本概念1.系统与环境热力学研究问题时,首先要确定研究对象。
从周围其它部分划分出来的作为研究对象的那一部分物质或空间,叫系统、体系或物系。
第二章热力学第一定律

Note:
(1)热力学中所谈的功都 是指体系与环境通过 它们的边界相互作用 的功; (2)关于功的规定,采用 1970年IUPAC所建议 的W或W代表环境对 体系所作之功。
正、负规定: 环境对系统作功,W >0; 系统对环境作功,W <0 单位:J、cal、atm· l等
体积功 W 机械功 电功 功 / 非体积功 W 表面功
对于可逆电池,若既有体积功也有电功时,电 池作的微功为 W ' W pdV EdQ Note:功不是体系能量的形式,而是能量传递或转 化的一种方式。
2.2
体积功计算实例
p33~35
例1、2、3
2.3 热 Q
历史上关于热本质的两种观点: 热质说:热是物质,称为热质是守恒的 (18世纪初代替热动说,1850年:传递着的能量) 热动说:热来源于运动
表示法:由于功是途径函数,所以宏观过程 的功用W 表示,微小过程的微量功 用W 表示
(2)体积功
本质是机械功
在压力作用下,体系(或物体)的外参量体积发 生改变时环境对体系(或者体系对环境)所作的功。
据机械功的定义,流体在准 静态过程中对环境所作的微功为:
W ' f dx pA dx pAdx pdV
(17世纪:笛卡尔、玻意尔、胡克、牛顿等)
热的唯象定义:
热是由于温差而引起的传递着的能量。
也就是说:热是能量的一种形式,但它不是体系(或物体)所 贮存的能量,也不是通过宏观作功的方式所传递的能量, 而是由于温差所引起的能流,它是在分子水平上的转移。
热力学中热的定义:系统与环境间因温差而交换的能量
正、负规定:吸热,Q >0;放热, Q <0 单位:J、cal、atm· l等 表示法:宏观过程的热用Q 表示,微小过程的微量热 用Q 表示。注意与状态函数表示法区分
物理化学第2章热力学第一定律

第二章热力学第一定律2.1 热力学的理论基础与方法1.热力学的理论基础热力学涉及由热所产生的力学作用的领域,是研究热、功及其相互转换关系的一门自然科学。
热力学的根据是三件事实:①不能制成永动机。
②不能使一个自然发生的过程完全复原。
③不能达到绝对零度。
热力学的理论基础是热力学第一、第二、第三定律。
这两个定律是人们生活实践、生产实践和科学实验的经验总结。
它们既不涉及物质的微观结构,也不能用数学加以推导和证明。
但它的正确性已被无数次的实验结果所证实。
而且从热力学严格地导出的结论都是非常精确和可靠的。
不过这都是指的在统计意义上的精确性和可靠性。
热力学第一定律是有关能量守恒的规律,即能量既不能创造,亦不能消灭,仅能由一种形式转化为另一种形式,它是定量研究各种形式能量(热、功—机械功、电功、表面功等)相互转化的理论基础。
热力学第二定律是有关热和功等能量形式相互转化的方向与限度的规律,进而推广到有关物质变化过程的方向与限度的普遍规律。
利用热力学第三定律来确定规定熵的数值,再结合其他热力学数据从而解决有关化学平衡的计算问题。
2.热力学的研究方法热力学方法是:从热力学第一和第二定律出发,通过总结、提高、归纳,引出或定义出热力学能U,焓H,熵S,亥姆霍茨函数A,吉布斯函数G;再加上可由实验直接测定的p,V,T等共八个最基本的热力学函数。
再应用演绎法,经过逻辑推理,导出一系列的热力学公式或结论。
进而用以解决物质的p,V,T变化、相变化和化学变化等过程的能量效应(功与热)及过程的方向与限度,即平衡问题。
这一方法也叫状态函数法。
热力学方法的特点是:(i)只研究物质变化过程中各宏观性质的关系,不考虑物质的微观结构;(ii)只研究物质变化过程的始态和终态,而不追究变化过程中的中间细节,也不研究变化过程的速率和完成过程所需要的时间。
因此,热力学方法属于宏观方法。
2.2 热力学的基本概念1.系统与环境系统:作为某热力学问题研究对象的部分;环境:与系统相关的周围部分;按系统与环境交换内容分为:(1)敞开系统(open system) :体系与环境间既有物质交换又有能量交换的体系。
(完整版)第二章热力学第一定律

(完整版)第⼆章热⼒学第⼀定律第⼆章热⼒学第⼀定律1、如果⼀个系统从环境吸收了J 40的热,⽽系统的热⼒学能却增加了J 200,问系统从环境中得到了多少功?如果该系统在膨胀过程中对环境作了kJ 10的功,同时收了kJ 28的热,求系统的热⼒学能变化值。
解:根据W Q U +=?热⼒学第⼀定律,可知J Q U W 160)40200(=-=-?=(系统从环境吸热,0>Q ) kJ W Q U 181028=-=+=?(系统对环境做功,02、有mol 10的⽓体(设为理想⽓体),压⼒为kPa 1000,温度为K 300,分别求出等温时下列过程的功:(1)在空⽓中压⼒为kPa 100时,体积胀⼤31dm ;(2)在空⽓中压⼒为kPa 100时,膨胀到⽓体压⼒也是kPa 100;(3)等温可逆膨胀⾄⽓体的压⼒为kPa 100;解:(1)外压始终维持恒定,系统对环境做功 J V p W e 1001011010033-=-=?-=-(2))11()()(12112212p p nRTp p nRT p nRT p V V p V p W e e e e --=--=--=?-=343311108.31430010010() 2.21010010100010J =--=-???(3)等温可逆膨胀:2112ln ln21p p nRT V V nRT dV p W V V e -=-=-=?J 41074.51001000ln 300314.810?-=-=3、1mol 单原⼦理想⽓体,,32V m C R =,始态(1)的温度为273K ,体积为322.4dm ,经历如下三步,⼜回到始态,请计算每个状态的压⼒,Q ,W 和U ?。
(1)等容可逆升温由始态(1)到546K 的状态(2);(2)等温(546K )可逆膨胀由状态(2)到44.8dm 3的状态(3);(3)经等压过程由状态(3)回到始态10mol,300K 1000kPa,V 1 10mol,300K 100kPa,V 2(1);解:(1)等容可逆升温过程:()21,0318.3145462733404.582e T V V m T W P V U Q W Q nC dT J=-?=?=+===-=? (2)等温可逆膨胀过程:0U ?=2144.8ln 18.314546ln 3146.5022.43146.50V W nRT JV Q W J=-==-=-=(3)等压过程:()()()()()2131231,18.31427322.444.8102269.7222.4103527354618.3142735674.31225674.312269.723404.59e T p P m T nRT W P V V V J V Q H nC dT n R R J U Q W J--??=-?=--=-?-?==?=+?-=-=-=+=-+=-4、在K 291和kPa 100下,)(1s molZn 溶于⾜量稀盐酸中,置换出)(12g molH ,并放热kJ 152。
02章 热力学第一定律

3. 几种典型可逆过程: (1)可逆膨胀和可逆压缩:力学平衡 (2)可逆传热:热平衡 (3)可逆相变:相平衡 (4)可逆化学反应:A + B
E反=E-dE + 电 池(E) A+B C -
C
§ §2 2- -4 4 热的计算 热的计算 (How (How to to calculate calculate heat) heat)
§2-1 基本概念 (Important concepts)
一、系统和环境 (System and surroundings) ¾ 定义:系统——研究对象(也称体系) 环境——与系统有相互作用的外界 ¾ 系统的分类 敞开系统 系统 封闭系统 孤立系统
二、热力学平衡状态 (Thermodynamic equilibrium state)
V1 V1 V1
V2
V2
V2
= −∫
V2
V1
nRT V dV = − nRT ln 2 V V1
等温膨胀 W=? H2(1000Pa, 3m3)
例:1mol H2 (3000Pa, 1m3)
(1) 若 p外=0 (自由膨胀):W=0 (2) 若 p外=1000 Pa (一次膨胀):W=-1000×(3-1) J =-2000 J (3) 可逆膨胀:
∆U = ∫ CV dT
T1
T2
¾ 理气 H = U + pV = U + nRT = f(T)
⎛ ∂H ⎜ ⎜ ∂p ⎝
⎞ ⎟ ⎟ =0 ⎠T
对任意物质的任意(p V T)过程 ⎛ ∂H ⎞ d H = C p dT + ⎜ ⎜ ∂p ⎟ ⎟ dp ⎝ ⎠T 理想气体
dH = C p dT
T2
第二章 热力学第一定律 概念及公式总结

2.10.3 化学反应的热效应:
反应物
等压 r H I 0
Qp H
H
、 QV U H
T1 、 p1 、v2 、
T1 、 p1 、 v1
H 3
由于 H 是状态函数,所以
r H1 r H2 r H3
pV 2 n RT1 或 r H rU n RT
nR
k 1 1 1 1 = W 1 V2 V1
nR T2 T 1
1
= W CV T2 T1 (适
(1)
用于理想气体) 2.8.4Carnot
P
A
Tc Th
以上四个过程构成一个可逆循环,系统又回到了始态:
U 0 、 Q W 、 Q Qh QC Qc 0 、
W W1 W2 W3 W4 = W1 W3 ( W2 与 W4 对消)= nRTh ln
v v1 nRTc ln 3 v2 v4
V1 】 V2
Q2 0 、 W2 U 2 nCv ,m dT
Th TC
过程(3) :等温可逆压缩
v U3 0 、 QC W3 、 W3 v3 pdv nRTc ln
4
V3 、 w3 v4
0 、 QC 0
过程(4) :绝热可逆压缩
W4 U 4 nCV ,m dT 、 Q4 0 、
1 1 1 1 在等温下当体积变化时 U a 、 H a pVm V V V V m ,1 m ,2 m ,1 m ,2
实际气体的
U U 和 的都不等于零, H 也不等于零 V T p T
第2章-热力学第一定律

内能及闭口系热一律表达式
定义 dU = Q - W 内能U 状态函数
Q = dU + W Q=U+W
闭口系热一律表达式
!!!两种特例 绝功系 Q = dU 绝热系 W = - dU
内能U 的物理意义
dU = Q - W
Q
W
dU 代表某微元过程中系统通过边界 交换的微热量与微功量两者之差值,也 即系统内部能量的变化。
Q
Q + min(u + c2/2 + gz)in - mout(u + c2/2 + gz)out - Wnet = dEcv
开口系能量方程微分式
Q + min(u + pv+c2/2 + gz)in - Wnet - mout(u + pv+c2/2 + gz)out = dEcv
适用条件: 任何流动工质 任何稳定流动过程
单位质量工质的开口与闭口
闭口系(1kg)
q u w
容积变化功 等价
wsh
技术功wt
q
稳流开口系
1 2 q h c gz wsh 2
稳流开口与闭口的能量方程
闭口 稳流开口
q u w q ຫໍສະໝຸດ h wt等价容积变化功 w 技术功 wt 轴功 ws 几种功的关系?
稳定流动能量方程
Steady State Steady Flow(SSSF)
min 稳定流动条件 uin 1 2 1、 mout min m cin 2 gzin 2、 Q const
Wnet
mout uout 1 2 cout 2 gzout
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
H2与N2以3:1的比例在绝热钢瓶中反应生成NH3,此过程:
(A) H = 0 (B) p = 0 (C) U = 0 (D) T = 0
3. 理想气体的热力学能和焓 焦耳实验(1845)图2.2.1
§2.4
热
容
或
δQV dU m
CV ,m
或
U m ( )V f (T ) T
热力学第一定律表述之一:
自然界一切物质都有能量,能量有各种不同形式并可互相转 化,在转化过程中总值不变(即能量守恒与转化定律)。
热力学第一定律表述之二:
第一类永动机是造不成的。
热力学第一定律的数学表述: 系统从状态 (1) 状态(2),与环境交换热Q,交换功W, 则有: U2 = U1 + Q + W, 或 U = Q +W dU = Q + W (封闭系统)
4. 过程与途径 系统的一切变化均称之为过程。 在相同的始终态间,可有不同的变化方式,称之为 途径 。状态函数的变化与途径无关!。 常见的过程有: 恒温过程:T2 = T1 = T (环) 恒压过程:p2 = p1 = p (环) 恒容过程:V = 0 绝热过程:无热交换,但可以有功的传递 循环过程:回到初始状态 5. 热力学平衡态(无环境影响下) (1) 热平衡 (2) 力平衡 (3) 相平衡 (4) 化学平衡 T (环)为环境温度 p (环)为环境压力
W 与途径有关,微小变化用W表示(不能用dW).
p(环)
p(环)
A
体积功的计算:
W = Fdl
= p(环) Adl
= p(环) dV
(能否用系统的压力p ?) dl
对于一有限过程:
若环境压力恒定, V1 = p(环)(V2 V1) = p(环)V (恒外压过程) 与恒压过程比较。 V2 V
= 625 J
3. 热力学能(U):
系统内部能量之总和(内能),包括分子运动的平动
能、分子内的转动能、振动能、电子能、核能以及各种粒子 之间的相互作用势能等。 U 是状态函数,其变化只取决于始终态。 对于纯物质单相封闭系统,可认为是 T,V 的函数, U = U(T,V) 全微分: 或 U =U (T, p)
可知, 的数值与反应式的书写有关。
物质的标准态及标准摩尔反应焓 压力的标准态: 历史沿革: 1 atm (大气压) 101.325 kPa 100 kPa
例如:
表示:298.15K,反应物和生成物都处于标准态, 反应进度为1mol 时的焓变。( p 为标准态压力) 焓的变化 反应(reaction) 反应物和生成物都处于标准态 反应温度 反应进度为1mol
或
§2.5 相 变 焓
例: 已知 100º C、101.325 kPa 下,H2O的摩尔蒸发焓
Δ vapH m (100 C) 40.64 kJ mol 1
100 – 142.9 º 之间水蒸气的摩尔定压热容 C
Cp,m(g,T) =(29.16 +14.49 10-3 T 2.022 10-6 T2 ) J K-1 mol-1
= (47.40 +14.49 10-3 T 2.022 10-6 T2 ) J K-1 mol-1
代入并积分得
38.64 kJ mol-1
§2.6 溶解焓与稀释焓(略) §2.7 化学反应焓
例 10 mol N2(g) 和 20 mol H2(g)混合通过合成氨塔,经过多次循环 反应,最后有5mol NH3(g)生成。试分别以如下两个反应方程式为基 础,计算反应进度。 (a) N2 + 3H2 → 2NH3 1 3 ( b) N 2 + H2 → NH 3 2 2
2. 状态与状态函数 状态:系统物理化学性质的综合。 状态函数:描述系统状态的宏观性质,p, V, T …..
状态函数的特征: (1) 状态确定,状态函数有确定值; (2) 状态函数的变化值与途径无关,仅取决于始终态; (3) 系统复原,状态函数改变量为零。 状态函数的微小变化可用全微分表示,e.g. dp, d , dT….. V 3. 广度性质和强度性质 广度性质:其值与系统物质的量成正比,在一定条件下有加 和性,e.g. V, n, U 强度性质:其值与系统物质的量无关, e.g. T, p , 无加和性。
(A) 降低 (B) 升高 (C) 不变 (D) 不能确定
思考题: 有一电炉丝浸于水中,以未通电时为初态,以通电一定时间 后为终态。如果按下列几种情况选择系统,问U、Q 和W 为正、为负、还是为零?(设电池放电过程中没有热效应)。 (1) (2) (3) (4) (5) (6) 水和电炉丝 水 电炉丝 电池 电池和电炉丝 电池、电炉丝和水 (1) W Q U + 0 + (2) (3) + – + (4) 0 –
水的平均摩尔热容C
p, m (l)
76. 56 J K1 mol 1
求H2O(l)在142.9C平衡条件下的蒸发焓vapHm(142.9C) 解: 假设水蒸气为理想气体,并忽略其蒸发焓随压力的变化。
其中: vapCp,m = Cp,m(g,T) Cp,m(l) = (29.16 + 14.49 10-3 T 2.022 10-6 T2 76.56 )
2
θ Δ rH m (T
θ Δf H m (C2H4O, g, T ) )=
§2.2 热力学第一定律
热与功 能量交换的两种形式,是过程量,不是系统的性质。 热(Q) 系统与环境间因温度不同而产生的能量交换。 符号规定 :系统吸热 + ,系统放热 显热 相变热(潜热) 化学反应热 Q 与途径有关,微小变化用Q 表示(不能用dQ).
功(W)
系统与环境间除热以外所有其它形式的能量交换。 符号规定 :系统作功 ,环境作功 + 功的分类:体积功,非体积功 W ’(电功、表面功等);
§2.8 标准摩尔反应焓的计算
C2H4(g) + 1 O2(g) p, T
2
θ r H m (T )
C2H4O(g) p, T
H1
途径 I
途径 II
H2
2C(石墨) + 2H2(g) +1 O2(g) p, T
θ H2 = H1 + Δ rH m (T )
θ Δ rH m (T ) = H2 H1
U dT U dV dU V T T V
U dT U dp dU p T p T
U U T T V p
4. 热力学第一定律
1mol理想气体从始态 A 经途径 1 到达终态 B 时,系
统与环境交换热量Q1 = 15 kJ,做功 W1 = 10 kJ。若 该气体从同一始态 A 经途径 2 到达同一终态 B 时,Q2 = 10 kJ,则W2 = ___。
绝热房间内放有一电冰箱,将冰箱门打开的同时供以
电能使冰箱运行 2小时,达平衡后室内的温度将 ____。
解: n(N2)/mol t = 0, = 0 10 t = t, = 7.5
n(H25
(a) 以NH3为基准 = (5 0)/2 = 2.5mol
以H2为基准, = (12.5 20)/ 3 = 2.5mol 以N2为基准, = (7.5 10)/ 1 = 2.5mol (b) 分别以NH3, H2和N2为基准 = (50)/1 = (12.520)/(3/2) = (7.510)/(1/2)= 5mol
(2)Cu在试管中氧化为CuO,然后再通入H2 还原为Cu。 (以Cu为系统和以Cu+O2为系统有何不同?) 解:(1) 是循环过程. 1 ( 2) Cu O2 = CuO CuO + H2 = Cu + H2O 2 以Cu 为系统是循环过程,以Cu + O2 为系统不是循环过程。 因H = Qp,所以只有恒压过程才有H。对否?
热力学最基本的公式之一!
思考题:
一绝热容器中放有绝热、无质量和无摩擦的活塞,该活塞将 容器分隔为左、右两室,两室中均充有n, p1 ,T1 的理想气体。若 右室中装有一电热丝,并通电缓慢加热右室气体,于是活塞逐渐 向左移动。此时,若以右室气体为系统,则过程的Q (右) > 0 , <0 =0 W (右) ____ ; 若以左室气体为系统, 则过程的 Q (左) ____ , >0 >0 W (左) ____ ;若以整个容器的气体为系统,则过程的Q ____, =0 W _____。
例:1mol 理想气体从 p1 = 100 kPa, T1 = 298K 分别经历以 下三条不同途径,恒温变化到 p2 = 50 kPa, 求W。 (1) 向真空膨胀(自由膨胀)至终态; (2) 恒定 p(环) = 50 kPa 至终态;
(3) 先被 200 kPa 恒外压压缩至一中间态,然后在50 kPa 恒 外压下膨胀至终态。 解: (1) 向真空膨胀,p(环) = 0, W1 = 0;
(2) p (环) = 常数,V1 = 0.025 m3,V2 = 0.050 m3 W2 = -p (环)(V2 V1)
= 50 103 (0.050 0.025) = 1250 J
(3) 两步都是恒外压过程, W3 = 200 103 (0.01250.025)50103 (0.050.0125)
绝热壁 水
(5)
(6)
0
+ +
0
– –
0
0
0
§2.3 恒容热、恒压热与焓
1. 恒容热QV 恒容且非体积功W' = 0 条件下的热交换。 恒容过程 d = 0,Q = QV ,体积功W (体) = 0 V
由热一律 U = Q + W
