初三数学-极差与方差练习
7.1.4 2020中考数学复习:《极差、方差、标准差》近8年全国中考题型大全(含答案)

极差、方差、标准差一、选择题1. (2017 浙江省舟山市) 已知一组数据c,的平均数为5,方差为4,那么数a,b据2ba的平均数和方差分别是()-c-,2-,2A.3,2 B.3,4 C.5,2 D.5,42. (2017 贵州省六盘水市) 已知A组四人的成绩分别为90、60、90、60,B组四人的成绩分别为70、80、80、70,用下列哪个统计知识分析区别两组成绩更恰当( )A.平均数B.中位数C.众数D.方差3. (2018 浙江省杭州市) (3分)测试五位学生的“一分钟跳绳”成绩,得到五个各不相同的数据,在统计时,出现了一处错误:将最高成绩写得更高了,计算结果不受影响的是()A.方差B.标准差C.中位数D.平均数4. (2018 新疆建设兵团) (5分)甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字个数的统计结果如下表:某同学分析上表后得出如下结论:1(1)甲、乙两班学生的平均成绩相同;(2)乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字的个数≥150为优秀);(3)甲班成绩的波动比乙班大.上述结论中,正确的是()A.①②B.②③C.①③D.①②③5. (2018 新疆乌鲁木齐) (4分)甲、乙两名运动员参加射击预选赛.他们的射击成绩(单位:环)如表所示:第一次第二次第三次第四次第五次甲7 9 8 6 10乙7 8 9 8 8设甲、乙两人成绩的平均数分别为,,方差分别s甲2,s乙2,下列关系正确的是()A.=,s甲2>s乙2 B.=,s甲2<s乙2C.>,s甲2>s乙2 D.<,s甲2<s乙26. (2018 四川省自贡市) (4分)在一次数学测试后,随机抽取九年级(3)班5名学生的成绩(单位:分)如下:80、98、98、83、91,关于这组数据的说法错误的是()A.众数是98 B.平均数是90 C.中位数是91 D.方差是5627. (2018 四川省资阳市) (3分)某单位定期对员工的专业知识、工作业绩、出勤情况三个方面进行考核(考核的满分均为100分),三个方面的重要性之比依次为3:5:2.小王经过考核后所得的分数依次为90、88、83分,那么小王的最后得分是()A.87 B.87.5 C.87.6 D.888. (2019 黑龙江省齐齐哈尔市)小明和小强同学分别统计了自己最近10次“一分钟跳绳”的成绩,下列统计量中能用来比较两人成绩稳定程度的是()A.平均数B.中位数C.方差D.众数9. (2019 湖北省孝感市) (3分)下列说法错误的是()A.在一定条件下,可能发生也可能不发生的事件称为随机事件B.一组数据中出现次数最多的数据称为这组数据的众数C.方差可以刻画数据的波动程度,方差越大,波动越小;方差越小,波动越大D.全面调查和抽样调查是收集数据的两种方式10. (2019 辽宁省沈阳市) (2分)下列说法正确的是()A.若甲、乙两组数据的平均数相同,20.1S=甲,20.04S=乙,则乙组数据较稳定B.如果明天降水的概率是50%,那么明天有半天都在降雨C.了解全国中学生的节水意识应选用普查方式D.早上的太阳从西方升起是必然事件311. (2019 山东省潍坊市) (3分)小莹同学10个周综合素质评价成绩统计如下:这10个周的综合素质评价成绩的中位数和方差分别是()A.97.5 2.8; B.97.5 3; C.97 2.8; D.97 312. (2019 山东省烟台市) (2019年烟台)某班有40人,一次体能测试后,老师对测试成绩进行了统计,由于小亮没有参加本次集体测试,因此计算其他39人的平均成绩为90分,方差为s2=41.后来小亮进行了补测,成绩为90分.关于该班40人的测试成绩,下列说法中确的是()A.平均分不变,方差变大 B.平均分不变,方差变小C.平均分和方差都不变 D.平均分和方差都改变13. (2019 四川省达州市) (3分)一组数据1,2,1,4的方差为()A.1 B.1.5 C.2 D.2.514. (2019 四川省自贡市) (4分)在5轮“中国汉字听写大赛”选拔赛中,甲、乙两位同学的平均分都是90分,甲的成绩方差是15,乙的成绩方差是3,下列说法正确的是()A.甲的成绩比乙的成绩稳定 B.乙的成绩比甲的成绩稳定C.甲、乙两人的成绩一样稳定D.无法确定甲、乙的成绩谁更稳定15. (2019 浙江省宁波市) (4分)去年某果园随机从甲、乙、丙、丁四个品种的4葡萄树中各采摘了10棵,每棵产量的平均数(单位:千克)及方差S2(单位:千克2)如表所示:甲乙丙丁24 24 23 20S2 2.1 1.9 2 1.9要选出一种产量既高又稳定的葡萄树进行种植,应选的品种是()A.甲B.乙C.丙D.丁16. (2019 浙江省台州市) (4分)方差是刻画数据波动程度的量.对于一组数据x1,x2,x3,…,x n,可用如下算式计算方差:s2=[(x1﹣5)2+(x2﹣5)2+(x3﹣5)2+…+(x n﹣5)2],其中“5”是这组数据的()A.最小值B.平均数C.中位数D.众数17. (2019 四川省攀枝花市) (3分)比较A组、B组中两组数据的平均数及方差,以下说法正确的是()A.A组、B组平均数及方差分别相等 B.A组、B组平均数相等,B组方差大C.A组比B组的平均数、方差都大D.A组、B组平均数相等,A组方差大5二、填空题18. (2015 山东省济宁市) 甲乙两地9月上旬的日平均气温如图所示,则甲乙两地这10天日平均气温方差大小关系为S甲2S乙2(填>或<).19. (2019 贵州省安顺市) (4分)已知一组数据x1,x2,x3,…,x n的方差为2,则另一组数据3x1,3x2,3x3,…,3x n的方差为.20. (2019 湖南省郴州市) (3分)如图是甲、乙两人6次投篮测试(每次投篮10个)成绩的统计图,甲、乙两人测试成绩的方差分别记作s甲2、s乙2,则s甲2 s乙2.(填“>”,“=”或“<”)21. (2019 内蒙古通辽市) (3分)某机床生产一种零件,在6月6日至9日这4天中出现次品的数量如下表:6日期6月6日6月7日6月8日6月9日次品数量(个) 1 0 2 a若出现次品数量的唯一众数为1,则数据1,0,2,a的方差等于.22. (2019 山东省菏泽市) (3分)一组数据4,5,6,x的众数与中位数相等,则这组数据的方差是.23. (2019 内蒙古赤峰市) (3分)如图是甲、乙两名射击运动员10次射击成绩的统计表和折线统计图.平均数中位数众数甲8 8 8乙8 8 8你认为甲、乙两名运动员,的射击成绩更稳定.(填甲或乙)三、应用题24. (2012 福建省厦门市) 本题满分7分)已知A组数据如下:0,1,-2,-1,0,-1,3.(1)求A组数据的平均数;(2)从A组数据中选取5个数据,记这5个数据为B组数据. 要求B组数78据满足两个条件:①它的平均数与A 组数据的平均数相等;②它的方差比A 组数据的方差大.你选取的B 组数据是 ,请说明理由. 注:A 组数据的方差的计算式是S A 2=17[(x 1-—x )2+(x 2-—x )2+(x 3-—x )2+(x 4-—x )2+(x 5-—x )2+(x 6-—x )2+(x 7-—x )2]25. (2013 四川省绵阳市) 为了从甲.乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表: 图1 甲、乙射击成绩统计表图2 甲、乙射击成绩折线图乙甲y x命中环数射击次数1234567891010987654321(1)请补全上述图表(请直接在表中填空和补全折线图);(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?26. (2014 黑龙江省大庆市) 甲、乙两名同学进入初四后某科6次考试成绩如图所示:请根据右图填写下表;平均数方差中位数众数极差甲75 75乙33 .3 159请你从以下两个不同的方面对甲、乙两名同学6次考试成绩进行分析:①从平均数和方差结合看;②从折线图上两名同学分数的走势上看,你认为反应出什么问题?27. (2015 河北省) 某厂生产A,B两种产品,其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了如表统计表及不完整的折线图.A,B产品单价变化统计表第一次第二次第三次A产品单价(元/件) 6 5.2 6.5B产品单价(元/件) 3.5 4 3并求得了A产品三次单价的平均数和方差:=5.9,s A2=[(6﹣5.9)2+(5.2﹣5.9)2+(6.5﹣5.9)2]=(1)补全如图中B产品单价变化的折线图.B产品第三次的单价比上一次的单价降低了%(2)求B产品三次单价的方差,并比较哪种产品的单价波动小;10(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.28. (2016 山东省青岛市) 甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:根据以上信息,整理分析数据如下:(1)写出表格中a,b,c的值;(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?29. (2019 浙江省杭州市) (8分)称量五筐水果的质量,若每筐以50千克为基准,超过基准部分的千克数记为正数,不足基准部分的千克数记为负数,甲组为实际称量读数,乙组为记录数据,并把所得数据整理成如下统计表和未完成的统计图(单位:千克).实际称量读数和记录数据统计表数据 1 2 3 4 5甲组48 52 47 49 54乙组﹣2 2 ﹣3 ﹣1 4(1)补充完成乙组数据的折线统计图.(2)①甲,乙两组数据的平均数分别为,,写出与之间的等量关系.②甲,乙两组数据的方差分别为S甲2,S乙2,比较S甲2与S乙2的大小,并说明理由.参考答案一、选择题 1. 答案B.试题分析:平均数为13(a −2 + b −2 + c −2 )=13(3×5-6)=3;原来的方差:2221(5)(5)(5)43a b c ⎡⎤-+-+-=⎣⎦;新的方差:2221(23)(23)(23)3a b c ⎡⎤--+--+--=⎣⎦2221(5)(5)(5)43a b c ⎡⎤-+-+-=⎣⎦,故选B.考点: 平均数;方差.2. 考点方差;平均数;中位数;众数.分析根据A 组和B 组成绩,求出中位数,平均数,众数,方差差,即可做出判断. 解答解:A 组:平均数=75,中位数=75,众数=60或90,方差=225A 组:平均数=75,中位数=75,众数=70或80,方差=25故选D .3. 分析根据中位数的定义解答可得.解答解:因为中位数是将数据按照大小顺序重新排列,代表了这组数据值大小的“中点”,不易受极端值影响,所以将最高成绩写得更高了,计算结果不受影响的是中位数,故选:C.4.分析两条平均数、中位数、方差的定义即可判断;解答解:由表格可知,甲、乙两班学生的成绩平均成绩相同;根据中位数可以确定,乙班优秀的人数多于甲班优秀的人数;根据方差可知,甲班成绩的波动比乙班大.故(1)(2)(3)正确,故选:D.5.分析分别计算平均数和方差后比较即可得到答案.解答解:(1)=(7+8+9+6+10)=8;=(7+8+9+8+8)=8;=[(7﹣8)2+(8﹣9)2+(8﹣8)2+(6﹣8)2+(10﹣8)2]=2;=[(7﹣8)2+(8﹣8)2+(9﹣8)2+(8﹣8)2+(8﹣8)2]=0.2;∴=,s>s故选:A.6.分析根据众数、中位数的概念、平均数、方差的计算公式计算.解答解:98出现的次数最多,∴这组数据的众数是98,A说法正确;=(80+98+98+83+91)=90,B说法正确;这组数据的中位数是91,C说法正确;S2=[(80﹣90)2+(98﹣90)2+(98﹣90)2+(83﹣90)2+(91﹣90)2]=×278=55.6,D说法错误;故选:D.7.分析将三个方面考核后所得的分数分别乘上它们的权重,再相加,即可得到最后得分.解答解:小王的最后得分=90×+88×+83×=27+44+16.6=87.6(分),故选:C.8.分析根据方差的意义:体现数据的稳定性,集中程度,波动性大小;方差越小,数据越稳定.要比较两位同学在五次数学测验中谁的成绩比较稳定,应选用的统计量是方差.解答解:能用来比较两人成绩稳定程度的是方差,故选:C.点评此题主要考查统计的有关知识,主要包括平均数、中位数、众数、方差的意义.反映数据集中程度的统计量有平均数、中位数、众数方差等,各有局限性,因此要对统计量进行合理的选择和恰当的运用.9.分析分别根据随机事件的定义、众数的定义、方差的意义以及调查方式判断即可.解答解:A.在一定条件下,可能发生也可能不发生的事件称为随机事件,正确,故选项A不合题意;B.一组数据中出现次数最多的数据称为这组数据的众数,正确,故选项B不合题意;C.方差可以刻画数据的波动程度,方差越大,波动越大;方差越小,波动越小.故选项C符合题意;D.全面调查和抽样调查是收集数据的两种方式,正确,故选项D不合题意.故选:C.点评本题主要考查了随机事件的定义、众数的定义、方差的意义以及调查的方式,属于基础题.10.分析根据方差、概率、全面调查和抽样调查以及随机事件的意义分别对每一项进行分析即可得出答案.解答解:A、20.1S=Q甲,20.04S=乙,22S S∴>乙甲,∴乙组数据较稳定,故本选项正确;B、明天降雨的概率是50%表示降雨的可能性,故此选项错误;C、了解全国中学生的节水意识应选用抽样调查方式,故本选项错误;D、早上的太阳从西方升起是不可能事件,故本选项错误;故选:A.点评本题考查了方差、概率、全面调查和抽样调查以及随机事件,熟练掌握定义是解题的关键.11.分析根据中位数和方差的定义计算可得.解答解:这10个周的综合素质评价成绩的中位数是=97.5(分),平均成绩为×(94+95×2+97×2+98×4+100)=97(分),∴这组数据的方差为×[(94﹣97)2+(95﹣97)2×2+(97﹣97)2×2+(98﹣97)2×4+(100﹣97)2]=3(分2),故选:B.点评本题主要考查中位数和方差,解题的关键是掌握中位数和方差的定义.12. {答案}B{解析}本题考查了统计量的意义与计算,由平均数和方差的计算公式知平均分不变,方差变小.因此本题选B.13.分析先求得这组数据平均值,再根据方差公式,计算即可解答解:平均数为==2方差S2=[(1﹣2)2+(2﹣2)2+(1﹣2)2+(4﹣2)2]=故选:B.点评此题主要考查方差的计算公式,熟记方差的计算公式:S2=×[(x1﹣)2+(x)2+…+(x n﹣1﹣)2+(x n﹣)2]是解题的关键2﹣14.分析根据方差的意义求解可得.解答解:∵乙的成绩方差<甲成绩的方差,∴乙的成绩比甲的成绩稳定,故选:B.点评本题主要考查方差,方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.15. 分析先比较平均数得到甲组和乙组产量较好,然后比较方差得到乙组的状态稳定.解答解:因为甲组、乙组的平均数丙组、丁组大, 而乙组的方差比甲组的小, 所以乙组的产量比较稳定,所以乙组的产量既高又稳定,故选:B .点评本题考查了方差:一组数据中各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差.方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.也考查了平均数的意义.16. 解答解:方差s 2=[(x 1﹣5)2+(x 2﹣5)2+(x 3﹣5)2+…+(x n ﹣5)2]中“5”是这组数据的平均数,故选:B .17. 分析由图象可看出A 组的数据为:3,3,3,3,3,2,2,2,2,B 组的数据为:2,2,2,2,3,0,0,0,0,则分别计算出平均数及方差即可 解答解:由图象可看出A 组的数据为:3,3,3,3,3,2,2,2,2,B 组的数据为:2,2,2,2,3,0,0,0,0则A 组的平均数为111(333332222)99A x =⨯++++++++=B 组的平均数为111(222230000)99B x =⨯++++++++=∴A B x x =A 组的方差:22222222221111111111111111111320[(3)(3)(3)(3)(3)(1)(1)(1)(1)]999999999981A S =⨯-+-+-+-+-+--+--+--+--=B 组的方差:22222222221111111111111111111104[(2)(2)(2)(2)(3)(0)(0)(0)(0)]999999999981B S =⨯-+-+-+-+-+-+-+-+-=22A B S S ∴>综上,A 组、B 组的平均数相等,A 组的方差大于B 组的方差 故选:D .点评本题考查了平均数,方差的意义.平均数平均数表示一组数据的平均程度;方差是用来衡量一组数据波动大小的量.二、填空题18. 分析: 根据气温统计图可知:贵阳的平均气温比较稳定,波动小,由方差的意义知,波动小者方差小.解答: 解:观察平均气温统计图可知:乙地的平均气温比较稳定,波动小; 则乙地的日平均气温的方差小, 故S 2甲>S 2乙. 故答案为:>.点评: 本题考查方差的意义:方差反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.19.分析如果一组数据x1、x2、…、x n的方差是s2,那么数据kx1、kx2、…、kx n 的方差是k2s2(k≠0),依此规律即可得出答案.解答解:∵一组数据x1,x2,x3…,x n的方差为2,∴另一组数据3x1,3x2,3x3…,3x n的方差为32×2=18.故答案为18.点评本题考查了方差的定义.当数据都加上一个数时,平均数也加上这个数,方差不变,即数据的波动情况不变;当数据都乘以一个数时,平均数也乘以这个数(不为0),方差变为这个数的平方倍.20.分析根据数据偏离平均数越大,即波动越大,数据越不稳定,方差越大;数据偏离平均数越小,即波动越小,数据越稳定,方差越小进行判断.解答解:由图象可知:乙偏离平均数大,甲偏离平均数小,所以乙波动大,不稳定,方差大,即S甲2<S乙2.故答案为:<.点评本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.21.分析求一组数据的众数的方法:找出频数最多的那个数据,若几个数据频数都是最多且相同,此时众数就是这多个数据.一组数据中各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差.解答解:Q 出现次品数量的唯一众数为1,1a ∴=,∴102114x +++==, 22222(11)(01)(21)(11)142S -+-+-+-∴==,故答案为12.点评本题考查了方差,熟练运用方差公式是解题的关键.22. 分析分别假设众数为4,5,6,分类讨论,找到符合题意的x 的值,再根据方差的定义求解可得.解答解:若众数为4,则数据为4,4,5,6,此时中位数为4.5,不符合题意; 若众数为5,则数据为4,5,5,6,中位数为5,符合题意, 此时平均数为=5,方差为[(4﹣5)2+(5﹣5)2+(5﹣5)2+(6﹣5)2]=;若众数为6,则数据为4,5,6,6,中位数为5.5,不符合题意; 故答案为.点评本题主要考查众数、中位数及方差,根据众数的可能情况分类讨论求解是解题的关键.23. 分析根据题意和统计图中的数据可以解答本题. 解答解:由统计表可知,甲和乙的平均数、中位数和众数都相等, 由折线统计图可知,乙的波动小,成绩比较稳定, 故答案为:乙.点评本题考查折线统计图、平均数、中位数、众数,解答本题的关键是明确波动越小,成绩越稳定. 三、应用题 24. 本题满分7分)(1)解:A 组数据的平均数是0+1-2-1+0-1+371分 =0.3分 (2)解1:选取的B 组数据:0,-2,0,-1,3. 4分 ∵ B 组数据的平均数是0.5分∴ B 组数据的平均数与A 组数据的平均数相同. ∴ S B 2=145 ,S A 2=167 .6分 ∴ 145 >167.7分∴ B 组数据:0,-2,0,-1,3.解2:B 组数据:1,-2,-1,-1,3. 4分 ∵ B 组数据的平均数是0.5分∴ B 组数据的平均数与A 组数据的平均数相同. ∵S A 2=167, S B 2=165 .6分 ∴165>1677分∴ B 组数据:1,-2,-1,-1,3.25.解:(1)如右图(2)甲胜出。
(完整版)方差专项练习

极差、方差与标准差专项练习⑴极差极差=最大值-最小值.⑵方差:用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况,这个结果叫方差,通常用s 2来表示。
⑶标准差:标准差=⑷方差(或标准差)越大,,稳定性越小;反之,方差越小,稳定性越好.一、填空题1、数据-2,-1,3,1,2的方差是_________极差是 _______2、 七个数1,2,5,3,4,a ,3的平均数是3,则a =________,这七个数的方差是________。
3、若一组数据3,一1,a ,-3,3的平均数是a 的则这组数据的标准差是_________。
4、已知,一组数据1, 2,……,n 的平均数是10,方差是2, ①数据1+3, 2+3,……,n+3的平均数是 方差是 , ②数据2×1,2×2,……,2×n 的平均数是 方是 , ③数据2×1+3,2×2+3,……,2×n+3的平均数是 方差是 。
5、数据:2-,1-,0,x ,1的平均数是0,则x = .方差=2S .6、如果样本方差[]242322212)2()2()2()2(41-+-+-+-=x x x x S ,那么这个样本的平均数为 .样本容量为 .7、已知321,,x x x 的平均数=x 10,方差=2S 3,则3212,2,2x x x 的平均数为 ,方差为 .二、选择题:8、样本方差的作用是A 、估计总体的平均水平B 、表示样本的平均水平C 、表示总体的波动大D 、表示样本的波动大小,从而估计总体的波动大小9、一个样本的方差是0,若中位数是a ,那么它的平均数是A 、等于aB 、不等于 aC 、大于 aD 、小于a10、已知样本数据101,98,102,100,99,则这个样本的标准差是 A、0 B、1 C、2 D、211、如果给定数组中每一个数都减去同一非零常数,则数据的A、平均数改变,方差不变B、平均数改变,方差改变C、平均数不变,方差不变D、平均数不变,方差改变三、问答题:1、为了考察甲、乙两种农作物的长势,分别从中抽取了10株苗,测得苗高如下:(单位:mm)甲:9,10,11,12,7,13,10,8,12,8乙:8,13,12,11,10,12,7,7,9,11请你经过计算后回答如下问题:(1)哪种农作物的10株苗长的比较高?(2)哪种农作物的10株苗长的比较整齐?2. 从甲、乙两种农作物中各抽取1株苗,分别测得它的苗高如下:(单位:cm)甲:9、10、11、12、7、13、10、8、12、8;乙:8、13、12、11、10、12、7、7、9、11;问:(1)哪种农作物的苗长的比较高?(2)哪种农作物的苗长得比较整齐?3. 段巍和金志强两人参加体育项目训练,近期的5次测试成绩如4.甲、乙两名学生在相同的条件下各射靶10次,命中的环数如下:甲:7、8、6、8、6、5、9、10、7、4乙:9、5、7、8、7、6、8、6、7、7经过计算,两人射击环数的平均数相同,但S2甲 S2乙,所以确定去参加比赛。
极差、方差及标准差典型例题及习题(2)

典型例题例1计算下列一组数据的极差、方差及标准差(精确到0.01);50,55,96,98,65,100,70,90,85,100.解极差为100-50=50.平均数为.方差为:标准差为.于是,这组数据的极差、方差和标准差分别为50,334.69,18.29.例2若样本,,…,的平均数为10,方差为2,则对于样本,,…,,下列结论正确的是()(A)平均数为10,方差为2 (B)平均数为11,方差为3(C)平均数为11,方差为2 (D)平均数为12,方差为4解由已知条件,得故应选(C)说明此题充分应用了已知条件来进行整体计算,使运算十分简捷.例3 如图,公园里有两条石级路,哪条石级走起来更舒适?(图中数字表示每一级的高度,单位:厘米)解由于15+14+14+16+16+15=90,19+10+17+18+15+11=90,所以两条石级路总高度一样,都是90厘米;由于都是6个台阶,所以台阶的平均高度也一样,都15厘米.上台阶是否舒适,就看台阶的高低起伏情况如何,因此,需要计算两条石级路台阶高度的极差、方差和标准差.左边石级路台阶高度的极差为16-14=2,方差为:,标准差为;右边石级路台阶高度的极差为19-10=9,方差为:,标准差为.由以上计算可见,左边石级路的极差、方差和标准差都比右边小,所以左边石级路起伏小,走起来舒服些.例4要从甲、乙、丙三位射击运动员中选拔一名参加比赛,在预选赛中,他们每人各打10发子弹,命中的环数如下:甲:10 10 9 10 9 9 9 9 9 9 ;乙:10 10 10 9 10 8 8 10 10 8;丙:10 9 8 10 8 9 10 9 9 9 .根据这次成绩,应该选拔谁去参加比赛?分析本题着重考查对方差的意义及实际运用.解经计算,甲、乙、丙三人命中的总环数分别为93,93,91.所以丙应先遭淘汰.设甲、乙的命中环数分别为和,方差分别是和,则:.∵∴在总成绩相同的条件下,应选择水平发挥较稳定的运动员甲参加比赛.说明丙的总成绩显著,应先遭淘汰,然后利用方差的含义,来考查甲、乙二人成绩的稳定性.例5 小明和小华假期到工厂体验生活,加工直径为100毫米的零件,为了检验他们的产品的质量.从中各随机抽出6件进行测量,测得数据如下:(单位:毫米)小明:99 10 98 100 100 103小华:99 100 102 99 100 100(1)分别计算小明和小华这6件产品的极差、平均数与方差.(2)根据你的计算结果,说明他们两人谁加工的零件更符合要求.解(1)小明:极差=5,平均数=100,方差,小华:极差=3,平均数=100,方差=1.(2)计算结果说明,小明加工的零件极差大,方差也大,小华加工的零件极差小,方差小,所以小华加工的零件更符合要求。
(完整版)方差专项练习

极差、方差与标准差专项练习⑴极差极差=最大值-最小值.⑵方差:用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况,这个结果叫方差,通常用s 2来表示。
⑶标准差:标准差=⑷方差(或标准差)越大,,稳定性越小;反之,方差越小,稳定性越好.一、填空题1、数据-2,-1,3,1,2的方差是_________极差是 _______2、 七个数1,2,5,3,4,a ,3的平均数是3,则a =________,这七个数的方差是________。
3、若一组数据3,一1,a ,-3,3的平均数是a 的则这组数据的标准差是_________。
4、已知,一组数据1, 2,……,n 的平均数是10,方差是2, ①数据1+3, 2+3,……,n+3的平均数是 方差是 , ②数据2×1,2×2,……,2×n 的平均数是 方是 , ③数据2×1+3,2×2+3,……,2×n+3的平均数是 方差是 。
5、数据:2-,1-,0,x ,1的平均数是0,则x = .方差=2S .6、如果样本方差[]242322212)2()2()2()2(41-+-+-+-=x x x x S ,那么这个样本的平均数为 .样本容量为 .7、已知321,,x x x 的平均数=x 10,方差=2S 3,则3212,2,2x x x 的平均数为 ,方差为 .二、选择题:8、样本方差的作用是A 、估计总体的平均水平B 、表示样本的平均水平C 、表示总体的波动大D 、表示样本的波动大小,从而估计总体的波动大小9、一个样本的方差是0,若中位数是a ,那么它的平均数是A 、等于aB 、不等于 aC 、大于 aD 、小于a10、已知样本数据101,98,102,100,99,则这个样本的标准差是 A、0 B、1 C、2 D、211、如果给定数组中每一个数都减去同一非零常数,则数据的A、平均数改变,方差不变B、平均数改变,方差改变C、平均数不变,方差不变D、平均数不变,方差改变三、问答题:1、为了考察甲、乙两种农作物的长势,分别从中抽取了10株苗,测得苗高如下:(单位:mm)甲:9,10,11,12,7,13,10,8,12,8乙:8,13,12,11,10,12,7,7,9,11请你经过计算后回答如下问题:(1)哪种农作物的10株苗长的比较高?(2)哪种农作物的10株苗长的比较整齐?2. 从甲、乙两种农作物中各抽取1株苗,分别测得它的苗高如下:(单位:cm)甲:9、10、11、12、7、13、10、8、12、8;乙:8、13、12、11、10、12、7、7、9、11;问:(1)哪种农作物的苗长的比较高?(2)哪种农作物的苗长得比较整齐?3. 段巍和金志强两人参加体育项目训练,近期的5次测试成绩如4.甲、乙两名学生在相同的条件下各射靶10次,命中的环数如下:甲:7、8、6、8、6、5、9、10、7、4乙:9、5、7、8、7、6、8、6、7、7经过计算,两人射击环数的平均数相同,但S2甲 S2乙,所以确定去参加比赛。
极差、方差与标准差 边讲边练(含答案)-
极差、方差与标准差学习目标1.理解极差、方差、标准差可以用来表示一组数据的波动情况,•知道三个统计量各自的长处与不足.2.学会用极差、方差与标准差来处理数据.3.会用计算器(计算机)求方差和标准差.知识网络背景材料1.反映一组数据集中程度的指标有哪些?2.如何反映一组数据的离散程度?反映一组数据离散程度的量有哪些?3.什么是极差?什么是方差?什么是标准差?方差与标准差的关系是什么?预习反馈1.极差是___________,它反映了____________.2.方差是标准差的__________,如果一组数据的方差是3,那么它的标准差是_________.知识要点详解1.表示一组数据离散程度的指标(1)极差用一组数据中的最大数据减去最小的数据所得到的差来反映这组数据的变化范围,这个差就称为极差.(2)方差①定义一组数据中各数据与这组数据的平均数的差的平方和的平均数叫做这组数据的方差.②方差的意义方差是反映一组数据波动大小的量,它表示的是一组数据偏离平均值的情况上.方差越大,数据组的波动就越大.③方差的计算公式数据x1,x2,x3, …,x n的方差是S2=1n(x1-x)2+(x2-x)2+(x3-x)2+…+(x n-x)注意:①上面的计算公式是一般情况下计算方差的办法;②当数据组中的数据个数比较少且绝对值比较小时,又可以采用下面的公式来计算方差:S2=1n[(x12+x22+x32+…+x n2)-n x2]③如果数据组中的每一个数比较接近于常数a时,•也可以采用下面的公式计算方差:S=1n[(x`12+x`22+x`32+…+x`x n2)-n x`2](其中x1`、x2`、x3`……x n`分别等于x1-a、x2-a、x3-a……x n-a,•x`是数据组x1`、x2`、x3`……x n`的平均数)(3)标准差方差的算术平方根叫做标准差.标准差和方差一样,也是反映一组数据波动大小的指标.同样,标准差越大,数据组的波动就越大.触类旁通1.求数据组9、10、11、12的方差.2.若小明参加体育项目训练近期的5次测试成绩为13、14、13、12、13.求测试成绩的极差、标准差和方差.典型例题例1 计算下面两组数据的方差(1)-1 2 -2 3 -1(2)40 38 42 45 41 39分析:第(1)组数据的绝对值比较小,可以利用公式②计算方差;第(2)•题中的数据比较接近于40,可以利用公式③计算方差.解:(1)平均数为:(-1+2-2+3-1)÷5=0.2,方差为:15[(-1)2+22+(-2)2+(-1)2+32-5×0.22]=3.76.(2)原数据组中的每一个数都减去40,得:0 -2 2 5 1 -1新数据组的平均数为:16(0-2+2+5+1-1)=56.方差是:16[02+(-2)2+22+52+12+(-1)-6×(56)2]≈5.14例2 八(1)班在一次单元测验中的数学成绩如下:83 74 81 50 87 92 75 94 87 92 83 77 74 70 80 9178 66 92 89 93 89 87 86 78 89 75 86 78 49 86 7592 79 90 75 72 99 80 76 88 84 79 80 82 84 85 9983 90 82 88 70 90 79 88 63 73 91 63 68请你计算出该班数学成绩的平均分、方差与标准差.分析:这里的数据比较多,我们可以采用计算器或计算机来计算平均数、方差、标准差.注意操作方法要正确.答案:该班数学成绩的平均分约为82.3,方差约为101.5,标准差约为10.1.例3 为了考察两种优质玉米良种的生长情况,在相同时间里把它们种在同一块实验田里,经过一段时间后,分别抽取了其中10株幼苗,测得苗高如下(单位:厘米):甲:12 8 7 13 9 10 11 9 12 11乙:11 9 12 7 13 8 7 10 12 9分析:要判断哪种玉米长得整齐,显然就是看哪种玉米高度波动较小,•因此我们可计算方差来解决这个问题.解:甲种玉米的平均高度:(12+8+7+13+9+10+11+9+12+11)÷10=10.2(厘米);•乙种玉米的平均高度是:(11+9+12+7+13+8+7+10+12+9)÷10=9.8(厘米).S甲2=110(122+82+72+132+92+102+112+92+122+112-10×10.22)=3.36S乙2=110(112+92+122+72+132+82+72+102+122+92-10×9.82)=4.16S甲2<S乙2,所以甲种玉米的幼苗长得比较整齐.变式练习1.小明和小刚要去参加一项比赛,近5次他们的测验成绩如下:你认为该选谁去?2.计算数据组:25 23 27 26 24 22 24 28 23 21的方差.3.为了从甲、乙两名学生中选拔一人参加电脑知识竞赛,•在相同条件下对他们的电脑知识进行了10次测验,成绩如下:(单位:分)甲:76 84 90 86 81 87 86 82 85 83 乙:82 84 85 89 79 80 91 89 74 79 回答下列问题:(1)甲学生成绩的众数是______(分),乙学生成绩的中位数是_____(分);(2)若甲学生成绩的平均数是x甲,•乙学生成绩的平均数是x乙,•则x甲与x乙的大小关系是:_________;(3)经计算知:S甲2=13.2,S乙2=26.36,这表明____________________________;(用简明的文字语言表述)(4)若测验分数在85分(含85分)以上为优秀,则甲的优秀率为________;•乙的优秀率为________.误区警示解析1.混用极差与方差.例1数据A:1 6 4 3 4;数据B:2 6 6 2 3.哪一组数据更稳定?错解:数据组A的极差是6-1=5,数据组B的极差是6-2=4,所以数据组B更稳定.错因分析:极差只能描述一组数据的波动范围,并不能准确地描述一组数据的波动情况,方差才能够描述出一组数据的波动情况.所以计算出方差,根据方差大,波动就大来作出判断.正解:∵S A2=2.64,S B2=3.36,∴S A2<S B2.所以数据组A更稳定.2.将标准差当作方差的平方根.例2 判断语句是否正确标准差的平方等于方差,方差是标准差的平方根.错解:正确.错因分析:没有正确掌握标准差的概念,先有方差,再有标准差.标准差是方差的算术平方根,而非平方根.正解:错误.活学活用甲、乙两台包装机同时分装质量为400g的奶粉,•从它们各自分装的奶粉中随机抽取了10袋,测得它们的实际质量(单位:克)如下:甲:401 400 408 406 410 409 400 393 394 394乙:403 404 396 399 402 401 405 397 402 399试问:哪台包装机包装的奶粉质量比较稳定?历年考题回顾例1 (2005年常州)小明同学参加某体育项目训练,近期的五次测试成绩得分情况如图所示:试分别求出五次成绩的平均数和方差.分析:观察折线图,知道小明同学五次测试成绩如:10 13 12 14 16,根据平均数和方差的计算公式分别计算出平均数和方差.答案:五次成绩的平均数是13分,方差是4.例2(2005福建)张老师为了从平时在班级里数学成绩比较优秀的王军、•张成两位同学中选拔一人参加“全国初中数学联赛”,对两位同学进行了辅导,•并在辅导期间进行了10次测验,两位同学测验成绩记录如下:王军10次成绩分别是:•68 •8078 79 81 77 78 84 83 92;张成10次成绩分别是:86 80 75 83 85 77 •79 •80 •8075.利用提供的数据,解答下列问题:(1)填写完成下表:2=33.2,•请你(2)张老师从测验成绩记录表中,求得王军10次测验成绩的方差S王2;帮助张老师计算张成10次测验成绩的方差S张(3)请你根据上面的信息,运用所学的统计知识,帮助张老师做出选择,并简要说明理由.分析:从题中数据不难得出众数和中位数,计算张成10次测验成绩的方差可以先将这10个数据都减去80计算方差.张老师应该选择成绩稳定的同学去,所以比较它们方差的大小.答案:(1)王军成绩的众数是78,张成成绩的中位数是80;(2)S张2=13;(3)•张老师应该选择张成去.因为张成10次成绩的方差较小,也就是说他的成绩波动小,•所以应该选择他去.例3 (2005年沪州)一组数据:2,-2,0,4的方差是_________.分析:这里的数据都比较小,所以可以用公式②计算方差,不过要先计算平均数.答案:5点石成金在中考中,重点考查本节的知识点是方差,所以掌握方差的计算办法(记住方差计算公式)是关键,•在明白方差意义的基础上能够运用方差解决一些简单的实际问题.全真模拟1.三明中学初三(1)班篮球队有10名队员,在一次投篮训练中,这10•名队员各投篮50次的进球情况如下表:针对这次训练,请解答下列问题:(1)求这10名队员进球数的平均数、中位数和众数;(2)求这支球队整体投篮命中率;(投篮命中率=进球数投篮次数×100%)(3)若队员小华的投篮命中率为40%,•请你分析一下小华在这支球队中的投篮水平.2.某职业中学为选派一名学生参加全市实践活动技能竞赛,A、B•两位同学在学校实习基地现场进行加工直径为20mm的零件的测试,他俩各加工的10•个零件的相关数据依次如下图表所示(单位:mm)(其中虚线表示A同学,实线表示B同学)根据测试得到的有关数据,试解答下列问题:(1)考虑平均数与完全符合要求的个数,你认为________的成绩好些?(2)计算出S B2的大小,考虑平均数与方差,说明谁的成绩好些;(3)考虑图中折线走势及竞赛中加工零件个数远远超过10个的实际情况,你认为派谁去参赛较合适?说明你的理由.3.甲、乙两班举行汉字输入比赛,•参赛学生每分钟输入汉字的个数经统计计算后,填入下表:分析此表得出如下结论:()(1)甲、乙两班学生成绩的平均水平相同;(2)乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字150个为优秀)(3)甲班学生成绩的波动情况比乙班成绩波动大.A.(1)(2) B.(1)(2)(3) C.(2)(3) D.(1)(3)答案:预习反馈1.数据中最大数据与最小数据的差,一组数据的波动范围;2触类旁通1.解:计算每个数据与10的差,分别是:-1、0、1、2,计算新数据组的平均数:14(-1+0+1+2)=0.5.计算方差:S2=14[(-1)2+02+12+22-4×0.52]=1.252.解:极差:14-12=2.α=15(13+14+13+12+13)=13方差:S2=15[(13-13)2+(14-13)2+(13-13)2+(12-13)2+(13-13)2]=0.4变式练习1.解:我们一般采用方差来判断数据组,小明成绩的方差是0.4,小刚成绩的方差是4,显然小刚的成绩不够稳定,应该小明去.[点拨]我们常常使用方差来判断一组数据是否稳定,方差越大,数据波动就越大.2.解:(1)原数据组的每一个数都减去25得:0 -2 2 1 -1 -3 -1 3 -2 -4.(2)新数据组的平均数是(0-2+2+1-1-3-1+3-2-4)÷10=-0.7.(3)方差为:S2=110[02+(-2)2+22+12+(-1)2+(-3)2+(-1)2+3+(-2)2+(-4)2-10×(-0.7)2]=4.41.3.解:(1)86,83;(2)x甲<x乙[点拨]:∵x甲=84,x乙=83.2,∴x甲<x乙.(3)∵S甲2<S乙2,∴甲的成绩更稳定;(4)50%,40%.活学活用1.解:S甲2=38.05,S乙2=7.96.因为S甲2>S乙2,所以乙包装机包装的奶粉质量比较稳定.全真模拟1.(1)22,19,19和15,(2)44%,(3)从表格中的数据看,命中率在40%以上的有4人,所以它在这支球队中从命中率的角度看是中等偏上的.2.(1)经计算A的平均数为20,B的平均数不足20,但A符合要求的有2个,B•符合要求的有4个,所以B的成绩好些.(2)S B2=0.008225,S A2=0.026,所以B的成绩要好些.(3)通过图表和上面的计算,B同学的成绩要稳定得多,所以应选B去参加比赛.3.B。
九年级数学上册 第二章 数据的离散程度 2.2 方差与标准差训练题 苏科版
第二章 数据的离散程度【知识回顾】1.描述一组数据的离散程度(即波动大小)的量:等。
2.极差:(1)极差计算公式:。
注意:极差越小,这组数据的离散程度(即波动大小)就越 ,这组数据就越。
(2)用极差来衡量一组数据的离散程度(即波动大小)的优缺点:(回忆) 3.方差(或标准差): (1)方差计算公式:; 标准差计算公式:。
注意:①方差的单位是;而标准差的单位是。
②方差(或标准差)越小,这组数据的离散程度(即波动大小)就越 ,这组数据就越。
③两组数据比较时,一组数据的极差大,这组数据的方差(或标准差)不一定...就大! (2)填表:样本平均数方差标准差1x , 2x ,3x ,4x ,5x ,… , n x x2SSa x +1, a x +2,… , a x n + 1kx , 2kx , 3kx ,4kx ,… , n kx a kx +1, a kx +2,… , a kx n +(3)区分“二选一”和“对二者做出评价”这两类题型的回答的不同:(回忆) 【基础训练】一、选一选,看完四个选项再做决定(每小题3分,共24分)1.某住宅小区六月份中1日至6日每天用水量变化情况如图所示,那么这6天用水量的极差是()A.7B.9 C2.小伟五次数学考试成绩分别为:86分,78分,80分,85分,92分,李老师想了解小伟数学学习变化情况,则李老师最关注小伟数学成绩的()100米短跑进行5次测试,他们的成绩通过计算得;x甲=x乙,S2甲=0.025,S2乙=0.026,下列说法正确的是()4. 样本方差的计算式S2=120[(x1-30)2+(x2-30)]2+…+(x n-30)2]中,数字20和30分别表示样本中的()A.众数、中位数B.方差、标准差C.样本中数据的个数、平均数D.样本中数据的个数、中位数5. 一组数据的方差为S2,将该数据每一个数据,都乘以2,所得到的一组新数据的方差是()A.22S2 C.2 S2 D.4 S26. 观察图中两组数据的折线图,你认为下列说法中正确的是( )A.离散程度较大的是甲组数据C.甲、乙两组数据离散程度一样大7.在2,3,4,5,x五个数据中,平均数是4,那么这组数据的方差是()A.2B.10 2108.在学校对学生进行的晨检体温测量中,学生甲连续10天的体温在36℃的上下波动数据为:0.2, 0.3, 0.1, 0.1, 0, 0.2, 0.1, 0.1, 0.1, 0,则对这10天中该学生的体温波动数据分析不正确的是( )0.1 C二、填一填,要相信自己的能力(每题3分,共24分)1.若一组数据1、2、3、x的极差是6,则x的值为.2. 数据8,9,10,11,12的方差S2为.3.甲、乙、丙三台包装机同时分装质量为400克的茶叶.从它们各自分装的茶叶中分别随机抽取了10盒,测得它们的实际质量的方差如下表所示:根据表中数据,可以认为三台包装机中,包装机包装的茶叶质量最稳定。
初三数学极差、方差、标准差

【知识点】
(1)极差是用来反映一组数据变化范围的大小.一组数据中的最大数据与最小数据所得的
差来称为极差;
(2)方差记作 S 2
1 n
[(
x1
x)2
(x2
x)2
(xn
x)2 ]
;在实际应用时常常将求出
的方差 算术平方根,这就是标准差.
【例题】
1、(2016 广西百色)一组数据 2,4,a,7,7 的平均数 x =5,则方差 S2=
C.甲和乙一样稳定
D.甲、乙稳定性没法对比
3、下面是甲、乙两人 10 次射击成绩(环数)的条形统计图,则下列说法正确的是( )
A.甲比乙的成绩稳定 C.甲、乙两人的成绩一样稳定
B.乙比甲的成绩稳定 D.无法确定谁的成绩更稳定
4.已知 A 样本的数据如下:72,73,76,76,77,78,78,78,B 样本的数据恰好是 A 样
A.平均数 3
B.众数是﹣2
C.中位数是 1
D.极差为 8
2.在一次射击训练中,甲、乙两人各射击 10 次,两人 10 次射击成绩的平均数均是 9.1 环, 方差分别是 S 甲 2=1.2,S 乙 2=1.6,则关于甲、乙两人在这次射击训练中成绩稳定的描述正确 的是( )
A.甲比乙稳定
B.乙比甲稳定
本数据每个都加 2,则 A,B 两个样本的下列统计量对应相同的是( )
A.平均数
B.标准差
C.中位数
D.众数
【练习解析】
1、【答案】D.
2、【答案】A 【解析】根据方差的意义可作出判断.方差是用来衡量一组数据波动大小的量,方差越小, 表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
极差、方差标准差测试题(含答案)

极差、方差标准差测试题一、选择题:(每小题3分,共18分)1.若数据2,x,4,8的平均数是6,则该组数据的极差是().A.4 B.6 C.8 D.102.观察图形,下列结论中不正确的是().A.a组数据的极差较大B.a组数据的方差较大C.b组数据比较稳定D.b组数据的标准差较大3.甲乙两中学生在一年里学科平均分相等,但他们的方差不相等,能正确评价他们学习情况的是().A.因为他们的平均分相等,所以学习水平一样B.表面上看这两个学生平均成绩一样,但方差小的学习成绩稳定C.成绩虽然一样,方差较大的,说明潜力大,学习态度踏实D.平均分相等,方差不等,说明学习的方法不一样,但效果一样4.一个样本有10个数据,各数据与样本平均数的差依次是-4,5,-2,4,-1,3,2,0,-2,-5,那么这个样本的方差是().A.0 B.3.2 C.10.4 D.1045.某工厂为了选拔1名车工参加加工直径为10mm的精密零件的技术比赛,随机抽取甲、乙两名车工加工的5个零件,现测得的结果如下表,请你用计算器比较S 2甲、S 2乙的大小().A.S 2甲>S 2乙B.S 2甲=S 2乙C.S 2甲<S 2乙D.S 2甲≤S 2乙6.已知一组数据x1、x2、x3、x4、x5的平均数是2,方差是1,那么另一组数据:10 x1-2、10 x2-2、10 x3-2、10 x4-2、10 x5-2的平均数和方差分别是().A.2、1 B.18、1 C.2、100 D.18、100二、填空题:(每小题4分,共24分)7. 一组数据:1,-2,0,4的极差为______________.8.小明在计算某组数据的方差时列式22221281[( 1.5)( 1.5)( 1.5)]8S x x x=-+-+⋅⋅⋅+-,那么该组数据的平均数是.9.甲乙两人进行射击比赛,他们在相同条件下各射击10 次,平均成绩均为7 环,10 次射击成绩的方差分别是:3S2=甲,2.1S2=乙.成绩较为稳定的是__________.(填“甲”或“乙”)10. 计算样本1,2,2,-3,3的方差为____________.11.数据3,2,1,0,-1的标准差S= .12.甲、乙、丙三台机床生产直径为60mm的螺丝,为了检验产品质量,从三台机床生产的螺丝中各抽查了20个测量其直径,进行数据处理后,发现这三组数据的平均数都是60mm,它们的方差依次为S2甲=0.162,S2乙=0.058,S2丙=0.149.根据以上提供的信息,你认为生产螺丝质量最好的是__ __机床.三、解答题(本题5个小题,共55分)13.(本题满分10分)甲、乙两位同学五次数学测验成绩如下表:请你在表中的空白处填上适当的数,用学到的统计知识对两位同学的成绩进行分析,并写出一条合理化建议.14.(本题满分10分)甲、乙两名车工都加工要求尺寸是直径10mm的零件.从他们所生产的零件中,各取5件,测得直径如下(单位:mm)甲:10.05 10.02 9.97 9.95 10.01乙:9.99 10.0210.02 9.98 10.01分别计算两组数据的标准差(精确到0.01),说明在尺寸符合规格方面,谁做得较好?15.(本题满分10分)将10盒同一品种的花施用甲、乙两种花肥,随意分成两组,每组5 盆,其花期的记录结果如下(单位:天).(1)施用哪种花肥,使得花的平均花期较长?(2)施用哪种保花肥效果比较可靠?16.(本题满分12分)(1)计算下列各组数据的方差:①2、3、4、5、6;②12、13、14、15、16;③102、103、104、105、106;④20、30、40、50、60.(2)将其他各组的方差与第一组进行比较,你有何发现?(写一条即可)17.(本题满分13分)张阿姨下岗后开了一个牛奶销售店,主要经营“学生奶”、“酸牛奶”、“原味奶”.可张阿姨由于经验不足,经常有的牛奶没卖完,有的牛奶又不够卖,一段时间下来,通过盘点不但没有挣钱反而亏损了.热心的小红结合所学的统计知识帮张阿姨统计了一个星期牛奶的销售情况,并绘制了下表:(1)计算各品种牛奶的日平均销售量,并说明哪种牛奶销量最高?(2)计算各品种牛奶的方差(保留两位小数),并比较哪种牛奶销量最稳定?(3)假如你是小红,你对张阿姨有哪些好的建议.四、扩广探索(本题20分)18.第一次月考中,A、B、C、D、E五位同学的数学、英语成绩等有关信息如下表所示:(1)求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是标准分=(个人成绩-平均成绩)÷成绩标准差,从标准分看,标准分大的考试成绩更好,请问A同学在第一次月考中,数学与英语哪个学科考得更好.极差、方差标准差测试题参考答案一、选择题:二、填空题:7.6;8.1.5;9.乙;10.4.4;1112.乙. 三、解答题13.解:甲平均数:85,方差53.2;乙平均数85,方差70.4;从上述数据看乙同学数学成绩不稳定,波动较大,应在数学学习上多下功夫,加强能力训练. 14.解:甲组标准差是0.04,乙组标准差是0.02,0.04>0.02∴乙组做得较好. 15.解:(1)施用两种花肥的平均花期一样长;(2)∵S 2甲=5.2,S 2乙=2.8,∴施用乙种花肥的效果更可靠一些. 16.解:(1)①S 12=2,②S 22=2,S 32=2,S 42=200;(2)第一组数据中,每个数据分别加上10就变成了第二组数据,并且它的方差不变,若分别加上100就成了第三组数据,其方差仍然为2,但是如果将第一组数据扩大10倍变成了第四组数据,其方差变为原来的102倍.17.解:(1)∵3,80,40,x x x ===学生奶酸牛奶原味奶 ∴酸牛奶的销量最高;(2)∵S 2学生奶=12.57,S 2酸牛奶=92.86,S 2原味奶=96.86,∴学生奶的销量最稳定;(3)建议张阿姨学生奶平常尽量少进或不进,周末适当进一点. 四、拓广探索18.解:(1)数学考试成绩的平均分70, 英话考试成绩的标准差6;(2)设A 同学数学考试成绩标准分为P 数学,英语考试成绩标准分为P 英语,则P 数学=(71-702,P 英语=(88-85)÷6=0.5,∵P 数学>P 英语, ∴从标准分看,A 同学数学比英语考得更好.。
九年级数学上册极差、方差、标准差复习题 试题

蠡园中学九年级数学上册?极差、方差、HY 差?复习苏科版制卷人:打自企; 成别使; 而都那。
审核人:众闪壹; 春壹阑; 各厅…… 日期:2022年二月八日。
〔一〕新课概念1.极差:我们可以用一组数据中的__________减去__________所得的差来反映这组数据的变化范围.用这种方法得到的差称为________.2.方差:方差实际上是一种表示一组数据的_________的量,我们可以用“先平均,_________, 然后_________,最后再________〞的方法得到.3.HY 差:与方差有什么关系? 这二者与原数据在单位上有什么关系? . 4.反映数据离散程度的指标是 . 〔二〕课后作业1.下表给出了05年5月28日至6月3日的最高气温,那么这些最高气温的极差是_____℃.2.〔〔2〕假设样本1,2,3,x 的平均数为5,又样本1,2,3,x ,y 的平均数为6,那么样本1,2,3,x ,y 的极差是_______,方差是_______,HY 差是______.3.〔1〕一组数据0,1,2,3,4的方差为2,那么数据20,21,22,23,24的方差为_____,• HY 差为________.〔2〕321,,x x x 的平均数=x 10,方差=2S 3,那么3212,2,2x x x 的平均为 ,方差为.4.利用计算器求一组数据的方差和HY差:78,84,98,92,66,77,75,80,79,815.为了考察甲、乙两种农作物的长势,分别从中抽取了10株苗,测得苗高如下:〔单位:mm〕甲:9,10,11,12,7,13,10,8,12,8乙:8,13,12,11,10,12,7,7,9,11请你经过计算后答复如下问题:〔1〕哪种农作物的10株苗长的比拟高?〔2〕哪种农作物的10株苗长的比拟整齐?6.某校要从甲、乙两名跳远运发动中挑选一人参加一项校际比赛.在最近的10次选拔赛中,他们的成绩〔单位:cm〕如下:甲:585 596 610 598 612 597 604 600 613 601乙:613 618 580 574 618 593 585 590 598 624〔1〕他们的平均成绩分别是多少?〔2〕他们的极差分别是多少?〔3〕甲、乙这10次比赛成绩的方差分别是多少?〔4〕这两名运发动的运动成绩各有什么特点?12 35 689 10 11 12(月份〕29 10 11 12(月份〕7.某公司为了评价甲、乙两位营销员去年的营销业绩,统计了这两人去年12个月的营销业绩〔所推销甲 乙〔1〕利用图中信息,完成下表:〔2〕假假设你是公司主管,请你根据〔1〕中图表信息,应用所学的统计知识,对两人的营销业绩作出评价.8.体校准备挑选一名跳高运发动参加全中学生运动会,对跳高运动队的甲、乙两名运发动进展了8次选拔比赛.他们的成绩〔单位:m 〕如下:甲:1.70 1.65 1.68 1.69 1.72 1.73 1.68 1.67乙:1.60 1.73 1.72 1.61 1.62 1.71 1.70 1.75〔1〕甲、乙两名运发动的跳均成绩分别是多少?〔2〕哪位运发动的成绩更为稳定?〔3〕假设预测,跳过1.65m就很可能获得冠HY,该校为了获得冠HY,可能选哪位运发动参赛?假设预测跳过1.70m才能得冠HY呢?9.某校初三〔1〕班、〔2〕班各有49名学生,两班在一次数学测验中的成绩统计如下表:班级平均分众数中位数HY差一班79 70 87二班79 70 79〔1〕请你对下面的一段话给予简要分析:初三〔1〕班的小刚回家对妈妈说:“昨天的数学测验,全班平均79分,得70分的人最多,我得了85分,在班里可算上游了!〞〔2〕请你根据表中数据,对这两个班的测验情况进展简要分析,并提出教学建议.10.王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活98%.现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示.〔1〕分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;〔2〕试通过计算说明,哪个山上的杨梅产量较稳定?11.一次期中考试中,A、B、C、D、E五位同学的数学、英语成绩等有关信息如下表所示:〔单位:分〕A B C D E 平均分 HY差数学 71 72 69 68 70〔1〕求这五位同学在本次考试中数学成绩的平均分和英语成绩的HY差;〔2〕为了比拟不同学科考试成绩的好与差,采用HY分是一个合理的选择,HY分的计算公式是:HY分=〔个人成绩一平均成绩〕÷成绩HY差.从HY分看,HY分大的考试成绩更好.请问A同学在本次考试中,数学与英语哪个学科考得更好?12.甲、乙两人在一样的条件下各射靶5次,每次射靶的成绩情况如下图.〔1〕请你根据图中的数据填写上下表:姓名平均数〔环〕众数〔环〕方差甲乙〔2〕从平均数和方差相结合看,分析谁的成绩好些.制卷人:打自企;成别使;而都那。
初中数学极差和方差测试5

测试5 极差和方差(一)学习要求了解极差和方差的意义和求法,体会它们刻画数据波动的不同特征.课堂学习检测一、填空题1.一组数据100,97,99,103,101中,极差是______,方差是______.2.数据1,3,2,5和x 的平均数是3,则这组数据的方差是______.3.一个样本的方差[(x 1-3)2+(x 2-3)2+…+(x n -3)2],则样本容量是______,样本平均数是______.二、选择题4.一组数据-1,0,3,5,x 的极差是7,那么x 的值可能有( ).(A)1个 (B)2个 (C)4个 (D)6个5.已知样本数据1,2,4,3,5,下列说法不正确的是( ).(A)平均数是3(B)中位数是4 (C)极差是4 (D)方差是2三、解答题6.甲、乙两组数据如下:甲组:10 9 11 8 12 13 10 7;乙组:7 8 9 10 11 12 11 12.分别计算出这两组数据的极差和方差,并说明哪一组数据波动较小.1212 s7.为检测一批橡胶制品的弹性,现抽取15条皮筋的抗拉伸程度的数据(单位:牛):5 4 4 4 5 7 3 3 5 56 6 3 6 6(1)这批橡胶制品的抗拉伸程度的极差为______牛;(2)若生产产品的抗拉伸程度的波动方差大于1.3,这家工厂就应对机器进行检修,现在这家工厂是否应检修生产设备?通过计算说明.综合、运用、诊断一、填空题8.随机从甲、乙两块试验田中各抽取100株麦苗测量高度,计算平均数和方差的结果:=13,=13,=3.6,=15.8,则小麦长势比较整齐的试验田是______.9.把一组数据中的每个数据都减去同一个非零数,则平均数______,方差______.(填“改变”或“不变”)二、选择题10.关于数据-4,1,2,-1,2,下面结果中,错误的是( ).(A)中位数为1 (B)方差为26(C)众数为2 (D)平均数为011.某工厂共有50名员工,他们的月工资方差是s2,现在给每个员工的月工资增加200元,那么他们的新工资的方差( ).(A)变为s2+200 (B)不变(C)变大了(D)变小了12.数据-1,0,3,5,x的极差为7,那么x等于( ).(A)6 (B)-2 (C)6或-2 (D)不能确定三、解答题13.甲、乙两个组各10名同学进行英语口语会话测试,每个人测试5次,每个同学合格的次数分别如下:甲组:4 1 2 2 1 3 3 1 2 1;乙组:4 3 0 2 1 3 3 0 1 3.(1)如果合格3次以上(含3次)为及格标准,请你说明哪个小组的及格率高;(2)请你比较两个小组口语会话的合格次数谁比较稳定.测试5 极差和方差(一)1.6;4. 2.2. 3.12;3. 4.B. 5.B.6.甲组的极差是6,方差是3.5;乙组的极差是5,方差是3;说明乙组的波动较小.7.(1)4;(2)方差约是1.5,大于1.3,说明应该对机器进行检修.8.甲. 9.改变;不变. 10.B. 11.B. 12.C.13.(1)甲组及格率是30%,乙组及格率是50%,乙组及格率高;(2)=2,=2,=1,=1.8,甲组更稳定.。
专题17方差极差标准差综合题(原卷版)

专题17 方差、极差、标准差(综合题)知识点:极差、方差和标准差1.极差一组数据中 ,称为极差,极差= 细节剖析:极差是 ,它受 的影响较大.一组数据极差越小,这组数据就越 2.方差方差是 .方差的计算公式是:,其中,是,,…的 细节剖析:(1)方差反映的是一组数据 的情况.方差越大,数据的 越大;方差越小,数据的波动 .(2)一组数据的每一个数都 同一个常数,所得的一组新数据的方差 (3)一组数据的每一个数据都变为原来的倍,则所得的一组新数据的方差变为原来的倍. 3.标准差方差的算术平方根叫做这组数据的标准差,用符号表示,即:;标准差的数量单位与原数据一致.4.极差、方差和标准差的联系与区别联系:极差与方差、标准差都是表示 .区别:极差表示 ,它受 的影响较大;方差反映了 .方差越大,稳定性也 ;反之,则稳定性 .所以一般情况下只求 用极差,在考虑到 时用方差.2s ()[]222212)(...)(1x x x x x x nS n -++-+-=x 1x 2x n x k 2k s 易错点拨易错题专训一.选择题1.(2021秋•汝州市期末)描述一组数据的离散程度,我们还可以用“平均差”.在一组数x1、x2、x3、…、x n中,各数据与它们的平均数x的差的绝对值的平均数,即T=(|x1﹣x|+|x2﹣x|+…+|x n﹣x|)叫做这组数据的“平均差”.“平均差”也能描述一组数据的离散程度,“平均差”越大说明数据的离散程度越大,稳定性越小.现有甲、乙两组数据,如表所示,则下列说法错误的是()甲12 13 11 15 13 14乙10 16 10 18 17 7 A.甲、乙两组数据的平均数相同B.乙组数据的平均差为4C.甲组数据的平均差是2D.甲组数据更加稳定2.(2021秋•青羊区期末)甲、乙、丙、丁四人进行射击测试,他们在相同条件下各射击10次,成绩(单位:环)统计如表:甲乙丙丁平均数9.7 9.6 9.6 9.7方差0.25 0.25 0.27 0.28如果从这四人中,选出一位成绩较好且状态稳定的选手参加比赛,那么应选()A.甲B.乙C.丙D.丁3.(2022春•定海区期末)若一组数据x1+1,x2+1,…,x n+1的平均数为17,方差为2,则另一组数据x1+2,x2+2,…,x n+2的平均数和方差分别为()A.17,2 B.18,2 C.17,3 D.18,34.(2021秋•历下区期中)在2020东京奥运会女子10米气步枪的项目中,杨倩以251.8环的好成绩一举夺冠,为中国体育代表团斩获奥运首金.现将决赛淘汰阶段中国选手杨倩每一轮(两轮之和)的数据进行汇总,并进行一定的数据处理作出以下表格.姓名第1轮第2轮第3轮第4轮第5轮第6轮第7轮总计杨倩20.9 21.7 21.0 20.6 21.1 21.3 20.5 147.1 根据表格信息可以得到杨倩在决赛淘汰阶段成绩的极差和中位数分别为多少()A.1.1,20.6 B.1.2,20.6 C.1.2,21.0 D.1.1,21.35.(2020秋•泰山区期末)甲,乙两个班参加了学校组织的“国学小名士”国学知识竞赛选拔赛,他们成绩的平均数、中位数、方差如下表所示,规定成绩大于等于95分为优异,则下列说法正确的是()参加人数平均数中位数方差甲40 93 92 5.2乙40 93 94 4.7 A.甲、乙两班的平均水平相同B.甲、乙两班竞赛成绩的众数相同C.甲班的成绩比乙班的成绩稳定D.甲班成绩优异的人数比乙班多6.(2021•天心区模拟)去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了10棵,每棵产量的平均数(单位:千克)及方差S2(单位:千克2)如下表所示.今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植,应选的品种是()甲乙丙丁24 24 23 20S2 1.9 2.1 2 1.9 A.甲B.乙C.丙D.丁二.填空7.(2021秋•开江县期末)某班有50人,一次数学测试后,老师对测试成绩进行了统计.由于小颖没有参加此次集体测试,因此计算其他49人的平均分为92分,方差s2=23.后来小颖进行了补测,成绩是92分,则该班50人的数学测试成绩的方差(填“变小”、“不变”、“变大”).8.(2021秋•福田区期末)新兴农场果农随机从甲、乙、丙三个品种的枇杷树中各选10棵,每棵产量的平均数(单位:千克)及方差(单位:千克2)如下表所示,他准备从这三个品种中选出一种产量既高又稳定的枇杷树进行种植,则应选的品种是.甲乙丙44 44 42S2 1.7 1.5 1.7 9.(2021秋•巨野县期末)在对一组样本数据进行分析时,小华列出了方差的计算公式:S2=,由公式提供的信息,①样本的容量是4,②样本的中位数是3,③样本的众数是3,④样本的平均数是3.5,则说法错误的是(填序号)10.(2022春•黄陵县期末)甲、乙两地6月上旬的日平均气温如图所示,则甲、乙两地这10天日平均气温的方差大小关系为S甲2S乙2(填>或<)11.(2021秋•莱州市期中)跳远运动员李强在一次训练中,先跳了6次的成绩如下:7.6,7.8,7.7,7.8,8.0,7.9(单位:m).这六次成绩的平均数为7.8,方差为.如果李强再跳两次,成绩分别为7.6,8.0,则李强这8次跳远成绩与前6次的成绩相比较,其方差.(填“变大”、“不变”或“变小”)12.(2021秋•海曙区校级期末)已知一组数据的方差s2=[(x1﹣6)2+(x2﹣6)2+(x3﹣6)2+(x4﹣6)2],那么这组数据的总和为.三.解答题13.(2021秋•中牟县期末)为增强防疫意识,某初中在元旦举行了疫情防控知识竞赛活动,现从本校甲、乙两班中各随机抽取10名同学的测试成绩进行整理、描述和分析,如图所示:班级平均数/分中位数/分众数/分方差乙班83.7 82 46.21甲班83.7 86 13.21 请将乙班学生成绩按从小到大的顺序写在横线上.(1)两组数据的平均数、中位数、众数、方差如上表所示,请补充完整.(2)根据上述数据,请从两个不同角度评价甲班与乙班掌握防疫知识的情况.14.(2021秋•平顶山期末)某校为了改善学生伙食,准备午餐为学生提供鸡腿.现有A、B两家副食品厂可以提供规格为75g的鸡腿,而且它们的价格相同,品质也相近.质检人员分别从两家随机各抽取10个,记录它们的质量(单位:g)如下:A加工厂74 74 74 75 73 77 78 72 76 77B加工厂78 74 77 73 75 75 74 74 75 75并对以上数据进行整理如下:平均数中位数众数方差A加工厂a74.5 c 3.4B加工厂75 b75 2根据以上分析,回答下列问题:(1)统计表中a=;b=;c=;(2)根据以上信息估计B加工厂加工的100个鸡腿中,质量为75g的鸡腿有多少个?(3)如果考虑鸡腿的规格,学校应该选购哪家加工厂的鸡腿?说明理由.15.(2021秋•渭城区期末)某学校从九年级同学中任意选取40人,平均分成甲、乙两个小组进行“引体向上”体能测试,根据测试成绩绘制出如下的统计表和统计图(成绩均为整数,满分为10分).甲组成绩统计表成绩7 8 9 10人数 1 9 5 5 请根据上面的信息,解答下列问题:(1)m=,甲组成绩的众数是,乙组成绩的中位数是;(2)已知甲组成绩的方差s=0.81,求出乙组成绩的方差,并判断哪个小组的成绩更加稳定?16.(2021秋•乾县期末)某中学开展“唱歌”比赛活动,八(1),八(2)班各选出5名选手参加复赛,5名选手的复赛成绩(满分为100分),如图所示:(1)根据图示填写下表:班级中位数/分众数/分八(1)班85八(2)班100 (2)通过计算得知八(2)的平均成绩为85分,请计算八(1)的平均成绩.(3)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好.(4)经计算八(1)班复赛成绩的方差为70,请计算八(2)班复赛成绩的方差,并说明哪个班学生的成绩比较稳定.17.(2021秋•新民市期末)某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.(1)根据图示填写下表:平均数/分中位数/分众数/分A校85B校85 100(2)结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;(3)计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.18.(2022春•宁武县期末)市体校射击队要从甲、乙两名射击队员中挑选一人参加省级比赛,因此,让他们在相同条件下各射击10次,成绩如图所示.为分析成绩,教练根据统计图算出了甲队员成绩的平均数为8.5环、方差为1.05,请观察统计图,解答下列问题:(1)先写出乙队员10次射击的成绩,再求10次射击成绩的平均数和方差;(2)根据两人成绩分析的结果,若要选出总成绩高且发挥稳定的队员参加省级比赛,你认为选出的应是,理由是:.19.(2021秋•驻马店期末)某校八年级学生开展踢毽子比赛活动,每班派5名学生参加.按团体总分多少排列名次,在规定时间每人踢100个以上(含100个)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个),经统计发现两班总分相等,此时有学生建议,可通过考查数据中的其他信息作为参考.请你回答下列问题:1号2号3号4号5号总分甲班100 98 110 89 103 500乙班86 100 98 119 97 500(1)根据上表提供的数据填写下表:班级参加人数优秀率中位数方差甲 5乙 5(2)根据以上信息,你认为应该把冠军奖状发给哪一个班级?简述理由.20.(2021•锡林浩特市校级模拟)我市某中学举办“网络安全知识答题竞赛”,初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.平均分(分)中位数(分)众数(分)方差(分2)初中部a85 b s初中2高中部85 c100 160(1)根据图示计算出a、b、c的值;(2)结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?(3)计算初中代表队决赛成绩的方差s初中2,并判断哪一个代表队选手成绩较为稳定.。
中考方差试题及答案

中考方差试题及答案试题1:某班学生数学成绩如下:85,90,95,100,90。
求这组数据的方差。
答案:首先计算这组数据的平均数,即(85+90+95+100+90)/5=92。
然后计算每个数据与平均数的差的平方,分别为(85-92)^2=49,(90-92)^2=4,(95-92)^2=9,(100-92)^2=64,(90-92)^2=4。
将这些差的平方相加得到49+4+9+64+4=130。
最后,将总和除以数据个数5,得到方差为130/5=26。
试题2:一组数据的方差为s^2,若将这组数据中的每个数都乘以2,则新的方差是多少?答案:若原数据的方差为s^2,当每个数据都乘以2时,新的方差为(2^2)*s^2=4s^2。
这是因为方差是衡量数据波动大小的指标,当数据整体放大时,波动也会相应放大。
试题3:已知一组数据的平均数为50,方差为25,求这组数据的标准差。
答案:标准差是方差的平方根。
已知方差为25,所以标准差为√25=5。
试题4:一组数据的方差为0,这组数据有什么特点?答案:方差为0意味着这组数据中的所有数值都相等。
因为方差是衡量数据分布的离散程度,当所有数据值都相同时,方差为0。
试题5:某次考试中,小明的数学成绩是85分,全班的平均成绩是80分,求小明成绩的方差。
答案:首先计算小明成绩与全班平均成绩的差,即85-80=5。
然后计算差的平方,即5^2=25。
方差是每个数据与平均数差的平方的平均值,但这里只给出了一个数据,所以小明成绩的方差为25。
试题6:一组数据的方差为10,如果将这组数据中的每个数都加上3,新的方差是多少?答案:方差是衡量数据分布的离散程度,与数据的平移无关。
所以,将这组数据中的每个数都加上3,新的方差仍然是10。
试题7:一组数据的方差为s^2,若将这组数据中的每个数都除以2,则新的方差是多少?答案:若原数据的方差为s^2,当每个数据都除以2时,新的方差为(1/2)^2*s^2=s^2/4。
极差、方差标准差测试题(包含答案)

极差、方差标准差测试题(包含答案) 极差、方差标准差测试题一、选择题:(每小题3分,共18分)1.若数据2,x,4,8的平均数是6,则该组数据的极差是().A.4 B.6 C.8 D.102.观察图形,下列结论中不正确的是().A.a组数据的极差较大B.a组数据的方差较大C.b组数据比较稳定D.b组数据的标准差较大3.甲乙两中学生在一年里学科平均分相等,但他们的方差不相等,能正确评价他们学习情况的是().A.因为他们的平均分相等,所以学习水平一样B.表面上看这两个学生平均成绩一样,但方差小的学习成绩稳定C.成绩虽然一样,方差较大的,说明潜力大,学习态度踏实D.平均分相等,方差不等,说明学习的方法不一样,但效果一样4.一个样本有10个数据,各数据与样本平均数的差依次是-4,5,-2,4,-1,3,2,0,-2,-5,那么这个样本的方差是().A.0 B.3.2 C.10.4 D.1045.某工厂为了选拔1名车工参加加工直径为10mm的精密零件的技术比赛,随机抽取甲、乙两名车工加工的5个零件,现测得的结果如下表,请你用计算器比较S 2甲、S 2乙的大小().A.S 2甲>S 2乙B.S 2甲=S 2乙C.S 2甲<S 2乙D.S 2甲≤S 2乙6.已知一组数据x1、x2、x3、x4、x5的平均数是2,方差是1,那么另一组数据:10 x1-2、10 x2-2、10 x3-2、10 x4-2、10 x5-2的平均数和方差分别是().A.2、1 B.18、1 C.2、100 D.18、100二、填空题:(每小题4分,共24分)7. 一组数据:1,-2,0,4的极差为______________.8.小明在计算某组数据的方差时列式22221281[( 1.5)( 1.5)( 1.5)]8S x x x=-+-+⋅⋅⋅+-,那么该组数据的平均数是.9.甲乙两人进行射击比赛,他们在相同条件下各射击10 次,平均成绩均为7 环,10 次射击成绩的方差分别是:3S2=甲,2.1S2=乙.成绩较为稳定的是__________.(填“甲”或“乙”)10. 计算样本1,2,2,-3,3的方差为____________.11.数据3,2,1,0,-1的标准差S= .12.甲、乙、丙三台机床生产直径为60mm的螺丝,为了检验产品质量,从三台机床生产的螺丝中各抽查了20个测量其直径,进行数据处理后,发现这三组数据的平均数都是4010 060mm,它们的方差依次为S2甲=0.162,S2乙=0.058,S2丙=0.149.根据以上提供的信息,你认为生产螺丝质量最好的是__ __机床.三、解答题(本题5个小题,共55分)13.(本题满分10分)甲、乙两位同学五次数学测验成绩如下表:请你在表中的空白处填上适当的数,用学到的统计知识对两位同学的成绩进行分析,并写出一条合理化建议.14.(本题满分10分)甲、乙两名车工都加工要求尺寸是直径10mm的零件.从他们所生产的零件中,各取5件,测得直径如下(单位:mm)甲:10.05 10.02 9.97 9.95 10.01乙:9.99 10.0210.02 9.98 10.01分别计算两组数据的标准差(精确到0.01),说明在尺寸符合规格方面,谁做得较好?15.(本题满分10分)将10盒同一品种的花施用甲、乙两种花肥,随意分成两组,每组5 盆,其花期的记录结果如下(单位:天).(1)施用哪种花肥,使得花的平均花期较长?(2)施用哪种保花肥效果比较可靠?16.(本题满分12分)(1)计算下列各组数据的方差:①2、3、4、5、6;②12、13、14、15、16;③102、103、104、105、106;④20、30、40、50、60.(2)将其他各组的方差与第一组进行比较,你有何发现?(写一条即可)17.(本题满分13分)张阿姨下岗后开了一个牛奶销售店,主要经营“学生奶”、“酸牛奶”、“原味奶”.可张阿姨由于经验不足,经常有的牛奶没卖完,有的牛奶又不够卖,一段时间下来,通过盘点不但没有挣钱反而亏损了.热心的小红结合所学的统计知识帮张阿姨统计了一个星期牛奶的销售情况,并绘制了下表:(1)计算各品种牛奶的日平均销售量,并说明哪种牛奶销量最高?(2)计算各品种牛奶的方差(保留两位小数),并比较哪种牛奶销量最稳定?(3)假如你是小红,你对张阿姨有哪些好的建议.四、扩广探索(本题20分)18.第一次月考中,A、B、C、D、E五位同学的数学、英语成绩等有关信息如下表所示:(1)求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是标准分=(个人成绩-平均成绩)÷成绩标准差,从标准分看,标准分大的考试成绩更好,请问A同学在第一次月考中,数学与英语哪个学科考得更好.极差、方差标准差测试题参考答案一、选择题:二、填空题:7.6;8.1.5;9.乙;10.4.4;11;12.乙. 三、解答题13.解:甲平均数:85,方差53.2;乙平均数85,方差70.4;从上述数据看乙同学数学成绩不稳定,波动较大,应在数学学习上多下功夫,加强能力训练. 14.解:甲组标准差是0.04,乙组标准差是0.02,0.04>0.02∴乙组做得较好.15.解:(1)施用两种花肥的平均花期一样长;(2)∵S 2甲=5.2,S 2乙=2.8,∴施用乙种花肥的效果更可靠一些. 16.解:(1)①S 12=2,②S 22=2,S 32=2,S 42=200;(2)第一组数据中,每个数据分别加上10就变成了第二组数据,并且它的方差不变,若分别加上100就成了第三组数据,其方差仍然为2,但是如果将第一组数据扩大10倍变成了第四组数据,其方差变为原来的102倍.17.解:(1)∵3,80,40,xx x ===学生奶酸牛奶原味奶 ∴酸牛奶的销量最高;(2)∵S 2学生奶=12.57,S 2酸牛奶=92.86,S 2原味奶=96.86,∴学生奶的销量最稳定;(3)建议张阿姨学生奶平常尽量少进或不进,周末适当进一点. 四、拓广探索18.解:(1)数学考试成绩的平均分70, 英话考试成绩的标准差6;(2)设A 同学数学考试成绩标准分为P 数学,英语考试成绩标准分为P 英语,则P 数学=(71-70,P 英语=(88-85)÷6=0.5,∵P 数学>P 英语, ∴从标准分看,A 同学数学比英语考得更好.。
中考数学分类汇编-1.4极差、方差、标准差(2014年)
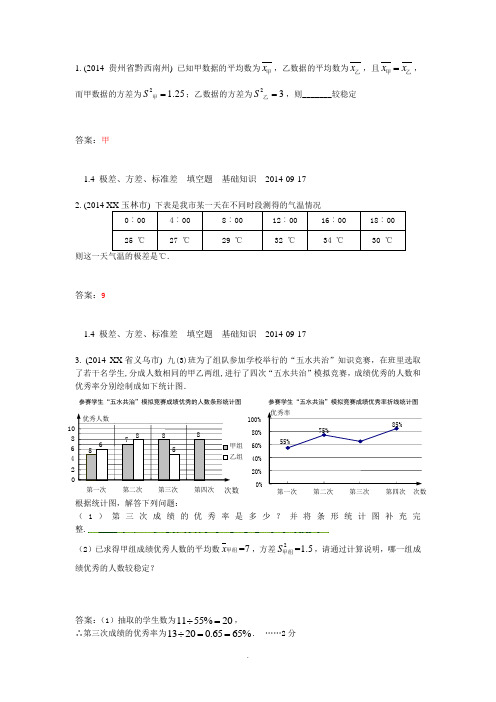
1. (2014 贵州省黔西南州) 已知甲数据的平均数为x 甲,乙数据的平均数为x 乙,且x x =乙甲,而甲数据的方差为2 1.25S=甲;乙数据的方差为23S =乙,则_______较稳定答案:甲1.4 极差、方差、标准差 填空题 基础知识 2014-09-172. (2014 XX 玉林市) 下表是我市某一天在不同时段测得的气温情况0︰00 4︰00 8︰00 12︰00 16︰00 18︰00 25 ℃27 ℃29 ℃32 ℃34 ℃30 ℃则这一天气温的极差是℃.答案:91.4 极差、方差、标准差 填空题 基础知识 2014-09-173. (2014 XX 省义乌市) 九(3)班为了组队参加学校举行的“五水共治”知识竞赛,在班里选取了若干名学生,分成人数相同的甲乙两组,进行了四次“五水共治”模拟竞赛,成绩优秀的人数和优秀率分别绘制成如下统计图.根据统计图,解答下列问题:(1)第三次成绩的优秀率是多少?并将条形统计图补充完整.(2)已求得甲组成绩优秀人数的平均数=7x 甲组,方差2=1.5S 甲组,请通过计算说明,哪一组成绩优秀的人数较稳定?答案:(1)抽取的学生数为1155%20÷=,∴第三次成绩的优秀率为13200.6565%÷==. ……2分参赛学生“五水共治”模拟竞赛成绩优秀的人数条形统计图次数2 64 56 78 8 第一次第二次第三次第四次优秀人数甲组 乙组 8 85参赛学生“五水共治”模拟竞赛成绩优秀率折线统计图85%75%55%0%20%40%60% 80%100%第一次第二次第三次第四次 优秀率次数第四次成绩优秀的人数为2085%17⨯=,乙组成绩优秀的人数1789-=, 补充后的条形统计图如下图所示:……2分(2)1=6+8+5+9=74x 乙组(),222221=6-78-7(57)(97) 2.54S ⎡⎤+-+-=⎣⎦乙组()+(), 因为22S S 甲组乙组<,所以甲组成绩优秀的人数较稳定. ……4分1.4 极差、方差、标准差 应用题 基础知识 2014-09-154. (2014 四川省遂宁市) 我市射击队为了从甲、乙两名运动员中选出一名运动员参加省运动会比赛,组织了选拔测试,两人分别进行了五次射击,成绩(单位:环)如下:则应选择 甲 运动员参加省运动会比赛.答案:甲1.4 极差、方差、标准差 填空题 基础知识 2014-09-155. (2014 XX 省营口市) 小华和小苗练习射击,两人的成绩如图所示,小华和小苗两人成绩的方差分别为21S 、22S ,根据图中的信息判断两人方差的大小关系为.答案:S 12<S 221.4 极差、方差、标准差 填空题 基础知识2014-09-15参赛学生“五水共治”模拟竞赛成绩优秀的人数条形统计图次数2468第一次第二次第三次第四次小苗小华6. (2014 重庆市B卷) 某校将举办一场“中国汉字听写大赛”,要求各班推选一名同学参加比赛。
九年级数学上册(极差)同步练习试题

轧东卡州北占业市传业学校睢宁县新世纪九年级数学上册<极差>同步练习1、数据1,6,3,9,8的极差是〔〕A.1 B.5 C.6 D.82、一次数学测试后,随机抽取九年级二班5名学生的成绩如下:78,85,91,98,98.关于这组数据的错.误说法...是〔〕A.极差是20 B.众数是98 C.中位数是91 D.平均数是913、2007年5月下旬,的天气特点是潮湿、闷热。
张小敏同学对这11天的最高气温进行统计,得到的数据如下表:那么五月下旬最高气温的众数和极差分别是〔〕A、31,5B、31,6C、31,7D、32,64、为了了解某小区居民的用水情况,随机抽查了10户家庭的月用水量,结果如下表:那么关于这10户家庭的月用水量,以下说法错误的选项是......〔〕A.中位数是5吨B.众数是5吨 C.极差是3吨D.平均数是吨5、一服装店新进某种品牌五种尺码的衬衣,经过试卖一周,各尺码衬衣的销售量列表如下:据上表给出的信息,仅就经营该品牌衬衣而言,你认为最能影响服装店经理决策的统计量是〔〕A.平均数B.中位数C.众数D.极差6、小明同学将某班级毕业升学体育测试成绩〔总分值30分〕统计整理,得到下表,那么以下说法错误的选项是〔〕分数20 21 22 23 24 25 26 27 28 人数 2 4 3 8 10 9 6 3 1 A.该组数据的众数是24分B.该组数据的平均数是25分C.该组数据的中位数是24分D.该组数据的极差是8分7、我国著名的珠穆朗玛峰海拔高达8844米,在它周围2千米的附近,耸立的几座著名山峰的高度如下表:山峰名珠穆朗玛洛子峰卓穷峰马卡鲁峰章子峰努子峰普莫里峰海拔高度8844m 8516m 7589m 8463m 7543m 7855m 7145m那么这七座山峰海拔高度的极差为米.7、如图是日报2006年2月17日发布的我六年来专利申请量〔项〕的统计图,那么这六年中平均每年专利申请量是项,极差是项.8、5名同学目测同一本教科书的宽度时,产生的误差如下〔单位:cm〕:2,2-,1-,1,0,那么这组数据的极差为cm.9、2007年1月,在举行了第六届亚洲冬季运动会.我国在各届亚冬会上获得金牌数如下列图,那么这六届获得金牌数的极差是枚。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初三数学
极差与方差练习
一、填空题
1. 一组数据中的最大数据与最小数据的差叫做这组数据的 ,它反映了这组数据
的 。
2、下表给出了合肥市2006年5月28日至6月3日的最高气温,•则这些最高气温的极差是_____℃
日期
5月 28日 5月 29日 5月 30日 5月 31日 6月 1日 6月 2日 6月 3日
最高气温 26℃ 27℃ 30℃ 28℃ 27℃ 29℃ 33℃ 3、______,平均数是______
4、体育课上,八(1)班两个组各10人参加立定跳远,要判断哪一组成绩比较整齐,通常需 要知道这两个组立定
跳远成绩的( ) A .平均数 B.众数 C .方差 D .频率
分布
5、人数相同的八年级甲、乙两班学生在同一次数学单元测试,班级平均分和方差如下:
80==乙甲x x ,2402
=甲s ,1802=乙
s ,则成绩较为稳定的班级是( ) A.甲班 B.乙班 C.两班成绩一样稳定 D.无法确定 6、计算下列三组数据的平均值、方差.
数据
平均数 标准差 方差 (1) 1,2,3,4 (2) 3,6,9,12 (3) 5,8,11,14
165.0cm ,其结果如下: −1.2,0.1,−8.3,1.2,10.8,−7.0 这6名男生中最高身高与最低身高的差是 ;
这6名男生的平均身高约为 (结果保留到小数点后第一位) 8、一组数据2-,1-,0,x ,1的平均数是0,则x = ,方差=2S .
9、如果样本方差[]
242322212)2()2()2()2(4
1
-+-+-+-=
x x x x S ,那么这个样本的平均数为 .样本容量为 . 二、解答题
9、下表是掷两颗骰子的实验中得到的数据.
投掷次数 5 10 15 20 25 30 35 40 45 50 出现数字之和为奇
数的频数 2 4 8 10 14 17 20 22 25 26 出现数字之和为奇
0.4
0.4
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
求出其标准差,说说哪一段的频率表现得更为稳定.
解:
10、某年A,B两座城市四季的平均气温如下表所示:
(1)分别计算A,B两座城市的年平均气温
(2)哪座城市四季的平均气温较为接近?
x
A
x=
B
(2)
11、下表是两种股表在2003年某周的交易日收盘价格(单位:元),计算它们的平均数和方差,比较这两种股票在这段时间内的张跌变化情况。
x
A
2
s=
A
x=
B
2
s=
B
12、为了从甲、乙两名学生中选择一人参加电脑知识竞赛,•在相同条件下对他们的电脑知识进行了10次测验,成绩如下:(单位:分)(9分)
甲成绩76 84 90 84 81 87 88 81 85 84
乙成绩82 86 87 90 79 81 93 90 74 78
(1)请填写下表
平均数中位数众数方差标准差85分以上的频率
甲 84 84 14.4 0.3
乙 84 84 90
(2
13、小红的奶奶开了一个金键牛奶销售店,主要经营“金键学生奶”、“金键酸牛奶”、“金键原
味奶”,可奶奶经营不善,经常有品种的牛奶滞销(没卖完)或脱销(量不够),造成了浪费或亏损,细心的小红结合所学的统计知识帮奶奶统计了一个星期牛奶的销售情况,并绘制了下表:
(1)计算各品种牛奶的日平均销售量,并说明哪种牛奶销量最高?
(2)计算各品种牛奶的方差(保留两位小数),并比较哪种牛奶销量最稳定?
(3)假如你是小红,你会对奶奶有哪些好的建议.
= ,
答:(1)x
学生奶
x酸牛奶= ,
x原味奶= ,
所以牛奶销量高,
(2)2S学生奶= ,2S酸牛奶= ,2S原味奶= ,
所以牛奶销量最稳定,
(3)
14、为了了解某校八年级女生的身体情况,从中抽取了60名女生的身高进行了测量,结果如下(单位:㎝):
167 154 159 166 169 159 156 166 162 158
159 156 166 160 164 160 157 156 157 161
158 158 153 158 164 158 163 158 153 157
162 162 159 154 165 166 157 151 146 151
158 160 165 158 163 163 162 161 154 165
162 162 159 157 159 149 164 168 159 153
(1)计算这组数据的极差,这个极差说明什么问题?
(2)根据分组原则“数据在50~100之间时分8~12组较合适”,请将本题数据适当分组,设计并填好频数分布表;
(3)绘制频数分布直方图;
(4)根据图文信息,请你估计并说出你有何结论。
