RLC串联电路的谐振
RLC串联电路电流谐振曲线

contents
目录
• RLC串联电路基础 • 电流谐振曲线 • RLC串联电路的谐振频率 • 电流谐振曲线的应用 • 结论
01 RLC串联电路基础
RLC串联电路的定义
RLC串联电路是由电阻(R)、电感 (L)和电容(C)三个元件串联而成 的电路。
在RLC串联电路中,电流通过电阻、 电感和电容三个元件,形成一个闭合 的电流回路。
在电力电子系统中的应用
逆变器
在逆变器中,RLC串联电路电流 谐振曲线可用于实现高频化,提 高逆变器的转换效率和功率密度 。
无功补偿
利用电流谐振曲线,可以设计无 功补偿装置,实现对电网的无功 补偿,提高电网的功率因数和稳 定性。
在无线电系统中的应用
发射机
在无线电发射机中,RLC串联电路电流谐振曲线可用于实现信号的高频化和功 率放大,提高信号的覆盖范围和传输质量。
自动控制
在自动控制系统,利用RLC串联电 路的谐振特性,实现系统的频率 响应控制和稳定性控制。
04 电流谐振曲线的应用
在通信系统中的应用
信号传输
RLC串联电路电流谐振曲线可用于信 号传输,通过调整电路参数,使信号 在特定频率上产生谐振,从而提高信 号传输效率和稳定性。
滤波器设计
利用电流谐振曲线,可以设计具有特 定频响特性的滤波器,用于提取或抑 制特定频率的信号,实现信号的筛选 和处理。
分析应用范围
根据电流谐振曲线的特点,可以确定RLC串 联电路在不同频率下的应用范围。
03 RLC串联电路的谐振频率
谐振频率的计算方法
公式法
根据RLC串联电路的阻抗公式,通过求解一元二次方程得到谐振频 率。
图形法
通过绘制RLC串联电路的阻抗圆,找到与实轴交点的频率即为谐振 频率。
RLC串联谐振频率与其计算公式

RLC串联谐振频率及其计算公式串联谐振是指所研究的串联电路部分的电压和电流达到同相位,即电路中电感的感抗和电容的容抗在数值上时相等的,从而使所研究电路呈现纯电阻特性,在给定端电压的情况下,所研究的电路中将出现最大电流,电路中消耗的有功功率也最大.1. 谐振定义:电路中L、C 两组件之能量相等,当能量由电路中某一电抗组件释出时,且另一电抗组件必吸收相同之能量,即此两电抗组件间会产生一能量脉动。
2. 电路欲产生谐振,必须具备有电感器L及电容器C 两组件。
3. 谐振时其所对应之频率为谐振频率(resonance),或称共振频率,以f r表示之。
4. 串联谐振电路之条件如图1所示:当Q=Q ⇒I2X L = I2 X C也就是X L =X C时,为R-L-C串联电路产生谐振之条件。
图1 串联谐振电路图5. 串联谐振电路之特性:(1) 电路阻抗最小且为纯电阻。
即 Z =R+jX L−jX C=R(2) 电路电流为最大。
即(3) 电路功率因子为1。
即(4) 电路平均功率最大。
即P=I2R(5) 电路总虚功率为零。
即Q L=Q C⇒Q T=Q L−Q C=06. 串联谐振电路之频率:(1) 公式:(2) R - L -C串联电路欲产生谐振时,可调整电源频率f 、电感器L 或电容器C使其达到谐振频率f r,而与电阻R完全无关。
7. 串联谐振电路之质量因子:(1) 定义:电感器或电容器在谐振时产生的电抗功率与电阻器消耗的平均功率之比,称为谐振时之品质因子。
(2) 公式:(3) 品质因子Q值愈大表示电路对谐振时之响应愈佳。
一般Q值在10~100 之间。
8. 串联谐振电路阻抗与频率之关系如图(2)所示:(1) 电阻R 与频率无关,系一常数,故为一横线。
(2) 电感抗X L=2 πfL ,与频率成正比,故为一斜线。
(3) 电容抗与频率成反比,故为一曲线。
(4) 阻抗Z = R+ j(X L−X C)当 f = f r时, Z = R 为最小值,电路为电阻性。
rlc串联谐振电路总结

rlc串联谐振电路总结RLC串联谐振电路总结引言RLC串联谐振电路是一种基础的电路,广泛应用于各个领域,如通信、电力系统、医疗设备等。
本文将详细介绍RLC串联谐振电路的基本原理、特性以及应用,并结合实际案例进行分析和讨论。
一、RLC串联谐振电路的基本原理1.1 RLC电路元件介绍RLC电路由电阻(R)、电感(L)和电容(C)组成。
电阻是消耗电能的元件,电感是储存电能的元件,电容是储存电能的元件。
1.2 谐振的概念谐振是指电路中某些电压或电流的幅度具有最大值的现象。
RLC串联电路中,当电感、电容和电阻的参数选择合适时,可以实现谐振。
1.3 LRC电路的阻抗RLC串联电路的总阻抗可表示为Z = R + j(Xl - Xc),其中R是电阻,j是虚数单位,Xl是电感的感抗(即感性阻抗),Xc是电容的容抗(即容性阻抗)。
感抗和容抗在不同频率下具有不同的大小和方向。
1.4 谐振频率谐振频率是指电路中感抗和容抗大小相等,阻抗最小的频率。
谐振频率可通过求解总阻抗为实数的频率得出。
二、RLC串联谐振电路的特性2.1 幅频特性幅频特性是指在不同频率下电压或电流的大小变化规律。
RLC串联电路在谐振频率附近,电压或电流的幅度较大,达到最大值;而在谐振频率之外,幅度逐渐减小。
2.2 相频特性相频特性是指在不同频率下电压或电流的相位差变化规律。
在谐振频率附近,电压与电流的相位差为0,即电压和电流完全同相;而在谐振频率之外,相位差逐渐增大。
2.3 幅相特性幅相特性是指在不同频率下电压或电流的幅值与相位差的关系。
在RLC串联电路中,幅值与相位差之间存在一定的关系,通常在Bode图中表示。
三、RLC串联谐振电路的应用3.1 通信领域RLC串联谐振电路在通信领域中被广泛应用于滤波器、调谐器等电路中。
通过合理选择电阻、电感和电容参数,可以实现滤波、频率选择功能。
3.2 电力系统RLC串联谐振电路在电力系统中用于电力因数校正、电力滤波等应用。
RLC串联谐振的频率及计算公式
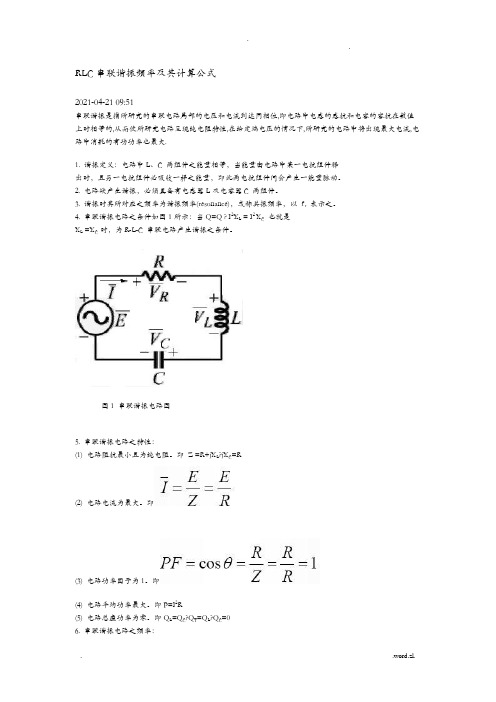
RLC串联谐振频率及其计算公式2021-04-21 09:51串联谐振是指所研究的串联电路局部的电压和电流到达同相位,即电路中电感的感抗和电容的容抗在数值上时相等的,从而使所研究电路呈现纯电阻特性,在给定端电压的情况下,所研究的电路中将出现最大电流,电路中消耗的有功功率也最大.1. 谐振定义:电路中L、C 两组件之能量相等,当能量由电路中某一电抗组件释出时,且另一电抗组件必吸收一样之能量,即此两电抗组件间会产生一能量脉动。
2. 电路欲产生谐振,必须具备有电感器L及电容器C 两组件。
3. 谐振时其所对应之频率为谐振频率(resonance),或称共振频率,以f r表示之。
4. 串联谐振电路之条件如图1所示:当Q=Q ? I2X L = I2 X C也就是X L =X C 时,为R-L-C 串联电路产生谐振之条件。
图1 串联谐振电路图5. 串联谐振电路之特性:(1) 电路阻抗最小且为纯电阻。
即Z =R+jX L?jX C=R(2) 电路电流为最大。
即(3) 电路功率因子为1。
即(4) 电路平均功率最大。
即P=I2R(5) 电路总虚功率为零。
即Q L=Q C?Q T=Q L?Q C=06. 串联谐振电路之频率:(1) 公式:(2) R - L -C 串联电路欲产生谐振时,可调整电源频率f 、电感器L 或电容器C 使其到达谐振频率f r ,而与电阻R完全无关。
7. 串联谐振电路之质量因子:(1) 定义:电感器或电容器在谐振时产生的电抗功率与电阻器消耗的平均功率之比,称为谐振时之品质因子。
(2) 公式:(3) 品质因子Q值愈大表示电路对谐振时之响应愈佳。
一般Q值在10~100 之间。
8. 串联谐振电路阻抗与频率之关系如图(2)所示:(1) 电阻R 与频率无关,系一常数,故为一横线。
(2) 电感抗X L=2 π fL ,与频率成正比,故为一斜线。
(3) 电容抗与频率成反比,故为一曲线。
(4) 阻抗Z = R+ j(X L ?X C)当f = f r时,Z = R 为最小值,电路为电阻性。
rlc串联谐振的谐振频率(3篇)

第1篇一、RLC串联谐振电路的基本原理RLC串联谐振电路由电阻R、电感L和电容C三个元件组成。
当电路中电压或电流的频率发生变化时,电路的阻抗Z也会随之变化。
当电路的阻抗Z达到最小值时,电路处于谐振状态,此时的频率称为谐振频率。
二、谐振频率的计算1. 谐振频率的定义谐振频率是指RLC串联电路在谐振状态下,电路的阻抗Z达到最小值时的频率。
在谐振状态下,电路的电流I与电压U之间的相位差为0,即电流和电压同相位。
2. 谐振频率的计算公式RLC串联电路的谐振频率可以通过以下公式计算:\[ f_0 = \frac{1}{2\pi\sqrt{LC}} \]其中,\( f_0 \)表示谐振频率,L表示电感,C表示电容。
三、谐振频率的影响因素1. 电感L和电容C谐振频率与电感L和电容C的乘积成反比。
当电感L或电容C增大时,谐振频率会减小;反之,当电感L或电容C减小时,谐振频率会增大。
2. 电阻R电阻R对谐振频率没有直接影响,但会影响电路的品质因数Q。
品质因数Q定义为:\[ Q = \frac{f_0}{\Delta f} \]其中,\( \Delta f \)表示谐振曲线的带宽。
当电阻R增大时,品质因数Q减小,电路的带宽增大,谐振频率基本不变。
四、谐振频率在实际应用中的重要性1. 选择合适的谐振频率在实际应用中,选择合适的谐振频率可以提高电路的性能。
例如,在无线通信、信号传输等领域,通过选择合适的谐振频率,可以减小信号损耗,提高传输效率。
2. 提高电路的稳定性在电路设计和分析过程中,通过调整电感L和电容C的值,可以使电路在特定的频率下达到谐振状态,从而提高电路的稳定性。
3. 优化电路性能通过调整谐振频率,可以优化电路的性能。
例如,在滤波器设计中,通过选择合适的谐振频率,可以实现对特定频率信号的滤波。
五、总结RLC串联谐振电路的谐振频率是电路设计和分析中的一个重要参数。
通过掌握谐振频率的计算方法、影响因素以及在实际应用中的重要性,有助于我们更好地进行电路设计和优化。
RLC串联电路的谐振特性研究实验报告.doc

RLC串联电路的谐振特性研究实验报告.doc 实验目的:1. 了解RLC串联电路的工作原理及其谐振特性;2. 掌握测量RLC串联电路谐振频率和谐振带宽的方法。
实验仪器:1. RLC串联电路实验箱;2. 信号源;3. 示波器。
实验原理:RLC串联电路是由电阻、电感和电容串联形成的电路,它可以产生共振现象。
当其频率为共振频率时,电路中流过电流的大小取决于电路中的电感和电容。
此时,电路呈现出很高的阻抗,电流最大。
谐振频率 f0 由以下公式给出:f0 = 1 / (2π√LC)其中,L 为电路中的电感,C 为电路中的电容。
Z0 = R + j(XL - XC)谐振带宽 BW 的计算公式为:BW = Δf = f2 - f1其中,f1 和 f2 分别为电路总阻抗等于Z0/√2 时的频率。
实验步骤:1. 连接实验电路:将电阻、电感和电容串联起来,组成 RLC 串联电路,并连接信号源和示波器。
2. 设置信号源:将信号源的频率调节旋钮设置到最小值,同时将信号源电压调节旋钮调整到最大值。
3. 测量谐振频率:将示波器调节到 X-Y 模式,然后调节信号源频率调节旋钮,逐渐增大频率,直到示波器屏幕上显示出一个正弦波。
此时,记录下示波器显示的频率值,即为电路的谐振频率 f0。
实验结果:1. 在本次实验中,使用的电阻、电感和电容的值分别为:R = 1kΩ,L = 10mH,C = 0.1μF。
2. 在逐渐增大信号源频率的过程中,当频率达到 2231 Hz 时,电路中开始出现正弦波,此时记录下的频率值即为电路的谐振频率 f0。
3. 继续增大信号源频率,当频率达到 2358 Hz 时,电路总阻抗等于Z0/√2 时,记录下此时信号源频率调节旋钮的读数。
5. 通过计算,得到电路的谐振带宽为 157 Hz。
1. RLC串联电路可以产生共振现象,其频率为谐振频率 f0。
2. 对于给定的 RLC 串联电路,谐振频率 f0 取决于电路中的电感和电容的值。
rlc串联电路的谐振实验报告

rlc串联电路的谐振实验报告一、实验目的二、实验原理1. RLC串联电路的基本概念2. 谐振现象及其特点三、实验器材和仪器1. 实验器材清单2. 实验仪器清单四、实验步骤1. 实验前准备工作2. 测量电路中各元件的参数值3. 测量谐振频率和带宽五、实验数据处理与分析1. 计算电路品质因数Q和谐振频率f0的理论值2. 绘制电路的幅频特性曲线和相频特性曲线,并分析其特点。
六、实验结论与思考七、参考文献一、实验目的本次实验主要是通过对RLC串联电路进行谐振实验,掌握测量RLC串联电路中各元件参数值以及谐振频率和带宽的方法,了解谐振现象及其特点,掌握计算电路品质因数Q和谐振频率f0理论值的方法,并绘制出幅频特性曲线和相频特性曲线。
二、实验原理1. RLC串联电路的基本概念RLC串联电路是由电阻R、电感L和电容C三种元件串联而成的电路。
当交流电源接入这个电路时,由于电感和电容的存在,会产生阻抗,从而影响电路中的电流和电压。
在RLC串联电路中,当交流信号频率等于某一特定值时,会出现谐振现象。
2. 谐振现象及其特点谐振是指在某一特定频率下,RLC串联电路的阻抗达到最小值或最大值的现象。
当交流信号频率等于谐振频率f0时,RLC串联电路中的阻抗为纯阻抗,即只有R存在。
此时,如果在该频率下加入一个外加信号,则可以得到最大幅度的响应。
谐振现象具有以下特点:(1)在谐振频率f0处,RLC串联电路中的阻抗为纯阻抗。
(2)在谐振频率f0处,输入信号与输出信号之间相位差为0。
(3)当输入信号频率偏离f0时,输出信号幅度将随着频率增加而降低。
三、实验器材和仪器1. 实验器材清单:电阻箱、电容箱、电感箱、万用表、示波器等。
2. 实验仪器清单:Tektronix TDS2002C数字示波器等。
四、实验步骤1. 实验前准备工作(1)检查实验仪器是否正常工作。
(2)连接RLC串联电路,调整各元件的参数,使其符合实验要求。
(3)将示波器连接到电路中,以便观察信号的变化情况。
rlc串联电路谐振时,电路中的电流与信号源电压相位一致

RLC串联电路谐振时,电路中的电流与信号源电压相位一致1. 引言RLC串联电路的谐振特性在电子和通信领域中具有广泛的应用。
当电路发生谐振时,电路中的电流与信号源电压之间存在一定的相位关系。
本文将详细探讨RLC串联电路谐振时,电路中的电流与信号源电压相位一致的现象、原理、实验验证、实际应用和展望。
2. RLC串联电路基础RLC串联电路由电阻(R)、电感(L)和电容(C)三个元件串联而成。
在正弦交流电源的作用下,电路中会产生一定的电流。
电流与元件参数及电源频率有关,其行为受到KVL(基尔霍夫电压定律)的支配。
3. 谐振现象及其产生条件当RLC串联电路中的电阻、电感和电容满足一定条件时,电路发生谐振。
此时,电路的阻抗最小,电流最大。
谐振的产生条件由品质因数Q决定,即Q=ωL/R=1/ωC=√(L/C)/R,其中ω是角频率。
4. 电流与信号源电压相位一致的原理在RLC串联电路谐振时,由于电路的阻抗最小,因此电流的幅度最大。
此外,由于电感和电容的相位相反,导致电流与信号源电压的相位一致。
这一现象可以通过复数阻抗和相量图进行解释。
在相量图上,电感和电容的相量在复平面上的角度相反,因此在某一特定频率下,它们的相量之和为零,导致整个电路的阻抗最小。
此时,电流与信号源电压的相位一致。
5. 实验验证与结论为了验证RLC串联电路谐振时电流与信号源电压相位一致的现象,我们可以通过搭建实验电路并使用示波器和信号源进行测量。
首先,我们需要选择适当的电阻、电感和电容元件值,以满足谐振条件。
然后,通过信号源向RLC串联电路施加适当频率的正弦信号,观察并记录示波器上电流与信号源电压的波形及相位关系。
实验结果将验证在谐振条件下,电流与信号源电压相位一致的现象。
6. 实际应用与展望RLC串联电路谐振时电流与信号源电压相位一致的现象在通信、电子和微波等领域中有着广泛的应用。
例如,在通信系统中,利用这一现象可以实现频率选择和信号过滤功能。
RLC串联谐振

1Ω
0.1H 1μF
2. 求下图电路的谐振角频率
C2 i C
R
C1
L1
i
L
19
R j(ω C 2 ω L 2 ) R 2 (ω L)2 R (ω L)
G jB
ω0 L 0 谐振时 B=0,即 ω0 C 2 2 R (ω0 L)
求得
ω0
1 ( R )2 LC L
由电路参数决定。
当电路发生谐振时,电路相当于一个电阻:
R 2 (ω0 L) 2 Z (ω0 ) R0 L R RC
C2
ω1
1 串联谐振 L1 (C 2 C 3 )
ω2
1 L1C 2
并联谐振
ω1 ω2
15
阻抗的频率特性: Z ( )=jX( ) X( )
(a)
O
1
2
X( ) (b) O
1
2
16
LC串并联电路的应用: 可构成各种无源滤波电路 (passive filter)。 例: 激励 u1(t),包含两个频率1、2分量 (1<2): u1(t) =u11(1)+u12(2) 要求响应u2(t)只含有1频率电压。 如何实现? + u1(t) _ 可由下列滤波电路实现: u2(t)
对(b)电路可作类似定性分析。
13
1 定量分析: jω L ( ) 1 L1 jω C2 jω L 2 (a) Z (ω) jω L 3 3 ω L C 1 1 1 2 jω L 1 jω C2 L3 3 ω L1 L3C 2 ω( L1 L3 ) j ω2 L1C 2 1 L1 当Z( )=0,即分子为零,有: 3 ω2 L1 L3 C 2 ω2 ( L1 L3 ) 0
RLC串联电路的谐振

RLC串联电路的谐振一、实验目的1.观察谐振现象,加深对串联谐振电路特点的理解。
2. 学习测定RLC 串联谐振电路频率特性的方法。
二、实验原理图5-1 RLC 串联电路图在图5-1 所示的RLC 串联电路上,施加一正弦电压,电路中电流的有效值上式中,电抗是角频率的函数。
当外施电压的角频率时,。
这时电路的工作状态称为串联谐振。
ω0称为谐振角频率,称为谐振频率,可由下式求得可见要使电路满足谐振条件,可以通过改变L 、C 或f 来实现。
本实验是采用改变外施正弦电压的频率来使电路达到谐振。
谐振时,电路的阻抗为最小值。
若外施电压的有效值U 及电路中的电阻R 为定值,则谐振时电路中电流的有效值达到最大根据这个特点可以判断电路是否发生了谐振。
如果保持外施电压的有效值U 及电路参数R 、L 、C 不变,改变信号源的频率 f ,便可得到电流的幅频特性如图5-2 所示。
曲线也称为电流谐振曲线。
从曲线可以看出,串联电路中的电阻R 愈小,曲线的尖锐程度就愈大。
以为横坐标,为纵坐标,画出的曲线称为串联谐振电路的通用曲线。
如图5-3 所示。
图中图5-2 串联谐振电路的电流谐振曲线图5-3 串联谐振电路的通用曲线式中称为电路的品质因数。
可以看出,Q 愈大,曲线的尖锐程度就愈大,谐振电路的选择性也就愈好。
三、实验仪器四、实验内容1 .按图5-4 接通电路,改变信号源频率,观察电路的谐振现象,找出电路的谐振频率f0。
2 .在串联电阻R=50 Ω时,改变信号源频率 f ,并维持信号源的输出电压为6V 不变,测量R 两端的电压,将测试数据分别以表格形式列出。
每条曲线需测量9-11 个数据。
图5-4 RLC 串联电路图3 .在串联电阻R=500 Ω时,改变信号源频率 f ,并维持信号源的输出电压为6V 不变, 测量R 两端的电压,将测试数据分别以表格形式列出。
每条曲线需测量9-11 个数据。
4 .分别测量电阻在50Ω及500Ω两种情况下,测量谐振时电容器两端的电压U C。
RLC串联谐振频率及其计算公式

RLC串联谐振频率及其计算公式串联谐振是指所研究的串联电路部分的电压和电流达到同相位,即电路中电感的感抗和电容的容抗在数值上时相等的,从而使所研究电路呈现纯电阻特性,在给定端电压的情况下,所研究的电路中将出现最大电流,电路中消耗的有功功率也最大.1. 谐振定义:电路中L、C 两组件之能量相等,当能量由电路中某一电抗组件释出时,且另一电抗组件必吸收相同之能量,即此两电抗组件间会产生一能量脉动。
2. 电路欲产生谐振,必须具备有电感器L及电容器C 两组件。
3. 谐振时其所对应之频率为谐振频率(resonance),或称共振频率,以f r 表示之。
4. 串联谐振电路之条件如图1所示:当Q=Q ?I2X L = I2 X C也就是X L =X C时,为R-L-C串联电路产生谐振之条件。
???????????? 图1 串联谐振电路图5. 串联谐振电路之特性:(1) 电路阻抗最小且为纯电阻。
即 Z =R+jX L?jX C=R(2) 电路电流为最大。
即(3) 电路功率因子为1。
即(4) 电路平均功率最大。
即P=I2R(5) 电路总虚功率为零。
即Q L=Q C?Q T=Q L?Q C=06. 串联谐振电路之频率:(1) 公式:(2) R - L -C串联电路欲产生谐振时,可调整电源频率f 、电感器L 或电容器C使其达到谐振频率f r,而与电阻R完全无关。
7. 串联谐振电路之质量因子:(1) 定义:电感器或电容器在谐振时产生的电抗功率与电阻器消耗的平均功率之比,称为谐振时之品质因子。
(2) 公式:(3) 品质因子Q值愈大表示电路对谐振时之响应愈佳。
一般Q值在10~100 之间。
8. 串联谐振电路阻抗与频率之关系如图(2)所示:(1) 电阻R 与频率无关,系一常数,故为一横线。
(2) 电感抗X L=2 πfL ,与频率成正比,故为一斜线。
(3) 电容抗与频率成反比,故为一曲线。
(4) 阻抗Z = R+ j(X L?X C)当 f = f r时, Z = R 为最小值,电路为电阻性。
RLC串联谐振频率和计算公式

RLC串联谐振频率及其计算公式串联谐振是指所研究的串联电路部分的电压和电流达到同相位,即电路中电感的感抗和电容的容抗在数值上时相等的,从而使所研究电路呈现纯电阻特性,在给定端电压的情况下,所研究的电路中将出现最大电流,电路中消耗的有功功率也最大.1. 谐振定义:电路中L、C 两组件之能量相等,当能量由电路中某一电抗组件释出时,且另一电抗组件必吸收相同之能量,即此两电抗组件间会产生一能量脉动。
2. 电路欲产生谐振,必须具备有电感器L及电容器C 两组件。
3. 谐振时其所对应之频率为谐振频率(resonance),或称共振频率,以f r表示之。
4. 串联谐振电路之条件如图1所示:当Q=Q ⇒I2X L = I2 X C也就是X L =X C时,为R-L-C串联电路产生谐振之条件。
图1 串联谐振电路图5. 串联谐振电路之特性:(1) 电路阻抗最小且为纯电阻。
即 Z =R+jX L−jX C=R(2) 电路电流为最大。
即(3) 电路功率因子为1。
即(4) 电路平均功率最大。
即P=I2R(5) 电路总虚功率为零。
即Q L=Q C⇒Q T=Q L−Q C=06. 串联谐振电路之频率:(1) 公式:(2) R - L -C串联电路欲产生谐振时,可调整电源频率f 、电感器L 或电容器C使其达到谐振频率f r,而与电阻R完全无关。
7. 串联谐振电路之质量因子:(1) 定义:电感器或电容器在谐振时产生的电抗功率与电阻器消耗的平均功率之比,称为谐振时之品质因子。
(2) 公式:(3) 品质因子Q值愈大表示电路对谐振时之响应愈佳。
一般Q值在10~100 之间。
8. 串联谐振电路阻抗与频率之关系如图(2)所示:(1) 电阻R 与频率无关,系一常数,故为一横线。
(2) 电感抗X L=2 πfL ,与频率成正比,故为一斜线。
(3) 电容抗与频率成反比,故为一曲线。
(4) 阻抗Z = R+ j(X L−X C)当 f = f r时, Z = R 为最小值,电路为电阻性。
RLC串联电路的幅频特性和谐振

)
2.改变电阻R=100,重复1 2.改变电阻 改变电阻R=100,重复1 3.改变L==200mH,重复1。计算值,并 3.改变 改变L==200mH,重复1 计算值, 测定该值所对应的f值通频带f 测定该值所对应的f值通频带f 4.Q值的测定 用毫伏表测L(或C)上两端的 4.Q值的测定, 用毫伏表测L(或C)上两端的 值的测定, 谐振时的电压,此值即Q 谐振时的电压,此值即Q值;用数字万用表 电阻档测L的直流也阻r R0=R+r) 电阻档测L的直流也阻r(R0=R+r)带入 上面的公式,看它们的Q值误差有多大。 上面的公式,看它们的Q值误差有多大。
实验七 RLC串联电路的幅频特性和谐振 RLC串联电路的幅频特性和谐振
一、实验目的 l、研究RLC 串联电路的幅频特性(也就是谐 研究RLC 串联电路的幅频特性( 振曲线) 振曲线) 2、研究串联谐振现象及电路参数对谐振特性 的影响。 的影响。
二、实验说明
在RLC串联电路中,阻抗值是: RLC串联电路中 阻抗值是: 串联电路中,
三 实验内容
测量幅频特性的实验电路如下,信号发生器 测量幅频特性的实验电路如下, 输出正弦电压,频率可在20赫到 千赫范 赫到20 输出正弦电压,频率可在20赫到20千赫范 围内变化
1、测量RLC串联电路的幅频特性I(f),并测出 测量RLC串联电路的幅频特性 串联电路的幅频特性I ),并测出 谐振频率f 谐振频率f。 具体方法:采用电阻取样法测定回路电流, 具体方法:采用电阻取样法测定回路电流,取样电 阻采用Ro=10。调整信号源频率, 阻采用Ro=10。调整信号源频率,取样电阻两 端接的交流毫伏表指示值最大时,调整信号源幅度, 端接的交流毫伏表指示值最大时,调整信号源幅度, Us=1V,重新调整频率使电流最大,此时f 使Us=1V,重新调整频率使电流最大,此时f即为 f ,电流为I 。Q2>Q1 电流为I
实验八 RLC串联电路的谐振实验

C1L ω=ωfC 21πC1ωLC21πLC1LC实验八 R 、L 、C 串联电路的谐振实验一、实验目的1、研究交流串联电路发生谐振现象的条件。
2、研究交流串联电路发生谐振时电路的特征。
3、研究串联电路参数对谐振特性的影响。
二、实验原理1、R L C 串联电压谐振在具有电阻、 电感和电容元件的电路中,电路两端的电压与电路中的电流一般是不同相的。
如果我们调节电路中电感和电容元件的参数或改变电源的频率就能够使得电路中的电流和电压出现了同相的情况。
电路的这种情况即电路的这种状态称为谐振。
R 、L 、C 串联谐振又称为电压谐振。
在由线性电阻R 、电感L 、电容c 组成的串联电路中,如图8-1所示。
图8-1 R L C 串联电路图当感抗和容抗相等时,电路的电抗等于零即X L = X C ; ; 2πf L=X = ω L - = 0则 ϕ = arc tg = 0即电源电压u 与电路中电流i 同相,由于是在串联电路中出现的谐振故称为串联谐振。
谐振频率用f 0表示为f = f 0 = 谐振时的角频率用ω 0表示为ω = ω 0 =谐振时的周期用T 0表示为T = T 0 = 2 π 串联电路的谐振角频率ω 0频率f 0,周期T 0,完全是由电路本身的有关参数来决定的,它们是电路本身的固有性质,而且每一个R 、L 、C 串联电路,只有一个对应的谐振频f 0和 周期T 0。
因而,对R 、L 、C 串联电路来说只有将外施电压的频率与电路的谐振频率相等时候,电路才会发生谐振。
在实际应用中,往往采用两种方法使电路发生谐振。
一种是当外施()2CL2X X R -+RU UU U电压频率f 固定时,改变电路电感L 或电容C 参数的方法,使电路满足谐振条件。
另一种是当电路电感L 或电容C 参数固定时,可用改变外施电压频率f 的方法,使电路在其谐振频率下达到谐振。
总之,在R 、L 、C 串联电路中,f 、L 、C 三个量,无论改变哪一个量都可以达到谐振条件,使电路发生谐振。
RLC串联谐振频率和其计算公式

RLC串联谐振频率及其计算公式串联谐振是指所研究的串联电路部分的电压和电流达到同相位,即电路中电感的感抗和电容的容抗在数值上时相等的,从而使所研究电路呈现纯电阻特性,在给定端电压的情况下,所研究的电路中将出现最大电流,电路中消耗的有功功率也最大.1. 谐振定义:电路中L、C 两组件之能量相等,当能量由电路中某一电抗组件释出时,且另一电抗组件必吸收相同之能量,即此两电抗组件间会产生一能量脉动。
2. 电路欲产生谐振,必须具备有电感器L及电容器C 两组件。
3. 谐振时其所对应之频率为谐振频率(resonance),或称共振频率,以f r表示之。
4. 串联谐振电路之条件如图1所示:当Q=Q ⇒I2X L = I2 X C也就是X L =X C时,为R-L-C串联电路产生谐振之条件。
图1 串联谐振电路图5. 串联谐振电路之特性:(1) 电路阻抗最小且为纯电阻。
即Z =R+jX L−jX C=R(2) 电路电流为最大。
即(3) 电路功率因子为1。
即(4) 电路平均功率最大。
即P=I2R(5) 电路总虚功率为零。
即Q L=Q C⇒Q T=Q L−Q C=06. 串联谐振电路之频率:(1) 公式:(2) R - L -C串联电路欲产生谐振时,可调整电源频率f 、电感器L 或电容器C使其达到谐振频率f r,而与电阻R完全无关。
7. 串联谐振电路之质量因子:(1) 定义:电感器或电容器在谐振时产生的电抗功率与电阻器消耗的平均功率之比,称为谐振时之品质因子。
(2) 公式:(3) 品质因子Q值愈大表示电路对谐振时之响应愈佳。
一般Q值在10~100 之间。
8. 串联谐振电路阻抗与频率之关系如图(2)所示:(1) 电阻R 与频率无关,系一常数,故为一横线。
(2) 电感抗X L=2 πfL ,与频率成正比,故为一斜线。
(3) 电容抗与频率成反比,故为一曲线。
(4) 阻抗Z = R+ j(X L−X C)当f = f r时,Z = R 为最小值,电路为电阻性。
RLC串联谐振频率及其计算公式

R L C串联谐振频率及其计算公式The document was finally revised on 2021RLC串联谐振频率及其计算公式串联谐振是指所研究的串联电路部分的电压和电流达到同相位,即电路中电感的感抗和电容的容抗在数值上时相等的,从而使所研究电路呈现纯电阻特性,在给定端电压的情况下,所研究的电路中将出现最大电流,电路中消耗的有功功率也最大.1. 谐振定义:电路中L、C 两组件之能量相等,当能量由电路中某一电抗组件释出时,且另一电抗组件必吸收相同之能量,即此两电抗组件间会产生一能量脉动。
2. 电路欲产生谐振,必须具备有电感器L及电容器C 两组件。
3. 谐振时其所对应之频率为谐振频率(resonance),或称共振频率,以f r 表示之。
4. 串联谐振电路之条件如图1所示:当Q=Q I2X L = I2 X C也就是X L =X C时,为R-L-C串联电路产生谐振之条件。
图1 串联谐振电路图5. 串联谐振电路之特性:(1) 电路阻抗最小且为纯电阻。
即 Z =R+jX L jX C=R(2) 电路电流为最大。
即(3) 电路功率因子为1。
即(4) 电路平均功率最大。
即P=I2R(5) 电路总虚功率为零。
即Q L=Q C Q T=Q L Q C=06. 串联谐振电路之频率:(1) 公式:(2) R - L -C串联电路欲产生谐振时,可调整电源频率f 、电感器L 或电容器C使其达到谐振频率f r,而与电阻R完全无关。
7. 串联谐振电路之质量因子:(1) 定义:电感器或电容器在谐振时产生的电抗功率与电阻器消耗的平均功率之比,称为谐振时之品质因子。
(2) 公式:(3) 品质因子Q值愈大表示电路对谐振时之响应愈佳。
一般Q值在10~100 之间。
8. 串联谐振电路阻抗与频率之关系如图(2)所示:(1) 电阻R 与频率无关,系一常数,故为一横线。
(2) 电感抗X L=2 πfL ,与频率成正比,故为一斜线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
