最新全等三角形的判定(SSS)练习题
11.2 三角形全等的判定(SSS)(含答案)

11.2 三角形全等的判定(SSS)题号一1 二2 三3 四4 五5 六6 七7 八8 得分度的反复训练才能取得跟多的收获,我们设计的试卷主要就是从这点出发,所以从你下载这张试卷开始,就与知识接近了一步。
◆课堂测控测试点边边边1.如图,点B,E,C,F在同一直线上,AB=DE,AC=DF,BE=CF,∠A=•43°,求∠D的度数,下面是小红同学的求解过程,请你说明每一步的理由.解:因为BE=CF,所以BE+EC=CF+EC,即BC=EF.在△ABC与△DEF中,,,AB DEAC DFBC EF=⎧⎪=⎨⎪=⎩所以△ABC≌△DEF().所以∠D=∠A=43°().2.已知:如图,C是AB的中点,AD=CE,CD=BE,求证:△ACD≌△CBE.◆课后测控3.如图,AC=BD,AB=DC,求证:∠B=∠C.4.已知:如图,点A,C,B,D都在一条直线上,AC=BD,AM=CN,BM=DN.求证:AM∥CN.5.三月三放风筝,下图是小明制作的风筝,他根据DE=DF,EH=FH,不用度量,就知道∠DEH=∠DFH.请你用所学知识给予证明.◆拓展测控6.有一块三角形的厚铁板(如图),根据实际生产需要,工人师傅要把∠MAN平分开,现在他手边只有一把尺子(没有刻度)和一根细绳,•你能帮助工人师傅想个办法吗?并说明你这样做的理由.答案:1.SSS 全等三角形对应角相等2.∵C是AB的中点,∴AC=BC.在△ACD与△CBE中,,,,AC CBAD CECD BE=⎧⎪=⎨⎪=⎩∴△ACD≌△CBE(SSS).[总结反思]三条边对应相等的两个三角形全等,•运用此结论可证明两个三角形全等.3.证明:在△ABD与△DCA中,,,,AB DCDB ACAD DA=⎧⎪=⎨⎪=⎩∴△ABD≌△DCA(SSS),∴∠B=∠C.[解题规律]证明线段相等或角相等时,常证明它们所在的两个三角形全等,本题中证明两个三角形全等已具备两个条件,运用公共边这个隐含条件是解题关键.4.∵AC=BD,∴AC+CB=BD+CB,即AB=CD.在△AMB和△CND中,,,,AM CNBM DNAB CD=⎧⎪=⎨⎪=⎩∴△AMB≌△CND(SSS).∴∠A=∠NCD,∴AM∥CN.[解题技巧]题目中条件AC=BD不能直接用来证明,可运用等式的性质变为AB=CD.5.证明:连结DH.在△DEH和△DFH中,,,.DE DFEH FHDH DH=⎧⎪=⎨⎪=⎩∴△DEH≌△DFH(SSS),∴∠DEH=∠DFH.[解题规律]连结EH即将原图形分成一对三角形,利用公共边运用SSS可得两个三角形全等.6.用绳子的一定长度在AM,AN边上截取AB=AC,再选取适当长度的绳子,将其对折,得绳子的中点D,把绳子的两端点固定在B,C两点,拽住绳子中点D,向外拉直BD和CD,•再在铁板上点出D的位置,作射线AD,则AD平分∠MAN.理由如下:如图,∵在△ABD和△ACD中,,,,AB ACBD CDAD AD=⎧⎪=⎨⎪=⎩∴△ABD≌△ACD(SSS),∴∠BAD=∠CAD,即AD平分∠MAN.[解题技巧]这是一道实际应用问题,通过构造两个三角形全等将∠MAN平分,•解题关键是得到绳子的中点并拉直绳子,从而可知DB=DC.可以编辑的试卷(可以删除)This document is collected from the Internet, which is convenient for readers to use. If there is any infringement, please contact the author and delete it immediately.。
全等三角形判定SSS练习题
5、已知:如图,AB=DC,AD=BC, 求证:∠A=∠C
A
D
B
C
全等三角形判定SSS练习题
6、已知:如图 , AB=AC , AD=AE , BD=CE.求证:∠BAC=∠DAE.
A
E
D
B
C
全等三角形判定SSS练习题
此课件下载可自行编辑修改,供参考! 感谢你的支持,我们会努力做得更好!
4、 如图,已知AB=CD,AC=BD, 求证:∠A=∠D.
AD
O
B
C
全等三角形判定SSS练习题
5、如图,已知AB=AD,AC=AE, BC=DE,求证:∠1=∠2
A
12ELeabharlann CBD全等三角形判定SSS练习题
1、已知AD=BE,BC=EF, AC=DF,求证EF//BC
D
A
E
F
B
C
全等三角形判定SSS练习题
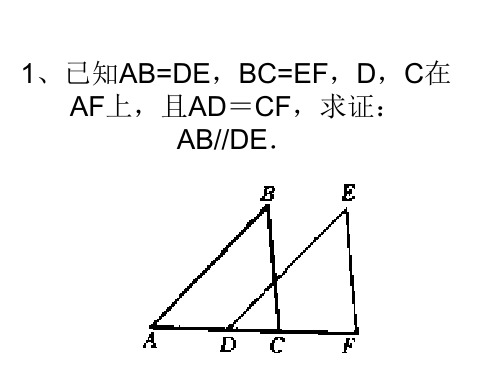
1、已知AB=DE,BC=EF,D,C在 AF上,且AD=CF,求证: AB//DE.
全等三角形判定SSS练习题
2、已知AB=DE,BC=EF,AF=CD, 求证EF//BC:
E
F1
A
2
C
D
B
全等三角形判定SSS练习题
3、如图,已知AB=AC,AD为 △ABC的中线,求证:AD⊥BC
A
BD C
全等三角形判定SSS练习题
2、如图,△ABC中,D是BC边的中 点,AB=AC,求证:∠B=∠C
A
B
D
C
全等三角形判定SSS练习题
3、已知:如图,B、E、C、F在一 条直线上,且BE=CF,AB=DE, AC=DF。 求证:△ABC≌△DEF
全等三角形的判定(SSS)

。 A
c
D
=
=
。B
E
图1
F
(2)∵△ABC≌△FDE(已证) ∴∠C=∠E(全等三角形的对应角相等)
(3)∵△ABC≌△FDE(已证) ∠A=∠F(全等三角形的对应角相等)
AC//EF(内错角相等,两直线平行)
例.有一种作已知角的平分线的方法,如图,在∠AOB的两边上 分别取点D、E,使OD=OE,再分别以D、E为圆心,大于DE一 半的长为半径作弧,两弧相交于点C,作射线OC,则OC就是 ∠AOB的平分线。试说明这种作法的正确性。
3.两个等腰直角三角形全等
(×)
4.都有两边长分别为3厘米和5厘米的两个 等腰三角形全等
(×)
5.都有两边长分别为3厘米和8厘米的两个
等腰三角形全等
(√ )
练习
已知:如图,AB=AC,DB=DC,
求证:∠B =∠C.
A
证:连接AD
在△ABD和△ACD中,
AB=AC (已知)
DB=DC (已知)
D
AD=AD (公共边)
3.连接线段A′B′ , A′C′.
A
A
B
C
B
C
△A′ B′ C′ 与 △ABC 能不能重合?是不是全等?
边边边公理:
三边对应相等的两个三角形全等。 简写为“边边边”或“SSS”
注:这个定理说明,只要三角形的三边的长度确定了, 这个三角形的形状和大小就完全确定了, 这也是三角形具有稳定性的原理。
A
B
C
∴△ABD≌△ACD (SSS)
∴∠B =∠C (全等三角形的对应角相等)
练习
已知:AC=AD,BC=BD, 求证:AB是∠DAC的平分线.
全等三角形判定SSS练习题(优选)
A
C
F
E
B
D
11
2、如图,△ABC中,D是BC边的中 点,AB=AC,求证:∠B=∠C
A
B
D
C
12
3、已知:如图,B、E、C、F在一 条直线上,且BE=CF,AB=DE, AC=DF。 求证:△ABC≌△DEF
A
D
B
E
C
F
13
4、已知:如图,AD=BC,AC=BD. 求证:∠OCD=∠ODC
14
A
D
B
C
8
4、已知C是BD上一点, AC=CE,AB=CD,BC=DE, ∠B=900 求证:AC⊥CE
A
B C
E D
9
5、如图,已知AE=AB,AF=AC, EC=BF,求证:∠CMF=∠CAF
F
ቤተ መጻሕፍቲ ባይዱ
E
A
M
B
C
10
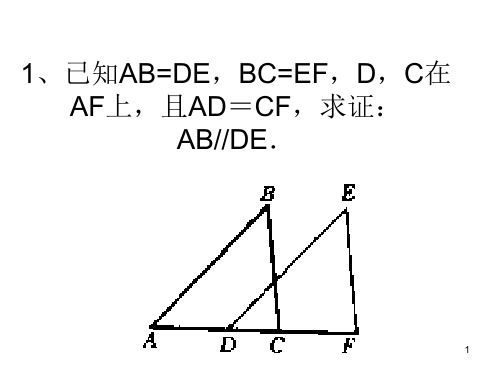
1、已知:如图,A、B、E、F在一条 直线上,且AC=BD,CE=DF, AF=BE。求证:△ACE≌△BDF
5、已知:如图,AB=DC,AD=BC, 求证:∠A=∠C
A B
D C
15
6、已知:如图 , AB=AC , AD=AE , BD=CE.求证:∠BAC=∠DAE.
A
E
D
B
C
16
点击此处添加标题
欢迎使用 可删
AD
O
B
C
4
5、如图,已知AB=AD,AC=AE, BC=DE,求证:∠1=∠2
A
12
E
C
B
D
5
1、已知AD=BE,BC=EF, AC=DF,求证EF//BC
全等三角形的判定精选练习题分SSSSASAASASAHL分专题

全等三角形的判定(SSS)1、如图1,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是()A。
120°B.125°C。
127° D。
104°2、如图2,线段AD与BC交于点O,且AC=BD,AD=BC,•则下面的结论中不正确的是( )A.△ABC≌△BAD B。
∠CAB=∠DBA C.OB=OC D。
∠C=∠D3、在△ABC和△A1B1C1中,已知AB=A1B1,BC=B1C1,则补充条件____________,可得到△ABC≌△A1B1C1.4、如图3,AB=CD,BF=DE,E、F是AC上两点,且AE=CF.欲证∠B=∠D,可先运用等式的性质证明AF=________,再用“SSS”证明______≌_______得到结论。
5、如图,已知AB=CD,AC=BD,求证:∠A=∠D.6、如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.请推导下列结论:⑴∠D=∠B;⑵AE∥CF.7、已知如图,A、E、F、C四点共线,BF=DE,AB=CD.⑴请你添加一个条件,使△DEC≌△BFA;⑵在⑴的基础上,求证:DE∥BF.全等三角形的判定(SAS)1、如图1,AB∥CD,AB=CD,BE=DF,则图中有多少对全等三角形( )A.3 B。
4 C.5 D。
6CBA 2、如图2,AB=AC ,AD=A E,欲证△A BD ≌△A CE ,可补充条件( ) A 。
∠1=∠2B .∠B=∠C C.∠D=∠ED 。
∠BAE=∠C AD 3、如图3,AD=B C,要得到△AB D和△CD B全等,可以添加的条件是( )A .AB∥CD B。
AD ∥B CC .∠A=∠C D.∠ABC =∠CDA4、如图4,AB 与CD 交于点O ,O A=OC ,OD =OB ,∠A OD =________,•根据_________可得到△AOD ≌△COB ,从而可以得到AD=_________.5、如图5,已知△ABC 中,AB=AC ,A D平分∠BAC ,请补充完整过程说明△A BD≌△ACD 的理由。
三角形全等的判定(SSS,SAS)同步训练

1、如图,AB=AC ,BD=CD ,求证:∠1=∠2.
2.如图, DA DB = ,AC BC =。
求证:DAC
DBC ∆≅∆
3、如图,已知AB=CD ,AC=BD ,求证:∠A=∠D .
4、如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.请推导下列结论:⑴∠D=∠B;⑵AE∥CF.
5.如图,点E,F在BD上,且AB=CD,BF=DE,AE=CF,AC与BD相交于点O.求证:AE∥CF.
6、已知如图,A、E、F、C四点共线,BF=DE,AB=CD.
⑴请你添加一个条件,使△DEC≌△BFA;
⑵在⑴的基础上,求证:DE∥BF.
C B A 7、如图6,已知AB=A
D ,AC=A
E ,∠1=∠2,求证∠ADE=∠B.
8、如图,已知AB=AD ,若AC 平分∠BAD ,问AC 是否平分∠BCD ?为什么?
9.如图,已知在ABC △中,AB AC =,12∠=∠.
求证:AD BC ⊥,BD DC =.
A C
2 1
3 4
10. 如图,CF BE =, DC AB =, C B ∠=∠ ,求证:DCE ABF ∆≅∆
11.如图,点C 是BD 的中点 ,EC AC =, , ECB ACD ∠=∠ ,求证:EDC ABC ∆≅∆
12.如图,点M ,N 在线段AC 上,AM =CN ,AB ∥CD ,AB =CD.求证:∠1=∠2.。
全等三角形的性质与判定(SSS、SAS、ASA、AAS)练习题

全等三角形的性质与判断(SSS、SAS、ASA 、AAS )练习题1.如图,在△2.如图,把△则∠ A=A ABC中,∠ A=90°, D、 E 分别是 AC、 BC上的点,若△ ADB≌△ EDB≌△ EDC,则∠ C= ABC 绕点 C 顺时针旋转35°,获得△ A′ B′ C, A′ B′交 AC 于点 D,若∠ A′ DC=90°,A' BEDAD D A' C FCB'B'AB E CB CO A B1题图2题图3题图4题图3.如图,△ AOB 中,∠ B=3 0°,将△ AOB 绕点 O 顺时针旋转 52°,获得△ A′ OB′,边 A′B′与边OB交于点 C( A′不在 OB上),则∠ A′ CO=4.如图,△ AB C≌△ ADE , BC 的延伸线过点 E,∠ ACB= ∠ AED=10 5°,∠ CAD=1 0°,∠ B=50°,则∠ DEF=5.如图, Rt △ ABC中,∠ BAC=90°, AB=AC,分别过点 B、 C 作过点 A 的垂线 BC、CE,垂足分别为 D、E,若 BD=3 , CE=2 ,求 DE 的长 .BCD A E6.如图, AD 是△ ABC的角均分线, DE⊥AB, DF⊥AC,垂足分别是 E、 F,连结 EF,交 AD 于 G,试判断AD与 EF的关系,并证明你的结论。
AEGFBDC7.如下图,在△ ABC 中, AD 为∠ BAC 的角均分线, DE⊥ AB 于 E, DF⊥ AC 于 F,△ ABC 的面积是28cm2,AB=20cm,AC=8cm,求 DE的长。
AE FB D C8.如图, AD=BD , A D⊥ BC于 D, BE⊥ AC于 E, AD与 BE 订交于点 H,则 BH与 AC相等吗?为何?AEH- 1 -B D C1 / 49.已知: BD 、 CE 是△ ABC 的高,点 F 在 BD 上, BF=AC ,点 G 在 CE 的延伸线上, CG=AB ,求证: A G⊥AFG AE DFB C10.如图:在△ ABC中, BE、 CF 分别是 AC、AB 两边上的高,在 BE 上截取 BD=AC,在 CF 的延伸线上截取CG=AB,连结 AD、 AG.试判断 AD与 AG的关系怎样?并证明之.AGF EDHB C11.已知,如图:AB=AE,∠ B=∠ E,∠ BAC=∠ EAD,∠ CAF=∠ DAF,求证:AF⊥ CDAEBC F DA12.已知:∠ B=∠ E,且AB=AE。
全等三角形综合练习题含答案

全等三角形的判定(SSS)1、如图1,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是( )°°°°2、如图2,线段AD与BC交于点O,且AC=BD,AD=BC,•则下面的结论中不正确的是( )A.△ABC≌△BADB.∠CAB=∠DBA =OC D.∠C=∠D3、在△ABC和△A1B1C1中,已知AB=A1B1,BC=B1C1,则补充条件____________,可得到△ABC≌△A1B1C1.4、如图3,AB=CD,BF=DE,E、F是AC上两点,且AE=CF.欲证∠B=∠D,可先运用等式的性质证明AF=________,再用“SSS”证明______≌_______得到结论.5、如图,AB=AC,BD=CD,求证:∠1=∠2.6、如图,已知AB=CD,AC=BD,求证:∠A=∠D.7、如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.请推导下列结论:⑴∠D=∠B;⑵AE∥CF.8、已知如图,A、E、F、C四点共线,BF=DE,AB=CD.⑴请你添加一个条件,使△DEC≌△BFA;⑵在⑴的基础上,求证:DE∥BF.全等三角形的判定方法SAS专题练习1.如图,AB=AC,AD=AE,欲证△ABD≌△ACE,可补充条件( )A.∠1=∠2B.∠B=∠CC.∠D=∠ED.∠BAE=∠CAD2.能判定△ABC≌△A′B′C′的条件是()A.AB=A′B′,AC=A′C′,∠C=∠C′B. AB=A′B′,∠A=∠A′,BC=B′C′C. AC=A′C′,∠A=∠A′,BC=B′CD. AC=A′C′,∠C=∠C′,BC=B′C3.如图,AB与CD交于点O,OA=OC,OD=OB,∠AOD= ,根据_________可得到△AOD≌△COB,从而可以得到AD=_________.4.如图,已知BD=CD,要根据“SAS”判定△ABD≌△ACD,则还需添加的条件是。
全等三角形的判定精选练习题(分SSS、SAS、AAS、ASA、HL分专题)

全等三角形的判定(SSS)之南宫帮珍创作1、如图1, AB=AD, CB=CD, ∠B=30°, ∠BAD=46°, 则∠ACD的度数是( )°°°°2、如图2, 线段AD与BC交于点O, 且AC=BD, AD=BC, •则下面的结论中不正确的是( )A.△ABC≌△BADB.∠CAB=∠DBAC.OB=OCD.∠C=∠D3、在△ABC和△A1B1C1中, 已知AB=A1B1, BC=B1C1, 则弥补条件____________, 可获得△ABC≌△A1B1C1.4、如图3, AB=CD, BF=DE, E、F是AC上两点, 且AE=CF.欲证∠B=∠D, 可先运用等式的性质证明AF=________, 再用“SSS”证明______≌_______获得结论.5、如图, 已知AB=CD, AC=BD, 求证:∠A=∠D.6、如图, AC与BD交于点O, AD=CB, E、F是BD上两点, 且AE=CF, DE=BF.请推导下列结论:⑴∠D=∠B;⑵AE∥CF.7、已知如图, A、E、F、C四点共线, BF=DE, AB=CD.⑴请你添加一个条件, 使△DEC≌△BFA;⑵在⑴的基础上, 求证:DE∥BF.全等三角形的判定(SAS)1、如图1, AB∥CD, AB=CD, BE=DF, 则图中有几多对全等三角形( )2、如图2, AB=AC, AD=AE, 欲证△ABD≌△ACE, 可弥补条件( )A.∠1=∠2B.∠B=∠CC.∠D=∠ED.∠BAE=∠CAD3、如图3, AD=BC, 要获得△ABD和△CDB全等, 可以添加的条件是( )∥∥BC C.∠A=∠C D.∠ABC=∠CDA4、如图4, AB与CD交于点O, OA=OC, OD=OB, ∠AOD=________,•根据_________可获得△AOD≌△COB,从而可以获得AD=_________.DC BA5、如图5, 已知△ABC 中, AB=AC, AD 平分∠BAC, 请弥补完整过程说明△ABD ≌△ACD 的理由.∵AD 平分∠BAC, ∴∠________=∠_________(角平分线的界说).在△ABD 和△ACD 中,∵____________________________, ∴△ABD ≌△ACD ( )6、如图6, 已知AB=AD, AC=AE, ∠1=∠2, 求证∠ADE=∠B.7、如图, 已知AB=AD, 若AC 平分∠BAD, 问AC 是否平分∠BCD ?为什么?8、如图, 在△ABC 和△DEF 中, B 、E 、F 、C, 在同一直线上, 下面有4个条件, 请你在其中选3个作为题设, 余下的一个作为结论, 写一个真命题, 并加以证明.①AB=DE ;②AC=DF ;③∠ABC=∠DEF ;④BE=CF.9、如图⑴, AB ⊥BD, DE ⊥BD, 点C 是BD 上一点, 且BC=DE, CD=AB .⑴试判断AC 与CE 的位置关系, 并说明理由.⑵如图⑵, 若把△CDE 沿直线BD 向左平移, 使△CDE 的极点C 与B 重合, 此时第⑴问中AC 与BE 的位置关系还成立吗?(注意字母的变动)全等三角形(三)AAS 和ASA 【知识要点】1.角边角定理(ASA ):有两角及其夹边对应相等的两个三角形全等.2.角角边定理(AAS ):有两角和其中一角的对边对应相等的两个三角形全等. 【典范例题】例1.如图, AB ∥CD, AE=CF, 求证:AB=CD例2.如图, 已知:AD=AE, ABE ACD ∠=∠, 求证:BD=CE.例3.如图, 已知:ABD BAC D C ∠=∠∠=∠., 求证:OC=OD.例4.如图已知:AB=CD, AD=BC, O 是BD 中点, 过O别交DA 和BC 的延长线于E, F.求证:AE=CF.例5.如图, 已知321∠=∠=∠, AB=AD.求证:例6.如图, 已知四边形ABCD 中点E 在BC 上, AF=CE, EF 的对角线BD交于征?【经典练习】1.△ABC 和△C B A '''中, C B C B A A ''='∠=∠,', ∠C B A '''.2.如图, 点C, F 在BE 上, ,,21EF BC =∠=∠请弥补一个条件, 使△ABC ≌DFE,弥补的条件是.3.在△ABC 和△C B A '''中, C B A '''全等的个数有( )①A A '∠=∠B B '∠=∠, C B BC ''=②A A '∠=∠, B B '∠=∠, C A C A ''='③A A '∠=∠B B '∠=∠, C B AC ''=④A A '∠=∠,B B '∠=∠,C A B A ''='A . 1个B. 2个C. 3个D. 4个4.如图, 已知MB=ND, NDC MBA ∠=∠, 下列条件不能判定是△ABM ≌△CDN 的是( )A . N M ∠=∠ B. AB=CD C . AM=CN D. AM ∥CN5.如图2所示, ∠E =∠F =90°, ∠B =∠C , AE =AF , 给出下列结论:C①∠1=∠2 ②BE=CF ③△ACN≌△ABM ④CD=DN其中正确的结论是__________________.(注:将你认为正确的结论填上)图2 图36.如图3所示, 在△ABC和△DCB中, AB=DC, 要使△ABO≌DCO, 请你弥补条件________________(只填写一个你认为合适的条件). 7. 如图, 已知∠A=∠C, AF=CE, DE∥BF, 求证:△ABF≌△CDE. 8.如图, CD⊥AB, BE⊥AC, 垂足分别为D、E, BE交CD于F, 且AD=DF, 求证:AC= BF.9.如图, AB, CD相交于点O, 且AO=BO, 试添加一个条件, 使△AOC≌△BOD, 并说明添加的条件是正确的.(很多于两种方法)10.如图, 已知:BE=CD, ∠B=∠C, 求证:∠1=∠2.11.如图, 在Rt△ABC中, AB=AC, ∠BAC=90º, 多点AAN, BD⊥AN于D,CE⊥AN于E, 你能说说DE=BD-CE的理由吗?直角三角形全等HL【知识要点】斜边直角边公理:有斜边和直角边对应相等的两个直角三角形全等.【典范例题】例1 如图, B、E、F、C在同一直线上, AE⊥BC, DF⊥BC, AB=DC, BE=CF, 试判断AB与CD的位置关系. A例2 已知 如图, AB ⊥BD, CD ⊥BD, AB=DC, 求证:AD ∥BC.例 3 公路上A 、B为两村落(视为两个点), DA ⊥AB 于点A, CB DA=16km, BC=10km, 现要在公路AB 上建一个土特产收购站CD两村落到E 站的距离相等, 那么E 站应建在距A 理?例4 如图, AD 是△ABC 的高, E 为AC 上一点, BE 交AD 于F, 具有BF=AC, FD=CD, 试探究BE 与AC 的位置关系.例 5 如图, A 、E 、F 、B 四点共线, AC ⊥CE AC=BD, 求证:△ACF ≌△BDE. 【经典练习】1.在Rt △ABC 和Rt △DEF 中, ∠ACB=∠DFE=90那么Rt △ABC 与Rt △DEF(填全等或不全等)2.如图, 点C 在∠DAB 的内部, CD ⊥AD 于D, CB ⊥AB 于B, CD=CB 那么Rt △ADC ≌Rt △ABC 的理由是( )A .SSS B. ASA C. SAS D. HL3.如图, CE ⊥AB, DF ⊥AB, 垂足分别为E 、F, AC ∥DB, 且AC=BD, 那么Rt △AEC ≌Rt △BFC 的理由是( ).A .SSSB. AASC. SASD. HL 4.下列说法正确的个数有( ).②有两边对应相等的两个直角三角形全等;③有两边和一角对应相等的两个直角三角形全等;BBC BC④有两角和一边对应相等的两个直角三角形全等. A .1个B. 2个C. 3个D. 4个5.过等腰△ABC 的极点A 作底面的垂线, 就获得两个全等三角形, 其理由是.6.如图, △ABC 中, ∠C=︒90, AM 平分∠CAB, CM=20cm, 那么M 到AB 的距离是( )cm.7.在△ABC 和△C B A '''中, 如果AB=B A '', ∠B=∠B ', AC=C A '', 那么这两个三角形( ).A .全等B. 纷歧定全等 C. 不全等D. 面积相等, 但不全等 8.如图, ∠B=∠D=︒90, 要证明△ABC 与△ADC 全等, 还需要弥补的条件是.9.如图, 在△ABC 中, ∠ACB=︒90, AC=BC, 直线MN 经过点C, 且AD ⊥MN 于D, BE ⊥MN 于E,求证:DE=AD+BE.10.如图, 已知AC ⊥BC, AD ⊥BD, AD=BC, CE ⊥AB, DF ⊥AB,垂足分别为E 、F, 那么, CE=DF 吗?谈谈你的理由! 11.如图, 已知AB=AC, AB ⊥BD, AC ⊥CD, AD, BC 相交于点E, 求证:(1)CE=BE ;(2)CB ⊥AD.提高题型: 1.如图, △ABC 中, D 是BC 上一点, DE⊥AB, DF⊥AC, E、F 分别为垂足, 且AE=AF, 试说明:DE=DF, AD 平分∠BAC.2.如图, 在ABC 中, D 是BC 的中点, DE⊥AB, DF⊥AC, 垂足分别是E 、F, 且DE=DF, 试说明AB=AC.3.如图, AB=CD, DF ⊥AC 于F, BE ⊥AC 于E, DF=BE, 求证:AF=CE.4.如图, △ABC 中, ∠C=90°, AB=2AC, M 是AB 的中点, 点N 在BC 上, MN ⊥AB.求证:AN 平分∠BAC.创作时间:二零二一年六月三十日┐ AB M CAC DBA DB ENC A B C DE F AE DBCAD C BFEM。
全等三角形的判定精选练习题 简单(分SSS、SAS、AAS、ASA、HL分专题)

CBA全等三角形的判定(SSS)不要写在上面,答案写在纸上1、如图1,已知AB=CD,AC=BD,求证:∠A=∠D.图1 图2 图3 图42、如图2,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.请推导下列结论:⑴∠D=∠B;⑵AE∥CF.3、已知如图3,A、E、F、C四点共线,BF=DE,AB=CD.⑴请你添加一个条件,使△DEC≌△BFA;⑵在⑴的基础上,求证:DE∥BF.4、如图4,AB=AC,BD=CD,求证:∠1=∠2.全等三角形的判定(SAS)4、如图4,AB与CD交于点O,OA=OC,OD=OB,求证AD=CB.图7 图8 图95、如图5,已知△ABC中,AB=AC,AD平分∠BAC,求证△ABD≌△ACD6、如图6,已知AB=AD,AC=AE,∠1=∠2,求证∠ADE=∠B.7、如图7,已知AB=AD,若AC平分∠BAD,求证AC平分∠BCD8、如图8,在△ABC和△DEF中,B、E、F、C,在同一直线上,①AB=DE;③∠ABC=∠DEF;④BE=CF. 证明AC=DF9、如图9,AB⊥BD,DE⊥BD,点C是BD上一点,且BC=DE,CD=AB.⑴如图1证明AC与CE垂直⑵如图2,若把△CDE沿直线BD向左平移,使△CDE的顶点C与B重合,此时第⑴问中AC与BE的位置关系还成立吗?(注意字母的变化)【典型题】1.如图1,AB∥图5图2 图32.如图2,已知:AD=AE,ABEACD∠=∠,求证:BD=CE.3.如图3,已知:ABDBACDC∠=∠∠=∠.,求证:OC=OD. 图64.如图4已知:AB=CD,AD=BC,O是BD中点,过O点的直线分别交DA和BC的延长线于E,F.求证:AE=CF.5.如图5,已知321∠=∠=∠,AB=AD.求证:BC=DE.6.如图6,已知四边形ABCD中,AB=DC,AD=BC,点F在AD上,点E在BC上,AF=CE,EF的对角线BD交于O,求证:OF=OE 7. 如图7,已知∠A=∠C,AF=CE,DE∥BF,求证:△ABF≌△CDE.8.如图8,CD⊥AB,BE⊥AC,垂足分别为D、E,BE交CD于F,且AD=DF,求证:AC= BF。
全等三角形判定(SSS)

E
F
用 数学语言表述:
在△ABC和△ DEF中
∴ △ABC ≌△ DEF(SSS)
AB=DE BC=EF CA=FD
结论:三边分别都相等的两个三角形全等(SSS)
例1. 如下图,△ABC是一个刚架,AB=AC,AD是连接A与BC中点D的支架。 求证:△ ABD≌ △ ACD
添加标题
小结
添加标题
知道三角形三条边的长度怎样画三角形。
添加标题
①只给一条边:
②只给一个角:
60°
60°
60°
探究:
只给出一个条件时不能保证所画的两个三角形一定全等.
2.给出两个条件:
①一边一内角:
②两内角:
③两边:
30°
30°
30°
30°
30°
50°
50°
2cm
2cm
4cm
4cm
可以发现按两个条件画的两个三角形也不能保证一定全等。
已知一个三角形的三个内角是80°、60°、40°,它们全等吗?
∴ △ ABD≌ △ACD(SSS)
A
B
C
D
证明:∵D是BC的中点 ∴BD=CD 在△ABD和△ACD中,
AB=AC(已知) AD=AD(公共边) DB=DC
∴ △ ABD≌ △ACD(SSS)
∴∠1= ∠2(全等三角形对应角相等) ∵ ∠1+∠2=180º
∴∠1= ∠BDC=90º
结论:三个内角对应相等的两个三角形不一定全等。
A
B
C
60°
80°
40°
D
E
F
60°
40°
80°
3、给出三个条件:(三个角相等)
三角形全等的判定(SSS、SAS) 习题

全等三角形(SSS 、SAS)之羊若含玉创作例1:如图, CE=DE ,EA=EB ,CA=DB ,求证:∠CAB=∠DBA 证明∵CE=DE , EA=EB ( )∴________=________即:_______=________在△ABC 和△BAD .中,∵()()()⎪⎩⎪⎨⎧===___________________________________________已证已知∴△ABC ≌△BAD .( )∴∠CAB=∠DBA ( )练一练:1、如图,AC =BD ,BC =AD ,说明.∠C=∠D证明:在△ABC 与△BAD 中,∴△ABC ≌△BAD ( )∴∠C=∠___ ( ) 2、如图,AB=DF ,AC=DE ,BE=FC ,问:(1)ΔABC 与ΔDFE 全等吗? (2)AB 与DF 平行吗?请说明你的来由.3、如图1所示,点C 、F 在直线AD 上,且AF=DC ,AB=DE ,BC=EF.(1)试说明AB ∥DE;(2)不雅察图2,图3,指出它们是怎样由图1变换得到的?(3)在知足已知条件的情况下依据图2,试证明BC ∥EF. A DF B AC B A C A BF C4、已知AB ⊥BD ,ED ⊥BD ,AB=CD ,BC=DE ,点B 、C 、D 在一条直线上,求证:AC ⊥CE.5、(多变题)已知AB=CD ,AD=CB ,求证:∠A=∠C一变:已知AD ∥BC ,AD=CB ,试证明:△ADC ≌△CBA 二变:已知AD ∥BC ,AD=CB ,AE=CF.试证:△AFD ≌△CEB 6、(实际运用)有一湖的湖岸在A 、B 之间呈不规矩形状,A 、B 之间的距离不克不及直接丈量,你能用已学过的知识或办法设计丈量计划并求出A 、B 之间的距离吗?做一做:7、如图所示,有一块三角形的镜子,小明不小心弄破裂成1、2两块,现需配成同样大小的一块.为了便利起见,需带上________块,其来由是__________.8、如图所示,AB ,CD 相交于O ,且AO =OB ,不雅察图形,图中已具备的另一相等的条件是________,联想到SAS ,只需填补条件________,则有△AOC ≌△_______9、如图,已知CA=CB ,AD=BD ,E ,F 分离为CB ,CA 的中点,求证:DE=DF10、如图,已知AB =AE ,∠B =∠E ,BC =ED ,点F 是CD 的中点.求证:AF ⊥CD.11、已知△ABE 和三角形DEC 均为等边三角形,衔接BD ,AC ,求证:AC =BD D E B A C FE C B DA。
全等三角形的判定精选练习题(分专题)
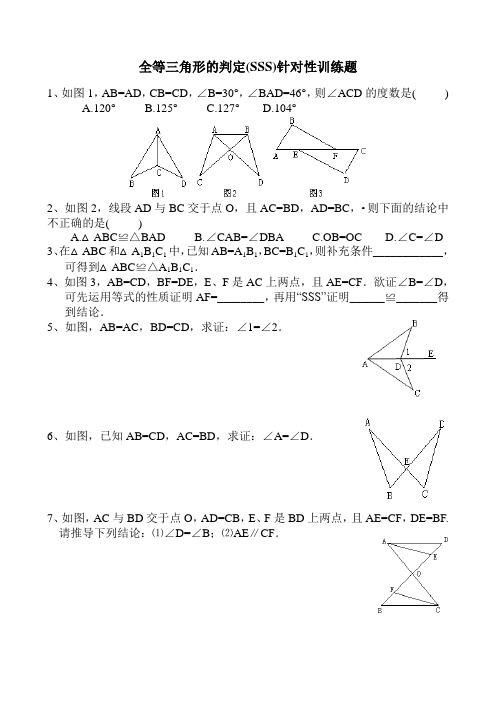
全等三角形的判定(SSS)针对性训练题1、如图1,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是( )A.120°B.125°C.127°D.104°2、如图2,线段AD与BC交于点O,且AC=BD,AD=BC,•则下面的结论中不正确的是( )A.△ABC≌△BADB.∠CAB=∠DBAC.OB=OCD.∠C=∠D3、在△ABC和△A1B1C1中,已知AB=A1B1,BC=B1C1,则补充条件____________,可得到△ABC≌△A1B1C1.4、如图3,AB=CD,BF=DE,E、F是AC上两点,且AE=CF.欲证∠B=∠D,可先运用等式的性质证明AF=________,再用“SSS”证明______≌_______得到结论.5、如图,AB=AC,BD=CD,求证:∠1=∠2.6、如图,已知AB=CD,AC=BD,求证:∠A=∠D.7、如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.请推导下列结论:⑴∠D=∠B;⑵AE∥CF.8、已知如图,A、E、F、C四点共线,BF=DE,AB=CD.⑴请你添加一个条件,使△DEC≌△BFA;⑵在⑴的基础上,求证:DE∥BF.全等三角形的判定(SAS)针对性训练题1、如图1,AB∥CD,AB=CD,BE=DF,则图中有多少对全等三角形( )A.3B.4C.5D.62、如图2,AB=AC,AD=AE,欲证△ABD≌△ACE,可补充条件( )A.∠1=∠2B.∠B=∠CC.∠D=∠ED.∠BAE=∠CAD3、如图3,AD=BC,要得到△ABD和△CDB全等,可以添加的条件是( )A.AB∥CDB.AD∥BCC.∠A=∠CD.∠ABC=∠CDA4、如图4,AB与CD交于点O,OA=OC,OD=OB,∠AOD=________,•根据_________可得到△AOD≌△COB,从而可以得到AD=_________.5、如图5,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程说明△ABD≌△ACD的理由.∵AD平分∠BAC,∴∠________=∠_________(角平分线的定义).在△ABD和△ACD中,∵____________________________,∴△ABD≌△ACD()DC BA 6、如图6,已知AB=AD ,AC=AE ,∠1=∠2,求证∠ADE=∠B.7、如图,已知AB=AD ,若AC 平分∠BAD ,问AC 是否平分∠BCD ?为什么?8、如图,在△ABC 和△DEF 中,B 、E 、F 、C ,在同一直线上,下面有4个条件,请你在其中选3个作为题设,余下的一个作为结论,写一个真命题,并加以证明.①AB=DE ; ②AC=DF ; ③∠ABC=∠DEF ; ④BE=CF.9、如图⑴,AB ⊥BD ,DE ⊥BD ,点C 是BD 上一点,且BC=DE ,CD=AB .⑴试判断AC 与CE 的位置关系,并说明理由. ⑵如图⑵,若把△CDE 沿直线BD 向左平移,使△CDE 的顶点C 与B 重合,此时第⑴问中AC 与BE 的位置关系还成立吗?(注意字母的变化)全等三角形的判定(AAS)和(ASA)针对性训练题 【典型例题】例1.如图,AB ∥CD ,AE=CF ,求证:AB=CD例2.如图,已知:AD=AE ,ABE ACD ∠=∠,求证:BD=CE.例3.如图,已知:ABD BAC D C ∠=∠∠=∠.,求证:OC=OD.例4.如图已知:AB=CD ,AD=BC ,O 是BD 中点,过O 点的直线分别交DA和BC 的延长线于E ,F.求证:AE=CF. 例5.如图,已知321∠=∠=∠,AB=AD.求证:BC=DE.例6.如图,已知四边形ABCD 中,AB=DC ,AD=BC ,点F 在AD 上,点E 在BC 上,AF=CE ,EF 的对角线BD 交于O ,请问O 点有何特征?AEABDC EO12 3 AFDOBECABCDO【经典练习】1.△ABC 和△C B A '''中,C B C B A A ''='∠=∠,',C C '∠=∠则△ABC 与△C B A ''' .2.如图,点C ,F 在BE 上,,,21EF BC =∠=∠请补充一个条件,使△ABC ≌DFE,补充的条件是 .3.在△ABC 和△C B A '''中,下列条件能判断△ABC 和△C B A '''全等的个数有( ) ①A A '∠=∠ B B '∠=∠,C B BC ''= ②A A '∠=∠,B B '∠=∠,C A C A ''=' ③A A '∠=∠ B B '∠=∠,C B AC ''= ④A A '∠=∠,B B '∠=∠,C A B A ''='A . 1个B. 2个C. 3个D. 4个4.如图,已知MB=ND ,NDC MBA ∠=∠,下列条件不能判定是△ABM ≌△CDN 的是( )A .N M ∠=∠ B. AB=CDC . AM=CND. AM ∥CN5.如图所示, ∠E =∠F =90°,∠B =∠C ,AE =AF , 给出下列结论①∠1=∠2 ②BE=CF ③△ACN ≌△ABM④CD=DN ,其中正确的结论是_________。
全等三角形的判定精选练习题(分SSS、SAS、AAS、ASA、HL分专题)
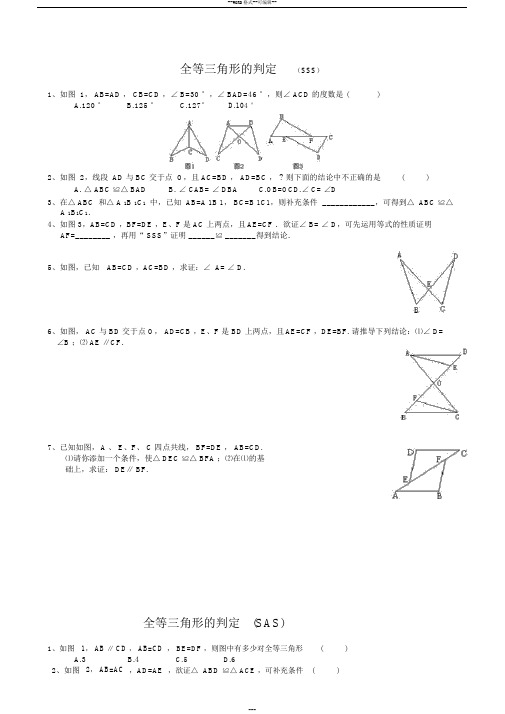
全等三角形的判定(SSS)1、如图 1, AB=AD , CB=CD ,∠ B=30 °,∠ BAD=46 °,则∠ ACD 的度数是 ()A.120 °B.125 °C.127°D.104 °2、如图 2,线段 AD 与 BC 交于点 O,且 AC=BD , AD=BC , ? 则下面的结论中不正确的是()A. △ ABC ≌△ BADB. ∠ CAB= ∠ DBAC.OB=OCD.∠ C= ∠D3、在△ ABC 和△ A 1B 1C1中,已知 AB=A 1B 1, BC=B 1C1,则补充条件 ____________,可得到△ ABC ≌△A 1B1C1.4、如图 3,AB=CD ,BF=DE ,E、F 是 AC 上两点,且AE=CF .欲证∠ B= ∠ D,可先运用等式的性质证明AF=________ ,再用“ SSS”证明 ______≌ _______得到结论.5、如图,已知AB=CD ,AC=BD ,求证:∠ A= ∠ D.6、如图, AC 与 BD 交于点 O, AD=CB ,E、F 是 BD 上两点,且AE=CF ,DE=BF. 请推导下列结论:⑴∠ D=∠B ;⑵ AE ∥CF.7、已知如图,A 、 E、F、 C 四点共线, BF=DE , AB=CD.⑴请你添加一个条件,使△ DEC ≌△ BFA ;⑵在⑴的基础上,求证: DE∥ BF.全等三角形的判定(SAS)1、如图1, AB ∥ CD , AB=CD, BE=DF ,则图中有多少对全等三角形()A.3B.4C.5D.62、如图2, AB=AC,AD=AE,欲证△ABD≌△ ACE ,可补充条件()A. ∠ 1= ∠23、如图 3, AD=BCA.AB ∥ CDB.∠ B= ∠ C,要得到△ ABDB.AD ∥ BCC.∠ D= ∠ ED. ∠BAE= ∠CAD 和△CDB 全等,可以添加的条件是 ( C.∠A=∠ C D. ∠ABC= ∠ CDA)4、如图 4, AB 与 CD 交于点 O, OA=OC , OD=OB ,∠ AOD=________ , ? 根据 _________可得到△ AOD≌△ COB,从而可以得到AD=_________ .5、如图 5,已知△ ABC 中, AB=AC , AD 平分∠ BAC ,请补充完整过程说明△∵ AD 平分∠ BAC ,∴∠ ________=∠ _________(角平分线的定义).在△ ABD 和△ ACD 中,∵ ____________________________ ,∴△ ABD≌△ ACD(ABD)≌△ ACD的理由.6、如图 6,已知 AB=AD , AC=AE ,∠ 1= ∠ 2,求证∠ ADE= ∠ B.7、如图,已知AB=AD ,若 AC 平分∠ BAD ,问 AC 是否平分∠ BCD ?为什么?BA CD8、如图,在△ABC 和△ DEF 中, B 、 E、 F、 C,在同一直线上,下面有 4 个条件,请你在其中选 3 个作为题设,余下的一个作为结论,写一个真命题,并加以证明.①AB=DE ;② AC=DF ;③∠ ABC= ∠ DEF ;④ BE=CF.9、如图⑴, AB ⊥ BD , DE⊥ BD ,点 C 是 BD 上一点,且BC=DE , CD=AB .⑴试判断AC 与 CE 的位置关系,并说明理由.⑵如图⑵,若把△CDE 沿直线 BD 向左平移,使△CDE 的顶点 C 与 B 重合,此时第⑴问中的位置关系还成立吗?(注意字母的变化)AC与BE全等三角形(三) AAS和 ASA【知识要点】1.角边角定理( ASA):有两角及其夹边对应相等的两个三角形全等.2 .角角边定理( AAS):有两角和其中一角的对边对应相等的两个三角形全等.【典型例题】例 1.如图, AB∥ CD, AE=CF,求证: AB=CDD FC O例 2.如图,已知: AD=AE,ACD ABE ,求证:BD=CE.AE BAD E例 3.如图,已知:CD . BAC ABD ,求证:OC=OD.B CD COA B例 4.如图已知: AB=CD,AD=BC,O是 BD中点,过 O点的直线分别交DA和 BC的延长线于E,F. 求证: AE=CF.FDCOAB例 5.如图,已知123 ,AB=AD.求证:BC=DE.EA2E1OB D 3C例6.如图,已知四边形 ABCD中, AB=DC,AD=BC,点 F 在 AD 上,点 E 在 BC上, AF=CE, EF 的对角线 BD 交于 O,请问 O点有何特征?A F DOB EC【经典练习】1. △ ABC和△A B C中,A A' , BC B C ,C C 则△ABC与△ A B C.2.如图,点 C,F 在 BE上,12, BC EF ,请补充一个条件,使△ABC≌DFE,补充的条件是.A DB 12EC F3.在△ ABC和△A B C中,下列条件能判断△ABC和△A B C全等的个数有()① A AB B , BC B C② AA , B B , AC A C③ A AB B , AC B C④ AA , B B , AB A CA . 1 个 B. 2 个 C. 3 个 D. 4 个4.如图,已知 MB=ND,MBA NDC ,下列条件不能判定是△ABM≌△CDN的是()A.M NB. AB=CD M NC. AM=CND. AM∥ CN5.如图 2 所示,∠E=∠ F=90°,∠ B=∠ C, AE=AF,给出下列结论:①∠ 1=∠2② BE=CF③△ ACN≌△ ABM④ CD=DN A C B D 其中正确的结论是_________ _________ 。
三角形全等的判定(SSS)同步作业(含答案)
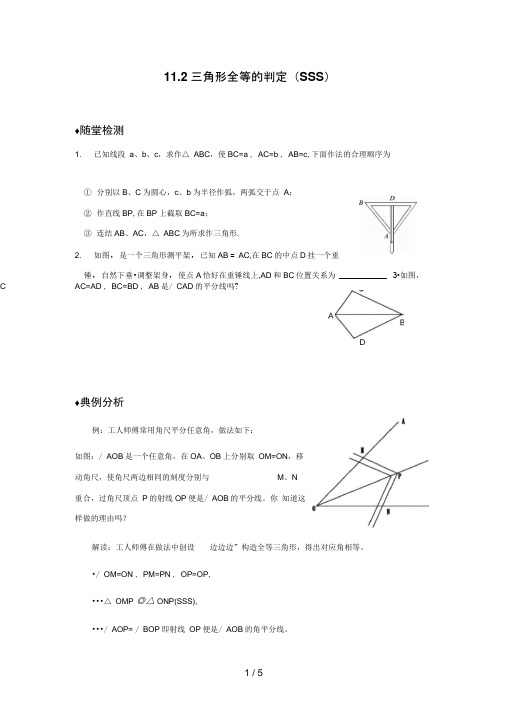
11.2三角形全等的判定(SSS)♦随堂检测1. 已知线段a、b、c,求作△ ABC,使BC=a , AC=b , AB=c,下面作法的合理顺序为①分别以B、C为圆心,c、b为半径作弧,两弧交于点A;②作直线BP,在BP上截取BC=a;③连结AB、AC,△ ABC为所求作三角形.2. 如图,是一个三角形测平架,已知AB = AC,在BC的中点D挂一个重锤,自然下垂•调整架身,使点A恰好在重锤线上,AD和BC位置关系为 ____________ 3•如图,CAC=AD , BC=BD , AB是/ CAD的平分线吗?♦典例分析例:工人师傅常用角尺平分任意角,做法如下:如图:/ AOB是一个任意角,在OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M、N重合,过角尺顶点P的射线OP便是/ AOB的平分线。
你知道这样做的理由吗?解读:工人师傅在做法中创设边边边”构造全等三角形,得出对应角相等。
•/ OM=ON , PM=PN , OP=OP,•••△ OMP ◎△ ONP(SSS),•••/ AOP= / BOP即射线OP便是/ AOB 的角平分线。
♦课下作业•拓展提高1 如图,AC=DF , BC=EF , AD=BE,/ BAC=72°,/ F=32 ° 则/ ABC=2. 如图,已知AB=AC , BD=DC,那么下列结论中不正确的是()A . △ABD ◎△ ACDB . Z ADB=90°C . Z BAD 是Z B 的一半 D . AD 平分Z BAC3. 如图,是一个风筝模型的框架,由DE=DF , EH=FH,4.如图,已知线段AB、CD相交于点O,AD、CB的延长线交于点E,OA=OC,EA=EC。
就说明Z DEH= Z DFH。
试用你所学的知识说明理由。
请说明Z A= Z C.•感受中考1. (2009 年怀化)如图,AD=BC,AB=DC.求证:/ A+ / D=1802. (2009年四川省宜宾市)已知:如图,在四边形ABCD中,AB=CB,AD=CD. 求证:/ C=Z A.随堂检测:1、②①③.解读:本题是利用 SSS 画全等三角形的尺规作图步骤, 作直线BP ,在BP 上截 取Bc=a 也可表达为画线段Bc=a2、 由全等可得 AD 垂直平分BC3、 公共边相等是两个三角形全等的一个条件.由于 AC=AD , BC=BD , AB=AB ,所以,△ ABC ◎△ ABD (SSS ),所以,/ CAB= / DAB , 即AB 平分/ CAD.拓展提高:1、76°.解读:先证明全等,再利用全等三角形的对应角相等和三角形内角和定理答案:2、 C .解读:利用SSS 证明两个三角形全等3、 由于已知 DE=DF , EH=FH ,连结DH ,这是两三所以△ DEH DFH ( SSS ),所以/ DEH= / DFH (全等三角形的对应角相等)。
三角形全等的判定SSS练习
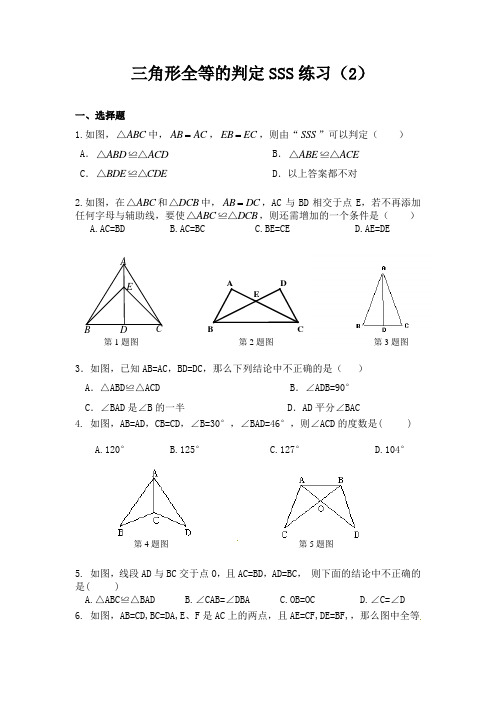
三角形全等的判定SSS 练习(2)一、选择题1.如图,ABC △中,AB AC =,EB EC =,则由“SSS ”可以判定( ) A .ABD ACD △≌△ B .ABE ACE △≌△ C .BDE CDE △≌△D .以上答案都不对2.如图,在ABC △和DCB △中,AB DC =,AC 与BD 相交于点E ,若不再添加任何字母与辅助线,要使ABC DCB △≌△,则还需增加的一个条件是( ) A.AC=BD B.AC=BC C.BE=CE D.AE=DE3.如图,已知AB=AC ,BD=DC ,那么下列结论中不正确的是( ) A .△ABD ≌△ACD B .∠ADB=90° C .∠BAD 是∠B 的一半D .AD 平分∠BAC4. 如图,AB=AD ,CB=CD ,∠B=30°,∠BAD=46°,则∠ACD 的度数是( )A.120°B.125°C.127°D.104°5. 如图,线段AD 与BC 交于点O ,且AC=BD ,AD=BC , 则下面的结论中不正确的是( )A.△ABC ≌△BADB.∠CAB=∠DBAC.OB=OCD.∠C=∠D6. 如图,AB=CD,BC=DA,E 、F 是AC 上的两点,且AE=CF,DE=BF,,那么图中全等EDCB AAEB DC 第1题图第2题图 第3题图第4题图第5题图三角形共有( )对A .4对B .3对C .2对D .1对7. 如图 ,AB=CD ,BC=AD ,则下列结论不一定正确的是( ).A.AB ∥DCB. ∠B =∠DC. ∠A =∠CD. AB=BC8. 如果△ABC 的三边长分别为3,5,7,△DEF 的三边长分别为3,3x -2,2x -1,若这两个三角形全等,则x 等于( ) A .73B .3C .4D .5二、填空题9.(2011湖北十堰)工人师傅常用角尺平分一个任意角。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形的判定(SSS )练习题
1.如图,ABE ∆≌DCF ∆,
点A 和点D 、点E 和点F 分别是对应点,则AB= ,=∠A ,AE= ,CE= ,AB// ,若BC AE ⊥,则DF 与BC 的关系是 .
2.如图,ABC ∆≌AED ∆,
若=∠︒=∠︒=∠︒=∠BAC C EAB B 则,45,30,40 ,=∠D ,=∠DAC .
3.已知ABC ∆≌DEF ∆,若ABC ∆的周长为23,AB=8,BC=6,则AC= ,EF= .
4.如图,若AB=AC ,BE=CD ,AE=AD ,则ABE ∆ ACD ∆,所以
=∠AEB ,=∠BAE ,=∠BAD .
5.如图,ABC ∆≌ADC ∆,点B 与点D 是对应点,︒=∠26BAC ,且︒=∠20B ,1=∆ABC S ,求ACD D CAD ∠∠∠,,的度数及ACD ∆的面积.
6.如图,ABC ∆≌DEF ∆,cm CE cm BC A 5,9,50==︒=∠,求DEF ∠的度数及CF 的长.
7.如图,已知:AB=AD ,AC=AE ,BC=DE ,求证:CAD BAE ∠=∠
B
第1题图
D
第2题图
第
4题图
8.如图,在,90︒=∠∆C ABC 中D 、E 分别为AC 、AB 上的点,且BE=BC ,DE=DC ,求证:(1)AB DE ⊥;(2)BD 平分ABC ∠
9.如图,已知AB=EF ,BC=DE ,AD=CF ,求证:①ABC ∆≌FED ∆;②AB//EF
10.如图,已知AB=AD ,AC=AE ,BC=DE ,求证:CAE BAD ∠=∠
D
F
E。
