江苏省南京市2020届高三年级第一学期期初联考数学试题(word版有答案)
南京市六校联合体2020届高三上学期期初测试 数学(含答案)

1272Pr int i S Whilei S S ii i EndWhileS ←←<←⨯←+南京市六校联合体2019-2020学年度第一学期期初测试 高三数学 2019.08.09Ⅰ试题注意事项:1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
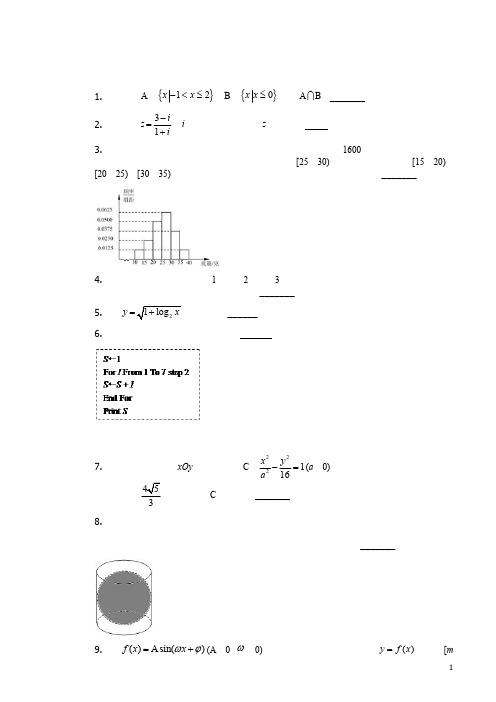
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.1.集合{}1,0,1A =-,{}|20B x x =-<<,则A B 中元素的个数是________. 2.已知复数z 满足1i 1z z-=-+,则z =________. 3.某校共有学生1600人,其中高一年级400人.为了解各年级学生的兴趣爱好情况,用分层抽样的方法从中抽取容量为80的样本,则应抽取高一学生________人.4.已知函数)0)(4cos()(>+=ωπωx x f 的最小正周期为4,则ω=________. 5.若“存在R x ∈,使042<-+a ax x ”为假命题,则实数a 的取值范围是________. 6.执行如图所示的伪代码,则输出的S 的值为________. 7.从分别写有1,2,3,4的4张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为________.8.已知焦点在x 轴上的双曲线的渐近线方程为340x y ±=,则双曲线离心率为________.9.已知实数,x y 满足条件⎪⎩⎪⎨⎧-≥-≤+≥+144222y x y x y x ,则函数3z x y =+的取值范围为________.10.已知圆C :22(1)()16x y a -+-=,若直线20ax y +-=与圆C 相交于A ,B 两点,且CA CB ⊥,则实数a 的值为________.11.设n S 是数列{}n a 的前n 项和,且11a =-,11n n n a S S ++=,则n S =________. 12.已知0a >,0b >,且113a b b a+=-,则b 的最大值为________. 13.如图,在平面四边形ABCD 中,90CBA CAD ∠=∠=︒,30ACD ∠=︒,AB BC =,点E 为线段BC 的中点.若AC AD AE λμ=+(,R λμ∈),则λμ的值为________.14.已知函数330()ln 0x mx m x f x x m x ,,,⎧--≤=⎨->⎩有三个不同的零点,则实数m 的取值范围是________.二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(本小题满分14分)在ABC ∆中,2sin 3A =,A π(,π)2∈. (1)求sin2A 的值;(2)若1sin 3B =,求cos C 的值.。
2020高考一模联考数学试卷原卷及解析卷完整版

南京市六校联合体2020届高三年级一模联考试卷数学Ⅰ试题2019.12一、填空题(本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上)1.已知集合A ={1,2,3,4},B ={x |x 2-4x <0},则A ∩B =__________. 2.已知复数2i 12++=iz ,则复数z 的共轭复数为__________. 3.某校有教师300人,男学生1500人,女学生1200人,现用分层抽样的办法从全校师生中抽取200人进行某项调查,则应抽取的女学生人数为__________. 4.根据如图所示的伪代码,可知输出的结果S 为__________.5.甲、乙两人依次从标有数字1,2,3的三张卡片中各抽取一张(不放回),则两人均未抽到标有数字3的卡片的概率为__________.6.若抛物线210y x =的焦点到双曲线222116x y a -=的一条渐近线的距离是2,则该双曲线的离心率为__________.7.已知f (x )是定义在R 上的奇函数,且当x ≥0时f (x )=x +a ,a 为实数,则f (-4)的值是__________.8.已知等差数列{}n a 的前n 项和为n S ,等比数列{}n b 前n 项和为n T ,若918S =-,1352S =-,且55b a =,77b a =,则42T T 的值为__________.9.已知()sin(2)3f x x π=+,若)20)((πϕϕ<<-=x f y 是偶函数,则=ϕ__________.10.已知矩形ABCD 中AB =4,BC =3,若沿对角线AC 折叠,使得平面DAC Ⅰ平面BAC ,则三棱锥D -ABC 的体积是__________.11.已知实数x ,y 满足条件xy +1=4x +y 且x >1,则(x +1)(y +2)的最小值是__________. 12.若直线04:=-+a y ax l 上存在相距为2的两个动点A ,B ,圆1:22=+y x O 上存在点C ,使得ABC ∆为等腰直角三角形(C 为直角顶点),则实数a 的取值范围为__________.13.如图,在平面直角坐标系x O y 中,已知点(1,0)A -,点P 是圆O :224x y +=上的任意一点,过点(1,0)B 作直线BT 垂直于AP ,垂足为T ,则2P A +3PT 的最小值是__________.14.已知函数4)(,)(22-+-=+-=x mx x h bx x x g ,若不等式)(01)(R x b x g ∈≤++恒成立,4)(+x h 为奇函数,函数⎩⎨⎧>≤=tx x h tx x g x f ),(),()(恰有两个零点,则实数t 的取值范围为__________.二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内) 15.(本小题满分14分)已知c b a ,,分别为ABC ∆三个内角A ,B ,C 的对边,且3tan 4A =. (1)若65a =,2b =,求边c 的长;(2)若()sin 10A B -=,求tan B 的值.如图,在直三棱柱ABC -A 1B 1C 1中,AC ⅠBC ,A 1B 与AB 1交于点D ,A 1C 与AC 1交于点E .求证:(1)DE Ⅰ平面B 1BCC 1; (2)平面A 1BC Ⅰ平面A 1ACC 1.17.(本小题满分14分)如图,在平面直角坐标系xOy 中,椭圆C :2222+10)x y a b a b=>>(的左、右顶点分别为A B ,.已知4AB =,且点3(,5)4e 在椭圆上,其中e 是椭圆的离心率. (1)求椭圆C 的方程;(2)设P 是椭圆C 上异于 A 、B 的点,与x 轴垂直的直线l 分别交直线AP ,BP 于点M ,N ,求证:直线AN 与直线BM 的斜率之积是定值.ED B 1A 1C 1CBAB xy OPA M NlCB AD东北如图,甲、乙两观察哨所位于海岸线l (一条南北方向的直线)上的点A 、B 处,两观察哨所相距32 n mile ,在海岸线东侧有一半径为6 n mile 圆形暗礁区,该暗礁区中心点C 位于乙观察哨所北偏东53︒的方向上,与甲观察哨所相距2193,暗礁中心与乙观察哨所的距离大于2193;(1)求暗礁中心点C 到海岸线l 的距离;(2)某时刻,甲观察哨所发现在其正南方向且位于暗礁中心正西方向的点D 处有一走私船正欲逃窜,甲观察哨所立即派缉私艇进行追击.已知缉私艇的最大航速是走私船最大航速的(1)λλ>倍.假设缉私艇和走私船均按直线方向以最大航速航行.问:无论走私船沿何方向逃窜,要保证缉私艇总能在暗礁区(不包含暗礁区边界)以外的海域内拦截成功,求λ的取值范围.19.(本小题满分16分)已知函数x x x x f 23)(23+-=,R t tx x g ∈=,)(,xe x x=)(ϕ.(1)求函数)()(x x f y ϕ⋅=的单调增区间;(2)令)()()(x g x f x h -=,且函数)(x h 有三个彼此不相等的零点n m ,,0,其中n m <.Ⅰ若n m 21=,求函数)(x h 在m x =处的切线方程; Ⅰ若对][n m x ,∈∀,t x h -≤16)(恒成立,求实数t 的取值范围.等差数列{a n }公差大于零,且a 2+a 3=52,a 22+a 32=134,记{a n }的前n 项和为S n ,等比数列{b n }各项均为正数,公比为q ,记{b n }的前n 项和为T n .(1)求S n ;(2)若q 为正整数,且存在正整数k ,使得T k ,T 3k ∈{S 2,S 5,S 6},求数列{b n }的通项公式;(3)若将S n 中的整数项按从小到大的顺序排列构成数列{c n },求{c n }的一个通项公式.南京市六校联合体2020届高三年级一模联考试卷数学Ⅰ试题2019.12一、填空题(本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上)1.已知集合A ={1,2,3,4},B ={x |x 2-4x <0},则A ∩B =__________. 解:{1A =Q ,2,3,4},{|04}B x x =<<, {1A B ∴=I ,2,3}.故答案为:{1,2,3}. 2.已知复数2i 12++=iz ,则复数z 的共轭复数为__________. 解:22(1)221211(1)(1)i z i i i i i i i i -=+=+=-+=+++-Q , 故z 的共轭复数是:1i -3.某校有教师300人,男学生1500人,女学生1200人,现用分层抽样的办法从全校师生中抽取200人进行某项调查,则应抽取的女学生人数为__________. 解:女学生人数所占的比例为12002300150012005=++,则应抽取的女学生人数为2200805⨯=, 故答案为:80.4.根据如图所示的伪代码,可知输出的结果S 为__________.答案:模拟演示:解:1S =,1I =;3S =,4I =;7S =,7I =;15S =,10I =此时结束循坏输出15S = 故答案为:15.5.甲、乙两人依次从标有数字1,2,3的三张卡片中各抽取一张(不放回),则两人均未抽到标有数字3的卡片的概率为__________.解:甲、乙两人依次从标有数字1,2,3的三张卡片中各抽取一张(不放回), 基本事件总数326n =⨯=,两人均未抽到标有数字3的卡片包含的基本事件个数212m =⨯=, 则两人均未抽到标有数字3的卡片的概率为2163m p n ===. 故答案为:13.6.若抛物线210y x =的焦点到双曲线222116x y a -=的一条渐近线的距离是2,则该双曲线的离心率为__________.解:抛物线210y x =的焦点为5(,0)2,双曲线222116x y a -=的一条渐近线方程为4y x a=±,542⨯=,解得3a =,则5c =,所以双曲线的离心率53e = 故答案为:537.已知f (x )是定义在R 上的奇函数,且当x ≥0时f (x )=x +a ,a 为实数,则f (-4)的值是__________.解:()f x Q 是定义在R 上的奇函数,且0x …时()f x a =, (0)0f a ∴==,0x ∴…时,()f x =,∴(4)(4)2f f -=-==-.故答案为:2-.8.已知等差数列{}n a 的前n 项和为n S ,等比数列{}n b 前n 项和为n T ,若918S =-,1352S =-,且55b a =,77b a =,则42T T 的值为__________. 解:918S =-,则5918a =-,所以52a =-,即52b =-1352S =-,则71352a =-,所以74a =-,即74b =-设等比数列{}n b 的公比为22q =4124212(1)1=13(1)1b q T q q b q T q--=+=-- 故答案为:39.已知()sin(2)3f x x π=+,若)20)((πϕϕ<<-=x f y 是偶函数,则=ϕ__________.解:函数()sin(2)3f x x π=+,所以函数()sin(22)3y f x x πϕϕ=-=-+,由于函数为偶函数, 所以2()32k k Z ππϕπ-+=+∈,解得()212k k Z ππϕ=--∈, 由于02πϕ<<,所以当1k =-时,512πϕ=. 故答案为:512π. 10.已知矩形ABCD 中AB =4,BC =3,若沿对角线AC 折叠,使得平面DAC Ⅰ平面BAC ,则三棱锥D -ABC 的体积是__________.解:过B 作BE AC ⊥于E ,4AB =Q ,3BC =,5AC ∴=,125AB BC BE AC ==g , Q 平面DAC ⊥平面BAC ,平面DAC ⋂平面BAC AC =,BE AC ⊥,BE ⊂平面ABC ,BE ∴⊥平面DAC ,11112243433255ACD D ABC B ACD V V S BE ∆--∴==⋅=⨯⨯⨯⨯=棱锥棱锥. 故答案为245.11.已知实数x ,y 满足条件xy +1=4x +y 且x >1,则(x +1)(y +2)的最小值是__________. 解:14xy x y +=+Q ,且1x >, 114y x y -∴=>-,解得,4y >, (1)(2)2212(3)x y xy x y x y ∴++=+++=++ 33912()12[7(4)]44y y y y y -=++=++-+-- 12(76)27++=….(1)(2)x y ∴++取最小值为27.故答案为:27.12.若直线04:=-+a y ax l 上存在相距为2的两个动点A ,B ,圆1:22=+y x O 上存在点C ,使得ABC ∆为等腰直角三角形(C 为直角顶点),则实数a 的取值范围为__________.解:根据题意,若ABC ∆为等腰直角三角形,其中C 为直角顶点且||2AB =, 则C 到AB 的距离为||12AB =, 若圆22:1O x y +=上存在点C ,使得ABC ∆为等腰直角三角形, 则圆心O 到直线l 的距离2d „2,解可得:a ,即a 的取值范围[;故答案为:[.13.如图,在平面直角坐标系x O y 中,已知点(1,0)A -,点P 是圆O :224x y +=上的任意一点,过点(1,0)B 作直线BT 垂直于AP ,垂足为T ,则2P A +3PT 的最小值是__________.解:由中线长公式可得PO =22=10PA PB + 222cos 2PA PB AB P PA PB +-=⋅,则3cos P PA PB=⋅在Rt PBT ∆中,cos PT PB P =,即3PT PA=所以9232PA PT PA PA+=+≥=(当且仅当2PA =时取等)14.已知函数4)(,)(22-+-=+-=x mx x h bx x x g ,若不等式)(01)(R x b x g ∈≤++恒成立,4)(+x h 为奇函数,函数⎩⎨⎧>≤=tx x h tx x g x f ),(),()(恰有两个零点,则实数t 的取值范围为__________.解:若不等式()10()g x b x R ++∈„恒成立, 即210x bx b ---…恒成立, 则△24(1)0b b =++„,解得:2b =-, 故2()2g x x x =--, 若()4h x +为奇函数,则224444mx x mx x ---+=--+,解得:0m =, 故()4h x x =-,画出函数()g x ,()h x 的图象,如图所示:若函数()()()()()g x x t f x h x x t ⎧=⎨>⎩…恰有两个零点,结合图象:[2t ∈-,0)[4U ,)+∞, 故答案为:[2-,0)[4U ,)+∞.二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内) 15.(本小题满分14分)已知c b a ,,分别为ABC ∆三个内角A ,B ,C 的对边,且3tan 4A =. (1)若65a =,2b =,求边c 的长; (2)若()sin A B -=,求tan B 的值. 解:(1)在ABC ∆中,由3tan 4A =可知(0,)2A π∈, 由22sin 3cos 4sin cos 1A A A A ⎧=⎪⎨⎪+=⎩解得3sin 54cos 5A A ⎧=⎪⎪⎨⎪=⎪⎩, 由余弦定理得2222cos a b c bc A =+-,得2226422255c c ⎛⎫=+-⋅⋅⋅ ⎪⎝⎭,即216640525c c -+=,解得85c =. (2)由(0,)2A π∈且(0,)B π∈,得(,)2A B ππ-∈-, 又()10sin 0A B -=>,则(0,)2A B π-∈,则()cos 0A B ->, 所以()2310cos 1sin ()A B A B -=--=, 所以()sin()1tan cos()3A B A B A B --==-,所以()31tan tan()143tan tan 311tan tan()3143A AB B A A B A A B ---=--===⎡⎤⎣⎦+⋅-+⋅ 16.(本小题满分14分)如图,在直三棱柱ABC -A 1B 1C 1中,AC ⅠBC ,A 1B 与AB 1交于点D ,A 1C 与AC 1交于点E .求证:(1)DE Ⅰ平面B 1BCC 1; (2)平面A 1BC Ⅰ平面A 1ACC 1.证明:(1)直三棱柱ABC -A 1B 1C 1中,1AA //1BB , 所以四边形11ABB A 是平行四边形,且11A B AB DE =I , 所以D 为1A B 中点, 同理E 为1A C 中点, 所以//DE BC ,又因为DE ⊄平面11B BCC ,BC ⊂平面11B BCC , 所以//DE 11B BCC .ED B 1A 1C 1CBA(2)直三棱柱ABC -A 1B 1C 1中,1C C ⊥平面ABC , 因为BC ⊂平面ABC ,所以1C C BC ⊥,因为AC BC ⊥,1AC C C C =I ,1AC C C ⊂、平面11A ACC , 所以BC ⊥平面11A ACC , 又因为BC ⊂平面1A BC , 所以平面1A BC ⊥平面11A ACC . 17.(本小题满分14分)如图,在平面直角坐标系xOy 中,椭圆C :2222+10)x y a b a b=>>(的左、右顶点分别为A B ,.已知4AB =,且点3(,5)4e 在椭圆上,其中e 是椭圆的离心率. (1)求椭圆C 的方程;(2)设P 是椭圆C 上异于 A 、B 的点,与x 轴垂直的直线l 分别交直线AP ,BP 于点M ,N ,求证:直线AN 与直线BM 的斜率之积是定值.解:(1)因为4AB =,所以24a =,即2a =,又点3(,5)4e 在椭圆上,故22245+116e a b =,即2245+11616c b =, 又2224b c a +==, 联立方程组,解得2=3b ,故椭圆方程为22+143x y =.(2)设P 点坐标为(,s t ),M ,N 的横坐标均为2)mm ≠±(, 则直线AP 的方程为(2)2ty x s =++, B xy O PAM NlCB AD东北故(,(2))2tM m m s ++, 故直线BM 的斜率1(2)(2)(2)t m k s m +=+-,同理可得直线AN 的斜率2(-2)(2)(+2)t m k s m =-,故2122(2)(-2)=(2)(2)(2)(+2)4t m t m t k k s m s m s +=+---,又因为P 点在椭圆上,故有22+143s t =,即223(4)4t s =--,因此有21223=44t k k s =--,故直线AN 与直线BM 的斜率之积是定值. 18.(本小题满分16分)如图,甲、乙两观察哨所位于海岸线l (一条南北方向的直线)上的点A 、B 处,两观察哨所相距32 n mile ,在海岸线东侧有一半径为6 n mile 圆形暗礁区,该暗礁区中心点C 位于乙观察哨所北偏东53︒的方向上,与甲观察哨所相距2193,暗礁中心与乙观察哨所的距离大于2193;(1)求暗礁中心点C 到海岸线l 的距离;(2)某时刻,甲观察哨所发现在其正南方向且位于暗礁中心正西方向的点D 处有一走私船正欲逃窜,甲观察哨所立即派缉私艇进行追击.已知缉私艇的最大航速是走私船最大航速的(1)λλ>倍.假设缉私艇和走私船均按直线方向以最大航速航行.问:无论走私船沿何方向逃窜,要保证缉私艇总能在暗礁区(不包含暗礁区边界)以外的海域内拦截成功,求λ的取值范围.解:(1)在三角形ABC 中,由余弦定理可得2222cos AC AB BC AB BC ABC =+-⋅⋅∠,即2223322325BC BC =+-⨯⨯⨯,整理得2519212600BC BC -+=,解得30BC =或425BC =(舍去), 过点C 作CD 垂直于l ,垂足为D ,在直角三角形CDB 中,CD =BC 4sin 30245ABC ∠=⋅=, 故暗礁中心点C 到海岸线l 的距离为24n mile . (2)由(1)可知14AD =,18BD =,以点C 为坐标原点,建立如图所示平面直角坐标系,则A (24-,14),D (24-,0),暗礁区域边界所在的圆的方程为2236x y +=, 假设缉私艇在点T (x ,y )处拦截成功,则ATDTλ=,则点T λ=,化简得222221414(24)()()11x y λλλ+++=--要保证缉私艇总能在暗礁区(不包含暗礁区边界)以外的海域内拦截成功, 只需要圆222221414(24)()()11x y λλλ+++=--与圆2236x y +=外离,214()61λλ>+-,整理得1352421840λλ-->,解得43λ>或4645λ<-(舍去). 答:(1)暗礁中心点C 到海岸线l 的距离是24n mile ; (2)当43λ>时,就能保证无论走私船沿何方向逃窜,缉私艇总能在暗礁区(不包含暗礁区边界)以外的海域内拦截成功. 19.(本小题满分16分)已知函数x x x x f 23)(23+-=,R t tx x g ∈=,)(,xe x x=)(ϕ.(1)求函数)()(x x f y ϕ⋅=的单调增区间;(2)令)()()(x g x f x h -=,且函数)(x h 有三个彼此不相等的零点n m ,,0,其中n m <.Ⅰ若n m 21=,求函数)(x h 在m x =处的切线方程; Ⅰ若对][n m x ,∈∀,t x h -≤16)(恒成立,求实数t 的取值范围. 解:(1)xe x x x xf y )23()()(2+-=⋅=ϕ, 所以xe x x y )1(2'--=,令0'>y 得到251251+>-<x x 或, 所以)()(x x f y ϕ⋅=的单调增区间是),251()251,(+∞+--∞,. (2)由方程()0h x =得,m n 是方程23(2)0x x t -+-=的两实根, 故3,2m n mn t +==-,且由判别式得14t >-, Ⅰ若n m 21=,得1,2m n ==,故22mn t =-=,得0t =, 因此'(1)1h =-,故函数()h x 在1=x 处的切线方程为1y x =-+.②若对任意的[,]x m n ∈,都有()16h x t ≤-成立,所以max ()16h x t ≤-, 因为3,m n m n +=<,所以n m n m <<<<<0230或, 当302m n <<<时,对[,]x m n ∈有max ()0h x =, 所以016t ≤-, 解得16t ≤,又因为20mn t =->,得2t <,则有124t -<<; 当0m n <<时,2'()36(2)h x x x t =-+-,则存在()h x 的极大值点1(,0)x m ∈,且211362t x x =-+, 由题意得321111()3(2)16h x x x t x t =-+-≤-, 将211362t x x =-+代入得321113370x x x -++≥,进而得到31(1)8x -≥-,得110x -≤<, 又因为211362t x x =-+,得211t <≤,综上可知t 的取值范围是124t -<<或211t <≤.20.(本小题满分16分)等差数列{a n }公差大于零,且a 2+a 3=52,a 22+a 32=134,记{a n }的前n 项和为S n ,等比数列{b n }各项均为正数,公比为q ,记{b n }的前n 项和为T n .(1)求S n ;(2)若q 为正整数,且存在正整数k ,使得T k ,T 3k ∈{S 2,S 5,S 6},求数列{b n }的通项公式;(3)若将S n 中的整数项按从小到大的顺序排列构成数列{c n },求{c n }的一个通项公式. 解:(1)设{a n }公差为d ,d >0, 因为a 2+a 3=52,a 22+a 32=134,所以a 1+d +a 1+2d =52,(a 1+d )2+(a 1+2d )2=134,解得a 1=12,d =12,于是S n =12n +n (n -1)2×12=n 2+n 4.(2){S 2,S 5,S 6}={32,152,212}当q =1时,T k =kb 1,T 3k =3kb 1,T 3kT k=3,舍去;当q ≠1时,T k =b 1(1-q k )1-q ,T 3k =b 1(1-q 3k )1-q ,所以T 3kT k =1+q k +q 2k ,因为q ⅠN *且q ≠1,所以q ≥2, 因此T 3kT k ≥1+2+4=7,于是T k =32,T 3k =212,因此1+q k +q 2k =7,解得q k =2或-3(舍去), 从而q =2,k =1,代入T k =b 1(1-q k )1-q 得b 1=32所以b n =3×2n-2(3)因为S n =n 2+n4为整数项,所以n =4k 或者4k -1,k ⅠN *当n =4k -1,k ⅠN *时,S n =k (4k -1); 当n =4k ,k ⅠN *时,S n =k (4k +1);因为S n 中的整数项按从小到大的顺序排列构成数列{c n }, 且k (4k -1)<k (4k +1)<(k +1)[4(k +1)-1]<(k +1)[4(k +1)+1], 所以当n 为奇数时,c n =(4×n +12-1)×n +12=2n 2+3n +12;当n 为偶数时,c n =n2×(2n +1)=2n 2+n 2;所以c n =⎩⎨⎧2n 2+3n +12,n 为奇数,2n 2+n2,n 为偶数.。
2020届江苏省南京市六校联合体高三上学期一模联考数学试题(word版)

南京市六校联合体2020届高三年级一模联考试卷数学I试题2019.12一、填空题(本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上)1.已知集合A = {1 , 2, 3, 4}, B = {x|x2—4x v 0},则A A B= _____________ .答案为:{1 , 2, 3}.22•已知复数z —— 2i ,则复数z的共轭复数为1 i答案为:1 i3. 某校有教师300人,男学生1500人,女学生1200人,现用分层抽样的办法从全校师生中抽取200人进行某项调查,则应抽取的女学生人数为_____________ .答案为:80.4. 根据如图所示的伪代码,可知输出的结果S为 .WhileS—2S+1End WhilePrint S(弟4瞇)答案:模拟演示:答案为:15.5•甲、乙两人依次从标有数字1, 2, 3的三张卡片中各抽取一张(不放回),则两人均未抽到标有数字3的卡片的概率为____________ .答案为:1.32 26 •若抛物线y310x的焦点到双曲线笃L 1的一条渐近线的距离是2,则该双曲线的离心率为a 16答案为:537.已知f (x)是定义在R 上的奇函数,且当 寸f (x) =>/x + a , a 为实数,则f (— 4)的值是 ____________ .答案为:2 .&已知等差数列{a n }的前n 项和为S n ,等比数列{b n }前n 项和为T n ,若S 918 , S 13 52,且b s a s ,b 7 a 7,则-的值为 ________________ .T2答案为:39•已知 f(x) sin(2x -),若 y f (x )(0-)是偶函数,则 _________________ .32答案为:乞.1210. 已知矩形 ABCD 中AB = 4, BC = 3,若沿对角线 AC 折叠,使得平面 DAC 丄平面BAC ,则三棱锥 D —ABC 的体积是 ___________ . 答案为24 .511. ___________________________________________________________________________ 已知实数 x , y 满足条件xy + 1 = 4x + y 且x > 1,则(x + 1)(y + 2)的最小值是 __________________________________ . 答案为:27.12. 若直线丨:ax y 4a 0上存在相距为2的两个动点A, B,圆O : x 2 y 2 1上存在点C ,使得 ABC为等腰直角三角形(C 为直角顶点),则实数a 的取值范围为2 213.如图,在平面直角坐标系 xOy 中,已知点A( 1,0),点P 是圆O : x y4上的任意一点,过点B(1,0)作直线BT 垂直于AP ,垂足为T ,贝U 2PA+3PT 的最小值是h V*p1 f2 2 222解:由中线长公式可得 PO . 2( PA PB ) AB ,贝y PA PB =102答案为:33T ,T ]cosP —PB~~,则cosP2 PA PB PA PB在Rt PBT 中,PT PBcosP,即PTPA所以2 PA 3PT2PA 9 2 .18 6. 2 (当且仅当PAPA3 2时取等)214.已知函数g(x) 2 x2bx, h(x) mx x 4,若不等式g(x) b 1 0(x R)恒成立,h(x) 4为奇函数,函数f(x)g(x),x t恰有两个零点,则实数h(x),x tt的取值范围为解:若不等式g(x) b1, 0(x R)恒成立,即x2 bx b1…0恒成立,则厶b24(b1),0, 解得:b 2,故g(x) 2 x2x,若h(x) 4为奇•函数,2 2则mx x 4 4 mx x 4 4,解得:m 0, 故h(x) x 4 ,结合图象:t [ 2 , 0)U【4 , ),故答案为:[2 , 0)U【4 , ) •、解答题(本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写画出函数g(x) , h(x)的图象,如图所示:在答题纸的指定区域内) 15.(本小题满分 14分)2 已知a , b , c 分别为 ABC 三个内角A , B , C 的对边,且tan A -. 4(1)若 a 6 , b 5(2)若 sin A B解得c2,求边c 的长;1010 ,解:(1)在 ABC 中, , 3由 tan A - 可知A (0,-4 2sin A 33sin A由 cos A 4 解得 5 sin A cos 2 A 1 cos A45o46 c 16i52c14 - 5c222c22(2)由 (0三)且B (0,),,2),又 sin A B(0,—),则 cos所以cos A B1 sin 2(A B) 3 .10 10由余弦定理得a 2 b 2 c 2 2bccosA ,求tan B 的值.103 1tan A tan(A B) 43 11 tan A tan(A B) 13 134 316. (本小题满分14分)如图,在直三棱柱 ABC — A 1B 1C 1中,AC 丄BC , A 1B 与AB 1交于点D , AQ 与AC 1交于点E .求证: (1) DE //平面 B 1BCC 1; (2) 平面A 1BC 丄平面A 1ACC 1.所以tan A Bsin(A B) 1 cos(A B) 3所以 tan B tan A A Bx直线AN 与直线BM 的斜率之积是定值.证明:(1)直三棱柱 ABC — A I B I C I 中,A^ / / BB 1, 所以四边形 ABB 1A 1是平行四边形,且 ABI AB i DE , 所以D 为A ,B 中点, 同理E 为AC 中点, 所以 DE//BC ,又因为DE 平面B 1BCC 1,BC 平面B 1BCC 1, 所以 DE// B 1BCC 1 .(2)直三棱柱 ABC — A 1B 1C 1中,C 1C 平面ABC , 因为BC 平面ABC ,所以C 1C BC ,因为 AC BC , AC I C 1C C , AC 、C 1C 平面 A 1ACC 1, 所以BC 平面AACG , 又因为BC 平面ABC , 所以平面A BC 平面A ACG . 17. (本小题满分14分)2 2如图,在平面直角坐标系 xOy 中,椭圆C : — +1( a b 0)的左、右顶点分别为 A , B .已a b3 \_知AB 4,且点(e,.5)在椭圆上,其中e 是椭圆的离心率. 4(1)求椭圆C 的方程;(2)设P 是椭圆C 上异于A 、B 的点,与x 轴垂直的直线l 分别交直线AP , BP 于点M , N ,求证:5第解:(1)因为AB 4,所以2a 4,即a 2 ,又 b 2 c 2 a 2 4 , 联立方程组,解得b 2=3 ,2 2故椭圆方程为―+^ 1.4 3(2)设P 点坐标为(s,t ), M ,N 的横坐标均为 m( m 2),则直线AP 的方程为y1 (x 2), s 2故 M (m,—(m 2)),s 2故直线BM 的斜率k 1t(m 2) (s 2)(m 2)t(m 2) t(m-2) = t 2又点(e,3・,5)在椭圆上,故4e 2 + 45 a 2 + T6b 2同理可得直线AN 的斜率k 2t(m-2)(s 2)(m+2)故 k 1k 2(s 2)(m 2)(s 2)(m+2) = s24又因为P点在椭圆上,故有2 .2s t+4 31,即t2 3 23(s4),因此有故直线AN与直线BM的斜率之积是定值.18.(本小题满分16分)如图,甲、乙两观察哨所位于海岸线l (一条南北方向的直线)上的点A、B处,两观察哨所相距32 n mile ,在海岸线东侧有一半径为 6 n mile圆形暗礁区,该暗礁区中心点C位于乙观察哨所北偏东53的方向上,与甲观察哨所相距2・.193 n mile,暗礁中心与乙观察哨所的距离大于2.193 n mile;(1)求暗礁中心点C到海岸线I的距离;(2 )某时刻,甲观察哨所发现在其正南方向且位于暗礁中心正西方向y私艇进行追C一丿(1)倍.假设缉私艇和走私船均按直线方向以最大航速航行•问:无论走私船沿何方向逃窜,要保证缉私艇总能在暗礁区(不包含暗礁区边界)以外的海域内拦截成功,求的取值范围.解:(1)在三角形ABC中,由余弦定理可得AC3 4 AB2 BC2 2AB BC cos ABC,即(2 197)2 322 BC2 2 32 BC 5 6,整理得5BC2 192BC 1260 0,542解得BC 30或BC 42(舍去),5过点C作CD垂直于I,垂足为D,在直角三角形CDB中,CD=BCsin ABC 30 - 24,5故暗礁中心点C到海岸线I的距离为24n mile •(2)由(1)可知AD 14, BD 18 ,以点C为坐标原点,建立如图所示平面直角坐标系,则A (24 , 14 ), D (24 , 0),暗礁区域边界所在的圆的方程为x2y236,假设缉私艇在点T (x,y)处拦截成功,则丛 ,DT则点T满足方程•(x=24)(y 14),J(x 24)2 y2化简得(x 24)2(y壬;)2(占)21 1要保证缉私艇总能在暗礁区(不包含暗礁区边界)以外的海域内拦截成功,只需要圆(x 24)2(y -4^)2(TT)2与圆x2y236外离,1 1故(0 24)2(0 2141)2(单^)6,4 46整理得135 42 184 0,解得-或一(舍去).5 45答:(1)暗礁中心点C到海岸线I的距离是24n mile ;6(2)当-时,就能保证无论走私船沿何方向逃窜,缉私艇总能在暗礁区(不包含暗礁区边界)以外的3海域内拦截成功.21 2,19. (本小题满分16分)x 已知函数 f(x) x 3 3x 2 2x , g(x) tx , t R ,(x)—.x(1)求函数y f(x) (x)的单调增区间;(2)令h(x) f (x) g (x),且函数h(x)有三个彼此不相等的零点 0, m , n ,其中1① 若m n ,求函数h(x)在x m 处的切线方程;2② 若对 x [m , n],h(x) 16 t 恒成立,求实数t 的取值范围.解:(1) y f (x)(x) (x 2 3x 2)e x ,所以 y ' (x 2 x 1)e x , 1 15令y 0得到x 或x2所以y f(x) (x)的单调增区间是( 丄 5),(!5,).2 2 (2)由方程h(x) 0得m,n 是方程x 2 3x (2 t) 0的两实根,1 故m n 3,mn2 t ,且由判别式得t -, 41 ①若 m n ,得 m 1,n 2,故 mn2 t 2,得 t 0 , 2因此 h '(1)1 , 故函数h(x)在x 1处的切线方程为y x 1. ②若对任意的x [m, n],都有h(x) 16 t 成立,所以h(x)max 16 t ,3因为m n 3,m n ,所以0 mn 或m 0 n 2 , t 3当 0 m n 时,对 x [m, n]有 h(x) max 0 , 2所以016 t , 解得t 16 ,1又因为mn 2 t 0 ,得t 2,则有一t 2 ;4当 m 0 n 时,h'(x) 3x 2 6x (2 t),一 _ 2则存在h(x)的极大值点x1(m,0),且t 3x i 6x1 2 ,由题意得h(为)为3 3为7 (2 t)x, 16 t ,2 3 2将t 3为6为2代入得X i 3x i 3x i 7 0 ,进而得到(X i 1)38,得1 x1 0,2又因为t 3x16x1 2,得2 t 11 ,1综上可知t的取值范围是—t 2或2 t 11 .420. (本小题满分16分)5 13等差数列{a n}公差大于零,且a2+ a3=勺a?2+ a32=才,记{a.}的前n项和为S n,等比数列{b n}各项均为正数,公比为q,记{b n}的前n项和为T n.(1 )求S n;(2)若q为正整数,且存在正整数k,使得T k, T3k€ {S2, S5, S6},求数列{b n}的通项公式;(3 )若将S n中的整数项按从小到大的顺序排列构成数列{c n},求{c n}的一个通项公式.解:(1)设{a n}公差为d, d> 0,因为a2+ a3= 8, a22+ a32=乎,7{S2, S5, S6} = {|,字,21}T3k当q = 1 时,T k= kb1, T3k= 3kb1,云=3,舍去;8所以a1 + d + a1 + 2d= 5,212,13⑻ + d)2+ ⑻ + 2d)2盲,因为q € N *且q M l ,所以q 》2因此1 + q k + q 2k = 7,解得q k = 2或一3 (舍去),于是n(n — 1) 1 2为 n 2+ n 4T k = b 1(1 - q k ) 1 — q ,T 3k = b 1(1-q 3k ) 1 — q ,所以 T 3k T k 1 + q k + q 2k ,因此 T 3k T k >1 2+ 4 = 7, 于是 T k = 3,T 3k =k从而 q = 2, k = J 代入 T k =得 b 1 =- 所以 b n = 3 X2n —2 (3)因为S n = 为整数项,所以n = 4k 或者4k — 1,k € N * 当 n = 4k — 1, k € N *时,S n = k(4k — 1);当 n = 4k , k € N *时,S n = k(4k + 1);因为S n 中的整数项按从小到大的顺序排列构成数列 { c n }, 且 k(4k — 1)v k(4k + 1)v (k + 1)[4(k + 1)— 1]v (k + 1)[4(k + 1)+ 1],n + 1 所以当n 为奇数时,C n = (4疋■厂—1)_2n 2n 2+ n当 n 为偶数时,C n = 2*2n +1) = —2 ■;2所以 C n = c2+n-^2—, n 为偶数.1 1解得 a 1 = 2, d = 2,n + 1 2n 2 + 3n + 1- ;2n 2+ 3n + 1门为奇数,。
江苏省南京市六校联合体2020届高三年级第一学期期中检测试卷数学

江苏省南京市六校联合体2020届高三年级第一学期期中检测试卷数学Ⅰ试题命题: 审核:一、填空题:本部分共14题,每题5分,满分70分。
1.设全集={25}U x Z x ∈-≤≤,若集合{}24A x Z x =∈≤,则=U C A __________.2.已知命题:4p x >,命题2:540q x x -+≥,那么p 是q 的__________条件(选填“充分不必要”、“充要”、“既不充分也不必要”).3.命题“若20x x -≥,则2x >”的否命题是__________.4.函数y =log 7(x 2−4x +3)的定义域为__________.5.已知()f x 是R 上的奇函数,当0x ≥时,()25f x x x =-,则()()1f x f x ->的解集为__________.6.若函数()(21)()xf x x x a =+-为奇函数,则(1)f =__________.7.化简:tan17tan133(tan17tan13)++=__________.8.若将一个圆锥的侧面沿一条母线剪开,是半径为3,圆心角为23π的扇形,则该圆锥的体积为__________. 9.已知函数,1()4,1x a e x f x x x x ⎧-<⎪=⎨+≥⎪⎩,若()y f x =的最小值是4,则实数a 的取值范围为__________. 10.正方形ABCD 的边长为1,O 为正方形ABCD 的中心,过中心O 的直线与边AB 交于点M ,与边CD 交于点N ,P 为平面上一点,满足2(1)OP OB OC λλ=+-,则PM PN ⋅的最小值为__________.11.在△ABC 中,cos 2A+cos 2B+cos 2C<1,C =4π,则tan A +tan B 的最小值为__________. 12.已知椭圆22221(0)x y a b a b+=>>上有一个点A ,它关于原点的对称点为B ,点F 为椭圆的右焦点,且满足AF△BF ,当△ABF =12π时,椭圆的离心率为__________.13.已知圆1C :22(1)(6)25x y ++-=,圆2C :222(17)(30)x y r -+-=.若圆2C 上存在一点P ,使得过点P 可作一条射线与圆1C 依次交于点A ,B ,满足2PA AB =,则半径r 的取值范围是__________.14.已知函数()ln f x x x =,2()(12)2g x x a x a =-+++,若不等式()()f x g x ≤的解集中恰有两个整数,则实数a 的取值范围是__________.二、解答题:本部分共6题,满分70分。
江苏省南京市2020高三数学上学期期初联考试题(含解析)

江苏省南京市2020届高三数学上学期期初联考试题(含解析)一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卷相应的位置上.)1.已知集合A ={}12x x -<≤,B ={}0x x ≤,则A I B =_______. 【答案】{}10x x -<≤ 【解析】 【分析】根据交集定义直接求得结果.【详解】由交集定义可得:{}10A B x x ⋂=-<≤ 本题正确结果:{}10x x -<≤【点睛】本题考查集合运算中的交集运算,属于基础题.2.已知复数z 31ii-=+(i 是虚数单位),则z 的虚部是 . 【答案】-2 【解析】 【分析】直接利用复数代数形式的除法运算化简,则复数z 的虚部可求. 【详解】∵z ()()()()31324121112i i i ii i i i ----====-++-, ∴z 的虚部是﹣2. 故答案为﹣2.【点睛】本题考查了复数代数形式的除法运算,考查了复数的基本概念,是基础题.3.对一批产品的质量(单位:克)进行抽样检测,样本容量为1600,检测结果的频率分布直方图如图所示.根据标准,单件产品质量在区间[25,30)内为一等品,在区间[15,20),[20,25)和[30,35)内为二等品,其余为三等品.则样本中三等品件数为_______.【答案】200. 【解析】 【分析】根据频率分布直方图求得三等品对应频率,根据频数等于频率乘以总数求得结果. 【详解】由题意可知,单间产品质量在[)10,15和[)35,40的为三等品∴三等品对应的频率为:0.0125250.125⨯⨯=∴三等品件数为:16000.125200⨯=本题正确结果:200 【点睛】本题考查根据频率分布直方图计算频数的问题,属于基础题.4.现有三张卡片,分别写有“1”、“2”、“3”这三个数字.将这三张卡片随机排序组成一个三位数,则该三位数是偶数的概率是_______.【答案】13. 【解析】 【分析】计算出三位数个数和其中偶数个数,根据古典概型概率公式求得结果.【详解】三张卡片随机排序组成一个三位数,共有:336A =个,其中偶数有:222A =个∴该三位数是偶数的概率:2163p == 本题正确结果:13【点睛】本题考查古典概型概率问题的求解,属于基础题.5.函数21log y x =+______.【答案】1[,)2+∞ 【解析】 【分析】直接由根式内部的代数式大于等于0,然后求解对数不等式得答案. 【详解】由21log 0x +≥,得12x ≥, ∴函数21log y x =+的定义域为1,2⎡⎫+∞⎪⎢⎣⎭.故答案为:1,2⎡⎫+∞⎪⎢⎣⎭.【点睛】本题考查了函数的定义域及其求法,考查对数不等式的解法,是基础题.6.运行如图所示的伪代码,其结果为 .【答案】17 【解析】试题分析:第一次循环,I=1,S=1+1=2;第二次循环,I=3,S=2+3=5;第三次循环,I=5,S=5+5=10;第四次循环,I=7,S=10+7=17,结束循环输出S=17 考点:循环结构流程图7.在平面直角坐标系xOy 中,双曲线C :222116x y a -=(a >0)的右顶点到双曲线的一条渐近线的距离为53,则双曲线C 的方程为_______. 【答案】2212016x y -=.【解析】 【分析】由方程得到顶点坐标和渐近线方程,利用点到直线距离公式构造方程求得2a ,从而得到所求方程.【详解】由双曲线方程知,右顶点为(),0a ,渐近线方程为:4y x a=±,即40x ay ±-= ∴右顶点到双曲线渐近线距离2445316ad a ±=+,解得:220a =∴双曲线C 的方程为:2212016x y -=本题正确结果:2212016x y -=【点睛】本题考查双曲线标准方程的求解,关键是能够利用点到直线距离公式构造方程求得未知量.8.如图所示是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,相传这个图形表达了阿基米德最引以为自豪的发现.我们来重温这个伟大发现,圆柱的表面积与球的表面积之比为_______.【答案】32. 【解析】 分析】设球的半径为R ,可知圆柱高为2R ;根据圆柱表面积和球的表面积公式分别求得表面积,作比得到结果.【详解】设球的半径为R ,则圆柱的底面半径为R ,高为2R∴圆柱的表面积2212226S R R R R πππ=+⋅=;球的表面积224S R π=∴圆柱的表面积与球的表面积之比为21226342S R S R ππ== 本题正确结果:32【点睛】本题考查圆柱表面积和球的表面积公式的应用,属于基础题.9.函数()Asin()f x x ωϕ=+(A >0,ω>0)的部分图象如图所示.若函数()y f x =在区间[m ,n ]上的值域为[2-,2],则n ﹣m 的最小值是_______.【答案】3. 【解析】 【分析】根据三角函数图象求得函数解析式()2sin4f x x π=;利用()2f x =-()2f x =求得x的取值,可知当12k k =时取最小值,从而得到结果.【详解】由图象知:()max 2f x = 2A ∴=,又()22628T πω==⨯-= 4πω∴=()22sin 22f πϕ⎛⎫=+= ⎪⎝⎭Q 2k ϕπ∴=,k Z ∈()2sin 22sin 44f x x k x πππ⎛⎫∴=+= ⎪⎝⎭当()2f x =-1244x k πππ=-+或15244x k πππ=+,1k Z ∈ 181x k ∴=-或185x k =+,1k Z ∈当()2f x =时,2242x k πππ=+,2k Z ∈ 282x k ∴=+若n m -最小,则12k k = ()min 3n m ∴-= 本题正确结果:3【点睛】本题考查利用三角函数图象求解函数解析式、根据值域求解定义域的问题;关键是能够通过特殊角三角函数值确定角的取值.10.在公比为q 且各项均为正数的等比数列{}n a 中,n S 为{}n a 的前n 项和.若121a q =,且527S S =+,则首项1a 的值为_______.【答案】14. 【解析】 【分析】首先验证1q =时,不符合题意,可知1q ≠;利用()252317S S a q q -=++=和2311aa q ==可构造方程求得q ,代入求得结果.【详解】当1q =时,由527S S =+得:11527a a =+,解得:173a = 与11a =矛盾,可知1q ≠()252345317S S a a a a q q -=++=++=Q ,2311a a q ==260q q ∴+-=,又0q >,解得:2q = 114a ∴=本题正确结果:14【点睛】本题考查等比数列通项公式的应用,关键是能够利用已知等式构造出关于公比的方程.11.已知()f x 是定义在区间(﹣1,1)上的奇函数,当x <0时,()(1)f x x x =-.已知m 满足不等式2(1)(1)0f m f m -+-<,则实数m 的取值范围为_______. 【答案】(0,1). 【解析】 【分析】根据二次函数性质和奇偶性可知()f x 在()1,1-上单调递减;将不等式变为()()211f m f m -<-,根据单调性和定义域可得不等式组,解不等式组求得结果.【详解】()f x Q 为定义在()1,1-上的奇函数 ()00f ∴=(]1,0x ∴∈-时,()221124f x x x x ⎛⎫=-=-- ⎪⎝⎭ ()f x ∴在(]1,0-上单调递减()f x Q 为奇函数 ()f x ∴在[)0,1上单调递减 ()f x ∴在()1,1-上单调递减由()()2110f m f m-+-<得:()()()22111f m f m f m-<--=-2211111111m m m m -<-<⎧⎪∴-<-<⎨⎪->-⎩,解得:01m <<,即m 的取值范围为:()0,1 本题正确结果:()0,1【点睛】本题考查利用单调性和奇偶性求解函数不等式的问题,关键是能够将问题转化为函数值之间的比较,根据单调性将函数值的比较变为自变量的比较;易错点是忽略定义域的要求,造成求解错误.12.已知圆O :x 2+y 2=4和圆O 外一点P(0x ,0y ),过点P 作圆O 的两条切线,切点分别为A ,B ,且∠AOB=120°.若点C(8,0)和点P 满足PO =λPC ,则λ的范围是_______. 【答案】1,13⎡⎤⎢⎥⎣⎦. 【解析】 【分析】根据4PO =可知220016x y +=,利用PO PC λ=构造方程可求得0215x λ=-;根据044x -≤≤且0λ>可解不等式求得结果.【详解】120AOB ∠=o Q ,2OA OB == 4cos60AO PO ∴==o,即220016x y += 又PC =PO PC λ= ()22200816x y λ⎡⎤∴-+=⎣⎦且0λ> 解得:20225115x λλλ-==-220016x y +=Q 044x ∴-≤≤ 21454λ∴-≤-≤,解得:1,13λ⎡⎤∈⎢⎥⎣⎦本题正确结果:1,13⎡⎤⎢⎥⎣⎦【点睛】本题考查直线与圆的综合应用问题,涉及到两点间距离公式的应用、点的轨迹方程的求解;关键是能够利用λ表示出动点的横坐标,从而根据横坐标范围构造不等式.13.如图,已知梯形ABCD ,//AD BC ,23BC AD =,取BD 中点E ,连接AE 并延长交CD 于F ,若2AB AD FA CD ⋅=⋅u u u v u u u v u u u v u u u v ,则ABAD=_______.【答案】33. 【解析】 【分析】作//FG AD ,根据三角形相似得到比例关系证得34DF DC =;利用平面向量线性运算可用AD uuu v ,AB u u u v表示出CD uuu v ,FA u u u v ,根据数量积的运算律可整理得到223122AB AD =u u u v u u u v ,从而得到结果.【详解】作//FG AD ,交BD 于点GAED FEG ∆∆Q : GF EG AD DE ∴=,又2FG GD DE EGBC BD DE+== 又23BC AD =,可得:2DE EG = 3344DF DG EG DC DB EG ∴=== 2133CD CB BA AD DA BA AD AD AB =++=++=-u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v Q()3313344344FA AD DF AD DC AD AD AB AD AB ⎡⎤⎛⎫⎛⎫∴=-+=-+=-+-+=-- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦u u u v u u u v u u u v u u uv u u u v u u u v u u u v u u u v u u u v u u u v22133********2FA CD AD AB AD AB AB AD AB AD ⎛⎫⎛⎫∴⋅=-⋅--=+⋅- ⎪ ⎪⎝⎭⎝⎭u u u v u u u v u u uv u u u v u u u v u u u v u u u v u u u v u u u v u u u v又2AB AD FA CD ⋅=⋅u u u v u u u v u u u v u u u v 223122AB AD ∴=u u u v u u u v ,即223122AB AD =u u uv u u u v33AB AB AD AD ∴==u u u v u u u v 本题正确结果:33【点睛】本题考查平面向量的综合应用问题,涉及到向量的线性运算、向量数量积的运算律等知识;关键是能够用基底准确的表示向量,将数量积运算转化为模长之间的关系,属于较难题.14.已知函数()1ln ,111,122x x f x x x +≥⎧⎪=⎨+<⎪⎩,若12x x ≠,且()()122f x f x +=,则12x x +的取值范围是________.【答案】[32ln 2,)-+∞ 【解析】 【分析】首先可根据题意得出12x x 、不可能同时大于1,然后令121x x <<,根据()()122f x f x +=即可得出122212ln x x x x +=-+,最后通过构造函数()()12ln 1g x x x x =-+>以及对函数()()12ln 1g x x x x =-+>的性质进行分析即可得出结果。
2020江苏南京高三一模数学试卷详解

一、填空题
(本大题共14小题,每小题5分,共70分)
1. 已知集合
,全集
,则
.
【答案】
【解析】 集合 集合 故答案为
,
,
.
.
2. 设复数
,其中 为虚数单位,则
.
【答案】
【解析】
,
,
∴
. 故答案为: .
3. 学校准备从甲,乙,丙三位学生中随机选两位学生参加问卷调查,则甲被选中的概率为
平面
,
与四棱锥
的
/
∴无论 位于何处, 到底面 的面积设为 ,
∴
,
而
.
∴
故答案为 .
的距离都一样,不妨设为 ,将底面
10. 设函数 个最低点的横坐标为 ,则 的值为
的图象与 轴交点的纵坐标为 .
, 轴右侧第一
【答案】
【解析】 由函数
函数过
,
的图象与 轴交点的纵坐标为 ,
,
,
.
由 轴右侧第一个最底点的横坐标为 ,
中裁剪出两块全等的圆形铁皮⊙ 与⊙ 做圆柱的底面,裁剪出一个矩形
做圆柱的侧面
(接缝忽略不计), 为圆柱的一条母线,点 , 在⊙ 上,点 、 在⊙ 的一条直径
上,
,⊙ 、⊙ 分别与直线 、 相切,都与⊙ 内切.
( 1 ) 求圆形铁皮⊙ 半径的取值范围. ( 2 ) 请确定圆形铁皮⊙ 与⊙ 半径的值,使得油桶的体积最大.(不取近似值)
小值为四分之一图的切线与双曲线渐近线之间的距离,正好为四分之一图的半径 .
第一象限:
切线方程为:
.
/
第二象限: 第四象限:
2020年江苏省南京市新城中学高三数学理联考试题含解析

2020年江苏省南京市新城中学高三数学理联考试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 如果执行右边的程序框图,输入=,那么输出的结果是()A.9 B.3 C. D.参考答案:C略2. 已知函数是上的偶函数,且,当,则函数的零点个数()A.3 B.4 C.5 D.6参考答案:D3. 某几何体的三视图如图所示,图中的四边形都是边长为1的正方形,两条虚线互相垂直,则该几何体的体积是()A.1 B. C .D.参考答案:D略4. 函数的反函数是(A) (B)(C) (D)参考答案:答案:D5. 在△ABC中,若,则△ABC是………………………………()A.有一内角为30°的直角三角形 B.等腰直角三角形C.有一内角为30°的等腰三角形 D.等边三角形参考答案:B6. 已知为等差数列,若,则的值为()A.B.C.D.参考答案:A略7. 设集合 M={ x | x 2+3 x+2<0} , 集合 , 则M∪N= ()A.{ x | x-2} B.{ x | x>-1} C.{ x | x<-1} D.{ x | x -2}参考答案:A【知识点】集合及其运算A1∵集合M={x|x2+3x+2<0}={x|-2<x<-1},集合N={x|()x≤4}={x|2-x≤22}={x|-x≤2}={x|x≥-2},∴M∪N={x|x≥-2},【思路点拨】根据题意先求出集合M和集合N,再求M∪N.8. 设直线x=k 与函数的图像分别交于点M,N,则当达到最小时k的值为A.1 B. C.D.参考答案:D9. 已知在三棱锥P﹣ABC中,V P﹣ABC=,∠APC=,∠BPC=,PA⊥AC,PB⊥BC,且平面PAC⊥平面PBC,那么三棱锥P﹣ABC外接球的体积为()A.B.C.D.参考答案:D【考点】球的体积和表面积.【分析】利用等体积转换,求出PC,PA⊥AC,PB⊥BC,可得PC的中点为球心,球的半径,即可求出三棱锥P﹣ABC外接球的体积.【解答】解:由题意,设PC=2x,则∵PA⊥AC,∠APC=,∴△APC为等腰直角三角形,∴PC边上的高为x,∵平面PAC⊥平面PBC,∴A到平面PBC的距离为x,∵∠BPC=,PA⊥AC,PB⊥BC,∴PB=x,BC=x,∴S△PBC==,∴V P﹣ABC=V A﹣PBC==,∴x=2,∵PA⊥AC,PB⊥BC,∴PC的中点为球心,球的半径为2,∴三棱锥P﹣ABC外接球的体积为=.故选:D.10. 如图,半圆的直径AB=6,O为圆心,C为半圆上不同于A、B的任意一点,若P为半径OC上的动点,则的最小值是( )A、 B、 C、 D、参考答案:A略二、填空题:本大题共7小题,每小题4分,共28分11. 已知函数,则f[f(﹣2)]=.参考答案:【考点】有理数指数幂的化简求值.【分析】根据解析式从内到外逐次求解.【解答】解:根据题意:f(﹣2)=22﹣1=3,所以,故答案为.【点评】本题考察函数求值,属基础题.关键是根据自变量选择对应的解析式.12. 设,定义P ※Q=,则P※Q中元素的个数为 .参考答案:1213. 14.已知是定义域为的偶函数,当≥时,,那么,不等式的解集是____________.参考答案:(-7,3)14. 复数在复平面内对应的点位于第象限.参考答案:四15. (5分)设m是一个正整数,对两个正整数a、b,若a﹣b=km(k∈Z,k≠0),我们称a、b模m同余,用符号a=b(Modm)表示;在6=b(Modm)中,当,且m>1时,b的所有可取值为.参考答案:2或3或4由两个数同余的定义,可得6=b(Modm)中,则称6﹣b=km(k是非零整数),即6=b+km,又∵,且m>1,∴m是6的正约数,可得m=2、3或6①当m=2时,6=b+2k,可得b=2或4符合题意;②当m=3时,6=b+3k,可得b=3符合题意;⑥当m=6时,根据定义不符合题意,舍去故答案为:2或3或416. 已知实数满足约束条件,则的取值范围是参考答案:[-1,1]17. 圆C:的圆心到直线的距离是.参考答案:3圆C化成标准方程为,圆心为,到直线的距离,故答案为:3.三、解答题:本大题共5小题,共72分。
南京市2020届高三数学上学期期初联考试卷附答案详析
f x1
1 f x2
1 2
x1
3 2
ln x2
11
f x1 f x2 2
1 2
x1
ln x2
1 2
x1 1 2 ln x2
x1 x2 1 2 ln x2 x2
g x 1 2 ln x x x 1
gx
1
2 x
gx 0
1
2 x
0
x2
gx 0
1
2 x
0
x2
gx 0
1
2 x
0
1 x 2
g x 1, 2
f
2
2 sin
2
2
2k k Z
f
x
2 sinቤተ መጻሕፍቲ ባይዱ
4
x
2k
2 sin
4
x
f x 2
4
x
4
2k1
4
x
5 4
2k1
k1 Z
x 8k1 1 x 8k1 5 k1 Z
q 1
S5 S2 7
5a1 2a1 7
a1
7 3
a1 1
q 1
S5 S2 a3 a4 a5 a3 1 q q2 7
a3 a1q2 1
q2 q 6 0 q 0
q2
a1
1 4
1 4
a3 a1q2 1
5
1 2
AOB 120 OA OB 2
2020届江苏省南京市高三年级第一学期期中模拟试卷 数学试题含答案全解全析

绝密★启用前2020届江苏省南京市高三年级第一学期期中模拟试卷数学 答案全解全析数学Ⅰ卷一、填空题:本大题共14小题,每小题5分,共计70分.1. (本小题满分5分) 【答案】0【解析】()222i 12i z a a a =+=-+是实数,则0a =. 2. (本小题满分5分) 【答案】 5【解析】z =21-i-i 3=1+i +i =1+2i ,所以| z |=5. 3. (本小题满分5分) 【答案】(]2,3【解析】图中阴影部分所表示的集合为()U C M N ,即为(]2,3.4. (本小题满分5分) 【答案】18【解析】校A 专业对视力要求不低于0.9的学生数为45()10.750.250.218⨯++⨯=. 5. (本小题满分5分) 【答案】4860【解析】由题设可知,S =100+99+98+…+20=4860. 6. (本小题满分5分) 【答案】6 3【解析】由体积得球半径R =1,三棱柱的高为2,底面边长为23.V =34(23)2×2=63. 7. (本小题满分5分)【解析】由题意,235k -=,即4k =,所以双曲线为2214x y -=.8. (本小题满分5分) 【答案】128π【解析】设圆锥底面半径为r ,高为h ,由题意,π1080πr ⨯=,得8r =.所以6h =,容积为2211ππ8633128πr h =⨯⨯=. 9. (本小题满分5分) 【答案】6-因为23AE AD =,12AF AD DF AD AB =+=+;23BE BA AE AD AB =+=-,那么AF BE ⋅=()()1223AD AB AD AB +⋅-22212323AD AB AB AD =--⋅6846=--=-. 10. (本小题满分5分) 【答案】{}1,3【解析】由2,1,()2,11,2, 1.x x f x x x x -<-⎧⎪=-⎨⎪>⎩≤≤由(23)()f a f a -=,得23a a -=或230a a -+=或11,1231,a a -⎧⎨--⎩≤≤≤≤解得1a =或3a =.11. (本小题满分5分) 【答案】72+. 【解析】如图所示AF 的斜率为3,所以60BAF ∠=︒且AF =AB ,所以ABF ∆是等边三角形, 所以130F BF ∠=︒,所以1234BF c BF c ==,, 所以c AF 721=,由双曲线的定义可知c c a 4722-=,所以双曲线的离心率为327+.12. (本小题满分5分) 【答案】15.【解析】令AB BC CA ===,,c a b ,则11tan tan 32A C ==,, 所以tan tan(π)tan()1B AC A C =--=-+=-,所以3π4B =,由正弦定理可得22||,||510==c a ,所以15⋅=a c .y xO ABF 第11题13. (本小题满分5分).【解析】由2PB PA ≥得224PB PA ≥,所以2244(1)PC PO --≥,所以224PC PO ≥,设()P x y ,,所以22816033x y x ++-≤,即22464()39x y ++≤,点P 在圆964)34(22=++y x 上及圆内,所以EF 为直线截圆所得的弦,所以EF =3392.14. (本小题满分5分)【答案】[32]-【解析】① 若1a -≤,222222110()2210 1.x ax a a x f x ax a a x ⎧-+++-<⎪=⎨-+++⎪⎩,≤,,≤≤ 当01x ≤≤时,2()221f x ax a a =-+++为递增函数,且2(0)(1)f a =+, 当10x -<≤时,22()2221f x x ax a a =-+++的对称轴为2a x =,若存在0[11]x ∈-,,使得0()0f x ≤,则12(1)0a f ⎧-⎪⎨⎪-⎩≤≤或12()02a a f ⎧>-⎪⎨⎪⎩≤,即22430a a a -⎧⎨++⎩≤≤或221420a a a -<-⎧⎨++⎩≤≤,解得31a --≤≤.② 若10a -<<,22222211()222102210 1.ax a a x a f x x ax a a a x ax a a x ⎧-++-<⎪=-+++<⎨⎪-+++⎩,≤,,≤,,≤≤当01x ≤≤时,2()221f x ax a a =-+++为递增函数,且2(0)(1)f a =+, 当1x a -<≤时,2()221f x ax a a =-++为递减函数,且2()(1)f a a =+, 当0a x <≤时,22()2221f x x ax a a =-+++的对称轴为2a x =,若存在[]011x ∈-,,使得0()0f x ≤, 则()02a f ≤,即2420a a ++≤,解得22a --+≤10a -<<,所以12a -<.综上可得,32a -≤,即a的取值范围为[32]--. 二、解答题:本大题共6小题,共计90分. 15.(本小题满分14分) 【答案与解析】(1)因为 m ∥n ,所以sin α=-2cos α.所以原式=4.(2)因为 |m -n |=2,所以2sin α-cos α=2.所以cos 2α=4(sin α-1)2,所以1-sin 2α=4(sin α-1)2, 所以α∈()ππ2,, 所以34sin ,cos 55αα==-.所以原式=10-. 16.(本小题满分14分) 【答案与解析】(1)由题可得△BCD 为正三角形,E 为BC 中点,故DE ⊥BC . 又PO ⊥平面ABCD ,BC ⊂平面ABCD ,则PO ⊥BC , 而DE ∩PO =O ,,DE PO ⊂平面PDE ,所以BC ⊥平面PDE . 又PD ⊂平面PDE ,故PD ⊥BC . (2)取AP 中点为F ,再取PD 中点为G ,连结FG . 则FG 为△P AD 中位线,故FG =∥ 12AD , 又BE =∥ 12AD ,所以FG =∥BE ,于是四边形BFGE 为平行四边形, 因此BF ∥EG .又BF ⊄平面PDE ,EG ⊂平面PDE ,所以BF ∥平面PDE . 由(1)知,BC ⊥平面PDE .则有BC ⊥PE ,BC ⊥DE , 而BC ∥FG ,故FG ⊥PE ,FG ⊥DE ,且DE ∩PE =E ,所以FG ⊥平面PDE .A BCDPM(第16题)O于是四面体PDEF 的体积为V=13S △PDE ·FG =13×12×23×3×1=1.另解(等体积转化):因为BF //面PDE ,则B ,F 两点到平面PDE 的距离相等,所以四面体PDEF 的体积等于四面体PDEB , 因为PO ⊥平面ABCD ,所以V P-BDE =13·PO ·S △BDE =1.17.(本小题满分14分) 【答案与解析】(1)因为CD ∥OA ,所以rad ODC AOD x ∠=∠=, 在△OCD 中,23OCD π∠=,3COD x π∠=-,2OD =km ,由正弦定理得22sin sin()sin 33OC CD x x ===ππ-(注:正弦定理要呈现,否则扣2分)得sin 3OC x =km,sin()33CD x π=- km . 又圆弧DB 长为2()3x π- km .所以2sin [sin()2()]3333y a x a x x ππ=⨯+⨯-+-2cos )3a x x x π=⨯+-+,(0)3x π∈,. (2)记()2cos )3f x a x x x π=⨯+-+,则()2sin 1)2[2cos()1]6f x a x x a x π'=⨯--=⨯+-, 令()0f x '=,得6x π=. 当x 变化时,()f x ',()f x 的变化如下表:所以()f x 在6x π=处取得极大值,这个极大值就是最大值. 即()2)66f a ππ=⨯.答:(1)y 关于x 的函数解析式为2cos )3y a x x x π=⨯+-+,其定义域为 (0)3π,;(2)广告位出租的总收入的最大值为)6a π元. 18.(本小题满分16分) 【答案与解析】(1)设点()M x y ,PQ =,得()P x .因为P 为圆O :222x y +=上的动点, 所以)222x +=,即2212x y +=,所以当点P 运动时,点M 始终在定椭圆2212x y +=上.(2)①设11()A x y ,,22()B x y ,,当10y ≠时,直线AT 的方程为:()1111x y y x x y -=--,即221111x x y y x y +=+, 因为22112x y +=,所以112x x y y +=, 当10y =时,直线AT 的方程为:x = 综上,直线AT 的方程为:112x x y y +=. 同理,直线BT 的方程为:222x x y y +=.又点T ()2()t t -∈R ,在直线AT ,BT 上, 则1122x ty -+=,① 2222x ty -+=,② 由①②知,直线AB 的方程为:22x ty -+=.BCAl 3l 2l 1 图1D E所以直线AB 过定点()10-,. ②设33()C x y ,,44()D x y ,,则O 到AB的距离d =AB =由222212x ty x y -+=⎧⎪⎨+=⎪⎩,得22(8)440t y ty +--=, 于是34248t y y t +=+,34248y y t -=+,所以34CD y =-,于是AB CD =,AB CD ⇔⇔()222(8)2t t ++2≤()222(4)4t t ++ ⇔42(6)t t +≥0(显然)所以AB CD .19.(本小题满分16分) 【答案与解析】(1)当16b =时,31()16f x ax x =++,则21()36f x ax '=+.由0a >可知()0f x '>恒成立,故函数()f x 在[33]-,上单调递增, 所以min 1()(3)2702f x f a =-=-+≥,解得1054a <≤,所以集合1{|0}54A a a =<≤.(2)① 由3()1f x ax bx =++得2()3f x ax b '=+,因为00a b ><,,则由()0f x '=,得1,212)x x x =<.在R 上列表如下:(ⅰ)当23x ≥,即027b a <-≤时,则12[33][]x x -⊆,,,所以()f x 在[33]-,上单调递减;(ⅱ)当23x <,即27b a >-时,此时13x >-,()f x 在1[3]x -,和2[3]x ,上单调递增;在12()x x ,上单调递减. 综上,当027b a <-≤时,()f x 在[33]-,上单调递减; 当27b a >-时,()f x 在3⎡-⎢⎣,,3⎤⎥⎦上单调递增; 在(上单调递减.②(方法一)当1b <-时,由①可知,(ⅰ)当027b a<-≤时,()f x 在[33]-,上单调递减,所以min ()(3)2731312110f x f a b b b b ==++-++=+<-<≤, 这与()0x D f x ∀∈,≥恒成立矛盾,故此时实数a 不存在; (ⅱ)当27b a >-时,()f x 在3⎡-⎢⎣,,3⎤⎥⎦上单调递增; 在(上单调递减,所以min 2()min{(3)()}f x f f x=-,. 若(3)27310f a b -=--+<,这与()0x D f x ∀∈,≥恒成立矛盾, 故此时实数a 不存在;若(3)27310f a b -=--+>,此时3222()1f x ax bx =++, 又222()30f x ax b '=+=,则223b ax =-, 32222222()1()111133bx b f x ax bx x bx =++=-++=+==.下面证明10<,也即证:3427b a ->.因为27ba >-,且27310a b --+>,则2731a b <-+, 下证:3431b b ->-+.令3()431(1)g b b b b =-+<-,则2()1230g b b '=->,所以()g b 在(,1]-∞-上单调递增,所以()(1)0g b g <-=,即2()0f x <. 这与()0x D f x ∀∈,≥恒成立矛盾,故此时实数a 不存在. 综上所述,A =∅. (方法二)(ⅰ)当0x =时,(0)1f =≥0成立;(ⅱ)当(0,3]x ∈时,由题意可知31ax bx -≥-恒成立,则231b a x x -≥-,设231()b g x x x =--,则3442323()b bx g x x x x+'=+=, 令()0g x '=,解得32x b =-.因为1b <-,所以3032b<-<,所以()g x 在3(0)2b -,上单调递增,在3(3]2b-,上单调递减, 所以333max3484()()292727b b b g x g b =-=-+=-,所以3427b a ≥-; (ⅲ)当[30)x ∈-,时,由题意可知31ax bx -≥-恒成立,则231b a x x -≤-.设231()b g x x x =--,则3442323()b bx g x x x x+'=+=, 因为1b <-,所以()0g x '>恒成立,所以()g x 在[3,0)-上单调递增, 所以min 1()(3)927b g x g =-=-+,所以1927b a -+≤.若A ≠∅,则存在实数a 满足34127927b b a -+-≤≤,则34127927b b -+-≤成立,即34310b b -+≥,也即2(1)(21)0b b +-≥成立,则1b -≥,这与1b <-矛盾,所以A =∅. 20.(本小题满分16分) 【答案与解析】(1) 由A ={1,2},得a 1=b 1,a 2=b 2.设数列{a n }公差为d ,数列{b n }公比为我q ,由a 2=b 2⇒ a 1+ d =a 1q ,故d =a 1(q -1) ①因为a n =n ,a 1=b 1=1,a 2=b 2=2,所以数列{b n }的公比q =b 2b 1=2,所以,b n =2n -1.……2分② 答:a n <b n (n =1,2,…).证明如下: 因为a 1>0,q >0,q ≠1,所以b n -a n =a 1q n -1-[(a 1+(n -1) a 1(q -1)]=a 1( q n -1-1)-a 1(q -1) (n -1)=a 1(q -1)(q n -2+q n -1+…+1)-a 1(q -1) (n -1)=a 1(q -1)[q n -2+q n -3+…+1-(n -1)] =a 1(q -1)[(q n -2-1)+( q n -3-1)+…+(q -1)]=a 1(q -1)2[(q n -3+q n -4+…+1)+(q n -4+q n -5+…+1)+…+(q +1)+1]>0. 所以a n <b n (n =1,2,…).(2)不妨设a n =a +bn (b ≠0),b n =pq n ,由a n =b n ⇔ a +bn =pq n ⇒a p +bp n =q n .令s =a p ,t =bp,(t ≠0),原问题转化为关于n 的方程q n -tn -s =0 ① 最多有多少个解.下面我们证明:当q >0时,方程①最多有2个解;q <0时,方程②最多有3个解. 当q >0时,考虑函数f (x )=q x -tx -s ,则f ′(x )=q x ln q -t如果t ln q <0,则f (x )为单调函数,故方程①最多只有一个解;如果t ln q >0,且不妨设由f ′(x )=0得f ′(x )有唯一零点x 0=log q tln q ,于是当x >x 0时,f ′(x )恒大于0或恒小于0,当x <x 0时,f ′(x )恒小于0或恒大于0, 这样f (x )在区间(0,x 0)与(x 0,+∞)上是单调函数,故方程①最多有2个解. 当q <0时,如果t >0.如果n 为奇数,则方程①变为 |q |n +tn +s =0,显然方程最多只有一个解,即最多只有一个奇数满足方程①. 如果n 为偶数,则方程①变为|q |n -tn -s =0.由q >0的情形,上式最多有2个解,即满足①的偶数最多有2个. 这样,最多有3个正数满足方程①.对于t <0,同理可以证明,方程①最多有3个解. 综上所述,集合A 中的元素个数最多有3个. 再由当a n =6n -8,,b n =(-2)n ,则a 1=b 1,a 2=b 2,a 4=b 4.A ={1,2,4}. 由此,可知集合A 中的元素个数最多有3个.数学Ⅱ卷(附加题)21.【选做题】本题包括A 、B 、C 三小题。
江苏南通市2020届高三学校第一次大联考数学试题含附加题及参考答案

2020届高三基地学校第一次大联考数学 I参考公式:样本数据1x ,2x ,…,n x 的方差2211()n i i s x x n ==-∑,其中11n i i x x n ==∑.柱体的体积公式V Sh =柱体,其中S 为柱体的底面积,h 为高. 球体的体积公式34π3V R =球体,其中R 为球体的半径. 一、填空题:本大题共14小题,每小题5分,共计70分.把答案填写在答题卡相应位置........ 1. 已知集合{}11A x x =-<<,{}101B =-,,,则AB = ▲ .2. 已知复数z 满足10i z z =-(i 为虚数单位),则z 的虚部为 ▲ . 3. 根据如图所示的伪代码,可知输出的结果S 为 ▲ . 4. 若样本数据3,4,5,x ,y 的平均数为4,且12xy =, 则此样本的方差为 ▲ .5. 从1,2,3,4,5中随机取出两个不同的数,则两数之积大于10 的概率为 ▲ .6. 现有一个半径为3 cm 的实心铁球,将其高温融化后铸成一个底面圆半径为3 cm 的圆柱状实心铁器(不计损耗),则该圆柱铁器的高为 ▲ cm .7. 已知函数π()2sin()(0)3f x x ωω=+>的图象关于点π(0)2,对称,则ω的最小值为▲ .8. 设等差数列{}n a 的前n 项和为n S ,若10a ≠,323a a =,则105S S 的值为 ▲ . 9. 在平面直角坐标系xOy 中,设抛物线C :22(0)x py p =>在点1x =处的切线为(第3题)l .若l 与该抛物线的准线的交点横坐标为732,则p 的值为 ▲ . 10. 已知()f x 是定义在R 上的奇函数,当x ≥0时,()log 2(1)f x x =+.则满足不等式2(2)40f a a -+>的实数a 的取值范围是 ▲ . 11. 已知x ,y 为正实数,则292y x x x y++的最小值为 ▲ . 12. 在ABC ∆中,已知π3A =,3AB =.若D 为BC 中点,且72AD =,则AC AD ⋅=▲ .13. 在平面直角坐标系xOy 中,已知AB 是圆O :224x y +=的直径.若与圆O 外离的圆1O :222(6)(8)(0)x y r r -+-=>上存在点M ,连接AM 与圆O 交于 点N ,满足BMON ,则半径r 的取值范围是 ▲ .14. 已知函数2()(1)1f x x m x =-+-与()ln 22g x x x m =--的零点分别为12x x ,和34x x ,.若1324x x x x <<<,则实数m 的取值范围是 ▲ . 二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤.15.(本小题满分14分)如图,在三棱锥A BCD -中,AB AD =,BC BD ⊥.E 为CD 的中点,O 为BD 上 一点,且AO ⊥平面BCD . 求证:(1)BC平面AOE ;(2)平面ABD ⊥平面AOE .(第15题)16.(本小题满分14分)在△ABC 中,角A B C ,,所对边分别为a b c ,,.已知sin sin 2B Ca Bb +=. (1)求角A 的值; (2)若π1cos()64B +=,求cosC 的值.17.(本小题满分14分)在平面直角坐标系xOy 中,已知椭圆C :22221(0)x y a b a b +=>>的左焦点为(0)F,点1()2A ,在椭圆C 上.(1)求椭圆C 的方程;(2)已知圆O :222x y a +=,连接FA 并延长交圆O 于点B ,H 为椭圆长轴上一点(异于左、右焦点),过点H 作椭圆长轴的垂线分别交椭圆C 和圆O 于点P ,Q (P ,Q 均在x 轴上方).连接PA ,QB ,记PA 的斜率为1k ,QB 的斜率为2k .①求21k k 的值; ②求证:直线PA ,QB 的交点在定直线上.(第17题)18.(本小题满分16分)某生态农场有一矩形地块,地块内有一半圆形池塘(如图所示),其中4AB =百米,2AD =百米,半圆形池塘的半径为 1 百米,圆心O 与线段AB 的中点重合,半圆与AB 的左侧交点为E .该农场计划分别在AE 和CD 上各选一点P ,Q ,修建道路A P Q C →→→,要求 PQ 与半圆相切.(1)若 60QPE ∠=︒,求该道路的总长;(2)若AP ,PQ 为观光道路,修建费用是4万元/百米,CQ 为便道,修建费用是 1 万元/百米,求修建观光道路与便道的总费用的最小值.19.(本小题满分16分)设n S 为数列{}n a 的前n 项和,若2n n n S Aa Ba C =++(A B C ,,为常数)对任意n *∈N 恒成立.(1)若2nn a =,求A B C ,,的值;(2)若16A =,12B =,13C =,且1n a >. ①求数列{}n a 的通项公式;②若数列{}n b 满足212n an n b b +=,且238b b =,求证:数列{}n b 为等比数列.(第18题)20.(本小题满分16分)已知函数()ln f x a x x =-,(a ∈R ,0a ≠),1()()gx x x=-+(0x >). (1)若函数()f x 与()g x 有相同的极值点(极值点是指函数取极值时对应的自变量的值),求a 的值; (2)记()()()F x f x g x =-.①若在区间(]0e ,(e 为自然对数底数)上至少存在一点0x ,使得0()0F x <成立,求a 的取值范围;②若函数()F x 图象存在两条经过原点的切线,求a 的取值范围.2020届高三基地学校第一次大联考数 学 II (附加题)21.【选做题】本题包括A 、B 、C 三小题,请选定其中两题,并在相应的答题区域内作答....................若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. A .[选修4–2:矩阵与变换] (本小题满分10分)已知矩阵231t ⎡⎤=⎢⎥⎣⎦A 的一个特征值为4,求矩阵A 的逆矩阵1-A .B .[选修4–4:坐标系与参数方程](本小题满分10分)在平面直角坐标系xOy 中,已知直线l 的参数方程为11,22x t y ⎧=+⎪⎪⎨⎪=⎪⎩(t 为参数),曲线C的参数方程为2,2x s y s ⎧=⎨=⎩(s 为参数).若直线l 与曲线C 相交于A B ,两点,求弦AB 的长.C .[选修4–5:不等式选讲](本小题满分10分)已知关于x 的不等式x a b -<的解集为{}24x x <<,【必做题】第22、23题,每小题10分,共计20分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤.22.(本小题满分10分)在某次数学测验中,学号为(1234)i i =,,,的四位同学的考试成绩{}()90929698f i ∈,,,,且满足(1)f ≤(2)f ≤(3)f ≤(4)f .(1)求四位同学的考试成绩互不相同的概率;(2)设四位同学中恰有X 位同学的考试成绩为96分,求随机变量X 的概率分布列及数学期望.23.(本小题满分10分)已知2012(1)()n n n x a a x a x a x n *+=+++⋅⋅⋅+∈N .(1)若215a =,求n 的值; (2)求01(1)nkn k kS a ==-∑的值.。
江苏省南京市2020届高三上学期期初联考试卷数学试题 (含解析答案)

江苏省南京市2020届高三年级第一学期期初联考考试数学试题一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卷相应的位置上.) 1.已知集合A ={}12x x -<≤,B ={}0x x ≤,则A I B = . 答案:(﹣1,0] 考点:集合的运算 解析:(﹣1,0] 2.已知复数z =3i1i-+(i 是虚数单位),则z 的虚部是 . 答案:﹣2 考点:虚数解析:z =223i (3i)(1i)i 4i 34i 22i 11i (1i)(1i)1i 2----+-+====-+++--,所以则z 的虚部是﹣2. 3.对一批产品的质量(单位:克)进行抽样检测,样本容量为1600,检测结果的频率分布直方图如图所示.根据标准,单件产品质量在区间[25,30)内为一等品,在区间[15,20),[20,25)和[30,35)内为二等品,其余为三等品.则样本中三等品件数为 .答案:200考点:统计,抽样调查 解析:2004.现有三张卡片,分别写有“1”、“2”、“3”这三个数字.将这三张卡片随机排序组成一个三位数,则该三位数是偶数的概率是 . 答案:13考点:古典概型解析:将这三张卡片随机排序组成一个三位数如下:123,132,213,231,312,321,共6种,其中偶数有2种,所以该三位数是偶数的概率是1263÷=. 5.函数21log y x =+的定义域为 . 答案:[12,+∞) 考点:函数的定义域解析:由21log 00x x +≥⎧⎨>⎩,解得12x ≥,所以原函数定义域为[12,+∞).6.运行如图所示的伪代码,其结果为 .答案:17考点:算法初步,伪代码解析:根据伪代码所示的顺序,逐框分析程序中各变量、各语句的作用可知:该程序的作用是累加并输出S =1+1+3+5+7的值,所以S =1+1+3+5+7=17.7.在平面直角坐标系xOy 中,双曲线C :222116x y a -=(a >0)的右顶点到双曲线的一条渐近线的距离为453,则双曲线C 的方程为 . 答案:2212016x y -= 考点:双曲线的性质解析:由题意可知双曲线的右顶点为(a ,0),渐近线方程为4y x a=±,根据点到线的距离公式求得右顶点到双曲线渐近线距离为:216a +,即可得方程216a +=45,解得a 2=20,所以双曲线C 的方程为2212016x y -=. 8.如图所示是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,相传这个图形表达了阿基米德最引以为自豪的发现.我们来重温这个伟大发现,圆柱的表面积与球的表面积之比为 .答案:32考点:圆柱、球的表面积解析:设球的半径为R ,则圆柱的底面半径为R ,高为2R ,S 圆柱=2πR ×2R +2×πR 2=6πR 2,S 球=4πR 2.所以22S 63S 42R R ππ==圆柱球. 9.函数()Asin()f x x ωϕ=+(A >0,ω>0)的部分图象如图所示.若函数()y f x =在区间[m ,n ]上的值域为[2-,2],则n ﹣m 的最小值是 .答案:3考点:三角函数的图像与性质解析:由函数的最大值为2,可得A =2.由12•2πω=4,可得4πω=.由五点法作图可得4π×2+ϕ=2π,∴ϕ=0,函数()2sin()4f x x π=.由于函数在[2,5]上是减函数,x =2时,()f x =2,x =5时,()f x =2-,故n ﹣m 的最小值是5﹣2=3. 10.在公比为q 且各项均为正数的等比数列{}n a 中,n S 为{}n a 的前n 项和.若121a q=,且527S S =+,则首项1a 的值为 . 答案:14考点:等比数列解析:因为527S S =+,所以3457a a a ++=,则2341()7a q q q ++=,将121a q =代入可得:260q q +-=,因为q >0,所以q =2,从而首项1a 的值为14. 11.已知()f x 是定义在区间(﹣1,1)上的奇函数,当x <0时,()(1)f x x x =-.已知m满足不等式2(1)(1)0f m f m -+-<,则实数m 的取值范围为 . 答案:(0,1)考点:函数性质综合解析:当x <0时,()(1)f x x x =-,可得()f x 在(﹣1,0)单调递减;由()f x 是定义在区间(﹣1,1)上的奇函数,可得()f x 也是区间(﹣1,1)上的减函数.因为2(1)(1)0f m f m -+-<,所以2(1)(1)f m f m -<-,可得如下不等式组:2211111111m m m m -<-<⎧⎪-<-<⎨⎪->-⎩,得02022021m m m m <<⎧⎪<<-<<⎨⎪-<<⎩或,解得:01m <<.所以实数m的取值范围为(0,1).12.已知圆O :x 2+y 2=4和圆O 外一点P(0x ,0y ),过点P 作圆O 的两条切线,切点分别为A ,B ,且∠AOB =120°.若点C(8,0)和点P 满足PO =λPC ,则λ的范围是 . 答案:113λ≤≤ 考点:圆的方程解析:首先求得PO =4,设P(x ,y ),则2216x y +=①,由PO =λPC ,得PO 2=λPC 2,则x 2+y 2=λ2[(x ﹣8)2+y 2],化简得222220(1)()1664x y x λλλ=-+-+②,由①②得:2251x λλ-=,根据﹣4≤2251λλ-≤4,求得113λ≤≤. 13.如图,已知梯形ABCD ,AD ∥BC ,BC 2AD 3=,取BD 中点E ,连接AE 并延长交CD 于F ,若AB AD 2FA CD ⋅=⋅u u u r u u u r u u u r u u u r ,则AB AD= .3 考点:平面向量的数量积解析:根据题意可得CF 1FD 3=,21CD CB BA AD AD AB AD AD AB 33=++=--+=-u u u r u u u r u u u r u u u r u u ur u u u r u u u r u u u r u u u r ,2331132FA CD 2(CD AD)CD 2[(AD AB)AD](AD AB)AB 44332⋅=-⋅=--⋅-=u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r21AD AB AD 2-+⋅u u ur u u u r u u u r ,所以由AB AD 2FA CD ⋅=⋅u u u r u u u r u u u r u u u r ,得2231AB AD AB AD 22⋅=-+u u u r u u u r u u u r u u u rAB AD ⋅u u u r u u u r ,所以22AD 3AB =u u u r u u u r ,所以ABAD314.已知函数1ln 1()11122x x f x x x +≥⎧⎪=⎨+<⎪⎩,,,若12x x ≠,且12()()2f x f x +=,则12x x +的取值范围是 .答案:[32ln 2-,+∞) 考点:函数与方程 解析:设121x x <<,则12111ln 222x x +++=,得:1212ln x x =-,所以12x x +=1﹣22ln x +2x .令222()12ln g x x x =-+,2222()x g x x -'=,当1<2x <2,2()g x '<0,2()g x 在(1,2)上单调递减,当2x >2,2()g x '>0,2()g x 在(2,+∞)上单调递增,∴当x =2时,2()g x 有最小值为32ln 2-,所以12x x +≥32ln 2-,即12x x +的取值范围是[32ln 2-,+∞).二、解答题(本大题共6小题,共计90分,请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.) 15.(本小题满分14分)如图,在四棱锥P —ABCD 中,底面ABCD 是正方形,PA ⊥底面ABCD ,且PA =AD ,点F 是棱PD 的中点,点E 为CD 的中点.(1)证明:EF ∥平面PAC ; (2)证明:AF ⊥PC .解:16.(本小题满分14分)在△ABC 中,A =34π,AB =6,AC =32(1)求sinB的值;(2)若点D在BC边上,AD=BD,求△ABD的面积.解:(1)∵A=34π,AB=6,AC=32∴由余弦定理可得:BC2=AB2+AC2﹣2AB·AC·cosA=90∴BC=310由正弦定理可得:232AC sin A102sin BBC10310⨯⋅===.(2)∵A=34π,B为锐角∴cosB=310由余弦定理:AD2=AB2+BD2﹣2AB·BD·cosB因为AD=BD,所以BD=AB102cos B3102==⨯所以S△ABD=12AB·BD·sinB=1106102⨯⨯⨯=3所以△ABD的面积为3.17.(本小题满分14分)窗花是贴在窗纸或窗户玻璃上的剪纸,是中国古老的传统民间艺术之一.图中的窗花是由一张圆形纸片剪去一个正十字形剩下的部分,正十字形的顶点都在圆周上.已知正十字形的宽和长都分别为x,y(单位:dm)且x<y,若剪去的正十字形部分面积为4dm2.(1)求y关于x的函数解析式,并求其定义域;(2)现为了节约纸张,需要所用圆形纸片面积最小.当x取何值时,所用到的圆形纸片面积最小,并求出其最小值.解:(1)由题意可得:224xy x-=,则242xyx+=,∵y x>,∴0<x<2∴y 关于x 的函数解析式242x y x+=,定义域为(0,2).(2)设正十字形的外接圆的直径为d ,由图可知22222222454()2224x x d x y x x x+=+=+=++≥,当且仅当2x =时,正十字形的外接圆直径d 最小,则半径最小值为2d =,∴正十字形的外接圆面积最小值为2142ππ⨯=答:当x . 18.(本小题满分16分)已知椭圆C :22221x y a b+=(a >b >0),左、右焦点分别为F 1(﹣1,0),F 2(1,0),椭圆离心率为12,过点P(4,0)的直线l 与椭圆C 相交于A 、B 两点(A 在B 的左侧). (1)求椭圆C 的方程;(2)若B 是AP 的中点,求直线l 的方程;(3)若B 点关于x 轴的对称点是E ,证明:直线AE 与x 轴相交于定点. 解:(1)∵左、右焦点分别为F 1(﹣1,0),F 2(1,0) ∴c =1, ∵椭圆离心率为12∴a =2∴b 2=a 2﹣c 2=4﹣1=3∴椭圆C 的方程为22143x y +=. (2)设B(0x ,0y ),根据B 是AP 的中点,得A(024x -,02y ) 由于A 、B 两点都在椭圆上,可得方程组:22002200143(24)4143x y x y ⎧+=⎪⎪⎨-⎪+=⎪⎩,解得0074x y ⎧=⎪⎪⎨⎪=⎪⎩或0074x y ⎧=⎪⎪⎨⎪=⎪⎩所以B(74,8)或(74,8-)设直线l 的斜率为k ,则k=8744-或8744--,即k所以直线l的方程为:4)6y x =±-,60y --=60y +-=. (3)设A(1x ,1y ),B(2x ,2y ),则E(2x ,2y -) 设D 为直线AE 与x 轴的焦点,且D(d ,0) 根据A 、D 、E 三点共线得:1212y y x d x d -=--,解得122112x y x y d y y +=+ 设直线l 为:(4)y k x =-,其中k ≠0 则11(4)y k x =-,22(4)y k x =-,代入122112x y x y d y y +=+得12121224()8x x x x d x x -+=+-22(4)143y k x x y =-⎧⎪⎨+=⎪⎩,化简得:2222(34)3264120k x k x k +-+-= 所以21223234k x x k +=+,2122641234k x x k -=+则2222121221226412322424()34341328834k k x x x x k k d k x x k ---+++===+--+所以直线AE 与x 轴相交于定点(1,0).19.(本小题满分16分)在数列{}n a 中,已知12a =,13()n n a a f n +=+. (1)若()f n k =(k 为常数),314a =,求k ;(2)若()21f n n =-.①求证:数列{}n a n +为等比数列;②记(1)n n b a n λ=+-,且数列{}n b 的前n 项和为n T ,若3T 为数列{}n T 中的最小项,求λ的取值范围. 解:(1)k 的值为﹣1; (2)①②20.(本小题满分16分)已知函数()ln 2f x x x =--.(1)求曲线()y f x =在x =1处的切线方程;(2)函数()f x 在区间(k ,k +1)(k ∈N)上有零点,求k 的值; (3)记函数21()2()2g x x bx f x =---,设1x ,2x (1x <2x )是函数()g x 的两个极值点,若32b ≥,且12()()g x g x k -≥恒成立,求实数k 的最大值. 解:(1)∵()ln 2f x x x =-- ∴1()1f x x'=-则(1)0k f '== 又∵(1)1f =-∴曲线()y f x =在x =1处的切线方程y =﹣1. (2)k =3. (3)所以实数k的最大值为152ln28.11。
江苏省南京市六校联合体2020届高三年级一模联考数学试卷解析版

1南京市六校联合体2020届高三年级一模联考试卷数学Ⅰ试题2019.12一、填空题(本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上)1.已知集合A ={1,2,3,4},B ={x |x 2-4x <0},则A ∩B =__________. 解:{1A =Q ,2,3,4},{|04}B x x =<<, {1A B ∴=I ,2,3}.故答案为:{1,2,3}. 2.已知复数2i 12++=iz ,则复数z 的共轭复数为__________. 解:22(1)221211(1)(1)i z i i i i i i i i -=+=+=-+=+++-Q , 故z 的共轭复数是:1i -3.某校有教师300人,男学生1500人,女学生1200人,现用分层抽样的办法从全校师生中抽取200人进行某项调查,则应抽取的女学生人数为__________. 解:女学生人数所占的比例为12002300150012005=++,则应抽取的女学生人数为2200805⨯=, 故答案为:80.4.根据如图所示的伪代码,可知输出的结果S 为__________.答案:模拟演示:解:1S =,1I =;3S =,4I =;7S =,7I =;15S =,10I =此时结束循坏输出15S =2故答案为:15.5.甲、乙两人依次从标有数字1,2,3的三张卡片中各抽取一张(不放回),则两人均未抽到标有数字3的卡片的概率为__________.解:甲、乙两人依次从标有数字1,2,3的三张卡片中各抽取一张(不放回), 基本事件总数326n =⨯=,两人均未抽到标有数字3的卡片包含的基本事件个数212m =⨯=, 则两人均未抽到标有数字3的卡片的概率为2163m p n ===. 故答案为:13.6.若抛物线210y x =的焦点到双曲线222116x y a -=的一条渐近线的距离是2,则该双曲线的离心率为__________.解:抛物线210y x =的焦点为5(,0)2,双曲线222116x y a -=的一条渐近线方程为4y x a=±,542⨯=,解得3a =,则5c =,所以双曲线的离心率53e = 故答案为:537.已知f (x )是定义在R 上的奇函数,且当x ≥0时f (x )=x +a ,a 为实数,则f (-4)的值是__________.解:()f x Q 是定义在R 上的奇函数,且0x …时()f x a =, (0)0f a ∴==,0x ∴…时,()f x =,∴(4)(4)2f f -=-==-.故答案为:2-.8.已知等差数列{}n a 的前n 项和为n S ,等比数列{}n b 前n 项和为n T ,若918S =-,1352S =-,且55b a =,77b a =,则42T T 的值为__________.3解:918S =-,则5918a =-,所以52a =-,即52b =-1352S =-,则71352a =-,所以74a =-,即74b =-设等比数列{}n b 的公比为22q =4124212(1)1=13(1)1b q T q q b q T q--=+=-- 故答案为:39.已知()sin(2)3f x x π=+,若)20)((πϕϕ<<-=x f y 是偶函数,则=ϕ__________.解:函数()sin(2)3f x x π=+,所以函数()sin(22)3y f x x πϕϕ=-=-+,由于函数为偶函数, 所以2()32k k Z ππϕπ-+=+∈,解得()212k k Z ππϕ=--∈, 由于02πϕ<<,所以当1k =-时,512πϕ=. 故答案为:512π. 10.已知矩形ABCD 中AB =4,BC =3,若沿对角线AC 折叠,使得平面DAC Ⅰ平面BAC ,则三棱锥D -ABC 的体积是__________.解:过B 作BE AC ⊥于E ,4AB =Q ,3BC =,5AC ∴=,125AB BC BE AC ==g , Q 平面DAC ⊥平面BAC ,平面DAC ⋂平面BAC AC =,BE AC ⊥,BE ⊂平面ABC ,BE ∴⊥平面DAC ,11112243433255ACD D ABC B ACD V V S BE ∆--∴==⋅=⨯⨯⨯⨯=棱锥棱锥. 故答案为245.411.已知实数x ,y 满足条件xy +1=4x +y 且x >1,则(x +1)(y +2)的最小值是__________. 解:14xy x y +=+Q ,且1x >, 114y x y -∴=>-,解得,4y >, (1)(2)2212(3)x y xy x y x y ∴++=+++=++ 33912()12[7(4)]44y y y y y -=++=++-+-- 12(76)27++=….(1)(2)x y ∴++取最小值为27.故答案为:27.12.若直线04:=-+a y ax l 上存在相距为2的两个动点A ,B ,圆1:22=+y x O 上存在点C ,使得ABC ∆为等腰直角三角形(C 为直角顶点),则实数a 的取值范围为__________.解:根据题意,若ABC ∆为等腰直角三角形,其中C 为直角顶点且||2AB =, 则C 到AB 的距离为||12AB =, 若圆22:1O x y +=上存在点C ,使得ABC ∆为等腰直角三角形, 则圆心O 到直线l 的距离2d „2,解可得:a ,即a的取值范围[;故答案为:[.513.如图,在平面直角坐标系x O y 中,已知点(1,0)A -,点P 是圆O :224x y +=上的任意一点,过点(1,0)B 作直线BT 垂直于AP ,垂足为T ,则2P A +3PT 的最小值是__________.解:由中线长公式可得PO =22=10PA PB + 222cos 2PA PB AB P PA PB +-=⋅,则3cos P PA PB=⋅在Rt PBT ∆中,cos PT PB P =,即3PT PA=所以9232PA PT PA PA+=+≥=(当且仅当2PA =时取等)14.已知函数4)(,)(22-+-=+-=x mx x h bx x x g ,若不等式)(01)(R x b x g ∈≤++恒成立,4)(+x h 为奇函数,函数⎩⎨⎧>≤=tx x h tx x g x f ),(),()(恰有两个零点,则实数t 的取值范围为__________.解:若不等式()10()g x b x R ++∈„恒成立, 即210x bx b ---…恒成立, 则△24(1)0b b =++„,解得:2b =-, 故2()2g x x x =--, 若()4h x +为奇函数,则224444mx x mx x ---+=--+,解得:0m =,6故()4h x x =-,画出函数()g x ,()h x 的图象,如图所示:若函数()()()()()g x x t f x h x x t ⎧=⎨>⎩…恰有两个零点,结合图象:[2t ∈-,0)[4U ,)+∞, 故答案为:[2-,0)[4U ,)+∞.二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内) 15.(本小题满分14分)已知c b a ,,分别为ABC ∆三个内角A ,B ,C 的对边,且3tan 4A =. (1)若65a =,2b =,求边c 的长; (2)若()sin A B -=,求tan B 的值. 解:(1)在ABC ∆中,由3tan 4A =可知(0,)2A π∈, 由22sin 3cos 4sin cos 1A A A A ⎧=⎪⎨⎪+=⎩解得3sin 54cos 5A A ⎧=⎪⎪⎨⎪=⎪⎩,7由余弦定理得2222cos a b c bc A =+-,得2226422255c c ⎛⎫=+-⋅⋅⋅ ⎪⎝⎭,即216640525c c -+=,解得85c =. (2)由(0,)2A π∈且(0,)B π∈,得(,)2A B ππ-∈-, 又()10sin 0A B -=>,则(0,)2A B π-∈,则()cos 0A B ->, 所以()2310cos 1sin ()A B A B -=--=, 所以()sin()1tan cos()3A B A B A B --==-,所以()31tan tan()143tan tan 311tan tan()3143A AB B A A B A A B ---=--===⎡⎤⎣⎦+⋅-+⋅ 16.(本小题满分14分)如图,在直三棱柱ABC -A 1B 1C 1中,AC ⅠBC ,A 1B 与AB 1交于点D ,A 1C 与AC 1交于点E .求证:(1)DE Ⅰ平面B 1BCC 1; (2)平面A 1BC Ⅰ平面A 1ACC 1.证明:(1)直三棱柱ABC -A 1B 1C 1中,1AA //1BB , 所以四边形11ABB A 是平行四边形,且11A B AB DE =I , 所以D 为1A B 中点, 同理E 为1A C 中点,ED B 1A 1C 1CBA8所以//DE BC ,又因为DE ⊄平面11B BCC ,BC ⊂平面11B BCC , 所以//DE 11B BCC .(2)直三棱柱ABC -A 1B 1C 1中,1C C ⊥平面ABC , 因为BC ⊂平面ABC ,所以1C C BC ⊥,因为AC BC ⊥,1AC C C C =I ,1AC C C ⊂、平面11A ACC , 所以BC ⊥平面11A ACC , 又因为BC ⊂平面1A BC , 所以平面1A BC ⊥平面11A ACC . 17.(本小题满分14分)如图,在平面直角坐标系xOy 中,椭圆C :2222+10)x y a b a b=>>(的左、右顶点分别为A B ,.已知4AB =,且点3(,5)4e 在椭圆上,其中e 是椭圆的离心率. (1)求椭圆C 的方程;(2)设P 是椭圆C 上异于 A 、B 的点,与x 轴垂直的直线l 分别交直线AP ,BP 于点M ,N ,求证:直线AN 与直线BM 的斜率之积是定值.解:(1)因为4AB =,所以24a =,即2a =,又点3(,5)4e 在椭圆上,故22245+116e a b =,即2245+11616c b =, 又2224b c a +==,B xy OPAM Nl9CA D联立方程组,解得2=3b ,故椭圆方程为22+143x y =.(2)设P 点坐标为(,s t ),M ,N 的横坐标均为2)m m ≠±(,则直线AP 的方程为(2)2ty x s =++, 故(,(2))2tM m m s ++, 故直线BM 的斜率1(2)(2)(2)t m k s m +=+-,同理可得直线AN 的斜率2(-2)(2)(+2)t m k s m =-,故2122(2)(-2)=(2)(2)(2)(+2)4t m t m t k k s m s m s +=+---,又因为P 点在椭圆上,故有22+143s t =,即223(4)4t s =--,因此有21223=44t k k s =--,故直线AN 与直线BM 的斜率之积是定值. 18.(本小题满分16分)如图,甲、乙两观察哨所位于海岸线l (一条南北方向的直线)上的点A 、B 处,两观察哨所相距32 n mile ,在海岸线东侧有一半径为6 n mile 圆形暗礁区,该暗礁区中心点C 位于乙观察哨所北偏东53︒的方向上,与甲观察哨所相距2193,暗礁中心与乙观察哨所的距离大于2193;(1)求暗礁中心点C 到海岸线l 的距离;(2)某时刻,甲观察哨所发现在其正南方向且位于暗礁中心正西方向的点D 处有一走私船正欲逃窜,甲观察哨所立即派缉私艇进行追击.已知缉私艇的最大航速是走私船最大以最大航速航行.问:航速的(1)λλ>倍.假设缉私艇和走私船均按直线方向无论走私船沿何方向逃窜,要保证缉私艇总能在暗礁区(不包含暗礁区边界)以外的海域内拦截成功,求λ的取值10范围.解:(1)在三角形ABC 中,由余弦定理可得2222cos AC AB BC AB BC ABC =+-⋅⋅∠,即2223322325BC BC =+-⨯⨯⨯,整理得2519212600BC BC -+=,解得30BC =或425BC =(舍去), 过点C 作CD 垂直于l ,垂足为D ,在直角三角形CDB 中,CD =BC 4sin 30245ABC ∠=⋅=, 故暗礁中心点C 到海岸线l 的距离为24n mile . (2)由(1)可知14AD =,18BD =,以点C 为坐标原点,建立如图所示平面直角坐标系,则A (24-,14),D (24-,0),暗礁区域边界所在的圆的方程为2236x y +=, 假设缉私艇在点T (x ,y )处拦截成功,则ATDTλ=, 则点Tλ=,化简得222221414(24)()()11x y λλλ+++=--要保证缉私艇总能在暗礁区(不包含暗礁区边界)以外的海域内拦截成功, 只需要圆222221414(24)()()11x y λλλ+++=--与圆2236x y +=外离,214()61λλ>+-,整理得1352421840λλ-->,解得43λ>或4645λ<-(舍去). 答:(1)暗礁中心点C 到海岸线l 的距离是24n mile ;11(2)当43λ>时,就能保证无论走私船沿何方向逃窜,缉私艇总能在暗礁区(不包含暗礁区边界)以外的海域内拦截成功.19.(本小题满分16分)已知函数x x x x f 23)(23+-=,R t tx x g ∈=,)(,x e x x=)(ϕ. (1)求函数)()(x x f y ϕ⋅=的单调增区间;(2)令)()()(x g x f x h -=,且函数)(x h 有三个彼此不相等的零点n m ,,0,其中n m <.Ⅰ若n m 21=,求函数)(x h 在m x =处的切线方程; Ⅰ若对][n m x ,∈∀,t x h -≤16)(恒成立,求实数t 的取值范围.解:(1)x e x x x x f y )23()()(2+-=⋅=ϕ,所以x e x x y )1(2'--=,令0'>y 得到251251+>-<x x 或, 所以)()(x x f y ϕ⋅=的单调增区间是),251()251,(+∞+--∞,. (2)由方程()0h x =得,m n 是方程23(2)0x x t -+-=的两实根,故3,2m n mn t +==-,且由判别式得14t >-, Ⅰ若n m 21=,得1,2m n ==,故22mn t =-=,得0t =, 因此'(1)1h =-,故函数()h x 在1=x 处的切线方程为1y x =-+.②若对任意的[,]x m n ∈,都有()16h x t ≤-成立,所以max ()16h x t ≤-, 因为3,m n m n +=<,所以n m n m <<<<<0230或,12当302m n <<<时,对[,]x m n ∈有max ()0h x =, 所以016t ≤-,解得16t ≤,又因为20mn t =->,得2t <,则有124t -<<; 当0m n <<时,2'()36(2)h x x x t =-+-,则存在()h x 的极大值点1(,0)x m ∈,且211362t x x =-+,由题意得321111()3(2)16h x x x t x t =-+-≤-,将211362t x x =-+代入得321113370x x x -++≥,进而得到31(1)8x -≥-,得110x -≤<,又因为211362t x x =-+,得211t <≤,综上可知t 的取值范围是124t -<<或211t <≤.20.(本小题满分16分) 等差数列{a n }公差大于零,且a 2+a 3=52,a 22+a 32=134,记{a n }的前n 项和为S n ,等比数列{b n }各项均为正数,公比为q ,记{b n }的前n 项和为T n .(1)求S n ;(2)若q 为正整数,且存在正整数k ,使得T k ,T 3k ∈{S 2,S 5,S 6},求数列{b n }的通项公式;(3)若将S n 中的整数项按从小到大的顺序排列构成数列{c n },求{c n }的一个通项公式. 解:(1)设{a n }公差为d ,d >0,因为a 2+a 3=52,a 22+a 32=134, 所以a 1+d +a 1+2d =52,(a 1+d )2+(a 1+2d )2=134, 解得a 1=12,d =12, 于是S n =12n +n (n -1)2×12=n 2+n 4.13(2){S 2,S 5,S 6}={32,152,212} 当q =1时,T k =kb 1,T 3k =3kb 1,T 3k T k=3,舍去; 当q ≠1时,T k =b 1(1-q k )1-q ,T 3k =b 1(1-q 3k )1-q,所以T 3k T k =1+q k +q 2k , 因为q ⅠN *且q ≠1,所以q ≥2,因此T 3k T k≥1+2+4=7, 于是T k =32,T 3k =212, 因此1+q k +q 2k =7,解得q k =2或-3(舍去),从而q =2,k =1,代入T k =b 1(1-q k )1-q得b 1=32 所以b n =3×2n -2(3)因为S n =n 2+n 4为整数项,所以n =4k 或者4k -1,k ⅠN * 当n =4k -1,k ⅠN *时,S n =k (4k -1);当n =4k ,k ⅠN *时,S n =k (4k +1);因为S n 中的整数项按从小到大的顺序排列构成数列{c n },且k (4k -1)<k (4k +1)<(k +1)[4(k +1)-1]<(k +1)[4(k +1)+1],所以当n 为奇数时,c n =(4×n +12-1)×n +12=2n 2+3n +12; 当n 为偶数时,c n =n 2×(2n +1)=2n 2+n 2; 所以c n =⎩⎨⎧2n 2+3n +12,n 为奇数,2n 2+n 2,n 为偶数.。
江苏省南京市六校联合体2020届高三上学期期初测试数学试题(二卷)及参考答案

南京市六校联合体2019-2020学年度第一学期期初测试 高三数学 2019.08.09Ⅱ试题注意事项:1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
21.【选做题】本题包括A 、B 、C 三小题,请选定其中两小题,并在相应的答题区域内作答.若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.A .[选修4-2:矩阵与变换](本小题满分10分)已知矩阵01M ⎡=⎢⎣ 10-⎤⎥⎦,21N ⎡=⎢-⎣ 12⎤⎥-⎦. (1)求MN ;(2)若曲线1C :122=-y x 在矩阵MN 对应的变换作用下得到另一曲线2C ,求2C 的方程.B .[选修4-4:坐标系与参数方程](本小题满分10分)在极坐标系下,已知圆C :cos sin ρθθ=+和直线l :20x y -+=.(1)求圆C 的直角坐标方程和直线l 的极坐标方程;(2)求圆C 上的点到直线l 的最短距离.【必做题】第22题、第23题,每题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.22.(本小题满分10分)某超市在节日期间进行有奖促销,凡在该超市购物满200元的顾客,将获得一次摸奖机会,规则如下:一个袋子装有5只形状和大小均相同的玻璃球,其中两只是红色,三只是绿色,顾客从袋子中一次摸出两只球,若两只球都是红色,则奖励20元;共两只球都是绿色,则奖励10元;若两只球颜色不同,则不奖励.(1)求一名顾客在一次摸奖活动中获得20元的概率;(2)记X 为两名顾客参与该摸奖活动获得的奖励总数额,求随机变量X 的概率分布列和数学期望.23.(本小题满分10分)在平面直角坐标系xOy中,已知抛物线)0(22>=ppxy上一点),43(mP到准线的距离与到原点O的距离相等,抛物线的焦点为F.(1)求抛物线的标准方程;(2)若A为抛物线上一点(异于原点O),点A处的切线交x轴于点B,过A作准线的垂线,垂足为点E.试判断四边形AEBF的形状,并证明你的结论.参考答案21.A(1)1221⎡⎤⎢⎥⎣⎦(2)22 3.y x -=21.B(1)C :220x y x y +--=,l :cos sin 20ρθρθ-+= 22.(1)110 (2)见解析23.(1)x y 62= (2)菱形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏省南京市 2020 届高三年级第一学期期初联考考试
数学试题
2019.9
一、填空题(本大题共 14 小题,每小题 5 分,共 70 分,请将答案填写在答题卷相应的位置上.)
1.已知集合{}21≤<-=x x A ,{}0≤=x x B ,则=B A .
2. 已知复数i
i z +-=13(i 是虚数单位),则z 的虚部是 . 3. 对一批产品的质量(单位:克)进行抽样检测,样本容量为 1600,检测结果的频率分布 直方图如图所示.根据标准,单件产品质量在区间[25,30)内为一等品,在区间[15,20),
[20,25)和[30,35)内为二等品,其余为三等品.则样本中三等品件数为 .
4.现有三张卡片,分别写有“1”、“2”、“3”这三个数字.将这三张卡片随机排序组成一个 三位数,则该三位数是偶数的概率是 .
5. 函数x y 2log 1+=的定义域为 .
6. 运行如图所示的伪代码,其结果为 .
7. 在平面直角坐标系xOy 中,双曲线 C :)0(116
2
22>=-a y a x 的右顶点到双曲线的一条渐近线的距离为3
54 ,则双曲线 C 的方程为 . 8. 如图所示是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,相传这个图形表达了阿基米德最引以为自豪的发现.我们来重温这个伟大发现,圆柱的表面积与球的表面积之比为 .
9. 函数)0,0)(sin()(>>+=ωϕωA x A x f 的部分图象如图所示.若函数)(x f y =在区间],[n m 上的值域为]2,2[-,则m n -的最小值是 .
10. 在公比为q 且各项均为正数的等比数列{}n a 中,n S 为{}n a 的前n 项和.若211q a =
,且725+=S S ,则首项1a 的值为 .
11. 已知是定义在区间(﹣1,1)上的奇函数,当0<x 时,)1()(-=x x x f .已知m 满足不等式0)1()1(2<-+-m f m f ,则实数m 的取值范围为 .
12. 已知圆O :422=+y x 和圆O 外一点),(00y x P ,过点P 作圆O 的两条切线,切点分别为A ,B ,且∠AOB =120°.若点 C(8,0)和点 P 满足 PO =λPC ,则 的范围是 .
13. 如图,已知梯形ABCD ,AB// BC ,
32=AD BC ,取BD 中点E ,连接AE 并延长交CD 于F ,若⋅=⋅2,则=AD
AB .
14. 已知函数11,212
1,ln 1)(<≥⎪⎩⎪⎨⎧++=x x x x x f ,若21x x ≠,且2)()(21=+x f x f ,则21x x +的取值范围是 . 二、解答题(本大题共 6 小题,共计 90 分,请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.)
15.(本小题满分 14 分)
如图,在四棱锥 P —ABCD 中,底面 ABCD 是正方形,PA ⊥底面 ABCD ,且 PA =AD , 点 F 是棱 PD 的中点,点 E 为 CD 的中点.
(1)证明:EF ∥平面 PAC ;
(2)(2)证明:AF ⊥PC .
16.(本小题满分 14 分)
在ABC ∆中,4
3π=A ,6=AB ,23=AC . (1)求 sinB 的值;
(2)若点 D 在 BC 边上,AD =BD ,求△ABD 的面积.
17.(本小题满分 14 分)
窗花是贴在窗纸或窗户玻璃上的剪纸,是中国古老的传统民间艺术之一.图中的窗花是 由一张圆形纸片剪去一个正十字形剩下的部分,正十字形的顶点都在圆周上.已知正十字形 的宽和长都分别为 x ,y (单位:dm )且 x <y ,若剪去的正十字形部分面积为 4dm 2.
(1)求 y 关于 x 的函数解析式,并求其定义域;
(2)现为了节约纸张,需要所用圆形纸片面积最小.当 x 取何值时,所用到的圆形纸 片面积最小,并求出其最小值.
18.(本小题满分 16 分)
已知椭圆 C :12222=+b y a x (a >b >0),左、右焦点分别为 F 1(﹣1,0),F 2(1,0),椭圆离心率为2
1,过点 P(4,0)的直线l 与椭圆 C 相交于 A 、B 两点(A 在B 的左侧).
(1)求椭圆 C 的方程;
(2)若 B 是 AP 的中点,求直线l 的方程;
(3)若 B 点关于 x 轴的对称点是 E ,证明:直线 AE 与 x 轴相交于定点.
19.(本小题满分 16 分)
在数列{}n a 中,已知 21=a ,)(31n f a a n n +=+ .
(1)若 k n f =)((k 为常数), 143=a ,求 k ;
(2)若12)(-=n n f .①求证:数列{}n a n +为等比数列;②记n a b n n )1(λ-+=,且数列{}n b 的前n 项和为n T ,若3T 为数列{}n T 中的最小项,求λ的取值范围.
20.(本小题满分 16 分)
已知函数 2ln )(--=x x x f .
(1)求曲线)(x f y = 在 x =1 处的切线方程;
(2)函数)(x f 在区间(k ,k +1)(k ∈N)上有零点,求k 的值;
(3)记函数 )(221)(2x f bx x x g ---=,设 )(2121x x x x <⋅是函数)(x g 的两个极值点,若 23≥b ,且k x g x g ≥-)()(21恒成立,求实数 k 的最大值.
参考答案
一、填空题
1.]0,1(-
2.2-
3.200
4.31
5.)21[∞+,
6.17
7.1162022=-y x
8.23
9.3 10.41 11.)1,0( 12.131≤≤λ 13. 33 14.),2ln 23[+∞-
二、解答题
15. 略
16. (1)10
10sin =B ;(2)3=∆ABD S . 17. (1))2,0(;(2)当x 取
554,所用到的圆形纸片面积最小,最小值为π215+. 18. (1)13
42
2=+y x ;(2)05465=--y x 或05465=-+y x ;(3)略. 19. (1)1-=k ;(2)①略;②4
819≤≤λ. 20. (1)切线方程为1-=y ;(2)3=k ;(3)k 的最大值为
2ln 2815-.。
