初二期末几何压轴题答案详解共27页

合集下载

初二数学压轴几何证明题(含答案)

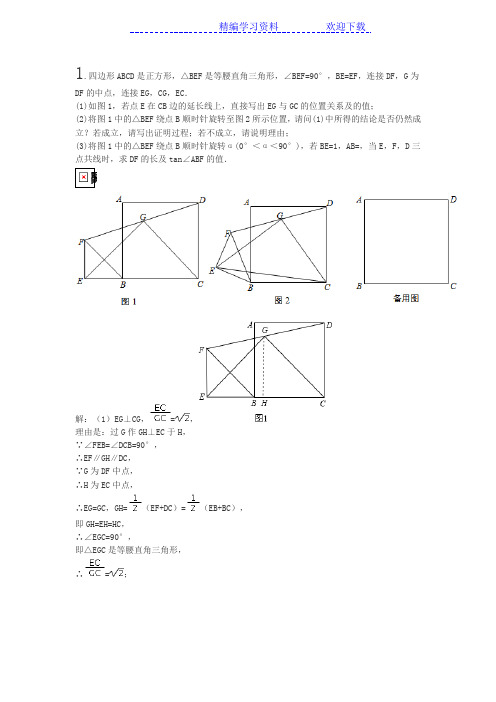
1.四边形ABCD是正方形，△BEF是等腰直角三角形，∠BEF=90°，BE=EF，连接DF，G为DF的中点，连接EG，CG，EC．(1)如图1，若点E在CB边的延长线上，直接写出EG与GC的位置关系及的值；(2)将图1中的△BEF绕点B顺时针旋转至图2所示位置，请问(1)中所得的结论是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由；(3)将图1中的△BEF绕点B顺时针旋转α(0°＜α＜90°)，若BE=1，AB=，当E，F，D三点共线时，求DF的长及tan∠ABF的值．解：（1）EG⊥CG，=，理由是：过G作GH⊥EC于H，∵∠FEB=∠DCB=90°，∴EF∥GH∥DC，∵G为DF中点，∴H为EC中点，∴EG=GC，GH=（EF+DC）=（EB+BC），即GH=EH=HC，∴∠EGC=90°，即△EGC是等腰直角三角形，∴=；（2）解：结论还成立，理由是：如图2，延长EG到H，使EG=GH，连接CH、EC，过E作BC的垂线EM，延长CD，∵在△EFG和△HDG中∴△EFG≌△HDG（SAS），∴DH=EF=BE，∠FEG=∠DHG，∴EF∥DH，∴∠1=∠2=90°-∠3=∠4，∴∠EBC=180°-∠4=180°-∠1=∠HDC，在△EBC和△HDC中∴△EBC≌△HDC．∴CE=CH，∠BCE=∠DCH，∴∠ECH=∠DCH+∠ECD=∠BCE+∠ECD=∠BCD=90°，∴△ECH是等腰直角三角形，∵G为EH的中点，∴EG⊥GC，=，即（1）中的结论仍然成立；（3）解：连接BD，∵AB=，正方形ABCD，∴BD=2，∴cos∠DBE==，∴∠DBE=60°，∴∠ABE=∠DBE-∠ABD=15°，∴∠ABF=45°-15°=30°，∴tan∠ABF=，∴DE=BE=，∴DF=DE-EF=-1．解析：（1）过G作GH⊥EC于H，推出EF∥GH∥DC，求出H为EC中点，根据梯形的中位线求出EG=GC，GH=（EF+DC）=（EB+BC），推出GH=EH=BC，根据直角三角形的判定推出△EGC是等腰直角三角形即可；（2）延长EG到H，使EG=GH，连接CH、EC，过E作BC的垂线EM，延长CD，证△EFG≌△HDG，推出DH=EF=BE，∠FEG=∠DHG，求出∠EBC=∠HDC，证出△EBC≌△HDC，推出CE=CH，∠BCE=∠DCH，求出△ECH是等腰直角三角形，即可得出答案；（3）连接BD，求出cos∠DBE==，推出∠DBE=60°，求出∠ABF=30°，解直角三角形求出即可．2.已知正方形ABCD和等腰直角三角形BEF，BE=EF，∠BEF=90°，按图1放置，使点E在BC 上，取DF的中点G，连接EG，CG．(1)延长EG交DC于H，试说明：DH=BE．(2)将图1中△BEF绕B点逆时针旋转45°，连接DF，取DF中点G(如图2)，莎莎同学发现：EG=CG且EG⊥CG．在设法证明时他发现：若连接BD，则D，E，B三点共线．你能写出结论“EG=CG且EG⊥CG”的完整理由吗？请写出来．(3)将图1中△BEF绕B点转动任意角度α(0＜α＜90°)，再连接DF，取DF的中点G(如图3)，第2问中的结论是否成立？若成立，试说明你的结论；若不成立，也请说明理由．（1）证明：∵∠BEF=90°，∴EF∥DH，∴∠EFG=∠GDH，而∠EGF=∠DGH，GF=GD，∴△GEF≌△GHD，∴EF=DH，而BE=EF，∴DH=BE；（2）连接DB，如图，∵△BEF为等腰直角三角形，∴∠EBF=45°，而四边形ABCD为正方形，∴∠DBC=45°，∴D，E，B三点共线．而∠BEF=90°，∴△FED为直角三角形，而G为DF的中点，∴EG=GD=GC，∴∠EGC=2∠EDC=90°，∴EG=CG且EG⊥CG；（3）第2问中的结论成立．理由如下：连接AC、BD相交于点O，取BF的中点M，连接OG、EM、MG，如图，∵G为DF的中点，O为BD的中点，M为BF的中点，∴OG∥BF，GM∥OB，∴四边形OGMB为平行四边形，∴OG=BM，GM=OB，而EM=BM，OC=OB，∴EM=OG，MG=OC，∵∠DOG=∠GMF，而∠DOC=∠EMF=90°，∴∠EMG=∠GOC，∴△MEG≌△OGC，∴EG=CG，∠EGM=∠OCG，又∵∠MGF=∠BDF，∠FGC=∠GDC+∠GCD，∴∠EGC=∠EGM+∠MGF+∠FGC=∠BDF+∠GDC+∠GCD+∠OCG=45°+45°=90°，∴EG=CG且EG⊥CG．解析：（1）由∠BEF=90°，得到EF∥DH，而GF=GD，易证得△GEF≌△GHD，得EF=DH，而BE=EF，即可得到结论．（2）连接DB，如图2，由△BEF为等腰直角三角形，得∠EBF=45°，而四边形ABCD为正方形，得∠DBC=45°，得到D，E，B三点共线，而G为DF的中点，根据直角三角形斜边上的中线等于斜边的一半得到EG=GD=GC，于是∠EGC=2∠EDC=90°，即得到结论．（3）连接AC、BD相交于点O，取BF的中点M，连接OG、EM、MG，由G为DF的中点，O为BD的中点，M为BF的中点，根据三角形中位线的性质得OG∥BF，GM∥OB，得到OG=BM，GM=OB，而EM=BM，OC=OB，得到EM=OG，MG=OC，又∠DOG=∠GMF，而∠DOC=∠EMF=90°，得∠EMG=∠GOC，则△MEG≌△OGC，得到EG=CG，∠EGM=∠OCG，而∠MGF=∠BDF，∠FGC=∠GDC+∠GCD，所以有∠EGC=∠EGM+∠MGF+∠FGC=∠BDF+∠GDC+∠GCD+∠OCG=45°+45°=90°．3.已知正方形ABCD和等腰Rt△BEF，BE=EF，∠BEF=90°，按图①放置，使点F在BC上，取DF的中点G，连接EG、CG．(1)探索EG、CG的数量关系和位置关系并证明；(2)将图①中△BEF绕B点顺时针旋转45°，再连接DF，取DF中点G(如图②)，问(1)中的结论是否仍然成立．证明你的结论；(3)将图①中△BEF绕B点转动任意角度(旋转角在0°到90°之间)，再连接DF，取DF的中点G(如图③)，问(1)中的结论是否仍然成立，证明你的结论．解：（1）EG=CG且EG⊥CG．证明如下：如图①，连接BD．∵正方形ABCD和等腰Rt△BEF，∴∠EBF=∠DBC=45°．∴B、E、D三点共线．∵∠DEF=90°，G为DF的中点，∠DCB=90°，∴EG=DG=GF=CG．∴∠EGF=2∠EDG，∠CGF=2∠CDG．∴∠EGF+∠CGF=2∠EDC=90°，即∠EGC=90°，∴EG⊥CG．（2）仍然成立，证明如下：如图②，延长EG交CD于点H．∵BE⊥EF，∴EF∥CD，∴∠1=∠2．又∵∠3=∠4，FG=DG，∴△FEG≌△DHG，∴EF=DH，EG=GH．∵△BEF为等腰直角三角形，∴BE=EF，∴BE=DH．∵CD=BC，∴CE=CH．∴△ECH为等腰直角三角形．又∵EG=GH，∴EG=CG且EG⊥CG．（3）仍然成立．证明如下：如图③，延长CG至H，使GH=CG，连接HF交BC于M，连接EH、EC．∵GF=GD，∠HGF=∠CGD，HG=CG，∴△HFG≌△CDG，∴HF=CD，∠GHF=∠GCD，∴HF∥CD．∵正方形ABCD，∴HF=BC，HF⊥BC．∵△BEF是等腰直角三角形，∴BE=EF，∠EBC=∠HFE，∴△BEC≌△FEH，∴HE=EC，∠BEC=∠FEH，∴∠BEF=∠HEC=90°，∴△ECH为等腰直角三角形．又∵CG=GH，∴EG=CG且EG⊥CG．解析：（1）首先证明B、E、D三点共线，根据直角三角形斜边上的中线等于斜边的一半，即可证明EG=DG=GF=CG，得到∠EGF=2∠EDG，∠CGF=2∠CDG，从而证得∠EGC=90°；（2）首先证明△FEG≌△DHG，然后证明△ECH为等腰直角三角形．可以证得：EG=CG且EG ⊥CG．（3）首先证明：△BEC ≌△FEH ，即可证得：△ECH 为等腰直角三角形，从而得到：EG=CG 且EG ⊥CG ．已知，正方形ABCD 中，△BEF为等腰直角三角形，且BF 为底，取DF 的中点G ，连接EG 、CG ．（1）如图1，若△BEF 的底边BF 在BC 上，猜想EG 和CG 的数量关系为______；（2）如图2，若△BEF 的直角边BE 在BC 上，则（1）中的结论是否还成立？请说明理由；（3）如图3，若△BEF 的直角边BE 在∠DBC 内，则（1）中的结论是否还成立？说明理由．解：（1）GC=EG ，（1分）理由如下：∵△BEF 为等腰直角三角形， ∴∠DEF=90°，又G 为斜边DF 的中点， ∴EG=DF ， ∵ABCD 为正方形， ∴∠BCD=90°，又G 为斜边DF 的中点，∴CG= DF ， ∴GC=EG ；（2）成立．如图，延长EG 交CD 于M ，∵∠BEF=∠FEC=∠BCD=90°，∴EF ∥CD ，∴∠EFG=∠MDG ，又∠EGF=∠DGM ，DG=FG ，∴△GEF ≌△GMD ，∴EG=MG ，即G 为EM 的中点．∴CG 为直角△ECM 的斜边上的中线，∴CG=GE= EM ；（3）成立．取BF 的中点H ，连接EH ，GH ，取BD 的中点O ，连接OG ，OC ．∵CB=CD ，∠DCB=90°，∴CO= BD1 2 1 21212 12．∵DG=GF，∴GH∥BD，且GH= BD，OG∥BF，且OG= BF，∴CO=GH．为等腰直角三角形．∵△BEF∴EH= BF∴EH=OG．∵四边形OBHG为平行四边形，∴∠BOG=∠BHG．∵∠BOC=∠BHE=90°．∴∠GOC=∠EHG．∴△GOC≌△EHG．∴EG=GC．此题考查了正方形的性质，以及全等三角形的判定与性质．要求学生掌握直角三角形斜边上的中线等于斜边的一半，以及三角形的中位线与第三边平行且等于第三边的一半．掌握这些性质，熟练运用全等知识是解本题的关键．解析：（1）EG=CG，理由为：根据三角形BEF为等腰直角三角形，得到∠DEF为直角，又G为DF中点，根据在直角三角形中，斜边上的中线等于斜边的一半，得到EG为DF的一半，同理在直角三角形DCF中，得到CG也等于DF的一半，利用等量代换得证；（2）成立．理由为：延长EG交CD于M，如图所示，根据“ASA”得到三角形EFG与三角形GDM 全等，由全等三角形的对应边相等得到EG与MG相等，即G为EM中点，根据直角三角形斜边上的中线等于斜边的一半得到EG与CG相等都等于斜边EM的一半，得证；（3）成立．理由为：取BF的中点H，连接EH，GH，取BD的中点O，连接OG，OC，如图所示，1212因为直角三角形DCB中，O为斜边BD的中点，根据斜边上的中线等于斜边的一半得到OC等于BD 的一半，由HG为三角形DBF的中位线，根据三角形的中位线平行于第三边且等于第三边的一半，得到GH等于BD一半，OG等于BF的一半，又根据直角三角形斜边上的中线等于斜边的一半得到EH等于BF的一半，根据等量代换得到OG与EH相等，再根据OBHG为平行四边形，根据平行四边形的性质得到对边相等，对角相等，进而得到∠GOC与∠EHG相等，利用“SAS”得到△GOC与△EHG全等，利用全等三角形的对应边相等即可得证．。

初二期末压轴题训练附解析

参考答案与试题解析1．如图，已知AB∥CD，M为平行线之间一点，连接AM，CM，N为AB上方一点，连接AN，CN，E为NA延长线上一点，若AM，CM分别平分∠BAE，∠DCN，则∠M与∠N 的数量关系为（）A．∠M﹣∠N＝90°B．2∠M﹣∠N＝180°C．∠M+∠N＝180°D．∠M+2∠N＝180°【解答】解：过点M作MO∥AB，过点N作NP∥AB，∵AB∥CD，∴MO∥AB∥CD∥NP，∴∠AMO＝∠1，∠OMC＝∠MCD，∵AM，CM分别平分∠BAE，∠DCN，∴∠BAE＝2∠1，∠NCD＝2∠2，∠2＝∠MCD，∴∠AMC＝∠1+∠2，∵CD∥NP，∴∠PNC＝∠NCD＝2∠2，∴∠CNE＝2∠2﹣∠3，∵NP∥AB，∴∠3＝∠NAB＝180°﹣2∠1，∴∠CNE＝2∠2﹣（180°﹣2∠1）＝2（∠1+∠2）﹣180°＝2∠AMC﹣180°，∴2∠AMC﹣∠CNE＝180°，故选：B．2.随着时代的进步，人们对P M 2.5（空气中直径小于等于2.5微米的颗粒）的关注日益密切．某市一天中P M 2.5的值y 1(u g /m 3)随时间t (h )的变化如图所示，设y 2表示0时到t 时P M 2.5的值的极差（即0时到t 时P M 2.5的最大值与最小值的差），则y 2与t 的函数关系大致是()A ．B ．C ．D ．【解答】解：当t =0时，极差y 2=85−85=0，当100≤t ＜时，极差y 2随t 的增大而增大，最大值为43；当2010≤t ＜时，极差y 2随t 的增大保持43不变；当2420≤t ＜时，极差y 2随t 的增大而增大，最大值为98．故选：B ．2.已知长方形纸带ABCD ，将纸带沿EF 折叠后，点C 、D 分别落在H 、G 的位置，再沿BC 折叠成图b ，若∠DEF ＝72°，则∠GMN ＝72°．【解答】解：∵AD ∥CB ，∴∠EFC +∠DEF ＝180°，∠EFB ＝∠DEF ，即∠EFC ＝180°﹣72°＝108°，∠EFB ＝72°，∴∠BFH ＝108°﹣72°＝36°．∵∠H ＝∠D ＝90°，∴∠HMF ＝180°﹣90°﹣36°＝54°．由折叠可得：∠NMF ＝∠HMF ＝54°，∴∠GMN ＝72°．4．如图，在△ABC中，BO、CO分别平分∠ABC，∠ACB，BO的延长线交外角∠ACD的角平分线于点E．以下结论：①∠1＝2∠2；②∠BOC＝3∠2；③∠BOC＝90°+∠2；④∠BOC＝90°+∠1．其中正确的结论有①③（填序号）．【解答】解：∵CE为外角∠ACD的平分线，BE平分∠ABC，∴∠DCE＝∠ACD，∠DBE＝∠ABC，又∵∠DCE是△BCE的外角，∴∠2＝∠DCE﹣∠DBE，＝（∠ACD﹣∠ABC）＝∠1，故①正确；∵BO，CO分别平分∠ABC，∠ACB，∴∠OBC＝ABC，∠OCB＝∠ACB，∴∠BOC＝180°﹣（∠OBC+∠OCB）＝180°﹣（∠ABC+∠ACB）＝180°﹣（180°﹣∠1）＝90°+∠1，故②、④错误；∵OC平分∠ACB，CE平分∠ACD，∴∠ACO＝∠ACB，∠ACE＝ACD，∴∠OCE＝（∠ACB+∠ACD）＝×180°＝90°，∵∠BOC是△COE的外角，∴∠BOC＝∠OCE+∠2＝90°+∠2，故③正确；故答案为：①③．5.正方形111A B C O ，2221A B C C ，3332A B C C ，⋯按如图所示的方式放置．点1A ，2A ，3A ，⋯和点1C ，2C ，3C ，⋯分别在直线(0)y kx b k =+>和x 轴上，已知点1(1,1)B ，2(3,2)B ，则n B 的坐标是(21n -，12)n -．【解答】解：点1(1,1)B ，2(3,2)B ，1(0A ∴，21)(1A ，32)(3,4)A ，∴直线(0)y kx b k =+>为1y x =+，∴n A 的横坐标数列为121--n ，纵坐标为12n -，Bn ∴的横坐标为1n A +的横坐标，纵坐标为An 的纵坐标Bn ∴的坐标为(21n -，12)n -．故答案为：(21n -，12)n -．6.问题情境：（1）如图1，AB ∥CD ，∠PAB ＝130°，∠PCD ＝120°．求∠APC 度数．小颖同学的解题思路是：如图2，过点P 作PE ∥AB ，请你接着完成解答问题迁移：（2）如图3，AD ∥BC ，点P 在射线OM 上运动，当点P 在A 、B 两点之间运动时，∠ADP ＝∠α，∠BCP ＝∠β．试判断∠CPD 、∠α、∠β之间有何数量关系？（提示：过点P 作PE ∥AD ），请说明理由；（3）在（2）的条件下，如果点P 在A 、B 两点外侧运动时（点P 与点A 、B 、O 三点不重合），请你猜想∠CPD 、∠α、∠β之间的数量关系．【解答】解：（1）过P作PE∥AB，∵AB∥CD，∴PE∥AB∥CD，∴∠APE＝180°﹣∠A＝50°，∠CPE＝180°﹣∠C＝60°，∴∠APC＝50°+60°＝110°；（2）∠CPD＝∠α+∠β，理由如下：如图3，过P作PE∥AD交CD于E，∵AD∥BC，∴AD∥PE∥BC，∴∠α＝∠DPE，∠β＝∠CPE，∴∠CPD＝∠DPE+∠CPE＝∠α+∠β；（3）当P在BA延长线时，∠CPD＝∠β﹣∠α；理由：如图4，过P作PE∥AD交CD于E，∵AD∥BC，∴AD∥PE∥BC，∴∠α＝∠DPE，∠β＝∠CPE，∴∠CPD＝∠CPE﹣∠DPE＝∠β﹣∠α；当P在BO之间时，∠CPD＝∠α﹣∠β．理由：如图5，过P作PE∥AD交CD于E，∵AD∥BC，∴AD∥PE∥BC，∴∠α＝∠DPE，∠β＝∠CPE，∴∠CPD＝∠DPE﹣∠CPE＝∠α﹣∠β．7.在平面直角坐标系中，一次函数(0)y kx b k =+≠的图象由函数12y x =的图象向下平移1个单位长度得到．（1）求这个一次函数的解析式；（2）求一次函数与x 轴，y 轴的交点坐标；（3）当2x >-时，对于x 的每一个值，函数(0)y mx m =≠的值大于一次函数y kx b =+的值，请直接写出m 的取值范围．【解答】解：（1）函数12y x =的图象向下平移1个单位长度得到112y x =-，一次函数(0)y kx b k =+≠的图象由函数12y x =的图象向下平移1个单位长度得到，∴这个一次函数的表达式为112y x =-．（2）把0y =代入112y x =-中，得2x =，∴一次函数与x 轴的交点坐标为(2,0)；把0x =代入112y x =-中，得1y =-，∴一次函数与y 轴的交点坐标(0,1)-；（3）把2x =-代入112y x =-，求得2y =-，∴函数(0)y mx m =≠与一次函数112y x =-的交点为(2,2)--，把点(2,2)--代入y mx =，求得1m =，当2x >-时，对于x 的每一个值，函数(0)y mx m =≠的值大于一次函数112y x =-的值，∴121≤≤m ．8.如图1，一张三角形ABC纸片，点D，E分别是△ABC边上两点．研究（1）：如果沿直线DE折叠，使点A落在CE上的点A'处，则∠BDA'与∠A的数量关系是∠BDA′＝2∠A；研究（1）：如果折成图2的形状，猜想∠BDA'，∠CEA'和∠A的数量关系是∠BDA′+∠CEA′＝2∠A；研究（3）：如果折成图3的形状，猜想∠BDA'，∠CEA'和∠A的数量关系是什么，并说明理由．【解答】解：（1）∠BDA′与∠A的数量关系是∠BDA′＝2∠A；（2）∠BDA′+∠CEA′＝2∠A，理由：在四边形ADA′E中，∠A+∠DA′E+∠ADA′+∠A′EA＝360°，∴∠A+∠DA′E＝360°﹣∠ADA′﹣∠A′EA，∵∠BDA′+∠ADA′＝180°，∠CEA′+∠A′EA＝180°，∴∠BDA′+∠CEA′＝360°﹣∠ADA′﹣∠A′EA，∴∠BDA′+∠CEA′＝∠A+∠DA′E，∵△A′DE是由△ADE沿直线DE折叠而得，∴∠A＝∠DA′E，∴∠BDA′+∠CEA′＝2∠A；故答案为：∠BDA′+∠CEA′＝2∠A；（3）∠BDA′﹣∠CEA′＝2∠A．理由：DA′交AC于点F，∵∠BDA′＝∠A+∠DFA，∠DFA＝∠A′+∠CEA′，∴∠BDA′＝∠A+∠A′+∠CEA′，∴∠BDA′﹣∠CEA′＝∠A+∠A′，∵△A′DE是由△ADE沿直线DE折叠而得，∴∠A＝∠DA′E，∴∠BDA′﹣∠CEA′＝2∠A．9.同学们以“一块直角三角板和一把直尺”开展数学活动，提出了很多数学问题，请你解答：（1）如图1，∠α和∠β具有怎样的数量关系？请说明理由；（2）如图2，∠DFC的平分线与∠EGC的平分线相交于点Q，求∠FQG的大小．【解答】解：（1）如图1，延长AC交EG于M．∠β+∠α＝90°，理由如下：由题意知：DF∥EG，∠ACB＝90°．∴∠α＝∠GMC，∠ACB＝∠GMC+∠CGM＝90°．∵∠EGB和∠CGM是对顶角，∴∠β＝∠CGM．∴∠β+∠α＝90°．（2）如图2，延长AC交EG于N．由题意知：DF∥EN，∠ACB＝90°．∴∠1＝∠GNC，∠CGN+∠GNC＝90°．∴∠1+∠CGN＝90°．∵QF平分∠DFC，∴∠QFC＝∠DFC＝（180°﹣∠1）＝90°﹣∠1，∠GQC＝90°﹣∠CGN同理可得：∠GQC＝90°﹣∠CGN，∵四边形QFCG的内角和等于360°．∴∠FQG＝360°﹣∠QFC﹣∠QGC﹣∠ACB＝360°﹣（90°﹣∠1）﹣（90°﹣∠CGN）﹣90°．∴∠FQG＝135°．。

初二下期末几何压轴题及解析

初二下期末几何及解析1、以四边形ABCD 的边AB 、AD 为边分别向外侧作等边三角形ABF 和ADE ，连接EB 、FD ，交点为G ．（1）当四边形ABCD 为正方形时（如图1），E B 和FD 的数量关系是_____________；（2）当四边形ABCD 为矩形时（如图2），EB 和FD 具有怎样的数量关系?请加以证明；（3）四边形ABCD 由正方形到矩形到一般平行四边形的变化过程中，∠EGD 是否发生变化?如果改变，请说明理由；如果不变，请在图3中求出∠EGD 的度数．难度一般：证全等即可（第三问，图1中就能看出是45°。

）解（1）EB=FD 。

（2）EB=FD 。

证：∵△AFB 为等边三角形,∴AF=AB ，∠FAB=60°∵△ADE 为等边三角形，∴AD=AE ，∠EAD=60°,∴∠FAB+∠BAD=∠EAD+∠BAD即∠FAD=∠BAE,∴△FAD ≌△BAE,∴EB=FD（3）解：∵△ADE 为等边三角形，∴∠AED=∠EDA=60° ∵△FAD ≌△BAE ，∴∠AEB=∠ADF 设∠AEB 为x °，则∠ADF 也为x °于是有∠BED 为（60-x ）°，∠EDF 为（60+x ）° ∴∠EGD=180°-∠BED-∠EDF =180°-（60-x ）°-（60+x ）°=60°2、已知：如图，在□ABCD 中，点E 是BC 的中点，连接AE 并延长交DC 的延长线于点F ，连接BF ．（1）求证：△ABE ≌△FCE ；（2）若AF =AD ，求证：四边形ABFC 是矩形．FA BC DE简单题证明：（1）如图1．在△ABE 和△FCE 中，∠1=∠2， ∠3=∠4，BE =CE ， ∴△ABE ≌△FCE ．（2）∵△ABE ≌△FCE ，∴AB =FC ．∵AB ∥FC ，∴四边形ABFC 是平行四边形． ∵四边形ABCD 是平行四边形，∴AD =BC ． ∵AF =AD ，∴AF =BC ．∴四边形ABFC 是矩形．3、已知：△ABC 是一张等腰直角三角形纸板，∠B =90°，AB =BC =1．（1）要在这张纸板上剪出一个正方形，使这个正方形的四个顶点都在△ABC 的边上．小林设计出了一种剪法，如图1所示．请你再设计出一种不同于图1的剪法，并在图2中画出来．（2）按照小林设计的图1所示的剪法来进行裁剪，记图1为第一次裁剪，得到1个正方形，将它的面积记为1S ，则1S =___________；余下的2个三角形中还按照小林设计的剪法进行第二次裁剪（如图3），得到2个新的正方形，将此次所得2个正方形的面积的和．记为2S ，则2S =___________；在余下的4个三角形中再按照小林设计的的剪法进行第三次裁剪（如图4），得到4个新的正方形，将此次所得4个正方形图EFA BCD 图AB C图图B图2CBA图14321EDC BAF的面积的和．记为3S；按照同样的方法继续操作下去……，第n次裁剪得到_________个新的正方形，它们的面积的和．nS=______________．（题外题：把你剪出的正方形的面积与图1中的正方形面积进行比较。

初二期末压轴题答案及解析

1．（2009•铁岭）△ABC是等边三角形，点D是射线BC上的一个动点（点D不与点B、C重合），△ADE 是以AD为边的等边三角形，过点E作BC的平行线，分别交射线AB、AC于点F、G，连接BE．（1）如图（a）所示，当点D在线段BC上时．①求证：△AEB≌△ADC；②探究四边形BCGE是怎样特殊的四边形？并说明理由；（2）如图（b）所示，当点D在BC的延长线上时，直接写出（1）中的两个结论是否成立；（3）在（2）的情况下，当点D运动到什么位置时，四边形BCGE是菱形？并说明理由．考点：全等三角形的判定；平行四边形的判定；菱形的判定。

专题：几何综合题。

分析：此题要熟练多方面的知识，特别是全等三角形和平行四边形和菱形的判定．解答：证明：（1）①∵△ABC和△ADE都是等边三角形，∴AE=AD，AB=AC，∠EAD=∠BAC=60°．（1分）又∵∠EAB=∠EAD﹣∠BAD，∠DAC=∠BAC﹣∠BAD，∴∠EAB=∠DAC，∴△AEB≌△ADC．（3分）②方法一：由①得△AEB≌△ADC，∴∠ABE=∠C=60°．又∵∠BAC=∠C=60°，∴∠ABE=∠BAC，∴EB∥GC．（5分）又∵EG∥BC，∴四边形BCGE是平行四边形．（6分）方法二：证出△AEG≌△ADB，得EG=AB=BC．（5分）由①得△AEB≌△ADC．得BE=CG．∴四边形BCGE是平行四边形．（6分）（2）①②都成立．（8分）（3）当CD=CB （∠CAD=30°或∠BAD=90°或∠ADC=30°）时，四边形BCGE是菱形．（9分）理由：方法一：由①得△AEB≌△ADC，∴BE=CD（10分）又∵CD=CB，∴BE=CB．（11分）由②得四边形BCGE是平行四边形，∴四边形BCGE是菱形．（12分）方法二：由①得△AEB≌△ADC，∴BE=CD．（9分）又∵四边形BCGE是菱形，∴BE=CB（11分）∴CD=CB．（12分）方法三：∵四边形BCGE是平行四边形，∴BE∥CG，EG∥BC，∴∠FBE=∠BAC=60°，∠F=∠ABC=60°（9分）∴∠F=∠FBE=60°，∴△BEF是等边三角形．（10分）又∵AB=BC，四边形BCGE是菱形，∴AB=BE=BF，∴AE⊥FG（11分）∴∠EAG=30°，∵∠EAD=60°，∴∠CAD=30度．（12分）点评：本题考查三角形的全等以及菱形的判定．2．如图，在Rt△ABC中，∠ACB=90°，∠B=60°，BC=2．点O是AC的中点，过点O的直线l与AB边相交于点D．过点C作CE∥AB交直线l于点E，设∠AOD=α．（1）当α等于多少度时，四边形EDBC是等腰梯形？并求此时AD的长；（2）当α=90°时，判断四边形EDBC是否为菱形，并说明理由．考点：菱形的判定；等腰梯形的判定。

八年级数学期末几何压轴题

26．（本题满分10分）已知：在矩形ABCD 中，AB =10，BC =12，四边形EFGH 的三个顶点E 、F 、H 分别在矩形ABCD 边AB 、BC 、DA 上，AE =2.（1）如图①，当四边形EFGH 为正方形时，求△GFC 的面积；（5分）（2）如图②，当四边形EFGH 为菱形，且BF = a 时，求△GFC 的面积（用含a 的代数式表示）；（5分）D(第26题图1)FD CA BE (第26题图2)FH G26．解：（1）如图①，过点G 作GM BC ⊥于M . …………………………………………（1分）在正方形EFGH 中，90,HEF EH EF ∠==. …………………………………………………………（1分）90.90,.AEH BEF AEH AHE AHE BEF ∴∠+∠=∠+∠=∴∠=∠又∵90A B ∠=∠=，∴⊿AH E ≌⊿BEF …………………………………………………………（1分）同理可证：⊿MFG ≌⊿BEF . …………………………………………………………（1分） ∴GM=BF=AE =2.∴FC=BC-BF =10. …………………………………………………………（1分）（2）如图②，过点G作GM BC ⊥于M .连接HF . …………………………………………（1分）//,.//,.AD BC AHF MFH EH FG EHF GFH ∴∠=∠∴∠=∠.AHE MFG ∴∠=∠ …………………………………………………（1分）又90,,A GMF EH GF ∠=∠==∴⊿AHE ≌⊿MFG . ………………………………………………………（1分）∴GM=AE =2. ……………………………………………………………（1分）11(12)12.22GFCSFC GM a a ∴=⋅=-=- …………………………………………（1分）3（1）求点A 和点B 的坐标；（2）过点A 作AC ⊥y 轴于点C ，过点B 作直线l ∥y 轴．动点P 从点O 出发，以每秒1个单位长的速度，沿O ﹣C ﹣A 的路线向点A 运动；同时直线l 从点B 出发，以相同速度向左平移，在平移过程中，直线l 交x 轴于点R ，交线段BA 或线段AO 于点Q ．当点P 到达点A 时，点P 和直线l 都停止运动．在运动过程中，设动点P 运动的时间为t 秒)0( t ．①当t 为何值时，以A 、P 、R 为顶点的三角形的面积为8？②是否存在以A 、P 、Q 为顶点的三角形是QA=QP 的等腰三角形？若存在，求t 的值；若不存在，请说明理由．3∴y ＝－x +7，0＝x +7，∴x ＝7，∴B 点坐标为：（7，0），----------------------------1分 ∵y ＝－x +7＝x 34，解得x ＝3，∴y ＝4，∴A 点坐标为：（3，4）；-------------------1分（2）①当0＜t ＜4时，PO ＝t ，PC ＝4－t ，BR ＝t ，OR ＝7－t ，--------------1分过点A 作AM ⊥x 轴于点M∵当以A 、P 、R 为顶点的三角形的面积为8，∴S 梯形ACOB －S △ACP －S △POR －S △ARB ＝8， ∴21（AC +BO ）×CO －21AC ×CP －21PO ×RO －21AM ×BR ＝8， ∴（AC +BO ）×CO －AC ×CP －PO ×RO －AM ×BR ＝16，∴（3+7）×4－3×（4－t ）－t ×（7－t ）－4t ＝16，∴t 2－8t +12＝0. -----------------1分解得t 1＝2，t 2＝6（舍去）. --------------------------------------------------------------------1分当4≤t ≤7时，S △APR ＝21AP ×OC =2（7－t ）＝8，t=3(舍去)；--------------1分 ∴当t ＝2时，以A 、P 、R 为顶点的三角形的面积为8； ②存在．当0＜t ≤4时,直线l 与AB 相交于Q ，∵一次函数y ＝－x +7与x 轴交于B （7，0）点，与y 轴交于N （0，7）点，∴NO ＝OB ，∴∠OBN ＝∠ONB ＝45°.∵直线l ∥y 轴，∴RQ ＝RB=t ，AM=BM=4∴QB=t 2,AQ=t 224-----------------1分 ∵RB ＝OP ＝QR ＝t ，∴PQ//OR,PQ=OR=7-t --------------------------------------1分 ∵以A 、P 、Q 为顶点的三角形是等腰三角形，且QP =QA ，∴7-t=t 224-，t=1-32（舍去）--------------------------------------------1分当4＜t ≤7时，直线l 与O A 相交于Q ，若QP ＝QA ，则t －4+2（t －4）＝3，解得t ＝5；---------------------------------------1分 ∴当t =5，存在以A 、P 、Q 为顶点的三角形是PQ ＝AQ 的等腰三角形．已知边长为1的正方形ABCD 中， P 是对角线AC 上的一个动点（与点A 、C 不重合），过点P 作 PE ⊥PB ，PE 交射线DC 于点E ，过点E 作EF ⊥AC ，垂足为点F . （1）当点E 落在线段CD 上时（如图10），① 求证：PB=PE ；② 在点P 的运动过程中，PF 的长度是否发生变化？若不变，试求出这个不变的值，若变化，试说明理由；（2）当点E 落在线段DC 的延长线上时，在备用图上画出符合要求的大致图形，并判断上述（1）中的结论是否仍然成立（只需写出结论，不需要证明）；（3）在点P 的运动过程中，⊿PEC 能否为等腰三角形？如果能，试求出AP 的长，如果不能，试说明理由．D CAE P 。

初二期末几何压轴题答案详解课件

解题方法
首先分析题目给出的条件，明确所涉及的三角形和四边形，然后根据性质和判定定理进行推理，最后得出结论。
角度与线段的计算题
总结词
考察角度和线段的计算
详细描述
这类题目通常涉及角度和线段的计算，需要学生掌握角度和线段的计算公式，并能够灵活运用。
解题方法
首先根据题目给出的条件，明确所涉及的角度和线段，然后根据计算公式进行计算，最后得出结论。
初二期末几何压轴题答案详解课件
目录
• 几何压轴题概述 • 常见几何压轴题类型与解题方法 • 几何压轴题的解题技巧与注意事项 • 学生常见问题与解答 • 练习与巩固 • 总结与展望
01
几何压轴题概述
几何压轴题的定义与特点
定义
几何压轴题通常指在期末考试中难度较大、分值较高、考察学生综合运用几何知识能力的题目。
解题方法
首先分析题目给出的条件，明确所涉及的折叠和旋转，然后根据性质和判定定理进行推理，最后得出结论。
03
几何压轴题的解题技巧与注意事项
解题技巧：如何快速找到解题突破口
仔细审题
理解题目的要求和条件，明确解题的目标。
寻找关键信息
从题目中提取关键信息，如特殊角、特殊图形等。
利用已知条件进行推导
注重实践应用
将所学的几何知识应用到实际生活中，加深对知识的理解，提高自己的实践能力。
3
提前预习下一学期的学习内容
提前了解下一学期的学习内容，做好预习工作，为新的学习做好准备。
THANKS
感谢观看
答案与解析：答案+解析答案与解析：答案+解析
练习题二：填空题
01
填空题一：题目内容
02

期末考试勾股定理与几何翻折压轴题专项训练—2023-2024学年八年级数学下学期(人教版)(解析版)

期末考试勾股定理与几何翻折压轴题专项训练【例题精讲】例1．（三角形翻折问题）如图，在Rt ABC △中，9086ABC AB BC ∠=︒==，，，分别在AB AC ，边上取点E F ，，将AEF △沿直线EF 翻折得到A EF '△，使得点A 的对应点A '恰好落在CB 延长线上，当60EA B '∠=︒时，AE 的长为，当A F AC '⊥时，AF 的长为．【答案】 32− 407【分析】由折叠的性质可得AE A E '=，先求出30A EB '∠=︒，从而可得1122A B A E AE ''==，再由勾股定理可得BE AE =，最后由AE BE AB +=，进行计算即可；令A F '交AB 于G ，连接CG ，由折叠的性质可得：A EA F '∠=∠，AFE A FE '∠=∠，AEF A EF '∠=∠，AF A F '=，由A F AC '⊥得出90A FA A FC ''∠=∠=︒，45AFE A FE '∠=∠=︒，证明()ASA A FC AFG '≌得到CF FG =，设CF FG x ==，则10AF x =−，AG ，根据1122ACG S AC FG AG BC =⋅=⋅建立方程，解方程即可得出CF 的长，即可求解．【详解】解：由折叠的性质可得：AE A E '=，90ABC ∠=︒，18090A BE ABC '∴∠=︒−∠=︒，60EA B '∠=︒，9030A EB EA B ''∴∠=︒−∠=︒，1122A B A E AE ''∴==，BE AE∴==，AE BE AB+=，8AE AE∴=，32AE∴=−如图，令A F'交AB于G，连接CG，A F AC'⊥，90A FA A FC''∴∠=∠=︒，由折叠的性质可得：A EA F'∠=∠，AFE A FE'∠=∠，AEF A EF'∠=∠，AF A F'=，90AFE A FE'∠+∠=︒，45AFE A FE'∴∠=∠=︒，设A EA Fα'∠=∠=，则45FEB AFEα∠=∠=+︒，180135AEF FEB A EFα'∴∠=︒−∠=︒−=∠，()13545902A EB A EF BEFααα''∴∠=∠−∠=︒−−︒+=︒−，902EA B A EBα''∴∠=︒−∠=，FA C EA B EA F Aα'''∴∠=∠−∠==∠，在A FC'和AFG中，CA F AA F AFA FC AFG∠=∠⎧⎪=⎨⎪∠=∠''⎩'，()ASAA FC AFG'∴≌，CF FG∴=，在Rt ABC△中，9086ABC AB BC∠=︒==，，，10AC∴，设CF FG x==，则10AF x=−，AG∴==1122ACGS AC FG AG BC=⋅=⋅，106x∴⋅=，整理得：271809000x x+−=，即29014400749x⎛⎫+=⎪⎝⎭，9012077x∴+=±，解得：307x=或30x=−（不符合题意，舍去），307CF∴=，30401077AF AC CF∴=−=−=，故答案为：32−407．【点睛】本题考查了折叠的性质、全等三角形的判定与性质、勾股定理、三角形的面积公式、等腰直角三角形的判定与性质、三角形外角的定义及性质、三角形内角和定理等知识，熟练掌握以上知识点，添加适当的辅助线是解此题的关键．例2．（坐标系中折叠问题）如图，在平面直角坐标系中，长方形ABCO的边OC OA、分别在x轴、y轴上，6AB=，点E在边BC上，将长方形ABCO沿AE折叠，若点B的对应点F 恰好是边OC的三等分点，则点E的坐标是．【答案】⎛−⎝⎭或(−【分析】本题主要考查了勾股定理与折叠问题，坐标与图形，由折叠的性质可得6AF AB==，BE EF=，90AFE B∠=∠=︒，再分当点F靠近点C时，24CF OF==，，当点F靠近点O 时，则42CF OF==，，两种情况利用勾股定理先求出OA的长，进而得到BC的长，设出CE 的长，进而得到EF的长，在Rt EFC△中，由勾股定理建立方程求解即可．【详解】解：在长方形ABCO 中，6CO AB ==，90BCO B AOC ∠=∠=∠=︒，由折叠的性质可得6AF AB ==，BE EF =，90AFE B ∠=∠=︒，F 恰好是边OC 的三等分点，∴当点F 靠近点C 时，24CF OF ==，，在Rt AFO V中，OA =，∴BC OA ==设CE x =，则BE EF x ==，在Rt EFC △中，由勾股定理得到222EF CF CE =+，∴()2222xx =+，解得x =，∴点E的坐标是⎛− ⎝⎭；当点F 靠近点O 时，则42CF OF ==，，在Rt AFO V中，OA ==∴BC OA ==设CE x =，则BE EF x ==，在Rt EFC △中，由勾股定理得到222CF CE =+，∴()2224x x =+，解得x =∴点E的坐标是(−；综上所述，点E的坐标是⎛− ⎝⎭或(−，故答案为：⎛− ⎝⎭或(−．例3．（四边形折叠问题）如图，已知矩形ABCD ，4AB =，5BC =，点P 是射线BC 上的动点，连接AP ，AQP △是由ABP 沿AP 翻折所得到的图形．(1)当点Q 落在边AD 上时，QC = ；(2)当直线PQ 经过点D 时，求BP 的长；(3)如图2，点M 是DC 的中点，连接MP 、MQ ．①MQ 的最小值为；②当PMQ 是以PM 为腰的等腰三角形时，请直接写出BP 的长．【答案】(2)2BP =或8BP =(3) 2.9BP =或4BP =或10BP =【分析】（1）根据折叠的性质和勾股定理进行求解即可；（2）分点P 在线段BC 上，点P 在线段BC 的延长线上，两种情况，进行讨论求解；（3）①连接AM ，勾股定理求出AM 的长，折叠求出AQ 的长，根据MQ AM AQ ≥−，求出最小值即可；②分PM MQ =和PM PQ =两种情况，再分点P 在线段BC 上，点P 在线段BC 的延长线上，进行讨论求解即可．【详解】（1）解：当点Q 落在边AD 上时，如图所示，∵矩形ABCD ，4AB =，5BC =，∴4,5CD AB AD BC ====，90BAD B BCD ADC ∠=∠=∠=∠=︒，∵翻折，∴4,90AQ AB AQP B ==∠=∠=︒，∴1DQ AD AQ =−=，在Rt CDQ △中，CQ ==（2）当直线PQ 经过点D 时，分两种情况：当点P 在线段BC 上时，如图：∵翻折，∴4AQ AB ==，90AQP B ∠=∠=︒，BP PQ =，∴90AQD ∠=︒，∴3DQ ==，设BP PQ x ==，则：5PC BC BP x =−=−，3DP DQ PQ x =+=+，在Rt PCD △中，222DP CP CD=+，即：()()222345x x +=+−，∴2x =；∴2BP =；②当P 在线段BC 的延长线上时：∵翻折，∴4,90AQ AB Q B ==∠=∠=︒，BP PQ =，∴3DQ ==，设BP PQ x ==，则：5PC BP BC x =−=−，3DP PQ DQ x =−=−，在Rt PCD △中，222DP CP CD =+，即：()()222345x x −=+−，∴8x =；∴8BP =；综上：2BP =或8BP =；（3）①连接AM ，∵M 是CD 的中点， ∴122DM CM CD ===，∴AM =∵翻折，∴4AQ AB ==，∵MQ AM AQ ≥−，∴当,,A Q M 三点共线时，MQ 的值最小，即：4MQ AM AQ =−=4；②当PM PQ =时，如图：∵翻折，∴BP PQ PM ==，设BP x =，则：,5PM x CP BC BP x ==−=−，在Rt PCM 中，222PM CM PC =+，即：()22225x x =+−，解得： 2.9x =，即： 2.9BP =；当PM QM =，点P 在线段BC 上时，如图：∵,QM PM DM CM ==，90D C ∠=∠=︒，∴()HL MDQ MCP ≌，∴CP DQ =，点Q 在AD 上，由（1）知：1DQ =，∴1CP DQ ==，∴4BP BC CP =−=；当点P 在BC 的延长线上时：如图：此时点M 在AP 上，连接BM ，∵翻折，∴BM MQ PM ==，∵MC BP ⊥，∴210BP BC ==；综上： 2.9BP =或4BP =或10BP =．质，综合性强，难度大，属于压轴题．利用数形结合和分类讨论的思想进行求解，是解题的关键．【模拟训练】1．如图，在长方形ABCD 中，点E 是AD 的中点，将ABE 沿BE 翻折得到FBE ，EF 交BC 于点H ，延长BF DC 、相交于点G ，若8DG =，10BC =，则DC = ．【答案】258【分析】本题考查了全等三角形的判定与性质，折叠的性质，勾股定理，连接EG ，根据点E 是AD 的中点得DE AE EF ==，根据四边形ABCD 是长方形得90D A ∠=∠=︒，根据将ABE 沿BE 翻折得到FBE 得90BFE D A ∠=∠=∠=︒，利用HL 证明Rt Rt EFG EDG △≌△，得8FG DG ==，设DC x =，则8CG DG DC x =−=−，8BG BF FG AB FG DC FG x =+=+=+=+，在Rt BCG V △中，根据勾股定理得，222CG BC BG +=，进行计算即可得．【详解】解：如图所示，连接EG ，∵点E 是AD 的中点，∴DE AE EF ==，∵四边形ABCD 是长方形，∴90D A ∠=∠=︒，∵将ABE 沿BE 翻折得到FBE ，∴90BFE D A ∠=∠=∠=︒在Rt EFG △和Rt EDG △中，EF ED EG EG =⎧⎨=⎩，∴()Rt Rt HL EFG EDG V V ≌，∴8FG DG ==，设DC x =，则8CG DG DC x =−=−，8BG BF FG AB FG DC FG x =+=+=+=+，在Rt BCG 中，根据勾股定理得，222CG BC BG +=，∴222(8)10(8)x x −+=+，解得258x =，故答案为：258．2．如图，在Rt ABC △中，90ACB ∠=︒，254AB =，154=AC ，点D 是AB 边上的一个动点，连接CD ，将BCD △沿CD 折叠，得到CDE ，当DE 与ABC 的直角边垂直时，AD 的长是．【答案】154或54【分析】本题考查了勾股定理，平行四边形的判定和性质，折叠的性质，全等三角形的判定和性质，分DE BC ⊥和DE AB ⊥两种情况进行求解即可得到答案，根据题意，正确画出图形是解题的关键．【详解】解：如图，当DE BC ⊥时，延长ED 交BC 于点F ，CE 与AB 相交于点M ，∵EF BC ⊥，∴90EFC EFB ∠=∠=︒，∴90E ECF ∠+∠=︒，由折叠得，B E ∠=∠，CE CB =，MCD FCD ∠=∠，∴90B ECF ∠+∠=︒，∴90CMB ∠=︒，即C M A B ⊥，∵90ACB ∠=︒，254AB =，154=AC ，∴5BC ==， ∵1122ABC S AC BC AB CM ==△，∴11512552424CM ⨯⨯=⨯⨯，解得3CM =，∴4BM =，∵90CFD CMD FCD MCD CD CD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩， ∴()AAS CFD CMD ≌，∴3CF CM ==，DF DM =，∴532BF BC CF =−=−=，设DF DM x ==，则4BD x =−，在Rt BFD 中，222DF BF BD +=，∴()22224x x +=−，解得32x =， ∴35422BD =−=， ∴25515424AD AB BD =−=−=；当DE AB ⊥时，如图，设DE 与AC 相交于点M ，由折叠可得，BCD ECD ∠=∠，DE DB =，ED BD =，5EC BC ==，∵DE AB ⊥，90ACB ∠=︒，∴DE BC ∥，∴EDC BCD ∠=∠，∴EDC ECD ∠=∠，∴5ED EC ==，∴5BD ED ==， ∴255544AD AB BD =−=−=；综上，AD 的长是154或54，故答案为：154或54．3．如图，等边三角形ABC 中，16AB BD AC =⊥，于点D ，点E F 、分别是BC DC 、上的动点，沿EF 所在直线折叠CEF △，使点C 落在BD 上的点C '处，当BEC '△是直角三角形时，BE 的值为．【答案】24−或323【分析】本题考查了翻折变换，等边三角形的性质，折叠的性质，熟练运用折叠的性质是本题的关键．由等边三角形的性质可得30DBC ∠=︒，分9090BEC BC E ''∠=︒∠=︒，两种情况讨论，由直角三角形的性质即可求解．【详解】解：ABC 是等边三角形，BD AC ⊥，30,DBC ∴∠=︒ 由折叠的性质可得：,CE C E '=若90,BEC ∠'=︒且30,C BE ∠'=︒,2,BE E B E C C ∴='''=16,BE CE BC +==16,CE +=8,E E C C ∴'==24BE ∴=−若90,30,E C B E C B ∠'=︒='∠︒2,,BE E B C E C ∴'''=16,BE CE BC +==16,3CE E C =='∴ 32.3BE ∴=故答案为∶ 24−323．4．如图，在ABC 中，120ACB ∠=︒，8AC =，4BC =，将边BC 沿CE 翻折，使点B 落在AB 上的点D 处，再将边AC 沿CF 翻折，使点A 落在CD 的延长线上的点A '处，两条折痕与斜边AB 分别交于点E 、F ，则线段FA '的长为．【答案】【分析】本题考查了折叠的性质，勾股定理，直角三角形的性质，添加恰当辅助线构造直角三角形是本题的关键．过点A 作AH BC ⊥交BC 的延长线于H ，由直角三角形的性质可求142HC AC ==，AH =AB 的长，由面积法可求CE 的长，由折叠的性质可求90BEC DEC ∠=∠=︒，BCE DCE ∠=∠，ACF DCF ∠=∠，然后再求解即可．【详解】解：如图，过点A 作AH BC ⊥，交BC 的延长线于H ，120ACB ∠=︒，ACB H HAC ∠=∠+∠，30HAC ∴∠=︒，142HC AC ∴==，AH ==，448BH ∴=+=，AB ∴1122ACB S BC AH AB CE =⨯⨯=⨯⨯，4CE ∴=，CE ∴，将边BC 沿CE 翻折，使点B 落在AB 上的点D 处，再将边AC 沿CF 翻折，90BEC DEC ∴∠=∠=︒，BCE DCE ∠=∠，ACF DCF ∠=∠，1602ECF ACB ∴∠=∠=︒，30CFE ∴∠=︒，EF ∴，在Rt BCE中，BE ===，AF AB EF BE ∴=−−==FA AF '∴==故答案为：5．如图，点D 是ABC 的边AB 的中点，将BCD △沿直线CD 翻折能与ECD 重合，若4AB =，2CD =，1AE =，则点C 到直线AB 的距离为．【答案】【分析】连接BE ，延长CD 交BE 于点G ，作CH AB ⊥于点H ，如图所示，由折叠的性质及中点性质可得AEB △为直角三角形，且G 为BE 中点，从而CG BE ⊥，由勾股定理可得BE的长，再根据2ABC BDC S S =△△，即11222AB CH CD BG ⋅=⨯⋅，从而可求得CH 的长．【详解】解：连接BE ，延长CD 交BE 于点G ，作CH AB ⊥于点H ，如图所示，由折叠的性质可得：BD ED =，CB CE =，∴CG 为BE 的中垂线， ∴12BG BE =，∵点D 是AB 的中点，4AB =，2CD =，1AE =， ∴122BD AD AB ===，CBD CAD S S =，AD DE =，∴DBE DEB ∠=∠，DEA DAE ∠=∠，∵180EDA DEA DAE ∠+∠+∠=︒，即22180DEB DEA ∠+∠=︒，∴90DEB DEA ∠+∠=︒，即90BEA ∠=︒，∴BE∴12BG BE ==， ∵2ABC BDCS S =△△， ∴11222AB CH CD BG ⋅=⨯⋅，∴422CH =⨯，∴CH ，∴点C 到直线AB 的距离为．故答案为：．【点睛】本题考查翻折变换，线段中垂线的判定，等腰三角形的性质，点到直线的距离，直角三角形的判定，勾股定理，利用面积相等求相应线段的长，解题的关键是得出CG 为BE 的中垂线，2ABC BDC S S =△△．6．如图，在ABC 中，90,A AB AC ∠=︒==D 为AC 边上一动点，将C ∠沿过点D 的直线折叠，使点C 的对应点C '落在射线CA 上，连接BC '，当Rt ABC '△的某一直角边等于斜边BC '长度的一半时，CD 的长度为．【答案】或【分析】由翻折得，12CD CC '=，分三种情况：①当点C '在边AC 上，且12AC BC ''=（即2BC AC ''=）时；②当点C '在CA 的延长线上，且12AC BC ''=（即2BC AC ''=）时；③当点C '在CA 的延长线上，且12AB BC '=（即2BC AB '==时，分别根据勾股定理求出AC '的长，再求出CC '的长即可【详解】解：由翻折得，12CD CC '=，分三种情况：①当点C '在边AC 上，且12AC BC ''=（即2BC AC ''=）时，90,A AB AC ∠=︒==∴由勾股定理得，222BC AC AB ''−=，即222(2)AC AC ''−=，AC '∴=CC '∴CD ∴；②当点C '在CA 的延长线上，且12AC BC ''=（即2BC AC ''=）时，同理得AC 'CC '∴CD ∴；③当点C '在CA 的延长线上，且12AB BC '=（即2BC AB '==由勾股定理得，222AC BC AB ''=−，即22218AC '=−=，AC '∴=CC '∴CD ∴=，0>，CD AB ∴>，此时点D 不在边AC 上，不符合题意，舍去，综上，当Rt ABC '△的某一直角边等于斜边BC '长度的一半时，CD 的长度为或．故答案为：或．【点睛】本题主要考查图形的翻折变换（折叠问题），勾股定理，等腰直角三角形的性质等知识，灵活运用折叠的性质及勾股定理是解答本题的关键，同时要注意分类思想的运用．7．如图，在ABC 中，90ACB ∠=︒，3AC =，4BC =，P 为斜边AB 上的一动点（不包含A ，B 两端点），以CP 为对称轴将ACP △翻折得到A CP '，连结BA '．当A P AB '⊥时，BA '的长为．【答案】【分析】当A P AB '⊥时，过点C 作CD AB ⊥于D ，可知125CD =，95AD =，得出PDC △为等腰直角三角形，得到PD CD =，求出PA '和BP 的长，利用勾股定理即可求出BA '的长．【详解】过点C 作CD AB ⊥于D ，在Rt ADC 中，90ACB ∠=︒，3AC =，4BC =，∴5AB = ∵1122AC BC AB CD ⨯=⨯，125CD ∴=，在Rt ADC 中，3AC =∴95AD ==，当A P AB '⊥时，如图由折叠性质可知12∠=∠，PA PA '=，又1290A PA '∠=∠+∠=︒145∠=∠2=︒∴，又2390∠+∠=︒，345∴∠=︒，23∴∠=∠，125PD CD ∴==，又PA PD AD =+，12921555PA ∴=+=，又PA PA '=，215PA '∴=，又BP AB PA =−，214555BP ∴=−=，在Rt BPA '△中，90BPA ∠='︒，222BP PA BA ∴='+，2224214575525BA ⎛⎫⎛⎫'∴=+= ⎪ ⎪⎝⎭⎝⎭，BA '∴=，故答案为：．【点睛】本题考查了勾股定理的应用，折叠问题，熟练掌握勾股定理是解题的关键．8．如图，在ABC 中，90ACB ∠=︒，AC BC =，D 为AB 上一点，连接DC ，将BDC 沿DC 翻折，得到EDC △，连接AE ，若AE CE =，4BC =，则D 到CE 的距离是．【答案】2【分析】本题考查等腰直角三角形中的折叠问题，涉及等边三角形判定与性质，勾股定理应用、面积法等知识．设BE 交CD 于G ，过E 作EF BC ⊥交BC 延长线于F ，根据将BDC 沿DC 翻折，得到EDC △，AC BC =，AE CE =，可得ACE △是等边三角形，即知60ACE ∠=︒，而90ACB ∠=︒，故150BCE ∠=︒，30ECF ∠=︒，可得75BCD ECD ∠=∠=︒，122EF CE ==，CF =BE =15CBE ∠=︒，可得90BGC ∠=︒，即CG BE ⊥，从而12BG BE GE ===，由勾股定理得CG ，在Rt BDG △中，DG ，即得CD DG CG =+，由面积法可得D 到CE 的距离是2．【详解】解：设BE 交CD 于G ，过E 作EF BC ⊥交BC 延长线于F ，如图：将BDC 沿DC 翻折，得到EDC △，4BC CE ∴==，BCD ECD ∠=∠，AC BC =，AE CE =，AC BC CE AE ∴===，ACE ∴是等边三角形，60ACE ∴∠=︒，90ACB ∠=︒，150BCE ∴∠=︒，30ECF ∠=︒，75BCD ECD ∴∠=∠=︒，122EF CE ==，CF =在Rt BEF △中，BE ==BCE 中，BC CE =，150BCE ∠=︒，15CBE ∴∠=︒，18090BGC BGC BCD ∴∠=︒−∠−∠=︒，即CG BE ⊥，12BG BE GE ∴==，CG ∴===，45ABC ∠=︒，15CBE ∠=︒，30DBG ∴∠=︒，在Rt BDG△中，DG =，CD DG CG ∴=+=，设D 到CE 的距离是h ，2DCE S CE h DC GE ∆=⋅=⋅，324DC GE h CE ⋅∴===，故答案为：2．9．在生活中、折纸是一种大家喜欢的活动、在数学中，我们可以通过折纸进行探究，探寻数学奥秘．【纸片规格】三角形纸片ABC ，120ACB ∠=︒，CA CB =，点D是底边AB 上一点．【换作探究】(1)如图1，若6AC =，AD =CD ，求CD 的长度；(2)如图2，若6AC =，连接CD ，将ACD 沿CD 所在直线翻折得到ECD ，点A 的对应点为点.E 若DE 所在的直线与ABC 的一边垂直，求AD 的长；(3)如图3，将ACD 沿CD 所在直线翻折得到ECD ，边CE 与边AB 交于点F ，且DE BC ∥，再将DFE △沿DF 所在直线翻折得到DFG ，点E 的对应点为点G ，DG 与CE 、BC 分别交于H ，K ，若1KH =，请直接写出AC 边的长．【答案】(1)(2)3或(3)3【分析】（1）作CE AB ⊥于E ，求得30A B ==︒∠∠，从而得出132CE AC ==，AE AC =进而得出DE AE AD =−=（2）当DE AB ⊥时，连接AE ，作CG AB ⊥于G ，依次得出45DAE DEA ∠=∠=︒，304575CAE CAD DAE ∠=∠+∠=︒+︒=︒，75CEA CAE ∠=∠=︒，30ACE ∠=︒，15ACD DCE ∠=∠=︒，45CDG CAB DAC ∠=∠+∠=︒，从而DG CG =，进一步得出结果；当ED AC ⊥时，设ED 交AC 于点W CE ，交AB 于V ，可推出90AVC ∠=︒，60ACE ∠=︒，从而30ACD DCE ∠=∠=︒，进一步得出结果；当DE BC ⊥时，可推出180ACB BCE ∠+∠=︒，从而90ACD DCE ∠=∠=︒，进一步得出结果；（3）可推出CKH 和CDH △及CHK 是直角三角形，且30HCK ∠=︒，30HDF ∠=︒，45DCH ∠=︒，进一步得出结果．【详解】（1）解：如图1，作CE AB ⊥于E ，90AEC ∴∠=︒，CA CB =，120ACB ∠=︒，30A B ∴∠=∠=︒，132CE AC ∴==，AE =，DE AE AD ∴=−==CD ∴=；（2）解：如图2，当DE AB ⊥时，连接AE ，作CG AB ⊥于G ，由翻折得：AD DE =，CAD CED =∠∠，AC CE =，45DAE DEA ∠∠∴==︒，304575CAE CAD DAE ∴∠=∠+∠=︒+︒=︒，75CEA CAE ∴∠=∠=︒，30ACE ∴∠=︒，15ACD DCE ∴∠=∠=︒，45CDG CAB DAC ∴∠=∠+∠=︒，DG CG ∴=，由（1）知：3CG =，AG =3AD AG DG ∴=−=；如图3，当ED AC ⊥时，设ED 交AC 于点W CE ，交AB 于V ，90E ACE ∴∠+∠=︒，E A ∠=∠，90A ACE ∴∠+∠=︒，90AVC ∴∠=︒，60ACE∴∠=︒，30ACD DCE∴∠=∠=︒，ACD A∴∠=∠，AD CD∴=，3CV =，CD∴=，AD CD∴==如图4，当DE BC⊥时，30E A∠=∠=︒，60BCE∴∠=︒，180ACB BCE∴∠+∠=︒，90ACD DCE∴∠=∠=︒，AD∴=，综上所述：3AD=或（3）解：如图5，∵DE BC ∥，30B C ∠=∠=︒，30BCF E ∴∠=∠=︒，30EDF B ∠=∠=︒，120ACB ∠=︒，90ACE ∴∠=︒，1452ECD ACD ACE ∴∠=∠=∠=︒，将DFE △沿DF 所在直线翻折得到DFG ，30GDF EDF ∴∠=∠=︒，60EDG ∴∠=︒，90CHK EHD ∴∠=∠=︒，DH CH ∴=1FH ∴==，1CF CH FH ∴=+，3AC ∴==．【点睛】本题考查了等腰三角形的判定和性质，直角三角形的性质等知识，解决问题的关键是正确分类，画出图形．10．如图，在ABC 中，90BAC ∠=︒，AB AC =，点D 为线段BC 延长线上一点，以AD 为腰作等腰直角DAF △，使90DAF ∠=︒，连接CF ．(1)请判断CF 与BC 的位置关系，并说明理由；(2)若8BC =，4CD BC =，求线段AD 的长；(3)如图2，在（2）的条件下，将DAF △沿线段DF 翻折，使点A 与点E 重合，连接CE ，求线段CE 的长．【答案】(1)CF BC ⊥，理由见解析(2)(3)【分析】（1）证明()SAS ABD ACF △≌△，则ADB AFC ∠=∠，如图1，记AD CF 、的交点为O ，根据180FAO AFO AOF DCO CDO COD ∠+∠+∠=︒=∠+∠+∠，AOF COD ∠=∠，可得90FAO DCO ∠=∠=︒，进而可得CF BC ⊥；（2）如图2，过A 作AH BC ⊥于H ，则142BH CH AH BC ====，6DH =，由勾股定理得，AD =（3）由翻折的性质可知，DE AD =，45EDF ADF ∠=∠=︒，90ADE ∠=︒，如图3，过A 作AM BC ⊥于M ，过E 作EN BC ⊥于N ，证明()AAS ADM DEN ≌，则46DN AM EN DM ====，，6CN =，由勾股定理得，CE =计算求解即可．【详解】（1）解：CF BC ⊥，理由如下：∵等腰直角DAF △，90DAF ∠=︒，∴AD AF =，又∵90BAC ∠=︒，∴BAC CAD DAF CAD ∠+∠=∠+∠，即BAD CAF ∠=∠，∵AB AC =，BAD CAF ∠=∠，AD AF =，∴()SAS ABD ACF △≌△，∴ADB AFC ∠=∠，如图1，记AD CF 、的交点为O ，∵180FAO AFO AOF DCO CDO COD ∠+∠+∠=︒=∠+∠+∠，AOF COD ∠=∠，∴90FAO DCO ∠=∠=︒，∴CF BC ⊥；（2）解：∵8BC =，4CD BC =，∴2CD =，如图2，过A 作AH BC ⊥于H ，∵ABC 是等腰直角三角形， ∴142BH CH AH BC ====，∴6DH =，由勾股定理得，AD =∴线段AD 的长为（3）解：由翻折的性质可知，DE AD =，45EDF ADF ∠=∠=︒，∴90ADE ∠=︒，如图3，过A 作AM BC ⊥于M ，过E 作EN BC ⊥于N ，∴90AMD DNE ∠=︒=∠，同理（2）可知，4AM =，6MD =，∵90ADM EDN EDN DEN ∠+∠=︒=∠+∠，∴ADM DEN ∠=∠，∵90AMD DNE ∠=︒=∠，ADM DEN ∠=∠，AD DE =，∴()AAS ADM DEN ≌，∴46DN AM EN DM ====，，∴6CN =，由勾股定理得，CE =，∴线段CE 的长为【点睛】本题考查了全等三角形的判定与性质，三角形内角和定理，勾股定理，折叠的性质，等腰三角形的性质．熟练掌握全等三角形的判定与性质，折叠的性质是解题的关键．11．如图1，在Rt ABC △中，90C ∠=︒，5AC =，12BC =，点D 为BC 边上一动点，将ACD 沿直线AD 折叠，得到AFD △，请解决下列问题．(1)AB =______；当点F 恰好落在斜边AB 上时，CD =______；(2)连接CF ，当CBF V 是以CF 为底边的等腰三角形时，请在图2中画出相应的图形，并求出此时点F 到直线AC 的距离；(3)如图3，E 为边BC 上一点，且4，连接EF ，当DEF 为直角三角形时，CD = ．（请写出所有满足条件的CD 长）【答案】(1)13，103(2)画图见解析，600169(3)52或或5或10【分析】（1）根据勾股定理可得AB 的长，再利用等积法求出CD 即可；（2）过点F 作FG AC ^，交CA 的延长线于G ，首先由等积法求出CH 的长，再根据勾股定理求出AH 的长，再次利用等积法可得FG 的长；（3）分90DEF ∠=︒或90EDF ∠=︒或90EFD ∠=︒分别画出图形，从而解决问题．【详解】（1）解：在Rt ABC △中，由勾股定理得，13AB ，当点F 落在AB 上时，由折叠知，CD DF =， ∴111222AC CD AB DF AC BC ⋅+⋅=⋅，51360CD CD ∴+=，103CD ∴=，故答案为：13，103；（2）过点F 作FG AC ^，交CA 的延长线于G ，BC BF =，AC AF =，AB ∴垂直平分CF ，由等积法得6013AC BC CH AB ⋅==，在Rt ACH 中，由勾股定理得，2513AH ===， 1122ACF S AC FG CF AH =⋅=⋅△，6025260013135169CF AH FG AC ⨯⨯⋅∴===；（3）当90DEF ∠=︒时，当点D 在CE 上时，作FH AC ⊥于H ，则4HF CE ==，5AF AC ==，3AH ∴=，2CH EF AC AH ∴==−=，设CD x =，则4DE x =−，在Rt EDF 中，由勾股定理得，222(4)2x x =−+，解得52x =，52CD ∴=，当点D 在EB 上时，同理可得538CH AC AH =+=+=，设CD DF x ==，则4DE x =−，在Rt EDF 中，由勾股定理得，222(4)8x x −+=，解得10x =，10CD ∴=，当90DFE ∠=︒时，由勾股定理得AE设CD DF x ==，则520x +=，x ∴，CD ∴=；当90FDE ∠=︒时，则45ADC ADF ∠=∠=︒，5CD AC ∴==，综上：52CD =或或5或10，故答案为：52或或5或10．【点睛】本题是三角形综合题，主要考查了翻折的性质，直角三角形的性质，勾股定理，等腰直角三角形的判定与性质等知识，利用等积法求垂线段的长是解题的关键．。

初二数学全等三角形压轴几何题知识点总结及答案

初二数学全等三角形压轴几何题知识点总结及答案一、全等三角形旋转模型1．ABC △和ADE 都是等腰直角三角形，CE 与BD 相交于点,M BD 交AC 于点,N CE 交AD 于点H .试确定线段BD CE 、的关系.并说明理由.解析：BD CE ⊥且BD CE =【分析】由已知条件可证明BAD CAE ≅△△，再根据全等三角形的性质，得到BD CE ∴= ADB AEC ∠=∠，在AEH △中90AEC AHE ∠+∠=︒，又AHE MHD ∠=∠，可得：90HMD ∠=︒，即可证明BD CE ⊥且BD CE =.【详解】解： ABC 和ADE 是直角三角形BAC DAE ∴∠=∠AB AC =AD AE =则BAC CAD DAE CAD ∠+∠=∠+∠即BAD CAE ∠=∠在BAD 与CAE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩S )AS BAD CAE ∴≅（△△BD CE ∴= ADB AEC ∠=∠在AEH △中90AEC AHE ∠+∠=︒又AHE MHD ∠=∠90ADB MHD ∴∠+∠=︒则MHD 中90HMD ∠=︒，即，BD CE ⊥，综上所述，BD CE ⊥且BD CE =.【点睛】本题主要考查三角形全等的判定方法和性质定理和等腰直角三角形的性质，从复杂的图形中找到全等三角形和“8”字形三角形是解题的关键.2．探究问题：(1)方法感悟：如图①，在正方形ABCD中，点E，F分别为DC，BC边上的点，且满足∠BAF＝45°，连接EF，求证DE＋BF＝EF．感悟解题方法，并完成下列填空：将△ADE绕点A顺时针旋转90°得到△ABG，此时AB与AD重合，由旋转可得：AB＝AD，BG＝DE，∠1＝∠2，∠ABG＝∠D＝90°，∴∠ABG＋∠ABF＝90°＋90°＝180°，因此，点G，B，F在同一条直线上．∵∠EAF＝45°∴∠2＋∠3＝∠BAD－∠EAF＝90°－45°＝45°．∵∠1＝∠2，∠1＋∠3＝45°．即∠GAF＝∠________．又AG＝AE，AF＝AE∴△GAF≌△________．∴ _________＝EF，故DE＋BF＝EF．(2)方法迁移：如图②，将Rt△ABC沿斜边翻折得到△ADC，点E，F分别为DC，BC边上的点，且∠EAF ＝∠DAB．试猜想DE，BF，EF之间有何数量关系，并证明你的猜想．答案：E解析：(1)EAF、△EAF、GF；(2)DE＋BF＝EF.【解析】【分析】（1）利用角之间的等量代换得出∠GAF=∠FAE，再利用SAS得出△GAF≌△EAF，得出答案；（2）将△ADE顺时针旋转90°得到△ABG，再证明△AGF≌△AEF，即可得出答案；【详解】解：（1）如图①所示；根据等量代换得出∠GAF=∠FAE，利用SAS得出△GAF≌△EAF，∴GF=EF，故答案为：FAE；△EAF；GF；(2)DE＋BF＝EF，理由如下：假设∠BAD的度数为m，将△ADE绕点A顺时针旋转，m°得到△ABG，如图，此时AB与AD重合，由旋转可得：AB＝AD，BG＝DE，∠1＝∠2，∠ABG＝∠D＝90°，∴∠ABG＋∠ABF＝90°＋90°＝180°，因此，点G，B，F在同一条直线上．∵，∴．∵∠1＝∠2，∴∠1＋∠3＝．即∠GAF＝∠EAF．∵在△AGF和△AEF中，，∴△GAF≌△EAF（SAS）．∴GF＝EF．又∵GF＝BG＋BF＝DE＋BF，∴DE＋BF＝EF．【点睛】此题主要考查了全等三角形的判定和性质、以及折叠的性质和旋转变换性质等知识，证得△GAF≌△EAF是解题的关键．3．如图，△ABC中，O是△ABC内一点，AO平分∠BAC，连OB，OC．（1）如图1，若∠ACB＝2∠ABC，BO平分∠ABC，AC＝5，OC＝3，则AB＝；（2）如图2，若∠CBO+∠ACO＝∠BAC＝60°，求证：BO平分∠ABC；（3）如图3，在（2）的条件下，若BC＝3B绕点O逆时针旋转60°得点D，直接写出CD的最小值为．答案：A解析：（1）8；（2）见解析；（3）33【分析】（1）先补充证明角平分线的性质定理：如图，△ABC中，AD是角平分线，则：BD DC＝AB AC ．如图1中，延长CO交AB于E，由OA平分∠EAC，推出AEAC＝OEOC，推出AEEO＝AC OC ＝53，设AE＝5k，OE＝3k，利用相似三角形的性质构建方程求出k即可解决问题．（2）如图2中，过点O作EF⊥OA交AB于E，交AC于F，作CG∥EF交AB于G，连接OG．证明△AGO≌△ACO（SAS），推出OG＝OC，推出∠OGC＝∠OCG，证明O，G，B，C 四点共圆，可得结论．（3）如图3中，以BC为边向上作等边△BCH，连接OH，作HM⊥BC于M．证明△HBO≌△CBD（SAS），推出OH＝CD，由（2）可知∠BOC＝120°，推出当点O落在HM 上时，OH的值最小．【详解】解：（1）先补充证明角平分线的性质定理：如图，△ABC中，AD是角平分线，则：BD DC＝AB AC．理由：过C作CE∥DA，交BA的延长线于E，∵CE∥DA，∴∠1＝∠E，∠2＝∠3，∠1＝∠2，∴∠E＝∠3，∴AE＝AC，∵BDDC ＝BAAE，∴BDDC ＝ABAC．如图1中，延长CO交AB于E，∵OA平分∠EAC，∴AEAC＝OEOC，∴AEEO ＝ACOC＝53，设AE＝5k，OE＝3k，∵OB平分∠ABC，∴OC平分∠ACB，∵∠ACB＝2∠ABC，∴∠BCE＝12∠ACB＝∠EBC，∴EB＝EC＝3k+3，∵∠ACE＝∠ABC，∠CAE＝∠BAC，∴△ACE∽△ABC，∴ACAB ＝AEAC，∴5533k k ＝55k，解得k＝58或﹣1（舍弃），∴AB＝8k+3＝8．故答案为：8．（2）如图2中，过点O作EF⊥OA交AB于E，交AC于F，作CG∥EF交AB于G，连接OG．∵AO平分∠AEF，∴∠OAE＝∠OAF，∵AO＝AO，∠AOE＝∠AOF＝90°，∴△AOE≌△AOF（ASA），∴AE＝AF，∵∠EAF＝60°，∴△AEF是等边三角形，∴∠AEF＝∠AFE＝60°＝∠FOC+∠FCO，∵∠OBC+∠FCO＝60°，∴∠FOC＝∠OBC，∵EF∥CG，∴∠AGC＝∠AEF＝60°，∠ACG＝∠AFE＝60°，∴∠AGC＝∠ACG，∴AG＝AC，∵∠GAO＝∠CAO，AO＝AO，∴△AGO≌△ACO（SAS），∴OG＝OC，∴∠OGC＝∠OCG，∵∠FOC＝∠OCG，∴∠OBC＝∠OGC，∴O，G，B，C四点共圆，∴∠ABO＝∠OCG，∴∠ABO＝∠OBC，∴OB平分ABC．（3）如图3中，以BC为边向上作等边△BCH，连接OH，作HM⊥BC于M．∵△OBD，△BCH都是等边三角形，∴∠HBC＝∠OBD＝60°，BH＝BC，BO＝BD，∴∠HBO＝∠CBD，∴△HBO≌△CBD（SAS），∴OH＝CD，由（2）可知∠BOC＝120°，∴当点O落在HM上时，OH的值最小，此时OH＝HM﹣OM＝33∴CD的最小值为33．故答案为：33【点睛】本题主要考查角平分线、三角形相似的判定和性质、三角形全等的判定和性质、等边三角形等相关知识点，解题关键在于作出辅助线构造相应图形．4．定义：按螺旋式分别延长n边形的n条边至一点，若顺次连接这些点所得的图形与原多边形相似，则称它为原图形的螺旋相似图形．例如：如图1，分别延长多边形A1A2…A n 的边得A1′，A2′，…，A n′，若多边形A1′A2′…A n′与多边形A1A2…An相似，则多边形A1′A2′…A n′就是A1A2…A n的螺旋相似图形．（1）如图2，已知△ABC是等边三角形，作出△ABC的一个螺旋相似图形，简述作法，并给以证明．（2）如图3，已知矩形ABCD，请探索矩形ABCD是否存在螺旋相似图形，若存在，求出此时AB与BC的比值；若不存在，说明理由．（3）如图4，△ABC是等腰直角三角形，AC＝BC＝2，分别延长CA，AB，BC至A′，B′，C′，使△A′B′C′是△ABC的螺旋相似三角形．若AA′＝kAC，请直接写出BB′，CC′的长（用含k的代数式表示）答案：A解析：（1）见解析；（2）AB：BC＝1；（3）BB′＝2k，CC′＝k．【分析】（1）如图2中，延长AB到E，延长BC到F，延长CA到D，使得BE＝CF＝AD，连接EF，DF，DE．则△DEF是△ABC的一个螺旋相似图形，证明△DEF是等边三角形即可解决问题．（2）如图3中，假设存在．四边形EFGH是矩形ABCD的螺旋相似图形，设AB＝CD＝a，BC＝AD＝b，BE＝DG＝x，CF＝AH＝y．分两种情形，利用相似三角形的性质以及相似矩形的性质，构建关系式证明a＝b即可解决问题．（3）如图4中，作B′T⊥CB交CB的延长线于T．设TB＝TB′＝m，证明△A′CC′≌△A′TB′（ASA），推出A′C＝TC′，CC′＝TB′＝BT，构建关系式推出m＝k即可解决问题．【详解】解：（1）如图2中，延长AB到E，延长BC到F，延长CA到D，使得BE＝CF＝AD，连接EF，DF，DE．则△DEF是△ABC的一个螺旋相似图形．理由：∵△ABC是等边三角形，∴AB＝BC＝AC，∠CAB＝∠ABC＝∠ACB，∴∠DAE＝∠FCD＝∠EBF＝120°，∵BE＝CF＝AD，∴CD＝AE＝BF，∴△FCD≌△DAE≌△EBF（SAS），∴DF ＝DE ＝EF ，∴△DEF 是等边三角形，∴△DEF ∽△ABC ，∴△DEF 是△ABC 的一个螺旋相似图形．（2）如图3中，假设存在．四边形EFGH 是矩形ABCD 的螺旋相似图形，设AB ＝CD ＝a ，BC ＝AD ＝b ，BE ＝DG ＝x ，CF ＝AH ＝y ．由题意：△BEF ∽△AHE ， ∴EF EH ＝BE AH ＝BF AE， ∴x y ＝b y a x++，当EF HE ＝BC AB ＝b a 时，b a ＝x y ＝b y a x++， ∴x ＝b a•y ，ax +x 2＝by +y 2， ∴by +22b a•y 2＝by +y 2， ∴a 2＝b 2，∴a ＝b ，即AB ：BC ＝1．当EF EH ＝AB BC ＝a b 时．a b ＝x y ＝b y a x ++， ∴x ＝a b•y ，ax +x 2＝by +y 2， ∴2a b •y +22a b•y 2＝by +y 2， ∴22a b b -•y （1+y b）＝0， ∵y ≠0，1+y b≠0，∴a2＝b2，∴a＝b，即AB：BC＝1，综上所述，AB：BC＝1．（3）如图4中，作B′T⊥CB交CB的延长线于T．∵AC＝BC＝2，∠ACB＝90°，∴∠ABC＝∠CAB＝45°，∴∠TBB′＝∠ABC＝45°，∴∠TB′B＝∠TBB′＝45°，∴TB＝TB′，设TB＝TB′＝m，∵△A′B′C′是△ABC的螺旋相似三角形，∴A′C′＝B′C′，∠A′C′B′＝90°，∵∠A′C′C+∠B′C′＝90°，∠A′CC+∠C′A′C＝90°，∴∠C′A′C＝∠B′C′T，∵∠A′CC′＝∠T＝90°，∴△A′CC′≌△A′TB′（ASA），∴A′C＝TC′，CC′＝TB′＝BT，∴2+2k＝2+2m，∴m＝k，∴BB′2k，CC′＝k．【点睛】本题属于相似形综合题，考查了等边三角形的性质，矩形的性质，等腰直角三角形的判定和性质等知识，解题的关键是理解题意，学会利用参数解决问题，学会用分类讨论的思想思考问题，属于中考压轴题．5．△CDE和△AOB是两个等腰直角三角形，∠CDE＝∠AOB＝90°，DC＝DE＝1，OA＝OB＝a（a＞1）．（1）将△CDE的顶点D与点O重合，连接AE，BC，取线段BC的中点M，连接OM．①如图1，若CD，DE分别与OA，OB边重合，则线段OM与AE有怎样的数量关系？请直接写出你的结果；②如图2，若CD在△AOB内部，请你在图2中画出完整图形，判断OM与AE之间的数量关系是否有变化？写出你的猜想，并加以证明；③将△CDE绕点O任意转动，写出OM的取值范围（用含a式子表示）；（2）是否存在边长最大的△AOB，使△CDE的三个顶点分别在△AOB的三条边上（都不与顶点重合）？如果存在，请你画出此时的图形，并求出边长a的值；如果不存在，请说明理由．答案：A解析：（1）①OM ＝12AE ；②OM ＝12AE ，证明详见解析；③12a -≤OM ≤12a +；（2）5【分析】（1）①利用△CDE ≌△AOB 得出BC ＝AE ，再由直角三角形斜边的中线等于斜边的一半求解．②作辅助线，利用△COF ≌△EOA 及三角形中位线得出OM ＝12AE ． ③分两种情况，当OC 与OB 重合时OM 最大，当OC 在BO 的延长线上时OM 最小，据此求出OM 的取值范围．（2）分两种情况：当顶点D 在斜边AB 上时，设点C ，点E 分别在OB ，OA 上．由DM +OM ≥OF 求出直角边a 的最大值；当顶点D 在直角边AO 上时，点C ，点E 分别在OB ，AB 上时，利用△EHD ≌△DOC ，得出OD ＝EH ，在Rt △DHE 中，运用勾股定理ED 2＝DH 2+EH 2，得出方程，由△判定出a 的最大值．【详解】解：（1）①∵△CDE 和△AOB 是两个等腰直角三角形，∴CD ＝ED ，AO ＝B 0，∠CDE ＝∠AOB ，在△CDE 和△AOB 中，CD ED CDE AOB AO BO =⎧⎪∠=∠⎨⎪=⎩∴△CDE ≌△AOB （SAS ），∴BC ＝AE∵M 为BC 中点，∴OM ＝12BC ，∴OM ＝12AE ． ②猜想：OM ＝12AE ．证明：如图2，延长BO 到F ，使OF ＝OB ，连接CF ，∵M 为BC 中点，∴OM ＝12CF ， ∵△CDE 和△AOB 是两个等腰直角三角形，∴CD ＝ED ，AO ＝BO ＝OF ，∠CDE ＝∠AOB ，∵∠AOC +∠COB ＝∠BOE +∠COB ＝90°，∴∠AOC ＝∠BOE ，∠FOC ＝∠AOE ，在△COF 和△EOA 中，CD ED FOC AOE OF AO =⎧⎪∠=∠⎨⎪=⎩∴△COF ≌△EOA ，∴CF ＝AE ，∴OM ＝12AE ． ③Ⅰ、如图3，当OC 与OB 重合时，OM 最大，OM＝11122 a a-++=Ⅱ、如图4，当OC在BO的延长线上时，OM最小，OM＝12a+﹣1＝12a-，所以12a-≤OM≤12a+，（2）解：根据△CDE的对称性，只需分两种情况：①如图5，当顶点D在斜边AB上时，设点C，点E分别在OB，OA上．作OF⊥AB于点F，取CE的中点M，连接OD，MD，OM．∵△AOB和△CDE是等腰直角三角形，∠AOB＝∠CDE＝90°，OA＝OB＝a（a＞1），DC＝DE＝1，∴AB ＝2a ，OF ＝12AB ＝22a ， ∴CE ＝2，DM ＝12CE ＝22，在RT △COE 中，OM ＝12CE ＝22，在RT △DOM 中，DM +OM ≥OD ，又∵OD ≥OF ， ∵DM +OM ≥OF ，即22+22≥22a ， ∴a ≤2，∴直角边a 的最大值为2．②如图6，当顶点D 在直角边AO 上时，点C ，点E 分别在OB ，AB 上，作EH ⊥AO 于点H ． ∵∠AOB ＝∠CDE ＝∠DHE ＝90°，∵∠HED +∠EDH ＝∠CDO +∠EDH ＝90°，∴∠HED ＝∠CDO ，∵DC ＝DE ，在△EHD 和△DOC 中，EHD COD HED CDO DE DC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△EHD ≌△DOC （AAS ）设OD ＝x ，∴OD ＝EH ＝AH ＝x ，DH ＝a ﹣2x ，在Rt △DHE 中，ED 2＝DH 2+EH 2，∴1＝x 2+（a ﹣2x ）2，整理得，5x 2﹣4ax +a 2﹣1＝0，∵x 是实数，∴△＝（4a ）2﹣4×5×（a 2﹣1）＝20﹣4a 2≥0，∴a 2≤5，∴a 2的最大值为5，∴a的最大值为5．综上所述，a的最大值为5．【点睛】本题主要考查了几何变换综合题及三角形全等的判定和性质，解题的关键是在取最大值时，对三角形的位置进行讨论分别求值．6．已知：在△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点(点D不与B、C重合)．以AD为边作正方形ADEF，连接CF．（1）如图1，当点D在线段BC上时，请直接写出线段BD与CF的数量关系：；（2）如图2，当点D在线段BC的延长线上时，其它条件不变，若AC=2，CD=1，则CF= ；（3）如图3，当点D在线段BC的反向延长线上时，且点A、F分别在直线BC的两侧，其它条件不变：①请直接写出CF、BC、CD三条线段之间的关系：；②若连接正方形对角线AE、DF，交点为O，连接OC，探究△AOC的形状，并说明理由．答案：B解析：（1）BD=CF；（2）221；（3）①CD=CF+BC，②等腰三角形，见解析【分析】（1）△ABC是等腰直角三角形，利用SAS即可证明△BAD≌△CAF；（2）同（1）相同，利用SAS即可证得△BAD≌△CAF，从而证得BD=CF，即可得到CF=CD+BC，然后求出答案；（3）中的①与（1）相同，可证明BD=CF，又点D、B、C共线，故：CD=BC+CF；②由（1）猜想并证明BD⊥CF，从而可知△FCD为直角三角形，再由正方形的对角线的性质判定△AOC三边的特点，再进一步判定其形状．【详解】解：（1）证明：∵∠BAC=90°，AB=AC，∴∠ABC=∠ACB=45°，∵四边形ADEF是正方形，∴AD=AF，∠DAF=90°，∵∠BAC=∠BAD+∠DAC=90°，∠DAF=∠CAF+∠DAC=90°，∴∠BAD=∠CAF，在△BAD和△CAF中，AB AC BAD CAF AD AF =⎧⎪∠=∠⎨⎪=⎩，∴△BAD ≌△CAF （SAS ），∴BD=CF ，（2）与（1）同理，证△BAD ≌△CAF ；∴BD=CF ，∴CF=BC+CD ，∵AC=AB=2，CD=1，∴BC ==∴CF=1；（3）①BC 、CD 与CF 的关系：CD=BC+CF理由：与（1）同法可证△BAD ≌△CAF ，从而可得：BD=CF ，即：CD=BC+CF②△AOC 是等腰三角形理由：与（1）同法可证△BAD ≌△CAF ，可得：∠DBA=∠FCA ，又∵∠BAC=90°，AB=AC ，∴∠ABC=∠ACB=45°，则∠ABD=180°-45°=135°，∴∠ABD=∠FCA=135°∴∠DCF=135°-45°=90°∴△FCD 为直角三角形．又∵四边形ADEF 是正方形，对角线AE 与DF 相交于点O ，∴OC=12DF ， ∴OC=OA ∴△AOC 是等腰三角形．【点睛】本题考查了等腰三角形、正方形的性质及全等三角形的判定与性质等知识点，一般情况下，要证明两条线段相等，就得证明这两条线段所在的两个三角形全等，关键是掌握图形特点挖掘题目所隐含的条件．7．问题提出（1）如图①，在ABC 中，AD 是BC 边上的高，若∠BAD ＝45°，∠DAC ＝30°，则ABD ACD S S ＝．问题探究（2）如图②，在正方形ABCD 中，边长为8，点E 是AB 的中点，作∠EDF ＝45°，交BC 于点F ，求DEF 的面积．问题解决（3）如图③，某市为迎接城市运动会，打造融体育、文化、饮食、旅游为一体的综合商业品牌，规划了如图所示的矩形ABCD 观光区，如图，在矩形ABCD 中，AB ＝16km ，AD ＝12km ，要求在边AB 上确定一点E 为观光区的南门，在边BC 上确定一点F 为观光区的东门，且∠EDF ＝30°，同时为了方便市民游览，还要修建一条观光通道FG ，使FG ∥AB ，交DE 于点G （观光带的宽度不计），为了节约成本，要使FG 的长度最小，那么是否存在符合条件的修建方案？若存在，请求出FG 的最小值；若不存在，请说明理由．答案：B解析：3(2)803，(3) 323．【分析】(1)根据∠BAD ＝45°，∠DAC ＝30°，求出BD 、AD 、DC 的关系即可；(2)将△DCF 绕点D 顺时针旋转90°得到△DAG ，可证△DEF ≌△DEG ，得到EF =CF +AE ，求出CF 长即可；(3) 作DM ⊥DF ，交BA 延长线于点M ，作EN ⊥DF 于N ，EH ⊥DM 于H ，作△DME 的外接圆⊙O ，连接OD 、OE 、OM ，作OQ ⊥ME 于Q ，求出△DEF 的面积最小值，再用面积求FG 最小值．【详解】解:(1)∵AD 是BC 边上的高，若∠BAD ＝45°，∠DAC ＝30°，∴AD =BD ，AD = tan 603DC DC ︒=，12312ABD ACD BD AD SS CD AD ⋅==⋅ (2) 将△DCF 绕点D 顺时针旋转90°得到△DAG ，∵∠DAG =∠C =90°，∠DAE =90°，∴G 、A 、E 三点共线，由旋转可知，∠FDG =∠CDA =90°，DF =DG ，∴∠GDE =∠FDE =45°，DE =DE ,∴△GDE ≌△FDE ，∴GE =EF ，∴EF =AE +CF ，设EF 为x ，则CF =x -4，BF =12-x ，2224(12)x x +-=，解得，x =203, DEF 的面积=DEG 的面积=120808233⨯⨯=；(3)作DM ⊥DF ，交BA 延长线于点M ，作EN ⊥DF 于N ，EH ⊥DM 于H ，作△DME 的外接圆⊙O ，连接OD 、OE 、OM ，作OQ ⊥ME 于Q ，∵∠FDM =∠CDA =90°， ∴∠ADM =∠CDF ，∵∠C =∠DAM =90°，∴△ADM ∽△CDF ，∴34MD AD DF DC ==, ∵∠FDE =30°，∴∠EDM =60°， ∵1sin 302EN DE DE =︒=,3sin 60EH DE DE =︒=, ∴3EH EN =,1432192DEFDME DF EN S S DM EH ⋅==⋅, 设⊙O 的半径为R ，∵∠MDE =60°，∴∠MOE =120°， ∠MOQ =60°，3sin 602R MQ OM =︒=，ME 3R ,OQ =12R , OD +OQ ≥AD , 1122R R +≥,解得，8R ≥，138122DME S ≥⨯⨯⨯，即483DME S ≥，DME S △的最小值为483，DEF S △的最小值为43483649⨯=， 1()62DEF DGF EGF S S S FG CF BF FG =+=+=, FG 的最小值为643263=．【点睛】本题考查了全等三角形的判定与性质，相似三角形的判定与性质，三角形的外接圆，解直角三角形等，解题关键是充分理解题意，恰当的构建全等三角形、相似三角形和外接圆． 8．如图1，在等腰Rt △ABC 中，∠ABC ＝90°，AB ＝BC ＝6，过点B 作BD ⊥AC 交AC 于点D ，点E 、F 分别是线段AB 、BC 上两点，且BE ＝BF ，连接AF 交BD 于点Q ，过点E 作EH ⊥AF 交AF 于点P ，交AC 于点H ．（1）若BF ＝4，求△ADQ 的面积；（2）求证：CH ＝2BQ ；（3）如图2，BE ＝3，连接EF ，将△EBF 绕点B 在平面内任意旋转，取EF 的中点M ，连接AM ，CM ，将线段AM 绕点A 逆时针旋转90°得线段AN ，连接MN 、CN ，过点N 作NR ⊥AC 交AC 于点R ．当线段NR 的长最小时，直接写出△CMN 的周长．答案：A解析：（1）1.8；（2）证明见解析；（3）2+．【分析】（1）利用等腰直角三角形的性质求出12BD AD CD AC ====积相等和勾股定理分别求出AQ 和QD ，最后利用三角形面积公式即可求解；（2）如图，先作辅助线构造()AEH CFG ASA ∆∆≌，得到AH CG =，再通过转化得到2AH DQ =，最后利用AC ，得到一个相等关系，即()2AH HC BQ QD +=+，利用等式性质即可得到所求；（3）如图，通过做辅助线构造全等三角形确定出当HN ⊥AC ，且N 点位于H 、R 之间时，此时NR 的长最小，接着利用勾股定理和等腰直角三角形的性质，分别求出CM 、MN 、CN 的长，相加即可．【详解】解：6AB BC ==，°90ABC =∠，AC ==∴又∵AC BD ⊥∴BD 平分AC ，且BD 是∠ABC 的角平分线∴12BD AD CD AC ====Q 点到BA 和BC 边的距离相等； ∵4BF =， ∴6342ABQ BFQ S S ∆∆==， ∴32AQ FQ =，∵AF ===∴355AQ AF ==，∴5QD ===，∴1 1.82ADQ S ∆==， ∴△ADQ 的面积为1.8．（2）如图，作CG ⊥AC ，垂足为C ，交AF 的延长线于点G ，∴°90ACG =∠∵°45ACB CAB ==∠∠，∴°45GCB CAB ==∠∠，∵EH ⊥AF ，∴°90EAP AEP +=∠∠,又∵°90EAP AFB +=∠∠∴AEP AFB =∠∠，∴AEP CFG =∠∠∵BE BF =，BA BC =∴AE CF =，在AEH ∆和CFG ∆中，AEH CFG AE CFEAH FCG ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()AEH CFG ASA ∆∆≌∴AH CG =；∵BD ⊥AC ，CG ⊥AC ，∴BD ∥CG ，∵D 点是AC 的中点，且BD ∥CG ，∴DQ 是ACG ∆的中位线， ∴12DQ CG =， ∴2DQ CG AH ==； ∵AC =2BD ，∴()2AH HC BQ QD +=+，∵2AH DQ =，∴CH ＝2BQ ．（3）如图①，作AH ⊥AB ,且AH =AB ，∴∠NAH +∠HAM =∠HAM +∠BAM =90°，∴∠BAM =∠NAH ，∵AB =AH ，AM =AN ，∴()ABM AHN SAS ∆∆≌，∴HN =BM ，∵BE =BF =3，∠EBF =90°， ∴EF ==∴由M 点是EF 的中点，可得122BM EF ==，∴2NH =，∴N 点在以H 点为圆心，2为半径的圆上，如图②，当HN ⊥AC ，且N 点位于H 、R 之间时，此时NR 的长最小，为2NR HR HN HR =-=-， ∵∠BAC =45°，∴∠HAC =45°，∴∠AHN =45°，HR =AR ，∵222HR AR AH +=，∴HR AR ===，∴22NR HR =-=， ∵AC == ∴CR AC AR =-=∴CN AN === ∵∠MAN =90°，AM =AN ，∴MN ==∴∠ABM =45°，∴∠EBM =45°，∴F 点在BA 上，E 点在CB 延长线上，如图，作MP ⊥EC ，垂足为P ，∴1322BP MP EB ===， ∴315622PC PB BC =+=+=，∴2MC ==∴3263351022MC MN CN ++=++， ∴△CMN 的周长为3263351022++．【点睛】本题综合考查了等腰直角三角形的性质、全等三角形的判定与性质、旋转的性质、勾股定理、圆等知识，要求学生熟练掌握相关概念并能灵活应用它们，本题的综合性较强，难点在于作辅助线构造全等三角形以及线段之间的关系转化等，考查了学生综合分析和推理论证以及计算的能力，本题属于压轴题，蕴含了数形结合和转化的思想方法等．9．在ABC 中，,AB AC BAC α=∠=，点P 为线段CA 延长线上一动点，连接PB ，将线段PB 绕点P 逆时针旋转，旋转角为α，得到线段PD ，连接,DB DC ．（1）如图1，当60α=︒时，请直接写出线段PA 与线段CD 的数量关系是__________，DCP ∠为______度；（2）如图2，当120α=︒时，写出线段PA 和线段DC 的数量关系，并说明理由；（3）如图2，在（2）的条件下，当23AB =13BP PC +的最小值．答案：A解析：（1）PA ＝DC ，60；（2）CD ＝3PA ．理由见详解；（2）3+22【分析】（1）先证明△ABC ，△PBD 是等边三角形，再证明△PBA ≌△DBC ，进而线段PA 与线段CD 的数量关系，利用全等三角形的性质以及三角形内角和等于180°，解决问题即可；（2）证明△CBD ∽△ABP ，可得3CD BC PA AB==，解决问题；（3）过点C 作射线CM ，使得sin ∠ACM =13，过点P 作PN ⊥CM 于点N ，则PN =13PC ，过点B 作BG ⊥BA 于点G ，当点B 、P 、N 共线时，BP +PN 最小，即13BP PC +最小，由BGP CNP ∽，得13GP NP BP CP ==，结合勾股定理求出GP ，从而得CP ，进而即可求解．【详解】（1）①证明： ∵将线段PB 绕点P 逆时针旋转，旋转角为α，得到线段PD ， ∴PB ＝PD ，∵AB ＝AC ，PB ＝PD ，∠BAC ＝∠BPD ＝60°，∴△ABC ，△PBD 是等边三角形，∴∠ABC ＝∠PBD ＝60°，∴∠PBA ＝∠DBC ，∵BP ＝BD ，BA ＝BC ，∴△PBA ≌△DBC （SAS ），∴PA ＝DC ．设BD 交PC 于点O ，如图1，∵△PBA ≌△DBC ，∴∠BPA ＝∠BDC ，∵∠BOP ＝∠COD ，∴∠OBP ＝∠OCD ＝60°，即∠DCP ＝60°．故答案是：PA ＝DC ，60；（2）解：结论：CD 3．理由如下：∵AB ＝AC ，PB ＝PD ，∠BAC ＝∠BPD ＝120°，∴BC ＝2•AB •cos30°，BD ═2BP •cos30°， ∴BC BDBA BP= ∵∠ABC ＝∠PBD ＝30°，∴∠ABP ＝∠CBD ，∴△CBD ∽△ABP ，∴CD BC PA AB== ∴CD；（3）过点C 作射线CM ，使得sin ∠ACM =13，过点P 作PN ⊥CM 于点N ，则PN =13PC ，过点B 作BG CA ⊥于点G ，则BG =AB ×sin ∠BAG =3，AG = AB ×cos ∠BAG 当点B 、P 、N 共线时，BP +PN 最小，即13BP PC +最小， ∵∠BGP =∠CNP =90°，∠BPG =∠CPN ， ∴BGP CNP ∽， ∴13GP NP BP CP ==，设GP =x ，则AP -x ，BP =3x ，∴()22233x x +=，解得：x∴BPAP∴CP =AC +AP∴13BP PC +最小值13+【点睛】本题属于几何变换综合题，考查了全等三角形的判定和性质，相似三角形的判定和性质，解直角三角形等知识，第（1）（2）题解题的关键是正确寻找全等三角形或相似三角形解决问题，第（3）题的关键是过点C 作射线CM ，使得sin ∠ACM =13，过点P 作PN ⊥CM 于点N ．10．如图1，在正方形ABCD 中，点,E F 分别在边,AB AD 上，且AE AF =，延长FD 到点G ，使得DG DF =，连接,,EF GE CE ．（特例感知）（1）图1中GE 与CE 的数量关系是______________．（结论探索）（2）图2，将图1中的AEF 绕着点A 逆时针旋转()090αα︒<<︒，连接FD 并延长到点G ，使得DC DF =，连接,,GE CE BE ，此时GE 与CE 还存在（1）中的数量关系吗？判断并说明理由．（拓展应用）（3）在（2）的条件下，若5,32AB AE ==EFG 是以EF 为直角边的直角三角形时，请直接写出GE 的长．答案：G解析：(1) GE 2CE ，(2)存在，证明见解析，（3）25810或16或4．【分析】(1)连接GC，证△CDG≌△CBE，得出△GCE为等腰直角三角形即可；(2)类似（1）的方法，先证△AFD≌△AEB，再证△CDG≌△CBE，得出△GCE为等腰直角三角形即可；(3)根据E、F是直角顶点分类讨论，结合（2）中结论，利用勾股定理求解即可．【详解】解：(1)连接GC，∵AE=AF，AD=AB，∴DF=BE，，∵DG DF∴DG = BE，∵∠GDC=∠B=90°，DC=BC，∴△CDG≌△CBE，∴CE=CG，∠GCD=∠ECB，∵∠ECB+∠DCE=90°，∴∠GCE=∠GCD+∠DCE=90°，∴GE=2CE；故答案为：GE=2CE；(2) 存在，连接GC，∵AE=AF，AD=AB，∠FAE=∠DAB=90°，∴∠FAD=∠EAB，∴△FAD≌△EAB，∴FD=EB=GD，∠FDA=∠EBA，∵∠GDC+∠FDA=90°，∠EBC+∠EBA=90°，∴∠GDC=∠EBC，∵DC=BD，∴△CDG≌△CBE，与（1）同理，GE=2CE；(3)当∠FEG=90°时，如图1，因为∠FEA=∠GEC=45°，所以，A、E、C在一条直线上，∵AB=5，∴AC=52,CE=52-32=22,GE=2EC=4；如图2，E在CA延长线上，同理可得，EC2，GE2EC=16；当∠EFG =90°时，如图3，∠AFD =∠EFG +∠AFE =135°，由（2）得，∠AFD =∠AEB =135°，DF =BE ，所以，B 、E 、F 在一条直线上，作AM ⊥EF ，垂足为M ， ∵5,32AB AE ==，∴EF =6，AM =ME =MF =3，224BM AB AM =-=，BE =DF =1,FG =2，22210GE FG EF =+=；如图4，同图3，BE =DF =7，FG =14，EF =6，22258GE FG EF =+=，综上，GE 的长为258或210或16或4．【点睛】本题考查了旋转的性质、全等三角形的判定与性质、勾股定理和等腰直角三角形的性质，解题关键是恰当的连接辅助线，构造全等三角形；会分类讨论，结合题目前后联系，解决问题．11．回答下列问题：（1）（发现）如图1，点A 为线段BC 外一动点，且4BC =，2AB =．填空：线段AC 的最大值为．图1（2）（应用）点A 为线段BC 外一动点，且3BC =，2AB =，如图2所示，分别以AB ，AC 为边，作等腰直角ABD △和等腰直角ACE ，连接CD ，BE ．图2①证明：BE DC =．②求线段BE 的最大值．（3）（拓展）如图3，在平面直角坐标系中，直线l ；4y x =+与坐标轴交于点A 、B 两点，点C 为线段AB 外一动点，且2CB =，以AC 为边作等边ACD △，连接BD ，求线段BD 长的最大值并直接写出此时点C 的横坐标．图3答案：A解析：（1）6（2）①证明见解析． ②322+（3）42226-26+ 【分析】(1)根据点A 位于CB 的延长线上时，线段AC 的长取得最大值，即可得到结论；(2) ①由“SAS” 可证△DAC ≌△BAE ，可得BE=DC ；②由于线段长BE 的最大值=线段DC 的最大值，根据(1)中的结论即可得到结果，(3)以BC 为边作等边三角形BCE ，可以证明△ACE ≌△DCB(SAS) ，从而得到BD=AE ，BE=BC ，由AE≤AB+BE ，当且仅当A 、B 、E 三点共线时，AE 取得最大值，即BD 取得最大值，当BD 取得最大值时，①当C 在直线AB 的上方时，过C 作CH ⊥y 轴于H ，作BC 的垂直平分线交BH 于N ，求出CH 的长度，即可求出点C 的横坐标，②当C 在直线AB 的下方时，按同①的方法也可以求出点C 的横坐标．【详解】（1）当A 在选段BC 的延长线上时， max 6AC AB BC =+=．（2）①∵等腰直角AEC 与等腰直角三角形ABD ，∴AD AB =，AE AC =，90DAB EAC ∠=∠=︒，∴DAB BAC EAC BAC ∠+∠=∠+∠，∴DAC EAB ∠=∠，在DAC △和BAE 中，DA BA DAC BAE AB AE =⎧⎪∠=∠⎨⎪=⎩，∴()SAS DAC BAE ≌△△， ∴BE CD =．②由①可知，BE DC =，∵线段BE 的最大值即线段DC 的最大值．在等腰直角ABD △中，222BD AB ==，∵CD BC BD ≤+，∴当点D 在CB 的延长线上时， CD 取得最大值为322+．∴线段BE 的最大值为322+．（3）如图，以BC 为边作等边三角形BCE ，则BC CE =，60BCE ∠=︒．∵60ACD ∠=︒，∴ACD ECD BCE ECD ∠-∠=∠-∠，∴ACE DCB ∠=∠．在ACE 与DCB 中，AC DC ACE DCB CE CB =⎧⎪∠=∠⎨⎪=⎩，∴()SAS ACE DCB ≌△△， ∴BD AE =．对于一次函数4y x =+，令0x =，则4y =，∴()0,4B ，令0y =，则4x =-，∴()4,0A -．∴224442AB =+=又∵2BE BC ==，∴AE AB BE ≤+，∴当且仅当A 、B 、E 三点共线时，AE 取得最大值，即BD 取得最大值为422+；当BD 取得最大值时，①当C 在直线AB 的上方时过C 作CH y ⊥轴于H ，∵45ABO HBE ∠=∠=︒，60CBE ∠=︒，∴15CBH CBE HBE ∠=∠-∠=︒，作BC 的垂直平分线交BH 于N ，∴CN BN =，15NCB NBC ∠=∠=︒，∴30CNB ∠=︒，在Rt CHN △中，设CH x =．则3HN x =，2CN x =，∴2BN x =，∴)32BH HN BN x =+=，在Rt BHC △中，22222HC BH BC +==，∴)222322x x ⎡⎤+=⎣⎦，整理得(227434x x ++=， 223x =，)12312x =，)22312x =-（舍）， ∴62CH -=2②当C 在直线AB 的下方时，过C 作CL ⊥y 轴于L ，∵∠ABO=45°，∠CBE=60°，∴∠CBL=180°-∠CBE−∠ABO=75°，∴∠BCL=15°，作BC 的垂直平分线交BL 于M ，∴CM=BM ，∠MCB=∠MBC=15°，∴∠LMB=30°，在Rt △CLB 中，设BL=y ．则3，BM=2y ，∴CM=2y ，∴3+2)y ，在Rt △BLC 中，BL 2+CL 2=BC 2=22，∴)222322y y ⎡⎤+=⎣⎦，整理得(227434y y ++=， 223y = )1231y =，)2231y =（舍去）， 622BL =∴CL=)32BL 26+2综合以上可得点C 的横坐标为：262-或 262+ 【点睛】本题是三角形综合题，考查了全等三角形的判.定和性质，等腰直角三角形的性质，最大值问题，旋转的性质正确的作出辅助线构造全等三角形是解题的关键.12．已知等腰三角形底边中点，可以考虑与顶点连接用“三线合一”．请利用上面信息解决以下问题：已知Rt ABC 中，AC BC =，90C ∠=︒，D 为AB 边的中点，90EDF ∠=︒，EDF ∠绕D 点旋转，它的两边分别交AC 、CB （或它们的延长线）于E 、F ．（1）当EDF ∠绕D 点旋转到DE AC ⊥于E 时（如图①），求证：12DEF CEF ABC S S S +=△△△；（2）当EDF ∠绕D 点旋转到DE 和AC 不垂直时，在图②和图③这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，DEF S △、CEF S △、ABCS又有怎样的数量关系？请写出你的猜想，不需要证明．答案：D解析：（1）见解析；（2）图2成立，图3不成立：12DEF CEF ABC S S S -=△△△ 【分析】（1）根据等腰直角三角形和正方形的性质得到AED 、DFB △、EDF 、ECF △为全等的等腰直角三角形，据此即可证明；（2）对于图2：过点D 作DM AC ⊥，DN BC ⊥，根据中位线的性质和等量代换证得MD ND =和MDE NDF ∠=∠，结合90DME DNF ∠=∠=︒，证得DME DNF ∆≅∆，根据全等三角形的性质即可求证；对于图3：根据ASA 证明DME DNF ∆≅∆，根据全等三角形的性质即可求证．【详解】（1）证明：连接CD∵D 为AB 边的中点，AC BC =∴AD=CD=BD∴45DAC DCA DCB DBC ∠=∠=∠=∠=︒又∵DE AC ⊥，90EDF ∠=︒，90C ∠=︒，∴四边形ECFD 为矩形∴∠CFD=90°又∵∠DCF=45°∴CF=DF∴四边形ECFD 是正方形∴DE=DF∴DEF CEF DEC DFC S S S S +=+△△△△又∵12DCF DBF ABC S S S +=△△△，且DCF DBF S S =△△ ∴12DEF CEF ABC S S S +=△△△ （2）图2成立，图3不成立对于图2：过点D 作DM AC ⊥，DN BC ⊥，如图2，则90DME DNF MDN ∠=∠=∠=︒又∵90C ∠=︒∴DM BC ，DN AC∵D 为AB 边的中点 ∴根据中位线定理得到：12DN AC =，12MD BC = ∵AC=BC∴MD=ND∵90EDF ∠=︒∴90MDE EDN ∠+∠=︒，90NDF EDN ∠+∠=︒∴MDE NDF ∠=∠在DME ∆与DNF ∆中DME DNF MD NDMDE NDF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴DME DNF ∆≅∆∴DME DNF S S ∆∆=∴DEF CEF DMCN DECF S S S S ∆∆==+四边形四边形 ∴12DMCN ABC S S =△ ∴12DEF CEF ABC S S S +=△△△ 对于图3：连接DC ，在DEC ∆与DBF ∆中135DCE DBF DC DBCDE BDF ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩∴DEC DBF ∆≅∆∴12DEF CFE DBC CFE ABC DBFEC S S S S S S ∆∆∆∆∆==+=+五边形 ∴12DEF CEF ABC S S S ∆∆∆-=．【点睛】本题考查了全等三角形的判定和性质，中位线的性质，等腰直角三角形的性质，题目较为综合，利用作出的辅助线将不规则的三角形转化为直角三角形进行解决．13．矩形ABCD 中，6,8AB BC ==，点,M N 分别在边,BC AD 上，且3,2BM DN ==，连接MN 并延长，交CD 的延长线于点E ，点Q 为射线MN 上一动点，过点Q 作AQ 的垂线，交CD 于点P ．（1）特例发现，如图，若点P 恰好与点D 重合，填空：①DE =________；②QA 与QP 的等量关系为_________．（2）拓展探究如图，若点Q 在MN 的延长线上，QA 与QP 能否相等？若能，求出DP 的长；若不能，请说明理由．（3）思维延伸如图，点G 是线段CD 上异于点D 一点，连接AG ，过点G 作直线GI AG ⊥，交直线MN 于点I ，是否存在点G ，使,AG GI 相等？若存在，请直接写出DG 的长；若不存在，请说明理由．答案：E解析：（1）①4； ②QA QP =；（2）QA 与QP 能够相等，理由详见解析；（3）（3）,AG GI 能够相等，43DG =【分析】（1）①根据END EMC ，利用对应边成比例列式求出ED 长；②过点Q 作//HG BC ，交AB 于点H ，交DC 于点G ，设QG x =，利用AHQ QGD ，对应边成比例列式求出x ，得到这两个三角形其实是全等的，所以QA QP =；（2）过点Q 作QF AB ⊥，交BA 的延长线于点F ，延长FQ 交CE 于点G ，构造“k”字型全等三角形，设AF x =，再利用相似三角形的性质列式求解；（3）过点G 作GK AB ⊥于点K ，过点I 作IS KG ⊥，交KG 的延长线于点S ，延长AD 交IS 于点T ，同（2）构造“k”字型全等三角形，DG y =，再利用相似三角形的性质列式求解．【详解】（1）①∵//ND MC ，∴END EMC ，∴ED ND EC MC=，835MC BC BM =-=-=，6DC =， 265ED ED =+，解得4ED =，故答案是：4；②如图，过点Q 作//HG BC ，交AB 于点H ，交DC 于点G ，可得HG AB ⊥，HG DC ⊥，∴90AHQ QGD ∠=∠=︒，∵AQ QD ⊥，∴90AQH DQG ∠+∠=︒，∵90QAH AQH ∠+∠=︒，∴QAH DQG ∠=∠，∴AHQ QGD ，∴AH HQ QG GD=，设QG x =，8HQ x =-， ∵//QG MC ，∴EQG EMC ， ∴QG EG MC EC =，4510x DG +=，得24DG x =-， ∴24AH x =-，根据AH HQ QG GD =，得24824x x x x --=-，解得4x =， ∴4AH HQ QG GD ====，∴AHQ QGD ≅，∴AQ QD QP ==，故答案是：QA QP =；（2）QA 与QP 能够相等，163PD =，如图，过点Q 作QF AB ⊥，交BA 的延长线于点F ，延长FQ 交CE 于点G ， 90,90,AQF PQG GPQ PQG AQF GPQ ∠+∠=︒∠+∠=︒∴∠=∠，又90,,,,AFQ PGQ AQ PQ FAQ GDP AF QG FQ PG ∠=∠=︒=∆≅∆∴==，设AF x =，则,,4QG x DG x EG x ===-，42,2EG ED x QG ND x -==∴=，解得43x =，经检验，43x =是该分式方程的根，42020204168,,333333FQ PG PD ∴=-=∴==-=；（3）,AG GI 能够相等，43DG =，如图，过点G 作GK AB ⊥于点K ，过点I 作IS KG ⊥，交KG 的延长线于点S ，延长AD 交IS 于点T ，根据“k ”字型全等得,,8AKG GSI AK GS IS KG ∆≅∆∴===，设DG y =，则,8,2AK TS GS DT y IT y NT y ====∴=-=+，84tan ,22IT ED y INT NT ND y -∠==∴=+，解得43y =，故DG 的长为43．【点睛】本题考查“k ”字型全等三角形，相似三角形的性质和判定，解题的关键是作辅助线构造“k ”字型全等，再利用相似三角形对应边成比例列式求解．14．如图，在四边形ABCD 中，AB AC =，AD 是对角线，60BAC ∠=︒，4B C ADB BAC ∠+∠+∠=∠，（1）求ADC ∠的度数；（2）若AD BD CD =+，求证：AD 平分BDC ∠；（3）在（2）的条件下，E 、F 分别在AC 、AB 上，连接BE 、CF ，交于点P ，使得BPC BDC ∠=∠，若7BD EF ==，15AD =，求EFP ∆的面积答案：A解析：（1）=60∠︒ADC ；（2）证明见详解；（3）4003129．【分析】（1）先由四边形内角和得到++300B C BDC ∠∠∠=︒，再由4B C ADB BAC ∠+∠+∠=∠可得答案；（2）把ABD △绕点A 逆时针旋转60︒得到ACE △，由（1）及题意易得D 、C 、E 三点共线，从而得到ADE 是等边三角形，由等边三角形的性质及旋转的性质易得60ADB E ∠=∠=︒，故得证；（3）过点B 、点F 分别作BG ⊥CD ，FH ⊥AC ，分别交CD 的延长线于点G 、AC 于点H ，连接BC ，由（2）及题意易得DC=8，由BPC BDC ∠=∠易得EBC FCA ∠=∠，进而得到AFC CEB △≌△，设AF=CE=x ，根据勾股定理得到AF 、CE 、BC 的长，最后根据BFE BPC 、的面积比等于FP 与PC 的比，进而求解即可．【详解】（1）解：=60BAC ∠︒，∴++36060300B C BDC ∠∠∠=︒-︒=︒，又BDC ADB ADC ∠=∠+∠，4B C ADB BAC ∠+∠+∠=∠，∴30024060ADC ∠=︒-︒=︒；（2）证明：把ABD △绕点A 逆时针旋转60︒得到ACE △，由（1）得：∴AD=AE ，BD=CE ，=ADC=60DAE ∠∠︒AD BD CD =+，DE=DC+CE ，∴D 、C 、E 三点共线，。

人教版八年级数学上册期末专题复习：几何压轴题强化训练试题(含答案)

人教版八年级数学上册期末专题复习：几何压轴题强化训练试题1、如图，AB＞AC，∠BAC的平分线与BC边的中垂线GD相交于点D，过点D作DE⊥AB于点E，DF⊥AC于点F，求证：BE=CF．2、如图，△ABC中，∠ACB=90°，AC=BC，将△ABC绕点C逆时针旋转角α．（0°＜α＜90°）得到△A1B1C1，连接BB1．设CB1交AB于D，A1B1分别交AB、AC于E、F．（1）在图中不再添加其它任何线段的情况下，请你找出一对全等的三角形，并加以说明（△ABC与△A1B1C1全等除外）；（2）当△BB1D是等腰三角形时，求α．3、如图，在△ABC中，∠BAC=120°，AD，BE分别为△ABC的角平分线，连结DE．（1）求证：点E到DA，DC的距离相等；（2）求∠DEB的度数．4、在△ABC中，∠ACB=90°，AC=BC，直线，MN经过点C，且AD⊥MN于点D，BE⊥MN于点E．（1）当直线MN绕点C旋转到如图1的位置时，求证：DE=AD+BE；（2）当直线MN绕点C旋转到如图2的位置时，求证：DE=AD﹣BE；（3）当直线MN绕点C旋转到如图3的位置时，线段DE、AD、BE之间又有什么样的数量关系？请你直接写出这个数量关系，不要证明．5、概念学习：规定：如果一个三角形的三个角分别等于另一个三角形的三个角，那么称这两个三角形互为“等角三角形”．从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原来三角形是“等角三角形”，我们把这条线段叫做这个三角形的“等角分割线”．理解概念（1）如图1，在Rt△ABC中，∠ACB＝90°，CD⊥AB，请写出图中两对“等角三角形”．概念应用（2）如图2，在△ABC中，CD为角平分线，∠A＝40°，∠B＝60°．求证：CD为△ABC的等角分割线．（3）在△ABC中，∠A＝42°，CD是△ABC的等角分割线，直接写出∠ACB的度数．6、如图,∠ABC=∠BAD=90°，点E，F分别是AC，BC的中点。

北师大版八年级下册数学期末几何压轴题专练(含答案)

八下数学期末复习专题几何压轴题专练1．如图1，在△ABC中，AB＝AC，点D是直线BC上一点（不与点BC重合），以AD 为一边在AD的右侧作△ADE，使AD＝AE，△DAE＝△BAC，连接CE.设△BAC＝α，△DCE＝β.（1）求证：△DAB△△EAC.（2）当点D在线段BC上运动时，①α＝50°，则β＝°.②猜想α与β之间的数量关系，并对你的结论进行证明.（3）如图2，当点D在线段BC的反向延长线上运动时，猜想α与β之间的数量关系，并对你的结论给出证明.2．如图，在矩形ABCD中，E是BC上一动点，将△ABE沿AE折叠后得到△AFE，点F在矩形ABCD内部，延长AF交CD于点G，AB＝3，AD＝4.（1）如图1，当△DAG＝30°时，求BE的长；（2）如图2，当点E是BC的中点时，求线段GC的长；（3）如图3，点E在运动过程中，当△CFE的周长最小时，直接写出BE的长. 3．如图（1）如图1，在□ABCD中，AE平分△BAD交CD边于点E，已知AB=5cm，AD=3cm，则EC等于cm。

（2）如图2，在□ABCD中，若AE，BE分别是△DAB，△CBA的平分线，点E在DC边上，且AB=4，则▱ABCD的周长为。

（3）如图3，已知四边形ABCD是平行四边形，AD=BC，若AF，BE分别是△DAB，△CBA的平分线。

求证：DF=EC（4）在（3）的条件下，如果AD=3，AB=5，则EF的长为。

4．已知,在▱ABCD中, AB⊥BD, AB＝BD, E为射线BC上一点,连接AE交BD 于点F．（1）如图1,若点E与点C重合,且AF=√5,求AB的长;（2）如图2,当点E在BC边上时,过点D作DG⊥AE于G,延长DG交BC于H,连接FH．求证: AF=DH+FH;（3）如图3,当点E在射线BC上运动时,过点D作DG⊥AE于G, M为AG 的中点,点N在BC边上且BN=1,已知AB=5√2,请直接写出MN的最小值．5．如图，在△ABC中，△ACB＝90°，AC＝a，BC＝b，a＞b，点P是边AB上一点，连接CP，将△ACP沿CP翻折得到△QCP．（1）若PQ△AB，由折叠性质可得△BPC＝°；（2）若a＝8，b＝6，且PQ△AB，求C到AB的距离及BP的长；（3）连接BQ，若四边形BCPQ是平行四边形，直接写出a与b之间的关系式．6．如图，在平行四边形ABCD中，AB△AC，对角线AC，BD相交于点O，将直线AC 绕点O顺时针旋转一个角度α(0°<α≤90°)，分别交线段BC，AD于点E，F，连接BF.（1）如图1，在旋转的过程中，写出线段AF与EC的数量关系，并证明；（2）如图2，当旋转至90°时，判断四边形ABEF的形状，并说明理由；（3）若AB＝1，BC＝√5，求当α等于多少度时，BF＝DF？7．在Rt△ABC中，∠ABC=90°，BA=BC=4，将△ABC绕点C顺时针旋转得到△A1B1C，其中点A，B的对应点分别为点A1，B1.连接AA1，BB1交于点D.（1）如图1，当点A1落在BC的延长线上时，求线段AB1的长；（2）如图2，当△ABC旋转到任意位置时，求证：点D为线段AA1中点；（3）若△A1B1C从图1的位置绕点C继续顺时针旋转α（0°<α≤90°），当直线AB与直线A1B1相交构成的4个角中最小角为30°时，求α的值.8．如图①，在平行四边形ABCD中，AD＝BD＝2，BD△AD，点E为对角线AC上一动点，连接DE，将DE绕点D逆时针旋转90°得到DF，连接BF．（1）求证BF＝AE；（2）如图②，若F点恰好落在AC，求OF的长；（3）如图③，当点F落在△OBC的外部，构成四边形DEMF时，求四边形DEMF 的面积.9．如图（1）如图①，在Rt△ABC中，AB＝AC，D为BC边上一点(不与点B，C重合)，将线段AD绕点A逆时针旋转90°得到AE，连接EC，证明线段BC，DC，EC之间满足的等量关系;（2）如图②，在Rt△ABC与Rt△ADE中，AB＝AC，AD＝AE，将△ADE绕点A旋转，使点D落在BC边上，探索线段AD，BD，CD之间满足的等量关系，并证明结论;（3）如图③，在四边形ABCD中，∠ABC＝∠ACB＝∠ADC＝45°若BD＝12，CD＝4，求AD的长.10．把△ABC绕着点A逆时针旋转α，得到△ADE.（1）如图1，当点B恰好在ED的延长线上时，若α=60°，求△ABC的度数；（2）如图2，当点C恰好在ED的延长线上时，求证：CA平分△BCE；（3）如图3，连接CD，如果DE=DC，连接EC与AB的延长线交于点F，直接写出△F的度数（用含α的式子表示）.11．如图1，在平面直角坐标系中.直线y=−12x+3与x轴、y轴相交于A、B两点，动点C在线段OA上，将线段CB绕着点C顺时针旋转90∘得到CD，此时点D 恰好落在直线AB上时，过点D作DE⊥x轴于点E．（1）求证：△BOC△ △CED；（2）如图2，将△BCD沿x轴正方向平移得△B′C′D′，当直线B′C′经过点D时，求点D的坐标及△BCD平移的距离；（3）若点P在y轴上，点Q在直线AB上.是否存在以C、D、P、Q为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的Q点坐；若不存在，请说明理由．12．在等边三角形ABC中，AD⊥BC于D，AB=2．（1）如图①，点E为AD的中点，则点E到AB的距离为；（2）如图②，点M为AD上一动点，求12AM+MC的最小值．（3）（问题解决）如图③，A，B两地相距600km，AC是笔直地沿东西方向向两边延伸的一条铁路，点B到AC的距离为360km．今计划在铁路线AC上修一个中转站M，再在BM间修一条笔直的公路．如果同样的物资在每千米公路上的运费是铁路上的两倍，那么为使通过铁路由A到M再通过公路由M到B的总运费达到最小值，中转站M应修在使AM=（千米）处．13．已知Rt△ABC中，△BAC=90°，AB=AC，点E为△ABC内一点，连接AE，CE，CE△AE，过点B作BD△AE，交AE的延长线于D．（1）如图1，求证BD=AE；（2）如图2，点H为BC中点，分别连接EH，DH，求△EDH的度数；（3）如图3，在（2）的条件下，点M为CH上的一点，连接EM，点F为EM的中点，连接FH，过点D作DG△FH，交FH的延长线于点G，若GH：FH=6：5，△FHM 的面积为30，△EHB=△BHG，求线段EH的长．14．阅读下面材料，并解决问题：（1）如图①等边△ABC内有一点P，若点P到顶点A、B、C的距离分别为3，4，5，求△APB的度数．为了解决本题，我们可以将△ABP绕顶点A旋转到△ACP′处，此时△ACP′△△ABP，这样就可以利用旋转变换，将三条线段PA、PB、PC转化到一个三角形中，从而求出△APB ＝；（2）基本运用请你利用第（1）题的解答思想方法，解答下面问题：已知如图②，△ABC中，△CAB＝90°，AB＝AC，E、F为BC上的点且△EAF＝45°，求证：EF2＝BE2+FC2；（3）能力提升如图③，在Rt△ABC中，△C＝90°，AC＝1，△ABC＝30°，点O为Rt△ABC内一点，连接AO，BO，CO，且△AOC＝△COB＝△BOA＝120°，求OA+OB+OC的值．15．在△ABC和△ADE中，∠BAC=∠DAE=90°，且AB=AC，AD=AE.（1）如图1，如果点D在BC上，且BD=4，CD=3，求DE的长；（2）如图2，AD与BC相交于点N，点D在BC下方，连接BD，且AD⊥BD，连接CE并延长与BA的延长线交于点F，点M是CA延长线上一点，且CM=AF，求证：CF=AN+MN；（3）如图3，若AD=AB，△ADE绕着点A旋转，取DE中点M，连接BM，取BM中点N，连接AN，点F为BC中点，连接DN，若DN恰好经过点F，请直接写出DF:DN:AN的值.16．如图1，△ABC是直角三角形，△ACB＝90°，点D在AC上，DE△AB于E，连接BD，点F是BD的中点，连接EF，CF.（1）EF和CF的数量关系为；（2）如图2，若△ADE绕着点A旋转，当点D落在AB上时，小明通过作△ABC和△ADE斜边上的中线CM和EN，再利用全等三角形的判定，得到了EF和CF的数量关系，请写出此时EF和CF的数量关系；（3）若△AED继续绕着点A旋转到图3的位置时，EF和CF的数量关系是什么？写出你的猜想，并给予证明.17．我们定义：如图1、图2、图3，在ΔABC中，把AB绕点A顺时针旋转α(0∘<α<180∘)得到AB′，把AC绕点A逆时针旋转β得到AC′，连接B′C′，当α+β=180∘时，我们称ΔAB′C′是ΔABC的“旋补三角形”，ΔAB′C′边B′C′上的中线AD叫做ΔABC的“旋补中线”，点A叫做“旋补中心”.图1、图2、图3中的ΔAB′C′均是ΔABC的“旋补三角形”.（1）①如图2，当ΔABC为等边三角形时，“旋补中线” AD与BC的数量关系为：AD=BC；②如图3，当∠BAC=90∘，BC=8时，则“旋补中线” AD长为.（2）在图1中，当ΔABC为任意三角形时，猜想“旋补中线” AD与BC的数量关系，并给予证明.18．在平行四边形ABCD中，∠BAD的角平分线交直线BC于点E，交直线DC于点F．（1）在（图25-1）中证明CE=CF；（2）若∠ABC=90°，G是EF的中点（如图25-2），求∠BDG的度数；（3）若∠ABC=120°，FG//CE，FG=CE，分别连接BD、DG（如图25--3），直接写出∠BDG的度数．19．在△ABCD中，对角线AC、BD交于点O，将过点A的直线l绕点A旋转，交射线CD于点E，BF△l于点F，DG△l于点G，连接OF，OG．（1）如图①当点E与点C重合时，请直接写出线段OF，OG的数量关系；（2）如图②，当点E在线段CD上时，OF与OG有什么数量关系？请证明你的结论；（3）如图③，当点E在线段CD的延长线上时，上述的结论是否仍成立？请说明理由．20．如图，在平行四边形ABCD中，AB△AC，对角线AC，BD相交于点O，将直线AC绕点O顺时针旋转一个角度α（0°＜α≤90°），分别交线段BC，AD于点E，F，连接BF.（1）如图1，在旋转的过程中，求证：OE＝OF；（2）如图2，当旋转至90°时，判断四边形ABEF的形状，并证明你的结论；（3）若AB＝1，BC＝√5，且BF＝DF，求旋转角度α的大小.21．如图1，在Rt△ABC中，△A＝90°，AB＝AC，点D，E分别在边AB，AC上，AD ＝AE，连接DC，点M，P，N分别为DE，DC，BC的中点.（1）观察猜想：图1中，线段PM与PN的数量关系是，位置关系是；（2）探究证明：把△ADE绕点A逆时针方向旋转到图2的位置，连接MN，BD，CE，判断△PMN 的形状，并说明理由；（3）拓展延伸：把△ADE绕点A在平面内自由旋转，若AD＝4，AB＝10，请直接写出△PMN面积的最大值.22．如图，已知函数y=﹣12x+b的图象与x轴、y轴分别交于点A、B，与函数y=x的图象交于点M，点M的横坐标为2．（1）求点A的坐标；（2）在x轴上有一动点P（a，0）（其中a＞2），过点P作x轴的垂线，分别交函数y=﹣12x+b和y=x的图象于点C、D．①若OB=2CD，求a的值；②是否存在这样的点P，使以B、O、C、D为顶点的四边形是平行四边形？若存在，直接写出点P的坐标；若不存在，请说明理由．答案与解析1．【答案】（1）证明：∵△DAE＝△BAC，∴△CAD﹣△DAE＝△CAD﹣△BAC，∴△CAE＝△BAD，在△DAB和△EAC中，{AB=AC∠BAD=∠CAF AD=AE∴△DAB△△EAC（SAS）（2）解：①130；②α+β＝180°，理由：由（1）知，△DAB△△EAC，∴△ABC＝△ACE，在△ABC中，AB＝AC，△BAC＝α，∴△ABC＝△ACB＝12（180°﹣△BAC）＝12（180°﹣α）＝90°﹣12α，∴β＝△ACB+△ACE＝△ACB+△ABC＝90°﹣12α+90°﹣12α＝180°﹣α，∴α+β＝180°（3）解：β＝α；理由：∵△DAE＝△BAC，∴△DAE﹣△BAE＝△BAC﹣△BAE，∴△CAE＝△BAD，在△DAB和△EAC中，{AB=AC∠BAD=∠CAB AD=AE∴△DAB△△EAC（SAS），∴△ABD＝△ACE，在△ABC中，AB＝AC，△BAC＝α，∴△ABC＝△ACB＝12（180°﹣△BAC）＝12（180°﹣α）＝90°﹣12α，∴△ACE＝△ABD＝180°﹣△ABC＝180°﹣（90°﹣12α）＝90°+12α，∴β＝△ACE﹣△ACB＝90°+ 12α﹣（90°﹣12α）＝α.2．【答案】（1）解：∵四边形ABCD是矩形，∴△BAD＝90°，∵△DAG ＝30°，∴△BAG ＝60°由折叠知，△BAE ＝12△BAG ＝30°，在Rt△BAE 中，△BAE ＝30°，AB ＝3，∴BE ＝√3（2）解：如图4，连接GE ，∵E 是BC 的中点，∴BE ＝EC ，∵△ABE 沿AE 折叠后得到△AFE ，∴BE ＝EF ，∴EF ＝EC ，∵在矩形ABCD 中，∴△C ＝90°，∴△EFG ＝90°，∵在Rt△GFE 和Rt△GCE 中，{EG =EG EF =EC∴Rt△GFE△Rt△GCE （HL ），∴GF ＝GC ；设GC ＝x ，则AG ＝3+x ，DG ＝3﹣x ，在Rt△ADG 中，42+（3﹣x ）2＝（3+x ）2，解得x ＝43. （3）解：BE ＝323．【答案】（1）2（2）12（3）证明：∵在▱ABCD 中，CD△AB ，∴△DFA=△FAB.又∵AF是△DAB的平分线∴△DAF=△FAB，∴△DAF=△DFA，∴AD=DF，同理可得EC=BC.∵AD=BC，∴DF=EC（4）14．【答案】（1）解：如图1中，∵AB⊥BD,∴∠ABD=90°,∵AB=BD,∠BAD=45°,∴∠BDA=∠BAD=45°,∵四边形ABCD是平行四边形,∴E、C重合时BF=12BD=12AB,在RtΔABF中,∵AF2=AB2+BF2,∴(√5)2=(2BF)2+BF2,∴BF=1, AB=2,∴AB=2;（2）证明：如图2中，在AF上截取AK=HD,连接BK,∵AB⊥BD, DG⊥AE,∴∠ABF=∠FGD=90°,∵∠AFD=∠ABF+∠2=∠FGD+∠3, ∠ABF=∠FGD=90°,∴∠2=∠3,在ABK和ΔDBH中, {AB=BD ∠2=∠3 AK=HD,∴ΔABK≅ΔDBH,∴BK=BH, ∠6=∠1,∵四边形ABCD是平行四边形,∴AD//BC,∴∠4=∠1,由（1）知∠4=45°,∴∠l=∠6=45°,∴∠5=∠ABD−∠6=45°,∠5=∠1,在ΔFBK和ΔFBH中, {BF=BF ∠5=∠1 BK=BH,∴ΔFBK≅ΔFBH,∴KF=FH,∵AF=AK+KF，∴AF=DH+FH；（3）解：MN的最小值为√149−52．5．【答案】（1）45（2）解：如图，作CH△AB于H由翻折的性质可知：△APC=△QPC∵CH△AB，△BPC=45°∴CH=PH在Rt△ABC中，AB=√AC2+BC2=√82+62=10∵12⋅AB ⋅CH =12⋅AC ⋅BC ，即 5CH =24 ∴CH= 245；（3）解：如图:连接BQ由翻折的性质可得：PA=PQ ，△QPC=△APC∵四边形BCPQ 是平行四边形∴PQ=BC=PA=b ，PQ//BC ，∴△QPC+△PCB=180°∵△BPC+△APC=180°∴△PCB=△BPC∴PB=BC=b∴AP=PB=b ，AB=2b ，在Rt△ABC 中，则有（2b ）2=a 2+b 2∴a 2=3b 2∵a>0.b>0，∴a= √3b ．6．【答案】（1）解：AF=CE.理由如下：∵四边形ABCD 为平行四边形，∴AD // CB ，OA=OC.∴△FAO=△ECO.在 △AOF 和 △COE 中，∵{∠AOF =∠COE,OA =OC,∠FAO =∠ECO,∴△AOF ≌△COE(ASA) .∴AF=CE.（2）解：当旋转至90°时，四边形ABEF为平行四边形.理由如下：∵△AOF= 90°，△BAC= 90°，∴AB //EF.又∵四边形ABCD是平行四边形，∴AD//BC，即AF//BE.∴四边形ABEF为平行四边形（3）解：当α等于45度时，BF＝DF.理由如下：∵AB=1，BC= √5，AB△AC，∴AC= √BC2−AB2=√(√5)2−12=2.∵四边形ABCD为平行四边形，∴OA=12AC=12×2=1，BO=DO.∴OA=AB=1.点O在线段BD的垂直平分线上.∴△ABO为等腰直角三角形.∴△AOB= 45°.当F在线段BD的垂直平分线上时，BF=DF，∴FO垂直平分BD.∴△BOF=90°.∴∠AOF=∠BOF−∠AOB=90°−45°=45°，即α=45°.∴当α等于45度时，BF＝DF.7．【答案】（1）解：∵Rt△ABC中，∠ABC=90°，BA=BC=4，∴∠ACB=45°，AC=√AB2+BC2=√42+42=4√2.∵△ABC绕点C顺时针旋转得到△A1B1C，∴∠A1CB1=45°，B1C=BC=4.∴∠ACB1=180°−∠ACB−∠A1CB1=90°.∴AB1=√AC2+B1C2=√(4√2)2+42=4√3（2）证明：过点A1作A1E//AB交BB1的延长线于点E，∴∠ABD=∠DEA1.∵B1C=BC，∴∠CBB1=∠CB1B.∵∠ABC=∠A1B1C=90°，∴∠ABD+∠CBB1=∠CB1B+∠A1B1E=90°.∴∠A1B1E=∠ABD=∠DEA1.∴A1B1=A1E.∵AB=A1B1，∴AB=A1E.∵∠ADB=∠A1DE，∴△ADB≅△A1DE.∴AD=∠A1D.∴点D为线段AA1中点（3）解：如图3，当直线AB与直线A1B1相交于点A上方，延长BC交A1B1于点E，∵∠ABC=90°，∠P=30°，∴∠PEB=60°.∵∠CA1B1=45°，∴∠A1CE=∠PEB−∠CA1E=15°.如图4，当直线AB与直线A1B1相交于点A下方，延长BC交A1B1的延长线于点E，∵∠ABC=90°，∠P=30°，∴∠PEB=60°.∵∠A1B1C=90°，∴∠B1CE=∠A1B1C−∠PEB=30°.∴∠A1CE=∠B1CE+∠A1CB=75°.∴当直线AB与直线A1B1相交构成的4个角中最小角为30°时，α的值为15°或75°.8．【答案】（1）证明：根据旋转的性质可得，DE=DF，△EDF=90°∵BD△AD∴△ADB=90°∴△ADE=△BDF∵AD=BD∴△ADE△△BDF∴BF=AE（2）过点D 作DG△AC 于点G ，∵DE=DF ，△EDF=90°∴△DEF=△DFE=45°，△DEA=135°根据（1）可得，△ADE△△BDF∴△BFD=△DEA=135°，AE=BF∴△BFO=90°∵四边形ABCD 为平行四边形∴OB=OD∴△DGO△△BFO∴DG=BF ，OF=OG∴DG=EG=AE=BF设DG=a （a ＞0），则AG=2a在直角三角形ADG 中，∵AG 2+DG 2=AD 2∴（2a ）2+a 2=22解得a=2√55 ∴OF=OG=12×2√55=√55（3）过点D 作DN△AC 于点N ，将△DEN 绕点D 逆时针旋转90°得到△DFH ，∴DH=DN ，△DNE=△DH=90°，△DEN=△DFG∵△DEF=△FME=90°∴△DEM+△DFM=180°∴△DFH+△DFM=180°∴点H ，点F ，点M 三点共线∵△DHF=△DNM=△FMN=90°∴四边形DNMG 为矩形∵DN=DH∴四边形DNMH 为正方形∴S 四边形DEMF=S 四边形DNMH=（2√55）2=459．【答案】（1）解：∵线段AD绕点A逆时针旋转90°得到AE∵Rt△ABC中AB=AC∴∠BAD=∠CAE∴△ABD≌△ACE(SAS)∴DB=EC∴BC=DC+DB=DC+EC（2）解：连结CE∵Rt△ABC与Rt△ADE中AB＝AC，AD＝AE∴∠B=∠ACE=45°，DE2=AD2+AE2=2AD2，∵由（1）同理可得△ABD≌△ACE∴DB=EC,∠ABD=∠ACE=45°∴∠ECD=90°∴Rt△ECD中，DE2=EC2+CD2=BD2+CD2∴2AD2=BD2+CD2（3）解：过点A作AE⊥AD，且AE=AD，连结DE,CE∵∠ABC=∠ACB=45°∴AB⊥AC,AB=AC∵AE⊥AD,AE=AD∴由（1）同理可得△ABD≌△ACE∴DB=EC=12∵∠ADC=45°∴∠EDC=∠ADC+∠ADE=90°∴DE=√CE2−CD2=√122−42=8√2∴等腰直角△ADE中AD=810．【答案】（1）解：∵α=60°，△ABC△△ADE，∴ AD=AB，△ABC=△ADE.∴ △ABD=△DAB=60°.∴ △ABC=△ADE=△DAB+△ABD=120°.（2）解：∵ AC=AE,△EAC= α，∴ △E=△ACE.∵ △ABC△△ADE，∴ △ACB=△E.∴ △ACB=△ACE.∴ CA平分△BCE.（3）解：△F= 90°−α.如下图：延长AD交EF于点G，则根据图形旋转的性质得，△GAF=α，∵△ABC△△ADE∴AC=AE，∴△AEC为等腰三角形，在△AED和△ACD中，{AE=AC DE=CD AD=AD，∴ △AED △ △ACD（SSS），∴ △DAE=△DAC，∴ AD平分△EAC，∵△AEC为等腰三角形，∴AG△EF，即△AGF=90°，∴∠EAF=3∠CAF=32α，∴∠F=180°−∠GAF−∠AGF=90°−α.11．【答案】（1）证明：∵∠BOC=∠BCD=∠CED=90∘，∴∠OCB+∠DCE=90∘，∠DCE+∠CDE=90∘，∴∠BCO=∠CDE，∵BC=CD，∴△BOC△ △CED．（2）解：∵△BOC△ △CED，∴OC=DE=m，BO=CE=3，∴D(m+3,m)，把D(m+3,m)代入y=−12x+3得到，m=−12(m+3)+3，∴2m=−m−3+6，∴m=1，∴D(4,1)，∵B(0,3)，C(1,0)，∴直线BC的解析式为y=−3x+3，设直线B′C′的解析式为y=−3x+b，把D(4,1)代入得到b=13，∴直线B′C′的解析式为y=−3x+13，∴C′(133,0)，∴CC′=103，∴△BCD平移的距离是103个单位．（3）点Q的坐标为(3,32)或(5,12)或(−3,92).12．【答案】（1）√34（2）解：如图，作CN⊥AB，垂足为N，此时12AM+MC最小，最小值等于CN，∵在正三角形ABC中，AB=BC=AC=2，∠ANC=90°，∴AN=1，由勾股定理得，CN=√3由（1）知，MN=12AM∴MN+CM=12AM+MC=CN=√3，即12AM+MC的最小值为√3（3）( 480−120√3 )13．【答案】（1）证明：∵CE△AE，BD△AE，∴△AEC＝△ADB＝90°，∵△BAC＝90°，∴△ACE+CAE＝△CAE+△BAD＝90°，∴△ACE＝△BAD，在△CAE与△ABD中{∠ACE=∠BAD ∠AEC=∠ADB AC=AB∴△CAE△△ABD（AAS），∴AE＝BD；（2）解：连接AH∵AB＝AC，BH＝CH，∴△BAH＝12∠BAC=12×90°=45°，△AHB＝90°，∴△ABH＝△BAH＝45°，∴AH＝BH，∵△EAH＝△BAH﹣△BAD＝45°﹣△BAD，△DBH＝180°﹣△ADB﹣△BAD﹣△ABH＝45°﹣△BAD，∴△EAH＝△DBH，在△AEH与△BDH中{AE=BD∠EAH=∠DBH AH=BH∴△AEH△△BDH（SAS），∴EH＝DH，△AHE＝△BHD，∴△AHE+△EHB＝△BHD+△EHB＝90°即△EHD＝90°，∴△EDH ＝△DEH ＝ 180°−90°2=45° ；（3）解：过点M 作MS△FH 于点S ，过点E 作ER△FH ，交HF 的延长线于点R ，过点E 作ET△BC ，交HR 的延长线于点T ．∵DG△FH ，ER△FH ，∴△DGH ＝△ERH ＝90°，∴△HDG+△DHG ＝90°∵△DHE ＝90°，∴△EHR+△DHG ＝90°，∴△HDG ＝△HER在△DHG 与△HER 中{∠HDG =∠HER ∠DGH =∠ERH DH =EH∴△DHG△△HER （AAS ），∴HG ＝ER ，∵ET△BC ，∴△ETF ＝△BHG ，△EHB ＝△HET ，△ETF ＝△FHM ，∵△EHB ＝△BHG ，∴△HET ＝△ETF ，∴HE ＝HT ，在△EFT 与△MFH 中{∠ETF =∠FHM ∠EFT =∠MFH EF =FM，∴△EFT△△MFH （AAS ），∴HF ＝FT ，∴HF·MS 2=FT·ER 2， ∴ER ＝MS ，∴HG＝ER＝MS，设GH＝6k，FH＝5k，则HG＝ER＝MS＝6k，HF·MS 2=5k·6k2=30，k＝√2，∴FH＝5 √2，∴HE＝HT＝2HF＝10 √2．14．【答案】（1）150°（2）解：如图2，把△ABE绕点A逆时针旋转90°得到△ACE′，由旋转的性质得，AE′＝AE，CE′＝BE，△CAE′＝△BAE，△ACE′＝△B，△EAE′＝90°，∵△EAF＝45°，∴△E′AF＝△EAE′-△EAF=45°，∴△EAF＝△E′AF，在△EAF和△E′AF中，{AE=AE′∠EAF=∠E′AFAF=AF∴△EAF△△E′AF（SAS），∴E′F＝EF，∵△CAB＝90°，AB＝AC，∴△B＝△ACB＝45°，∴△E′CF＝45°+45°＝90°，由勾股定理得，E′F2＝CE′2+FC2，即EF2＝BE2+FC2．（3）解：如图3，将△AOB绕点B顺时针旋转60°至△A′O′B处，连接OO′，∵在Rt△ABC中，△ACB＝90°，AC＝1，△ABC＝30°，∴AB＝2，∴BC＝√AB2−AC2=√3，∵△AOB绕点B顺时针方向旋转60°，△ABC=30°，∴△A′BC＝△ABC+60°＝30°+60°＝90°，∵△C＝90°，AC＝1，△ABC＝30°，∴AB＝2AC＝2，∵△AOB绕点B顺时针方向旋转60°，得到△A′O′B，∴A′B＝AB＝2，BO＝BO′，A′O′＝AO，∴△BOO′是等边三角形，∴BO＝OO′，△BOO′＝△BO′O＝60°，∵△AOC＝△COB＝△BOA＝120°，∴△COB+△BOO′＝△BO′A′+△BO′O＝120°+60°＝180°，∴C、O、A′、O′四点共线，在Rt△A′BC中，A′C＝√BC2+A′B2=√(√3)2+22=√7，∴OA+OB+OC＝A′O′+OO′+OC＝A′C＝√7．15．【答案】（1）解：连接EC，又AB=AC，AD=AE，∴BD=CE=4，∠ACE=∠ABC，∵∠ABC+∠ACB=90°∴∠ACE+∠ACB=90°∴△ACE是直角三角形，∴DE=√CD2+CE2=√32+42=5；（2）解：∵∠BAD+∠DAC=90°,∠EAC+∠DAC=90°∴∠BAD=∠EAC∵{AB=AC∠BAD=∠EACAD=AE∴△BAD≅△CAE(SAS)∴∠ABD=∠ACE∵AD⊥BD∴∠BAD=90°−∠ABD∵∠BAC=90°∴∠DAC=90°−∠BAD∴∠DAC=∠ABD∴∠ACF=∠DAC∴AD//CF过点A作AP//BC交FC于点P，∴四边形ANCP是平行四边形∴AN=CP，NC=AP∵AP//BC∴∠FAP=∠ABC=45°{PA=NC∠PAF=∠NCM AF=CN∴△PAF≅△NCM(SAS)∴MN=PF∴AN+MN=CP+FP=CF；（3）DF:DN:AN=1:2:216．【答案】（1）EF＝CF（2）EF＝CF（3）解：猜想，EF＝CF，理由：如图3中，取AB的中点M，AD的中点N，连接MC，MF，EN，FN.∵BM＝MA，BF＝FD，∴MF△AD，MF＝12AD，∵AN＝ND，∴MF＝AN，MF△AN，∴四边形MFNA是平行四边形，∴NF＝AM，△FMA＝△ANF，在Rt△ADE中，∵AN＝ND，△AED＝90°，∴EN＝12AD＝AN＝ND，同理CM＝12AB＝AM＝MB，在△AEN和△ACM中，△AEN＝△EAN，△MCA＝△MAC，∵△MAC＝△EAN，∴△AMC＝△ANE，又∵△FMA＝△ANF，∴△ENF＝△FMC，∵AM＝FN，AM＝CM，∴CM＝NF，在△MFC和△NEF中，{MF=EN∠FMC=∠ENFMC=NF，∴△MFC△△NEF（SAS），∴FE＝FC.17．【答案】（1）12；4（2）解：结论：AD=12BC.理由：如图1中，延长AD到M，使得AD=DM，连接B′M，C′M，∵B′D=DC′，AD=DM，∴四边形AC′MB′是平行四边形，∴AC′=B′M=AC，∵∠BAC+∠B′AC′=180∘，∠B′AC′+∠AB′M=180∘，∴∠BAC=∠MB′A，∵AB=AB′，∴ΔBAC≅ΔAB′M，∴BC=AM，∴AD=12BC.18．【答案】（1）证明：在平行四边形ABCD中，AB△CD，AD△BC∴△BAF=△F，△DAF=△CEF又∵AE平分△BAD∴△BAF=△DAF∴△F=△CEF∴CE=CF（2）如图，连接CG、BG.∵ABCD是平行四边形，△ABC＝90°∴平行四边形ABCD是矩形∴AB=DC，AB△DC，AD△BC，△BAD＝△ADC=△BCD＝△ECF＝90° ∴△F=△BAE，△DBC=△ADB∵△BAD＝90° ，△BAE＝12△BAD=45°∴AB=BE，△F=△BAE=45°∴CE=CF∴BC=BE+EC=AB+CF=CD+CF=DF又∵G 是EF 的中点，△ECF ＝90° ,CE=CF∴CG=FG=12EF,△ECG=12△ECF=45° ∴△ECG=△F∴△DFG△△BCG∴△FDG ＝△CBG ，DG=BG∴△DBG=△BDG∵△DBC=△ADB,△FDG ＝△CBG∴△DBC+△CBG=△ADB+△FDG即△DBG=△ADB+△FDG∴△BDG=△ADB+△FDG又∵△BDG+（△ADB+△FDG ）=90°∴△BDG=12△ADC=45° （3）如图，连接GB 、GE 、GC 。

八年级数学下册期末压轴题带答案

1． (1)如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE.求证：CE=CF；(2)如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE=45°，请你利用(1)的结论证明：GE=BE+GD.(3)运用(1)(2)解答中所积累的经验和知识，完成下题：如图3，在直角梯形ABCD中，AD∥BC(BC＞AD)，∠B=90°，AB=BC，E是AB上一点，且∠DCE=45°，BE=4，DE=10，求直角梯形ABCD的面积.2.如图，已知等腰Rt△ABC和△CDE，AC=BC,CD=CE，连接BE、AD，P为BD中点，M为AB中点、N为DE中点，连接PM、PN、MN.（1）试判断△PMN的形状，并证明你的结论；（2）若CD=5，AC=12，求△PMN的周长.3.已知正方形ABCD和正方形AEFG有公共顶点A，将正方形AEFG绕点A旋转．（1）①当E点旋转到DA的延长线上时（如图1），△ABE与△ADG的面积关系是：．②当E点旋转到CB的延长线上时（如图2），△ABE与△ADG的面积关系是：（2）当正方形AEFG旋转任意一个角度时（如图3），（1）中的结论是否仍然成立？若成立请证明，若不成立请说明理由．（3）已知△ABC，AB=5cm，BC=3cm，分别以AB、BC、CA为边向外作正方形（如图4），则图中阴影部分的面积和的最大值是 cm2．4.一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动：将△MNK的直角顶点M 放在△ABC的斜边AB的中点处，设AC=BC=a．（1）如图1，两个三角尺的重叠部分为△ACM，则重叠部分的面积为，周长为；（2）将图1中的△MNK绕顶点M逆时针旋转45°，得到图2，此时重叠部分的面积为，周长为；（3）如果将△MNK绕M旋转到不同于图1，图2的位置，如图3所示，猜想此时重叠部分的面积为多少？并试着加以验证．5.在正方形ABCD中，点E，F分别在边BC，CD上，且∠EAF=∠CEF=45°．（1）将△ADF绕着点A顺时针旋转90°，得到△ABG（如图①），求证：△AEG≌△AEF；（2）若直线EF与AB，AD的延长线分别交于点M，N（如图②），求证：EF2=ME2+NF2；（3）将正方形改为长与宽不相等的矩形，若其余条件不变（如图③），请你直接写出线段EF，BE，DF之间的数量关系．答案1.(1)证明：∵四边形ABCD是正方形，∴BC=CD，∠B=∠CDF=90°，∵∠ADC=90°，∴∠FDC=90°.∴∠B=∠FDC，∵BE=DF，∴△CBE≌△CDF(SAS).∴CE=CF.(2)证明：如图2，延长AD至F，使DF=BE，连接CF.由(1)知△CBE≌△CDF，∴∠BCE=∠DCF.∴∠BCE+∠ECD=∠DCF+∠ECD，即∠ECF=∠BCD=90°，又∠GCE=45°，∴∠GCF=∠GCE=45°.∵CE=CF，GC=GC，∴△ECG≌△FCG.∴GE=GF，∴GE=GF=DF+GD=BE+GD.(3)解：如图3，过C作CG⊥AD，交AD延长线于G.在直角梯形ABCD中，∵AD∥BC，∴∠A=∠B=90°，又∵∠CGA=90°，AB=BC，∴四边形ABCG为正方形.∴AG=BC.…∵∠DCE=45°，根据(1)(2)可知，ED=BE+DG.…∴10=4+DG，即DG=6.设AB=x，则AE=x﹣4，AD=x﹣6，在Rt△AED中，∵DE2=AD2+AE2，即102=(x﹣6)2+(x﹣4)2.解这个方程，得：x=12或x=﹣2(舍去).…∴AB=12.∴S梯形ABCD=0.5(AD+BC)•AB=0.5×(6+12)×12=108.即梯形ABCD的面积为108.…2.解：（1）①∵正方形ABCD和正方形AEFG有公顶点A，将正方形AEFG绕点A旋转，E点旋转到DA的延长线上，∴AE=AG，AB=AD，∠EAB=∠GAD，∴△ABE≌△ADG（SAS），∴△ABE的面积=△ADG的面积；②作GH⊥DA交DA的延长线于H，如图2，∴∠AHG=90°，∵E点旋转到CB的延长线上，∴∠ABE=90°，∠HAB=90°，∴∠GAH=∠EAB，在△AHG和△AEB中，∴△AHG≌△AEB，∴GH=BE，∵△ABE的面积=0.5EB•AB，△ADG的面积=0.5GH•AD，∴△ABE的面积=△ADG的面积；（2）结论仍然成立．理由如下：作GH⊥DA交DA的延长线于H，EP⊥BA交BA的延长线于P，如图3，∵∠PAD=90°，∠EAG=90°，∴∠PAE=∠GAH，在△AHG和△AEP中，∴△AHG≌△AEP（AAS），∴GH=BP，∵△ABP的面积=0.5EP•AB，△ADG的面积=0.5GH•AD，∴△ABP的面积=△ADG的面积；（3）∵AB=5cm，BC=3cm，∴AC==4cm，∴△ABC的面积=0.5×3×4=6（cm2）；根据（2）中的结论得到阴影部分的面积和的最大值=△ABC的面积的3倍=18cm2．故答案为相等；相等；18．3.解：（1）∵AM=MC=AC=a，则∴重叠部分的面积是△ACB的面积的一半为0.25a2，周长为（1+）a．（2）∵重叠部分是正方形∴边长为0.5a，面积为0.25a2，周长为2a．（3）猜想：重叠部分的面积为0.25a2．理由如下：过点M分别作AC、BC的垂线MH、MG，垂足为H、G设MN与AC的交点为E，MK与BC的交点为F∵M是△ABC斜边AB的中点，AC=BC=a∴MH=MG=0.5a又∵∠HME+∠HMF=∠GMF+∠HMF，∴∠HME=∠GMF，∴Rt△MHE≌Rt△MGF∴阴影部分的面积等于正方形CGMH的面积∵正方形CGMH的面积是MG•MH=0.5a×0.5a =0.25a2,∴阴影部分的面积是0.25a2．4.（1）证明：∵△ADF绕着点A顺时针旋转90°,得到△ABG,∴AF=AG,∠FAG=90°，∵∠EAF=45°,∴∠GAE=45°，在△AGE与△AFE中，，∴△AGE≌△AFE（SAS）；（2）证明：设正方形ABCD的边长为a.将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM．则△ADF≌△ABG，DF=BG．由（1）知△AEG≌△AEF，∴EG=EF．∵∠CEF=45°，∴△BME、△DNF、△CEF均为等腰直角三角形，∴CE=CF，BE=BM，NF=DF，∴a﹣BE=a﹣DF，∴BE=DF，∴BE=BM=DF=BG，∴∠BMG=45°，∴∠GME=45°+45°=90°，∴EG2=ME2+MG2，∵EG=EF，MG=BM=DF=NF，∴EF2=ME2+NF2；（3）解：EF2=2BE2+2DF2．如图所示，延长EF交AB延长线于M点，交AD延长线于N点，将△ADF绕着点A顺时针旋转90°，得到△AGH，连结HM，HE．由（1）知△AEH≌△AEF，则由勾股定理有（GH+BE）2+BG2=EH2，即（GH+BE）2+（BM﹣GM）2=EH2又∴EF=HE，DF=GH=GM，BE=BM，所以有（GH+BE）2+（BE﹣GH）2=EF2，即2（DF2+BE2）=EF2。

人教版八年级数学上册期末专题复习：几何压轴题强化训练试题(含答案)

初二数学全等三角形压轴几何题(讲义及答案)含答案

初二数学全等三角形压轴几何题(讲义及答案)含答案一、全等三角形旋转模型1．问题背景：如图1，在四边形ABCD 中，90BAD ∠=︒，90BCD ∠=︒，BA BC =，120ABC ∠=︒，60MBN ∠=︒，MBN ∠绕B 点旋转，它的两边分别交AD 、DC 于E 、F ．探究图中线段AE ，CF ，EF 之间的数量关系．小李同学探究此问题的方法是：延长FC 到G ，使CG AE =，连接BG ，先证明BCG BAE △≌△，再证明BFC BFE △≌△，可得出结论，他的结论就是_______________；探究延伸1：如图2，在四边形ABCD 中，90BAD ∠=︒，90BCD ∠=︒，BA BC =，2ABC MBN ∠=∠，MBN ∠绕B 点旋转，它的两边分别交AD 、DC 于E 、F ．上述结论是否仍然成立？请直接写出结论（直接写出“成立”或者“不成立”），不要说明理由．探究延伸2：如图3，在四边形ABCD 中，BA BC =，180BAD BCD ∠+∠=︒，2ABC MBN ∠=∠，MBN ∠绕B 点旋转，它的两边分别交AD 、DC 于E 、F ．上述结论是否仍然成立？并说明理由．实际应用：如图4，在某次军事演习中，舰艇甲在指挥中心（O 处）北偏西30的A 处舰艇乙在指挥中心南偏东70︒的B 处，并且两舰艇到指挥中心的距离相等接到行动指令后，舰艇甲向正东方向以75海里/小时的速度前进，同时舰艇乙沿北偏东50︒的方向以100海里/小时的速度前进，1.2小时后，指挥中心观测到甲、乙两舰艇分别到达E 、F 处，且指挥中心观测两舰艇视线之间的夹角为70︒，试求此时两舰艇之间的距离．答案：E解析：EF=AE+CF ．探究延伸1：结论EF=AE+CF 成立．探究延伸2：结论EF=AE+CF 仍然成立．实际应用：210海里．【分析】延长FC 到G ，使CG AE =，连接BG ，先证明BCG BAE △≌△，可得BG=BE ，∠CBG=∠ABE ，再证明BGF BEF ≌，可得GF=EF ，即可解题；探究延伸1：延长FC 到G ，使CG AE =，连接BG ，先证明BCG BAE △≌△，可得BG=BE ，∠CBG=∠ABE ，再证明BGF BEF ≌，可得GF=EF ，即可解题；探究延伸2：延长FC 到G ，使CG AE =，连接BG ，先证明BCG BAE △≌△，可得BG=BE ，∠CBG=∠ABE ，再证明BGF BEF ≌，可得GF=EF ，即可解题；实际应用：连接EF ，延长AE ，BF 相交于点C ，然后与探究延伸2同理可得EF=AE+CF ，将AE 和CF 的长代入即可．【详解】解：EF=AE+CF理由：延长FC 到G ，使CG AE =，连接BG ，在△BCG 和△BAE 中，90BC BA BCG BAE CG AE =⎧⎪∠=∠=︒⎨⎪=⎩，∴BCG BAE △≌△（SAS ），∴BG=BE ，∠CBG=∠ABE ，∵∠ABC=120°，∠MBN=60°，∴∠ABE+∠CBF=60°，∴∠CBG+∠CBF=60°，即∠GBF=60°，在△BGF 和△BEF 中，BG BE GBF EBF BF BF =⎧⎪∠=∠⎨⎪=⎩，∴△BGF ≌△BEF （SAS ），∴GF=EF ，∵GF=CG+CF=AE+CF ，∴EF=AE+CF ．探究延伸1：结论EF=AE+CF 成立．理由：延长FC 到G ，使CG AE =，连接BG ，在△BCG 和△BAE 中，90BC BA BCG BAE CG AE =⎧⎪∠=∠=︒⎨⎪=⎩，∴BCG BAE △≌△（SAS ），∴BG=BE ，∠CBG=∠ABE ，∵∠ABC=2∠MBN ，∴∠ABE+∠CBF=12∠ABC ， ∴∠CBG+∠CBF=12∠ABC ，即∠GBF=12∠ABC ，在△BGF 和△BEF 中，BG BE GBF EBF BF BF =⎧⎪∠=∠⎨⎪=⎩，∴△BGF ≌△BEF （SAS ），∴GF=EF ，∵GF=CG+CF=AE+CF ，∴EF=AE+CF ．探究延伸2：结论EF=AE+CF 仍然成立．理由：延长FC 到G ，使CG AE =，连接BG ，∵180BAD BCD ∠+∠=︒，∠BCG+∠BCD=180°，∴∠BCG=∠BAD在△BCG 和△BAE 中，BC BA BCG BAE CG AE =⎧⎪∠=∠⎨⎪=⎩，∴BCG BAE △≌△（SAS ），∴BG=BE ，∠CBG=∠ABE ，∵∠ABC=2∠MBN ，∴∠ABE+∠CBF=12∠ABC ， ∴∠CBG+∠CBF=12∠ABC ，即∠GBF=12∠ABC ，在△BGF 和△BEF 中，BG BE GBF EBF BF BF =⎧⎪∠=∠⎨⎪=⎩，∴△BGF ≌△BEF （SAS ），∴GF=EF ，∵GF=CG+CF=AE+CF ，∴EF=AE+CF ．实际应用：连接EF ，延长AE ，BF 相交于点C ，∵∠AOB=30°+90°+(90°-70°)=140°，∠EOF=70°，∴∠EOF=12∠AOB ∵OA=OB ，∠OAC+∠OBC=(90°-30°)+(70°+50°)=180°，∴符合探索延伸中的条件∴结论EF= AE+CF 仍然成立即EF=75×1.2+100×1.2=210（海里）答：此时两舰艇之间的距离为210海里．【点睛】本题考查了全等三角形的判定与性质．作辅助线构造全等三角形是解题的关键． 2．一位同学拿了两块45︒三角尺MNK ∆，ACB ∆做了一个探究活动：将MNK ∆的直角顶点M 放在ACB ∆的斜边AB 的中点处，设4AC BC ==.（1）如图1所示，两三角尺的重叠部分为ACM ∆，则重叠部分的面积为______，周长为______.（2）将如图1所示中的MNK ∆绕顶点M 逆时针旋转45︒，得到如图2所示，此时重叠部分的面积为______，周长为______.（3）如果将MNK ∆绕M 旋转到不同于如图1所示和如图2所示的图形，如图3所示，请你猜想此时重叠部分的面积为______.（4）在如图3所示情况下，若1AD =，求出重叠部分图形的周长.答案：A解析：（1）4，4+；（2）4，8；（3）4；（4）4+【分析】()1根据4AC BC ==，90ACB ∠=，得出AB 的值，再根据M 是AB 的中点，得出AM MC =，求出重叠部分的面积，再根据AM ，MC ，AC 的值即可求出周长；()2易得重叠部分是正方形，边长为12AC ，面积为214AC ，周长为2.AC ()3过点M 分别作AC 、BC 的垂线MH 、ME ，垂足为H 、.E 求得Rt MHD ≌Rt MEG ，则阴影部分的面积等于正方形CEMH 的面积. ()4先过点M 作ME BC ⊥于点E ，MH AC ⊥于点H ，根据DMH EMH ∠∠=，MH ME =，得出Rt DHM ≌Rt EMG ，从而得出HD GE =，CE AD =，最后根据AD 和DF 的值，算出DM =.【详解】解：()14AC BC ==，90ACB ∠=，AB ∴== M 是AB 的中点，AM ∴=45ACM ∠=，AM MC ∴=，∴重叠部分的面积是42=， ∴周长为：44AM MC AC ++==+故答案为4，4+；()2重叠部分是正方形，∴边长为1422⨯=，面积为14444⨯⨯=，周长为248⨯=．故答案为4，8．()3过点M 分别作AC 、BC 的垂线MH 、ME ，垂足为H 、E ， M 是ABC 斜边AB 的中点，4AC BC ==， 12MH BC ∴=， 12ME AC =， MH ME ∴=，又90NMK HME ∠∠==，90NMH HMK ∠∠∴+=，90EMG HMK ∠∠+=， HMD EMG ∠∠∴=，在MHD 和MEG 中，HMD GME MH MEDHM MEG ∠=∠⎧⎪=⎨⎪∠=∠⎩， MHD ∴≌()MEG ASA ，∴阴影部分的面积等于正方形CEMH 的面积，正方形CEMH 的面积是1144422ME MH ⋅=⨯⨯⨯=； ∴阴影部分的面积是4；故答案为4．()4如图所示，过点M 作ME BC ⊥于点E ，MH AC ⊥于点H ，∴四边形MECH 是矩形，MH CE ∴=，45A ∠=，45AMH ∠∴=，AH MH ∴=，AH CE ∴=，在Rt DHM 和Rt GEM 中，DMH EMG MH MEDHM GEM ∠=∠⎧⎪=⎨⎪∠=∠⎩， Rt DHM ∴≌.Rt GEMGE DH ∴=，AH DH CE GE ∴-=-，CG AD ∴=，1AD =，1.DH ∴= 145DM ∴=+= ．∴四边形DMGC 的周长为：CE CD DM ME +++2AD CD DM =++425=+．【点睛】此题考查了等腰直角三角形，利用等腰直角三角形的性质，等腰直角三角形的面积公式，正方形的面积公式，全等三角形的判定和性质求解．3．如图1，在Rt △ABC 中，∠A ＝90°，AB ＝AC ，点D ，E 分别在边AB ，AC 上，AD ＝AE ，连接DC ，点M ，P ，N 分别为DE ，DC ，BC 的中点．（1）观察猜想：图1中，线段PM 与PN 的数量关系是，位置关系是；（2）探究证明：把△ADE 绕点A 逆时针方向旋转到图2的位置，连接MN ，BD ，CE ，判断△PMN 的形状，并说明理由；（3）拓展延伸：把△ADE 绕点A 在平面内自由旋转，若AD ＝4，AB ＝10，请直接写出△PMN 面积的最大值．解析：（1）PM ＝PN ，PM ⊥PN ；（2）△PMN 是等腰直角三角形．理由见解析；（3）S △PMN 最大＝492．【分析】（1）由已知易得BD CE =，利用三角形的中位线得出12PM CE =，12PN BD =，即可得出数量关系，再利用三角形的中位线得出//PM CE 得出DPM DCA ∠=∠，最后用互余即可得出位置关系；（2）先判断出ABD ACE ∆≅∆，得出BD CE =，同（1）的方法得出12PM BD =，12PN BD =，即可得出PM PN =，同（1）的方法由MPN DCE DCB DBC ACB ABC ∠=∠+∠+∠=∠+∠，即可得出结论；（3）方法1：先判断出MN 最大时，PMN ∆的面积最大，进而求出AN ，AM ，即可得出MN 最大AM AN =+，最后用面积公式即可得出结论．方法2：先判断出BD 最大时，PMN ∆的面积最大，而BD 最大是14AB AD +=，即可得出结论．【详解】解：（1）点P ，N 是BC ，CD 的中点，//PN BD ∴，12PN BD =，点P ，M 是CD ，DE 的中点， //PM CE ∴，12PM CE =， AB AC =，AD AE =，BD CE ∴=，PM PN ∴=，//PN BD ，DPN ADC ∴∠=∠，//PM CE ，DPM DCA ∴∠=∠，90BAC ∠=︒，90ADC ACD ∴∠+∠=︒，90MPN DPM DPN DCA ADC ∴∠=∠+∠=∠+∠=︒，PM PN ∴⊥，故答案为：PM PN =，PM PN ⊥；（2）PMN ∆是等腰直角三角形．由旋转知，BAD CAE ∠=∠，AB AC =，AD AE =，()ABD ACE SAS ∴∆≅∆，ABD ACE ∴∠=∠，BD CE =，利用三角形的中位线得，12PN BD =，12PM CE =， PM PN ∴=，PMN ∴∆是等腰三角形，同（1）的方法得，//PM CE ，DPM DCE ∴∠=∠，同（1）的方法得，//PN BD ，PNC DBC ∴∠=∠，DPN DCB PNC DCB DBC ∠=∠+∠=∠+∠，MPN DPM DPN DCE DCB DBC ∴∠=∠+∠=∠+∠+∠BCE DBC ACB ACE DBC =∠+∠=∠+∠+∠ACB ABD DBC ACB ABC =∠+∠+∠=∠+∠，90BAC ∠=︒，90ACB ABC ∴∠+∠=︒，90MPN ∴∠=︒，PMN ∴∆是等腰直角三角形；（3）方法1：如图2，同（2）的方法得，PMN ∆是等腰直角三角形，MN ∴最大时，PMN ∆的面积最大，//DE BC ∴且DE 在顶点A 上面，MN ∴最大AM AN =+，连接AM ，AN ，在ADE ∆中，4AD AE ==，90DAE ∠=︒，22AM ∴=在Rt ABC ∆中，10AB AC ==，52AN =22522MN ∴=最大，222111149(72)22242PMN S PM MN ∆∴==⨯=⨯=最大．方法2：由（2）知，PMN ∆是等腰直角三角形，12PM PN BD ==， PM ∴最大时，PMN ∆面积最大，∴点D 在BA 的延长线上，14BD AB AD ∴=+=，7PM ∴=，2211497222PMN S PM ∆∴==⨯=最大．【点睛】此题属于几何变换综合题，主要考查了三角形的中位线定理，等腰直角三角形的判定和性质，全等三角形的判断和性质，直角三角形的性质的综合运用；解（1）的关键是判断出12PM CE =，12PN BD =，解（2）的关键是判断出ABD ACE ∆≅∆，解（3）的关键是判断出MN 最大时，PMN ∆的面积最大．4．如图，△ABC 中，O 是△ABC 内一点，AO 平分∠BAC ，连OB ，OC ．（1）如图1，若∠ACB ＝2∠ABC ，BO 平分∠ABC ，AC ＝5，OC ＝3，则AB ＝；（2）如图2，若∠CBO +∠ACO ＝∠BAC ＝60°，求证：BO 平分∠ABC ；（3）如图3，在（2）的条件下，若BC ＝3B 绕点O 逆时针旋转60°得点D ，直接写出CD 的最小值为．答案：A解析：（1）8；（2）见解析；（3）33【分析】（1）先补充证明角平分线的性质定理：如图，△ABC 中，AD 是角平分线，则：BD DC＝AB AC ．如图1中，延长CO 交AB 于E ，由OA 平分∠EAC ，推出AE AC ＝OE OC，推出AE EO ＝AC OC ＝53，设AE ＝5k ，OE ＝3k ，利用相似三角形的性质构建方程求出k 即可解决问题．（2）如图2中，过点O 作EF ⊥OA 交AB 于E ，交AC 于F ，作CG ∥EF 交AB 于G ，连接OG ．证明△AGO ≌△ACO （SAS ），推出OG ＝OC ，推出∠OGC ＝∠OCG ，证明O ，G ，B ，C 四点共圆，可得结论．（3）如图3中，以BC 为边向上作等边△BCH ，连接OH ，作HM ⊥BC 于M ．证明△HBO ≌△CBD （SAS ），推出OH ＝CD ，由（2）可知∠BOC ＝120°，推出当点O 落在HM 上时，OH 的值最小．【详解】解：（1）先补充证明角平分线的性质定理：如图，△ABC 中，AD 是角平分线，则：BD DC ＝AB AC．理由：过C 作CE ∥DA ，交BA 的延长线于E ，∵CE∥DA，∴∠1＝∠E，∠2＝∠3，∠1＝∠2，∴∠E＝∠3，∴AE＝AC，∵BDDC ＝BAAE，∴BDDC ＝ABAC．如图1中，延长CO交AB于E，∵OA平分∠EAC，∴AEAC＝OEOC，∴AEEO ＝ACOC＝53，设AE＝5k，OE＝3k，∵OB平分∠ABC，∴OC平分∠ACB，∵∠ACB＝2∠ABC，∴∠BCE＝12∠ACB＝∠EBC，∴EB＝EC＝3k+3，∵∠ACE＝∠ABC，∠CAE＝∠BAC，∴△ACE∽△ABC，∴ACAB ＝AEAC，∴5533k k ＝55k，解得k＝58或﹣1（舍弃），∴AB＝8k+3＝8．故答案为：8．（2）如图2中，过点O作EF⊥OA交AB于E，交AC于F，作CG∥EF交AB于G，连接OG．∵AO平分∠AEF，∴∠OAE＝∠OAF，∵AO＝AO，∠AOE＝∠AOF＝90°，∴△AOE≌△AOF（ASA），∴AE＝AF，∵∠EAF＝60°，∴△AEF是等边三角形，∴∠AEF＝∠AFE＝60°＝∠FOC+∠FCO，∵∠OBC+∠FCO＝60°，∴∠FOC＝∠OBC，∵EF∥CG，∴∠AGC＝∠AEF＝60°，∠ACG＝∠AFE＝60°，∴∠AGC＝∠ACG，∴AG＝AC，∵∠GAO＝∠CAO，AO＝AO，∴△AGO≌△ACO（SAS），∴OG＝OC，∴∠OGC＝∠OCG，∵∠FOC＝∠OCG，∴∠OBC＝∠OGC，∴O，G，B，C四点共圆，∴∠ABO＝∠OCG，∴∠ABO＝∠OBC，∴OB平分ABC．（3）如图3中，以BC为边向上作等边△BCH，连接OH，作HM⊥BC于M．∵△OBD，△BCH都是等边三角形，∴∠HBC＝∠OBD＝60°，BH＝BC，BO＝BD，∴∠HBO＝∠CBD，∴△HBO≌△CBD（SAS），∴OH＝CD，由（2）可知∠BOC＝120°，∴当点O落在HM上时，OH的值最小，此时OH＝HM﹣OM＝3﹣3，∴CD的最小值为3﹣3．故答案为：3﹣3．【点睛】本题主要考查角平分线、三角形相似的判定和性质、三角形全等的判定和性质、等边三角形等相关知识点，解题关键在于作出辅助线构造相应图形．5．已知：在△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点(点D不与B、C重合)．以AD为边作正方形ADEF，连接CF．（1）如图1，当点D在线段BC上时，请直接写出线段BD与CF的数量关系：；（2）如图2，当点D在线段BC的延长线上时，其它条件不变，若AC=2，CD=1，则CF= ；（3）如图3，当点D在线段BC的反向延长线上时，且点A、F分别在直线BC的两侧，其它条件不变：①请直接写出CF、BC、CD三条线段之间的关系：；②若连接正方形对角线AE、DF，交点为O，连接OC，探究△AOC的形状，并说明理由．答案：B解析：（1）BD=CF；（2）221；（3）①CD=CF+BC，②等腰三角形，见解析【分析】（1）△ABC 是等腰直角三角形，利用SAS 即可证明△BAD ≌△CAF ；（2）同（1）相同，利用SAS 即可证得△BAD ≌△CAF ，从而证得BD=CF ，即可得到CF=CD+BC ，然后求出答案；（3）中的①与（1）相同，可证明BD=CF ，又点D 、B 、C 共线，故：CD=BC+CF ； ②由（1）猜想并证明BD ⊥CF ，从而可知△FCD 为直角三角形，再由正方形的对角线的性质判定△AOC 三边的特点，再进一步判定其形状．【详解】解：（1）证明：∵∠BAC=90°，AB=AC ， ∴∠ABC=∠ACB=45°， ∵四边形ADEF 是正方形， ∴AD=AF ，∠DAF=90°，∵∠BAC=∠BAD+∠DAC=90°，∠DAF=∠CAF+∠DAC=90°， ∴∠BAD=∠CAF ，在△BAD 和△CAF 中，AB AC BAD CAF AD AF =⎧⎪∠=∠⎨⎪=⎩， ∴△BAD ≌△CAF （SAS ）， ∴BD=CF ，（2）与（1）同理，证△BAD ≌△CAF ； ∴BD=CF ， ∴CF=BC+CD ， ∵AC=AB=2，CD=1，∴BC ==∴CF=1；（3）①BC 、CD 与CF 的关系：CD=BC+CF理由：与（1）同法可证△BAD ≌△CAF ，从而可得： BD=CF ，即：CD=BC+CF②△AOC 是等腰三角形理由：与（1）同法可证△BAD ≌△CAF ，可得：∠DBA=∠FCA ，又∵∠BAC=90°，AB=AC ， ∴∠ABC=∠ACB=45°，则∠ABD=180°-45°=135°， ∴∠ABD=∠FCA=135° ∴∠DCF=135°-45°=90° ∴△FCD 为直角三角形．又∵四边形ADEF是正方形，对角线AE与DF相交于点O，∴OC=12DF，∴OC=OA∴△AOC是等腰三角形．【点睛】本题考查了等腰三角形、正方形的性质及全等三角形的判定与性质等知识点，一般情况下，要证明两条线段相等，就得证明这两条线段所在的两个三角形全等，关键是掌握图形特点挖掘题目所隐含的条件．6．综合与探究问题情境在Rt△ABC中，∠BAC＝90°，AB＝AC，点D是射线BC上一动点，连接AD，将线段AD绕点A逆时针旋转90°至AE，连接DE，CE．探究发现（1）如图1，BD＝CE，BD⊥CE，请证明；探究猜想；（2）如图2，当BD＝2DC时，猜想AD与BC之间的数量关系，并说明理由；探究拓广（3）当点D在BC的延长线上时，探究并直接写出线段BD，DC，AD之间的数量关系．答案：B解析：（1）证明见解析；（2）10AD BC=，理由见解析；（3）2222BD CD AD+=．【分析】（1）根据题意计算得∠BAD=∠CAE；再根据旋转的性质，通过证明△BAD≌△CAE，从而完成求解；（2）结合（1）的结论，通过△BAD≌△CAE，得CE；通过勾股定理，得2DE=；再通过勾股定理计算，记得得到答案；（3）过点A作AM BC⊥交BC于点M；根据等腰三角形三线合一的性质，得BM CM=，再根据直角三角形斜边中线的性质，得12AM BM CM BC===；根据勾股定理的性质，通过计算，即可得到线段BD，DC，AD之间的数量关系．【详解】（1）由题意得，∠BAC =∠DAE =90° ∵∠BAD +∠CAD =∠CAE +∠CAD ∴∠BAD =∠CAE∵线段AD 绕点A 逆时针旋转90°至AE ∴AD=AE 又∵AB=AC ， ∴△BAD ≌△CAE ∴BD=CE ，∠B =∠ACE =45° ∴∠ECD =90°，BD ⊥CE ．（2）由（1）得：△BAD ≌△CAE ∴BD=CE ，∠B =∠ACE =45° ∵13CD BC =，BD ＝2DC ，即23BD BC =, ∴23BD CE BC ==， ∵AD=AE ∴222DE AD AE AD =+=∴∠B =∠ACB =45° ∴∠BCE =∠ACB+∠ACE =90°∴CD 2+CE 2=DE 2，即22212()()233BC BC AD +=， ∴106AD BC =；（3）如图，过点A 作AM BC ⊥交BC 于点M∵∠BAC ＝90°，AB ＝AC ∴12BM CM BC ==∴12AM BM CM BC ===∴()1122AM BC BD CD ==-，()1122DM CM CD BC CD BD CD =+=+=+ ∵222AM DM AD +=∴()()2221122BD CD BD CD AD ⎡⎤⎡⎤-++=⎢⎥⎢⎥⎣⎦⎣⎦∴2222BD CD AD +=．【点睛】本题考查了旋转、等腰直角三角形、勾股定理、直角三角形斜边中线的知识；解题的关键是熟练掌握旋转、等腰三角形三线合一、勾股定理、直角三角形斜边中线的性质，从而完成求解．7．如图1所示，在Rt ABC △中90BAC ∠=︒，AB AC =，2BC =，以BC 所在直线为x 轴，边BC 的垂直平分线为y 轴建立平面直角坐标系，将ABC 绕P 点0,1顺时针旋转．（1）填空：当点B 旋转到y 轴正半轴时，则旋转后点A 坐标为______；（2）如图2所示，若边AB 与y 轴交点为E ，边AC 与直线1y x =-的交点为F ，求证：AEF 的周长为定值；（3）在（2）的条件下，求AEF 内切圆半径的最大值．解析：（1）2,21；（2）见解析；（3）324【分析】（1）作出图形，'''A B C 是ABC 绕 P 点0,1顺时针旋转，点B 旋转到y 轴正半轴时得到的图形，连接 BP ，CP ，根据2BC =，y 轴垂直平分BC ， AB AC =，()0,1P -可证得四边形ABPC 是正方形，则有 '''2BP B PAB A B ，'0'21B B PPO，可得点 A 坐标；（2）作BPQ CPF ∠=∠，交AB 延长线于Q 点，根据四边形ABPC 是正方形，得到90QBP FCP ∠=∠=︒，BP CP =，可证BPQ CPF ASA ≌△△，得BQ CF =，QP FP =，利用ASA 再可证得QPE FPE ≌△△，得QE FE =则AEF 的周长22AB AC =+=（3）设EF m =，AE n =，Rt AEF 的内切圆半径为r ，由（2）可得22AF m n =--则2AE AF EF r +-=222n m n m+---=2m =-，当m 最小时，r 最大．得到22222n m nm 整理得：2224220nm n m，关于n的一元二次方程有解，即22244220m m化简得24280m m +-≥，利用二次函数图像可得422m ≥-或422m ≤--（不合题意，舍去）可得m 的最小值为422-，即r 的最大值为2422324，则有AEF 内切圆半径的最大值为324-．【详解】解：（1）如图示，'''A B C 是ABC 绕 P 点0,1顺时针旋转，点B 旋转到y 轴正半轴时得到的图形，连接 BP ，CP ，∵2BC =，y 轴垂直平分BC ∴1BO CO ==又∵Rt ABC △中，AB AC = ∴1AO =，2AB AC ==∵()0,1P - ∴1PO =∴AO BO CO PO === ∴四边形ABPC 是正方形 ∴'''2BP B P AB A B∴'0'21B B PPO∴点A 坐标为2,21（2）如图2所示，作BPQ CPF ∠=∠，交AB 延长线于Q 点 ∵四边形ABPC 是正方形∴90QBP FCP ∠=∠=︒， BP CP = ∴BPQ CPF ASA ≌△△∴ BQ CF =，QP FP =∵点F 在直线1y x =-∴45FPE ∠=︒∴ 45BPE FPC ∠+∠=︒ ∴45BPE BPQ ∠+∠=︒∴45QPE FPE ∠=∠=︒ ∵EP EP =∴QPE FPE ASA ≌△△∴ QE FE =∴AEF 的周长AE EF AF AE QE AF =++=++ AE BE BQ AF AE BE FC AF =+++=+++22AB AC =+=（3）设EF m =，AE n =，Rt AEF 的内切圆半径为 r ，由（2）可得22AF m n =-则2AE AF EFr +-=22n m n m+---=2m =∴当m 最小时，r 最大．∵在Rt AEF 中，222AE AF EF +=∴22222n m nm 整理得： 2224220nm nm ∵关于n 的一元二次方程有解∴22244220m m∴24280m m +-≥利用二次函数图像可得422m ≥-422m ≤--（不合题意，舍去） ∴m 的最小值为422-r 2422324即AEF 内切圆半径的最大值为324．【点睛】本题主要考查了一次函数的综合应用以及根的判别式、全等三角形的判定与性质、旋转、三角形内切圆等知识，能熟练应用相关性质是解题关键． 8．问题解决一节数学课上，老师提出了这样一个问题：如图①，点P 是等边ABC 内的一点，6PA =，8PB = ，10PC =．你能求出APB ∠的度数和等边ABC 的面积吗？小明通过观察、分析、思考，形成了如下思路：如图①将BPC △绕点B 逆时针旋转60°，得到BPA △，连接PP '，可得BPP '是等边三角形，根据勾股定理逆定理可得AP P '是直角三角形，从而使问题得到解决．（1）结合小明的思路完成填空：PP '=_____________，APP '∠=_______________，APB ∠=_____________ ，ABCS= ______________．（2）类比探究Ⅰ如图②，若点P 是正方形ABCD 内一点，1PA = ，2PB =，3PC =，求APB ∠的度数和正方形的面积．Ⅱ如图③，若点P 是正方形ABCD 外一点，3PA = ，1PB =， 11PC =，求APB ∠的度数和正方形的面积．答案：B解析：（1）8，90˚，150˚，25336；（2）Ⅰ135APB ∠=︒， 722ABCD S =+正方形；Ⅱ45APB ∠=︒， 1032ABCD S =-正方形【分析】（1）根据小明的思路，然后利用等腰三角形和直角三角形性质计算即可；（2）Ⅰ将△BPC 绕点B 逆时针旋转90°，得到△BP′A ，连接PP′，求出∠APB 的度数；先利用旋转求出∠PBP'=90°，BP'=BP=2，AP'=CP=3，利用勾股定理求出PP'，进而判断出△APP'是直角三角形，得出∠APP'=90°，即可得出结论；过B 作BE ⊥AP 于点E ，然后利用勾股定理求出AB 的长度即可求出正方形面积；Ⅱ将△BPC 绕点B 逆时针旋转90°，得到△BP′A ，连接PP′，求出∠APB 的度数；先利用旋转求出∠PBP'=90°，BP'=BP=2，AP'=CP=3，利用勾股定理求出PP'，进而判断出△APP'是直角三角形，得出∠APP'=90°，即可得出结论；过B 作BF ⊥AP 于点F ，然后利用勾股定理求出AB 的长度即可求出正方形面积；【详解】解:（1）由题易有P BP '∆是等边三角形，AP P '∆是直角三角形 ∴PP '=BP=8，90?APP '=∠，60?P PB '=∠，∴APB ∠=APP '∠+=P PB '∠150˚，如图1，过B 作BD ⊥AP 于点D∵APB ∠=150°∴30?BPD =∠在Rt △BPD 中，30?BPD =∠，BP=8∴BD=4，PD=43 ∴AD=6+43∴AB 2=AD 2+BD 2=100+483∴ABC S =234AB =25336+ （2）Ⅰ．如图2，将△BPC 绕点B 逆时针旋转90°，得到△BP′A ，连接PP′，∴△ABP'≌△CBP ，∴∠PBP'=90°，BP'=BP=2，AP'=CP=3，在Rt △PBP'中，BP=BP'=2，∴∠BPP'=45°，根据勾股定理得，PP'=2BP=22，∵AP=1，∴AP 2+PP'2=1+8=9，∵AP'2=32=9，∴AP 2+PP'2=AP'2，∴△APP'是直角三角形，且∠APP'=90°，∴∠APB=∠APP'+∠BPP'=90°+45°=135°；过B 作BE ⊥AP 于点E ，∵∠APB=135°∴∠BPE=45°∴△BPE 是等腰直角三角形∴BE=BP=22BP =2 ∴AE=1+2∴AB 2=AE 2+BE 2=7+22 ∴2722ABCD S AB ==+正方形Ⅱ．如图3，将△BPC 绕点B 逆时针旋转90°，得到△BP′A ，连接PP′，∴△ABP'≌△CBP ，∴∠PBP'=90°，BP'=BP=1，AP'=CP=11，在Rt △PBP'中，BP=BP'=1，∴∠BPP'=45°，根据勾股定理得，PP'=2BP=2，∵AP=3，∴AP 2+PP'2=9+2=11，∵AP'2=（11）2=11，∴AP 2+PP'2=AP'2，∴△APP'是直角三角形，且∠APP'=90°，∴∠APB=∠APP'-∠BPP'=90°-45°=45°．过B 作BF ⊥AP 于点F∵∠APB=45°∴△BPF 为等腰直角三角形∴PF=BF=22BP =22 ∴2 ∴AB 2=AF 2+BF 2=1032-∴21032ABCD S AB ==-正方形【点睛】此题是四边形综合题，主要考查了正方形的性质，旋转的性质，直角三角形的性质和判定，勾股定理，正确作出辅助线是解本题的关键．9．如图１，在△ABC 和△ADE 中，∠DAE=∠BAC ，AD=AE ，AB=AC ．（1）求证：△ABD ≌△ACE ；（2）如图2，在△ABC 和△ADE 中，∠DAE=∠BAC ，AD=AE ，AB=AC ，∠ADB=90°，点E 在△ABC 内，延长DE 交BC 于点F ，求证：点F 是BC 中点；（3）△ABC 为等腰三角形，∠BAC=120°，AB=AC ，点P 为△ABC 所在平面内一点，∠APB=120°，AP=2，BP=4，请直接写出 CP 的长．答案：D解析：（1）证明见详解；（2）证明见详解；（3）2713【分析】（1）因为∠DAE=∠BAC ，可以得到∠DAB=∠EAC ，因为AD=AE ，AB=AC ，即可得到△ABD ≌△ACE ；（2）连接CE ，延长EF 至点H ，取CF=CH ，连接CH ，由（1）可得△ABD ≌△ACE ，所以∠AEC=90°和CE=BD ，可以推出∠BDF=∠CEF ，再证明△DBF ≌△ECH ，所以BF=CH ，等量代换即可得到BF=FC ，即可解决；（3）点P 在△ABC 内部，将△ABP 逆时针旋转120°，得到ACP ∆'，连接PP '和PC ，可以得到△PP C '是直角三角形，利用勾股定理即可求出PC 的值；当点P 在△ABC 外部，将△APB 绕点A 逆时针旋转120︒得到PDC ∆，连接PP '和PC ，过点P 作PD ⊥'CP 于点D ，连接PD 可以得到△PP D '，△PP D '是直角三角形和，利用勾股定理即可求出'DP 及PC 的值．【详解】解：（1）证明：∵∠DAE=∠BAC∴∠DAB=∠EAC∵AD=AE ，AB=AC∴△ABD ≌△ACE（2）证明：连接CE ，延长EF 至点H ，取CF=CH ，连接CH ，如图所示：∵△ADB≌△AEC∴BD=EC，∠ADB=∠AEC=90°∵AD=AE∴∠ADE=∠AED∵∠ADE+∠EDB=∠AED+∠CEH=90°∴∠EDB=∠CEH∵CF=CH∴∠CFH=∠CHF∴∠DFB=∠H∵CE=BD∴△DBF≌△ECH∴BF=CH∴BF=CF∴点F是BC的中点∆'，连接（3）当点P在△ABC内部，如图所示，将△ABP逆时针旋转120°，得到ACPPP'和PC∆'∵将△ABP旋转120°得到ACP∴∠PAP'=120°，AP='AP=2，BP=CP'=4∴PP'3∵∠AP C'=120°，∠AP P'=30°，∴∠PP C'=90°，∴()2223427+=．当点P在△ABC外部，如图所示，将△APB 绕点A 逆时针旋转120︒到△'AP C ，过点P 作PD ⊥'CP 于点D ，连接PD ， ∵将△ABP 旋转120°得到ACP ∆'∴∠PAP '=120°，AP='AP =2，BP=CP '=4，∴PP '=23， ∵∠AP C '=120°,∠AP P '=30°，∴∠PP C '=150°，∴∠PP D '=30°，在Rt 'PDP 中，1'32PD PP ==， 22''3DP PP PD ∴=-=，''347DC DP P C ∴=+=+=，()222237213PC PD DC ∴=+=+= ．综上所述，27213PC =或【点睛】本题主要考查了全等三角形以及旋转，合理的作出辅助线以及熟练旋转的性质是解决本题的关键．10．如图，直线y ＝﹣x +c 与x 轴交于点B （3，0），与y 轴交于点C ，过点B ，C 的抛物线y ＝﹣x 2+bx +c 与x 轴的另一个交点为A ．（1）求抛物线的解析式和点A 的坐标；（2）P 是直线BC 上方抛物线上一动点，PA 交BC 于 D ．设t ＝PD AD，请求出t 的最大值和此时点P 的坐标；（3）M 是x 轴上一动点，连接MC ，将MC 绕点M 逆时针旋转90°得线段ME ，若点E 恰好落在抛物线上，请直接写出此时点M 的坐标．答案：A解析：（1）y＝﹣x2+2x+3，A（﹣1，0）；（2）t的最大值为916，此时P （32，154）；（3）M（9332-，0）或（9332+，0）．【分析】（1）利用待定系数法解决问题即可；（2）连接AC，PC，PB，过点A作AE⊥BC于E，过等P作PF⊥BC于F．设P（m，﹣m2+2m+3）．利用相似三角形的性质构建二次函数解决问题即可；（3）过点E作EH⊥x轴于H．设M（m，0），利用全等三角形的性质求出点E的坐标（用m表示），再利用待定系数法解决问题即可．【详解】解：（1）∵直线y＝﹣x+c与x轴交于点B（3，0），与y轴交于点C，∴0＝﹣3+c，解得c＝3，∴C（0，3），∵抛物线经过B，C，∴9303b cc-++=⎧⎨=⎩，解得23bc=⎧⎨=⎩，∴抛物线的解析式为y＝﹣x2+2x+3，令y＝0，得到﹣x2+2x+3＝0，解得x＝﹣1或3，∴A（﹣1，0）；（2）如图，连接AC，PC，PB，过点A作AE⊥BC于E，过点P作PF⊥BC于F．设P（m，﹣m2+2m+3）．∵AE∥PF，∴△PFD∽△AED，∴PDAD ＝PFAE，∵S△PBC＝12•BC•PF，S△ACB＝12•BC•AE，∴PDAD ＝PBCABCSS∆∆，∵S △ABC ＝12•AB •OC ＝12×4×3＝6， ∴t ＝PD AD ＝6PBC S ∆＝211133(23)332226m m m ⨯⨯+⨯⨯-++-⨯⨯＝﹣14m 2+34m ＝﹣14（m ﹣32）2+916， ∵﹣14＜0， ∴m ＝32时，t 有最大值，最大值为916，此时P （32，154）；（3）如图，过点E 作EH ⊥x 轴于H ，∵∠COM ＝∠EHM ＝∠CME ＝90°，∴∠EMH +∠CMH ＝90°，∠EMH +∠MEH ＝90°，∴∠MEH ＝∠CMO ，∵MC ＝ME ，∴△COM ≌△MHE （AAS ），∴OC ＝MH ＝3，OM ＝EH ，设M （m ，0），则E （m ﹣3，﹣m ），把E （m ﹣3，﹣m ）代入y ＝﹣x 2+2x +3，可得﹣（m ﹣3）2+2（m ﹣3）+3＝﹣m ，整理得，m 2﹣9m +12＝0，解得m 933-933+， ∴M 933-，0933+0）．【点睛】本题考查的是二次函数综合题，涉及全等三角形的性质和判定，相似三角形的性质和判定，解题的关键是利用数形结合的思想，在二次函数图象上构造全等三角形或相似三角形，利用几何的性质进行点坐标的求解．11．综合与实践实践操作：①如图1，ABC ∆是等边三角形，D 为BC 边上一个动点，将ACD ∆绕点A 逆时针旋转60︒得到AEF ∆，连接CE ．②如图2，在ABC ∆中，AD BC ⊥于点D ，将ABD ∆绕点A 逆时针旋转90︒得到AEF ∆，延长FE 与BC 交于点G ．③如图3，将图2中得到AEF ∆沿AE 再一次折叠得到AME ∆，连接MB ．问题解决：（1）小明在探索图1时发现四边形ABCE 是菱形．小明是这样想的：请根据小明的探索直接写出图1中线段CD ，CF ，AC 之间的数量关系为：（2）猜想图2中四边形ADGF 的形状，并说明理由；问题再探：（3）在图3中，若AD=6，BD=2，则MB 的长为．答案：C解析：（1）CD+CF=AC ；（2）四边形ADGF 为正方形；理由见解析；（3）13【分析】（1）先证明C 、F 、E 在同一直线上，再证明△BAD ≌△CAF （SAS ），则∠ADB=∠AFC ，BD=CF ，可得AC=CF+CD ；（2）先根据∠ADC=∠DAF=∠F=90°，证明得四边形ADGF 是矩形，由邻边相等可得四边形ADGF 是正方形；（3）证明△BAM ≌△EAD （SAS ），根据BM=DE 及勾股定理可得结论．【详解】解：（1）如图：由旋转得：∠DAF=60°=∠BAC，AD=AF，∴∠BAD=∠CAF，∵△ABC是等边三角形，∴AB=AC，∴△BAD≌△CAF（SAS），∴∠ADB=∠AFC，BD=CF，∵∠ADC+∠ADB=∠AFC+∠AFE=180°，∴C、F、E在同一直线上，∴AC=BC=BD+CD=CF+CD，+=；故答案为：CD CF AC（2）四边形ADGF是正方形，理由如下：如图：∵Rt△ABD绕点A逆时针旋转90°得到△AEF，∴AF=AD，∠DAF=90°，∵AD⊥BC，∴∠ADC=∠DAF=∠F=90°，∴四边形ADGF是矩形，∵AF=AD，∴四边形ADGF是正方形；（3）如图3，连接DE，∵四边形ADGF是正方形，DG=FG=AD=AF=6，∵△ABD绕点A逆时针旋转90°，得到△AEF，∴∠BAD=∠EAF，BD=EF=2，∴EG=FG-EF=6-2=4，∵将△AFE沿AE折叠得到△AME，∴∠MAE=∠FAE，AF=AM，∴∠BAD=∠EAM，∴∠BAD+∠DAM=∠EAM+∠DAM，即∠BAM=∠DAE，∵AF=AD，∴AM=AD，在△BAM和△EAD中，∵AM ADBAM DAEAB AE=⎧⎪∠=∠⎨⎪=⎩，∴△BAM≌△EAD（SAS），∴BM=DE=22EG DG+=2246213+=．故答案为：213．【点睛】本题属于四边形综合题，主要考查了旋转的性质、全等三角形的判定与性质、等边三角形的判定与性质、正方形的性质以及勾股定理的综合应用，解决问题的关键是熟练掌握等边三角形和全等三角形的性质，依据图形的性质进行计算求解．12．如图，BC⊥CA，BC＝CA，DC⊥CE，DC＝CE，直线BD与AE交于点F，交AC于点G，连接CF．（1）求证：△ACE≌△BCD；（2）求证：BF⊥AE；（3）请判断∠CFE与∠CAB的大小关系并说明理由．答案：C解析：（1）见解析；（2）见解析；（3）∠CFE＝∠CAB，见解析【分析】（1）根据垂直的定义得到∠ACB ＝∠DCE ＝90°，由角的和差得到∠BCD ＝∠ACE ，即可得到结论；（2）根据全等三角形的性质得到∠CBD ＝∠CAE ，根据对顶角的性质得到∠BGC ＝∠AGE ，由三角形的内角和即可得到结论；（3）过C 作CH ⊥AE 于H ，CI ⊥BF 于I ，根据全等三角形的性质得到AE ＝BD ，S △ACE ＝S △BCD ，根据三角形的面积公式得到CH ＝CI ，于是得到CF 平分∠BFH ，推出△ABC 是等腰直角三角形，即可得到结论．【详解】（1）证明：∵BC ⊥CA ，DC ⊥CE ，∴∠ACB ＝∠DCE ＝90°，∴∠BCD ＝∠ACE ，在△BCD 与△ACE 中，BC CA ACD ACE CD CE =⎧⎪∠=∠⎨⎪=⎩，∴△ACE ≌△BCD ；（2）∵△BCD ≌△ACE ，∴∠CBD ＝∠CAE ，∵∠BGC ＝∠AGE ，∴∠AFB ＝∠ACB ＝90°，∴BF ⊥AE ；（3）∠CFE ＝∠CAB ，过C 作CH ⊥AE 于H ，CI ⊥BF 于I ，∵△BCD ≌△ACE ，∴ACE BCD AE BD,S S ∆∆==，∴CH ＝CI ，∴CF 平分∠BFH ，∵BF ⊥AE ，∴∠BFH ＝90°，∠CFE ＝45°，∵BC ⊥CA ，BC ＝CA ，∴△ABC 是等腰直角三角形，∴∠CAB ＝45°，∴∠CFE ＝∠CAB ．【点睛】角的和差、对顶角的性质这些知识点在证明全等和垂直过程中经常会遇到，需要掌握。

八年级压轴题期末复习试卷专题练习(解析版)

八年级压轴题期末复习试卷专题练习（解析版）一、压轴题1．如图，直线2y x m =-+交x 轴于点A ，直线122y x =+交x 轴于点B ，并且这两条直线相交于y 轴上一点C ，CD 平分ACB ∠交x 轴于点D ．（1）求ABC 的面积．（2）判断ABC 的形状，并说明理由．（3）点E 是直线BC 上一点，CDE △是直角三角形，求点E 的坐标．2．如图，在平面直角坐标系中，直线y ＝2x ＋4与x 轴交于点A ，与y 轴交于点B ，过点B 的另一条直线交x 轴正半轴于点C ，且OC ＝3．图1 图2（1）求直线BC 的解析式；（2）如图1，若M 为线段BC 上一点，且满足S △AMB ＝S △AOB ，请求出点M 的坐标；（3）如图2，设点F 为线段AB 中点，点G 为y 轴上一动点，连接FG ，以FG 为边向FG 右侧作正方形FGQP ，在G 点的运动过程中，当顶点Q 落在直线BC 上时，求点G 的坐标；3．在等边△ABC 的顶点A 、C 处各有一只蜗牛，它们同时出发，分别以每分钟1米的速度由A 向B 和由C 向A 爬行，其中一只蜗牛爬到终点时，另一只也停止运动，经过t 分钟后，它们分别爬行到D 、E 处，请问：（1）如图1，在爬行过程中，CD 和BE 始终相等吗，请证明？（2）如果将原题中的“由A 向B 和由C 向A 爬行”，改为“沿着AB 和CA 的延长线爬行”，EB 与CD 交于点Q ，其他条件不变，蜗牛爬行过程中∠CQE 的大小保持不变，请利用图2说明：∠CQE =60°；（3）如果将原题中“由C 向A 爬行”改为“沿着BC 的延长线爬行，连接DE 交AC 于F ”，其他条件不变，如图3，则爬行过程中，证明：DF =EF4．已知在△ABC 中，AB =AC ，∠BAC =α，直线l 经过点A （不经过点B 或点C ），点C 关于直线l 的对称点为点D ，连接BD ，CD ．（1）如图1，①求证：点B ，C ，D 在以点A 为圆心，AB 为半径的圆上；②直接写出∠BDC 的度数（用含α的式子表示）为；（2）如图2，当α=60°时，过点D 作BD 的垂线与直线l 交于点E ，求证：AE =BD ；（3）如图3，当α=90°时，记直线l 与CD 的交点为F ，连接BF ．将直线l 绕点A 旋转的过程中，在什么情况下线段BF 的长取得最大值？若AC 2a ，试写出此时BF 的值．5．如图，在平面直角坐标系中，直线334y x =-+分别交,x y 轴于A B ，两点，C 为线段AB 的中点，(,0)D t 是线段OA 上一动点（不与A 点重合），射线//BF x 轴，延长DC 交BF 于点E ．（1）求证：AD BE =；（2）连接BD ，记BDE 的面积为S ，求S 关于t 的函数关系式；（3）是否存在t 的值，使得BDE 是以BD 为腰的等腰三角形？若存在，求出所有符合条件的t 的值；若不存在，请说明理由．6．ABC 是等边三角形，作直线AP ，点C 关于直线AP 的对称点为D ，连接AD ，直线BD 交直线AP 于点E ，连接CE ．（1）如图①，求证：CE AE BE +=；（提示：在BE 上截取BF DE =，连接AF ．）（2）如图②、图③，请直接写出线段CE ，AE ，BE 之间的数量关系，不需要证明；（3）在（1）、（2）的条件下，若26BD AE ==，则CE =__________．7．如图1中的三种情况所示，对于平面内的点M ，点N ，点P ，如果将线段PM 绕点P 顺时针旋转90°能得到线段PN ，就称点N 是点M 关于点P 的“正矩点”．（1）在如图2所示的平面直角坐标系xOy 中，已知(3,1),(1,3),(1,3)S P Q ---，(2,4)M -．①在点P ，点Q 中，___________是点S 关于原点O 的“正矩点”；②在S ，P ，Q ，M 这四点中选择合适的三点，使得这三点满足：点_________是点___________关于点___________的“正矩点”，写出一种情况即可；（2）在平面直角坐标系xOy 中，直线3(0)y kx k =+<与x 轴交于点A ，与y 轴交于点B ，点A 关于点B 的“正矩点”记为点C ，坐标为(,)C C C x y ．①当点A 在x 轴的正半轴上且OA 小于3时，求点C 的横坐标C x 的值；②若点C 的纵坐标C y 满足12C y -<≤，直接写出相应的k 的取值范围．8．阅读下面材料，完成(1)-(3)题．数学课上，老师出示了这样一道题：如图1，已知等腰△ABC中，AB＝AC，AD为BC边上的中线，以AB为边向AB左侧作等边△ABE，直线CE与直线AD交于点F．请探究线段EF、AF、DF之间的数量关系，并证明．同学们经过思考后，交流了自已的想法：小明：“通过观察和度量，发现∠DFC的度数可以求出来．”小强：“通过观察和度量，发现线段DF和CF之间存在某种数量关系．”小伟：“通过做辅助线构造全等三角形，就可以将问题解决．”......老师：“若以AB为边向AB右侧作等边△ABE，其它条件均不改变，请在图2中补全图形,探究线段EF、AF、DF三者的数量关系，并证明你的结论．”（1）求∠DFC的度数；（2）在图1中探究线段EF、AF、DF之间的数量关系，并证明；（3）在图2中补全图形，探究线段EF、AF、DF之间的数量关系，并证明．9．在等腰△ABC与等腰△ADE中，AB＝AC，AD＝AE，∠BAC＝∠DAE，且点D、E、C三点在同一条直线上，连接BD．（1）如图1，求证：△ADB≌△AEC（2）如图2，当∠BAC＝∠DAE＝90°时，试猜想线段AD，BD，CD之间的数量关系，并写出证明过程；（3）如图3，当∠BAC ＝∠DAE ＝120°时，请直接写出线段AD ，BD ，CD 之间的数量关系式为：（不写证明过程）10．已知在△ABC 中，AB ＝AC ，射线BM 、BN 在∠ABC 内部，分别交线段AC 于点G 、H ．（1）如图1，若∠ABC ＝60°，∠MBN ＝30°，作AE ⊥BN 于点D ，分别交BC 、BM 于点E 、F ．①求证：∠1＝∠2；②如图2，若BF ＝2AF ，连接CF ，求证：BF ⊥CF ；（2）如图3，点E为BC 上一点，AE 交BM 于点F ，连接CF ，若∠BFE ＝∠BAC ＝2∠CFE ，求ABFACF S S 的值．11．如图，四边形ABCD 是直角梯形，AD ∥BC ，AB ⊥AD ，且AB ＝AD +BC ，E 是DC 的中点，连结BE 并延长交AD 的延长线于G ．（1）求证：DG ＝BC ；（2）F 是AB 边上的动点，当F 点在什么位置时，FD ∥BG ；说明理由．（3）在（2）的条件下，连结AE 交FD 于H ，FH 与HD 长度关系如何？说明理由．12．如图，在平面直角坐标系中，直线y ＝2x +6与x 轴交于点A ，与y 轴交于点B ，过点B 的直线交x 轴于点C ，且AB ＝BC ．（1）求直线BC 的解析式；（2）点P 为线段AB 上一点，点Q 为线段BC 延长线上一点，且AP ＝CQ ，设点Q 横坐标为m ，求点P 的坐标（用含m 的式子表示，不要求写出自变量m 的取值范围）；（3）在（2）的条件下，点M 在y 轴负半轴上，且MP ＝MQ ，若∠BQM ＝45°，求直线PQ 的解析式．【参考答案】***试卷处理标记，请不要删除一、压轴题1．（1）5；（2）直角三角形，理由见解析；（3）44,33E ⎛⎫-⎪⎝⎭或82,33E ⎛⎫- ⎪⎝⎭ 【解析】【分析】（1）先求出直线122y x =+与x 轴的交点B 的坐标和与y 轴的交点C 的坐标，把点C 代入直线2y x m =-+，求出m 的值，再求它与x 轴的交点A 的坐标，ABC 的面积用AB 乘OC 除以2得到；（2）用勾股定理求出BC 的平方，AC 的平方，再根据AB 的平方，用勾股定理的逆定理证明ABC 是直角三角形；（3）先根据角平分线求出D 的坐标，再去分两种情况构造全等三角形，利用全等三角形的性质求出对应的边长，从而得到点E 的坐标．【详解】解：（1）令0x =，则10222y =⨯+=， ∴()0,2C ，令0y =，则1202x +=，解得4x =-， ∴()4,0B -，将()0,2C 代入2y x m =-+，得2m =，∴22y x =-+，令0y =，则220x -+=，解得1x =，∴1,0A ，∴5AB =，2OC =， ∴152ABC S AB OC =⋅=△；（2）根据勾股定理，222224220BC BO OC =+=+=，22222125AC AO OC =+=+=，且22525AB ==，∴222AB BC AC =+，则ABC 是直角三角形；（3）∵CD 平分ACB ∠， ∴12AD AC BD BC ==， ∴1533AD AB ==， ∴23OD AD OA =-=， ∴2,03D ⎛⎫- ⎪⎝⎭①如图，CED ∠是直角，过点E 作EN x ⊥轴于点N ，过点C 作CM EN ⊥于点M ，由（2）知，90ACB ∠=︒，∵CD 平分ACB ∠，∴45ECD ∠=︒，∴CDE △是等腰直角三角形，∴CE DE =，∵90NED MEC ∠+∠=︒，90NED NDE ∠+∠=︒，∴MEC NDE ∠=∠，在DNE △和EMC △中，NDE MEC DNE EMC DE EC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴()DNE EMC AAS ≅，设DN EM x ==，EN CM y ==，根据图象列式：DO DN CM EN EM CO +=⎧⎨+=⎩，即232x y x y ⎧+=⎪⎨⎪+=⎩，解得2343x y ⎧=⎪⎪⎨⎪=⎪⎩， ∴43EN CM ==， ∴44,33E ⎛⎫- ⎪⎝⎭；②如图，CDE ∠是直角，过点E 作EG x ⊥轴于点G ，同理CDE △是等腰直角三角形，且可以证得()CDO DEG AAS ≅，∴2DG CO ==，23EG DO ==， ∴28233GO GD DO =+=+=， ∴82,33E ⎛⎫- ⎪⎝⎭，综上：44,33E ⎛⎫-⎪⎝⎭，82,33E ⎛⎫- ⎪⎝⎭．【点睛】本题考查一次函数综合，解题的关键是掌握一次函数解析式的求解，与坐标轴交点的求解，图象围成的三角形面积的求解，还涉及勾股定理、角平分线的性质、全等三角形等几何知识，需要运用数形结合的思想去求解．2．（1）443y x =-+；（2）612(,)55M ；（3）23(0,)7G 或(0,-1)G 【解析】【分析】（1）求出点B ，C 坐标，再利用待定系数法即可解决问题；（2）结合图形，由S △AMB ＝S △AOB 分析出直线OM 平行于直线AB ，再利用两直线相交建立方程组求得交点M 的坐标；（3）分两种情形：①当n＞2时，如图2-1中，点Q落在BC上时，过G作直线平行于x 轴，过点F，Q作该直线的垂线，垂足分别为M，N．求出Q（n-2，n-1）．②当n＜2时，如图2-2中，同法可得Q（2-n，n+1），代入直线BC的解析式解方程即可解决问题．【详解】解：（1）∵直线y=2x+4与x轴交于点A，与y轴交于点B，∴A（-2，0），B（0，4），，又∵OC=3，∴C（3，0），设直线BC的解析式为y=kx+b，将B、C的坐标代入得：304k bb+=⎧⎨=⎩，解得：434kb⎧=-⎪⎨⎪=⎩，∴直线BC的解析式为443y x=-+；（2）连接OM，∵S△AMB＝S△AOB，∴直线OM平行于直线AB，故设直线OM解析式为：2y x=,将直线OM的解析式与直线BC的解析式联立得方程组2443y xy x=⎧⎪⎨=-+⎪⎩，解得：65125xy⎧=⎪⎪⎨⎪=⎪⎩故点612(,)55M；（3）∵FA=FB，A（-2，0），B（0，4），∴F （-1，2），设G （0，n ），①当n ＞2时，如图2-1中，点Q 落在BC 上时，过G 作直线平行于x 轴，过点F ，Q 作该直线的垂线，垂足分别为M ，N ．∵四边形FGQP 是正方形，易证△FMG ≌△GNQ ，∴MG=NQ=1，FM=GN=n-2，∴Q （n-2，n-1），∵点Q 在直线443y x =-+上， ∴41(2)43n n -=--+， ∴23=7n , ∴23(0,)7G ． ②当n ＜2时，如图2-2中，同法可得Q （2-n ，n+1），∵点Q 在直线443y x =-+上， ∴4+1(2)43n n =--+， ∴n=-1，∴(0,-1)G ．综上所述，满足条件的点G坐标为23(0,)7G或(0,-1)G【点睛】本题属于一次函数综合题，考查了待定系数法，三角形的面积，全等三角形的判定和性质，正方形的性质等知识，解题的关键是学会用分类讨论的思想思考问题，学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．3．（1)相等，证明见解析；（2)证明见解析；（3)证明见解析．【解析】【分析】（1）先证明△ACD≌△CBE，再由全等三角形的性质即可证得CD=BE；（2）先证明△BCD≌△ABE，得到∠BCD=∠ABE，求出∠DQB=∠BCQ+∠CBQ=∠ABE+∠CBQ=180°-∠ABC，∠CQE=180°-∠DQB，即可解答；（3）如图3，过点D作DG∥BC交AC于点G，根据等边三角形的三边相等，可以证得AD=DG=CE；进而证明△DGF和△ECF全等，最后根据全等三角形的性质即可证明．【详解】（1）解：CD和BE始终相等，理由如下：如图1，AB=BC=CA，两只蜗牛速度相同，且同时出发，∴CE=AD，∠A=∠BCE=60°在△ACD与△CBE中，AC=CB，∠A=∠BCE，AD=CE∴△ACD≌△CBE（SAS），∴CD=BE，即CD和BE始终相等；（2）证明：根据题意得：CE=AD，∵AB=AC，∴AE=BD，∴△ABC是等边三角形，∴AB=BC，∠BAC=∠ACB=60°，∵∠EAB+∠ABC=180°，∠DBC+∠ABC=180°，∴∠EAB=∠DBC，在△BCD和△ABE中，BC=AB，∠DBC=∠EAB，BD=AE∴△BCD≌△ABE（SAS），∴∠BCD=∠ABE∴∠DQB=∠BCQ+∠CBQ=∠ABE+∠CBQ=180°-∠ABC=180°-60°=120°，∴∠CQE=180°-∠DQB=60°，即CQE=60°；（3）解：爬行过程中，DF始终等于EF是正确的，理由如下：如图，过点D作DG∥BC交AC于点G，∴∠ADG=∠B=∠AGD=60°，∠GDF=∠E，∴△ADG为等边三角形，在△DGF 和△ECF 中，∠GFD=∠CFE ，∠GDF=∠E ，DG=EC∴△DGF ≌△EDF （AAS ），∴DF=EF.【点睛】本题主要考查了全等三角形的判定与性质和等边三角形的性质；题弄懂题中所给的信息，再根据所提供的思路寻找证明条件是解答本题的关键．4．（1）①详见解析；②12α；（2）详见解析；（3）当B 、O 、F 三点共线时BF 最长，(10+2)a【解析】【分析】（1）①由线段垂直平分线的性质可得AD=AC=AB ，即可证点B ，C ，D 在以点A 为圆心，AB 为半径的圆上；②由等腰三角形的性质可得∠BAC=2∠BDC ，可求∠BDC 的度数；（2）连接CE ，由题意可证△ABC ，△DCE 是等边三角形，可得AC=BC ，∠DCE=60°=∠ACB ，CD=CE ，根据“SAS”可证△BCD ≌△ACE ，可得AE=BD ；（3）取AC 的中点O ，连接OB ，OF ，BF ，由三角形的三边关系可得，当点O ，点B ，点F 三点共线时，BF 最长，根据等腰直角三角形的性质和勾股定理可求10BO a =，2OF OC a ==，即可求得BF【详解】（1）①连接AD ，如图1．∵点C 与点D 关于直线l 对称，∴AC = AD ．∵AB = AC ，∴AB = AC = AD ．∴点B ，C ，D 在以A 为圆心，AB 为半径的圆上．∴∠ADB=∠ABD，∠ADC=∠ACD，∵∠BAM=∠ADB+∠ABD，∠MAC=∠ADC+∠ACD，∴∠BAM=2∠ADB，∠MAC=2∠ADC，∴∠BAC=∠BAM+∠MAC=2∠ADB+2∠ADC=2∠BDC=α∴∠BDC=12α故答案为：12α．（2连接CE，如图2．∵∠BAC=60°，AB=AC，∴△ABC是等边三角形，∴BC=AC，∠ACB=60°，∵∠BDC=12α，∴∠BDC=30°，∵BD⊥DE，∴∠CDE=60°，∵点C关于直线l的对称点为点D，∴DE=CE，且∠CDE=60°∴△CDE是等边三角形，∴CD=CE=DE，∠DCE=60°=∠ACB，∴∠BCD=∠ACE，且AC=BC，CD=CE，∴△BCD≌△ACE（SAS）∴BD=AE，（3）如图3，取AC的中点O，连接OB，OF，BF，，F是以AC为直径的圆上一点，设AC中点为O，∵在△BOF中，BO+OF≥BF，当B、O、F三点共线时BF最长；如图，过点O 作OH ⊥BC ，∵∠BAC=90°，2a ，∴24BC AC a ==，∠ACB=45°，且OH ⊥BC ，∴∠COH=∠HCO=45°，∴OH=HC ，∴2OC HC =， ∵点O 是AC 中点，AC 2a ，∴2OC a =， ∴OH HC a ==，∴BH=3a ，∴10BO a =，∵点C 关于直线l 的对称点为点D ，∴∠AFC=90°， ∵点O 是AC 中点，∴2OF OC a ==，∴102BF a =， ∴当B 、O 、F 三点共线时BF 最长；最大值为102)a ．【点睛】本题是三角形综合题，考查了全等三角形的判定和性质，等腰三角形的性质，勾股定理，三角形的三边关系，灵活运用相关的性质定理、综合运用知识是解题的关键．5．（1）详见解析；（2）36(04)2BDE t t S-+≤<=；（3）存在，当78t =或43时，使得BDE 是以BD 为腰的等腰三角形．【解析】【分析】（1）先判断出EBC DAC ∠=∠，CEB CDA ∠=∠，再判断出BC AC =，进而判断出△BCE ≌△ACD ，即可得出结论；（2）先确定出点A ，B 坐标，再表示出AD ，即可得出结论；（3）分两种情况：当BD BE =时，利用勾股定理建立方程2223(4)t t +=-，即可得出结论；当BD DE =时，先判断出Rt △OBD ≌Rt △MED ，得出DM OD t ==，再用OM BE =建立方程求解即可得出结论．【详解】解：（1）证明：射线//BF x 轴，EBC DAC∴∠=∠，CEB CDA ∠=∠，又C 为线段AB 的中点，BC AC ∴=，在△BCE 和△ACD 中， CEB CDA EBC DAC BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△BCE ≌△ACD （AAS ），BE AD ∴=；（2）解：在直线334y x =-+中，令0x =，则3y =，令0y =，则4x =，A ∴点坐标为(4,0)，B 点坐标为(0,3)，D 点坐标为(,0)t ，4AD t BE ∴=-=，113(4)36(04)222BDE ABD B S S AD y t t t ∴==⋅=-⨯=-+<；（3）当BD BE =时，在Rt OBD ∆中，90BOD ∠=︒，由勾股定理得：222OB OD DB +=，即2223(4)t t +=-解得：78t =；当BD DE =时，过点E 作EM x ⊥轴于M ，90BOD EMD ∴∠=∠=︒，//BF OA ，OB ME ∴=在Rt △OBD 和Rt △MED 中，==BD DE OB ME ⎧⎨⎩，∴Rt △OBD ≌Rt △MED （HL ），OD DM t ∴==，由OM BE =得：24t t =- 解得：43t =，综上所述，当78t =或43时，使得△BDE 是以BD 为腰的等腰三角形．【点睛】本题是一次函数综合题，主要考查了平行线的性质，全等三角形的判定和性质，勾股定理，用方程的思想解决问题是解本题的关键．6．（1）见解析；（2）图②中，CE+BE=AE ，图③中，AE+BE=CE ；（3）1.5或4.5【解析】【分析】（1）在BE 上截取BF DE =，连接AF ，只要证明△AED ≌△AFB ，进而证出△AFE 为等边三角形，得出CE+AE= BF+FE ，即可解决问题；（2）图②中，CE+BE=AE ，延长EB 到F ，使BF=CE ，连接AF ，只要证明△ACE ≌△AFB ，进而证出△AFE 为等边三角形，得出CE+BE= BF+BE ，即可解决问题；图③中，AE+BE=CE ，在EC 上截取CF=BE ，连接AF ，只要证明△AEB ≌△AFC ，进而证出△AFE 为等边三角形，得出AE+BE =CF+EF ，即可解决问题；（3）根据线段CE ，AE ，BE ，BD 之间的数量关系分别列式计算即可解决问题．【详解】（1）证明：在BE 上截取BF DE =，连接AF ，在等边△ABC 中，AC=AB ，∠BAC=60°由对称可知：AP 是CD 的垂直平分线，AC=AD ，∠EAC=∠EAD ，设∠EAC=∠DAE=x ．∵AD=AC=AB ，∴∠D=∠ABD=12（180°-∠BAC-2x）=60°-x，∴∠AEB=60-x+x=60°．∵AC=AB，AC=AD，∴AB=AD，∴∠ABF=∠ADE，∵BF DE，∴△ABF≌△ADE，∴AF=AE，BF=DE，∴△AFE为等边三角形，∴EF=AE，∵AP是CD的垂直平分线，∴CE=DE，∴CE=DE=BF，∴CE+AE= BF+FE =BE；（2）图②中，CE+BE=AE，延长EB到F，使BF=CE，连接AF在等边△ABC中，AC=AB，∠BAC=60°由对称可知：AP是CD的垂直平分线，AC=AD，∠EAC=∠EAD，∴AB =AD，CE=DE，∵AE =AE∴△ACE≌△ADE，∴∠ACE=∠ADE∵AB =AD，∴∠ABD=∠ADB∴∠ABF=∠ADE=∠ACE∵AB=AC，BF=CE，∴△ACE≌△ABF，∴AE=AF，∠BAF=∠CAE∵∠BAC=∠BAE+∠CAE =60°∴∠EAF=∠BAE+∠BAF =60°∴△AFE为等边三角形，∴AE=BE+BF= BE+CE ，即CE+BE=AE ；图③中，AE+BE=CE ，在EC 上截取CF=BE ，连接AF ，在等边△ABC 中，AC=AB ，∠BAC=60°由对称可知：AP 是CD 的垂直平分线，AC=AD ，∠EAC=∠EAD ，∴AB =AD ，CE=DE ，∵AE =AE∴△ACE ≌△ADE ，∴∠ACE=∠ADE∵AB =AD ，∴∠ABD=∠ADB∴∠ABD=∠ADE=∠ACE∵AB=AC ，BE=CF ，∴△ACF ≌△ABE ，∴AE=AF ，∠BAE=∠CAF∵∠BAC=∠BAF+∠CAF =60°∴∠EAF=∠BAF+∠BAE =60°∴△AFE 为等边三角形，∴EF=AE ，∴CE =EF+CF= AE + BE ，即AE+BE=CE ；（3）在（1）的条件下，若26BD AE ==，则AE=3，∵CE+AE=BE ，∴BE-CE=3，∵BD=BE+ED=BE+CE=6，在（2）的条件下，若26BD AE ==，则AE=3，因为图②中，CE+BE=AE ，而BD=BE-DE=BE-CE ，所以BD 不可能等于2AE ；图③中，若26BD AE ==，则AE=3，∵AE+BE=CE ，∴CE-BE=3，∵BD=BE+ED=BE+CE=6，∴CE=4.5．即CE=1.5或4.5．【点睛】本题考查几何变换，等边三角形的性质，线段垂直平分线的性质，全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．7．（1）①点P ；②见解析；（2）①点C 的横坐标C x 的值为-3；②334k -≤<-【解析】【分析】（1）①在点P ，点Q 中，点OS 绕点O 顺时针旋转90°能得到线段OP ，故S 关于点O 的“正矩点”为点P ；②利用新定义得点S 是点P 关于点M 的“正矩点”（答案不唯一）；（2）①利用新定义结合题意画出符合题意的图形，利用新定义的性质证明△BCF ≌△AOB ，则FC=OB 求得点C 的横坐标；②用含k 的代数式表示点C 纵坐标，代入不等式求解即可．【详解】解：（1）①在点P ，点Q 中，点OS 绕点O 顺时针旋转90°能得到线段OP ，故S 关于点O 的“正矩点”为点P ，故答案为点P ；②因为MP 绕M 点顺时针旋转90︒得MS ，所以点S 是点P 关于点M 的“正矩点”，同理还可以得点Q 是点P 关于点S 的“正矩点”．（任写一种情况就可以）（2）①符合题意的图形如图1所示，作CE ⊥x 轴于点E ，CF ⊥y 轴于点F ，可得 ∠BFC=∠AOB=90°．∵直线3(0)y kx k =+<与x 轴交于点A ，与y 轴交于点B ，∴点B 的坐标为3(0,3),(,0)B A k-在x 轴的正半轴上， ∵点A 关于点B 的“正矩点”为点(,)C C C x y ，∴∠ABC=90°，BC=BA ，∴∠1＋∠2=90°，∵∠AOB=90°，∴∠2＋∠3=90°，∴∠1=∠3．∴△BFC ≌△AOB ，∴3FC OB ==，可得OE ＝3．∵点A 在x 轴的正半轴上且3OA <，0C x ∴<，∴点C 的横坐标C x 的值为－3．②因为△BFC ≌△AOB ，3(,0)A k-，A 在x 轴正半轴上，所以BF ＝OA ，所以OF ＝OB-OF ＝33k +点3(3,3)C k -+，如图2， -1＜C y ≤2，即：-1＜33k+ ≤2，则334k -≤<-．【点睛】本题考查的是一次函数综合运用，涉及到三角形全等、解不等式，新定义等，此类新定义题目，通常按照题设的顺序，逐次求解．8．（1）60°；（2）EF=AF+FC，证明见解析；（3）AF=EF+2DF，证明见解析．【解析】【分析】（1）可设∠BAD＝∠CAD＝α，∠AEC＝∠ACE＝β，在△ACE中，根据三角形内角和可得2α＋60＋2β＝180°，从而有α＋β＝60°，即可得出∠DFC的度数；（2）在EC上截取EG＝CF，连接AG，证明△AEG≌△ACF，然后再证明△AFG为等边三角形，从而可得出EF＝EG＋GF＝AF＋FC；（3）在AF上截取AG＝EF，连接BG，BF，证明方法类似（2），先证明△ABG≌△EBF，再证明△BFG为等边三角形，最后可得出结论．【详解】解：（1）∵AB=AC，AD为BC边上的中线，∴可设∠BAD＝∠CAD＝α，又△ABE为等边三角形，∴AE=AB=AC，∠EAB=60°，∴可设∠AEC＝∠ACE＝β，在△ACE中，2α＋60°＋2β＝180°，∴α＋β＝60°，∴∠DFC=α＋β＝60°；（2）EF=AF+FC，证明如下：∵AB=AC，AD为BC边上的中线，∴AD⊥BC，∴∠FDC=90°，∵∠CFD＝60°，则∠DCF=30°，∴CF＝2DF，在EC上截取EG＝CF，连接AG，又AE=AC，∴∠AEG=∠ACF，∴△AEG≌△ACF（SAS）,∴∠EAG＝∠CAF，AG＝AF，又∠CAF=∠BAD，∴∠EAG=∠BAD，∴∠GAF＝∠BAD+∠BAG=∠EAG+∠BAG=∠60°，∴△AFG为等边三角形，∴EF＝EG＋GF＝AF＋FC，即EF=AF+FC；（3）补全图形如图所示，结论：AF=EF+2DF．证明如下：同（1）可设∠BAD＝∠CAD＝α，∠ACE＝∠AEC＝β，∴∠CAE＝180°－2β，∴∠BAE＝2α＋180°－2β＝60°，∴β－α＝60°，∴∠AFC=β－α＝60°，又△ABE为等边三角形，∴∠ABE=∠AFC=60°，∴由8字图可得：∠BAD＝∠BEF，在AF上截取AG＝EF，连接BG，BF，又AB=BE，∴△ABG≌△EBF（SAS），∴BG＝BF，又AF垂直平分BC，∴BF=CF，∴∠BFA=∠AFC=60°，∴△BFG为等边三角形，∴BG=BF，又BC⊥FG，∴FG=BF=2DF，∴AF＝AG＋GF＝BF＋EF＝2DF＋EF．【点睛】本题考查了全等三角形的判定和性质、等边三角形的性质、等腰三角形的性质等知识，解决问题的关键是常用辅助线构造全等三角形，属于中考常考题型．9．（1）见解析；（2）CD＝2AD+BD，理由见解析；（3）CD＝3AD+BD【解析】【分析】（1）由“SAS”可证△ADB≌△AEC；（2）由“SAS”可证△ADB≌△AEC，可得BD＝CE，由直角三角形的性质可得DE＝2AD，可得结论；（3）由△DAB≌△EAC，可知BD＝CE，由勾股定理可求DH＝3AD，由AD＝AE，AH⊥DE，推出DH＝HE，由CD＝DE+EC＝2DH+BD＝3AD+BD，即可解决问题；【详解】证明：（1）∵∠BAC＝∠DAE，∴∠BAD＝∠CAE，又∵AB＝AC，AD＝AE，∴△ADB≌△AEC（SAS）；（2）CD＝2AD+BD，理由如下：∵∠BAC＝∠DAE，∴∠BAD＝∠CAE，又∵AB＝AC，AD＝AE，∴△ADB≌△AEC（SAS）；∴BD＝CE，∵∠BAC＝90°，AD＝AE，∴DE＝2AD，∵CD＝DE+CE，∴CD＝2AD+BD；（3）作AH⊥CD于H．∴∠BAD＝∠CAE，又∵AB＝AC，AD＝AE，∴△ADB≌△AEC（SAS）；∴BD＝CE，∵∠DAE＝120°，AD＝AE，∴∠ADH＝30°，∴AH＝12 AD，∴DH＝22AD AH＝32AD，∵AD＝AE，AH⊥DE，∴DH＝HE，∴CD＝DE+EC＝2DH+BD＝3AD+BD，故答案为：CD＝3AD+BD．【点睛】本题是结合了全等三角形的性质与判定，勾股定理等知识的综合问题，熟练掌握知识点，有简入难，层层推进是解答关键.10．（1）①见解析；②见解析；（2）2【解析】【分析】（1）①只要证明∠2+∠BAF＝∠1+∠BAF＝60°即可解决问题；②只要证明△BFC≌△ADB，即可推出∠BFC＝∠ADB＝90°；（2）在BF上截取BK＝AF，连接AK．只要证明△ABK≌CAF，可得S△ABK＝S△AFC，再证明AF＝FK＝BK，可得S△ABK＝S△AFK，即可解决问题；【详解】（1）①证明：如图1中，∵AB＝AC，∠ABC＝60°∴△ABC是等边三角形，∴∠BAC＝60°，∵AD⊥BN，∴∠ADB＝90°，∠BFD＝60°＝∠1+∠BAF＝∠2+∠BAF，∴∠1＝∠2②证明：如图2中，在Rt△BFD中，∵∠FBD＝30°，∴BF＝2DF，∵BF＝2AF，∴BF＝AD，∵∠BAE＝∠FBC，AB＝BC，∴△BFC≌△ADB，∴∠BFC＝∠ADB＝90°，∴BF⊥CF（2）在BF上截取BK＝AF，连接AK．∵∠BFE＝∠2+∠BAF，∠CFE＝∠4+∠1，∴∠CFB＝∠2+∠4+∠BAC，∵∠BFE＝∠BAC＝2∠EFC，∴∠1+∠4＝∠2+∠4∴∠1＝∠2，∵AB＝AC，∴△ABK≌CAF，∴∠3＝∠4，S△ABK＝S△AFC，∵∠1+∠3＝∠2+∠3＝∠CFE＝∠AKB，∠BAC＝2∠CEF，∴∠KAF＝∠1+∠3＝∠AKF，∴AF＝FK＝BK，∴S△ABK＝S△AFK，∴ABFAFCS2S∆∆=．本题考查全等三角形的判定和性质、等边三角形的性质、等腰三角形的判定和性质、直角三角形30度角性质等知识，解题的关键是能够正确添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．11．（1）见解析；（2）当F运动到AF＝AD时，FD∥BG，理由见解析；（3）FH＝HD，理由见解析【解析】【分析】（1）证明△DEG≌△CEB（AAS）即可解决问题．（2）想办法证明∠AFD＝∠ABG＝45°可得结论．（3）结论：FH＝HD．利用等腰直角三角形的性质即可解决问题．【详解】（1）证明：∵AD∥BC，∴∠DGE＝∠CBE，∠GDE＝∠BCE，∵E是DC的中点，即DE＝CE，∴△DEG≌△CEB（AAS），∴DG＝BC；（2）解：当F运动到AF＝AD时，FD∥BG．理由：由（1）知DG＝BC，∵AB＝AD+BC，AF＝AD，∴BF＝BC＝DG，∴AB＝AG，∵∠BAG＝90°，∴∠AFD＝∠ABG＝45°，∴FD∥BG，故答案为：F运动到AF＝AD时，FD∥BG；（3）解：结论：FH＝HD．理由：由（1）知GE＝BE，又由（2）知△ABG为等腰直角三角形，所以AE⊥BG，∵FD∥BG，∴AE⊥FD，∵△AFD为等腰直角三角形，∴FH＝HD，故答案为：FH＝HD．本题考查了全等三角形的判定和性质，平行线的判定，等腰直角三角形的性质，掌握三角形全等的判定和性质是解题的关键．12．（1）y＝﹣2x+6；（2）点P（m﹣6，2m﹣6）；（3）y＝﹣x+3 2【解析】【分析】（1）先求出点A，点B坐标，由等腰三角形的性质可求点C坐标，由待定系数法可求直线BC的解析式；（2）证明△PGA≌△QHC（AAS），则PG＝HQ＝2m﹣6，故点P的纵坐标为：2m﹣6，而点P在直线AB上，即可求解；（3）由“SSS”可证△APM≌△CQM，△ABM≌△CBM，可得∠PAM＝∠MCQ，∠BQM＝∠APM＝45°，∠BAM＝∠BCM，由“AAS”可证△APE≌△MAO，可得AE＝OM，PE＝AO＝3，可求m的值，进而可得点P，点Q的坐标，即可求直线PQ的解析式．【详解】（1）∵直线y＝2x+6与x轴交于点A，与y轴交于点B，∴点B(0，6)，点A(﹣3，0)，∴AO＝3，BO＝6，∵AB＝BC，BO⊥AC，∴AO＝CO＝3，∴点C(3，0)，设直线BC解析式为：y＝kx+b，则036k bb=+⎧⎨=⎩，解得：26kb=-⎧⎨=⎩，∴直线BC解析式为：y＝﹣2x+6；（2）如图1，过点P作PG⊥AC于点G，过点Q作HQ⊥AC于点H，∵点Q横坐标为m，∴点Q(m，﹣2m+6)，∵AB＝CB，∴∠BAC＝∠BCA＝∠HCQ，又∵∠PGA＝∠QHC＝90°，AP＝CQ，∴△PGA≌△QHC（AAS），∴PG＝HQ＝2m﹣6，∴点P的纵坐标为：2m﹣6，∵直线AB的表达式为：y＝2x+6，∴2m﹣6＝2x+6，解得：x＝m﹣6，∴点P(m﹣6，2m﹣6)；（3）如图2，连接AM，CM，过点P作PE⊥AC于点E，∵AB＝BC，BO⊥AC，∴BO是AC的垂直平分线，∴AM＝CM，且AP＝CQ，PM＝MQ，∴△APM≌△CQM（SSS）∴∠PAM＝∠MCQ，∠BQM＝∠APM＝45°，∵AM＝CM，AB＝BC，BM＝BM，∴△ABM≌△CBM（SSS）∴∠BAM＝∠BCM，∴∠BCM＝∠MCQ，且∠BCM+∠MCQ＝180°，∴∠BCM＝∠MCQ＝∠PAM＝90°，且∠APM＝45°，∴∠APM＝∠AMP＝45°，∴AP＝AM，∵∠PAO+∠MAO＝90°，∠MAO+∠AMO＝90°，∴∠PAO＝∠AMO，且∠PEA＝∠AOM＝90°，AM＝AP，∴△APE≌△MAO（AAS）∴AE＝OM，PE＝AO＝3，∴2m﹣6＝3，∴m＝92，∴Q(92，﹣3)，P(﹣32，3)，设直线PQ的解析式为：y＝ax+c，∴932332a ca c⎧-=+⎪⎪⎨⎪=-+⎪⎩，解得：132ac=-⎧⎪⎨=⎪⎩，∴直线PQ的解析式为：y＝﹣x+32．【点睛】本题主要考查三角形全等的判定和性质定理，等腰直角三角形的性质定理以及一次函数的图象和性质，添加辅助线，构造全等三角形，是解题的关键．。

人教版数学八年级上册期末考试几何压轴20题带答案解析河南各地期末试卷

1．如图，在△ABC中，∠ABC为锐角，点D为直线BC上一动点，以AD为直角边且在AD 的右侧作等腰直角三角形ADE，∠DAE＝90°，AD＝AE．（1）如果AB＝AC，∠BAC＝90°．①当点D在线段BC上时，如图1，线段CE、BD的位置关系为，数量关系为②当点D在线段BC的延长线上时，如图2，①中的结论是否仍然成立，请说明理由．（2）如图3，如果AB≠AC，∠BAC≠90°，点D在线段BC上运动．探究：当∠ACB 多少度时，CE⊥BC？请说明理由．2．如图，在平面直角坐标系中，△AOP为等边三角形，A（0，2），点B为y轴上一动点，以BP为边作等边△PBC，延长CA交x轴于点E．（1）求证：OB＝AC；（2）∠CAP的度数是；（直接写出答案，不需要说明理由．）（3）当B点运动时，猜想AE的长度是否发生变化？并说明理由；（4）在（3）的条件下，在y轴上存在点Q，使得△AEQ为等腰三角形，请写出点Q的坐标：．（直接写出答案，不需要说明理由．）3．（1）在等边三角形ABC中，①如图①，D，E分别是边AC，AB上的点且AE＝CD，BD与EC交于点F，则∠BFE的度数是度；②如图②，D，E分别是边AC，BA延长线上的点且AE＝CD，BD与EC的延长线交于点F，此时∠BFE的度数是度；（2）如图③，在△ABC中，AC＝BC，∠ACB是锐角，点O是AC边的垂直平分线与BC的交点，点D，E分别在AC，OA的延长线上，AE＝CD，BD与EC的延长线交于点F，若∠ACB＝α，求∠BFE的大小．（用含α的代数式表示）．4．如图，∠ACB＝90°，AC＝BC，BE⊥CE于E，AD⊥CE于D，BE＝3cm，AD＝9cm．求：（1）DE的长；（2）若CE在△ABC的外部（如图），其它条件不变，DE的长是多少？5．在平面直角坐标系中，直线AB分别交x轴，y轴于A（a，0），B（0，b），且满足a2+b2+4a ﹣8b+20＝0．（1）求a，b的值；（2）点P在直线AB的右侧；且∠APB＝45°，①若点P在x轴上（图1），则点P的坐标为；②若△ABP为直角三角形，求P点的坐标．6．在Rt△ABC中，∠ACB＝90°，CA＝CB，点D是直线AB上的一点，连接CD，将线段CD绕点C逆时针旋转90°，得到线段CE，连接EB．（1）操作发现如图1，当点D在线段AB上时，请你直接写出AB与BE的位置关系为；线段BD、AB、EB的数量关系为；（2）猜想论证当点D在直线AB上运动时，如图2，是点D在射线AB上，如图3，是点D在射线BA 上，请你写出这两种情况下，线段BD、AB、EB的数量关系，并对图2的结论进行证明；（3）拓展延伸若AB＝5，BD＝7，请你直接写出△ADE的面积．7．已知AB∥CD（1）如图，∠A＝40°，∠C＝78°，BP是∠ABG的平分线，DP是∠CDG的平分线，求∠P的度数；（2）如果∠A＝α，∠P＝β，其它条件不变，则∠C＝．8．如图，△ACB和△ECD都是等边三角形，点A、D、E在同一直线上，连接BE．（1）求证：AD＝BE；（2）求∠AEB的度数．9．（1）问题发现：如图1，已知：在△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．试写出线段DE，BD和CE之间的数量关系为；（2）思考探究：如图2，将（1）中的条件改为：在△ABC中，AB＝AC，D，A、E三点都在直线m上，并且∠BDA＝∠AEC＝∠BAC＝α，其中α为任意锐角或钝角．请问（1）中结论还是否成立？若成立，请给出证明；若不成立，请说明理由．（3）拓展应用：如图3，D、E是D、A、E三点所在直线m上的两动点（D，A，E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD，CE，若∠BDA＝∠AEC＝∠BAC，试判断△DEF的形状并说明理由．10．如图，在△ABC与△ABD中，AC＝BD，∠C＝∠D＝90°，AD与BC交于点E．（1）求证：BC＝AD．（2）若AC＝6，BC＝8，求△ACE的周长．11．如图，在四边形ABCD中，AB∥CD，∠ABC的平分线交CD的延长线于点E，F是BE 的中点，连接CF并延长交AD于点G．（1）求证：CG平分∠BCD．（2）若∠ADE＝110°，∠ABC＝52°，求∠CGD的度数．12．知识背景我们在第十一章《三角形》中学习了三角形的边与角的性质，在第十二章《全等三角形》中学习了全等三角形的性质和判定，在第十三章《轴对称》中学习了等腰三角形的性质和判定．在一些探究题中经常用以上知识转化角和边，进而解决问题．问题：如图1，△ABC是等腰三角形，∠BAC＝90°，D是BC的中点，以AD为腰作等腰△ADE，且满足∠DAE＝90°，连接CE并延长交BA的延长线于点F，试探究BC与CF之间的数量关系．发现：（1）BC与CF之间的数量关系为．探究：（2）如图2，当点D是线段BC上任意一点（除B、C外）时，其他条件不变，试猜想BC与CF之间的数量关系，并证明你的结论．拓展：（3）当点D在线段BC的延长线上时，在备用图中补全图形，并直接写出△BCF 的形状．13．（1）如图①，OP是∠MON的平分线，点A为OP上一点，请你作一个∠BAC，B、C 分别在OM、ON上，且使AO平分∠BAC（保留作图痕迹）；（2）如图②，在△ABC中，∠ACB是直角，∠B＝60°，△ABC的平分线AD，CE相交于点F，请你判断FE与FD之间的数量关系（可类比（1）中的方法）；（3）如图③，在△ABC中，如果∠ACB≠90°，而（2）中的其他条件不变，请问（2）中所得的结论是否仍然成立？若成立，请证明，若不成立，说明理由．14．如图，在平面直角坐标系中，点A的坐标为（1，0），以线段OA为边在第四象限内作等边三角形△AOB，点C为x正半轴上一动点（OC＞1），连接BC，以线段BC为边在第四象限内作等边三角形△CBD，连接DA并延长，交y轴于点E．（1）求证：△OBC≌△ABD．（2）在点C的运动过程中，∠CAD的度数是否会变化？如果不变，请求出∠CAD的度数；如果变化，请说明理由．（3）当点C运动到什么位置时，以A，E，C为顶点的三角形是等腰三角形？15．如图所示，△ABC是等腰三角形，AB＝AC，点D，E，F分别在AB，BC，AC边上，且BD＝CE，BE＝CF．（1）求证：△DEF是等腰三角形；（2）猜想：当∠A满足什么条件时，△DEF是等边三角形？并说明理由．16．如图，在△ABC中，AB＝AC，点D、E、F分别在AB、BC、AC边上，且BE＝CF，BD＝CE．（1）求证：△DEF是等腰三角形；（2）当∠A＝40°时，求∠DEF的度数．17．在△ABC中，∠ACB＝2∠B，如图①，当∠C＝90°，AD为∠BAC的平分线时，在AB上截取AE＝AC，连接DE．（1）求证：AB＝AC+CD；（2）如图②，当∠C≠90°，AD为∠BAC的平分线时，线段AB、AC、CD之间又有怎样的数量关系？只写出你的猜想，不用证明；（3）如图③，当AD为△ABC的外角平分线时，线段AB、AC、CD之间又有怎样的数量关系？请写出你的猜想，并对你的猜想给予证明．18．“我们应该讨论一般化、特殊化和类比这些过程本身，他们是获得发现的伟大源泉”﹣﹣乔治•波利亚．（1）观察猜想如图1，在△ABC中，CA＝CB，∠ACB＝90°．点D在AC上，点E在BC上，且CD ＝CE．则BE与AD的数量关系是，直线BE与直线AD的位置关系是；（2）拓展探究如图2，在△ABC和△CDE中，CA＝CB，CD＝CE，∠ACB＝∠DCE＝90°．则BE与AD的数量关系怎样？直线BE与直线AD的位置关系怎样？请说明理由；（3）解决问题如图3，在△ABC中，CA＝CB，∠ACB＝90°，BD是△ABC的角平分线，点M是AB 的中点．点P在射线BD上，连接PM，以点M为中心，将PM逆时针旋转90°，得到线段MN，请直接写出点A，P，N在同一条直线上时∠CPM的值．19．已知：三角形ABC中，∠A＝90°，AB＝AC，D为BC的中点，（1）若点E，F分别是AB，AC的中点，则△DEF是三角形；（2）如图，E，F分别是AB，AC上的点，且BE＝AF，求证：△DEF为等腰直角三角形；（3）若E，F分别为AB，CA延长线上的点，仍有BE＝AF，其他条件不变，那么，△DEF是否仍为等腰直角三角形？证明你的结论．20．在Rt△ABC中，∠ACB＝90°，AC＝BC，D为BC中点，CE⊥AD于E，BF∥AC交CE的延长线于F．（1）求证：△ACD≌△CBF；（2）求证：AB垂直平分DF．参考答案与解析1．如图，在△ABC中，∠ABC为锐角，点D为直线BC上一动点，以AD为直角边且在AD 的右侧作等腰直角三角形ADE，∠DAE＝90°，AD＝AE．（1）如果AB＝AC，∠BAC＝90°．①当点D在线段BC上时，如图1，线段CE、BD的位置关系为垂直，数量关系为相等②当点D在线段BC的延长线上时，如图2，①中的结论是否仍然成立，请说明理由．（2）如图3，如果AB≠AC，∠BAC≠90°，点D在线段BC上运动．探究：当∠ACB 多少度时，CE⊥BC？请说明理由．【分析】（1）①根据∠BAD＝∠CAE，BA＝CA，AD＝AE，运用“SAS”证明△ABD≌△ACE，根据全等三角形性质得出对应边相等，对应角相等，即可得到线段CE、BD之间的关系；②先根据“SAS”证明△ABD≌△ACE，再根据全等三角形性质得出对应边相等，对应角相等，即可得到①中的结论仍然成立；（2）先过点A作AG⊥AC交BC于点G，画出符合要求的图形，再结合图形判定△GAD ≌△CAE，得出对应角相等，即可得出结论．【解答】解：（1）CE与BD位置关系是CE⊥BD，数量关系是CE＝BD．理由：如图1，∵∠BAD＝90°﹣∠DAC，∠CAE＝90°﹣∠DAC，∴∠BAD＝∠CAE．又BA＝CA，AD＝AE，∴△ABD≌△ACE（SAS）∴∠ACE＝∠B＝45°且CE＝BD．∵∠ACB＝∠B＝45°，∴∠ECB＝45°+45°＝90°，即CE⊥BD．故答案为：垂直，相等；②都成立．∵∠BAC＝∠DAE＝90°，∴∠BAC+∠DAC＝∠DAE+∠DAC，∴∠BAD＝∠CAE，在△DAB与△EAC中，∴△DAB≌△EAC（SAS），∴CE＝BD，∠B＝∠ACE，∴∠ACB+∠ACE＝90°，即CE⊥BD；（2）当∠ACB＝45°时，CE⊥BD（如图2）．理由：过点A作AG⊥AC交CB的延长线于点G，则∠GAC＝90°，∵∠ACB＝45°，∠AGC＝90°﹣∠ACB，∴∠AGC＝90°﹣45°＝45°，∴∠ACB＝∠AGC＝45°，∴AC＝AG，…（8分）在△GAD与△CAE中，∴△GAD≌△CAE（SAS），∴∠ACE＝∠AGC＝45°，∠BCE＝∠ACB+∠ACE＝45°+45°＝90°，即CE⊥BC．【点评】此题为三角形综合题，主要考查了全等三角形的判定与性质及等腰直角三角形的性质，解决问题的关键是作辅助线构造全等三角形，根据全等三角形的对应边相等，对应角相等进行求解．2．如图，在平面直角坐标系中，△AOP为等边三角形，A（0，2），点B为y轴上一动点，以BP为边作等边△PBC，延长CA交x轴于点E．（1）求证：OB＝AC；（2）∠CAP的度数是60°；（直接写出答案，不需要说明理由．）（3）当B点运动时，猜想AE的长度是否发生变化？并说明理由；（4）在（3）的条件下，在y轴上存在点Q，使得△AEQ为等腰三角形，请写出点Q的坐标：（0，﹣2）或（0，6）．（直接写出答案，不需要说明理由．）【分析】（1）根据等边三角形性质得出OP＝AP，BP＝PC，∠APO＝∠CPB＝60°，求出∠OPB＝∠APC，证出△PBO≌△PCA即可；（2）当点B在y轴正半轴上时，由（1）知∠PBO＝∠PCA，根据∠BAC＝∠BPC＝60°，当点B在y轴负半轴上时，判断出△APC≌△OPB（SAS），即可求出答案．（3）∠EAO＝60°，求出∠AEO＝30°，得出AE＝2AO，求出即可．（4）分点Q在y轴正半轴和负半轴两种情况计算即可．【解答】（1）证明：∵△BPC和△AOP是等边三角形，∴OP＝AP，BP＝PC，∠APO＝∠CPB＝60°，∴∠APO+∠APB＝∠BPC+∠APB，即∠OPB＝∠APC，在△PBO和△PCA中，∴△PBO≌△PCA（SAS），∴OB＝AC；（2）解：当点B在y轴正半轴上时，由（1）知∠PBO＝∠PCA，∴∠BAC＝∠BPC＝60°，又∵∠OAP＝60°，∴∠CAP＝60°．当点B在y轴负半轴上时，如图，∵△AOP和△BCP是等边三角形，∴AP＝OP，PC＝PB，∠AOP＝∠APO＝∠BPC＝60°，∴∠APC＝∠OPB，∴△APC≌△OPB（SAS），∴∠CAP＝∠BOP＝180°﹣∠AOP＝120°，∵延长CA交x轴于点E，∴此种情况不符合题意，舍去，故答案为60°；（3）解：当B点运动时，AE的长度不发生变化，理由是：∵A（0，2），∴OA＝2，∵∠EAO＝∠BAC＝60°，∠AOE＝90°，∴∠AEO＝30°，∴AE＝2AO＝4，即当B点运动时，AE的长度不发生变化．（4）由（3）知，AE＝4，∠OAE＝60°，当点Q在y轴负半轴时，∵OA⊥AE，∴点Q与点A关于x轴对称，∴Q（0，﹣2），当点Q在y轴正半轴时，EQ＝AE＝4，∴OQ＝OA+EQ＝6，∴Q（0，6）．即：满足条件的点Q的坐标为（0，﹣2）或（0，6），故答案为（0，﹣2）或（0，6）．【点评】此题是三角形综合题，主要考查了等边三角形的性质，全等三角形的性质和判定，含30度角的直角三角形性质的应用，主要考查学生的推理能力．3．（1）在等边三角形ABC中，①如图①，D，E分别是边AC，AB上的点且AE＝CD，BD与EC交于点F，则∠BFE的度数是60度；②如图②，D，E分别是边AC，BA延长线上的点且AE＝CD，BD与EC的延长线交于点F，此时∠BFE的度数是60度；（2）如图③，在△ABC中，AC＝BC，∠ACB是锐角，点O是AC边的垂直平分线与BC的交点，点D，E分别在AC，OA的延长线上，AE＝CD，BD与EC的延长线交于点F，若∠ACB＝α，求∠BFE的大小．（用含α的代数式表示）．【分析】（1）只要证明△ACE≌△CBD，可得∠ACE＝∠CBD，推出∠BFE＝∠CBD+∠BCF＝∠ACE+∠BCF＝∠BCA＝60°；（2）只要证明△ACE≌△CBD，可得∠ACE＝∠CBD＝∠DCF，即可推出∠BFE＝∠D+∠DCF＝∠D+∠CBD＝∠BCA＝60°；（3）只要证明△AEC≌△CDB，可得∠E＝∠D，即可推出∠BFE＝∠D+∠DCF＝∠E+∠ECA＝∠OAC＝α；【解答】解：（1）如图①中，∵△ABC是等边三角形，∴AC＝CB，∠A＝∠BCD＝60°，∵AE＝CD，∴△ACE≌△CBD，∴∠ACE＝∠CBD，∴∠BFE＝∠CBD+∠BCF＝∠ACE+∠BCF＝∠BCA＝60°．故答案为60．（2）如图②中，∵△ABC是等边三角形，∴AC＝CB，∠A＝∠BCD＝60°，∴∠CAE＝∠BCD＝′120°∵AE＝CD，∴△ACE≌△CBD，∴∠ACE＝∠CBD＝∠DCF，∴∠BFE＝∠D+∠DCF＝∠D+∠CBD＝∠BCA＝60°．故答案为60．（3）如图③中，∵点O是AC边的垂直平分线与BC的交点，∴OC＝OA，∴∠EAC＝∠DCB＝α，∵AC＝BC，AE＝CD，∴△AEC≌△CDB，∴∠E＝∠D，∴∠BFE＝∠D+∠DCF＝∠E+∠ECA＝∠OAC＝α．【点评】本题考查全等三角形的判定和性质、等腰三角形的性质和判定、等边三角形的性质、线段的垂直平分线的性质等知识，解题的关键是正确寻找全等三角形解决问题．4．如图，∠ACB＝90°，AC＝BC，BE⊥CE于E，AD⊥CE于D，BE＝3cm，AD＝9cm．求：（1）DE的长；（2）若CE在△ABC的外部（如图），其它条件不变，DE的长是多少？【分析】（1）由余角的性质，推出∠CBE＝∠ECA，再依据全等三角形的判定定理“AAS”，推出△BEC和△CDA全等，然后即得BE＝CD，CE＝AD，再由BE＝3cm，AD＝9cm，结合图形即可推出DE＝6cm，（2）根据余角的性质推出∠CBE＝∠ACD，再依据全等三角形的判定定理“AAS”，推出△BEC和△CDA全等，然后即得BE＝CD，CE＝AD，再由BE＝3cm，AD＝9cm，结合图形即可推出DE＝12cm．【解答】解：（1）∵∠ACB＝90°，BE⊥CE，∴∠BCE+∠CBE＝90°，∠BCE+∠ECA＝90°，∴∠CBE＝∠ECA，∠BEC＝∠CDA，∵在△BEC和△CDA中，，∴△BEC≌△CDA（AAS），∴BE＝CD，CE＝AD，∵BE＝3cm，AD＝9cm，∴CD＝3cm，CE＝9cm，∴DE＝CE﹣CD＝6cm．（2）∵∠ACB＝90°，BE⊥CE于E，AD⊥CE于D，∴∠BCE+∠CBE＝90°，∠BCE+∠DCA＝90°，∠BEC＝∠CDA＝90°，∴∠CBE＝∠ACD，∵在△CBE和△ACD中，，∴△CBE≌△ACD（AAS），∴BE＝CD，CE＝AD，∵BE＝3cm，AD＝9cm，∴DE＝CD+CE＝BE+AD＝12cm．【点评】本题主要考查垂直的性质、全等三角形的判定与性质，关键在于根据相关的判定定理推出相关的三角形全等．5．在平面直角坐标系中，直线AB分别交x轴，y轴于A（a，0），B（0，b），且满足a2+b2+4a ﹣8b+20＝0．（1）求a，b的值；（2）点P在直线AB的右侧；且∠APB＝45°，①若点P在x轴上（图1），则点P的坐标为（4，0）；②若△ABP为直角三角形，求P点的坐标．【分析】（1）利用非负数的性质解决问题即可．（2）①根据等腰直角三角形的性质即可解决问题．②分两种情形：如图2中，若∠ABP＝90°，过点P作PC⊥OB，垂足为C．如图3中，若∠BAP＝90°，过点P作PD⊥OA，垂足为D．分别利用全等三角形的性质解决问题即可．【解答】解：（1）∵a2+4a+4+b2﹣8b+16＝0∴（a+2）2+（b﹣4）2＝0∴a＝﹣2，b＝4．（2）①如图1中，∵∠APB＝45°，∠POB＝90°，∴OP＝OB＝4，∴P（4，0）．故答案为（4，0）．②∵a＝﹣2，b＝4∴OA＝2OB＝4又∵△ABP为直角三角形，∠APB＝45°∴只有两种情况，∠ABP＝90°或∠BAP＝90°①如图2中，若∠ABP＝90°，过点P作PC⊥OB，垂足为C．∴∠PCB＝∠BOA＝90°，又∵∠APB＝45°，∴∠BAP＝∠APB＝45°，∴BA＝BP，又∵∠ABO+∠OBP＝∠OBP+∠BPC＝90°，∴∠ABO＝∠BPC，∴△ABO≌△BPC（AAS），∴PC＝OB＝4，BC＝OA＝2，∴OC＝OB﹣BC＝4﹣2＝2，∴P（4，2）．②如图3中，若∠BAP＝90°，过点P作PD⊥OA，垂足为D．∴∠PDA＝∠AOB＝90°，又∵∠APB＝45°，∴∠ABP＝∠APB＝45°，∴AP＝AB，又∵∠BAD+∠DAP＝90°，∠DP A+∠DAP＝90°，∴∠BAD＝∠DP A，∴△BAO≌△APP（AAS），∴PD＝OA＝2，AD＝OB＝4，∴OD＝AD﹣0A＝4﹣2＝2，∴P（2，﹣2）．综上述，P点坐标为（4，2），（2，﹣2）．【点评】本题属于三角形综合题，考查了等腰直角三角形的判定和性质，全等三角形的判定和性质等知识，解题的关键是学会用分类讨论的思想思考问题，学会添加常用辅助线，构造全等三角形解决问题，属于中考常考题型．6．在Rt△ABC中，∠ACB＝90°，CA＝CB，点D是直线AB上的一点，连接CD，将线段CD绕点C逆时针旋转90°，得到线段CE，连接EB．（1）操作发现如图1，当点D在线段AB上时，请你直接写出AB与BE的位置关系为AB⊥BE；线段BD、AB、EB的数量关系为AB＝BD+BE；（2）猜想论证当点D在直线AB上运动时，如图2，是点D在射线AB上，如图3，是点D在射线BA 上，请你写出这两种情况下，线段BD、AB、EB的数量关系，并对图2的结论进行证明；（3）拓展延伸若AB＝5，BD＝7，请你直接写出△ADE的面积．【分析】（1）证明△ACD≌△BCE（SAS）利用全等三角形的性质可得结论．（2）分两种情形，在图2和图3中，利用全等三角形的性质证明即可．（3）分两种情形，在图2和图3中，利用全等三角形的性质以及三角形的面积解决问题即可．【解答】解：（1）如图1中，∵∠ACB＝∠DCE＝90°，∴∠ACD＝∠BCE，∵CA＝CB，CD＝CE，∴△ACD≌△BCE（SAS），∴AD＝BE，∠CBE＝∠A，∵CA＝CB，∠ACB＝90°，∴∠A＝∠CBA＝45°，∴∠CBE＝∠A＝45°，∴∠ABE＝90°，∴AB⊥BE，∵AB＝AD+BD，AD＝BE，∴AB＝BD+BE，故答案为AB⊥BE，AB＝BD+BE．（2）①如图2中，结论：BE＝AB+BD．理由：∵∠ACB＝∠DCE＝90°，∴∠ACD＝∠BCE，∵CA＝CB，CD＝CE，∴△ACD≌△BCE（SAS），∴AD＝BE，∵AD＝AB+BD，AD＝BE，∴BE＝AB+BD．②如图3中，结论：BD＝AB+BE．理由：∵∠ACB＝∠DCE＝90°，∴∠ACD＝∠BCE，∵CA＝CB，CD＝CE，∴△ACD≌△BCE（SAS）∴AD＝BE，∵BD＝AB+AD，AD＝BE，∴BD＝AB+BE．（3）如图2中，∵AB＝5，BD＝7，∴BE＝AD＝5+7＝12，∵BE⊥AD，∴S△AED＝•AD•EB＝×12×12＝72．如图3中，∵AB＝5，BD＝7，∴BE＝AD＝BD﹣AB＝7﹣5＝2，∵BE⊥AD，∴S△AED＝•AD•EB＝×2×2＝2．【点评】本题属于几何变换综合题，考查了等腰直角三角形的性质，全等三角形的判定和性质等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型．7．已知AB∥CD（1）如图，∠A＝40°，∠C＝78°，BP是∠ABG的平分线，DP是∠CDG的平分线，求∠P的度数；（2）如果∠A＝α，∠P＝β，其它条件不变，则∠C＝2β﹣α．【分析】（1）根据三角形的外角的性质，外角等于不相邻的两个内角的和以及平行线、角平分线的性质即可求解；（2）根据外角等于不相邻的两个内角的和可以求解．【解答】解：（1）∵AB∥CD，DP是∠CDG的平分线，∴∠CDA＝∠A＝40°，∠CDP＝∠PDA＝20°；同理，∠P AB＝∠CBP＝39°在△CDM中，∠DMG＝∠CDM+∠C＝78°+20°＝98°，在△BPM中，根据三角形的外角的性质可以得到：∠P＝∠DMG﹣∠PBM＝98°﹣39°＝59°；（2）∵AB∥CD∴∠ABP＝∠PBC＝∠C在△CDM和△PBM中，根据三角形的外角的性质，即可得到：∠DMB＝∠C+α＝∠P+∠PBC即：∠C+α＝β+∠C则∠C＝2β﹣α．【点评】本题主要考查了三角形的外角等于不相邻的两个内角的和，平行线和角平分线的性质，结合图形找出各角间的关系是解题的关键．8．如图，△ACB和△ECD都是等边三角形，点A、D、E在同一直线上，连接BE．（1）求证：AD＝BE；（2）求∠AEB的度数．【分析】（1）由条件△ACB和△DCE均为等边三角形，易证△ACD≌△BCE，从而得到对应边相等，即AD＝BE；（2）根据△ACD≌△BCE，可得∠ADC＝∠BEC，由点A，D，E在同一直线上，可求出∠ADC＝120°，从而可以求出∠AEB的度数；【解答】证明：（1）∵△ACB和△ECD都是等边三角形，∴AC＝BC，CD＝CE，∠ACB＝∠DCE＝60°，又∵∠ACD＝∠ACB﹣∠DCB，∠BCE＝∠DCE﹣∠DCB，∴∠ACD＝∠BCE，在△ACD和△BCE中，∴△ACD≌△BCE（SAS）．∴AD＝BE；（2）在等边△ECD中，∠CDE＝∠CED＝60°，∴∠ADC＝120°，∵△ACD≌△BCE，∴∠BEC＝∠ADC＝120°，∴∠AEB＝∠BEC﹣∠CED＝120°﹣60°＝60°．【点评】主要考查了全等三角形的判定方法和性质，等边三角形的性质的综合应用．在判定三角形全等时，关键是选择恰当的判定条件，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造三角形．9．（1）问题发现：如图1，已知：在△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．试写出线段DE，BD和CE之间的数量关系为DE＝BD+CE；（2）思考探究：如图2，将（1）中的条件改为：在△ABC中，AB＝AC，D，A、E三点都在直线m上，并且∠BDA＝∠AEC＝∠BAC＝α，其中α为任意锐角或钝角．请问（1）中结论还是否成立？若成立，请给出证明；若不成立，请说明理由．（3）拓展应用：如图3，D、E是D、A、E三点所在直线m上的两动点（D，A，E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD，CE，若∠BDA＝∠AEC＝∠BAC，试判断△DEF的形状并说明理由．【分析】（1）根据垂直的定义得到∠BDA＝∠CEA＝90°，根据等角的余角相等得到∠CAE＝∠ABD，根据“AAS”证明△ADB≌△CEA，根据全等三角形的性质得到AE＝BD，AD＝CE，结合图形得到DE＝BD+CE；（2）根据∠BDA＝∠AEC＝∠BAC，得到∠BAD＝∠ACE，由AAS定理证明△BAD≌△ACE，根据全等三角形的性质得到BD＝AE，DA＝CE，得出结论；（3）根据等边三角形的性质得到∠BAC＝120°，证明△BAD≌△ACE，得到BD＝AE，证明△BDF≌△AEF，得到DF＝EF，∠BFD＝∠AFE，求出∠DFE＝60°，根据等边三角形的判定定理得到答案．【解答】解：（1）如图1，∵BD⊥直线m，CE⊥直线m，∴∠BDA＝∠CEA＝90°，∵∠BAC＝90°，∴∠BAD+∠CAE＝90°∵∠BAD+∠ABD＝90°，∴∠CAE＝∠ABD，在△ADB和△CEA中，，∴△ADB≌△CEA（AAS），∴AE＝BD，AD＝CE，∴DE＝AE+AD＝BD+CE，故答案为：DE＝BD+CE；（2）（1）中结论成立，理由如下：如图2，∵∠BDA＝∠BAC＝α，∴∠DBA+∠BAD＝∠BAD+∠CAE＝180°﹣α，∴∠DBA＝∠CAE，在△ADB和△CEA中，，∴△ADB≌△CEA（AAS），∴AE＝BD，AD＝CE，∴DE＝AE+AD＝BD+CE；（3）△DEF是等边三角形，理由如下：如图3，由（2）可知，△ADB≌△CEA，∴BD＝AE，∠DBA＝∠CAE，∵△ABF和△ACF均为等边三角形，∴∠ABF＝∠CAF＝60°，BF＝AF，∴∠DBA+∠ABF＝∠CAE+∠CAF，即∠DBF＝∠EAF，∵在△DBF和△EAF中，，∴△DBF≌△EAF（SAS）∴DF＝EF，∠BFD＝∠AFE，∴∠DFE＝∠DF A+∠AFE＝∠DF A+∠BFD＝60°，∴△DEF为等边三角形．【点评】本题考查的是全等三角形的判定与性质以及等边三角形的判定与性质，掌握全等三角形的判定定理和性质定理是解题的关键．10．如图，在△ABC与△ABD中，AC＝BD，∠C＝∠D＝90°，AD与BC交于点E．（1）求证：BC＝AD．（2）若AC＝6，BC＝8，求△ACE的周长．【分析】（1）由HL证得Rt△ABC≌Rt△BAD，即可得出结论；（2）由Rt△ABC≌Rt△BAD，得出∠ABC＝∠BAD，则AE＝BE，即可得出结果．【解答】（1）证明：∵∠C＝∠D＝90°，∴△ABC与△ABD都是直角三角形，在Rt△ABC和Rt△BAD中，，∴Rt△ABC≌Rt△BAD（HL），∴BC＝AD；（2）解：由（1）知Rt△ABC≌Rt△BAD，∴∠ABC＝∠BAD，∴AE＝BE，∴△ACE的周长＝AC+AE+CE＝AC+BE+CE＝AC+BC＝6+8＝14．【点评】本题考查了全等三角形的判定与性质、等腰三角形的判定与性质等知识；熟练掌握全等三角形的判定与性质是解题的关键．11．如图，在四边形ABCD中，AB∥CD，∠ABC的平分线交CD的延长线于点E，F是BE 的中点，连接CF并延长交AD于点G．（1）求证：CG平分∠BCD．（2）若∠ADE＝110°，∠ABC＝52°，求∠CGD的度数．【分析】（1）根据角平分线的定义得到．根据平行线的性质得到∠ABF＝∠E，推出△BCE是等腰三角形．根据等腰三角形的性质即可得到结论．（2）根据平行线的性质待定的∠ABC+∠BCD＝180°．根据角平分线的定义即可得到结论．【解答】（1）证明：∵BE平分∠ABC，∴．∵AB∥CD，∴∠ABF＝∠E，∴∠CBF＝∠E，∴BC＝CE，∴△BCE是等腰三角形．∵F为BE的中点，∴CF平分∠BCD，即CG平分∠BCD．（2）解：∵AB∥CD，∴∠ABC+∠BCD＝180°．∵∠ABC＝52°，∴∠BCD＝128°．∵CG平分∠BCD，∴．∵∠ADE＝110°，∠ADE＝∠CGD+∠GCD，∴∠CGD＝46°．【点评】本题考查了等腰三角形的判定和性质，平行线的性质，判断出△BCE是等腰三角形是解题的关键．12．知识背景我们在第十一章《三角形》中学习了三角形的边与角的性质，在第十二章《全等三角形》中学习了全等三角形的性质和判定，在第十三章《轴对称》中学习了等腰三角形的性质和判定．在一些探究题中经常用以上知识转化角和边，进而解决问题．问题：如图1，△ABC是等腰三角形，∠BAC＝90°，D是BC的中点，以AD为腰作等腰△ADE，且满足∠DAE＝90°，连接CE并延长交BA的延长线于点F，试探究BC与CF之间的数量关系．发现：（1）BC与CF之间的数量关系为BC＝CF．探究：（2）如图2，当点D是线段BC上任意一点（除B、C外）时，其他条件不变，试猜想BC与CF之间的数量关系，并证明你的结论．拓展：（3）当点D在线段BC的延长线上时，在备用图中补全图形，并直接写出△BCF 的形状．【分析】（1）先判断出∠BAD＝∠CAE，进而判断出△ABD≌△ACE，得出∠ACE＝∠B ＝45°，进而得出∠BCF＝90°，即可得出结论；（2）同（1）的方法，即可得出结论；（3）同（1）的方法即可得出结论．【解答】解：（1）BC＝CF．理由：∵△ABC是等腰三角形，且∠BAC＝90°，∴AB＝AC，∠B＝∠ACB＝45°．∵∠DAE＝90°，∴∠DAE＝∠BAC，∴∠DAE﹣∠DAC＝∠BAC﹣∠DAC，∴∠BAD＝∠CAE．∵△ADE是以AD为腰的等腰三角形，∴AD＝AE．在△ABD与△ACE中，AB＝AC，∠BAD＝∠CAE，AD＝AE，∴△ABD≌△ACE（SAS），∴∠ACE＝∠B＝45°．∵∠ACB＝45°，∴∠BCF＝∠ACB+∠ACE＝90°，∴∠B+∠F＝90°，∴∠F＝45°，∴∠B＝∠F，∴BC＝CF．故答案为：BC＝CF；（2）BC＝CF．理由：∵△ABC是等腰三角形，且∠BAC＝90°，∴AB＝AC，∠B＝∠ACB＝45°．∵∠DAE＝90°，∴∠DAE＝∠BAC，∴∠DAE﹣∠DAC＝∠BAC﹣∠DAC，∴∠BAD＝∠CAE．∵△ADE是以AD为腰的等腰三角形，∴AD＝AE．在△ABD与△ACE中，AB＝AC，∠BAD＝∠CAE，AD＝AE，∴△ABD≌△ACE（SAS），∴∠ACE＝∠B＝45°．∵∠ACB＝45°，∴∠BCF＝∠ACB+∠ACE＝90°，∴∠B+∠F＝90°，∴∠F＝45°，∴∠B＝∠F，∴BC＝CF．（3）△BCF是等腰直角三角形．理由：如备用图，∵△ABC是等腰三角形，∠BAC＝90°，∴AB＝AC，∠B＝∠ACB＝45°．∵∠DAE＝90°，∴∠DAE＝∠BAC，∴∠DAE+∠DAC＝∠BAC+∠DAC，∴∠BAD＝∠CAE．∵△ADE是以AD为腰的等腰三角形，∴AD＝AE．在△ABD与△ACE中，AB＝AC，∠BAD＝∠CAE，AD＝AE，∴△ABD≌△ACE（SAS），∴∠ACE＝∠B＝45°．∵∠ACB＝45°，∴∠BCF＝∠ACB+∠ACE＝90°，∴∠B+∠BFC＝90°，∴∠BFC＝45°，∴∠B＝∠BFC，∴△BCF是等腰三角形，∵∠BCF＝90°，∴△BCF是等腰直角三角形．【点评】此题是几何变换综合题，主要考查了旋转的性质，全等三角形的判定和性质，等腰三角形的判定和性质，判断出△ABD≌△ACE是解本题的关键．13．（1）如图①，OP是∠MON的平分线，点A为OP上一点，请你作一个∠BAC，B、C 分别在OM、ON上，且使AO平分∠BAC（保留作图痕迹）；（2）如图②，在△ABC中，∠ACB是直角，∠B＝60°，△ABC的平分线AD，CE相交于点F，请你判断FE与FD之间的数量关系（可类比（1）中的方法）；（3）如图③，在△ABC中，如果∠ACB≠90°，而（2）中的其他条件不变，请问（2）中所得的结论是否仍然成立？若成立，请证明，若不成立，说明理由．【分析】（1）在射线OM，ON上分别截取OB＝OC，连接AB，AC，则AO平分∠BAC；（2）过点F作FG⊥AB于G，作FH⊥BC于H，作FK⊥AC于K，根据角平分线上的点到角的两边的距离相等可得FG＝FH＝FK，根据四边形的内角和定理求出∠GFH＝120°，再根据三角形的内角和定理求出∠AFC＝120°，根据对顶角相等求出∠EFD＝120°，然后求出∠EFG＝∠DFH，再利用“角角边”证明△EFG和△DFH全等，根据全等三角形对应边相等可得FE＝FD；（3）过点F分别作FG⊥AB于点G，FH⊥BC于点H，首先证明∠GEF＝∠HDF，再证明△EGF≌△DHF可得FE＝FD．【解答】解：（1）如图①所示；（2）如图②，过点F作FG⊥AB于G，作FH⊥BC于H，作FK⊥AC于K，∵AD、CE分别是∠BAC、∠BCA的平分线，∴FG＝FH＝FK，在四边形BGFH中，∠GFH＝360°﹣60°﹣90°×2＝120°，∵AD、CE分别是∠BAC、∠BCA的平分线，∠B＝60°，∴∠F AC+∠FCA＝（180°﹣60°）＝60°，在△AFC中，∠AFC＝180°﹣（∠F AC+∠FCA）＝180°﹣60°＝120°，∴∠EFD＝∠AFC＝120°，∴∠EFG＝∠DFH，在△EFG和△DFH中，，∴△EFG≌△DFH（ASA），∴FE＝FD；（3）成立，理由：如图c，过点F分别作FG⊥AB于点G，FH⊥BC于点H．∴∠FGE＝∠FHD＝90°，∵∠B＝60°，且AD，CE分别是∠BAC，∠BCA的平分线，∴∠F AC+∠FCA＝60°，F是△ABC的内心，∴∠GEF＝∠BAC+∠FCA＝60°+∠BAD，∵F是△ABC的内心，即F在∠ABC的角平分线上，∴FG＝FH（角平分线上的点到角的两边相等）．又∵∠HDF＝∠B+∠BAD（外角的性质），∴∠GEF＝∠HDF．在△EGF与△DHF中，，∴△EGF≌△DHF（AAS），∴FE＝FD．【点评】本题是三角形综合题，主要考查了全等三角形的判定与性质、三角形内角和定理、角平分线的性质等知识，熟练掌握角平分线的性质，证明三角形全等是解题的关键．14．如图，在平面直角坐标系中，点A的坐标为（1，0），以线段OA为边在第四象限内作等边三角形△AOB，点C为x正半轴上一动点（OC＞1），连接BC，以线段BC为边在第四象限内作等边三角形△CBD，连接DA并延长，交y轴于点E．（1）求证：△OBC≌△ABD．（2）在点C的运动过程中，∠CAD的度数是否会变化？如果不变，请求出∠CAD的度数；如果变化，请说明理由．（3）当点C运动到什么位置时，以A，E，C为顶点的三角形是等腰三角形？【分析】（1）先根据等边三角形的性质得∠OBA＝∠CBD＝60°，OB＝BA，BC＝BD，则∠OBC＝∠ABD，然后可根据“SAS”可判定△OBC≌△ABD；（2）由△AOB是等边三角形知∠BOA＝∠OAB＝60°，再由△OBC≌△ABD知∠BAD ＝∠BOC＝60°，根据∠CAD＝180°﹣∠OAB﹣∠BAD可得结论；（3）先根据全等三角形的性质以及等边三角形的性质，求得∠EAC＝120°，进而得出以A，E，C为顶点的三角形是等腰三角形时，AE和AC是腰，最后根据Rt△AOE中，OA＝1，∠OEA＝30°，求得AC＝AE＝2，据此得到OC＝1+2＝3，即可得出点C的位置．【解答】解：（1）∵△AOB，△CBD都是等边三角形，∴OB＝AB，CB＝DB，∠ABO＝∠DBC，∴∠OBC＝∠ABC，在△OBC和△ABD中，∵，∴△OBC≌△ABD（SAS）；（2）点C在运动过程中，∠CAD的度数不会发生变化，理由如下：∵△AOB是等边三角形，∴∠BOA＝∠OAB＝60°，∵△OBC≌△ABD，∴∠BAD＝∠BOC＝60°，∴∠CAD＝180°﹣∠OAB﹣∠BAD＝60°；（3）∵△OBC≌△ABD，∴∠BOC＝∠BAD＝60°，又∵∠OAB＝60°，∴∠OAE＝180°﹣60°﹣60°＝60°，∴∠EAC＝120°，∠OEA＝30°，∴以A，E，C为顶点的三角形是等腰三角形时，AE和AC是腰，∵在Rt△AOE中，OA＝1，∠OEA＝30°，∴AE＝2，∴AC＝AE＝2，∴OC＝1+2＝3，∴当点C的坐标为（3，0）时，以A，E，C为顶点的三角形是等腰三角形．【点评】本题是三角形的综合问题，主要考查了全等三角形的判定与性质，等边三角形的性质的运用．全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．解决本题的关键是利用等腰三角形的性质求出点C的坐标．15．如图所示，△ABC是等腰三角形，AB＝AC，点D，E，F分别在AB，BC，AC边上，且BD＝CE，BE＝CF．（1）求证：△DEF是等腰三角形；（2）猜想：当∠A满足什么条件时，△DEF是等边三角形？并说明理由．【分析】（1）首先根据条件证明△DBE≌△ECF，根据全等三角形的性质可得DE＝FE，进而可得到△DEF是等腰三角形；（2）∠A＝60°时，△DEF是等边三角形，首先根据△DBE≌△ECF，再证明∠DEF＝60°，可以证出结论．【解答】（1）证明：∵AB＝AC，∴∠B＝∠C，在△DBE和△ECF中，，∴△DBE≌△ECF，∴DE＝FE，∴△DEF是等腰三角形；（2）当∠A＝60°时，△DEF是等边三角形，理由：∵△BDE≌△CEF，∴∠FEC＝∠BDE，∴∠DEF＝180°﹣∠BED﹣∠FEC＝180°﹣∠DEB﹣∠EDB＝∠B要△DEF是等边三角形，只要∠DEF＝60°．所以，当∠A＝60°时，∠B＝∠DEF＝60°，则△DEF是等边三角形．【点评】此题主要考查了等腰三角形的判定，等边三角形的判定，关键是证明△DBE≌△ECF．16．如图，在△ABC中，AB＝AC，点D、E、F分别在AB、BC、AC边上，且BE＝CF，BD＝CE．（1）求证：△DEF是等腰三角形；（2）当∠A＝40°时，求∠DEF的度数．【分析】（1）由AB＝AC，∠ABC＝∠ACB，BE＝CF，BD＝CE．利用边角边定理证明△DBE≌△CEF，然后即可求证△DEF是等腰三角形．（2）根据∠A＝40°可求出∠ABC＝∠ACB＝70°根据△DBE≌△CEF，利用三角形内角和定理即可求出∠DEF的度数．【解答】证明：∵AB＝AC，∴∠ABC＝∠ACB，在△DBE和△CEF中，∴△DBE≌△CEF，∴DE＝EF，∴△DEF是等腰三角形；。

初二下期末几何压轴题及解析

初二下期末几何压轴题及解析初二下期末几何及解析1、已知四边形ABCD，以边AB、AD为边分别向外侧作等边三角形ABF和ADE，连接EB、FD，交点为G。

1) 当四边形ABCD为正方形时，EB和FD的数量关系是什么？2) 当四边形ABCD为矩形时，EB和FD具有什么数量关系？请证明。

3) 四边形ABCD由正方形到矩形到一般平行四边形的变化过程中，∠EGD是否发生变化？如果改变，请说明理由；如果不变，请在图3中求出∠EGD的度数。

解答：1) EB=FD。

2) EB=FD。

证明：因为△AFB为等边三角形，所以AF=AB，∠FAB=60°；因为△ADE为等边三角形，所以AD=AE，∠EAD=60°，所以∠FAB+∠BAD=∠EAD+∠BAD，即∠FAD=∠BAE。

因此，△FAD≌△BAE，从而EB=FD。

3) ∠EGD不发生变化，因为在任何情况下，∠EGD都等于60°。

2、已知：在□ABCD中，点E是BC的中点，连接AE并延长交DC的延长线于点F，连接BF。

1) 求证：△ABE≌△FCE；2) 若AF=AD，求证：四边形ABFC是矩形。

解答：1) 如图1.在△ABE和△XXX中，∠1=∠2，∠3=∠4，BE=CE，因此△ABE≌△XXX。

2) 因为△ABE≌△FCE，所以AB=FC。

又因为AB∥FC，所以四边形ABFC是平行四边形。

由于四边形ABCD是平行四边形，所以AD=BC。

又因为AF=AD，所以AF=BC，从而四边形ABFC是矩形。

3、已知△ABC是一张等腰直角三角形纸板，∠B=90°，AB=BC=1.1) 要在这张纸板上剪出一个正方形，使这个正方形的四个顶点都在△XXX的边上。

XXX设计出了一种剪法，如图1所示。

请你再设计出一种不同于图1的剪法，并在图2中画出来。

2) 请在图3和图4中画出两个不同于图1和图2的剪法。

解答：1) 另一种剪法如图2所示，将△XXX沿着AC折叠，使点C与点B重合，然后将纸张沿着BD剪去一部分，即可得到正方形。

几何压轴题-含答案

几何压轴题类型一线段数量关系探究命题角度❶利用“倍长中线”添加辅助线(2020·原创)如图1，在△ABC和△ADE中，AB＝AC，AD＝AE，∠BAC＝∠DAE ＝90°.连接BE，DC，点P是CD的中点，连接AP.(1)求证：BE＝2AP；(2)如图2，若∠CAE＝30°，AB＝6，AD＝4，求AP的长．图1 图2【分析】(1)要证BE＝2AP，由点P是CD的中点，可知，延长AP到G，使得AP ＝PG，则△APD≌△GPC，从而只需证明AG＝BE即可；(2)由(1)可知，只需过点E作AC，AB的垂线，构造直角三角形求出BE的长即可．【自主解答】1．(2019·安顺)(1)如图1，在四边形ABCD中，AB∥CD，点E是BC的中点，若AE是∠BAD的平分线，试判断AB，AD，DC之间的等量关系．解决此问题可以用如下方法：延长AE交DC的延长线于点F，易证△AEB≌△FEC 得到AB＝FC，从而把AB，AD，DC转化在一个三角形中即可判断．AB，AD，DC之间的等量关系为 ________．(2)问题探究：如图2，在四边形ABCD中，AB∥CD，AF与DC的延长线交于点F，点E是BC的中点，若AE是∠BAF的平分线，试探究AB，AF，CF之间的等量关系，并证明你的结论．图1 图2命题角度❷利用“截长补短”添加辅助线(2019·大渡口区三诊)如图，平行四边形ABCD中，∠BAC＝90°，AB＝AC，点E是边AD上一点，且BE＝BC，BE交AC于点F，过点C作BE的垂线，垂足为O，与AD交于点G.(1)若AB＝2，求AE的长；(2)求证：BF＝CO＋3EO.【分析】(1)要求AE的长，由AB＝AC，∠BAC＝90°可求BC的长，从而得到BE的长，进而过点B作DA的垂线，构造等腰直角三角形，利用勾股定理列方程可解；(2)要证BF＝CO＋3OE，可考虑在CO的延长线上取点P，使得OP＝3OE，再证明BF＝CP，由OE⊥OG，故连接PF，PE，则需证△PFE是等边三角形即可．【自主解答】1．(2019·贵港改编)如图，已知△ABC是等腰直角三角形，∠BAC＝90°，将△ABC绕点C顺时针方向旋转105°得到△A′B′C，过点A′作A′D⊥AC的延长线于D，A′D交CB′于E，EF平分∠A′EC交BC于F.(1)求证：A′E＋CE＝EF；(2)若AB＝2，求EF的长．命题角度❸“构造等腰直角三角形”(2019·重庆A卷)如图，在▱ABCD中，点E在边BC上，连接AE，EM⊥AE，垂足为E，交CD于点M，AF⊥BC，垂足为F，BH⊥AE，垂足为H，交AF于点N，点P是AD上一点，连接CP.(1)若DP＝2AP＝4，CP＝17，CD＝5，求△ACD的面积；(2)若AE＝BN，AN＝CE.求证：AD＝2CM＋2CE.【分析】(1)要求△ACD的面积，由已知得到AD的长，故只需过点C作CG⊥AD，求出CG的长即可；(2)要证AD＝2CM＋2CE，可先证AD＝2AF，从而只需证明AF＝22CM＋CE，由AF＝CF可知只需证明EF＝22CM，进而连接NE，构造“等腰Rt△EFN”，只需证明EN＝CM即可．【自主解答】1．(2019·大渡口区二诊)如图，在Rt△ABC中，AC＝BC，∠ACB＝90°，点D 是BC上一点，连接AD.过点D作DE⊥AB，垂足为E.点F是AD的中点，连接EF.(1)如图1，若∠DAC＝α，请用含α的式子表示∠EFD的大小；(2)如图2，过点B作BG⊥AB，BG＝BE，连接CG.求证：AD＝2CG.图1 图22．(2019·枣庄)在△ABC中，∠BAC＝90°，AB＝AC，AD⊥BC于点D.(1)如图1，点M，N分别在AD，AB上，且∠BMN＝90°，当∠AMN＝30°，AB＝2时，求线段AM的长；(2)如图2，点E，F分别在AB，AC上，且∠EDF＝90°，求证：BE＝AF；(3)如图3，点M在AD的延长线上，点N在AC上，且∠BMN＝90°，求证：AB ＋AN＝2AM.命题角度❹构造“K”字模型(2019·泰州)如图，线段AB＝8，射线BG⊥AB，P为射线BG上一点，以AP 为边作正方形APCD，且点C，D与点B在AP两侧，在线段DP上取一点E，使∠EAP＝∠BAP，直线CE与线段AB相交于点F.(1)求证：△AEP≌△CEP；(2)判断CF与AB的位置关系，并说明理由；(3)求△AEF的周长．【分析】(1)要证△AEP≌△CEP，可由正方形的对称性得到PC＝PA，∠CPE＝∠APE，即可得证；(2)判断CF与AB的位置关系，从图中可观察CF⊥AB，故只需证明∠AFC＝90°，从而设AP交CF于M，证明∠FAM＝∠PCM即可；(3)要求△AEF的周长，可先过点C作CN⊥BP，构造“K字”模型得到△APB≌△PCN，利用全等特性，将AE＋AF＋EF转化为CE＋EF＋AF即可得解．【自主解答】1．(2019·南岸区二模)如图，在△ABC中，AB＝BC，两条高AD，BE相交于P，过点E作EG⊥AB，垂足为G，交AD于点F，过点F作FH∥AB交BC于点H，交BE于点Q，连接DE.(1)若AD＝12，CD＝5，求DE的长；(2)若∠ABC＝45°，求证：BE＝(1＋2)BQ.命题角度❺构造“平行四边形”模型(2019·南开中学模拟)如图，在平行四边形ABCD中，E为AD上一点，连接BE，CE，满足BC＝BE＝CE.(1)如图1，若∠ABC＝90°，BC＝4，求AC的长；(2)如图2，过点A作AF⊥BE于点F，交CE于点G，连接BG，在BG上取点M，使得∠AMG＝60°，延长AM交BC于点N，求证：CN＝2AE.图1 图2【分析】(1)由∠ABC＝90°得到四边形ABCD是矩形，再由BC＝BE＝CE得到△BCE是等边三角形，利用锐角三角函数即可得解；(2)要证CN＝2AE，可先过点E 作AN的平行线交CN于H，从而只需证明CH＝NH即可．【自主解答】1．(2018·重庆B卷)如图，在平行四边形ABCD中，∠ACB＝45°，点E在对角线AC上，BE＝BA，BF⊥AC于点F，BF的延长线交AD于点G，点H在BC的延长线上，且CH＝AG，连接EH.(1)若BC＝122，AB＝13，求AF的长；(2)求证：EB＝EH.2．(2017·重庆B卷)如图，△ABC中，∠ACB＝90°，AC＝BC，点E是AC上一点，连接BE.(1)如图1，若AB＝42，BE＝5，求AE的长；(2)如图2，点D是线段BE延长线上一点，过点A作AF⊥BD于点F，连接CD，CF，当AF＝DF时，求证：DC＝BC.图1 图23．(2019·西南师大附中适应性考试)如图，在平行四边形ABCD中，AB⊥AC，过点D作DE⊥AD交直线AC于点E，点O是对角线AC的中点，点F是线段AD上一点，连接FO并延长交BC于点G.(1)如图1，若AC ＝4，cos ∠CAD ＝45，求△ADE 的面积；(2)如图2，点H 为DC 延长线上一点，连接HF ，若∠H ＝30°，DE ＝BG ，求证：DH ＝CE ＋32FH.图1 图2类型二角度数量关系探究(2017·重庆A卷)在△ABM中，∠ABM＝45°，AM⊥BM，垂足为M，点C是BM延长线上一点，连接AC.(1)如图1，若AB＝32，BC＝5，求AC的长；(2)如图2，点D是线段AM上一点，MD＝MC，点E是△ABC外一点，EC＝AC，连接ED并延长交BC于点F，且点F是线段BC的中点，求证：∠BDF＝∠CEF.图1 图2【分析】(1)由AM⊥BM，∠ABM＝45°，可得△ABM是等腰直角三角形，△AMC是直角三角形，再由AB＝32根据勾股定理求得AM与BM的长为3，因为BC＝5，可得MC＝5－3＝2，在Rt△AMC中，利用勾股定理即可求得AC的长；(2)延长EF至点H，使FH＝EF，连接BH，可得△BFH≌△CFE，从而得到BH＝CE，∠H＝∠CEF，故要证∠CEF＝∠BDF，只需证明∠H＝∠BDF即可．【自主解答】1．(2019·淮安改编)如图，在△ABC中，AB＝AC，∠BAC＝100°，AD是边BC 上的中线，点P在射线AD上，连接BP，将线段BP绕点P逆时针旋转80°，得到线段PE.(1)当点E落在AD的延长线上时，连接BE，求∠BEP的度数；(2)当点E在射线AD的右侧，连接CE并延长交射线AD于F，求证：∠CFD＝∠BAD.2．(2019·重庆八中开学考试)如图，平行四边形ABCD中，BF⊥DC于点F，且BF＝AB，点E是BC边上一点，连接AE交BF于G.(1)若AE平分∠DAB，∠C＝60°，BE＝3，求BG的长；(2)若AD＝BG＋FC，求证：AE平分∠DAB.类型三线段比值关系探究(2016·重庆A 卷)在△ABC 中，∠B ＝45°，∠C ＝30°，点D 是BC 上一点，连接AD ，过点A 作AG ⊥AD ，在AG 上取点F ，连接DF ，延长DA 至E ，使得AE ＝AF ，连接EG ，DG ，且GE ＝DF. (1)若AB ＝22，求BC 的长；(2)如图1，当点G 在AC 上时，求证：BD ＝12CG ；(3)如图2，当点G 在AC 的垂直平分线上时，直接写出ABCG的值．图1 图2【分析】(1)要求BC 的长，由已知∠B ＝45°，∠C ＝30°，从而过点A 作AH ⊥BC ，分别在Rt △ABH 和Rt △ACH 中求出BH 和CH 即可；(2)要证BD ＝12CG ，过点A 作AM ⊥AB 交BC 于M ，连接GM ，从而只需证明GM ＝BD ，且GM ⊥BC 即可；(3)要求ABCG ，可用相同的未知数分别表示AB ，CG ，再作比即可．【自主解答】1．(2016·重庆B 卷)已知△ABC 是等腰直角三角形，∠BAC ＝90°，CD ＝12BC ，DE ⊥CE ，DE ＝CE ，连接AE ，点M 是AE 的中点．(1)如图1，若点D 在BC 边上，连接CM ，当AB ＝4时，求CM 的长；(2)如图2，若点D 在△ABC 的内部，连接BD ，点N 是BD 中点，连接MN ，NE ，求证：MN ⊥AE ；(3)如图3，将图2中的△CDE 绕点C 逆时针旋转，使得∠BCD ＝30°，连接BD ，点N 是BD 中点，连接MN ，探索MNAC的值，并直接写出结果．参考答案【例1】(1)证明：延长AP到G，使得PG＝AP，连接CG，并延长交AE于H.解图1∵点P是CD的中点，∴PC＝PD，∵PG＝PA，∠CPG＝∠DPA，∴△PCG≌△PDA，∴CG＝AD＝AE，∠PGC＝∠PAD，∴CG∥AD.∵DA⊥AE，∴CH⊥AH，∴∠HAC＋∠HCA＝90°，∵∠HAC＋∠BAE＝90°，∴∠BAE＝∠ACG，解图2∵AB＝AC，∴△ABE≌△CAG，∴BE＝AG，∵AG＝2AP，∴BE＝2AP.(2)解：过点E分别作AC，AB的垂线，垂足记为G，H，∵∠CAE＝30°，∴∠AEG＝60°，∴EG＝2，AG＝23，∵∠BAC＝90°，∴四边形EGAH是矩形，∴AH＝EG＝2，EH＝AG＝23，∴BH＝AB－AH＝4，∴在Rt△BHE中，BE＝BH2＋EH2＝27，∴AP＝7. 跟踪训练1．解：(1)AD＝AB＋DC.理由：∵AE是∠BAD的平分线，∴∠DAE＝∠BAE.∵AB∥CD，∴∠F＝∠BAE.∴∠DAF＝∠F.∴AD＝DF.∵点E是BC的中点，∴CE＝BE，且∠F＝∠BAE，∠AEB＝∠CEF，∴△CEF≌△BEA(AAS)，∴AB＝CF.∴AD＝CD＋CF＝CD＋AB.(2)AB＝AF＋CF.理由：如解图，延长AE交DF的延长线于点G，∵E是BC的中点，∴CE＝BE，∵AB∥DC，∴∠BAE＝∠G.∵∠AEB＝∠GEC，∴△AEB≌△GEC(AAS)，∴AB＝GC.∵AE是∠BAF的平分线，∴∠BAG＝∠FAG.∵∠BAG＝∠G，∴∠FAG＝∠G.∴FA＝FG.∵CG＝CF＋FG，∴AB＝AF＋CF.【例2】解：(1)如解图1，过点B作BH⊥DA交DA延长线于H.解图1∵在Rt△ABC中，AB＝AC＝2，∠BAC＝90°，∴BC＝2AB＝2，∠ABC＝∠ACB＝45°，∴BE＝BC＝2，∵四边形ABCD是平行四边形，∴AD∥BC，∴∠HAB＝∠ABC＝45°，∴AH＝BH＝22AB＝1，在Rt△BEH中，由勾股定理得BH2＋HE2＝BE2，即1＋(AE＋1)2＝22，解得AE＝3－1(负值舍去)．(2)证明：如解图2，分别延长BA ，CO 交于点P ，连接PE ，PF.例2题解图2∵CO⊥BE，BA⊥CA，∴∠BAF＝∠COF＝∠CAP＝90°， ∵∠AFB＝∠OFC， ∴∠ABF＝∠PCA，在△ABF 和△ACP 中，⎩⎪⎨⎪⎧∠FAB＝∠PAC AB ＝AC∠ABF＝∠ACP ，∴△ABF≌△ACP， ∴CP＝BF ，AF ＝AP ， ∴∠AFP＝∠APF＝45°.过点E 作EQ⊥BC 于Q ，过点A 作AM⊥BC 于M ，易得四边形AMQE 是矩形，AM ＝12BC ，则EQ ＝AM ＝12BC ＝12BE ，∴∠EBQ＝30°，∴∠PBF＝15°， ∴∠PFE＝∠PBF＋∠BPF＝60°，在△PAE 和△FAE 中，⎩⎪⎨⎪⎧AP ＝AF ∠PAE＝∠FAE＝45°AE ＝AE ，∴△PAE≌△FAE，∴PE＝EF ，∴△PEF 是等边三角形，∴PO＝3OE ，∴BF＝CO＋PO＝CO＋3OE.跟踪训练1．(1)证明：如解图，在EF上截取EG＝EC，连接CG.∵△ABC是等腰直角三角形，∠BAC＝90°，∴AB＝AC，∠ABC＝∠ACB＝45°，∵△A′B′C是由△ABC绕点C顺时针旋转105°得到的，∴∠A′CE＝∠BCA＝45°，∠ACA′＝105°，∴∠A′CD＝180°－∠A′CA＝75°，∵A′D⊥AD，∴∠CA′E＝90°－∠A′CD＝15°，∴∠A′EC＝180°－∠CA′E－∠A′CE＝120°，∵EF平分∠A′EC，∴∠A′EF＝∠CEF＝60°，∵EG＝EC，∴△CEG是等边三角形，∴∠CGE＝60°，CG＝CE，∴∠FGC＝120°＝∠A′EC，∵∠BCB′＝105°，∠GCE＝60°，∴∠FCG＝45°＝∠A′CE，∴△FCG≌△A′CE，∴FG＝A′E，∵FE＝FG＋GE，∴FE＝A′E＋CE.(2)解：根据题意可知AC＝AB＝A′C＝ 2.如解图，过点A′作A′N⊥CB′于N，则A′N＝CN＝1，∵∠A′EC＝120°，∴∠CED＝∠A′EN＝60°， ∴EN＝A′N tan∠A′EN ＝33，∴A′E＝2EN ＝233，CE ＝CN －EN ＝1－33，∴E F ＝A′E＋CE ＝233＋1－33＝1＋33.【例3】(1)解：如解图，作CG⊥AD 于G.设PG ＝x ，则DG ＝4－x ，在Rt△PCG 中，由勾股定理得CG 2＝CP 2－PG 2＝17－x 2，在Rt△DGC 中，由勾股定理得CG 2＝CD 2－GD 2＝9＋8x －x 2， ∴17－x 2＝9＋8x －x 2，解得x ＝1，即PG ＝1，∴CG＝4， ∵AD＝DP ＋AP ＝6，∴S △ACD ＝12AD·CG＝12.(2)证明：连接NE ，如解图所示，∵BH⊥AE，AF⊥BC，AE⊥EM，∴∠AEB＋∠NBF＝∠AEB＋∠EAF＝∠AEB＋∠MEC＝90°， ∴∠NBF＝∠EAF＝∠MEC， ∵∠BFN＝∠AFE，BN ＝AE ，∴△NBF≌△EAF，∴BF＝AF ，NF ＝EF ， ∴∠ABC＝45°，∠ENF＝45°，FC ＝AF ＝BF ， ∴∠ANE＝∠BCD＝135°，AD ＝BC ＝2AF ， ∵∠MEC＝∠EAF，AN ＝CE ， ∴△ANE≌△ECM，∴CM＝NE.∴NF＝22NE＝22MC，∴AF＝22MC＋CE，∴AD＝2MC＋2CE.跟踪训练1．(1)解：∵在Rt△ABC中，AC＝BC，∠ACB＝90°，∴∠CAB＝∠CBA＝45°，∴∠EAF＝45°－α，∵DE⊥AB，点F是AD的中点，∴EF＝AF，∴∠EFD＝2∠EAF＝90°－2α.(2)证明：连接CE，CF，如解图，∵BG⊥AB，∴∠EBG＝90°，∵∠EBC＝45°，∴∠CBG＝45°，∴∠EBC＝∠GBC，∵BE＝BG，BC＝BC，∴△CEB≌△CGB(SAS)，∴CE＝CG，∵DE⊥AB，∠ACB＝90°，∴△AED和△ACD是直角三角形，∵点F 是AD 的中点，∴EF＝CF ＝12AD ，∴∠EFD＝2∠EAD，∠CFD＝2∠CAF， ∴∠EFC＝2∠EAC＝90°， ∴△EFC 是等腰直角三角形， ∴C E ＝2EF ＝2(12AD)，∴AD＝2CE ，∴AD＝2CG.2．(1)解：∵∠BAC＝90°，AB ＝AC ，AD⊥BC， ∴AD＝BD ＝DC ，∠ABC＝∠ACB＝45°， ∠BAD＝∠CAD＝45°， ∵AB＝2，∴AD＝BD ＝CD ＝2，∵∠AMN＝30°，∴∠BMD＝180°－90°－30°＝60°， ∴∠MBD＝30°，∴MB＝2DM.由勾股定理得BM 2－DM 2＝BD 2，∴(2DM)2－DM 2＝(2)2，解得DM ＝63，∴AM＝AD －DM ＝2－63.(2)证明：∵AD⊥BC，∠EDF＝90°， ∴∠BDE＝∠ADF， ∵∠B＝∠DAF，BD ＝DA ， ∴△BDE≌△ADF，∴BE＝AF.(3)证明：过点M 作ME∥BC 交AB 的延长线于E ，∴∠AME＝∠ADB＝90°，∵∠BAM＝45°，∴∠E＝45°＝∠MAN，AM＝ME，∵∠BMN＝90°，∴∠EMB＋∠BMA＝∠BMA＋∠AMN，即∠BME＝∠AMN，∴△BME≌△NMA，∴BE＝AN，∴AB＋AN＝AE＝2AM. 【例4】(1)证明：∵四边形APCD是正方形，∴PD平分∠APC，PC＝PA，∵PE＝PE，∴△PCE≌△PAE.(2)解：CF⊥AB.理由如下：设AP交CF于M，如解图，∵△AEP≌△CEP，∴∠EAP＝∠ECP，∵∠EAP＝∠BAP，∠PCM＋∠CMP＝90°，∠CMP＝∠AMF，∴∠MAF＋∠AMF＝90°，∴∠AFM＝90°，即CF⊥AB.(3)解：如解图，过点C作CN⊥PB于N，∵CF⊥AB，BG⊥AB，∴四边形CNBF是矩形，∴BF＝CN，CF＝BN.∵∠PCN＋∠CPN＝∠CPN＋∠APB＝90°，∴∠PCN＝∠APB， ∵∠CNP＝∠PBA，CP ＝AP ， ∴△ABP≌△PNC， ∴BP＝CN ＝BF ，AB ＝PN ， ∵△AEP≌△CEP，∴AE＝CE ，∴AE＋EF ＋AF ＝CE ＋EF ＋AF ＝BN ＋AF ＝PN ＋PB ＋AF ＝AB ＋AF ＋BF ＝2AB ＝16. 跟踪训练1．(1)解：在Rt△ADC 中，AD ＝12，CD ＝5，由勾股定理得AC ＝13，∵AB＝BC ，BE⊥AC，∴AE＝CE ， ∴DE＝AE ＝CE ＝132.(2)证明：∵∠ABC＝45°，AB ＝BC ， ∴∠BAC＝∠BCA＝67.5°，∵BE⊥AC，∴∠ABE＝∠C BE ＝22.5°， ∵EG⊥AG，∴∠AEG＝22.5°＝∠ABQ， ∵AD⊥BC，∴∠DAB＝∠DBA＝45°， ∴∠EAD＝∠DBE＝22.5°，DA ＝DB. 如解图，过点Q 作QM⊥AB 于M ，连接QD.∵FG⊥AB，FQ∥MG，∴四边形MGFQ 是矩形，∴GF＝MQ. ∵∠GAF＝45°，FG⊥AG，∴AG＝FG ＝MQ ，在△AGE 和△QMB 中，⎩⎪⎨⎪⎧∠AEG＝∠QBM ∠AGE＝∠QMB AG ＝QM，∴△AGE≌△QMB，∴AE＝BQ ＝DE. 在△AED 和△BQD 中，⎩⎪⎨⎪⎧AE ＝BQ ∠EAD ＝∠QBD AD ＝BD ，∴△AED≌△BQD，∴DQ＝DE ，∠QDB＝∠EDA， ∴∠QDA＋∠ADE＝∠BDQ＋∠QDA＝90°， ∴QE＝2DE. ∵BQ＝AE ＝DE ，∴BE＝BQ ＋QE ＝2BQ ＋BQ ， ∴BE＝(1＋2)BQ.【例5】(1)解：∵四边形ABCD 是平行四边形，∠ABC＝90°， ∴四边形ABCD 是矩形，∵在△BCE 中，BC ＝BE ＝CE ，∴△BCE 是等边三角形， ∴BE＝4，∠EBC＝60°，∴∠ABE＝30°，∵∠BAE＝90°，∴AB＝BEcos∠ABE＝4cos30°＝23，在Rt△ABC 中，由勾股定理得AC ＝AB 2＋BC 2＝（23）2＋42＝27. (2)证明：如解图，过点E 作EH∥AN 交BC 于H ，∵四边形ABCD 是平行四边形，∴AD∥BC， ∴四边形ANHE 是平行四边形，∴AE＝NH ，∠NHE＝∠NAE. ∵△BEC 是等边三角形， ∴∠EBC＝∠BEC＝∠ECB＝60°， ∴∠DEC＝∠ECB＝60°＝∠AMG， ∴∠AEG＋∠DEC＝∠AEG＋∠AMG＝180°， ∴∠EGM＋∠BGC＝∠EGM＋∠EAM＝180°， ∴∠BGC＝∠EAN＝∠EHN，∵∠EBG＋∠BEG＝∠BGC，∠HEC＋∠HCE＝∠BHE， ∴∠EBG ＝∠CEH，在△EBG 和△CEH 中， ⎩⎪⎨⎪⎧∠BEG＝∠EC H BE ＝EC∠EBG＝∠CEH， ∴△EBG≌△CEH，∴EG＝CH.∵AE∥BC，∴∠AEB＝∠EBC＝60°＝∠BEC， ∵AF⊥EF，∴∠AFE＝∠GFE，∵EF＝EF ， ∴△AEF≌△GEF，∴AE＝EG ＝HC ， ∵NC＝CH ＋NH ，∴NC＝2AE. 跟踪训练1．(1)解：∵BF⊥AC，∠ACB ＝45°，BC ＝122， ∴BF＝12，∵AB＝13，∴在Rt△AFB 中，AF ＝AB 2－BF 2＝5.(2)证明：如解图，连接GE，过点A作AP⊥AG，交BG于P，连接PE.∵BE＝BA，BF⊥AC，∴AF＝FE，∴BG是AE的垂直平分线，∴AG＝EG，AP＝EP，∵∠GAE＝∠ACB＝45°，∴△AGE是等腰直角三角形，即∠AGE＝90°，△APE 是等腰直角三角形，∠APE＝90°，∴∠APE＝∠PAG＝∠AGE＝90°，又AG＝EG，∴四边形APEG是正方形，∴PF＝EF，AP＝AG＝CH.又∵BF＝CF，∴BP＝CE，∵∠APG＝45°＝∠BCF，∴∠APB＝∠HCE＝135°，∴△APB≌△HCE，∴AB＝EH，又∵AB＝BE，∴BE＝EH.2．(1)解：∵AC＝BC，∠C＝90°，AB＝42，∴AC＝BC＝22·AB＝4，在Rt△BCE中，由勾股定理得CE＝BE2－BC2＝3，∴AE＝AC－CE＝4－3＝1.(2)证明：∵AC＝BC，∠ACB＝90°，∴∠CAB＝45°，∵AF⊥BF，∴点A，F，C，B共圆，∴∠CFB＝∠CAB＝45°，∴∠D FC＝180°－∠CFB＝135°，∠AFC＝∠AFB＋∠CFB＝135°，∴∠DFC＝∠AFC，∵DF＝AF ，CF ＝CF ， ∴△AFC≌△DFC，∴AC＝DC ， ∵AC＝BC ，∴CD＝CB.3．(1)解：∵四边形ABCD 是平行四边形， ∴CD∥AB，∵AB⊥AC，∴AC⊥CD. 在Rt△ACD 中，AC ＝4，cos∠CAD＝45，∴AD＝ACcos∠CAD ＝5，由勾股定理得CD ＝3，∵DE⊥AD，∴tan∠DAC＝DC AC ＝DEAD ，即34＝DE 5，则DE ＝154， ∴S △ADE ＝12AD·DE＝12·5·154＝758.(2)证明：如解图，连接BD ，过点F 作FM⊥DH 于M.∵四边形ABCD 是平行四边形，点O 是AC 的中点， ∴点O 是BD 的中点，即点B ，O ，D 在一条直线上， ∵AD∥BC，∴∠FDO＝∠GBO，∠OFD＝∠OGB， ∴△OFD≌△OGB，∴DF＝BG ＝DE. ∵∠FDE＝90°，∴∠FDM＋∠EDC＝90°， ∵FM⊥DC，∴∠FDM＋∠DFM＝90°， ∴∠EDC＝∠DFM.∵AC⊥DC，∴∠DCE＝∠ACD＝90°，∴∠ECD＝∠DMF，∴△FDM≌△DEC，∴DM＝CE.在Rt△HFM中，∵∠H＝30°，FM⊥HM，∴HM＝32 FH，∵DH＝DM＋MH，∴DH＝CE＋32 FH.【例6】(1)解：∵AM⊥BM，点C是BM延长线上一点，∴∠AMB＝∠AMC＝90°，∴△AMB和△AMC是直角三角形，∵∠ABM＝45°，AB＝32，∴AM＝BM＝3，∵BC＝5，∴MC＝5－3＝2，在Rt△AMC中，AM＝3，CM＝2，∴AC＝AM2＋MC2＝32＋22＝13 .(2)证明：延长EF至点H，使FH＝FE，连接BH，如解图，∵点F是BC的中点，∴BF＝CF，在△BFH和△CFE中，⎩⎪⎨⎪⎧BF＝CF∠BFH＝∠CFEFH＝FE，∴△BFH≌△CFE，∴BH＝CE，∠H＝∠CEF，又∵∠BMD＝∠AMC＝90°，AM＝BM，MD＝MC，∴△BMD≌△AMC，∴BD＝AC，又∵AC＝EC，∴BD＝EC＝BH，∴∠H＝∠BDF，∴∠BDF＝∠CEF.跟踪训练1．(1)解：∵PE是由BP绕点P逆时针旋转80°得到的，∴B P＝PE，∠BPE＝80°，∴∠BEP＝∠EBP＝50°.(2)证明：如解图，连接PC.∵AD是边BC上的中线，AB＝AC，∴AD平分∠BAC，∴∠BAP＝∠CAP＝50°，∵AP＝AP，∴△ABP≌△ACP，∴BP＝CP，∵BP＝PE，∴BP＝PE＝PC，∴点E，B，C在以P为圆心PB为半径的圆上，∴∠BCE＝12∠BPE＝40°，∵AB＝AC，AD平分∠B AC，∴AD⊥BC，∴∠CFD＝90°－∠DCF＝50°，∴∠BAD＝∠CFD.2．(1)解：∵四边形ABCD是平行四边形，∴AD∥BC，∠C＝∠BAD＝60°，CD∥AB，∴∠DAE＝∠AEB，∵AE平分∠DAB，∴∠DAE＝∠BAE＝30°，∴∠AEB＝∠BAE，∴AB＝BE＝3，∵BF⊥DC，∴∠DFB＝90°，∵CD∥AB，∴∠ABF＝90°，∴BG＝AB·tan∠BAE＝3×33＝3；(2)证明：如解图，作CH⊥AB于点H，延长AH到I，使HI＝BG，则四边形BFCH 是矩形，CF＝BH，CH＝BF＝AB.在△ABG和△CHI中，⎩⎪⎨⎪⎧AB＝CH∠ABG＝∠CHIBG＝HI，∴△ABG≌△CHI(SAS)．∴∠I＝∠AGB，∠4＝∠2，∵AD＝BG＋FC＝HI＋BH＝BI，AD＝BC，∴BC＝BI，∴∠BCI＝∠I，∵BF∥CH，∴∠FBC＝∠BCH，∵∠I＝∠AGB＝∠3＋∠FBC，∠BCI＝∠BCH＋∠4，∴∠3＝∠4.∵AD∥BC，∴∠1＝∠3，而∠2＝∠4，∴∠1＝∠2，∴AE平分∠DAB.【例7】(1)解：过点A作AH⊥BC于点H，如解图，在Rt△ABH中，∠ABH＝45°，AB＝22，∴BH＝AH＝2，在Rt△ACH中，∠ACH＝30°，∴CH＝23，∴BC＝BH＋CH＝2＋2 3.(2)证明：过点A作AM⊥AB交BC于点M，连接GM，如解图，∵∠BAM＝90°，∠ABM＝45°，∴AB＝AM，∠AMB＝45°，∵AG⊥AD，∴∠DAG＝∠EAG＝90°，∵AE＝AF，GE＝DF，∴Rt△ADF≌Rt△AGE，∴AD＝AG，∵∠BAM＝∠DAG＝90°，∴∠BAD＝∠MAG，∴△ABD≌△AMG，∴BD＝GM，∠B＝∠AMG＝45°，∵∠AMB＝45°，∴∠GMC＝90°，在Rt△CGM中，∠C＝30°，∴GM＝12CG，∴BD＝12CG.(3)1＋32.跟踪训练1．(1)解：∵∠BAC＝90°，AB＝AC＝4，∴BC＝4 2.∵CD＝12BC.∴CD＝2 2.∵DE⊥CE，DE＝CE，∴DE＝CE＝2，∠ECD＝45°，∵∠ACB＝45°，∴∠ACE＝90°，∴AE＝AC2＋CE2＝25，∵M是AE的中点，∴CM＝12AE＝ 5.(2)证明：延长EN至F，使得NF＝EN，连接AF，BF，如解图，在△NDE和△NBF中，⎩⎪⎨⎪⎧ND＝NB∠DNE＝∠BNFNE＝NF，∴△NDE≌△NBF，∴BF＝DE＝CE，∠FBN＝∠EDN.设∠DCB＝x°，∠DBC＝y°，则∠ACE＝∠ACB＋(∠DCE－x°)＝90°－x°，∴∠BDC＝180°－x°－y°，∴∠BDE＝135°－x°－y°，∵∠ABD＝45°－y°，∠ABF＝∠FBD－∠ABD＝135°－x°－y°－(45°－y°)＝90°－x°，即∠ABF＝∠ACE，∴△ABF≌△ACE，∴∠BAF＝∠EAC，∴∠EAF＝∠BAF＋∠BAE＝∠EAC＋∠BAE＝90°，∵M是AE的中点，∴MN∥AF，∴MN⊥AE.(3)7 4.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

6.如图，△ABC是等边三角形，△BDC 是顶角∠BDC=120°的等腰三角形，以 D为顶点作一个60°角∠NDM，角的两边分别交AB、AC边于M、N两点，连接 MN．试探究BM、MN、CN之间的数量关系，并加以证明．
证明：BM+CN=NM 延长AC至E，使CE=BM，连接DE， ∵△BDC是顶角∠BDC=120°的等腰三角形，△ABC是等边三角形， ∴∠BCD=30°， ∴∠ABD=∠ACD=90°， ∵DB=DC，CE=BM， ∴△DCE≌△BMD， ∵∠MDN=∠NDE=60° ∴DM=DE（上面已经全等） ∴DN=ND（公共边） ∴△DMN≌△DEN∴BM+CN=NM．
实数与二次根式
•
方程与不等式
用
二元一次方程与不等式组及其应
•
一次函数代数应用综合一次函数与二元一次方程
租不等式综合及其应用
•
一次函数几何综合一次函数的图像性பைடு நூலகம்与几何图形
综合
•
因式分解与分式代数式恒等变形，分式方程及其
应用
• 第四期2.24-2.28
• 代数预习专场反比例函数基础反比例函数的定义几基本性质
•
反比例函数进阶反比例函数综合难题，中考压轴
题
•
一元二次方程的解法
解法
一元二次方程的几种一般
•
一元二次方程判别式及根与系数的关系根与判别式
根与系数关系
•
一元二次方程应用题
题策略
一元二次方程的应用题解
• 第三期
• 2.10——2.14日
• 几何预习专场题型方法
矩形，菱形矩形；菱形的基本性质与中考
7.如图，ABCD为正方形，E为BC边上一点，且 AE=DE，AE与对角线BD交于点F，连接CF，交ED 于点G．判断CF与ED的位置关系，并说明理由．
解：垂直．理由：∵四边形ABCD为正方形， ∴∠ABD=∠CBD，AB=BC， ∵BF=BF， ∴△ABF≌△CBF， ∴∠BAF=∠BCF， ∵在RT△ABE和△DCE中，AE=DE， AB=DC， ∴RT△ABE≌△DCE， ∴∠BAE=∠CDE， ∴∠BCF=∠CDE， ∵∠CDE+∠DEC=90°， ∴∠BCF+∠DEC=90°， ∴DE⊥CF．
E
F
AH D
G O
K
B
C
4.如图，在正方形ABCD的边BC上任取一点M，过点 C作CN⊥DM交AB于N，设正方形对角线交点为O，试确定OM与ON之间的关系，并说明理由．
解：∵四边形ABCD是正方形， ∴DC=BC，∠DCM=∠NBC=90°，又∵CN⊥DM交AB于N， ∴∠NCM+∠CMD=90°，而∠CMD+∠CDM=90°， ∴∠NCM=∠CDM， ∴△DCM≌△CBN， ∴CM=BN，再根据四边形ABCD是正方形可以得到 OC=OB，∠OCM=∠OBN=45°， ∴△OCM≌△OBN． ∴OM=ON，∠COM=∠BON，而 ∠COM+∠MOB=90°， ∴∠BON+∠MOB=90°． ∴∠MON=90°． ∴OM与ON之间的关系是OM=ON； OM⊥ON．
∴∠ADB=∠FDC
3.如图，梯形ABCD中，AD∥BC， CD⊥BC，BC=CD，O是BD的中点， E是CD延长线上一点，作OF⊥OE交 DA的延长线于F，OE交AD于H，OF 交AB于G，FO的延长线交CD于K，求证：OE=OF
提示：由条件知△BCD为等腰Rt△，连接 OC，可证△OCK≌△ODH(AAS)，得OK=OH，再证 △FOH≌△EOK(AAS)，得OE=OF
∠BAD=∠ACG=90°
BA=CA ∴△BDA≌△AGC ∴DA=GC ∵D是AC中点，∴DA=CD ∴GC=CD 由∠1=45°，∠ACG=90°，故∠2=45°=∠1 在△GCF与△DCF中， ∵ GC=CD
∠2=45°=∠1
CF=CF ∴△GCF≌△DCF ∴∠G=∠FDC,又∠G=∠BDA
5.如图，正方形CGEF的对角线CE在正方形 ABCD的边BC的延长线上（CG＞BC），M是线段AE的中点，DM的延长线交CE于N．探究：线段MD、MF的关系，并加以证明．
证明：根据题意，知AD∥BC． ∴∠EAD=∠AEN（内错角相等）， ∵∠DMA=∠NME（对顶角相等），又∵M是线段AE的中点， ∴AM=ME． ∴△ADM≌△ENM（ASA）． ∴AD=NE,DM=MN．（对应边相等）．连接线段DF，线段FN，线段CE是正方形的对角线， ∠DCF=∠NEF=45°，根据上题可知线段AD=NE，又∵四边形CGEF是正方形， ∴线段FC等于FE． ∴△DCF≌△NEF（SAS）． ∴线段FD=FN． ∴△FDN是等腰三角形． ∴线段MD⊥线段MF．
• 第一期1.31——2.4日
• 几何复习提升专场
三角形综合一
• 三角形中的特殊点线角平分线，中点中线性质及对应辅助线作法
•
三角形综合二
等腰三角形，等
边三角形，直角三角形
•
几何三大变换
对称平移旋转
•
中位线定理三角形的中位线
•
平行四边形初步平行四边形的性
质与判定
• 第二期2.6-2.10
• 代数复习提升专场
•
正方形一
正方形的基本性质及常考题型
•
正方形二
正方形进阶，中考压轴题解题方法体验与归纳
•
梯形梯形的基本性质及常考题型
•
几何动点动态问题
几何图形中的点线面运动
1.如图，在直角梯形ABCD中，
A
AD∥BC，∠A＝90º，AB＝AD，
DE⊥CD交AB于E，DF平分∠CDE交 E
BC于F，连接EF．证明：CF＝EF
B
F
D C
解：
过D作DG⊥BC于G．由已知可得四边形ABGD为正方形，
∵DE⊥DC ∴∠ADE+∠EDG=90°=∠GDC+∠EDG， ∴∠ADE=∠GDC．又∵∠A=∠DGC且AD=GD， ∴△ADE≌△GDC， ∴DE=DC且AE=GC．在△EDF和△CDF中∠EDF=∠CDF，DE=DC，DF为公共边， ∴△EDF≌△CDF， ∴EF=CF
2.已知：在⊿ABC中，∠A=900，AB=AC，D是AC的中点， AE⊥BD，AE延长线交BC于F，求证：∠ADB=∠FDC。
证明：
过点C作CG⊥CA交AF延长线于G ∴∠G+∠GAC=90°…………① 又∵AE⊥BD ∴∠BDA+∠GAC=90°…………② 综合①②，∠G=∠BDA 在△BDA与△AGC中， ∵ ∠G=∠BDA

初二期末几何压轴题答案详解共27页

初二数学压轴几何证明题(含答案)

初二期末压轴题训练附解析

初二下期末几何压轴题及解析

初二期末压轴题答案及解析

八年级数学期末几何压轴题

初二期末几何压轴题答案详解课件

期末考试勾股定理与几何翻折压轴题专项训练—2023-2024学年八年级数学下学期(人教版)(解析版)

初二数学 全等三角形压轴几何题知识点总结及答案

人教版八年级数学上册期末专题复习：几何压轴题强化训练试题(含答案)

北师大版八年级下册数学期末几何压轴题专练(含答案)

八年级数学下册期末压轴题带答案

人教版八年级数学上册期末专题复习：几何压轴题强化训练试题(含答案)

初二数学全等三角形压轴几何题(讲义及答案)含答案

八年级压轴题 期末复习试卷专题练习(解析版)

人教版数学八年级上册期末考试几何压轴20题 带答案解析河南各地期末试卷

初二下期末几何压轴题及解析

几何压轴题-含答案

初二数学全等三角形压轴几何题知识点总结及答案

八年级压轴题期末复习试卷专题练习(解析版)

人教版数学八年级上册期末考试几何压轴20题带答案解析河南各地期末试卷