(完整版)一次函数及其图像练习(含答案详解)
一次函数的图象专题练习题(最新版) 含答案

一次函数的图象专题练习题1.画函数图象的方法.可以概括为_______,__ __,__ __三步,通常称为__ __.2.如果点M 在函数y =x -1的图象上,则M 点的坐标可以是( )A .(-1,0)B .(0,1)C .(1,0)D .(1,-1)3.(1)若点A(a ,-3)在函数y =-3x的图象上,则a =____; (2)下列各点M (1,2),N (3,32),P (1,-1),Q (-2,-4)中,在函数y =2x x +1的图象上的点是__________. 4. 小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,加快了骑车速度,下面是小明离家后他到学校剩下的路程s 关于时间t 的函数图象,那么符合小明行驶情况的图象大致是( )5. 小明的父亲从家走了20分钟到一个离家900米的书店,在书店看了10分钟书后,用15分钟返回家,下列图中表示小明的父亲离家的距离与时间的函数图象是( )6. 某星期六上午,小明从家出发跑步去公园,在公园停留了一会儿打车回家.图中折线表示小明离开家的路程y(米)和所用时间x(分)之间的函数关系,则下列说法中错误的是()A.小明在公园休息了5分钟B.小明乘出租车用了17分C.小明跑步的速度为180米/分D.出租车的平均速度是900米/分7. 一段笔直的公路AC长20千米,途中有一处休息点B,AB长15千米,甲、乙两名长跑爱好者同时从点A出发,甲以15千米/时的速度匀速跑至点B,原地休息半小时后,再以10千米/时的速度匀速跑至终点C;乙以12千米/时的速度匀速跑至终点C,下列选项中,能正确反映甲、乙两人出发后2小时内运动路程y(千米)与时间x(小时)函数关系的图象是()8. 李老师为锻炼身体一直坚持步行上下班.已知学校到李老师家总路程为2000米.一天,李老师下班后,以45米/分的速度从学校往家走,走到离学校900米时,正好遇到一个朋友,停下又聊了半小时,之后以110米/分的速度走回了家.李老师回家过程中,离家的路程s(米)与所用时间t(分)之间的关系如图所示.(1)求a,b,c的值;(2)求李老师从学校到家的总时间.9. 如果两个变量x,y之间的函数关系如图,则函数值y的取值范围是() A.-3≤y≤3 B.0≤y≤2C.1≤y≤3 D.0≤y≤310. 如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是()A.乙前4秒行驶的路程为48米B.在0到8秒内甲的速度每秒增加4米/秒C.两车到第3秒时行驶的路程相等D.在4至8秒内甲的速度都大于乙的速度11. 甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论:①出发1小时时,甲、乙在途中相遇;②出发1.5小时时,乙比甲多行驶了60千米;③出发3小时时,甲、乙同时到达终点;④甲的速度是乙速度的一半.其中,正确结论的个数是()A.4B.3C.2D.112. 有一个水箱,它的容积是500升,水箱内原有水200升,现需将水箱注满,已知每分钟注入水10升.(1)写出水箱内水量Q(升)与时间t(分)的函数关系式;(2)求自变量t的取值范围;(3)画出函数的图象.13.如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是()14. 如图①,底面积为30 cm2的空圆柱形容器内水平放置着由两个实心圆柱组成的“几何体”,现向容器内匀速注水,注满为止,在注水过程中,水面高度h(cm)与注水时间t(s)之间的关系如图②所示.请根据图中提供的信息,解答下列问题:(1)圆柱形容器的高为____cm,匀速注水的水流速度为____cm3/s;(2)若“几何体”的下方圆柱的底面积为15 cm2,求“几何体”上方圆柱的高和底面积.答案:1. 描点 连线 描点法2. C3. (1) 1 (2) 点N4. D5. B6. B7. A8. (1)李老师停留地点离他家路程为:2000-900=1100(米),900÷45=20(分).a =20,b =1100,c =20+30=50 (2)20+30+1100110=60(分).答:李老师从学校到家共用60分钟 9. D10. C11. B 点拨:①②④正确12. (1)Q =200+10t (2)令200≤Q≤500,则0≤t≤30 (3)图略13. B14. (1) 14 5(2) “几何体”下方圆柱的高为a ,则a·(30-15)=18×5,解得a =6,所以“几何体”上方圆柱的高为11 cm-6 cm =5 cm ,设“几何体”上方圆柱的底面积为S cm 2,根据题意得5(30-S )=5×(24-18),解得S =24,即“几何体”上方圆柱的底面积为24 cm 2。
一次函数的图像(作业)解析版

20.2 一次函数的图像(作业)一、单选题1.(2019·上海金山区·八年级期中)一次函数的图像不经过的象限是()A.第一象限B.第二象限C.第三象限D.第四象限.【答案】B【分析】先根据一次函数的解析式判断出k、b的符号,再根据一次函数的性质进行解答即可.【详解】解:∵解析式y=2x﹣1中,k=2>0,b=﹣1<0,∴图象过第一、三、四象限,∴图象不经过第二象限.故选:B.【点睛】本题考查的是一次函数的性质,即一次函数y=kx+b(k≠0)中,当k>0时,函数图象经过第一、三象限,当b<0时,函数图象与y轴相交于负半轴.2.(2018·上海闵行区·)一次函数y=-2(x-3)在y轴上的截距是( )A.2 B.-3 C.6 D.6【答案】D【分析】令x=0,则y=6,即一次函数与y轴交点为(0,6),即可得出答案.【详解】解:令x=0,则y=6,即一次函数与y轴交点为(0,6),∴一次函数y=-2(x-3)在y轴上的截距为6.故选D.【点睛】本题考查了一次函数图象上点的坐标特征,属于基础题,关键是令x=0求出与y轴的交点坐标.3.(2019·上海市西延安中学八年级期中)在同一真角坐标平面中表示两个一次函数,,正确的图像为()A.B.C. D.【答案】D【分析】根据的图像判断k、b的符号,再判断的图像所在的象限,即可得出正确答案.【详解】解:A.由的图像得k>0,b<0,所以的图像应在一、二、三象限,故A错误;B、由的图像得k>0,b>0,所以的图像应在一、二、四象限,故B错误;C、由的图像得k<0,b>0,所以的图像应在二、三、四象限,故C错误;D、由的图像得k>0,b>0,所以的图像应在一、二、四象限,故D正确.故选:D.【点睛】本题考查一次函数的图象,熟悉一次函数的性质是解题的关键.4.(2018·上海金山区·八年级期末)直线不经过点()A.(-2,3);B.(0,0);C.(3,-2);D.(-3,2).【答案】A【分析】直接把各点代入直线进行检验即可.【详解】A. 当x=−2时,y==≠3,故此点不在直线上,故本选项正确;B. 当x=0时,y==0,故此点在直线上,故本选项错误;C. 当x=3时,y==−2,故此点在直线上,故本选项错误;D. 当x=−3时,y==2,故此点在直线上,故本选项错误故选A.【点睛】本题考查一次函数图象上点的坐标特征,解题的关键是掌握直接代入的方法. 5.(2020·上海松江区·八年级期末)一次函数的图像经过()A.第一、二、三象限B.第一、三、四象限C.第一、二、四象限D.第二、三、四象限【答案】A【分析】根据一次函数的图象与性质解答即可.【详解】解:一次函数中,k=2>0,b=3>0,所以一次函数的图象经过第一、二、三象限.故选:A.【点睛】本题考查了一次函数的图象与性质,属于基础题型,熟练掌握一次函数的基本知识是解题的关键.6.(2020·上海八年级期中)如果直线y=2x+3和y轴相交于点M,那么M的坐标为()A.M(2,3)B.M(0,2)C.M(0,)D.M(0,3)【答案】D【分析】代入x=0求出与之对应的y值,进而可得出点M的坐标.【详解】当x=0时,y=2x+3=3,∴点M的坐标为(0,3).故选:D.【点睛】本题考查了一次函数图象上点的坐标特征,牢记直线上任意一点的坐标都满足函数关系式y=kx+b是解题的关键.7.(2019·上海市闵行区明星学校八年级月考)若bk<0,则直线y=kx+b一定通过()A.第一、二象限B.第二、三象限C.第三、四象限D.第一、四象限【答案】D【分析】根据题意讨论k和b的正负情况,然后可得出直线y=kx+b一定通过哪两个象限.【详解】解:由bk<0,知①b>0,k<0;②b<0,k>0,①当b>0,k<0时,直线经过第一、二、四象限,②b<0,k>0时,直线经过第一、三、四象限.综上可得,函数图象一定经过一、四象限.故选:D.【点睛】本题主要考查一次函数图象在坐标平面内的位置与k、b的关系.解答本题注意理解:直线y=kx+b所在的位置与k、b的符号有直接的关系:k>0时,直线必经过一、三象限;k<0时,直线必经过二、四象限;b>0时,直线与y轴正半轴相交;b=0时,直线过原点;b<0时,直线与y轴负半轴相交.8.(2018·上海民办浦东交中初级中学八年级月考)无论k取何值,一次函数的图像必经过点( )A.B.C.D.无法确定【答案】C【分析】先对一次函数进行整理,然后根据图象过定点,得到关于x,y的一个方程组,解方程组即可.【详解】由得∵一次函数过定点,∴解得,∴一次函数过点故选:C.【点睛】本题主要考查一次函数过定点问题,掌握一次函数的图象和性质是解题的关键.9.(2018·上海闵行区·八年级期末)已知直线y=kx+b与直线y=﹣2x+5平行,那么下列结论正确的是()A.k=﹣2,b=5 B.k≠﹣2,b=5 C.k=﹣2,b≠5 D.k≠﹣2,b=5【答案】C【分析】利用两直线平行问题得到k=-2,b≠5即可求解.【详解】∵直线y=kx+b与直线y=﹣2x+5平行,∴k=﹣2,b≠5.故选C.【点睛】本题考查了两条直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解.若两条直线是平行的关系,那么它们的自变量系数相同,即k值相同.10.(2019·上海·八年级期末)如图,直线交坐标轴于两点,则关于的不等式的解集是A.B.C.D.【答案】A试题分析:kx+b>0可看作是函数y=kx+b的函数值大于0,然后观察图象得到图象在x轴上方,对应的自变量的取值范围为x>-2,这样即可得到不等式kx+b>0的解集.kx+b>0即函数y=kx+b的函数值大于0,图象在x轴上方,对应的自变量的取值范围为x>-2,所以不等式kx+b>0的解集是x>-2.故选A.考点:本题考查了一次函数与一元一次不等式点评:对于一次函数y=kx+b,当y>0时对应的自变量的取值范围为不等式kx+b>0的解集.二、填空题11.(2021·上海市仙霞第二中学八年级期末)直线经过第_________象限.【答案】一、三【分析】根据k的正负性确定图像的增减性,根据b的正负性确定图像与y轴的交点位置即可.【详解】解:∵>0,∴y随着x的增大而增大,∴图像经过第一、三象限,∵b=0,∴图像过原点,∴直线经过第一、三象限,故答案为:一、三.【点睛】本题考查了一次函数图像的性质,熟练掌握一次函数图像的性质是解决本题的关键.12.(2018·上海崇明区·八年级期中)直线向上平移3个单位后,所得直线的表达式是___________.【答案】【分析】根据一次函数图象的平移规律即可得.【详解】由一次函数的平移规律得:所得直线的表达式是,即故答案为:.【点睛】本题考查了一次函数图象的平移规律,熟记平移规律是解题关键.13.(2019·上海市市西初级中学八年级期中)将直线向下平移5个单位后,所得直线的表达式为________.【答案】y=-x-3【分析】根据一次函数平移的特点即可求解.【详解】将直线向下平移5个单位后,所得直线的表达式为-5=-x-3故答案为:y=-x-3.【点睛】此题主要考查一次函数的图像,解题的关键是熟知一次函数平移的特点.14.(2019·上海普陀区·八年级期末)已知直线与直线平行,那么_______.【答案】5【分析】两直线平行,则两比例系数相等,据此可以求解.【详解】解:直线与直线平行,,故答案为:5.【点睛】本题考查了两条直线相交或平行问题,解题的关键是熟知两直线平行时两比例系数相等.15.(2019·上海市闵行区七宝第二中学八年级期中)直线与坐标轴围成的三角形的面积为________.【答案】【分析】求出直线与坐标轴的交点坐标即可解决问题.【详解】解:由题意可知直线与坐标轴的交点为和,∴三角形的底为高为,∴三角形的面积为,故答案为.【点睛】本题考查一次函数的应用、三角形的面积等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.16.(2018·上海崇明区·八年级期中)直线与轴和轴的交点分别为、,那么线段的长为_________.【答案】5【分析】先根据一次函数的表达式求出点A、B的坐标,再利用勾股定理即可得.【详解】如图,当时,,解得则点A的坐标为,当时,,则点B的坐标为,,故答案为:5.【点睛】本题考查了一次函数的图象、勾股定理,掌握一次函数的图象是解题关键.三、解答题17.(2018·上海虹口区·八年级期中)如图,是甲、乙两种机器人根据电脑程序工作时各自工作量y关于工作时间x的函数图像,线段OA表示甲机器人的工作量(吨)关于时间x(时)的函数图像,线段BC表示乙机器人的工作量(吨)关于时间x(时)的函数图像.根据图像信息回答下列填空题.(1)甲种机器人比乙种机器人早开始工作小时;甲种机器人每小时的工作量是吨;(2)直线BC的表达式为;当乙种机器人工作5小时后,它完成的工作量是吨.【答案】(1)3,; (2) , 5【分析】(1)由图像可以得到甲机器人比乙机器人早开始工作的时间,甲机器人的每小时的工作量.(2)利用甲机器人求得交点的坐标,再用待定系数法求BC的解析式.【详解】解:(1)由图像可知:甲机器人比乙机器人早工作3小时,甲机器人每小时的工作量吨,(2)设直线OA为,把代入得:,所以:,因为函数的交点的纵坐标为3,所以:横坐标为,设BC为:,又因为BC过,所以:,所以:,所以直线BC的解析式为;,当乙机器人工作5小时,即,所以:工作量.【点睛】本题考查的是一次函数的图像与图像信息问题,同时考查求一次函数的解析式,弄清楚关键点的坐标含义是解题关键.18.(2018·上海市行知实验中学八年级期中)一次函数图像经过(0,-4),与两坐标轴围成的三角形面积是6,求这个函数解析式.【答案】y=x-4或y=-x-4.【分析】设一次函数与x轴的交点是(a,0),根据三角形的面积公式即可求得a的值,然后利用待定系数法即可求得函数解析式.【详解】∵一次函数y=kx+b(k≠0)图象过点(0,-4),∴b=-4,设一次函数与x轴的交点是(a,0),则×4×|a|=6,解得:a=3或-3.把(3,0)代入y=kx-4,解得:k=,则函数的解析式是y=x-4;把(-3,0)代入y=kx-4,得k=-,则函数的解析式是y=-x-4.故这个函数解析式为y=x-4或y=-x-4.【点睛】本题考查了待定系数法求函数的解析式,正确求得与x轴的交点坐标是关键.19.(2019·上海市田林第三中学八年级月考)已知一次函数图像经过点A(2,2)、B(-2,-4).(1)求这个一次函数的解析式;(2)求这个一次函数图像与两坐标轴所围成的图形的面积.【答案】(1)y= x−1;(2)【分析】(1)运用待定系数设出函数解析式y=kx+b,再将两点代入可得出k和b的值.(2)求出函数解析式与x轴及y轴的交点坐标,根据s= |x||y|可计算出面积.【详解】(1)设这个函数解析式为y=kx+b,已知一次函数图像经过点A(2,2)、B(-2,-4),可得:,解得:,∴函数解析式为y= x−1.(2)直线y=x−1与x轴的交点坐标为( ,0),与y轴的交点坐标为(0,−1)所以S=××|−1|=.【点睛】此题考查待定系数法求一次函数解析式,一次函数的图象,解题关键在于把已知点代入解析式.20.(2019·上海松江区·八年级期中)已知一次函数y=kx+b(k、b是常数)的图像平行于直线,且经过点(2,-3).(1)求这个一次函数的解析式;(2)求这个一次函数与两坐标轴所围成的图形面积.【答案】(1) y=-3x+3;(2).【分析】(1)根据题意可得k=﹣3,将点(2,-3)代入求解即可得到答案;(2)先求得该一次函数与坐标轴的交点坐标,再利用三角形面积公式求解即可.【详解】解:(1)∵y=kx+b平行于直线,∴k=-3,∵一次函数经过点(2,-3),∴代入得b=3,∴y=-3x+3;(2)一次函数与x轴交于点(1,0),与y轴交于点(0,3),∴面积.【点睛】本题主要考查一次函数的性质,解此题的关键在于根据题意准确求得一次函数的解析式.21.(2018·上海全国·八年级期中)已知y+2与3x成正比例,当x=1时,y的值为4.(1)求y与x之间的函数表达式;(2)若点(-1,a),(2,b)是该函数图象上的两点,请利用一次函数的性质比较a,b的大小.【答案】(1)y=6x-2;(2)a<b.试题分析:(1)由y+2与3x成正比例,设y+2=3kx(k≠0).将x=1,y=4代入求出k的值,确定出y与x的函数关系式;(2)由函数图象的性质来比较a、b的大小.试题解析:(1)根据题意设y+2=3kx(k≠0).将x=1,y=4代入,得4+2=3k,解得:k=2.所以,y+2=6x,所以y=6x−2;(2)a<b.理由如下:由(1)知,y与x的函数关系式为y=6x−2.∴该函数图象是直线,且y随x的增大而增大,∵−1<2,∴a<b.22.(2019·上海全国·八年级期末)已知一次函数的图象经过(2,5)和(-1,-1)两点,(1)在给定坐标系中画出这个函数图象,(2)求这个一次函数解析式.【答案】(1)如图所示:(2)试题分析:(1)先在平面直角系内找到(2,5)和(-1,-1)两点,即可作出图象;(2)根据待定系数法列方程组求解即可。
(完整版)一次函数图像问题附答案

一次函数图像问题附答案一、基本识图问题1.(2007•常州)如图,图像(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的函数关系,下列说法中错误的是()A、第3分时汽车的速度是40千米/时B、第12分时汽车的速度是0千米/时C、从第3分到第6分,汽车行驶了120千米D、从第9分到第12分,汽车的速度从60千米/时减少到0千米/时二、行程问题1.(2009•滨州)小明外出散步,从家走了20分钟后到达了一个离家900米的报亭,看了10分钟的报纸然后用了15分钟返回到家.则下列图像能表示小明离家距离与时间关系的是()A、B、C、D、2.(2007•鄂尔多斯)如图,一只蚂蚁以均匀的速度沿台阶A1⇒A2⇒A3⇒A4⇒A5爬行,那么蚂蚁爬行的高度h随时间t变化的图像大致是()A 、B、C、D、三、行走路线问题1. 图1是韩老师早晨出门散步时,离家的距离(y)与时间(x)之间的函数图像。
若用黑点表示韩老师家的位置,则韩老师散步行走的路线可能是()图1四、速度问题1.如图4所示的函数图像反映的过程是:小明从家去书店,又去学校取封信后马上回家,其中x表示时间,y表示小明离他家的距离,则小明从学校回家的平均速度为千米/小时。
图42. 图中由线段OA、AB组成的折线表示的是小明步行所走的路程和时间之间的关系,其中x 轴表示步行的时间,y轴表示步行的路程.他在6分至8分这一时间段步行的速度是()A、120米/分B、108米/分C、90米/分D、88米/分五、图像变化快慢问题Ⅰ.直线变化1. (2009•金华)小明在一直道上骑自行车,经过起步、加速、匀速、减速之后停车.设小明骑车的时间为t(秒),骑车的路程为s(米),则s关于t的函数图像大致是()A、B、C、D、2.1、2004年6月3日中央新闻报道,为鼓励居民节约用水,北京市将出台新的居民用水收费标准:①若每月每户居民用水不超过4立方米,则按每立方米2元计算;②若每月每户居民用水超过4立方米,则超过部分按每立方米4.5元计算(不超过部分仍按每立方米2元计算).现假设该市某户居民某月用水x立方米,水费为y元,则y与x的函数关系用图像表示正确的是()Ⅱ.曲线变化3.(2005•余姚市)向高为10cm的容器中注水,注满为止,若注水量Vcm3与水深hcm之间的关系的图像大致如下图,则这个容器是下列四个图中的()A、B、C、D、六、特殊背景----------注水问题1. (2007•牡丹江)将一盛有部分水的圆柱形小玻璃杯放入事先没有水的大圆柱形容器内,现用﹣注水管沿大容器内壁匀速注水(如图所示),则小水杯内水面的高度h(cm)与注水时间t(min)的函数图像大致为()A、B、C、D、2. (2005•黄冈)有一个装有进、出水管的容器,单位时间进、出的水量都是一定的.已知容器的容积为600升,又知单开进水管10分钟可把空容器注满,若同时打开进、出水管,20分钟可把满容器的水放完,现已知水池内有水200升,先打开进水管5分钟后,再打开出水管,两管同时开放,直至把容器中的水放完,则能正确反映这一过程中容器的水量Q (升)随时间t(分)变化的图像是()A、B、C、D、七、图像对称问题1. (2007•呼和浩特)已知某函数图像关于直线x=1对称,其中一部分图像如图所示,点A (x1,y1),点B(x2,y2)在函数图像上,且﹣1<x1<x2<0,则y1与y2的大小关系为()A、y1>y2B、y1=y2C、y1<y2D、无法确定八、图像转换问题1. (2007•泰安)骆驼被称为“沙漠之舟”,它的体温随时间的变化而发生较大的变化,其体温(℃)与时间(时)之间的关系如图所示.若y(℃)表示0时到t时内骆驼体温的温差(即0时到t时最高温度与最低温度的差).则y与t之间的函数关系用图像表示,大致正确的是()A、B、C、D、九、易错----------细节理解问题1.汽车由重庆驶往相距400千米的成都。
八年级数学一次函数图像基础练习题(含答案)

八年级数学一次函数图像练习题一、选择题; ③y=−2x2; ④y=2; ⑤y=2x−1.下列函数关系式: ①y=−2x; ②y=2x1,其中是一次函数的是()A. ① ⑤B. ① ④ ⑤C. ② ⑤D. ② ④ ⑤2.在y=(k+1)x+k2−1中,若y是x的正比例函数,则k值为()A. 1B. −1C. ±1D. 无法确定3.图是一次函数的图象,则该函数的解析式是()A. y=2x+2B. y=−2x−2C. y=−2x+2D. y=2x−24.函数y=(m−2)x n−1+3是关于x的一次函数,则m,n的值为()A. m≠2,n=2B. m=2,n=2C. m≠2,n=1D. m=2,n=15.下列函数中,y随x的增大而增大的是()A. y=−2x+1B. y=−x−2C. y=x+1D. y=−2x−16.一次函数y=kx+3中,当x=2时,y=−3,则当x=−2时,y的值为()A. −1B. −3C. 7D. 97.下列曲线中,表示y是x的函数的是()A. B.C. D.8.已知正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=−kx+k的图象大致是()A. B. C. D.9.将直线y=−2x−1向上平移2个单位长度,平移后的直线所对应的函数关系式为()A. y=−2x−5B. y=−2x−3C. y=−2x+1D. y=−2x+310.在平面直角坐标系中,一次函数y=kx+b的图象如图所示,则k和b的取值范围是()A. k>0,b>0B. k>0,b<0C. k<0,b>0D. k<0,b<011.数形结合是解决数学问题常用的思想方法.如图,直线y=x+5和直线y=ax+b相交于点P,根据图象可知,方程x+5=ax+b的解是()A. x=20B. x=5C. x=25D. x=1512.点P(a,b)在函数y=3x+2的图象上,则代数式6a−2b+1的值等于()A. 5B. 3C. −3D. −113.直线y=kx+b在平面直角坐标系中的位置如图所示,则不等式kx+b≤2的解集是()A. x≤−2B. x≤−4C. x≥−2D. x≥−414.两个一次函数y=ax+b和y=bx+a在同一平面直角坐标系中的图象可能是()A. B.C. D.15.2020年年初以来,红星消毒液公司生产的消毒液在库存量为m吨的情况下,日销售量与产量持平.自1月底抗击“新冠病毒”以来,消毒液需求量猛增,该公司在生产能力不变的情况下,消毒液一度脱销,下面表示2020年年初到脱销期间,该公司消毒液库存量y(吨)与时间t(天)之间的函数关系的大致图象是()A. B.C. D.16.如图,三个正比例函数的图象分别对应表达式: ①y=ax, ②y=bx, ③y=cx,将a,b,c从小到大排列为()A. a<b<cB. a<c<bC. b<a<cD. c<b<a17.已知点(−2,y1),(−1,y2),(1,y3)都在直线y=−3x+b上,则y1,y2,y3的值的大小关系是().A. y3<y2<y1B. y1<y2<y3C. y2<y1<y3D. y3<y1<y218.已知y=kx+2,当x<−1时,其图象在x轴下方;当x>−1时,其图象在x轴上方,则k的值为()A. −2B. 2C. −3D. 319.若一次函数y=kx+b(k≠0)的图象与直线y=−x+1平行,且过点(8,2),则此一次函数的解析式为()A. y=−x−2B. y=−x−6C. y=−x−1D. y=−x+1020.双胞胎兄弟小明和小亮在同一班读书,周五16:00时放学后,小明和同学走路回家,途中没有停留,小亮骑车回家,他们各自离学校的路程s(米)与用去的时间t(分)的关系如图所示,根据图象提供的有关信息,下列说法中错误的是()A. 兄弟俩的家离学校1000米B. 他们同时到家,用时30分钟C. 小明的速度为50米/分D. 小亮中间停留了一段时间后,再以80米/分的速度骑回家21.一元一次方程ax−b=0的解是x=5,则函数y=ax−b的图象与x轴的交点坐标是()A. (−5,0)B. (5,0)C. (a,0)D. (−b,0)二、填空题22.已知函数y=(k+1)x+k2−1.若它是一次函数,则k;若它是正比例函数,则k.23.如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x≥ax+4的解集为________.24.如图,分别表示A步行与B骑车在同一道路上行驶的路程s与时间t的关系。
完整版)一次函数图像与性质练习题

完整版)一次函数图像与性质练习题授课目的与考点分析:本文主要介绍了一次函数图像与系数的关系,包括直线的平移和位置关系,以及k、b对图像和性质的影响等内容。
文章还提供了一些例题,帮助读者更好地理解和掌握相关知识点。
一、一次函数图像与系数的关系1.函数y=kx+b(k、b为常数,且k≠0)的图像是一条直线:当b>0时,直线y=kx+b是由直线y=kx向上平移b个单位长度得到的;当b<0时,直线y=kx+b是由直线y=kx向下平移|b|个单位长度得到的。
2.一次函数y=kx+b(k、b为常数,且k≠0)的图像与性质:正比例函数的图像是经过原点(0,0)和点(1,k)的一条直线;一次函数y=kx+b(k≠0)图像和性质如下:3.k、b对一次函数y=kx+b的图像和性质的影响:k决定直线y=kx+b从左向右的趋势,b决定它与y轴交点的位置,k、b一起决定直线y=kx+b经过的象限。
4.两条直线l1:y=k1x+b1和l2:y=k2x+b2的位置关系可由其系数确定:1)k1≠k2,即斜率不相等,l1与l2相交;2)k1=k2,且b1≠b2,即斜率相等但截距不等,l1与l2平行;例题:1.若b<0,则直线y=kx+b一定通过()A.第一、二象限B.第二、三象限C.第三、四象限D.第一、四象限2.若直线y=kx+b(k≠0)不经过第一象限,则k、b的取值范围是()A.k>0,b0,b≤0 XXX<0,b<0 D.k<0,b≤03.已知直线y=kx+b,若k+b=-5,kb=6,那么该直线不经过第象限。
4.若实数a,b,c满足a+b+c=0,且a<b<c,则函数y=cx+a的图像可能是()A. B. C. D.5.已知点(k,b)为第四象限内的点,则一次函数y=kx+b的图像大致是()A. B. C. D.6.如果函数y=3x+m的图像一定经过第二象限,那么m的取值范围是()A.m>0 B.m≥0 C.m<0 D.m≤07.一次函数y=kx+k(k<0)的图像大致是()A. B. C. D.8.函数y=kx+k(k≠0)在直角坐标系中的图像可能是().已知一次函数y=−mx+n−2的图象如下图所示,则m、n的取值范围是()。
一次函数图像应用题(带解析版答案)
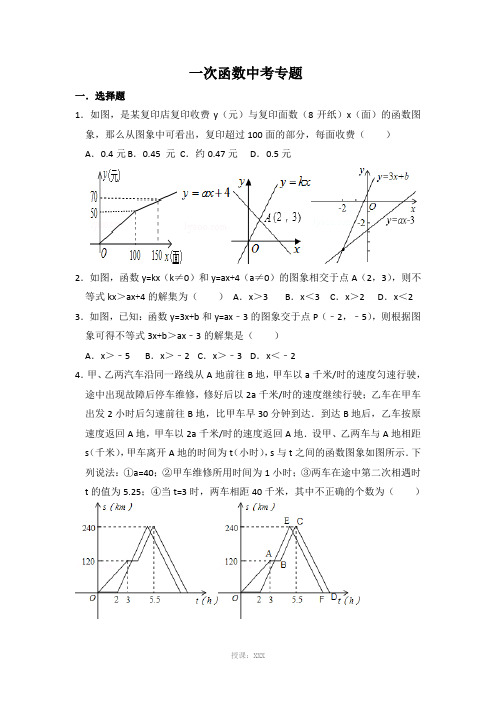
一次函数中考专题一.选择题1.如图,是某复印店复印收费y(元)与复印面数(8开纸)x(面)的函数图象,那么从图象中可看出,复印超过100面的部分,每面收费()A.0.4元 B.0.45 元C.约0.47元D.0.5元2.如图,函数y=kx(k≠0)和y=ax+4(a≠0)的图象相交于点A(2,3),则不等式kx>ax+4的解集为()A.x>3 B.x<3 C.x>2 D.x<2 3.如图,已知:函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),则根据图象可得不等式3x+b>ax﹣3的解集是()A.x>﹣5 B.x>﹣2 C.x>﹣3 D.x<﹣24.甲、乙两汽车沿同一路线从A地前往B地,甲车以a千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以2a千米/时的速度继续行驶;乙车在甲车出发2小时后匀速前往B地,比甲车早30分钟到达.到达B地后,乙车按原速度返回A地,甲车以2a千米/时的速度返回A地.设甲、乙两车与A地相距s(千米),甲车离开A地的时间为t(小时),s与t之间的函数图象如图所示.下列说法:①a=40;②甲车维修所用时间为1小时;③两车在途中第二次相遇时t的值为5.25;④当t=3时,两车相距40千米,其中不正确的个数为()A.0个B.1个 C.2个 D.3个【解答】①由函数图象,得a=120÷3=40故①正确,②由题意,得5.5﹣3﹣120÷(40×2),=2.5﹣1.5,=1.∴甲车维修的时间为1小时;故②正确,③如图:∵甲车维修的时间是1小时,∴B(4,120).∵乙在甲出发2小时后匀速前往B地,比甲早30分钟到达.∴E(5,240).∴乙行驶的速度为:240÷3=80,∴乙返回的时间为:240÷80=3,∴F(8,0).设BC的解析式为y1=k1t+b1,EF的解析式为y2=k2t+b2,由图象,得,解得,,∴y1=80t﹣200,y2=﹣80t+640,当y1=y2时,80t﹣200=﹣80t+640,t=5.25.∴两车在途中第二次相遇时t的值为5.25小时,故弄③正确,④当t=3时,甲车行的路程为120km,乙车行的路程为80×(3﹣2)=80km,∴两车相距的路程为:120﹣80=40千米,故④正确,故选:A.5.甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论:(1)a=40,m=1;(2)乙的速度是80km/h;(3)甲比乙迟h到达B地;(4)乙车行驶小时或小时,两车恰好相距50km.正确的个数是()A.1 B.2 C.3 D.4【解答】(1)由题意,得m=1.5﹣0.5=1.120÷(3.5﹣0.5)=40(km/h),则a=40,故(1)正确;(2)120÷(3.5﹣2)=80km/h(千米/小时),故(2)正确;(3)设甲车休息之后行驶路程y(km)与时间x(h)的函数关系式为y=kx+b,由题意,得解得:∴y=40x﹣20,根据图形得知:甲、乙两车中先到达B地的是乙车,把y=260代入y=40x﹣20得,x=7,∵乙车的行驶速度80km/h,∴乙车行驶260km需要260÷80=3.25h,∴7﹣(2+3.25)=h,∴甲比乙迟h到达B地,故(3)正确;(4)当1.5<x≤7时,y=40x﹣20.设乙车行驶的路程y与时间x之间的解析式为y=k'x+b',由题意得解得:∴y=80x﹣160.当40x﹣20﹣50=80x﹣160时,解得:x=.当40x﹣20+50=80x﹣160时,解得:x=.∴﹣2=,﹣2=.所以乙车行驶或小时,两车恰好相距50km,故(4)错误.故选(C)二.填空题(共3小题)6.如图,已知A1,A2,A3,…,A n是x轴上的点,且OA1=A1A2=A2A3=…=A n A n+1=1,分别过点A1,A2,A3,…,A n+1作x 轴的垂线交一次函数的图象于点B1,B2,B3,…,B n+1,连接A1B2,B1A2,A2B3,B2A3,…,A n B n+1,B n A n+1依次产生交点P1,P2,P3,…,P n,则P n 的坐标是(n+,).【解答】由已知得A1,A2,A3,…的坐标为:(1,0),(2,0),(3,0),…,又得作x轴的垂线交一次函数y=x的图象于点B1,B2,B3,…的坐标分别为(1,),(2,1),(3,),….由此可推出A n,B n,A n+1,B n+1四点的坐标为(n,0),(n ,),(n+1,0),(n+1,).所以得直线A n B n+1和A n+1B n的直线方程分别为解得故答案为:(n+,).7. 下图是护士统计一病人的体温变化图,这位病人中午12时的体温约为℃.8.某高速铁路即将在2019年底通车,通车后,重庆到贵阳、广州等地的时间将大大缩短.5月初,铁路局组织甲、乙两种列车在该铁路上进行试验运行,现两种列车同时从重庆出发,以各自速度匀速向A地行驶,乙列车到达A地后停止,甲列车到达A地停留20分钟后,再按原路以另一速度匀速返回重庆,已知两种列车分别距A地的路程y(km)与时间x(h)之间的函数图象如图所示.当乙列车到达A地时,则甲列车距离重庆km.【解答】设乙列车的速度为xkm/h,甲列车以ykm/h的速度向A地行驶,到达A 地停留20分钟后,以zkm/h的速度返回重庆,则根据3小时后,乙列车距离A地的路程为240,而甲列车到达A地,可得3x+240=3y,①根据甲列车到达A地停留20分钟后,再返回重庆并与乙列车相遇的时刻为4小时,可得x+(1﹣)z=240,②根据甲列车往返两地的路程相等,可得(﹣3﹣)z=3y,③由①②③,可得x=120,y=200,z=180,∴重庆到A地的路程为3×200=600(km),∴乙列车到达A地的时间为600÷120=5(h),∴当乙列车到达A地时,甲列车距离重庆的路程为600﹣(5﹣3﹣)×180=300(km),故答案为:300.三.解答题(共10小题)9.为倡导绿色出行,某共享单车近期登陆徐州,根据连续骑行时长分段计费:骑行时长在2h以内(含2h)的部分,每0.5h计费1元(不足0.5h按0.5h计算);骑行时长超出2h的部分,每小时计费4元(不足1h按1h计算).根据此收费标准,解决下列问题:(1)连续骑行5h,应付费多少元?(2)若连续骑行xh(x>2且x为整数)需付费y元,则y与x的函数表达式为;(3)若某人连续骑行后付费24元,求其连续骑行时长的范围.【解答】(1)当x=5时,y=2×2+4×(5﹣2)=16,∴应付16元;(2)y=4(x﹣2)+2×2=4x﹣4;故答案为:y=4x﹣4;(3)当y=24,24=4x﹣4,x=7,∴连续骑行时长的范围是:6<x≤7.10.如图,“十一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.根据以上信息,解答下列问题:(1)设租车时间为x小时,租用甲公司的车所需费用为y1元,租用乙公司的车所需费用为y2元,分别求出y1,y2关于x的函数表达式;(2)当租车时间为多少小时时,两种方案所需费用相同;(3)根据(2)的计算结果,结合图象,请你帮助小明选择怎样的出游方案更合算.【解答】(1)设y1=k1x+80,把点(1,95)代入,可得:95=k1+80,解得k1=15,∴y1=15x+80(x≥0);设y2=k2x,把(1,30)代入,可得30=k2,即k2=30,∴y2=30x(x≥0);(2)当y1=y2时,15x+80=30x,解得x=;答:当租车时间为小时时,两种方案所需费用相同;(3)由(2)知:当y1=y2时,x=;当y1>y2时,15x+80>30x,解得x<;当y1<y2时,15x+80<30x,解得x>;∴当租车时间为小时,任意选择其中的一个方案;当租车时间小于小时,选择方案二合算;当租车时间大于小时,选择方案一合算.11.如表给出A、B、C三种上网的收费方式:收费方式月使用费/元包时上网时间/小时超时费/(元/分钟)A30250.05B50500.05C120不限时(1)假设月上网时间为x小时,分别直接写出方式A、B、C三种上网方式的收费金额分别为y1、y2、y3与x的函数关系式,并写出自变量的范围(注意结果要化简);(2)给出的坐标系中画出这三个函数的图象简图;(3)结合函数图象,直接写出选择哪种上网方式更合算.【分析】从题意可知,本题中的一次函数又是分段函数,关键是理清楚自变量的取值范围,由取值来确定函数值,从而作出函数图象.【解答】(1)收费方式A:y=30 (0≤x≤25),y=30+3x (x>25);收费方式B:y=50 (0≤x≤50),y=50+3x (x>50);收费方式C:y=120 (0≤x);(2)函数图象如图:(3)由图象可知,上网方式C更合算。
专题06 一次函数图像的五种考法(解析版)(北师大版)

专题06一次函数图像的五种考法类型一、图像的位置关系问题例.直线y kx k =-与直线y kx =-在同一坐标系中的大致图像可能是()A .B .C .D .【答案】A【分析】根据直线y kx k =-与直线y kx =-图像的位置确定k 的正负,若不存在矛盾则符合题意,据此即可解答.【详解】解:A 、y kx =-过第二、四象限,则0k >,所以y kx k =-过第一、三、四象限,所以A 选项符合题意;B 、y kx =-过第二、四象限,则0k >,所以y kx k =-过第一、三、四象限,所以B 选项不符合题意;C 、y kx =-过第一、三象限,则0k <,所以y kx k =-过第二、一、四象限,所以C 选项不符合题意;D 、y kx =-过第一、三象限,则0k <,所以y kx k =-过第二、一、四象限,所以D 选项不符合题意.故选A .【点睛】本题主要考查了一次函数的图像:一次函数0y kx b k =+≠()的图像为一条直线,当0k >,图像过第一、三象限;当0k <,图像过第二、四象限;直线与y 轴的交点坐标为()0b ,.【变式训练1】在同一坐标系中,直线1l :()3y k x k =-+和2l :y kx =-的位置可能是()A .B ...【答案】B【分析】根据正比例函数和一次函数的图像与性质,对平面直角坐标系中两函数图像进行讨论即可得出答案.k>,故由一次函数图像与【详解】A、由正比例函数图像可知0,即0点的上方,故选项A不符合题意;....【答案】B【分析】先根据直线1l,得出k然后再判断直线2l的k和b的符号是否与直线.B...【答案】C【分析】根据一次函数的图象性质判断即可;ab>,【详解】∵0同号,A .B .C .D .【答案】A【分析】分别分析四个选项中一次函数和正比例函数m 和n 的符号,即可进行解答.【详解】解:A 、由一次函数图象得:0,0m n <>,由正比例函数图象得:0mn <,符合题意;B 、由一次函数图象得:0,0m n <>,由正比例函数图象得:0mn >,不符合题意;C 、由一次函数图象得:0,0m n >>,由正比例函数图象得:0mn <,不符合题意;D 、由一次函数图象得:0,0m n ><,由正比例函数图象得:0mn >,不符合题意;故选:A .【点睛】本题主要考查了一次函数和正比例函数的图象,解题的关键是掌握一次函数和正比例函数图象与系数的关系.类型二、图像与系数的关系则13k≥或3k≤-,故答案为:【点睛】本题考查了一次函数的图象与性质,熟练掌握数形结合思想是解题关键.类型三、图像的平移问题例.将直线y kx b =+向左平移2个单位,再向上平移4个单位,得到直线2y x =,则()A .2k =,8b =-B .2k =-,2b =C .1k =,4b =-D .2k =,4b =【答案】A【分析】根据直线y kx b =+向左平移2个单位,变为()2y k x b =++,再向上平移4个单位,变为()24y k x b =+++,然后结合得到直线2y x =,即可解出k 和b 的值.【详解】解:直线y kx b =+向左平移2个单位,变为()2y k x b =++,再向上平移4个单位,变为()24y k x b =+++,得到直线2y x =,2k ∴=,240k b ++=,2k ∴=,8b =-,故选:A .【点睛】本题考查了一次函数图像平移变换,熟练掌握图象左加右减,上加下减的变换规律是解答本题的关键.【变式训练1】对于一次函数24y x =-+,下列结论错误的是().A .函数的图象与x 轴的交点坐标是(0,4)B .函数的图象不经过第三象限C .函数的图象向下平移4个单位长度得2y x =-的图象D .函数值随自变量的增大而减小【答案】A【分析】分别根据一次函数的性质及函数图象平移的法则进行解答即可.【详解】A 选项:当0y =时,2x =,所以函数的图象与x 轴的交点坐标是(2,0),故A 选项错误;B 选项:函数的图象经过第一、二、四象限,不经过第三象限,故B 选项正确;C 选项:函数的图象向下平移4个单位长度,得到函数244y x =-+-,即2y x =-的图象,故C 选项正确;D 选项:由于20k =-<,所以函数值随x 的增大而减小,故D 选项正确.故选:C【点睛】本题考查一次函数的图象及性质,函数图象平移的法则,熟练运用一次函数的图象及性质进行判断是解题的关键.【变式训练2】把直线3y x =-先向右平移2个单位长度,再向下平移3个单位长度,平移后的新直线与x 轴的交点为()0m ,,则m 的值为()A .3B .1C .1-D .3-【答案】B【分析】由题意知,平移后的直线解析式为()32333y x x =---=-+,将()0m ,代入得033m =-+,计算求解即可.【详解】解:由题意知,平移后的直线解析式为()32333y x x =---=-+,将()0m ,代入得033m =-+,解得1m =,故选:B .【点睛】本题考查了一次函数图象的平移,一次函数与坐标轴的交点.解题的关键在于熟练掌握图象平移:左加右减,上加下减.类型四、规律性问题例.在平面直角坐标系中,直线:1l y x =-与x 轴交于点1A ,如图所示,依次作正方形111A B C O ,正方形2221A B C C ,…,正方形1n n n n A B C C -,使得点1A ,2A ,3A ,….在直线l 上,点1C ,2C ,3C ,…,在y 轴正半轴上,则点2023B 的坐标为()A .()202220232,21-B .()202320232,2C .()202320242,21-D .()202220232,21+【答案】A【分析】根据一次函数图象上点的坐标特征结合正方形的性质可得出点11A B 、的坐标,同理可得出2A 、3A 、4A 、5A …及2B 、3B 、4B 、5B …的坐标,根据点的坐标变化可找出变化规律()12,21n n n B --(n 为正整数),依此规律即可得出结论.【详解】解:当0y =时,由10x -=,解得:1x =,∴点1A 的坐标为()1,0,111A B C O 为正方形,()11,1B ∴,同理可得:()22,1A ,()34,3A ,()48,7A ,()516,15A ,…,∴()22,3B ,()34,7B ,()48,15B ,()516,31B ,…,【答案】20222022(21,2)-【分析】先求出1A 、2A 、3A 、4A 的坐标,找出规律,即可得出答案.【详解】解: 直线1y x =+和y 轴交于1A ,1A ∴的坐标()0,1,即11OA =,四边形111C OA B 是正方形,111OC OA ∴==,【答案】()20222,0【分析】根据1A 的坐标和函数解析式,即可求出点34,A A 探究规律利用规律即可解决问题.【详解】∵直线3y x =,点1A 的坐标为∴()11,3B 在11Rt OA B △中,11131,OA A B ==,类型五、增减性问题.B...A .()15,53B .()15,63C .()17,53D 【答案】D【答案】40432【分析】根据已知先求出2OA ,3OA ,33A B ,44A B ,然后分别计算出1S ,2S 【详解】解:∵11OA =,212OA OA =,∴22OA =,∵322OA OA =,∴34OA =,∵432OA OA =,。
中考数学复习----《一次函数之定义、图像与性质》知识点总结与专项练习题(含答案解析)

中考数学复习----《一次函数之定义、图像与性质》知识点总结与专项练习题(含答案解析)知识点总结1. 一次函数的定义:一般地,形如()0≠+=k b k b kx y 是常数且,的函数叫做一次函数。
2. 一次函数的图像:是不经过原点的一条直线。
3. 一次函数的图像与性质:一次函数与x 轴的交点坐标公式为:⎪⎭⎫ ⎝⎛−0 ,k b;与y 轴的交点坐标公式为:()b ,0。
专项练习题1.(2022•沈阳)在平面直角坐标系中,一次函数y =﹣x +1的图像是( )A .B .C .D .【分析】依据一次函数y =x +1的图像经过点(0,1)和(1,0),即可得到一次函数y =﹣x +1的图像经过一、二、四象限.【解答】解:一次函数y =﹣x +1中,令x =0,则y =1;令y =0,则x =1, ∴一次函数y =﹣x +1的图像经过点(0,1)和(1,0), ∴一次函数y =﹣x +1的图像经过一、二、四象限, 故选:C .2.(2022•安徽)在同一平面直角坐标系中,一次函数y =ax +a 2与y =a 2x +a 的图像可能是( )A .B .C .D .【分析】利用一次函数的性质进行判断.【解答】解:∵y=ax+a2与y=a2x+a,∴x=1时,两函数的值都是a2+a,∴两直线的交点的横坐标为1,若a>0,则一次函数y=ax+a2与y=a2x+a都是增函数,且都交y轴的正半轴,图像都经过第一、二、三象限;若a<0,则一次函数y=ax+a2经过第一、二、四象限,y=a2x+a经过第一、三、四象限,且两直线的交点的横坐标为1;故选:D.3.(2022•辽宁)如图,在同一平面直角坐标系中,一次函数y=k1x+b1与y=k2x+b2的图像分别为直线l1和直线l2,下列结论正确的是()A.k1•k2<0B.k1+k2<0C.b1﹣b2<0D.b1•b2<0【分析】根据一次函数y=k1x+b1与y=k2x+b2的图像位置,可得k1>0,b1>0,k2>0,b2<0,然后逐一判断即可解答.【解答】解:∵一次函数y=k1x+b1的图像过一、二、三象限,∴k1>0,b1>0,∵一次函数y=k2x+b2的图像过一、三、四象限,∴k2>0,b2<0,∴A、k1•k2>0,故A不符合题意;B、k1+k2>0,故B不符合题意;C、b1﹣b2>0,故C不符合题意;D、b1•b2<0,故D符合题意;故选:D.4.(2022•六盘水)如图是一次函数y=kx+b的图像,下列说法正确的是()A.y随x增大而增大B.图像经过第三象限C.当x≥0时,y≤b D.当x<0时,y<0【分析】根据一次函数的图像和性质进行判断即可.【解答】解:由图像得:图像过一、二、四象限,则k<0,b>0,当k<0时,y随x的增大而减小,故A、B错误,由图像得:与y轴的交点为(0,b),所以当x≥0时,从图像看,y≤b,故C正确,符合题意;当x<0时,y>b>0,故D错误.故选:C.5.(2022•兰州)若一次函数y=2x+1的图像经过点(﹣3,y1),(4,y2),则y1与y2的大小关系是()A.y1<y2B.y1>y2C.y1≤y2D.y1≥y2【分析】先根据一次函数的解析式判断出函数的增减性,再根据﹣3<4即可得出结论.【解答】解:∵一次函数y=2x+1中,k=2>0,∴y随着x的增大而增大.∵点(﹣3,y1)和(4,y2)是一次函数y=2x+1图像上的两个点,﹣3<4,∴y1<y2.故选:A.6.(2022•凉山州)一次函数y=3x+b(b≥0)的图像一定不经过()A.第一象限B.第二象限C.第三象限D.第四象限【分析】根据一次函数的图像与系数的关系即可得出结论.【解答】解:∵函数y=3x+b(b≥0)中,k=3>0,b≥0,∴当b=0时,此函数的图像经过一、三象限,不经过第四象限;当b>0时,此函数的图像经过一、二、三象限,不经过第四象限.则一定不经过第四象限.故选:D.7.(2022•济宁)已知直线y1=x﹣1与y2=kx+b相交于点(2,1).请写出一个b值(写出一个即可),使x>2时,y1>y2.【分析】由题意可知,当b>﹣1时满足题意,故b可以取0.【解答】解:直线y1=x﹣1与y2=kx+b相交于点(2,1).∵x>2时,y1>y2.∴b>﹣1,故b可以取0,故答案为:0(答案不唯一).8.(2022•上海)已知直线y=kx+b过第一象限且函数值随着x的增大而减小,请列举出来这样的一条直线:.【分析】根据一次函数的性质,写出符合条件的函数关系式即可.【解答】解:∵直线y=kx+b过第一象限且函数值随着x的增大而减小,∴k<0,b>0,∴符合条件的函数关系式可以为:y=﹣x+1(答案不唯一).故答案为:y=﹣x+1(答案不唯一).9.(2022•无锡)请写出一个函数的表达式,使其图像分别与x轴的负半轴、y轴的正半轴相交:.【分析】设函数的解析式为y=kx+b(k≠0),再根据一次函数的图像分别与x轴的负半轴、y轴的正半轴相交可知k>0,b>0,写出符合此条件的函数解析式即可.【解答】解:设一次函数的解析式为y=kx+b(k≠0),∵一次函数的图像分别与x轴的负半轴、y轴的正半轴相交,∴k>0,b>0,∴符合条件的函数解析式可以为:y=x+1(答案不唯一).故答案为:y=x+1(答案不唯一).10.(2022•湘潭)请写出一个y随x增大而增大的一次函数表达式.【分析】根据y随着x的增大而增大时,比例系数k>0即可确定一次函数的表达式.【解答】解:在y=kx+b中,若k>0,则y随x增大而增大,∴只需写出一个k>0的一次函数表达式即可,比如:y=x﹣2,故答案为:y=x﹣2(答案不唯一).11.(2022•宿迁)甲、乙两位同学各给出某函数的一个特征,甲:“函数值y随自变量x增大而减小”;乙:“函数图像经过点(0,2)”,请你写出一个同时满足这两个特征的函数,其表达式是.【分析】根据甲、乙两位同学给出的函数特征可判断出该函数为一次函数,再利用一次函数的性质,可得出k<0,b=2,取k=﹣1即可得出结论.【解答】解:∵函数值y随自变量x增大而减小,且该函数图像经过点(0,2),∴该函数为一次函数.设一次函数的表达式为y=kx+b(k≠0),则k<0,b=2.取k=﹣1,此时一次函数的表达式为y=﹣x+2.故答案为:y=﹣x+2(答案不唯一).12.(2022•甘肃)若一次函数y=kx﹣2的函数值y随着自变量x值的增大而增大,则k=(写出一个满足条件的值).【分析】根据函数值y随着自变量x值的增大而增大得到k>0,写出一个正数即可.【解答】解:∵函数值y随着自变量x值的增大而增大,∴k>0,∴k=2(答案不唯一).故答案为:2(答案不唯一).13.(2022•柳州)如图,直线y1=x+3分别与x轴、y轴交于点A和点C,直线y2=﹣x+3分别与x轴、y轴交于点B和点C,点P(m,2)是△ABC内部(包括边上)的一点,则m的最大值与最小值之差为()A.1B.2C.4D.6【分析】由于P的纵坐标为2,故点P在直线y=2上,要求符合题意的m值,则P点为直线y=2与题目中两直线的交点,此时m存在最大值与最小值,故可求得.【解答】解:∵点P(m,2)是△ABC内部(包括边上)的一点,∴点P 在直线y =2上,如图所示,当P 为直线y =2与直线y 2的交点时,m 取最大值, 当P 为直线y =2与直线y 1的交点时,m 取最小值, ∵y 2=﹣x +3中令y =2,则x =1, y 1=x +3中令y =2,则x =﹣1, ∴m 的最大值为1,m 的最小值为﹣1.则m 的最大值与最小值之差为:1﹣(﹣1)=2. 故选:B .14.(2022•遵义)若一次函数y =(k +3)x ﹣1的函数值y 随x 的增大而减小,则k 值可能是( ) A .2B .23C .﹣21 D .﹣4【分析】根据一次项系数小于0时,一次函数的函数值y 随x 的增大而减小列出不等式求解即可.【解答】解:∵一次函数y =(k +3)x ﹣1的函数值y 随着x 的增大而减小, ∴k +3<0, 解得k <﹣3.所以k 的值可以是﹣4, 故选:D .15.(2022•包头)在一次函数y =﹣5ax +b (a ≠0)中,y 的值随x 值的增大而增大,且ab >0,则点A (a ,b )在( ) A .第四象限B .第三象限C .第二象限D .第一象限【分析】根据一次函数的增减性,确定自变量x 的系数﹣5a 的符号,再根据ab >0,确定b 的符号,从而确定点A (a ,b )所在的象限.【解答】解:∵在一次函数y =﹣5ax +b 中,y 随x 的增大而增大, ∴﹣5a >0,∴a <0. ∵ab >0, ∴a ,b 同号, ∴b <0.∴点A (a ,b )在第三象限. 故选:B .16.(2022•眉山)一次函数y =(2m ﹣1)x +2的值随x 的增大而增大,则点P (﹣m ,m )所在象限为( ) A .第一象限B .第二象限C .第三象限D .第四象限【分析】根据一次函数的性质求出m 的范围,再根据每个象限点的坐标特征判断P 点所处的象限即可.【解答】解:∵一次函数y =(2m ﹣1)x +2的值随x 的增大而增大, ∴2m ﹣1>0, 解得:m >,∴P (﹣m ,m )在第二象限, 故选:B .17.(2022•天津)若一次函数y =x +b (b 是常数)的图像经过第一、二、三象限,则b 的值可以是 (写出一个即可).【分析】根据一次函数的图像可知b >0即可.【解答】解:∵一次函数y =x +b (b 是常数)的图像经过第一、二、三象限, ∴b >0, 可取b =1,故答案为:1.(答案不唯一,满足b >0即可) 18.(2022•邵阳)在直角坐标系中,已知点A (23,m ),点B (27,n )是直线y =kx +b(k <0)上的两点,则m ,n 的大小关系是( ) A .m <nB .m >nC .m ≥nD .m ≤n【分析】根据k <0可知函数y 随着x 增大而减小,再根>即可比较m 和n 的大小.【解答】解:点A (,m ),点B (,n )是直线y =kx +b 上的两点,且k <0,∴一次函数y 随着x 增大而减小, ∵>,∴m <n , 故选:A .19.(2022•株洲)在平面直角坐标系中,一次函数y =5x +1的图像与y 轴的交点的坐标为( ) A .(0,﹣1)B .(﹣51,0) C .(51,0) D .(0,1)【分析】一次函数的图像与y 轴的交点的横坐标是0,当x =0时,y =1,从而得出答案. 【解答】解:∵当x =0时,y =1,∴一次函数y =5x +1的图像与y 轴的交点的坐标为(0,1), 故选:D .20.(2022•绍兴)已知(x 1,y 1),(x 2,y 2),(x 3,y 3)为直线y =﹣2x +3上的三个点,且x 1<x 2<x 3,则以下判断正确的是( ) A .若x 1x 2>0,则y 1y 3>0 B .若x 1x 3<0,则y 1y 2>0C .若x 2x 3>0,则y 1y 3>0D .若x 2x 3<0,则y 1y 2>0【分析】根据一次函数的性质和各个选项中的条件,可以判断是否正确,从而可以解答本题.【解答】解:∵直线y =﹣2x +3,∴y 随x 的增大而减小,当y =0时,x =1.5,∵(x 1,y 1),(x 2,y 2),(x 3,y 3)为直线y =﹣2x +3上的三个点,且x 1<x 2<x 3, ∴若x 1x 2>0,则x 1,x 2同号,但不能确定y 1y 3的正负,故选项A 不符合题意; 若x 1x 3<0,则x 1,x 3异号,但不能确定y 1y 2的正负,故选项B 不符合题意; 若x 2x 3>0,则x 2,x 3同号,但不能确定y 1y 3的正负,故选项C 不符合题意;若x 2x 3<0,则x 2,x 3异号,则x 1,x 2同时为负,故y 1,y 2同时为正,故y 1y 2>0,故选项D 符合题意; 故选:D .21.(2022•盘锦)点A (x 1,y 1),B (x 2,y 2)在一次函数y =(a ﹣2)x +1的图像上,当x 1>x 2时,y 1<y 2,则a 的取值范围是 . 【分析】根据一次函数的性质,建立不等式计算即可.【解答】解:∵当x1>x2时,y1<y2,∴a﹣2<0,∴a<2,故答案为:a<2.22.(2022•永州)已知一次函数y=x+1的图像经过点(m,2),则m=.【分析】由一次函数y=x+1的图像经过点(m,2),利用一次函数图像上点的坐标特征可得出2=m+1,解之即可求出m的值.【解答】解:∵一次函数y=x+1的图像经过点(m,2),∴2=m+1,∴m=1.故答案为:1.。
一次函数及其图像练习(含答案详解)

一次函数及其图象一、选择题1.关于一次函数y =-x +1的图象,下列所画正确的是(C )【解析】 由一次函数y =-x +1知:图象过点(0,1)和(1,0),故选C.2.在同一平面直角坐标系中,若一次函数y =-x +3与y =3x -5的图象交于点M ,则点M 的坐标为(D )A .(-1,4)B .(-1,2)C. (2,-1)D. (2,1)【解析】 一次函数y =-x +3与y =3x -5的图象的交点M 的坐标即为方程组⎩⎪⎨⎪⎧y =-x +3,y =3x -5的解, 解方程组,得⎩⎪⎨⎪⎧x =2,y =1,∴点M 的坐标为(2,1). 3.已知直线y =kx +b ,若k +b =-5,kb =6,则该直线不经过(A )A .第一象限B .第二象限C. 第三象限D. 第四象限【解析】 由kb =6,知k ,b 同号.又∵k +b =-5,∴k <0,b <0,∴直线y =kx +b 经过第二、三、四象限,∴不经过第一象限.4.直线y =-32x +3与x 轴,y 轴所围成的三角形的面积为(A )A .3B .6C.34D.32【解析】直线y=-32x+3与x轴的交点为(2,0),与y轴的交点为(0,3),所围成的三角形的面积为12×2×3=3.5.已知正比例函数y=kx(k<0)的图象上两点A(x1,y1),B(x2,y2),且x1<x2,则下列不等式中恒成立的是(C)A.y1+y2>0 B.y1+y2<0C. y1-y2>0D. y1-y2<0【解析】∵正比例函数y=kx中k<0,∴y随x的增大而减小.∵x1<x2,∴y1>y2,∴y1-y2>0.(第6题)6.甲、乙两人沿相同的路线由A地到B地匀速前进,A,B两地间的路程为20 km.设他们前进的路程为s(km),甲出发后的时间为t(h),甲、乙前进的路程与时间的函数图象如图所示.根据图象提供的信息,下列说法正确的是(C) A.甲的速度是4 km/h B.乙的速度是10 km/hC.乙比甲晚出发1 h D.甲比乙晚到B地3 h【解析】根据图象知:甲的速度是204=5(km/h),乙的速度是202-1=20(km/h),乙比甲晚出发1-0=1(h),甲比乙晚到B地4-2=2(h),故选C.7.丁老师乘车从学校到省城去参加会议,学校距省城200 km,车行驶的平均速度为80 km/h.若x(h)后丁老师距省城y(km),则y与x之间的函数表达式为(D)A. y=80x-200B. y=-80x-200C. y=80x+200D. y=-80x+200【解析】∵丁老师x(h)行驶的路程为80x(km),∴x(h)后距省城(200-80x)km.8.如果一次函数y=kx+b的函数值y随x的增大而减小,且图象与y轴的负半轴相交,那么下列对k和b的符号判断正确的是(D)A.k>0,b>0 B.k>0,b<0C .k <0,b >0D .k <0,b <0【解析】 ∵y 随x 的增大而减小,∴k <0.∵图象与y 轴交于负半轴,∴b <0.(第9题)9.张师傅驾车从甲地到乙地,两地相距500km ,汽车出发前油箱有油25L ,途中加油若干升,加油前、后汽车都以100km/h 的速度匀速行驶,已知油箱中剩余油量y (L)与行驶时间t (h)之间的函数关系如图所示,则下列说法错误的是(C )A .加油前油箱中剩余油量y (L)与行驶时间t (h)的函数表达式是y =-8t +25B .途中加油21LC. 汽车加油后还可行驶4hD. 汽车到达乙地时油箱中还剩油6L【解析】 A .设加油前油箱中剩余油量y (L)与行驶时间t (h)的函数表达式为y =kt +b .将点(0,25),(2,9)的坐标代入,得⎩⎪⎨⎪⎧b =25,2k +b =9,解得⎩⎪⎨⎪⎧k =-8,b =25,∴y =-8t +25,故本选项正确.B .由图象可知,途中加油30-9=21(L),故本选项正确.C .由图象可知,汽车每小时用油(25-9)÷2=8(L),∴汽车加油后还可行驶30÷8=334(h)<4h ,故本选项错误.D .∵汽车从甲地到乙地所需时间为500÷100=5(h),又∵汽车油箱出发前有油25L ,途中加油21L ,∴汽车到达乙地时油箱中还剩油25+21-5×8=6(L),故本选项正确.故选C.二、填空题10.写出一个图象经过第一、三象限的正比例函数y=kx(k≠0)的表达式:y =2x.【解析】∵图象经过第一、三象限,∴k>0,∴k可以取大于0的任意实数.答案不唯一,如:y=2x.11.已知一次函数y=(2-m)x+m-3,当m>2时,y随x的增大而减小.【解析】由一次函数的性质可知:当y随x的增大而减小时,k=2-m<0,∴m>2.12.如图是一个正比例函数的图象,把该图象向左平移一个单位长度,得到的函数图象的表达式为y=-2x-2.【解析】设原函数图象的表达式为y=kx.当x=-1时,y=2,则有2=-k,∴k=-2,∴y=-2x.设平移后的图象的表达式为y=-2x+b.当x=-1时,y=0,则有0=2+b,∴b=-2,∴y=-2x-2.(第12题)(第13题)13.如图所示是某工程队在“村村通”工程中修筑的公路长度y(m )与时间x(天)之间的函数关系图象.根据图象提供的信息,可知该公路的长度是504m .【解析】 当2≤x ≤8时,设y =kx +b.把点(2,180),(4,288)的坐标代入,得⎩⎪⎨⎪⎧180=2k +b ,288=4k +b ,解得⎩⎪⎨⎪⎧k =54,b =72.∴y =54x +72.当x =8时,y =504.14.直线y =kx +b 经过点A(-2,0)和y 轴正半轴上的一点B ,如果△ABO(O 为坐标原点)的面积为6,那么b 的值为__6__.【解析】 S △ABO =12×2·b =6,∴b =6.(第15题)15.如图,矩形ABCD 的边AB 在x 轴上,AB 的中点与原点重合,AB =2,AD =1,过定点Q(0,2)和动点P(a ,0)的直线与矩形ABCD 的边有公共点,则a 的取值范围是-2≤a ≤2.【解析】 当QP 过点C 时,点P(2,0);当QP 过点D 时,点P(-2,0).∴-2≤a ≤2.16.一次越野跑中,当小明跑了1600 m 时,小刚跑了1400 m ,小明、小刚在此后所跑的路程y (m)与时间t (s)之间的函数关系如图所示,则这次越野跑的全程为2200m.,(第16题))【解析】 设小明的速度为a (m/s),小刚的速度为b (m/s),由题意,得 ⎩⎪⎨⎪⎧1600+100a =1400+100b ,1600+300a =1400+200b ,解得⎩⎪⎨⎪⎧a =2,b =4.∴这次越野跑的全程为1600+300×2=2200(m).17.已知直线y =k 1x +b 1(k 1>0)与y =k 2x +b 2(k 2<0)交于点A (-2,0),且两直线与y 轴围成的三角形的面积为4,那么b 1-b 2等于__4__.【解析】 如解图,设直线y =k 1x +b 1(k 1>0)与y 轴交于点B ,直线y =k 2x +b 2(k 2<0)与y 轴交于点C ,则OB =b 1,OC =-b 2.(第17题解)∵△ABC 的面积为4,∴12OA·OB +12OA·OC =4,∴12×2·b 1+12×2·(-b 2)=4,∴b 1-b 2=4.三、解答题(第18题)18.A ,B 两城相距600 km ,甲、乙两车同时从A 城出发驶向B 城,甲车到达B 城后立即返回.如图是它们离A 城的距离y (km)与行驶时间x (h)之间的函数图象.(1)求甲车行驶过程中y 与x 之间的函数表达式,并写出自变量x 的取值范围.(2)当它们行驶7 h 时,两车相遇,求乙车的速度.【解析】 (1)①当0≤x ≤6时,易得y =100x .②当6<x ≤14时,设y =kx +b .∵图象过点(6,600),(14,0),∴⎩⎪⎨⎪⎧6k +b =600,14k +b =0,解得⎩⎪⎨⎪⎧k =-75,b =1050.∴y =-75x +1050.∴y =⎩⎪⎨⎪⎧100x (0≤x ≤6),-75x +1050(6<x ≤14).(2)当x =7时,y =-75×7+1050=525,∴v 乙=5257=75(km/h).19.一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留了一段相同的时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x (h),两车之间的距离为y (km),如图中的折线表示y 与x 之间的函数关系.(第19题)请根据图象解决下列问题:(1)甲、乙两地之间的距离为__560__km.(2)求快车和慢车的速度.(3)求线段DE 所表示的y 关于x 的函数表达式,并写出自变量x 的取值范围.【解析】 (1)由图象可得:甲、乙两地之间的距离为560 km.(2)由图象可得:慢车往返分别用了4 h ,慢车行驶4 h 的距离,快车3 h 即可行驶完,∴可设慢车的速度为3x (km/h),则快车的速度为4x (km/h).由图象可得:4(3x +4x )=560,解得x =20.∴快车的速度为4x =80(km/h),慢车的速度为3x =60(km/h).(3)由题意可得:当x =8时,慢车距离甲地60×(4-3)=60(km),∴点D (8,60).∵慢车往返一次共需8h ,∴点E (9,0).设直线DE 的函数表达式为y =kx +b ,则⎩⎪⎨⎪⎧9k +b =0,8k +b =60,解得⎩⎪⎨⎪⎧k =-60,b =540.∴线段DE 所表示的y 关于x 的函数表达式为y =-60x +540(8≤x ≤9).20.小明家今年种植的“红灯”樱桃喜获丰收,采摘上市20天后全部销售完,小明对销售情况进行跟踪记录,并将记录情况绘成图象,日销售量y (kg)与上市时间x (天)的函数关系如图①所示,樱桃价格z (元/kg)与上市时间x (天)的函数关系如图②所示.(第20题)(1)观察图象,直接写出日销售量的最大值.(2)求小明家樱桃的日销售量y 与上市时间x 之间的函数表达式.(3)第10天与第12天的销售金额哪天多?请说明理由.【解析】 (1)日销售量的最大值为120 kg.(2)当0≤x ≤12时,设日销售量y 与上市时间x 之间的函数表达式为y =kx . ∵点(12,120)在y =kx 的图象上,∴120=12k ,∴k =10,∴函数表达式为y =10x .当12<x ≤20时,设日销售量y 与上市时间x 之间的函数表达式为y =k 1x +b 1.∵点(12,120),(20,0)在y =k 1x +b 1的图象上,∴⎩⎪⎨⎪⎧12k 1+b 1=120,20k 1+b 1=0,解得⎩⎪⎨⎪⎧k 1=-15,b 1=300.∴函数表达式为y =-15x +300.∴小明家樱桃的日销售量y 与上市时间x 之间的函数表达式为y =⎩⎪⎨⎪⎧10x (0≤x ≤12),-15x +300(12<x ≤20).(3)当5<x ≤15时,设樱桃价格z 与上市时间x 之间的函数表达式为z =k 2x +b 2.∵点(5,32),(15,12)在z =k 2x +b 2的图象上,∴⎩⎪⎨⎪⎧5k 2+b 2=32,15k 2+b 2=12,解得⎩⎪⎨⎪⎧k 2=-2,b 2=42.∴函数表达式为z =-2x +42.当x =10时,y =10×10=100,z =-2×10+42=22,∴销售金额为100×22=2200(元).当x =12时,y =10×12=120,z =-2×12+42=18,∴销售金额为120×18=2160(元).∵2200>2160,∴第10天的销售金额多.。
八年级数学一次函数图象性质 专项练习题(含答案)

参考答案 1、B 2、C ; 3、A 4、C 5、C 6、B 7、A 8、C 9、A 10、C 11、A 12、D 13、B 14、A 15、A 16、A 17、A 18、C 19、D 20、A 21、 22、y=23、答案为 1. 24、-3 25、一、二、三. 26、2 . 27、3 28、答案是:3. 29、答案为 y=3x+4. 30、(0,-1) ;
m313将直线ykx1向上平移2个单位长度可得直线的解析式为aykx3bykx1cykx3dykx114直线y2xb与x轴的交点坐标是20则关于x的方程2xb0的解是ax2bx4cx8dx1015如图直线ykxb与x轴y轴分别相交于点a30b02则不等式kxb0的解集是ax3bx3cx2dx216同一直角坐标系中一次函数y1k1xb与正比例函数y2k2x的图象如图所示则满足y1y2的x取值范围是ax2bx2cx2dx217点ax1y1点bx2y2是一次函数y2x4图象上的两点且x1x2则y1与y2的大小关系是ay1y2by1y20cy1y2dy1y218已知a320则一次函数yaxb的图象不经过6)在 y=k1x 上∴﹣6=3k1∴k1=﹣2 ∵点 P(3,﹣6)在 y=k2x﹣9 上∴﹣6=3k2﹣9∴k2=1; (2)∵k2=1,∴y=x﹣9∵一次函数 y=x﹣9 与 x 轴交于点 A 又∵当 y=0 时,x=9∴A(9,0). 33、(1) ;(2)23;
八年级数学一次函数图象性质 专项练习题
一、选择题: 1、下列函数(1)y=3πx;(2)y=8x-6;(3)y= ( ) A.4 个 2、函数 A.(3,5); B.3 个 C.2 个 D.1 个
1 ;(4)y= -8x;(5)y=5x2-4x+1 中,是一次函数的有 x
最全一次函数图像专题(带解析)完整版.doc

最全一次函数图像专题(带解析)完整版.doc最全一次函数图像专题(带解析)完整版一次函数也称为一次方程或线性方程,是数学中的重要概念。
在本专题中,我们将详细讨论一次函数的图像及相关概念和性质。
一、一次函数的定义与性质一次函数是指形如y = kx + b的函数,其中k和b为常数,k 称为斜率,b称为截距。
一次函数的图像是一条直线,其斜率决定了直线的倾斜程度,截距决定了直线与y轴的交点位置。
二、一次函数的图像特征1. 斜率k的正负决定了直线的倾斜方向。
当k为正数时,直线向右上方倾斜;当k为负数时,直线向右下方倾斜。
2. 斜率k的绝对值决定了直线的倾斜程度。
绝对值越大,倾斜程度越大。
3. 当k为0时,直线为水平线;当k不存在时,直线为竖直线。
三、一次函数图像的基本形状1. 当k>0时,直线从左下方向右上方倾斜。
2. 当k=1时,直线为45°斜线。
3. 当k=-1时,直线为水平斜线。
4. 当k=0时,直线为水平线。
5. 当k不存在时,直线为竖直线。
四、一次函数的图像平移1. 沿x轴平移的结果:将y = kx + b中的b替换为b',则得到的函数为y = kx + b'。
平移后的直线与原直线平行,斜率不变,但截距发生了变化。
2. 沿y轴平移的结果:将y = kx + b中的k替换为k',则得到的函数为y = k'x + b。
平移后的直线与原直线平行,截距不变,但斜率发生了变化。
五、一次函数的图像伸缩1. 垂直伸缩的结果:将y = kx + b中的k替换为ak,其中a 为正数。
当a>1时,直线变得更陡峭;当0<a<1时,直线变得更平缓。
2. 水平伸缩的结果:将y = kx + b中的x替换为x/a,其中a为正数。
当a>1时,直线变得更平缓;当0<a<1时,直线变得更陡峭。
六、一次函数的解析法与图像的关系1. 斜率k的正负决定了图像的倾斜方向。
初中数学一次函数的图像专项练习30题(有答案)

初中数学一次函数的图像专项练习30题(有答案)1.本题为选择题,无需改写。
2.在图中,当x>2时,y2>y1,因此结论③正确。
由于y1=kx+b与y2=x+a的图象相交于第三象限,因此a<0,结论②也正确。
而k<0,因此结论①错误。
因此选项C正确。
3.根据题目中的条件,k<0,b>0,因此函数的图象是下降的直线,截距为正数,应该是选项A。
4.本题为选择题,无需改写。
5.根据题目中的条件,k<0,b>0,因此函数的图象是下降的直线,截距为正数,斜率的绝对值小于1,应该是选项B。
6.将直线l1和直线l2的方程化简可得y=2x+1和y=-x-1,因此直线l1的斜率为2,直线l2的斜率为-1.由于x+y=0,因此该点在第三部分。
因此选项C正确。
7.根据两个函数的表达式可知它们的图象分别是斜率为负数的直线和斜率为正数的直线,应该是选项B。
8.函数y=2x+3的斜率为2,截距为3,应该是选项A。
9.根据图象可知,选项C表示的是y=-x-1的图象,因此选项C正确。
10.将函数kx-y=2化简可得y=kx-2,因此函数的图象是斜率为正数的直线,截距为-2,应该是选项C。
11.由于b1<b2,因此直线y1在直线y2的下方。
由于k1k2<0,因此直线y1和直线y2的斜率异号,相交于第二象限。
因此选项B正确。
12.根据图象可知,选项D表示的是y=abx的图象,因此选项D正确。
13.根据图象可知,降雨后,蓄水量每天增加5万立方米,因此选项B正确。
14.本题为选择题,无需改写。
15.将y=kx代入y=kx-k可得y=k(x-1),因此函数的图象是斜率为正数的直线,截距为-k,应该是选项C。
16.当x增加时,y的值也会增加,且当x大于某个值时,y会大于2.17.当x增加时,y的值也会增加,但当x大于某个值时,y会小于某个值。
18.当x增加时,y的值也会增加,且当x大于某个值时,y会大于某个值。
19.正确的判断是:①k0;③当x=3时,y1=y2;④当03时,y1>y2.20.当x增加时,y1的值也会增加,且当x大于某个值时,y1会大于y2.21.当y小于某个值时,x的取值范围是一定的,具体取值范围需要根据具体函数图象来确定。
(完整版)一次函数的图像和性质练习题

一次函数的图像和性质练习题一、填空题1.正比例函数(0)y kx k =≠一定经过 点,经过(1), ,一次函数(0)y kx b k =+≠经过(0),点,(0) ,点. 2.直线26y x =-+与x 轴的交点坐标是 ,与y 轴的交点坐标是 。
与坐标轴围成的三角形的面积是 。
3.若一次函数(44)y mx m =--的图象过原点,则m 的值为 .4.如果函数y x b =-的图象经过点(01)P ,,则它经过x 轴上的点的坐标为 . 5.一次函数3+-=x y 的图象经过点( ,5)和(2, )6.某函数具有下面两条性质:(1)它的图象是经过原点的一条直线;(2)y 随x 的增大而减小.请你写出一个满足上述条件的函数 7.在同一坐标系内函数y=2x 与y=2x+6的图象的位置关系是 . 8. 若直线y=2x+6与直线y=mx+5平行,则m=____________.9.在同一坐标系内函数y=ax+b 与y=3x+2平行,则a, b 的取值范围是 . 10.将直线y= -2x 向上平移3个单位得到的直线解析式是 ,将直线y= -2x 向下移3个单得到的直线解析式是 .将直线y= -2x+3向下移2个单得到的直线解析式是 .11.直线y kx b =+经过一、二、三象限,则k 0,b 0,经过二、三、四象限,则有k 0,b 0,经过一、二、四象限,则有k 0,b 0.12.一次函数(2)4y k x k =-+-的图象经过一、三、四象限,则k 的取值范围是 . 13.如果直线3y x b =+与y 轴交点的纵坐标为2-,那么这条直线一定不经过第 象限. 14. 已知点A(-4, a),B(-2,b)都在一次函数y=21x+k(k 为常数)的图像上,则a 与b 的大小关系是a____b(填”<””=”或”>”) 15.一次函数y=kx+b 的图象如图所示,看图填空:(1)当x=0时,y=____________;当x=____________时,y=0. (2)k=__________,b=____________.(3)当x=5时,y=__________;当y=30时,x=___________. 二、选择题1.已知函数(3)2y m x =+-,要使函数值y 随自变量x 的增大而减小,则m 的取值范围是( )A.3m -≥B.3m >-C.3m -≤D.3m <-2.已知直线y kx b =+,经过点11()A x y ,和点22()B x y ,,若0k <,且12x x <,则1y 与2y 的大小关系是( ) A.12y y >B.12y y <C.12y y =D.不能确定3.若直线23y mx m =--经过第二、三、四象限,则m 的取值范围是( )A.32m <B.302m -<<C.32m >D.0m >4.一次函数31y x =-的图象不经过( )A.第一象限B.第二象限 C.第三象限D.第四象限5. 如果点P(a,b)关于x 轴的对称点p ,在第三象限,那么直线y=ax+b 的图像不经过 ( )A.第一象限 B.第二象限 C.第三象限 D.第四象限 6. 若一次函数y=kx+b 的图像经过(-2,-1)和点(1,2),则这个函数的图像不经过 ( )A.第一象限 B.第二象限 C.第三象限 D.第四象限 7.下列图象中不可能是一次函数(3)y mx m =--的图象的是( )8.两个一次函数1y ax b =+与2y bx a =+,它们在同一直角坐标系中的图象可能是( )三、解答题1.已知一次函数y=(3-k)x-2k+18, (1) k 为何值时,它的图像经过原点; (2) k 为何值时,它的图像经过点(0,-2);(3) k 为何值时,它的图像与y 轴的交点在x 轴的上方; (4) k 为何值时,它的图像平行于直线y=-x; (5) k 为何值时,y 随x 的增大而减小.2. 设一次函数)0(≠+=k b kx y ,当2=x 时,3-=y ,当1-=x 时,4=y 。
一次函数经典题型 习题(精华 含答案)

一次函数题型一、点的坐标方法: x 轴上的点纵坐标为0,y 轴上的点横坐标为0;若两个点关于x 轴对称,则他们的横坐标相同,纵坐标互为相反数; 若两个点关于y 轴对称,则它们的纵坐标相同,横坐标互为相反数; 若两个点关于原点对称,则它们的横坐标互为相反数,纵坐标也互为相反数;1、 若点A (m,n )在第二象限,则点(|m|,-n )在第____象限;2、 若点P (2a-1,2-3b )是第二象限的点,则a,b 的范围为______________________;3、 已知A (4,b ),B (a,-2),若A ,B 关于x 轴对称,则a=_______,b=_________;若A,B 关于y 轴对称,则a=_______,b=__________;若若A ,B 关于原点对称,则a=_______,b=_________;4、 若点M (1-x,1-y )在第二象限,那么点N (1-x,y-1)关于原点的对称点在第______象限。
题型二、关于点的距离的问题方法:点到x 轴的距离用纵坐标的绝对值表示,点到y 轴的距离用横坐标的绝对值表示;若AB ∥x 轴,则(,0),(,0)A B A x B x 的距离为A B x x -; 若AB ∥y 轴,则(0,),(0,)A B A y B y 的距离为A B y y -;点B (2,-2)到x 轴的距离是_________;到y 轴的距离是____________; 1、 点C (0,-5)到x 轴的距离是_________;到y 轴的距离是____________;到原点的距离是____________;2、 点D (a,b )到x 轴的距离是_________;到y 轴的距离是____________;到原点的距离是____________; 3、 已知点P (3,0),Q(-2,0),则PQ=__________,已知点110,,0,22M N ⎛⎫⎛⎫-⎪ ⎪⎝⎭⎝⎭,则MQ=________; ()()2,1,2,8E F --,则EF 两点之间的距离是__________;已知点G (2,-3)、H (3,4),则G 、H 两点之间的距离是_________;4、 两点(3,-4)、(5,a )间的距离是2,则a 的值为__________;5、 已知点A (0,2)、B (-3,-2)、C (a,b ),若C 点在x 轴上,且∠ACB=90°,则C 点坐标为___________.题型三、一次函数与正比例函数的识别方法:若y=kx+b(k,b 是常数,k ≠0),那么y 叫做x 的一次函数,特别的,当b=0时,一次函数就成为y=kx(k 是常数,k ≠0),这时,y 叫做x 的正比例函数,当k=0时,一次函数就成为若y=b ,这时,y 叫做常函数。
最全一次函数图像专题(带解析)完整版.doc

2018/06/10一.选择题(共15小题)1.(2016•武汉)下列函数:①y=x;②y=;③y=;④y=2x+1,其中一次函数的个数是()A.1 B.2 C.3 D.42.函数y=(m﹣2)x n﹣1+n是一次函数,m,n应满足的条件是()A.m≠2且n=0 B.m=2且n=2 C.m≠2且n=2 D.m=2且n=03.已知函数y=3x+1,当自变量x增加m时,相应函数值增加()A.3m+1 B.3m C.m D.3m﹣14.在一次函数y=kx+b中,k为()A.正实数B.非零实数 C.任意实数 D.非负实数5.(2017•台湾)如图的坐标平面上有四直线L1、L2、L3、L4.若这四直线中,有一直线为方程式3x﹣5y+15=0的图形,则此直线为何?()A.L1B.L2C.L3D.L46.(2017•清远)一次函数y=x+2的图象大致是()A .B .C .D .7.(2017•滨州)关于一次函数y=﹣x+1的图象,下列所画正确的是()A .B .C .D .8.(2016•台湾)如图,有四直线L1,L2,L3,L4,其中()是方程式13x﹣25y=62的图象.A.L1B.L2C.L3D.L49.(2016•贵阳)一次函数y=kx+b的图象如图所示,当y<0时,x的取值范围是()A.x>0 B.x<0 C.x>2 D.x<210.(2015•芜湖)关于x的一次函数y=kx+k2+1的图象可能正确的是()A .B .C .D .11.(2017•乐山)若实数k,b满足kb<0且不等式kx<b的解集是x >,那么函数y=kx+b的图象只可能是()A .B .C .D .12.(2015•江津区)已知一次函数y=2x﹣3的大致图象为()1A. B.C.D.13.(2014•河北)如图所示的计算程序中,y与x之间的函数关系所对应的图象应为()A.B.C.D.14.(2017•达州)函数y=kx+b的图象如图所示,则当y<0时x的取值范围是()A.x<﹣2 B.x>﹣2 C.x<﹣1 D.x>﹣115.(2016•安徽)已知函数y=kx+b的图象如图,则y=2kx+b的图象可能是()A.B.C.D.二.填空题(共10小题)16.(2017•丽水)已知一次函数y=2x+1,当x=0时,函数y的值是_________.17.已知一次函数y=(k﹣1)x|k|+3,则k=_________.18.当m=_________时,函数y=(m﹣3)x2+4x﹣3是一次函数.19.已知2x﹣3y=1,若把y看成x的函数,则可表示为_________.20.已知函数y=(m﹣1)+1是一次函数,则m=_________.21.若函数y=(m﹣)+m是一次函数,则m的值是_________.22.已知函数是一次函数,则m=_________,此函数图象经过第_________象限.23.根据图中的程序,当输入数值x为﹣2时,输出数值y为_________.24.在函数y=﹣2x﹣5中,k=_________,b=_________.25.购某种三年期国债x元,到期后可得本息和为y元,已知y=kx,则这种国债的年利率为(用含k的代数式表示)_________.三.解答题(共5小题)26.已知函数是一次函数,求k和b的取值范围.27.已知+(b﹣2)2=0,则函数y=(b+3)x﹣a+1﹣2ab+b2是什么函数?当x=﹣时,函数值y是多少?28.已知是y关于x的一次函数,并且y的值随x值的增大而减小,求m的值.29.说出下面两个问题中两个量的函数关系,并指出它们是不是正比例函数,是不是一次函数.①汽车以40千米/小时的平均速度从A站出发,行驶了t小时,那么汽车离开A站的距离s(千米)和时间t(小时)之间的函数关系是什么?的函数关系式为_________,它是_________函数;②汽车离开A站4千米,再以40千米/小时的平均速度行驶了t小时,那么汽车离开A站的距离s(千米)与时间t(小时)之间的函数关系是什么?的函数关系式为_________,它是_________函数.30.已知函数y=(m﹣3)x|m|﹣2+3是一次函数,求解析式.答案与评分标准一.选择题(共15小题)1.下列函数:①y=x;②y=;③y=;④y=2x+1,其中一次函数的个数是()A.1 B.2 C.3 D.4考点:一次函数的定义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一次函数及其图象一、选择题1.关于一次函数y =-x +1的图象,下列所画正确的是(C )【解析】 由一次函数y =-x +1知:图象过点(0,1)和(1,0),故选C.2.在同一平面直角坐标系中,若一次函数y =-x +3与y =3x -5的图象交于点M ,则点M 的坐标为(D )A .(-1,4)B .(-1,2)C. (2,-1)D. (2,1)【解析】 一次函数y =-x +3与y =3x -5的图象的交点M 的坐标即为方程组⎩⎪⎨⎪⎧y =-x +3,y =3x -5的解, 解方程组,得⎩⎪⎨⎪⎧x =2,y =1,∴点M 的坐标为(2,1). 3.已知直线y =kx +b ,若k +b =-5,kb =6,则该直线不经过(A )A .第一象限B .第二象限C. 第三象限D. 第四象限【解析】 由kb =6,知k ,b 同号.又∵k +b =-5,∴k <0,b <0,∴直线y =kx +b 经过第二、三、四象限,∴不经过第一象限.4.直线y =-32x +3与x 轴,y 轴所围成的三角形的面积为(A )A .3B .6C.34D.32【解析】直线y=-32x+3与x轴的交点为(2,0),与y轴的交点为(0,3),所围成的三角形的面积为12×2×3=3.5.已知正比例函数y=kx(k<0)的图象上两点A(x1,y1),B(x2,y2),且x1<x2,则下列不等式中恒成立的是(C)A.y1+y2>0 B.y1+y2<0C. y1-y2>0D. y1-y2<0【解析】∵正比例函数y=kx中k<0,∴y随x的增大而减小.∵x1<x2,∴y1>y2,∴y1-y2>0.(第6题)6.甲、乙两人沿相同的路线由A地到B地匀速前进,A,B两地间的路程为20 km.设他们前进的路程为s(km),甲出发后的时间为t(h),甲、乙前进的路程与时间的函数图象如图所示.根据图象提供的信息,下列说法正确的是(C) A.甲的速度是4 km/h B.乙的速度是10 km/hC.乙比甲晚出发1 h D.甲比乙晚到B地3 h【解析】根据图象知:甲的速度是204=5(km/h),乙的速度是202-1=20(km/h),乙比甲晚出发1-0=1(h),甲比乙晚到B地4-2=2(h),故选C.7.丁老师乘车从学校到省城去参加会议,学校距省城200 km,车行驶的平均速度为80 km/h.若x(h)后丁老师距省城y(km),则y与x之间的函数表达式为(D)A. y=80x-200B. y=-80x-200C. y=80x+200D. y=-80x+200【解析】∵丁老师x(h)行驶的路程为80x(km),∴x(h)后距省城(200-80x)km.8.如果一次函数y=kx+b的函数值y随x的增大而减小,且图象与y轴的负半轴相交,那么下列对k和b的符号判断正确的是(D)A.k>0,b>0 B.k>0,b<0C .k <0,b >0D .k <0,b <0【解析】 ∵y 随x 的增大而减小,∴k <0.∵图象与y 轴交于负半轴,∴b <0.(第9题)9.张师傅驾车从甲地到乙地,两地相距500km ,汽车出发前油箱有油25L ,途中加油若干升,加油前、后汽车都以100km/h 的速度匀速行驶,已知油箱中剩余油量y (L)与行驶时间t (h)之间的函数关系如图所示,则下列说法错误的是(C )A .加油前油箱中剩余油量y (L)与行驶时间t (h)的函数表达式是y =-8t +25B .途中加油21LC. 汽车加油后还可行驶4hD. 汽车到达乙地时油箱中还剩油6L【解析】 A .设加油前油箱中剩余油量y (L)与行驶时间t (h)的函数表达式为y =kt +b .将点(0,25),(2,9)的坐标代入,得⎩⎪⎨⎪⎧b =25,2k +b =9,解得⎩⎪⎨⎪⎧k =-8,b =25,∴y =-8t +25,故本选项正确.B .由图象可知,途中加油30-9=21(L),故本选项正确.C .由图象可知,汽车每小时用油(25-9)÷2=8(L),∴汽车加油后还可行驶30÷8=334(h)<4h ,故本选项错误.D .∵汽车从甲地到乙地所需时间为500÷100=5(h),又∵汽车油箱出发前有油25L ,途中加油21L ,∴汽车到达乙地时油箱中还剩油25+21-5×8=6(L),故本选项正确.故选C.二、填空题10.写出一个图象经过第一、三象限的正比例函数y=kx(k≠0)的表达式:y =2x.【解析】∵图象经过第一、三象限,∴k>0,∴k可以取大于0的任意实数.答案不唯一,如:y=2x.11.已知一次函数y=(2-m)x+m-3,当m>2时,y随x的增大而减小.【解析】由一次函数的性质可知:当y随x的增大而减小时,k=2-m<0,∴m>2.12.如图是一个正比例函数的图象,把该图象向左平移一个单位长度,得到的函数图象的表达式为y=-2x-2.【解析】设原函数图象的表达式为y=kx.当x=-1时,y=2,则有2=-k,∴k=-2,∴y=-2x.设平移后的图象的表达式为y=-2x+b.当x=-1时,y=0,则有0=2+b,∴b=-2,∴y=-2x-2.(第12题)(第13题)13.如图所示是某工程队在“村村通”工程中修筑的公路长度y(m )与时间x(天)之间的函数关系图象.根据图象提供的信息,可知该公路的长度是504m .【解析】 当2≤x ≤8时,设y =kx +b.把点(2,180),(4,288)的坐标代入,得⎩⎪⎨⎪⎧180=2k +b ,288=4k +b ,解得⎩⎪⎨⎪⎧k =54,b =72.∴y =54x +72.当x =8时,y =504.14.直线y =kx +b 经过点A(-2,0)和y 轴正半轴上的一点B ,如果△ABO(O 为坐标原点)的面积为6,那么b 的值为__6__.【解析】 S △ABO =12×2·b =6,∴b =6.(第15题)15.如图,矩形ABCD 的边AB 在x 轴上,AB 的中点与原点重合,AB =2,AD =1,过定点Q(0,2)和动点P(a ,0)的直线与矩形ABCD 的边有公共点,则a 的取值范围是-2≤a ≤2.【解析】 当QP 过点C 时,点P(2,0);当QP 过点D 时,点P(-2,0).∴-2≤a ≤2.16.一次越野跑中,当小明跑了1600 m 时,小刚跑了1400 m ,小明、小刚在此后所跑的路程y (m)与时间t (s)之间的函数关系如图所示,则这次越野跑的全程为2200m.,(第16题))【解析】 设小明的速度为a (m/s),小刚的速度为b (m/s),由题意,得 ⎩⎪⎨⎪⎧1600+100a =1400+100b ,1600+300a =1400+200b ,解得⎩⎪⎨⎪⎧a =2,b =4.∴这次越野跑的全程为1600+300×2=2200(m).17.已知直线y =k 1x +b 1(k 1>0)与y =k 2x +b 2(k 2<0)交于点A (-2,0),且两直线与y 轴围成的三角形的面积为4,那么b 1-b 2等于__4__.【解析】 如解图,设直线y =k 1x +b 1(k 1>0)与y 轴交于点B ,直线y =k 2x +b 2(k 2<0)与y 轴交于点C ,则OB =b 1,OC =-b 2.(第17题解)∵△ABC 的面积为4,∴12OA·OB +12OA·OC =4,∴12×2·b 1+12×2·(-b 2)=4,∴b 1-b 2=4.三、解答题(第18题)18.A ,B 两城相距600 km ,甲、乙两车同时从A 城出发驶向B 城,甲车到达B 城后立即返回.如图是它们离A 城的距离y (km)与行驶时间x (h)之间的函数图象.(1)求甲车行驶过程中y 与x 之间的函数表达式,并写出自变量x 的取值范围.(2)当它们行驶7 h 时,两车相遇,求乙车的速度.【解析】 (1)①当0≤x ≤6时,易得y =100x .②当6<x ≤14时,设y =kx +b .∵图象过点(6,600),(14,0),∴⎩⎪⎨⎪⎧6k +b =600,14k +b =0,解得⎩⎪⎨⎪⎧k =-75,b =1050.∴y =-75x +1050.∴y =⎩⎪⎨⎪⎧100x (0≤x ≤6),-75x +1050(6<x ≤14).(2)当x =7时,y =-75×7+1050=525,∴v 乙=5257=75(km/h).19.一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留了一段相同的时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x (h),两车之间的距离为y (km),如图中的折线表示y 与x 之间的函数关系.(第19题)请根据图象解决下列问题:(1)甲、乙两地之间的距离为__560__km.(2)求快车和慢车的速度.(3)求线段DE 所表示的y 关于x 的函数表达式,并写出自变量x 的取值范围.【解析】 (1)由图象可得:甲、乙两地之间的距离为560 km.(2)由图象可得:慢车往返分别用了4 h ,慢车行驶4 h 的距离,快车3 h 即可行驶完,∴可设慢车的速度为3x (km/h),则快车的速度为4x (km/h).由图象可得:4(3x +4x )=560,解得x =20.∴快车的速度为4x =80(km/h),慢车的速度为3x =60(km/h).(3)由题意可得:当x =8时,慢车距离甲地60×(4-3)=60(km),∴点D (8,60).∵慢车往返一次共需8h ,∴点E (9,0).设直线DE 的函数表达式为y =kx +b ,则⎩⎪⎨⎪⎧9k +b =0,8k +b =60,解得⎩⎪⎨⎪⎧k =-60,b =540.∴线段DE 所表示的y 关于x 的函数表达式为y =-60x +540(8≤x ≤9).20.小明家今年种植的“红灯”樱桃喜获丰收,采摘上市20天后全部销售完,小明对销售情况进行跟踪记录,并将记录情况绘成图象,日销售量y (kg)与上市时间x (天)的函数关系如图①所示,樱桃价格z (元/kg)与上市时间x (天)的函数关系如图②所示.(第20题)(1)观察图象,直接写出日销售量的最大值.(2)求小明家樱桃的日销售量y 与上市时间x 之间的函数表达式.(3)第10天与第12天的销售金额哪天多?请说明理由.【解析】 (1)日销售量的最大值为120 kg.(2)当0≤x ≤12时,设日销售量y 与上市时间x 之间的函数表达式为y =kx . ∵点(12,120)在y =kx 的图象上,∴120=12k ,∴k =10,∴函数表达式为y =10x .当12<x ≤20时,设日销售量y 与上市时间x 之间的函数表达式为y =k 1x +b 1.∵点(12,120),(20,0)在y =k 1x +b 1的图象上,∴⎩⎪⎨⎪⎧12k 1+b 1=120,20k 1+b 1=0,解得⎩⎪⎨⎪⎧k 1=-15,b 1=300.∴函数表达式为y =-15x +300.∴小明家樱桃的日销售量y 与上市时间x 之间的函数表达式为y =⎩⎪⎨⎪⎧10x (0≤x ≤12),-15x +300(12<x ≤20).(3)当5<x ≤15时,设樱桃价格z 与上市时间x 之间的函数表达式为z =k 2x +b 2.∵点(5,32),(15,12)在z =k 2x +b 2的图象上,∴⎩⎪⎨⎪⎧5k 2+b 2=32,15k 2+b 2=12,解得⎩⎪⎨⎪⎧k 2=-2,b 2=42.∴函数表达式为z =-2x +42.当x =10时,y =10×10=100,z =-2×10+42=22,∴销售金额为100×22=2200(元).当x =12时,y =10×12=120,z =-2×12+42=18,∴销售金额为120×18=2160(元).∵2200>2160,∴第10天的销售金额多.。
