第四章 微光学元件与应用(白底)
光学原理及应用

光学的基本原理及应用人类很早就开始了对光的观察研究,逐渐积累了丰富的知识。
远在2400多年前,我国的墨翟(公元前468—前376)及其弟子们所著的《墨经》一书,就记载了光的直线传播、影的形成、光的反射、平面镜和球面镜成像等现象,可以说是世界上最早的光学著作。
现在,光学已成为物理学的一个重要分支,并在实际中有广泛应用.光学既是物理学中一门古老的基础学科,又是现代科学领域中最活跃的前沿科学之一,具有强大的生命力和不可估量的发展前景。
按研究目的的不同,光学知识可以粗略地分为两大类.一类利用光线的概念研究光的传播规律,但不研究光的本质属性,这类光学称为几何光学;另一类主要研究光的本性(包括光的波动性和粒子性)以及光和物质的相互作用规律,通常称为物理光学。
一、光学现象原理光的传播速度很快,地球上的光源发出的光,到达我们眼睛所用的时间很短,根本无法觉察,所以历史上很长一段时间里,大家都认为光的传播是不需要时间的.直到17世纪,人们才认识到光是以有限的速度传播的。
光速是物理学中一个非常重要的基本常量,科学家们一直努力更精确地测定光速.目前认为真空中光速的最可靠的值为c=299 792 458 m/s在通常的计算中可取c=3.00×108m/s玻璃、水、空气等各种物质中的光速都比真空中的光速小.(一)直线传播光能够在空气、水、玻璃透明物质中传播,这些物质叫做介质.在小学自然和初中物理中我们已经学过,光在一种均匀介质中是沿直线传播的.自然界的许多现象,如影、日食、月食、小孔成像等,都是光沿直线传播产生的.由于光沿直线传播,因此可以沿光的传播方向作直线,并在直线上标出箭头,表示光的传播方向,这样的直线叫做光线。
物理学中常常用光线表示光的传播方向。
有的光源,例如白炽灯泡,它发出的光是向四面八方传播的;但是有的光源,例如激光器,它产生的光束可以射得很远,宽度却没有明显的增加.在每束激光中都可以作出许多条光线,这些光线互相平行,所以叫做平行光线.做简单实验的时候,太阳光线也可以看做平行光线.(二)反射与折射阳光能够照亮水中的鱼和水草,同时我们也能通过水面看到烈日的倒影;这说明光从空气射到水面时,一部分光射进水中,另一部分光被反射,回到空气中.一般说来,光从一种介质射到它和另一种介质的分界面时,一部分光又回到这种介质中的现象叫做光的反射;而斜着射向界面的光进入第二种介质的现象,叫做光的折射。
高中物理选择性必修件第四章光及其应用本章整合

THANKS
反射光线和入射光线不会重合,而是分别位于法线的两侧。
反射角等于入射角
反射角是反射光线与法线之间的夹角,入射角是入射光线与法线之间的夹角。根据反射定 律,这两个角度是相等的。
光的折射定律
折射光线、入射光线和法线在同一平面内
与反射定律类似,折射光线也会沿着与入射光线和法线所构成的平面内的路径进行折射 。
在激光加工、激光医疗、光计算等领 域有广泛应用。例如,利用非线性光 学效应可以实现激光束的变换和控制 ,用于材料加工和医疗治疗等。
量子光学简介及前景展望
量子光学简介
研究光场的量子性质以及与物质相互作用中的量子效应的科 学。它是现代物理学的重要分支,对于理解光的本质和开发 新的光学技术具有重要意义。
光通过一个小孔或障碍物时,会在屏幕上 形成衍射图样,表明光具有波动性质。
晶体中的原子排列具有周期性,当光通过 晶体时,会发生衍射现象,形成特定的衍 射图样。
光的偏振现象
偏振光的定义
01
光在传播过程中,只沿着某个特定方向振动的光称为偏振光。
偏振片的原理
02
偏振片只允许与其透振方向一致的光通过,其他方向的光则被
折射光线和入射光线分居法线两侧
折射光线和入射光线同样不会重合,而是分别位于法线的两侧。
折射角与入射角满足一定的关系
折射角是折射光线与法线之间的夹角,而入射角是入射光线与法线之间的夹角。这两个 角度之间的关系取决于两种介质的折射率。
全反射与临界角
全反射现象
当光从光密介质射向光疏介质时,如果入射角大于或等于 某一特定角度(临界角),则光会完全反射回光密介质中 ,这种现象称为全反射。
现。
02
薄膜干涉
光在薄膜的上下表面反射后相 互叠加,形成干涉现象,如肥
微光学元器件

ZW
n0 0 A
2 n 12 0
l0
l0
2
C-Lens:
R2
l0 2 R R2 2 2 n 1 n 1 0
C-Lens在长工作距离应用中具有优势, 而Grin-Lens是TFF型DWDM中不可缺少的。
C-Lens与Grin-Lens对比I
0.2
0.3
0.4
0.5
0.6
0.7
0.8
Tilting Angle of Incident Light to GRIN Lens Axis (Degree)
Collimator Assembly UV Adhesive P/M
Positioner #1 (to be assembled) Positioner #2 (Reference)
T
E
2
1
E dxdy
* 2
2
E1 dxdy E 2 dxdy
2
高斯光束的耦合失配情况 两高斯光束之间的耦合,存在:径向失配,轴向失配和角向失配。
高斯光束的能量耦合
两高斯光束耦合损耗与各种失配量之间的关系
束腰半径分别为200um和5um,对应一般准直器和光纤的模场半径。 束腰半径为200um的光束,对角向失配比较敏感,对径向失配次之,对轴向失配有较大容差; 束腰半径为5um的光束,对轴向失配比较敏感,对径向失配次之,对角向失配有较大容差。
近轴光线传输矩阵
1
R n
r2 r1
r1 r2
2
1
1 n 2 r1 n1 R
1 0 A B C D (1 n) / R n
球面传输矩阵
光电工程中微纳光学元件设计与应用

光电工程中微纳光学元件设计与应用微纳光学元件是光电工程中的重要组成部分,广泛应用于光传感、光通信、光计算等领域。
它们具有体积小、重量轻、高度集成、高效能等特点,被誉为光电工程中的“微型英雄”。
本文旨在探讨微纳光学元件的设计原理和应用技术,并介绍其在光电工程中的重要应用。
首先,我们来了解微纳光学元件的设计原理。
微纳光学元件的设计基于光学原理,主要涉及到光的折射、反射、漫反射等现象。
通过合理设计光学构造、选择适当的材料,可实现对光信号的控制和调节。
例如,利用微纳光学元件的折射特性,可以实现光信号的聚焦、分离等功能;利用光学透明材料的反射特性,可以实现光的反射,从而改变光的传播方向和角度。
其次,我们来探讨微纳光学元件的应用技术。
微纳光学元件的应用技术涉及到光学材料选择、加工工艺、光学模拟和测试等方面。
首先,光学材料的选择对于微纳光学元件的性能和应用起到关键的作用。
常见的光学材料有硅、玻璃、聚合物等,每种材料都有其特殊的光学性能和适用范围。
其次,加工工艺是实现微纳光学元件设计的关键环节。
传统的加工工艺包括光刻、薄膜沉积、离子刻蚀等,而近年来,随着纳米加工技术的发展,还涌现出了诸如离子束刻蚀、电子束曝光等新的加工方法。
最后,光学模拟和测试是微纳光学元件设计中不可缺少的环节。
通过模拟光的传播和反射行为,可以优化微纳光学元件的设计;而光学测试可以验证设计结果的准确性和可行性。
接下来,我们来介绍微纳光学元件的重要应用。
微纳光学元件在光电工程领域有着广泛的应用。
首先是光传感领域,微纳光学元件可以实现对光信号的探测和分析。
例如,利用微纳光学元件的折射特性和表面增强拉曼散射效应,可以实现高灵敏度的化学传感器。
其次,微纳光学元件在光通信领域也有重要应用。
它们可以实现光信号的调制、解调和复用等功能。
例如,利用微纳光学元件的小尺寸和高效能,可以实现更高密度的光纤连接和高速光通信。
此外,微纳光学元件还可以应用于光计算、光存储等领域,为光电工程的发展提供了新的机遇和挑战。
光电传感器应用技术第4章 第2节

如图4-22(a)所示的“CIEl931-RGB系统标准色度观 察 者三刺激值曲线σrgb”。从曲线中看到、、光谱三刺激值有 一部分为负值,计算很不方便,又难以理解。因此1931年
CIE
新的国际通用色度系统,称为“CIEl931-XYZ系 统”。它是在CIE1931-RGB系统的基础上改用三个假想 的原色x、y、z所建立的一个新的色度系统。
1.双色硅色敏器件的工作原理
双色硅色敏光传感器的结构和等效电路如图4-19所示。 它是在同一硅片上制作两个深浅不同PN结的光电二极管 PD1和PD2组成的。
浅PN结的PD1 的光谱响应峰值 在蓝光范围,深 结PD2的光谱响应 峰值在红光范围。
双结光电二极管只能通过测量单色光的光谱辐射功率与黑体
辐射相接近的光源色温来确定颜色。用双结光电二极管测量颜色 时,通常测量两个光电二极管的短路电流比(ISC2/ ISC1)与入射波 长的关系(如图4-21所示),从关系曲线中不难看出,每一种波长 的光都对应于一个短路电流比值,根据短路电流比值判别入射光 的波长,达到识别颜色的目的。
x y
(Ix' Iy ) (Ix Iy')
Ix Ix' Iy Iy' (Ix' Iy') (Ix Iy )
Ix Ix' Iy Iy'
斑在边缘的测量误差被大大地减少。
4.3 光生伏特器件的偏置电路
• 4.3.1 反向偏置电路
图4-40所示为光生伏特器件的反向偏置电路。其中图(a)为反 向偏置电路的原理电路图,图(b)为反向偏置电路图。光生伏特 器件在反向偏置状态,PN结势垒区加宽,有利于光生载流子的漂移 运动,使光生伏特器件的线性范围和光电变换的动态范围加宽。
现代光学基础课件:第四章 光学仪器的基本原理

• 放大镜放大率的公式,通常采用以下形式
M 250 f'
• 放大镜的放大率仅由放大镜的焦距f ′ 所决定,焦 距越大则放大率越小。
§4-3 目 镜
放大镜是一种通过直接放大实物达到增大视角的助视仪器。下面将介绍 一种放大像的助视仪器——目镜。 一、目镜
• 由于场镜的物为虚物,所以这种目镜无法对物镜所成的像进行测量。
• 此目镜的视角较大(可达400),在250范围内像更清晰。而且结构 紧凑,适用于生物显微镜。
2、冉斯登目镜 1
Q 'Q
2
⑴ 结构:如图示 3
⑵ 特点:
F2 F
o1
• 场镜、视镜均为同种材
3
F1' 3
o2
2
2
料的平凸透镜,二镜凸 面相向,平面朝外。
网膜 脉络膜 黄斑中心凹
前室
晶状体
盲斑
总能将像成在网膜上。
后室
角膜和晶状体之间的空间称为前室;充满1.336的水状液;
晶状体和网膜所包围的空间称为后室;充满1.336的玻状体
人眼的构造剖视图
瞳孔 虹膜 角膜
1.376
前室
1.336
晶状体
巩膜
网膜 脉络膜 黄斑中心凹
视轴
光轴
盲斑
后室 1.336
眼睛的像方节点与中心凹的连线为眼睛的视轴, 在观察物 体时眼睛本能地把物体瞄准在这根轴上。
x'
f1' f1'
• 物镜的像被目镜放大,其放大率为
Me
250 f2 '
• 式中: f2' 为目镜的焦距。由此,显微镜系统的
《光学》全套课件

Δ
=2en2
(
1 cosγ
sin2 γ) +λ cosγ 2
Δ
=
2en2
c
os
γ
+
λ 2
Δ =2e n22
n12
sin2 i +λ 2
干涉条件
2e
n22
n12
sin2
i
2
k
k 1,2, 加强(明)
( 2k 1 ) 2 k 0,1,2, 减弱(暗)
额外程差的确定 不论入射光的的入射角如何
M1
x
S1S2 平行于 WW '
d
S1
S2
C M2
o
W'
d <<D
D
屏幕上O点在两个虚光源连线的垂直平分线上,屏幕 上明暗条纹中心对O点的偏离 x为:
x =kλ D d
x = 2k +1 λ D 2d
明条纹中心的位置 暗条纹中心的位置
k =0,±1,±2L
2 洛埃镜
E
S1
d
S2
光栏
E
p
p'
Q'
M
L
橙 630nm~590nm 黄 590nm~570nm 绿 570nm~500nm
折射率
n=c = u
εrμr
青 500nm~460nm 蓝 460nm~430nm 紫 430nm~400nm
u = c ,λ = λ0 nn
§1-2 光源 光的相干性
一、光源
1.光源的发光机理 光源的最基本发光单元是分子、原子
§1-3 光程与光程差
干涉现象决定于两束相干光的位相差 两束相干光通过不同的介质时, 位相差不能单纯由几何路程差决定。
《光学教程》姚启钧原著第四章光学仪器基本基本原理

《光学教程》姚启钧原著第四章光
7
学仪器基本基本原理
(四)、像面弯曲
1.现象:对较大物平面经透镜后成的像是抛物面。 2. 消除方法:采用组合系统,适当的选配各透镜
的焦距和折射率。
《光学教程》姚启钧原著第四章光
8
学仪器基本基本原理
(五)、畸变
物平面
枕形畸变
桶形畸变
1、现象:像和物不能保持几何相似。
2、成因:由于物点离主轴的距离不同,而使得横 向放大率不同所引起。
Q
说明:
P
O
l
U
① 须将物放在同一特定位置比较两像大小。
② 放大镜和显微镜:明视距离处(25cm);
望远镜:无穷远《处光。学教程》姚启钧原著第四章光
23
学仪器基本基本原理
三、放大镜
Q`
最简单的放大镜--凸透镜:
L
U‘
y`
Q
使用放大镜的视角:
P`
y
O
FP
l'
U `
y`
s`
y
f
y f`
Q
-s`
-f U‘
一、目镜
1、定义:用于放大其它光具组所成像的助视仪器。 要求:A、放大本领高;
B、能校正像差、色差。 2、结构:场镜+视镜+分划板(刻度尺)
• 场镜: 面向物体的透镜(或透镜组)
• 视镜: 接近人眼的透镜(或透镜组)
• 分划板:包含透明刻度尺,用于提高测量精度。
《光学教程》姚启钧原著第四章光
27
学仪器基本基本原理
未用放大镜的视角: y
P
U y 25
放大镜的放大本领:
25cm
O
微光学课件教材课程

典型微光学器件
微透镜
一种具有微小尺寸和焦距的透镜,用于实现光的 聚焦和成像。
光栅
一种具有周期性结构的光学元件,用于实现光的 分光、合光等功能。
微棱镜
一种具有微小尺寸和特定几何形状的棱镜,用于 实现光的反射和折射。
光子晶体
一种具有周期性折射率变化的光学材料,用于实 现光的带隙、禁带等特性。
03
微光学器件设计与制作
生物医学成像技术简介
生物医学成像技术概述
简要介绍生物医学成像技术的定义、分类、发展历程及现状。
常见生物医学成像技术
详细介绍X射线成像、核磁共振成像、超声成像、光学成像等常见 生物医学成像技术的原理、特点及应用范围。
生物医学成像技术挑战
阐述生物医学成像技术面临的挑战,如分辨率、对比度、成像深度、 实时性等方面的限制。
降低插入损耗
采用高透过率、低反射的微光学 元件,减少光信号在传输过程中
的能量损失。
提高耦合效率
利用微光学器件的精确对准和高 效耦合特性,提高光源与光纤之
间的耦合效率。
实现高速传输
通过优化微光学系统设计,降低 色散和非线性效应对信号传输的 影响,实现高速、大容量的光通
信。
05
微光学在生物医学领域应光 学胶合、微纳加工等制作工艺,
掌握其基本原理和操作流程。
制作设备
熟悉超精密研磨机、抛光机、镀膜 机、光刻机、刻蚀机等制作设备, 了解其性能参数和使用方法。
工艺控制
掌握工艺过程中的温度、湿度、洁 净度等环境控制要求,确保制作质 量。
器件性能评价与测试
02
微光学基础知识
光学基本概念
01
02
03
光的本质
微流控光学及应用PPT课件

第1页/共35页
固体器件还是流体器件?
• 液体材料外型不定、难以操控,传统光学系统主 要采用玻璃、金属和半导体等固体材料。
布拉格分布反馈(DFB)光栅。
在 5 3 2 nm-Nd:YAG 脉 冲 激 光 泵
浦下,从芯片一端可得到单模
❖Z. Y. Li, Z. Y. Zhang, T. Emery, A. Scherer, and D. Psaltis. Single mode optofluidic distributed feedback dye laser. Opt. Express. 14(2), 696-701(2006).
第14页/共35页
微流控光学变焦透镜
• Philips公司的 液体变焦透镜 FluidFocus
第15页/共35页
微流控变焦透镜阵列
1. 梁忠诚,陈陶,徐宁,涂兴华,电调谐微流控变焦透镜阵列芯片. 发明专 利,申请号:200610161275.9 2. 梁忠诚,涂兴华,徐宁,陈陶,电调谐微流控变焦透镜阵列芯片的制作方 法.发明专利,申请号:200610161276.3
– Biological analysis – Medical diagnosis – Chemical analysis and synthesis – Drug discovery – Drug Delivery
第5页/共35页
什么是Optofluidics?
• 微流控光学是现代光学、光电子学与微流控技术相结合而形成的新型交叉前沿学科与技术。微流控技术 (microfluidics)意图实现微量化学或生物样品的合成与分析,而微流控光学技术则是在微观尺度上通过操 控流体达到调节系统的光学或光电子学特性的目的。
微光学技术及其应用(最新版)

13
CODE V中的GRIN Lens
ZEMAX中的GRIN Lens
14
二、折射型微光学元件的设计
1、规则面型微透镜的设计 几何光学成像公式计算、追迹
曲率半径
透镜玻璃牌号
非球面系数
15
2、特殊面型的微光学元件 折射定律、边界条件、能量守恒原则
x
z
微光学 元件
入射光强度分布
像面
像面强度分布
h(x) T1 . | x | p .w2 .[ x .erf (x / w) 1 ex2 /w2 1/ p ], 0 | x | L / 2
2
2A w
p
18
设计仿真结果:
微光学元件浮雕分布
19
高斯→环形的典型应用:
信号探测
副镜
主镜
卡赛格林望远系统示意图
20
利用公式(1)、(2)和(3)计算得到的微光学元件,可以 将任意输入光强分布变换为想要的分布,比如:
– 焦距:f = -1/[n0A1/2sin(A1/2L)] – 聚焦参数:A = 2/a2
– 数值孔径:NA = n0(2)1/2 – 节距:P = 2p/A1/2
• 成像特性:与透镜长度有关:
– 1/4 节距透镜
– 1/2 节距透镜
– 0.23节距透镜
– 0.29 节距透镜
– ……
11
典型应用: 光通信、微型光学系统、医用光学仪器、 光学复印机、传真机、扫描仪
ei(x) comb((x)) *{rect[(x)].L1 eik .rect[k 2p k / L]}
2p
2p k 0
2p / L
L——台阶数
将其代入衍射级的振幅公式中,得到:
应用光学内容

镜观测天体四百周年。
TMT:Thirty Meter Telescope宇宙喷泉遥远星系哈勃望远镜(主镜口径2.4米)光是电磁波的一种,覆盖特定的波长范围。
图1-1 电磁波按波长的分类图1-2 球面波和平面波图1-3 光线的反射入射光线、法线和反射光线在同一平面内;入射光线和反射光线在法线的两侧;反射角等于入射角图1-4 光线的折射入射光线、法线和折射光线在同一平面内;入射光线和折射光线在法线的两侧;入射角与折射角的正弦之比与入射角无关,是一个与介质与光的波长有关的常数:n′=−n,折射定律可推导出反射定律图1-5 光线在玻璃块中的折射和反射45°§1.1.3 光学材料及色散光的色散、典型玻璃的色散曲线516.7491Fe K393.3666Ca图1-8 透镜对光线的作用与透镜成像图1-7 透镜对波面的作用与透镜成像图1-10 光程图1-9 光线与波面的正交关系光线从P到P',经历时间:图1-11 遵守反射定律的光线图1-12 回转椭球面凹面反射镜图1-13 内切于回转椭球面的凹面反射镜图1-14 由费马原理导出折射定律22()z z d +−=('')('') d d−•−aδaδl'(u')l'(0)图1-15 完善成像(等光程)=Δ=−=[LMP'][OO'P'] [PP'][PP'][PP']0球面顶点图1-16 球面方程中所用的坐标系图1-17 入射光线与球面的两个交点211()ch z −−==22z r r h =±−图1-18 回转椭球面z 在许多商用光学设计程序中zOlympus手机摄像头透镜组富瑞丰公司头盔式显示器。
光学教程-总结ppt课件

U f2
f 2
聚光本领
物镜的聚光本领是描述物镜聚集光通量能力的物理量,可以 用象面的照度来量度。
分辨本领
瑞利判据:总照度分布曲线中央有下凹部分,其对应强度不超过每 一分布曲线最大值的74%,当一个中央亮斑的最大值位置恰和另一个中 央亮斑的最小值位置相重合时,两个像点刚好能被分辨。
36
第四章 光学仪器的基本原理
32
第三章 几何光学基本原理
球面折射对光束单心性的破坏
n
l P
A
n
l P
Or C
s
s
B
近轴光线条件下球面折射的物像公式
n n n n s s r
33
第三章 几何光学基本原理
横向放大率
在近轴光线和近轴物
Q
的条件下,垂直于主轴的 y
物所成的像仍然是垂直于
P
O
主轴的,像的横向大小与 物的大小之比值为横向放
棱镜
棱镜是一种常见的光学元件,它的主要用途有两种:作为色散 元件和利用光的棱镜内的全反射来改变光束的方向,即转向元件。
棱镜材料的折射率为:
n
sin i1
sin
0
2
A
sin i2
sin A
2
30
第三章 几何光学基本原理
符号法则
球面的中心点O称为顶 点,球面的球心C称为 曲率中心,球面的半径 称为曲率半径,连接顶 点和曲率中心的直线CO 称为主轴,通过主轴的 平面称为主平面。主轴 对于所有主平面具有对 称性。
u
sin2 N(d sin
sin2(d sin )
)
I0
s in 2 u2
u
sin2 Nv sin2 v
物理光学第四章学习教案

3.渥拉斯顿棱镜
光轴方向
B
C
由两直角棱镜组成,材料“方解e
石”
θO
A
D
(或水晶)
特点:两光轴互相垂直。
功能:能产生两束互相分开(fēn
kā2is)i的n 1、n振0 动ne方tg向 ,互相为垂棱直镜角的度线
偏光。
第20页/共71页
原因:进入第一晶体和第二晶
第二十一页,共71页。
若波片的厚n度0 为cd,v0则, o光ne和ec光v通e不过波同片时的光程也不同。
在麦克斯韦电磁场理论中,用介电常数ε来表征物质的极化 状关D况系 。是E 在:各向同性媒质(méizhì)中,电位移矢量与电场强度
,这里ε是介电常数,是一标量,此式表明D与E的 方向一致。
第8页/共71页
第九页,共71页。
在各向异性媒质中, D与E在一般情况下方向是不一致的, 为一张量,将
麦克斯韦方程组和物质方程应用于晶体,可得出单色平面波在晶体中的传
ν为光在折射介t质中B的B波'
c
速)在折射介质中作半圆(实际上是半球面),这就是另一边缘入射线 到达B’点时由A点发出的次波面。
(4)通过B’点作上述半圆的切线(实际上是切面(qiēmiàn))这就是折 射线的波面(包络面)
(5)从A联接到切点A’的方向便是折射线的方向。
B A
空气
B'
A' 介质
第11页/共71页
而e光则因受到界面强烈散射以致无法通过。 散射型偏振片本身是无色的,而且它对可见光范围的各种 色光的透过率几乎相同,又能做成较大的通光面积,因 此,特别适用于需要真实地反映自然光中各种色光成分(chéng fèn)
的 彩色电影、电视中。
光学微腔特性研究及其应用ppt课件

光学微腔分类
➢依据工作介质不同 1.有源微腔:“有源”是指腔内的工作介质具有增益,这类微腔在外部光激
励或者电激励的时通过谐振腔的模式选择产生激光出射 2.无源微腔:“无源”指腔内工作介质无增益,这种微腔主要通过微腔的本征 光学模式选择对入射光进行调制,主要应用于信号处理中的滤波器、光开关、 或者传感器等。
普通谐振腔
.
光学微腔
光学微腔的研究背景
集成光路包括光波的发射、传输、调制-解调、上载、下载、接收、存储、显 示等一系列的过程。近年来,随着微电子学的薄膜工艺提高,研究者们将微波理 论和激光技术相结合,采用微纳加工技术在各种均匀的光学材料中制备各种波长 尺度的结构来控制光信号的传播或产生新的物理效应,从而创造出新型光子学器 件。微腔型光电子器件正式基于此背景提出的。这类器件具有尺寸小、易于集成、 功耗低以及品质因子高等优点,在信号的发射、处理和传感等方面表现出很大的 前景,例如高性能光源,光存储器、光开关、密集波分复用系统(DWDM)的上下 载滤波器以及生化传感器等。除此之外,由于光学微腔可以在极小的空间内产生 巨大的光强,同时降低了腔内模式数目,影响腔内物质原子的自发福射特性,因 此在揭示物质世界本质的自然科学领域。
.
回音壁式微腔制作流程图
.
基片准备
第一步包括在基片表面不同成分或者厚度的功能膜层的生成,来得到所需要 的垂直方向结构。膜层的生成可根据选用材料的不同使用不同的膜层生成方式, 例如分子束外延(MBE),化学或物理气相沉积,以及膜层粘接等等。具体如何选 择生成方式与所要得到的微谐振腔结构、材料以及要求的制造精度密切相关。例 如,半导体材料通常要使用几步连续的生长来得到垂直结构,而高分子聚合物层 只需要简单地涂敷在基片上即满足要求。
微光学课件

欧洲和美国“微世界”的研究是由半导体工艺技
术启动,即带有机械的微电子技术,固称之为微 电子机械系统(Micro Electro Mechanical Systems, 美国惯用词)或称之为微系统(Microsystems,欧洲 惯用词)。 日本实现“微世界”(Micro World)以系统方式 从机械电子(Machatronics)开始。固称之微型机械 (Micromachine,日本惯用词)。
可用于全光网络的MEMS器件包括微型光开关阵列、可调衰减器
和光滤波器等。对上述技术的研究是MEMS用于光通讯领域的关 键。 在全光通信网中,光交换技术的好坏直接决定了传输网的规模、 复杂性和灵活性等技术指标。光开关是光交换技术中的核心器 件,是影响光交换技术的关键。微机械光开关在开关速度、透 明性、功耗和串扰等性能比其它各类光开关具有明显的优点。 除此之外,微机械光开关还用于光信息处理系统和光学测量系 统,实现光路的转换、切换和光信息处理。在军事领域中,微 机械光开关用于核弹、导弹等的引信装置。且因其巨大的商业 应用前景,而备受关注。
信息处理单元 力 传 光 声 温度 其它 感 器 模 拟 信 号 处 理 器 数 字 信 号 处 理 器 模 拟 信 号 处 理 器 运动 能力 信息 其它
执 行 器
感测量
通讯/接口单元
控制量
光、电、磁
-4-
Peking University
MEMS发展回顾
1959年就有科学家提出微型机械
的设想,但直到1962年才出现属 于微机械范畴的产品—硅微型压 力传感器。其后尺寸为50~500 微米的齿轮、齿轮泵、气动蜗轮 及联接件等微型机构相继问世。 而1987年由华裔留美学生冯龙生 等人研制出转子直径为60微米和 100微米的硅微型静电电机,显 示出利用硅微加工工艺制作微小 可动结构并与集成电路兼容制造 微小系统的潜力,在国际上引起 轰动,科幻小说中描述把自己变 成小昆虫钻到别人的居室或心脏 中去的场景将要成为现实展现在 人们面前。同时,也标志着微电 子机械系统(MEMS)的诞生。
微光学资料

• 利用微纳加工设备对材料进行切割、刻蚀等处理
• 制备复杂结构的微光学元件
• 实现微光学元件的制备和集成
• 实现微光学系统的集成化和智能化
03
微光学元件的应用领域
微光学元件在通信领域的应用
光纤通信
激光通信
• 微光学元件用于光纤的连接、分路等功能
• 微光学元件用于激光器的调制、扫描等功能
• 提高光纤通信的传输速率和容量
• 微光学技术将成为光学领域的重要发展方向
CREATE TOGETHER
谢谢观看
THANK YOU FOR WATCHING
DOCS
• 微光学技术是光学技术的一个重要分支
• 微光学元件在许多领域具有广泛应用前景
• 微光学技术的发展推动了光学仪器的微型化、集成化和智能化
微光学元件的分类与特点
微光学元件的分类
微光学元件的特点
• 按功能分:透镜、反射镜、衍射光栅等
• 微小尺寸:尺寸在微米甚至纳米量级
• 按材料分:光学玻璃、石英、塑料等
薄膜技术在微光学元件制备中的应用
薄膜技术原理
• 通过沉积、蒸发等方法在基底上形成薄膜
• 对薄膜进行刻蚀、抛光等处理形成微光学元件
薄膜技术在微光学元件制备中的应用
• 制备具有特殊光学性能的薄膜微光学元件
• 实现微光学元件的多功能性和高性能
微纳加工技术在微光学元件制备中的应用
微纳加工技术原理
微纳加工技术在微光学元件制备中的应用
• 提高微光学系统的集成度和性能
微光பைடு நூலகம்系统的优化设计
优化设计原理
• 通过光学设计、结构设计等方法优化微光学系统
• 实现微光学系统的性能优化和成本降低
微光学第4章a
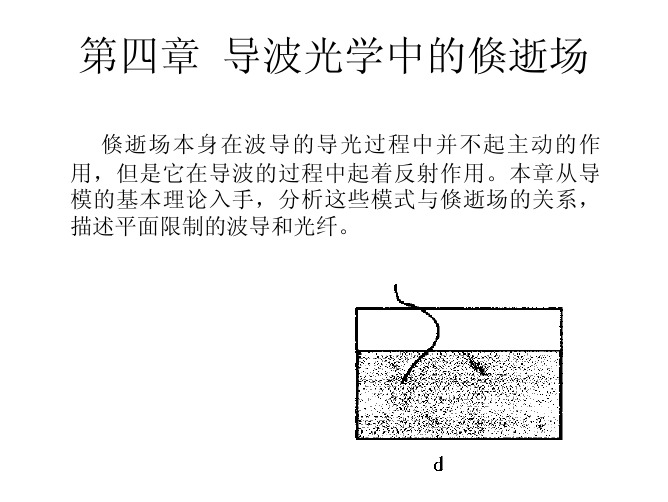
d 2 E z (r ) 1 dE z (r ) ⎛ 2 v2 ⎞ 2 + + ⎜ ω εμ 0 − β − 2 ⎟ Ez (r ) = 0 2 ⎜ dz r rdz r ⎟ ⎠ ⎝ d 2 H z (r ) 1 dH z (r ) ⎛ 2 v2 ⎞ 2 + + ⎜ ω εμ 0 − β − 2 ⎟ H z (r ) = 0 2 ⎜ dz r dz r ⎟ ⎠ ⎝ (4.12)
4.2 受限波导
波导内的场在横向受到限制。Fig4.6是用不同方法制作的波导。 (a,b掩埋波导,c条形波导)
用扩散和注入法制作受限波导的方法见Fig.4.7。形成条形波导的 方法见Fig.4.8。
用扩散和注入法制作受限波导的方法
形成条形波导的方法
受限波导中的传输模式计算是很复杂的。通常没有通用的分析解。 一般采用有限元技术或光束传输法(BPM)。我们将在后面章介绍 这种方法。
(4.7)
对应的本征值方程为
(2aq ) = (n tan
p + n 2 2 r n1 q 0 2 4 n 2 2 n3 q 2 − n1 pr
2 2
)
(4.8)
波导内的场是正弦或余弦函数,而在皮层(介质折射率n2、n3) 中,场是指数衰减的。倏逝波的形式和平面内全反射相似。
光学微细结构光学器件与应用

微细结构光学器件及其应用文:何凤英也许光自人类诞生以来,就一直让我们的生活充满光彩。
即使人类的科技如何发达,我们依然无法离开光的世界。
人类通过光来观察世界,万物从阳光中获取能量,光的作用在我们的生活中显得既普遍又基本。
光正以崭新的姿态影响着我们的生活,这种影响在几十年前是无法想象的。
光正渐渐成为一切技术的核心。
人们对光的各种利用探索不断应用在生活方方面面,小到人们日常生活方面的照明领域、电子显示、包装印刷,到模拟仿真、太阳能利用到国防科技等,随着生活水平的提高,光的利用仍然呈现巨大潜力。
微细结构光学器件是博大而精深的光学领域中极为微小的部分。
微细结构光学器件在光学领域犹如沧海一粟,就如这些微细结构光学器件所具有的光学结构尺寸一样微小,其微细程度若以长度单位来表示,通常是微米甚至纳米。
如果说毫米(mm)我们还能以肉眼可见的话,而微米是毫米的千分之一,基本上人的肉眼不易看出。
微细结构光学器件是指表面具有微细透镜结构,对光进行调整利用的光学器件;其包含以下三个方面的含义:1)光学器件,其本身无法单独发挥作用,须配合光的一定条件才能使用;2)对光进行调整利用,是指其本身并不产生光能,只是对现有光能的调整和利用;3)其发挥作用的本质其表面有一个或多个光学透镜,这些透镜尺寸很微小,在微米级以下,面形精度可达亚微米级,表面粗糙度可达纳米级。
下面我们就介绍一些带有微细透镜结构的光学器件以及应用。
比较常见光学透镜有凸透镜、棱镜、柱面镜等。
我们生活中最简单最熟悉的透镜就是凸透镜,凸透镜是中央较厚,边缘较薄,类似一个球体表面,凸透镜有会聚作用故又称聚光透镜,较厚的凸透镜则有望远、会聚等作用,这与透镜的厚度有关。
19世纪末,法国物理学家奥古斯汀.菲涅尔(Augustin.Fresnel)从凸透镜基础上发明了菲涅尔透镜(Fresnel Lense)。
其工作原理是透镜的折射能量仅仅发生在光学表面(如:透镜表面),拿掉尽可能多的光学材料,而保留表面的弯曲度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
更一般的方法是设 a h
0 1 通过调整 a
rl
2 H (n n 0 )lf H 2 (n n 0 ) 2 l 2 Ln L2 n 2
,可以适当调整台阶高度h.
2 3
f lch f d - d v 3 d 2
6
2014-6-3
7
2014-6-3
光学元件的温度特性由光热膨胀系数(即单位 温度变化引起的光焦度相对变化)决定。 在薄透镜模型和空气介质条件下,折射元件和 衍射元件的的光热膨胀系数分别为
d 1 df 1 dn g dT f dT n 1 dT d (2 g )
特性 光焦度 阿贝数 部分色散 注:
折射透镜
(n 1)c0
V P n1 1 0 n2 n3 n1 n3 n2 n3
衍射透镜
K
V P
1 1 0 2 3
1 3 2 3
3 1 2 , K 是常数
BOE的色散仅与 波长有关,与基底材料无关. DOE 具有负等效Abbe常数的特性,与折射光学 相反. 因此衍射/折射组合可消除色差。
I n An sin c 2 n / L
2
r
2
集中于主焦点(n=-1)处的光强被 定义为FZP的衍射效率η :
A1 sin c2 (1/ L)
2
多相位正透镜的透过率函数可表达为:
N ( L 1)
u (r 2 )
k 0
r 2 krp 2 / L rp 2 /( 2 L) i 2k exp rect 2 rp / L L
根据FZP的径向对称性和沿r2方 向的周期性,可以将复振幅分 布表示成一个傅里叶级数,求 在光轴上光强峰值,得到焦点 的位置.
ux, y u x 2 y 2 u r 2 mrp2
u x, y
n 1 0 ,则在光轴上将产生一个光 2 2 z rp 强峰值,即所谓的焦点。此时,焦距为:
当n>0时,Zn为负值,对应于发散光波;n<0时, Zn 为正值,对应于会聚光波;n=0时, Zn为∞,表示直 接透射波;
多台阶相位衍射透镜: 目的是消除高衍射级次,使 光能量尽可能多地集中到一个主焦点(n=-1)上.
在 zn 2pn , n jL 1, j Z 处有一系列焦点,且产生会 聚和发散两种作用。各焦点处的光强为:
菲涅尔微透镜
菲涅尔波带片(FZP): 一系列同心圆环组成的二元 振幅图形。沿 r2方向呈周期性分布。
rm mrp
第 m个透明环带半径:
不同的量化方法: a) 基于菲涅尔透镜的传统量化; b) 超级子区概念,增加衍射透镜孔径; c) 定常像素尺寸量化,如实现空间量化液晶调制器
4
2014-6-3
h(r )
(r ) 0 n 2
hl hM
l 1 , l 1,2,, L. L
非全波长高度浮雕结构的量化: 对于小口径尺寸,长焦距的衍射微透镜,其最大的 位相往往小于2π。在这种情况下,为了利用微电子 工艺进行制作,可以直接对连续浮雕采用等相位量 化方法进行设计。
4.3 折衍混合光学
式中N为台阶数,m为量化水平,m=1,2,3,… 当N->∞时,其图形就是DOE;当m取很大时,就是轮 廓接近连续的微浮雕。
3
2014-6-3
衍射效率分析
对于DOE或BOE,其振幅 分布为周期函数:
其中傅立叶系数为
Ci
e jT ( )
1 2m
i
C e
i
j i
当N=2m,i=1(只计算±1),q=1时, 1 sinc(
1 N
N 1 i 0
i Ci
2
2
i 0 sin c(qm i)
1
j 2 (qm i ) exp N
i sin c N
2
2
对于衍射透镜的效率,也可以用上述公式来估计。 透镜的结构可视为具有变周期的局部光栅。在中心 部分,光栅周期大,量化要求不高,边缘部分,光 栅周期小,受光刻制作分辨率限制。需要优化的量 化方案。
比较折射透镜和衍射透镜的焦距:
f r ( ) c0 1 1 n( ) 1 c1 c2 n( ) 1
H hm
n n0
a h H /L
h
f d ( ) f 0
0
L 2N
rl f
2 2
f
H (n n0 )l , Ln
对于折射透镜 ,焦距相对于波长的变化不减少色差的方法: a.采用 v 玻璃阿贝常数: 纵向色差: 大,取决于系数n-1.色散用 Abbe数描述: 大的材料;b.采用双组胶合 f n(1 ) 1 lch 1 结构,其中一组采用负透镜, vr vr 但结构复杂. n(2 ) n(3 ) 对于衍射透镜,焦距与波长成线性比例, 等 1 1 1 衍 效 Abbe 数为 等效 v
★ 随后相位数L的增加,FZP器件的衍射效率也随之增加,且在 主焦点衍射效率的增加较次焦点快得多。当L≥8时,衍射效率增 加缓慢。一般,既要达到高衍射效率,又不至于加工太复杂, 选择L=4或8是比较合适的。
★当 L变化时,FZP环带周期并不改变,焦距也保持不变。
★ FZP的作用机理是衍射,意味着出射波前只由器件的横向尺 寸决定,而与纵向尺寸无关。
2n
, n 0,1,2,
设u(x,y)处于z=0平面并被平面波照明,则在z>0的任意 平面上的衍射光的振幅由菲涅尔积分求得:
n 1 i u ( x' , y ' , z ) An exp ( x' 2 y ' 2 ) expi 2 ( 2 )( x 2 y 2 ) rp 2z z n xx' yy' exp i 2 ( ) dxdy z
g 为材料的热膨胀系数;n和n0分别为光学材料和环境介 质的折射率.
▲ 对于 混合光学,总的光焦度是各 个组成光焦度之和,即 ▲总的光热膨胀系数为:
r d 1
f r r d d
hyb( ) ref ( ) dif ( )
混合光学系统要消色差,须满足消色差方程:
也就是衍射面的光焦度应满足:
ref
dif
eff
0
dif
ref eff
优点: (1) 正光焦度的衍射元件具有负色散,不仅为校正色差 提供了条件,还分担了光焦度,有利于减小单色像差;(2)混合 消色差透镜可以不使用那些难以加工或稀少昂贵的大色散材料, 对红外波段的应用尤为有利,可大大降低红外光学的成本。
2014-6-3
内 容
第四章 微光学元件与应用
微透镜阵列 衍射光学器件与二元光学器件
参考文献: 1. 二元光学, 金国藩等编著,国防工业出版社 2. 微光学与系统, 杨国光等编著,浙江大学出版社
折衍混合光学系统
谐衍射光学 亚波长结构 光束成形 阵列光学
4.1 微透镜阵列
- 三种类型: - 折射型 - 衍射型 - 折 /衍混合型 衍射微透镜
i ) N
2
N=2(m=1), η=41%; N=4(m=2), η=81%; N=8(m=3), η=95%; N=16(m=4), η=99%;
2 m
0
i exp jT ( )exp j d m
第i衍射级的相位分布为iφ(p), 则衍射效率为 • 对于DOE,衍射效率为: • 对于BOE,衍射效率为:iB
对折射光学系统,由于光学材料的折射率与温度有关 。温度升高,折射率变小,光学系统光焦度变小,焦 距变长;温度降低,焦距变小。 常规光学,需要温度膨胀的补偿设计,但由于光学材 料、镜筒的金属材料、塑料等壳体材料的热膨胀系数 均为正值,无法实现消热差设计,故只能设计调焦机 构。 衍射光学表面微结构对温度不敏感,且具有负热差特 性,与折射光学结合组成折/衍混合光学,可消热差。
相位函数的变换
相位元件的相位函数由一个多项式 描述:
对BOE, 当取整函数量化函数N=2m时,则有
(x, y)
2
a
mn
mn
xm yn
TB ( )
intT ( ) N 2m q N
• 对于DOE(相位连续型), 当变换函数用2mπ向下取整时, 则有 ( x, y) TD ( ) ( x, y) int 2m q 2m 其中int(x)是取整函数,即取小于x的最大整数;q是闪耀 系数,精确闪耀时,q=1,而q≠1表示存在误差,如加工误 差、波长误差等
• 应用1外 - 材料:硅,玻璃,聚合物 - 类型: 折射型,衍射型 可见光 CCD
凸透镜阵列
凹透镜阵列
折 /衍微透镜
1
2014-6-3
• 应用2——光束微扫描
传统光学透镜扫描器 微透镜阵列扫描器
• 应用3——折/衍混合光学成像系统
体积大,运动路径大, 速度慢
若
zn rp
2
图2-5 入射波通过菲涅耳波带透镜时的衍射
n
A
n
x2 y2 exp i 2n rp2
An
1 rp2 r2 u ( r 2 ) exp i 2n 2 d ( r 2 ) rp2 0 rp
· 消热差方程:
