自动控制原理第六章课后习题答案(免费)
自动控制原理第6章习题解——邵世凡

习 题 66-1 设控制系统的开环传递函数为:()()()s s s s G 1.015.0110++= 绘出系统的Bode 图并求出相角裕量和幅值裕量。
若采用传递函数为(1+0.23s)/(1+0.023s)的串联校正装置,试求校正后系统的幅值和相角裕度,并讨论校正后系统的性能有何改进。
6—2设控制系统的开环频率特性为()()()()ωωωωωj j j j H j G 25.01625.011++= ①绘出系统的Bode 图,并确定系统的相角裕度和幅值裕度以及系统的稳定性; ②如引入传递函数()()()0125.025.005.0++=s s s G c 的相位滞后校正装置,试绘出校正后系统的Bode 图,并确定校正后系统的相角裕度和幅值裕度。
6 3设单位反馈系统的开环传递函数为()()()8210++=s s s s G 设计一校正装置,使静态速度误差系数K v =80,并使闭环主导极点位于s=-2±j23。
6-4设单位反馈系统的开环传递函数为()()()93++=s s s K s G ①如果要求系统在单位阶跃输入作用下的超凋量σ =20%,试确定K 值;②根据所确定的K 值,求出系统在单位阶跃输入下的调节时间t s 。
,以及静态速度误差系数; ③设计一串联校正装置,使系统K v ≥20,σ≤25%,t s 减少两倍以上。
6 5 已知单位反馈系统开环传递函数为()()()12.011.0++=s s s K s G 设计校正网络,使K v ≥30,γ≥40º,ωn ≥2.5,K g ≥8dB 。
6-6 由实验测得单位反馈二阶系统的单位阶跃响应如图6-38所示.要求①绘制系统的方框图,并标出参数值;②系统单位阶跃响应的超调量σ =20%,峰值时间t p =0.5s ,设计适当的校正环节并画出校正后系统的方框图。
6-7设原系统的开环传递函数为()()()15.012.010++=s s s s G 要求校正后系统的相角裕度γ=65º。
自动控制原理 题库第六章 线性系统校正 习题

6-1证明RC 无源超前校正环节 最大超前相角为采用半对数坐标时最大超前相角所对应的频率位于两个转折频率的中间或等于零、极点乘积的平方根,即 6-2某单位反馈控制系统的设计指标为上升时间0.1r t ≤秒,超调量%16%σ≤,斜坡输入下的稳态误差0.05ssv e ≤。
(a )试问系统开环频率特性的低频段需要满足什么要求?中频段需要满足什么要求?(b )在s 平面内绘制出能满足设计要求的系统主导极点所在的区域。
6-3某系统框图如下图所示,误差c r e -=,01≥K ,02≥K 。
(a )要求系统对单位斜坡输入t t r =)(的稳态误差3.0≤,主导极点的阻尼比707.0≥ξ,调节时间 2.33s t ≤秒(按5%误差考虑),请在s 平面上绘制出满足上述设计要求的闭环极点的可行区域,给出1K 、2K 应满足的条件。
(b )设11=K 、2、10,绘制三种情况下以2K 为可变参数的根轨迹。
(c )设101=K ,确定满足(a )中性能指标的2K 的值。
6-4下图所示为钟摆的角度控制系统,其中被控对象为阻尼为零的二阶系统。
(a )试问控制器()c G s 必须满足什么条件,才能使系统为非条件稳定系统?(b )选用常规调节器,使得系统对阶跃扰动输入w 稳态误差为零,系统还可以做到非条件稳定吗?(c )选用PID 控制器应用根轨迹方法分析p k 、i T 和d k 发生变化时对系统快速性、稳定性的影响。
答案:应用关系12d i TT k T =和12p i TT k T +=容易给出分析结果。
6-5力、转矩的积分为速度、转速,速度、转速的积分为位置、转角,许多重要的运动控制系统的被控对象可以描述为二重积分器传递函数,即用根轨迹法分析比例控制p k 、比例微分控制(1)p d k k s k s +=+和超前校正(1)(12)k s s ++、(1)(9)k s s ++、(1)(4)k s s ++几种情况下闭环根轨迹的情况和闭环系统的性能。
自动控制原理简明教程第二版课后答案第六章习题答案

7
胡寿松自动控制原理第六章习题解答 电三刘晓峰制作
-40
-20 14 -20
L(ω)
-40 4 1 ω -60
ω1
ω2
-10 -40
-60
校正后的系统传递函数为:
5(s / ω 2 +1) G(s)Gc(s) = s(s /ω 1 +1)(s +1)(0.25s +1)
设校正后系统中频段宽度为 16,校正后的截止频率 ω c' = 1/ 4 = 0.25 ω 2 = 1/16
8 G(s) = s(2s +1)
若采用滞后—超前校正装置
Gc(s) = (10s +1)(2s +1) (100s +1)(0.2s +1)
对系统进行串联校正,试绘制系统校正前后的对数幅频渐近特性,并计算系统校正前后的 相角裕度。 解:
8
系统校正前的开环传递函数为 G(s) = ,其对数幅频渐近特性如下:
-40 1 ω 4.47
截止频率为 ω c = 4.47 ,相角裕量 γ (ω c) =12.60 不满足要求。 其希望的对数频率渐进曲线如下(按二阶最佳校正) : -20 26 L(ω)
-40 20 1 4.47 40 ω
20
校正后的开环传递函数为 G(s)Gc(s) =
s(s/ 40 +1) G(s)Gc (s) 所以 Gc(s) = = s +1
1 ess < 15
(3)截止频率 ω c ≥ 7.5rad / s 。
rad
1 解:在单位斜坡输入下的稳态误差由于 ess < rad ,所以 K >15 取 K = 20 15 20
自动控制原理(孟华)第6章习题答案(含过程)

第六章习题6-1.已知单位反馈控制系统的开环传递函数为)11.0(200)(+=s s s G试设计一个串联校正网络,使系统的相角裕量︒≥45γ,剪切频率s rad c /50≥ω。
解:方法一:原系统的截止频率为44.16rad/s ,相稳定裕度为180°-90°-arctan4.416=12.76°截止频率和相角裕度均不满足要求,需加入串联超前校正,选择校正网络的传递函数为TsaTsKs G c ++=11)(取校正后系统的截止频率s rad c /52=ω,相角裕度︒=50γ。
则Ta c 1=ω,6.2lg 10lg 20=+a K ,︒=+-+︒5011arctan11a a 由上述3式的64.0,01.0,4.4===K T a)101.0)(11.0()104.0(128)()(+++=s s s s s G s G c校正后系统的截止频率为s rad c /53=ω,相角裕度︒=5.49γ,满足要求。
方法二:按二阶系统最佳模型设计,设校正后系统的开环传递函数为)1()(+=Ts s Ks G则闭环系统的传递函数为222222//1/)(nn n s s T K Ts s TK K s Ts K s ωζωωφ++=++=++= 令50=K ,707.0=ζ由T n /12=ζω,T K n /2=ω,得01.0=T 。
即)101.0(50)()(+=s s s G s G c ,101.011.041)(++=s s s G c 。
易验证该校正环节满足要求。
6-2.已知单位反馈控制系统的开环传递函数为)104.0()(+=s s s G要求系统对单位斜坡输入信号的稳态误差%1≤ss e ,相角裕量为︒≥45γ,试确定系统串联校正网络。
解:本题可首先检验系统得性能指标,针对系统在性能上的缺陷并结合校正网络的作用,选用合适的校正网络,再按相应的步骤确定校正网络的参数。
自控原理习题解答(第六章)(课堂PPT)

2
900 2 1 2025 2 1
yt Gj 0.8sin0.1t Gj
3.2 0.8
sin 0.1t 2tg130 0.1 tg1 45 0.1
900 0.12 1 2025 0.12 1
2.56 sin0.1t 143.13 77.47
10 21.25
0.056sin0.1t 220.6
1
GjHj
5 12
1 0.12 1 0.22 1 22
GjHj tg1 tg1 0.1- tg1 0.2 tg1 2
0 : M 5, 0
: M 0, 90 90 90 90 180
13
答6 41 3.MATLAB画法
GsHs
0.04s3
5s 1 0.62s2
kT1s 1
T2s 1
k
T1s
1
T2
1 s
1
R1 R2
k
R2 R1 R2
, T1
R1C, T2
R1R 2C R1 R2
T1 T2 , k 1
1
1 T1
2
1 T2
22
L dB
1
2
90 45
0
1
2
- 45
- 90
23
答6 5b
E0 s Ei s
R2
1 Cs
1 R 2 R1 Cs
R1
R
R1C1s 1R 2C2s 1 2C2s 1R 2C1s 1 R1C2s
R1C1s 1R 2C2s 1 R1C1R 2C2s 2 R1C1 R 2C2 R1C2
s
1
Tas 1Tbs 1 Ta Tbs 2 Ta Tb Ta Tb
胡寿松《自动控制原理》(第6版)笔记和课后习题(含考研真题)详解2

6-2 设单位反馈 统 开环 函 为
试设计 联 前校正装置, 统满
(1) 角裕度r≥45°;
(2) 单位
入下 态 差
下 标:
(3)截止频率ωc≥7.5rad/s。
解: 开环
取
则开环 函 为:
令
,解得校正前
rad/s
则校正前 角裕度为:
不 合题 要求,
前校正。
取
rad/s,可得:
,可得:
则 前校正环节 校正后 统开环 其 角裕度为
统性能得:
3.某 反馈 统开环 函
合要求。
(1)求 统 角裕度 幅 裕度。
(2) 角裕度
联 前校正 联滞后校正 主要特点。为 统
,试分 统应
联 前校正还 联滞后校正?
[
技 2009 ]
解:(1)求截止频率与
裕度:
求幅 裕度:
(2)要 节 校正。
统 角裕度
,
前校正,则需要校正环
不合
前校正,可以
联滞后
为 习重点, 此,本 分也就没
考 题。
第二部分 课后习题
第6章 线性系统的校正方法
6-1 设 单位反馈 火炮
统,其开环 函 为
若要求 统最 2°,试求:
出速度为12°/s, 出位置
许 差小
(1) 满 上 幅 裕度;
标 最小K ,计 该K 下 统
角裕度
(2) 前
前校正网络
计 校正后 统 能影。
角裕度 幅 裕度,
解:(1) 题可
则 统 特征表 式为
统特征 为:
令
,则
则
可得:
所以 统 状态 应为
(2)求 统 出范 最小 刻t
(完整版)自动控制原理课后习题及答案

第一章绪论1-1 试比较开环控制系统和闭环控制系统的优弊端.解答: 1 开环系统(1)长处 :构造简单,成本低,工作稳固。
用于系统输入信号及扰动作用能早先知道时,可获得满意的成效。
(2)弊端:不可以自动调理被控量的偏差。
所以系统元器件参数变化,外来未知扰动存在时,控制精度差。
2闭环系统⑴长处:不论因为扰乱或因为系统自己构造参数变化所惹起的被控量偏离给定值,都会产生控制作用去消除此偏差,所以控制精度较高。
它是一种按偏差调理的控制系统。
在实质中应用宽泛。
⑵弊端:主要弊端是被控量可能出现颠簸,严重时系统没法工作。
1-2什么叫反应?为何闭环控制系统常采纳负反应?试举例说明之。
解答:将系统输出信号引回输入端并对系统产生控制作用的控制方式叫反应。
闭环控制系统常采纳负反应。
由1-1 中的描绘的闭环系统的长处所证明。
比如,一个温度控制系统经过热电阻(或热电偶)检测出目前炉子的温度,再与温度值对比较,去控制加热系统,以达到设定值。
1-3试判断以下微分方程所描绘的系统属于何种种类(线性,非线性,定常,时变)?2 d 2 y(t)3 dy(t ) 4y(t ) 5 du (t ) 6u(t )(1)dt 2 dt dt(2) y(t ) 2 u(t)(3)t dy(t) 2 y(t) 4 du(t) u(t ) dt dtdy (t )u(t )sin t2 y(t )(4)dtd 2 y(t)y(t )dy (t ) (5)dt 2 2 y(t ) 3u(t )dt(6)dy (t ) y 2 (t) 2u(t ) dty(t ) 2u(t ) 3du (t )5 u(t) dt(7)dt解答: (1)线性定常(2)非线性定常 (3)线性时变(4)线性时变(5)非线性定常(6)非线性定常(7)线性定常1-4 如图 1-4 是水位自动控制系统的表示图, 图中 Q1,Q2 分别为进水流量和出水流量。
控制的目的是保持水位为必定的高度。
《自动控制原理》第六章习题答案

119第六章习题及解答6-1 试求下列函数的z 变换T ta t e =)()1(()()223e t t e t=- 21)()3(ss s E +=)2)(1(3)()4(+++=s s s s s E解 (1)∑∞=---=-==0111)(n nnaz z azza z E(2)[]322)1()1(-+=z z z T t Z由移位定理:[]333323333232)()()1()1(TTTTTTte z ez zeT ze ze zeT et Z -----+=-+=(3)22111)(ssss s E +=+=2)1(1)(-+-=z Tz z z z E (4)21)(210++++=s c s c sc s E21)1(3lim212)2(3lim23)2)(1(3lim221100=++=-=-=++==+++=-→-→→s s s c s s s c s s s c s s s2211223+++-=s s s)(22)1(23)(2TT e z ze z z z z z E ---+---=6-2 试分别用部分分式法、幂级数法和反演积分法求下列函数的z 反变换。
120()()()()11012E z z z z =-- 211213)()2(---+-+-=z zz z E 解 (1))2)(1(10)(--=z z zz E① 部分分式法)12(10210110)()2(10)1(10)(210110)2)(1(10)(-=⨯+⨯-=-+--=-+--=---=nnnT e z zz z z E z z z z zz E② 幂级数法:用长除法可得+-+-+-=+++=+-=--=---)3(70)2(30)(10)(7030102310)2)(1(10)(*3212T t T t T t t e z z z z z z z z z z E δδδ③ 反演积分法[][])()12(10)()12(10210110)(210110lim)(Re 10210lim)(Re 0*221111nT t t e nT e z zzz E s z z z z E s n nnnnnz z n nz z n --=-=⨯+⨯-=⨯=-=⋅-=-=⋅∑∞=→→-→→-δ(2) 2221)1()13(12)13(213)(-+-=+-+-=+-+-=--z z z z z z z zz zz E① 部分分式法∑∑∞=∞=---=-⎥⎦⎤⎢⎣⎡--=⨯--=----=----=--=0*222)()32()(32)()(132)(13)1(2)(13)1(2)1(31)(n n nT t n nT t nT Tt e t t Tt e z z z z z E z z z z zz E δδ121② 幂级数法:用长除法可得--------=-----=+-+-=---)3(9)2(7)(5)(3)(9753123)(*32122T t T t T t t t e zzzz z z z z E δδδδ③ 反演积分法[][]12111)3(lim!11)(Re )(-→→-⋅+-=⋅=n s z n zz zdzd z z E s nT e[]32)1(3lim 11--=++-=-→n nzz n n ns∑∞=---=*)()32()(n nT t n t e δ6-3 试确定下列函数的终值()()()11112E z Tzz =--- )208.0416.0)(1(792.0)()2(22+--=z z z zz E解 (1)∞=--=---→21111)1()1(lim zTz z e z ss(2)1208.0416.01792.0208.0416.0792.0lim)()1(lim 2211=+-=+-=-=→→z z zz E z e z z ss6-4 已知差分方程为c k c k c k ()()()-+++=4120初始条件:c(0)=0,c(1)=1。
自动控制原理第六章课后习题答案(免费)

自动控制原理第六章课后习题答案(免费)线性定常系统的综合6-1 已知系统状态方程为:()100102301010100x x uy x•-⎛⎫⎛⎫ ⎪ ⎪=--+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭=试设计一状态反馈阵使闭环系统极点配置为-1,-2,-3. 解: 由()100102301010100x x u y x•-⎛⎫⎛⎫ ⎪ ⎪=--+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭=可得:(1) 加入状态反馈阵()012K k k k =,闭环系统特征多项式为:32002012()det[()](2)(1)(2322)f I A bK k k k k k k λλλλλ=--=++++-+--+- (2) 根据给定的极点值,得期望特征多项式:*32()(1)(2)(3)6116f λλλλλλλ=+++=+++(3) 比较()f λ与*()f λ各对应项系数,可得:0124,0,8;k k k ===即:()408K =6-2 有系统:()2100111,0x x u y x•-⎛⎫⎛⎫=+ ⎪ ⎪-⎝⎭⎝⎭= (1) 画出模拟结构图。
(2) 若动态性能不能满足要求,可否任意配置极点? (3) 若指定极点为-3,-3,求状态反馈阵。
解(1) 模拟结构图如下:(2) 判断系统的能控性;0111c U ⎡⎤=⎢⎥-⎣⎦满秩,系统完全能控,可以任意配置极点。
(3)加入状态反馈阵01(,)K k k =,闭环系统特征多项式为:()2101()det[()](3)22f I A bK k k k λλλλ=--=+++++ 根据给定的极点值,得期望特征多项式:*2()(3)(3)69f λλλλλ=++=++比较()f λ与*()f λ各对应项系数,可解得:011,3k k ==即:[1,3]K =6-3 设系统的传递函数为:(1)(2)(1)(2)(3)s s s s s -++-+试问可否用状态反馈将其传递函数变成:1(2)(3)s s s -++若能,试求状态反馈阵,并画出系统结构图。
自动控制理论课后习题详细解答答案(夏德钤翁贻方版)第六章
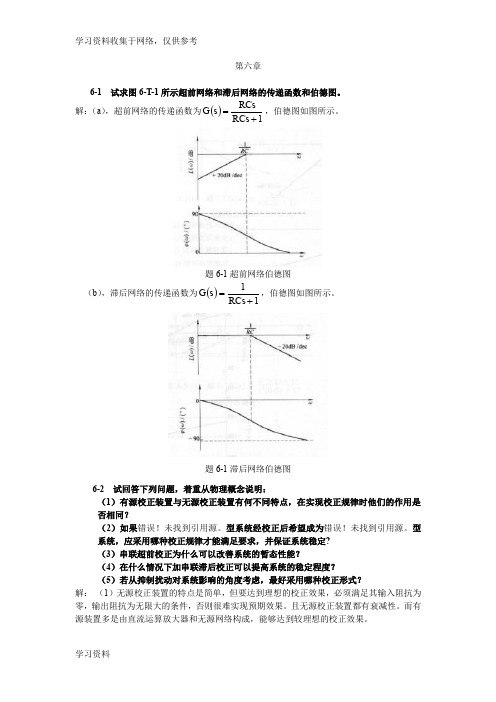
第六章6-1 试求图6-T-1所示超前网络和滞后网络的传递函数和伯德图。
解:(a ),超前网络的传递函数为()1+=RCs RCss G ,伯德图如图所示。
题6-1超前网络伯德图(b ),滞后网络的传递函数为()11+=RCs s G ,伯德图如图所示。
题6-1滞后网络伯德图6-2 试回答下列问题,着重从物理概念说明:(1)有源校正装置与无源校正装置有何不同特点,在实现校正规律时他们的作用是否相同?(2)如果错误!未找到引用源。
型系统经校正后希望成为错误!未找到引用源。
型系统,应采用哪种校正规律才能满足要求,并保证系统稳定? (3)串联超前校正为什么可以改善系统的暂态性能?(4)在什么情况下加串联滞后校正可以提高系统的稳定程度?(5)若从抑制扰动对系统影响的角度考虑,最好采用哪种校正形式?解: (1)无源校正装置的特点是简单,但要达到理想的校正效果,必须满足其输入阻抗为零,输出阻抗为无限大的条件,否则很难实现预期效果。
且无源校正装置都有衰减性。
而有源装置多是由直流运算放大器和无源网络构成,能够达到较理想的校正效果。
(2)采用比例-积分校正可使系统由I 型转变为II 型。
(3)利用串联超前校正装置在剪切频率附近提供的相位超前角,可增大系统的相角裕度 ,从而改善系统的暂态性能。
(4)当ω减小,相频特性)(ωϕ朝0方向变化且斜率较大时,加串联滞后校正可以提高系统的稳定程度。
(5)可根据扰动的性质,采用带有积分作用的串联校正,或采用复合校正。
6-3 某单位反馈系统的开环传递函数为6418)(2++=s s s G (1)计算校正前系统的剪切频率和相角裕度。
(2)串联传递函数为1125.014.0)(++=s s s G c 的超前校正装置,求校正后系统的剪切频率和相角裕度。
(3)串联传递函数为1100110)(++=s s s G c 的滞后校正装置,求校正后系统的剪切频率和相角裕度。
(4)讨论串联超前校正、串联滞后校正的不同作用。
自动控制原理第6章 习题及解析

第6章 习题及参考解答6-9 已知单位负反馈控制系统校正前对数幅频特性)(0ωL 如图6-63中点画线所示,串联校正装置对数幅频特)(c ωL 如图6-63中实线所示,要求1)作出校正后系统开环对数幅频渐进特性)(ωL 。
2)比较校正前、后的开环对数幅频特性)(0ωL 和)(ωL ,说明校正装置的作用。
习题 6-9 参考解答:1)校正后系统开环对数幅频渐进特性)(ωL 是)(0ωL 和)(c ωL 的线性叠加,如图右上图中红色实线所示。
2)校正装置的传递函数为2(1)()101c s G s s +=+,为滞后校正装置。
它的作用:①抬高了低频段幅值,可提高速度输入的稳态精度;②固有特性以-40dB/dec 穿越0dB 线,校正后的Bode 图以-20dB/dec 穿越0dB 线,中频段变缓,平稳性变好;校正后系统Bode 图的高频段幅值降低了,抗干扰能力提高;校正后系统的开环截止频率减小了,滞后校正是靠牺牲系统的快速性来换取平稳性的。
6-10 图6-64为三种校正装置的对数渐近幅频特性,它们都是由最小相位环节组成。
系统为单位负反馈 系统,其开环传递函数为02400()(0.011)G s s s =+试问: 1)这些校正网络特性中,哪一种使已校正系统的稳定性最好?2)为了将12Hz 的正弦噪声削弱10倍左右,你确定采用哪种校正网络特性?习题 6-10 参考解答: 校正装置传递函数分别是12310.110.510.51(),(),().1010.0111010.0251c c c s s s s G s G s G s s s s s ++++===++++。
1)a )使用滞后校正网络,校正后021400()(0.011)1().101c G G s s s s s s =+++10()()1c G j G j ωω==L (图6-63 题6-9图图6-64 题6-10图102400()()1110180arctan 6.32180arctan 0.01 6.32arctan16.3211.7063.2cc c co oo c G j G j ωωωωωγω⨯=⇒⨯⨯≈=-=+--⨯-⨯=b )使用超前校正网络,校正后022400()(0.011)0.11().0.011c G G s s s s s s =+++10()()1c G j G j ωω==1024000.1()()11180arctan 0.140180arctan 0.0140arctan 04032.4.0140c occ c o o G j G j ωγωωωω⨯=⇒⨯=+⨯---⨯==⨯≈c )使用滞后-超前校正网络,校正后0223400()(0.011)(0.51)().(101)(0.0251)c G G s s s s s s s =++++2230224000.5()()11011180(arctan 0.510)180arctan 1041010arctan 0.02510arctan 0.01108.2cc c c o o c oG j G j ωγωωωωω⨯=⇒⨯⨯⨯=+⨯--⨯-⨯-⨯=≈=由上述结果可知,在这些校正网络特性中,滞后-超前校正网络,其相角裕量γ=48o 最大,所以滞后-超前网络使已校正系统的稳定性最好。
自动控制原理课后答案第6章

串联超前校正
一般而言,当控制系统的开环增益增大到满足其稳态精度时,有可能其稳定裕量不够甚 至不稳定,或者即使稳定,其动态性能一般也不会满足设计要求。为此,需要在系统前向通 道中增设一个超前校正装置,已实现在开环增益增大的情况下,使系统的动态性能也能满足 设计要求。本节先讨论超前校正装置的特点,然后介绍超前校正装置的设计方法。
a ) 按给定补偿的复合校正 图 6-3 复合校正 3
b)按扰动补偿的复合校正
复合控制系统充分利用开环控制与闭环控制的优点,解决了系统静态与动态性能方面, 以及对扰动的抑制与对给定的跟随两方面的矛盾,极大地改善了系统的性能。 在系统设计中,究竟采用那种校正方式,取决于系统中的信号性质、技术实现的方便性、 可供选用的元件、抗干扰性、经济性、环境使用条件以及设计者的经验等因素。一般来说, 对于一个具体的单输入、单输出线性定常系统,宜选用串联校正或反馈校正。通常由于串联 校正比较简单,易于实现,所以工程实际中应用较多,也是本章学习的重点内容。
图 6-1 串联校正
为了减少校正装置的输出功率,降低系统功率损耗和成本,串联校正装置一般装设在前 向通道综合放大器之前,误差测量点之后的位置。串联校正的特点是结构简单,易于实现, 但需附加放大器,且对于系统参数变化比较敏感。 串联校正按照校正装置的特点分为超前校正、滞后校正和滞后-超前校正。校正后系统开 环传递函数为
自动控制原理研究的范畴有两方面:一方面已知控制系统的结构和参数,研究和分析其 三个基本性能,即稳定性、动态性能和稳态性能,称此过程为系统分析。本书的第 3 章~第 5 章就是采用不同的方法进行系统分析;另一方面在是被控对象已知的前提下,根据工程实 际对系统提出的各项性能要求,设计一个新系统或改善原性能不太好的系统,使系统的各项 性能指标均能满足实际需要,称此过程为系统校正(或综合) 。本章就是研究控制系统校正的 基本问题,并介绍基于 MATLAB 和 Simulink 的线性控制系统较正的一般方法。 通过本章的学习,建立系统校正的概念,掌握校正的方法和步骤,并能利用 MATLAB 和 Simulink 对系统进行校正分析,为进行实际系统设计建立理论基础。
中国矿业大学常俊林版自动控制原理6章课后习题解答

第一章1. 1图1・18是液位自动控制系统原理示意图。
在任意情况下,希望液而髙度c维持不变, 试说明系统工作原理并画出系统方块图。
解:系统的控制任务是保持液而髙度不变。
水箱是被控对彖,水箱液位是被控变量。
电位器用来设置期望液位髙度c•(通常点位器的上下位移来实现)。
当电位器电刷位于中点位置时,电动机不动,控制阀门有一左的开度,使水箱的流入水屋与流岀水量相等,从而使液面保持在希望高度C•上。
一旦流出水量发生变化(相当于扰动),例如当流岀水量减小时,液面升髙,浮子位置也相应升高,通过杠杆作用使电位器电刷从中点位宜下移,从而给电动机提供一定的控制电压,驱动电动机通过减速器减小阀门开度,使进入水箱的液体流量减少。
这时,水箱液位下降.浮子位巻相应下降,直到电位器电刷回到中点位置为止,系统重新处于平衡状态,液位恢复给定髙度。
反之,当流出水量在平衡状态基础上增大时,水箱液位下降,系统会自动增大阀门开度,加大流入水量,使液位升到给左髙度cl 系统方框图如图解1・4・1所示。
图解1.4.1液位自动控制系统方框图1. 2恒温箱的温度自动控制系统如图1. 19所示。
(1) 画出系统的方框图:(2) 简述保持恒温箱温度恒左的工作原理;(3) 指出该控制系统的被控对象和被控变疑分别是什么。
「调压器220〜图1.19恒温箱的温度自动控制系统解:恒温箱采用电加热的方式运行,电阻丝产生的热量与调压器电压平方成正比,电压增 高,炉温就上升。
调压器电压由其滑动触点位苣所控制,滑臂则由伺服电动机驱动.炉子的 实际温度用热电偶测量,输出电压作为反馈电压与给左电圧进行比较,得岀的偏差电压经放 大器放大后,驱动电动机经减速器调宵调压器的电压。
在正常情况下,炉温等于期望温度T,热电偶的输岀电压等于给泄电压。
此时偏差为零, 电动机不动,调压器的滑动触点停留在某个合适的位置上。
这时,炉子散失的热量正好等于 从电阻丝获取的热量,形成稳定的热平衡状态,温度保持恒定。
自动控制原理(北大丁红版)第六章习题解答

解: G ( j )
j 0.05 j 0.01
=0 时, G (0) 5 ,在低频段, L ( ) 20 lg 5 14dB ; 时, G ( j) 1 ,在高频段,
L( ) 20 lg1 0dB 。转折频率 1 0.01 , 2 0.05 。串联校正装置是滞后校正装置。
令 L( ) 0 ,可得 c 4.8
180 o 90 o arctan(0.4 c ) arctan(0.2 c ) arctan(0.5 c ) arctan(0.08 ) 20.2 o 0 o
第 169 页(共 34 页)
可见串入超前校正网络后,
解: (1) k
R 希望的输出速度 2.360 o / 60 6 e ss 容许的位置误差 2o G ( s) 6 s (0.2 s 1)(0.5s 1)
6 20 lg , 3 6 L( ) 20 lg ,2 5 0.5 6 20 lg , 5 0.5 0.2
6-6 设开环传递函数
G(s)
k s ( s 1)(0.01s 1)
*
单位斜坡输入 R (t ) t ,输入产生稳态误差 e 0.0625 。若使校正后相位裕度 不低于 45°,截止 频率 c 2( rad / s ) ,试设计校正系统。
*
解:
e
1 0.0625, k 16 k
20 lg15 40 lg c 20 lg c ,
2
15 c2
得到,
c 15 3.87 。
相角裕量:
180 0 ( c ) 180 0 90 0 arctan 3.87 14.50
自动控制原理胡寿松主编课后习题答案详解-胡寿松第六版自控答案

X 0 (s) =
f1 f2s2 + ( f1K2 + K1 f2 )s + K1K2
= K1K2
K 1
K2
X i (s) f1 f2s2 + ( f1K2 + K1 f1 + K1 f2 )s + K1K2
f1 f2 s2 + ( f1 + f2 )s +1+ f1
K1 K 2
K 1
K2
K2
( f1 s + 1)( f 2 s + 1)
于是传递函数为
X 0 (s) =
f1
X i (s) ms + f1 + f 2
②图 2—57(b):其上半部弹簧与阻尼器之间,取辅助点 A,并设 A 点位移为 x ,方向朝下;而在其下半部工。
引出点处取为辅助点 B。则由弹簧力与阻尼力平衡的原则,从 A 和 B 两点可以分别列出如下原始方程:
K1 (xi − x) = f (x& − x&0 )
=
1 C2s
(R2C2s + 1) =
1 C2
s
(T2
s
+ 1)
所以: U 0 (s) = Z 2 =
1 C2
s
(T2
s
+
1)
=
(T1s + 1)(T2 s + 1)
Ui (s)
Z1 + Z2
R1 T1s +
1
+
1 C2
s
(T2
s
+
1)
R1C2 s + (T1s + 1)(T2 s + 1)
自动控制原理 第6章 控制系统的频域分析习题答案
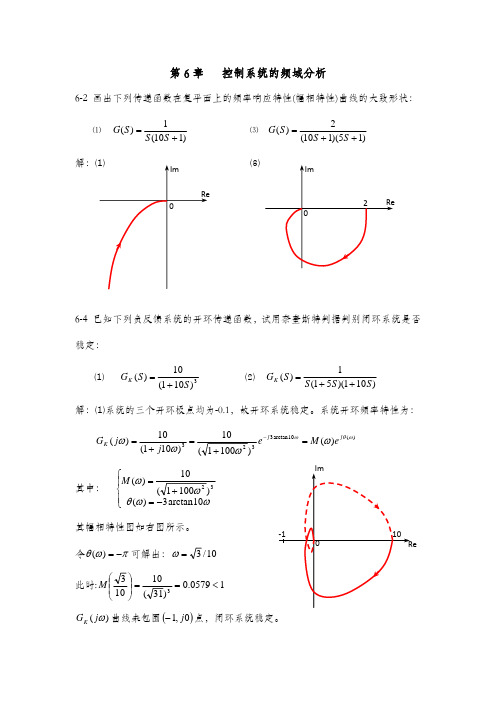
GK (S )
10 (1 10S ) 3
⑵
GK (S )
1 S (1 5S )(1 10S )
解:⑴系统的三个开环极点均为-0.1,故开环系统稳定。系统开环频率特性为:
G K ( j )
10 10 e j 3 arctan 10 M ( )e j ( ) 3 2 3 (1 j10 ) ( 1 100 )
Im
其幅相特性图如右图所示。 令 ImG K ( j ) 0 可解出:
1 50
1 5 2
Re ‐1 0
10 1 此时: G K j 1 3 5 2
G K ( j ) 曲线顺时钟包围 1, j 0 点两圈,
故闭环系统不稳定,有两个正根。
第6章
控制系统的频域分析
6-2 画出下列传递函数在复平面上的频率响应特性(幅相特性)曲线的大致形状:
⑴
G(S )
1 S (10 S 1)
Im Re 0
⑶
G(S )
2 (10 S 1)(5S 1)
Im
Байду номын сангаас
解:⑴
⑶
2 0
Re
6-4 已知下列负反馈系统的开环传递函数,试用奈奎斯特判据判别闭环系统是否 稳定: ⑴
Im
其中:
10 M ( ) ( 1 100 2 ) 3 ( ) 3 arctan 10
‐1
其幅相特性图如右图所示。 令 ( ) 可解出: 3 / 10
10 0 Re
3 10 此时: M 10 ( 31) 3 0.0579 1
6-7 控制系统如图 6-25 所示,求出使系统闭环稳定的最小δ的取值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自动控制原理第六章课后习题答案(免费)线性定常系统的综合6-1 已知系统状态方程为:()100102301010100x x uy x•-⎛⎫⎛⎫ ⎪ ⎪=--+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭=试设计一状态反馈阵使闭环系统极点配置为-1,-2,-3.解: 由()100102301010100x x u y x •-⎛⎫⎛⎫ ⎪ ⎪=--+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭=可得:(1) 加入状态反馈阵()012K k k k =,闭环系统特征多项式为:32002012()det[()](2)(1)(2322)f I A bK k k k k k k λλλλλ=--=++++-+--+-(2) 根据给定的极点值,得期望特征多项式:*32()(1)(2)(3)6116f λλλλλλλ=+++=+++(3) 比较()f λ和*()f λ各对应项系数,可得:0124,0,8;k k k ===即:()408K =6-2 有系统:()2100111,0x x u y x•-⎛⎫⎛⎫=+ ⎪ ⎪-⎝⎭⎝⎭= (1) 画出模拟结构图。
(2) 若动态性能不能满足要求,可否任意配置极点? (3) 若指定极点为-3,-3,求状态反馈阵。
解(1) 模拟结构图如下:∫∫-1-21u++y(2) 判断系统的能控性;0111c U ⎡⎤=⎢⎥-⎣⎦满秩,系统完全能控,可以任意配置极点。
(3)加入状态反馈阵01(,)K k k =,闭环系统特征多项式为:()2101()det[()](3)22f I A bK k k k λλλλ=--=+++++ 根据给定的极点值,得期望特征多项式:*2()(3)(3)69f λλλλλ=++=++比较()f λ和*()f λ各对应项系数,可解得:011,3k k ==即:[1,3]K =6-3 设系统的传递函数为:(1)(2)(1)(2)(3)s s s s s -++-+试问可否用状态反馈将其传递函数变成:1(2)(3)s s s -++若能,试求状态反馈阵,并画出系统结构图。
解:若希望采用状态反馈将(1)(2)(1)(2)(3)s s s s s -++-+变成1(2)(3)s s s -++,则根据状态反馈不改变系统传递函数的零点的原理,可知经过状态反馈之后的系统传递函数必为()()212(2)(3)s s s s -+++。
因此期望的特征多项式为232(2)(3)71612λλλλλ++=+++由于原系统的传递函数为232(1)(2)2(1)(2)(3)256s s s s s s s s s s -++-=+-++--,则状态反馈阵[]18215K=。
6-4 是判断下列系统通过状态反馈能否镇定。
210402105,00200517050A b -⎛⎫⎛⎫ ⎪ ⎪- ⎪ ⎪⎪ ⎪==- ⎪ ⎪- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭解:该系统为约旦标准型,很显然,其不能控不能所对应的特征值具有负实部,是渐进稳定的,因此可以通过状态反馈进行镇定。
6-5 设系统状态方程为:01000010100010001101x x u •⎛⎫⎛⎫ ⎪ ⎪- ⎪ ⎪=+ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭(1) 判断系统能否稳定。
系统能否镇定。
(2) 若能,试设计状态反馈使之稳定。
解:(1)()4100010det 000100110I A λλλλλλλ-⎡⎤⎢⎥⎢⎥-===⎢⎥-⎢⎥⎣⎦= 原系统处于临界稳定状态。
010110100101110110c U ⎡⎤⎢⎥⎢⎥=⎢⎥--⎢⎥--⎣⎦,可知矩阵满秩,系统完全能控,所以可以通过状态反馈实现系统的镇定。
(2)自定义期望的系统极点,然后采用极点配置的方法进行即可。
6-6 设计一前馈补偿器,使系统:1112()11(1)s s W s s s s ⎛⎫ ⎪++⎪= ⎪ ⎪+⎝⎭解耦,且解耦后的极点为-1,-1,-2,-2.解:根据题意可知解耦后的系统传递函数矩阵为()()212101()102s W s s ⎛⎫⎪+ ⎪= ⎪⎪ ⎪+⎝⎭, 则前馈补偿器为()()()12211101121110(1)2d s s s W s s s s s -⎛⎫⎛⎫ ⎪ ⎪+++ ⎪⎪= ⎪ ⎪ ⎪ ⎪ ⎪+⎝⎭+⎝⎭, 所以()()()()()()2232122122d s s s s W s s s s s s +⎛⎫- ⎪++⎪= ⎪+- ⎪ ⎪+++⎝⎭6-7 已知系统:100100230110101100011x x u y x•-⎛⎫⎛⎫ ⎪ ⎪=--+ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎛⎫= ⎪⎝⎭(1) 判别系统能否用状态反馈实现解耦。
(2) 设计状态反馈使系统解耦,且极点为-1,-2,-3. 解:原系统的传递函数矩阵为:()()()()1101001010002301011101011011012s W s C sI A B s s s s s --+⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥=-=+⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥---⎣⎦⎣⎦⎡⎤⎢⎥+⎢⎥=⎢⎥⎢⎥++⎣⎦系统存在耦合。
下面判断系统能否通过状态反馈进行解耦:[][]0110101011001c A B ⎡⎤⎢⎥==≠⎢⎥⎢⎥-⎣⎦0,所以10d =;[][][][]02121001101000110010011023011010101c A B c A B ⎡⎤⎢⎥===⎢⎥⎢⎥-⎣⎦-⎡⎤⎡⎤⎢⎥⎢⎥=--=≠⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦00所以21d =。
因此1212100122d d c A D c A ⎡⎤⎡⎤==⎢⎥⎢⎥--⎣⎦⎣⎦,1010010011221001E DB ⎡⎤⎡⎤⎡⎤⎢⎥===⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎢⎥-⎣⎦, 可知E 为非奇异阵,所以该系统不能通过状态反馈的办法实现解耦。
6-8 已知系统:()01000110x x u y x•⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭= 试设计一状态观测器,使观测器的极点为-r,-2r(r>0). 解 (1) 检验能观性因10,,01o c U cA ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭满秩系统能观可构造全维观测器.(2) 原系统的对偶系统为:[]001,,01100TT TA c b ⎡⎤⎡⎤===⎢⎥⎢⎥⎣⎦⎣⎦()201det ,0,0T I A a a λλ-===所以另观测器的期望多项式为()()22232r r r r λλλλ++=++则2012,3a r a r **==所以()22,3T KE r r ==下面求转换矩阵1100101100110T TT T TTP A cc A cc P -⎡⎤⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎡⎤=⎢⎥⎣⎦所以原系统对应的()1222012,3321032TTE E P r r r r r E r -⎡⎤⎡⎤=⋅==⎢⎥⎣⎦⎣⎦⎡⎤=⎢⎥⎣⎦对应的全维观测器为:223103ˆˆ()2012rr x A Ec x bu Ey x u y r r -⎛⎫⎛⎫⎛⎫=-++=++ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭6-9* 已知系统:()21001110x x uy x•-⎛⎫⎛⎫=+ ⎪ ⎪-⎝⎭⎝⎭= 设状态变量2x 不能测取,试设计全维和降维观测器,使观测器极点为-3,-3.解:[]201,,01110TT TA c b -⎡⎤⎡⎤===⎢⎥⎢⎥-⎣⎦⎣⎦()201det 32,2,3T I A a a λλλ-=++==所以另观测器的期望多项式为()22369λλλ+=++则019,6a a **==所以()7,3T KE ==下面求转换矩阵1101131100111T TT T TTP A cc A cc P -⎡⎤⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎡⎤=⎢⎥-⎣⎦所以原系统对应的()[]1017,3341134TTE E P E -⎡⎤=⋅==⎢⎥-⎣⎦⎡⎤=⎢⎥⎣⎦对应的全维观测器为:5103ˆˆ()4114x A Ec x bu Ey x u y -⎛⎫⎛⎫⎛⎫=-++=++ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭6-11* 设受控对象传递函数为31s : (1) 设计状态反馈,使闭环极点配置为133,2--± 解:期望的特征多项式为()320121313344322223,4,4j j a a a λλλλλλ***⎛⎫⎛⎫++-++=+++ ⎪⎪⎝⎭⎝⎭=== 原系统0120,0,0a a a ===所以[]344K=。
