试卷3(AB)

合集下载

人教版2022——2023学年小学三年级上册期末数学调研试卷AB卷(含答案)

第1页/总36页【人教版】2022-2023学年小学三年级上册期末数学调研试卷（A 卷）第I 卷（选一选）评卷人得分一、选一选1．下面的运动哪个没有是旋转？（）A．B ．C ．2．，像这样一一间隔排成一行，如果有45根，有（）个。

A ．44B ．45C ．463．比较下面三个图形的周长。

（）A ．图1的周长要长一些B ．图3的周长要长一些C ．三个图形的周长是相等的4．下面哪个分数可以表示图中的涂色部分？（）A ．12B ．38C ．145．三年级有510人去参观博物馆，要求每组有多少人，可以补充哪个条件？（）A ．每组有170人B ．平均分成3组C ．四年级有400人去参观博物馆6．用48根彩带做纸花，每3根做一朵，可以做多少朵？小华用竖式计算出了结果。

竖式中箭试卷第2页，共5页…○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※没有※※要※※在※※装※※订※※线※※内※※答※※题※※头所指的数表示的是（）。

A ．已经用去3根B ．还剩下30根C ．已经用去了30根7．看线段图，要求篮球有多少个，正确的列式是哪一个？（）A ．18＋32＋11B ．18＋32－11C ．18×2＋118．将下面的分数条铺在白色直条中（分数条使用次数没有限），哪一种铺法刚好将白色直条铺满。

（）A ．12；14；14B ．12；14；18；116C ．12；14；18第II 卷（非选一选）评卷人得分二、填空题9．军军很喜欢写数学日记，下面这段话是他在学习了“克与千克”后，写的一篇日记，你能帮他补充完整吗？我叫军军，今年8岁了。

我喜欢运动，所以身体很健壮，体重已经有28()了，身高135()。

为了补充营养，我每天早上要吃一个重约50()的鸡蛋，吃一袋250()的面包。

上学时我背着一个重约3()的书包。

10．400×6可以看作4个()乘6，结果是()。

河南公务员考试行测数学运算专项强化真题试卷3(题后含答案及解析)

河南公务员考试行测数学运算专项强化真题试卷3(题后含答案及解析)题型有：1.1．某商品的单位利润和进货量的大小相关，进货总额低于5万元时利润率为5％，低于或等干10万元时一高干5万元的部分利润在10％，高干10万元时，高于10万元的部分利润在15％。

问当进货量在20万元时，一共有多少万元的利润?A．1．75B．2．25C．3．15D．4．05正确答案：B解析：当进货量在20万元时，一共有5×5％＋(10－5)×10％＋(20－10)×15％＝2．25万元的利润，选B。

2．在7×7的队列中，先随机给一个队员戴上红绶带，再给另一个队员戴上蓝绶带，要求戴两种颜色绶带的这两位队员不在同一行也不在同一列。

问有多少种戴法?A．1048B．1374C．1764D．1858正确答案：C解析：7×7的队伍共有49人，先从49人中任选1人戴上红绶带，要求两人不同行不同列，相当于从6×6的队伍再选一人．即从36人中任取1人戴上蓝绶带，共有49×36＝1764种戴法。

3．某单位举行大型比赛，其中，舞台布置费占总费用的。

舞台布置所花费用比原来计划的少用20％，节约了3000元。

问总预算是多少元?A．25000B．30000C．40000D．45000正确答案：C解析：舞台布置费为3000÷20％＝15000元，总费用为15000÷＝40000元，选C。

4．箱子里有标号1至10共10个球，小张随机取了三个球并记下号码后将球放回，小李也随机取了三个并记下号码。

这时发现两人取的球的号数之积都恰好是144。

已知小张的号数之和比小李的大．那么小张取的球的号数之和是多少?A．19B．17C．16D．14正确答案：A解析：144＝2×2×2×2×3×3，小张和小李记下的号码为1～10中的三个，则只能是2，8，9和3，6，8。

山东省济南市2022——2023学年小学三年级上册数学期末调研试卷AB卷(含答案)

山东省济南市2022-2023学年小学三年级上册数学期末调研试卷（A卷）一、计算1．直接写得数。

40×60＝450÷9＝200×8＝5600÷8＝31×3＝140×5＝120×4＝8000÷4＝300×40＝300÷5＝32×20＝68÷2＝700×80＝400÷8＝15×6＝50×80＝600×7＝0÷7＝48÷4＝90÷3＝2．估算。

901÷3≈718÷9≈58÷2≈544÷6≈3．列竖式计算。

（带★的要验算）26×18＝20﹣12.5＝824÷4＝8.4+2.5＝35×87＝＝★548÷3＝二、填空4．在横线里填上合适的数。

9平方米＝平方分米200平方厘米＝平方分米2年＝个月6分米＝米＝米（填小数）1日＝小时2元7角＝元（填小数）5．在横线里填上合适的单位名称。

一块黑板的面积大约是4一张奖状的面积约是6小明身高1.3篮球场的面积是420一粒纽扣的面积约是16．每根跳绳8元，用245元钱买跳绳，可以买根，还剩元。

7．2022年3月23日，神舟十三号飞行乘组航天员翟志刚、王亚平、叶光富在中国空间站讲授“天宫课堂”第二课，开始时间为15时40分，结束时间为17时，授课时间共小时分。

8．2022年2月4日至2月20日，北京成功举办冬季奥运会。

今年2月份共有天，全年共有天。

9．在横线里填上“＞”“＜”或“＝”。

5元 4.9元 2.3 2.78.9米9.8米10．照样子填一填。

14：00下午2：0019：30上午8：1511．□14÷5，要使商是三位数，□里最小可以填；要使商是两位数，□里最大可以填。

12．商店运进250个桃子，放在4个筐里售卖，每个筐里大约放个桃子。

2022——2023学年小学三年级下册北师大版数学期末调研试卷AB卷(含答案)

2022-2023学年小学三年级下册北师大版数学期末调研试卷（A卷）一、选一选。

（每题2分，共10分）1．（2分）29×34，用第二个乘数十位上的数字3去乘29，结果是（）A．87B．870C．87002．（2分）下面的图形中，是轴对称图形的有（）个。

A．3B．4C．53．（2分）下面的图形中阴影部分没有表示的是（）A．B．C．4．（2分）一头猪的重量相当于2只羊的重量，一头牛的重量相当于3头猪的重量，那一头牛的重量相当于（）只羊的重量．A．6B．7C．85．（2分）图中，长方形被分为甲、乙两部分，这两部分的（）A．周长相等，面积没有相等B．周长和面积都没有相等C．周长和面积都相等二、认真读题，准确填空。

（每空1分，共18分）6．（2分）用分数表示涂色部分。

7．（2分）168÷3的商是位数；35×40的积的末尾有个0。

8．（2分）拉开抽屉是现象，拧水龙头是现象．9．（2分）在横线处填上合适的单位名称。

一袋大米重20；一张课桌面的面积是35。

10．（1分）正方形的周长为84厘米，它的面积为平方厘米。

11．（2分）400平方分米＝平方米；2000千克＝吨．12．（2分）比大小。

13．（5分）三、请你判断，认为对的打上“√”，错的打上“×”。

（共5分）14．（1分）三角形是轴对称图形．15．（1分）分母相同的分数，分子大的分数比较大．．16．（1分）小明家的客厅面积为20平方分米．．17．（1分）320÷（4×2）与320÷4×2的结果相等。

18．（1分）所有的分数都比1小。

四、直接写出得数。

（每小题8分，共8分）19．（8分）直接写出得数。

618÷6＝11×50＝560÷8＝35×4＝4×5+20＝五、计算题。

（9+9＝18分）20．（9分）用竖式计算下面各题。

24×75＝39×18＝636÷6＝21．（9分）用递等式计算。

【部编版】2022-2023学年小学语文三年级上册期末调研试卷AB卷(含解析)

【部编版】2022-2023学年小学语文三年级上册期末调研试卷（A卷）第I卷（选一选）评卷人得分一、选一选1．下列诗句按“一年四季”的顺序排列正确的一项是（）①墙角数枝梅，凌寒独自开。

②小荷才露尖尖角，早有蜻蜓立上头。

③竹外桃花三两枝，春江水暖鸭先知。

④荷尽已无擎雨盖，菊残犹有傲霜枝。

A．③②①④B．③②④①C．②③①④D．②③④①2．下面这段话缺个开头，以下哪个开头最能激发你的阅读兴趣（）一踏进水果店，浓浓的果香扑鼻而来。

放眼望去，果架上摆满了新鲜娇嫩的水果：有红得发紫的葡萄，有椭圆形的哈蜜瓜，有又大又圆的西瓜，有像小船儿一样的香蕉，还有像乒乓球一般的枇杷……A．今天，我和妈妈到水果店买水果。

B．我家楼下有一家水果店。

C．你可知道，超市的水果品种有多么丰富吗？第II卷（非选一选）评卷人得分二、书写3．请把下面这句话抄写在横线里，做到格式正确，字迹工整。

幻想是极其可贵的品质。

——列宁____________________________________评卷人得分三、填空题4．看拼音写字词，并写规范整。

kuà yuè ( ) má fan ( ) ōu zhōu ( ) dài jià( )xùn sù ( )jì xù ( )ǒuěr( )xiū jiàn( )5．火眼金睛。

我能填空，并能在正确的音节和意思下面画“ ”。

我发现“诫、谣、辩”都有，因为它们的意思都和有关。

我猜“讷”的音节是（①nè②hūn），它的意思是（①说话迟钝②表示里头）。

我还能写两个带有这个偏旁的字、。

6．我能按课文内容填空，还能巧妙运用。

（1）这地方的火烧云变化极多，一会儿_________，一会儿_________，一会儿_________，一会儿_________。

（2）没有努力，指望靠好运气过日子，是没有会有好结果的。

化工操作工(高级)模拟试卷3(题后含答案及解析)

化工操作工（高级）模拟试卷3(题后含答案及解析) 题型有：1. 单项选择题 2. 判断题请判断下列各题正误。

单项选择题下列各题的备选答案中，只有一个是符合题意的。

1．用“φ外径mm×壁厚mm”来表示规格的是( )。

A．铸铁管B．钢管C．铅管D．水泥管正确答案：B2．离心泵中Y型泵为( )。

A．单级单吸清水泵B．多级清水泵C．耐腐蚀泵D．油泵正确答案：D3．流体运动时，能量损失的根本原因是由于流体存在着( )。

A．压力B．动能C．湍流D．粘性正确答案：D4．下列物系中，不可以用旋风分离器加以分离的是( )。

A．悬浮液B．含尘气体C．酒精水溶液D．乳浊液正确答案：C5．下列四种不同的对流给热过程：空气自然对流α1，空气强制对流α2（流速为3m/s）,水强制对流α3（流速为3 m/s），水蒸汽冷凝α4。

α值的大小关系为( )。

A．α3>α4>α1 >α2B．α4>α3>α2>α1C．α4>α2>α1>α3D．α3>α2>α1>α4正确答案：B6．对于间壁式换热器，流体的流动速度增加，其热交换能力将( )。

A．减小B．不变C．增加D．不能确定正确答案：C7．料液随浓度和温度变化较大时，若采用多效蒸发，则需采用( )。

A．并流加料流程B．逆流加料流程C．平流加料流程D．以上都可采用正确答案：B8．精馏塔塔底产品纯度下降，可能是( )。

A．提馏段板数不足B．精馏段板数不足C．再沸器热量过多D．塔釜温度升高正确答案：A9．在精馏塔操作中，若出现塔釜温度及压力不稳时，产生的原因可能是( )。

A．蒸汽压力不稳定B．疏水器不畅通C．加热器有泄漏D．以上三种原因正确答案：D10．在吸收操作中，当吸收剂用量趋于最小用量时，为完成一定的任务，则( )。

A．回收率趋向最高B．吸收推动力趋向最大C．总费用最低D．填料层高度趋向无穷大正确答案：D11．吸收塔内，不同截面处吸收速率( )。

工程测量测验试卷3

l s 90 l s2 ls l s3 l s p q m，缓和曲线长 = 100 m，计算曲线测设元素及主点里程。( 0 、、 ) R 24R 2 240R 2
（ TH ( R p ) tan

2
q 、 LH R 2 0

180

2l s LY 2l s 、 E H ( R p) sec
D
B
班级
2．如图所示支导线，AB 边的坐标方位角为 AB 125 30'30' ' ，转折角如图，则 CD 边的坐第 2 页共 6 页

2011～2012 学年第二学期《公路工程测量》模块考核试卷
标方位角

CD 为（
） B ． 15 30'30' '

A ． 75 30'30' ' D． 25 29'30' '
AB 312°00′54″， S AB 105.22，则△X，△Y 分别为（
）。
A 36.4m B 36.6m C 37.4m D 37.6m 4.已知水准点 A 的高程为 8.500m，要测设高程为 8.350m 的 B 点，若在 A、B 两点间，架设仪器后视 A 点的读数为 1.050m，则视线高和前视 B 点的读数应为（）； A) 9.400m ；0.900m B) 9.400m ；1.200m C) 9.550m ；0.900 D) 9.550m ；1.200m 5. 按照二分之一的基本等高距加密等高线是指（）。 A) 首曲线 B) 间曲线 C) 计曲线 D) 助曲线 6、测量地物、地貌特征点并进行绘图的工作通常称为（）。 A 控制测量 B 水准测量 C 导线测量 D 碎部测量 7、等高距是两相邻等高线之间的（）。 A、高程之差； B、平距； C、间距 D、斜距 8、在比例尺为 1：2000，等高距为 2m 的地形图上，如果按照指定坡度 i 5 ％，从坡脚到坡顶 B 来选择路线，其通过相邻等高线时在图上的长度为（） A． 10mm B． 20mm C． 25mm D．30mm 9、两不同高程的点，其坡度应为两点（）之比，再乘以 100％。 A．高差与其水平距离； B．高差与其斜距； C．平距与其斜距 D．斜距与其高差 10. 一组闭合的等高线是山丘还是盆地，可根据（）来判断。 A. 助曲线； B. 首曲线； C. 高程注记 D.等高距 11.公路中线里程桩测设时，短链是指（）。 A 实际里程大于原桩号 B 实际里程小于原桩号 C 原桩号测错 D 实际里程等于原里程 12.路线中平测量的观测顺序是（）。 A 沿路线前进方向按先后顺序观测 B 先观测中桩点，后观测转点 C 先观测水准点，后观测转点，再观测中桩点 D 先观测转点，后观测中桩点 13.横断面的绘图顺序是从图纸的（）依次按桩号绘制。 A 左上方自上而下，由左向右 C 左下方自下而上，由左向右 B 右上方自上而下，由右向左 D 右下方自下而上，由右向左第 3 页共 6 页公高 1136

考研数学三N维向量-试卷3_真题(含答案与解析)-交互

考研数学三（N维向量）-试卷3(总分54, 做题时间90分钟)1. 选择题选择题下列每题给出的四个选项中，只有一个选项符合题目要求。

1.下列向量组α1，α2，…，α3中，线性无关的是SSS_SINGLE_SELA (1，2，3，4)，(4，3，2，1)，(0，0，0，0)．B (a，b，c)，(b，c，d)，(c，d，e)，(d，e，f)．C (a，l，b，0，0)，(c，0，d，2，3)，(e，4，f，5，6)．D (a，1，2，3)，(b，1，2，3)，(c，4，2，3)，(d，0，0，0)．分值: 2答案:C解析：有零向量的向量组肯定线性相关，任意n+1个n维向量必线性相关．因此(A)，(B)均线性相关．对于(D)，若d=0，肯定线性相关；若d≠0，则 (a，1，2，3)-(b，1，2，3)= (d，0，0，0)，即α1，α2，α4线性相关，而线性相关的向量组再增加向量肯定仍是线性相关，因此不论哪种情况，(D)是线性相关的．由排除法可知(C)入选．另一方面，若能观察出β1=(1，0，0)，β2 =(0，2，3)，β3=(4，5，6)所构成的行列式则可知β1，β2，β3线性无关，而α1，α2，α3是其延伸组，即不论如何扩充均线性无关，故选(C)．2.已知向量组α1，α2，α3，α4线性无关，则命题正确的是SSS_SINGLE_SEL Aα1+α2，α2+α3，α3+α4，α4+α1线性无关．Bα1 -α2，α2-α3，α3-α4，α4-α1线性无关．Cα1+α2，α2+α3，α3-α4，α4-α1线性无关．Dα1+α2，α2-α3，α3-α4，α4-α1线性无关．分值: 2答案:D解析：由观察法可知(α1+α2)-(α2+α3)+(α3+α4)-(α4+α1 )=0，即(A)线性相关．对于(B)，(α1-α2)+(α2-α3)+(α3-α4)+(α4-α1)=0，即(B)线性相关．而(C)中，(α1+α2)-(α2+α3)+(α3-α4)+(α4-α1)=0，即(C)线性相关．由排除法可知(D)正确．作为复习并掌握基本方法，请读者直接证明(D)线性无关.3.设α1，α2，…，αs是n维向量，则下列命题中正确的是SSS_SINGLE_SELA如αs 不能用α1，α2，…，αs-1线性表出，则α1，α2，…，αs线性无关．B如α1，α2，…，αs线性相关，αs不能由α1，α2，…，αs-1线性表出，则α1，α2，…，αs-1线性相关．C如α1，α2，…，αs中，任意s-1个向量都线性无关，则α1，α2，…，αs线性无关．D零向量0不能用α1，α2，…，αs线性表出．分值: 2答案:B解析：(A)，(C)，(D)均错，仅(B)正确． (A)中当αs 不能用α1，α2，…，αs-1线性表出时，并不保证每一个向量αi(i=1，2，…，s-1)都不能用其余的向量线性表出．例如，α1 =(1，0)，α2=(2，0)，α3=(0，3)，虽α3不能用α1，α2线性表出，但2α1-α2+0α3=0，α1，α2，α3是线性相关的． (C)如α1，α2，…，αs线性无关，可知它的任何一个部分组均线性无关．但任一部分组线性无关并不能保证该向量组线性无关．例如 e1 =(1，0，0，…，0)，e2=(0，1，0，…，0)，…，en=(0，0，0，…，1)，α=(1，1，1，…，1)，其中任意n个都是线性无关的，但这n+1个向量是线性相关的． (D)在线性表出的定义中，对组合系数没有任何约束条件，因此，零向量可以用任何向量组线性表出，最多组合系数全取为0，即0=0α1+0α2，+ 0s．其实，零向量0用α1，α2，…，αs 表示时，如果组合系数可以不全为0，则表明α1，α2，…，αs是线性相关的，否则线性无关．关于(B)，由于α1，α2，…，αs线性相关，故存在不全为0的ki (i=1，2，…，s)，使 k1α1+k2α2+…+ksαs =0．显然，ka=0(否则αs可由α1，…，αs-1线性表出)，因此α1，α2，…，αs-1线性相关．4.设向量组Ⅰ：α1，α2，…，αr可由向量组Ⅱ：β1，β2，…，βs线性表出，则下列命题正确的是SSS_SINGLE_SELA 若向量组Ⅰ线性无关，则ar≤s．B 若向量组Ⅰ线性相关，则r＞s．C 若向量组Ⅱ线性无关，则r≤s．D 若向量组Ⅱ线性相关，则r＞s．分值: 2答案:A解析：因为Ⅰ可由Ⅱ线性表出，故r(Ⅰ)≤r(Ⅱ)．当向量组Ⅰ线性无关时，有r(Ⅰ)=r(α1，α2，…，αr)=r．由向量组秩的概念自然有r(Ⅱ)=r(β1，β2，…，βs)≤s．从而(A)正确．若α1= ，可见(B)、(D)均不正确．若α1= ，可知(C)．不正确．2. 填空题1.已知向量组α1 =(1，2，-1，1) T，α2=(2，0，a，0) T，α3=(0，-4，5，1-a) T的秩为2，则a=______．SSS_FILL分值: 2答案:正确答案：3解析：根据三秩相等定理及经初等变换秩不变定理，对(α1，α2，α3)作初等变换，有所以a=3．2.若α1 =(1，0，5，2) T，α2=(3，-2，3，-4) T，α3=(-1，1，t，3) T线性相关，则t=______.SSS_FILL分值: 2答案:正确答案：1解析：α1，α2，α3线性相关的充要条件是齐次方程组x1α1+x2α2 +x3α3=0有非零解．对系数矩阵高斯消元，化为阶梯形，于是有因为齐次方程组有三个未知数，它若有非零解则阶梯形方程组中方程个数必不大于2，故知t=1．3.若α1 =(1，-1，2，4) T，α2=(0，3，1，2) T，α3=(3，0，7，a)T，α4=(1，-2，2，0) T线性无关，则a的取值范围为________．SSS_FILL分值: 2答案:正确答案：a≠14解析：n个n维向量α1，α2，…，αn线性无关｜α1，α2，…，αn｜≠0．因为所以a≠14．4.若β=(1，2，t) T可由α1 =(2，1，1) T，α2=(-1，2，7) T，α3=(1，-1，-4) T线性表出，则t=_______.SSS_FILL分值: 2答案:正确答案：5解析：β可以由向量组α1，α2，α3线性表出的充要条件是线性方程组x1α1+x2α2+x3α3=β有解．对增广矩阵高斯消元，化为阶梯形，即5.设α1 =(1，2，1) T，α2=(2，3，a) T，α3=(1，a+2，-2) T，若β1=(1，3，4) T可以由α1，α2，α3线性表出，β2=(0，1，2) T不能由α1，α2，α3线性表出，则a=_____.SSS_FILL分值: 2答案:正确答案：-1解析：依题意，方程组x1α1+x2α2+x3α3=β1有解，而方程组x1α1 +x2α2+x3α3=β2无解.因为两个方程组的系数矩阵相同，故可合并一次加减消元，即可见a=-1时，方程组x1α1+x2α2+x3α3=β1有解，而x1α1+x2α2+x3α3=β2无解，故a=-1.3. 解答题解答题解答应写出文字说明、证明过程或演算步骤。

数据结构(第二版) 模拟试题自测卷AB卷带答案3

试卷B一、选择题（本题共20分,每题2分）1．在数据结构中，从逻辑上可以把数据结构分成（）。

A ．动态结构和静态结构 B. 线性结构和非线性结构 C. 紧凑结构和非紧凑结构 D. 内部结构和外部结构 2. 下列程序段的时间复杂度是（）count=0;for(k=1;k<=n;k*=2) for(j=1;j<=n;j++) count++;A.O(nlog2n)B.O(n)C.O(log2n)D.O(n2) 3. 以下描述错误的是：（）A. 线性表是n 个数据元素的有限非空集合。

B. 栈和队列都是操作受限的线性表。

C. 串（或字符串）是由零个或多个字符组成的有限序列。

D. 非空栈中的栈顶指针top 始终指向栈顶元素的下一个位置。

4. 若采用少用一个队列空间的方法来区分队满队空两种状态，则判定一个顺序循环队列 Q （最大队列长度MAXSIZE ）为满队列的条件是( )。

A. Q.front=Q.rearB. Q.front!=Q.rearC. Q.front=(Q.rear+1) % MAXSIZED. Q.front!=(Q.rear+1) % MAXSIZE 5. 按照二叉树的定义，具有 3 个结点的二叉树有（）种。

A. 3 B. 4 C. 5 D. 66. 设矩阵A （如下图所示）是一个对称矩阵，为了节省存储，将其下三角（包括对角线）部分按行序存放在一维数组 B[n(n+1)/2]中，对下三角部分中任一元素 ai,j(i ≥j)，在一维数组 B 的下标位置k 的值是（）。

A. i(i-1)/2+j-1 B. i(i-1)/2+j C. i(i+1)/2+j-1 D. i(i+1)/2+j0,01,01,11,01,11,1...............n n n n a a a A a a a ----⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦7. 有一个有序表为｛5, 18，23, 33, 42, 54,56,78｝，当折半查找56时，经过（）次比较后查找成功。

人教版2022——2023学年小学三年级下册数学期末专项提升模拟试卷AB卷(含答案)

【人教版】2022-2023学年小学三年级下册数学期末专项提升模拟试卷（A 卷）一、选一选1．下面的算式中，得数小于2400的是（）。

A ．7842⨯B ．5325⨯C ．4962⨯2．小明从学校出来往西走300米，再往北走100米，就到了家，小明家在学校的（）。

A ．东南方B ．南方C ．西3．2088年的季度有()天．A ．89B ．90C ．914．9□×6□的积是()位数．A ．三B ．四C ．三或四5．正方形的边长4米，它的周长与面积（）。

A ．周长＞面积B ．周长＜面积C ．无法比较D ．周长＝面积6．从红、黄、白、绿、黑五个颜色球中，任意选出两个球装进纸箱中，至多可有（）种没有重复的方法。

A ．12B ．11C ．10D ．87．学校食堂运来84千克大米，吃了6天正好吃完。

用84÷6计算的是（）。

A ．平均每天吃多少千克B ．还剩多少千克C ．5天吃多少千克8．“0.6元6角”,比较大小,在○里应填的符号是（）A．＞B．＜C．=D．÷二、填空题9．69□÷3的商是()位数，如果商的个位是0，□里可以填()。

时，他先算________，再在积的末尾添写________个0，积是________。

10．小明在口算154011．早晨，你面对太阳时，你的后面是()面，右面是()面。

12．红红买一条毛巾花了19.4元，丽丽买一条毛巾花了7.8元，红红买的毛巾比丽丽贵()元，她们买毛巾一共花了()元。

13．周长是48分米的正方形，如果它的边长扩大到原来的2倍，那么它的周长是()分米，面积是()平方分米。

14．今年7月1日是中国100周岁生日，这个月在()季度，这个月共有()星期零()天。

15．一个周长是8分米的正方形，如果它的边长扩大到原来的3倍，那么它的周长变成()分米，面积变成()平方分米。

16．计算42－36÷6时，应先算()法，计算结果是()；计算（42－36）÷6时，应先算()法，计算结果是()。

化工基础期末试卷3(含答案)

word 格式-可编辑-感谢下载支持太原师范学院2008-2009学年第一学期期末考试化工基础试卷（A ）题号一二三四五六总分分数核分人签字一、填空题(每空1分，共25分。

将正确答案写在横线上)1.气体的粘度值随温度的升高而；液体的粘度值随温度的升高而。

2.用常压蒸馏塔的塔底重油加热原油。

重油的初始温度为300 ℃，最终温度为220 ℃；原油的初始温度为25 ℃，最终温度为180 ℃。

若采用并流操作，其平均温差：△t m = ℃；若采用逆流操作，其平均温差：△t m ′= ℃。

由上述计算结果可以看出：当热交换双方流体无相变，且进、出口温度不变时，采用操作的传热平均温差比操作的传热平均温差大，对热交换有利。

3. 在计算摩擦阻力时，若流体作层流，摩擦系数λ与相对粗糙度__________，与雷诺数之间的关系为，λ＝_______。

4.流体在管道中流动。

层流时，其平均流速等于管道中心最大流速的倍；湍流时，则约为倍。

5.流体流动的连续性方程u 1A 1=u 2A 2适用于的流体，它是原理在化学工程中的应用。

6.在右图中,不同位置的q 线表示不同的进料状态,ef 2线表示进料为 , ef 4线表示进料为。

7.对于连续精馏过程,若回流比增大,则在y-x 图上所标绘的精馏段操作线的斜率 ,所需理论塔板数。

在全回流时,所需理论塔板数。

8.雷诺数Re 是流体流动的判据。

流体在管道中流动，当Re 时为稳定层流；当Re 时，可以形成湍流。

9.同一容器中有A,B,C 三点，B 点的压强为1atm ，且P A >P B >P C ，若B 点的压强增加0.6atm ，则P A 增加_______Pa ，P A -P C 增加__________mmHg 。

10.某连续精馏塔中，若精馏段操作线的截距为零，则馏出液流量为_________。

11.实验证明，流体在管路中流动时，同一截面上各点的流速是不同的，管心处流速__________，管壁处等于__________。

备战2023年北京市中考数学全真模拟试卷三(解析版)

备战2023年北京市中考数学全真模拟试卷三（满分100分，考试用时120分钟）一、选择题（本大题共8小题，每小题2分，共16分）1．用3个同样的小正方体摆出的几何体，从三个方向看到的图形分别如图，这个几何体是（）A．B．C．D．【答案】B【详解】解：根据题意得，小正方体摆出的几何体为：，故选：B．2．北斗卫星导航系统是我国着眼于经济社会发展需要，自主建设、独立运行的卫星导航系统，属于国家重要空间基础设施．截至2022年3月，北斗高精度时空服务覆盖全球百余个国家和地区，累计服务超11亿人口，请将11亿用科学记数法表示为（）A．1.1×108B．1.1×109C．1.1×1010D．1.1×1011【答案】B【详解】解：11亿9=．=⨯00110000000 1.11故选：B．3．如图，在△ABC中，∠1是它的一个外角，E为边AC上一点，延长BC到D，连接DE．则下列结论正确的是（）A．∠1＞∠D B．∠D＞∠2C．∠1＝∠2＋∠3D．∠3＝∠A【详解】解：A．∵∠1是△ABC的外角，∴∠1＞∠2，∵∠2是△DEC的外角，∴∠2＞∠D，∴∠1＞∠D，故选项A正确；B．∵∠2是△DEC的外角，∴∠2＞∠D，故选项B不正确；C．延长DE交AB于G，∴∠3=∠AEG，∵∠1＝∠2+∠A＝∠D+∠3+∠A，∠2+∠3＝∠D+∠3+∠3＝2∠3+∠D，当AG=EG时，∠A=∠AEG=∠3，此时∠1=∠2+∠3，当AG≠EG时，∠A≠∠AEG=∠3，∴∠1≠∠2+∠3∴∠1和∠2+∠3不一定相等，故选项C不不正确；D．由C可得∠3和∠A不一定相等，故选项D不不正确；故选：A．4．下列图形中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．【详解】解：A 、不是轴对称图形，是中心对称图形，故A 选项不合题意； B 、是轴对称图形，不是中心对称图形，故B 选项不符合题意； C 、既不是轴对称图形，也不是中心对称图形，故C 选项不合题意； D 、既是轴对称图形，又是中心对称图形，故D 选项合题意．故选：D ．5．一个多边形的内角和是它的外角和的2倍，那么这个多边形的边数是（） A ．3 B ．4C ．5D ．6【答案】D【详解】解：设这个多边形是n 边形，根据题意得，()21802360n −⋅︒=⨯︒，解得6n =．故选：D ．6．实数a 在数轴上的对应点的位置如图所示，若实数b 满足0a b +>，则b 的值可以是（）A ．－2B ．－1C ．1D ．2【答案】D【详解】解∶根据题意得∶21a −<<−， ∴1a >， ∵0a b +>，∴0b >，且1b a >>， ∴1b a >−>， ∴b 的值可以是2．故选：D7．不透明的袋子中有三个小球，上面分别写着数字“1”，“2”，“3”，除数字外三个小球无其他差别．从中随机摸出一个小球，记录其数字，放回并摇匀，再从中随机摸出一个小球，记录其数字，那么两次记录的数字之和为4的概率是（）A ．14B ．13C ．12D ．23【答案】B【详解】列树状图如下：共有9种等可能的情况，其中两次记录的数字之和为4的有3种，∴P （两次记录的数字之和为4）=3193=，故选：B ．8．线段5AB =，动点P 以每秒1个单位长度的速度从点A 出发，沿线段AB 运动至点B ．以点A 为圆心、线段AP 长为半径作圆心角为90︒的扇形PAC ，以线段PB 为边作等边PBD △．设点P 的运动时间为t ，扇形PAC 的弧CP 的长为y ，等边PBD △的面积为S ，则y 与t ，S 与t 满足的函数关系分别是（）A ．正比例函数关系，一次函数关系B ．正比例函数关系，二次函数关系C ．一次函数关系，一次函数关系D ．二次函数关系，正比例函数关系【答案】B【详解】解：设点P 的运动时间为t ，则AP t =，5BP t =−，则901ππ1802y t t =⨯=，))22252510S t t t =−=−+=， ∴y 与t ，S 与t 满足的函数关系分别是正比例函数关系，二次函数关系，故选：B ．二、填空题（本大题共8小题，每小题2分，共16分） 9．如果分式31x +有意义，那么实数x 的取值范围是______．【答案】x ≠-1【详解】解：∵x +1≠0， ∴x ≠-1．故答案为：x ≠-1．10．设12,x x 分别是一元二次方程2230x x −−=的两个不相等的实数根，则12x x ⋅的值为___________．【答案】3−【详解】解：1x Q ，2x 是一元二次方程2230x x −−=的两个不相等的实数根，∴123x x =−，故答案为：3−．11的整数：________．【答案】2（或3）【详解】解：因为12,34<<<的整数有2，3．故答案为：2（或3）．12．方程组335x y x y −=⎧⎨+=⎩的解为______．【答案】21x y =⎧⎨=−⎩ 【详解】解：335x y x y −=⎧⎨+=⎩①②，①+②得：4x =8，解得x =2．把x =2代入①得：2-y =3，解得y =-1．∴方程组的解是21x y =⎧⎨=−⎩．故答案为：21x y =⎧⎨=−⎩．13．在平面直角坐标系xOy 中，直线y x =−与双曲线my x=交于A ，B 两点．若点A ，B 的纵坐标分别为1y ，2y ，则12y y +的值为______．【答案】0【详解】解：∵正比例函数和反比例函数均关于坐标原点O 对称， ∴正比例函数和反比例函数的交点亦关于坐标原点中心对称， ∵直线y x =−与双曲线my x=交于A 、B 两点， ∴A 、B 两点关于原点对称， ∴120y y +=，故答案为：0．14．如图，点B 、F 、C 、E 在一条直线上，90A D ∠=∠=︒，AB DE =，若用“HL ”判定ABC DEF ≌△△，则添加的一个条件是___________．【答案】BC EF =（答案不唯一）【详解】解：添加条件：BC EF =，在Rt ABC △和Rt DEF △中，AB DEBC EF =⎧⎨=⎩， ∴()Rt Rt HL ABC DEF ≌△△，故答案为：BC EF =（答案不唯一）．15．如图所示的网格是正方形网格，A ，B ，C ，D ，E 是网格线的交点，那么ADE 的面积与ABC V 的面积的比是___________．【答案】14##1:4【详解】解：∵AE ==AC =1AD =，2AB =，∴12AE AC ==，12AD AB =， ∴AE ADAC AB=， ∵A A ∠=∠， ∴ADE ABC △△∽，∴221124ADE ABC S AD S AB ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭△△, 故答案为：1416．我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”（如图）就是一例．这个三角形给出了（a+b ）n （n=1，2，3，4，5，6）的展开式的系数规律．例如，在三角形中第三行的三个数1，2，1，恰好对应（a+b ）2=a 2+2ab+b 2展开式中各项的系数；第四行的四个数1，3，3，1，恰好对应着（a+b ）3=a 3+3a 2b+3ab 2+b 3展开式中各项的系数，等等．有如下四个结论：①（a+b ）5=a 5+5a 4b+10a 3b 2+10a 2b 3+5ab 4+b 5；②当a=-2，b=1时，代数式a 3+3a 2b+3ab 2+b 3的值是-1；③当代数式a 4+4a 3b+6a 2b 2+4ab 3+b 4的值是0时，一定是a=-1，b=1； ④（a+b ）n 的展开式中的各项系数之和为2n ．上述结论中，正确的有______（写出序号即可）．【答案】①②【详解】解：∵在杨辉三角形中第三行的三个数1，2，1，恰好对应222()2a b a ab b +=++展开式中各项的系数；第四行的四个数1，3，3，1，恰好对应着+=+++33223()33a b a a b ab b 展开式中各项的系数，等等∴在杨辉三角形中第n 行的n 个数，对应1()n a b −+展开式中各项的系数，①∵5()a b +展开式中各项的系数，为杨辉三角形中第6行的6个数， ∴554322345()510105a b a a b a b a b ab b +=+++++；②∵322333a a b ab b +++各项系数对应杨辉三角中的第4行的4个数， ∴3223333()a a b ab b a b +++=+，当21a b =−=，时，代数式=3(21)1−+=−；③∵++++432234a 4a b 6a b 4ab b 各项系数对应杨辉三角中的第5行的5个数， ∴4322344464()a a b a b ab b a b ++++=+，当代数式时，0a b +=，不一定是11a b =−=，； ④∵当11a b ==，时，展开式各项之和便是系数之和， ∴()n a b +的展开式中的各项系数之和为(11)=2n n +，故答案为：①②．三、解答题（共68分，第17-20题，每题5分，第21题6分，第22题5分，第23-24题，每题6分，第25题5分，第26题6分，第27-28题，每题7分） 17．（5(2112tan 603−⎛⎫+︒+ ⎪⎝⎭【答案】8(2112tan 603−⎛⎫+︒+ ⎪⎝⎭19=+8=．18．（5分）解不等式组()21581252x x x x ⎧+≤+⎪⎨−−<⎪⎩．【答案】3x ≤<-2【详解】解：()21581252x x x x ⎧+≤+⎪⎨−−<⎪⎩①②，解①得：2x ≥−，解②得：3x <， ∴3x ≤<-2．19．（5分）已知m 是方程23250x x −−=的一个根，求代数式()()()221211m m m +−−+的值．【答案】3【详解】解：由m 是方程23250x x −−=的一个根可得23250m m −−=，即2325m m −=，()()()221211m m m +−−+()221421m m m −−++= 224121m m m −−−−=2322m m =−−将2325m m −=代入，可得原式523=−=20．（5分）下面是小元设计的“作已知角的角平分线”的尺规作图过程．已知：如图，AOB ∠．求作：AOB ∠的角平分线OP ．作法：如图，①在射线OA 上任取点C ； ②作ACD AOB ∠=∠；③以点C 为圆心CO 长为半径画圆，交射线CD 于点P ； ④作射线OP ；所以射线OP 即为所求．根据小元设计的尺规作图过程，完成以下任务． (1)补全图形； (2)完成下面的证明：证明：∵ACD AOB ∠=∠，∴______（______）（填推理的依据）． ∴BOP ∠=______．又∵OC CP =，∴COP CPO ∠=∠（______）（填推理的依据）． ∴COP BOP ∠=∠．∴OP 平分AOB ∠．【答案】(1)见解析(2)CD OB ∥；同位角相等，两直线平行；OPC ∠；等边对等角【详解】（1）解：如图，OP 为所作；（2）证明：∵ACD AOB ∠=∠，∴CD OB ∥（同位角相等，两直线平行）． ∴BOP OPC ∠=∠（两直线平行，内错角相等）．又∵OC CP =，∴COP CPO ∠=∠（等边对等角）． ∴COP BOP ∠=∠． ∴OP 平分AOB ∠．故答案为：CD OB ∥；同位角相等，两直线平行；OPC ∠；等边对等角． 21．（6分）如图，在△ABC 中，AB ＝AC ，D 为BC 中点，AE ∥BD ，且AE ＝BD ．（1）求证：四边形AEBD 是矩形；（2）连接CE 交AB 于点F ，若∠ABE ＝30°，AE ＝2，求EF 的长．【答案】（1）证明见解析；（2．【详解】（1）证明：∵AE ∥BD ，AE ＝BD ， ∴四边形AEBD 是平行四边形， ∵AB ＝AC ，D 为BC 的中点， ∴AD ⊥BC ， ∴∠ADB ＝90°，∴四边形AEBD 是矩形．（2）解：∵四边形AEBD 是矩形， ∴∠AEB ＝90°， ∵∠ABE ＝30°，AE ＝2，∴BE ＝BC ＝4，∴EC ＝ ∵AE ∥BC ， ∴△AEF ∽△BCF ， ∴12EF AE CFBC ，∴EF 13=EC ．22．（5分）在平面直角坐标系xOy 中，反比例函数()10my m x=≠的图象经过点()1,6A −−，一次函数()210y kx k =−≠的图象与y 轴交于点B ． (1)求反比例函数的表达式并直接写出点B 的坐标；(2)当2x >时，对于x 的每一个值，都有12y y <，直接写出k 的取值范围．【答案】(1)反比例函数的表达式为6y x=；()0,1B − (2)2k ≥【详解】（1）解：依题意，把点()1,6A −−，代入()10my m x=≠ 得()()166m =−⨯−=， ∴反比例函数的表达式为6y x=；由()210y kx k =−≠的图象与y 轴交于点B ，令0x =，得1y =−，∴()0,1B −；（2）解：如图，令6y x=中，2x =，解得：3y =，当直线()210y kx k =−≠经过点()2,3时，321k =−解得：2k =，根据函数图象可知，当2k ≥时，当2x >时，对于x 的每一个值，都有12y y <， ∴2k ≥23．（6分）如图，O e 是ABC V 的外接圆，直径BD 与AC 交于点E ，过点D 作O e 的切线，与BC 的延长线交于点F ．(1)求证：F BAC ∠=∠；(2)若DF AC ∥，若8AB =，2CF =，求AC 的长．【答案】(1)见解析(2)AC =【详解】（1）证明：∵DF 是O e 的切线， ∴OD DF ⊥， ∴90ODF ∠=︒，∴90F DBC ∠+∠=︒， ∵BD 是O e 的直径， ∴90BAD ∠=︒， ∴90BAC DAC ∠+∠=︒， ∵DBC DAC ∠=∠， ∴F BAC ∠=∠；（2）解：连接CD ，∵DF AC ∥，90ODF ∠=︒， ∴90BEC ODF ∠=∠=︒， ∴直径BD AC ⊥于E ， ∴12AE CE AC ==， ∴8AB BC ==， ∵BD 是O e 的直径， ∴90BCD ∠=︒， ∴90DBC BDC ∠+∠=︒， ∵90DBC F ∠+∠=︒， ∴BDC F ∠=∠， ∵90BCD FCD ∠=∠=︒， ∴BCD DCF ∽V V ， ∴BC DC DC CF =，即82DCDC =， ∴4DC =，∴BD == ∵在BCD △中，1122BCD S BC CD BD CE ∆=⋅=⋅，∴118422CE ⨯⨯=⨯，∴CE =∴2AC CE ==24．（6分）己知一个二次函数图象上部分点的横坐标x 与纵坐标y 的对应值如下表所示：(1)求m 的值和这个二次函数的表达式；(2)在给定的平面直角坐标系中画出这个二次函数的图象（无需再单独列表）； (3)当14x <≤时，直接写出y 的取值范围．【答案】(1)0m =，()221y x =−− (2)见解析 (3)13y −≤≤【详解】（1）解：∵当0x =和4x =时，3y =；∴抛物线的顶点为2,1，当1x =和3x =时，函数值都是0，即0m =，设这个二次函数的表达式为：()()2210y a x a =−−≠，将()0,3代入得413a −=，解得1a =，∴这个二次函数的表达式为()221y x =−−；（2）解：如图：（3）解：由函数图象得：当14x <≤时，13y −≤≤．25．（5分）某年级共有300名学生，为了解该年级学生A ，B 两门课程的学习情况，从中随机抽取30名学生进行测试，获得了他们的成绩（百分制），并对数据（成绩）进行整理、描述和分析，相关信息如下： α．30名学生A ，B 两门课程成绩统计图：b ．30名学生A ，B 两门课程成绩的平均数如下：根据以上信息，回答下列问题：(1)在这30名学生中，甲同学A 课程成绩接近满分，B 课程成绩没有达到平均分，请在图中用“○”圈出代表甲同学的点；(2)这30名学生A 课程成绩的方差为21s ，B 课程成绩的方差为22s ，直接写出21s ，22s 的大小关系； (3)若该年级学生都参加此次测试，估计A ，B 两门课程成绩都超过平均分的人数．【答案】(1)见解析(2)2212s s <(3)90人【详解】（1）解：如图所示：（2）∵方差体现了某组数据的波动情况，波动越大，方差越大，由a 可知，B 课程成绩的波动大，A 课程成绩的波动小，∴2212s s <；（3）由统计图可知在这30名学生中，A ，B 两门课程成绩都超过平均分的有9人，所以若该年级学生都参加此次测试，估计A ，B 两门课程成绩都超过平均分的人数为93009030⨯=（人）． 26．（6分）在平面直角坐标系xOy 中，点()2,A m −在抛物线()20y ax c a =+>上，抛物线与x 轴有两个交点()1,0B x ，()2,0C x ，其中12x x <．(1)当1,3a m c ==−时，求抛物线的表达式及顶点坐标； (2)点()13,D x n +在抛物线上，若0m n >>，求1x 的取值范围．【答案】(1)21y x =−，()0,1− (2)1312x −<<−【详解】（1）解：当1,3a m c ==−，将点()2,A m −代入得：34c c −=+，解得：1c =−，故抛物线的解析式为：21y x =−，顶点坐标为()0,1−；（2）解：∵()1,0B x ，()2,0C x 是抛物线()20y ax c a =+>与x 轴的两个交点，12x x <，∴21120,ax c x x +==−，∵点()2,A m −在抛物线上，∴()'2,A m 在抛物线上 ∵点()13,D x n +在抛物线上，∴21(3)a x c n ++=，∴21169ax ax a c n +++=，∴169n ax a =+， ∵0n >，∴1690,0ax a a +>>， ∴132x >−，又∵0x >时，y 随x 增大而增大，0m n >>， ∴132x +<， ∴11x <−， ∴1312x −<<−．27．（7分）在ABC ∆中，90ACB AC BC ∠=︒=，，D 是直线AB 上一点（点D 不与点A 、B 重合），连接DC 并延长到E ，使得CE CD =，过点E 作EF BC ⊥，交直线BC 于点F ．(1)如图1，当点D 为线段AB 的上任意一点时，用等式表示线段EF CF AC 、、的数量关系，并证明； (2)如图2，当点D 为线段BA 的延长线上一点时，依题意补全图2，猜想线段EF CF AC 、、的数量关系是否发生改变，并证明．【答案】(1)AC EF FC =+，证明见解析； (2)改变，EF FC AC =+，补图和证明见解析．【详解】（1）解：结论：AC EF FC =+．理由如下：过D 作DH CB ⊥于H ，∵EF CF ⊥于F ， ∴90EFC DHC ︒∠=∠=， ∵,FCE DCH EC DC ∠=∠=， ∴()FEC HDC AAS ≌V V ， ∴,CH FC DH EF ==， ∵90,45DHB B ︒︒∠=∠=， ∴DH HB EF ==，∴AC BC CH BH FC EF ==+=+，即AC EF FC =+（2）解：依题意补全图形．结论：EF FC AC =+．证明：过D 作DH CB ⊥交CB 的延长线于H ，∵EF CF ⊥于F ， ∴90EFC DHC ︒∠=∠=， ∵,FCE DCH EC DC ∠=∠=， ∴()FEC HDC AAS ≌V V ，∴,CH FC DH EF ==，∵90,45DHB B ︒︒∠=∠=， ∴DH HB EF ==，∴EF CH BC FC AC =+=+，即EF FC AC =+．28．（7分）对于平面内三个点P ，A ，B ，给出如下定义：将线段PA 与线段PB 长度的和叫做线段AB 关于点P 的折线距离，记为(,)d P AB ．例如下图中，A ，B ，C 三点共线，2AB =，1BC =，则线段AC 关于点B 的折线距离(,)213d B AC BA BC =+=+=，线段AB 关于点C 的折线距离(,)314d C AB CA CB =+=+=．(1)如图，ABC V 中，AB AC ==90BAC ∠=︒，D 是AB 中点．①(,)d A DC =_______．②P 是线段BC 上动点，确定点P 的位置使得(,)d P AD 的值最小，并求出(,)d P AD 的最小值．(2)ABC V 中，2AB AC ==，过点C 作AC 的垂线l ，点Q 在直线l 上，直接写出(,)d Q AB 的最小值的取值范围．【答案】(1)①(,)d P AD (2)2(,)6d Q AB <<．【详解】（1）解：如图，连接CD ，∵AB AC ==90BAC ∠=︒，D 是AB 中点．∴12AD AB ==∴(,)d A DC AD AC =+==②如图，作A 关于BC 的对称点K ，连接AK 交BC 于T ，连接DK 交BC 于P ，过D 作DM AK ⊥于M ，则AT KT =，AK BC ⊥，AP KP =，∴DM BC ∥， (,)d P AD AP DP DP KP DK =+=+=，此时值最小，∵AB AC ==90BAC ∠=︒， ∴45B C ∠==︒∠，由DM BC ∥可得45ADM B ∠=∠=︒， ∴ADM △，ABT V 都为等腰直角三角形，∵AD =AB =∴22222AM DM DM +==，(222228AT BT AT +===，∴1AM DM ==，2AT BT ==，则2TK =， ∴3MK，∴DK =∴(,)d P AD（2）如图，延长AC 至F ，使2AC FC ==，连接FB 交l 于Q ，而l AC ⊥，则l 是AF 的垂直平分线， ∴AQ FQ =，∴(,)d Q AB QA QB QB QF BF =+=+=，此时(,)d Q AB 最小， ∵2AB AC ==， ∴4AF =，∴AF AB BF AF AB −<<+，即26BF <<， ∴2(,)6d Q AB <<．。

人教版安徽省铜陵市2022——2023学年小学三年级上册期末数学调研试卷AB卷(含答案)

【人教版】安徽省铜陵市2022-2023学年小学三年级上册期末数学调研试卷（A卷）第I卷（选一选）评卷人得分一、选一选1．小丁家、学校、图书馆在迎宾大道的一旁，学校离小丁家230米，图书馆离小丁家480米，学校和图书馆相距（）。

A．250米B．710米C．250米或710米2．箱子里有30个球，其中红球占总数的35，红球有（）个。

A．6B．12C．183．要使345×□的积是一个三位数，□是（）。

A．1B．2C．3D．44．一个长方形的周长是24厘米，恰好能剪成两个完全一样的正方形。

剪成的正方形的边长是（）厘米。

A．6B．4C．85．下面三个图形中，（）的周长最长。

A．B．C．第II卷（非选一选）评卷人得分二、填空题6．4分＝()秒1070米＝()千米()米6000克＝()千克试卷第2页，共4页○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※没有※※要※※在※※装※※订※※线※※内※※答※※题※※3吨－1吨＝()千克8分米＝()毫米56毫米－6毫米＝()厘米7．用分数表示下面各图中的阴影部分。

()()()8．500×6积的末尾有_____个“0”，501×6积的中间有_____个“0”。

9．248的7倍是_____，8个205的和是_____。

10．在括号里填上合适的单位。

①一节课的时间是40()。

②2019铜陵国际半程马拉松比赛路线长约21()。

③小明身高大约是14()。

④一辆小型货车至多载货物5()。

11．在括号里填上“>”“<”或“=”。

13()1527()57121314150++++()121318150⨯⨯⨯⨯5073⨯()3507⨯400秒()6分6吨2000-千克()3吨12．用一根20厘米长的铁丝围成一个正方形，它的边长是()厘米；如果用它围成一个长是7厘米的长方形，这个长方形的宽是()厘米。

2022——2023学年江苏省南通三年级下册数学期末试卷AB卷(含答案)

2022-2023学年江苏省南通三年级下册数学期末试卷（A卷）一、选择题（满分16分）1．从镜子中看图形是下面的图()．A．B．C．2．从一张长9厘米，宽6厘米的长方形纸板上，剪下一个最大的正方形，这个正方形的面积是（）。

A．81cm2B．36cm2C．54cm2D．9cm23．18个鸡蛋大约重1（）．A．克B．米C．千克4．0乘任何数都等于0．（）A．对B．错5．59加上（）个19得1。

A．49B．4C．96．四年级4个班共浇花392盆，平均每个班浇花（）盆。

A．45B．72C．987．两头牛大约重1吨，一头牛大约重（）。

A．50千克B．200千克C．500千克8．280÷2×3＝()，商“2”写在()位数上．A．个位数B．十位数C．百位数二、填空题（满分16分）9．□12÷4要使商是三位数，□里最小填()；要使商是两位数，□里最大填()。

10．“一箱苹果吃去了34”，这是把一箱苹果平均分成了()份，吃去的苹果有这样的()份。

11．○÷9=38……△，△里最大能填()，这时○是()。

12．在括号里填上“平移”或“旋转”。

开关水龙头时水龙头的运动。

()钟面上分针的运动。

()升降机上下的运动。

()自行车车轮的转动。

()国旗的升降。

()13．一个正方形的边长是6厘米，它的面积是()平方厘米。

14．王师傅平均每小时做16个零件，工作12小时做了多少个零件？在括号里填上合适的数。

15．如果A×7＝147，那么A×75＝()。

16．一头猪重l50千克，6头同样大小的猪共重()千克，比l吨少()千克。

三、判断题（满分8分）17．试商时，当余数大于除数，说明商小了。

()18．一根火腿肠的质量为100千克。

()19．火箭升空时所做的运动属于平移现象；陀螺的转动属于旋转现象。

()20．()×70＜4200，括号里最大能填60.()四、图形计算题（满分6分）21．(6分)计算图中阴影部分的面积。

2022——2023学年河北省邢台市小学三年级下学期数学期末调研试卷AB卷(含答案)

2022-2023学年河北省邢台市小学三年级下学期数学期末调研试卷（A卷）一、口算(共8分)1．(本题8分)直接写得数。

970－60＝900×70＝600÷3＝324＋125＝986－244＝4×44＝63×7＝311×6＝二、竖式计算(共12分)2．(本题12分)列竖式计算。

38×24＝45×68＝37×45＝465÷6＝843÷7＝576÷8＝三、脱式计算(共9分)3．(本题9分)脱式计算。

6×8×2419×53－47626＋324÷3四、选择题(共16分)4．(本题2分)学校的南面是操场，那么学校在操场的（）。

A．东面B．北面C．南面5．(本题2分)爸爸早上9时上班，下午5时下班，爸爸每天工作（）小时。

A．8B．12C．4的积最大是（）。

6．(本题2分)□312A．1563B．143C．1116D．337．(本题2分)一张100元可以换成（）张10元。

A．5B．10C．208．(本题2分)在计算□58÷6时，□里填（）时，商是三位数。

A．2B．4C．5D．79．(本题2分)220×5的积有（）个0。

A．1B．2C．310．(本题2分)用9、1、3、0这四个数字组成的最小的四位数是（）。

A．1039B．1093C．139011．(本题2分)王叔叔从南京乘动车回合肥，车票如下图，正点出发，经过1小时14分到达，王叔叔到达合肥的时间是2021年（）。

A．8月30日24：44B．8月31日00：44C．9月1日00：44五、填空题(共21分)12．(本题1分)如图所示，两条平行线的距离为4厘米，在两条平行线之间画一个正方形，那么正方形的面积最大为()平方厘米。

13．(本题1分)小阳6分钟拍球540下，小明5分钟拍球505下，()拍得快。

2020年高考理数全国卷3 试题详解

2020年普通高等学校招生全国统一考试理科数学注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上．2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在本试卷上无效.3．考试结束后，将本试卷和答题卡一并交回.一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{(,)|,,}A x y x y y x =∈≥*N ，{(,)|8}B x y x y =+=，则A B 中元素的个数为（）A.2 B.3C.4D.6【答案】C【解析】∵A B 中的元素满足8y xx y ≥⎧⎨+=⎩，且*,x y N ∈，∴满足8x y +=的有(1,7),(2,6),(3,5),(4,4),∴A B 中元素的个数为4.故选C.2.复数113i-的虚部是（）A.310-B.110-C.110D.310【答案】D 【解析】∵1131313(13)(13)1010i z i i i i +===+--+，∴113z i =-的虚部为310.故选D.3.在一组样本数据中，1，2，3，4出现的频率分别为1234,,,p p p p ，且411i i p ==∑，则下面四种情形中，对应样本的标准差最大的一组是（）A.14230.1,0.4p p p p ====B.14230.4,0.1p p p p ====C.14230.2,0.3p p p p ====D.14230.3,0.2p p p p ====【答案】B【解析】对于A 选项，数据的平均数为()()140.1230.4 2.5A x =+⨯++⨯=，方差为()()()()222221 2.50.12 2.50.43 2.50.44 2.50.10.65A s =-⨯+-⨯+-⨯+-⨯=；对于B 选项，数据的平均数为()()140.4230.1 2.5B x =+⨯++⨯=，方差为()()()()222221 2.50.42 2.50.13 2.50.14 2.50.4 1.85B s =-⨯+-⨯+-⨯+-⨯=；对于C 选项，数据的平均数为()()140.2230.3 2.5C x =+⨯++⨯=，方差为()()()()222221 2.50.22 2.50.33 2.50.34 2.50.2 1.05C s =-⨯+-⨯+-⨯+-⨯=；对于D 选项，该组数据的平均数为()()140.3230.2 2.5D x =+⨯++⨯=，方差为()()()()222221 2.50.32 2.50.23 2.50.24 2.50.3 1.45D s =-⨯+-⨯+-⨯+-⨯=.综上，B 选项这一组的标准差最大.故选B.4.Logistic 模型是常用数学模型之一，可应用于流行病学领城．有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I (t )(t 的单位：天)的Logistic 模型：0.23(53)()=1e t I K t --+，其中K 为最大确诊病例数．当I (*t )=0.95K 时，标志着已初步遏制疫情，则*t 约为（）（ln19≈3）A.60 B.63C.66D.69【答案】C 【解析】()()0.23531t K I t e--=+ ，∴()()0.23530.951t KI t K e **--==+，则()0.235319t e *-=，∴()0.2353ln193t *-=≈，解得353660.23t *≈+≈.故选C.5.设O 为坐标原点，直线2x =与抛物线C ：22(0)y px p =>交于D ，E 两点，若OD OE ⊥，则C 的焦点坐标为（）A.1,04⎛⎫ ⎪⎝⎭B.1,02⎛⎫ ⎪⎝⎭C.(1,0)D.(2,0)【答案】B【解析】∵直线2x =与抛物线22(0)y px p =>交于,E D 两点且OD OE ⊥，根据抛物线的对称性可以确定4DOx EOx π∠=∠=，∴()2,2D ，代入抛物线方程44p =，求得1p =，∴其焦点坐标为1(,0)2，故选B.6.已知向量,a b 满足||5a =，||6b =，6a b ⋅=-，则cos ,=+a a b （）A.3135-B.1935-C.1735D.1935【答案】D【解析】∵5a = ,6b = ,6a b ⋅=-，∴()225619a a b a a b ⋅+=+⋅=-= .∴7a b +=，∴()1919cos ,5735a a b a a b a a b⋅+<+>===⨯⋅+ .故选D.7.在△ABC 中，cos C =23，AC =4，BC =3，则cos B =（）A.19B.13C.12D.23【答案】A【解析】∵在ABC ∆中，2cos 3C =，4AC =，3BC =根据余弦定理2222cos AB AC BC AC BC C=+-⋅⋅2224322433AB =+-⨯⨯⨯,可得29AB =,即3AB =22299161cos 22339AB BC AC B AB BC +-+-===⋅⨯⨯,故1cos 9B =.故选A.8.下图为某几何体的三视图，则该几何体的表面积是（）A.B.C.D.【答案】C【解析】根据三视图特征，在正方体中截取出符合题意的立体图形根据立体图形可得：12222ABC ADC CDB S S S ===⨯⨯=△△△根据勾股定理可得：AD DB ==∴ADB △是边长为根据三角形面积公式可得：211sin 6022ADB S ABAD =⋅⋅︒=⋅△∴该几何体的表面积是632=⨯++ C.9.已知2tan θ–tan(θ+π4)=7，则tan θ=（）A.–2B.–1C.1D.2【答案】D【解析】2tan tan 74πθθ⎛⎫-+= ⎪⎝⎭ ,∴tan 12tan 71tan θθθ+-=-，令tan ,1t t θ=≠，则1271tt t+-=-，整理得2440t t -+=，解得2t =，即tan 2θ=.故选D.10.若直线l 与曲线y 和x 2+y 2=15都相切，则l 的方程为（）A.y =2x +1 B.y =2x +12 C.y =12x +1 D.y =12x +12【答案】D【解析】设直线l 在曲线y =上的切点为(0x ，则00x >，函数y =的导数为y '=，则直线l的斜率k=，设直线l 的方程为)0y x x =-，即00x x -+=，由于直线l与圆2215x y+==，两边平方并整理得2005410x x --=，解得01x =，015x =-（舍），则直线l 的方程为210x y -+=，即1122y x =+.故选D.11.设双曲线C ：22221x y a b-=（a >0，b >0）的左、右焦点分别为F 1，F 2，离心率为5．P 是C 上一点，且F 1P ⊥F 2P ．若△PF 1F 2的面积为4，则a =（）A.1 B.2 C.4 D.8【答案】A【解析】∵5ca=，∴5c a =，根据双曲线的定义可得122PF PF a -=，12121||42PF F PF F S P =⋅=△，即12||8PF PF ⋅=，∵12F P F P ⊥，∴()22212||2PF PF c +=，∴()22121224PF PF PF PF c -+⋅=，即22540a a -+=，解得1a =，故选A.12.已知55<84，134<85．设a =log 53，b =log 85，c =log 138，则（）A.a <b <c B.b <a <c C.b <c <a D.c <a <b 【答案】A【解析】由题意可知a 、b 、()0,1c ∈，58log 3lg3lg8log 5lg5lg5a b ==⋅()22221lg3lg8lg3lg8lg 24122lg5lg 25lg5⎛⎫⎛⎫++⎛⎫<⋅==<⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，∴a b <；由8log 5b =，得85b =，由5458<，得5488b <，∴54b <，可得45b <；由13log 8c =，得138c =，由45138<，得451313c <，∴54c >，可得45c >.综上所述，a b c <<.故选A.二、填空题：本题共4小题，每小题5分，共20分.13.若x ，y 满足约束条件0,201,x y x y x +≥⎧⎪-≥⎨⎪≤⎩，，则z =3x +2y 的最大值为_________．【答案】7【解析】不等式组所表示的可行域如图∵32z x y =+，∴322x z y =-+，易知截距2z越大，则z 越大，平移直线32xy =-，当322x zy =-+经过A 点时截距最大，此时z 最大，由21y x x =⎧⎨=⎩，得12x y =⎧⎨=⎩，(1,2)A ，∴max 31227z =⨯+⨯=.故答案为7.14.262()x x+的展开式中常数项是__________（用数字作答）．【答案】240【解析】 622x x ⎛⎫+ ⎪⎝⎭,其二项式展开通项()62612rrr r C x x T -+⎛⎫⋅⋅ ⎪⎝⎭=1226(2)r r r r x C x --⋅=⋅1236(2)r r r C x -=⋅，令1230r -=得4r =,∴622x x ⎛⎫+ ⎪⎝⎭的展开式中常数项是664422161516240C C ⋅=⋅=⨯=.15.已知圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为_________．【解析】易知半径最大球为圆锥的内切球，球与圆锥内切时的轴截面如图所示，其中2,3BC AB AC ===，且点M 为BC 边上的中点，设内切圆的圆心为O，由于AM =，∴122S =⨯⨯=△ABC 设内切圆半径为r ，则ABC AOB BOC AOCS S S S =++△△△△111222AB r BC r AC r =⨯⨯+⨯⨯+⨯⨯()13322r =⨯++⨯=解得r =，其体积34233V r π==.故答案为3.16.关于函数f （x ）=1sin sin x x+有如下四个命题：①f （x ）的图像关于y 轴对称．②f （x ）的图像关于原点对称．③f （x ）的图像关于直线x =2π对称．④f （x ）的最小值为2．其中所有真命题的序号是__________．【答案】②③【解析】∵152622f π⎛⎫=+= ⎪⎝⎭,152622f π⎛⎫-=--=- ⎪⎝⎭,则66ff ππ⎛⎫⎛⎫-≠ ⎪ ⎪⎝⎭⎝⎭,∴函数()f x 的图象不关于y 轴对称，命题①错误；∵函数()f x 的定义域为{},x x k k Z π≠∈，定义域关于原点对称，()()()()111sin sin sin sin sin sin f x x x x f x x x x ⎛⎫-=-+=--=-+=- ⎪-⎝⎭，∴函数()f x 的图象关于原点对称，命题②正确；11sin cos 22cos sin 2f x x x x x πππ⎛⎫⎛⎫-=-+=+⎪ ⎪⎛⎫⎝⎭⎝⎭- ⎪⎝⎭ ，11sin cos 22cos sin 2f x x x x x πππ⎛⎫⎛⎫+=++=+ ⎪ ⎪⎛⎫⎝⎭⎝⎭+ ⎪⎝⎭，则22f x f x ππ⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭，∴函数()f x 的图象关于直线2x π=对称，命题③正确；∵当0x π-<<时，sin 0x <，则()1sin 02sin f x x x=+<<，命题④错误.∴答案为②③.三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.（一）必考题：共60分.17.设数列{a n }满足a 1=3，134n n a a n +=-．（1）计算a 2，a 3，猜想{a n }的通项公式并加以证明；（2）求数列{2n a n }的前n 项和S n ．【答案】（1）25a =，37a =，21n a n =+，证明见解析；（2）1(21)22n n S n +=-⋅+.【解析】（1）由题意可得2134945a a =-=-=，32381587a a =-=-=，由数列{}n a 的前三项可猜想数列{}n a 是以3为首项，2为公差的等差数列，即21n a n =+，证明如下：当1n =时，13a =成立；假设n k =时，21k a k =+成立.那么1n k =+时，1343(21)4232(1)1k k a a k k k k k +=-=+-=+=++也成立.∴对任意的*n N ∈，都有21n a n =+成立；（2）由（1）可知，2(21)2n nn a n ⋅=+⋅231325272(21)2(21)2n n n S n n -=⨯+⨯+⨯++-⋅++⋅ ，①23412325272(21)2(21)2n n n S n n +=⨯+⨯+⨯++-⋅++⋅ ，②由①-②得()23162222(21)2n n n S n +-=+⨯+++-+⋅ ()21121262(21)212n n n -+-=+⨯-+⋅⨯-1(12)22n n +=-⋅-，即1(21)22n n S n +=-⋅+.18.某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次，整理数据得到下表（单位：天）：锻炼人次空气质量等级[0，200](200，400](400，600]1（优）216252（良）510123（轻度污染）6784（中度污染）72（1）分别估计该市一天的空气质量等级为1，2，3，4的概率；（2）求一天中到该公园锻炼的平均人次的估计值（同一组中的数据用该组区间的中点值为代表）；（3）若某天的空气质量等级为1或2，则称这天“空气质量好”；若某天的空气质量等级为3或4，则称这天“空气质量不好”．根据所给数据，完成下面的2×2列联表，并根据列联表，判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关？人次≤400人次>400空气质量好空气质量不好附：22()()()()()n ad bc K a b c d a c b d -=++++，P (K 2≥k )0.0500.0100.001k3.8416.63510.828【答案】（1）该市一天的空气质量等级分别为1、2、3、4的概率分别为0.43、0.27、0.21、0.09；（2）350；（3）有，理由见解析.【解析】（1）由频数分布表可知，该市一天的空气质量等级为1的概率为216250.43100++=，等级为2的概率为510120.27100++=，等级为3的概率为6780.21100++=，等级为4的概率为7200.09100++=；（2）由频数分布表可知，一天中到该公园锻炼的人次的平均数为100203003550045350100⨯+⨯+⨯=（3）22⨯列联表如下：人次400≤人次400>空气质量不好3337空气质量好228()221003383722 5.820 3.84155457030K ⨯⨯-⨯=≈>⨯⨯⨯，∴有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关.19.如图，在长方体1111ABCD A B C D -中，点,E F 分别在棱11,DD BB 上，且12DE ED =，12BF FB =．（1）证明：点1C 在平面AEF 内；（2）若2AB =，1AD =，13AA =，求二面角1A EF A --的正弦值．【答案】（1）证明见解析；（2）427.【解析】（1）在棱1CC 上取点G ，使得112C G CG =，连接DG 、FG 、1C E 、1C F ，在长方体1111ABCD A B C D -中，//AD BC 且AD BC =，11//BB CC 且11BB CC =，∵112C G CG =，12BF FB =，∴112233CG CC BB BF ===且CG BF =，∴四边形BCGF 为平行四边形，则//AF DG 且AF DG =，同理可证四边形1DEC G 为平行四边形，∴1//C E DG 且1C E DG =，∴1//C E AF 且1C E AF =，则四边形1AEC F 为平行四边形，∴点1C 在平面AEF 内；（2）以点1C 为坐标原点,11C D 、11C B 、1C C 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系1C xyz -，则()2,1,3A 、()12,1,0A 、()2,0,2E 、()0,1,1F ，()0,1,1AE =-- ，()2,0,2AF =-- ，()10,1,2A E =- ，()12,0,1A F =-，设平面AEF 的法向量为()111,,m x y z =，由00m AE m AF ⎧⋅=⎪⎨⋅=⎪⎩，得11110220y z x z --=⎧⎨--=⎩取11z =-，得111x y ==，则()1,1,1m =-，设平面1A EF 的法向量为()222,,n x y z =，由1100n A E n A F ⎧⋅=⎪⎨⋅=⎪⎩，得22222020y z x z -+=⎧⎨-+=⎩，取22z =，得21x =，24y =，则()1,4,2n =，cos ,7m n m n m n⋅<>===⋅，设二面角1A EF A --的平面角为θ，则cos 7θ=，∴sin 7θ==.∴二面角1A EF A --的正弦值为7.20.已知椭圆222:1(05)25x y C m m +=<<的离心率为4，A ，B 分别为C 的左、右顶点．（1）求C 的方程；（2）若点P 在C 上，点Q 在直线6x =上，且||||BP BQ =，BP BQ ⊥，求APQ 的面积．【答案】（1）221612525x y +=；（2）52.【解析】（1） 222:1(05)25x y C mm +=<<,∴5a =，bm =，∴离心率4c ea ====，解得54m =或54m =-(舍)，∴C 的方程为22214255x y ⎛⎫ ⎪⎝⎭+=，即221612525x y +=；（2）不妨设P ,Q 在x 轴上方，点P 在C 上，点Q 在直线6x =上，且||||BP BQ =,BP BQ ⊥，过点P 作x 轴垂线，交点为M ，设6x =与x 轴交点为N 根据题意画出图形，如图∵||||BP BQ =,BP BQ ⊥,90PMB QNB ∠=∠=︒，又 90PBM QBN ∠+∠=︒,90BQN QBN ∠+∠=︒，∴PBM BQN ∠=∠,∴PMB BNQ ≅△△，221612525x y +=，∴(5,0)B ，∴651PM BN ==-=，设P 点为(,)P P x y ，可得P 点纵坐标为1P y =，将其代入221612525x y +=，可得21612525P x +=，解得3P x =或3P x =-，∴P 点为(3,1)或(3,1)-，①当P 点为(3,1)时，532MB =-=，PMB BNQ ≅△△，∴||||2MB NQ ==，∴Q 点为(6,2)，画出图象，如图 (5,0)A -,(6,2)Q ,∴直线AQ 的直线方程211100x y -+=，∴P 到直线AQ的距离为5d ===，∴AQ ==，APQ ∆面积为15252⨯=；②当P 点为(3,1)-时，5+38MB ==，PMB BNQ ≅△△，∴||||8MB NQ ==，∴Q 点为(6,8)，画出图象，如图(5,0)A -,(6,8)Q ，可求得直线AQ 的直线方程为811400x y -+=，∴P 到直线AQ 的距离为：d===，AQ ==，∴APQ ∆面积为522=，综上所述,APQ ∆面积为52.21.设函数3()f x x bx c =++，曲线()y f x =在点(12，f (12))处的切线与y 轴垂直．（1）求b ．（2）若()f x 有一个绝对值不大于1的零点，证明：()f x 所有零点的绝对值都不大于1．【答案】（1）34b =-；（2）证明见解析【解析】（1）因为'2()3f x x b =+，由题意，'1()02f =，即21302b ⎛⎫⨯+= ⎪⎝⎭，则34b =-；（2）由（1）可得33()4f x x x c =-+，'2311()33()()422f x x x x =-=+-，令'()0f x >，得12x >或21x <-；令'()0f x <，得1122x -<<，∴()f x 在11(,22-上单调递减，在1(,)2-∞-，1(,)2+∞上单调递增，且111111(1),(),(,(1)424244f c f c f c f c -=--=+=-=+，若()f x 所有零点中存在一个绝对值大于1的零点0x ，则(1)0f ->或(1)0f <，即14c >或14c <-.当14c >时,111(1)0,()0424f c f c -=->-=+>，111(0,(1)0244f c f c =->=+>又32(4)6434(116)0f c c c c c c -=-++=-<，由零点存在性定理知()f x 在(4,1)c --上存在唯一一个零点0x ，即()f x 在(,1)-∞-上存在唯一一个零点，在(1,)-+∞上不存在零点，此时()f x 不存在绝对值不大于1的零点，与题设矛盾；当14c <-时,111(1)0,()0424f c f c -=-<-=+<，111()0,(1)0244f c f c =-<=+<又32(4)6434(116)0f c c c c c c -=++=->，由零点存在性定理知()f x 在(1,4)c -上存在唯一一个零点0x '，即()f x 在(1,)+∞上存在唯一一个零点，在(,1)-∞上不存在零点，此时()f x 不存在绝对值不大于1的零点，与题设矛盾；综上，()f x 所有零点的绝对值都不大于1.（二）选考题：共10分.请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分.[选修4—4：坐标系与参数方程]（10分）22.在直角坐标系xOy 中，曲线C 的参数方程为22223x t t y t t ⎧=--⎨=-+⎩（t 为参数且t ≠1），C 与坐标轴交于A 、B 两点．2020年全国卷3理数第11页共11页（1）求||AB ；（2）以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，求直线AB 的极坐标方程．【答案】（1）（2）3cos sin 120ρθρθ-+=【解析】（1）令0x =，则220t t +-=，解得2t =-或1t =（舍），则26412y =++=，即(0,12)A .令0y =，则2320t t -+=，解得2t =或1t =（舍），则2244x =--=-，即(4,0)B -.∴AB ==（2）由（1）可知12030(4)AB k -==--，则直线AB 的方程为3(4)y x =+，即3120x y -+=.由cos ,sin x y ρθρθ==可得，直线AB 的极坐标方程为3cos sin 120ρθρθ-+=.[选修4—5：不等式选讲]（10分）23.设a ，b ，c ∈R ，a +b +c =0，abc =1．（1）证明：ab +bc +ca <0；（2）用max{a ，b ，c }表示a ，b ，c 中的最大值，证明：max{a ，b ，c．【答案】（1）证明见解析（2）证明见解析.【解析】（1）2222()2220a b c a b c ab ac bc ++=+++++= ，∴()22212ab bc ca a b c ++=-++.∵1abc =,∴,,a b c 均不为0，∴2220a b c ++>，∴()222210ab bc ca a b c ++=-++<；（2）不妨设max{,,}a b c a =，由0,1a b c abc ++==可知，0,0,0a b c ><<，∵1,a b c a bc =--=，∴()222322224b c b c bc bc bc a a a bc bc bc++++=⋅==≥=.当且仅当b c =时，取等号，∴a ≥max{,,}a b c .。

《材料力学》期末考试试卷AB卷及答案

***学院期末考试试卷考试科目《材料力学》考试成绩试卷类型 A 考试形式闭卷考试对象土木本科一、填空题(总分20分,每题2分)1、杆件在外力作用下,其内部各部分间产生的 ,称为内力。

2、杆件在轴向拉压时强度条件的表达式就是。

3、低碳钢拉伸时,其应力与应变曲线的四个特征阶段为阶段, 阶段, 阶段, 阶段。

4、线应变指的就是的改变,而切应变指的就是的改变。

5、梁截面上弯矩正负号规定,当截面上的弯矩使其所在的微段梁凹向下时为。

6、梁必须满足强度与刚度条件。

在建筑中,起控制做用的一般就是条件。

7、第一与第二强度理论适用于材料,第三与第四强度理论适用于材料。

8、求解组合变形的基本方法就是。

9、力作用于杆端方式的不同,只会使与杆端距离在较小的范围内受到影响,该原理被称为。

10、欧拉公式就是用来计算拉(压)杆的 ,它只适用于杆。

二、单项选择(总分20分,每题2分)1、用截面法可求出图示轴向拉压杆a-a 截面的内力12N P P =-,下面说法正确的就是( ) A 、 N 其实就是应力 B 、 N 就是拉力C 、 N 就是压力D 、 N 的作用线与杆件轴线重合2、构件的强度就是指( )A 、在外力作用下构件抵抗变形的能力B 、在外力作用下构件保持原有平衡态的能力C 、在外力作用下构件抵抗破坏的能力D 、在外力作用下构件保持原有平稳态的能力 3、现有钢、铸铁两种杆材,其直径相同。

从承载能力与经济效益两个方面考虑,图示结构中两种合理选择方案就是( )A 、 1杆为钢,2杆为铸铁B 、 1杆为铸铁,2杆为钢C 、 2杆均为钢D 、 2杆均为铸铁4、从拉压杆轴向伸长(缩短)量的计算公式EANll =∆可以瞧出,E 与A 值越大,l ∆越小,故( )。

A. E 为杆的抗拉(压)刚度。

B 、乘积EA 表示材料抵抗拉伸(压缩)变形的能力。

C. 乘积EA 为杆的抗拉(压)刚度 D 、以上说法都不正确。

统计学基础3套期末考试卷AB试卷模拟测试卷-带答案

统计学基础3套期末考试卷AB试卷模拟测试卷-带答案考试时间：100分钟总分：100分1．下⾯属于品质标志的是（）。

A、⼯⼈年龄B、⼯⼈性别C、⼯⼈⽉⼯资D、⼯⼈体重2．构成统计总体的个别事物称为( )A、调查单位B、总体单位C、调查对象D、填报单位3．2000年11⽉1⽇零点的第五次全国⼈⼝普查是（）A、典型调查B、重点调查C、⼀次性调查D、经常性调查4．⼯⼚对⽣产的⼀批零件进⾏检查，通常采⽤（）A、普查B、抽样调查C、重点调查D、典型调查5．某班的⼈均⽉⽣活费是450元，这个指标是（）A、结构相对指标B、⽐较相对指标C、强度相对指标D、平均指标6．⼀个企业产品销售收⼊计划增长8％，实际增长20％，则计划超额完成程度为（）A、12％B、150％C、111.11％D、11.11％7．时点指标的数值（）A、与其时间间隔长短⽆关B、通常连续登记C、时间间隔越长，指标数值越⼤D、具有可加性8．总体各部分指标数值与总体数值计算求得的结构相对数之和（）A、⼤于100％B、⼩于100％C、等于100％9．统计分组的核⼼问题是（）A、划分各组界限B、选择分组标志C、确定组数D、确定组距10．平均指标反映了（）A、总体次数分布的集中趋势B、总体分布的特征C、总体单位的集中趋势D、总体次数分布的离中趋势11．在抽样推断中应⽤⽐较⼴泛的指标是（）A、全距B、平均差C、标准差D、标准差系数12．抽样调查和重点调查的主要区别是（）A、选取调查单位的⽅式不同B、调查的⽬的不同C、调查的单位不同D、两种调查没有本质区别13．⼈均收⼊，⼈⼝密度，平均寿命，⼈⼝净增数，这四个指标中属于质量指标的有（）。

A、1个B、2个C、3个D、4个14. 已知环⽐增长速度为9.2％、8.6％、7.1％、7.5％，则定基增长速度为（）A 、9.2％×8.6％×7.1％×7.5％B、（9.2％×8.6％×7.1％×7.5％）－100％C、109.2％×108.6％×107.1％×107.5％D、（109.2％×108.6％×107.1％×107.5％）－100％15．累计增长量与其相应的各个逐期增长量的关系表现为（）A、累计增长量等于相应的各个逐期增长量之积B、累计增长量等于相应的各个逐期增长量之和C、累计增长量等于相应的各个逐期增长量之差16．某外商投资企业按⼯资⽔平分为四组：1000元以下，1000~1500元；1500~2000元；2000元以上。

电子技术基础试卷3套期末考试卷AB卷期末测试卷带答案

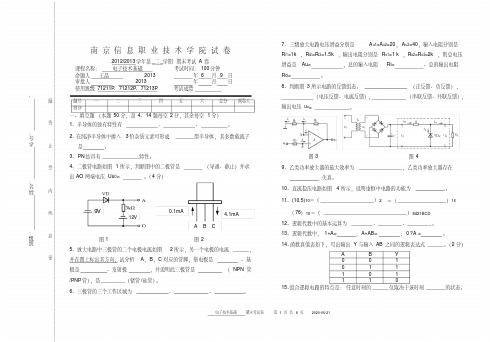
。（ 4 分）
9V
12V
0.1mA
4.1mA ABC
图1
图2
5、放大电路中三极管的二个电极电流如图 2 所示，另一个电极的电流
，
并在图上标出其方向；试分析 A ，B，C 对应的管脚，集电极是
、基
极是
、发射极
，并说明此三极管是
（ NPN 管
/PNP 管），是
（锗管 /硅管）。
6、三极管的三个工作区域为
； A+AB=
； 0 ?A =
。
14、函数真值表如下，写出输出 Y 与输入 AB 之间的逻辑表达式
。（2 分）
A
B
0
0
0
1
1
0
1
1
15、组合逻辑电路的特点是：任意时刻的
Y 1 1 1 0 仅取决于该时刻
的状态。
电子技术基础期末考试卷
第 1 页共 8 页 2020-06-21
16、LED 数码管根据其原理分为
。（4 分）
A
线
0
0
0
封
0 1
1
密
1
1
10、(21.5)10 ＝（
B
C
Y
0
0
1
0
1
0
1
0
0
1
1
1
0
0
0
0
1
0
1
0
0
1
1
1
）2 ＝（
）16
＝（
） 8421BCD（ 3 分）
11、在米利型电路中，输出信号不仅取决于
状态，还取决于
状
态；在摩尔型电路中，输入信号仅取决