川农在线《工程力学》平时作业及答案
(完整版)工程力学课后详细答案
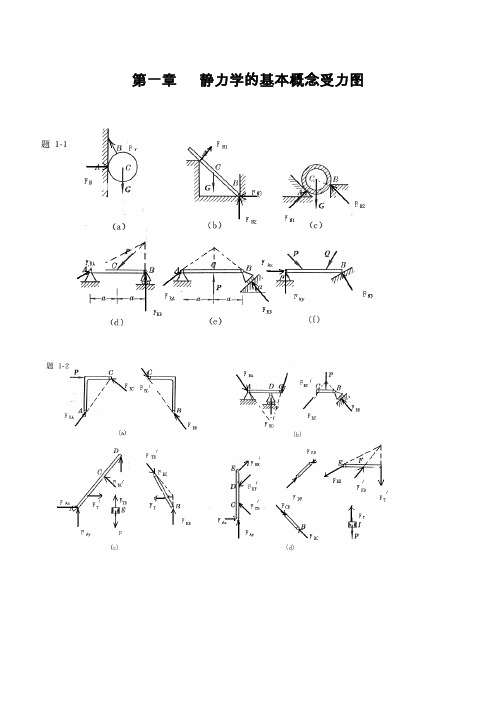
第一章静力学的基本概念受力图第二章 平面汇交力系2-1解:由解析法,23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故:22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==2-2解:即求此力系的合力,沿OB 建立x 坐标,由解析法,有123cos45cos453RX F X P P P KN==++=∑13sin 45sin 450RY F Y P P ==-=∑故: 223R RX RY F F F KN=+= 方向沿OB 。
2-3 解:所有杆件均为二力杆件,受力沿直杆轴线。
(a ) 由平衡方程有:0X =∑sin 300AC AB F F -=0Y =∑cos300AC F W -=0.577AB F W=(拉力)1.155AC F W=(压力)(b ) 由平衡方程有:0X =∑ cos 700AC AB F F -=0Y =∑sin 700AB F W -=1.064AB F W=(拉力)0.364AC F W=(压力)(c ) 由平衡方程有:0X =∑cos 60cos300AC AB F F -=0Y =∑sin 30sin 600AB AC F F W +-=0.5AB F W= (拉力)0.866AC F W=(压力)(d ) 由平衡方程有:0X =∑sin 30sin 300AB AC F F -=0Y =∑cos30cos300AB AC F F W +-=0.577AB F W= (拉力)0.577AC F W= (拉力)2-4 解:(a )受力分析如图所示:由x =∑ 22cos 45042RA F P -=+15.8RA F KN∴=由Y =∑ 22sin 45042RA RB F F P +-=+7.1RB F KN∴=(b)解:受力分析如图所示:由x =∑3cos 45cos 45010RA RB F F P ⋅--=0Y =∑1sin 45sin 45010RA RB F F P ⋅+-=联立上二式,得:22.410RA RB F KN F KN==2-5解:几何法:系统受力如图所示三力汇交于点D ,其封闭的力三角形如图示所以:5RA F KN= (压力)5RB F KN=(与X 轴正向夹150度)2-6解:受力如图所示:已知,1R F G = ,2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2-7解:受力分析如图所示,取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CBRA F F '-=联立后,解得:0.707RA F P=0.707RB F P=由二力平衡定理0.707RB CB CBF F F P '===2-8解:杆AB ,AC 均为二力杆,取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600AB AC F F W +-=联立上二式,解得:7.32AB F KN=-(受压)27.3AC F KN=(受压)2-9解:各处全为柔索约束,故反力全为拉力,以D ,B 点分别列平衡方程(1)取D 点,列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==(2)取B 点列平衡方程:由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解:取B 为研究对象:由0Y =∑sin 0BC F P α-=sin BC PF α∴=取C 为研究对象:由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式,且有BCBC F F '= 解得:2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象:由0Y =∑ cos 0NH CEF F α'-=CECE F F '= 故有:22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解:取A 点平衡:x =∑sin 75sin 750AB AD F F -=0Y =∑cos 75cos 750AB AD F F P +-=联立后可得: 2cos 75AD AB PF F ==取D 点平衡,取如图坐标系:x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD P F F F KN'∴===⋅=2-12解:整体受力交于O 点,列O 点平衡由x =∑cos cos300RA DC F F P α+-=0Y =∑sin sin 300RA F P α-=联立上二式得:2.92RA F KN=1.33DC F KN=(压力)列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得: 1.67AC F KN=(拉力)1.0BC F KN=-(压力)2-13解:(1)取DEH 部分,对H 点列平衡x =∑05RD REF F '= 0Y =∑05RD F Q =联立方程后解得: 5RD F Q =2REF Q '=(2)取ABCE 部分,对C 点列平衡x =∑cos 450RE RA F F -=0Y =∑sin 450RB RA F F P --=且RE REF F '=联立上面各式得: 22RA F Q =2RB F Q P=+(3)取BCE 部分。
工程力学课后习题答案(静力学和材料力学)
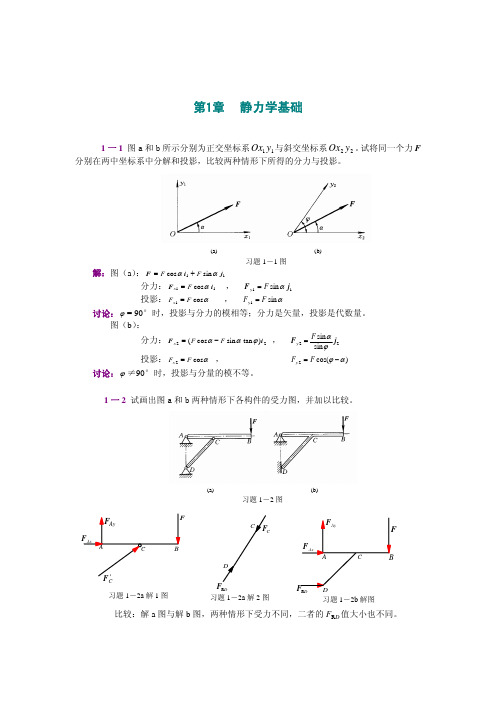
解:图(a):θ = arcsin 4 ,
5
∑ Fx = 0 ,
F sin(60° − θ ) − W sinθ = 0 , F = 1672 N
图(b):θ = 53.13° ,
∑ Fx = 0 , F cos(θ − 30°) − W sinθ = 0 , F = 217N
Fy
x
30D B
Wθ
y
可推出图(b)中 FAB = 10FDB = 100F = 80 kN。
FED αD
FDB FD′ B
FCB
α
B
F 习题 1-12 解 1 图
F AB 习题 1-12 解 2 图
1—13 杆 AB 及其两端滚子的整体重心在 G 点,滚子搁置在倾斜的光滑刚性平面上,如
图所示。对于给定的θ 角,试求平衡时的 β 角。
=
25 kN 6
即
FR
= ( 5 , 10 )kN 23
作用线方程: y = 4 x + 4 3
讨论:本题由于已知数值的特殊性,实际 G 点与 E 点重合。
2-3三个小拖船拖着一条大船,如图所示。每根拖缆的拉力为5kN。试求:(1)作用于大 船上的合力的大小和方向。(2)当A船与大船轴线x的夹角θ为何值时,合力沿大船轴线方向。
投影: Fx1 = F cosα , Fy1 = F sinα
讨论: ϕ = 90°时,投影与分力的模相等;分力是矢量,投影是代数量。
图(b):
分力: Fx2 = (F cosα − F sin α tan ϕ )i2 ,
Fy2
=
F sinα sinϕ
j2
投影: Fx2 = F cosα ,
Fy2 = F cos(ϕ − α )
工程力学课后习题答案解析
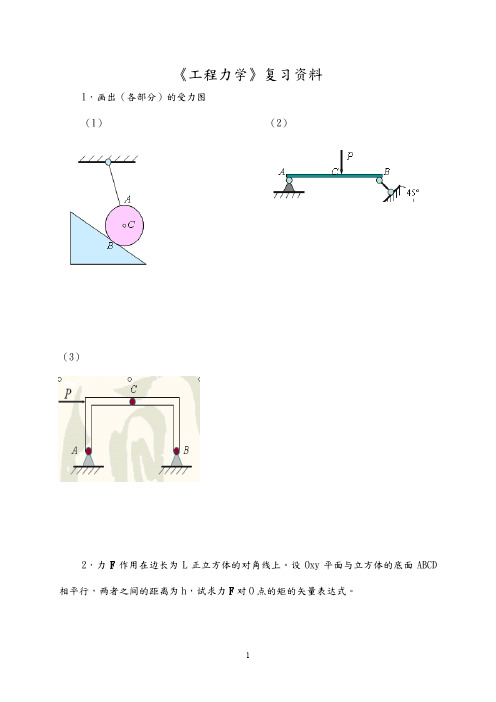
《工程力学》复习资料1.画出(各部分)的受力图(1)(2)(3)2.力F作用在边长为L正立方体的对角线上。
设Oxy平面与立方体的底面ABCD 相平行,两者之间的距离为h,试求力F对O点的矩的矢量表达式。
解:依题意可得:ϕθcos cos ⋅⋅=F F xϕθsin cos ⋅⋅=F F y θsin ⋅=F F z 其中33sin =θ 36cos =θ 45=ϕ 点坐标为:()h l l ,, 则()3)()(3333333j i h l F k F j F i F F M +⋅+=-+-= 3.如图所示力系由F 1,F 2,F 3,F 4和F 5组成,其作用线分别沿六面体棱边。
已知:的F 1=F 3=F 4=F 5=5kN, F 2=10 kN ,OA=OC/2=1.2m 。
试求力系的简化结果。
解:各力向O 点简化 0.0.0.523143=-==-==+-=C O F A O F M C B F A O F M C O F C O F M Z Y X 即主矩的三个分量 kN F F Rx 55==kN F F Ry 102==kN F F F F RZ 5431=+-=即主矢量为: k j i 5105++合力的作用线方程 Z y X ==24.多跨梁如图所示。
已知:q=5kN ,L=2m 。
试求A 、B 、D 处的约束力。
取CD 段0=∑ci M 0212=-⋅ql l F D 解得 kN F D 5=取整体来研究,0=∑iy F02=+⋅-+D B Ay F l q F F 0=∑ix F 0=Ax F0=∑iAM 032=⋅+⋅-⋅l F l ql l F D B 联合以上各式,解得 kN F F Ay A 10-== kN F B 25=5.多跨梁如图所示。
已知:q=5kN ,L=2m ,ψ=30°。
试求A 、C 处的约束力。
(5+5=10分)取BC 段0=∑iy F0cos 2=⋅+⋅-ϕC B F l q F 0=∑ix F 0sin =⋅-ϕC Bx F F0=∑icM 022=⋅⋅+⋅-l l q l F By联合以上各式,解得 kN F Bx 77.5= kN F By 10= kN F C 574.11=取整体研究0=∑ix F0sin =⋅-ϕC Ax F F 0=∑iy F 0cos 2=⋅+⋅-ϕC Ay F l q F0=∑iAM 04cos 32=⋅⋅+⋅⋅-l F l l q M C A ϕ 联合以上各式,解得 kN F Ax 774.5= kN F Ay 10= m kN M A ⋅=406.如图无底的圆柱形容器空筒放在光滑的固定地面上,内放两个重球。
工程力学练习题及参考答案.doc

)一、判断题(正确的在括号中打“√”,错误的在括号中打“×”。
1、加减平衡力系公理一般不适用于一个变形体。
(√)2、合力一定比分力大。
(×)3、物体相对于地球静止时,它一定平衡;物体相对于地球运动时,它一定不平衡。
(×)4、约束力的作用位置在约束与被约数物体的相互接触处。
(√)5、凡是只受到两个力作用的杆件都是二力杆件。
(×)6、汇交力系中各个力的作用点为同一点。
(×)7、力偶矩的单位与力矩的单位是相同的。
(√)8、力偶不能够合成为一个力,也不能用一个力来等效替代。
(√)9、平面一般力系的主矢与简化中心无关。
(√)10、平面力系与其作用面内的两个不同点简化,有可能得到主矩相等,但力系的主矢和主矩都不为零。
(×)11、平面汇交力系中各力在任意轴上投影的代数和分别等于零,则该力系平衡。
(√)12、一个汇交力系如果不是平衡力系,则必然有合力。
(√)13、在应用平面汇交力系的平衡方程解题时,所选取的两个投影轴必须相互垂直。
(×)14、平面力系的平衡方程可以是三个彼此独立的投影式的平衡方程。
(×)15、材料力学的任务是尽可能保证构件的安全工作。
(√)16、作用在刚体上的力偶可以任意平移,而作用在变形固体上的力偶一般不能平移。
(√)17、线应变是构件中单位长度的变形量。
(√)18、若构件无位移,则其内部不会产生内力。
(×)19、用圆截面低碳钢试件做拉伸试验,试件在颈缩处被拉断,断口呈杯锥形。
(√)20、一般情况下,脆性材料的安全系数要比塑性材料取得小些。
(×)21、胡克定律只适用于弹性变形范围内。
(√)22、塑性材料的应力 - 应变曲线中,强化阶段的最高点所对应的应力为强度极限。
(√)23、发生剪切变形的构件都可以称为剪切构件。
(×)24、在剪切构件中,挤压变形也是一个次要的方面。
(×)25、构件的挤压面和剪切面一般是垂直的。
川农在线《工程力学》平时作业及答案

川农在线《工程力学》平时作业及答案计算题(每题25分,共100分)1)锻锤头对工件打击力P=1000kN,偏心距e=20mm,锤头高度h=200mm,试求锤头施加于两侧导轨的压力为多大。
FN1N2F´解:取锤头为研究对象,画受力图根据锤头受力特征:锻击力F与锻件反作用力大小相等、方向向相反F´构成一个力偶,水平受力仅有两个约束力N1和N2 ,因而导轨对锻锤的约束力N1和N2也必构成一力偶与之平衡。
根据平面力偶系平衡充要条件得:∑m=0,F×e-N1×h =0∴N1 = N2 = F×e÷h = 1000×20÷200= 100(kN)2)用重力为G=4kN的扒杆AB起吊重物W=10kN,杆的A点可视为铰链,在B点系有拉绳拉起重物,求在下图所示的位置时的拉力T和A点的反力。
解:对A点取矩得:T*s-G*h-W*L=0其中s为A点到T的距离;h为A到G的距离;L为A到W的距离。
S=AB*sin30=0.5AB h=0.5AB*sin30=0.25ABL=AB*sin30=0.5AB所以T*0.5=G*0.25+W*0.5=1+5=6 ,T=12KN对A点有受力平衡得:Fay=T*sin30+G+W=6+4+10=20KNFax=T*cos30=12*cos30=19.4 KN3)压路机碾子直径500mm,重量为250N。
在拉力作用下越过100mm高的台阶,拉力都沿AB方向,与水平面成30˚。
求拉力。
解:图(a):θ = arcsin , ∑ Fx = 0, F sin (60° ? θ ) ? W sin θ = 0, F = 1672 N 4 5图(b)θ = 53.13°, ∑ Fx = 0, F cos(θ ? 30°) ? W sin θ = 0, F = 217 N4)平面桁架的尺寸和受力如图所示。
工程力学课后习题答案

工程力学课后习题答案工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC 或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)(d)(e)(f)(g)1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)(b)(c)(d)(e)(f)(g)第一章静力学基础 9第二章平面力系2-1 电动机重P=5000N,放在水平梁AC 的中央,如图所示。
梁的A端以铰链固定,另一端以撑杆BC支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A、B处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F F F F FB A y A B x 30sin 30sin ,0030cos 30cos ,0 解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F F P F F FBC y BC AB x解得:P F P F AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
题2-3图以AC 段电线为研究对象,三力汇交N F NF F F F F F FC A GA y C A x 200020110/1tan sin ,0,cos ,0=======∑∑解得:ααα2-4 图示为一拔桩装置。
(完整版)工程力学课后习题答案

工程力学练习册学校学院专业学号教师姓名第一章静力学基础 1第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)2 第一章静力学基础(d)(e)(f)(g)第一章静力学基础 3 1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)4 第一章静力学基础1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)第一章静力学基础 5 (b)(c)(d)6 第一章静力学基础(e)第一章静力学基础7 (f)(g)8 第二章 平面力系第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如第二章 平面力系 9图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
川农《工程力学(II)(材料)》18春平时作业2

(单选题) 1: 确切反映圆轴扭转变形剧烈程度的量是()。
A: 剪应力B: 扭转角C: 扭矩D: 单位扭转角正确答案:(单选题) 2: 集中力作用处的截面剪力()。
A: 大于零B: 小于零C: 等于零D: 不确定正确答案:(单选题) 3: 矩形截面简支梁满跨受均布荷载作用,若将其横截面高度增大一倍,其他条件不变,最大转角是原来的()。
A: 1/2B: 1/4C: 1/8D: 1/16正确答案:(单选题) 4: 由低碳钢组成的细长压杆,经冷作硬化后,其( )。
A: 稳定性提高,强度不变B: 稳定性不变,强度提高C: 稳定性和强度都提高D: 稳定性和强度都不变正确答案:(单选题) 5: 弯曲变形的变形特点是()。
A: 轴线伸长B: 相邻截面相互错动C: 杆件表面纵向线变成螺旋线D: 杆件的轴线由直线变成曲线正确答案:(单选题) 6: 梁的挠度是()。
A: 横截面上任一点沿梁轴垂直方向的线位移B: 横截面形心沿梁轴垂直方向的线位移C: 横截面形心沿梁轴方向的线位移D: 横截面形心的位移正确答案:(单选题) 7: 若将受扭圆轴的横截面面积增加一倍,则该轴的单位扭转角是原来的()倍。
A: 16B: 8C: 1/16D: 1/4正确答案:(单选题) 8: 虎克定律使用的条件是()。
B: σ>σpC: σ<σsD: σ>σs正确答案:(单选题) 9: 压杆临界力的大小()。
A: 与压杆所承受的轴向压力大小有关B: 与压杆的柔度大小有关C: 与压杆的长度大小无关D: 与压杆的柔度大小无关正确答案:(单选题) 10: 根据杆件横截面正应力分析过程,中性轴在什么情形下才会通过截面形心?关于这一问题,有以下四种答案,试分析哪一种是正确的()。
A: My=0或Mz=0,FNx≠0B: My=Mz=0,FNx≠0C: My=0,Mz≠0,FNx≠0D: My≠0或Mz≠0,FNx=0正确答案:(多选题) 1: 下列结论中正确的是()。
奥鹏四川农业大学2020年6月课程考试考试《工程力学(专科)》网考资料及答案.doc
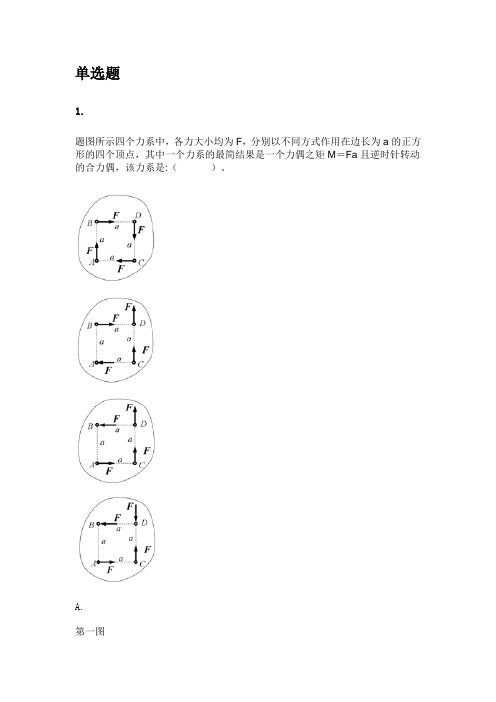
单选题1.题图所示四个力系中,各力大小均为F,分别以不同方式作用在边长为a的正方形的四个顶点,其中一个力系的最简结果是一个力偶之矩M=Fa且逆时针转动的合力偶,该力系是:()。
A.第一图B.第二图C.第三图D.第四图答案: D2.应力是指()。
A.受力物体截面上内力的分力B.受力物体截面上内力分布的集度C.受力物体截面上每一点的内力D.受力物体内部对外力的响应力答案: B3.1A.AB.BC.CD.D答案: D4.1A.AB.BC.CD.D答案: C5.1A.AB.BC.CD.D答案: C6.5.如题图所示,一个重为G的均质圆柱在夹板AB与墙壁AC之间,夹板A端有固定铰链支座与墙壁连接,B端用绳索CB拉住,CB垂直于墙壁,若不计夹板AB的自重和各接触处的摩擦。
从右侧所示的四个受力图(A)、(B)、(C)、(D)中找出题图中AB杆的正确受力图()选项:A.选项图一为AB.选项图二为B C.选项图三为C D.选项图四为D 答案: B7.1A.AB.BC.CD.D答案: C多选题1A.AB.BC.CD.D答案: B, C 2.5A.AB.BC.CD.DE.E答案: C, D, EA.AB.BC.CD.DE.E答案: A, B, C 计算题1.2答案:答案: 3.3答案:答案: 5.5答案: 简答题1.1答案: 2.2答案:。
工程力学课后习题答案

题5-1图
5-2试求图示各杆在1-1、2-2截面上的扭矩。并作出各杆的扭矩图。
题5-2图
5-3在变速箱中,低速轴的直径比高速轴的大,何故?
变速箱中轴传递的扭矩与轴的转速呈反比,低速轴传递的扭矩大,故轴径大。
5-4某传动轴,由电机带动,已知轴的转速 (转/分),电机输入的功率 ,试求作用在轴上的外力偶矩。
以整体为研究对象
以AB杆为研究对象
2-26 图示两无重杆在B处用套筒式无重滑块连接,在AD杆上作用一力偶,其力偶矩MA=40N.m,滑块和AD间的摩擦因数fs=0.3。求保持系统平衡时力偶矩MC的范围。
题2-26图
以AD杆为研究对象
以BC杆为研究对象
当摩擦力反向处于临界平衡态,如b图所示,则
以AD杆为研究对象
题5-9图
题5-9图
5-10图示外伸梁,承受集度为 的均布载荷作用。试问当 为何值时梁内的最大弯矩之值(即 )最小。
题5-10图
为保证梁的最大弯矩值最小,即最大正弯矩等于最大负弯矩
第六章 杆件的应力
6-1图示的杆件,若该杆的横截面面积 ,试计算杆内的最大拉应力与最大压应力。
题6-1图
6-2图示阶梯形圆截面杆,承受轴向载荷 与 作用, 与 段的直径分别为 与 ,如欲使 与 段横截面上的正应力相同,试求载荷 之值。
以BC杆为研究对象
2-27 尖劈顶重装置如图所示。在B块上受力P的作用。A与B块间的摩擦因数为fs(其他 有滚珠处表示光滑)。如不计A和B块的重量,求使系统保持平衡的力F的值。
题2-27图
以整体为研究对象,显然水平和铅直方向约束力分别为
以A滑块为研究对象,分别作出两临界状态的力三角形
工程力学课后习题答案

工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)(d)(e)(f)(g)1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)(b)(c)(d)(e)(f)(g)第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000=== 2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
题2-3图以AC 段电线为研究对象,三力汇交NF N F F F FF F F C A GA yC A x 200020110/1tan sin ,0,cos ,0=======∑∑解得:ααα2-4 图示为一拔桩装置。
工程力学课后习题答案

工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)(d)(e)(f)(g)1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)(b)(c)(d)(e)(f)(g)第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图解得: P F PF AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
题2-3图以AC 段电线为研究对象,三力汇交2-4 图示为一拔桩装置。
在木桩的点A 上系一绳,将绳的另一端固定在点C ,在绳的点B 系另一绳BE ,将它的另一端固定在点E 。
然后在绳的点D 用力向下拉,并使绳BD 段水平,AB 段铅直;DE 段与水平线、CB 段与铅直线成等角α=0.1rad (弧度)(当α很小时,tanα≈α)。
如向下的拉力F=800N ,求绳AB 作用于桩上的拉力。
题2-4图 作BD 两节点的受力图 联合解得:kN F F F A80100tan 2=≈=α 2-5 在四连杆机构ABCD 的铰链B 和C 上分别作用有力F 1和F 2,,机构在图示位置平衡。
工程力学课后习题答案

工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)(d)(e)(f)(g)1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)(b)(c)(d)(e)(f)(g)第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000=== 2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
题2-3图以AC 段电线为研究对象,三力汇交NF N F F F FF F F C A GA yC A x 200020110/1tan sin ,0,cos ,0=======∑∑解得:ααα2-4 图示为一拔桩装置。
工程力学课后习题答案

工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)(d)(e)(f)(g)1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)(b)(c)(d)(e)(f)(g)第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
题2-3图以AC 段电线为研究对象,三力汇交NF N F F F FF F F C A GA yC A x 200020110/1tan sin ,0,cos ,0=======∑∑解得:ααα2-4 图示为一拔桩装置。
《工程力学》课后习题与答案全集

相对运动:滑块E沿斜滑槽作直线运动;
牵连运动:随摇杆 相对于机架作定轴转动。
根据速度合成定理:
式中各参数为:
速度
大小
未知
未知
方向
水平
由图示速度平行四边形可得:
m/s,方向水平相左。
6.L形直OAB以角速度 绕O轴转动, ,OA垂直于AB;通过滑套C推动杆CD沿铅直导槽运动。在图示位置时,∠AOC= ,试求杆CD的速度。
(3).图(c)中动点是L形状的端点A,动系固结于矩形滑块M;
(4).图(d)中动点是脚蹬M,动系固系于自行车车架;
(5).图(e)中动点是滑块上的销钉M,动系固结于L形杆OAB。
(a)
(c)(d)
解:(1)绝对运动:向左做直线运动;相对运动:斜相上方的直线运动;牵连运动:向下直线运动。牵连速度 如图(a)。
5.2解;分别研究重物A与鼓轮,受力与加速度
分析如图,对重物A有:
对轮子有:
其中 ,
,
解得
5.3解:该系统初动能为零,设曲柄转过 角时的角速度为w,则有
式中
解得
对时间求一阶导数且 解得
习题五
4.如图所示机构中,已知均质杆AB长为l,质量为m,滑块A的质量不计。 , 试求当绳子OB突然断了瞬时滑槽的约束力即杆AB的角加速度。
由 , (1)
, (2)
式中 (3)
联立(1)、(2)、(3)可得:
,
第三章点的合成运动
判断题:
1.√;2.×;3.√
习题三
1.指出下述情况中绝对运动、相对运动和牵连运动为何种运动?画出在图示的牵连速度。定系固结于地面;
(1).图(a)中动点是车1,动系固结于车2;
(完整版)工程力学课后详细答案

第一章静力学的基本概念受力图第二章 平面汇交力系2-1解:由解析法,23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故:22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==2-2解:即求此力系的合力,沿OB 建立x 坐标,由解析法,有123cos45cos453RX F X P P P KN==++=∑13sin 45sin 450RY F Y P P ==-=∑故: 223R RX RY F F F KN=+= 方向沿OB 。
2-3 解:所有杆件均为二力杆件,受力沿直杆轴线。
(a ) 由平衡方程有:0X =∑sin 300AC AB F F -=0Y =∑cos300AC F W -=0.577AB F W=(拉力)1.155AC F W=(压力)(b ) 由平衡方程有:0X =∑ cos 700AC AB F F -=0Y =∑sin 700AB F W -=1.064AB F W=(拉力)0.364AC F W=(压力)(c ) 由平衡方程有:0X =∑cos 60cos300AC AB F F -=0Y =∑sin 30sin 600AB AC F F W +-=0.5AB F W= (拉力)0.866AC F W=(压力)(d ) 由平衡方程有:0X =∑sin 30sin 300AB AC F F -=0Y =∑cos30cos300AB AC F F W +-=0.577AB F W= (拉力)0.577AC F W= (拉力)2-4 解:(a )受力分析如图所示:由x =∑ 22cos 45042RA F P -=+15.8RA F KN∴=由Y =∑ 22sin 45042RA RB F F P +-=+7.1RB F KN∴=(b)解:受力分析如图所示:由x =∑3cos 45cos 45010RA RB F F P ⋅--=0Y =∑1sin 45sin 45010RA RB F F P ⋅+-=联立上二式,得:22.410RA RB F KN F KN==2-5解:几何法:系统受力如图所示三力汇交于点D ,其封闭的力三角形如图示所以:5RA F KN= (压力)5RB F KN=(与X 轴正向夹150度)2-6解:受力如图所示:已知,1R F G = ,2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2-7解:受力分析如图所示,取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CBRA F F '-=联立后,解得:0.707RA F P=0.707RB F P=由二力平衡定理0.707RB CB CBF F F P '===2-8解:杆AB ,AC 均为二力杆,取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600AB AC F F W +-=联立上二式,解得:7.32AB F KN=-(受压)27.3AC F KN=(受压)2-9解:各处全为柔索约束,故反力全为拉力,以D ,B 点分别列平衡方程(1)取D 点,列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==(2)取B 点列平衡方程:由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解:取B 为研究对象:由0Y =∑sin 0BC F P α-=sin BC PF α∴=取C 为研究对象:由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式,且有BCBC F F '= 解得:2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象:由0Y =∑ cos 0NH CEF F α'-=CECE F F '= 故有:22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解:取A 点平衡:x =∑sin 75sin 750AB AD F F -=0Y =∑cos 75cos 750AB AD F F P +-=联立后可得: 2cos 75AD AB PF F ==取D 点平衡,取如图坐标系:x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD P F F F KN'∴===⋅=2-12解:整体受力交于O 点,列O 点平衡由x =∑cos cos300RA DC F F P α+-=0Y =∑sin sin 300RA F P α-=联立上二式得:2.92RA F KN=1.33DC F KN=(压力)列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得: 1.67AC F KN=(拉力)1.0BC F KN=-(压力)2-13解:(1)取DEH 部分,对H 点列平衡x =∑05RD REF F '= 0Y =∑05RD F Q =联立方程后解得: 5RD F Q =2REF Q '=(2)取ABCE 部分,对C 点列平衡x =∑cos 450RE RA F F -=0Y =∑sin 450RB RA F F P --=且RE REF F '=联立上面各式得: 22RA F Q =2RB F Q P=+(3)取BCE 部分。
工程力学习题 及最终答案

工程力学习题及最终答案(总63页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第一章 绪论思 考 题1) 现代力学有哪些重要的特征2) 力是物体间的相互作用。
按其是否直接接触如何分类试举例说明。
3) 工程静力学的基本研究内容和主线是什么 4) 试述工程力学研究问题的一般方法。
第二章 刚体静力学基本概念与理论习 题2-1 求图中作用在托架上的合力F R 。
2-2 已知F 1=7kN ,F 2=5kN, 求图中作用在耳环上的合力F R 。
习题2-1图NN22-3 求图中汇交力系的合力F R 。
2-4 求图中力F 2的大小和其方向角?。
使 a )合力F R =, 方向沿x 轴。
b)合力为零。
2-5 二力作用如图,F 1=500N 。
为提起木桩,欲使垂直向上的合力为F R =750N ,且F 2力尽量小,试求力F 2的大小和?角。
2习题2-2图(b )F 1F 1F 2习题2-3图(a )F 1习题2-4图2-6 画出图中各物体的受力图。
F12习题2-5图(b) B(a)A(c)(d)(eA42-7 画出图中各物体的受力图。
) 习题2-6图(b ))(d(a ) A BC DB ABCB52-8 试计算图中各种情况下F 力对o 点之矩。
2-9 求图中力系的合力F R 及其作用位置。
习题2-7图习题2-8图P(d )(c ))) 1F 362-10 求图中作用在梁上的分布载荷的合力F R 及其作用位置。
q 1=600N/m2习题2-9图F 3F 2( c1F 4F 372-11 图示悬臂梁AB 上作用着分布载荷,q 1=400N/m ,q 2=900N/m, 若欲使作用在梁上的合力为零,求尺寸a 、b 的大小。
第三章 静力平衡问题q=4kN/m( b )q( c )习题2-10图B习题2-11图8习 题3-1 图示液压夹紧装置中,油缸活塞直径D=120mm ,压力p =6N/mm 2,若?=30?, 求工件D 所受到的夹紧力F D 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
川农在线《工程力学》平时作业及答案
计算题(每题25分,共100分)
1)锻锤头对工件打击力P=1000kN,偏心距e=20mm,锤头高度h=200mm,试求锤头施加于两侧导轨的压力为多大。
F
N1
N2
F´
解:取锤头为研究对象,画受力图
根据锤头受力特征:锻击力F与锻件反作用力大小相等、方向向相反F´构成一个力偶,水平受力仅有两个约束力N1和N2 ,因而导轨对锻锤的约束力N1和N2也必构成一力偶与之平衡。
根据平面力偶系平衡充要条件得:
∑m=0,F×e-N1×h =0
∴N1 = N2 = F×e÷h = 1000×20÷200= 100(kN)
2)用重力为G=4kN的扒杆AB起吊重物W=10kN,杆的A点可视为铰链,在B点系有拉绳拉起重物,求在下图所示的位置时的拉力T和A点的反力。
解:对A点取矩得:T*s-G*h-W*L=0
其中s为A点到T的距离;h为A到G的距离;L为A到W的距离。
S=AB*sin30=0.5AB h=0.5AB*sin30=0.25AB
L=AB*sin30=0.5AB
所以T*0.5=G*0.25+W*0.5=1+5=6 ,T=12KN
对A点有受力平衡得:Fay=T*sin30+G+W=6+4+10=20KN
Fax=T*cos30=12*cos30=19.4 KN
3)压路机碾子直径500mm,重量为250N。
在拉力作用下越过100mm高的台阶,拉力都沿AB方向,与水平面成30˚。
求拉力。
解:
图(a):θ = arcsin , ∑ Fx = 0, F sin (60° ? θ ) ? W sin θ = 0, F = 1672 N 4 5图(b)θ = 53.13°, ∑ Fx = 0, F cos(θ ? 30°) ? W sin θ = 0, F = 217 N
4)平面桁架的尺寸和受力如图所示。
P=10kN,求1,2,3,4杆所受的力。
解:取截面1——1将1,3,4杆件截断。
由受力分析可知,2号杆是零力杆。
因此F2=0 对整体分析由B点取力
矩平衡得,
Fax=0
Fay*4a=F*3a+F*2a+F*a
Fay=1.5F=15
将截面1-1截出的左边部分作为研究对象,由力的平衡,及A点力矩平衡得:
F3*cos45=Fay-F=5
F3=5根号2=7.07(拉)
F1*a+F3*a+F*a=0
F1=-20 (压力)
F4+F1+F3*cos45=0
F4=15 (拉)。
