东软数据结构实验报告通过栈和队列来实现进制转换
栈和队列的实验报告

栈和队列的实验报告栈和队列的实验报告引言:栈和队列是计算机科学中常用的数据结构,它们在算法设计和程序开发中起着重要的作用。
本实验旨在通过实际操作和观察,深入理解栈和队列的概念、特点以及它们在实际应用中的作用。
一、栈的实验1.1 栈的定义和特点栈是一种具有特殊操作约束的线性数据结构,它的特点是“先进后出”(Last-In-First-Out,LIFO)。
栈的操作包括入栈(push)和出栈(pop),入栈操作将元素放入栈顶,出栈操作将栈顶元素移除。
1.2 实验步骤在本次实验中,我们使用编程语言实现了一个栈的数据结构,并进行了以下实验步骤:1.2.1 创建一个空栈1.2.2 向栈中依次压入若干元素1.2.3 查看栈顶元素1.2.4 弹出栈顶元素1.2.5 再次查看栈顶元素1.3 实验结果通过实验,我们观察到栈的特点:最后入栈的元素最先出栈。
在实验步骤1.2.2中,我们依次压入了元素A、B和C,栈顶元素为C。
在实验步骤1.2.4中,我们弹出了栈顶元素C,此时栈顶元素变为B。
二、队列的实验2.1 队列的定义和特点队列是一种具有特殊操作约束的线性数据结构,它的特点是“先进先出”(First-In-First-Out,FIFO)。
队列的操作包括入队(enqueue)和出队(dequeue),入队操作将元素放入队尾,出队操作将队头元素移除。
2.2 实验步骤在本次实验中,我们使用编程语言实现了一个队列的数据结构,并进行了以下实验步骤:2.2.1 创建一个空队列2.2.2 向队列中依次插入若干元素2.2.3 查看队头元素2.2.4 删除队头元素2.2.5 再次查看队头元素2.3 实验结果通过实验,我们观察到队列的特点:最先入队的元素最先出队。
在实验步骤2.2.2中,我们依次插入了元素X、Y和Z,队头元素为X。
在实验步骤2.2.4中,我们删除了队头元素X,此时队头元素变为Y。
三、栈和队列的应用栈和队列在实际应用中有广泛的应用场景,下面简要介绍一些常见的应用:3.1 栈的应用3.1.1 表达式求值:通过栈可以实现对表达式的求值,如中缀表达式转换为后缀表达式,并计算结果。
数据结构栈和队列实验报告

数据结构栈和队列实验报告实验报告:数据结构栈和队列一、实验目的1.了解栈和队列的基本概念和特点;2.掌握栈和队列的基本操作;3.掌握使用栈和队列解决实际问题的方法。
二、实验内容1.栈的基本操作实现;2.队列的基本操作实现;3.使用栈和队列解决实际问题。
三、实验原理1.栈的定义和特点:栈是一种具有后进先出(LIFO)特性的线性数据结构,不同于线性表,栈只能在表尾进行插入和删除操作,称为入栈和出栈操作。
2.队列的定义和特点:队列是一种具有先进先出(FIFO)特性的线性数据结构,不同于线性表,队列在表头删除元素,在表尾插入元素,称为出队和入队操作。
3.栈的基本操作:a.初始化:建立一个空栈;b.入栈:将元素插入栈的表尾;c.出栈:删除栈表尾的元素,并返回该元素;d.取栈顶元素:返回栈表尾的元素,不删除。
4.队列的基本操作:a.初始化:建立一个空队列;b.入队:将元素插入队列的表尾;c.出队:删除队列表头的元素,并返回该元素;d.取队头元素:返回队列表头的元素,不删除。
四、实验步骤1.栈的实现:a.使用数组定义栈,设置栈的大小和栈顶指针;b.实现栈的初始化、入栈、出栈和取栈顶元素等操作。
2.队列的实现:a.使用数组定义队列,设置队列的大小、队头和队尾指针;b.实现队列的初始化、入队、出队和取队头元素等操作。
3.使用栈解决实际问题:a.以括号匹配问题为例,判断一个表达式中的括号是否匹配;b.使用栈来实现括号匹配,遍历表达式中的每个字符,遇到左括号入栈,遇到右括号时将栈顶元素出栈,并判断左右括号是否匹配。
4.使用队列解决实际问题:a.以模拟银行排队问题为例,实现一个简单的银行排队系统;b.使用队列来模拟银行排队过程,顾客到达银行时入队,处理完业务后出队,每个顾客的业务处理时间可以随机确定。
五、实验结果与分析1.栈和队列的基本操作实现:a.栈和队列的初始化、入栈/队、出栈/队以及取栈顶/队头元素等操作均能正常运行;b.栈和队列的时间复杂度均为O(1),操作效率很高。
数据结构-进制转换实验报告

计算机科学与技术系实验报告专业名称计算机科学与技术课程名称《数据结构》项目名称栈实现进制的转换班级学号姓名同组人员无实验日期一、实验目的与要求:(简述本次实验要求达到的目的,涉及到的相关知识点,实验的具体要求。
)(一)实验目的:应用栈来实现对数据的操作。
掌握,进栈,出栈(二)实验要求:用栈实现对数据进制的转换(三)实验环境:VC++6.0.二、实验内容#include <stdio.h>#include <malloc.h>#define maxlen 100typedef int dataType;typedef struct{dataType data[maxlen];int top;}seqstack;/*置空栈*/seqstack *Initstack(seqstack *S){S->top = -1;return S;}/*初始化栈*/seqstack *setstack(){seqstack *S;S = (seqstack *) malloc (sizeof(seqstack));S->top = -1;return S;}/*判断栈空*/int stackEmpty(seqstack *S){if(S->top<0)return 1;elsereturn 0;}/*判断栈满*/int stackFull(seqstack *S){if(S->top < (maxlen -1) && S->top >= -1) return 0;elsereturn 1;}/*入栈*/void push(seqstack *S, dataType x){if(stackFull(S))printf("此栈已经满\n");else{S->top ++;S->data[S->top] = x;}}/*出栈*/dataType pop(seqstack *S){dataType x;if(stackEmpty(S))printf("此栈为空\n");else{x = S->data[S->top];S->top--;}return x;}void main(){seqstack *S;dataType e;int m,n;S = setstack();printf("请输入一个十进制的数:");scanf("%d", &e);printf("请输入你想转出成的进制:");scanf("%d", &m);while(e){n = e%m;push(S,n);e = e/m;}printf("转换成%d进制为:", m);while(!stackEmpty(S)){e = pop(S);printf("%d",e);}printf("\n");}三、实验分析与小结(实验过程中的问题分析、产生的原因以及解决方法;实验结果分析;有待优化思路)(一)实验结果截图(二)总结通过栈,先进后出的特点,我们可以对数据实现进制的转换。
数据结构实验报告 栈进制转换

数据结构实验报告栈进制转换数据结构实验报告栈进制转换一、实验目的栈是一种常见的数据结构,本实验的目的在于通过实现栈的基本操作,设计并实现一个进制转换的程序,并通过实验验证程序的正确性和效率。
二、实验原理1.栈的定义和基本操作栈是一种后进先出(Last In First Out,简称LIFO)的数据结构。
它可以通过一个指针来标识当前栈顶元素,栈顶指针top的起始值为-1,空栈时top=-1.2.栈的进制转换将一个十进制数转换为其他进制(如二进制、八进制、十六进制)的过程中,可以通过栈来实现。
具体步骤如下:- 初始化一个空栈;- 将十进制数依次除以目标进制的基数,将余数依次入栈,直到商为0;- 依次出栈,将出栈的余数组合起来,得到转换后的目标进制数。
三、实验内容1.实现栈的基本操作(1)定义栈结构,包括元素数组和栈顶指针;(2)实现入栈操作push(),将元素插入到栈顶;(3)实现出栈操作pop(),从栈顶删除一个元素并返回其值;(4)实现获取栈顶元素的操作getTop(),返回栈顶元素的值;(5)实现判断栈是否为空的操作isEmpty(),返回布尔值;(6)实现判断栈是否已满的操作isFull(),返回布尔值。
2.设计并实现进制转换的程序(1)初始化一个空栈用于存放转换后的数字;(2)输入十进制数num和目标进制target;(3)通过栈的操作将num转换为target进制数;(4)输出转换后的结果。
四、实验步骤1.实现栈的基本操作(1)定义栈的结构和相关操作;(2)编写相应的测试代码,验证栈的基本操作是否正确。
2.设计并实现进制转换的程序(1)根据原理部分的步骤,设计转换程序的具体逻辑;(2)编写相应的测试代码,验证转换程序的正确性和效率。
五、实验结果与分析1.给定一个十进制数num=12345,目标进制为二进制(target=2),经过进制转换后得到的结果为.111.2.给定一个十进制数num=456,目标进制为八进制(target=8),经过进制转换后得到的结果为.710.本实验的结果表明,转换程序能够正确地将十进制数转换为目标进制数,并且具有较高的效率。
数据结构栈与队列的实验报告

数据结构栈与队列的实验报告实验概述本次实验的目的是通过对栈和队列进行实现和应用,加深对数据结构中的栈和队列的理解和巩固操作技能。
栈和队列作为常见的数据结构在程序开发中得到了广泛的应用,本次实验通过 C++ 语言编写程序,实现了栈和队列的基本操作,并对两种数据结构进行了应用。
实验内容1. 栈的实现栈是一种先进后出的数据结构,具有后进先出的特点。
通过使用数组来实现栈,实现入栈、出栈、输出栈顶元素和清空栈等操作。
对于入栈操作,将元素插入到数组的栈顶位置;对于出栈操作,先将数组的栈顶元素弹出,再使其下移,即将后面的元素全部向上移动一个位置;输出栈顶元素则直接输出数组的栈顶元素;清空栈则将栈中所有元素全部清除即可。
3. 栈和队列的应用利用栈和队列实现八皇后问题的求解。
八皇后问题,是指在8×8 的国际象棋盘上放置八个皇后,使得任意两个皇后都不能在同一行、同一列或者同一对角线上。
通过使用栈来保存当前八皇后的位置,逐个放置皇后并检查是否有冲突。
如果当前位置符合要求,则将位置保存到栈中,并继续查询下一个皇后的位置。
通过使用队列来进行八数码问题的求解。
八数码问题,是指在3×3 的矩阵中给出 1 至 8 的数字和一个空格,通过移动数字,最终将其变为 1 2 3 4 5 6 7 8 空的排列。
通过使用队列,从初始状态出发,枚举每种情况,利用队列进行广度遍历,逐一枚举状态转移,找到对应的状态后进行更新,周而复始直到找到正确的答案。
实验结果通过使用 C++ 语言编写程序,实现了栈和队列的基本操作,并对八皇后和八数码问题进行了求解。
程序执行结果如下:栈和队列实现的基本操作都能够正常进行,并且运行效率较高。
栈和队列的实现方便了程序编写并加速了程序运行。
2. 八皇后问题的求解通过使用栈来求解八皇后问题,可以得到一组成立的解集。
图中展示了求解某一种八皇后问题的过程。
从左到右是棋盘的列数,从上到下是棋盘的行数,通过栈的操作,求出了在棋盘上符合不同要求(不在同一行、同一列和斜线上)的八皇后位置。
数据结构栈和队列实验报告

数据结构栈和队列实验报告数据结构栈和队列实验报告1.实验目的本实验旨在通过设计栈和队列的数据结构,加深对栈和队列的理解,并通过实际操作进一步掌握它们的基本操作及应用。
2.实验内容2.1 栈的实现在本实验中,我们将使用数组和链表两种方式实现栈。
我们将分别实现栈的初始化、入栈、出栈、判断栈是否为空以及获取栈顶元素等基本操作。
通过对这些操作的实现,我们可将其用于解决实际问题中。
2.2 队列的实现同样地,我们将使用数组和链表两种方式实现队列。
我们将实现队列的初始化、入队、出队、判断队列是否为空以及获取队头元素等基本操作。
通过对这些操作的实现,我们可进一步了解队列的特性,并掌握队列在实际问题中的应用。
3.实验步骤3.1 栈的实现步骤3.1.1 数组实现栈(详细介绍数组实现栈的具体步骤)3.1.2 链表实现栈(详细介绍链表实现栈的具体步骤)3.2 队列的实现步骤3.2.1 数组实现队列(详细介绍数组实现队列的具体步骤)3.2.2 链表实现队列(详细介绍链表实现队列的具体步骤)4.实验结果与分析4.1 栈实验结果分析(分析使用数组和链表实现栈的优缺点,以及实际应用场景)4.2 队列实验结果分析(分析使用数组和链表实现队列的优缺点,以及实际应用场景)5.实验总结通过本次实验,我们深入了解了栈和队列这两种基本的数据结构,并利用它们解决了一些实际问题。
我们通过对数组和链表两种方式的实现,进一步加深了对栈和队列的理解。
通过实验的操作过程,我们也学会了如何设计和实现基本的数据结构,这对我们在日后的学习和工作中都具有重要意义。
6.附件6.1 源代码(附上栈和队列的实现代码)6.2 实验报告相关数据(附上实验过程中所产生的数据)7.法律名词及注释7.1 栈栈指的是一种存储数据的线性数据结构,具有后进先出(LIFO)的特点。
栈的操作主要包括入栈和出栈。
7.2 队列队列指的是一种存储数据的线性数据结构,具有先进先出(FIFO)的特点。
数据结构栈和队列实验报告

3检查一遍已输入的程序是否有错〔包括输入时输错的和编程中的错误〕,如发现有错,及时改正。
4进展编译和连接。如果在编译和连接过程中发现错误,频幕上会出现"报错信息〞,根据提示找到出错位置和原因,加以改正。再进展编译,如此反复直到不出错为止。
5运行程序并分析运行结果是否合理。在运行是要注意当输入不同的数据时所得结果是否正确,应运行屡次,分别检查在不同情况下结果是否正确。
s->ne*t=NULL;
}
void DestroyStack(LiStack *&s)//销毁栈
{LiStack *p=s,*q=s->ne*t;
while (q!=NULL)
{free(p);
p=q;
q=p->ne*t;
}
free(p);//此时p指向尾节点,释放其空间
}
bool StackEmpty(LiStack *s)//判断栈是否为空
printf("栈s的根本运算如下:\n");
printf(" (1)初始化栈s\n");
InitStack(s);
printf(" (2)栈为%s\n",(StackEmpty(s)""空":"非空"));
printf(" (3)依次进栈元素a,b,c,d,e\n");
Push(s,'a');Байду номын сангаас
Push(s,'b');
#include <stdio.h>
#include <malloc.h>
#define Ma*Size 100
SDUT2131数据结构实验之栈与队列一:进制转换
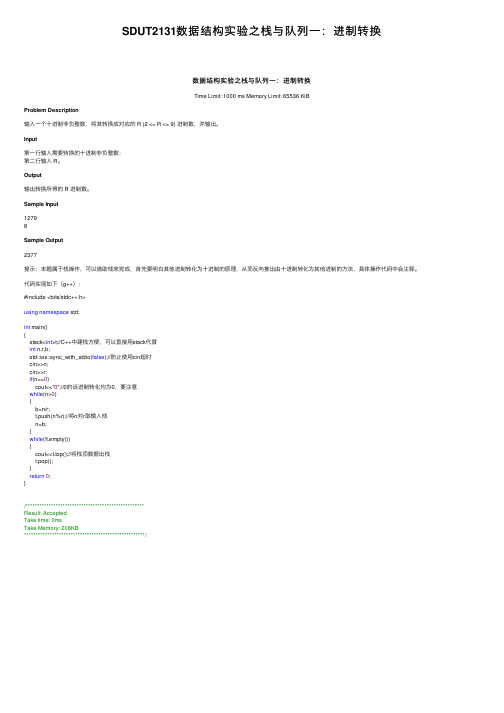
SDUT2131数据结构实验之栈与队列⼀:进制转换数据结构实验之栈与队列⼀:进制转换Time Limit: 1000 ms Memory Limit: 65536 KiBProblem Description输⼊⼀个⼗进制⾮负整数,将其转换成对应的 R (2 <= R <= 9) 进制数,并输出。
Input第⼀⾏输⼊需要转换的⼗进制⾮负整数;第⼆⾏输⼊ R。
Output输出转换所得的 R 进制数。
Sample Input12798Sample Output2377提⽰:本题属于栈操作,可以借助栈来完成,⾸先要明⽩其他进制转化为⼗进制的原理,从⽽反向推出由⼗进制转化为其他进制的⽅法,具体操作代码中会注释。
代码实现如下(g++):#include <bits/stdc++.h>using namespace std;int main(){stack<int>t;//C++中建栈⽅便,可以直接⽤stack代替int n,r,b;std::ios::sync_with_stdio(false);//防⽌使⽤cin超时cin>>n;cin>>r;if(n==0)cout<<"0";//0的话进制转化均为0,要注意while(n>0){b=n/r;t.push(n%r);//将n对r取模⼊栈n=b;}while(!t.empty()){cout<<t.top();//将栈顶数据出栈t.pop();}return0;}/***************************************************Result: AcceptedTake time: 0msTake Memory: 208KB****************************************************/。
数据结构栈和队列实验报告

num=Pop(top);
printf("%d",num);
}
printf("\n");
}
void Push(LinkStack *top,DataType x) /*压栈操作*/
i--;
}
q->rear->next=p;
q->rear=p;
}
void PutQ(LinkQueue *q,int i,int t)
{
int j=t-i-1;
p=q->front->next;
while(j){printf(" ");j--;}
scanf("%d",&t);
top=(LinkStack*)malloc(sizeof(LinkStack));
IniStack(top);
while(num!=0){
Push(top,num%t);
num=num/t;
}
printf("转化后的数为:");
数据结构栈和队列实验报告
(以下写实验内容、分析与程序清单、调试报告等)
一、 实验目的
1.掌握栈这种数据结构特性及其主要存储结构,并能在现实生活中灵活运用。
2.掌握队列这种数据结构特性及其主要存储结构并能在现实生活中灵活运用。
}
}
return 0;
栈与队列实验报告总结

栈与队列实验报告总结实验报告总结:栈与队列一、实验目的本次实验旨在深入理解栈(Stack)和队列(Queue)这两种基本的数据结构,并掌握其基本操作。
通过实验,我们希望提高自身的编程能力和对数据结构的认识。
二、实验内容1.栈的实现:我们首先使用Python语言实现了一个简单的栈。
栈是一种后进先出(LIFO)的数据结构,支持元素的插入和删除操作。
在本次实验中,我们实现了两个基本的栈操作:push(插入元素)和pop(删除元素)。
2.队列的实现:然后,我们实现了一个简单的队列。
队列是一种先进先出(FIFO)的数据结构,支持元素的插入和删除操作。
在本次实验中,我们实现了两个基本的队列操作:enqueue(在队尾插入元素)和dequeue(从队头删除元素)。
3.栈与队列的应用:最后,我们使用所实现的栈和队列来解决一些实际问题。
例如,我们使用栈来实现一个算术表达式的求值,使用队列来实现一个简单的文本行编辑器。
三、实验过程与问题解决在实现栈和队列的过程中,我们遇到了一些问题。
例如,在实现栈的过程中,我们遇到了一个“空栈”的错误。
经过仔细检查,我们发现是因为在创建栈的过程中没有正确初始化栈的元素列表。
通过添加一个简单的初始化函数,我们解决了这个问题。
在实现队列的过程中,我们遇到了一个“队列溢出”的问题。
这是因为在实现队列时,我们没有考虑到队列的容量限制。
通过添加一个检查队列长度的条件语句,我们避免了这个问题。
四、实验总结与反思通过本次实验,我们对栈和队列这两种基本的数据结构有了更深入的理解。
我们掌握了如何使用Python语言实现这两种数据结构,并了解了它们的基本操作和实际应用。
在实现栈和队列的过程中,我们也学到了很多关于编程的技巧和方法。
例如,如何调试代码、如何设计数据结构、如何优化算法等。
这些技巧和方法将对我们今后的学习和工作产生积极的影响。
然而,在实验过程中我们也发现了一些不足之处。
例如,在实现栈和队列时,我们没有考虑到异常处理和性能优化等方面的问题。
数据结构栈与队列的实验报告

s->stacksize=stack_init_size;
return 1;
int Push(sqst->base>=s->stacksize)
{
s->base=(int *)realloc(s->base,(s->stacksize+stackincrement)*sizeof(int));
实验三 栈与队列
一、实验目的:
(1)熟练掌握栈和队列的结构以及这两种数据结构的特点、栈与队列的基 本操作。
(2)能够在两种存储结构上实现栈的基本运算,特别注意栈满和栈空的判 断条件及描述方法;
(3)熟练掌握链队列和循环队列的基本运算,并特别注意队列满和队列空 的判断条件和描述方法;
(4)掌握栈的应用;
if(!s->base)
return 0;
s->top=s->base+s->stacksize;
s->stacksize+=stackincrement;
*(s->top++)=e;
return e;
}
int Pop(sqstack *s,int e)
{
if(s->top==s->base)
return 0;
while(!stackempty(s)) { e=Pop(s,e); switch(e) { case 10: printf("A"); break; case 11: printf("B"); break; case 12: printf("C"); break; case 13: printf("D"); break; case 14: printf("E"); break; case 15: printf("F"); break;
东软数据结构实验报告——通过栈和队列来实现进制转换

实验报告(一)实验过程一、项目简介进制转换通过编写函数实现十进制浮点数到R进制的转换,在十进制浮点数的整数部分利用栈结构实现,小数部分用队列结构实现。
二、项目实施:1.读取数据并获得小数点位置2.将字符串转为整数形式.3.对整数部分进行入栈4.获得小数部分并入队5.整数和小数的联合输出6.源代码:#include <stdio.h>#include <string.h>#include <math.h>#define size 10 //小数部分大小#define maxsize 20 //整数部分大小//*********************************//*********************************//小数部分——队列typedef struct{char data[10]; //读取转制后的小数部分int front,rear; //队首尾指针}Queue; //循环队列//*********************************//初始化队列void init_Queue(Queue* q){q->front=q->rear=0;}//*********************************//入队int push_Queue(Queue *q,int x){if((q->rear+1)%size==q->front) //判断队满{printf("队列满!不允许入队\n");return 0;}else{q->rear=(q->rear+1) % size;q->data[q->rear]=x;return 1;}}//********************************* //出队int pop_Queue(Queue *q,int *x){if(q->rear==q->front){printf("队空!");return 0;}else{q->front=(q->front+1)%size;*x=q->data[q->front]; //读取队头元素return 1;}}//*********************************//*********************************//整数部分——栈typedef struct{char dataint[100];int top;}Stack;//*********************************//-制空栈void init_Stack(Stack *s){s->top=0;}//*********************************//进栈int push_Stack(Stack *s,int x){if(s->top==maxsize){printf("栈已满!");return 0;}else{s->dataint[s->top]=x; //数据进栈s->top++;return 1;}}//*********************************//出栈int pop_Stack(Stack *s,int *x){if(s->top==0){printf("栈空,无数据可取!");return 0;}else{s->top--;*x=s->dataint[s->top]; //取处数据return 1;}}//********************************* 主程序int main(){//*********************************//读入数据char a[20];int aim;printf("请输入一个十进制浮点数:"); //以字符串形式输入一个浮点数gets(a);printf("请输入目标进制:");scanf("%d",&aim);if(aim==1) {printf("ERROR! PLEASE INPUT A NUMBER AND IT IS BIGGER THAN 1");return 0;}//*********************************//读取小数点位置int i;int pos;//小数点位置for(i=0;i<strlen(a);++i){if(a[i]=='.'){pos=i;break;}}//*********************************//定义栈对整数部分转化后并入栈Stack ss;init_Stack(&ss);//初始化栈//*********************************//将整数部分转换为int 型int begin=1;int bnum;if(a[0]=='-') {int bnum = a[1]-'0'; //判断是否为负数begin=2;}else bnum=a[0]-'0';for(i=begin;i<pos;i++){bnum=bnum*10+a[i]-'0';}// printf("整数部分:%d\n",bnum);//依次求得所转进制的每一位并入栈while(bnum){// if(bnum/aim!=0)push_Stack(&ss,bnum%aim);bnum=bnum/aim;}//*********************************//出栈读取整数部分结果int flag,z;flag=pop_Stack(&ss,&z);if(flag==1){printf("目的进制数为:");for(i=ss.top;i>=0;i--) //先从顶端出栈printf("%d ",ss.dataint[i]);}else printf("无数据!");// printf("\n");//定义队列并将小数部分转化后入队Queue q,*cq=&q;init_Queue(cq);//*********************************//将小数点后面的部分转为浮点数int c=1;int anum=a[pos+1]-'0';for(i=pos+2;i<strlen(a);i++){anum=anum*10+(a[i]-'0');c++;}double small=((double)anum)/pow(10,c); // printf("小数部分:%lf\n",small);//*********************************// 依次求得小数部分的每一位并入队int zz;int innum;for(i=0;i<6;i++){innum=(((int)(small*aim)))%10; //取出小数点前的部分small=small*aim-innum; //得到减去小数点前段的部分继续与aim相乘push_Queue(cq,innum);}//*********************************//出队列printf(".") ;if(pop_Queue(cq,&zz)){for(i=(cq->front)%size;i!=(cq->rear+1)%size;i=(i+1)%size)printf("%d ",cq->data[i]);}//*********************************return 0;}实验总结通过对数据的单个读取并入栈,后续的出栈顺序为从上到下,先进后出,读取数据后为相反的顺序,而队列的顺序出队为先进先出,对小数的存储可直接进行读取。
数据结构栈和队列实验报告

数据结构栈和队列实验报告一、实验目的本次实验的主要目的是深入理解和掌握数据结构中的栈和队列的基本概念、操作原理以及实际应用。
通过编程实现栈和队列的相关操作,加深对其特性的认识,并能够运用栈和队列解决实际问题。
二、实验环境本次实验使用的编程语言为C++,开发工具为Visual Studio 2019。
三、实验原理(一)栈栈(Stack)是一种特殊的线性表,其操作遵循“后进先出”(Last In First Out,LIFO)的原则。
可以将栈想象成一个只有一端开口的容器,元素只能从开口端进出。
入栈操作(Push)将元素添加到栈顶,出栈操作(Pop)则从栈顶移除元素。
(二)队列队列(Queue)也是一种线性表,但其操作遵循“先进先出”(FirstIn First Out,FIFO)的原则。
队列就像是排队买票的队伍,先到的人先接受服务。
入队操作(Enqueue)将元素添加到队列的末尾,出队操作(Dequeue)则从队列的头部移除元素。
四、实验内容(一)栈的实现与操作1、定义一个栈的数据结构,包含栈顶指针、存储元素的数组以及栈的最大容量等成员变量。
2、实现入栈(Push)操作,当栈未满时,将元素添加到栈顶,并更新栈顶指针。
3、实现出栈(Pop)操作,当栈不为空时,取出栈顶元素,并更新栈顶指针。
4、实现获取栈顶元素(Top)操作,返回栈顶元素但不进行出栈操作。
5、实现判断栈是否为空(IsEmpty)和判断栈是否已满(IsFull)的操作。
(二)队列的实现与操作1、定义一个队列的数据结构,包含队头指针、队尾指针、存储元素的数组以及队列的最大容量等成员变量。
2、实现入队(Enqueue)操作,当队列未满时,将元素添加到队尾,并更新队尾指针。
3、实现出队(Dequeue)操作,当队列不为空时,取出队头元素,并更新队头指针。
4、实现获取队头元素(Front)操作,返回队头元素但不进行出队操作。
5、实现判断队列是否为空(IsEmpty)和判断队列是否已满(IsFull)的操作。
数据结构实验报告-栈进制转换

数据结构实验报告-栈进制转换数据结构实验报告栈进制转换一、实验目的本实验旨在通过使用栈这种数据结构,实现不同进制之间的转换,加深对栈的基本概念、操作和应用的理解,提高编程能力和问题解决能力。
二、实验环境操作系统:Windows 10编程语言:C++开发工具:Visual Studio 2019三、实验原理进制转换是将一个数从一种进制表示形式转换为另一种进制表示形式的过程。
常见的进制有二进制、八进制、十进制和十六进制。
栈是一种特殊的线性表,它遵循“后进先出”(Last In First Out,LIFO)的原则。
在进制转换中,可以利用栈来存储转换过程中的余数,从而实现进制的转换。
以十进制转换为二进制为例,将十进制数除以 2 取余数,然后将商继续除以 2 取余数,直到商为 0。
将依次得到的余数从栈中取出,即可得到对应的二进制数。
四、实验内容与步骤(一)数据结构定义```cppclass Stack {private:int stackArray;int top;int capacity;public:Stack(int size) {capacity = size;stackArray = new intcapacity;top =-1;}~Stack(){delete stackArray;}void push(int element) {if (isFull()){std::cout <<"Stack Overflow" << std::endl; return;}stackArray++top = element;}int pop(){if (isEmpty()){std::cout <<"Stack Underflow" << std::endl; return -1;}return stackArraytop;}int peek(){if (isEmpty()){std::cout <<"Stack is empty" << std::endl; return -1;}return stackArraytop;}bool isEmpty(){return top ==-1;}bool isFull(){return top == capacity 1;}};```(二)十进制转二进制函数```cppvoid decimalToBinary(int decimalNumber) {Stack stack(32);while (decimalNumber > 0) {int remainder = decimalNumber % 2;stackpush(remainder);decimalNumber /= 2;}std::cout <<"十进制"<< decimalNumber <<"转换为二进制为: ";while (!stackisEmpty()){std::cout << stackpop();}std::cout << std::endl;}```(三)十进制转八进制函数```cppvoid decimalToOctal(int decimalNumber) {Stack stack(16);while (decimalNumber > 0) {int remainder = decimalNumber % 8;stackpush(remainder);decimalNumber /= 8;}std::cout <<"十进制"<< decimalNumber <<"转换为八进制为: ";while (!stackisEmpty()){std::cout << stackpop();}std::cout << std::endl;}```(四)十进制转十六进制函数```cppvoid decimalToHexadecimal(int decimalNumber) {Stack stack(16);while (decimalNumber > 0) {int remainder = decimalNumber % 16;if (remainder < 10) {stackpush(remainder +'0');} else {stackpush(remainder 10 +'A');}decimalNumber /= 16;}std::cout <<"十进制"<< decimalNumber <<"转换为十六进制为: ";while (!stackisEmpty()){std::cout << stackpop();}std::cout << std::endl;}```(五)主函数```cppint main(){int decimalNumber;std::cout <<"请输入一个十进制数: ";std::cin >> decimalNumber; decimalToBinary(decimalNumber);decimalToOctal(decimalNumber);decimalToHexadecimal(decimalNumber);return 0;}```五、实验结果与分析(一)实验结果输入十进制数 25,得到以下结果:二进制:11001八进制:31十六进制:19(二)结果分析通过实验,成功实现了将十进制数转换为二进制、八进制和十六进制。
数据结构栈和队列实验报告

数据结构栈和队列实验报告数据结构栈和队列实验报告1.引言本实验旨在通过设计和实现栈和队列的数据结构,掌握栈和队列的基本操作,并进一步加深对数据结构的理解和应用。
2.实验目的本实验的主要目标包括:________●掌握栈和队列的数据结构实现。
●熟悉栈和队列的基本操作:________入栈、出栈、入队、出队。
●理解栈和队列的应用场景,并能够灵活运用。
3.实验原理3.1 栈栈是一种特殊的数据结构,它采用“后进先出”的方式对元素进行操作。
栈的主要操作包括入栈和出栈,入栈将元素压入栈顶,出栈将栈顶元素弹出。
3.2 队列队列也是一种特殊的数据结构,它采用“先进先出”的方式对元素进行操作。
队列的主要操作包括入队和出队,入队将元素放入队列尾部,出队将队列头部的元素移除。
4.实验过程4.1 栈的实现a. 定义栈的数据结构在实现栈之前,首先要定义栈的数据结构,包括数据存储结构和相关操作方法。
b. 定义入栈操作入栈操作将元素压入栈顶。
c. 定义出栈操作出栈操作将栈顶元素弹出。
4.2 队列的实现a. 定义队列的数据结构在实现队列之前,首先要定义队列的数据结构,包括数据存储结构和相关操作方法。
b. 定义入队操作入队操作将元素放入队列尾部。
c. 定义出队操作出队操作将队列头部的元素移除。
5.实验结果与分析将栈和队列的数据结构实现后,可以进行测试和验证。
通过将不同类型的元素入栈和入队,然后再进行出栈和出队操作,最后检查栈和队列的状态,验证其正确性。
6.实验总结本实验通过设计和实现栈和队列的数据结构,掌握了栈和队列的基本操作。
并通过对栈和队列的应用,加深了对数据结构的理解和应用。
附件:________无法律名词及注释:________无。
栈和队列实验报告

栈和队列实验报告引言:计算机科学中的数据结构是解决问题的关键。
栈和队列这两种常用的数据结构,无疑在许多实际应用中起着重要的作用。
本篇报告旨在探讨栈和队列的实验结果,并展示它们的实际应用。
一、栈的实验结果及应用1. 栈的实验结果在实验中,我们设计了一个基于栈的简单计算器,用于实现基本的四则运算。
通过栈的先进后出(Last In First Out)特性,我们成功实现了表达式的逆波兰表示法,并进行了正确的计算。
实验结果表明,栈作为一个非常有效的数据结构,可以很好地处理栈内数据的存储和检索。
2. 栈的应用栈在计算机科学中有许多实际应用。
其中之一是程序调用的存储方式。
在程序调用过程中,每个函数的返回地址都可以通过栈来保存和恢复。
另一个应用是浏览器的历史记录。
浏览器中每个访问网页的URL都可以通过栈来存储,以便用户能够追溯他们之前访问的网页。
二、队列的实验结果及应用1. 队列的实验结果在实验中,我们模拟了一个简单的出租车调度系统,利用队列的先进先出(First In First Out)特性实现乘客的排队和叫车。
实验结果表明,队列作为一个具有高效性和可靠性的数据结构,能够很好地处理排队问题。
2. 队列的应用队列在许多方面都有应用。
一个常见的应用是消息队列。
在网络通信中,消息队列可以用于存储和传递信息,确保按照特定的顺序进行处理。
另一个应用是操作系统的进程调度。
操作系统使用队列来管理各个进程的执行顺序,以实现公平和高效的资源分配。
三、栈和队列的比较及选择1. 效率比较栈和队列在实际应用中的效率取决于具体问题的需求。
栈的操作更简单,仅涉及栈顶元素的插入和删除,因此具有更高的执行速度。
而队列涉及到队头和队尾元素的操作,稍复杂一些。
但是,队列在某些问题中的应用更为广泛,例如调度问题和消息传递问题。
2. 如何选择在选择栈和队列时,需要根据实际问题的性质和需求进行综合考虑。
如果问题需要追溯历史记录或按照特定顺序进行处理,则应选择栈作为数据结构。
东北大学计算机软件技术基础实验报告.pdf

计算机软件技术基础实验专业:学生姓名:[哈哈哈]学号:[哈哈哈]实验时间:[2016年8月22日]实验一:线性表的排序与查找#include<stdio.h>int aryLinearList[15];int x=0;void printout();void sort();void deleteit(int n);void insert(int n);void main(){int i,t,a;printf("请输入10个数:\n");for(i=0;i<10;i++){scanf("%d",&aryLinearList[i]);x=x+1;}printf("您的输入为:\n");printout();printf("排序后为:\n");sort();printf("请输入插入的数:\n");scanf("%d",&a);insert(a);printf("请输入要删除的数:\n");scanf("%d",&a);deleteit(a);}void sort()//冒泡法排序{int i,j,t;for(j=0;j<x-1;j++)for(i=0;i<x-1-j;i++)if(aryLinearList[i]>aryLinearList[i+1]){t=aryLinearList[i];aryLinearList[i]=aryLinearList[i+1];aryLinearList[i+1]=t;}printout();}void insert(int n)//插入并排序{aryLinearList[x]=n;x=x+1;sort();}void deleteit(int n)//删除{int i,j;for(i=0;i<x;i++)if(aryLinearList[i]==n){for(j=i;j<x;j++)aryLinearList[j]=aryLinearList[j+1];x=x-1;printout();}}void printout()//显示{int i;for(i=0;i<x;i++)printf("%d",aryLinearList[i]);printf("\n");}实验二:栈与队列的应用#include<stdio.h>#include<String.h>#include<stdlib.h>#include<math.h>#define MAX_LEN10//字符串长度#define MAX_SIZE30//栈或队最大元素个数struct QUEUE//定义队列{int nMaxSize;int nCount;int nFront;//队头int nRear;//队尾char szQueue[MAX_SIZE][MAX_LEN];};struct STACK//定义栈{int nMaxSize;int nTop;//栈顶char szStack[MAX_SIZE][MAX_LEN];};void InitQueue(QUEUE*q,int nMaxSize)//初始化队列{q->nMaxSize=nMaxSize;q->nCount=0;q->nFront=0;q->nRear=0;q->szQueue[MAX_SIZE][MAX_LEN]=0;}void InQueue(QUEUE*q,char*pItem)//入队{if(q->nCount==q->nMaxSize){printf("The Queue is full!\n");return;}strcpy(q->szQueue[q->nRear],pItem);if(q->nRear++==MAX_SIZE)q->nRear=0;q->nCount++;}void OutQueue(QUEUE*q,char*pItem)//出队{if(q->nCount==0){printf("The Queue is empty!\n");return;}strcpy(pItem,q->szQueue[q->nFront]);if(q->nFront++==MAX_SIZE)q->nFront=0;q->nCount--;}void InitStack(STACK*s,int nMaxSize)//初始化栈{s->nMaxSize=nMaxSize;s->nTop=0;s->szStack[MAX_SIZE][MAX_LEN]=0;}void PushStack(STACK*s,char*pItem)//入栈{char*p;if(s->nTop<s->nMaxSize){p=s->szStack[s->nTop];strcpy(p,pItem);s->nTop++;}else{printf("The stack overflow!\n");return;}}void PopStack(STACK*s,char*pItem)//出栈{char*p;if(s->nTop==0){printf("stack is empty!\n");return;}else{p=s->szStack[--s->nTop];strcpy(pItem,p);}}void GetTopStack(STACK*s,char*pItem)//获得栈顶运算符{char*p;char a[10]={0};if(s->nTop==0){a[0]=';';strcpy(pItem,a);}else{p=s->szStack[s->nTop-1];strcpy(pItem,p);}}int isdigit(char x)//判断字符{if(x>='0'&&x<='9')return1;return0;}int Priority(char*op)//获得操作符的优先级{int nPriority=0;switch(op[0]){case'^':nPriority=3;break;case'*':case'/':nPriority=2;break;case'+':case'-':nPriority=1;break;case';':nPriority=0;}return nPriority;}void Compute(char*num1,char*num2,char*op,char*chResult)//计算表达式的值{double fNum1,fNum2;double fResult=0;fNum1=atof(num1);fNum2=atof(num2);switch(op[0]){case'^':fResult=pow(fNum1,fNum2);break;case'*':fResult=fNum1*fNum2;break;case'/':fResult=fNum1/fNum2;break;case'+':fResult=fNum1+fNum2;break;case'-':fResult=fNum1-fNum2;break;}sprintf(chResult,"%.4f",fResult);return;}int main()//主程序{char x[MAX_LEN];//表达式char op[MAX_LEN];//栈顶运算符char num1[MAX_LEN],num2[MAX_LEN];//操作数char chResult[MAX_LEN];//运算结果struct QUEUE q1;//声明队列struct QUEUE*q;struct STACK OS;//声明OS栈和NS栈struct STACK NS;struct STACK*o;struct STACK*n;int i=0;//初始化int j=0;int k=0;q=&q1;o=&OS;n=&NS;InitStack(o,20);InitStack(n,20);InitQueue(q,20);printf("please input the expression end with\';'\n");do//输入表达式{printf("next\n");scanf("%s",x);InQueue(q,x);}while(x[0]!=';');printf("expression\n");while(true){if(q->nCount!=0){OutQueue(q,x);printf("%s",x);}if(isdigit(x[0]))//输入为数字PushStack(n,x);else//输入运算符{GetTopStack(o,op);//获得OS栈顶运算符if(x[0]==';'&&op[0]==';')//输入’;’结束表达式{printf("\n result is");break;}if(Priority(x)>Priority(op))//运算符的优先级〉栈顶运算符{PushStack(o,x);continue;}while((Priority(x)<=Priority(op))&&Priority(op))//运算符优先级<=栈顶运算符{PopStack(n,num1);PopStack(n,num2);PopStack(o,op);Compute(num2,num1,op,chResult);PushStack(n,chResult);GetTopStack(o,op);}PushStack(o,x);}}PopStack(n,chResult);printf("%s\n",chResult);return0;}实验三:关系数据语言的应用create table Stu(Sno char(4)primary key,Sname char(15),Sex char(2),Age numeric,Birthday datetime,Class char(10));create table Course(Cno char(2)primary key,Cname char(20),Chour numeric);create table Score(sno char(4),cno char(2),primary key(sno,cno),grade numeric);insert into Stuvalues('0101','zhangqiang','m','20','1994-02-20','zi1');insert into Stu values('0102','lihong','f','20','1994-08-10','zi1'); insert into Stu values('0103','wangtao','m','21','1993-05-18','zi1'); insert into Stu values('0104','liuli','f','19','1995-03-05','zi2'); insert into Stu values('0105','sundong','m','21','1993-12-17','zi2'); insert into Stu values('0106','wangping','m','22','1992-11-30','zi2'); insert into Stuvalues('0201','ouyangyan','f','20','1994-04-11','dian1');insert into Stuvalues('0202','yangrui','m','20','1994-05-13','dian1');insert into Stu values('0203','liuyan','f','18','1996-01-21','dian1'); insert into Stu values('0204','zhouyu','m','20','1994-07-10','dian1'); select*from stu;insert into course values('01','jisuanji','48'); insert into course values('02','java','32'); select*from course;insert into score values('0101','01','87'); insert into score values('0102','01','90'); insert into score values('0103','01','79'); insert into score values('0104','01','89'); insert into score values('0105','01','58'); insert into score values('0106','01','77'); insert into score values('0201','01','95'); insert into score values('0202','01','80'); insert into score values('0203','01','76'); insert into score values('0204','01','70'); insert into score values('0101','02','91'); insert into score values('0102','02','88'); insert into score values('0103','02','75'); insert into score values('0104','02','91'); insert into score values('0105','02','76'); insert into score values('0106','02','76'); insert into score values('0201','02','90'); insert into score values('0202','02','84'); insert into score values('0203','02','83'); insert into score values('0204','02','57'); select*from score;1.查询学生出生日期(Sno,Sname,BirthDay);Select sno,sname,birthDay from stu;2.按学号顺序查询自动化02班的所有学生(Class,Sname);Select Class,Sname from Stu where class='zi2'order by Sno;3.列出学生选择各门课程的成绩(Sname,Cname,Grade);Select Sname,Cname,Grade from Stu,Course,Score where Stu.Sno=Score.Sno and o=o;4.列出有过不及格成绩的学生名单(Sno,Sname,Class);Select distinct Stu.Sno,Sname,Class from Stu,Score whereStu.Sno=Score.Sno and Grade<60;5.求学生的平均成绩和总成绩(Sname,PJCJ,ZCJ);Select Sname,avg(Grade)PJCJ,sum(Grade)ZCJ from Stu,Score where Score.Sno=Stu.Sno group by Stu.Sname;6查找各科成绩都>=85分的学生(Sname,Class);Select Sname,Class from Stu where exists(Select*from Score where Stu.Sno=Score.Sno and o='01'and Score.Grade>=85)and exists(Select*from Score where Stu.Sno=Score.Sno and o='02' and Score.Grade>=85);7将课程号为“01”的课程名称修改为“软件技术”;Update Course set Cname='RuanJianJiShu'where Cno='01';select*from course;8修改一名学生的姓名、性别、年龄;Update Stu set Sname='gaoyu',Sex='f',age='20'where Sno='0204'; select*from stu;9将成绩为55~59分的男生的成绩修改为60分;Update Score set Grade=60where Sno in(Select Sno from Stu where Sex='m') and Grade between55and59;select*from score;ÎÒÈ¥10删除年龄不是20的学生的所有信息(包括选课和成绩);Delete Stu where Sno in(select Sno from Stu where age<'20'or age>'20');Select Sname,Cname,Grade,Age from Stu,Course,Score where;Stu.Sno=Score.Sno and o=o Array11删除一个班级的所有学生;Delete from Stu where Class='dian1';select*from stu;12删除所有数据表和数据库Drop database MyDB;。
数据结构栈和队列实验报告

数据结构栈和队列实验报告实验目的:掌握数据结构栈和队列的基本概念和操作,通过实验加深对栈和队列的理解。
1.实验原理1.1 栈的原理栈是一种具有后进先出(LIFO)特点的数据结构。
在栈中,只允许在栈顶进行插入、删除和访问操作,并且这些操作仅限于栈顶元素。
1.2 队列的原理队列是一种具有先进先出(FIFO)特点的数据结构。
在队列中,元素的插入操作只能在队列的一端进行,称为队尾。
而元素的删除操作只能在队列的另一端进行,称为队头。
2.实验要求2.1 实现栈和队列的基本操作●栈的基本操作:压栈、弹栈、获取栈顶元素和判断栈是否为空。
●队列的基本操作:入队、出队、获取队头元素和判断队列是否为空。
2.2 进行相应操作的测试●对栈进行插入、删除、访问等操作的测试,并输出测试结果。
●对队列进行插入、删除、访问等操作的测试,并输出测试结果。
3.实验环境●操作系统:Windows 10●开发工具:C++编译器4.实验步骤4.1 栈的实现步骤1:定义栈的结构体,包含栈的容量和栈顶指针。
步骤2:根据栈的容量动态分配内存。
步骤3:实现栈的基本操作函数:压栈、弹栈、获取栈顶元素和判断栈是否为空。
步骤4:进行栈的相关测试。
4.2 队列的实现步骤1:定义队列的结构体,包含队列的容量、队头和队尾指针。
步骤2:根据队列的容量动态分配内存。
步骤3:实现队列的基本操作函数:入队、出队、获取队头元素和判断队列是否为空。
步骤4:进行队列的相关测试。
5.实验结果与分析5.1 栈的测试结果●压栈操作测试:将若干元素压入栈中。
●弹栈操作测试:依次弹出栈中的元素。
●获取栈顶元素测试:输出栈顶元素。
●判断栈是否为空测试:输出栈是否为空的结果。
5.2 队列的测试结果●入队操作测试:将若干元素入队。
●出队操作测试:依次出队元素。
●获取队头元素测试:输出队头元素。
●判断队列是否为空测试:输出队列是否为空的结果。
6.结论通过本次实验,我们掌握了栈和队列的基本概念和操作。
数据结构栈和队列实验报告简版

数据结构栈和队列实验报告数据结构栈和队列实验报告1. 实验目的本实验的主要目的是通过实践的方式理解并掌握数据结构中栈和队列的概念、特点和基本操作。
通过实验,我们可以加深对栈和队列的理解,掌握栈和队列的应用方法,并能够设计和实现基于栈和队列的算法。
2. 实验内容本实验分为两个部分:栈的应用和队列的应用。
2.1 栈的应用栈是一种具有特定限制的线性表,它只允许在表的一端进行插入和删除操作,该端被称为栈顶。
栈的特点是“后进先出”(Last In First Out, LIFO),即最后进栈的元素最先出栈。
在本实验中,我们将实现一个简单的栈类,并应用栈来解决一个问题。
假设有一个字符串,其中包含了括号(圆括号、方括号和花括号),我们需要判断该字符串中的括号是否匹配。
为了达到这个目的,我们可以使用栈来辅助实现。
在实现过程中,我们可以定义一个栈来存储左括号,然后依次遍历字符串的每个字符。
当遇到左括号时,将其入栈;当遇到右括号时,判断栈顶是否是对应的左括号,如果是,则将栈顶元素出栈,否则说明括号不匹配。
最后,当栈为空时,表明所有的括号都匹配,否则说明括号不匹配。
2.2 队列的应用队列是一种具有特定限制的线性表,它只允许在表的一端进行插入操作(队尾),在表的另一端进行删除操作(队头)。
队列的特点是“先进先出”(First In First Out, FIFO),即最早进队列的元素最先出队列。
在本实验中,我们将实现一个简单的队列类,并应用队列来解决一个问题。
假设有一群人在排队等候,我们需要按照一定规则进行排队并输出结果。
为了达到这个目的,我们可以使用队列来进行模拟。
在实现过程中,我们可以定义一个队列来存储等候的人,然后依次将人入队列。
当需要输出结果时,我们可以通过队列的出队列操作,按照先后顺序依次输出到达队头的人。
通过使用队列,我们可以模拟人们排队等候的实际情况,并能够按照一定规则输出结果。
3. 实验过程本实验的实验过程如下:1. 首先,我们需要实现一个栈类。
数据结构栈和队列实验报告

数据结构栈和队列实验报告数据结构栈和队列实验报告引言:数据结构是计算机科学中非常重要的一个概念,它用于组织和存储数据,以便于程序的运行和管理。
栈和队列是数据结构中最基本的两种形式之一,它们在实际应用中有着广泛的应用。
本实验旨在通过实际操作和观察,深入理解栈和队列的特性和应用。
一、实验目的:1. 了解栈和队列的基本概念和特性;2. 掌握栈和队列的基本操作;3. 理解栈和队列在实际应用中的作用。
二、实验过程:本次实验我们使用Python语言来实现栈和队列的操作。
首先,我们定义了栈和队列的类,并编写了相应的操作方法。
1. 栈的实现:栈是一种后进先出(LIFO)的数据结构,类似于我们日常生活中的弹簧簿记本。
我们首先定义了一个栈类,其中包括了栈的初始化、入栈、出栈、获取栈顶元素等方法。
通过这些方法,我们可以对栈进行各种操作。
2. 队列的实现:队列是一种先进先出(FIFO)的数据结构,类似于我们日常生活中的排队。
我们同样定义了一个队列类,其中包括了队列的初始化、入队、出队、获取队首元素等方法。
通过这些方法,我们可以对队列进行各种操作。
三、实验结果:我们通过实验,成功实现了栈和队列的基本操作。
在测试过程中,我们发现栈和队列在实际应用中有着广泛的用途。
1. 栈的应用:栈在计算机系统中有着重要的作用,例如在函数调用中,每次函数调用时都会将返回地址和局部变量等信息存储在栈中,以便于函数执行完毕后能够正确返回。
此外,栈还可以用于表达式求值、括号匹配等场景。
2. 队列的应用:队列在操作系统中常用于进程调度,通过维护一个就绪队列,操作系统可以按照一定的策略选择下一个要执行的进程。
此外,队列还可以用于消息传递、缓冲区管理等场景。
四、实验总结:通过本次实验,我们深入了解了栈和队列的特性和应用。
栈和队列作为数据结构中最基本的两种形式,它们在计算机科学中有着广泛的应用。
在实际编程中,我们可以根据具体的需求选择合适的数据结构,以提高程序的效率和可读性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验报告(一)实验过程一、项目简介进制转换通过编写函数实现十进制浮点数到R进制的转换,在十进制浮点数的整数部分利用栈结构实现,小数部分用队列结构实现。
二、项目实施:1.读取数据并获得小数点位置2.将字符串转为整数形式.3.对整数部分进行入栈4.获得小数部分并入队5.整数和小数的联合输出6.源代码:#include <stdio.h>#include <string.h>#include <math.h>#define size 10 //小数部分大小#define maxsize 20 //整数部分大小//*********************************//*********************************//小数部分——队列typedef struct{char data[10]; //读取转制后的小数部分int front,rear; //队首尾指针}Queue; //循环队列//*********************************//初始化队列void init_Queue(Queue* q){q->front=q->rear=0;}//*********************************//入队int push_Queue(Queue *q,int x){if((q->rear+1)%size==q->front) //判断队满{printf("队列满!不允许入队\n");return 0;}else{q->rear=(q->rear+1) % size;q->data[q->rear]=x;return 1;}}//*********************************//出队int pop_Queue(Queue *q,int *x){if(q->rear==q->front){printf("队空!");return 0;}else{q->front=(q->front+1)%size;*x=q->data[q->front]; //读取队头元素return 1;}}//*********************************//*********************************//整数部分——栈typedef struct{char dataint[100];int top;}Stack;//*********************************//-制空栈void init_Stack(Stack *s){s->top=0;}//*********************************//进栈int push_Stack(Stack *s,int x){if(s->top==maxsize){printf("栈已满!");return 0;}else{s->dataint[s->top]=x; //数据进栈s->top++;return 1;}}//*********************************//出栈int pop_Stack(Stack *s,int *x){if(s->top==0){printf("栈空,无数据可取!");return 0;}else{s->top--;*x=s->dataint[s->top]; //取处数据return 1;}}//********************************* 主程序int main(){//*********************************//读入数据char a[20];int aim;printf("请输入一个十进制浮点数:"); //以字符串形式输入一个浮点数gets(a);printf("请输入目标进制:");scanf("%d",&aim);if(aim==1) {printf("ERROR! PLEASE INPUT A NUMBER AND IT IS BIGGER THAN 1");return 0;}//*********************************//读取小数点位置int i;int pos;//小数点位置for(i=0;i<strlen(a);++i){if(a[i]=='.'){pos=i;break;}}//*********************************//定义栈对整数部分转化后并入栈Stack ss;init_Stack(&ss);//初始化栈//*********************************//将整数部分转换为int 型int begin=1;int bnum;if(a[0]=='-') {int bnum = a[1]-'0'; //判断是否为负数begin=2;}else bnum=a[0]-'0';for(i=begin;i<pos;i++){bnum=bnum*10+a[i]-'0';}// printf("整数部分:%d\n",bnum);//*********************************//依次求得所转进制的每一位并入栈while(bnum){// if(bnum/aim!=0)push_Stack(&ss,bnum%aim);bnum=bnum/aim;}//*********************************//出栈读取整数部分结果int flag,z;flag=pop_Stack(&ss,&z);if(flag==1){printf("目的进制数为:");for(i=ss.top;i>=0;i--) //先从顶端出栈printf("%d ",ss.dataint[i]);}else printf("无数据!");// printf("\n");//*********************************//定义队列并将小数部分转化后入队Queue q,*cq=&q;init_Queue(cq);//*********************************//将小数点后面的部分转为浮点数int c=1;int anum=a[pos+1]-'0';for(i=pos+2;i<strlen(a);i++){anum=anum*10+(a[i]-'0');c++;}double small=((double)anum)/pow(10,c);// printf("小数部分:%lf\n",small);//*********************************// 依次求得小数部分的每一位并入队int zz;int innum;for(i=0;i<6;i++){innum=(((int)(small*aim)))%10; //取出小数点前的部分small=small*aim-innum; //得到减去小数点前段的部分继续与aim相乘push_Queue(cq,innum);}//*********************************//出队列printf(".") ;if(pop_Queue(cq,&zz)){for(i=(cq->front)%size;i!=(cq->rear+1)%size;i=(i+1)%size)printf("%d ",cq->data[i]);}//*********************************return 0;}实验总结通过对数据的单个读取并入栈,后续的出栈顺序为从上到下,先进后出,读取数据后为相反的顺序,而队列的顺序出队为先进先出,对小数的存储可直接进行读取。
